Dicke模型^[1]描述了单模光场与N个二能级原子系综之间的集体耦合, 实现了从正常相(原子都处于基态, 平均光子数为零)到超辐射相(部分原子处于激发态, 平均光子数不为零)的二级量子相变^[2–4], 可以通过探测腔内的平均光子数来表征^[5,6]. 基于变分法可以对Dicke模型的量子相变进行较好的理论研究^[1,7,8].

近年来, 利用高品质光学腔模增强了光场与机械振子之间的相互作用^[9–13], 不仅可以对机械运动状态进行高精密测量, 而且能对机械振子的运动进行精确操控^[14–16]. 光机械腔系统中加入原子, 可以实现机械振子的基态冷却^[17], 增强作用在机械振子上的辐射压力^[18], 出现稳态腔内光子数和原子布居数反转的双稳行为^[19], 研究耦合二能级原子的单模光机械腔系统中的量子相变^[20–22], 通过机械振动可检测到量子相变^[23–26]的发生. Wang等^[27]在光机械腔量子相变中取得了重大的进展, 可用于探索新的临界现象.

在许多情况下, 创建一个具有单一模式高质量的环境, 是一件要求很高的事情. 因此, 多模化提供了一个更现实的场景. 此外, 在固态光子晶体、人造原子系统和离子阱结构等方面的重大进展, 使得对丰富多样的原子-场耦合机制的实验研究成为可能. 两个交叉的光腔中玻色凝聚体的超辐射跃迁实验, 证明了光可以在两个腔模的任意叠加状态下发射, 可以驱动超辐射跃迁^[28–30]. 双模Dicke模型量子相变^[31–33]的研究, 在N个二能级原子与两个量子化光场同时相互作用的系综中, 实现了从正常相到超辐射相的二阶量子相变, 相变点可以通过多种方式进行调节.

本文在双模Dicke模型的基础上, 研究双模光机械系统的量子相变和超辐射相塌缩, 其中水平方向(模式1)构成光-机械腔系统, 垂直方向(模式2)固定腔镜. 两模光场使计算更加复杂, 带来了新的挑战. 采用相干态^{[9,20,33–36]}及变分法^[9,20,33]得到了基态能量泛函, 采用Hessian矩阵^[37]和二阶偏导判定基态解的稳定性. 数值计算从点-线-面进行递进研究, 首先选定参量绘制了平均光子数、原子布居数差、平均基态能量的线图, 给出了光子数稳定分布的基态相图. 其次, 相边界由点到线, 发现存在正常相和反转正常相的双稳态, 超辐射相和反转正常相的共存态, 以及单独存在的反转正常相. 最后, 原子与两模光场的相互作用强度的不同会影响相变点的大小, 存在正常相经过相变点到超辐射相的量子相变. 机械振子诱导了超辐射相的塌缩, 存在一个转折点, 经过转折点还可以实现超辐射相到反转的正常相的量子相变. 超辐射相的区域随着光-声子非线性耦合的增大而减小, 在耦合的临界值处收缩为零, 即转折点和相变点重合, 并且有可能出现两个正常相之间的原子布居数的反转, 可通过实验检测光子数和声子数来检验. 机械腔内加入原子, 通过探究对光机械振子的影响可研究光子和声子的量子效应, 将机械振子制备到所需量子态, 从而提高测量弱力和轻质量的精度^[38].

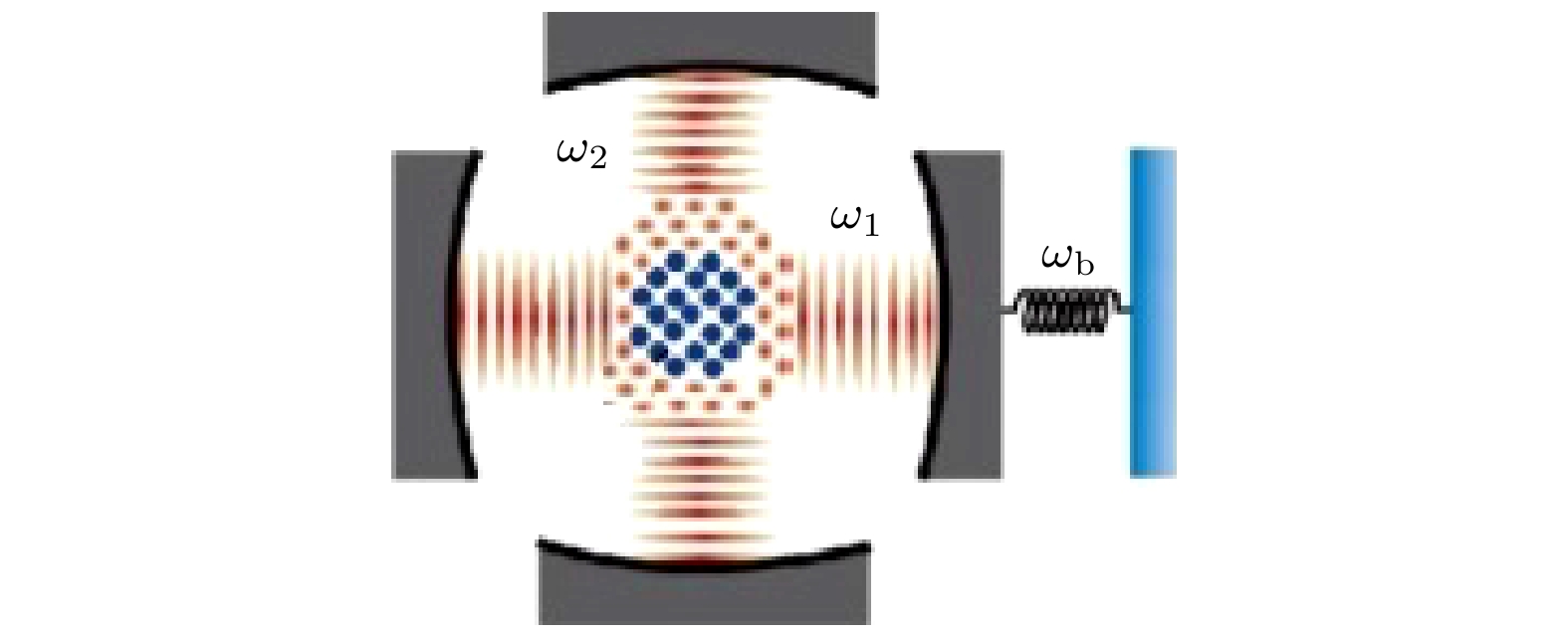
图1展示了双模光机械腔的示意图. 在水平方向上是光学机械系统, 频率为$ {\omega _1} $的高精度单模光腔一端固定, 另一端腔镜可移动, 耦合到一个机械振子上, 机械振子的频率为$ {\omega _{\text{b}}} $. 在垂直方向上腔场的频率为$ {\omega _2} $. 系统中有N个二能级$ {}^{87}{\text{Rb}} $冷原子, 其跃迁频率表示为$ {\omega _{\text{a}}} $. 光场采用二次量子化的场, 机械振子采用声子模. 此实验装置不同与Baumann等^[5]报道的, 在垂直方向是标准的Dicke模型, 不考虑原子与光场的非线性项, 而在水平方向增加了光机械腔, 考虑原子与两模光场都有偶级相互作用, 水平方向的光场(模式1)与机械振子有光-声子非线性耦合. 虽然量子相变已经通过外泵浦激光器实验实现^[2–4], 但是从理论上考虑拓展的Dicke模型, 可以用一种简洁的方式来说明机械振子的影响. 包含N个全同原子的光机械腔可以用下面的哈密顿量^[20–22]来描述($ \hbar = 1 $):

其中

方程(2)是标准双模Dicke模型的哈密顿量^[32]. $ a_l^\dagger \left( {{a_l}} \right) \left( {l = 1, 2} \right) $是两模光子的产生(湮灭)算符, N个二能级原子集体用自旋算符$ {J_z}, {J_ \pm } $表示. $ {g_l} {\text{ (}}l = 1, 2{)} $表示集体原子-场偶级相互作用. 考虑模式1与机械振子有光-声子的非线性相互作用, 强度用$ \zeta $表示, $\zeta = \sqrt N {\zeta _0}$, ${\zeta _0}$是等效的单光子光力耦合强度. $ b\left( {{b^\dagger }} \right) $是声子的湮灭算符和产生算符.

对方程(1)求平均值, 光场和声子采用谐振子相干态($ {a_l}\left| {{\alpha _l}} \right\rangle = {\alpha _l}\left| {{\alpha _l}} \right\rangle $, $ b\left| \beta \right\rangle = \beta \left| \beta \right\rangle $, 本征值采用复数表示, 设$ {\alpha _l} = {\gamma _l} + {\text{i}}{\tau _l} $, $ l = 1, 2 $, $ \beta = {\gamma _{\text{b}}} + {\text{i}}{\tau _{\text{b}}} $, $\gamma $和$\tau $均为实数). 三个态的直积组成了部分试探波函数$ \left| u \right\rangle = \left| {{\alpha _1}} \right\rangle \left| {{\alpha _2}} \right\rangle \left| \beta \right\rangle $, 由此可得哈密顿量:

其中

是一个有效的自旋哈密顿量.

用自旋相干态^[33–36]求解方程(4), 定义态$| \xi , j, m \rangle = T(\xi )\left| {j, m} \right\rangle = \exp [\xi {J_ + } - {\xi ^*}{J_ - })\left| {j, m} \right\rangle $, 其中$\xi = ({\theta }/{2}){ {\mathrm{exp}} ({- {\mathrm{i}}\varphi }})$, $ \theta\in\left[0,\pi\right) $, $ \varphi\in\left[0,2\pi\right) $, $\left| {j, m} \right\rangle $为$ J^2 $和$ J_z $的共同本征态.

角动量算符${J_ + }, {J_ - }, {J_z}$满足对易关系$[ {J_ + }, {J_ - } ] = 2{J_z}, \left[ {{J_ \pm }, {J_z}} \right] = \mp {J_ \pm }$, 且有${J_z}\left| {j, m} \right\rangle = m\left| {j, m} \right\rangle $, ${J_ \pm }\left| {j, m} \right\rangle = \sqrt {\left( {j \mp m} \right)\left( {j \pm m + 1} \right)} \left| {j, m \pm 1} \right\rangle $. 当$m = \mp j$时, 对应的$\left| {\xi , j, \mp j} \right\rangle $是通常自南极和北极规范的相干态. 当$\theta = 0$时, $\left| {0, j, m} \right\rangle = \left| {j, m} \right\rangle $回到${J^2}$和${J_z}$的共同本征态.

定义自旋相干态$ |\theta , \varphi \rangle =|\xi , j, \mp j\rangle= {\mathrm{exp}}\left[\dfrac{\theta }{2}\left({J}_{+}{\text{e}}^{-\text{i}\varphi }-J_{-}{\text{e}}^{\text{i}\varphi }\right)\right]|j, \mp j\rangle $, 相干态是归一化的, 具有超完备性$\displaystyle\frac{{2 j + 1}}{{4\pi }}\int {{\text{d}}\varOmega } \left| {\theta , \varphi } \right\rangle \left\langle {\theta , \varphi } \right| = 1$. 对于大j满足:

$ |\theta , \varphi \rangle $指的是一个方向, $ {\boldsymbol{n}} = \hat k{\text{cos}}\theta + (\hat i\cos \varphi + \hat j\sin \varphi )\sin \theta $. 定义$ {J_ \pm } = {J_x} \pm {\text{i}}{J_y} $, 满足不确定关系$ \Delta {J_x} \cdot \Delta {J_y} \geqslant \dfrac{1}{2}\left| {\left\langle {{J_z}} \right\rangle } \right| $. 对于一定的$ \theta , \varphi $, 相干态可为理想态及最小测不准态, 此时体系的量子噪音较小^[36].

将(5)式代入(4)式可以得到$ {E_{{\text{sp}}}} = \left\langle {\theta , \varphi \left| {{H_{{\text{sp}}}}} \right|} {\theta , \varphi } \right\rangle = \mp j\bigg( {{\omega _{\mathrm{a}}}\cos \theta - \displaystyle \sum\limits_{l = 1}^2 {\frac{{2{g_l}{\gamma _l}}}{{\sqrt N }}\sin \theta \cos \eta } } \bigg)$, 对$ \eta $求变分得$ \dfrac{{\partial {H_{{\text{sp}}}}}}{{\partial \eta }} = 0 $, $ \sin \eta = 0 $, 取$ \cos \eta = - 1 $, $ r = \sqrt {\omega _{\mathrm{a}}^2 + \dfrac{{4{{({g_1}{\gamma _1} + {g_2}{\gamma _2})}^2}}}{N}} $, $ \cos \theta = \dfrac{{{\omega _{\mathrm{a}}}}}{r} $, $ \sin \theta = \dfrac{{2({g_1}{\gamma _1} + {g_2}{\gamma _2})}}{{r\sqrt N }} $, ${H_{{\text{sp}}}}$的本征值$ {E_{{\text{sp}}}} = \mp jr $, $ j = N/2 $. 由此可得多个参量的基态能量泛函:

对(6)式的参量变分可得

将(7)式代入(6)式得到简化为两个参量$ {\gamma _1} $, $ {\gamma _2} $的基态能量泛函:

若基态能量是两个参量的函数, 用Hessian矩阵判定稳定性; 如果是单个参量的函数, 用二阶偏导大于零或小于零判断.

方程(8)中的$ {E_ - } $分别对参量$ {\gamma _1} $, $ {\gamma _2} $求极值:

方程(9)中总存在零解和可能存在有$ \gamma _1^ - , {\text{ }}\gamma _2^ - $的非零光子数解, γ上标$ - $对应于能量取$ {E_ - } $.

方程(8)中的$ {E_ + } $分别对参量$ {\gamma _1} $, $ {\gamma _2} $求极值:

方程(10)中总存在零解, 而

模式2光场在基态能量取$ {E_ + } $时不存在非零光子数解, 表示为$ \gamma _2^ + \ne 0 $的值不存在, 但当$ \gamma _2^ + = 0 $时, $ \gamma _1^ + $存在并满足:

对(11)式求二阶偏导, 判断其解的稳定性:

$ {{{\partial ^2}{E_ + }}}/({{\partial \gamma _1^2}}) \gt 0 $, 二阶导数大于零, 属于稳定的状态, $ {{{\partial ^2}{E_ + }}}/({{\partial \gamma _1^2}}) \lt 0 $, 属于不稳定状态.

通过以上分析可知, 可能有多种非零解存在. 利用Hessian矩阵可以判断零光子数解和方程(8)中能量为$ {E_ - } $的稳定性. 方程(8)中能量为$ {E_ + } $时, 基态能量泛函变成了单参量的函数, 所以用二阶偏导数大于零或小于零来判断稳定性.

定义点$ p\left( {{g_1}, {g_2}} \right) $处的函数$ {E_ \mp }\left( {{\gamma _1}, {\gamma _2}} \right) $的2×2的Hessian矩阵^[37,39]:

能量函数$ {E_ \mp }\left( {{\gamma _1}, {\gamma _2}} \right) $的二阶偏导为

当(14)式中的$ {\gamma _2} = 0 $, 基态能量取$ {E_ + } $时, 回到(12)式.

总是存在零解$ {\gamma _1} = 0 $, $ {\gamma _2} = 0 $, $ {{\text{N}}_ - } $表示的正常自旋态$ \left( \Downarrow \right) $和$ {{\text{N}}_{+}} $表示的反转自旋态$ \left( \Uparrow \right) $都属于正常相NP状态.

对于零解用Hessian矩阵判断稳定性, 其方法是Hessian矩阵的一切顺序主子式均为正, 函数在这些点有极小值是稳定点.

正常自旋$ {{\text{N}}_ - } $满足的Hessian矩阵:

$ {{\text{N}}_ - } $的正常自旋$ \left( \Downarrow \right) $的NP状态只存在于两个主子式$ 2{\omega _1} - \dfrac{{2 g_1^2}}{{{\omega _{\mathrm{a}}}}} $和$ \left| {\begin{array}{*{20}{c}} {2{\omega _1} - \dfrac{{2 g_1^2}}{{{\omega _{\mathrm{a}}}}}}&{ - \dfrac{{2{g_1}{g_2}}}{{{\omega _{\mathrm{a}}}}}} \\ { - \dfrac{{2{g_1}{g_2}}}{{{\omega _{\mathrm{a}}}}}}&{2{\omega _2} - \dfrac{{2 g_2^2}}{{{\omega _{\mathrm{a}}}}}} \end{array}} \right| $ 同时大于零时, 由此可得$ {{\text{N}}_ - } $只存在于:

在上述范围内正常相$ {{\text{N}}_ - } $是稳定状态, 满足的临界方程为

机械振子不影响正常相$ {{\text{N}}_ - } $和临界方程. 对于N₊表示的反转自旋态的Hessian矩阵为

当$ \left( {{g_1}, {g_2}} \right) $$ \in $实数, $ \left[ {{H_ + }} \right] $的一切顺序主子式均为正; 在整个区域中, 正常相N₊存在, 并且是稳定.

参考有关实验参数, 对于波长为780 nm的⁸⁷Rb原子的D₂谱线, 实际空腔频率$ {\omega _l} $和原子共振频率$ {\omega _{\text{a}}} $分别为10⁹ MHz数量级. 在实验中, 这些频率 可以通过控制弱泵浦激光器的频率$ {\omega _{\text{p}}} $来调谐, 可调谐频率从负千兆赫到千兆赫连续变化, 甚至超 过这个范围^[5,6]. 原子-光子的集体耦合强度${g_l}$也 在千兆赫数量级. 另一方面, 由于制造技术的快速发展, 纳米力学振荡器的质量已经达到了10^–15 g. 此外, 频率$ {\omega _{\text{b}}} $的范围从兆赫到千兆赫^[12,13]. 因此, 真空光力相互作用速率${\zeta _0}$可以从$ 2\pi \times 100{\text{ Hz}} $调谐到$ 2\pi \times 100{\text{ kHz}} $^[9], 增加了因子$\sqrt N $, 非线性光-声子的非线性耦合强度$\zeta $原则上可以达到千兆赫数量级^[21]. 为简单起见, 能量均以原子频率$ {\omega _{\text{a}}} $为单位. 本文假设$ {\omega _{\text{b}}} = 10{\omega _{\text{a}}} $与Zhao等^[22]报道的结果一致, 在文章中可比较双模与单模的不同.

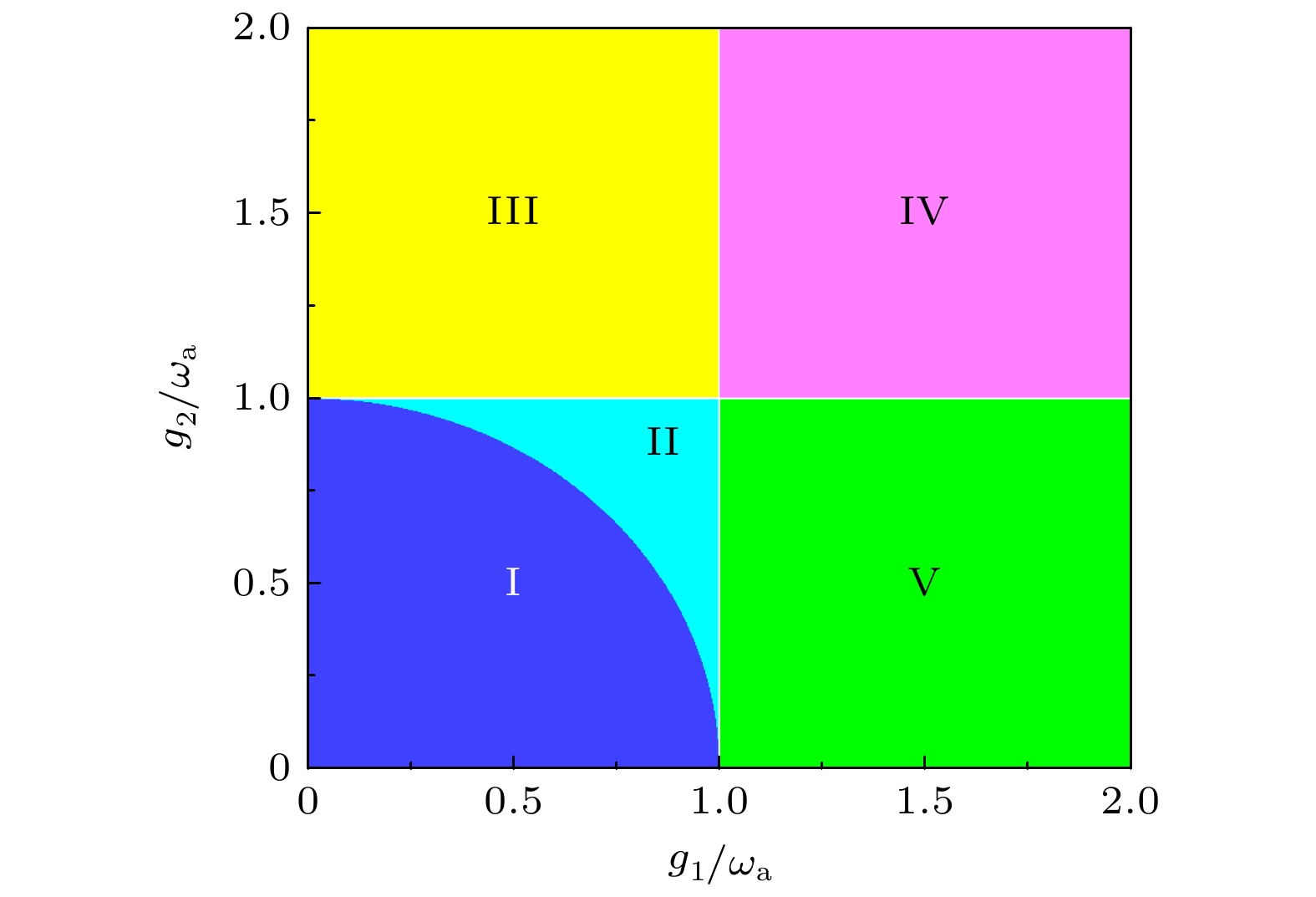
选取光场的频率为$ {\omega _1}/{\omega _{\text{a}}} = {\omega _2}/{\omega _{\text{a}}} = 1 $, 选取点计算, 因为计算过程非常复杂, 为了表述方便, 将原子集体与两模光场偶级相互作用参量构成的$ {g_1}/{\omega _{\text{a}}} $-$ {g_2}/{\omega _{\text{a}}} $的平面划分为五个区域取点, 范围为$ \left[ {0, 2} \right] $, 如图2所示.

在每个区域中选择一个点($ {g_1}/{\omega _{\text{a}}} $, $ {g_2}/{\omega _{\text{a}}} $), 用数值解法, 由(8)式—(12)式计算出对应的平均光子数的值、基态能量、Hessian矩阵中的值, 由Hessian矩阵的特征值确定稳定性. 如果特征值都是正值是稳定的, 对应最小值; 如果特征值有正有负, 对应鞍点是不稳定的; 如果都是负值那是极不稳定的, 对应最大的值. 每个区域获取的数据在经过计算后列在一系列表中.

定义平均光子数$ {\text{ }}\overline {\gamma _1^2} = \dfrac{{\gamma _1^2}}{N} $, $ \overline {\gamma _2^2} = \dfrac{{\gamma _2^2}}{N} $, 平均基态能量$ {\varepsilon _ \mp } = \dfrac{{{E_ \mp }}}{{{\omega _{\text{a}}}N}} $. 表1为取光-声子的非线性参量$ \zeta = 0 $时标准的双模Dicke模型, 在基态能量(8)式取$ {E_ - } $, 得出的平均基态能量$ {\varepsilon _ - } $和Hessian矩阵$ \left[ {{H_ - }} \right] $的特征值.

从表1可知, 在I区, 有正常相($ \Downarrow $)平均光子数零解, 基态能量取最小值–0.5, 是稳定解, 在其他四个区域总是存在一组非零解且是稳定的.

表2为双模加机械振子模型, 取光-声子的非线性参量$ \zeta /{\omega _{\text{a}}} = 1.0 $, 基态能量取(8)式中的$ {E_ - } $, 结合(8), (9), (13)式进行数值计算, 得出的$ {\varepsilon _ - } $和Hessian矩阵$ \left[ {{H_ - }} \right] $的特征值.

从表2可知, 在I区有1组不稳定的光子数非零解; 在其他四个区域有两组解, 一组是稳定解, 另一组是不稳定解, 由此可知考虑机械振子的作用增加了非零光子数解.

表3中取模式2光场$ {\gamma _2} = 0 $, 同样考虑机械振子的作用取$ \zeta /{\omega _{\text{a}}} = 1.0{\text{ }} $, 相当于单模光机械腔, (8)式中取基态能量$ {E_ + } $, 对应于平均基态能量$ {\varepsilon _ + } $, 由(11)式给出$ \overline {\gamma _1^2} $的数值和(12)式给出$ \dfrac{{{\partial ^2}{\varepsilon _ + }}}{{\partial \gamma _1^2}} $的数值. 从表3可知, 对应于图2中的$ {g_1}/{\omega _{\text{a}}} $不同的值, 由(11)式所得的解是不稳定的.

当$ \zeta /{\omega _{\text{a}}} = 1.{5} $时, 结果类似表2和表3. 从表1可以看出, 当不考虑机械振子的作用, 取$ \zeta = 0 $时, 能量泛函$ {E_ - } $对于一个给定的点$ \left( {{g_1}/{\omega _{\text{a}}}, {g_2}/{\omega _{\text{a}}}} \right) $, 可以得到一组解$ (\overline {\gamma _1^2} , {\text{ }}\overline {\gamma _2^2} ) $, 满足$ \partial {E_ - }/\partial {\gamma _1} = 0 $和$ \partial {E_ - }/ \partial {\gamma _2} = 0 $, 代入(8)式可得基态能量, 代入Hessian矩阵中判定是一组正数特征值, $ {E_ - } $具有最小值, 并且系统处于稳定状态, 存在稳定的正常相和超辐射相. 从表2可知, 考虑两模光场, 同时考虑机械振子的作用, 取$ \zeta /{\omega _{\text{a}}} = 1.0 $时, 在I区有一组不稳定非零光子数解, 在其他四个区域有两组非零的光子数解, 其中一组是不稳定解, 另一组解是稳定解. 从表3可知存在不稳定解. 由于计算很复杂, 还涉及到$ \zeta /{\omega _{\text{a}}} $的取值, 所以选取的点有限, 只是大致知道了平均光子数分布的情况及其稳定性. 下面取一些参量为固定值, 画出平均光子数、原子布居数差、平均基态能量线图加以说明, 并研究量子相变.

研究相变时的平均光子数、原子布居数差、平均基态能量、平均声子数. 系统总的波函数$ \left| {{\psi _ \mp }} \right\rangle = \left| u \right\rangle \left| {\theta , \varphi } \right\rangle $是光子、声子和自旋相干态的直积, 超辐射的平均光子数^[22,40]:

光子数有五个非零解, 对于波函数$ \left| {{\psi _ - }} \right\rangle $有两个非零解, 用$ \gamma _{{\text{s}}1}^ - $和$ \gamma _{{\text{s}}2}^ - $(上标“–”表示基态能量取$ {E_ - } $, 下标“s”表示稳定解)表示, 是稳定的超辐射光子数解, 对应能量泛函的极小值. 有两个是不稳定的解, 用$ \gamma _{{\text{us}}1}^ - $和$ \gamma _{{\text{us}}2}^ - $(下标“us”表示不稳定解)表示. 对于波函数$ \left| {{\psi _ + }} \right\rangle $有不稳定的解用$ \gamma _{{\text{us}}1}^ + $(上标“+”表示基态能量取$ {E_ + } $, 下标“us1”表示水平方向模式1有不稳定解)表示. 取光子数稳定零解是正常相$ {{\text{N}}_ - } $和反转正常相$ {{\text{N}}_ + } $.

原子布居数差^[9,20,33,41]:

一组稳定的光子解对应于正常相到超辐射相原子布居数差的分布, 另一组不稳定解对应的原子布居数差分布也是不稳定的, 还有不稳定的$ \gamma _{{\text{us}}1}^ + $产生的原子布居差分布. 对应于正常相NP, 状态$ {{\text{N}}_ - } $原子布居数差分布是$ \Delta {n_{{\text{a}} - }}\left( {{\gamma _ - } = 0} \right) = - 1/2 $, 状态$ {{\text{N}}_ + } $是$ \Delta {n_{{\text{a}} + }}\left( {{\gamma _ + } = 0} \right) = 1/2 $.

每个原子的平均基态能量^[42–44]:

每个原子的平均基态能量分布也对应三个值, 一组稳定的, 两组不稳定的, 还有正常相$ {{\text{N}}_ \mp } $对应于$ \mp {1}/{2} $.

平均声子数分布^[20,23]:

是与第一模光子数的平方成正比.

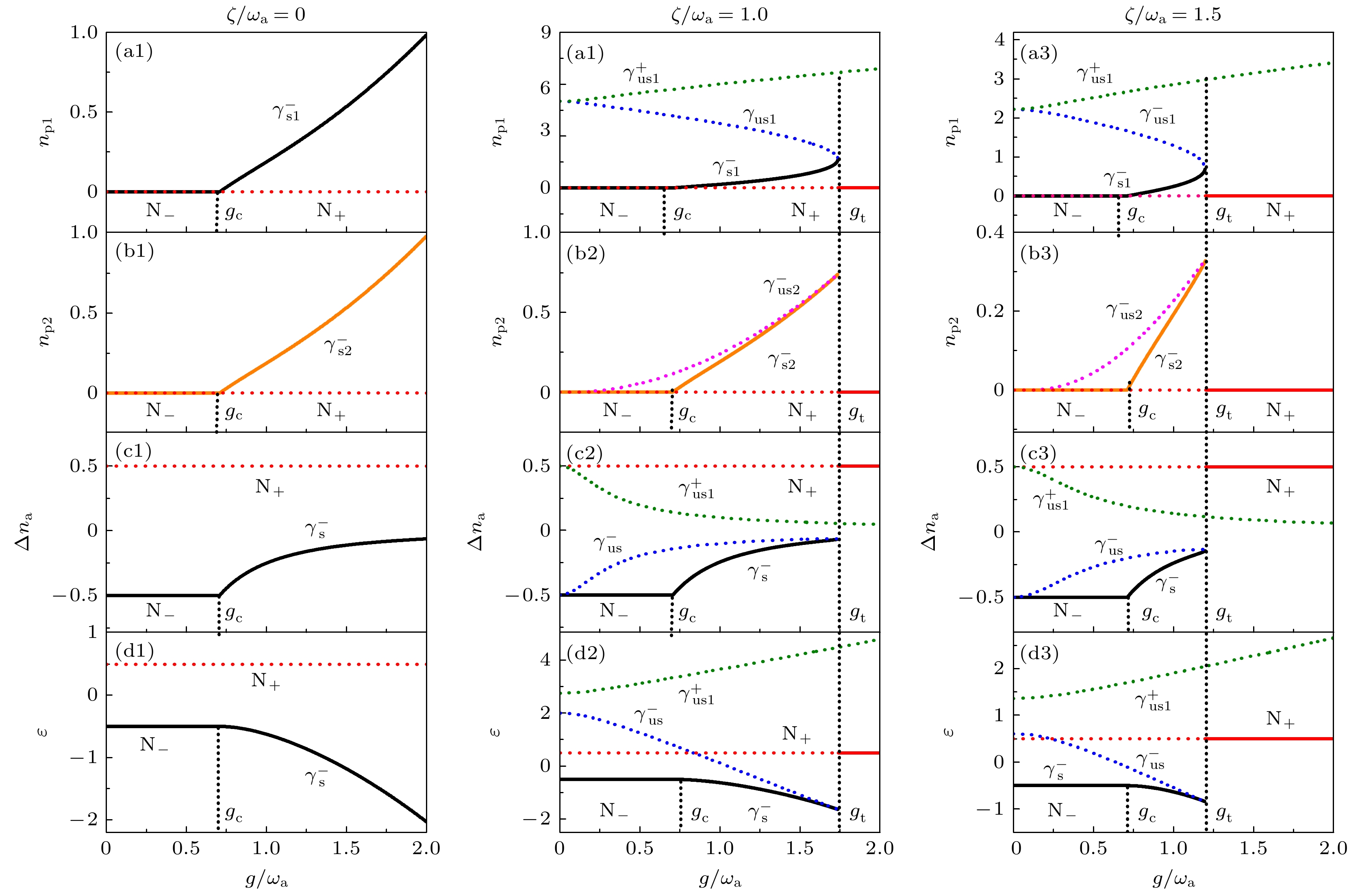
用线图表示解的情况. 原子与光场的相互作用参量取$ \dfrac{{{g_1}}}{{{\omega _{\text{a}}}}} = \dfrac{{{g_2}}}{{{\omega _{\text{a}}}}} = \dfrac{g}{{{\omega _{\text{a}}}}} $, 相当于图2中的对角线. 其他参数不变, 经过数值计算可画出以上物理量的线图, 如图3所示.

图3(a1)—(d1)展示了双模Dicke模型$ \left( {\zeta = 0} \right) $的正常相$ {{\text{N}}_ - } $到超辐射$ {{\text{S}}_ - } $的二级量子相变, 其中相变点是$ {\text{NP}}\left( {{{\text{N}}_ - }} \right) $(黑色实线)和$ {\text{SP}}(\gamma _{{\text{s}}1}^ - ) $(黑色实线)的交点, 数值是$ {g_{\text{c}}}/{\omega _{\text{a}}} = 0.707 $, 小于单模光机械腔^[22]相变点1.0, 所以相变更容易发生. 图3(a2)和图3(a3)中由于光与机械振子非线性耦合的作用$ {\zeta}/{\omega _{\text{a}}} = 1.0, {1}{.5} $, 增加了两条线, 即$ \gamma _{{\text{us}}1}^ - $(蓝色点线)的解在$ {g_{\text{t}}} $点反转向后上方有$ \gamma _{{\text{us}}1}^ + $(绿色点线, 由表3和线图可知, 这条线始终存在), 类似双稳态曲线, 但是这两个解是不稳定的, $ {g_{\text{t}}} $称为反转点, 也是超辐射相的塌缩点. 取图3(a2)和图3(a3)的反转点的值分别是$ {g_{\text{t}}}/{\omega _{\text{a}}} = {1}.7{\text{36, 1}}{.195} $, 同时也是一个相变点, 其左边是超辐射相(黑实线), 其右边是反转的正常相(红实线), 系统经历从SP到$ {\text{NP(}}{{\text{N}}_{+}}) $的量子相变. 随着光-声子非线性耦合强度$ \zeta /{\omega _{\text{a}}} $的增大, 反转点向左移动. 图中反转的正常$ {{\text{N}}_ + } $始终是稳定态, 在相变点$ {g_{\text{c}}}/{\omega _{\text{a}}} = 0.707 $之前是红色的虚线, 代表能量比正常相$ {{\text{N}}_ - } $高, $ {{\text{N}}_ + } $与$ {{\text{N}}_ - } $组成双稳态$ {\text{N}}{{\text{P}}_{{\text{bi}}}}\left( {{{\text{N}}_ - }{, }{{\text{N}}_{+}}} \right) $, 在相变点$ {g_{\text{c}}}/{\omega _{\text{a}}} $之后以及转折点$ {g_{\text{t}}}/{\omega _{\text{a}}} $之前与超辐射相$ {\text{SP}} $组成了共存态$ {\text{S}}{{\text{P}}_{{\text{co}}}}\left( {{{\text{S}}_ - }{, }{{\text{N}}_{+}}} \right) $, 在转折点$ {g_{\text{t}}}/{\omega _{\text{a}}} $后是实线代表最低能量状态$ {{\text{N}}_ + } $. 图3(b2)和图3(b3)是模式2光场的分布, 只增加了一条线$ \gamma _{{\text{us}}2}^ - $, 也展示超辐射相的塌缩. 图3(c2)与图3(c3)原子布居数差的分布和图3(d2)与图3(d3)平均基态能量分布都体现了双模光场与原子的相互作用和光-声子非线性耦合所引起的相变点、转折点在数值上的不同.

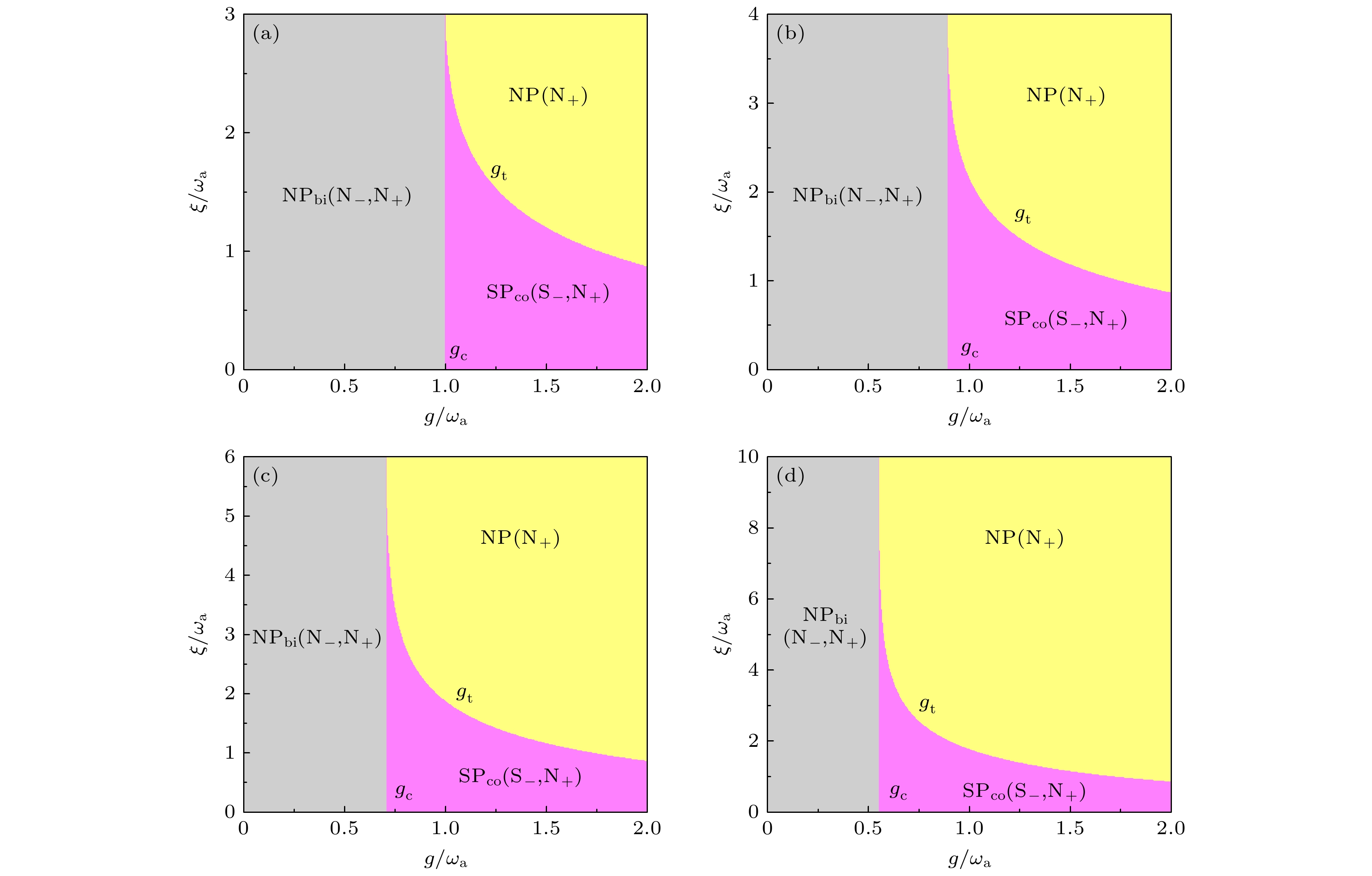
绘制$ g/{\omega _{\text{a}}}{\text{ - }}\zeta /{\omega _{\text{a}}} $基态相图, 取原子与模式1的相互作用变量$ {g_1}/{\omega _{\text{a}}} = g/{\omega _{\text{a}}} $, 原子与模式2的相互作用参量为$ {g_2}/{\omega _{\text{a}}} = \left( {1 + \delta } \right)g/{\omega _{\text{a}}} $, 其他参量不变. 取$ g/{\omega _{\text{a}}} $和$ \zeta /{\omega _{\text{a}}} $是变量时, $ \delta $取不同的确定值对相图的影响, 如图4所示.

图4展示了单模Dicke模型、单模光机械腔和双模光机械腔三种情况, 相边界由点到线, 通过操纵各种参数来控制相图. 在图4(a)中, 模式2光场为零, 当光-声子的非线性耦合参量$ \zeta = 0 $时是单模Dicke模型^[1], 其相变点$ {g_{\text{c}}}/{\omega _{\text{a}}} = 1.0 $^[1,7,8]. $ \zeta /{\omega _{\text{a}}} \gt 0 $是单模光机械腔^[22], 在$ \zeta /{\omega _{\text{a}}} = 3.0 $的位置附近, 导致了两个NP态NP (N_-)和NP (N₊)的直接转换. 图4(b)、图4(c)、图4(d)三个相图, 当$ \zeta = 0 $时是双模Dicke模型^[31,32], 由于$ \delta $的不同, 原子和光的偶级相互作用强度不同^[31], 对应的相变点也不同, 相变点依次为$ {g_{\text{c}}}/{\omega _{\text{a}}} $ = 0.8944, 0.7071, 0.5547都小于单模Dicke模型的相变点. 当$ \zeta /{\omega _{\text{a}}} \gt 0 $代表双模光机械腔, 相变点$ {g_{\text{c}}} $与$ \zeta $无关, 图4(a)—(d)中的相边界都是一条直线^[21,22]. 随着$ \delta $的增加, $ {g_2} $增大, 相变点向g减小的方向移动, 更加容易发生量子相变. 在图4(a)—(d)图中都有双稳态$ {\text{N}}{{\text{P}}_{{\text{bi}}}}( {{\text{N}}_ - }{, } {{\text{N}}_{+}} ) $到共存相$ {\text{S}}{{\text{P}}_{{\text{co}}}}\left( {{{\text{S}}_ - }{, }{{\text{N}}_{+}}} \right) $的二阶量子相变^{[1,26,27,31–33]}, 单独存在反转的正常相$ {{\text{N}}_{+}} $. 明显显示超辐射相$ {\text{S}}{{\text{P}}_{{\text{co}}}}\left( {{{\text{S}}_ - }{, }{{\text{N}}_{+}}} \right) $的塌缩. 可实现自旋反转的光-声子非线性耦合强度$ \zeta /{\omega _{\text{a}}} $的临界值从(3-4-6-10)依次增大, 即实现了正常相$ {{\text{N}}_ \mp } $之间的转化^[22].

本文利用自旋相干态和变分法得到了双模光机械腔中冷原子的基态能量泛函, 通过求解和判断稳定性得到共振时的基态性质. 存在稳定的三种态, 正常相和反转正常相的双稳态, 超辐射相和反转正常相的共存态, 单独的反转正常态. 分别有相变点和转折点, 原子与两模光场相互作用强度的不同对相变点的值有较大影响, 存在从正常相经过相变点到超辐射相的量子相变. 光-机械振子的非线性耦合强度不影响相变点, 光与机械振子耦合强度对超辐射相有影响, 由于机械振子的谐振阻尼, 超辐射相态在转折点坍塌, 塌缩的结果是反转自旋的零光子态变为基态, 并且发生了超辐射相经过转折点变为反转的正常相的量子相变. 特别是通过操纵光子-声子耦合强度, 可以使超辐射相塌缩为零, 转折点和相变点重合, 实现了两个原子能级之间的直接原子布居数的反转, 这一新的观察结果可能在激光物理学中有技术上的应用. 光-机械振子的非线性耦合还引起了不稳定的非零光子数分布, 与超辐射相相对应. 在没有机械振荡器($ \zeta = 0 $)的情况下, 回到双模Dicke模型的结果, 这个预测结果可以通过测量原子布居数、平均光子数和平均声子数来检测^{[5,6,20–22]}. 两模光场可以调控较多的因素, 使相变更易发生, 多模Dicke模型可能将成为一个新的探究方向^[45]. 后期我们也将与实验参数相结合进一步探讨多模Dicke模型混合系统的量子相变.