激光多普勒测振仪(laser doppler vibrometer, LDV)是一种利用激光多普勒效应实时获取目标振动参数的精密测量仪器, 相较于其他振动测量技术而言具有工作距离范围广^[1]、测量频带范围大^[2,3]、灵敏度高^[4]、非接触^[5]等优势. 基于光纤干涉光路的激光测振仪因具有杂散光抑制能力强、装调容易和集成度高等优点, 近年来获得快速发展^[6–9].

LDV系统常采用收发一体式望远镜结构, 其中收发望远镜口径和焦距直接影响激光能量的发射效率和接收效率, 同时由于激光测振仪实际测量目标大多为非合作目标, 粗糙目标散射回光产生的散斑效应影响耦合进入光纤的功率^[10], 进而影响测量分辨力和振动反演精度^[11]. 因此, 研究收发望远镜口径、焦距、光纤纤芯直径与粗糙目标回光功率的相互关系, 对提升激光测振仪的测量分辨力、可探测范围和振动测量精度具有重要意义.

国内外针对远距离目标光纤耦合能量已经进行了一定的研究. Rzasa等^[12]通过Lambertian目标假设和有限口径对应接收立体角近似计算耦合进入光纤的能量, 设定收发透镜焦距267 mm、口径88 mm, 目标距离2000 m内均能保障$ 3.6 \times {10^{-10}} $能量接收效率, 但忽略散斑效应和透镜衍射效应对结果的影响. Ruilier和Paris^[13]提出了光纤耦合效率计算公式, 但仅对理想平面光场经过口径受限单透镜耦合进入光纤的耦合效率进行讨论, 得到光纤最大耦合效率为0.81. Winzer和Leeb^[14]建立了远距离粗糙面目标的光纤耦合效率计算公式, 在未考虑激光发射过程的情况下, 得出最优耦合效率与透镜口径和散斑光斑直径比值量化关系.

国内外前期研究均缺乏对完整激光收发过程的讨论, 因此, 以菲涅耳衍射积分理论为激光收发过程基础框架, 结合高斯束腰传递理论、粗糙目标生成理论和光纤耦合理论建立光场传递仿真模型, 对理想高斯激光的发射传输过程和面目标回波接收耦合过程进行了系统分析. 基于散粒噪声受限假设并结合耦合能量与仪器噪声基底的关系, 提出LDV噪声基底评价方法. 经过数值仿真实验, 得到收发望远镜口径、焦距与仪器底噪的统计学关系, 验证了仿真模型的正确性. 仿真结果表明通过合理选择收发望远镜口径和焦距, 可提升激光测振仪接收回光信号能力和测量分辨力, 为激光测振仪和激光测风雷达等仪器收发望远镜参数设计提供理论依据.

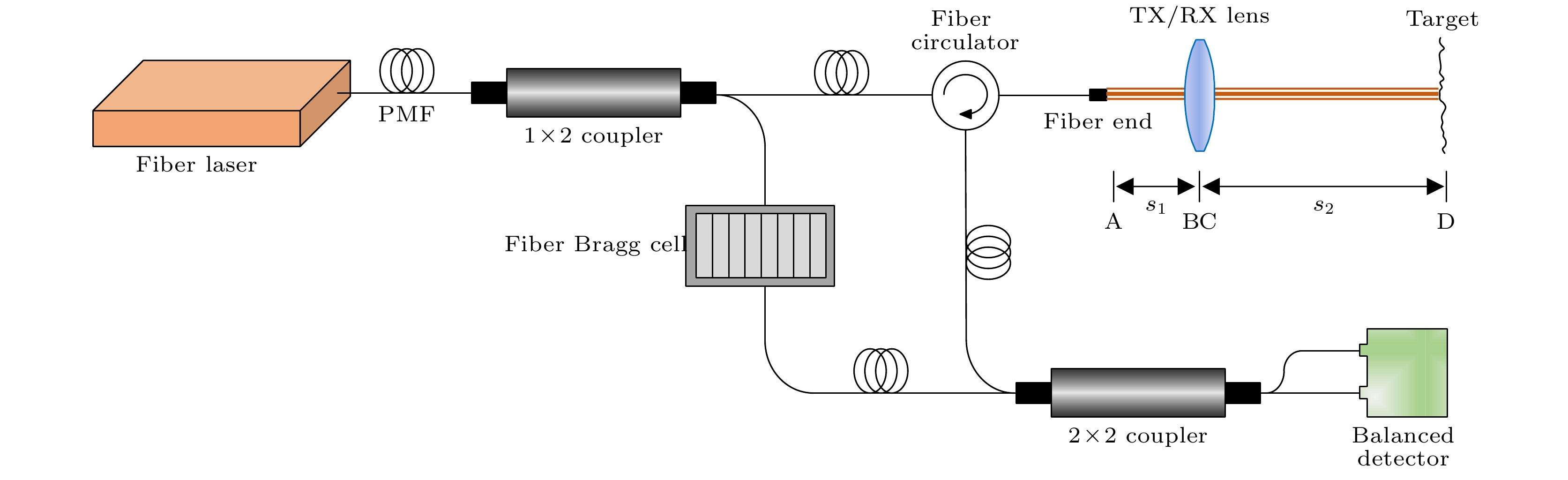
基于光纤的典型激光外差振动测量系统原理如图1所示, 该仪器采用马赫泽德干涉仪结构, 参考光经过光纤布拉格盒产生外差移频, 测量光输出采用光纤点衍射直接经过收发望远镜聚焦到粗糙目标上, 目标上激光束腰光斑的散射再次经过收发望远镜, 耦合进光纤头与参考光经过合束器形成外差干涉^[15], 最终在平衡探测器处经过光电转换形成光电流.

理想系统中, 平衡探测器接收到参考光和测量光干涉形成的光电流$ i(t) $可表示为^[15]

式中, $K$为探测器响应度, ${P_{\text{r}}}$和${P_{\text{m}}}$分别为参与干涉的参考光和测量光的光功率, $ {\omega _0} $为光纤布拉格盒外差角频率, $ {\varphi _{\text{r}}} $和$ {\varphi _{\text{m}}}(t) $分别为参考光初始相位和由粗糙目标振动引起的测量光相位变化. 在散粒噪声受限的激光外差测振系统中, 散粒噪声起到主导作用, 其噪声有效值${n_{{\text{shot}}}}$可写为

式中, B为测量带宽, q为电子所带电荷量. 研究表明散粒噪声受限系统位移频域噪声为白噪声, 采用单位带宽噪声有效值$ S_{\text{n}}' $表征仪器噪声基底^[16]:

式中, $\lambda $为激光波长, $ {\text{CNR}}_{{\text{rf}}}' $为单位带宽载噪比, $ {P_{\text{m}}} $为测量光光功率. 在激光外差测振系统中, 由于目标为非合作目标, 参考光功率远大于测量光功率, 散粒噪声大小由参考光功率决定, 因此$ S_{\text{n}}' $有(4)式近似结果:

(4)式表明, 参与干涉的测量光功率将直接决定信号获取的质量, 进而影响相位解调反演得到的位移信号质量. 显然, 测量光回光功率越大, 解得位移单位带宽噪声越小, 即仪器噪声基底越小, 仪器测量分辨力更高, 因此讨论如何提升收发望远镜能量利用率具有重要意义.

激光收发过程可分解为两个过程: 第1个过程是激光发射传输过程, 高斯激光经过收发望远镜将束腰传递到目标距离下的粗糙目标, 收发望远镜口径、焦距和空间位置等参数直接影响到发射能量传输效率以及到达目标端的光场分布; 第2个过程是激光回波接收耦合过程, 目标端粗糙表面对反射光场进行调制, 光场经过长距离传输、收发望远镜收集后到达光纤端面, 最后耦合进入单模光纤, 在光纤中以平整波前传输并与参考光干涉. 为了便于说明收发透镜口径和焦距对耦合效率的影响, 设定面目标距离典型值为1 km, 单模光纤模场半径为5 μm、激光波长为1550 nm. 下文将基于典型值对上述两个过程展开详细分析.

激光发射传输包含3个过程, 如图1和表1所示, 激光从光纤发射端面(A面)到透镜前表面(B面)的自由空间传输, 从B面到透镜后表面(C面)的透镜附加相位叠加, 以及从C面到粗糙目标面(D面)的自由空间传输.

激光从单模光纤中出射, 通过比较光纤内部稳定传输光场分布与束腰在出射端面的高斯光束下的空间光场分布^[17], 可用高斯光束对实际出射光场进行等效以简化运算, 光纤发射端面光场分布$ {U_{{\text{A,TX}}}}(x, y) $可表示为

式中, $ {A_0} $为光纤端面中心光场强度, ${w_1}$为光纤等效模场半径, 为保证激光到达目标面处波前平整并且光斑尽可能小, 根据高斯光束通过无限大薄透镜变换公式, 目标面与收发望远镜镜后表面的距离${s_2}$(后简称目标距离)和光纤端面到达收发望远镜镜前表面${s_1}$(后简称物距)须满足如下关系^[18]:

式中, f为透镜焦距. 为保证高斯光束能在目标位置处聚焦, 即(6)式能够解得实数${s_1}$, 根据仿真前提条件: 目标距离典型值为1 km, 单模光纤模场半径为5 μm、激光波长为1550 nm, 为保证${s_1}$存在实数解, 收发望远镜焦距需大于319 mm, 并作为后续仿真的输入范围.

收发望远镜口径受限也会产生衍射效应, 使得像面光斑与理想情况产生差异, 因此后文采用菲涅耳衍射理论估计像面光场分布. 根据高斯光束自由空间传输理论, 高斯光束从光纤端面传输至透镜前表面, 透镜前表面横向光场分布$ {U_{{\text{B,TX}}}}(x, y) $可表示为^[18]

式中, ${w_{{\text{lens}}}}({s_1})$为收发望远镜前表面束腰, $R\left( {{s_1}} \right)$为等相面曲率半径, $\psi \left( {{s_1}} \right)$为相位因子, 其中,

根据有一定口径的薄透镜假设, $ {U_{{\text{B,TX}}}}(x, y) $经过口径为$r$、焦距为$f$的理想薄透镜后${U_{{\text{C, TX}}}}(x, y)$可表达为^[19]

采用菲涅耳衍射积分过程对光场传输过程进行数值模拟仿真, 即通过傍轴近似假设, 得到物面光场经过距离为${s_2}$传输后的光场${U_{{\text{D,TX}}}}(\xi , \eta )$为^[20]

在数值计算中, 上述过程可通过快速傅里叶变换进行转换, 即

通过上述光场传递过程, 得到到达目标面处光场信息.

激光回波接收耦合包含5个过程, 如图1和表2所示, 粗糙表面叠加附加相位, 从D面到C面的自由空间传输, 从C面到B面的透镜附加相位叠加, 从B面到A面的自由空间传输, 以及光纤耦合过程.

粗糙面生成采用基于随机过程的数字滤波技术并通过Johnson转化系统的方法来模拟^[21], 利用该方法首先生成一个二维随机序列$ \eta \left( {x, y} \right) $并求得其傅里叶变换$ A\left( {{\omega _x}, {\omega _y}} \right) $, 该随机序列经过数字滤波调制后可得:

式中, $ H\left( {{\omega _x}, {\omega _y}} \right) $为滤波器的传递函数, $ Z\left( {{\omega _x}, {\omega _y}} \right) $是粗糙表面$ Z\left( {x, y} \right) $的傅里叶变换. 根据维纳辛钦定理^[22]: 宽平稳随机过程的功率谱密度是其自相关函数的傅里叶变换. 功率谱密度可看作传递函数数值的平方, 而传递函数是由给定的粗糙表面自相关函数$ R\left( {{z_x}, {z_y}} \right) $得到, 即

式中, $ {z_x}, {z_y} $分别为二维自相关函数的$x, y$坐标, 粗糙表面自相关函数由所需粗糙面的粗糙度决定, 即

式中, ${\sigma _z}$为指定粗糙表面均方根粗糙度; $ {\beta _x} $和$ {\beta _y} $分别为粗糙面$x$和$y$方向上的相关长度. 只要设定粗糙面的均方根粗糙度及粗糙面的相关长度就可得到$ Z\left( {{\omega _x}, {\omega _y}} \right) $, 再经傅里叶逆变换就可得到所需粗糙表面$ Z\left( {x, y} \right) $, 经过粗糙面光场调制, 粗糙面回光光场${U_{{\text{D, RX}}}}(x, y)$为

光场由D面传递到A面的过程与前文发射过程类似, 先通过菲涅耳衍射积分过程得到C面的光场分布${U_{{\text{C, RX}}}}(x, y)$, 经过口径受限的收发透镜调制, 得到B面的光场分布${U_{{\text{B, RX}}}}(x, y)$, 再次通过菲涅耳衍射积分过程得到A面的光场分布${U_{{\text{A, RX}}}}(x, y)$. 而光纤中稳定传输的光场可表达为

根据光纤耦合计算[13]式, 可将光纤中稳定传输的光场视为一空间向量, 待耦合的光场为另一空间向量, 光纤耦合效率即为两空间向量夹角模长的平方:

耦合进入光纤能量$P$为待耦合的光场在光纤光场上的投影, 因此可表示为

由(21)式可得当待耦合光场与光纤光场越一致, 最终可耦合进入光纤中稳定传输的能量也越多. 通过上述过程即可得到发射光场经过上述口径受限收发透镜和粗糙表面调制后最终耦合进入光纤的能量, 因此基于光纤的收发一体光学系统的能量利用率CE可表示为

式中, ${P_0}$为从光纤出射的能量. 不改变粗糙面的统计特性前提下进行蒙特卡罗实验, 可得出粗糙目标在该透镜参数下系统能量利用率的统计学分布, 通过改变透镜参数, 进而得到不同透镜参数下的系统能量利用率的统计学分布.

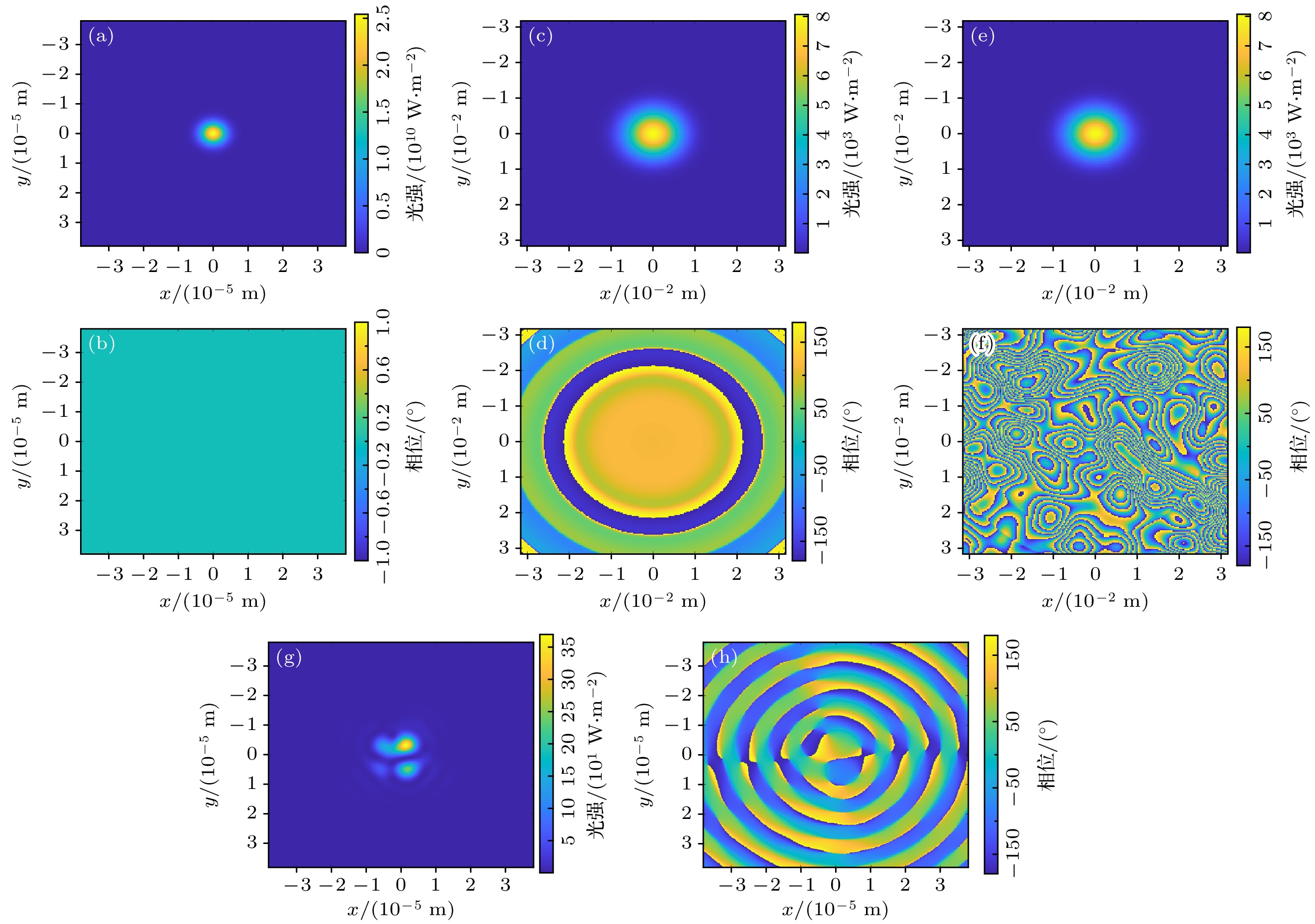
结合实际应用场景, LDV对1 km外粗糙目标进行微振动信号探测, 仪器选用的单模光纤模场半径为5 μm、激光波长为1550 nm, 发射面初始光强总和为1. 在上述约束下, 结合第2节讨论的激光光场传输过程, 获得各个观察面光场分布, 如图2所示.

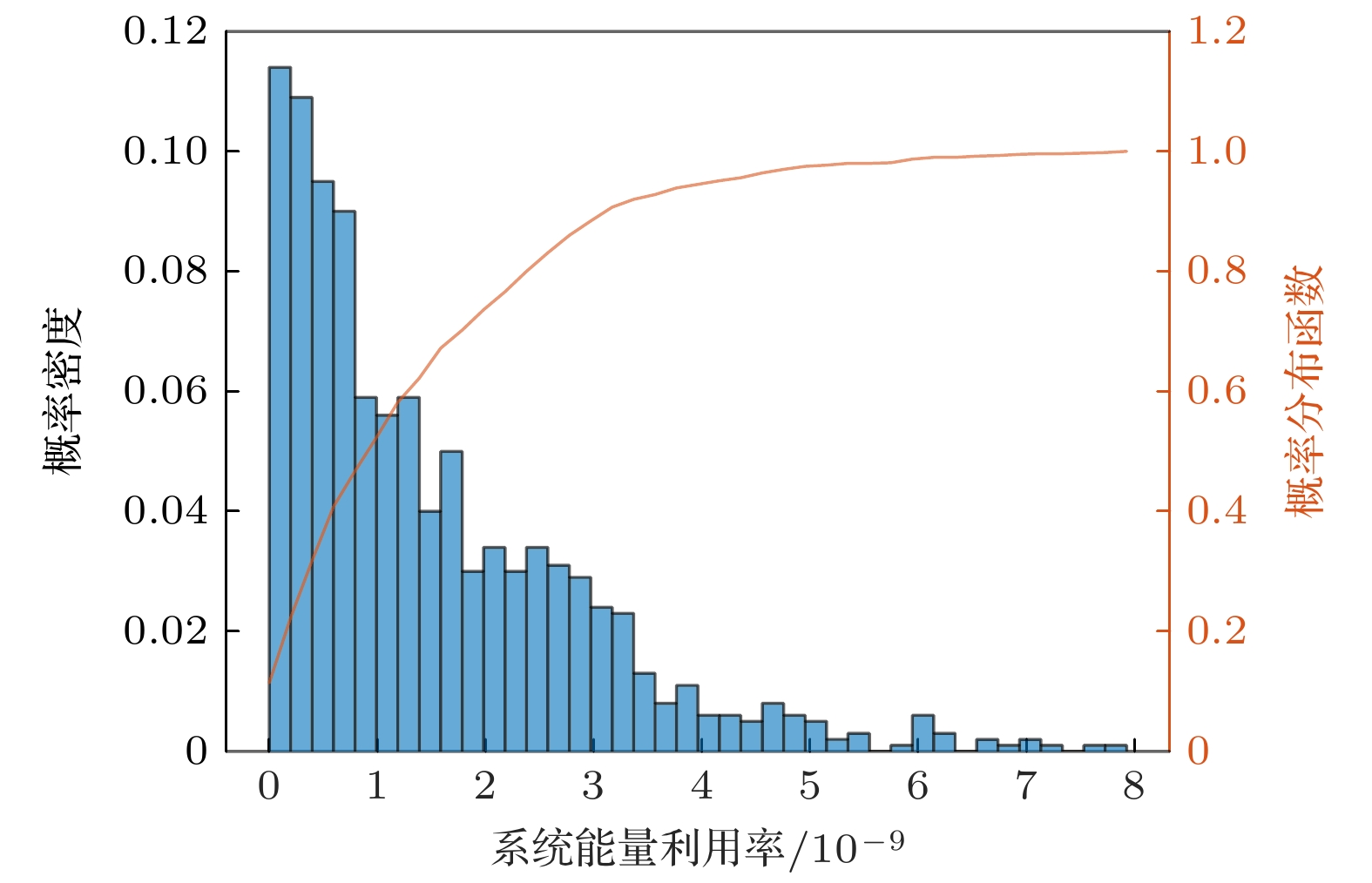
由图2(c), (d)可得, 虽然到达目标面仍然为高斯分布, 但因透镜口径受限, 到达D面波前并非为平面. 由图2(e), (f)可得, D面散射光场强度上虽然保持高斯分布, 但相位上由于叠加附加相位变为不规则相位分布. 由图2(g), (h)可得, 回光经过有限口径收发透镜接收, 由于相干光不同子孔径复振幅叠加, 产生散斑效应, 到达光纤端面的光场强度和相位均存在变形, 与图2(a), (b)展现的光纤内部稳定传输光场存在巨大差异. 显然, 当粗糙面发生变化时, 最终在光纤端面处得到的光场分布不同, 耦合进入光纤并参与外差干涉的能量也不同, 因此通过随机生成粗糙表面进行蒙特卡罗仿真实验, 如图3所示, 以焦距600 mm、口径200 mm的透镜参数为例得到系统能量利用率的概率密度分布.

如图3所示, 系统能量利用率概率密度分布集中于视窗左侧, 从概率分布函数可知系统能量利用率90%概率分布于视窗左侧, 这意味着大部分情况粗糙表面回光耦合进入光纤能量均为小值, 偶有极高耦合能量情况出现, 并且随着系统能量利用率增加, 出现概率趋势呈现单调递减状态. 由于散斑效应, 粗糙目标散射回光所得的测量光能量并不恒定, 根据(4)式关于噪声基底的讨论, 引入分辨力评价因子${\sigma _i}$来评价第i次实验噪声基底:

式中, 引入常系数$k = \dfrac{{2\sqrt 2 {\text{π}}}}{\lambda }\sqrt {\dfrac{{K{P_0}}}{q}} $, ${\text{C}}{{\text{E}}_i}$, ${P_i}$和$S_{{\text{n}}i}'$分别为第i次实验系统能量利用率计算结果, 耦合进入光纤能量和单位带宽噪声有效值. 为评估粗糙目标对系统噪声基底的统计学影响, 引入${\sigma _i}$均方根有效值$\sigma $作为某次实验条件下的分辨力评价因子:

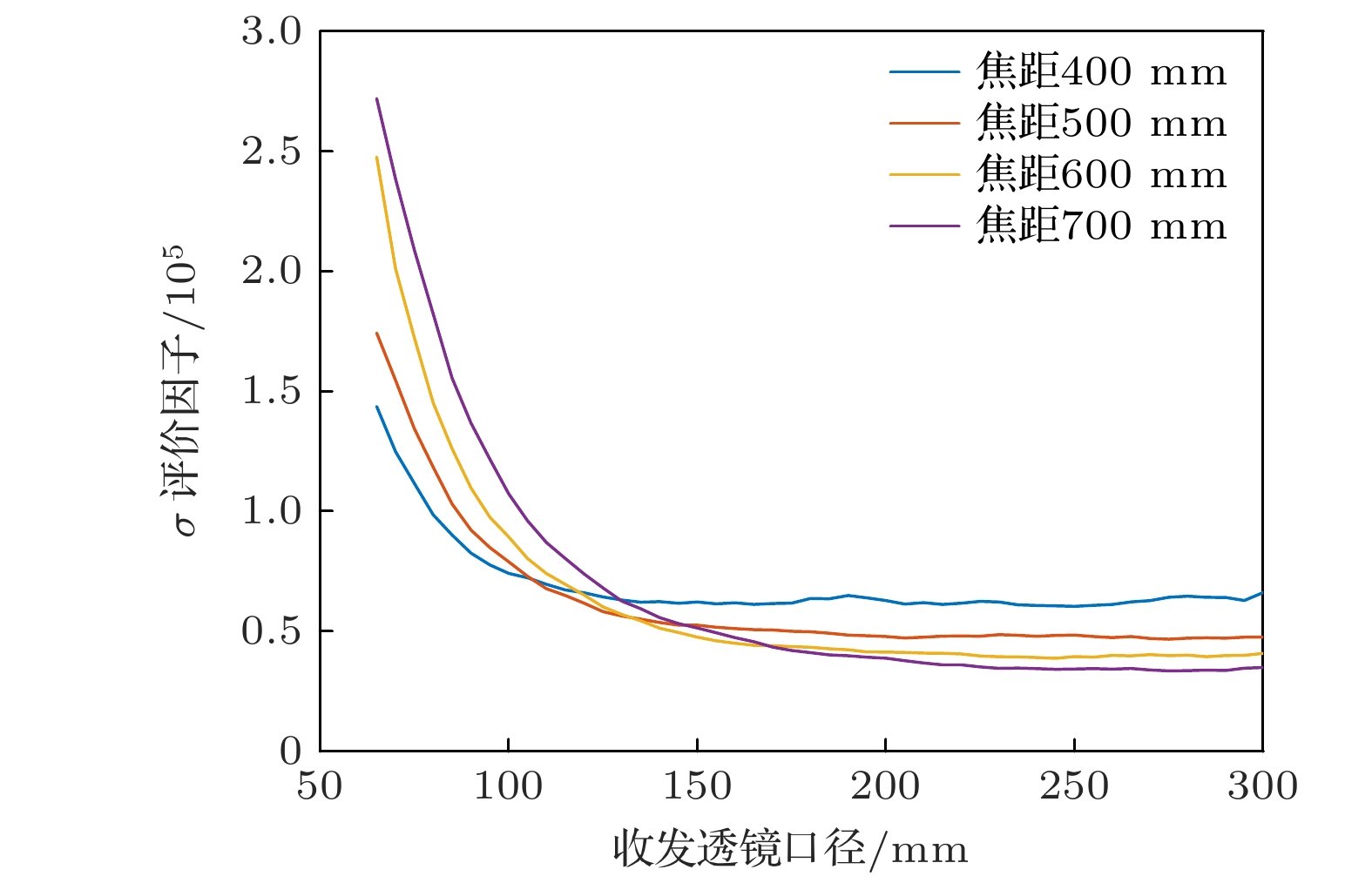
式中, n为单次实验条件下蒙特卡罗实验次数. 经过仿真检验, 对于不同透镜参数情况, ${\sigma _i}$分布几乎相同, 因此$\sigma $越小, 说明测振仪数据反演时噪声越小, 测量分辨力更高, 在上述仿真和讨论基础下, 变换透镜口径和焦距后进行蒙特卡罗实验, 获得不同透镜参数情况评价因子$\sigma $, 图4为滑动平均滤波后结果.

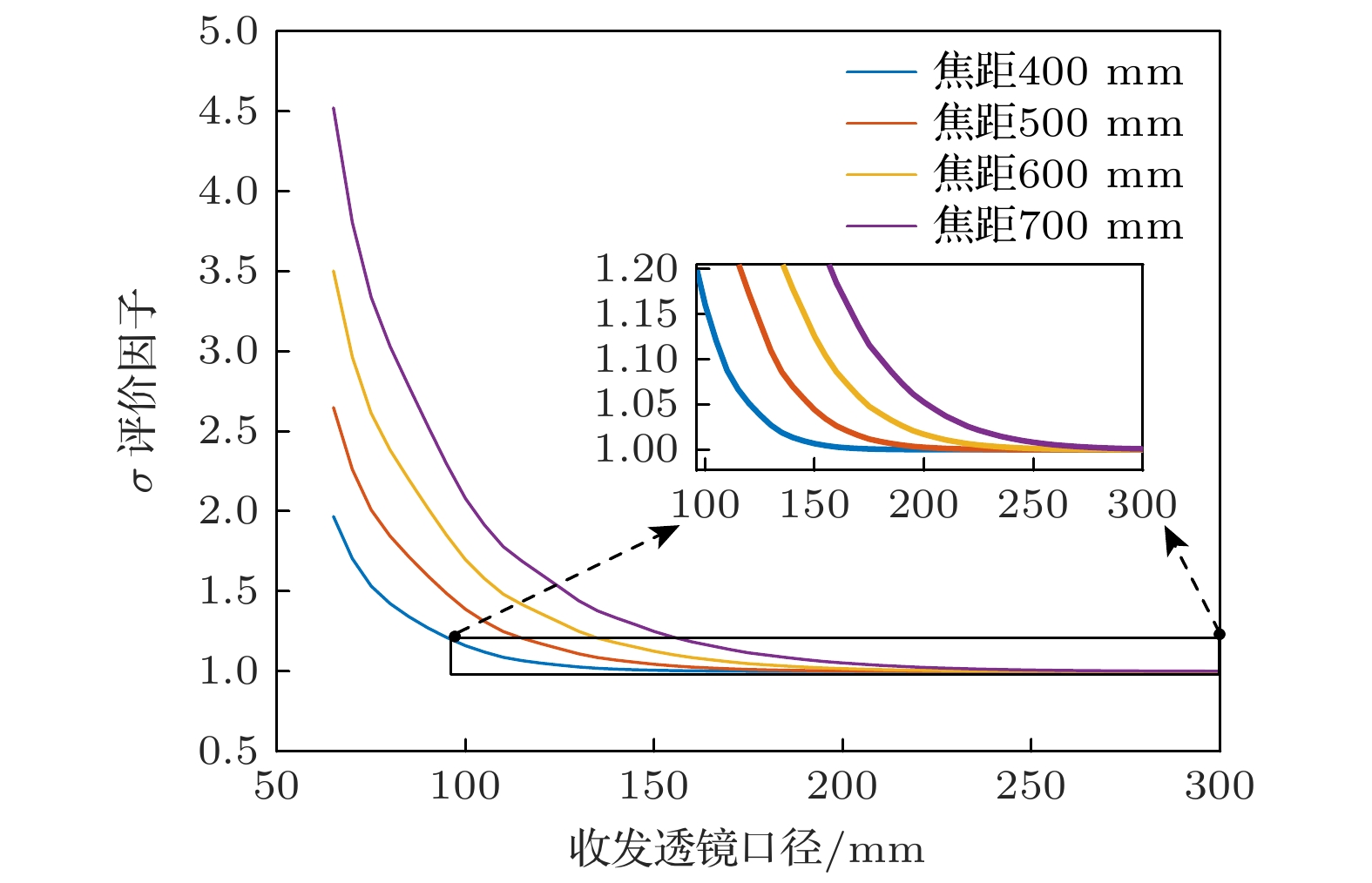
从图4可得: 1)当透镜焦距固定时, 随着收发透镜口径增大, $\sigma $先呈现快速下降趋势, 当F数低于3.3后, $\sigma $趋于稳定状态, 即收发系统不会由于口径增大而持续提升能量利用率, 仪器噪底也不再发生变化; 2)由图4曲线左侧同一口径不同焦距结果可知, 此时光纤F数远低于透镜F数, 光纤发射效率低, 因此收发透镜焦距越大, 仪器噪底越大; 3)由图4曲线右侧稳定状态结果可知, 极限情况仪器噪底与收发透镜焦距相关, 焦距越大, 极限情况仪器噪底越小.

将目标面设置为镜面, 通过相同仿真流程可获得镜面反射理想情况下不同收发透镜焦距和口径与$\sigma $关系, 如图5所示. 仿真表明:

1) 当透镜焦距固定时, 与粗糙目标趋势类似, 随着收发透镜口径增大, $\sigma $先呈现快速下降趋势, 当F数低于3.85后, $\sigma $趋于稳定状态, 这是由于高斯光束能量分布为中心高、边缘低, 当透镜口径增大时, 发射接收过程利用的能量先快速增加后趋于定值.

2) 口径足够大时, 不同焦距$\sigma $极限值相同, 当透镜口径足够大时, 接近于理论高斯光束腰传递, 即目标面和光纤端面处于共轭位置, 光纤收发过程无能量损失.

为更好比较不同焦距、不同目标$\sigma $拐点位置, 约定达到最小$\sigma $值的1.1倍作为该焦距下口径拐点及对应F数, 如表3所示. 从表1可得相同目标不同焦距下F数拐点基本一致, 镜面目标F数约为3.85, 粗糙目标F数约为3.3, 因此选择LDV收发透镜时需针对目标类型作出相应调整.

实际LDV使用场景为被测目标大部分为粗糙目标, 因此当设计收发透镜参数时, 可根据实际情况可以有两种选择方式.

1) 口径受限情况. 当透镜口径小于100 mm时, 更小焦距收发透镜能量利用率更高; 当透镜口径大于200 mm时, 结论相反, 因此可根据图4选择口径对应最小$\sigma $值时的焦距值.

2) 焦距受限情况. 尽可能选择大口径收发透镜, 但当F数小于3.3时, 仪器噪底几乎达到极限值, 同时口径增大到一定程度时, 会导致系统光学系统像差难以控制, 因此结合图4不同焦距曲线拐点信息, 可得无论何种焦距, 最优F数选择大约为3.3.

基于光纤耦合和菲涅耳衍射传递理论建立收发一体光纤LDV光场传递模型和系统能量利用率计算模型, 并根据散粒噪声受限模型提出粗糙目标回光情况仪器噪声基底评价方法. 与国内外研究仅考虑透镜接受情况与散斑理论计算工作相比, 基于光纤LDV基础结构出发全流程仿真收发过程可进一步得到系统能量利用率分布情况. 针对对准距离为1 km、单模光纤模场半径为5 μm、激光波长为1550 nm的典型光纤LDV应用场景进行光场传输和总耦合能量的数值仿真, 仿真结果表明当收发透镜F数达到3.3时, LDV趋近该焦距下最高能量利用率, 继续提升口径并不能持续提升系统能量利用率. 在工程应用中, 数值分析结果可为LDV收发透镜设计提供理论依据, 实现高灵敏外差干涉探测系统的优化设计, 仿真平台也可进一步指导激光测风雷达等领域收发透镜设计, 实现非合作目标更高测量分辨力.