声辐射力(ARF)是声场的非线性效应, 是声场与物体之间动量传递的结果. 声辐射力操控具有无创、适用性广、可操控粒子尺度跨度大等优点, 使其在生物医学、材料科学等领域拥有广泛的应用前景^[1,2], 这也要求粒子操控技术需要更高的精确性和有效性, 对声辐射力的研究尤为重要. 1934年, King^[3]提出了声辐射力的概念, 并对理想流体中刚性小球所受的声辐射力进行了研究, 基于此, Hasegawa和Yosioka ^[4]考虑粒子的弹性, 对理想流体中弹性球所受的声辐射力进行了计算. 除了平面波, 贝塞尔波、高斯波、马蒂厄波、驻波等新型声场对粒子的声辐射力也陆续被研究^[5–12]. 近来, Gong等^[13]通过共振黏附结构生成的声场实现了负的声辐射力的产生, 详细探讨和解释了声辐射力随入射声波频率和共振黏附结构各种参数的变化规律, 随后提出了一种基于多层球面结构实现负ARF的方案, 通过抑制后向散射来实现负ARF^[14]. Gaunaurd和Huang^[15]引入边界的影响, 结合镜像原理分析了边界附近球形粒子对平面波的声散射. Miri和Mitri^[16]为了与医学超声中血管壁附近的造影剂应用相结合, 建立了非刚性边界附近理想流体中弹性球壳的声辐射力理论模型, 对弹性聚乙烯材料的球形粒子的声辐射力进行了具体的分析和讨论. Westervelt^[17]首次考虑了实际应用中流体黏度这一因素对声辐射力的影响, 计算了固定球形粒子所受的声辐射力. Doinikov^[18]给出了黏性流体中的自由球体的声辐射力理论解析, 研究了黏性可压缩液体球在强耗散和弱耗散两种极限情况下的声辐射力. Qiao等^[19]计算了黏性流体中自由球形粒子的声辐射力, 得到的声辐射力表达式适用于任意黏度的流体, 并以聚苯乙烯球形粒子为例, 通过实验对其声辐射力进行了定量的测量. 在生物医学等领域的实际应用场景中, 为了提高声辐射力操控的精确性和有效性, 需要同时考虑到存在的多种因素, 如流体黏度、粒子自由状态、边界以及粒子的位置等. 基于此, 本文以球形粒子为主体, 推导了平面波垂直边界入射的情况下, 自由球形粒子在有界黏性流体中受到的声辐射力表达式, 分析了各因素对声辐射力的影响规律.

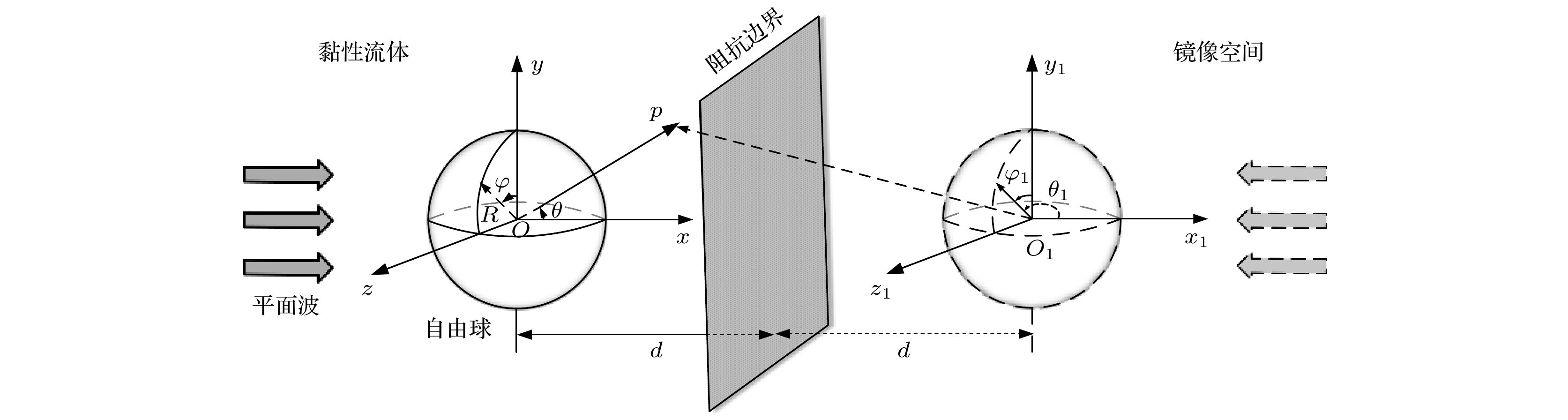
考虑一个半径为$R$的自由球形粒子位于黏性流体中的阻抗边界附近, 该边界视为局部反应边界(表面一给定点上的运动只与入射到这部分上的声压有关, 而与表面上任何其他部分的运动无关), 用边界反射系数$ {R_{\text{s}}} $来表示界面的物理特性^[16]. 粒子中心到边界的距离为$d$. 以球形粒子中心$O$为原点分别建立直角坐标系$\left( {x, {\text{ }}y, {\text{ }}z} \right)$和球坐标系$\left( {r, {\text{ }}\theta , {\text{ }}\varphi } \right)$, 如图1所示, $Ox$轴垂直于边界, 平面波沿$Ox$轴方向在液体中传播. 由镜像原理可知, 边界对声波的作用可视为在边界另一侧的镜像空间引入镜像粒子(与原粒子大小、材料、距离边界距离相同)和镜像声源(与原入射平面波振幅相同但方向相反的镜像平面波), 如图1所示. 为了理论分析, 以镜像球形粒子中心${O_1}$为原点分别建立直角坐标系$\left( {{x_1}, {\text{ }}{y_1}, {\text{ }}{z_1}} \right)$和球坐标系$\left( {{r_1}, {\text{ }}{\theta _1}, {\text{ }}{\varphi _1}} \right)$.

在球坐标系$\left( {r, {\text{ }}\theta , {\text{ }}\varphi } \right)$中, 入射平面波的速度势表示为

其中, $A = \sqrt {{2}{I_0}/{\rho _0}{c_0}{k^2}} $为入射波振幅, ${I_0}$为入射波声能量, ${\rho _0}$为黏性流体密度, ${c_0}$为流体中的声速, $k = {{\mathrm{Re}}} (\alpha )$, $\alpha = \left( {{\omega {/ } {{c_0}}}} \right){\left[ {1 - {\text{i}}\omega (\lambda ' + 2\mu ')/{\rho _0}c_0^2} \right]^{ - 1/2}}$为黏性流体中的纵波波数, $ \omega $为声波入射角频率, $ {{\text{j}}_n}( \cdot ) $为n阶球贝塞尔函数, ${{\text{P}}_n}( \cdot )$为n阶勒让德函数, $\lambda ' = \eta ' - {{2\mu '} {/ } 3}$, $ \mu ' $为动力黏性系数, $\eta '$为第二黏性系数或体膨胀黏性系数. 对于大多数的流体, 体积膨胀不是很大, 一般取$\eta ' \approx 0$, 则$\lambda ' = - {{2\mu '} {/ } 3}$, 这在许多应用中都适用^[20].

声波从球形粒子散射到黏性流体中有散射纵波${\phi _{\text{s}}}$与散射横波${\psi _{\text{s}}}$两种波, 在球坐标系$\left( {r, {\text{ }}\theta , {\text{ }}\varphi } \right)$中粒子的散射波方程为

其中, $\beta = (1 + {\text{i}})/\delta $为散射横波波数, $\delta = \sqrt {2\mu '/{\rho _0}\omega } $为黏性边界层, 表示黏性波的穿透深度.

球坐标系$\left( {r, \theta , \varphi } \right)$中, 解方程(2)和方程(3)可得粒子的散射波速度势:

其中, ${A_n}$和${B_n}$为边界条件决定的散射系数, ${\text{h}}_n^{(1)}( \cdot )$为第一类球汉克尔函数.

由镜像原理可知, 边界对声波的反射转化为镜像声源和镜像粒子的散射波, 其速度势在相应的坐标系表示为

其中, ${R_{\text{s}}}$为边界的声压反射系数, 反射系数的极限值${R_{\text{s}}} = + 1$和${R_{\text{s}}} = - 1$分别对应刚性边界和顺性边界.

在处理镜像粒子时, 利用球函数的加性定 理^[21,22]将镜像粒子的散射波(7)式和(8)式改写为

其中, Q_mn具体公式见附录.

根据(4)式—(6)式和(9)式—(10)式, 得球外总声场速度势为

为便于计算, 引入定义:

将(13)式和(14)式代入(11)式和(12)式, 整理得到球外散射总声场的速度势为

散射系数${A_n}$和${B_n}$为由球形粒子表面的边界条件确定, 在实际应用中, 如超声给药中, 许多药物粒子为液体和弹性材料, 因此, 本文中针对液体和弹性材料的球形粒子进行分析.

对于液体球形粒子, 其内部透射波只有纵波, 在球坐标系$\left( {r, {\text{ }}\theta , {\text{ }}\varphi } \right)$中透射纵波表示为

在黏性流体与液体球界面$r = R$处, 满足边界条件:

其中, $\overline p = {\text{i}}\omega {\rho _0}\overline \phi $, ${v_r}$和$\overline {{v_r}} $为相应的速度分量, ${\sigma _{rr}}$, ${\overline \sigma _{rr}}$, ${\sigma _{r\theta }}$, ${\overline \sigma _{r\theta }}$为相应的应力张量分量, 具体表达式为

考虑小球为自由状态, (21)式中的${{\partial \phi } {/ } {\partial t}}$应当在确定速度势的固定坐标系中进行计算, 因此有:

其中, ${\boldsymbol{u}}$小球速度, 由公式$ m\dot {\boldsymbol{u}} =\displaystyle \iint\nolimits_{{s_0}} {{\boldsymbol{\sigma }}{\text{d}}{\boldsymbol{S}}} $计算, 应力张量$ {\boldsymbol{\sigma }} = \left( { - {p_1} + \lambda '\nabla \cdot {\boldsymbol{v}}} \right){\boldsymbol{E}} + 2\mu '{\boldsymbol{e}} $, $ {\boldsymbol{E}} $为单位矢量, 变形张量$ {\boldsymbol{e}}{=}[ {\left( {\nabla {\boldsymbol{v}}} \right) + {{\left( {\nabla {\boldsymbol{v}}} \right)}^{\text{T}}}} ]/2 $, $m = {{4{\text{π}}{R^3}{\rho _{\text{s}}}} {/ } 3}$为球形粒子的质量, ${\rho _{\text{s}}}$为粒子密度, $ {\boldsymbol{v}} = \nabla \phi + \nabla \times \psi $为流体速度势. 注意, 在计算小球的速度时, 只需要将(22)式代入(21)式得到的表达式中保留一阶项^[23].

将(15)式—(17)式结合(19)式—(22)式代入(18)式, 得到黏性流体中阻抗边界附近的自由液体球散射系数方程组:

方程组的具体表达式为

若小球为弹性球, 球体对声波产生散射的同时, 声波透过弹性球, 在球体内折射为透射纵波与透射横波. 弹性球内部速度势在球坐标系$\left( {r, {\text{ }}\theta , {\text{ }}\varphi } \right)$中可以表示为

其中$ {k}_{\text{L}}=\omega /{c}_{\text{L}}和{k}_{\text{t}}=\omega /{c}_{\text{t}} $分别为球内透射纵波和横波波数, ${c_{\text{L}}} = \sqrt {(\lambda + 2\mu )/{\rho _{\text{s}}}} $和${c_{\text{t}}} = \sqrt {\mu /{\rho _{\text{s}}}} $为透射纵波和横波波速, $\lambda $和$\mu $为拉梅常数, ${\rho _{\text{s}}}$为弹性小球的密度.

在黏性流体中, 弹性球界面$r = R$处满足边界条件:

其中${v_r}$, $\overline {{v_r}} $, ${\sigma _{rr}}$, ${\sigma _{r\theta }}$如(19)式和(20)式所示, ${v_\theta }$, $\overline {{v_\theta }} $, ${\overline \sigma _{rr}}$, ${\overline \sigma _{r\theta }}$的具体表达式为

将(15)式和(16)式、(25)式和(26)式结合(19)式和(20)式、(28)式和(29)式代入边界条件(27)式, 计算整理, 可得黏性流体中阻抗边界附近的自由弹性球的散射系数方程组:

此方程式组具体公式为

声场中粒子所受声辐射力可以表示为

其中, $ {\boldsymbol{\sigma }} = \left( { - {p_1} + \lambda '\nabla \cdot {\boldsymbol{v}}} \right){\boldsymbol{E}} + 2\mu '{\boldsymbol{e}} $. 结合(21)式, (32)式写为

其中, $ \left\langle \cdot \right\rangle $表示时间平均, $ {\boldsymbol{E}} $为单位矢量, $ {\boldsymbol{e}} $为变形张量, $ {\text{d}}{\boldsymbol{S}} $为面元, $ S(t) $为球形粒子的表面, 该表 面是时间的函数. 声场在黏性流体中传播, 作用 在粒子上, 与粒子之间产生动量传递, 根据莱布 尼兹-雷诺传输定理^[20], 表面$ S(t) $界定的体积$ V(t) $内动量的变化率等于声场作用下该体积上的动 量变化率加上通过粒子表面的动量净输运量. 因此, 为了解决积分面是时间函数的难题, Yosioka 等^[24]将积分面$ S(t) $转化为粒子的初始表面积$ {S_0} $, 通过添加动量通量项$ {\rho _0}u \cdot \nabla \phi $来对声辐射力进 行修正. 令${{\partial \phi } {/ } {\partial t}} = {{{\text{d}}\phi } {/ } {{\text{d}}t}} - {\boldsymbol{u}} \cdot \nabla \phi $, (33)式可以改写为

其中$ V(t) $为表面$ S(t) $界定的体积. 结合下式^[20]:

可以得到:

此时${p_1}$的表达式已经通过${{\partial \phi } {/ } {\partial t}} = {{{\text{d}}\phi } {/ } {{\text{d}}t}} - {\boldsymbol{u }}\cdot \nabla \phi $关系转化为

在计算声辐射力时, 需将${p_1}$中的二阶项考虑在内.

(37)式写成分量的形式可以表示为

其中, $ {n_k} $为球形粒子面元$ {\text{d}}S $向外的方向单位矢量在$ k $方向的分量, $ {\sigma _{ik}} $为应力张量.

在有界黏性流体中, 平面波沿垂直边界方向入射情况下, 流体中自由球形粒子受到的声辐射力只有沿$Ox$轴的声辐射力, (38)式在$ x $轴方向的投影为

为计算方便, 将球形粒子外部总声场速度势(15)式和(16)式改写为

其中,

将(40)式代入(39)式, 结合球贝塞尔函数的递推公式和勒让德函数的性质, 推导得有界黏性流体中自由球形粒子的轴向声辐射力为

根据流体黏度、粒子材料、粒子位置、边界反射系数等不同, 散射系数${A_n}$和${B_n}$发生改变, 声辐射力大小不同.

为拓展有界黏性流体中自由球形粒子在声操控应用中的基础理论, 分析流体黏度、粒子材料、粒子位置以及边界等对平面波声场中自由球形粒子所受声辐射力, 本文选取一种常见的药物载体生物材料-聚乙烯(PE)开展数值分析. 为了分析粒子材料对声辐射力的影响, 另外对油酸和聚甲基丙烯酸甲酯(PMMA)两种材料粒子的声辐射力进行了数值计算, 数值仿真时不考虑流体的体积膨胀, 取第二黏性系数$\eta ' = 0$. 粒子材料和流体的声学参量由表1和表2给出.

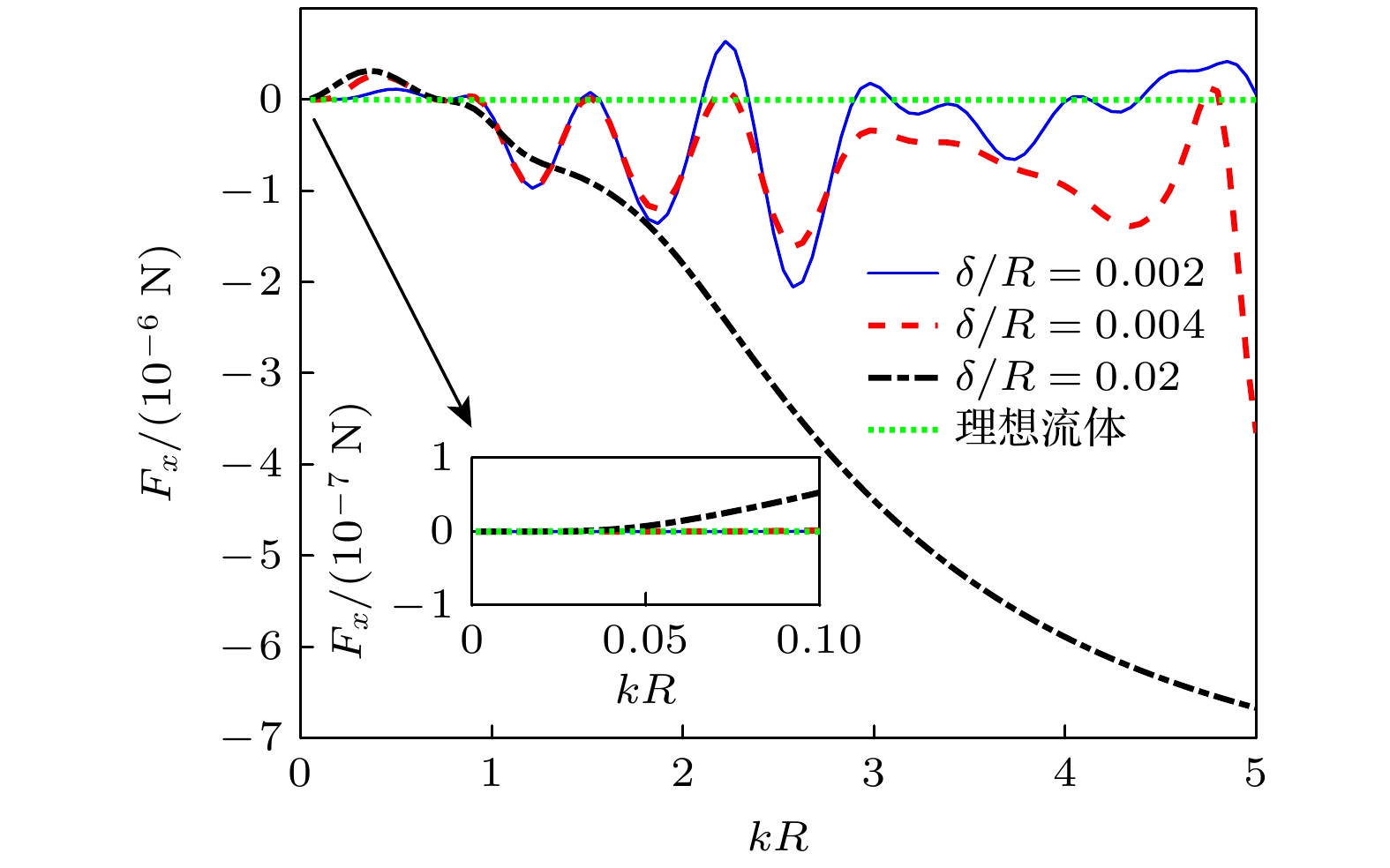
为了研究流体黏度对声辐射力的影响情况, 考虑半径$R = 0.5 {\text{ mm}}$的PE小球, 自由放置于距离刚性边界(${R_{\text{s}}} = 1$)距离$d = 4 R$的流体中, 不同${\delta {/ } R}$(边界层厚度-粒子半径比)以及理想流体情况下的声辐射力变化, 如图2所示.

由图2可以看出, 随着${\delta {/ } R}$的增大, 声辐射力先增大后减小, ${\delta {/ } R}$较小时, 声辐射力曲线的波峰和波谷较多. 因为, 随着${\delta {/ } R}$增大, 边界层越来越厚, 对声波的耗散和衰减就越大, 相应的共振峰被拓宽. 同时, 对比黏性流体和理想流体两种情况, 可以发现, 当$kR \ll {1}$时, 流体黏性影响较小, 黏性效应几乎可以忽略; 但$kR$较大时, 粒子处于黏性流体中所受声辐射力的幅值远大于其位于理想流体的情况, 流体黏性对声辐射力的影响很大, 不可忽略. 为了更加简单地显示两种情况的对比结果, 表3中给出了$kR$为1.0×10^–4, 1.0×10^–2, 1.0×10^–1, 1.0, 5.0时声辐射力的值. 从表3可以发现, $kR$=1.0×10^–4, 1.0×10^–2时, 流体黏性对声辐射力的影响可以忽略; 但对于$kR$ = 1.0×10^–1, 1.0, 5.0时, 流体黏性的影响使得声辐射力提高几个数量级.

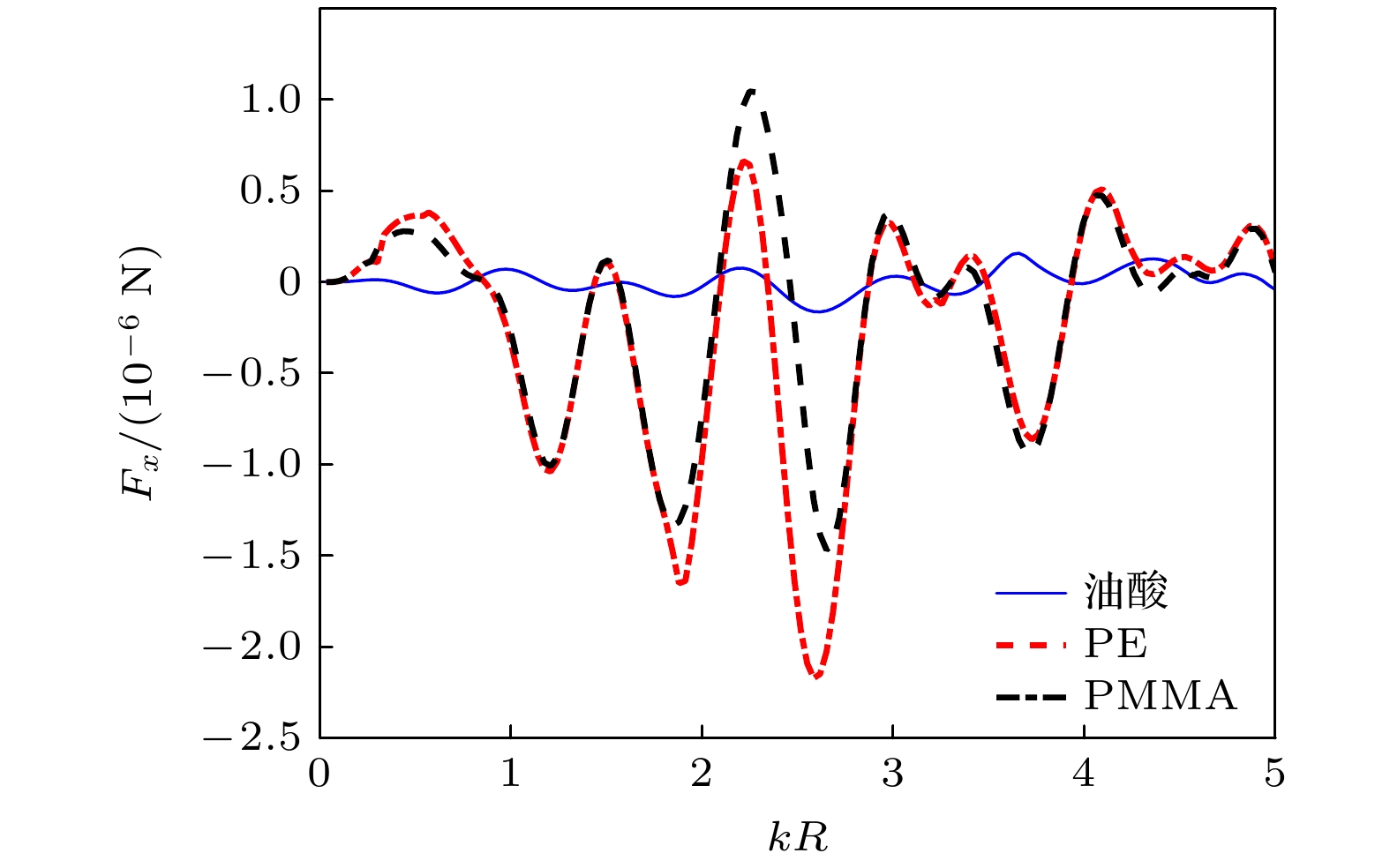
粒子的材料也是影响声辐射力的一个重要因素. 为了分析粒子材料的影响, 本次数值仿真中还选用了弹性材料聚甲基丙烯酸甲酯(PMMA)和液体材料油酸. 选取参数$d = 4 R$, 刚性边界(${R_{\text{s}}} = 1$), 考虑在低黏流体(水)中半径$R = 0.5\; {\text{mm}}$的自由球形粒子的声辐射力, 如图3所示. 由图3结果可知, 声辐射力受小球材料的影响较为显著. 弹性材料PE和PMMA的声辐射力总体上大于液体材料油酸小球, 声辐射力的振荡现象也更明显, 有更多的波峰和波谷; PMMA小球的声辐射力振幅总体略大于PE材料. 这是因为声波在弹性材料之间的动量传递大于与液体之间的传递.

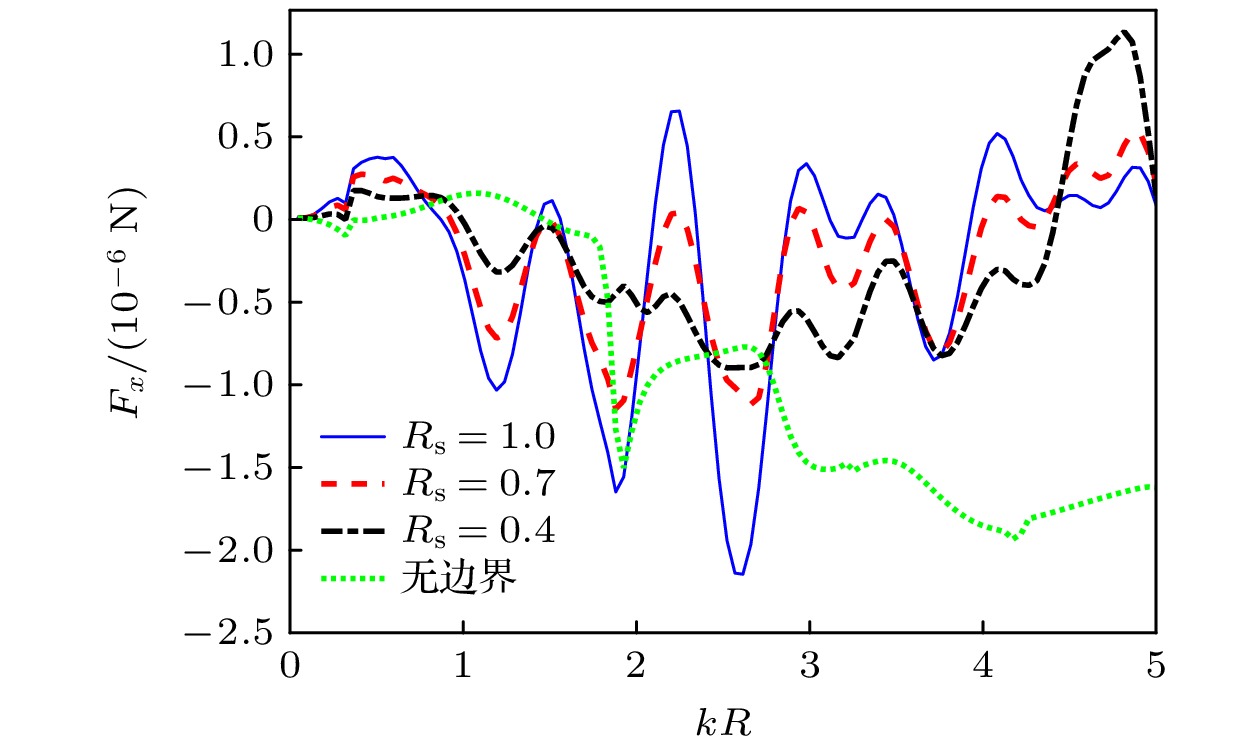
阻抗边界对PE小球的声辐射力影响情况如图4所示. 数值仿真选取参数$d = 4 R$, 粒子半径$R = 0.5 {\text{ mm}}$, 考虑粒子自由放置在低黏流体(水)中. 值得注意的是, 与无界空间相比, 阻抗边界的加入使得声辐射力曲线发生了变化. 除了声辐射力的振荡现象的变化外, 在有边界情况下, 随着边界反射系数的增大, 振幅增大. 而更多振荡的出现则是因为小球与边界反射的波相互作用的结果. 另外, 辐射力函数曲线的共振频率并没有因为反射系数变化而变化.

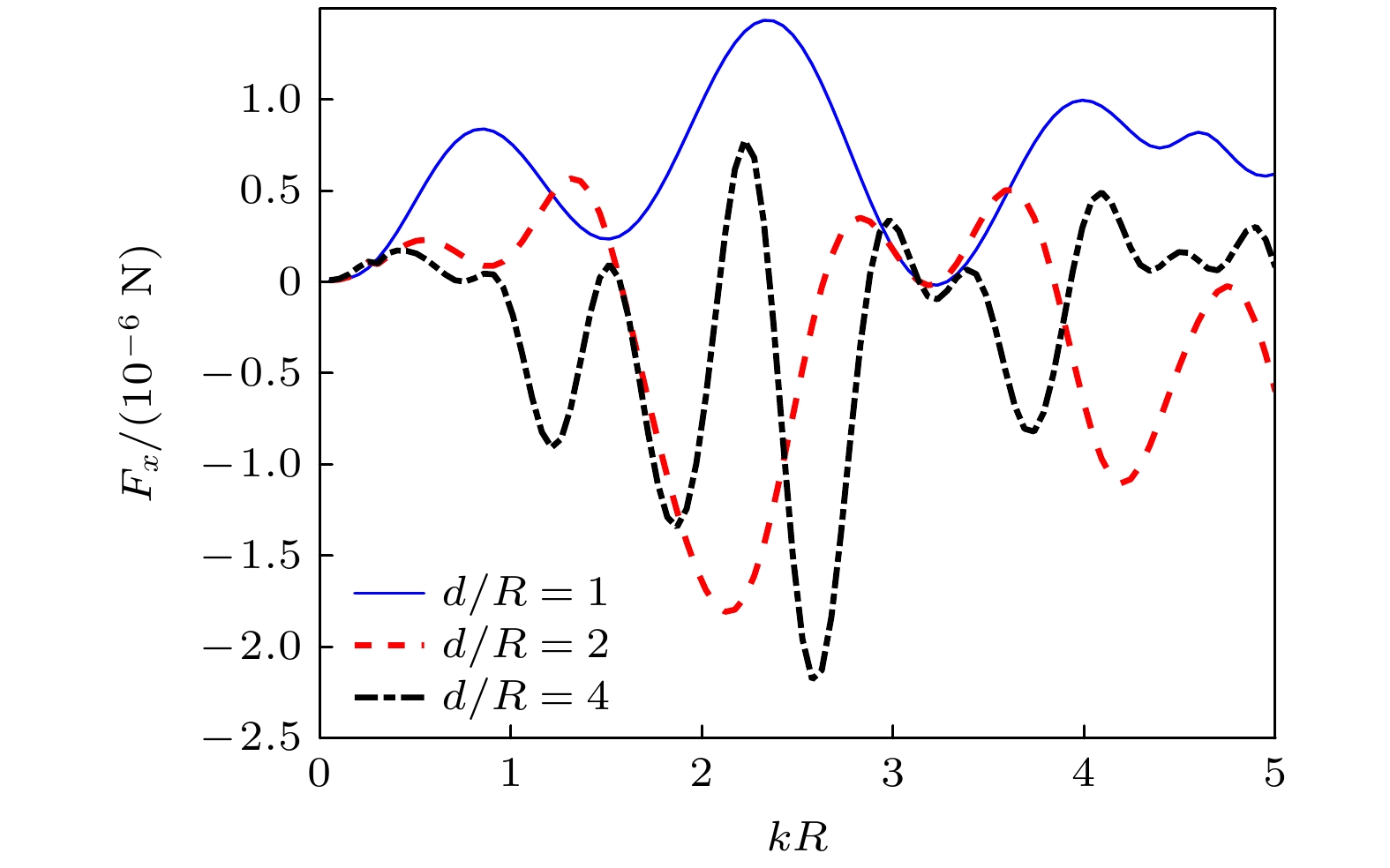
边界附近的小球所处的位置也是不可忽视的影响因素, 放置于不同位置的PE小球所受声辐射力变化如图5所示. 图5为代表小($d = R$)、中($d = 2 R$)、大($d = 4 R$) 3种不同位置的受力情况, 粒子半径$R = 0.5 {\text{ mm}}$, ${R_{\text{s}}} = 1$.

可以看出, 小球位置的不同主要影响声辐射力的振荡现象, 随着位置${d {/ } R}$的增大, 声辐射力的峰值变化更剧烈, 出现较多的波峰波谷. 主要是因为粒子的散射波与边界反射波之间的相互作用导致了振荡现象的产生. 值得一提的是, 这与反射系数的影响不同, 反射系数的改变主要影响声辐射力的振幅大小, 而小球位置的改变主要影响声辐射力周期的变化.

本文给出了平面波垂直入射时, 边界附近黏性流体中自由球形粒子的声辐射力通用公式, 计算过程中将粒子的动力学方程作为声辐射力的修正项. 考虑流体黏度、粒子材料、粒子位置以及边界等因素对声辐射力的影响, 并通过数值仿真直观地展现了不同情况下的声辐射力变化规律. 结果表明, 随着流体黏度的增大, 声辐射力曲线的波峰和波谷减少, 共振峰被拓宽; 声辐射力受小球材料的影响较为显著, 弹性材料比液体材料球形粒子的声辐射力的振荡现象更明显; 随着阻抗边界反射系数的增大, 声辐射力振幅增大, 但没有影响辐射力函数曲线的共振频率; 小球位置的不同主要影响其声辐射力的振荡周期, 随着距边界距离的增大, 声辐射力曲线出现较多的波峰波谷. 本文方法还可以推广到椭球以及其他形状粒子或多个目标粒子存在等, 以便于未来更加精确地对细胞、细菌、药物等进行靶向操控.

${Q_{mn}}$的具体表达式为

其中,

对于偶数q, $(mn00\left| {\sigma 0} \right.) = (\sigma + m + n)/2$; 对于奇数q, 则$(mn00\left| {\sigma 0} \right.) = 0$.