血流速度、方向等血流动力学参数的动态和精确测量具有重要临床意义^[1]. 此外, 血流阻抗指数(resistivity index, RI)作为一种表征动静脉血流搏动性的重要参数, 能够反映局部血管的血流阻力, 从而可作为间接评估血管病变的重要指标^[2]. 近年来的研究表明, 超快超声多普勒成像在脑血管疾病诊断以及脑功能监测中具有重要发展前景^[1,2]. 目前, 临床脑血管成像的主要技术仍是核磁共振和X射线计算机断层, 但它们在便捷性和实时性方面存在一定的局限性^[3,4]. 相比之下, 超声多普勒技术因其便携、低成本、非侵入性以及快速成像的优势, 现已成为临床血流动力学测量的重要手段^[5]; 此外, 其在评估血流速度、方向、血容量、阻抗指数等多参数评价方面, 还有重要发展潜力^[6].

多普勒效应无法检测垂直于声波传播方向的运动, 因而传统超声彩色多普勒只能实现轴向 速度分量测量^[7]. 矢量多普勒成像技术改进了传统的彩色多普勒成像, 通过获取真实血流速度在不同角度的投影信息, 可求解血流速度矢量^[8]. 横向 振荡(transverse oscillation)和散斑追踪(speckle tracking)方法也是两种常见的速度矢量化成像技术. 横向振荡对接收到的信号进行横向调制, 以估计横向和轴向运动^[9], 散斑追踪则基于散射强度分布的移动估计速度场^[10]. 相比之下, 矢量多普勒技术计算复杂度更低, 在实时成像方面具有优势.

1969年, Fahrbach^[11]利用两个固定90°夹角的超声探头, 计算了声波交叉处仿体的矢量化速度. 1974年, Peronneau等^[12]将该方法扩展到任意夹角, 但仍局限于固定位置的测量. 1982年, Wang与Yao^[13]设计了双波束超声矢量多普勒测量系统, 使得声束交叉区域与血管位置无关, 因此传感器无需根据不同深度的血管进行机械调整, 扩大了测量视野. 2009年, Tsang等^[14]提出了一种基于最小二乘(least squares, LS)的矢量速度估计方法, 该方法通过合成孔径技术增强测量角度多样性, 进而采用多个发射点源和多个接收孔径的模式, 实现了矢量速度估计.

近年来, 基于平面波发射的超快超声成像技术, 显著地克服了传统超声成像的帧率限制, 可突破万帧每秒^[15–17]. 基于奇异值分解的杂波滤除方法显著提升了超快超声多普勒对小血流检测的灵敏度^[18–22]. 2016年, Yiu与Yu^[23]通过发射多角度倾斜平面波, 给出了在宽视场上多角度多普勒速度投影的准确测量, 随后利用最小二乘法估计了体外血流仿体的速度矢量. 2022年, Wang等^[24]将多个角度平面波相干复合为两个交叉波束, 有效地提升了速度估算的准确度, 并在颈动脉仿体实验中进行了验证. 2023年, Yan等^[25]提出了超快矢量多普勒(ultrafast vector Doppler, UVD)技术, 将超快超声成像技术和多角度多普勒估计相结合, 显著提升了血流成像灵敏度, 为高时空分辨率下小血管的矢量化成像提供了可能, 并率先实现了小动物和人脑小血管网络的血流矢量速度测量. 虽然, 矢量多普勒技术近年来取得了显著进展, 但是在低信噪比(signal-to-noise ratio, SNR)条件下, 针对小血管的动态矢量血流测量仍面临技术挑战. 矢量多普勒需要保留各角度的回波信息用以计算速度矢量, 因此无法进行多角度相干复合, 其速度测量对噪声较为敏感. 特别在SNR和对比度较低的大脑深部区域, 易产生异常值估计^[25]. 在线性最小二乘法中, 异常值的残差将会对总误差有较大的贡献, 从而显著影响小血管速度矢量的估计准确性.

为了克服上述挑战, 本文提出了基于超快脉冲编码的矢量多普勒(pulse coded UVD, PC-UVD)脑血流速度动态测量方法. 实现方式是利用哈达玛(Hadamard)矩阵对每个发射事件中包含的多个连续的平面波进行脉冲极性编码和回波解码, 从而显著增强各角度下的速度投影估计准确度. 随后, 采用加权最小二乘(weighted least squares, WLS)法求解出速度矢量. 其中, WLS法通过为每个投影角度分配权重, 自适应降低噪声对速度估计的影响, 特别是通过残差迭代优化, 根据速度估计的误差动态调整权重. 具体地, 残差大的投影角度其权重逐渐减小, 从而显著提高低信噪比条件下速度矢量估计的准确性. 本文设计了一种包含多个螺旋环的流动仿真模型, 通过仿真实验分析了所提出的PC-UVD成像方法的可行性并量化了其测量误差. 此外, 本文进行了大鼠脑血流在体成像, 对比了提出的PC-UVD方法和现有UVD方法在大脑不同深度区域的速度矢量化估计准确度. 此外, 通过分析脑血流速度在心动周期内的变化特征, 可估计全脑血管网络阻抗指数, 实现小血管的动静脉判别.

基于平面波发射模式中, 每次发射一个单独的平面波脉冲并接收其对应的射频信号回波. 然而, 单个平面波发射获取的速度投影易受噪声干扰, 特别是在信号衰减较强的成像深部区域. 为此, 我们引入了Hadamard脉冲编码技术以增强信号质量^[26].

Hadamard矩阵是一种特殊的正交矩阵, 其中每一行的元素均为+1或–1, 并且行与行之间的点积为零. 对于$n$个发射角度, 使用一个$n \times n$的 Hadamard矩阵对每束平面波进行极性编码. 每次发射事件中发射的一连串脉冲信号极性由矩阵的一行决定. 如图1(a)所示, +1表示脉冲极性不变, –1表示脉冲极性反转. 以$n = 4$为例, Hadamard矩阵为

如图1(b)所示, 在每次发射事件中, 系统以固定的时延间隔${\tau _i}, {\text{ }}i = 1, {\text{ }}2, {\text{ }} \cdots , {\text{ }}n$连续发射$n$束倾斜角度不同、且极性经过Hadamard正交编码的平面波. 本文中相邻脉冲之间时间间隔为1 μs (图1(b)). 脉冲间隔过长会影响成像帧率, 脉冲间隔过短则会因拖尾效应导致信号干扰.

在接收阶段, 换能器接收到$n$个平面波回波的叠加信号. 由于Hadamard编码的正交性, 接收的回波数据可以通过矩阵反演来解码. 具体操作: 将接收到的所有回波信号按编码矩阵的转置矩阵进行线性加权组合, 从而实现各个角度下的回波数据分离, 实现无损解码. 将每次接收的回波信号记为M_i, 接收的$n$次回波信号组合为$ {\boldsymbol{M }}= [ {M_1}, {M_2}, \cdots , {M_n} ] $, 将其与编码矩阵的转置${\boldsymbol{H}}_n^{\text{T}}$相乘, 可解码出各个角度的射频回波信号$ {\bf{RF}} = [ {\mathrm{RF}}_1, {\mathrm{RF}}_2, \cdots , {\mathrm{RF}}_n ] $, 即^[27]

由于${{\boldsymbol{H}}_n} \cdot {\boldsymbol{H}}_n^{\text{T}} = n \cdot {{\boldsymbol{I}}_n}$, ${{\boldsymbol{I}}_n}$为$n$阶单位矩阵, 故解码得到每个独立散射回波的信号强度为非编码情况下得信号强度的$n$倍. 随后, 删除${\mathrm{R}}{{\mathrm{F}}_i}$信号靠前的${P_i}$行, 以在时间上对齐, 消除${\tau _i}$的影响:

其中${f_{\text{s}}}$为回波采样频率.

解码得到各个角度的射频回波信号${\mathrm{R}}{{\mathrm{F}}_{\theta i}}, i = 1, 2, {\text{ }} \cdots {\text{ }}n$后, 对每个角度回波信号分别独立进行延时叠加(delay and sum, DAS)波束合成、正交(in-phase/quadrature, I/Q)解调和基于奇异值分解(singular value decomposition, SVD)的组织杂波滤除, 提取出各个角度下的动态血流信号${S_{\theta i}}$. 随后基于延时自相关法获取各角度下的每个像素点的速度投影${V_{\theta i}}$^[28], 即

其中N_t表示重建一帧血流多普勒图像所需的帧数, ${{\boldsymbol{R}}_{\theta i}}$表示自相关矩阵, $c$表示组织中的声速, PRF表示脉冲发射频率, ${f_0}$表示发射信号中心频率. 随后, 可构建速度矢量与各角度下的速度投影${V_{\theta i}}$的几何关系, 即^[23]

其中$ {V_x} $和$ {V_z} $分别表示速度矢量在平面直角坐标系中在水平和竖直方向上的投影分量. 将(6)式表示为矩阵形式:

该方程组为超定方程组, 无精确解, 常规方法是采用最小二乘法求解方程组. 然而考虑到不同角度下的测量数据可能受到不同程度的噪声影响, 因此我们采用WLS法求解速度矢量:

其中${\boldsymbol{W}}$为对角权重矩阵, 每个对角线元素${w_\theta }_i$对应某个角度下残差的权重. 权重值的大小通过迭代进行优化, 保持所有权重值之和为1, 初始时将${w_\theta }_i$所有权重值都设置为$1/n$, 即

计算各角度下的残差${\mathrm{re}}{{\mathrm{s}}_{\theta i}}$为

然后根据残差大小更新权重值:

其中$\lambda $为正则化系数, 以避免分母为0, 这里设置$\lambda $为0.01. 更新后的权重归一化后继续进行下一轮迭代, 直至收敛, 即当权重的变化小于预设的阈值$ \varepsilon $时停止迭代:

其中$k$为迭代次数. 通过迭代, 最终我们得到每个像素点的水平速度分量${V_x}$和竖直速度分量${V_z}$的估计结果. 经过迭代优化的权重矩阵${\boldsymbol{W}}$则反映了每个角度下测量数据对速度矢量估计的贡献. 随后, 可计算出各像素点位置的总速度大小${V_{{\text{UVD}}}}$和方向${\theta _{{\text{UVD}}}}$:

通过分析矢量速度大小${V_{{\text{UVD}}}}$在心动周期内的搏动性特征, 可以提取血流收缩期峰值速度(peak systolic velocity, PSV)和舒张末期速度(end-diastolic velocity, EDV). 随后, 可计算出各像素位置的RI值^[29]:

仿真中探头参数设置与大鼠实验使用的探头相同, 探头型号为L22-14vX (Vermon, 中心频率18 MHz, 128阵元). 脉冲长度为2个周期, 采样频率为65 MHz, 声速为1540 m/s. 采用8阶Hadamard矩阵进行编解码, 脉冲重复频率为14.4 kHz, 8个倾斜角度(–15°—15°), 对应复合帧率为1.8 kHz, 共采集100个复合帧. 在进行解码之前, 将带限白噪声(–10 dB, 频率为1—22 MHz)添加到模拟信道数据中, 以生成指定的有效血液噪声对比度. 为了减少计算量, 仿真中不包括血管壁和周围组织, 因此没有应用杂波滤除.

为了模拟螺旋血流速度的层流特征, 首先定义了螺旋血管的几何形状. 血管中线为阿基米德螺线, 其极坐标方程如下:

其中$a$是螺旋起始点的半径, $b$控制螺线之间的间距, $\alpha $取值范围为0—${\alpha _{\max }}$. 我们设定$a = 1$ mm, $b = 0.28$ mm, ${\alpha _{\max }} = 4.2\pi $. 血管两侧血管壁的方程分别为

其中$R$为血管半径, 设定为0.6 mm.

为了模拟血流中的散射点, 每平方毫米设置300个散射点. 散射点的强度大小随机(平均值为0, 标准差为1), 散射点速度与其距离血管中线的位置关系为

其中${u_{\mathrm{c}}}$表示最大血流速度, 设置为25 mm/s; $l$表示散射点距离血管中心位置的距离, 其取值范围为($ - R, {\text{ }}R$). 这种流动模式为层流模式, 符合小血管内低速血流的流动特征. 散射点的速度决定了其角度$\alpha $在每一帧中的变化量(推导过程见附录):

设定成像帧率${f_{{\text{frame}}}}$为1000 Hz, 则时间步长$\Delta t$ = 1/1000 s. 为了确保散射点始终在定义的螺旋范围内, 当散射点的角度超过最大角度${\alpha _{\max }} = 4.2\pi $时, 将其循环回到起始位置. 最后, 将极坐标$\left( {r, \alpha } \right)$转换为直角坐标$\left( {{x_{\text{p}}}, {\text{ }}{z_{\text{p}}}} \right)$:

其中${x_{{\text{offset}}}} = 0$ mm和${z_{{\text{offset}}}} = 7$ mm分别表示坐标在水平方向和竖直方向的偏置.

仿真基于Field II (Release 3.30)软件实现, 该 软件可模拟生成真实的超声信号并建立传播模 型^[30,31]. 所有模拟和数据分析均在配备英特尔酷睿i7-12700 K处理器和32 GB内存的工作站上进行, 使用Matlab (R2022a, MathWorks, USA)软件. 单个角度平面波回波仿真耗时约93 s. 对于100个复合帧(每个复合帧由8个倾斜角度平面波回波复合得到)的完整仿真, 总计算时间约21 h.

相关动物实验已通过复旦大学动物实验科学部动物福利与伦理委员会审批(审批号: 202202020Z). 实验选用8周龄, 体重约200 g的雄性SD (Sprague-Dawley)大鼠. 使用2.5%的异氟烷气体对大鼠持续麻醉. 在超声成像前, 在大鼠颅骨顶部打开一个矩形颅窗(bregma +4 mm至–8 mm, 宽度13 mm). 剃除大鼠颅顶毛发, 使用碘伏对皮肤消毒, 随后用手术刀在颅顶切开切口, 用手术剪去除皮肤和骨膜, 暴露出头骨. 使用牙科钻将颅骨磨薄后, 轻轻将头骨取出, 并保留完整硬脑膜. 成像过程中, 使用脑立体定位仪固定大鼠头部, 使用39 ℃恒温加热垫保持大鼠体温, 超声探头固定在颅脑冠状面正上方(bregma –5.6 mm), 探头和鼠脑之间使用医用超声耦合剂耦合. 多通道超声数据发射与采集在自研可编程相控超声实验平台上进行. 实验所使用探头与仿真设置中介绍的相同, 使用8阶Hadamard矩阵对脉冲进行编解码, 脉冲重复频率为14.4 kHz, 8个倾斜角度(–15°—15°), 对应复合帧率为1.8 kHz, 采集时间0.2 s, 共采集360个复合帧, 具体参数设置见表1.

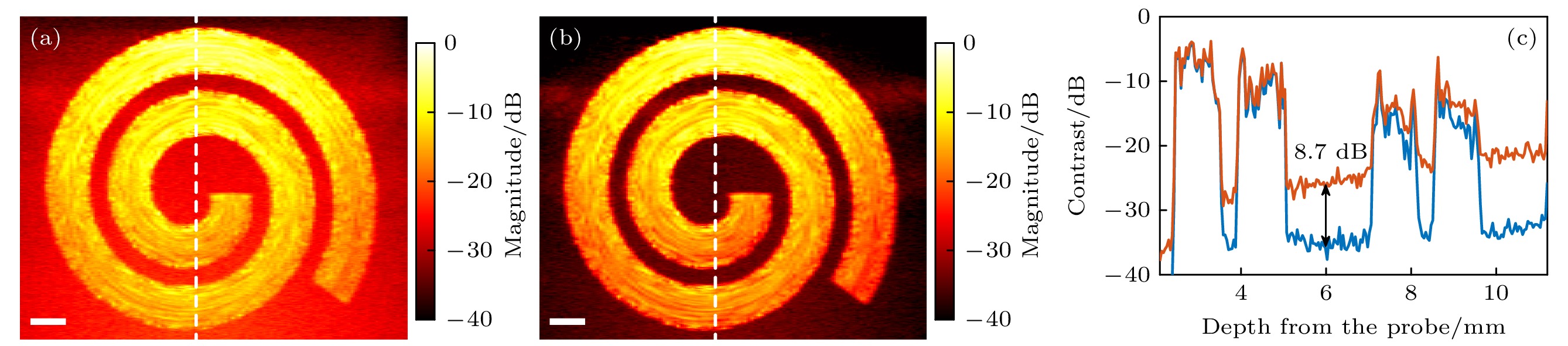
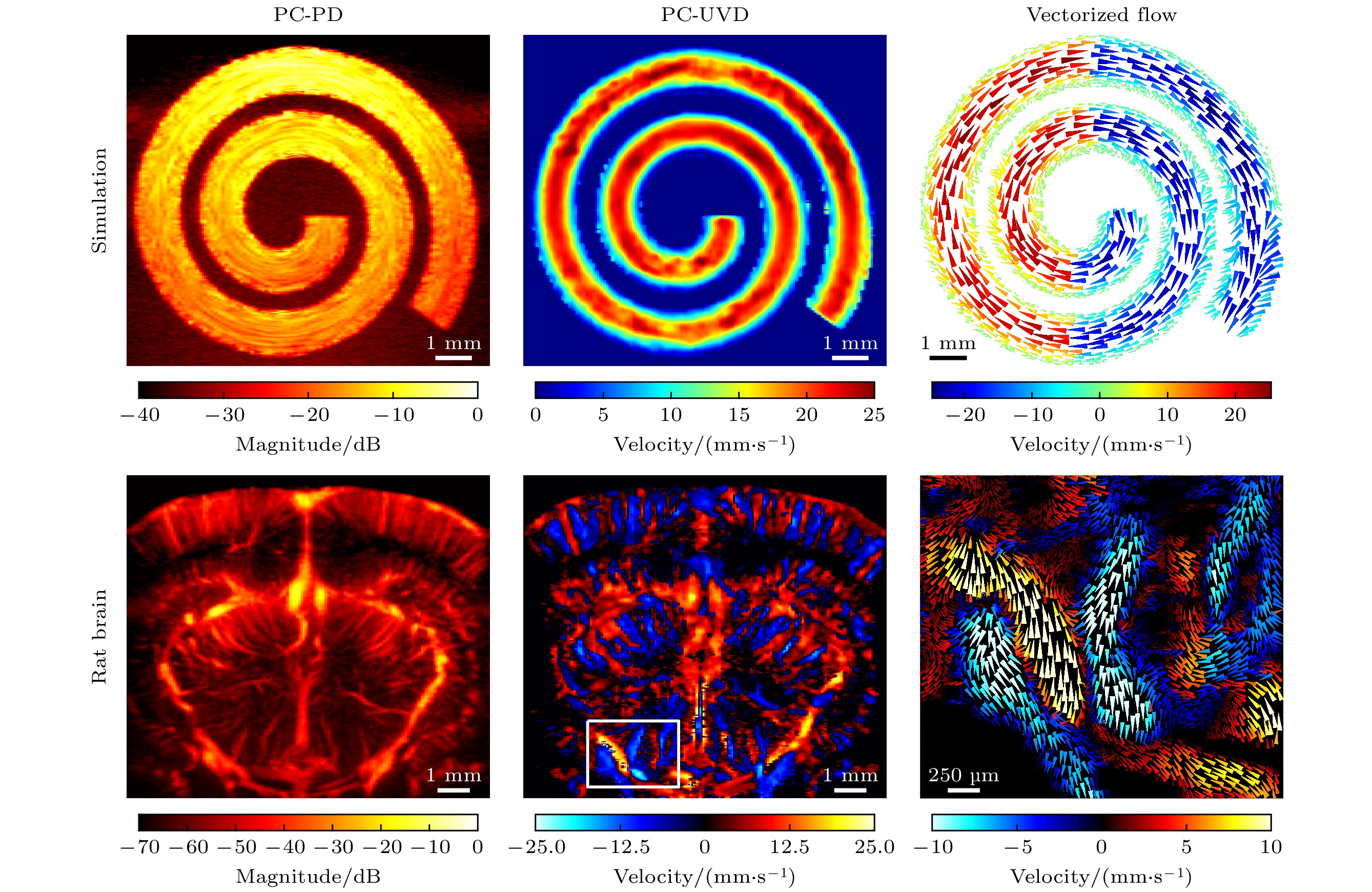
图2展示了基于超快PD和PC-PD的螺旋血流仿真成像结果. 图2(a)中, 血流信号显示出较为明显的衰减现象, 血流噪声对比度逐渐下降, 在成像较深位置, 血管边缘难以有效区分. 通过对比图2(a)与图2(b), 可以清晰地看到PC-PD相较于常规PD模式, 成像质量和SNR得到显著提升. 图2(c)展示了图2(a)和图2(b)中白色虚线位置处, 两种成像模式在不同深度上的SNR定量分析结果. 纵轴表示信号的对比度, 横轴表示成像深度, 橙色曲线代表常规PD模式, 蓝色曲线代表PC-PD模式. 通过对比可见, 在整个成像深度范围(0—11 mm), PC-PD模式的SNR均明显高于PD模式约8.7 dB. 这表明, 基于Hadamard矩阵的脉冲编解码技术有效地抑制了噪声强度.

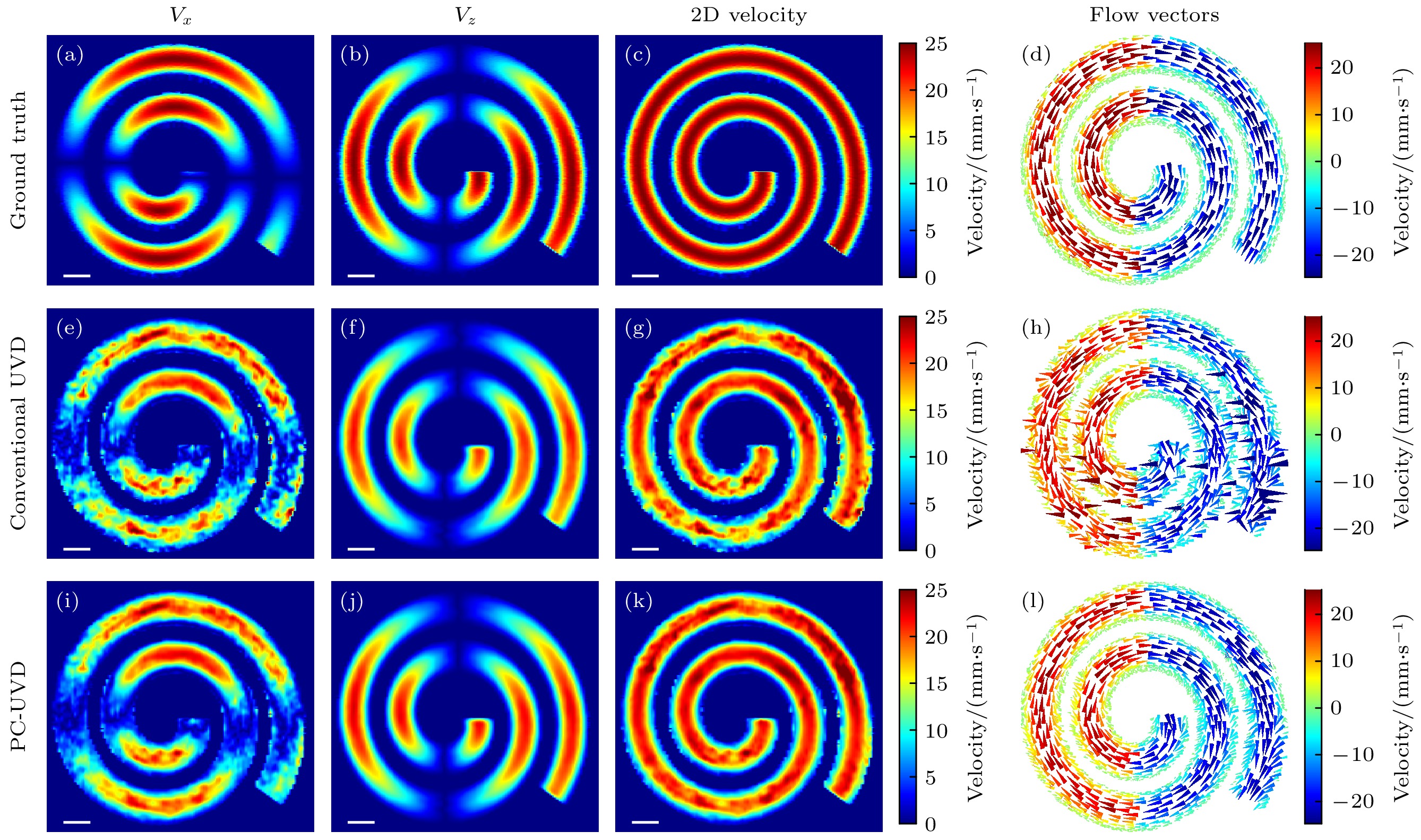
图3展示了螺旋血流的理论速度真值、以及基于常规UVD和提出的PC-UVD方法得到的矢量速度仿真结果. 图3(a)—(d)展示了螺旋血流速度的理论真值. 如图3(c)所示, 理论模型下, 二维速度图准确呈现了血流速度强度分布; 图3(d)中矢量图展示了速度大小和方向的精确分布, 清晰地显示了螺旋流场的特征. 图3(e)—(h)为基于常规UVD方法得到的速度估计结果. 相比理论真值, 常规UVD测量存在较大的误差. 图3(e)中, 水平速度分量V_x显示出明显的噪声干扰和测量误差, 特别是在SNR较差的深部区域. 由于多普勒测量对轴向运动敏感, 故与V_x相比, 竖直速度分量V_z (图3(f))测量结果相对较好, 测量得到速度分布较平滑, 无明显异常值, 然而其峰值估计速度相对理论真值稍低. 二维速度图(图3(g))的准确度也受到较大影响, 速度矢量图(图3(h))基本能够反映出螺旋流动模式, 但受限于深部区域的SNR较低, 可以观察到较多显著的异常测量值. 图3(i)—(l)展示了基于提出的PC-UVD方法获得的仿真结果. 如图3(i)所示, 相比于常规UVD结果相比, 提出的方法在水平方向速度估计更加准确, 特别是在较深区域, 测量误差显著降低, 速度分布更加平滑. V_z (图3(j))和二维速度图(图3(k))与理论真值更加接近. 图3(l)中速度矢量图显示, PC-UVD结果无明显的矢量速度异常测量值, 整体速度分布和方向更加接近理论模型.

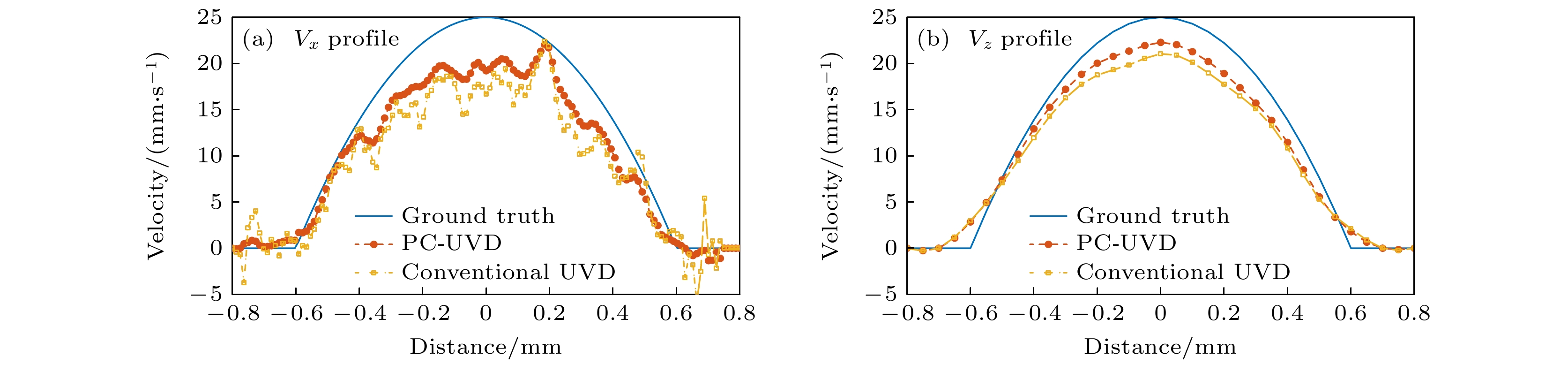
图4展示了所测得血流水平速度和竖直速度大小与距离血管中心距离的分布情况. 为了模拟层流模式, 在仿真设置中, 我们将速度大小设置为按抛物线规律分布, 如图4中蓝线所示, 血管中线速度最高为25 mm/s, 靠近血管壁的速度为0. 由图4(a)中可以看出, 尽管常规UVD和PC-UVD所测得横向血流速度在整个范围内都略低于理论速度, 但后者测得的横向血流速度更接近理论值, 且噪声影响的随机波动得到了较好的抑制. 图4(b)反映出PC-UVD方法对血流速度竖直方向分量的测量准确度也得到相对改善.

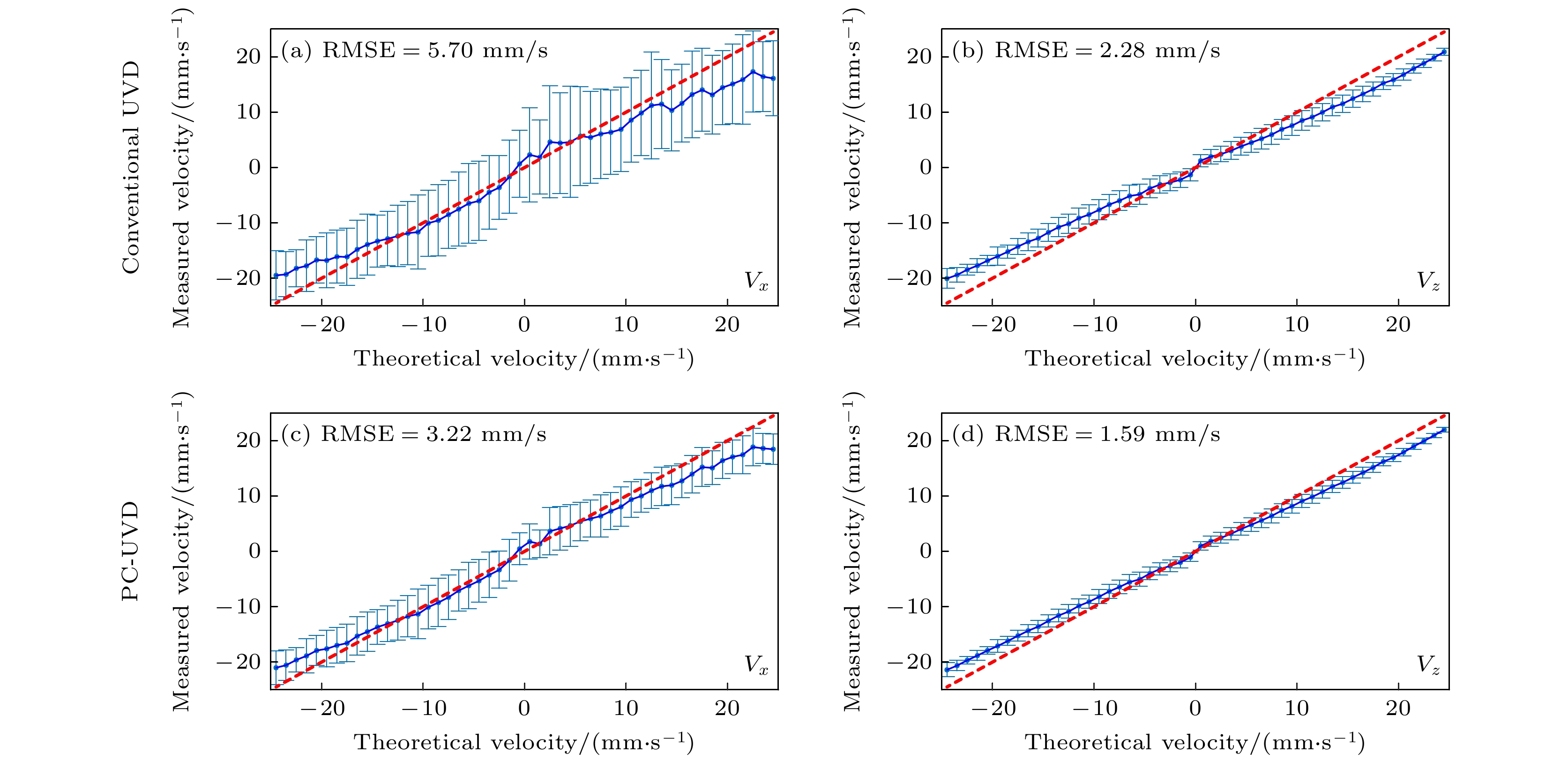
对全局矢量速度估计准确度进行了定量分析, 图5(a), (b)和图5(c), (d)分别是对常规UVD和PC-UVD速度估计误差的分析图. 图5(a), (c)和图5(b) , (d)分别绘制了估计的速度水平方向分量和竖直方向分量与标准值的对比图. 值得注意的是, 速度越大, 估计的偏差越大. 每1 mm/s内的所有测量误差值用来计算一个标准偏差, 并用误差条展示. 每个误差条表示最少100次测量的标准偏差. 图中左上角展示了所有像素位置测量值的均方根误差(root-mean-square error, RMSE). 对于水平方向速度估计, 常规UVD的测量RMSE为5.7 mm/s, PC-UVD的测量RMSE下降为3.22 mm/s, 准确度提高了43.51%. 对于竖直方向速度估计, 常规UVD的测量RMSE为2.28 mm/s, PC-UVD的测量RMSE下降为1.59 mm/s, 准确度提高了30.26%.

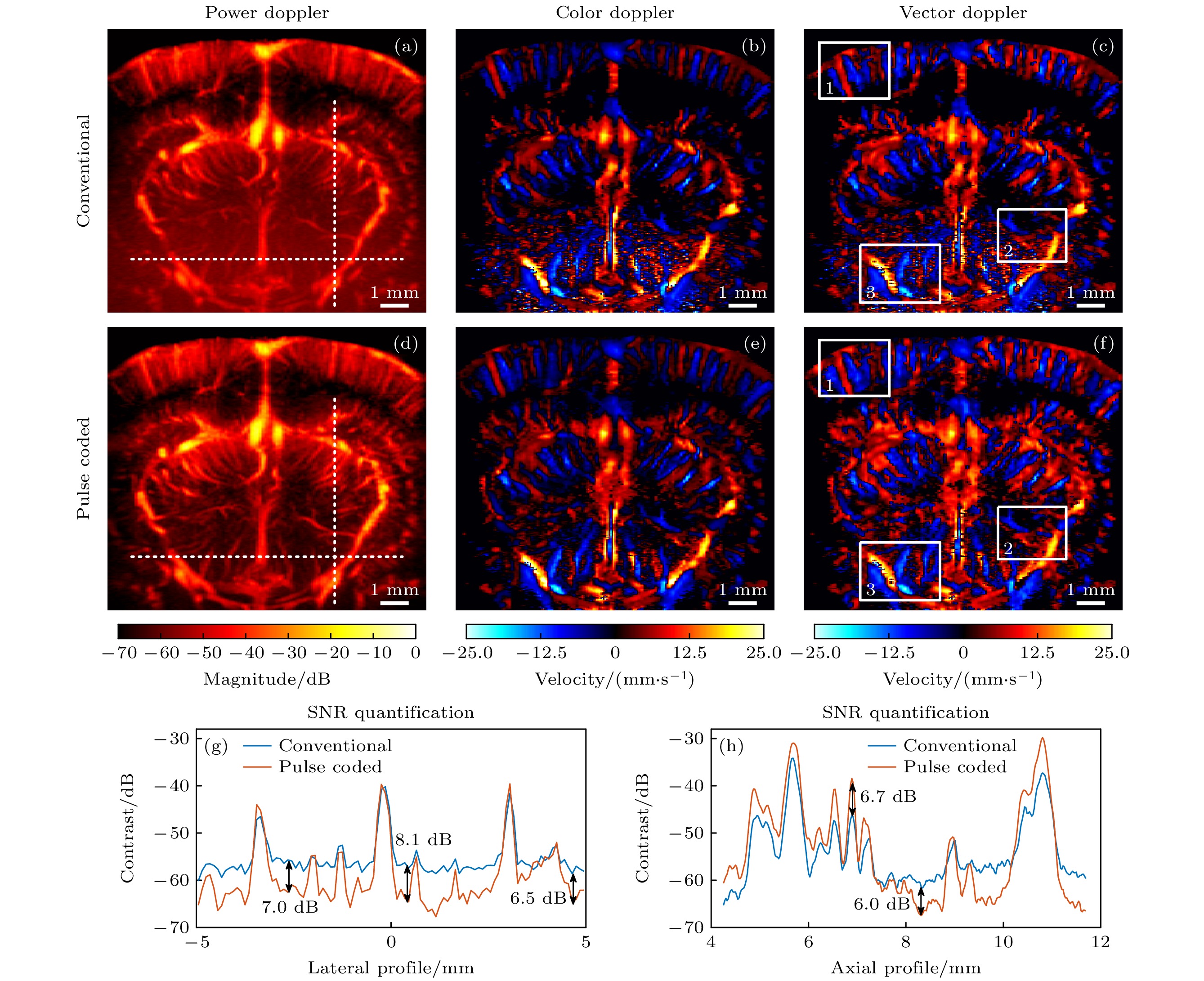
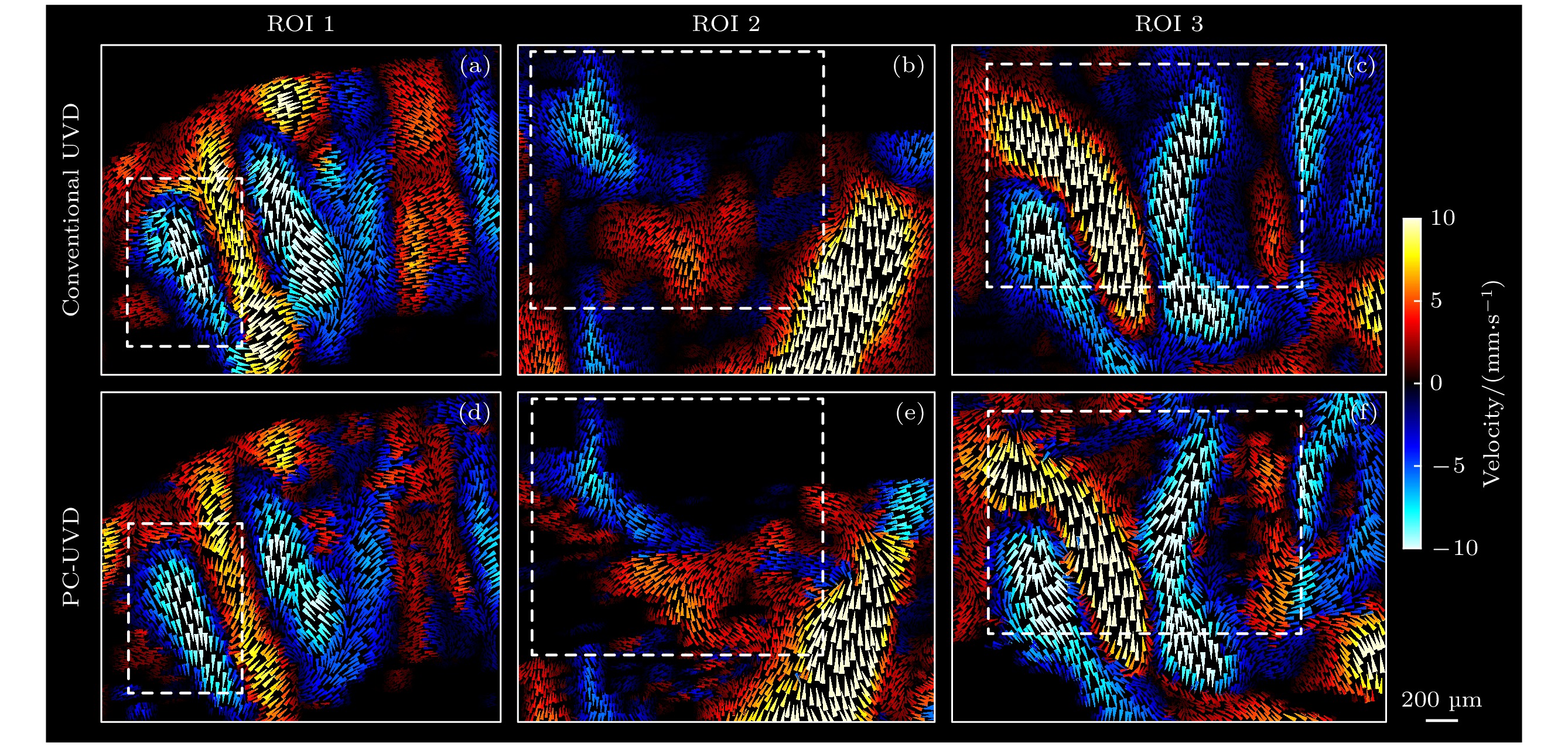
图6为大鼠脑血流超快多普勒冠状切面(bregma –5.6 mm)成像结果. 图6(a)和图6(d)分别为平面波常规发射模式和脉冲编码发射模式的超快功率多普勒血流图. 与图6(a)相比, 图6(d)中尤其是深部区域小血管与背景噪声之间的对比度显著提升, 可检出的小血管数量也有提升. 为了定量分析脉冲编码带来的SNR增强, 图6(g)和图6(h)分别展示了图6(a)和图6(d)中水平虚线和竖直虚线位置的信号强度剖面, 结果显示基于脉冲编码模式的超快多普勒血流成像SNR提升约6—8 dB. 图6(b)和图6(e)分别为平面波常规发射模式和脉冲编码发射模式的彩色多普勒血流图. 与图6(b)相比, 图6(e)中深脑区域的红蓝相间的随机噪声得到明显抑制. 图6(c)和图6(f)分别是常规UVD和PC-UVD速度图. 与彩色多普勒类似, 按照轴向速度分量的上、下方向不同, 将矢量速度值映射到红色和蓝色. 与彩色多普勒只能测得血流轴向速度分量相比, 矢量多普勒可测得更准确的血流速度. 在血流速度矢量图(图6(c)和图6(f))中不同深度上选定3个感兴趣的脑区(白色方框), 进行速度矢量可视化(图7), 用小三角形表示速度矢量, 三角形面积和颜色表示血流速度, 三角形锐角所指方向为血流速度方向. 常规UVD方法(图7(a)—(c))在复杂在体小血管环境中, 仍存在一些测量局限性. 例如, 图7(a)中虚线框内的速度矢量出现明显错误的“撞血管壁”现象, 反映了对靠近血管壁位置的血流速度大小和方向测量不准确; 图7(b)中深脑的成像SNR不足, 小血管出现明显模糊现象, 且有部份血管缺失; 图7(c)中血流矢量的横向分量测量明显错误, 使得估计的血流方向与血管走向不一致. 以上局限性在PC-UVD测量结果(图7(d)—(f))中得到明显的改善.

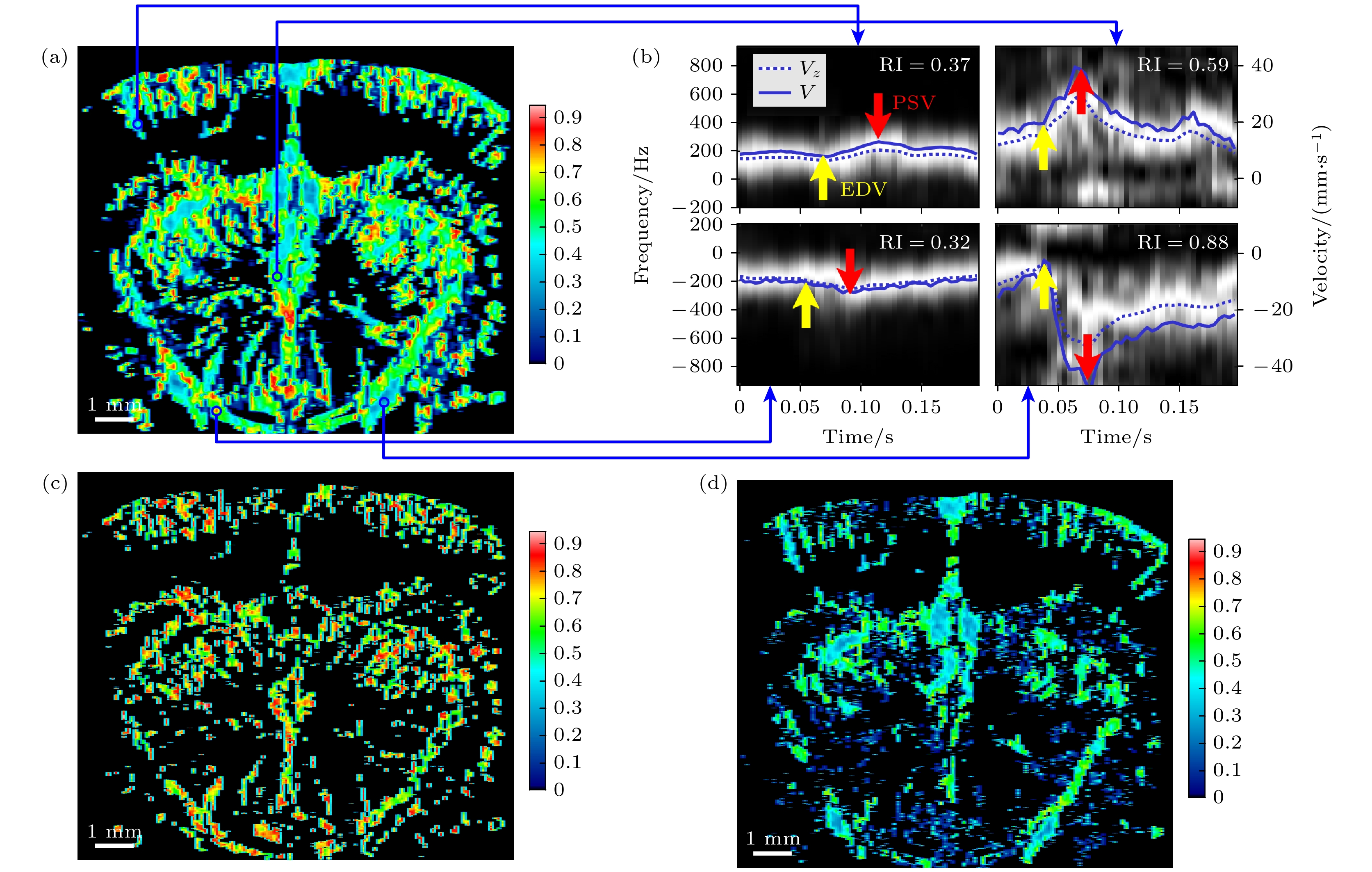
通过分析基于PC-UVD测量到的大鼠脑血流矢量速度在一个心动周期内的变化, 提取了全脑所有像素的血流搏动特征, 并进一步计算了血流RI值. 如图8(a)所示, 基于超快矢量多普勒技术获得的血流阻抗图显示了不同血管的RI分布. 图8(b)展示了不同位置的多角度相干复合后的血流多普勒频谱, 提取了每个心动周期中的最大收缩期速度和最小舒张末期速度. 频谱图中的虚线表示相干复合后多普勒频谱的中心频率, 对应超快彩色多普勒的动态速度估计, 实线表示测量的矢量多普勒动态速度, 二者具有同步的波动特征, 证明超快矢量多普勒速度动态估计的准确性. 图8(b)中红色箭头给出了血流在收缩期的峰值速度, 而黄色箭头则给出了舒张末期的最低速度. 左上和左下图分别显示了向上流动和向下流动的小静脉的动态速度特征, 右上和右下图则展示了向上流动和向下流动的小动脉的动态速度特征. 图8(c)和图8(d)分别展示了小动脉和小静脉血流网络图. 小动脉阻抗值一般介于0.55—0.9之间, 而小静脉阻抗值一般低于0.5^[29].

本文提出了一种超快脉冲编码矢量多普勒血流速度和阻抗成像方法, 该方法可在几乎不影响成像帧频和成像分辨率的情况下, 通过虚拟提高发射信号的幅度, 从而显著地提升射频回波数据的SNR, 并降低各角度下速度估计的异常值; 通过采用加权最小二乘估计和残差迭代优化的方法, 自适应降低异常值的权重, 增强了对噪声的适应性, 提升了速度矢量估计的精度. 本文通过螺旋血流仿真实验和大鼠脑小血管网络在体成像实验, 验证了PC-UVD方法对小血流速度动态估计的有效性, 尤其在信号衰减严重、SNR较低的深部区域, 相比常规的UVD方法表现出明显的优势. 以下讨论聚焦于PC-UVD方法的优势, 局限性及其应用潜力.

为了满足矢量多普勒测量对高SNR的需求, 本文实现了一种基于n个倾斜平面波级联发射的传输序列, 并进行了Hadamard幅度编码. 每次接收的回波信号均包含各个倾斜平面波的散射回波, 基于Hadamard矩阵的正交性, 通过对n次接收的回波信号进行简单加权复合, 即可解码得到各角度的回波信号. 此外, 解码后的信号强度相较于单次发射采集的回波信号增强了n倍, 等效于虚拟地将探头发射电压放大至$ \sqrt n $倍, 理论上可提升SNR达$20 \cdot \log (\sqrt n ) $dB^[32]. 本文仿真和在体实验中均采用n = 8, 因此理论SNR可增强9.03 dB, 仿真实验中测得SNR增益约8.7 dB, 与理论值接近. 在大鼠在体实验中, 测得SNR增益为6—8 dB, 也与理论值相符. Hadamard矩阵的阶数n可以取2或者是4的倍数, 即n = 2, 4, 8, 12, 16, 20, 24, ···等. 尽管理论上n越大, SNR增益越显著, 但成像帧率和时间分辨率限制决定了n值不宜过大. 成像帧率方面, 因为n不仅等于一次发射事件的脉冲个数, 也等于倾斜平面波的角度数, 随着n增大, 角度数相应增多, 最大复合成像帧率将会反比下降. 然而, 小血流成像要求高帧率以满足高灵敏度和避免频谱混叠, 因此n的取值不能过大. 成像分辨率方面, Hadamard无损解码的前提是n个发射和采集事件期间被测物体保持准静止, 然而血流速度是动态变化的, 尤其是在测量血流阻抗时, n取值过大可能带来较大的速度估计误差.

基于多脉冲编码激励的成像方法在临床实践中还面临安全性挑战. 超声检测的主要安全指标包括机械指数、热指数、时间平均峰值强度和脉冲平均峰值强度. 尽管直接增大发射电压能提高SNR, 但会同时增加所有安全指标. 相比之下, 多脉冲编码发射在不改变机械指数和脉冲平均峰值强度的前提下, 虚拟提高了发射电压, 从而提升了安全性. 然而, 由于单位时间内发射的脉冲数增多, 热指数和时间平均峰值强度依然会有所上升. 因此, 临床应用时需合理设置信号发射帧率以满足安全性要求.

超快超声相较于传统聚焦扫描模式, 显著地提升了成像帧率, 但在高速血流成像中, 仍需克服频率混叠问题以确保血流速度估计的准确性. 近年来, 研究者们针对克服频谱混叠问题提出了多种解决方案. 2016年, Posada等^[33]提出了一种基于交错脉冲重复频率的抗混叠方法, 利用两个不同的成像频率, 获取两个具有不同混叠倍数的多普勒速度值, 进而求解出无混叠的多普勒速度. 近似地, 2021年, Poree等^[34]提出了一种双波长抗混叠方法, 通过不同波长组合求解不同混叠倍数的多普勒速度. 2022年, Ecarlat等^[35]使用宽频带的啁啾波代替正弦脉冲波, 进一步改进了双波长法. 此外, 近年来深度学习方法也被引入, 有效地克服了彩色多普勒^[36]和矢量多普勒^[37]成像中的频谱混叠问题.

与彩色多普勒只能测量血流速度的单一分量(声波传播方向)不同, 本文研究的二维矢量多普勒方法可以获取血流速度在平面内的分量, 适用于血管走向与线阵探头平行的情况, 例如本文中的脑冠状切面. 然而, 对于复杂的小血管网络, 如肿瘤周围的血管流速测量, 未来需要进一步开发三维超快矢量多普勒成像方法. 目前, 研究人员已经实现了基于二维面阵^[32]和行列寻址^[38]阵列的三维超快功率和彩色多普勒成像方法, 因此, 在此基础上继续开发三维超快矢量多普勒成像(3D-UVD)方法具有可行性和研究价值.

本文提出了一种基于Hadamard多脉冲编码发射的超快超声矢量多普勒血流速度和阻抗测量方法. 通过螺旋血流仿真实验验证, 所提出的方法能够显著地提升血流成像的SNR和血流速度测量的准确性. 相较于常规的UVD方法, 该方法在血流成像中SNR提高了8.7 dB, 速度测量误差降低了30%以上, 同时有效地减少了由于SNR不足引起的速度异常估计. 大鼠脑血流在体实验证明了提出的PC-UVD方法具有大成像视野, 高SNR和高时间、空间分辨率的优势, 可以有效地测量全脑血流在单个心动周期内的波动特征, 并生成血流阻抗指数图, 对于脑小动静脉区分以及脑血管疾病的早期诊断和评估具有一定的临床价值.

在极坐标系中, 曲线的弧长公式为

其中$r(\alpha )$是半径随角度变化的函数. 对于任一粒子的螺旋轨迹:

其中$a$是螺旋起始点的半径; $b$控制螺线之间的间距; $l$表示散射点距离血管中心位置的距离. 结合(A1)式和(A2)式, 可得到:

弧长$s$和速度$u$的微分关系为

将(A3)式代入(A4)式, 可得到: