首页
登录
注册
下载:
-
颗粒体系[1–3]是大量离散颗粒组成的散粒体系统, 颗粒与颗粒之间通过非连续、非均匀的排布形成了复杂的接触网络, 具有介于连续和非连续介质之间的复杂特性. 当受到外界作用力时, 颗粒间接触力以接触点为载体逐级传递、相互影响, 具有牵一发而动全身的效应. 三维颗粒体系表现的宏观力学性能由颗粒间微观力学行为决定, 因此, 计算并研究颗粒间接触力作为探究颗粒体系的力学响应规律的基础, 具有重要意义.
颗粒体系内部接触力实验研究主要分为接触式检测法和非接触式检测法. 接触式检测法如高精度电子天平秤重法[4]、显色灵敏复写纸压痕方法[5]等, 借助工具介入内部检测颗粒体系中某位置的接触力分布, 对颗粒体系造成一定干扰, 影响检测结果. 随着数据采集技术、激光技术和图像处理技术等快速发展, 非接触式检测法应运而生, 如光弹法[6]、荧光共聚焦显微镜法[7]和磁共振弹性成像法[8], 通过确定颗粒的几何位置分析体系的结构特征, 从而得到三维颗粒体系中接触力分布信息. 2005年, Majmudar和Behringer[9]利用光弹法进行了一系列二维颗粒加载实验; 2009年, Sanfratello等[10]将磁共振弹性成像法应用于颗粒体系研究, 实现了三维空间中颗粒结构可视化; 2016年, 陈凡秀等[11]基于2D-DIC对集中力作用下颗粒体系动力学规律进行了探究; 2022年, Kondo等[12]基于数字图像处理, 对颗粒体系进行了桩模型贯入实验, 分析了实验过程中颗粒的荷载传递和位移变化情况; 2023年, 王潇等[13]利用显微CT (micro-CT)开展三维颗粒体系原位加载实验, 描述了三维颗粒体系中颗粒间微观力学行为. 以上研究对颗粒体系力学规律、接触力分布和演化进行了统计与分析, 并未得出具体接触力数值, 颗粒间接触力计算与研究仍是颗粒物质力学领域的重点和难点.
颗粒接触模型是计算颗粒间接触力的理论基础, 相关研究与发展对颗粒体系微细观角度力学行为探究具有先导意义. 颗粒接触模型研究与发展已有百余年历史, 逐渐形成了适用于不同接触条件和场合的接触理论模型. 1881年, Hertz[14]研究了无黏着的小变形球面接触, 解决了小变形球接触计算模型; 1971年, Johnson等[15]研究了基于Hertz模型的小变形球接触黏着问题, 即JKR黏着模型; 1975年, Derjaguin等[16]提出等效法向载荷是法向载荷和附着力之和, 即DMT黏着模型; 1991年, Tatara等[17,18]提出了具有非线性杨氏系数和接触面径向膨胀的橡胶大变形弹性球接触的理论模型; 2008年, 何思明等[19]以Hertz理论为基础, 提出了一种新的颗粒弹塑性接触理论; 2019年, 运睿德和丁北[20]基于经典的Hertz接触力学理论和现有的分形接触模型提出了一种考虑多尺度接触状 态的新接触模型; 2023年, Wu等[21]提出了一种用于匹配脆性岩石单轴抗压与抗拉强度比值的修正颗粒接触模型. 目前, 已有的颗粒接触模型大多 基于理想化假设, 在应用时可能与实际情况不符. 因此, 在具体应用理论模型计算时有必要结合实验验证.
显微CT (micro-CT)[22–25]是一种利用X射线束穿透被测物体, 通过光电信号变化形成一系列数字图像序列的技术. 该技术多用于物体内部结构无损检测, 近几年逐渐应用于三维颗粒体系的几何特性和受力研究中[26,27]. 显微CT为颗粒体系力学性能研究提供了三维可视化模型, 使提取三维颗粒体系中不易观测和量化的接触信息成为可能, 为探究颗粒微细观层面力学行为研究提供了可行性实验手段.
本文基于micro-CT实验对双弹性颗粒接触模型进行验证并得出接触力理论公式, 开展三维弹性球颗粒原位探针加载实验, 通过系列数字变化获得颗粒体系的三维数字模型, 构建颗粒的接触网络模型, 基于公式计算加载过程中颗粒间接触力. 该研究将指出并描述三维颗粒体系中接触力网络分布与演化情况, 为开展三维颗粒体系的力链[28]识别和演化规律分析工作提供支撑.
-
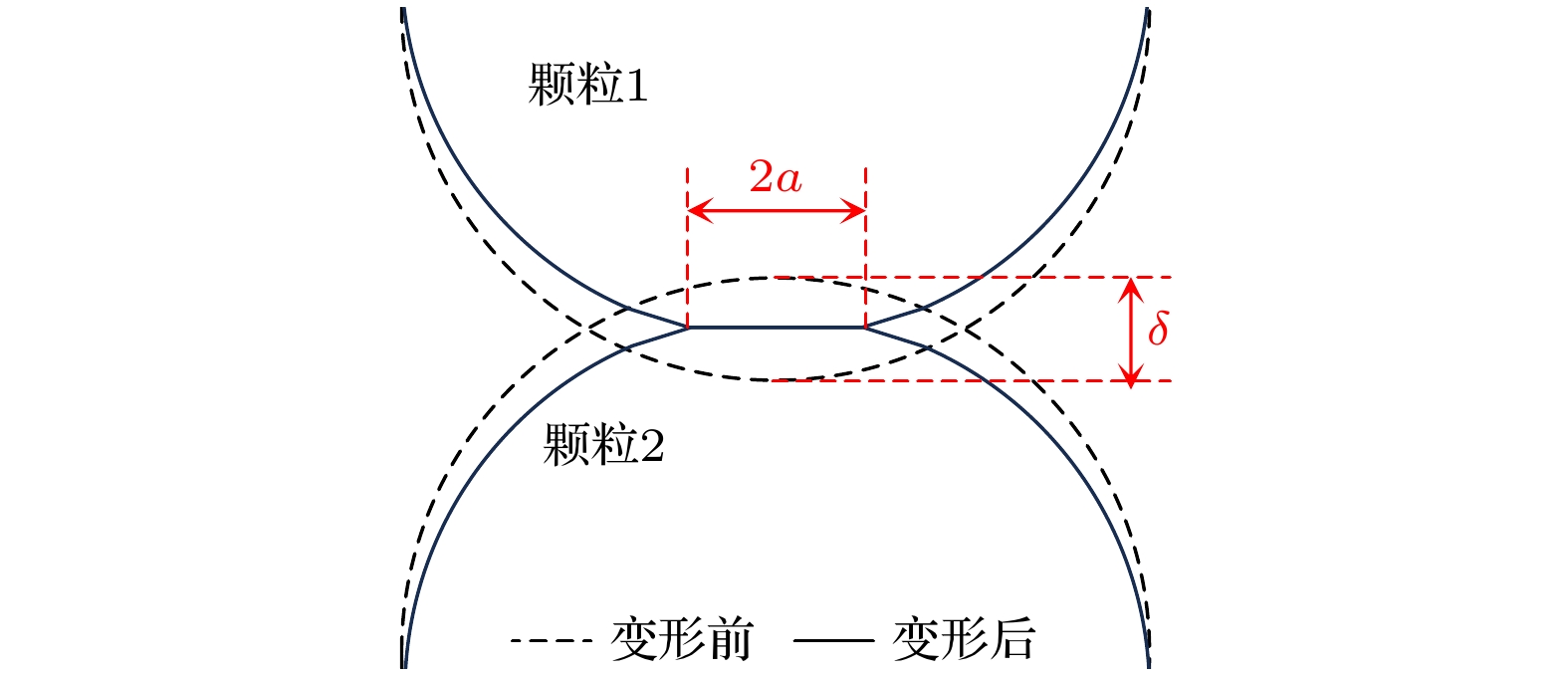
Hertz接触理论为1881年Hertz[14]提出的小变形下各向同性弹性球在非黏连无摩擦情况下的正压力接触理论, 该理论解释了载荷、法向接触力和几何变形的关系. 假设两球形颗粒间存在一处微小圆形接触区域, 该区域与颗粒表面相比面积很小, 在接触面上仅发生弹性变形且接触力垂直于该接触面. 如图1所示, 半径分别为R的两球形颗粒发生弹性接触, 法向接触力和接触面积计算见(1)式和(2)式.
式中, F为颗粒间法向接触力;
$ \delta $ 为颗粒间重叠量; A为颗粒间接触面积; a为接触半径; R为颗粒半径; E和v分别为颗粒弹性模量和泊松比.式中, K为接触面积与法向接触力比例系数, 该系数与颗粒弹性模量、泊松比和直径有关.
-
Tatara大变形接触理论为大变形下均匀非黏性弹性球压缩变形的一般理论[17], 该理论突破 了Hertz接触理论的两个限制, 即接触固体仅发生小变形且为线弹性固体, 考虑了大变形情况下, 基于橡胶变形的门尼定律对应非线性弹性材料的 行为.
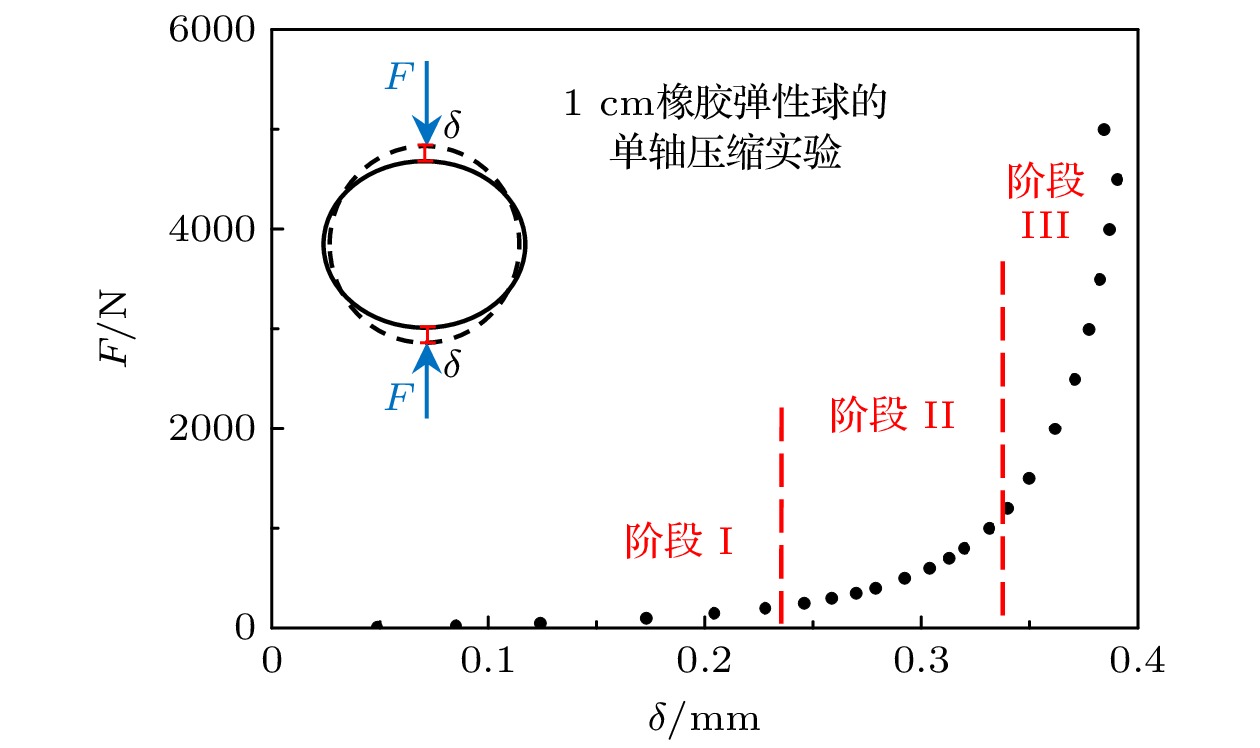
Tatara等[18]于1991年进行了大变形范围内1 cm橡胶弹性球的单轴压缩实验, 在10—5000 N外加荷载下测量了橡胶球的弹性位移和接触半径. 根据Tatara等[18]的实验数据, 得出单球颗粒法向重叠量
$ \delta $ 与接触力F的关系, 见图2.由图2可知, 单球轴向压缩变形可分为三个阶段. 阶段I为小变形接触, 计算结果与Hertz接触理论一致, 即接触力F与法向重叠量
$ \delta $ 的3/2次幂成正比; 阶段II为大变形接触, 接触力F与法向重叠量$ \delta $ 的幂次关系提升到3次方; 阶段II为超大变形接触, 接触力F与法向重叠量$ \delta $ 的幂次关系提升到5次方. Tatara等[18]的颗粒实验以颗粒与平面接触为基础, 只适用于单球颗粒, 通过单球轴向变形量计算法向重叠量. 实际颗粒体系为两球面间的接触, 与Tatara等[18]的颗粒实验不同. -
实验设备采用天津三英精密股份有限公司生产的高分辨率综合扫描分析系统nanoVoxel-2792, CT系统如图3所示, 主要由射线源、载物转台和探测器三者组成, 加载装置为基于该micro-CT设计的原位加载测试系统CT-020. 三者的相对位置由丝杆与步进电机控制, 以调整成像放大倍数. 图像采集过程中, 射线源发出X射线穿过加载装置及内部样品, 探测器接收射线, 完成一次曝光得到的射线投影图像称为二维断层灰度(digital radiography, DR)图像, 连续拍摄样品台旋转过程中的多幅DR图像并重建被测物三维空间结构称为计算机断层扫描(computed tomography)成像. 实验中, micro-CT系统采用最大管电压130 kV, 最大电流100 μA. 探测器阵列为1536 pixel × 1536 pixel, 有效成像视野为130 mm×130 mm, 曝光时间0.5 s, 采集帧率720 frame/s.
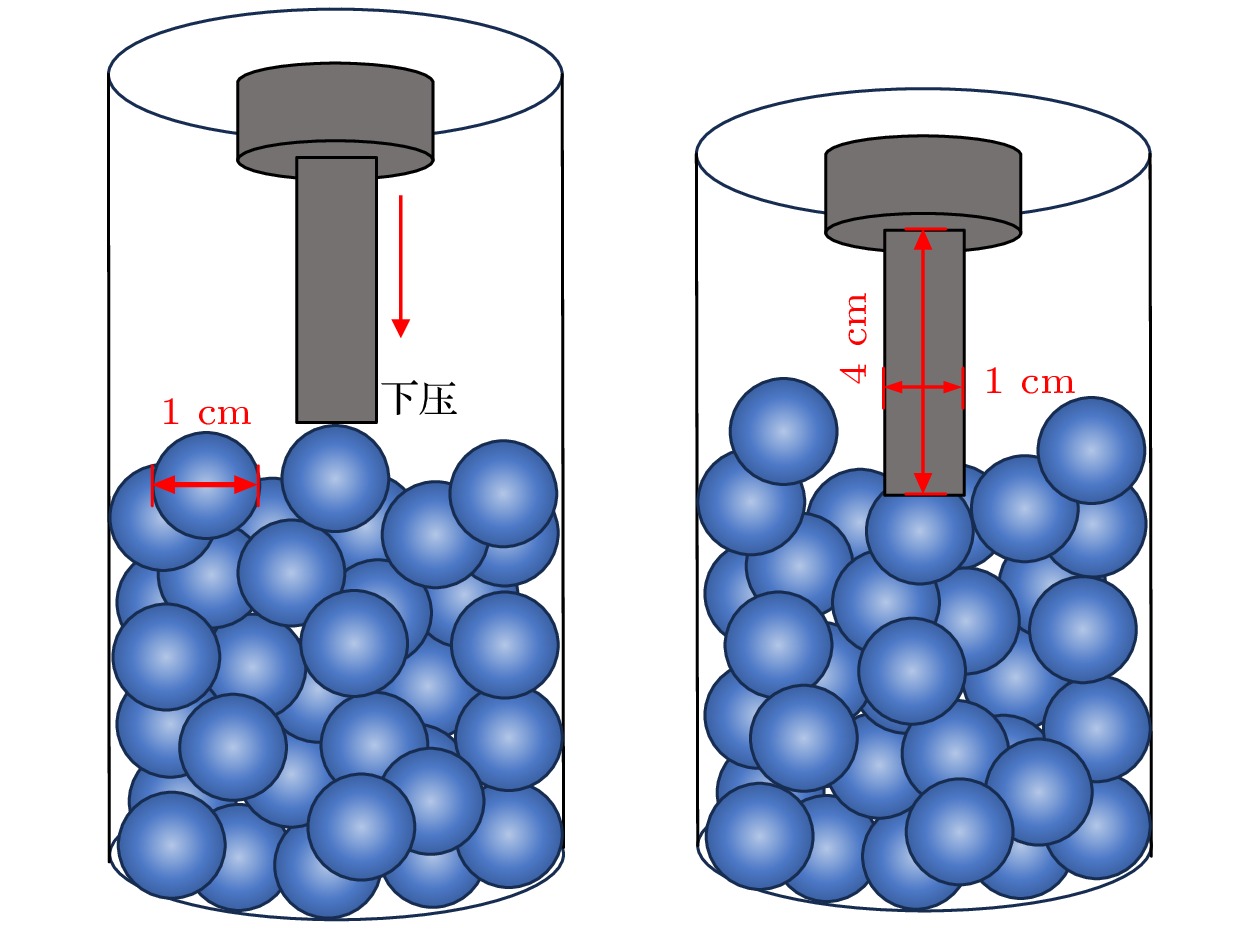
为获取颗粒体系内部接触力传递情况, 确保颗粒能够发生相对自由位移而不被压实, 实验模型采用直径1 cm、高4 cm的圆柱探针加载, 实验对象为90个直径为1 cm的橡胶弹性球颗粒. 实验模型见图4, 原位加载测试系统压头及试样见图5. 实验加载速率为0.5 mm/min, 压头每下压2 mm, 进行一次图像采集.
-
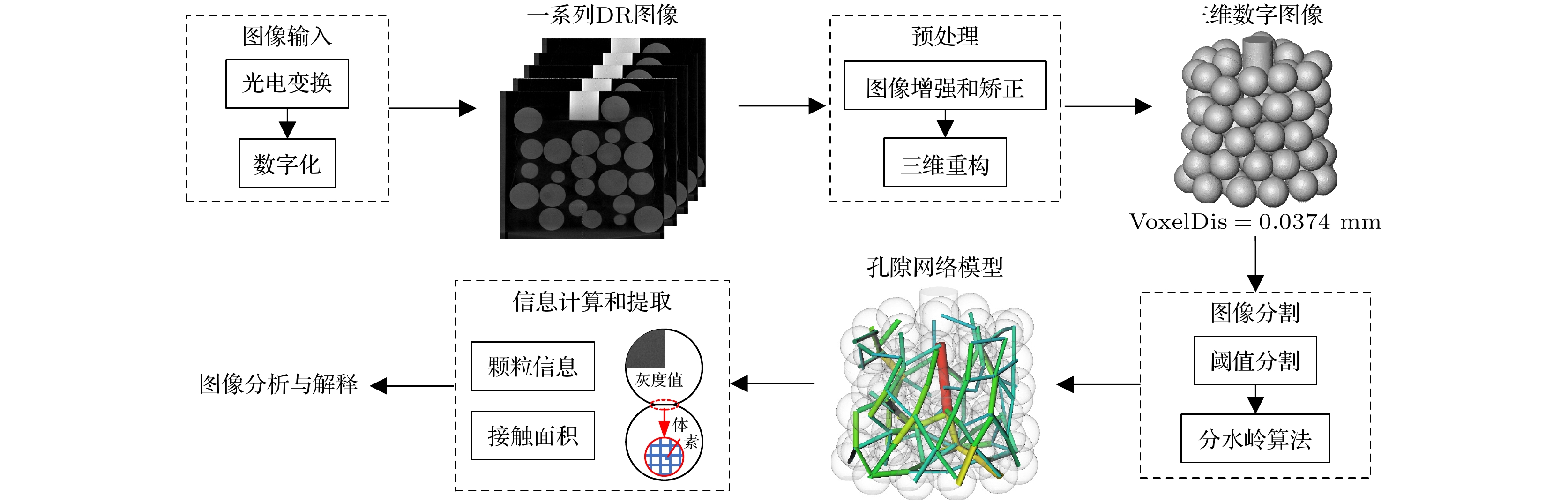
数字图像处理(digital image processing)是通过计算机对原始图像进行降噪、增强、复原、分割、提取信息的方法和技术[29–31]. 本实验中涉及的数字图像处理主要分为图像输入、图像预处理、图像分割和信息计算与提取四个步骤, 具体流程见图6. 1) 图像输入: 将光电信号进行转换, 将图像数字化获得一系列DR二维图像. 2) 图像预处理: 通过图像增强和矫正提高图像质量, 经三维重建(3D reconstruction)将一系列DR图像进行组合、修正, 通过数学运算得到重构的三维数字图像, 体素数量为1500×1500×1500, 体素尺寸VoxelDis为0.0374 mm. 3) 图像分割(image segmentation): 通过阈值分割提取灰度数据, 并基于分水岭算法把梯度图像中所有的像素按照灰度值分类, 完成颗粒数据的分割. 4) 构建孔隙网络模型(pore network model, PNM)[32,33]进行信息计算与提取: 基于PNM计算颗粒信息和接触面积, 用该模型表征颗粒接触网络模型, “孔隙”代表“颗粒”, “孔喉”代表“接触”. 结合体素坐标和灰度值提取颗粒的重心坐标、等效直径、配位数等颗粒信息, 采用分水岭算法分割颗粒单元后, 基于两颗粒单元接触位置体素的重叠量计算颗粒接触面积.
-
通过micro-CT实验对两橡胶颗粒的轴向压缩和扫描, 获取颗粒间接触力和接触面积, 基于Hertz小变形接触理论和Tatara大变形接触理论进行公式拟合, 得到接触面积与接触力的弹性球接触力计算公式.
-
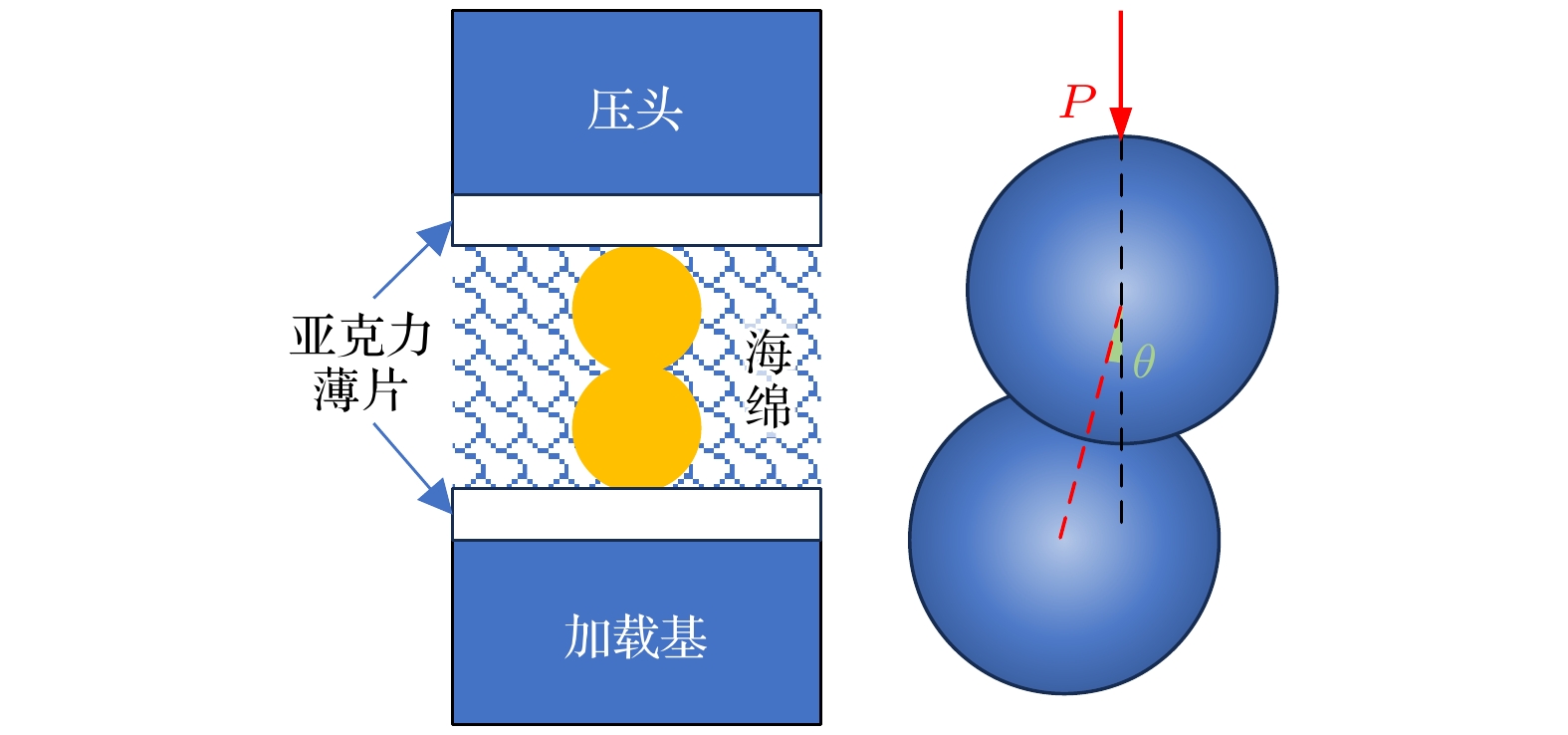
基于Tatara单球轴向压缩实验, 改进实验模型, 进行双球轴向压缩实验, 借助micro-CT获取颗粒接触信息. 对两直径为10 mm的橡胶球颗粒施加荷载P, 两颗粒球心与法向夹角为
$ \theta $ . 为保证在单轴加载过程中两颗粒基本保持轴向, 不发生大位移横向滑动, 两颗粒间受力主要为法向接触力, 颗粒四周包裹海绵以限制颗粒横向位移. 为方便后续颗粒与上下压头的图像分割, 在压头和颗粒之间以透明亚克力薄片隔开. 双弹性颗粒实验模型如图7所示, 原位加载测试系统压头及试样见图8. -
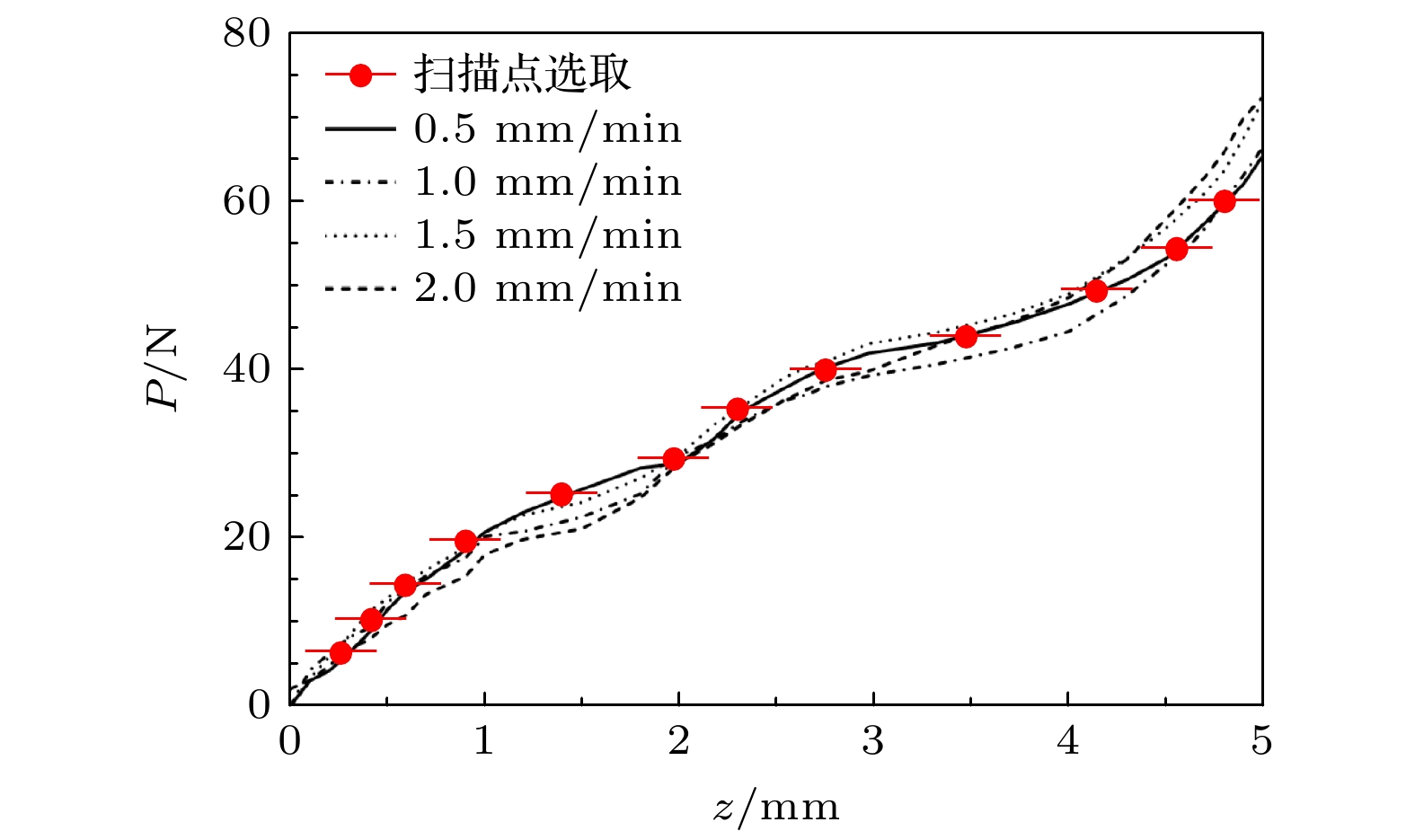
在验证实验正式开始前, 需确定合适的加载速度并预先选取扫描点, 确保扫描数据能够稳定有效地反映加载过程中双颗粒模型的变化. 分别采用0.5, 1.0, 1.5, 2.0 mm/min四种速度对颗粒体系进行持续加载, 由加载结果可知, 速度变化对P影响不大. 为保证扫描过程中, 颗粒状态变化更加均匀和稳定, 扫描加载速度采用0.5 mm/min. 根据P的变化曲线, 等力间隔选取12个合适的扫描点, 不同速度加载位移z与施加荷载P的变化以及扫描点选取见图9, 共选取扫描点12组.
-
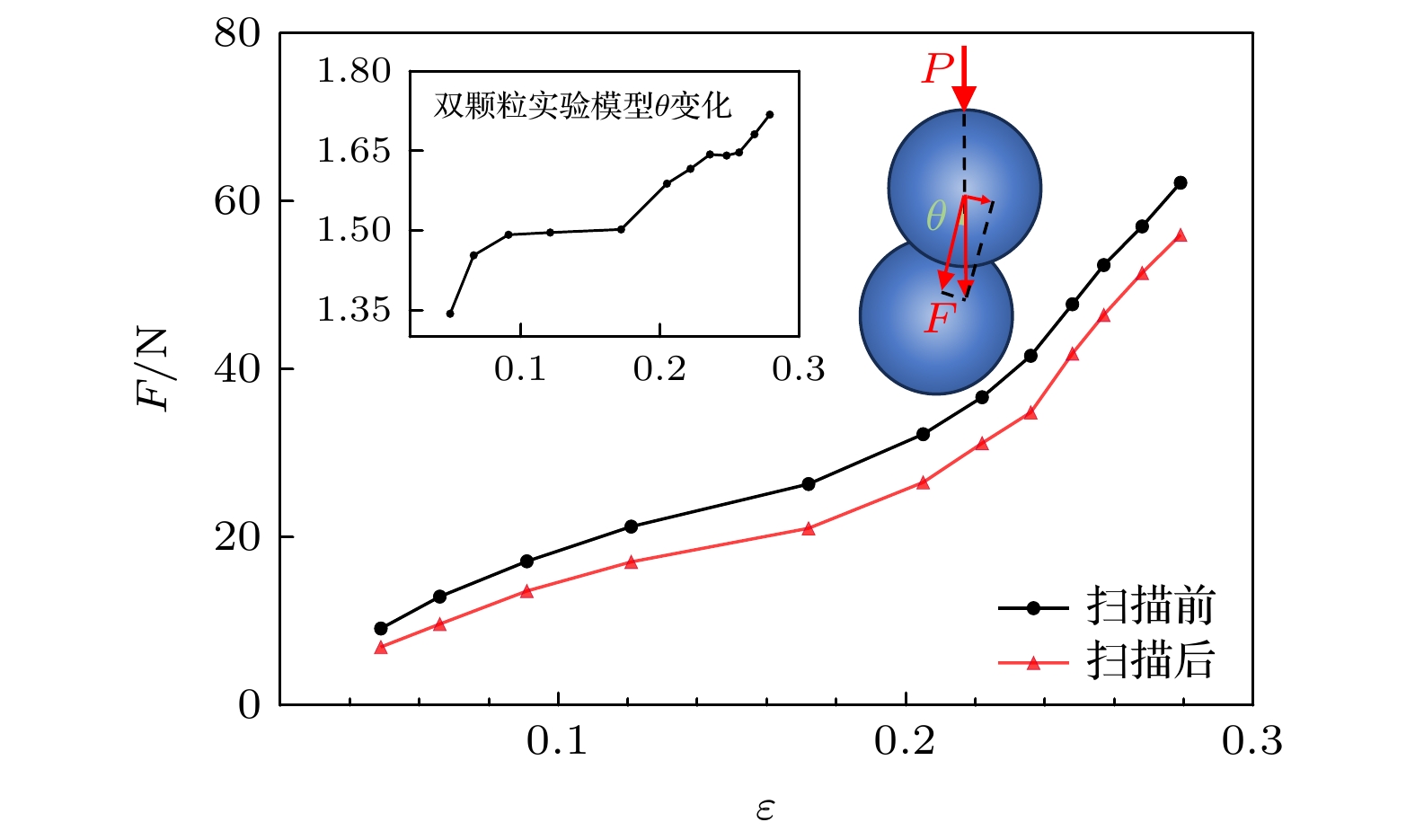
加载过程中, 加载到预设扫描点力值暂停加载, 开始扫描, 扫描结束后继续加载并重复此过程. 在扫描过程中, 由于颗粒的蠕变效应, 颗粒存在卸载情况, 加载过程中两颗粒可能发生角度偏移
$ \theta$ , 因此扫描前后接触力大小存在一定偏移量. 扫描前后的法向接触力F与应变$ \varepsilon $ 关系见图10. 由图10可知, 角度偏移$ \theta {\text{ }} $ 随应变$ \varepsilon $ 增大而增大, 本实验角度偏移$ \theta {\text{ }} $ 不超过1.8°, 修正后的颗粒法向接触力基本不变. 扫描前后颗粒接触力相差约5 N, 随着持续加载扫描, 该差值未发生明显变化. 颗粒体系应变$ \varepsilon $ 与接触力F呈正相关关系, 且随着应变$ \varepsilon $ 不断增大, 接触力F增加趋势升高. -
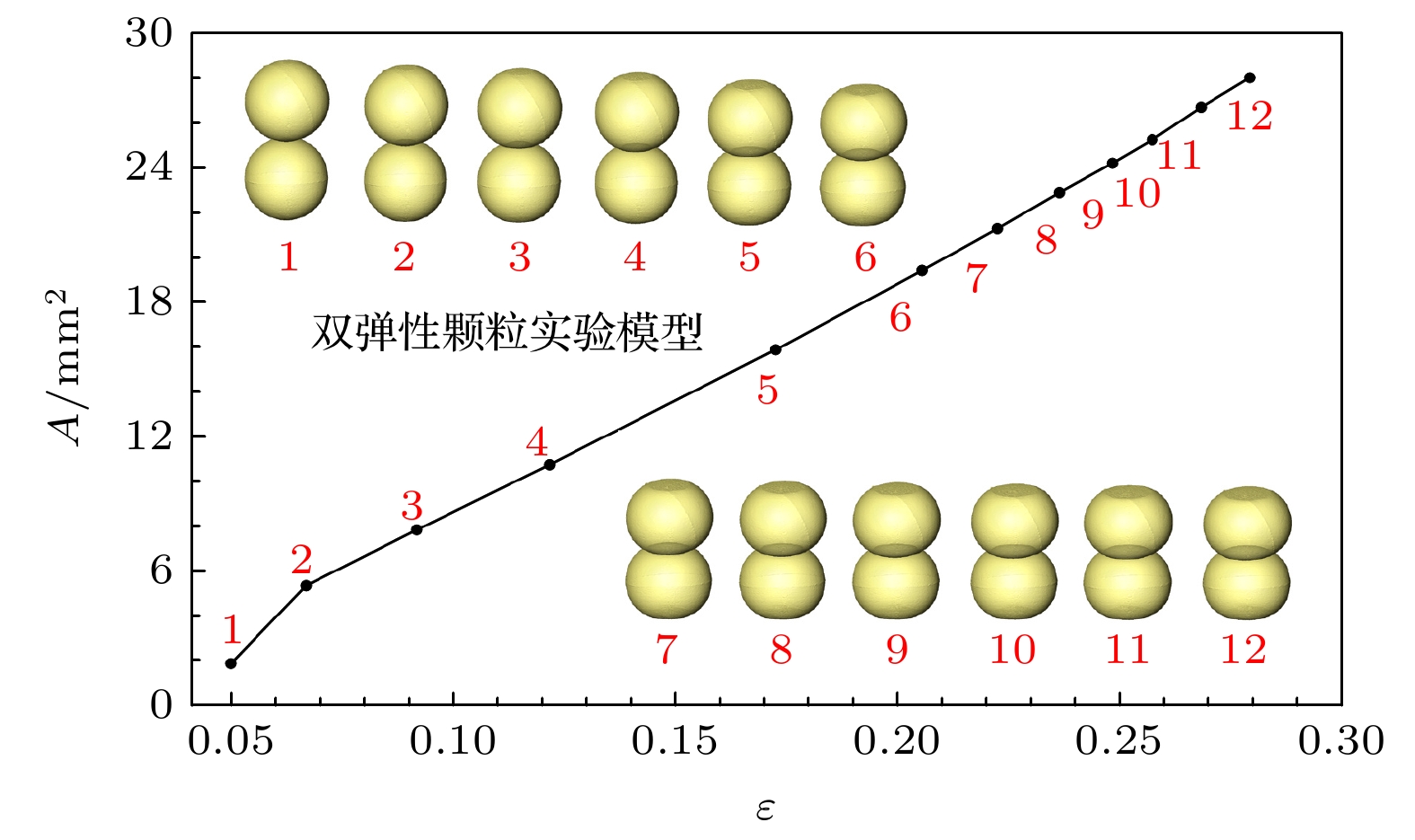
通过图像处理获取三维颗粒图像, 建立孔隙网络模型计算两颗粒间接触面积. 图11展示了12个扫描点处颗粒体系应变
$ \varepsilon $ 和接触面积A的关系, 随着应变$ \varepsilon $ 增加, 接触面积A呈线性增加趋势. -
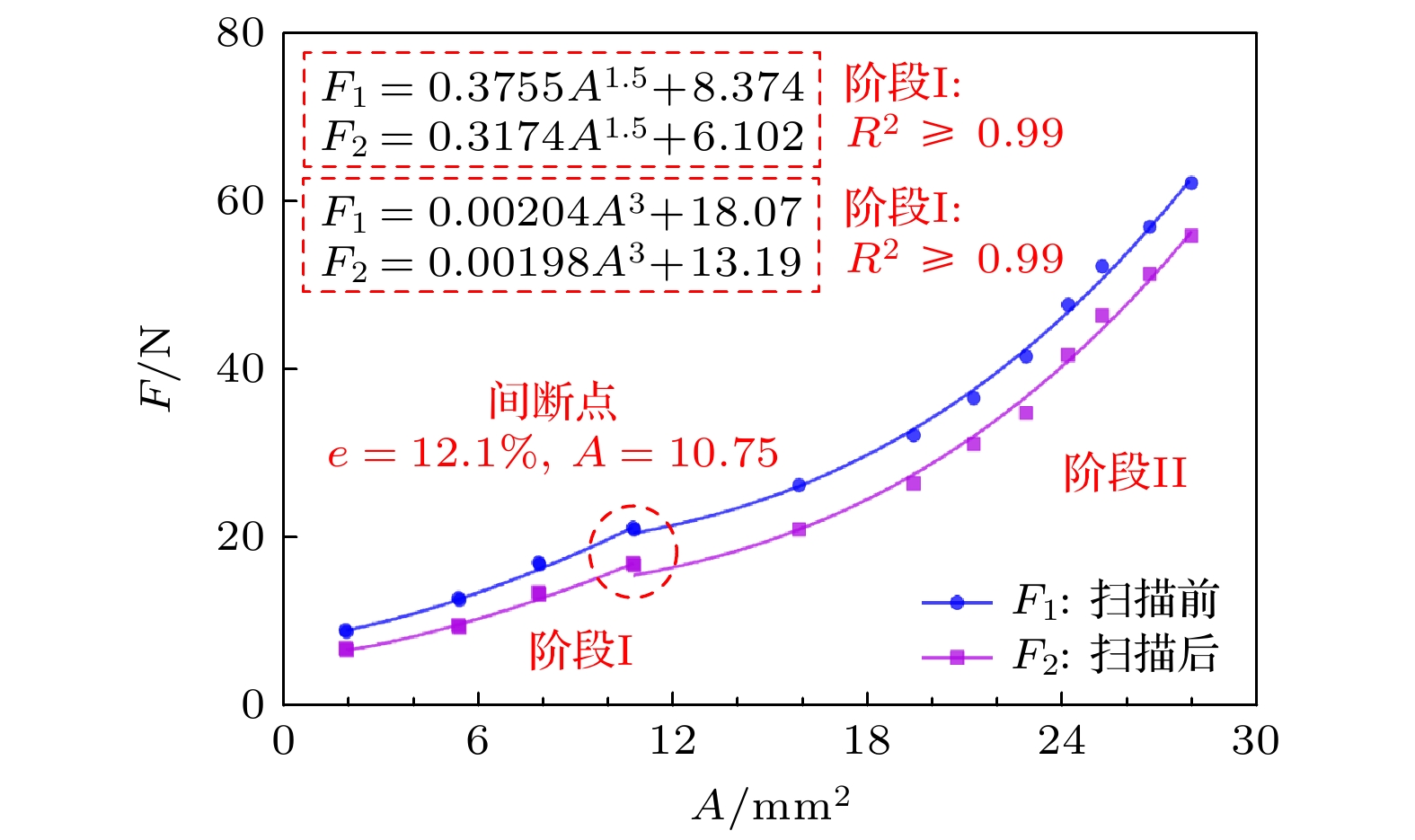
颗粒体系在探针加载状态过程中, 内部两颗粒应变和接触面积均处于较小范围, 均不超过双球轴向压缩实验的最大应变和接触面积. 因此, 实验探究接触面积A和接触力F两者关系时, 最大应变
$ \varepsilon $ = 28%, 最大接触面积A = 27.98 mm2. 分别对扫描前后的接触力进行公式拟合, 拟合结果以及R2值见图12. 为保证接触面积和接触力对应的唯一性, 分段拟合时间断点($ \varepsilon $ = 12.1%, A = 10.75)仅属于阶段I.由图12可知, 接触力随接触面积增大而增大, 具体可分为两个阶段. 当
$ \varepsilon $ $ \leqslant $ 12.1%即A$ \leqslant $ 10.75时, 接触力为接触面积的1.5次幂关系, 该阶段符合Hertz小变形接触理论; 当12.1%$\lt \varepsilon $ $ \leqslant $ 28%即$10.75 \lt A \leqslant 27.98$ 时, 接触力为接触面积的3次幂关系, 该阶段符合Tatara大变形接触理论.取扫描前后拟合公式系数平均值, 可得:
式中, 满足前提条件
$ \varepsilon $ $ \leqslant $ 28%即A$ \leqslant $ 27.98. 该式符合Hertz小变形理论和Tatara大变形理论$ N = K{A^n} + B $ 的关系, 式中, K代表接触面积与接触力比例系数, 与颗粒弹性模量、泊松比和直径有关; B代表偏移误差, 可能与颗粒材料、实验条件等因素有关. -
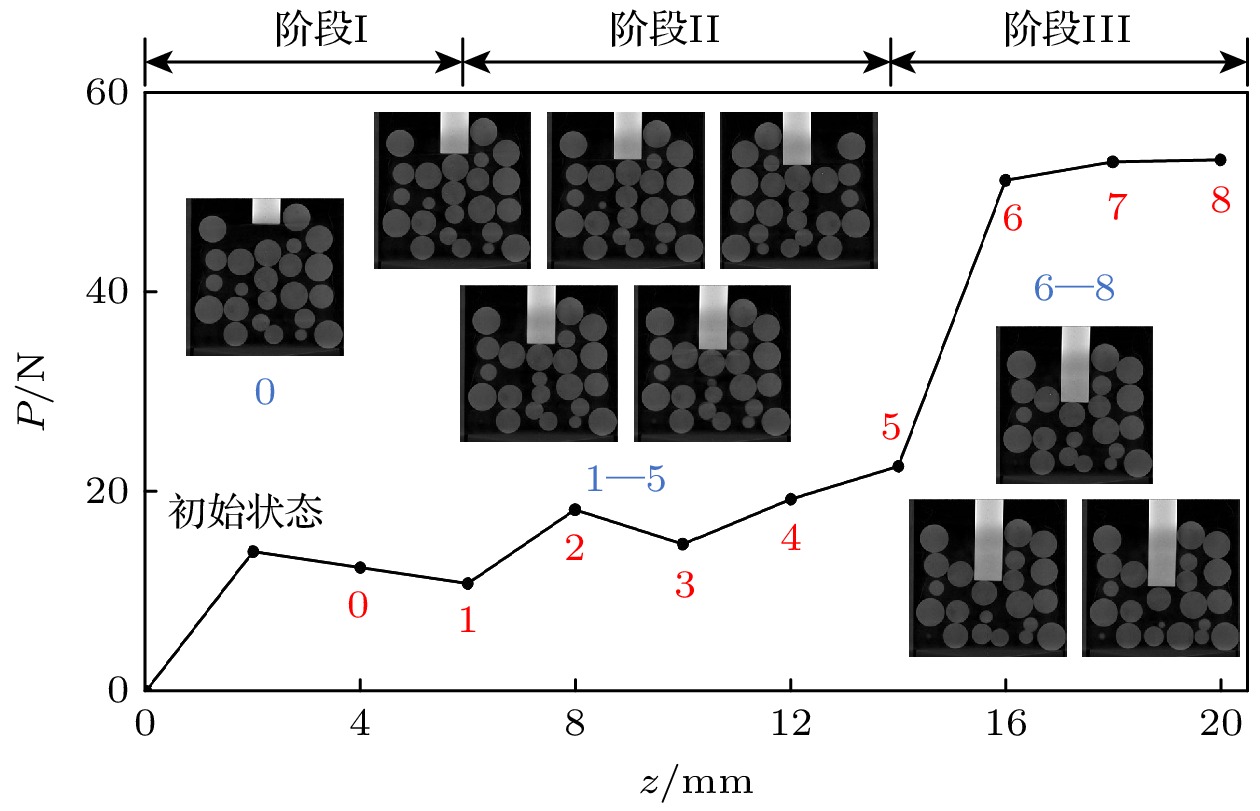
颗粒体系在受到探针加载作用时, 颗粒之间相互挤压但不被压实, 颗粒仍具有相对较高的自由度. 图13展示了加载过程中颗粒体系压力P随压头下压位移z的变化情况, 整个加载过程分为三个阶段. 1) 加载压头下压位移z = 0—6 mm为阶段I, 此时颗粒系统仍处于初始状态, 压头未完全压到某颗粒, 压力受压头触碰颗粒影响发生波动, 该阶段不存在明显的荷载传递特征, 不具备研究价值. 2) 加载压头下压位移z = 6—14 mm为阶段II, 此时探针压头压到某一颗粒, 并由该颗粒为起始点不断向下方和四周传递荷载作用. 大部分颗粒位置发生了微小的变化, 压头下方颗粒持续向下移动, 挤压四周颗粒向上移动, 系统所受压力逐渐上升, 该阶段颗粒系统处于一个相对稳定的阶段, 呈现出压力持续缓慢增长的特征. 3) 加载压头下压位移z = 14—20 mm为阶段III, 此时颗粒系统压力发生急剧上升后趋于缓慢增长. 表明在压头持续下压过程中, 打破了上一阶段的稳定状态, 并发生颗粒力链从破坏到重组直至稳定的新状态.
-
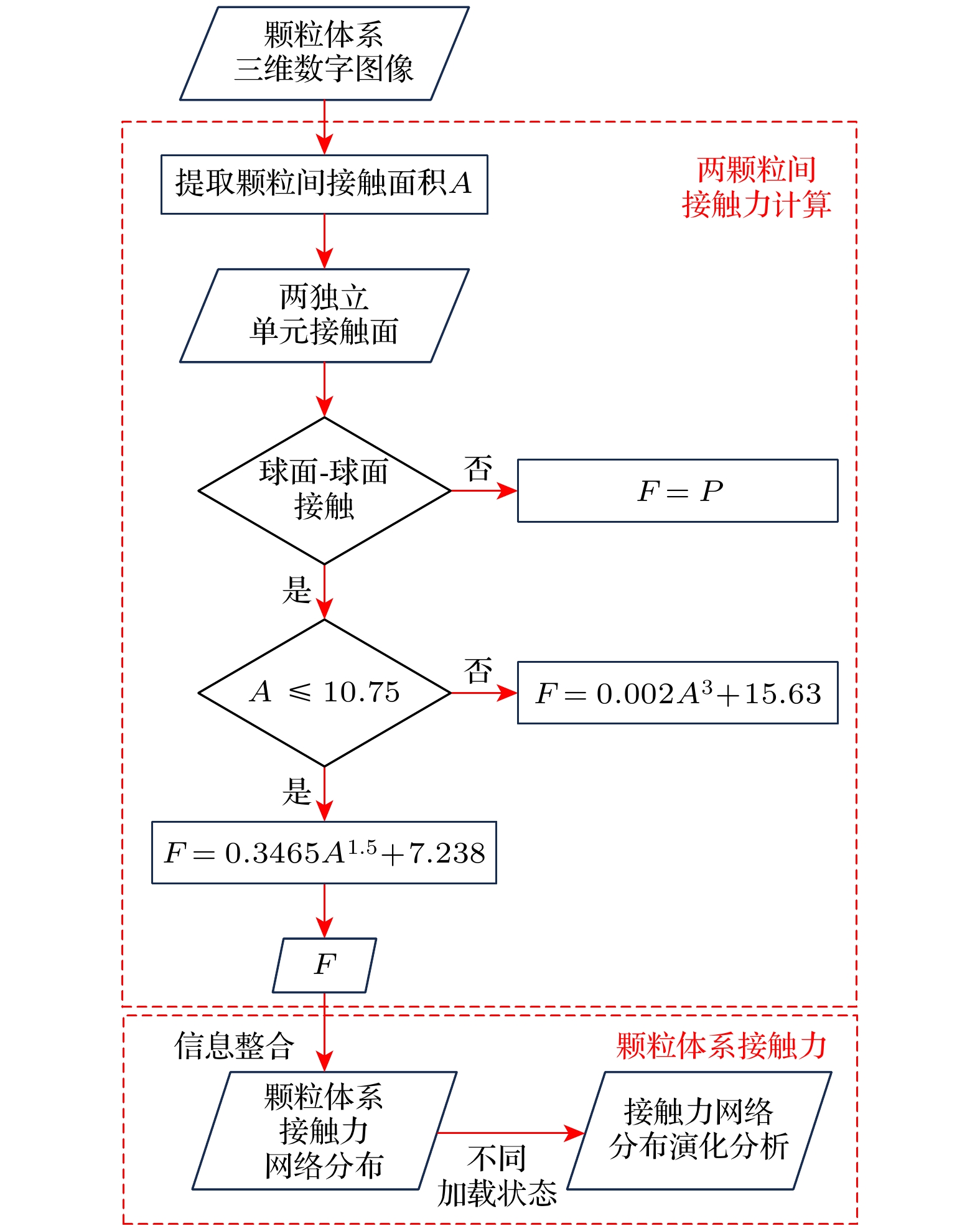
Mirco-CT实验获取颗粒体系三维数字图像, 通过建立孔隙网络模型提取颗粒间接触面积A, 前期经实验验证建立了接触力F和接触面积A公式关系, 以接触面积A为分段条件代入公式即可求得两颗粒间接触力F. 其中, 颗粒与压头间接触为球面-平面接触, 接触力F为压头施加荷载P; 颗粒间接触为球面-球面接触, 接触力基于micro-CT双球轴向压缩实验, 按照(5)式分段代入计算. 计算全部颗粒间接触力即可得到颗粒体系接触力网络分布, 分析不同加载状态下接触力网络分布演化情况, 计算流程见图14.
-
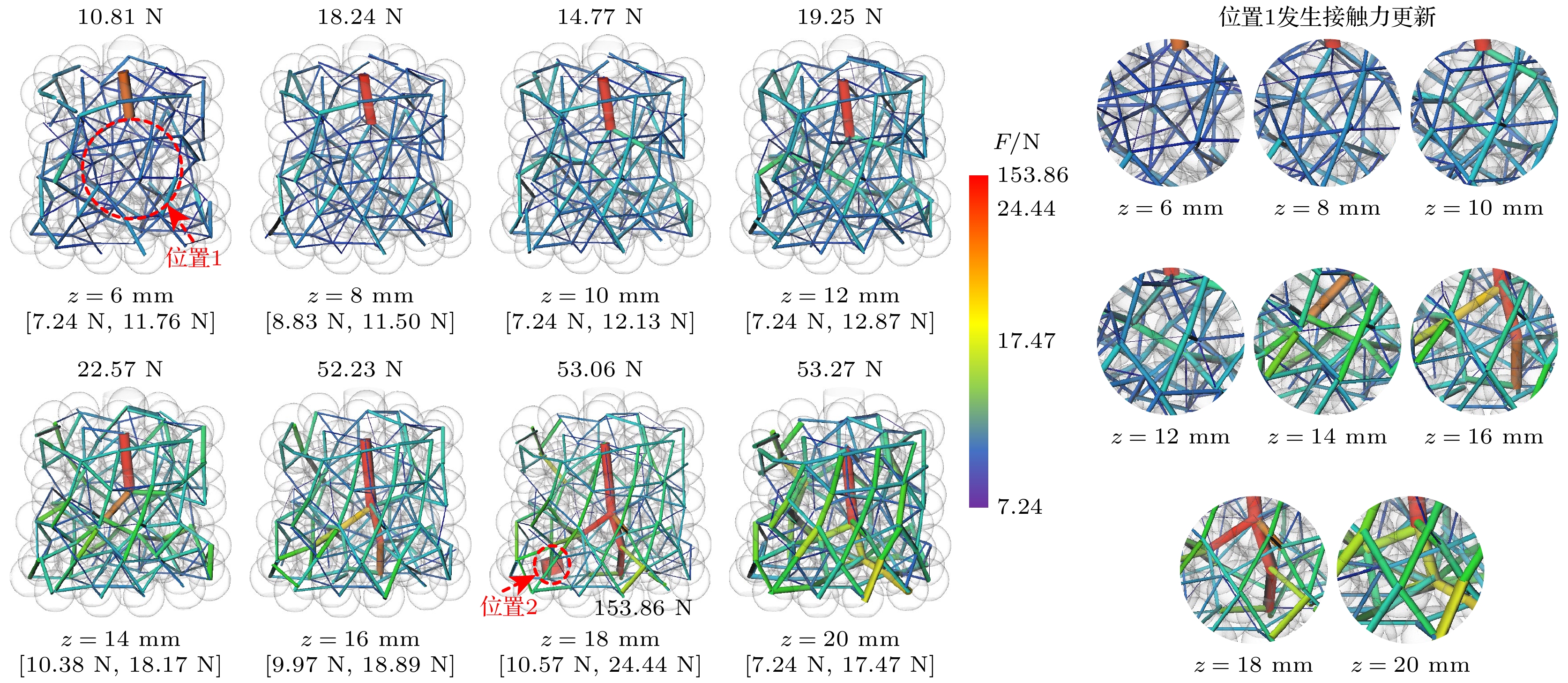
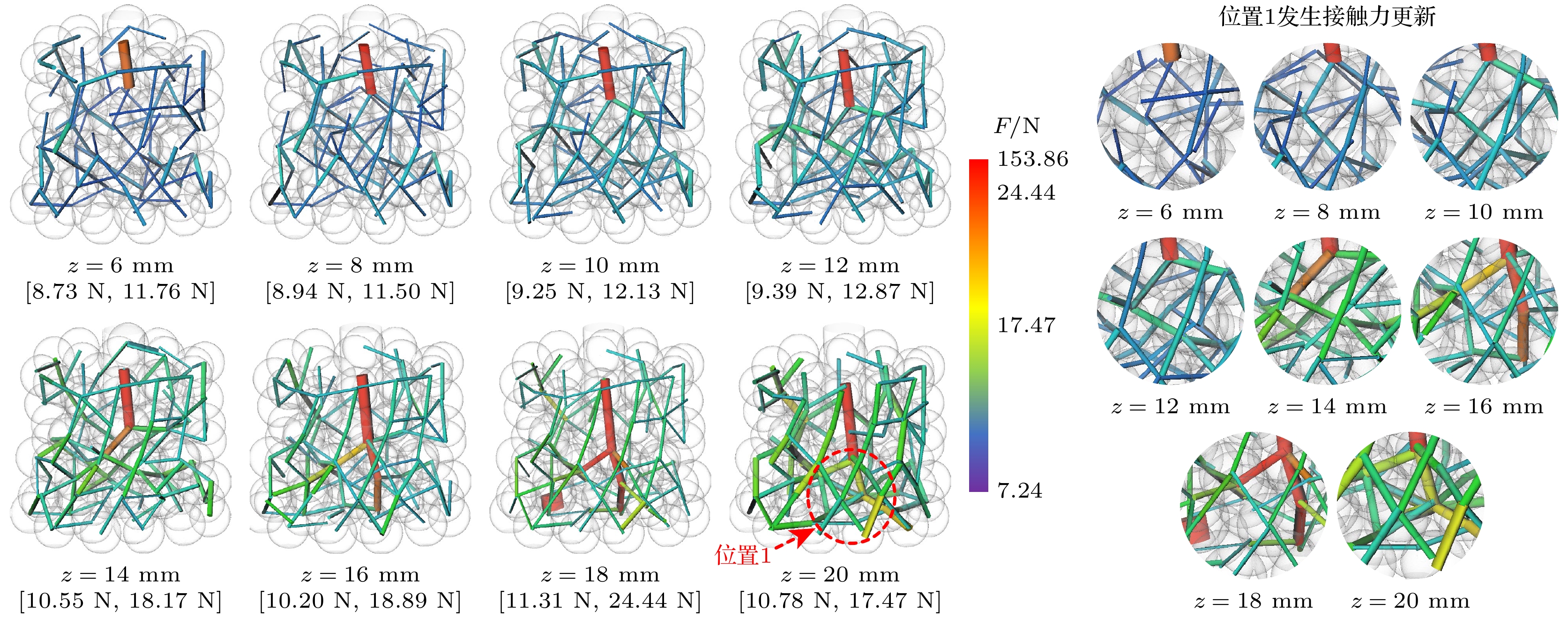
由于颗粒分布的随机性和无序性, 颗粒间接触关系错综复杂, 随着探针压头向下运动, 颗粒不断发生位移, 颗粒间接触力大小和方向随之更新, 以探针压头接触颗粒为起始点不断向下方和四周传递荷载. 图15展示了不同位移加载下三维颗粒体系接触力基本区间以及分布情况, 图中网络结构粗细和颜色均表示接触力大小. 可以看出, 颗粒体系受探针加载作用下, 接触力网络分布发生动态更新. 随着探针压头向下运动, 最大接触力基本产生在与压头接触的颗粒位置, 并挤压附近颗粒发生变形和位移, 接触力分布整体呈现出压头下方区域接触力较大, 由中心向四周发散的局面. 颗粒变形和移动伴随旋转、摩擦等能量的损耗, 在压头附近区域发生接触力消失或产生的情况, 部分区域伴随接触力大小和方向的改变. 图15中位置1压头附近接触力更迭最为明显, 在加载过程中接触力整体数值不断增大, 方向也随颗粒间移动挤压而发生变化, 持续发生接触力更新现象. 位置2发生随机性的力链断裂和重组现象, 导致该位置出现了最大接触力153.86 N, 下一加载状态该接触力消失, 附近区域力链网络结构更加趋于稳定.
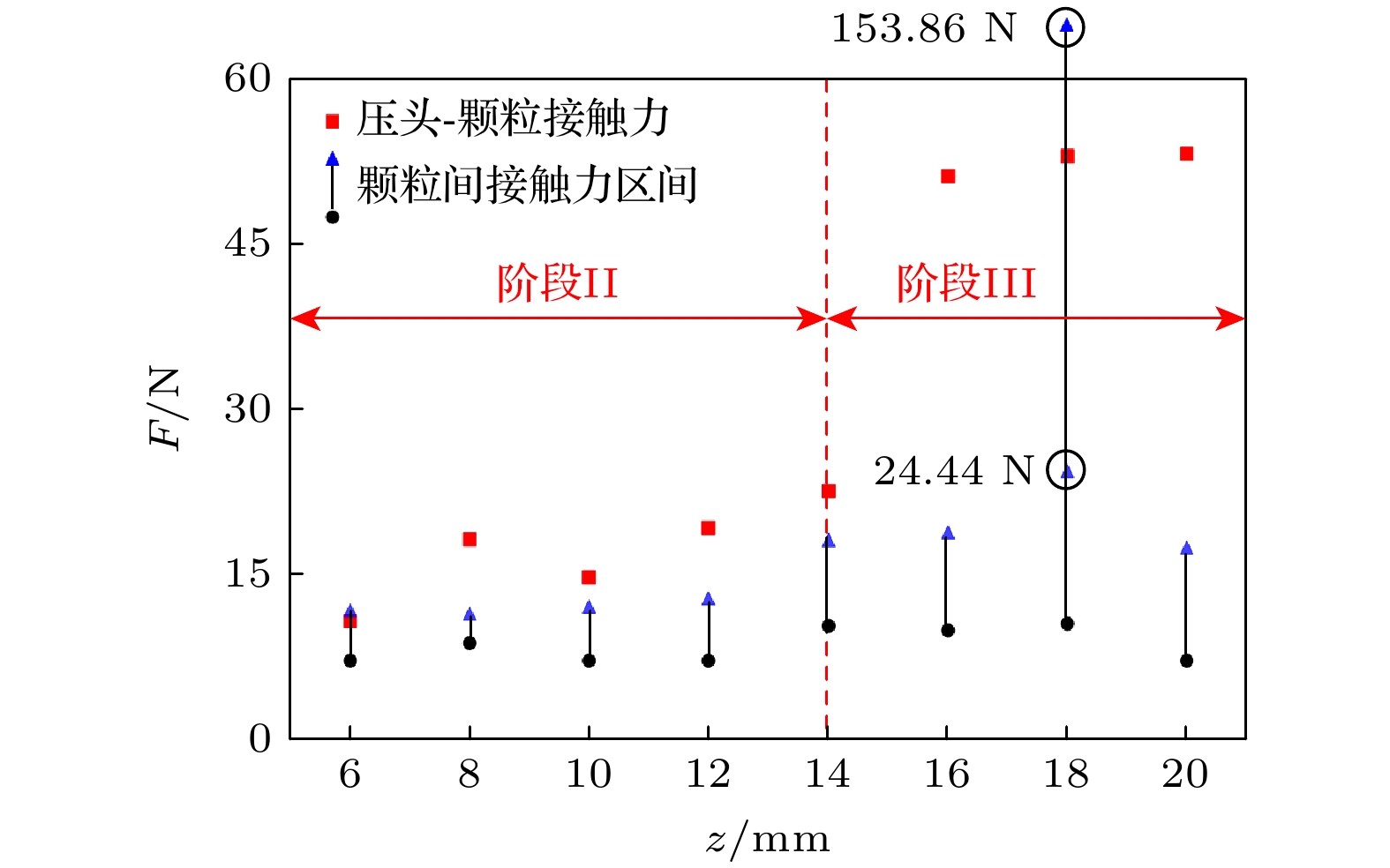
图16展示了不同加载位移下三维颗粒间的接触力区间和压头-颗粒接触力. 加载过程中, 压头与颗粒接触力基本为最大值, 标示在图15压头附近; 在z = 18 mm时, 颗粒体系内部力链断裂与重组, 位置2处出现较大接触力153.86 N, 并在下一加载状态再次被破坏导致消失. 颗粒接触力区间最小值基本不发生变化, 区间在阶段II和阶段III变化明显, 阶段II整体区间数值较小, 阶段III区间最大值出现上升并在最终加载状态下降, 结合图15可知z = 20 mm时最大接触力消失, 接触力网络分布较前一状态更加均匀稳定.
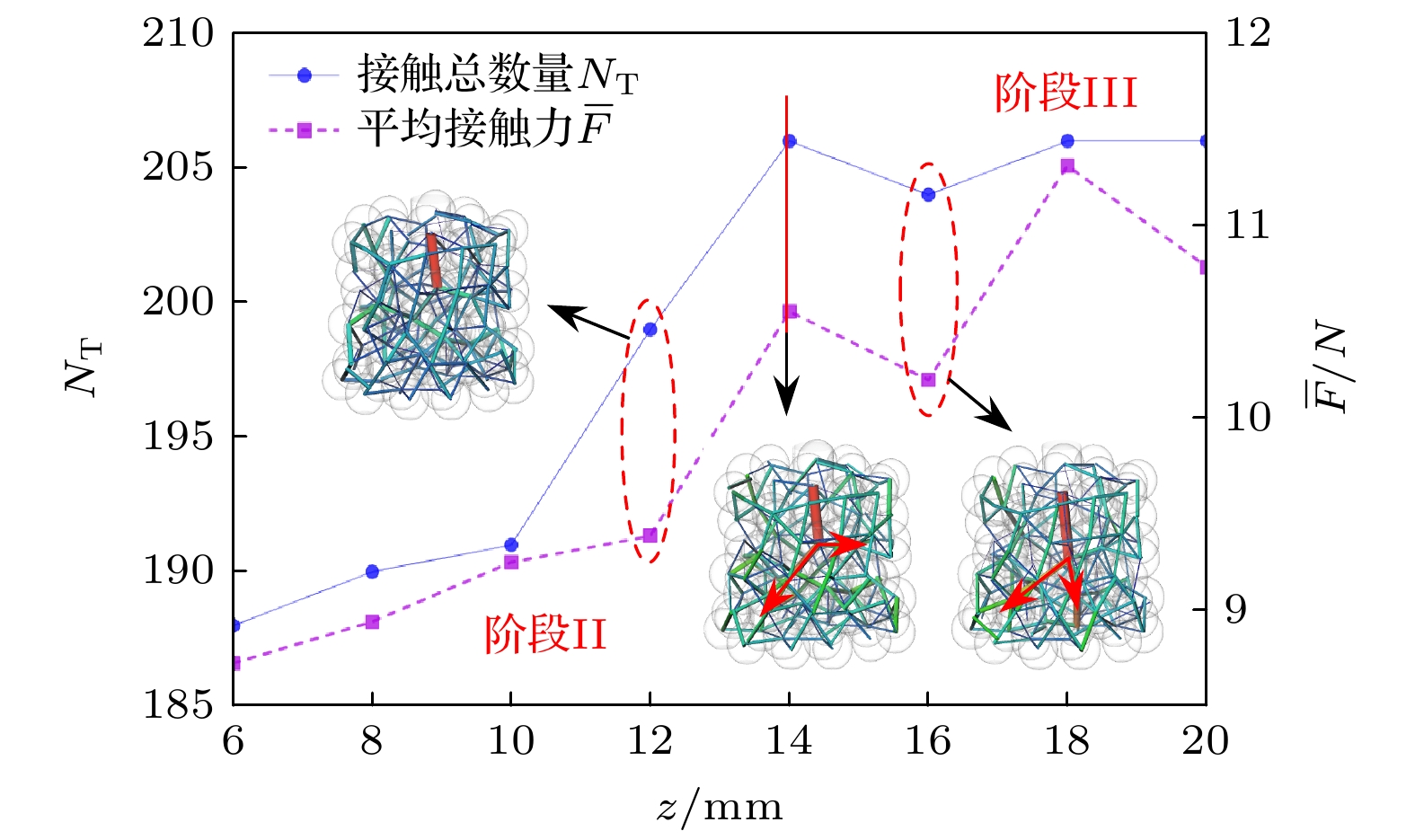
图17展示了加载过程中阶段II和阶段III接触总数量NT和平均接触力
$ \overline F $ 的变化情况. 在阶段II, 接触总数量NT呈现上升趋势; 在阶段III, 接触总数量NT基本稳定在206附近, 不再发生明显变化. 平均接触力$ \overline F $ 变化趋势与接触总数量NT保持一致, 表现出明显的阶段性变化. 接触数量越多, 颗粒间挤压更加频繁, 颗粒间接触力越大, 在阶段III稳定在10.5 N附近. z = 14 mm为阶段II和阶段III的转折点, 对比前后接触力网络分布情况可知, 阶段II接触力分布贯穿颗粒体系总网络, 力大小均匀; 阶段III转折点处接触力值出现明显的大小分化, 接触力较大者主要集中在压头下方, 以该点为中心向四周传递. -
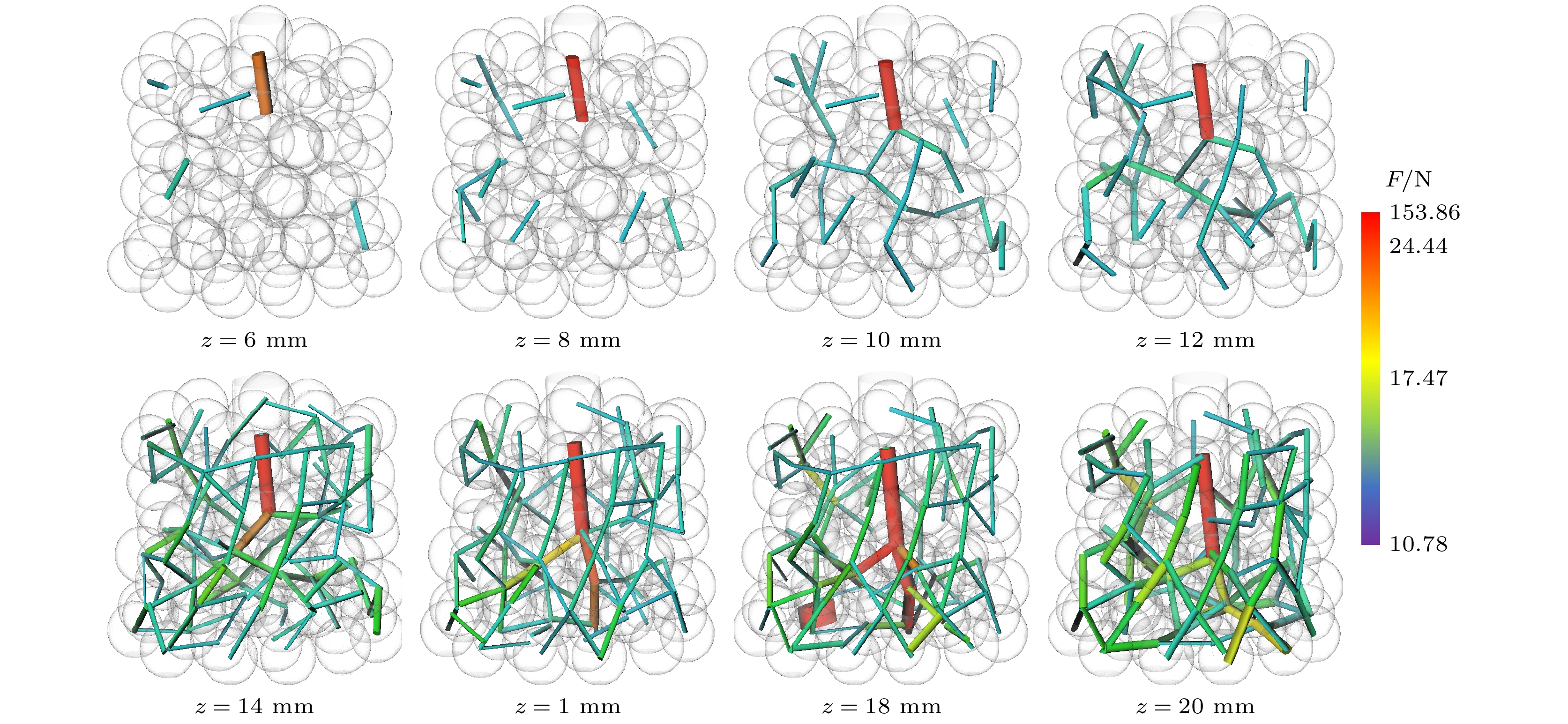
接触力大于颗粒体系内部平均接触力为强接触力. 作为颗粒体系力链的主要支撑和传力结构, 强接触力的分布与发展影响着整个颗粒体系的力学特征和性能. 图18展示了不同位移加载下三维颗粒体系强接触力基本区间以及分布情况, 图中网络结构粗细和颜色均表示接触力大小. 由图18可知, 强接触力分布贯穿于整个颗粒体系内部, 支撑起颗粒体系网络结构. 接触力值较大者多集中在探针压头下方, 并向四周传递和扩散, 接触力值也以该位置为中心点向外逐级减小. 随着压头不断下压, 强接触力值分布更加均匀, 整个颗粒体系网络结构逐渐趋于稳定. 图18中压头下方区域位置1在加载过程中强接触力整体增大, z = 18 mm时多个旧接触力消失, z = 20 mm时多个新接触力产生.
图19展示了颗粒体系高于最终位移加载状态接触力平均值10.78 N的接触力网络分布情况. 由图19可知, 高于10.78 N的接触力数量逐渐增多. 最开始出现在筒壁附近, 结构分散; z = 10 mm时在压头下方出现相互连接、较为稀疏的树杈状网络结构, 随着加载过程的进行, 该网络结构不断扩大, z = 14 mm时布满整个三维颗粒体系, 逐渐达到稳定状态.
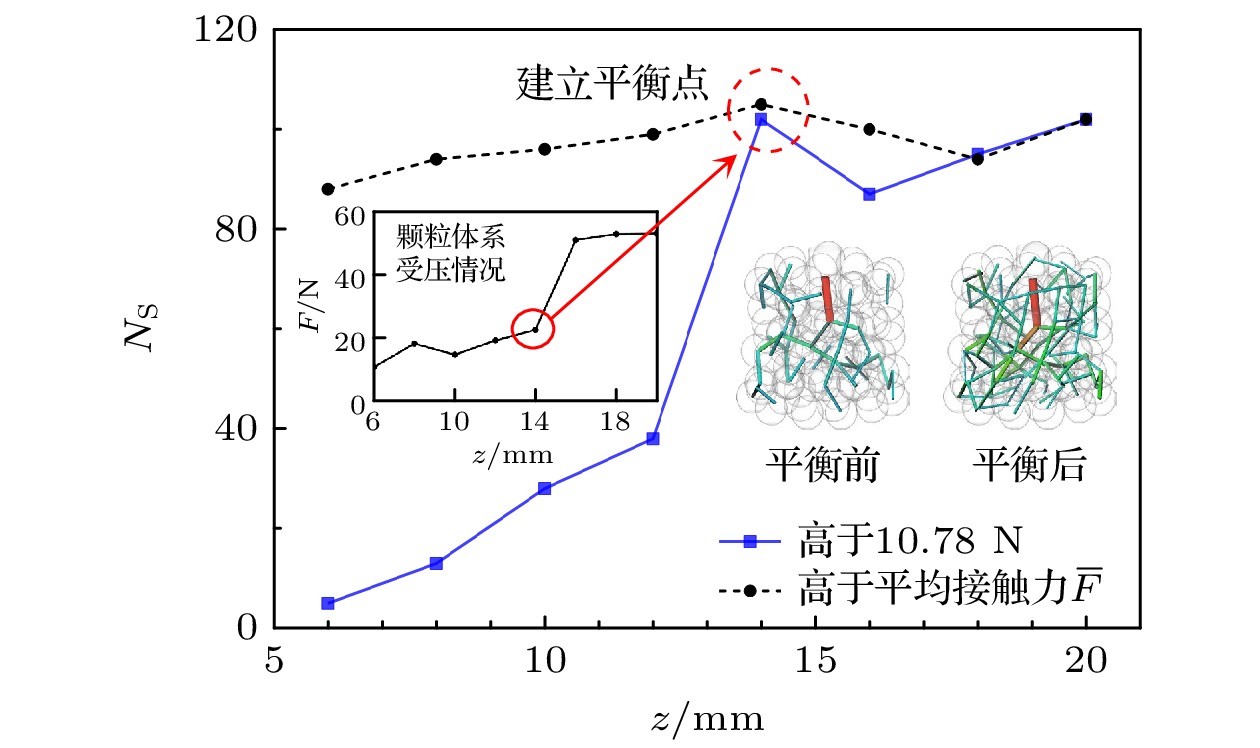
图20展示了高于平均接触力
$ \overline F $ 和高于最终加载状态平均接触力(10.78 N)的强接触数量NS变化情况. 随着探针压头下压, 强接触数量NS缓慢稳步增加, 在z = 14 mm处建立平衡点, 强接 触数量NS变化趋势改变, 呈现先递减又上升的 趋势. 平衡点的建立同样体现在颗粒体系受压变化中, z = 14 mm处颗粒体系受压出现陡增的趋势, 表明该处形成全新的承载能力更高的接触力网络结构, 高于10.78 N的强接触数量NS基本达到顶峰, 建立起承受外载荷的主要骨架. 平衡点前后强接触力网络状态截然不同, 建立平衡点后, 强接触力的整体数值更高, 在颗粒体系内部的分布也更加均匀.经计算, 强接触数量NS占接触总数量NT的45%—50%. 其中, 强接触作为强力链的主要核心, 是传递和承受外载荷并搭建起颗粒体系基本骨架, 弱接触作为体系网络结构的补充和黏结剂, 支撑着三维网络结构, 建立起颗粒间的联系并维持着整个颗粒体系网络结构的稳定.
-
本文基于mirco-CT对弹性球接触模型进行了验证, 得出适合本实验条件下的弹性球接触力计算公式. 通过开展弹性橡胶颗粒探针加载实验, 构建了三维颗粒体系的接触网络模型, 得到了加载过程中颗粒接触力网络分布情况. 从宏观上分析了颗粒体系受压情况, 从微观层面探究了颗粒体系接触力网络分布演化规律, 揭示了强接触数量及分布演化与颗粒体系稳定性的内在联系, 主要结论如下.
1) 验证了双弹性球接触模型符合Hertz接触理论和Tatara大变形接触理论规律, 拟合的接触力计算公式能合理有效表征两颗粒间接触力.
2) 弹性橡胶球颗粒体系受探针加载作用整个受压过程可分为初始状态、稳定受压、重组至稳定三个阶段. 阶段I压头未压到颗粒, 压力数值受周围颗粒扰动发生波动; 阶段II压头压到某一颗粒, 并以该颗粒为起点, 向与该颗粒接触的其他颗粒逐级传递荷载, 颗粒体系压力缓慢增长; 阶段III压头持续下压过程中, 颗粒力链发生从破坏到重组直至稳定的新状态, 颗粒体系压力发生急剧上升后趋于缓慢增长.
3)颗粒体系受探针加载作用下, 接触力网络分布发生动态更新, 接触力分布整体呈现出探针压头下方区域接触力较大, 由中心向四周发散的局面. 平均接触力变化趋势与接触数量保持一致, 表现出明显的阶段性变化. 接触数量越多, 颗粒间挤压更加频繁, 颗粒间接触力越大, 在阶段III稳定在10.5 N附近.
4) 强接触力分布贯穿于整个颗粒体系内部, 支撑起颗粒体系网络结构. 强接触数量NS占接触总数量NT的45%—50%, 随加载缓慢增加, 在z = 14 mm处建立平衡点, 变化趋势改变, 呈现轻微幅度的波动. 平衡点处, 高于10.78 N的强接触数量NS基本达到顶峰, 建立起承受外载荷的主要骨架, 在压头下方呈现树杈状分布. 平衡点后继续加载, 强接触力的整体数值更高, 在颗粒体系内部的分布也更加均匀.
基于micro-CT实验的颗粒体系接触力计算及演化分析
Contact force calculation and evolution analysis of granular systems based on micro-CT experiment
-
摘要: 三维颗粒体系颗粒间接触力计算是散体力学研究的重难点. 以双弹性橡胶球为研究对象, 开展显微CT (micro-CT)原位平压实验, 基于Hertz接触理论和Tatara大变形接触理论, 验证了弹性球接触模型, 获得了基于实验的弹性球接触力理论公式. 以三维颗粒体系为研究对象, 开展了micro-CT原位探针加载实验, 获取颗粒二维图像序列, 经过系列数字变换得到数字体图像, 获得了不同加载状态下三维颗粒体系接触力网络, 分析了颗粒体系接触力分布及演化规律, 探究了强接触数量及分布演化与颗粒体系稳定性的联系. 研究结果表明: 基于实验的弹性球接触力公式能合理有效表征两颗粒间的接触力; 探针加载下颗粒间接触力呈现以探针压头接触点为起点, 向下方和四周逐级传递接触力的网状分布; 强接触数量占接触总数量的45%—50%, 分布贯穿于整个颗粒体系内部, 支撑起颗粒体系网络结构, 较大值集中于压头下方呈现树杈状分布; 加载过程中, z = 14 mm处建立了平衡点, 平衡点处, 强接触数量达到顶峰, 强接触力网络结构布满整个三维颗粒体系, 建立起承受外载荷的主要骨架, 随着加载继续, 强接触力的整体数值更高, 在颗粒体系内部分布也更加均匀.Abstract: The calculation of inter-granule contact force in three-dimensional (3D) granular systems is a key and challenging aspect of granular mechanics research. Two elastic rubber balls are used as research objects for in-situ flat pressing micro-CT experiments. Based on the Hertzian contact theory and Tatara large deformation contact theory, the contact model of elastic balls is verified, and the theoretical formula of the contact force of elastic balls based on the experiment is obtained. Taking the 3D granular systems as research object, in-situ probe loading experiment of micro-CT is carried out to obtain the 2D image sequence of the granules, after a series of digital transformations, the digital body images emerge, the contact force networks of the 3D granular systems under different loading conditions are obtained by constructing pore network models. The contact force distribution and evolution law of the granular systems are analyzed. The relation among the number of strong contacts, the distribution evolution, and the stability of the granular system is explored. The results show that the two elastic ball contact model conforms to the Hertzian contact theory and Tatara large deformation contact theory, and the contact force fitting formula based on experiment can characterize the contact force between two granules reasonably and effectively. The contact force of granules under probe loading is distributed in a net-like pattern starting from the contact point of the indenter and gradually transmitted to the lower and the surrounding area. The trend of average contact force is consistent with the trend of the contact times, showing a significant phase transition. With the increase of contact times, the frequency of particle compression increases, resulting in a greater contact force between granules, ultimately stabilizing at about 10.5 N. The number of strong contacts accounts for 45% to 50% of the total number of contacts, distributed throughout the whole granular system and supporting the network structure of the granular system. The larger values are concentrated below the indenter and exhibit a branching distribution. In the loading process, an equilibrium point is established at z = 14 mm, where the number of strong contacts reaches the peak. The network structure of strong contact force is spread throughout the entire 3D granular system, establishing the main skeleton that can withstand external loads. As the loading continues, the total value of strong contact forces increases, and their distribution within the granular system becomes more uniform.
-
Key words:
- micro-CT /
- in-situ loading /
- contact model of granules /
- contact force .
-
-
图 2 单球颗粒法向重叠量
$ \delta $ 与接触力F关系Figure 2. Relationship between normal overlap
$ \delta $ and contact force F for single granule.
图 10 应变
$ \varepsilon $ -接触力F关系Figure 10. Relationship of strain
$ \varepsilon $ and contact force F.
图 11 应变
$ \varepsilon $ -接触面积A关系Figure 11. Relationship of strain
$ \varepsilon $ and contact area A.
图 14 接触力网络分布及演化计算流程图
Figure 14. Flowchart for calculation of contact force network distribution and evolution.
图 15 颗粒体系接触力网络分布及演化
Figure 15. Contact force network distribution and evolution of granular systems.
图 17 接触总数量NT和平均接触力
$ \overline F $ 变化Figure 17. Change in total number of contacts NT and average contact force
$ \overline F $ .
图 18 颗粒体系强接触力网络分布及演化
Figure 18. Strong contact force network distribution and evolution of granular systems.
图 19 颗粒体系高于10.78 N的强接触力网络分布及演化
Figure 19. Strong contact force network distribution and evolution more than 10.78 N of granular systems.
-
[1] 孙其诚 2015 物理学报 64 076101 doi: 10.7498/aps.64.076101 Sun Q C 2015 Acta Phys. Sin. 64 076101 doi: 10.7498/aps.64.076101 [2] 瞿同明, 冯云田, 王孟琦, 赵婷婷, 狄少丞 2021 力学学报 53 2404 doi: 10.6052/0459-1879-21-221 Qu T M, Feng Y T, Wang M Q, Zhao T T, Di S C 2021 Chin. J. Theor. Appl. Mech. 53 2404 doi: 10.6052/0459-1879-21-221 [3] Wang Y W, Liu R, Sun R H, Xu Z W 2023 Eng. Comput. 40 1390 doi: 10.1108/EC-09-2022-0590 [4] Lovoll G, Måloy K J, Flekkoy E G 1999 Phys. Rev. E 60 5872 doi: 10.1103/PhysRevE.60.5872 [5] Blair D L, Mueggenburg N W, Marshall A H, Jaeger H M, Nagel S R 2000 Phys. Rev. E 63 278 doi: 10.1103/PhysRevE.63.041304 [6] Anton K, Neverov S, Neverov A, Dmitry O, Ivan Z, Maria K 2023 Geohazard Mech. 1 128 doi: 10.1016/j.ghm.2023.03.001 [7] 鲁锋, 李照阳, 杨召, 张刘平, 刘金, 李璐璐, 刘向军 2023 石油实验地质 45 193 doi: 10.11781/sysydz202301193 Lu F, Li Z Y, Yang Z, Zhang L P, Liu J, Li L L, Liu X J 2023 Pet. Geol. Exp. 45 193 doi: 10.11781/sysydz202301193 [8] Wang S T, Chang Y H, Wang Z F, Su X X 2024 Energies 17 1370 doi: 10.3390/en17061370 [9] Majmudar T S, Behringer R P 2005 Nature 435 1079 doi: 10.1038/nature03805 [10] Sanfratello L, Fukushima E, Behringer R P 2009 Granular Matter 11 1 doi: 10.1007/s10035-008-0112-4 [11] 陈凡秀, 庄琦, 王日龙 2016 岩土力学 37 563 doi: 10.16285/j.rsm.2016.02.030 Chen F X, Zhuang Q, Wang R L 2016 Rock Soil Mech. 37 563 doi: 10.16285/j.rsm.2016.02.030 [12] Kondo A, Takano D, Kohama E, Bathurst R J 2022 Géotech. Lett. 12 203 [13] 王潇, 陈凡秀, 王远, 刘雨欣, 孙洁 2023 力学学报 55 1732 Wang X, Chen F X, Wang Y, Liu Y X, Sun J 2023 Chin. J. Theor. Appl. Mech. 55 1732 [14] Hertz H 1881 J. Reine Angew. Math. 92 156 doi: 10.1515/crll.1882.92.156/html [15] Johnson K L, Kendall K, Roberts A D 1971 Proc. R. Soc. London, Ser. A 324 301 doi: 10.1098/rspa.1971.0141 [16] Derjaguin B V, Muller V M, Toporov Y P 1975 J. Colloid Interface Sci. 53 314 doi: 10.1016/0021-9797(75)90018-1 [17] Tatara Y 1991 ASME J. Eng. Mater. Technol. 113 285 doi: 10.1115/1.2903407 [18] Tatara Y, Shima S, Lucero J C 1991 ASME J. Eng. Mater. Technol. 113 292 doi: 10.1115/1.2903408 [19] 何思明, 吴永, 李新坡 2008 工程力学 25 19 He S M, Wu Y, Li X P 2008 Eng. Mech. 25 19 [20] 运睿德, 丁北 2019 机械工程学报 55 80 Yun R D, Ding B 2019 J. Mech. Eng. 55 80 [21] Wu Y, Hao H C, Gao M Z, Gao Z, Gao Y N 2023 Geomech. Geophys. Geo-Energy Geo-Resour. 9 126 doi: 10.1007/s40948-023-00667-4 [22] 戚俊成, 陈荣昌, 刘宾, 陈平, 杜国浩, 肖体乔 2017 物理学报 66 054202 doi: 10.7498/aps.66.054202 Qi J C, Chen R C, Liu B, Chen P, Du G H, Xiao T Q 2017 Acta Phys. Sin. 66 054202 doi: 10.7498/aps.66.054202 [23] Lubner M G, Ziemlewicz T J, Wells S A, Li Ke, Wu P H, Hinshaw J L, Lee F T, Brace C L 2022 Abdominal Radiology 47 2658 doi: 10.1007/s00261-021-03333-z [24] Busch M, Hausotte T 2022 Prod. Eng. 16 411 doi: 10.1007/s11740-021-01100-z [25] 毛灵涛, 毕玉洁, 刘海洲, 陈俊, 王建强, 彭瑞东, 刘红彬, 吴昊, 孙跃, 鞠杨 2023 科学通报 68 380 doi: 10.1360/TB-2022-0405 Mao L T, Bi Y J, Liu H Z, Chen J, Wang J Q, Peng R D, Liu H B, Wu H, Sun Y, Ju Y 2023 Chin. Sci. Bill. 68 380 doi: 10.1360/TB-2022-0405 [26] Sakamoto S, Suzuki K, Toda K, Seino S 2022 Materials 15 7393 doi: 10.3390/ma15207393 [27] Zhuang C, Jianfeng W, Wei X 2023 Géotech. 21 1 doi: 10.1680/jgeot.21.00281 [28] 孙其诚, 王光谦 2008 物理学报 57 4667 doi: 10.7498/aps.57.4667 Sun Q C, Wang G Q 2008 Acta Phys. Sin. 57 4667 doi: 10.7498/aps.57.4667 [29] Pérez L G, Bernal P L J, Alés F V, del-Río J J M, Borreguero M, Ochoa J M A 2024 Boletín de la Sociedad Españ ola de Cerámicay Vidrio 63 216 [30] Wu Z H, Yang Y H, Zuo Y J, Meng X R, Wang W T, Lei W L 2023 Acta Geophys. 72 2503 doi: 10.1007/s11600-023-01228-9 [31] Fang H, He N 2023 Appl. Sci. 13 12270 doi: 10.3390/app132212270 [32] 雷健, 潘保芝, 张丽华 2018 地球物理学进展 33 653 doi: 10.6038/pg2018BB0108 Lei J, Pan B Z, Zhang L H 2018 Prog. Geophys. 33 653 doi: 10.6038/pg2018BB0108 [33] Hosseinzadegan A, Raoof A, Mahdiyar H, Nikooee E, Ghaedi M, Qajar J 2023 Geoenergy Sci. Eng. 226 211 -
图( 20)
计量
- 文章访问数: 530
- HTML全文浏览数: 530
- PDF下载数: 4
- 施引文献: 0