首页
登录
注册
下载:
-
里德伯原子是主量子数较高的激发态原子, 里德伯原子临近量子态跃迁频率覆盖射频、微波、太赫兹频段, 其广泛应用于量子测量、量子模拟等领域[1–5]. 碱金属原子里德伯态可以通过单光子激发[6]、双光子激发[7]、多光子激发[8]制备; 基于多光子干涉原理的电磁感应透明[9](electromagnetically induced transparency, EIT)光谱可以实现里德伯原子的非破坏性测量, 其广泛应用于室温气室原子的电磁场测量[10–12].
基于原子传感的电磁场测量依赖目标原子的数量或密度. 光学原子磁强计通常采用偏振光泵浦实现原子极化态的制备, 由于原子自发辐射以及原子碰撞退极化等效应, 单束激光泵浦通常不能实现高极化率的原子自旋态布居. 实验上通常引入反抽运光提高原子极化态的制备效率, 通过增加传感原子数量来提高原子磁强计测量灵敏度[13,14]. 基于里德伯原子的电场传感, 通过引入辅助场泵浦提高传感原子数量[15], 通过原子布居数的增加来改善电场测量极限灵敏度. 实际中, 室温气室原子多普勒速度分布对应的频率展宽远大于泵浦激光线宽, 单波长激光只能实现很窄速度群原子的里德伯态布居. 典型室温气室铯原子多普勒速度分布对应的频率分布~400 MHz, 其远大于852 nm和509 nm泵浦光场线宽, 双光子共振激发通常只能选择频移~MHz范围速度群原子布居到里德伯态. 特别是EIT光谱, 由于双光子共振激发的波长匹配[16,17]的要求以及激发光场空间几何要求, 通常选择共线反向传输的光束几何构型[18], 该构型通常只能激发相对光场波矢垂直的速度群原子, 即相对零速度群原子. 虽然该构型能够在室温原子气室中获得窄线宽光谱, 但是激发原子相对数量较少, 有限的原子数会影响EIT光谱的信噪比.
提高传感原子数量或密度是提高测量灵敏度的有效途径. 近年来, 为获得高数量或高密度目标态原子数, 在光学泵浦基础上又发展了射频泵浦、微波泵浦、空间分离泵浦、时间分离泵浦、光频梳锁频泵浦等辅助泵浦技术. 时域周期纳秒脉冲激光在频域上可以等效为动力学稳定的多频率激光, 频率分布或频谱包络依赖脉冲宽度, 激光频率间隔依赖脉冲重复频率. 通过脉冲宽度和脉冲重复频率的优化, 可以实现从连续到可控频率分布的频率梳激光. 20世纪80年代, Kocharovskaya和Khanin[19]提出了二能级原子系统的脉冲激发基本理论; 2003年, Felinto等[20]研究了基于锁模激光脉冲序列的原子态相干布居效应. 后续研究拓展到三能级与多能级模型, 并逐步完善原子脉冲激发的动力学特性. 相关工作包括飞秒脉冲激发冷原子双光子跃迁[21]、铷原子气室中的速度选择光泵浦[22]、任意形状脉冲与多能级原子相互作用[23]等. 时域周期纳秒脉冲通过傅里叶变换在频域上表现为高斯包络下的分立梳状谱, 梳状谱间隔为脉冲激光的重复频率. 基于微型脉冲频率梳技术可以实现覆盖大于400 MHz的激光频谱分布, 在此基础上, 利用双光子级联激发可以实现多个速度群原子的里德伯态布居, 该方案为获得高密度里德伯原子提供了技术手段.
本文利用1018 nm激光倍频获得509 nm脉冲激光, 利用852 nm连续激光和509 nm脉冲激光双光子级联激发, 在室温铯原子气室中实现了梳状里德伯原子光谱, 研究了脉冲激光泵浦的里德伯原子光谱特性. 实验利用电磁诱导透明(EIT)光谱进行里德伯态原子布居探测, 研究了脉冲频谱的参数依赖关系. 通过建立三能级原子系统的周期脉冲激发模型, 给出了相应的EIT光谱, 实验结果和理论相符合.
-
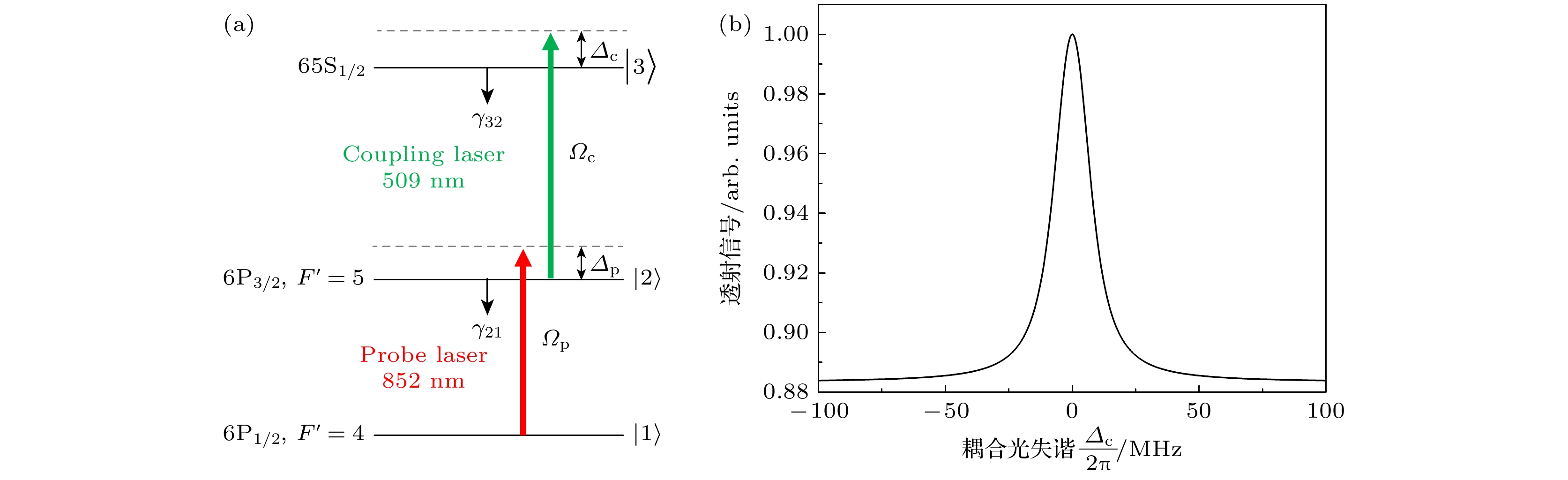
图1(a)为铯原子(133Cs)里德伯态的能级示意图. 能级
$\left| {1} \right\rangle $ ,$\left| {2} \right\rangle $ ,$\left| {3} \right\rangle $ 分别表示原子基态、中间态、里德伯态. EIT探测光和耦合光的角频率分别为${\omega _{\text{p}}}$ 和${\omega _{\text{c}}}$ , 对应原子$\left| {1} \right\rangle $ →$\left| {2} \right\rangle $ 和$\left| {2} \right\rangle $ →$\left| {3} \right\rangle $ 跃迁;${\varDelta _{\text{p}}}$ 与${\varDelta _{\text{c}}}$ 分别为探测光和耦合光相对原子共振跃迁的频率失谐, 相应拉比频率分别为${\varOmega _{\text{p}}} = {\mu _{12}}{E_{\text{p}}}/({\hbar})$ 和${\varOmega _{\text{c}}} = {\mu _{23}}{E_{\text{c}}}/(\hbar)$ ;$ \mu_{12} $ 和$ \mu_{23} $ 是相应跃迁的电偶极矩,${\gamma _{{32}}}$ 和${\gamma _{{21}}}$ 分别为里德伯态和中间态的衰减. 图1(b)为理论模拟的阶梯型三能级EIT光谱.原子与光场相互作用的哈密顿量为
其中, Ha为原子哈密顿量, Hl为光场哈密顿量, Hal为相互作用哈密顿量.
旋波近似和偶极近似条件下, 三能级原子系统哈密顿量矩阵形式表示为
其中
$ \hbar $ 为普朗克常量.密度矩阵随时间的演化可以描述三能级系统演化, 其动力学可以由Lindblad主方程表示:
其中,
$ {\boldsymbol{L}}\left( {\boldsymbol{\rho }} \right) $ 为退相位矩阵.$ {\boldsymbol{\rho }} $ 为原子的密度矩阵:三能级原子系统中描述衰减的退相位矩阵
$ {\boldsymbol{L}}\left( {\boldsymbol{\rho }} \right) $ 表示为式中,
${\gamma _{{32}}}$ 是里德伯态$\left| {3} \right\rangle $ 到中间态$\left| {2} \right\rangle $ 的衰减率,${\gamma _{{21}}}$ 是中间态$\left| {2} \right\rangle $ 到基态$\left| {1} \right\rangle $ 的衰减率.室温气室原子需要考虑多普勒效应导致的原子跃迁频移, 阶梯型三能级铯原子通过双光子级联激发构建EIT暗态, 其要满足单光子和双光子共振条件, 由于852 nm探测光与509 nm耦合光波长差较大, 双光子过程还需要考虑波长匹配效应. 里德伯EIT通常选择耦合光与探测光反向共线传输的几何模式, 其通过选择相对“零速度群原子”消除一阶多普勒展宽获得窄线宽光谱. 时域周期纳秒脉冲通过傅里叶变换在频域上表现为高斯包络下的分立梳状谱, 梳状谱间隔为脉冲激光的重复频率. 在铯原子阶梯型EIT能级结构中, 对锁定于6S1/2(F = 4) → 6P3/2(F' = 5)的852 nm探测光, 当特定速度群原子运动方向与852 nm光束的传播方向一致时, 由于多普勒效应, 其感受到的探测光频率低于6S1/2(F = 4)→6P3/2(F' = 5)跃迁的共振频率(失谐为Δ), 当509 nm脉冲光的重复频率经过波长匹配恰好等于Δ时, 该特定速度群原子被激发到里德伯态. 同理, 当特定速度群原子运动方向与852 nm光束的传播方向相反时, 509 nm脉冲光通过波长匹配将这一特定速度群原子激发到里德伯态. 由于多普勒效应, 原子不同的运动速度导致的多普勒展宽~400 MHz, 频率失谐在此范围内的跃迁都满足单光子共振条件. 在~400 MHz的多普勒频移范围, 相干频率梳激光可以实现多个速度群里德伯原子布居, 相应的光谱即为里德伯EIT干涉光谱或类频率梳光谱. 脉宽给出了光谱的整体包络, 脉冲重复频率给出干涉谱间隔. 室温气室原子典型的EIT线宽为10 MHz左右, 纳秒脉冲傅里叶变换频率谱宽为GHz左右, 当重复频率小于10 MHz时, 不同梳齿光谱重叠; 当重复频率大于10 MHz时, 不同梳齿分离, 谱线间隔为重复频率. 通过脉冲参数调谐可以实现可控速度群原子的里德伯态激发.
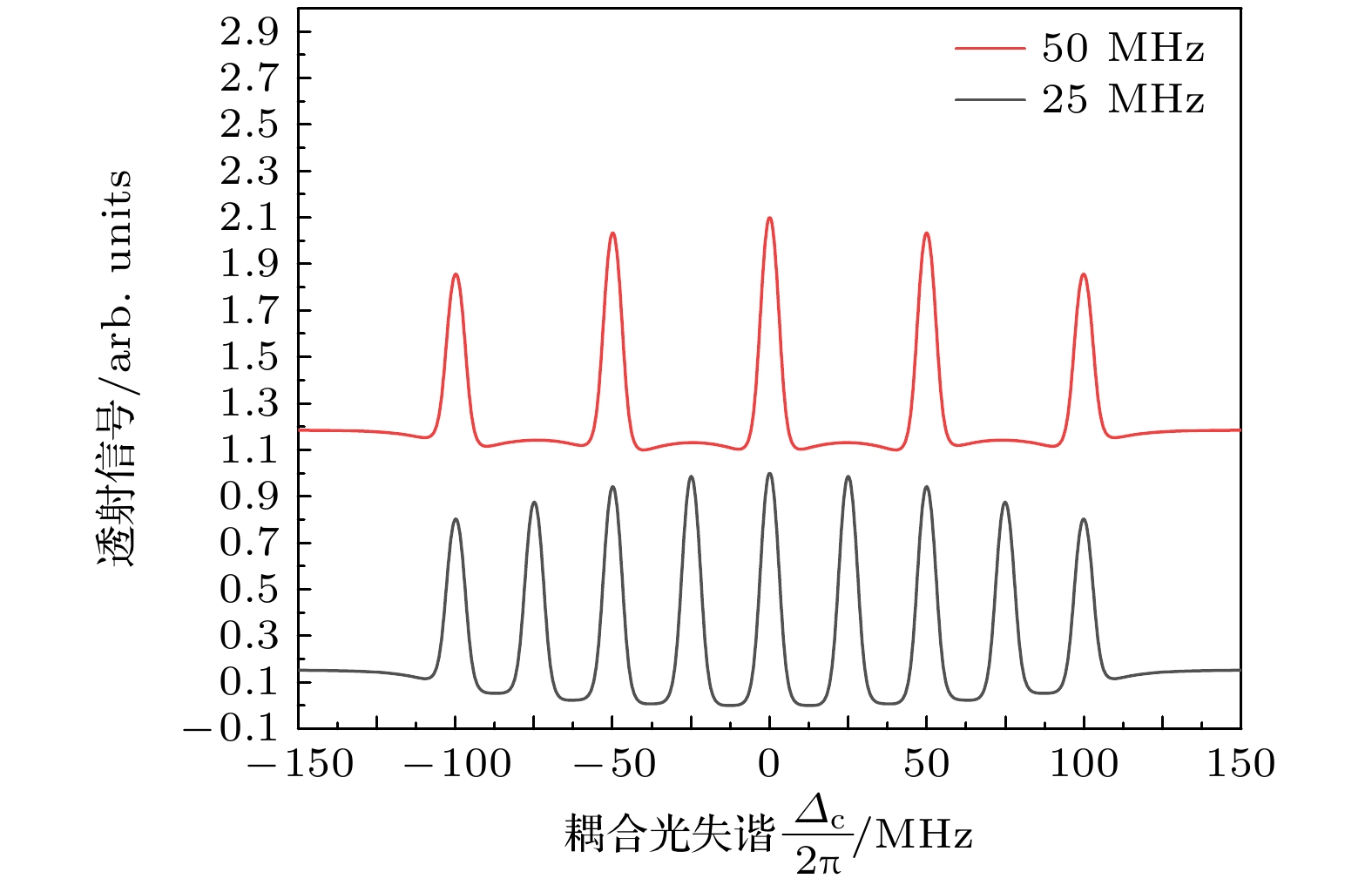
图1(b)数值模拟了连续光条件下特定速度群原子激发至里德伯态的光谱, 结果呈现出一个单峰, 即在中心频率15 MHz范围内的速度群原子被激发到里德伯态. 图2理论模拟了不同耦合光失谐下多速度群原子激发的EIT光谱. 探测光的强度为
${\varOmega _{\text{p}}}{{/(2\pi )}} = {\text{10 MHz}}$ , 耦合光的强度为${\varOmega _{\text{c}}}{{/(2\pi )}} = {\text{10 MHz}}$ , 中间态的衰减为${{2\pi \times 5}}{\text{.2 MHz}}$ , 里德伯态的衰减为$2\pi \times 1\; {\rm{MHz}}$ , 模拟光谱图中红色和黑色曲线的耦合光失谐量依次为${\varDelta _{\text{c}}}{{/(2\pi )}} = {\text{0, }} \pm {50}, \pm 100 {\rm MHz}$ ,${\varDelta _{\text{c}}}{{/(2\pi) }} = 0, \pm 25, \pm 50, \pm 75, \pm {\text{100 MHz}}$ . 不同耦合光失谐量下的EIT信号, 表示不同失谐处对应的速度群原子都被激发至里德伯态. 多个速度群原子里德伯态激发相对特定速度群激发的EIT光谱, 里德伯态原子数量分别提高4.5倍(红色曲线)和7倍(黑色曲线). -
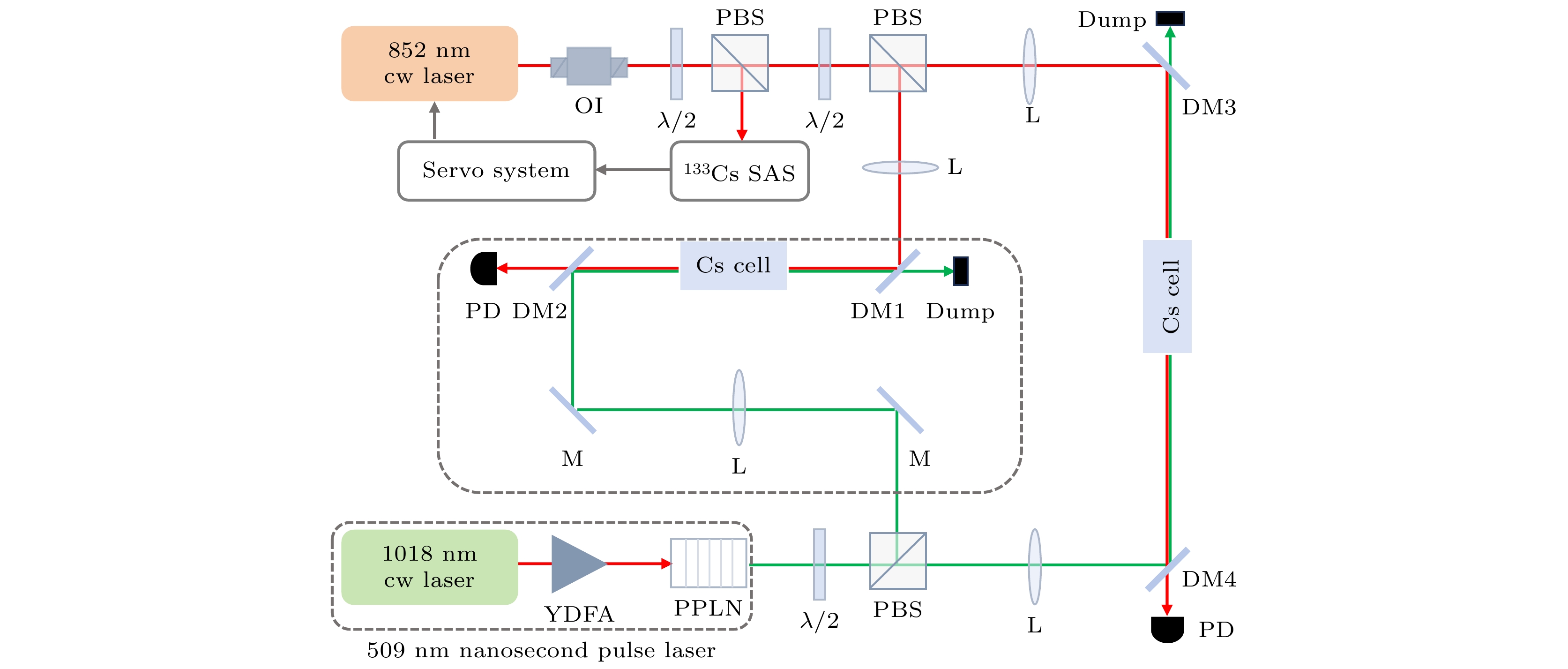
实验选择852 nm和509 nm激光分别作为探测光和耦合光. 852 nm探测光频率锁定于6S1/2 (F = 4) → 6P3/2(F' = 5), 509 nm耦合光频率在6P3/2(F' = 5) → 65S1/2跃迁之间扫描, 当满足双光子共振条件时可以得到EIT光谱. 实验装置如图3所示[24], 852 nm探测光由外腔半导体激光器(ECDL)提供, 典型线宽约为百kHz; 输出光经光隔离器、半波片和偏振分光棱镜分成两束, 一路搭建饱和吸收光谱(SAS), 用于激光稳频; 另一路经半波片和偏振分光棱镜分束, 一束与509 nm激光反向共线传输构建参考EIT用于509 nm激光稳频, 另一束与509 nm耦合光反向共线传输用于脉冲光谱实验测量. 1018 nm脉冲激光通过掺镱光纤放大器(YDFA)将功率放大, 典型峰值功率4600 W; 大功率1018 nm激光单次穿过周期极化铌酸锂(PPLN)晶体倍频获得509 nm脉冲激光, 典型脉冲激光峰值功率173 W. 测量所用圆柱体铯原子气室直径25 mm、长150 mm. 852 nm探测光通过二向色镜与509 nm光束分开, 透射光进入探测器, 探测器将光信号转换成电信号之后和示波器连接, 通过扫描509 nm耦合光获得EIT光谱.
-
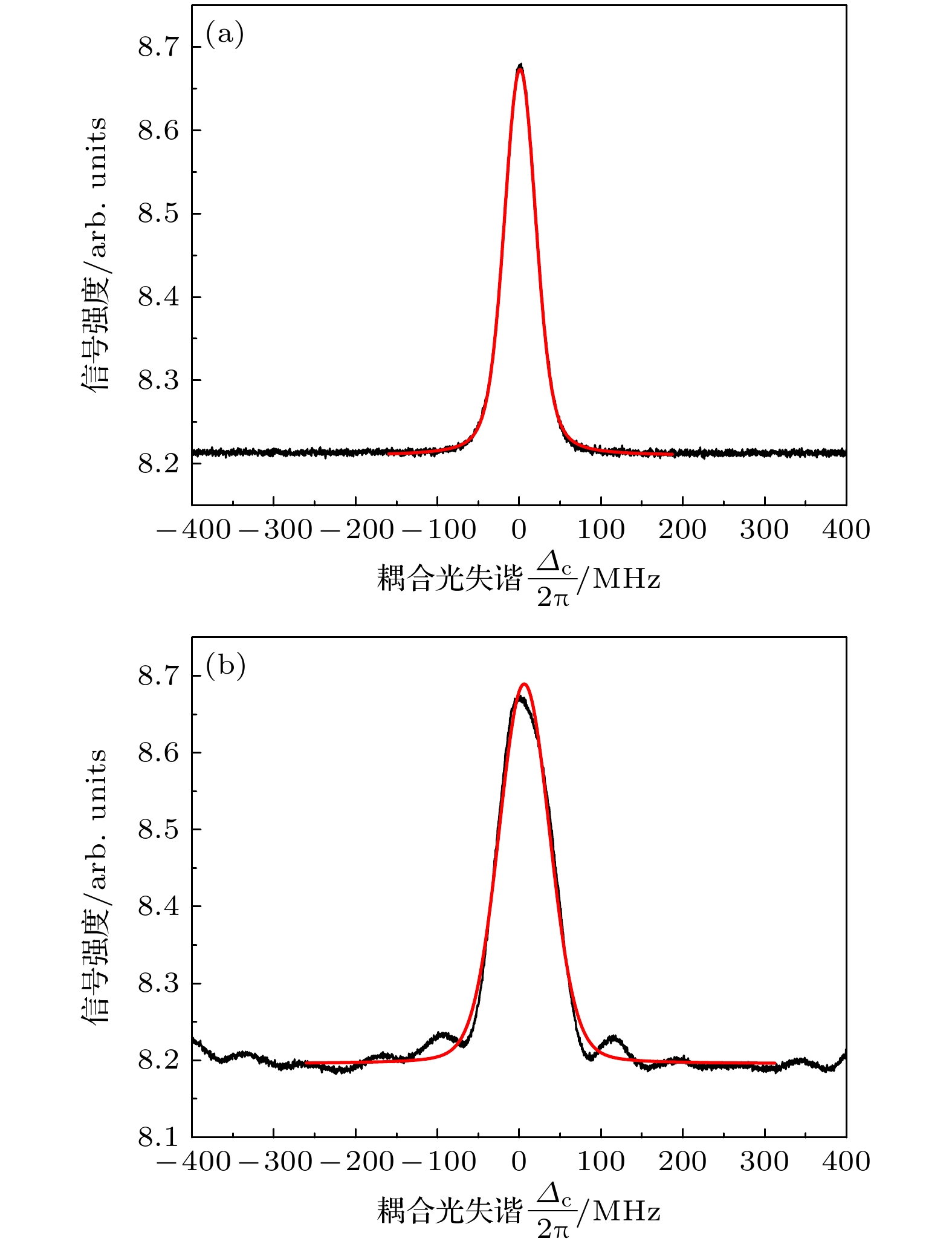
509 nm激光脉宽为
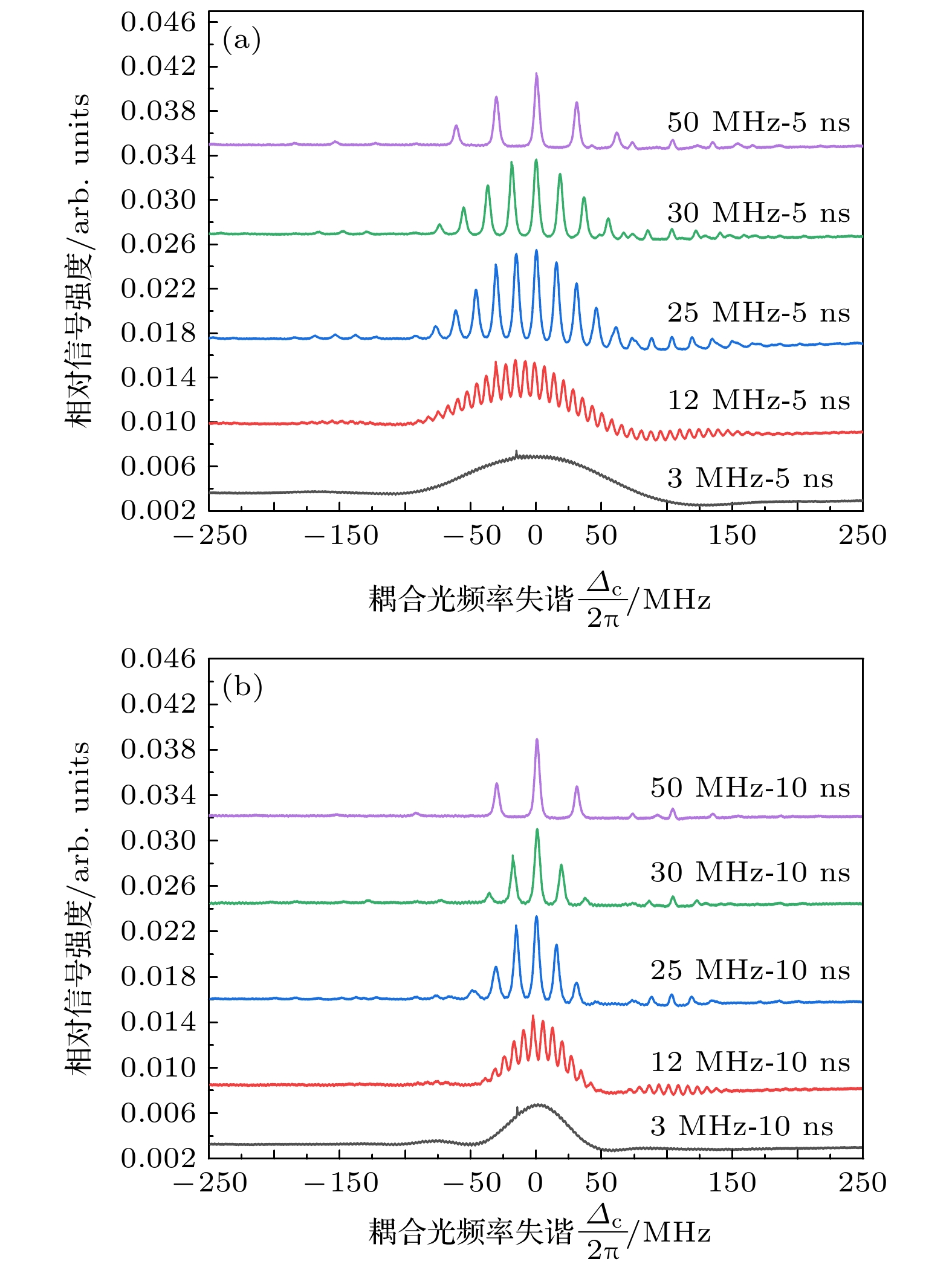
${\tau _{\text{p}}}$ , 重复周期为${T_{\text{R}}}$ , 重复频率为$f = {\text{1/}}{T_{\text{R}}}$ ; 脉宽在1—100 ns连续可调, 重复频率在300 kHz—100 MHz连续可调. 图4(a)为典型的连续激光里德伯原子EIT光谱, 图4(b)为脉冲509 nm激光的EIT光谱. 对应852 nm连续激光功率为12.3 μW, 509 nm脉冲激光功率为236 mW, 脉宽为10 ns、重复频率为10 MHz. 连续激光激发的EIT线宽约为15 MHz, EIT线宽主要由强耦合光的拉比频率决定; 脉冲光激发的EIT光谱包络由脉冲傅里叶变换对应的频谱决定, 当脉宽为10 ns时, EIT包络宽度约为100 MHz, 由于EIT线宽约为15 MHz, 重复频率为10 MHz 的梳齿信号表现为近连续光谱.实验研究了EIT光谱与激光脉冲重复频率、脉宽等参数的依赖关系. 当脉冲激光重复频率大于EIT线宽时, EIT信号由连续单峰光谱线型转换为多峰结构, 峰的间隔由脉冲光重复频率决定. 如图5(a)所示, 当激光脉宽为
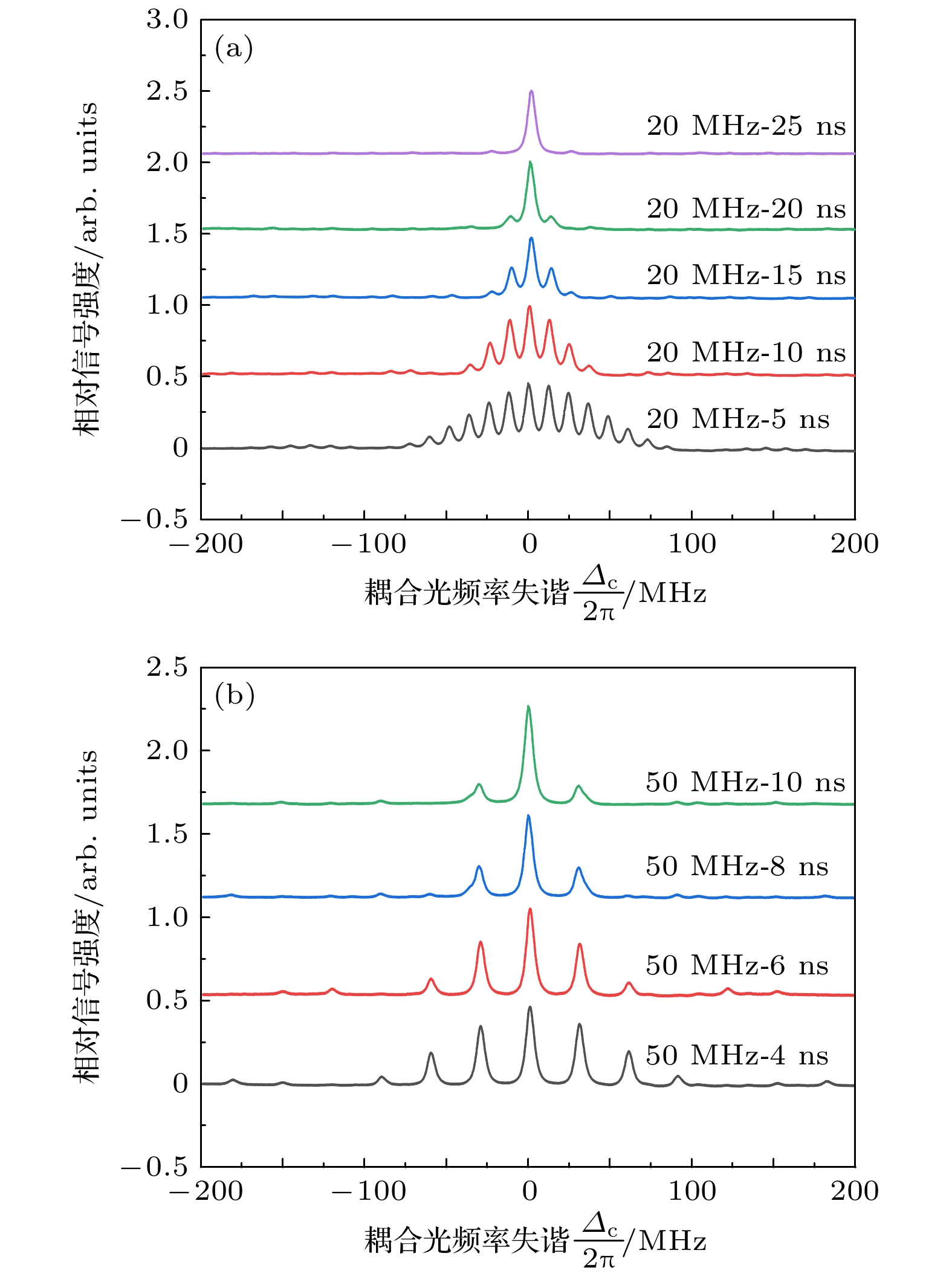
${\tau _{\text{p}}} = {\text{5 ns}}$ 、重复频率为$ f= \text{50 MHz} $ 时, 对应的光谱包络宽度为${\text{1/}}{\tau _{\text{p}}} = {\text{200 MHz}}$ , EIT线型由单峰结构变化为梳齿结构, 梳齿间隔均为50 MHz, 与脉冲激光重复频率一致. EIT中心峰频率失谐±50 MHz, ±100 MHz位置处的4个速度群原子同样被激发至里德伯态, 根据EIT信号的透射峰值可以计算出里德伯态的原子布居数是连续耦合光激发时的3倍. 由于基态原子多普勒速度分布为麦克斯韦-玻尔兹曼分布, 零速度群原子相对较多, 其信号相对较强, 同时远离共振的EIT谱峰的强度逐渐下降. 当重复频率为25 MHz时, 谱线的包络宽度为${\text{1/}}{\tau _{\text{p}}} = {\text{200 MHz}}$ , 梳齿间隔为25 MHz. 可以看到, 在200 MHz包络宽度内, 与中心峰频率失谐±25 MHz整数倍的速度群原子可以被激发至里德伯态, 此时里德伯态原子数量提高了5倍. 减小重复频率可以进一步提高里德伯态的原子数量, 当脉冲光重复频率接近EIT线宽时最大可以提高10倍, 脉冲光重复频率小于EIT线宽时, 里德伯原子激发光谱表现为近连续. 图5(b)中, 脉宽为${\tau _{\text{p}}} = {\text{10 ns}}$ , 相应的谱线包络宽度为${\text{1/}}{\tau _{\text{p}}} = {\text{100 MHz}}$ , 脉冲重复频率为50 MHz(紫色曲线)、25 MHz(蓝色曲线)时, 梳齿间隔或透射峰间隔同样与相应的激光重复频率一致. 与图2中理论模拟结果相比, 实验得到的EIT光谱由于双光束在铯原子气室中对向传输可以消除一部分多普勒效应的影响, 整体线型与模拟结果一致.实验研究了EIT光谱与脉冲光脉宽的依赖关系. 图6为脉冲重复频率分别为20 MHz和50 MHz时, 改变脉冲光脉宽得到的光谱结果. 图6(a)中不同脉宽下光谱中的梳齿间距均相等, 对应脉冲光重复频率20 MHz; 图6(b)中每一个谱线的透射峰间距均为50 MHz, 与脉冲重复频率一致. 可以看到, 相同重复频率条件下, 随着脉宽的减小, EIT峰齿数量增加, 激发到里德伯态的原子数量也增加, 在重复频率为50 MHz、脉宽为4 ns时激发的原子数量是50 MHz, 10 ns条件下的2倍.
考虑多普勒效应, 运动方向与光束传播方向一致或相反的速度群原子感受到光的频率有多普勒频移Δ = k·v, k是激光波矢量, v是原子速度矢量. 双光子激发过程中, 不同的速度群原子对应于不同的激光失谐Δ. 脉冲光由1/TR间隔的多频率激光组成, 当激光中心频率固定后, 失谐
$\varDelta = {\varDelta _n} \pm {{2\pi }}m{\text{/}}{T_{\text{R}}}$ 的速度群也满足共振条件, m为整数. 对于室温气室铯原子, 多普勒展宽范围约400 MHz内, 对应脉冲光包络下不同梳齿的速度群原子都可以激发到里德伯态, 使里德伯态的原子数量得到提高. 相较于连续光的单峰EIT光谱结果, 该实验利用纳秒脉冲可以激发不同速度群原子至里德伯态, 得到的EIT光谱峰齿数量增多, 有效提高了里德伯态的原子数量. 通过EIT光谱测量给出里德伯原子布居数量, 在较大失谐条件下, 由于原子速度群的麦克斯韦-玻尔兹曼分布, 远离共振中心的原子数量较少, EIT信号较弱, 图5和图6中 EIT信号光谱没有显示出更弱的高阶边带信号.时域周期纳秒脉冲激光, 在频域上可以等效为动力学稳定的多频率激光, 其频率分布依赖脉冲重复频率. 实验通过阶梯型双光子激发实现室温气室的里德伯原子制备和检测, 通过EIT光谱给出脉冲激发的光谱线型. 实验结果证实, 脉冲激发的EIT光谱, 脉宽的傅里叶变换给出了可激发热原子多普勒频率分布范围, 脉冲重复频率给出了干涉梳状光谱的谱线间隔. 当重复频率小于EIT线宽时, 脉冲激发给出近连续的里德伯原子激发光谱; 当重复频率大于EIT线宽时, 干涉光谱给出梳状的分离激发光谱.
-
本文利用双光子激发的实验方案制备铯原子里德伯态, 通过改变509 nm脉冲激光的重复频率和脉宽, 在室温铯原子气室中实现了梳状里德伯原子光谱. 在一定的重复频率和脉宽范围内, 谱线的包络呈现出规律的变化, 谱线中的透射峰间距与脉冲重复频率保持一致, 可以通过改变脉冲重复频率和脉宽的值来实现特定速度群原子的激发, 对于我们的脉冲激光系统, 相对中心峰频率失谐量可取范围为±100 MHz, 在光谱包络内, 失谐量整数倍位置处的速度群原子均可激发至里德伯态.
相对连续激光有限速度群原子泵浦, 脉冲509 nm耦合光激发时减小重复频率可以进一步提高里德伯态的原子数量, 当脉冲光重复频率接近EIT线宽时最大可以提高10倍. 优化参数过程中, 需要考虑多能级原子脉冲激发的动力学特性, 以及任意形状光脉冲与多能级系统相互作用特性等. 基于脉冲光泵浦可以实现光场与特定多普勒速度群原子的相互作用, 基于此发展的原子类频率梳光谱可以实现电场和磁场测量. 利用光谱的多峰结构可以更精确地确定微波电场的强度、频率和相位等信息, 这种高灵敏度和分辨率的测量能力对于微波电场的高精度测量[25,26]至关重要. 脉冲耦合光可以实现特定速度群原子激发至里德伯态, 高密度里德伯原子有利于改善测量光谱信噪比, 对基于里德伯原子的量子传感和量子测量有潜在的应用价值.
基于纳秒光脉冲激发的里德伯原子光谱
Rydberg atomic spectroscopy based on nanosecond pulsed laser excitation
-
摘要: 通过852 nm连续激光和509 nm脉冲激光级联激发, 在室温铯原子气室中实现了里德伯原子电磁诱导透明(EIT)光谱. 509 nm纳秒激光脉冲功率~173 W, 脉冲重复频率在300 kHz—100 MHz范围连续可调, 脉宽在1—100 ns范围连续可调. 实验研究了里德伯EIT光谱与509 nm脉冲激光参数的关系. 时域周期脉冲光在频域上等效为相干频率梳, 通过激光脉冲参数调节实现了可控速度群原子的里德伯态激发. 基于光脉冲激发的原子干涉光谱具有高信噪比, 在量子传感和量子模拟领域有潜在的应用价值.Abstract:
Through the cascade excitation of 852-nm continuous-wave (CW) laser and 509-nm nanosecond pulsed laser, the electromagnetically-induced transparency (EIT) spectroscopic signals of ladder-type three-level cesium atoms with Rydberg state are obtained by using a room-temperature cesium vapor cell. The power of 509-nm pulsed laser beam is ~176 W, while the pulse repetition frequency ranges from 300 kHz to 100 MHz and can be continuously adjusted. The laser pulse duration runs from 1 to 100 ns and can be continuously adjusted. The relationship between Rydberg EIT spectroscopic signals and 509-nm nanosecond pulsed laser parameters is investigated experimentally. By changing the pulse repetition frequency and the pulse duration of the 509-nm nanosecond pulsed laser, the comb-like Rydberg atomic spectrum is obtained by using a room-temperature cesium vapor cell. Within a certain range of repetition frequency and pulse duration, the envelope of spectral lines shows a regular pattern, and the spacing between the transmission peaks is consistent with the pulse repetition frequency. By changing the 509-nm laser pulse repetition frequency and pulse duration, atoms with the specific velocity group can be excited to Rydberg state. Reducing the repetition frequency of the 509-nm pulsed coupling laser can further increase the number of atoms in the Rydberg state in comparison with the case of finite velocity group pumping of cesium atoms by a continuous-wave laser. When the repetition frequency of the 509-nm pulsed laser approaches the EIT linewidth, the number of cesium Rydberg atoms can be increased by up to 10 times. In the parameter optimization process, the dynamic characteristics of pulsed excitation in multi-level atoms, as well as the interaction characteristics between arbitrarily shaped laser pulses and multi-level atomic systems, should be considered. Pulsed laser pumping can achieve the interaction between the laser field and atomic group with a specific velocity, and its developed atomic frequency comb spectra can be used for electric and magnetic field measurements. The multi-peak structure of the spectrum can be used to more accurately determine the intensity, frequency, and phase of the microwave electric field by measuring spectral variations. This high-sensitivity and high-resolution measurement capability is crucial for precisely measuring microwave electric fields. The pulsed coupling laser can excite atoms in a specific velocity group to the Rydberg state. High-density Rydberg atoms can improve the signal-to-noise ratio of the measured spectrum, which has potential applications in quantum sensing and quantum measurement based on Rydberg atoms. -
-
图 1 (a)铯原子里德伯EIT阶梯型能级图, 包括基态
$\left| 1 \right\rangle $ 、中间态$\left| {2} \right\rangle $ 和里德伯态$\left| {3} \right\rangle $ , 852 nm的弱探测激光束以拉比频率${\varOmega _{\text{p}}}$ 耦合态$\left| 1 \right\rangle $ 和态$\left| {2} \right\rangle $ , 而509 nm的强耦合激光束以拉比频率${\varOmega _{\text{c}}}$ 耦合态$\left| {2} \right\rangle $ 和态$\left| {3} \right\rangle $ ,${\varDelta _{\text{p}}}$ (${\varDelta _{\text{c}}}$ )是探测激光束(耦合激光束)的频率失谐量. (b)阶梯型多能级结构理论模拟EIT光谱, 横坐标为耦合光失谐, 纵坐标为EIT透射信号强度Figure 1. (a) Schematic of a ladder-type three-level cesium atomic system with the ground state
$\left| 1 \right\rangle $ , the intermediate state$\left| {2} \right\rangle $ , and Rydberg state$\left| {3} \right\rangle $ , the 852 nm weak probe laser beam couples states$\left| 1 \right\rangle $ and$\left| {2} \right\rangle $ with Rabi frequency${\varOmega _{\text{p}}}$ , while the 509 nm strong coupling laser couples states$\left| {2} \right\rangle $ and$\left| {3} \right\rangle $ with Rabi frequency${\varOmega _{\text{c}}}$ ,${\varDelta _{\text{p}}}$ (${\varDelta _{\text{c}}}$ ) is the frequency detuning of the probe laser beam (the coupling laser beam). (b) Transmission spectram of the probe laser beam versus the coupling laser detuning, the abscissa represents the detuning of the coupling light, while the ordinate represents the intensity of the EIT transmission signal.
图 2 耦合光为脉冲激光的阶梯型多能级结构理论模拟EIT光谱, 横坐标为耦合光失谐, 纵坐标为归一化的EIT透射信号强度
Figure 2. Transmission spectra of the probe laser beam versus the nanosecond pulsed coupling laser detuning, the abscissa represents the detuning of the coupling light, while the ordinate represents the intensity of the EIT transmission signal.
图 3 铯原子光谱实验装置图, 其中OI为光隔离器; YDFA为掺镱光纤放大器; λ/2为半波片; PBS为偏振分光棱镜; L为透镜; DM2, DM4为509 nm高反射率(HR)和852 nm高透射率(HT)双色镜; DM1, DM3为509 nm高透射率(HT)和852 nm高反射率(HR)双色镜; PD为光电探测器; PPLN为周期极化铌酸锂晶体; M为509 nm高反镜; SAS为饱和吸收光谱装置; Dump为光学垃圾堆
Figure 3. Experimental set-up, where OI is optical isolator; YDFA is ytterbium-doped fiber amplifier; λ/2 is half-wave plate; PBS is polarization beam splitter cube; L is Lens; DM2 and DM4 are 509 nm high reflectivity (HR) and 852 nm high transmissivity (HT) dichroic mirrors; DM1 and DM3 are 509 nm high transmissivity (HT) and 852 nm high reflectivity (HR) dichroic mirrors; PD is photodiode; PPLN is periodically poled lithium niobate crystals; M is 509 nm high reflectivity mirror; SAS is cesium atomic saturation absorption spectroscopic device; Dump is optical dump.
图 4 铯里德伯原子EIT光谱 (a) 连续509 nm耦合光扫描; (b) 脉冲509 nm耦合光扫描
Figure 4. EIT spectra of cesium Rydberg atoms: (a) The continuous-wave 509 nm coupling laser beam is frequency scanned; (b) the pulsed 509 nm coupling laser beam is frequency scanned.
图 5 不同重复频率下, 脉宽为(a) 5 ns和(b) 10 ns的 EIT信号光谱图
Figure 5. EIT spectra of cesium Rydberg atoms for the pulse duration is (a) 5 ns and (b) 10 ns.
图 6 EIT信号光谱图 (a) 重复频率为20 MHz, 脉宽分别为5 ns (灰色)、10 ns (红色)、15 ns (蓝色)、20 ns (绿色)、25 ns (紫色); (b) 重复频率为50 MHz, 脉宽分别为4 ns (灰色)、6 ns (红色)、8 ns (蓝色)、10 ns (绿色)
Figure 6. EIT spectra of cesium Rydberg atoms: (a) Repetition frequency is 20 MHz, while the pulse duration is 5 ns (gray), 10 ns (red), 15 ns (blue), 20 ns (green), and 25 ns (purple), respectively; (b) the repetition frequency is 50 MHz, while the pulse duration is 4 ns (gray), 6 ns (red), 8 ns (blue), and 10 ns (green), respectively.
-
[1] Adams C S, Pritchard J D, Shaffer J P 2020 J. Phys. B: At. Mol. Opt. Phys. 53 012002 doi: 10.1088/1361-6455/ab52ef [2] 周飞, 贾凤东, 刘修彬, 张剑, 谢锋, 钟志萍 2023 物理学报 72 045204 doi: 10.7498/aps.72.20222059 Zhou F, Jia F D, Liu X B, Zhang J, Xie F, Zhong Z P 2023 Acta Phys. Sin. 72 045204 doi: 10.7498/aps.72.20222059 [3] Zhang L J, Bao S X, Zhang H, Raithel G, Zhao J M, Xiao L T, Jia S T 2018 Opt. Express 26 29931 doi: 10.1364/OE.26.029931 [4] Bason M G, Tanasittikosol M, Sargsyan A, Mohapatra A K, Sarkisyan D, Potvliege R M, Adams C S 2010 New J. Phys. 12 065015 doi: 10.1088/1367-2630/12/6/065015 [5] Barredo D, Kubler H, Daschner R, Löw R, Pfau T 2013 Phys. Rev. Lett. 110 123002 doi: 10.1103/PhysRevLett.110.123002 [6] 王军民, 白建东, 王杰英, 刘硕, 杨保东, 何军 2019 中国光学 12 701 doi: 10.3788/co.20191204.0701 Wang J M, Bai J D, Wang J Y, Liu S, Yang B D, He J 2019 Chin. Opt. 12 701 doi: 10.3788/co.20191204.0701 [7] Hao L P, Xue Y M, Fan J B, Bai J X, Jiao Y C, Zhao J M 2020 Chin. Phys. B 29 033201 doi: 10.1088/1674-1056/ab6c49 [8] Fan J B, He Y H, Jiao Y C, Hao L P, Zhao J M, Jia S T 2021 Chin. Phys. B 30 034207 doi: 10.1088/1674-1056/abca25 [9] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003 doi: 10.1103/PhysRevLett.98.113003 [10] Zhao J M, Zhu X B, Zhang L J, Feng Z G, Li C Y, Jia S T 2009 Opt. Express 17 15821 doi: 10.1364/OE.17.015821 [11] Kübler H, Shaffer J P, Baluktsian T, Löw R, Pfau T 2010 Nat. Photonics 4 112 doi: 10.1038/nphoton.2009.260 [12] Huber B, Baluktsian T, Schlagmuller M, Kolle A, Kübler H, Löw R, Pfau T 2011 Phys. Rev. Lett. 107 243001 doi: 10.1103/PhysRevLett.107.243001 [13] Wang Y N, Meng Y L, Wan J Y, Yu M Y, Wang X, Xiao L, Cheng H D, Liu L 2018 Phys. Rev. A 97 023421 doi: 10.1103/PhysRevA.97.023421 [14] Li R J, Perrella C, Luiten A 2022 Opt. Express 30 31752 doi: 10.1364/OE.467513 [15] Prajapati N, Robinson A K, Berweger S, Simons M T, Artusio-Glimpse A B, Holloway C L 2021 Appl. Phys. Lett. 119 214001 doi: 10.1063/5.0069195 [16] Holloway C L, Simons M T, Gordon J A, Dienstfrey A, Anderson D A, Raithel G 2017 J. Appl. Phys. 121 233106 doi: 10.1063/1.4984201 [17] Schütz J, Martin A, Laschinger S, Birkl G 2022 J. Phys. B: At. Mol. Opt. Phys. 55 234004 doi: 10.1088/1361-6455/ac9c3a [18] Harris S E 1989 Phys. Rev. Lett. 62 1033 doi: 10.1103/PhysRevLett.62.1033 [19] Kocharovskaya O A, Khanin Y I 1986 Sov. Phys. JETP 63 945 [20] Felinto D, Bosco C A C, Acioli L H, Vianna S S 2003 Opt. Commun. 215 69 doi: 10.1016/S0030-4018(02)02230-7 [21] Marian A, Stowe M C, Lawall J R, Felinto D, Ye J 2004 Science 306 2063 doi: 10.1126/science.1105660 [22] Aumiler D, Ban T, Skenderović H, Pichler G 2005 Phys. Rev. Lett. 95 233001 doi: 10.1103/PhysRevLett.95.233001 [23] Felinto D, López C E E 2009 Phys. Rev. A 80 013419 doi: 10.1103/PhysRevA.80.013419 [24] 刘瑶, 何军, 苏楠, 蔡婷, 刘智慧, 刁文婷, 王军民 2023 物理学报 72 060303 doi: 10.7498/aps.72.20222286 Liu Y, He J, Su N, Cai T, Liu Z H, Diao W T, Wang J M 2023 Acta Phys. Sin. 72 060303 doi: 10.7498/aps.72.20222286 [25] Jia F D, Liu X B, Mei J, Yu Y H, Zhang H Y, Lin Z Q, Dong H Y, Zhang J, Xie F, Zhong Z P 2021 Phys. Rev. A 103 063113 doi: 10.1103/PhysRevA.103.063113 [26] Liu X B, Jia F D, Zhang H Y, Mei J, Yu Y H, Liang W C, Zhang J, Xie F, Zhong Z P 2021 AIP Adv. 11 085127 doi: 10.1063/5.0054027 -
计量
- 文章访问数: 473
- HTML全文浏览数: 473
- PDF下载数: 4
- 施引文献: 0