首页
登录
注册
-
原子质量是原子核物理、天体物理和核工程等领域研究中的关键参数[1,2]. 准确的原子质量数据在理解核结构[3]、核反应[4]、核衰变[5]以及星体演化过程[6]等方面具有至关重要的作用[7]. 这些数据支持核质量的计算和实验, 推动着核物理学科的深入研究和应用的发展.
20世纪30年代, Bethe, Bacher[8]以及Weizsäcker[9]融合理论计算和实验观测提出了一种半经验核质量公式用于计算原子核的结合能, 即著名的Bethe-Weizsäcker (BW)模型. BW模型考虑了核的体积效应、对称性效应、库仑排斥效应和原子核表面的效应. 为了提高计算结果的准确性, 2008年Kirson[10]在BW模型基础上添加了交换库仑项、Wigner项、表面对称项、配对项、曲率项和全局壳层修正项得出BW2模型, 即
其中,
$ \alpha_{v}\cdots\beta_{m} $ 表示核质量模型的各项系数. (2)式为(1)式部分项:式中
$ v_n $ 和$ v_p $ 是实际核子数$ N $ 和$ Z $ 与最接近的幻数[11–13]之差, 最常见的幻数有2, 8, 20, 28, 50, 82, 126和184. 使用最小二乘法[14,15]对实验测量的核质量进行拟合, 以确定理论模型中各项系数的理论值[10,16,17]. 通过计算理论值与实验值之间的均方根偏差(root mean square deviation, RMSD), 来描述理论模型的准确度. 具体的计算公式为在《原子质量评估AME2020》(
$ Z $ ,$ N $ $ \geqslant $ 8共3250个核素)[18,19] 的数据中, 原先系数的计算值与实验值的均方根偏差为1.92 MeV. 更新后的质量公式可以更准确地用于计算不同核素的结合能, 预测新的核素的性质, 进而研究核反应和核衰变等核物理过程, 在核物理研究中被广泛应用. 但存在在幻数附近和对重核元素[20–22]的预测偏差较大的问题, 不能更好地拟合实验数据.多层感知机(multilayer perceptron, MLP)作为一种神经网络模型, 隶属于机器学习中的深度学习领域, 专注使用深层神经网络来建模和解决复杂的任务. 在许多领域中, 特别是控制系统、模式识别和预测建模等方面, 多层感知器神经网络已经显示出卓越的性能. 它模拟了生物神经元的结构, 包括输入层、至少一个或多个隐藏层以及输出层. 其核心涉及多层神经元、权重、激活函数以及隐藏层等关键要素. 在这个模型训练过程中, 每个神经元与上一层的每个神经元相连, 通过更新优化器参数不断调整连接它们的权重和偏置, 以最小化模型在训练数据上的误差. 每个神经元都被赋予一个激活函数, 该函数根据输入的权重和偏置计算输出, 使得多层感知器能够学习和训练出更为复杂的模型结构. 通过层层堆叠的神经元, 以及逐渐优化的权重和激活函数, 实现了对复杂任务的学习和推断. 神经网络模型能够更好地自适应各种输入数据, 提高模型的泛化能力[23–26], 为设计神经网络寻找BW2模型较优系数提供了理论支持.
近年来, 神经网络方法已经应用到原子核质量的改进中, 特别是对于简单的液滴模型, 预测的结合能与实验数据的均方根偏差从2.455 MeV大幅降低到0.235 MeV (降低了90%)[27–32]. 在核质量模型改进的研究中, 更多的研究者通过改变质量公式[33]、传统数学算法[34]和利用神经网络方法优化核质量模型[35,36], 以此来提高预测的准确度. 而在核质量模型中, 模型的各项系数有很大的相关性[17], 局部核素结合能的计算值也有关联性[37]. 通过寻找到合适的方法拟合出更适合实验数据的系数具有很大的研究意义. 本文的重点工作是探索MLP神经网络在求解原子核质量半经验BW系列核质量模型中的最优系数问题的潜力. 在科学和工程领域中, 建立适当的数学模型以解决复杂的问题是一项关键任务. 这其中, 确定模型的最优参数对模型的准确性和预测能力至关重要. 其中, BW2核质量模型作为一种根据原子核的质子数和中子数来近似原子核质量的非线性模型, 在确定BW2模型最优系数的过程中往往涉及到非常庞大的参数空间, 传统的优化方法可能面临维度灾难和计算复杂度的问题. MLP神经网络以其强大的非线性建模能力和对大规模数据的适应性而受到广泛关注[38–41]. 本文将详细介绍MLP神经网络优化BW2核质量模型参数的方法, 通过评估不同参数下Adam优化器的训练效果, 寻找出更准确的模型参数. 阐述实验设计和实验结果, 并探讨MLP神经网络方法在解决参数优化问题中的优势.
-
本节将详细描述如何搭建MLP神经网络, 并选取合适的优化器训练神经网络模型进而改进现有的核质量模型参数.
-
本设计的关键是训练的神经网络能够将中子数、质子数和结合能作为输入, 并输出核质量模型的参数. (4)式为本文设计的神经网络数学模型,
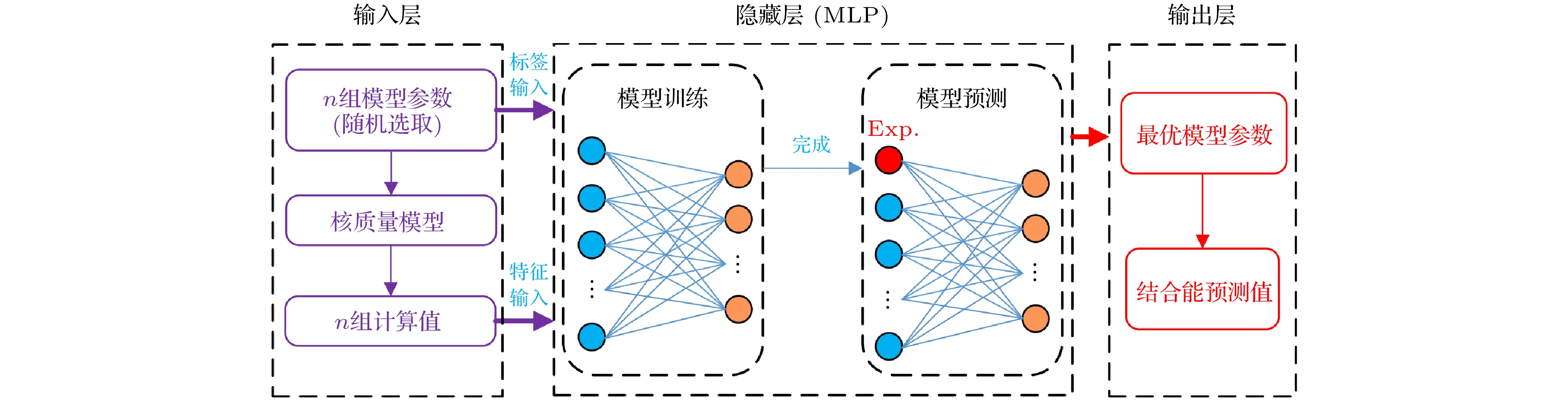
$ F({\alpha_v}, {\alpha_s}, \cdots, {\beta_m}) $ 是关于神经网络输出$ {\alpha_v}, {\alpha_s}, \cdots, {\beta_m} $ 的模型,$ G(N, Z, M) $ 为神经网络输入中子数$ N $ 、质子数$ Z $ 和结合能$ M $ 的模型, 即在计算机科学人工智能领域中, 模拟生物学、自然界或其他系统中的启发式方法, 如遗传算法[42]、模拟退火算法[43]、粒子群优化[44]、蚁群算法[45]等, 在寻找拟合问题中能提供一些近似解. 这类算法寻求的解集中随机选取n组模型参数作为神经网络模型的训练标签值. 将这些模型参数代入核质量模型得出的结合能计算值
$ {M}^{{\rm{BW2}}} $ 、中子数和质子数, 作为神经网络模型的训练特征值. 把《原子质量评估AME2020》的3250个原子核质量实验值$ {M}^{{\rm{EXP}}} $ ,$ Z $ 和$ N $ 代入训练完成的神经网络输出最优核质量模型参数$ {\alpha_v}, {\alpha_s}, \cdots, {\beta_m} $ . -
图1为本文神经网络的框架图, 其中紫色输入模块为神经网络训练的数据集, 红色输出模块为实验预测. 隐藏层展示的是该神经网络模型的第一层神经元连接第二层神经元, 构成了MLP双隐藏层神经网络. 其中, 第一层包含200个神经元, 第二层150个神经元. 在神经网络中, 每个神经元接收来自上一层神经元的输入, 通过对这些输入进行加权求和并加上偏置项后得到一个加权和, 将这个加权和传递给激活函数进行非线性变换. 激活函数将加权和映射到一个非线性的输出, 这个输出被传递到下一层的神经元. 再经过激活函数的变换后, 由优化器根据损失函数进行优化得到最优解. 由于Rectified Linear Unit (ReLu)函数在拟合效果中具有较好的非线性转换能力, 能更好地提升模型的表达能力. 因此本实验设计的神经网络各个神经元之间使用了ReLu激活函数, 该激活函数表达式为
此外, 根据Kirson[10]的BW2给定的系数, BW2模型系数的数值之间存在数量级差异. 然而, 特征值的数量级的差异会严重影响模型的稳定性, 导致某些权重学习得过大或过小. 对此, 在训练神经网络之前需要对训练的系数集进行归一化处理, 使数据具有统一的尺度和范围, 有助于平衡不同特征之间的权重, 从而帮助神经网络模型更好地收敛、提高性能、减少过拟合, 并提高模型对输入数据的鲁棒性[46].
-
在上述神经网络训练的过程中涉及到回归问题, 面对回归问题常用均方误差损失(mean squared error, MSE)作为训练的损失函数来评估模型的性能. 这种误差损失是衡量模型预测值
$ y $ 与真实值$ \hat{y} $ 之间的平方差. 在每个训练批次中, 模型会对数据进行均方误差计算后执行反向传播, 然后更新模型参数, 使得预测值与真实值之间的误差逐渐减小, 以提高预测的精确度. 当损失值越小, 神经网络训练得到的模型就越接近BW2核质量模型, 达到训练出的模型近似为BW2模型的效果. 损失函数表达式为合适的优化器能够快速减小神经网络训练中的损失值, 本实验设计自适应梯度优化器对神经元之间的权重和偏置的参数进行更新. 在Adam优化器中, 有两个影响神经网络训练的超参数: 学习率
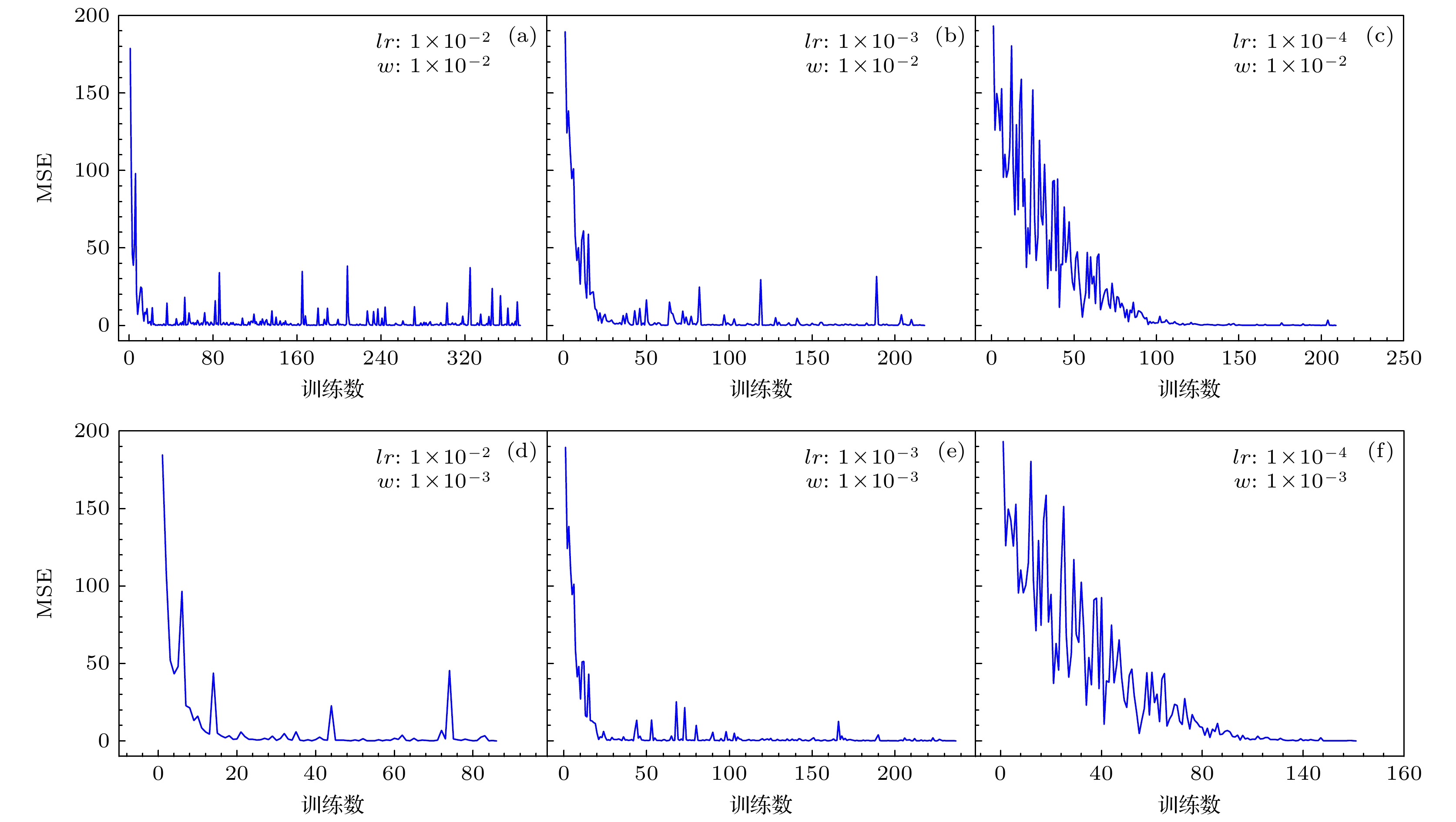
$ lr $ 和权重衰减参数$ w $ . 学习率控制参数更新的步长, 而权重衰减参数是一种常用的正则化技术, 选择合适的权重衰减值可以有更强的正则化效果, 有效地控制模型的复杂度, 提高其泛化能力. Adam优化器输出的参数值被用于更新神经网络模型, 从而使得损失函数逐渐减小, 使MLP在训练模型的收敛过程中更快速、更准确、更稳定地逼近BW2模型的特征, 达到输出最优系数组的效果.本节设计了Adam优化器在不同学习率和权重衰减参数下, 对神经网络模型损失值收敛到0.1%以下的速度和稳定性的影响. 在项目研究中进行了一系列的实验来验证不同学习率和权重衰减参数对模型性能的影响. 实验对优化器的学习率分别设置为0.0001, 0.001和0.01, 权重衰减参数分别设置为0.001和0.01进行了对比. 图2为不同学习率和权重衰减参数的损失函数损失值的变化图, 其中垂直坐标为损失值, 水平坐标为训练次数.
图2(a)—(c)和图2(d)—(f)具有相同的权重衰减参数与不同的学习率. 结果表明, 在权重衰减参数相同的情况下, 当学习率为0.0001时, 模型具有更加稳定的收敛性能, 然而收敛速度较慢, 而且在损失函数收敛的过程中收敛曲线下降不平缓; 当学习率为0.01时, 模型的收敛速度会加快, 但由于较大的学习步长, 也容易导致训练过程不稳定, 甚至出现振荡或无法收敛的情况. 同理, 图2(a), (d), 图2(b), (e)以及图2(c), (f)具有相同的学习率与不同的权重衰减参数. 在学习率相同的情况下, 0.001大小的权重衰减参数, 在收敛的过程中不容易出现损失值的振荡, 具有更好的稳定性, 有助于控制模型的复杂度并防止过拟合. 然而较大的权重衰减参数虽然能够有效地抑制模型的过拟合, 但降低了模型的训练速度, 甚至会导致欠拟合.
综合实验结果分析, 最终搭建的模型使用参数采用学习率为0.001, 权重衰减参数为0.001的Adam优化器训练的效果较好. 综合上述优化器实验结果可知, 优化器在不同学习率和权重衰减参数的组合下, MLP神经网络模型的收敛速度和稳定性呈现出不同的特征. 考虑到模型的复杂度、训练数据规模以及任务要求, 实验决定权衡收敛速度和稳定性, 最终选择的这组学习率和权重衰减参数能使得参数更新更为平缓, 更加有助于避免在参数空间中跳过局部最优解. 同时, 较为合适的学习率有助于实验过程中保持稳定的训练, 特别是在本项目利用深度神经网络寻找最合适参数中, 由于参数数量庞大, 模型很容易发生梯度消失或爆炸. 在0.001大小的学习率下, 能够确保模型参数在优化过程中更稳定地更新, 并且能够在寻找最优解过程中更好地收敛. 此外, 基于对模型数据的正则化需求, 选择了0.001大小的权重衰减参数. 最终实验表明当学习率为0.001且权重衰减参数为0.001时, 本模型在测试集上能够计算出更优秀的结果, 反映在损失函数的均方误差上其效果直接表现为更快的收敛速度、更低的损失值和更高的准确率. 这组参数更适用于本次实验的任务和数据集, 同时有助于模型更好地泛化到BW2模型数据上.
-
表1选取的是神经网络模型训练所得出的部分系数组. 其中第1组为初始系数, 第2—7组为神经网络训练出的BW2模型部分系数. 从表1可以看出, 第4组系数计算出的预测值与实验值(数据来源《原子质量评估AME2020》中的原子核中
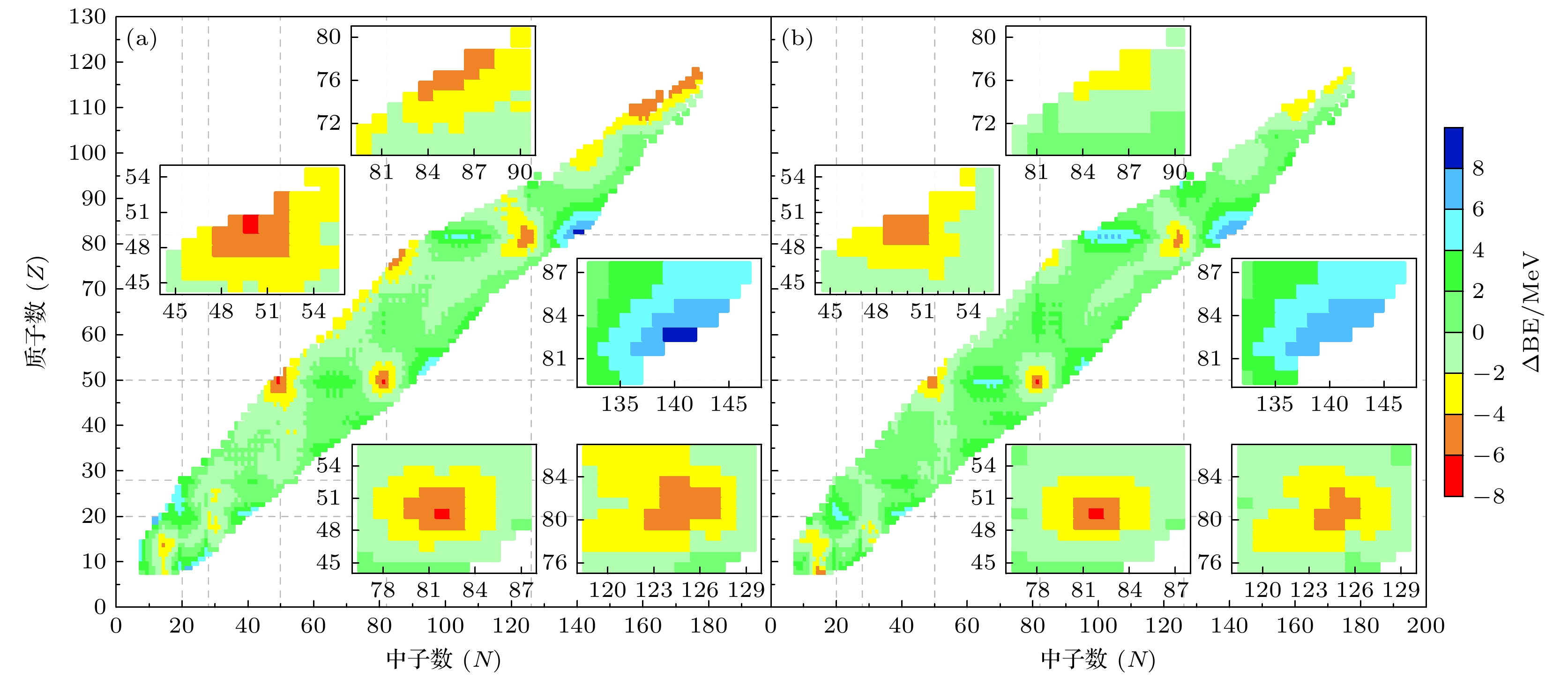
$ Z, N \geqslant 8 $ 共3250个核素)之间的均方根误差从原先的1.92 MeV降低到1.68 MeV, 降低了12.5%. 初始系数在$ Z=50,\; N=50 $ ,$ Z=50,\; N=82 $ ,$ Z= 82, N= 126 $ 等双幻数附近的计算值与实验值误差较大. 实验选取了$ Z=50, \; N=50 $ 附近($ 45\leqslant Z \leqslant 54,\; 45\leqslant N \leqslant 55 $ )合计70个核素,$ Z=50, N=82 $ 附近(45$ \leqslant Z \leqslant 55,\; 77\leqslant N \leqslant 87 $ )合计112个核素以及$ Z= 82, \;N=126 $ 附近($ 76\leqslant Z \leqslant 86, \;119\leqslant N \leqslant 129 $ )共118个核素, 对这三个双幻数附近区域进行分析并计算均方根误差. 计算发现该系数在这三组双幻数附近的表现并不理想, 故该系数组虽然在全局计算中误差更小但在局部区域泛化能力不足. 对其他几组系数进行计算并比较可以发现, 表1中第3组系数在选取的双幻数附近表现良好. 图3(a)和图3(b)分别给出的是BW2模型初始系数和表1中第3组优化系数下质量公式计算值与实验结合能的偏差值云图对比图. 可以看出, 新优化的系数在$ Z=50,\; N=50 $ ,$ Z=50,\; N=82 $ ,$ Z=82,\; N=126 $ 双幻数附近的局部色阶由红色变成橙色、黄色变成绿色, 表明了该区域的误差明显下降. 基于新系数再次对选取的核素进行计算得, 在$ Z=50, \; N=50 $ 附近的均方根误差由原先的3.32 MeV下降至2.39 MeV;$ Z=50, \; N=82 $ 附近的均方根误差由原先的2.45 MeV下降至2.14 MeV; 附近的均方根误差由原先的2.84 MeV下降至2.33 MeV. 全局均方根误差从原先的1.92 MeV降低到1.84 MeV, 降低了4%.此外, 根据图3所示, 该组系数在重核区域、
$ Z=76,\; N=85 $ 和$ Z=82, \;N=140 $ 附近, 误差的色阶也明显变浅. 通过计算,$ Z \geqslant 95 $ 且$ N \geqslant 135 $ 范围内合计278个核素的均方根误差由原先的2.37 MeV下降至1.23 MeV; 在$ Z=76,\; N=85 $ 附近($ 70\leqslant Z \leqslant 80,\; 80\leqslant N \leqslant 90 $ )合计71个核素的均方根误差由原先的2.49 MeV下降至1.29 MeV; 在$ Z = 82, \;N = 140 $ 附近($ 80 \leqslant Z \leqslant 87,\; 133 \leqslant N \leqslant 146 $ )合计73个核素的均方根误差由原先的4.90 MeV下降至4.72 MeV, 但该区域的误差仍然很大, BW2质量模型也远远低估了$ Z=82, \;N=140 $ 附近的结合能.由图4可以很清晰地看出在相同质子数的情况下, 红色点线图比黑色点线图更靠近零误差基准线. 优化后贫中子核结合能的计算值比原先计算值的误差更小, 而在质子数与中子数相近的稳定核素的计算中, 结合能优化可能出现较差的效果. 质子数较大的丰中子核素的结合能的计算值虽然有优化, 但优化效果不够明显. 实验分析, 由于贫中子核的能级结构更为简单, 而且核内的相互作用相对较少, 核子排布也更有序, BW2核质量模型能够反映出该情况下的核结构, 因此可能更容易通过对模型参数进行微调来提高拟合精度. 但随着中子数的增加, 核子之间的相互作用变得更加复杂. 在稳定核素的范围中, 有适度的中子数和质子数使核内部的相互作用力达到一种平衡状态, 核结构也相对稳定, 部分核素的误差可以通过BW2模型预测, 但也难以找到全局最优解. 对于丰中子, 虽然涉及到核子相互作用的饱和效应、屏蔽效应、相对论效应的饱和以及核结构的整体性质等因素的综合影响, 核结构也较为复杂, 但BW2核质量模型仍能考虑到这些相互作用的复杂度, 本实验所拟合的新系数也有优化的效果. 综合实验验证, 在计算不同组同位素链误差下, 新系数相对原先系数的效果更优, 贫中子核与丰中子核的误差更加接近, 误差曲线相对更平缓.
-
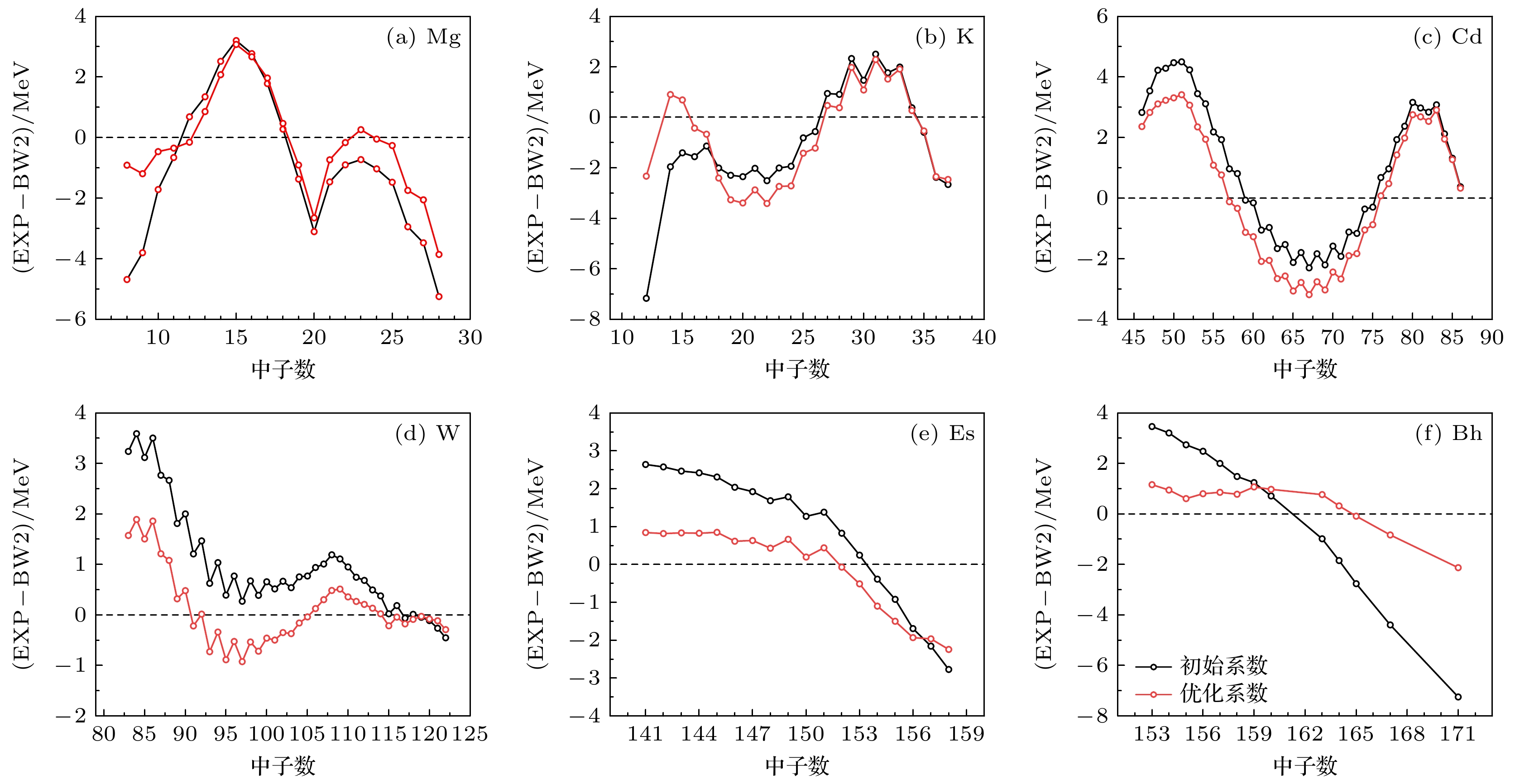
本实验结果选取表1中第3组系数, 为了验证新拟合系数的准确性, 进一步验证新系数对核素结合能优化的效果. 实验随机选取了6组不同元素的同位素链并计算在不同系数下BW2模型的预测值. 图4显示了实验测量值与初始系数和优化后系数的模型计算值之间的差异.
从图4可以看出, 随着中子数的逐渐增加, 曲线在中子数为幻数时会出现峰值. 这表明, 当中子数为幻数时, 核质量公式的预测值与实验值之间存在显著偏差. 因此, 这暗示了BW2质量模型在描述幻数附近的核素时仍然存在缺陷. 为BW系列模型后续发展与优化提供了一项参考, 即BW2质量模型需要添加幻数附近的矫正项. 由此得出, BW系列模型仍然有较大的优化空间. 通过对该组图的观察和分析, 很清晰地评估由MLP神经网络寻找的新拟合系数和原先系数对模型预测准确性的影响. 实验表明, 实验测量值与优化的新拟合系数计算值比原先系数的偏差更小, 新的系数能够更准确地描述核结合能, 进一步验证了本文对模型系数改进的有效性, 也为未发现的元素测量核质量提供了更可靠的数据参考.
-
在本文方法提出之前, 课题组在对BW2模型的研究过程中加入了对称能高阶项得到BW3核质量模型[47], 即
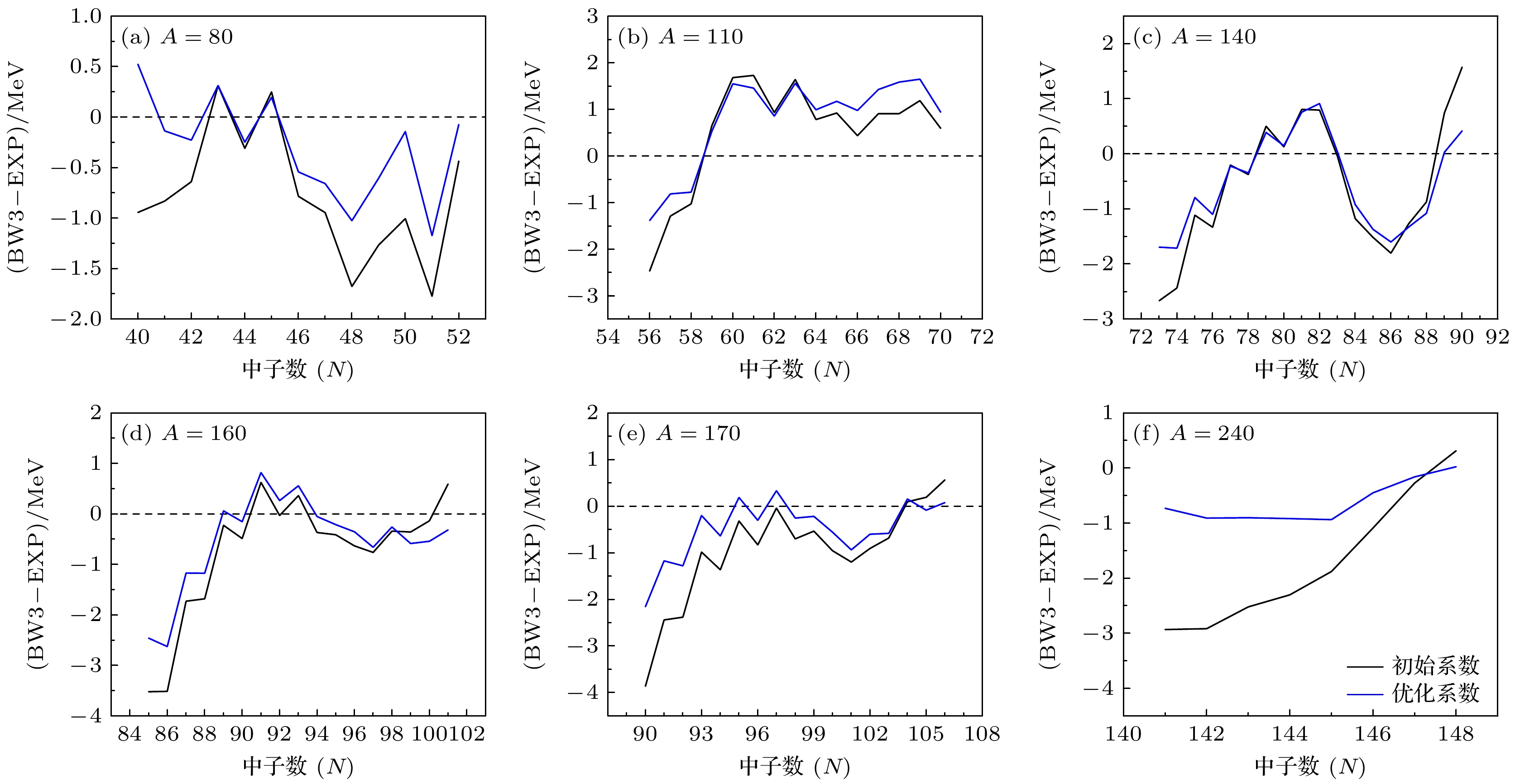
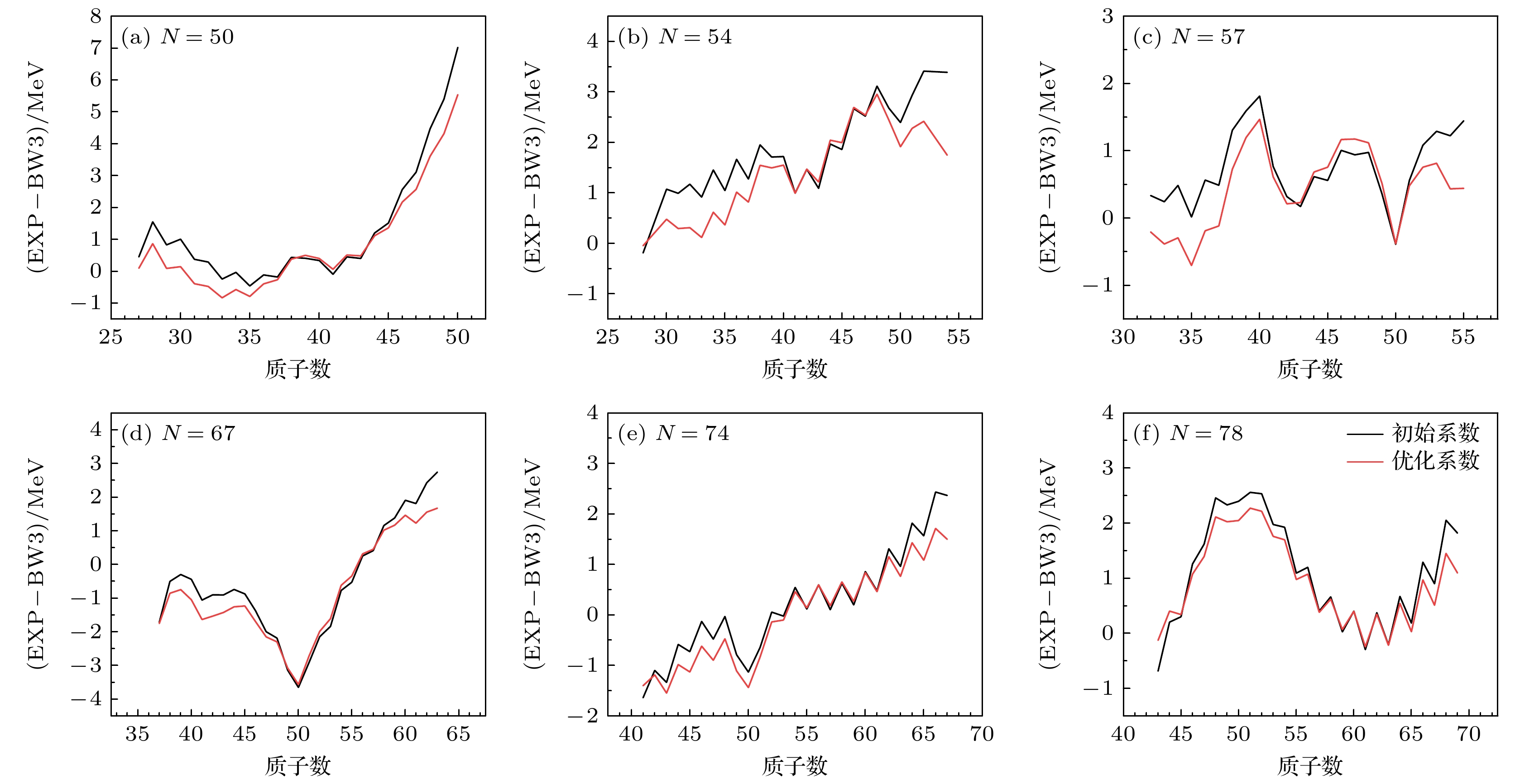
根据本文神经网络拟合系数的方法, 对BW3核质量模型进行系数更新以得到最适的拟合效果. 实验得出新系数组(表1第8组系数), 更新系数后的全局均方根误差从初始的1.86 MeV降低到1.63 MeV. 实验随机选取并计算6组质量数相同中子数不同的核素的结合能差值, 如图5所示. 图中横轴表示中子数, 纵轴表示结合能的计算值与实验值的差. 图中的蓝线表示更新系数后的偏差, 黑线表示初始系数的偏差.
由图5可知, 当
$ A=80 $ 时, 初始系数的计算结果在中子数较小时的误差较大, 重新拟合后, 误差有所减小, 但在特定的中子数($ N=48 $ 和$ 51 $ )仍有较大误差.$ A=110 $ , 初始系数的误差相对较大, 尤其是在$ N=56—58 $ 和$ N=60—62 $ 之间. 重新拟合后, 误差显著减少. 在$ A=140 $ , 初始系数在$ N=86 $ 附近有明显的误差峰值, 重新拟合后, 误差有所减小, 但在$ N=73—76 $ 和$ N=84—88 $ 之间仍存在较明显的误差. 当$ A=160 $ 时, 初始系数在$ N= 85—88 $ 之间误差较大, 拟合后误差显著减少, 显示出明显的改进. 当质量数为170, 初始系数的误差随中子数增加逐渐减小, 但仍然存在较大误差. 拟合后, 误差减少且在中子数较高时与实验值更接近. 当质量数为240时, 初始系数的误差较为明显, 尤其是在中子数相对较小时. 重新拟合后的误差显著减小, 几乎在整个区间内都得到了改进. 从图5(b)—(d)(A = 110, 140, 160)可以看出, 在中子数接近或达到幻数(如$ N=50, 82, 126 $ 等)时, 误差的变化较为剧烈. 这可能与幻数效应导致的核壳结构变化有关. 重新拟合后, 这些幻数附近的误差也有所改善, 表明模型在考虑这些效应时得到了优化. 重新拟合后的系数总体上改善了计算值与实验值的吻合度, 表现在误差的减少和波动的平滑. 这说明通过重新拟合, BW3质量公式能更准确地描述不同中子数下的核结合能, 表明该方法拟合的核质量模型系数对于这些核的结合能描述更加准确.对于偏差随质子数变化的情况, 我们选择了中子
$ N=50—82 $ 主壳层核素结合能计算误差随质子数据的变化进行研究. 这33条同中子素链的规律可以归纳为6种类型, 对应图6中的6条最具代表性的同中子素链. 在$ N=50 $ 时, 优化后的模型在质子数较小和较大的区间误差有所降低. 在$ Z= 27—30 $ 和$ Z=41 $ 时误差较低, 但在较大质子数上, 误差仍然较大. 如图6(b),$ Z=26—40 $ 时红线更接近零基准线, 更新系数的核质量模型误差明显降低.$ Z= 42—47 $ 时, 初始系数和更新系数下模型的计算值相近.$ Z=48—53 $ 时, 虽然误差值较大, 但更新系数后模型比初始模型误差显著减小了.$ N=57 $ 时, 当质子数较小时, 优化前后的模型误差交替变好. 质子数$ Z=36—42 $ 时, 新系数的计算误差降低.$ Z=43—50 $ 时, 拟合效果较差. 当质子数较大时, 优化效果则明显变好.当
$ N=67 $ 时, 在质子数接近$ Z=50 $ 质子幻数附近, 新旧模型的误差都出现了一个明显的低谷. 这表明具有幻数的核倾向于具有较大的偏差, 说明模型没有很好地捕捉到壳层效应. 在远离质子幻数的区域, 对于较小的质子数, 新模型拟合效果没有初始效果好, 但误差值也缩小在2 MeV以内. 对于较大的质子数, 新模型效果明显更好.$ N=74 $ 时, 随着质子数的增加, 误差逐渐变大, 特别是Z = 60—70之间, 误差明显增大. 初始系数和更新系数都呈现出相似的上升趋势, 说明在高质子数区域, 模型预测的误差相对较大.$ N=78 $ 时, 在质子幻数50附近, 误差达到局部最大值. 在质子数大于60时, 误差呈现出奇偶振荡的趋势. 新模型在此区间内的表现较初始模型有一定改进, 但仍然有较大的波动. 这说明BW模型对于预测奇偶效应引起的不同质子数核子配对能量效果较差.为验证新拟合系数的可靠性, 我们对重核区域及幻数附近的结合能进行了计算. 实验结果表明,
$ Z\geqslant 95 $ 且$ N\geqslant 135 $ 的重核区域中的278个核素, 均方根误差由原先的2.74 MeV降低到1.04 MeV; 在$ 70\leqslant Z \leqslant 80, 80\leqslant N \leqslant 90 $ 区域的71个核素中, 均方根误差由原先的2.49 MeV降低到1.68 MeV; 在$ 80\leqslant Z \leqslant 87, 133\leqslant N \leqslant 146 $ 区域的73个核素中, 均方根误差由原先的3.94 MeV降低到2.86 MeV. 实验表明, 新系数在重核区域和部分幻数区域的拟合效果都有显著优化.同时, 在质量实验值和理论值的偏差随中子数变化的图4和图5部分子图以及随质子数变化的图6部分子图均表现出奇偶性. 由于偶数个质子或中子的核子会通过配对效应更为稳定, 而奇数个核子则由于无法完全配对, 会更不稳定. 这一现象使得偶核与奇核之间的质量差异更大. 然而, BW系列模型主要基于宏观的液滴模型, 加上一些微观修正项, 如壳层修正和配对效应等. 这些修正通常是基于平均近似, 而非精确描述. 因此, BW系列模型在处理这些奇偶性有关的效应时可能出现不同的误估.
-
本文旨在研究利用MLP神经网络调整核质量模型的系数, 提升了模型的拟合效果, 进一步降低了模型预测的误差. 通过在神经网络中引入适当的输入特征和输出目标, 自动学习和调整得到模型系数. 最终得出泛化能力更好的系数组. 基于AME2020数据, 更新系数后的BW2核质量模型全局均方根误差有所降低, 在
$ Z = 76, N = 85 $ ,$ Z= 82, N=140 $ 附近区域和$ Z=50, N=50 $ ,$ Z=50, \; N=82 $ ,$ Z= 82, N=126 $ 等双幻数附近以及重核区域均有较好的优化效果. 实验得出, 神经网络拟合BW2模型在双幻数以及重核区域的拟合程度有着明显的优化. 通过比较随机选取的同位素链中的计算值与实验值的误差, 发现新系数相较于原先系数在贫中子核结合能计算中具有明显优势, 且在丰中子核结合能计算中也有较佳的优化效果, 进一步验证了新系数的泛化能力. 最后, 实验上对BW3质量模型系数进行重新拟合, 结果发现: 更新系数后的全局均方根误差从初始的1.86 MeV降低到1.63 MeV. 表明神经网络拟合BW3核质量模型能显著改善核结合能的计算精度, 尤其在幻数附近的误差减少, 整体模型对实验数据的拟合度提升明显. 这种基于MLP神经网络的方法为解决BW系列模型优化问题提供了一种新颖且有前景的途径. 实验表明MLP神经网络在求解原子核质量半经验核质量模型中的最优系数问题上有很大潜力.同时, 本研究介绍的利用MLP神经网络寻求最优拟合系数的方法抛弃了传统的数学公式, 不仅适用于BW2和BW3模型, 也为更复杂的原子核质量计算模型, 如FRDM[48], LDM[49], HFB[50], MS[51], DZ[52]等, 或具有隐函数而难以编程的核质量模型寻找最优拟合系数提供了一种新型的方法和思路, 为其他原子核质量非线性模型寻找最优系数提供了新的方法和洞见.
基于MLP神经网络优化改进的BW模型
Improved BW model based on MLP neural network optimization
-
摘要: 神经网络具有强大的建模能力和对大规模数据的适应性, 在拟合核质量模型参数方面表现出显著效果. 本研究旨在探索神经网络拟合核质量模型参数的问题: 采用多层感知机(multilayer perceptron, MLP)神经网络结构, 评估不同参数下Adam优化器的训练效果, 训练出准确的模型参数. 研究发现, 基于AME2020数据, 更新系数后的BW2核质量模型在双幻数以及重核区域的均方根误差降低明显; BW3模型重新拟合后的全局均方根误差为1.63 MeV, 较之前1.86 MeV有所降低. 结果表明, 该方法能够有效地拟合模型参数, 并具有良好的拟合性能和泛化能力. 这项研究为BW系列核质量模型的系数提供了新的拟合方法, 也为其他核质量寻求最佳拟合参数提供了有益的参考.Abstract: The nuclear mass model has significant applications in nuclear physics, astrophysics, and nuclear engineering. The accurate prediction of binding energy is crucial for studying nuclear structure, reactions, and decay. However, traditional mass models exhibit significant errors in double magic number region and heavy nuclear region. These models are difficult to effectively describe shell effect and parity effect in the nuclear structure, and also fail to capture the subtle differences observed in experimental results. This study demonstrates the powerful modeling capabilities of MLP neural networks, which optimize the parameters of the nuclear mass model, and reduce prediction errors in key regions and globally. In the neural network, neutron number, proton number, and binding energy are used as training feature values, and the mass-model coefficient is regarded as training label value. The training set is composed of the multiple sets of calculated nuclear mass model coefficients. Through extensive experiments, the optimal parameters are determined to ensure the convergence speed and stability of the model. The Adam optimizer is used to adjust the weight and bias of the network to reduce the mean squared error loss during training. Based on the AME2020 dataset, the trained neural network model with the minimum loss is used to predict the optimal coefficients of the nuclear mass model. The optimized BW2 model significantly reduces root-mean-square errors in double magic number and heavy nuclear regions. Specifically, the optimized model reduces the root-mean-square error by about 28%, 12%, and 18% near Z = 50 and N = 50; Z(N) = 50 and N = 82; Z = 82 and N = 126, respectively. In the heavy nuclear region, the error is reduced by 48%. The BW3 model combines higher-order symmetry energy terms, and after parameter optimization using the neural network, reduces the global root-mean-square error from 1.86 MeV to 1.63 MeV. This work reveals that the model with newly optimized coefficients not only exhibit significant error reduction near double magic numbers, but also shows the improvements in binding energy predictions for both neutron-rich and neutron-deficient nuclei. Furthermore, the model shows good improvements in describing parity effects, accurately capturing the differences related to parity in isotopic chains with different proton numbers. This study demonstrates the tremendous potential of MLP neural networks in optimizing the parameters of nuclear mass model and provides a novel method for optimizing parameters in more complex nuclear mass models. In addition, the proposed method is applicable to the nuclear mass models with implicit or nonlinear relationships, providing a new perspective for further developing the nuclear mass models.
-
Key words:
- nuclear mass model /
- magic numbers /
- multilayer perceptron neural network /
- Adam optimizer .
-
-
图 1 神经网络优化核质量模型系数框架图(MLP, 多层感知机神经网络; Exp., 实验结合能)
Figure 1. Framework diagram of neural network optimizing nuclear mass model coefficients (MLP, multi-layer perceptron neural network; Exp., experimental binding energy).
图 2 Adam优化器不同学习率和权重衰减参数实验对比图, 水平坐标为神经网络训练次数, 垂直坐标为神经网络损失值, 当损失值下降低于0.1%时停止训练(
$ lr $ 表示学习率,$ w $ 表示权重衰减参数)Figure 2. Comparison chart of Adam optimizer with different learning rates and weight decay parameters. The horizontal axis represents the number of neural network training iterations, and the vertical axis represents the neural network loss value. Training stops when the loss value drops below 0.1%. (
$ lr $ represents the learning rate,$ w $ represents the weight decay parameter)
图 3 BW2质量公式预测值与实验结合能的偏差对比图 (a)初始系数; (b)优化系数
Figure 3. Comparison plot of the deviation of the predicted value of the BW2 mass formula from the experimental binding energy: (a) Original coefficient; (b) optimization coefficient.
图 4 随机元素结合能的实验值与质量公式初始系数和优化系数计算值之间的差值折线图
Figure 4. Line plot of the difference between the experimental value of the binding energy of a random element and the calculated value of the original coefficient and optimization coefficient of the mass formula.
图 5 相同质量数下对比不同中子数的结合能偏差图
Figure 5. Graph of same mass number vs. different neutron numbers.
图 6 中子数相同对比不同质子数的结合能偏差图
Figure 6. Graph of same neutron number vs. differentproton numbers.
表 1 MLP神经网络寻找的系数组(部分, 单位: MeV)
Table 1. Coefficients identified by the MLP neural network (partial, unit: MeV).
1 2 3 4 5 6 7 8 $ \alpha_{v} $ 16.58 16.22 16.24 16.21 16.22 16.22 16.24 16.05 $ \alpha_{s} $ –26.95 –23.36 –23.42 –23.39 –23.38 –23.36 –23.40 –23.10 $ \alpha_{C} $ –0.77 –0.74 0.74 –0.74 –0.74 –0.75 –0.75 –0.74 $ \alpha_{t} $ –31.51 –31.53 –31.59 –31.54 –31.57 –31.53 –32.60 –31.62 $ \alpha_{xC} $ 2.22 1.39 1.38 1.39 1.40 1.39 1.40 1.59 $ \alpha_{W} $ –43.40 –57.38 –57.40 –57.42 –57.41 –57.40 –57.47 –72.97 $ \alpha_{s t} $ 55.62 54.98 55.02 54.96 55.03 54.99 55.09 64.10 $ \alpha_{p} $ 9.87 10.63 10.61 10.64 10.64 10.63 10.67 10.56 $ \alpha_{R} $ 14.77 9.89 9.94 9.91 9.91 9.89 9.93 9.89 $ \alpha_{m} $ –1.90 –1.89 –1.91 –1.90 –1.89 –1.89 –1.90 –1.88 $ \beta_{m} $ 0.14 0.14 0.13 0.14 0.14 0.15 0.15 0.14 $ b $ — — — — — — — –11.36 $ \sigma $ 1.92 1.90 1.84 1.68 1.76 1.81 1.89 1.63 
下载: 导出CSV
-
[1] Lunney D, Pearson J M, Thibault C 2003 Rev. Mod. Phys. 75 1021 doi: 10.1103/RevModPhys.75.1021 [2] 李涛, 黎春青, 周厚兵, 王宁 2021 物理学报 70 102101 doi: 10.7498/aps.70.20201734 Li T, Li C Q, Zhou H B, Wang N 2021 Acta Phys. Sin. 70 102101 doi: 10.7498/aps.70.20201734 [3] Ramirez E M, Ackermann D, Blaum K, Block M, Droese C, Düllmann C E, Dworschak M, Eibach M, Eliseev S, Haettner E, Herfurth F, Heßberger F P, Hofmann S, Ketelaer J, Marx G, Mazzocco M, Nesterenko D, Novikov Y N, Plaß W R, Rodríguez D, Scheidenberger C, Schweikhard L, Thirolf P G, Weber C 2012 Science 337 1207 doi: 10.1126/science.1225636 [4] Horoi M 2013 International Summer School for Advanced Studies Dynamics of Open Nuclear Systems (Predeal12) Predeal, Romania, July 9–20, 2012 p012020 [5] Wienholtz F, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, George S, Herfurth F, Holt J D, Kowalska M, Kreim S, Lunney D, Manea V, Menéndez J, Neidherr D, Rosenbusch M, Schweikhard L, Schwenk A, Simonis J, Stanja J, Wolf R N, Zuber K 2013 Nature 498 346 doi: 10.1038/nature12226 [6] Burbidge E M, Burbidge G R, Fowler W A, Hoyle F 1957 Rev. Mod. Phys. 29 547 doi: 10.1103/RevModPhys.29.547 [7] Ye W, Qian Y, Ren Z 2022 Phys. Rev. C 106 024318 doi: 10.1103/PhysRevC.106.024318 [8] Bethe H A, Bacher R F 1936 Rev. Mod. Phys. 8 82 doi: 10.1103/RevModPhys.8.82 [9] Weizsäcker C F V 1935 Zeitschrift für Physik 96 431 doi: 10.1007/BF01337700 [10] Kirson M W 2008 Nucl. Phys. A 798 29 doi: 10.1016/j.nuclphysa.2007.10.011 [11] Sorlin O, Porquet M G 2008 Prog. Part. Nucl. Phys. 61 602 doi: 10.1016/j.ppnp.2008.05.001 [12] Ozawa A, Kobayashi T, Suzuki T, Yoshida K, Tanihata I 2000 Phys. Rev. Lett. 84 5493 doi: 10.1103/PhysRevLett.84.5493 [13] Gherghescu R A, Poenaru D N 2022 Phys. Rev. C 106 034616 doi: 10.1103/PhysRevC.106.034616 [14] Björck Å 1990 Handb. Numer. Anal. 1 465 doi: 10.1016/S1570-8659(05)80036-5 [15] Jiang B N 1998 Comput. Methods Appl. Mech. Eng. 152 239 doi: 10.1016/S0045-7825(97)00192-8 [16] Mohammed-Azizi B, Mouloudj H 2022 Int. J. Mod. Phys. C 33 2250076 doi: 10.1142/S0129183122500760 [17] Cao Y, Lu D, Qian Y, Ren Z 2022 Phys. Rev. C 105 034304 doi: 10.1103/PhysRevC.105.034304 [18] Huang W, Wang M, Kondev F, Audi G, Naimi S 2021 Chin. Phys. C 45 030002 doi: 10.1088/1674-1137/abddb0 [19] Wang M, Huang W, Kondev F, Audi G, Naimi S 2021 Chin. Phys. C 45 030003 doi: 10.1088/1674-1137/abddaf [20] Sobiczewski A, Pomorski K 2007 Prog. Part. Nucl. Phys. 58 292 doi: 10.1016/j.ppnp.2006.05.001 [21] Yin X, Shou R, Zhao Y M 2022 Phys. Rev. C 105 064304 doi: 10.1103/PhysRevC.105.064304 [22] Wang N, Liu M, Wu X 2010 Phys. Rev. C 81 044322 doi: 10.1103/PhysRevC.81.044322 [23] Wu Y C, Feng J W 2018 Wirel. Pers. Commun. 102 1645 doi: 10.1007/s11277-017-5224-x [24] Popescu M C, Balas V E, Perescu-Popescu L, Mastorakis N 2009 WSEAS Trans. Cir. and Sys. 8 579 doi: 10.5555/1639537.1639542 [25] Xiang C, Ding S, Lee T H 2005 IEEE Trans. Neural Netw. 16 84 doi: 10.1109/TNN.2004.836197 [26] Pinkus A 1999 Acta Numerica 8 143 doi: 10.1017/S0962492900002919 [27] Sharma A, Gandhi A, Kumar A 2022 Phys. Rev. C 105 L031306 doi: 10.1103/PhysRevC.105.L031306 [28] Wu X H, Ren Z X, Zhao P W 2022 Phys. Rev. C 105 L031303 doi: 10.1103/PhysRevC.105.L031303 [29] Gao Z P, Wang Y J, Lü H L, Li Q F, Shen C W, Liu L 2021 Nucl. Sci. Tech. 32 109 doi: 10.1007/s41365-021-00956-1 [30] 庞龙刚, 周凯, 王新年 2020 原子核物理评论 37 720 doi: 10.11804/NuclPhysRev.37.2019CNPC41 Pang L G, Zhou K, Wang X N 2020 Nucl. Phys. Rev. 37 720 doi: 10.11804/NuclPhysRev.37.2019CNPC41 [31] Gernoth K A, Clark J W 1995 Neural Networks 8 291 doi: 10.1016/0893-6080(94)00071-S [32] Yüksel E, Soydaner D, Bahtiyar H 2021 Int. J. Mod. Phys. E 30 2150017 doi: 10.1142/S0218301321500178 [33] Liu M, Wang N, Deng Y, Wu X 2011 Phys. Rev. C 84 014333 doi: 10.1103/PhysRevC.84.014333 [34] Wang N, Liu M 2011 Phys. Rev. C 84 051303 doi: 10.1103/PhysRevC.84.051303 [35] Utama R, Piekarewicz J, Prosper H B 2016 Phys. Rev. C 93 014311 doi: 10.1103/PhysRevC.93.014311 [36] Utama R, Piekarewicz J 2018 Phys. Rev. C 97 014306 doi: 10.1103/PhysRevC.97.014306 [37] Ma C, Zong Y Y, Zhao Y M, Arima A 2020 Phys. Rev. C 102 024330 doi: 10.1103/PhysRevC.102.024330 [38] Özdoğan H, Üncü Y, Şekerci M, Kaplan A 2022 Appl. Radiat. Isot. 184 110162 doi: 10.1016/j.apradiso.2022.110162 [39] Chen X, Ma Q, Alkharobi T 2009 2nd IEEE International Conference on Computer Science and Information Technology Beijing, China, August 8–11, 2009 p291 [40] Ming X C, Zhang H F, Xu R R, Sun X D, Tian Y, Ge Z G 2022 Nucl. Sci. Tech. 33 48 doi: 10.1007/s41365-022-01031-z [41] Le X K, Wang N, Jiang X 2023 Nucl. Phys. A 1038 122707 doi: 10.1016/j.nuclphysa.2023.122707 [42] Slowik A, Kwasnicka H 2020 Neural Comput. Appl. 32 12363 doi: 10.1007/s00521-020-04832-8 [43] Amine K 2019 Adv. Oper. Res. 2019 8134674 doi: 10.1155/2019/8134674 [44] Wang D, Tan D, Liu L 2018 Soft Computing 22 387 doi: 10.1007/s00500-016-2474-6 [45] Chen A, Tan H, Zhu Y 2022 2nd International Conference on Applied Mathematics, Modelling, and Intelligent Computing (CAMMIC 2022) Kunming, China, March 25–27, 2022 p1472 [46] Huang L, Qin J, Zhou Y, Zhu F, Liu L, Shao L 2023 IEEE Trans. Pattern Anal. Mach. Intell. 45 10173 doi: 10.1109/TPAMI.2023.3250241 [47] Xu X Y, Deng L, Chen A X, Yang H, Jalili A, Wang H K 2024 Nucl. Sci. Tech. 35 91 doi: 10.1007/s41365-024-01450-0 [48] Möller P, Myers W D, Sagawa H, Yoshida S 2012 Phys. Rev. Lett. 108 052501 doi: 10.1103/PhysRevLett.108.052501 [49] Zhang H F, Wang L H, Yin J P, Chen P H, Zhang H F 2017 J. Phys. G: Nucl. Part. Phys. 44 045110 doi: 10.1088/1361-6471/aa5d78 [50] Samyn M, Goriely S, Heenen P H, Pearson J, Tondeur F 2002 Nucl. Phys. A 700 142 doi: 10.1016/S0375-9474(01)01316-1 [51] Moller P, Nix J, Myers W, Swiatecki W 1995 At. Data Nucl. Data Tables 59 185 doi: 10.1006/adnd.1995.1002 [52] Duflo J, Zuker A 1995 Phys. Rev. C 52 R23 doi: 10.1103/PhysRevC.52.R23 -
图( 6) 表( 1)
计量
- 文章访问数: 459
- HTML全文浏览数: 459
- PDF下载数: 3
- 施引文献: 0