-
金属纳米线凭借其在力学、电学和光学等方面的优异性能, 在芯片制造、航空航天和柔性传感器等领域具有广阔的应用前景, 近年来受到材料、化学和能源等相关领域研究者的广泛关注[1–3]. 随着纳米合成技术和微纳加工工艺的突破, 目前已成功制备得到直径为十几纳米甚至几个纳米的金属纳米线[4,5], 它们正逐渐成为微纳电子机械系统(micro- and Nano electromechanical system, M/NEMS)所不可或缺的基本结构单元. 在这些微纳电机系统服役过程中, 金属纳米线往往受到复杂的应力作用, 如弯曲和扭转等, 因此, 高性能微纳器件的设计和制造通常要求纳米线具有良好的力学性能. 由于金属的力学性能与其形变微观机制密切相关, 近年来研究者借助透射电子显微镜原位观测等微观分析手段对金属纳米线受载时的力学响应特征、结构演变规律和形变微观机制进行了深入研究[6–12]. 结果表明, 位错滑移、形变孪生以及固态相变是金属纳米线塑性变形的主要机制, 它们的主导地位取决于纳米线的晶体学取向、尺寸和加载方式等因素. Wang等[7]借助原位动态加载技术研究了不同取向单晶W纳米线的压缩形变行为, 他们发现
$\left\langle {111} \right\rangle $ ,$\left\langle {110} \right\rangle $ 和$\left\langle {100} \right\rangle $ 取向W纳米线塑性变形以形变孪生为主导机制, 而$\left\langle {112} \right\rangle $ 取向纳米线则以位错滑移为主导, 表现出高度的晶体取向依赖性. Yue等[8]对直径范围在70—1200 nm的单晶Cu 纳米线进行原位拉伸试验, 他们发现尺寸较大(>150 nm)的纳米线拉伸形变以全位错滑移为主. 而在尺寸较小的纳米线拉伸形变中则普遍观察到形变孪晶及部分位错. Seo等[9]也在直径约100 nm的Au纳米线拉伸变形中同样观察到类似的孪晶形核与长大过程. Wang等[12]通过原位拉伸试验研究了单晶Nb纳米线的塑性变形能力, 结果表明Nb纳米线在断裂前实现了超过269%的伸长率, 表现出超塑性特征, 而该形变特征源于纳米线通过应力诱发固态相变、形变孪生以及晶体旋转3种不同形变机制的协同作用.值得注意的是, 目前关于金属纳米线塑性变形行为的讨论主要集中在轴向拉伸和压缩变形. 相比之下, 金属纳米线在弯曲过程中的应力应变状态更为复杂, 然而, 针对纳米线弯曲变形的研究目前仍不多见. 实际地, 在微纳器件的成型、组装和应用过程中, 纳米线除受到轴向拉伸和压缩应变外, 往往还受到剧烈且反复的弯曲变形, 纳米线的弯曲性能在很大程度上决定了微纳器件的可靠性和使用寿命. 因此, 厘清金属纳米线在弯曲载荷作用下的力学响应特征和形变微观机制是评估微纳器件性能稳定性的重要依据, 对提高微纳器件可靠性和使用寿命具有十分重要的理论意义和工程价值. 在常规轴向拉伸和压缩载荷作用下, 纳米线内部产生均匀的应力应变场分布, 与之相比, 弯曲变形则在纳米线的横截面内产生复杂的应力应变梯度, 而应力状态的差异导致纳米线在弯曲时表现出不同于常规轴向变形的力学响应特征和形变机制. Wu等[13]利用原子力显微镜对单晶Au纳米线进行弯曲试验, 他们发现纳米线的弹性模量与纳米线尺寸无关且与相应的块体材料测量结果相当. Hu等[14]在单晶Al纳米线弯曲试验中观察到位错在纳米线内重排并形成小角度晶界, 表现出异于常规轴向加载时的形变特征. Wei等[15]对比分析了压缩和弯曲载荷作用下
$\left\langle {112} \right\rangle $ 取向单晶W纳米线的形变特征. 结果表明, 随着加载方式由单轴压缩转变为弯曲变形, 纳米线的形变主导机制由位错滑移转变为形变孪生, 表明载荷方式对金属纳米线形变行为具有重要影响. 最近, Sun等[16]在对比分析单晶Ag纳米线的拉伸和弯曲形变行为时也观察到类似的塑性变形机制对加载方式的依赖性.尽管原位力学观测技术为研究金属纳米线形变行为提供了有力手段, 但由于纳米材料形变过程涉及的时间和空间尺度较小, 仅依靠原位观测实验尚不足以在原子尺度下全面理解纳米线的力学性能与形变机制的相关性. 相比之下, 分子动力学(molecular dynamics, MD)模拟可在原子尺度下捕捉和复现材料微观结构的实时动态演变过程, 目前已成为研究纳米材料力学行为十分有效的理论方法. 借助MD模拟, 研究人员对金属纳米线的弯曲力学行为开展了相关研究工作, 并取得了一系列研究成果和进展. Olsson等[17]通过MD模拟对比分析了矩形和圆形横截面形状对纳米线弯曲形变行为的影响, 并验证了欧拉-伯努利弯杆理论(Euler-Bernoulli beam theory)在纳米尺度下的适用性. McDowell等[18]通过将Ag纳米线布置为悬臂梁结构, 讨论了纳米线弯曲弹性特征及晶体学取向和尺寸等因素的影响, 并将其与拉伸形变行为进行对比分析. Zhu等[19]分析讨论了不同晶体学取向Ni纳米线弯曲变形的微观机制, 发现
$\left\langle {112} \right\rangle $ 取向纳米线在弯曲载荷下可发生均匀的塑性变形, 其形变机制以扩展位错滑移为主导, 而$\left\langle {111} \right\rangle $ 和$\left\langle {010} \right\rangle $ 取向纳米线则由于大量位错塞积使形变局部化从而导致过早地断裂失效. Deb Nath[20]借助纳米压头施加弯曲载荷的方式讨论了温度和尺寸对Ag, Cu和Ni纳米线弯曲形变特征的影响. Zhang[21]通过对两端夹持固定的Ag纳米线施加作用力的方式实现纳米线的弯曲变形, 据此讨论了微观结构和加载方向对Ag纳米线弯曲形变的影响. 他们的结果表明, 纳米线的微观结构对其弯曲形变机制的影响有别于轴向拉伸变形, 且位错的形核位置与加载方向及纳米线的表面取向密切相关. Nöhring等[22]在Cu和Au纳米线的MD模拟弯曲试验中同样观察到塑性变形行为对加载方向具有类似的依赖性. Zhan和Gu[23]借助纳米压头模拟纳米线三点弯曲试验, 据此讨论了横截面尺寸对纳米线弯曲形变的影响. 他们指出, 当纳米线横截面尺寸较小时, 为获得恰当的模拟结果则需要综合考虑纳米线内的轴向拉伸效应, 而不能单纯考虑纳米线的表面效应. 特别地, Yang等[24,25]在模拟α-Fe纳米线的纯弯曲变形时发现, α-Fe纳米线在弯曲载荷作用下同样具有伪弹性特征, 且该力学特性可通过在纳米线中引入恰当的孪晶界而推广至更大的尺寸范围.另一方面, 上述有关金属纳米线形变行为的研究大多是围绕W, Ag, α-Fe, Au和Cu等纯金属纳米线展开, 而针对合金纳米线的相关讨论则相对有限, 尤其是对弯曲载荷条件下的形变行为. 相比于纯金属纳米线, 合金纳米线由于合金效应而具有更高的强度和热稳定性, 使其在高温下服役表现更好, 适用于更广泛的应用场景. 实际地, 目前尚不十分清楚合金纳米线是否具有与纯金属纳米线相似的形变特征和微观机制. 鉴于FeAl合金的高强度、良好高温抗氧化性和耐腐蚀性, 深入研究FeAl合金纳米线的力学行为和变形微观机制对高温条件下服役的微纳电子机械系统并解决其高温失效的问题, 具有深远的理论意义和潜在的工程应用价值. 因此, 本文以FeAl合金纳米线为研究对象, 采用MD模拟方法讨论不同取向FeAl合金纳米线在弯曲载荷下的形变行为, 同时考虑纳米线横截面尺寸及形状的影响, 分析纳米线在弯曲过程中的结构演变规律, 最终揭示其塑性形变微观机制, 为极端条件下服役的柔性微纳器件设计和制造提供理论参考和借鉴.
-
本文以B2结构的FeAl合金纳米线作为研究对象, 它具有CsCl型有序简单立方点阵结构, 空间群为Pm3m. 为分析晶体学取向对纳米线弯曲形变行为的影响, 本文分别构建轴向取向分别为
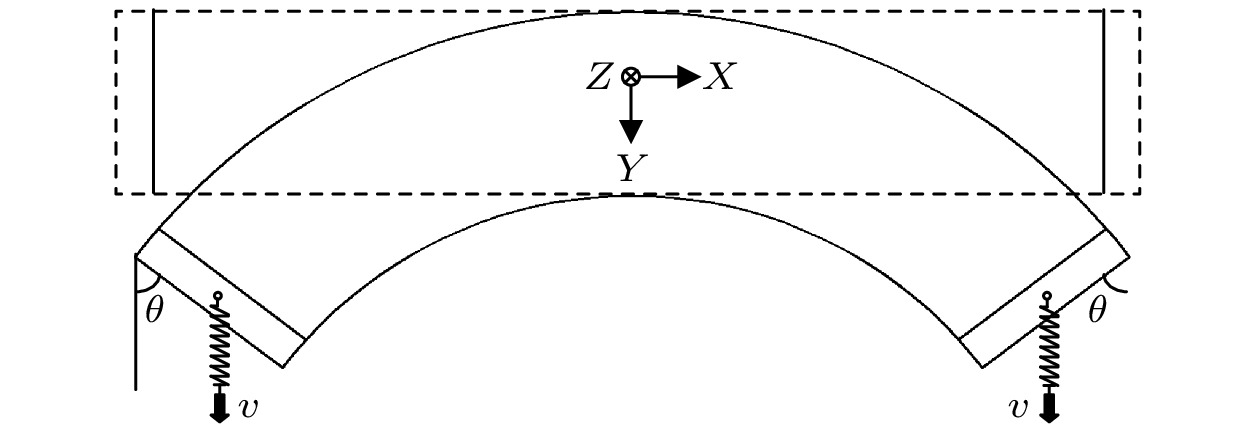
$\left\langle {111} \right\rangle $ ,$\left\langle {110} \right\rangle $ 和$\left\langle {001} \right\rangle $ 晶体学方向的B2结构FeAl合金纳米线, 这3种取向为立方点阵结构中典型的低指数晶向. FeAl合金纳米线初始构型的晶体学特征列于表1中, 其中, 模拟区域的X轴为纳米线的轴向, Y轴为弯曲形变加载方向, 且均为纳米线$ [1\bar 1 0] $ 方向, 据此消除加载方向不同所引入的差异. 同时, 以纳米线Y轴方向尺寸LY作为纳米线的直径, 并考虑LY = 2.9, 5.9和8.9 nm三种直径的纳米线以分析尺寸差异对弯曲行为的影响. 此外, 本文分别构建矩形和圆形横截面的FeAl合金纳米线, 据此讨论横截面形状的影响. 模拟采用Mendelev等[26]构建的嵌入原子势(embedded atom method, EAM)描述Fe和Al原子间的相互作用. 该势函数能够合理描述B2结构FeAl合金的晶格常数、内聚能和弹性常量等基本物理性质, 目前已成功应用于FeAl合金塑性变形分析和位错结构表征等有关模拟研究[27,28]. 在施加弯曲载荷前, 首先采用共轭梯度(conjugate gradient)法对纳米线初始构型进行能量最小化处理以获得原子势能最小的稳定结构, 然后在等温等体积系综(canonical ensemble)下弛豫50 ps至热力学平衡状态, 同时将弛豫温度设为室温300 K. 在整个模拟过程中, 时间步长取为1 fs并采用Verlet算法进行数值积分, 且在纳米线X, Y, Z三个方向上施加自由边界条件(free boundary condition).目前, 在纳米线弯曲变形的有关模拟研究中, 大多将纳米线布置为悬臂梁或简支梁结构, 并通过对纳米线施加弯曲位移、直接或借助压头施加弯曲作用力的方式实现纳米线的弯曲变形[17,18,21,23]. 这些方法在纳米线两端夹紧处及纳米线与压头接触位置易产生应力集中, 导致纳米线过早地发生断裂失效行为, 从而无法真实地反映纳米线弯曲的形变特征和微观机制. 为避免类似现象的发生, 本研究在纳米线两端厚度为0.5 nm的边界层上分别耦合一个加载弹簧, 如图1所示, 并使弹簧自由端沿弯曲加载方向(即Y轴方向)以恒定速度v = 0.005 nm/ps运动, 据此实现纳米线的弯曲变形. 同时, 记录弯曲过程中弹簧的作用力(F )及其自由端的位移(d ), 并绘制F-d曲线以表征纳米线的弯曲力学响应特征.
根据经典连续体力学[29]可知, 纳米线的弹性模量E与作用力F和位移d之间具有如下关系, 即:
式中, LX为纳米线长度, I为转动惯量. 当弯曲作用力F增大至弹性阶段最大值Fmax时, 纳米线屈服并进入塑性变形阶段, 其中, 作用力最大值Fmax表征纳米线弯曲变形时的屈服强度σs, 并可根据(2)式计算得到:
式中, LY为纳米线直径.
模拟借助分子动力学程序LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)[30]完成, 基于弯曲形变中的F-d响应曲线对比分析不同取向B2结构FeAl合金纳米线的弯曲形变特征, 利用可视化软件OVITO (open visualization tool)[31]中的公共近邻分析(common neighbor analysis, CNA)方法[32]可视化纳米线形变过程中的结构演变, 并基于位错提取算法(dislocation extraction algorithm, DXA)[33]分析纳米线中的位错结构特征, 同时采用原子尺度下剪切应变表征纳米线的应变状态[34].
-
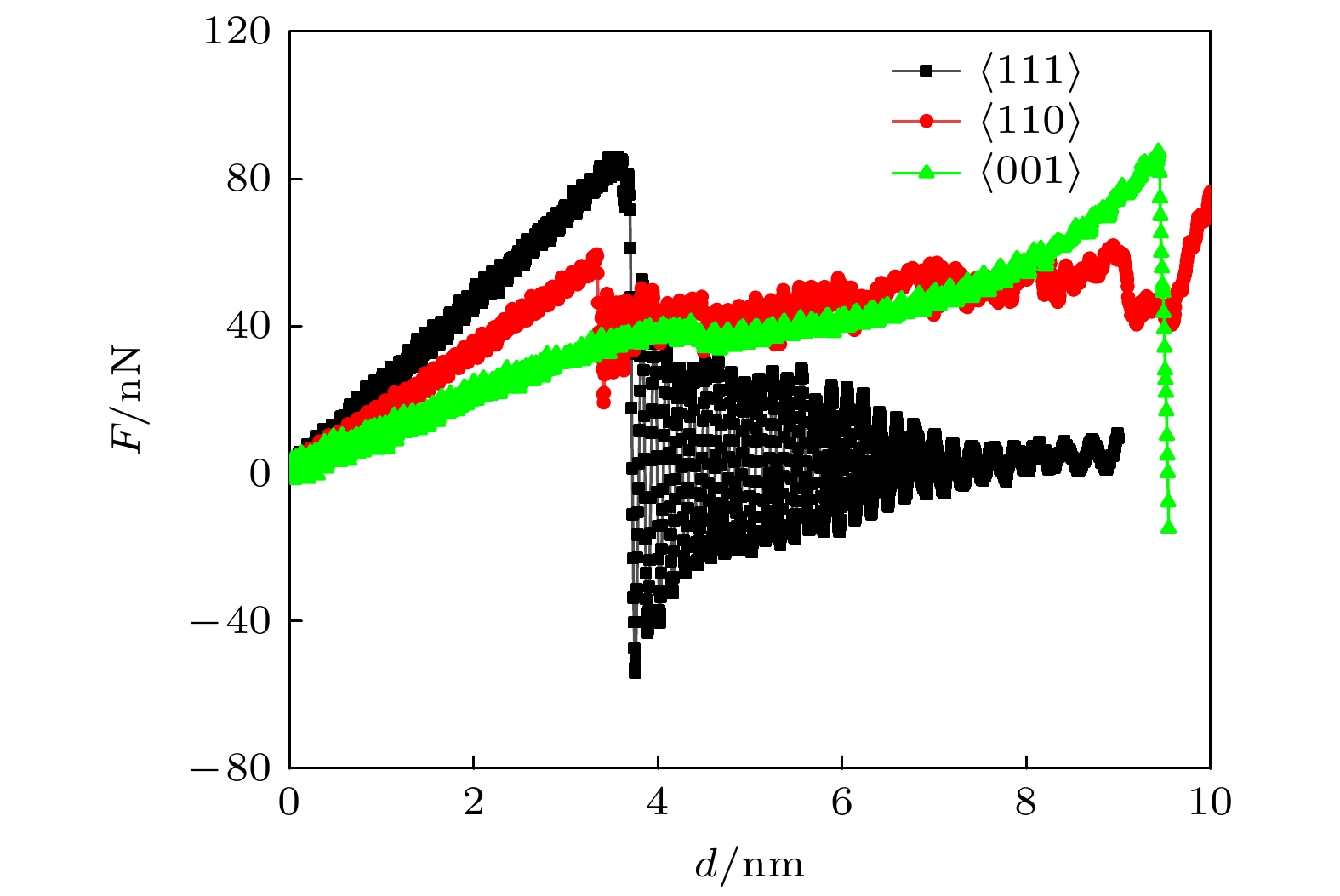
在弯曲过程中, 通过获取FeAl合金纳米线上耦合弹簧的作用力F及其自由端的位移d并绘制得到F-d曲线, 据此表征纳米线的力学响应特征, 如图2所示. 由于在同一取向下不同尺寸和横截面形状的纳米线弯曲形变时的F-d响应曲线呈现出相似的演化趋势, 即纳米线的弯曲行为不依赖于纳米线尺寸及其横截面形状, 因而图中仅给出直径为LY = 5.6 nm的矩形横截面FeAl合金纳米线的F-d曲线, 并且后续塑性形变机制的分析和讨论将围绕该纳米线展开. 图中可见弯曲作用力F在加载过程中存在一定幅度的振荡行为, 表明纳米线弯曲时表现出一定程度的不稳定性, 但即便如此, 这些F-d响应曲线的演化趋势依然十分清晰, 不影响本文对FeAl合金纳米线弯曲形变特征的分析. 从图2可以看出, 不同取向的纳米线在弯曲过程中呈现出完全不同的力学响应特征, 表明FeAl合金纳米线的弯曲形变行为对纳米线取向具有显著的依赖性.
根据F-d曲线的变化趋势可知, FeAl合金纳米线的弯曲变形包括弹性变形和塑性变形两个阶段. 在此过程中纳米线首先经历弹性变形, 且该阶段内弯曲作用力F随位移d的增大而线性增大, 符合直杆弯曲弹性变形规律. 据此, 通过拟合F-d曲线并得到F/d值, 根据(1)式可计算得到不同取向FeAl合金纳米线的弹性模量E具有
${E_{\left\langle {111} \right\rangle }} > {E_{\left\langle {110} \right\rangle }} > {E_{\left\langle {001} \right\rangle }}$ 关系. 可见, 弹性模量随晶体取向的变化而呈现出显著的差异, 表明FeAl合金纳米线的弹性特征具有较高的各向异性, 其主要源于FeAl合金中原子间相互作用力在不同晶体学取向上的差异. 其中,$\left\langle {111} \right\rangle $ 取向为B2结构的最密排方向, 其原子排列最紧密, 原子间相互作用最强, 因而在该取向上表现出最高的弹性模量, 而在$\left\langle {110} \right\rangle $ 取向上的原子排列相对稀疏, 原子间相互作用较弱, 导致该取向上具有较低的弹性模量[35].当弯曲作用力F达到弹性阶段的最大值Fmax时突然下降, 表明纳米线发生屈服并进入塑性变形阶段. 作用力最大值Fmax表征纳米线的屈服强度, 根据(2)式可计算得到不同取向FeAl合金纳米线的屈服强度存在
${\sigma _{\left\langle {111} \right\rangle }} > {\sigma _{\left\langle {110} \right\rangle }} > {\sigma _{\left\langle {001} \right\rangle }}$ 关系. 进一步地, 在塑性变形阶段不同取向FeAl合金纳米线的F-d响应曲线呈现不同的变化趋势. 在$\left\langle {111} \right\rangle $ 取向纳米线中, 弯曲作用力在达到屈服点后急剧下降并在较低载荷水平近邻振荡直至模拟结束, 而在$\left\langle {001} \right\rangle $ 和$\left\langle {110} \right\rangle $ 取向纳米线中, 作用力F在达到屈服点后略微下降并在一定弯曲位移区间内保持不变. 为进一步阐明晶体取向对FeAl合金纳米线弯曲形变机制的影响, 在3.2节中将借助可视化程序展示不同取向纳米线弯曲变形时微观结构演变过程, 进而揭示纳米线弯曲形变的微观机制及其晶体取向依赖性. -
图3给出了
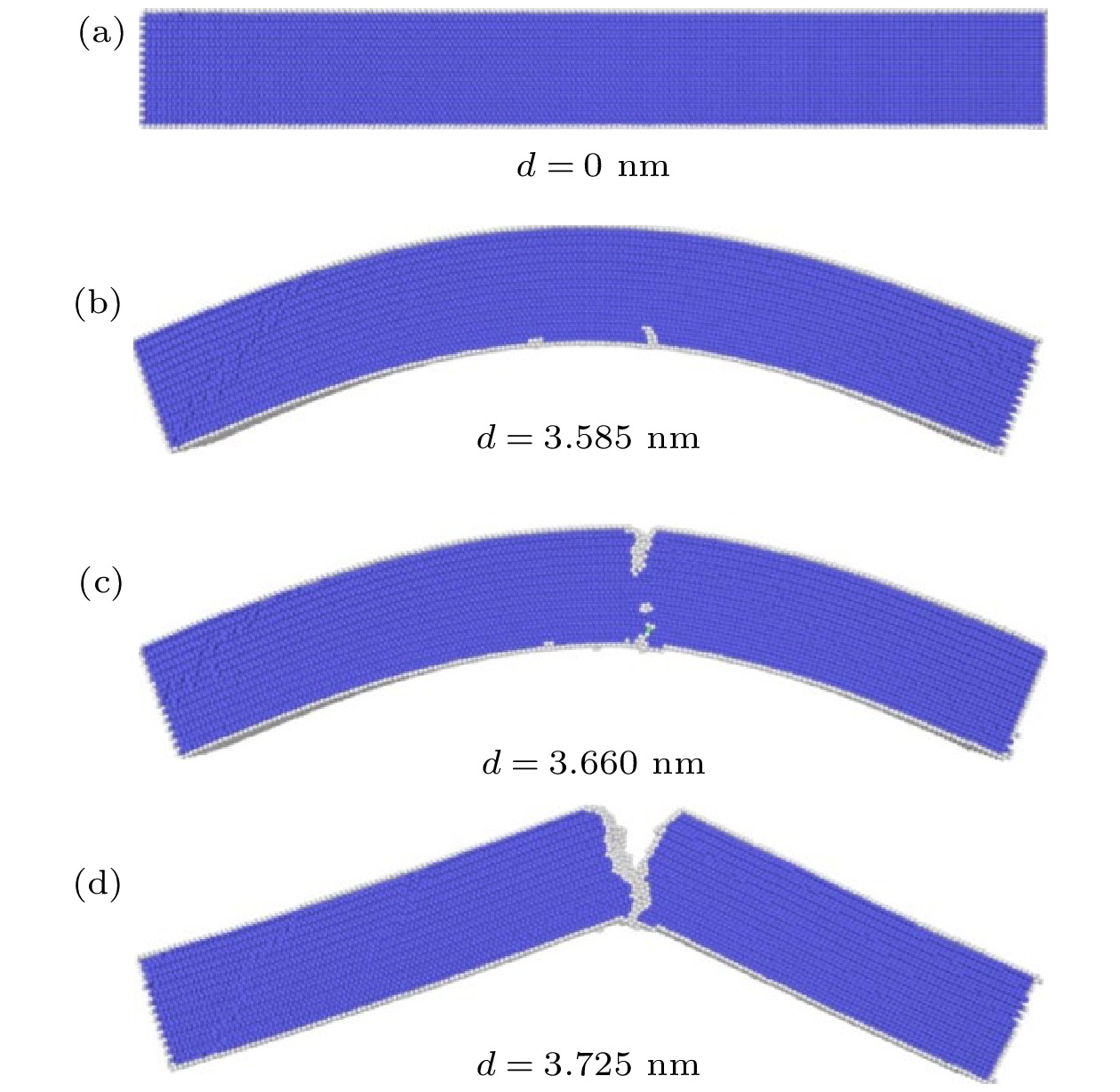
$\left\langle {111} \right\rangle $ 取向FeAl合金纳米线弯曲时各形变阶段的原子构型. 图中采用CNA分析方法辨识原子近邻环境的晶体结构并对其着色, 其中, 蓝色表示BCC结构, 绿色表示FCC结构, 而白色则为未知晶体结构, 通常表征缺陷结构或纳米线自由表面. 由于CNA方法无法区分原子类型, 因而将B2结构的FeAl合金辨识为BCC结构, 如图中蓝色原子所示. 图3(a)为FeAl合金纳米线在温度300 K下弛豫后得到的热力学平衡构型. 可以看出, 平衡态FeAl合金纳米线具有完整的B2结构, 弛豫过程未引入其他晶体缺陷. 纳米线在弯曲过程中首先发生弹性变形, 该阶段内纳米线晶体结构无显著变化. 当弯曲位移增大至d = 3.585 nm时, 可观察到位错从纳米线下表面形核, 如图3(b)所示, 标志着纳米线发生屈服, 对应F-d响应曲线上作用力F的急剧下降. 位错在形核后沿{011}面滑移并在纳米线下表面产生微台阶. 注意到位错在后续的滑移过程中未滑出纳米线的自由表面, 相反地, 它驻留在应力应变为零的纳米线中性层近邻区域. 类似的位错运动行为曾在Ni纳米线的弯曲模拟中被观察到[19], 其与弯曲形变在纳米线内引起的应力应变梯度相关. 随着弯曲形变的增大, V型裂纹在纳米线受拉应力的上表面形核, 并沿{011}面向纳米线内部快速扩展, 如图3(c), (d)所示. 当裂纹尖端扩展至纳米线下表面时, 纳米线发生断裂失效. 在整个弯曲过程中, 纳米线未发生显著的塑性变形, 且从图中可见纳米线的断口形貌较为平整, 表明$\left\langle {111} \right\rangle $ 取向FeAl合金纳米线发生脆性断裂行为.进一步地, 图4基于DXA方法[33]给出了纳米线断裂前的位错结构及其演化特征. 从图4(a)可以看出, 纳米线在屈服时产生的位错为BCC晶体结构中常见的
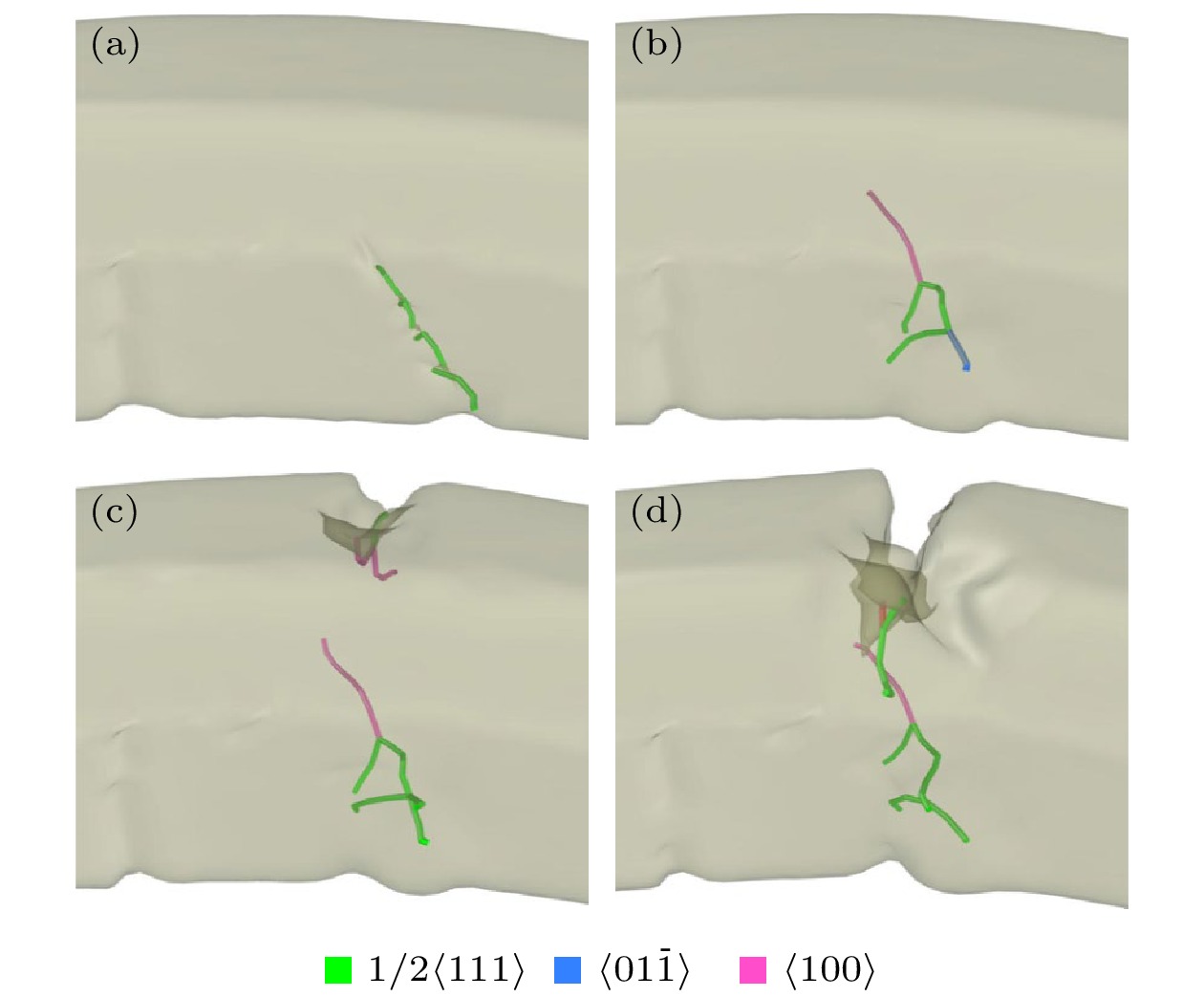
${1}/{2}\left\langle {11\bar 1} \right\rangle $ 螺型位错. 它们通过二元位错反应可进一步形成$\left\langle {100} \right\rangle $ 刃型位错, 即$ \left\langle {100} \right\rangle = {1}/{2}\left\langle {11\bar 1} \right\rangle +{1}/{2}\left\langle {1\bar 11} \right\rangle $ , 如图4(b)所示, 图中粉色线表示$ \left\langle {100} \right\rangle $ 位错. 该位错反应满足Frank能量条 件, 因而$ \left\langle {100} \right\rangle $ 刃型位错在纳米线中能够稳定存在. 此外, 图中还观察到这些螺型发生位错反应得到$ \left\langle {01\bar 1} \right\rangle $ 型位错, 即$ \left\langle {01\bar 1} \right\rangle ={1}/{2}\left\langle {11\bar 1} \right\rangle +{1}/{2}\left\langle {\bar 11\bar 1} \right\rangle $ , 如图4(b)中蓝色线所示, 但由于该位错反应不满足Frank能量条件, 因而$ \left\langle {01\bar 1} \right\rangle $ 型位错在形成后仅短暂停留便分解为两个${1}/{2}\left\langle {11\bar 1} \right\rangle $ 螺型位错. 当裂纹在纳米线上表面开始形核时, 可观察到裂纹尖端前沿伴随有位错形成, 并且在裂纹扩展过程中裂纹尖端向纳米线内部不断发射位错, 如图4(c), (d)所示, 类似裂纹尖端的位错行为在已有实验研究和MD模拟中被观察到[36,37]. -
类似地,
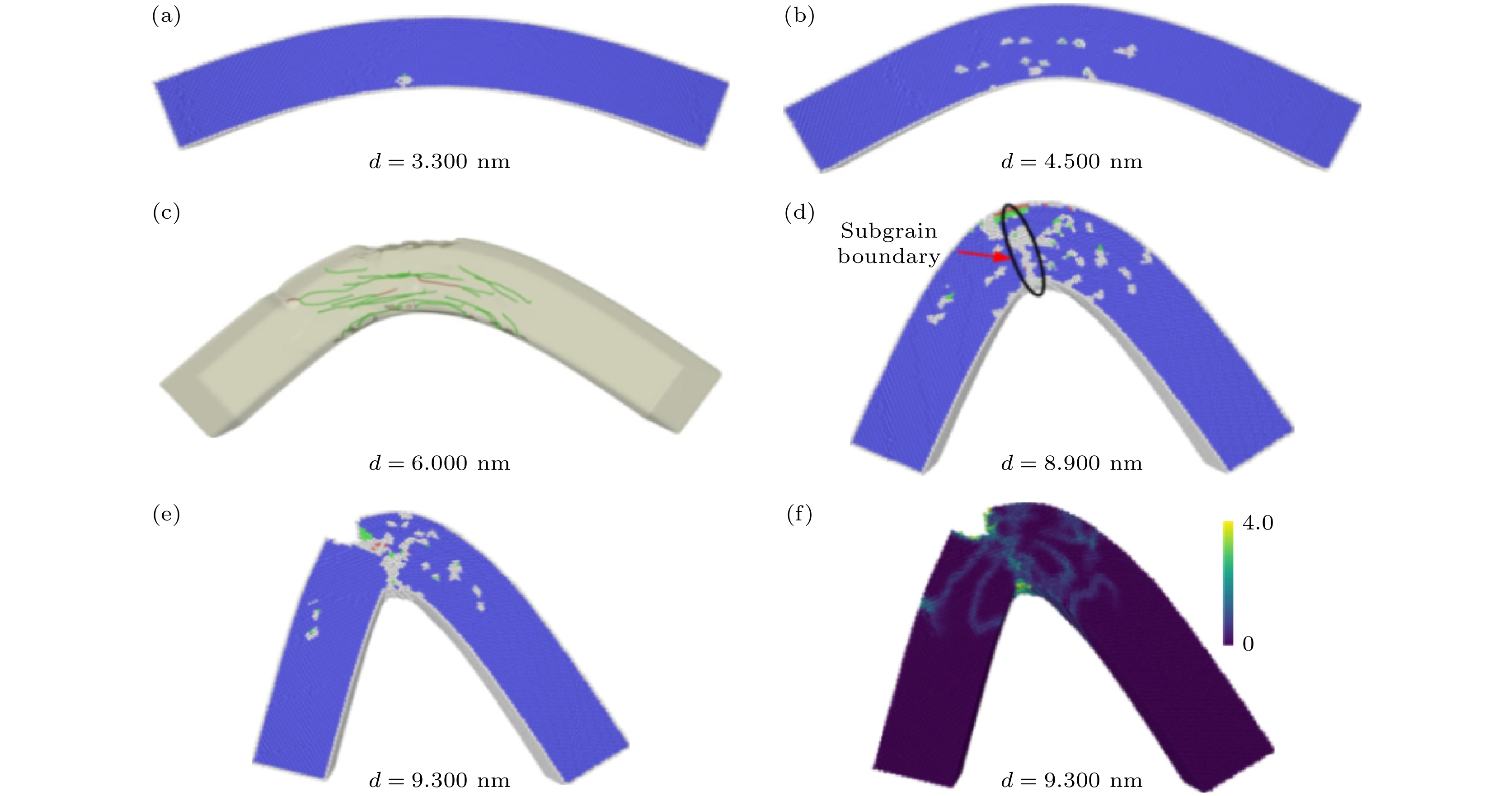
$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线的屈服行为同样源于位错形核过程, 但与$\left\langle {111} \right\rangle $ 取向纳米线的高脆性不同,$\left\langle {110} \right\rangle $ 取向纳米线在弯曲形变过程中表现出良好的塑性. 图5给出了$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线弯曲时各形变阶段的原子构型. 由图5(a)可见, 当弯曲位移d = 3.3 nm时位错开始从纳米线的下表面形核, 纳米线发生屈服. 由于初始完整B2结构的纳米线内部不存在其他缺陷的阻碍, 位错在形核后沿滑移面向纳米线内部滑移, 如图5(b), (c)所示. 基于DXA方法[33], 可以确定这些位错为B2结构晶体中常见的${1}/{2}\left\langle {111} \right\rangle $ 螺型位错, 表明$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线的弯曲塑性变形以位错滑移运动为主导机制. 此外, 从图5(c)可观察到这些螺型位错在滑移时始终平行于它们的Burgers矢量并保持笔直的位错形态, 推断这些位错在一组相互平行的滑移面上形核与滑移.在弯曲载荷的作用下, 位错连续地从纳米线下表面形核并向纳米线内部滑移运动, 从而在纳米线内形成稳定的塑性流动过程. 在此过程中, 从图2的F-d曲线可观察到弯曲作用力存在一定幅度的振荡, 其中, 作用力的每一次骤降则对应一个位错的形成. 虽然作用力表现出振荡特征, 但总体趋势变化较平缓并在F-d曲线上表现为一个覆盖弯曲位移量约6.0 nm的作用力平台区, 该平台区表征纳米线初始塑性变形过程中的“易滑移”阶段. 同时, 从图5(d)还观察到
$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线可均匀地弯曲变形得到一个光滑的圆弧形, 表现出良好的弯曲塑性及延展性. 随着弯曲形变的进一步增大, 一些位错沿纳米线轴向滑移并导致位错沿纳米线高度方向重新分布和排列得到一组位错墙, 形成如图5(d)所示的小角度亚晶界, 它将纳米线沿轴向分隔成两个亚晶粒. 类似亚晶界在金属纳米线弯曲试验中被观察到[38,39], 可见, 这种亚晶界结构在纳米线弯曲的形变中较为普遍, 其驱动力主要来自位错重新分布引起的应变能下降. 最后, 弯曲载荷的继续增大使亚晶界近邻区域发生剪切应变局部化从而在纳米线上表面产生V型裂纹, 如图5(e)和图5(f)所示, 最终导致纳米线发生断裂失效. 在整个弯曲形变过程中, 未观察到纳米线发生突然断裂, 即$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线以韧性断裂方式发生失效. -
根据上述结果可知, 位错的连续形核与稳定滑移使
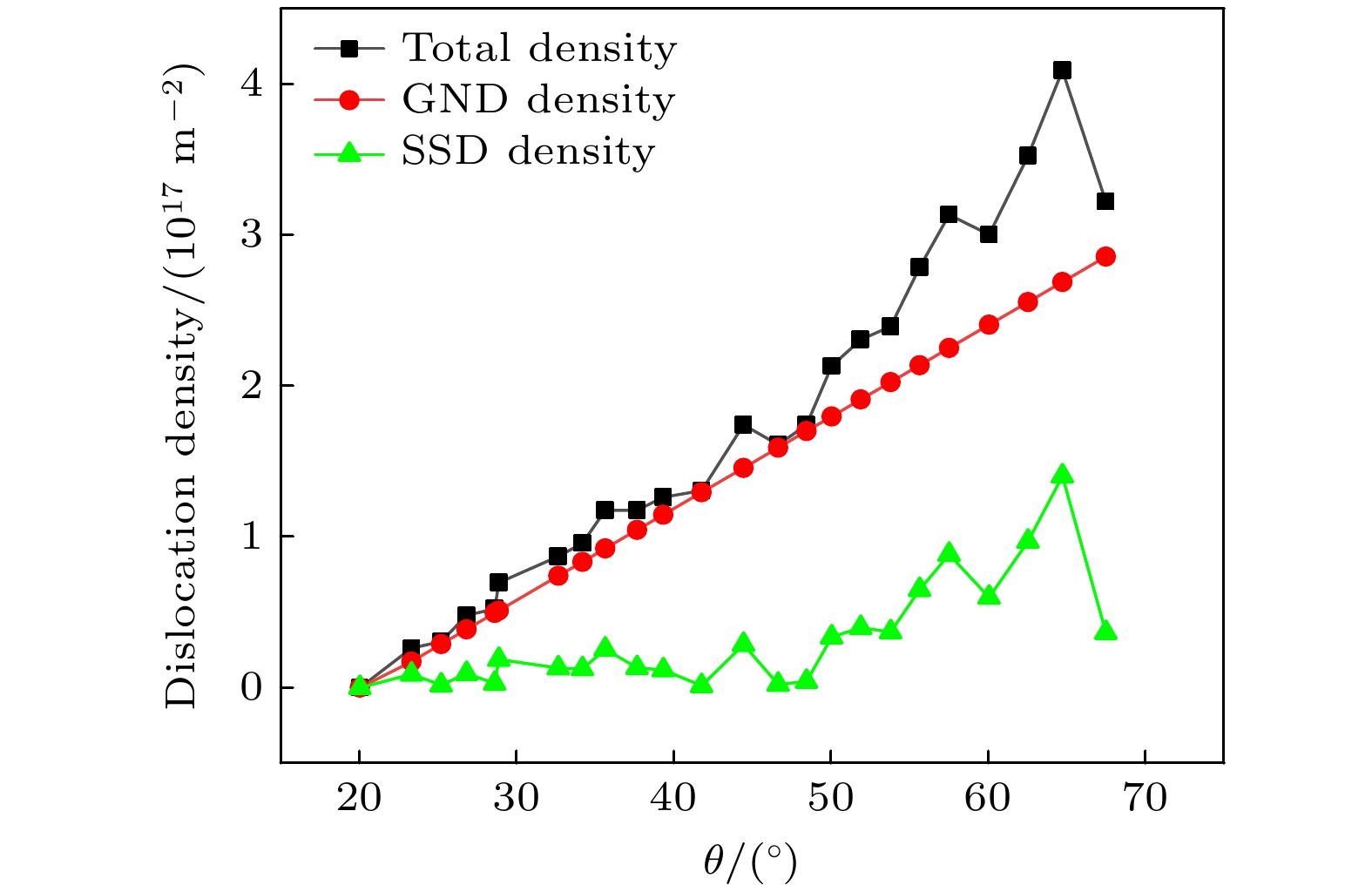
$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线在断裂失效前能够发生较大的弯曲塑性变形, 因而有必要讨论位错密度在弯曲形变过程中的演变规律. 一般地, 材料中的位错可分为几何必须位错(geometrically necessary dislocation, GND)和统计存储位错(statistically stored dislocation, SSD). 前者与非均匀变形引起的应变梯度相关, 如本研究中的弯曲变形, 而后者则来自均匀的塑性形变. 因此, 总位错密度为GND和SSD密度之和, 其中, GND密度可通过位错数量和晶体变形之间的几何关系来确定, 而SSD密度则通过从总位错密度中减去GND密度值得到. 本文中$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线弯曲变形所产生的GND密度ρGND可借助下式计算而得[40,41]其中, b为位错Burgers矢量, 其平行于纳米线轴向; κp表示弯曲纳米线的塑性曲率, 它与塑性弯曲角θp相关. (3)式表明GND密度ρGND与塑性曲率κp及塑性弯曲角θp成正比. 同时, 根据(3)式还可知, 将纳米线塑性弯曲形变至曲率κp需要引入一定密度的刃型GND以松弛相应的应变梯度. 另一方面, 本文中
$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线发生弯曲塑性变形时主要产生螺型位错, 因此, 这些螺型位错的Burgers矢量沿纳米线轴向分量则可松弛弯曲形变所产生的应变梯度, 进而(3)式中的$b= \dfrac{{\sqrt 3 }}{2}a \cos \varphi $ , 其中a为FeAl合金晶格常数,$\varphi $ 为${1}/{2}\left\langle {111} \right\rangle $ 螺型位错Burgers矢量与$\left\langle {110} \right\rangle $ 取向纳米线轴向间的夹角. 进一步地, 塑性弯曲角θp = θ – θe, 其中θ是图1中定义的弯曲角, θe表示弹性弯曲角. 基于理想Euler-Bernoulli梁假设, 可以通过几何方法确定纳米线在任意时刻的弯曲角θ, 特别地, 在弹性变形阶段弯曲角θ = θe. 此外, 本文考虑平面应变条件下的弯曲过程, 因此总位错密度可表征为单位面积内的位错数, 而位错数可通过DXA方法统计得到, 据此计算得到相应的位错密度. 图6给出了总位错密度以及GND和SSD密度随弯曲角θ的演变过程.从图6位错密度的演变过程可以看出, 当弯曲角小于50°时SSD密度处于较低水平, 可忽略不计, 而GND密度随弯曲角的增大而线性增大, 且与总位错密度的演变过程基本一致, 表明纳米线在纯弯曲形变过程中仅需要GND作为塑性变形的载体. 据此, 可以推断纳米线弯曲形变时产生的位错为“几何必须的”, 它们在滑移过程中未滑出纳米线的自由表面, 相反, 它们在纳米线内部停留以使纳米线适应与弯曲形变相关的几何不连续性, 如应变梯度和晶格曲率等. 同时, 随着位错密度的不断增大, 位错的进一步滑移受到来自其他位错的阻碍, 从而使位错的可动性降低, 最终导致位错在纳米线内部大量积累. 另一方面, 实验观察结果[42,43]表明, 在轴向拉伸和压缩形变过程中金属纳米线内部的位错极易从自由表面逃逸, 从而导致纳米线内部持续处于低位错密度的状态, 研究者称其为位错耗竭(dislocation starvation)[43]. 可见, 纳米线在弯曲过程中发生的位错堆积现象有别于轴向变形中的低位错密度状态, 两者间的差异主要源于应力应变状态的不同, 因而难以将纳米线轴向变形的微观机制直接应用于弯曲实验现象的解释中.
进一步地, 在弯曲形变的后期, 此时弯曲角大于50°, 从图6观察到SSD密度突然增大并迅速达到最大值2.4×1017 m–2, 而此时的总位错密度约为4.8×1017 m–2, 即塑性变形产生的位错约一半归为“统计存储的”. SSD密度的增大与弯曲变形后期高密度的GND有关. 一方面, GND阵列的应力场阻碍位错的进一步运动, 导致SSD发生位错增殖及随机捕获行为从而实现积累; 另一方面, 高位错密度使位错发生相互缠结并形成复杂的位错网结构, 该过程同样对SSD密度的快速增大产生贡献. 此外, 还注意到纳米线中产生的位错密度达1017 m–2数量级, 远高于实验测量值(1010—1015 m–2)[44,45]. 实际地, 在许多MD模拟研究中同样观测到类似的高位错密度值[46–48], 这与MD模拟中普遍使用的高应变率有关.
-
与上述两种取向纳米线的变形行为不同,
$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线的弯曲形变以固态相变为主导机制. 图7给出了$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线弯曲时各形变阶段的原子构型. 当弯曲位移d = 4.2 nm时, 观察到FCC结构相在纳米线上表面形核, 如图7(a)绿色原子所示, 此时纳米线发生屈服并进入塑性变形阶段; 图中FCC结构相为B2结构FeAl合金在应力诱发马氏体相变而得的面心四方结构(face-centered tetragonal) L10相. 由于CNA结构分析无法区分原子类型, 因而将L10相辨识为FCC结构. 如图7(b), (c)所示, L10相形核后在进一步加载作用下沿纳米线轴向快速长大, 表明$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线的弯曲塑性变形机制以应力诱发B2→L10相变为主导. 在此过程中弯曲作用力F保持不变并在F-d响应曲线上形成一个作用力平台区, 类似平台常见于B2结构合金材料的轴向拉伸测试. 相比于$\left\langle {110} \right\rangle $ 取向纳米线的作用力平台区,$\left\langle {001} \right\rangle $ 取向纳米线的平台区内由于作用力振幅较小而表现得较为平缓.基于相变晶体学分析可知, L10产物相与B2母相之间存在
$ {\left\langle {001} \right\rangle _{{\text{L10}}}}//{\left\langle {001} \right\rangle _{{\text{B2}}}} $ 和$ {\left\{ {111} \right\}_{{\text{L10}}}}//{\left\{ {011} \right\}_{{\text{B2}}}} $ 位向关系, 母相的$\left\langle {110} \right\rangle $ ,$\left\langle {1\bar 10} \right\rangle $ 和$\left\langle {001} \right\rangle $ 晶向分别对应于L10产物相的$ \left\langle {100} \right\rangle $ ,$\left\langle {010} \right\rangle $ 和$\left\langle {001} \right\rangle $ 晶向. 根据两相晶格常数可知, 在相变过程中B2相晶格结构需要沿$\left\langle {001} \right\rangle $ 方向发生拉伸变形, 并同时分别沿$\left\langle {110} \right\rangle $ 和$\left\langle {1\bar 10} \right\rangle $ 方向发生压缩变形从而得到L10相晶格结构. 可见, B2母相与L10产物相之间具有严格的晶体学对应关系, 该转变过程属于无扩散型马氏体相变. 进一步地, 可以看出纳米线中沿$\left\langle {001} \right\rangle $ 方向的拉伸和$\left\langle {110} \right\rangle $ 方向的压缩应力有助于B2→L10相变的发生. 另一方面, 弯曲变形在纳米线横截面内沿高度方向产生应力应变梯度, 其中, 纳米线中性层以上区域受拉伸应力, 可促进L10相形核, 而中性层以下区域则受相反方向的压缩应力并对相变具有抑制作用. 因此, 如图7(a)—(d)中所示B2→L10相变仅发生在纳米线中性层以上受拉伸应力作用的区域, 而中性层以下受压缩应力作用区域则未观察到相变的发生, 这与单轴拉伸过程中B2相可完全转变为L10相的相变行为不同[49].由图2中的F-d响应曲线可知, 当弯曲位移d = 8.0 nm时作用力F开始呈现显著上升趋势, 即纳米线产生应变硬化效应, 使纳米线具有更高的断裂应变. 当作用力达到应变硬化阶段的峰值时, L10相中的
${1}/{6}\left\langle {112} \right\rangle $ 部分位错从纳米线上表面形核并向纳米线内部滑移, 纳米线发生二次屈服行为, 如图7(d)所示. 进一步的弯曲变形使纳米线发生非晶化过程并伴随纳米线颈缩的发生, 如图7(e), (f)所示, 最终导致纳米线内剪切应变局部化进而发生断裂失效. 注意到$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线在断裂前可实现弯曲角接近90°的弯曲变形, 表现出优异的弯曲塑性和延展性. -
为探讨FeAl合金纳米线弯曲形变的回复行为, 在
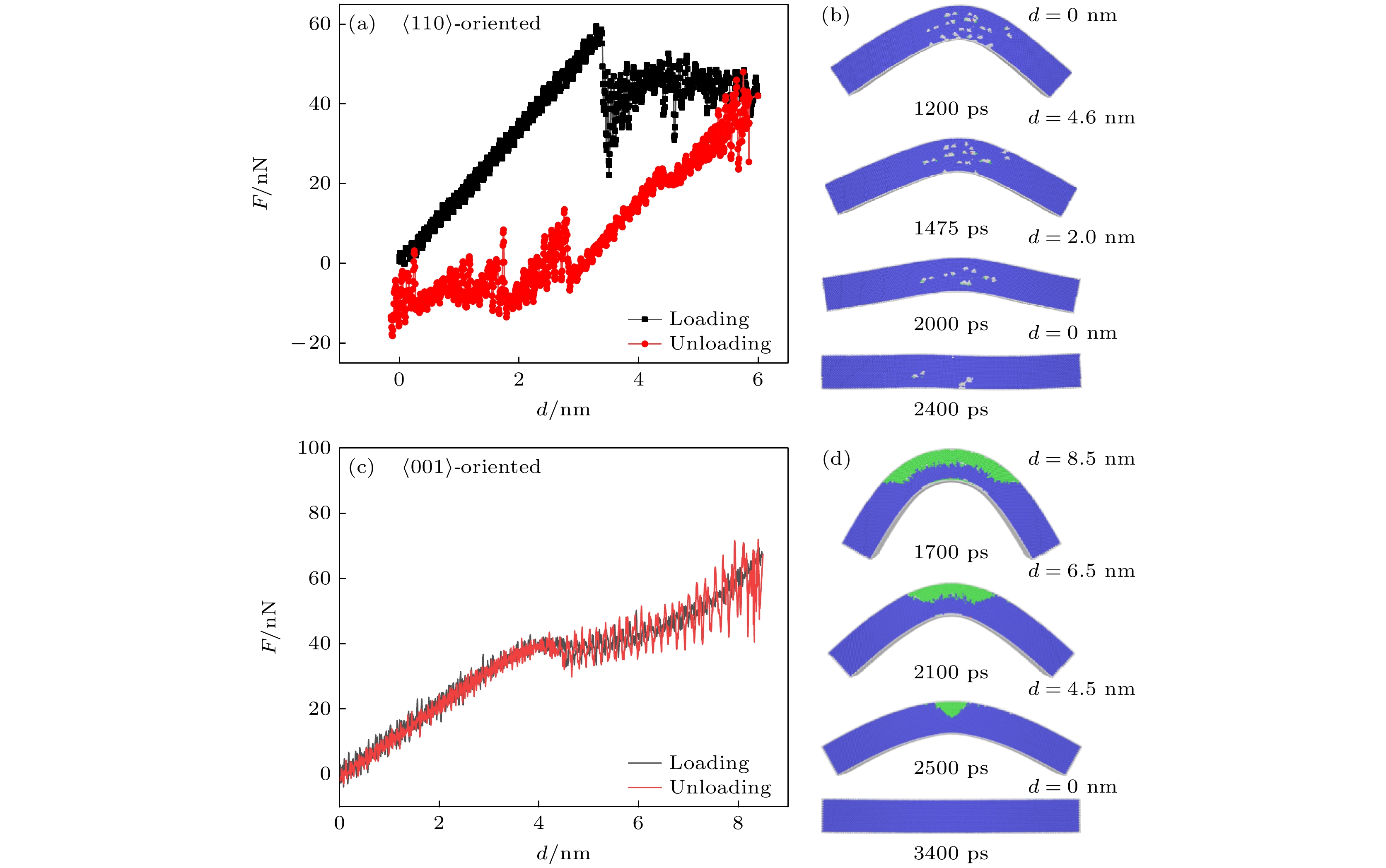
$\left\langle {110} \right\rangle $ 和$\left\langle {001} \right\rangle $ 取向纳米线发生断裂失效前以相同速率卸去弯曲载荷. 图8(a)给出了$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线弯曲形变加载和卸载时的F-d响应曲线, 其中黑色和红色曲线分别表示加载和卸载过程.$\left\langle {110} \right\rangle $ 取向纳米线从时刻t = 1200 ps开始卸载, 此时纳米线的弯曲角约为45°且未发生失效行为, 卸载完成后纳米线内存在不可回复的塑性变形. 图8(b)给出了卸载过程中各阶段的纳米线原子构型. 可以看出, 发生弯曲塑性变形后的纳米线在卸去载荷后可回复至初始形状, 且回复过程中未发生断裂失效, 表现出伪弹性(pseudoelasticity)形变特征. 在此过程中, 纳米线通过位错运动并被纳米线自由表面吸收从而实现形状的回复, 其中, 纳米线自由表面近邻的位错最先被吸收, 如图8(b)中时刻t = 1200 ps和1475 ps的原子构型所示, 而位于纳米线心部区域的位错则逐渐向自由表面运动并最终被吸收. 被吸收的位错在纳米线自由表面形成微台阶. 从图8(b)中时刻t = 2000 ps和2400 ps的原子构型可以看出, 当卸载完成时纳米线内部存在位错残留并且在位错滑过区域有空位形成, 表明位错滑移主导的$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线弯曲塑性变形为部分回复, 它与α-Fe纳米线通过去孪晶方式实现的弯曲形变完全回复不同[24,25]. 如前所述,$\left\langle {110} \right\rangle $ 取向纳米线在形变过程中产生的位错包括GND和SSD, 其中, GND松弛弯曲变形产生的应变梯度, 而SSD则与均匀塑性变形相关. 在卸载过程中, 纳米线内的应变梯度逐渐减弱, GND需要通过位错运动和重排的方式降低位错密度以响应纳米线内部应变状态的变化. 据此可以推断纳米线在回复过程中GND滑移运动并被自由表面吸收, 而与均匀塑性变形相关的SSD则残留在纳米线内.与
$\left\langle {110} \right\rangle $ 取向纳米线的卸载过程不同,$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线的弯曲塑性变形可完全回复. 图8(c)给出了$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线弯曲加载和卸载时的F-d响应曲线, 其中, 卸载时刻t = 1700 ps, 此时纳米线的弯曲角约为60°. 从F-d曲线可以看出, 纳米线的弯曲塑性变形完全回复. 相应地, 图8(d)给出了纳米线卸载时各阶段的原子构型. 可以看出, 卸载过程使$\left\langle {001} \right\rangle $ 方向上的拉应力松弛, 由于B2结构母相与L10产物相之间具有严格的晶体学对应关系, 亚稳态的L10结构产物相的点阵结构则沿原相变路径完全逆转变为初始的B2结构母相的点阵结构, 从而使塑性弯曲后的$\left\langle {001} \right\rangle $ 取向纳米线完全回复至初始形状, 表现出超弹性(superelasticity)行为. 可见, 即使在弯曲载荷作用下$\left\langle {001} \right\rangle $ 取向的FeAl合金纳米线同样具有类似拉伸变形时的超弹性力学特征. 此外, 注意到图8(c)中加载与卸载过程的F-d响应曲线几乎重合, 弯曲塑性变形沿原路径发生回复, 表明$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线在弯曲载荷作用下表现出近零滞后的超弹性行为. 类似的超弹性特征也同样在其他B2结构合金纳米材料的MD模拟[49–52]和实验研究[53,54]中观测到. 其中, 超弹性应力滞后的降低与材料尺寸减小到纳米尺度有关, 特别是当合金的特征尺寸减小到临界尺寸以下时应力滞后甚至消失, 而纳米尺度下显著的表面效应则对超弹性应力滞后的消除起到关键作用. -
本文采用分子动力学方法模拟研究了不同取向B2结构FeAl合金纳米线弯曲时的力学响应和形变机制, 并同时考虑了纳米线尺寸和横截面形状的影响. 从模拟结果可知, B2结构FeAl合金纳米线的弯曲形变行为高度依赖于纳米线轴向的晶体学取向, 而纳米线尺寸和横截面形状的差异则对其形变行为不产生显著影响. 在上述模拟结果中,
$\left\langle {111} \right\rangle $ 和$\left\langle {110} \right\rangle $ 取向纳米线的屈服机制均为位错形核, 但$\left\langle {111} \right\rangle $ 取向纳米线在屈服后随即发生脆性断裂行为, 而$\left\langle {110} \right\rangle $ 取向纳米线则在弯曲过程中表现出良好的弯曲塑性及延展性; 另一方面, 与前两种纳米线不同,$\left\langle {001} \right\rangle $ 取向纳米线的塑性变形机制为应力诱发B2→L10相变, 且同样表现出优异的弯曲塑性. 可以看出, 晶体学取向的差异使FeAl合金纳米线表现出完全不同的弯曲力学性能. 其中,$\left\langle {110} \right\rangle $ 和$\left\langle {001} \right\rangle $ 取向纳米线表现出较其相应块体合金材料更高的塑性和强度, 使其在柔性微纳米电子元器件的设计和制造中具有巨大的开发潜力和应用价值.进一步地, 上述FeAl合金纳米线弯曲形变行为对晶体学取向的依赖性可借助Schmid因子得到解释. 本研究中FeAl合金纳米线的上、下表面为
$ (1\bar 1 0) $ 面, 弯曲加载方向为$ [1\bar 1 0] $ 方向, 根据晶体学分析可知, 纳米线在形变过程中可开动的位错滑移系为${1}/{2}[11\bar 1 ]/(011) $ . 通过计算可得,$\left\langle {111} \right\rangle $ ,$\left\langle {110} \right\rangle $ 和$\left\langle {001} \right\rangle $ 取向纳米线在该滑移系上的Schmid因子分别为0.27, 0.41和0.41. 可见,$\left\langle {111} \right\rangle $ 取向纳米线在${1}/{2}[11\bar 1 ]/(011) $ 滑移系上的Schmid因子最小, 使其无法激活足够的位错以松弛塑性变形, 从而导致纳米线过早地发生脆性断裂; 此外, B2结构FeAl合金中的Fe和Al原子在$\left\langle {111} \right\rangle $ 方向上形成的共价键特征也增大了$\left\langle {111} \right\rangle $ 取向纳米线脆性断裂的趋势. 相比之下,$\left\langle {110} \right\rangle $ 取向纳米线在${1}/{2}[11\bar 1 ]/(011) $ 滑移系上具有较大的Schmid因子, 可激活并开动足够多的位错作为塑性变形的载体从而使塑性变形可稳定进行; 与此同时,$\left\langle {110} \right\rangle $ 取向纳米线还可开动${1}/{2}[111]/(01\bar 1 ) $ 滑移系, 并且在该滑移系上的Schmid因子也是0.41, 而$\left\langle {111} \right\rangle $ 取向纳米线则由于晶体结构特征的限制而无法开动该滑移系. 因此, 在上述弯曲过程中$\left\langle {110} \right\rangle $ 取向纳米线较$\left\langle {111} \right\rangle $ 取向纳米线具有更高的塑性. 另一方面, 注意到$\left\langle {110} \right\rangle $ 和$\left\langle {001} \right\rangle $ 取向纳米线在${1}/{2}[11\bar 1 ]/(011) $ 滑移系上具有相同的Schmid因子, 即这两种取向的纳米线在相同应力状态下激活该滑移系的概率相同. 然而, 从它们的F-d曲线可以看出,$\left\langle {110} \right\rangle $ 取向纳米线屈服时的作用力显著高于$\left\langle {001} \right\rangle $ 取向纳米线, 表明位错形核的临界作用力远高于应力诱发B2→L10相变. 因此,$\left\langle {001} \right\rangle $ 取向纳米线在弯曲载荷尚未达到位错形核的临界作用力时便通过应力诱发相变而发生屈服, 并导致弯曲作用力下降并维持在低于位错形核临界作用力的水平, 从而使$\left\langle {001} \right\rangle $ 取向纳米线的弯曲塑性变形以应力诱发固态相变为主导机制. -
本文采用分子动力学方法模拟不同取向B2结构FeAl合金纳米线的弯曲行为, 同时考虑了纳米线尺寸及其横截面形状的影响, 借助公共近邻分析和位错提取算法等可视化方法分析纳米线弯曲过程中的微观结构演变和形变机制, 并得到以下结论:
1) B2结构FeAl合金纳米线弯曲时的塑性变形微观机制不随纳米线尺寸及其横截面形状的变化而改变, 而只高度依赖于纳米线轴向的晶体学取向, 并且纳米线的弹性模量和屈服强度等力学性能也呈现出显著的取向依赖性.
2)
$\left\langle {111} \right\rangle $ 和$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线弯曲时的屈服机制均为位错形核, 但$\left\langle {111} \right\rangle $ 取向纳米线在屈服后发生脆性断裂行为, 而$\left\langle {110} \right\rangle $ 取向纳米线则通过位错的连续形核与滑移运动在纳米线内形成稳定的塑性流动, 从而表现出良好的塑性及延展性;$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线的弯曲塑性变形机制则为应力诱发B2→L10相变, 并同样表现出良好的弯曲塑性, 且具有较$\left\langle {110} \right\rangle $ 取向纳米线更高的断裂应变. FeAl合金纳米线弯曲形变机制的晶体学取向依赖性可基于Schmid因子得到解释.3)在卸载过程中, 塑性弯曲形变后的
$\left\langle {110} \right\rangle $ 和$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线均可回复至初始形状, 特别地,$\left\langle {001} \right\rangle $ 取向纳米线的弯曲塑性变形可实现完全回复, 表现出超弹性力学特征. 其中, 弯曲的$\left\langle {110} \right\rangle $ 取向纳米线在卸载过程中通过位错运动并被纳米线自由表面吸收而回复至初始形状, 而$\left\langle {001} \right\rangle $ 取向纳米线则通过L10→B2逆相变实现弯曲塑性变形的完全回复.上述结果阐明了B2结构FeAl合金纳米线在弯曲载荷作用下的形变特征和微观机制, 可为基于金属纳米线的微纳器件设计和应用提供有价值的参考.
不同取向B2结构FeAl合金纳米线弯曲行为的分子动力学模拟
Molecular dynamics simulation of bending behavior of B2-FeAl alloy nanowires with different crystallographic orientations
-
摘要: 金属纳米线的弯曲力学性能直接决定了微纳器件的可靠性和使用寿命. 厘清纳米线在弯曲载荷作用下的力学响应特征和形变微观机制, 对设计和制造高性能微纳器件具有十分重要的理论意义和巨大的工程价值. 本文采用分子动力学模拟方法对不同取向B2结构FeAl合金纳米线的弯曲行为展开研究, 并同时考虑纳米线尺寸和横截面形状的影响. 结果表明, 在本文考虑的尺寸范围内, FeAl合金纳米线弯曲塑性变形的微观机制不随纳米线尺寸及横截面形状的变化而改变, 而只取决于纳米线轴向的晶体学取向. 其中, $\left\langle {111} \right\rangle $和$\left\langle {110} \right\rangle $取向纳米线的屈服均源于位错形核, 但$\left\langle {111} \right\rangle $取向纳米线在屈服后随即发生脆性断裂, 而$\left\langle {110} \right\rangle $取向纳米线则在位错连续形核与滑移过程中产生稳定的塑性流动, 从而表现出良好的塑性及延展性; 与上述两种取向纳米线不同, $\left\langle {001} \right\rangle $取向纳米线的弯曲形变机制以应力诱发B2→L10相变为主导, 同样表现出良好的弯曲塑性, 且具有较$\left\langle {110} \right\rangle $取向纳米线更高的断裂应变. FeAl合金纳米线弯曲行为的晶体学取向依赖性可借助Schmid因子得到解释. 此外, 塑性弯曲的$\left\langle {110} \right\rangle $和$\left\langle {001} \right\rangle $取向纳米线在卸载过程中可回复至初始形状, 特别地, $\left\langle {001} \right\rangle $取向纳米线的弯曲塑性变形可完全回复, 表现出超弹性特征. 本文从原子尺度阐明B2结构FeAl合金纳米线的弯曲形变行为及其关键影响因素, 对基于金属纳米线的柔性微纳器件设计和性能优化具有重要指导意义.
-
关键词:
- B2结构FeAl合金纳米线 /
- 弯曲形变 /
- 位错密度 /
- 分子动力学模拟
Abstract: In nanosystems, the metallic nanowires are subjected to significant and cyclic bending deformation upon being integrated into stretchable and flexible nanoelectronic devices. The reliability and service life of these nanodevices depend fundamentally on the bending mechanical properties of the metallic nanowires that serve as the critical components. An in-depth understanding of the deformation behavior of the metallic nanowires under bending is not only essential but also imperative for designing and manufacturing high-performance nanodevices. To explore the mechanism of the bending plasticity of the metallic nanowire, the bending deformations of B2-FeAl alloy nanowires with various crystallographic orientations, sizes and cross-sectional shapes are investigated by using molecular dynamics simulation. The results show that the bending behavior of the B2-FeAl alloy nanowires is dependent on neither their size nor cross-sectional shape of the nanowire, but it is highly sensitive to its axial orientation. Specifically, both $\left\langle {111} \right\rangle $- and $\left\langle {110} \right\rangle $-oriented nanowires are generated through dislocation nucleation during bending, with the $\left\langle {111} \right\rangle $-oriented nanowires failling shortly after yielding due to brittle fracture, while the $\left\langle {110} \right\rangle $-oriented nanowires exhibit good ductility due to uniform plastic flow caused by continuous nucleation and stable motion of dislocations. Unlike the aforementioned two nanowires, the bending plasticity of the $\left\langle {001} \right\rangle $-oriented nanowire is mediated by the stress-induced transition from B2 phase to L10 phase, which leads to excellent ductility and higher fracture strain. The orientation dependence of bending deformation can be understood by considering the Schmid factor. Moreover, the plastically bent nanowires with $\left\langle {110} \right\rangle $ and $\left\langle {001} \right\rangle $ orientation are able to recover to their original shape upon unloading, particularly, the plastic deformation in the $\left\langle {001} \right\rangle $-oriented nanowire is recoverable completely via reverse transformation from L10 to B2 structures, exhibiting superelasticity. This work elucidates the deformation mechanism of the B2-FeAl alloy nanowires subjected to bending loads, which provides a crucial insight for designing and optimizing flexible and stretchable nanodevices based on metallic nanowires. -

-
图 3
$\left\langle {111} \right\rangle $ 取向FeAl合金纳米线弯曲变形在d = 0 nm (a), 3.585 nm (b), 3.660 nm (c)和3.725 nm (d)时的原子构型, 图中颜色表征晶体结构, 其中蓝色表示BCC结构, 绿色表示FCC结构以及白色表示未知结构Figure 3. Atomic configurations of the
$\left\langle {111} \right\rangle $ -oriented FeAl alloy nanowire upon bending deformation at d = 0 nm (a), 3.585 nm (b), 3.660 nm (c) and 3.725 nm (d), where colors denote the different local crystal structures: blue-BCC, green-FCC and white-unknown.图 4
$\left\langle {111} \right\rangle $ 取向FeAl合金纳米线断裂前的位错结构特征及其演化行为 (a) d = 3.585 nm; (b) d = 3.635 nm; (c) d = 3.660 nm; (d) d = 3.675 nmFigure 4. Structural characteristics and evolution of dislocations in the
$\left\langle {111} \right\rangle $ -oriented FeAl alloy nanowire before fracture: (a) d = 3.585 nm; (b) d = 3.635 nm; (c) d = 3.660 nm; (d) d = 3.675 nm.图 5
$\left\langle {110} \right\rangle $ 取向FeAl合金纳米线弯曲变形在d = 3.300 nm (a), 4.500 nm (b), 6.000 nm (c), 8.900 nm (d)和9.300 nm (e)时的原子构型, 图中颜色表征晶体结构, 其中, 蓝色表示BCC结构, 绿色表示FCC结构, 红色表示HCP结构以及白色表示未知结构; (f) d = 9.300 nm时纳米线在1860 ps时的应变分布图Figure 5. Atomic configurations of the
$\left\langle {110} \right\rangle $ -oriented FeAl alloy nanowire upon bending deformation at d = 3.300 nm (a), 4.500 nm (b), 6.000 nm (c), 8.900 nm (d) and 9.300 nm (e), where colors denote the different local crystal structures: blue-BCC, green-FCC, red-HCP and white-unknown; (f) strain distribution within the nanowire at 1860 ps and d = 9.300 nm, where atoms are colored by their local shear strain.图 7
$\left\langle {001} \right\rangle $ 取向FeAl合金纳米线弯曲变形在d = 4.200 nm (a), 6.000 nm (b), 8.000 nm (c), 9.440 nm (d) 和 9.540 nm (e)时的原子构型, 图中颜色表征晶体结构, 其中, 蓝色表示BCC结构, 绿色表示FCC结构, 红色表示HCP结构以及白色表示未知结构; (f) d = 9.540 nm时纳米线在1908 ps时的应变分布图Figure 7. Atomic configurations of the
$\left\langle {001} \right\rangle $ -oriented FeAl alloy nanowire upon bending deformation at d = 4.200 nm (a), 6.000 nm (b), 8.000 nm (c), 9.440 nm (d) and 9.540 nm (e), where colors denote the different local crystal structures: blue-BCC, green-FCC, red-HCP and white-unknown; (f) strain distribution within the nanowire at 1908 ps and d = 9.540 nm, where atoms are colored by their local shear strain.图 8
$\left\langle {110} \right\rangle $ 取向FeAl纳米线弯曲形变加载和卸载过程的F-d响应曲线(a)及卸载过程各阶段的原子构型(b);$\left\langle {001} \right\rangle $ 取向FeAl纳米线弯曲形变加载和卸载过程的F-d响应曲线(c)及卸载过程各阶段的原子构型(d)Figure 8. F-d curves of the
$\left\langle {110} \right\rangle $ -oriented FeAl alloy nanowire under loading and unloading (a) in addition to the atomic configurations during unloading (b); F-d curves of the$\left\langle {001} \right\rangle $ -oriented FeAl alloy nanowire under loading and unloading (c) in addition to the atomic configurations during unloading (d).表 1 FeAl合金纳米线初始模型的晶体学取向特征
Table 1. Crystallographic orientation of the FeAl alloy nanowires.
Orientation X Y Z $\left\langle {111} \right\rangle $ [111] $ [1\bar 1 0] $ $ [11\bar 2 ] $ $\left\langle {001} \right\rangle $ [001] $ [1\bar 1 0] $ [110] $\left\langle {110} \right\rangle $ [110] $ [1\bar 1 0] $ [001] -
[1] Wu Y, Xiang J, Yang C, Lu W, Lieber C M 2004 Nature 430 61 doi: 10.1038/nature02674 [2] Foss C A, Hornyak G L, Stockert J A, Martin C R 1992 J. Phys. Chem. 96 7497 doi: 10.1021/j100198a004 [3] Lee P, Lee J, Lee H, Yeo J, Hong S, Nam K H, Lee D, Lee S S, Ko S H 2012 Adv. Mater. 24 3326 doi: 10.1002/adma.201200359 [4] Kondo Y, Takayanagi K 1997 Phys. Rev. Lett. 79 3455 doi: 10.1103/PhysRevLett.79.3455 [5] Huo Z Y, Tsung C K, Huang W Y, Zhang X F, Yang P D 2008 Nano Lett. 8 2041 doi: 10.1021/nl8013549 [6] Marszalek P E, Greenleaf W J, Li H, Oberhauser A F, Fernandez J M 2000 Proc. Natl. Acad. Sci. U. S. A. 97 6282 doi: 10.1073/pnas.97.12.6282 [7] Wang J W, Zeng Z, Weinberger C R, Zhang Z, Zhu T, Mao S X 2015 Nat. Mater. 14 594 doi: 10.1038/nmat4228 [8] Yue Y H, Liu P, Deng Q S, Ma E, Zhang Z, Han X D 2012 Nano Lett. 12 4045 doi: 10.1021/nl3014132 [9] Seo J H, Yoo Y, Park N Y, Yoon S W, Lee H, Han S, Lee S W, Seong T Y, Lee S C, Lee K B, Cha P R, Park H S, Kim B, Ahn J P 2011 Nano Lett. 11 3499 doi: 10.1021/nl2022306 [10] Cao G, Wang J W, Du K, Wang X L, Li J X, Zhang Z, Mao S X 2018 Adv. Funct. Mater. 28 1805258 doi: 10.1002/adfm.201805258 [11] Hagen A B, Snartland B D, Thaulow C 2017 Acta Mater. 129 398 doi: 10.1016/j.actamat.2017.03.006 [12] Wang Q N, Wang J W, Li J X, Zhang Z, Mao S X 2018 Sci. Adv. 4 1 doi: 10.1126/sciadv.aas8850 [13] Wu B, Heidelberg A, Boland J J 2005 Nat. Mater. 4 525 doi: 10.1038/nmat1403 [14] Hu T, Ma K, Topping T D, Jiang L, Zhang D, Mukherjee A K, Schoenung J M, Lavernia E J 2016 Scr. Mater. 113 35 doi: 10.1016/j.scriptamat.2015.10.008 [15] Wei S Y, Wang Q N, Wei H, Wang J W 2019 Mater. Res. Lett. 7 210 doi: 10.1080/21663831.2019.1578833 [16] Sun S D, Li D W, Yang C P, Fu L B, Kong D L, Lu Y, Guo Y Z, Liu D M, Guan P F, Zhang Z, Chen J H, Ming W Q, Wang L H, Han X D 2022 Phys. Rev. Lett. 128 015701 doi: 10.1103/PhysRevLett.128.015701 [17] Olsson P A T, Melin S, Persson C 2007 Phys. Rev. B 76 224112 doi: 10.1103/PhysRevB.76.224112 [18] McDowell M T, Leach A M, Gall K 2008 Model. Simul. Mater. Sci. Eng. 16 045003 doi: 10.1088/0965-0393/16/4/045003 [19] Zhu W P, Wang H T, Yang W 2012 Acta Mater. 60 7112 doi: 10.1016/j.actamat.2012.09.018 [20] Deb Nath S K 2014 Comput. Mater. Sci. 87 138 doi: 10.1016/j.commatsci.2014.02.013 [21] Zhang S B 2014 Comput. Mater. Sci. 95 53 doi: 10.1016/j.commatsci.2014.07.016 [22] Nöhring W G, Möller J J, Xie Z, Bitzek E 2016 Extrem. Mech. Lett. 8 140 doi: 10.1016/j.eml.2016.03.001 [23] Zhan H F, Gu Y T 2012 J. Appl. Phys. 111 084305 doi: 10.1063/1.3703673 [24] Yang Y, Li S Z, Ding X D, Sun J, Salje E K H 2016 Adv. Funct. Mater. 26 760 doi: 10.1002/adfm.201504085 [25] Yang Y, Li S Z, Ding X D, Sun J 2021 Comput. Mater. Sci. 188 110128 doi: 10.1016/j.commatsci.2020.110128 [26] Mendelev M I, Srolovitz D J, Ackland G J, Han S 2005 J. Mater. Res. 20 208 doi: 10.1557/JMR.2005.0024 [27] Yan J X, Zhang Z J, Li K Q, Xia Z Y, Yang J B, Zhang Z F 2020 J. Alloys Compd. 815 152362 doi: 10.1016/j.jallcom.2019.152362 [28] Dong S, Liu X Y, Zhou C 2021 J. Mater. Sci. 56 17080 doi: 10.1007/s10853-021-06377-0 [29] Timoshenko S P, Gere J M 1961 Theory of Elastic Stability (New York: McGraw-Hill) p1 [30] Plimpton S 1995 J. Comput. Phys. 117 1 doi: 10.1006/jcph.1995.1039 [31] Stukowski A 2010 Model. Simul. Mater. Sci. Eng. 18 015012 doi: 10.1088/0965-0393/18/1/015012 [32] Faken D, Jonsson H 1994 Comput. Mater. Sci. 2 279 doi: 10.1016/0927-0256(94)90109-0 [33] Stukowski A, Albe K 2010 Model. Simul. Mater. Sci. Eng. 18 025016 doi: 10.1088/0965-0393/18/2/025016 [34] Shimizu F, Ogata S, Li J 2007 Mater. Trans. 48 2923 doi: 10.2320/matertrans.MJ200769 [35] 陈煜, 姚正军, 张平则, 魏东博, 罗西希, 韩培德 2014 稀有金属材料与工程 43 2112 Chen Y, Yao Z J, Zhang P Z, Wei D B, Luo X X, Han P D 2014 Rare Metal. Mat. Eng. 43 2112 [36] Wang Z, Shi X, Yang X S, He W, Shi S Q, Ma X 2021 J. Mater. Sci. 56 2275 doi: 10.1007/s10853-020-05401-z [37] Horton J A, Ohr S M 1982 J. Mater. Sci. 17 3140 doi: 10.1007/BF01203476 [38] Colorado H A, Navarro A, Prikhodko S V, Yang J M, Ghoniem N, Gupta V 2013 J. Appl. Phys. 114 233510 doi: 10.1063/1.4851055 [39] Hwang B, Kim T, Han S M 2016 Extrem. Mech. Lett. 8 266 doi: 10.1016/j.eml.2016.02.011 [40] Nye J F 1953 Acta Metall. 1 153 doi: 10.1016/0001-6160(53)90054-6 [41] Ashby M F 1969 Philos. Mag. 21 399 doi: 10.1080/14786437008238426 [42] Greer J R, Nix W D 2006 Phys. Rev. B 73 245410 doi: 10.1103/PhysRevB.73.245410 [43] Shan Z W, Mishra R K, Syed Asif S A, Warren O L, Minor A M 2008 Nat. Mater. 7 115 doi: 10.1038/nmat2085 [44] Norfleet D M, Dimiduk D M, Polasik S J, Uchic M D, Mills M J 2008 Acta Mater. 56 2988 doi: 10.1016/j.actamat.2008.02.046 [45] Lee S W, Han S M, Nix W D 2009 Acta Mater. 57 4404 doi: 10.1016/j.actamat.2009.06.002 [46] Rodriguez-Nieva J F, Ruestes C J, Tang Y, Bringa E M 2014 Acta Mater. 80 67 doi: 10.1016/j.actamat.2014.07.051 [47] Santhapuram R R, Spearot D E, Nair A K 2020 J. Mater. Sci. 55 16990 doi: 10.1007/s10853-020-05234-w [48] 袁用开, 陈茜, 高廷红, 梁永超, 谢泉, 田泽安, 郑权, 陆飞 2023 物理学报 72 136801 doi: 10.7498/aps.72.20221860 Yuan Y K, Chen Q, Gao T H, Liang Y C, Xie Q, Tian Z A, Zheng Q, Lu F 2023 Acta Phys. Sin. 72 136801 doi: 10.7498/aps.72.20221860 [49] Saitoh K, Liu W K 2009 Comput. Mater. Sci. 46 531 doi: 10.1016/j.commatsci.2009.04.025 [50] Zhang Z, Ding X D, Sun J, Suzuki T, Lookman T, Otsuka K, Ren X B 2013 Phys. Rev. Lett. 111 145701 doi: 10.1103/PhysRevLett.111.145701 [51] Mirzaeifar R, Gall K, Zhu T, Yavari A, Desroches R 2014 J. Appl. Phys. 115 194307 doi: 10.1063/1.4876715 [52] Morrison K R, Cherukara M J, Kim H, Strachan A 2015 Acta Mater. 95 37 doi: 10.1016/j.actamat.2015.05.015 [53] Ahadi A, Sun Q 2013 Appl. Phys. Lett. 103 021902 doi: 10.1063/1.4812643 [54] Ahadi A, Sun Q 2014 Acta Mater. 76 186 doi: 10.1016/j.actamat.2014.05.007 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: