高级搜索

链接杂质对一维量子Ising模型动力学性质的调控

downloadPDF

上一篇

下一篇

袁晓娟. 链接杂质对一维量子Ising模型动力学性质的调控[J]. 物理学报, 2025, 74(3): 037501-1. doi: 10.7498/aps.74.20241390
引用本文: 袁晓娟. 链接杂质对一维量子Ising模型动力学性质的调控[J]. 物理学报, 2025, 74(3): 037501-1. doi: 10.7498/aps.74.20241390
shu
Xiaojuan YUAN. Effects of link-impurity on spin dynamics of one-dimensional quantum Ising model[J]. Acta Physica Sinica, 2025, 74(3): 037501-1. doi: 10.7498/aps.74.20241390
Citation: Xiaojuan YUAN. Effects of link-impurity on spin dynamics of one-dimensional quantum Ising model[J]. Acta Physica Sinica, 2025, 74(3): 037501-1. doi: 10.7498/aps.74.20241390
shu

链接杂质对一维量子Ising模型动力学性质的调控

  • 齐鲁师范学院物理与电子工程学院, 济南　250200

    • 通讯作者: E-mail: yuanxiaojuan@163.com.

  • 中图分类号: 75.10.Pq, 75.40.Gb, 75.10.Jm, 75.50.Lk

Effects of link-impurity on spin dynamics of one-dimensional quantum Ising model

  • College of Physics and Electronic Engineering, Qilu Normal University, Jinan 250200, China

    • Corresponding author: Email: yuanxiaojuan@163.com.

  • MSC: 75.10.Pq, 75.40.Gb, 75.10.Jm, 75.50.Lk

  • 摘要: 自旋系统的动力学性质是量子统计和凝聚态理论研究的热点. 本文利用递推方法, 通过计算自旋关联函数及谱密度, 研究了链接杂质对一维量子Ising模型动力学性质的调控效应. 研究表明, 链接杂质的出现打破了主体格点自旋耦合$ J $和外磁场$ B $之间原有的竞争关系, 系统的动力学最终取决于链接杂质和主体格点自旋耦合的平均效应$ \bar J $、链接杂质的不对称程度及外磁场$ B $的强度等多因素之间的协同作用. 对于对称型链接杂质($ {J_{j - 1}} = {J_j} $), 随着杂质耦合强度的增大, 在$ B \geqslant J $的情况下, 系统的动力学出现了由集体模行为到中心峰值行为的交跨; 在$ B \lt J $的情况下, 出现了由类集体模行为到双峰行为, 再到中心峰值行为的两次交跨. 对于非对称型链接杂质($ {J_{j - 1}} \ne {J_j} $), 其杂质位型较多, 可以提供更多的调控自由度, 尤其当其中某个杂质耦合强度如$ {J_{j - 1}} $(或$ {J_j} $)较小时, 通过调节另一个杂质耦合强度$ {J_j} $(或$ {J_{j - 1}} $)可以得到多种动力学行为之间的交跨; 在$ B \gt J $情况下, 非对称型链接杂质的调控机制更为复杂, 出现了与以往研究经验不符的交跨顺序, 且出现了双频谱这种新的动力学模式. 一般来讲, 当平均自旋耦合$ \bar J $较弱或非对称型链接杂质的不对称程度较低时, 系统倾向于呈现集体模行为; 当$ \bar J $较强时, 系统倾向于呈现中心峰值行为; 但当非对称型链接杂质的不对称程度较明显时, 谱密度倾向于呈双峰、多峰或双频谱特征. 研究表明, 链接杂质的调控结果更加丰富, 且具有独特的调控优势, 因此利用链接杂质来调控量子自旋系统的动力学不失为一种新的尝试.
    Abstract: It is of considerable theoretical significance to study the effects of impurity on spin dynamics of quantum spin systems. In this paper, the dynamical properties of the one-dimensional quantum Ising model with symmetric and asymmetric link-impurity are investigated by the recursion method, respectively. The autocorrelation function $C\left( t \right) = \overline {\left\langle {\sigma _j^x\left( t \right)\sigma _j^x\left( 0 \right)} \right\rangle } $ and the associated spectral density $\varPhi \left( \omega \right) = \displaystyle\int_{ - \infty }^{ + \infty } {{\rm d}t{{\rm e}^{{\rm i}\omega t}}C\left( t \right)} $ are calculated. The Hamiltonian of the Ising model with link-impurity can be written as $\qquad\qquad\qquad\qquad\qquad H = - \displaystyle\frac{1}{2}({J_{j - 1}}\sigma _{j - 1}^x\sigma _j^x + {J_j}\sigma _j^x\sigma _{j + 1}^x) - \displaystyle\frac{1}{2}J\sum\limits_{i \ne j,j - 1}^N {\sigma _i^x\sigma _{i + 1}^x} - \frac{1}{2}B\sum\limits_i^N {\sigma _i^z} . $where $J$ is the nearest-neighbor exchange coupling of the main spin chain, $ B $ denotes the external transverse magnetic field, $\sigma _i^\alpha \left( {\alpha = x,y,z} \right)$ are Pauli matrices at site $ i $. The constant 1/2 is introduced for the convenience of theoretical deduction, and N is the number of spins. The so-called link-impurity $ {J_j} $ ($ {J_{j - 1}} $) is randomly introduced, which denotes the exchange coupling between the j th spin and the (j + 1)th spin (the (j – 1)th spin). The symmetric link-impurity and asymmetric link-impurity correspond to the case of $ {J_{j - 1}} = {J_j} $ and $ {J_{j - 1}} \ne {J_j} $, respectively. The periodic boundary conditions are assumed in the theoretical calculation.After introducing the link-impurity, the original competition between $ B $ and $J$ in the pure Ising model is broken. The dynamic behavior of the system depends on synergistic effect of multiple factors, such as the mean spin coupling $ \bar J $ between $J$ and the link-impurity, the asymmetry degree between $ {J_{j - 1}} $ and $ {J_j} $, and the strength of the external magnetic field. In calculation, the exchange couplings of the main spin chain are set to $J \equiv 1$ to fix the energy scale. We first consider the effects of symmetric link-impurity. The reference values can be set to $ {J_{j - 1}} = {J_j} \lt J $ (e.g. 0.4, 0.6 or 0.8) or $ {J_{j - 1}} = {J_j} \gt J $ (e.g. 1.2, 1.6, 2.0), which are called weak or strong impurity coupling. When the magnetic field $ B \geqslant J $ (e.g., $ B = 1 $, 1.5 or 2.0), it is found that the dynamic behavior of the system exhibits a crossover from a collective-mode behavior to a central-peak behavior as the impurity strength $ {J_{j - 1}} = {J_j} $ increases. Interestingly, for $ B \lt J $ (e.g. $ B = 0.4 $ or 0.7), there are two crossovers that are a collective-mode-like behavior to a double-peak behavior, then to a central-peak behavior as $ {J_{j - 1}} = {J_j} $ increases.For the case of asymmetric link-impurity, the impurity configuration is more complex. Using the cooperation between $ {J_{j - 1}} $ and $ {J_j} $, more freedoms of regulation can be provided and the dynamical properties are more abundant. For the case of $ B \leqslant J $ (e.g. $ B = 0.5 $, 1.0), the system tends to exhibit a collective-mode behavior when the mean spin coupling $ \bar J $ is weak, and a central-peak behavior when $ \bar J $ are strong. However, when the asymmetry between $ {J_{j - 1}} $ and $ {J_j} $ is obvious, the system tends to exhibit a double- or multi-peak behavior. For the case of $ B \gt J $ (e.g. $ B = 1.5 $, 2.0), when $ \bar J $ is weak or the asymmetry between $ {J_{j - 1}} $ and $ {J_j} $ is not obvious, the system tends to exhibit a collective-mode behavior. When $ \bar J $ is strong, it tends to show a central-peak behavior. However, when the asymmetry between $ {J_{j - 1}} $ and $ {J_j} $ is evident, the bispectral feature (two spectral peaks appear at $ {\omega _1} \ne 0 $ and $ {\omega _2} \ne 0 $) dominates the dynamics. Under the regulating effect of link-impurities, the crossover between different dynamic behaviors can be easily realized, and it is easier to stimulate new dynamic modes, such as the double-peak behavior, the collective-mode-like behavior or bispectral feature one. The results in this work indicate that using link-impurity to manipulate the dynamics of quantum spin systems may be a new try.
  • 加载中

  • 图 1  对称型链接杂质在不同杂质耦合强度下的连分式系数$ {\varDelta _\nu } $, 其中横向磁场$ B = J \equiv 1 $, 杂质耦合强度取值为$ {J_{j - 1}} = {J_j} = 0.4 $, 0.6, 0.8, 1.0, 1.2, 1.4和1.6

    Figure 1.  Recurrants $ {\varDelta _\nu } $ for the symmetric type of link-impurity. The transverse magnetic field $ B = J \equiv 1 $, and the impurity coupling strength $ {J_{j - 1}} = {J_j} = 0.4 $, 0.6, 0.8, 1.0, 1.2, 1.4 and 1.6.

    下载: 全尺寸图片 幻灯片

    图 2  对称型链接杂质在不同杂质耦合强度下的自旋关联函数$C\left( t \right)$(a)及谱密度$\varPhi \left( \omega \right)$(b), 其中横向磁场$ B = J \equiv 1 $, 杂质耦合强度$ {J_{j - 1}} = {J_j} = 0.4 $, 0.6, 0.8, 1.0和1.2

    Figure 2.  Spin autocorrelation function $C\left( t \right)$ (a) and spectral density $\varPhi \left( \omega \right)$ (b) for the symmetric type of link-impurity under different impurity coupling strengths. The transverse magnetic field $ B = J \equiv 1 $, and the impurity coupling strength $ {J_{j - 1}} = {J_j} = 0.4 $, 0.6, 0.8, 1.0 and 1.2.

    下载: 全尺寸图片 幻灯片

    图 3  对称型链接杂质在不同杂质耦合强度下的谱密度$\varPhi \left( \omega \right)$, 图(a)—(d)中横向磁场的取值分别为$ B = 0.4 $, 0.7, 1.5和2.0, 主体格点自旋耦合$ J \equiv 1 $

    Figure 3.  Spectral densities $\varPhi \left( \omega \right)$ for symmetric type of link-impurity under different impurity coupling strength. Without loss of generality, the parameter $ J \equiv 1 $, and the transverse magnetic field $ B = 0.4 $, 0.7, 1.5 and 2.0 in panel (a)–(d).

    下载: 全尺寸图片 幻灯片

    图 4  固定横场$ B = J \equiv 1 $, 非对称型链接杂质在不同杂质耦合强度下的谱密度$\varPhi \left( \omega \right)$, 其中固定$ {J_{j - 1}} = J' $, 图(a)—(d)中$ {J_{j - 1}} $分别取值为0.2, 0.5, 1.0和1.4; $ {J_j} = J'' $的取值从0.2变化到1.8

    Figure 4.  Spectral densities for non-symmetric type of link-impurity under different impurity coupling strength. The transverse magnetic field $ B = J \equiv 1 $, and the impurity coupling strength $ J_{j-1}=J'=0.2 $, 0.5, 1.0 and 1.4 are set in panels (a)–(d), respectively. The other impurity coupling strength $ {J_j} ({J_j} = J'')$ changes from 0.2 to 1.8.

    下载: 全尺寸图片 幻灯片

    图 5  固定横场$ B = 0.5 = J/2 $, 非对称型链接杂质在不同杂质耦合强度下的谱密度, 其中固定$ {J_{j - 1}} = J' $, 图(a)—(f)中$ {J_{j - 1}} $分别取值为0.2, 0.5, 0.8, 1.2, 1.6和2.0, $ {J_j} = J'' $的取值从0.2变化到1.8

    Figure 5.  Spectral densities for non-symmetric type of link-impurity under different impurity coupling strength. The transverse magnetic field $ B = 0.5 = J/2 $, and the impurity coupling strength $ {J_{j - 1}} =J'= 0.2 $, 0.5, 0.8, 1.2, 1.6 and 2.0 are set in panels (a)–(f), respectively. The other impurity coupling strength $ {J_j} ({J_j} = J'')$ changes from 0.2 to 1.8.

    下载: 全尺寸图片 幻灯片

    图 6  固定横场$ B = 1.5 = 1.5 J $, 给出非对称型链接杂质在不同杂质耦合强度下的谱密度, 固定$ {J_{j - 1}} = J' $, 图(a)—(d)中的$ {J_{j - 1}} $分别取值为0.4, 0.8, 1.2和1.6; $ {J_j} = J'' $的取值从0.2变化到1.8

    Figure 6.  Spectral densities for non-symmetric type of link-impurity under different impurity coupling strength. The transverse magnetic field $ B = 1.5 = 1.5 J $, and the impurity coupling strength $ J_{j-1}=J'=0.4 $, 0.8, 1.2和1.6 are set in panels (a)–(d), respectively. The other impurity coupling strength $ {J_j} ({J_j} = J'')$ changes from 0.2 to 1.8.

    下载: 全尺寸图片 幻灯片
  • [1] Young A P 1997 Phys. Rev. B 56 11691 doi: 10.1103/PhysRevB.56.11691
    [2] Florencio J, Sá Barreto F C 1999 Phys. Rev. B 60 9555 doi: 10.1103/PhysRevB.60.9555
    [3] Liu Z Q, Kong X M, Chen X S 2006 Phys. Rev. B 73 224412 doi: 10.1103/PhysRevB.73.224412
    [4] Yuan X J, Kong X M, Xu Z B, Liu Z Q 2010 Physica A 389 242 doi: 10.1016/j.physa.2009.08.021
    [5] Chen S X, Shen Y Y, Kong X M 2010 Phys. Rev. B 82 174404 doi: 10.1103/PhysRevB.82.174404
    [6] Nunes M E S, Florencio J 2003 Phys. Rev. B 68 014406 doi: 10.1103/PhysRevB.68.014406
    [7] Nunes M E S, Plascak J A, Florencio J 2004 Physica A 332 1 doi: 10.1016/j.physa.2003.10.049
    [8] Xu Z B, Kong X M, Liu Z Q 2008 Phys. Rev. B 77 184414 doi: 10.1103/PhysRevB.77.184414
    [9] Li Y F, Kong X M 2013 Chin. Phys. B 22 037502 doi: 10.1088/1674-1056/22/3/037502
    [10] Laflorencie N, Rieger H, Sandvik A W, Henelius P 2004 Phys. Rev. B 70 054430 doi: 10.1103/PhysRevB.70.054430
    [11] 李银芳, 申银阳, 孔祥木 2012 物理学报 61 107501 doi: 10.7498/aps.61.107501 Li Y F, Shen Y Y, Kong X M 2012 Acta Phys. Sin. 61 107501 doi: 10.7498/aps.61.107501
    [12] Silva da Conceição C M S, Maia R N P 2017 Phys. Rev. E 96 032121 doi: 10.1103/PhysRevE.96.032121
    [13] von Ohr S, Manssen M, Hartmann A K 2017 Phys. Rev. E 96 013315 doi: 10.1103/PhysRevE.96.013315
    [14] Theodorakis P E, Georgiou I, Fytas N G 2013 Phys. Rev. E 87 032119 doi: 10.1103/PhysRevE.87.032119
    [15] Crokidakis N, Nobre F D 2008 J. Phys. : Condens. Matter 20 145211 doi: 10.1088/0953-8984/20/14/145211
    [16] Liu Z Q, Jiang S R, Kong X M 2014 Chin. Phys. B 23 087505 doi: 10.1088/1674-1056/23/8/087505
    [17] Balcerzak T, Szałowski K, Jaščur M 2020 J. Magn. Magn. Mater. 507 166825 doi: 10.1016/j.jmmm.2020.166825
    [18] Silva R L, Guimarães P R C, Pereira A R 2005 Solid State Commun. 134 313 doi: 10.1016/j.ssc.2005.02.001
    [19] Sousa J M, Leite R V, Landim R R, Costa Filho R N 2014 Physica B 438 78 doi: 10.1016/j.physb.2014.01.004
    [20] Huang X, Yang Z 2015 Solid State Commun. 204 28 doi: 10.1016/j.ssc.2014.12.007
    [21] Çağlar T, Nihat Berker A 2015 Phys. Rev. E 92 062131 doi: 10.1103/PhysRevE.92.062131
    [22] Mazzitello K I, Candia J, Albano E V, 2015 Phys. Rev. E 91 042118 doi: 10.1103/PhysRevE.91.042118
    [23] Hadjiagapiou I A, Velonakis I N 2018 Physica A 505 965 doi: 10.1016/j.physa.2018.04.018
    [24] Hadjiagapiou I A, Velonakis I N 2021 Physica A 578 126112 doi: 10.1016/j.physa.2021.126112
    [25] 袁晓娟 2023 物理学报 72 087501 doi: 10.7498/aps.72.20230046 Yuan X J 2023 Acta Phys. Sin. 72 087501 doi: 10.7498/aps.72.20230046
    [26] Boechat B, Cordeiro C, Florencio J, Sá Barreto F C, de Alcantara Bonfim O F 2000 Phys. Rev. B 61 14327 doi: 10.1103/PhysRevB.61.14327
    [27] De Souza W L, de Mello Silva É, Martins P H L 2020 Phys. Rev. E 101 042104 doi: 10.1103/PhysRevE.101.042104
    [28] Nunes M E S, de Mello Silva É, Martins P H L, Plascak J A, Florencio J 2018 Phys. Rev. E 98 042124 doi: 10.1103/PhysRevE.98.042124
    [29] Guimarães P R C, Plascak J A, De Alcantara Bonfim O F, Florencio J 2015 Phys. Rev. E 92 042115 doi: 10.1103/PhysRevE.92.042115
    [30] Hu F M, Ma T, Lin H Q, Gubernatis J E 2011 Phys. Rev. B 84 075414 doi: 10.1103/PhysRevB.84.075414
    [31] Liu Q, Liu C X, Xu C, Qi X L, Zhang S C 2009 Phys. Rev. Lett. 102 156603 doi: 10.1103/PhysRevLett.102.156603
    [32] Cirillo A, Mancini M, Giuliano D, Sodano P 2011 Nuclear Phys. B 852 235 doi: 10.1016/j.nuclphysb.2011.06.014
    [33] Sindona A, Goold J, Lo Gullo N, Lorenzo S, Plastina F 2013 Phys. Rev. Lett. 111 165303 doi: 10.1103/PhysRevLett.111.165303
    [34] Li J, Wang Y P 2009 Europhys. Lett. 88 17009 doi: 10.1209/0295-5075/88/17009
    [35] Apollaro T J G, Francica G, Giuliano D, Falcone G, Palma G M, Plastina F 2017 Phys. Rev. B 96 155145 doi: 10.1103/PhysRevB.96.155145
    [36] Giuliano D, Campagnano G, Tagliacozzo A 2016 Eur. Phys. J. B 89 251 doi: 10.1140/epjb/e2016-70477-7
    [37] Rommer S, Eggert S 2000 Phys. Rev. B 62 4370 doi: 10.1103/PhysRevB.62.4370
    [38] Yuan X J, Zhao J F, Wang H, Bu H X, Yuan H M, Zhao B Y, Kong X M 2021 Physica A 583 126279 doi: 10.1016/j.physa.2021.126279
    [39] Eggert S, Affleck I 1992 Phys. Rev. B 46 10866 doi: 10.1103/PhysRevB.46.10866
    [40] Schuster C, Eckern U 2002 Ann. Phys. 514 901 doi: 10.1002/andp.20025141203
    [41] Huang X, Yang Z 2015 J. Magn. Magn. Mater. 381 372 doi: 10.1016/j.jmmm.2015.01.024
    [42] Viswanath V S, Müller G 1994 The Recursion Method—Application to Many-body Dynamics (Berlin: Springe-Verlag
    [43] Lee M H 1982 Phys. Rev. Lett. 49 1072 doi: 10.1103/PhysRevLett.49.1072
    [44] Lee M H 1982 Phys. Rev. B 26 2547 doi: 10.1103/PhysRevB.26.2547
    [45] Lee M H 2000 Phys. Rev. E 62 1769 doi: 10.1103/PhysRevE.62.1769
    [46] Yuan X J, Wang C Y, Kong X M, Zhao J F, Wang H, Bu H X 2023 J. Magn. Magn. Mater. 572 170632 doi: 10.1016/j.jmmm.2023.170632
    [47] Nunes M E S, Plascak J A 2024 Phys. Rev. E 109 014134 doi: 10.1103/PhysRevE.109.014134
    [48] Florencio J, de Alcantara Bonfim O F 2020 Front. Phys. 8 557277 doi: 10.3389/fphy.2020.557277
    [49] Florencio J, Lee M H 1987 Phys. Rev. B 35 1835 doi: 10.1103/PhysRevB.35.1835
  • 加载中
图( 6)
计量
  • 文章访问数:  128
  • HTML全文浏览数:  128
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-03
  • 刊出日期:  2025-02-05

链接杂质对一维量子Ising模型动力学性质的调控

    通讯作者: E-mail: yuanxiaojuan@163.com.
  • 齐鲁师范学院物理与电子工程学院, 济南　250200
  • 收稿日期:  2024-10-03

摘要: 自旋系统的动力学性质是量子统计和凝聚态理论研究的热点. 本文利用递推方法, 通过计算自旋关联函数及谱密度, 研究了链接杂质对一维量子Ising模型动力学性质的调控效应. 研究表明, 链接杂质的出现打破了主体格点自旋耦合$ J $和外磁场$ B $之间原有的竞争关系, 系统的动力学最终取决于链接杂质和主体格点自旋耦合的平均效应$ \bar J $、链接杂质的不对称程度及外磁场$ B $的强度等多因素之间的协同作用. 对于对称型链接杂质($ {J_{j - 1}} = {J_j} $), 随着杂质耦合强度的增大, 在$ B \geqslant J $的情况下, 系统的动力学出现了由集体模行为到中心峰值行为的交跨; 在$ B \lt J $的情况下, 出现了由类集体模行为到双峰行为, 再到中心峰值行为的两次交跨. 对于非对称型链接杂质($ {J_{j - 1}} \ne {J_j} $), 其杂质位型较多, 可以提供更多的调控自由度, 尤其当其中某个杂质耦合强度如$ {J_{j - 1}} $(或$ {J_j} $)较小时, 通过调节另一个杂质耦合强度$ {J_j} $(或$ {J_{j - 1}} $)可以得到多种动力学行为之间的交跨; 在$ B \gt J $情况下, 非对称型链接杂质的调控机制更为复杂, 出现了与以往研究经验不符的交跨顺序, 且出现了双频谱这种新的动力学模式. 一般来讲, 当平均自旋耦合$ \bar J $较弱或非对称型链接杂质的不对称程度较低时, 系统倾向于呈现集体模行为; 当$ \bar J $较强时, 系统倾向于呈现中心峰值行为; 但当非对称型链接杂质的不对称程度较明显时, 谱密度倾向于呈双峰、多峰或双频谱特征. 研究表明, 链接杂质的调控结果更加丰富, 且具有独特的调控优势, 因此利用链接杂质来调控量子自旋系统的动力学不失为一种新的尝试.

English Abstract

    全文HTML

    1.   引　言

    • 调控自旋系统的动力学性质一直是实验及理论研究的重点. 众多研究表明低维量子自旋系统在无序效应的调控下表现出丰富的物理性质, 因此考虑无序因素的随机量子自旋系统逐渐引起人们的关注, 例如随机Ising模型[1–5]、随机XY模型[6–9]、随机XXZ链[10]、Blume-Capel模型[11]等. 目前, 对随机自旋系统的平衡态性质已有大量研究, 且取得了丰硕的成果, 但对其动力学性质的研究仍然处于发展阶段. 这是因为在实际材料中无序因素非常复杂, 且其调控自旋动力学的物理机制尚不清楚.

      在随机自旋系统中, 自旋间的耦合相互作用或外加的磁场经常被处理为满足某种概率分布的随机变量, 如满足双模分布[2,5,12–13]、高斯分布[3,14]、双高斯分布[15,16]、幂律分布[17]等. 从数学角度来说, 概率分布可任意选取, 既定的随机分布也方便于理论计算. 但从物理角度来看, 纯数学的随机分布往往掩盖了某些物理特征, 如磁性或非磁性杂质[18–20]、键缺陷或空位的存在[21,22]等, 如何将这些实际因素引入到理论模拟中依然存在困难和挑战.

      研究者们提出可以将纯数学的随机分布进行扩展, 间接引入某些影响因素, 例如在改变版的双模分布中[23], 随机场的概率占比与磁场的强度有关. 在各向异性场依赖的双模分布中[24], 通过引入竞争参数使得双模分布的两个分支具有竞争性. 最近, 笔者利用三模分布的$ r $分支[25], 成功地将非磁性杂质效应引入理论模拟中. 此外, 研究者们还尝试将理论模型进行扩展, 使得扩展后的模型包含多尺度信息, 从物理本质上将实际因素引入进来. 例如在Ising模型或Heisenberg模型中引入四自旋相互作用[26,27]、Dzyaloshinskii-Moriya相互作用[9,28], 次近邻相互作用[4,29]等. 这两种常用的处理方式各有优势, 前者在理论计算时易于操作, 但随机场的实验实现存在困难; 后者更注重研究对象的物理本质, 但所模拟对象的范围存在局限.

      近几年来, 研究者们发现在石墨烯[30]、拓扑绝缘体[31]、Josephson-junction网络[32]、冷费米子气 体[33]、Ising超导体[34]及量子自旋链[35,36]等多种体系中, 利用杂质能够诱导系统的物理性质发生显著的变化, 且杂质的调控效应具有独特的优势. 本研究重点关注杂质对量子自旋系统动力学性质的调控. 在量子自旋系统中, 无序较复杂, 杂质类型比较多[37], 例如键杂质(bond impurity)、格点杂质(site impurity)、链接杂质(link impurity)、边界杂质(edge impurity)及近藤杂质(Kondo impurity)等, 在不同杂质类型下系统的动力学性质是否相同, 其调控机制有没有区别等问题均需要深入探讨. 前期笔者团队[38]在Ising模型中引入了键杂质, 发现键杂质对自旋动力学的影响比较明显, 同时积累了一定的研究经验. 本研究重点关注Ising模型中的链接杂质效应, 为了深入研究链接杂质对系统动力学性质的调控, 考虑了对称和非对称两种链接杂质位型, 得到了丰富的动力学结果.

    2.   模型及方法

    • 将Ising模型进行扩展, 引入链接杂质[37,39], 哈密顿量表示为

      其中$J$代表最近邻格点(主体格点)之间的自旋耦合相互作用, $ B $为横向磁场, 1/2是为了理论计算方便而引入的常数. $\sigma _i^\alpha \left( {\alpha = x, y, z} \right)$为格点$i$处的自旋泡利算符, 计算满足周期边界条件$\sigma _i^\alpha = \sigma _{i + N}^\alpha $. $ {J_j} $($ {J_{j - 1}} $)为格点$j$和$j + 1$($j - 1$)之间的自旋耦合相互作用, 称为链接杂质. 引起链接杂质最常见的情况是, 将自旋链中格点$j$处的主体离子用杂质离子来代替, 从而引起格点$j$左右两边的键长即$ {J_j} $和$ {J_{j - 1}} $发生变化[37]. 例如, 将Ni2+离子插入Cu2+链[39]; 将V用Nb代替[40], 形成Nb4+和V4+, 或Nb5+和V3+; 用Ca代替SrCuO3中的Sr等情况[41].

      求解含时自旋关联函数[42]是研究自旋动力学性质的关键, 其定义式为

      式中$\overline {\left\langle \cdot \right\rangle } $表示求统计平均后再对无序求平均. 对自旋关联函数进行Fourier变换得到谱密度的表达式:

      由于$ \varPhi \left( \omega \right) $可以通过中子散射实验、中子自旋回声实验等[33]进行测量, 因此谱密度的研究也非常关键.

      研究多体系统动力学性质的常用方法有级数展开法、严格求解法、格林函数法及递推方法(recursion method)等. 众多研究表明由Lee等[43–47]提出的递推方法是求解$C\left( t \right)$的最有效的方法之一, 目前该方法在研究谐振子链、多粒子系统、电子气、简单流体等[48]系统的动力学性质中被广泛采用.

      在量子自旋系统中, 力学量$\sigma _j^x\left( t \right)$的演化满足

      其中$L$为Liouville算符, 满足$LA = \left[ {H, A} \right] \equiv HA - AH$. 递推方法的核心是将力学量$\sigma _j^x\left( t \right)$按照一组完备的正交基矢$\left\{ {{f_\nu }} \right\}$展开:

      其中$\left\{ {{a_\nu }\left( t \right)} \right\}$表示$t$时刻$\sigma _j^x\left( t \right)$在基矢$\left\{ {{f_\nu }} \right\}$上的投影.

      将${f_0} = \sigma _j^x\left( 0 \right)$作为零阶基矢, 则$\left\{ {{f_\nu }} \right\}$满足如下递推关系:

      其中,

      称为递推因子或连分式系数, 其中$ {f_{ - 1}} \equiv 0 $, $ {\varDelta _0} \equiv 1 $. $ \left( {{f_\nu }, {f_\nu }} \right) $满足Kubo内积的形式:

      其中$ X\left( \lambda \right) = {{\text{e}}^{\lambda H}}X{{\text{e}}^{{{ - }}\lambda H}} $, $ \left\langle {XY} \right\rangle = \dfrac{{\text{Tr}}\left( {{{\text{e}}^{{{ - }}\beta H}}XY} \right)}{ {\text{Tr}}{{\text{e}}^{{{ - }}\beta H}}} $, $ \beta = {\left( {{k_{\text{B}}}T} \right)^{ - 1}} $, $T$为温度, ${k_{\text{B}}}$为Boltzmann常数. 在高温极限下$T \to \infty $, 内积可以简化为

      另外, 系数$\left\{ {{a_\nu }\left( t \right)} \right\}$满足如下递推关系:

      其中$ a_{-1}\left(t\right)\equiv0 $, 且可以证明${a_0}\left( t \right)$即为自旋关联函数$C\left( t \right)$. 将(10)式进行Laplace变换, 得到如下连分式:

      其中$z = \varepsilon + {\text{i}}\omega {\text{ }}(\varepsilon \gt 0)$. 由于连分式是无穷阶的, 故必须选用一种恰当的截断方法将其截断, 本研究适合采用高斯截断[2,3,42], 截断后得到${a_0}\left( z \right)$的近似解. 为了计算方便, 通常采用自旋关联函数的Laplace变换的极限形式求解谱密度, 即:

      从本质上说, Laplace变换与(3)式Fourier变换是等效的.

      本工作利用(6)式精确求解了前9个基矢$ {f_1}, {f_2}, \cdots , {f_9} $, 发现基矢${f_\nu }$随着$ \nu $的增大越来越复杂. 这里仅给出前4个基矢及前3个内积, 如下:

      利用(7)式计算了前9个连分式系数$ {\varDelta _1}, {\varDelta _2}, \cdots , {\varDelta _9} $, 进而得到自旋关联函数和谱密度. 对于Ising系统, 早期研究表明, 利用前9个连分式系数, 结合高斯截断方法, 即可给出较好的动力学结果[2].

    3.   对称型链接杂质的调控效应

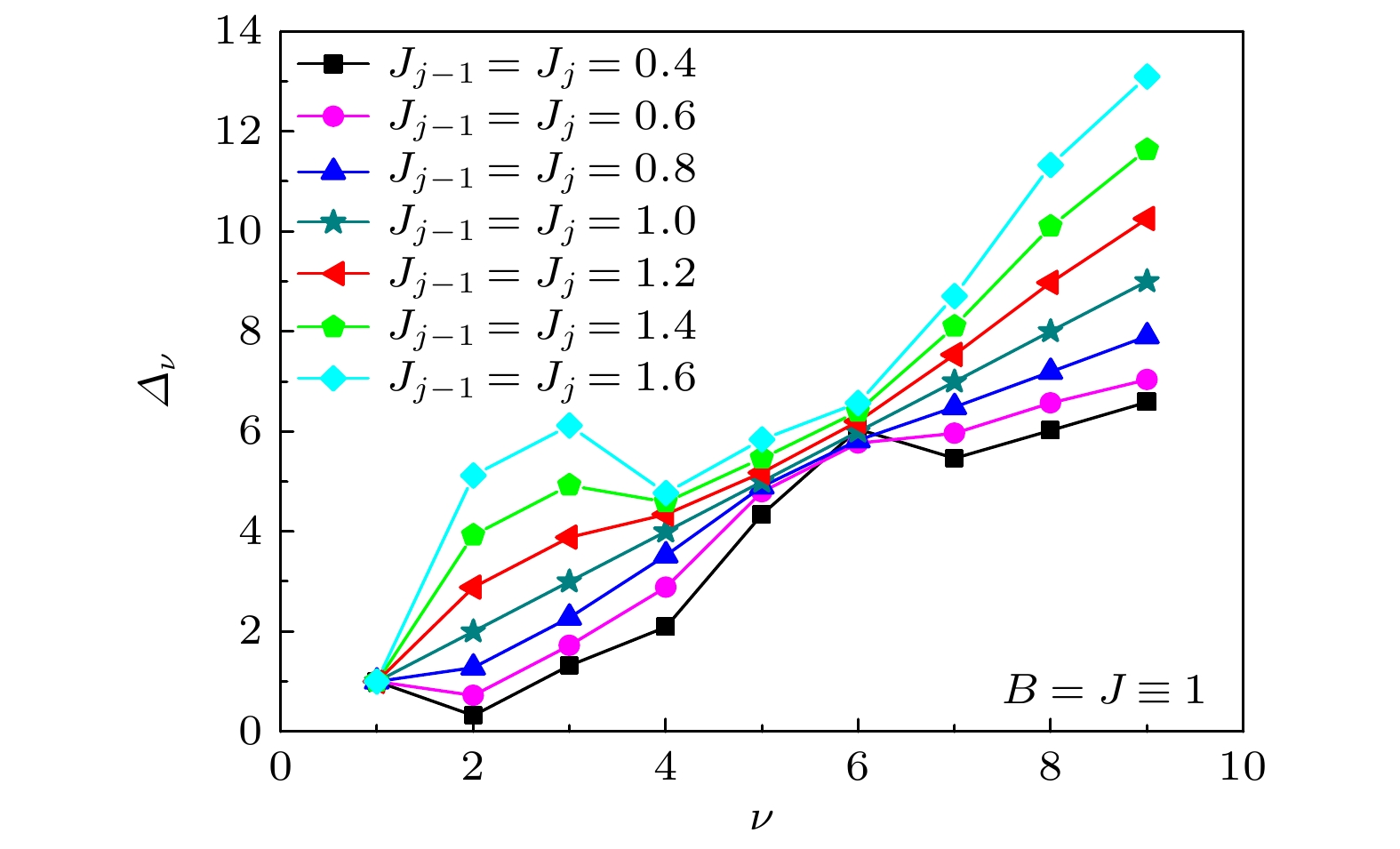
    • 由于链接杂质引起杂质两边的键长发生变化, 那么根据杂质两边的键长变化是否相等, 将杂质位型分为对称型和非对称型两种情况, 即$ {J_{j - 1}} = {J_j} $和$ {J_{j - 1}} \ne {J_j} $. 首先研究对称型链接杂质对系统动力学性质的影响, 为了不失一般性, 取主体格点自旋耦合相互作用$ J \equiv 1 $, 杂质强度可以取$ {J_{j - 1}} = {J_j} < J $和$ {J_{j - 1}} = {J_j} \gt J $, 分别称为弱杂质耦合和强杂质耦合. 特殊地, 当$ {J_{j - 1}} = {J_j} = J $时, 链接杂质模型蜕化为无杂质的一维横场Ising模型[2,49]. 首先考虑外加的横向磁场$ B = J \equiv 1 $, 此时主体格点自旋耦合相互作用与横场相等, 两者之间的竞争较小, 因而动力学行为之间的交跨将主要由链接杂质来调控. 图1给出了多组杂质耦合强度下的连分式系数, 当$ {J_{j - 1}} = {J_j} = J = 1.0 $时, 结果显示连分式系数呈线性变化, 斜率为1, 与严格解$ {\varDelta _{\nu}} = \nu \varDelta $[2,49]完全吻合, 证明本文计算可行. 但当杂质耦合强度较小如$ {J_{j - 1}} = {J_j} = 0.4 $, 或较大时如$ {J_{j - 1}} = {J_j} = 1.6$, 其线性关系将被破坏, 这意味着将会引发不同的动力学行为.

      图2所示为不同杂质耦合强度下的自旋关联函数和谱密度. 在杂质耦合强度较弱时, 如$ {J_{j - 1}} = {J_j} = 0.4 $或0.6, 关联函数$C\left( t \right)$以阻尼振荡形式衰减, 对应的谱密度$\varPhi \left( \omega \right)$其峰值出现在$ \omega \approx B \approx 1 $处, 表现为典型的集体模行为. 此时自旋随时间的演化是一种集体行为, 某自旋的演化要受到其他自旋的影响. 但随着杂质耦合强度的增大, 如$ {J_{j - 1}} = {J_j} = 1.2 $, 关联函数呈单调递减, 对应的谱密度峰值出现在$ \omega = 0 $处, 表现为典型的中心峰值行为. 特殊地, 当$ {J_{j - 1}} = {J_j} = 1.0 $时, 谱密度呈高斯衰减[2,3,49], 与已有结果吻合. 显然, 随着链接杂质耦合强度的增大, 系统的动力学出现了由集体模行为到中心峰值行为的交跨效应. 引起交跨效应的物理机制可以归结为链接杂质和横场之间的竞争关系: 在弱杂质耦合下, 横场在两者的竞争中占优势, 自旋对横场的响应较强, 表现为高频响应, 谱密度峰值出现在$ \omega \approx B \approx 1 $处; 在强杂质耦合下, 链接杂质在与横场竞争中占优势, 因此自旋对外场的响应较弱, 表现为低频响应, 谱密度峰值出现在$ \omega = 0 $处. 显然, 可以利用链接杂质来调控系统的动力学行为.

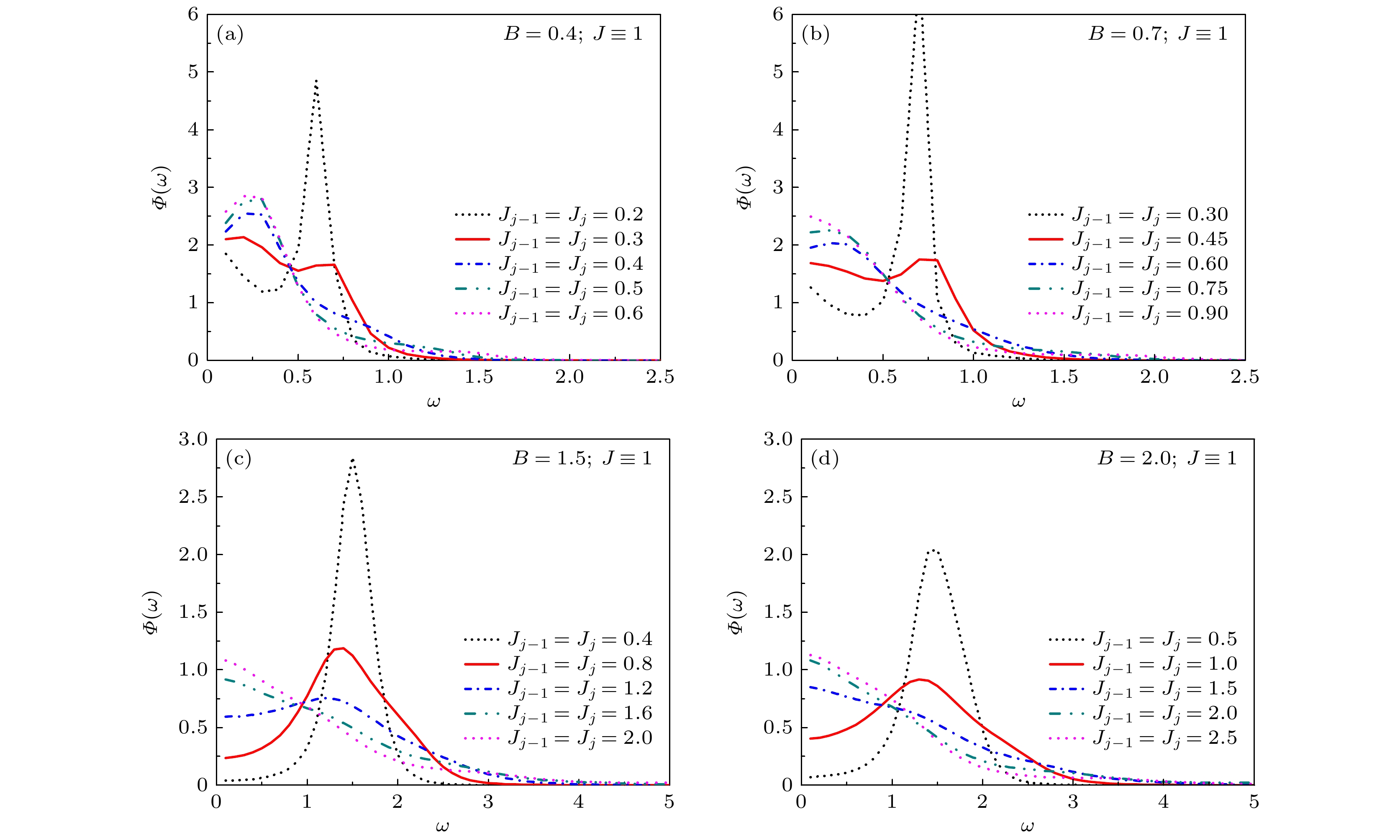
      图2是在$ B = J $的情况下给出的结果, 若$ B \ne J $, 如$ B \lt J $或$ B \gt J $, 则链接杂质效应有何不同? 为了不失一般性, 依然取$ J \equiv 1 $, 图3(a)—(d)分别给出了弱磁场$ B = 0.4 $, 0.7和强磁场$ B = 1.5 $, 2.0时的动力学结果. 由于关联函数和谱密度呈现的动力学结果一致, 这里仅给出谱密度结果. 已有研究表明, 当$ B \ne J $时, 外加的横向磁场与自旋耦合相互作用之间的竞争关系较明显[2,3]. 此时, 引入链接杂质, 由于磁场与链接杂质之间也存在竞争关系, 因此可预测引入链接杂质后系统的动力学行为将更加复杂.

      当$ B \lt J $时, 如$ B = 0.7 $, 根据以往的研究经验, 对于无杂质的纯Ising系统, 其动力学行为将表现为中心峰值行为. 图3(b)显示, 当链接杂质$ {J_{j - 1}} = {J_j} = 0.9 $或0.75时, 由于杂质耦合强度接近于主体格点自旋耦合强度$ J \equiv 1 $, 此时系统依然表现为中心峰值行为, 杂质效应不明显. 但当杂质耦合强度较小时, 如$ {J_{j - 1}} = {J_j} = 0.3 $, 谱密度在$ \omega \approx B \approx 0.7 $处出现了一个较高的峰, 系统主要表现为集体模行为. 显然, 在$ B \lt J $的情况下, 利用链接杂质的调控效应依然实现了不同动力学行为之间的交跨. 但与$ B = J $的情况不同的是, 除了中心峰值行为和集体模行为之外, 还出现了新的动力学模式. 例如在图3(b)中红色实线所示, 其参数对应$ {J_{j - 1}} = {J_j} = 0.45 $, 谱密度在$ \omega = 0 $和$ \omega \ne 0 $处均出现了峰值, 称为双峰行为.

      显然双峰行为的出现符合前期预测, 其物理机制可以归结为复杂的竞争关系. 对于纯Ising系统, 当$ B \lt J $时, 自旋耦合相互作用在与外场的竞争中占有优势[2,3], 但链接杂质的出现会打破两者的竞争, 最终杂质Ising系统的动力学行为取决于杂质耦合$ {J_{j - 1}} = {J_j} $和主体格点自旋耦合$ J $之间的平均效应, 这里用$ \bar J $表示平均自旋耦合强度. 当杂质耦合强度较强时, 使得$ \bar J $较强, 在与外场竞争中占有优势, 系统表现为中心峰值行为, 低频响应较明显; 但当杂质耦合强度较弱时, 使得$ \bar J $较弱, 此时外场占优势, 系统表现为集体模行为, 高频响应较明显; 但具有中等强度的杂质耦合会使得系统的竞争关系较复杂, 导致低频响应和高频响应同时出现, 表现为双峰行为. 可见, 系统的动力学取决于链接杂质、主体格点自旋耦合及外加磁场三者之间的协同作用. 将此双峰行为与以往研究中出现的双峰行为[25,38]进行比较, 发现其物理机制虽然不同, 但都可以归结为多种因素协同调控的结果. 因此, 要想得到新的动力学模式, 多因素之间的协同作用非常关键. 图3(a)为弱场$ B = 0.4 $时的谱密度, 通过调节链接杂质耦合强度, 也得到了类似的动力学结果.

      下面分析$ B \gt J $时的动力学结果, 图3(c), (d)分别给出$ B = 1.5 $和2.0时的谱密度, 为了不失一般性, 依然取主体格点自旋耦合强度$ J \equiv 1 $. 根据以往的研究经验, 当$ B \gt J $时, 纯Ising系统的动力学行为将表现为集体模行为. 但引入链接杂质后, 利用链接杂质的调控效应依然实现了不同动力学行为之间的交跨. 如图3(c)所示, 当杂质耦合强度较弱时, 如$ {J_{j - 1}} = {J_j} = 0.4 $或0.8, 系统表现为集体模行为, 但当杂质耦合强度较强时, 如$ {J_{j - 1}} = {J_j} = 1.6 $或2.0, 系统表现为中心峰值行为. 图3(d)也给出了类似的动力学结果.

      将图2和图3的结果进行比较发现, 新的动力学模式如双峰行为只出现在$ B \lt J $的情况下, 且$ B \lt J $时所呈现的集体模行为也比较特殊, 需要进一步分析. 如图3(a), (b)中的黑色虚线所示, 其参数分别对应$ B = 0.4 $, $ {J_{j - 1}} = {J_j} = 0.2 $和$ B = 0.7 $, $ {J_{j - 1}} = {J_j} = 0.3 $, 此时谱密度在$ \omega \ne 0 $处有一个峰值较大的峰, 称为主峰, 但同时在$ \omega = 0 $处存在一个峰值较小的峰, 称为次峰. 或者说, 系统的动力学以高频响应为主, 但同时也出现了低频响应. 这种特殊的动力学行为可以看作是由集体模行为到双峰行为过渡的一种中间状态, 称为类集体模行为, 这在以往研究中没有出现, 显然是由链接杂质的调控所引起. 从图3(b)可以看出, 随着链接杂质耦合强度的增大, 高频响应逐渐减弱, 低频响应逐渐增强, 系统的动力学经历了由类集体模行为到双峰行为, 再到中心峰值行为的两次交跨. 图3(a)也得到了类似的动力学结果.

      由此看出, 在外场较弱的情况下($ B \lt J $), 对称型链接杂质的调控机制更加复杂. 这是因为在弱场下, 链接杂质和主体格点自旋耦合之间的协同作用更加明显. 当链接杂质耦合强度较弱时(如$ {J_{j - 1}} = {J_j} = 0.2 $或0.3), 由于外场的作用系统依然倾向于呈现集体模行为, 但主体格点自旋耦合($ J \equiv 1 $)又使系统倾向于呈现中心峰值行为, 此时两者具有竞争关系. 但在磁场较强的情况下($ B \gt J $), 链接杂质和主体格点自旋耦合又是相互配合、共同协作的关系, 系统的动力学由两者的平均效应$ \bar J $和外场共同主导. 总的来说, 与纯Ising系统相比, 链接杂质Ising系统的动力学行为更加丰富, 且在链接杂质的调控下出现了新的动力学模式, 如双峰行为和类集体模行为. 与已有研究结果进行比较, 发现链接杂质的调控机理相对简单, 预测在实验中也较容易实现, 具有独特的优势. 因此利用链接杂质来调控量子自旋系统的动力学, 不失为一种新的尝试.

    4.   非对称型链接杂质的调控效应

    • 接下来重点研究非对称型链接杂质对系统动力学性质的影响, 为了不失一般性, 依然取主体格点自旋耦合相互作用$ J \equiv 1 $. 与对称型链接杂质类似, 首先考虑横场$ B = J \equiv 1 $, 此时横场$ B $与主体格点自旋耦合$ J $之间的竞争较小, 动力学行为的交跨将主要由非对称型链接杂质来主导. 对于非对称型链接杂质$ {J_{j - 1}} \ne {J_j} $, 其杂质位型有两个, 例如参数取值为$ {J_{j - 1}} = J' $, $ {J_j} = J'' $或$ {J_{j - 1}} = J'' $, $ {J_j} = J' $, 且$ J' \ne J'' $. 由于计算采用的是周期性边界条件, 初步预测两种位型下的动力学结果没有区别, 经计算证实我们的预测是正确的. 因此下面仅给出其中一种位型下的动力学结果, 例如可先固定$ {J_{j - 1}} = J' $, 然后取$ {J_j} = J'' $. 若$ J' \ne J'' \ne J $为非对称型链接杂质; 若$ J' = J'' \ne J $则蜕化为对称型链接杂质; 若$ J' \ne J'' $, 但$ J' = J $或$ J'' = J $, 则链接杂质蜕化为键杂质[38]; 若$ J' = J'' = J $, 则系统又蜕化为无杂质的纯Ising系统[2,3].

      固定$ {J_{j - 1}} = J' $, $ J' $的取值可以小于$ J $, 也可以大于$ J $, 如图4(a)—(d)分别对应$ {J_{j - 1}} = 0.2 $, 0.5, 1.0和1.4. 由于关联函数和谱密度呈现的动力学结果一致, 这里仅给出谱密度. 在图4(a)中, 固定$ {J_{j - 1}} = 0.2 $, $ {J_j} $的取值从小于$ J $变化到大于$ J $, 如取$ {J_j} = 0.2 $, 0.6, 1.0, 1.4和1.8. 当$ {J_j} = 0.2 $时, 此时$ {J_{j - 1}} = {J_j} $, 非对称型链接杂质蜕化为对称型链接杂质, 又由于$ {J_{j - 1}} = {J_j} = 0.2 \lt J $, 此时动力学表现为典型的集体模行为, 与图2所得结论一致. 继续增大$ {J_j} $的取值, 发现在$ {J_j} \lt J $的范围内, 如$ {J_j} = 0.6 $, 谱密度依然呈现为集体模行为. 其物理机制也非常容易理解, 当$ {J_{j - 1}} $和$ {J_j} $均小于$ J $时, 杂质耦合和主体格点自旋耦合的平均效应$ \bar J $小于外场($ B = J \equiv 1 $), 此时系统的动力学由外场主导, 表现为高频响应.

      在图4(a)中, 继续增大$ {J_j} $的取值, 如取$ {J_j} = 1.0 $, 则有$ {J_j} = J \equiv 1.0 $, 非对称型链接杂质蜕化为键杂质[38], 此时系统表现为多峰行为, 如图4(a)中蓝色虚线所示, 与已有结果吻合. 继续增大$ {J_j} $的取值, 则$ {J_j} $和$ {J_{j - 1}} $的差别越来越大, 不对称性越来越明显, 同时$ \bar J $也逐渐增强. 有趣的是, 在$ \bar J $较强的情况下, 系统没有表现为中心峰值行为, 而是表现为双峰行为, 这与以往的研究经验不符. 将此双峰行为与对称型链接杂质下的双峰行为进行比较, 发现两者的差别比较明显. 此双峰行为的主峰出现在$ \omega = 0 $处, 次峰出现在$ \omega \ne 0 $处, 且随着不对称性的增强, 主峰和次峰逐渐分离, 双峰特征更加明显, 见图4(a)中$ {J_j} = 1.4 $和$ {J_j} = 1.8 $所对应的曲线. 继续增大$ {J_j} $的取值, 也得到了类似的结果, 显然此双峰行为是由于链接杂质的不对称性增强所引起. 图4(b)对应参数$ {J_{j - 1}} = 0.5 $, $ {J_j} = 0.2 $, 0.6, 1.0, 1.4和1.8, 此时链接杂质的不对称程度有所降低, 但也得到了类似的结论.

      在图4(c)中, 固定$ {J_{j - 1}} = 1.0 $, 此时$ {J_{j - 1}} = J \equiv 1, $ 非对称型链接杂质蜕化为键杂质[38]. 通过改变$ {J_j} $的取值, 系统的动力学出现了由多峰行为(如$ {J_j} = 0.2 $)到中心峰值行为(如$ {J_j} = 1.4 $, 1.8)的交跨, 与已有结果吻合. 将图4(c)中的黑色实线(对应位型$ {J_{j - 1}} = 1.0 $, $ {J_j} = 0.2 $)与图4(a)中的蓝色虚线(对应位型$ {J_{j - 1}} = 0.2 $, $ {J_j} = 1.0 $)进行比较, 发现两条曲线完全重合, 均为多峰行为. 类似地, 图4(a)中位型$ {J_{j - 1}} = 0.2 $, $ {J_j} = 1.4 $对应的曲线和图4(d)中位型$ {J_{j - 1}} = 1.4 $, $ {J_j} = 0.2 $对应的曲线也完全重合, 均为双峰行为. 这也证实了前期预测: 当计算采用周期性边界条件时, 两种位型下的动力学结果没有区别. 更为特殊的是, 图4(c)中蓝色虚线对应位型$ {J_{j - 1}} = 1.0 $和$ {J_j} = 1.0 $, 此时$ {J_{j - 1}} = {J_j} = J \equiv 1 $, 且$ B = J \equiv 1 $, 非对称型链接杂质系统蜕化为纯Ising系统[2,3], 谱密度呈高斯衰减, 与已有结果吻合.

      继续增大$ {J_{j - 1}} $的取值, 在图4(d)中固定$ {J_{j - 1}} = 1.4 $, 依然取参数$ {J_j} = 0.2 $, 0.6, 1.0, 1.4和1.8. 发现仅在$ {J_j} = 0.2 $时出现了双峰行为, 其他情况下均为中心峰值行为, 这进一步证实了双峰行为的出现归因于链接杂质的不对称性较明显. 而中心峰值行为的出现归因于较强的平均自旋耦合$ \bar J $, 当$ {J_{j - 1}} $较大时, 平均自旋耦合$ \bar J $较强, 在与外场竞争中占优势, 系统表现为低频响应. 可见对于非对称型链接杂质, 在$ B = J $的情况下, 系统的动力学主要取决于平均自旋耦合$ \bar J $及链接杂质的非对称程度. 一般来说, 当平均自旋耦合$ \bar J $较弱时, 系统倾向于呈现集体模行为; 当$ \bar J $较强时, 倾向于呈中心峰值行为; 但当链接杂质的不对称性程度较明显时, 倾向于呈双峰行为. 可见, 利用$ {J_j} $和$ {J_{j - 1}} $的配合, 可以提供更多的调控自由度, 得到多种动力学行为之间的交跨.

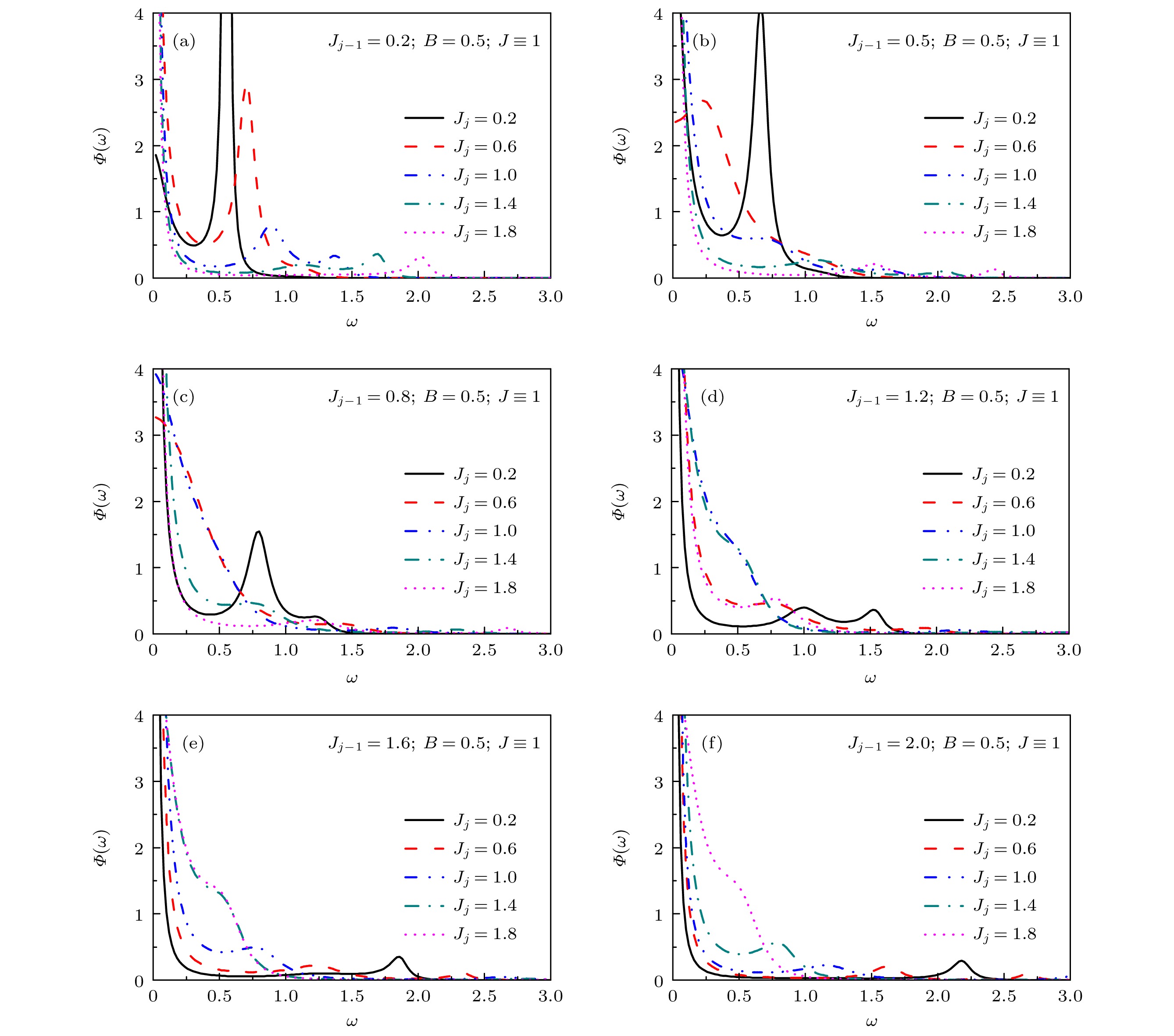
      图4是在$ B = J $的情况下给出的结果, 若$ B \ne J $, 如$ B \lt J $或$ B \gt J $, 此时非对称型链接杂质效应又有何变化? 根据对称型链接杂质下的结果, 预测非对称型链接杂质下的动力学结果在$ B \ne J $时将更加复杂. 首先讨论$ B \lt J $的情况, 图5给出$ B = 0.5 $, $ J \equiv 1 $时不同杂质位型下的谱密度, 图5(a)—(f)分别对应$ {J_{j - 1}} = 0.2 $, 0.5, 0.8, 1.2, 1.6和2.0. 当$ {J_{j - 1}} $的取值较小时, 例如$ {J_{j - 1}} = 0.2 $, 此时通过调节$ {J_j} $的取值, 如取$ {J_j} = 0.2 $, 0.6, 1.0, 1.4和1.8, 得到了多种动力学行为的交跨. 如图5(a)所示, 当$ {J_j} = 0.2 $时, 系统表现为类集体模行为, 主峰出现在$ \omega \approx B = 0.5 $处, 次峰出现在$ \omega = 0 $处, 动力学以高频响应为主. 随着$ {J_j} $取值的增大, 如$ {J_j} = 0.6 $, 高频响应逐渐减弱, 低频响应逐渐增强. 继续增大$ {J_j} $的取值, 如$ {J_j} = 1.4 $或1.8, 谱密度主峰出现在$ \omega = 0 $处, 次峰出现在$ \omega \ne 0 $处, 此时动力学以低频响应为主, 同时伴随着出现了高频响应. 显然这是由于$ {J_j} $取值的增大, 使得平均自旋耦合$ \bar J $逐渐增大, 在与外场竞争时逐渐占有优势. 有趣的是, 当$ {J_j} $取值较大时, 链接杂质的不对称性也逐渐明显, 此时动力学虽然以低频响应为主, 但不对称性导致了微弱的高频响应, 与图4所得结论一致.

      继续增大$ {J_{j - 1}} $取值, 如取$ {J_{j - 1}} = 0.5 $或0.8, 此时通过调节$ {J_j} $的取值, 虽然可以观察到高频响应, 但高频响应的强度明显减弱. 例如, 将图5(a)—(c)中的黑色实线(对应$ {J_j} = 0.2 $)或红色虚线(对应$ {J_j} = 0.6 $)进行比较, 发现随着$ {J_{j - 1}} $取值的增大, 高频响应逐渐减弱甚至消失, 低频响应逐渐增强. 显然这是由于较大的$ {J_{j - 1}} $同样使得平均自旋耦合$ \bar J $较大, 低频响应逐渐占优势. 当$ {J_{j - 1}} $的取值大于$ J \equiv 1 $时, 图5(d)—(f)分别对应$ {J_{j - 1}} = 1.2 $, 1.6和2.0, 结果显示仅在不对称性较明显时出现了微弱的高频响应(如图5(d)—(f)中$ {J_j} = 0.2 $所对应的黑色实线所示, 或图5(f) 中$ {J_j} = 0.6 $所对应的红色虚线所示), 其他情况几乎为低频响应. 可见, 在$ B \lt J $的情况下, $ {J_j} $和$ {J_{j - 1}} $的协同作用更加明显. 当其中某个链接杂质耦合强度如$ {J_{j - 1}} $较小时, 通过调节$ {J_j} $可以得到多种动力学行为之间的交跨; 但当$ {J_{j - 1}} $较大时, 系统的动力学将由$ {J_{j - 1}} $主导, 此时$ {J_j} $的调控不再明显. 但若两个杂质耦合强度差别较大, 即不对称性较明显时, 此时系统的动力学将由不对称性主导, 谱密度呈双峰甚至多峰特征, 与$ B = J $情况下的结论一致.

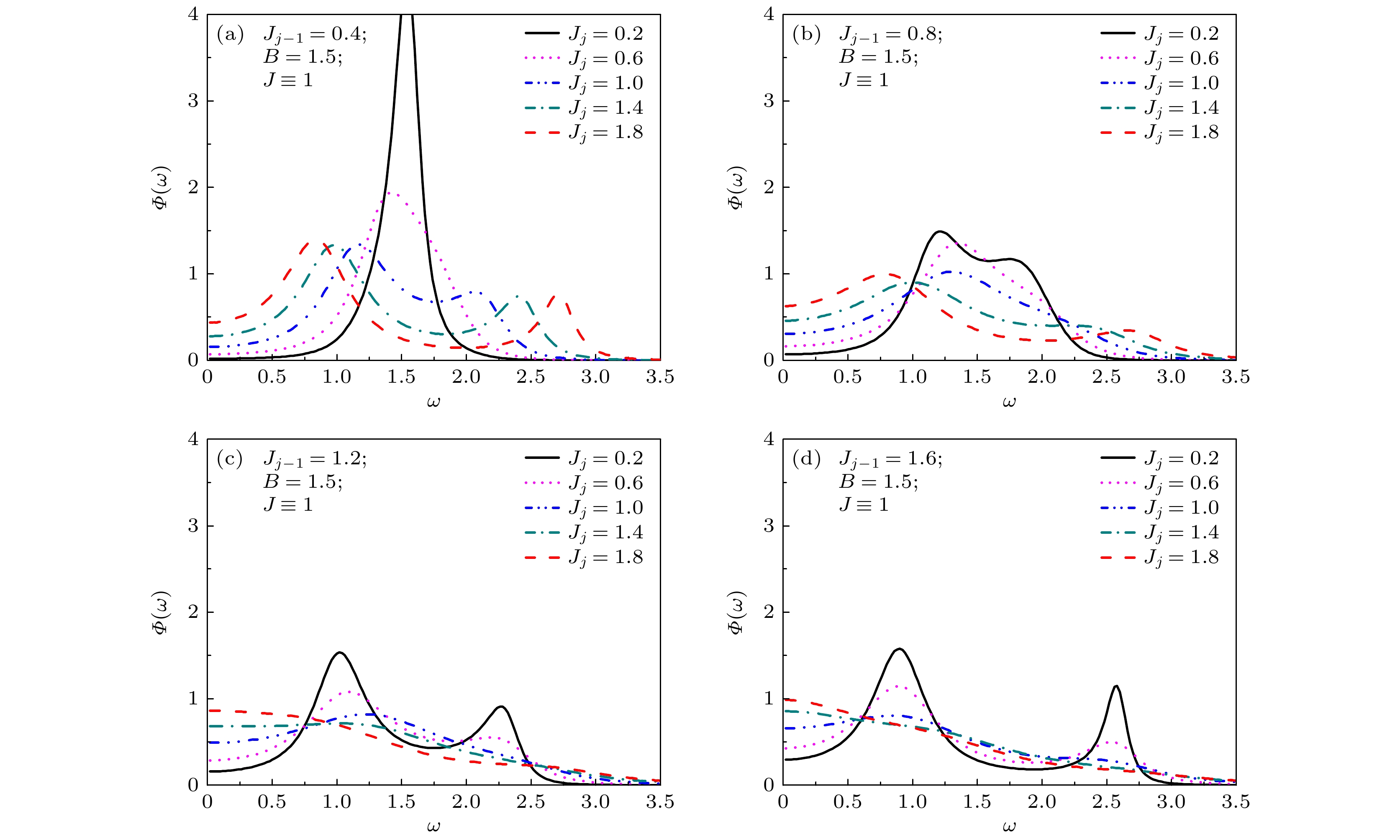
      下面分析$ B \gt J $时的非对称型链接杂质效应. 图6给出了$ B = 1.5 $, $ J \equiv 1 $时不同杂质位型下的谱密度. 图6(a)—(d)分别对应$ {J_{j - 1}} = 0.4 $, 0.8, 1.2和1.6. 当$ {J_{j - 1}} $的取值较小时, 例如$ {J_{j - 1}} = 0.4 $, 此时通过调节$ {J_j} $的取值, 如取$ {J_j} = 0.2 $, 0.6, 1.0, 1.4和1.8, 系统的动力学出现了由集体模行为到双峰行为的交跨. 如图6(a)所示, 当$ {J_j} = 0.2 $或0.6时系统表现为集体模行为, 此时平均自旋耦合$ \bar J $较弱, 系统的动力学由外场主导, 谱密度峰值出现在$ \omega \approx B \approx 1.5 $处, 表现为高频响应. 随着$ {J_j} $取值的增大, 如$ {J_j} = 1.0 $, 1.4和1.8, 平均自旋耦合$ \bar J $逐渐增强, 同时链接杂质的不对称性程度也逐渐明显, 谱密度由单峰逐渐扩展为双峰, 且两峰之间的距离也逐渐增大, 双峰特征更加明显. 有趣的是, 不同于前面出现的双峰行为(见图3和图4), 此双峰的两个峰值均出现在$ \omega \ne 0 $处. 如$ {J_j} = 1.8 $时, 两峰的位置分别位于低频$ {\omega _1} \approx 0.8 $和高频$ {\omega _2} \approx 2.7 $处, 将其称为双频谱. 这种特殊的双频谱在以往研究中均未出现, 显然这是非对称型链接杂质在强磁场下调控的结果.

      图6(b)对应$ {J_{j - 1}} = 0.8 $, 通过调节$ {J_j} $的取值, 也得到了不同动力学行为之间的交跨. 但与图6(a)不同的是, 随着$ {J_j} $取值的增大, 系统出现了由双峰行为(对应$ {J_j} = 0.2 $)到集体模行为(对应$ {J_j} = 0.6 $和1.0), 再到双峰行为(对应$ {J_j} = 1.4 $和1.8)的两次交跨, 此交跨顺序也与以往的研究经验不符. 分析认为双峰行为的出现主要取决于链接杂质的非对称性程度, 与平均自旋耦合$ \bar J $的关系不明显. 例如$ {J_j} = 0.6 $或1.0时, 其取值与$ {J_{j - 1}} = 0.8 $的取值均比较接近, 此时链接杂质的不对称程度较低, 系统表现为集体模行为; 但当不对称程度较明显时如$ {J_j} = 0.2 $或1.8时, 均为双峰行为. 分析图6(c)中的结果, 也得到了类似的结论. 图6(c)对应$ {J_{j - 1}} = 1.2 $, 结果显示随着$ {J_j} $取值的增大, 系统的动力学出现了由双峰行为(对应$ {J_j} = 0.2 $和0.6)到集体模行为(对应$ {J_j} = 1.0 $), 再到中心峰值行为(对应$ {J_j} = 1.4 $和1.8)的两次交跨. 此时双峰行为的出现依然归因于链接杂质的不对称性较明显; 集体模行为对应的位型为$ {J_j} = 1.0 $, $ {J_{j - 1}} = 1.2 $, 链接杂质的不对称程度较低; 而中心峰值行为的出现, 依然归因于较强的平均自旋耦合$ \bar J $. 图6(d)对应$ {J_{j - 1}} = 1.6 $, 也得到了类似的结果. 此外, 我们还计算了外场$ B = 2.0 $, $ J \equiv 1 $时不同杂质位型下的谱密度, 得到类似的结论.

      以上结果表明, 强磁场($ B \gt J $)下非对称型链接杂质的调控机制较为复杂, 明显不同于$ B \leqslant J $时的情况. 当平均自旋耦合$ \bar J $较弱或链接杂质的不对称程度较低时, 系统的动力学倾向于呈现集体模行为; 当平均自旋耦合$ \bar J $较强时, 倾向于呈中心峰值行为; 但当链接杂质的不对称程度较明显时, 倾向于呈双频谱特征. 总的来说, 对于非对称型链接杂质, 其杂质位型比较多, 可以提供更多的调控自由度, 调控结果也更加丰富, 且更容易激发新的动力学模式, 比如双频谱. 最终系统的动力学由平均自旋耦合$ \bar J $、链接杂质的不对称程度及外磁场$ B $的强度共同决定.

    5.   结　论

    • 本文利用递推关系方法研究了链接杂质对一维量子Ising模型动力学性质的调控, 考虑了对称型($ {J_{j - 1}} = {J_j} $)和非对称型($ {J_{j - 1}} \ne {J_j} $)两类链接杂质, 得到了丰富的动力学结果. 由于链接杂质的出现, 主体格点自旋耦合$ J $和外磁场$ B $之间原有的竞争关系被打破, 系统的动力学最终取决于链接杂质和主体格点自旋耦合的平均效应$ \bar J $、链接杂质的不对称程度及外磁场$ B $的强度等多因素之间的协同作用. 研究表明, 在链接杂质的调控下能够轻松实现不同动力学行为之间的交跨, 且更容易激发出新的动力学模式.

      对于对称型链接杂质, 不同动力学行为之间的交跨主要由链接杂质耦合强度来调控, 其调控机制为: 较弱的杂质耦合, 使得$ \bar J $较弱, 此时系统的动力学由外场主导, 倾向于呈集体模行为或类集体模行为; 而较强的杂质耦合, 使得$ \bar J $较强, 此时系统的动力学由自旋耦合主导, 倾向于呈中心峰值行为; 此调控机制同样适用于非对称型链接杂质. 有趣的是, 在非对称型链接杂质下, 除了杂质耦合强度的调控, 还存在链接杂质的非对称性这一调控机制. 当链接杂质的不对称程度较明显时, 系统的动力学将由不对称性主导, 能够出现与以往研究经验不符的交跨顺序, 且更容易激发出新的动力学模式, 如双峰、多峰或双频谱特征. 与已有研究结果进行比较, 发现链接杂质的调控结果更加丰富, 且具有独特的优势. 因此利用链接杂质来调控量子自旋系统的动力学, 不失为一种新的尝试.

    参考文献 (49)

目录

/

返回文章
返回