单羟基醇是一种重要的醇类液体, 其结构特点是分子中仅含有一个与羟基(—OH)直接相连的碳原子. 单羟基醇是常见的小分子玻璃形成液体, 而且其具有氢键作用, 与水具有相似性, 因此单羟基醇的研究与Science杂志创刊125周年时提出的125个重要的科学问题中“玻璃态物质的本质是什么”和“水的结构如何”^[1]这两个问题都有着密切关系, 而且单羟基醇自身还具有着一些特殊性质, 已成为重要的学术研究对象^[2–6].

在单羟基醇的研究中, 研究者们发现它们除了有最常见的结构弛豫(α弛豫)和次级弛豫(β弛豫)外, 在低频处还存在着一个比α弛豫更加缓慢的弛豫过程, 它具有德拜(Debye)方程所描述的理想指数特征, 因此被称为德拜弛豫^[7–11], 单羟基醇中的德拜介电弛豫过程一般认为来源于单羟基醇中因氢键作用而形成的氢键分子链^[12–14]. 在对该德拜弛豫的研究中还发现其介电弛豫强度在250 K附近存在着一个转折行为, 称为德拜介电弛豫强度的250 K异常^[11,15,16]. 除了介电弛豫强度之外, 近红外吸收率和核磁共振的化学位移在250 K附近也存在着异常变化^[11,15,16], 在微观上认为该异常变化是由单羟基醇中的氢键分子链因温度升高而变短所导致的^[11,16]. 基于Gainaru等^[13]提出的瞬态氢键分子链, Wang等^[17,18]建立了自由旋转赝自旋Ising链模型来描述德拜介电弛豫行为, 在一定的范围内与实验结果相符得较好. 对不同链长伯醇的德拜介电弛豫的研究表明, 单羟基醇的德拜介电弛豫动力学特征与链长具有相关性^[19].

研究中还发现, 单羟基醇中的探针离子的电导率也存在着异常变化情况, 即随着温度的升高探针离子的电导率出现了先增大后减小的变化趋势^[20,21], 明显不同于甘油等典型的小分子玻璃形成液体中探针离子电导率的行为. 单羟基醇不仅具有一些异常变化行为, 而且其弛豫动力学与分子链长等具有相关性, 对单羟基醇进行细致的研究, 将有利于探索和揭示新的现象与规律, 但是目前从分子的结构和链长方面探讨单羟基醇动力学特征变化情况的研究并不充足. 因此, 本文选择5种链长相近、结构又略有差异的线型伯醇和仲醇进行介电弛豫动力学研究. 本文不仅进一步表明单羟基醇中德拜弛豫动力学与分子链长具有相关性, 而且还揭示出异丙醇和正丁醇的介电谱存在着异常变化, 并探索了可能的原因. 这些研究将为单羟基醇中德拜弛豫动力学的深入认知提供切入点和支撑.

本文所测量的样品为异丙醇(2PRO)、正丙 醇(nPRO)、仲丁醇(2BUT)、正丁醇(nBUT)和仲戊醇(2PEN), 含量依次为≥ 99.7%, ≥ 99.8%, ≥ 99.5%, ≥ 99%和98%, 前3种样品是由福晨化学试剂有限公司生产, 后2种则分别由天津鑫铂特化工有限公司和阿拉丁公司生产, 它们的分子结构见表1. 单羟基醇的介电谱是通过Novocontrol公司生产的Beta-NB型宽频阻抗分析仪进行测量的, 测量频率的范围是10^–1—10⁷ Hz; 温度环境是通过Novocontrol公司配套的Qutro Cryosystem温度控制系统来实现的, 实验中的温度精度控制在0.1 K的范围内; 样品是放置在Novocontrol BDS 1308平行板液体样品池中进行测量的.

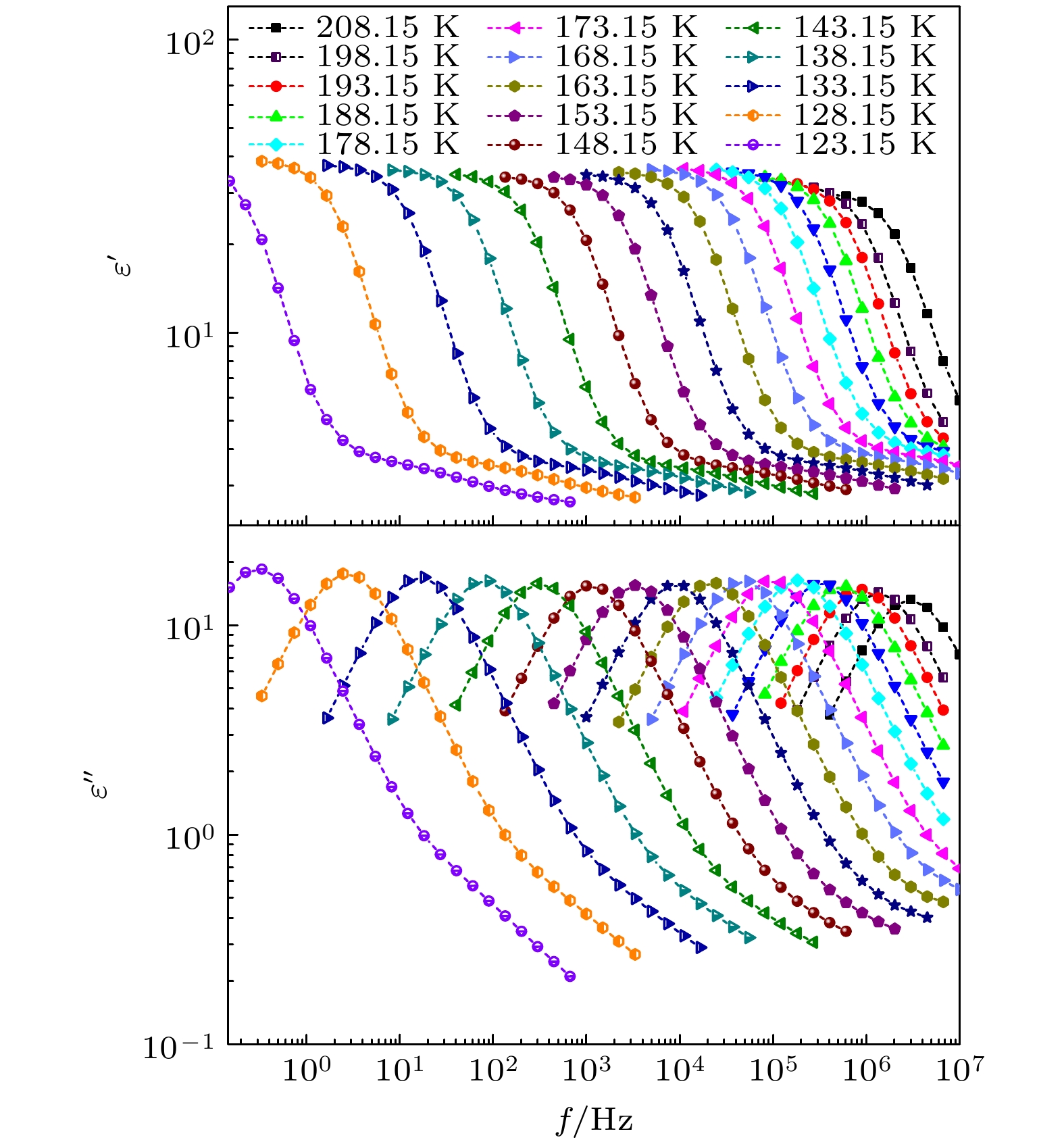
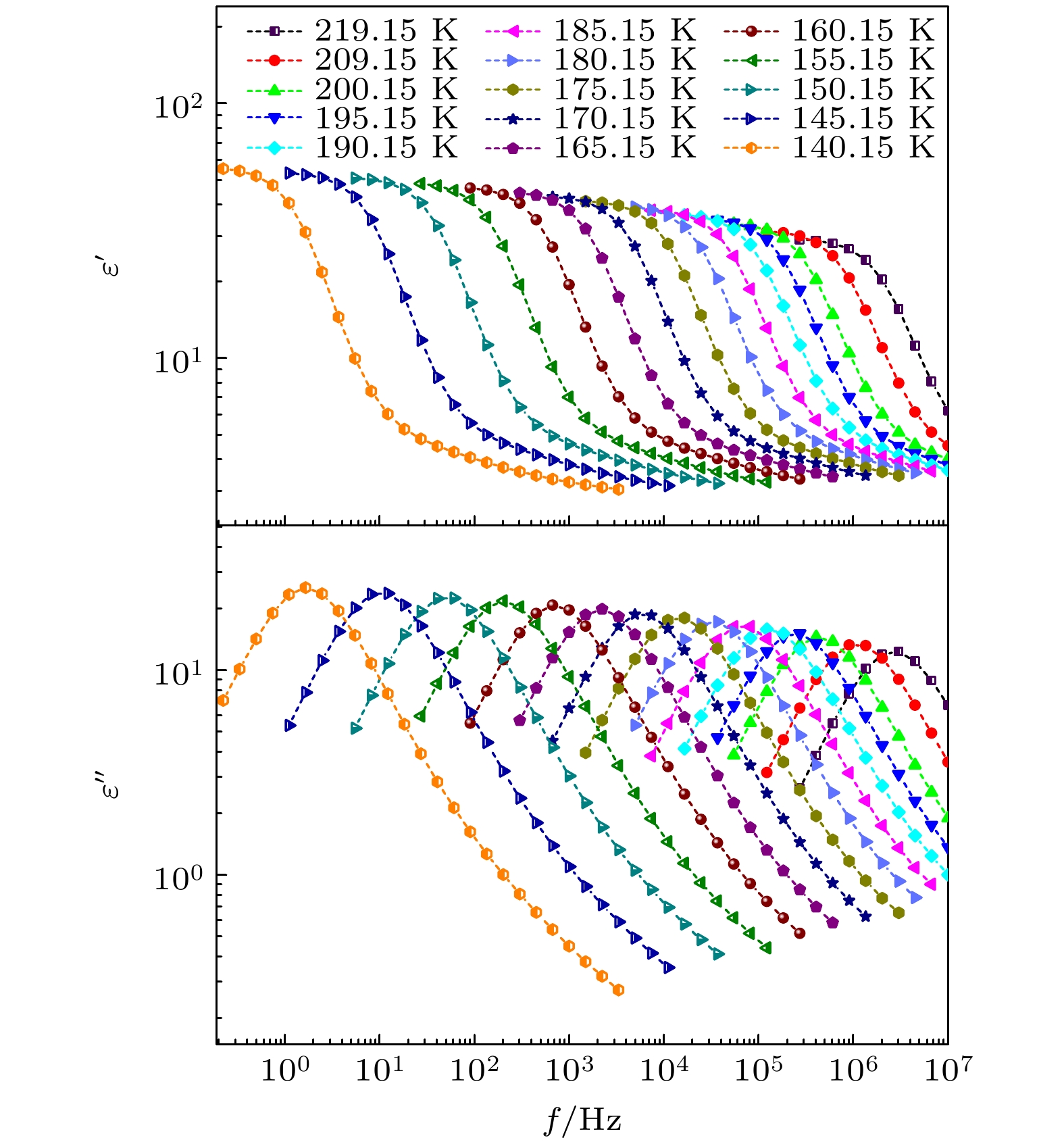
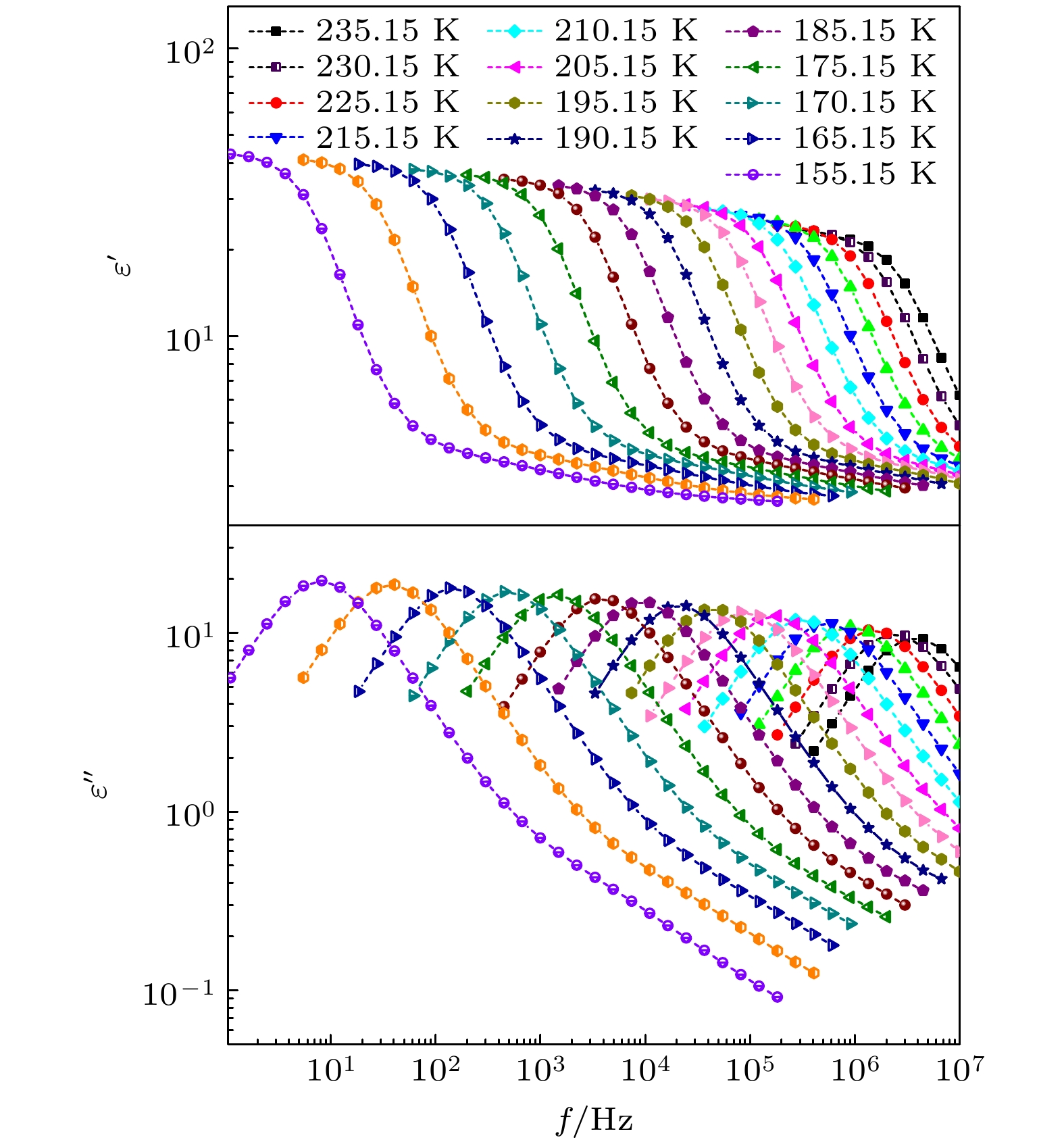
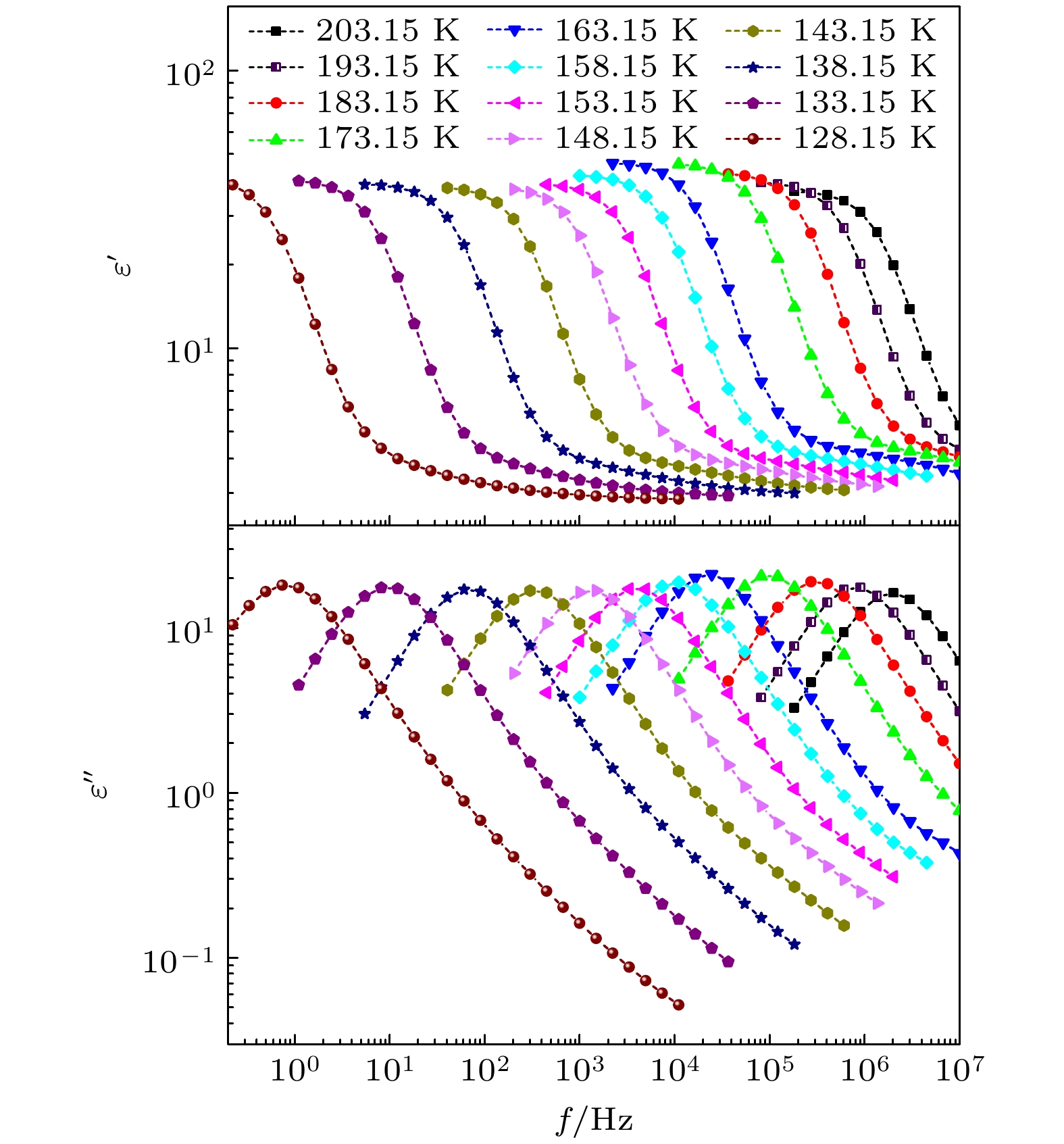
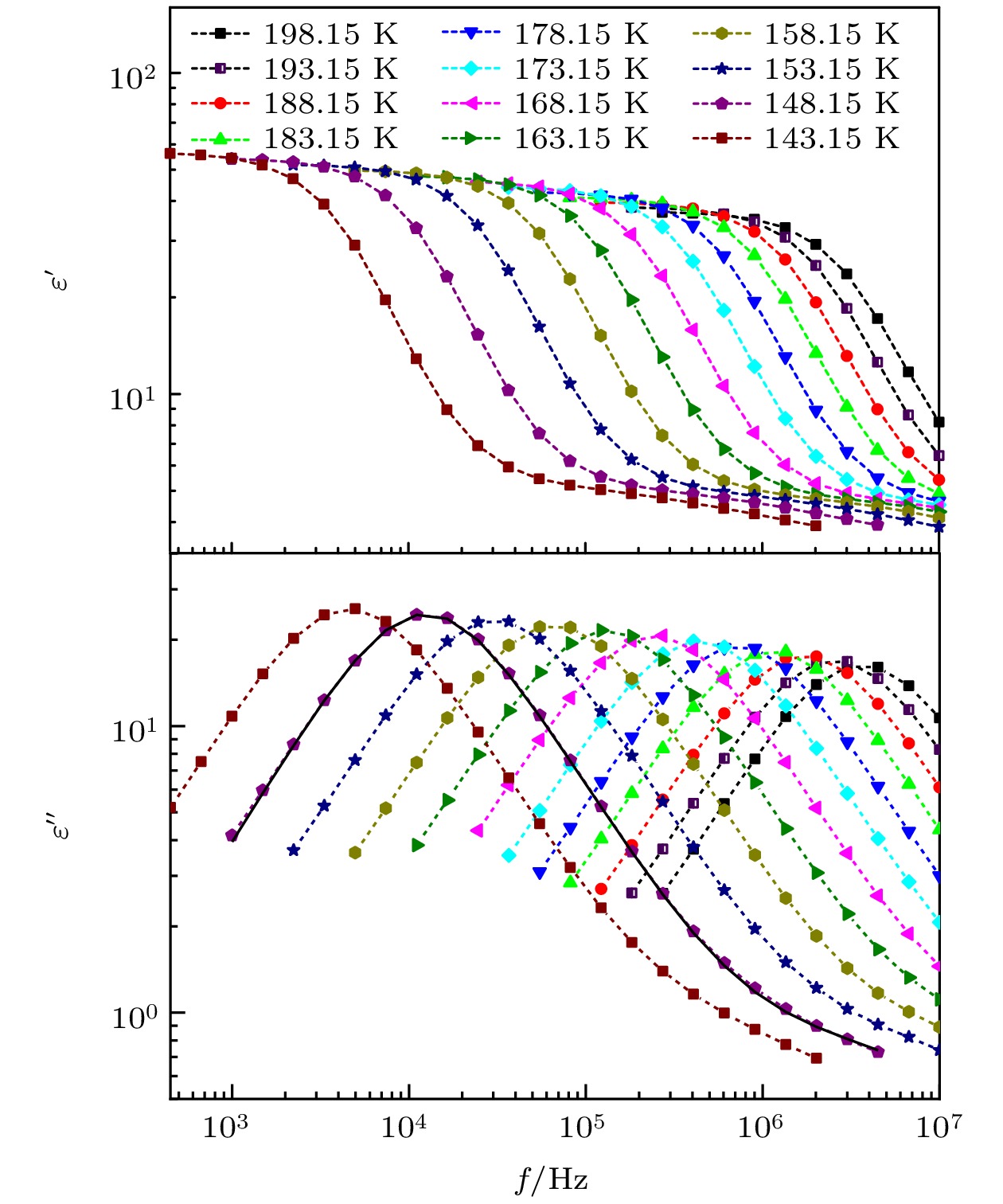
图1—图5所示为正丙醇、仲丁醇、仲戊醇、异丙醇和正丁醇在不同温度下的介电谱实部$ \varepsilon ' $和虚部$ \varepsilon '' $随频率$ f $的变化情况. 可以看出, 这几种单羟基醇在各温度下的$ \varepsilon ' $都出现了一个台阶式变化, 与此相对应的$ \varepsilon '' $上出现了一个峰, 这是弛豫型介电谱的典型特征. 在单羟基醇中, 一般认为介电谱上的这一最为明显的弛豫过程为德拜弛豫. 随着温度的升高, 正丙醇、仲丁醇和仲戊醇的$ \varepsilon '' $上弛豫峰逐渐降低, $ \varepsilon ' $上台阶的低频端也在逐渐下降, 但是在异丙醇和正丁醇中, $ \varepsilon '' $上弛豫峰和$ \varepsilon ' $上台阶的低频端都出现先减小、再增大、最后又减小的特征, 与其他3种单羟基醇的明显不同. 一般情况下, 弛豫峰的最大值和弛豫过程低频端的$ \varepsilon ' $值, 会随着温度的升高而降低, 但是上述异丙醇和正丁醇却出现了异常变化. 通过文献调研发现4-甲基-3-庚醇这种单羟基醇的介电谱上出现了弛豫峰的最大值和弛豫过程低频端的$ \varepsilon ' $值随温度升高而增大的现象, 但是在文献[16]所测量的温度范围内没有出现再次减小的过程.

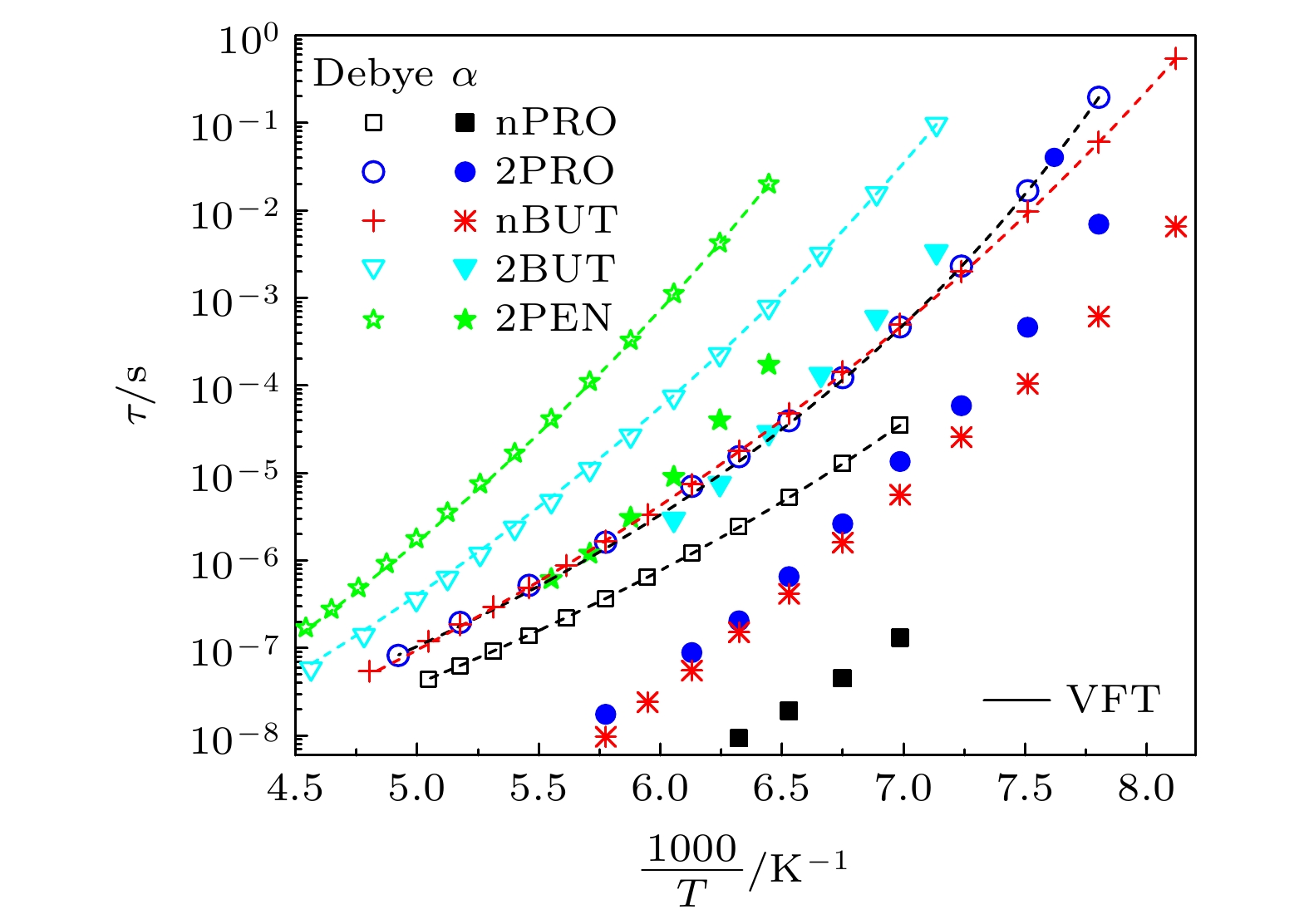
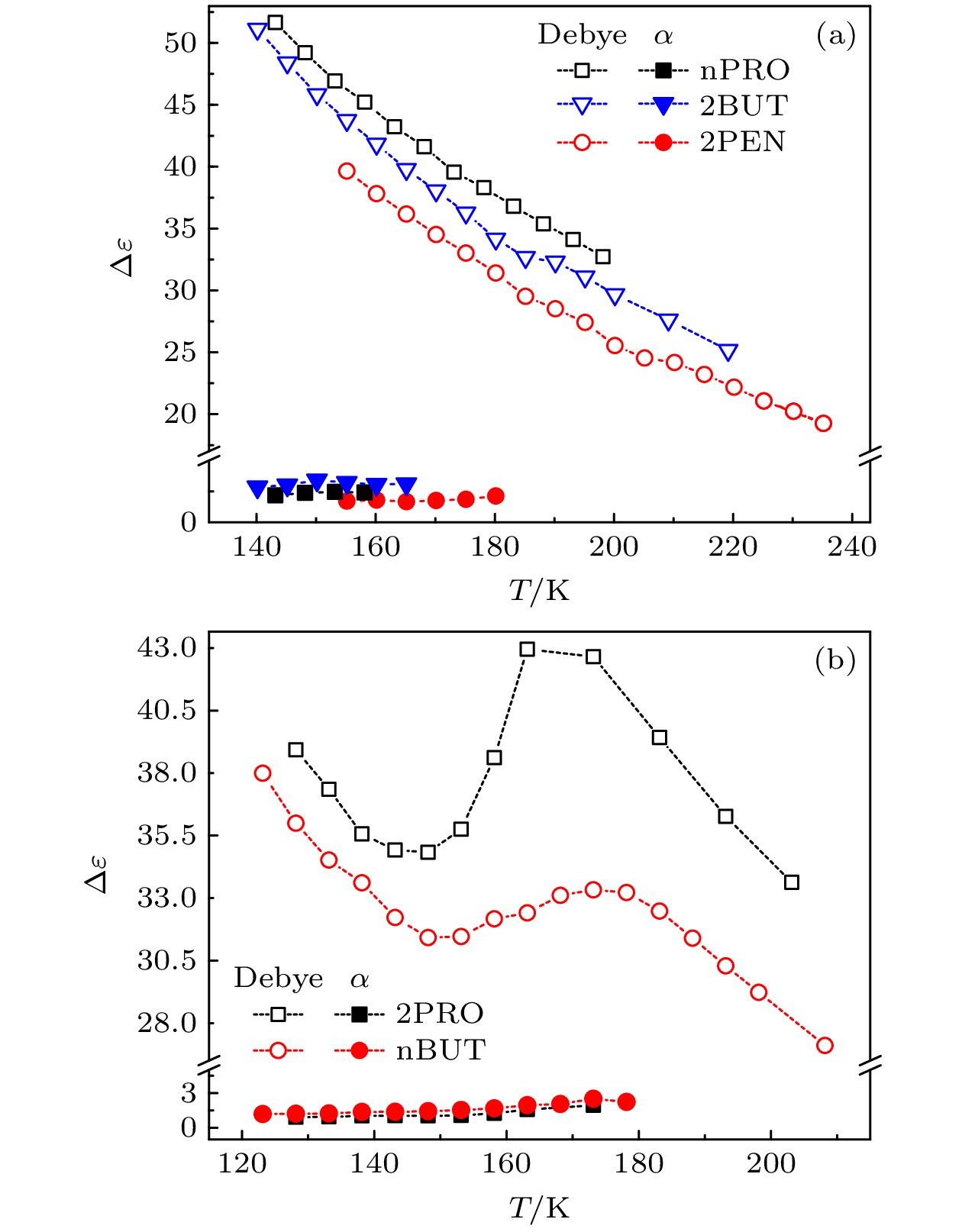
对于单羟基醇来说, 介电谱中除了有德拜弛豫过程之外, 还存在着α弛豫过程. 但α弛豫的强度$ {{{\Delta }}\varepsilon }_{{\mathrm{\alpha }}} $和弛豫时间$ {\tau }_{{\mathrm{\alpha }}} $一般要小于德拜弛豫的强度$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $和弛豫时间$ {\tau }_{{\mathrm{D}}} $, 在正丙醇和正丁醇的介电谱实部中可以看出在德拜弛豫过程的高频段还存在着一个比较小的台阶式变化, 即为α弛豫, 而其他3种单羟基醇则表现得更不明显. 单羟基醇中的弛豫过程可以通过Havriliak-Negami (HN)方程进行描述^[22], 利用HN方程拟合得到的$ {\tau }_{{\mathrm{D}}} $, $ {\tau }_{{\mathrm{\alpha }}} $, $ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $和$ {{{\Delta }}\varepsilon }_{{\mathrm{\alpha }}} $如图6和图7所示. 拟合中在对德拜弛豫进行描述时, HN方程中的形状因子$ \alpha $和$ \gamma $都设为了1, 即采用德拜方程描述该过程.

从图6可以看出, 这5种单羟基醇的$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $都随着温度的升高而减小, 就各单羟基醇之间的$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $来看, 异丙醇和正丁醇的$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $分别比较接近; 正丁醇的$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $最快, 仲戊醇的最慢; 异丙醇的、仲丁醇的和仲戊醇的则分别依次增大. 在图7中, 5种单羟基醇的$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $都远大于$ {{{\Delta }}\varepsilon }_{\alpha } $, 但是$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $的变化趋势并不相同; 其中正丙醇、仲丁醇和仲戊醇的$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $随着温度的升高而降低, 而异丙醇和正 丁醇的$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $却先减小再增大, 最后又降低的变化 情况, 也就是分别在145—175 K的范围内出现了随温度升高而增大的情况. 5种单羟基醇的$ {{{\Delta }}\varepsilon }_{\alpha } $在一个较小的值附近略微波动, 变化趋势不明显, 这可能是德拜弛豫的$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $比α弛豫的$ {{{\Delta }}\varepsilon }_{\alpha } $大得多, 对α弛豫造成了一定程度的掩盖, 导致拟合得到的$ {{{\Delta }}\varepsilon }_{\alpha } $有一定的偏差所造成的. 通过上面的分析, 可以看出异丙醇和正丁醇介电谱的异常变化在 介电弛豫参数上表现为德拜介电弛豫强度的异常变化.

通常$ {\tau }_{{\mathrm{D}}} $与热力学温度$ T $之间满足Vogel-Fulcher-Tammann (VFT)关系^[23,24]:

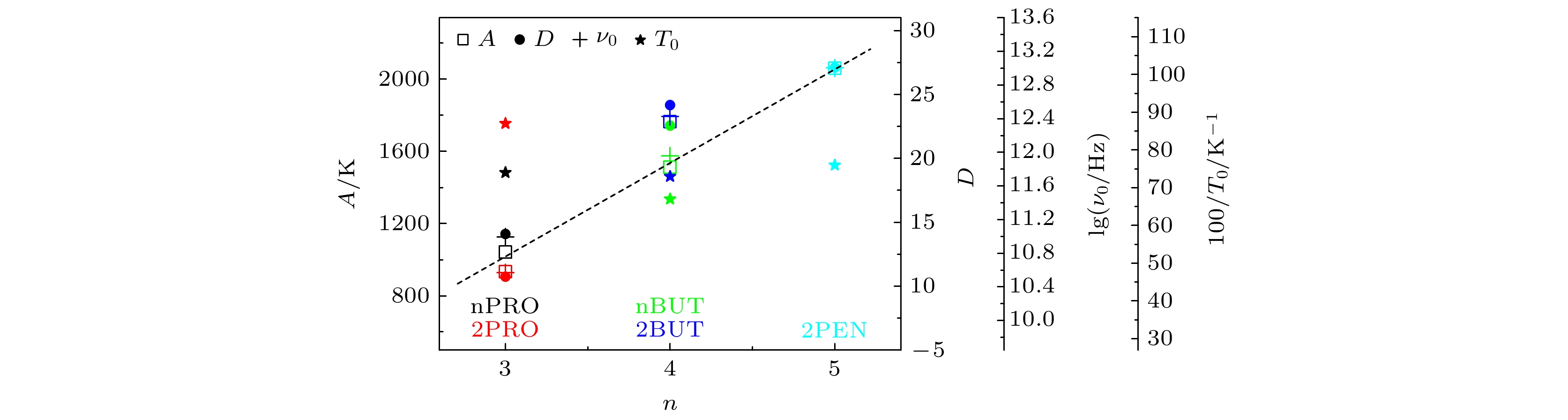
式中, $ {\tau }_{0} $, $ A $和$ {T}_{0} $都是与温度无关而与材料有关的常数, 其中$ {\tau }_{0} $与此时弛豫单元固有振动频率之间满足$ {\nu }_{0}=1/{\tau }_{0} $, $ A $可以理解为弛豫单元在高温极限下的激活能, $ {T}_{0} $为VFT温度, 对应于理想玻璃化转变温度. 利用VFT关系对实验结果进行拟合, 得到的$ {\nu }_{0} $, $ A $和$ {T}_{0} $如图8所示, 图中还给出了体系的强度参量$ D $, 其值由$ D=A/{T}_{0} $计算得到. 从图8可以看出, 无论是伯醇还是仲醇, $ A $, $ D $和$ {\mathrm{l}}{\mathrm{g}}{\nu }_{0} $随着$ n $的增大而增大, 其变化趋势与文献[19]中的结果是类似的, $ {T}_{0} $的值在一定的范围内变化, 并无明显的趋势.

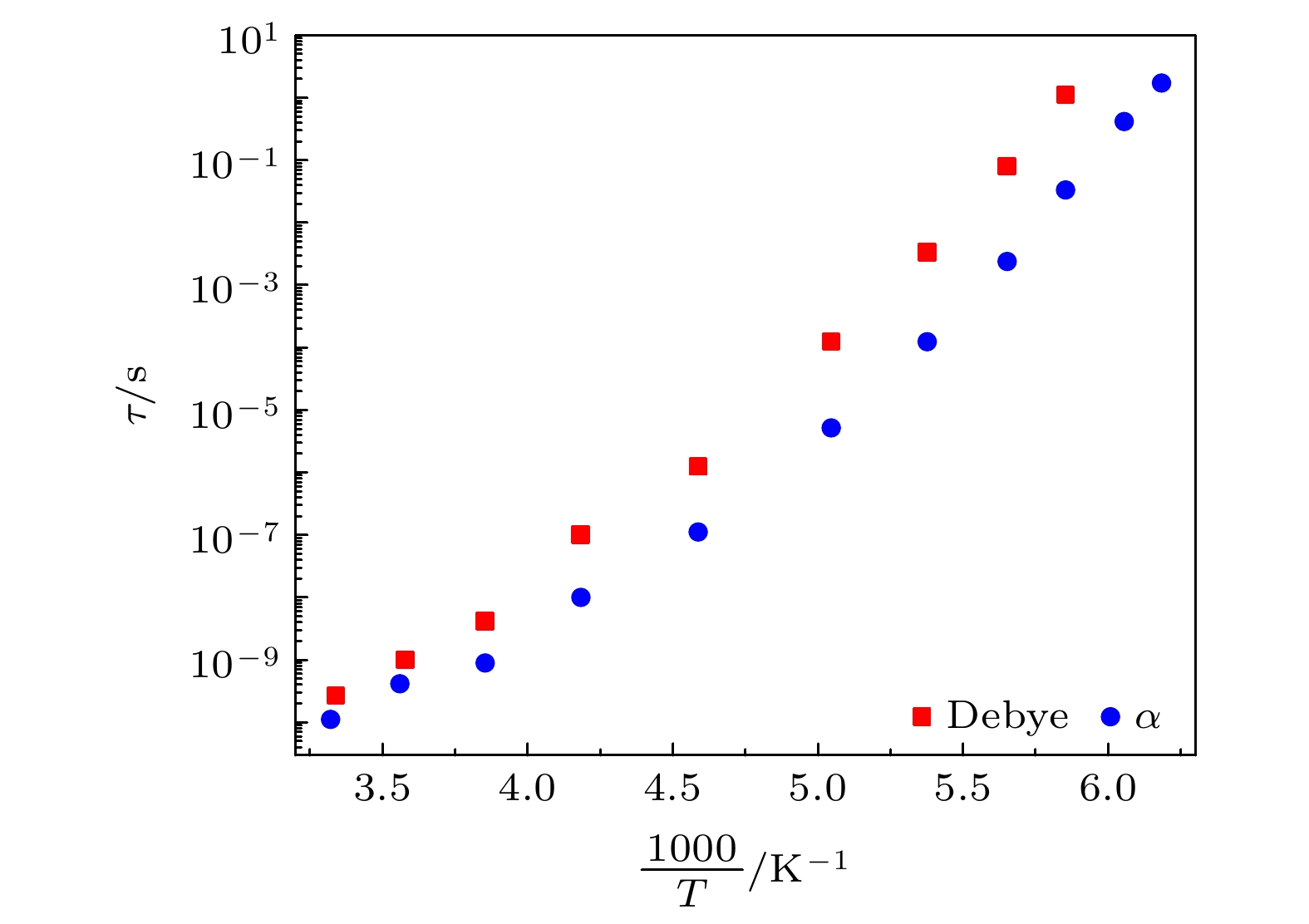
就介电谱随着温度出现异常变化来说, 除了本文中异丙醇和正丁醇之外, 在文献[16]中4-甲基-3-庚醇的介电谱上也出现了异常变化, 但是没有出现弛豫峰的最大值和弛豫过程低频端$ \varepsilon' $的值随温度增大后又再次减小的过程. 从文献[16]中4-甲基-3-庚醇的α过程与德拜过程的弛豫时间来看, 二者相差较小, 而且随着温度的升高, 彼此逐渐靠近, 如图9所示; 德拜介电弛豫强度也未出现随温度升高而增加的情况. 因此, 4-甲基-3-庚醇中介电谱上弛豫峰最大值随温度升高而逐渐增大的情 况, 应该是由α弛豫与德拜弛豫逐渐靠近时两峰彼此逐渐叠加所造成的. 将本文中异丙醇和正丁醇的α过程与德拜过程的弛豫时间进行对比, 可以发现在异丙醇与正丁醇的介电弛豫峰出现随温度升高而增大的区域内, 两个过程的弛豫时间并没有出现靠近的趋势, 而且德拜介电弛豫强度还出现了先降低再增大最后又减小的趋势, 也明显不同于4-甲基-3-庚醇中德拜介电弛豫强度随温度升高而持续减小的特征. 这说明异丙醇和正丁醇中介电谱上弛豫峰异常变化的原因与4-甲基-3-庚醇中的异常并不相同. 另外, 在4-甲基-3-庚醇中, 从其介电谱上可以看出α过程与德拜过程的介电弛豫强度相差并不大, 而在异丙醇与正丁醇中却是德拜介电弛豫强度远大于α弛豫的, 这也表明异丙醇和正丁醇中产生异常变化的原因可能与4-甲基-3-庚醇中的不同.

从介电谱分析的结果来看, 本文中异丙醇与正丁醇的介电谱异常变化应该是由德拜介电弛豫强度出现的新的异常变化所导致的, 即在145—175 K的范围内德拜介电弛豫强度出现了随温度升高而增大的变化趋势. 在研究中, 人们一般认为单羟基醇的德拜弛豫来源于氢键作用下单羟基醇分子所形成的氢键分子链, 理论分析和我们近来开展的分子动力学模拟结果都表明单羟基醇中的氢键分子链可以采用自由旋转链进行描述^[17,18]. 以自由旋转链为基础, Wang等^[17]建立了自由旋转赝自旋Ising链模型来描述单羟基醇中的德拜介电弛豫强度, 即:

其中$ N $是单位体积内的分子数目, $ \mu $是单个分子的电偶极矩在链切线方向上分量的大小, $ {\varepsilon }_{0} $是真空介电常数, $ {k}_{{\mathrm{B}}} $是玻尔兹曼常数, $ \gamma =J/\left({k}_{{\mathrm{B}}}T\right) $, 这里的$ J $和上述方程中的$ \theta $分别是相邻两分子的等效赝自旋之间的相互作用能和夹角.

从方程(2)可以看出, $ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $除了会受到温度的影响之外, 还会受到$ N $和$ \theta $的影响, 也就是受体系的分子数密度和相邻分子间夹角的影响, 具体为$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $分别正比于$ N $, 反比于温度, $ \theta $减小会导致$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $增大. 一般情况下, 随着温度的升高, $ N $略微减小, 而$ \theta $基本不变; 在温度的作用下, $ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $逐渐减小. 但是在实验中异丙醇和正丁醇的$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $却出现了随温度升高而增大的情况, 温度升高时, 方程(2)中$ T $的作用是使$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $减小; 因此, 导致$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $增大的原因只能来自于$ N $和$ \theta $. 通过文献调研并未发现体系的分子数密度在上述温度范围内出现增大的情况, 通过分子动力学方法对异丙醇的体积随温度的变化情况进行模拟, 显示其分子数密度在这一温度范围内略微减小. 对于$ \theta $来说, 随着温度升高, 如果其产生了变小, 那么将会产生使$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $增大的作用.

虽然理论上一般认为$ \theta $是与温度无关的, 但是在真实的体系中, 随着温度升高, 分子的动能会增大, 体系的体积也会增大, 平均每个分子将拥有更大的占有体积; 两个方面叠加在一起, 将导致分子的可动性增强. 氢键相互作用并没有化学键那么强, 因此分子的运动可能会对氢键分子链的结构形成影响, 进而导致$ \theta $发生变化. 在方程(2)中, 当$ \theta $的改变导致的增大量大于$ T $所导致的减小量时, $ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $就会表现出随温度的升高而增大的现象; 而当$ \theta $的改变导致的增大量小于$ T $所导致的减小量或者$ \theta $的改变导致的也是减小量时, $ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $将会表现出随温度的升高而降低的情况. $ A $可以对应于弛豫单元在高温极限下的激活能, 因此能够反映分子间羟基的相互作用. 从拟合所得$ A $的值来看, 异丙醇和正丁醇的值要分别小于正丙醇和仲丁醇的, 这说明在这两种单羟基醇中所形成的氢键相互作用相比于相同碳原子数的另一种醇的要弱. 因此, 温度升高时, 分子的可动性更容易对氢键分子链的结构形成明显的影响, 当这种影响所导致的方程(2)的增大量大于$ T $所导致的减小量时, 最终表现为$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $的增大.

当然, 这种影响强弱与最终结果, 不仅与氢键相互作用的大小有关, 而且应该也与分子中碳原子的多少以及分子结构有关. 从实验结果来看, 虽然正丙醇与异丙醇中碳原子数相同, 正丁醇与仲丁醇中的碳原子数也是相同的, 但是异丙醇和正丁醇的介电谱中存在着异常变化, 正丙醇与仲丁醇的介电谱中却没有表现出异常变化. 对比异丙醇和正丁醇的弛豫时间, 可以发现无论是德拜弛豫还是α弛豫, 两种单羟基醇中的$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $不仅整体上彼此比较接近, 而且在$ {{{\Delta }}\varepsilon }_{{\mathrm{D}}} $出现异常变化的温度区间内, 它们是十分接近的. 正丙醇中的碳原子数与异丙醇的相同, 但是由于正丙醇的羟基位于第一个碳原子上, 使得相对于异丙醇来说, 其可动性更强, 表现为其$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $小于异丙醇的; 而仲丁醇由于羟基位于第2个碳原子上, 其可动性比正丁醇要弱, 表现为其$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $小于正丁醇的. 由于正丙醇与异丙醇中分子的可动性以及分子间相互作用的强弱程度与异丙醇和正丁醇之间存在一些差异, 所以它们的介电谱上最终未表现出异常变化. 目前仅仅在在异丙醇和正丁醇这2种单羟基醇中观察到了上述异常变化, 其他单羟基醇中并未观察到, 也就是正常情况是更为常见的, 这说明要想形成上述异常变化需要的条件比较苛刻. 但是分子中碳原子的多少以及分子结构如何影响氢键分子链的结构, 所对应的规律又是如何, 尚不清楚, 还需要进一步研究. 另外, 虽然人们对小分子液体中不同弛豫过程的关联性进行了一些研究^[11,25–27], 但是单羟基醇中的德拜弛豫与α弛豫和β弛豫之间的关联性依然是一个值得研究的问题.

图8中$ A $的变化趋势, 表明随着单羟基醇中碳原子数的增加, 氢键作用将会得到增强, 而且无论是伯醇还是仲醇都满足这一规律. 虽然碳原子数相同的伯醇与仲醇中原子构成是完全一样的, 但是它们的结构却存在一些差异的. 因此, 上述伯醇和仲醇中$ A $, $ D $和$ {\mathrm{l}}{\mathrm{g}}{\nu }_{0} $都随着$ n $的增大而增大的结果, 说明单羟基醇中的$ A $, $ D $和$ {\mathrm{l}}{\mathrm{g}}{\nu }_{0} $随着$ n $的增大而增大的变化规律具有一定普遍性, 这可以为分子链长对单羟基醇动力学性质影响的研究提供参考.

在正丙醇、异丙醇、正丁醇、仲丁醇和仲戊醇5种单羟基醇的介电谱的测量与分析中, 发现了异丙醇和正丁醇的介电谱存在异常变化的情况, 即随着温度的升高, 介电谱中强度最大的弛豫峰出现了先降低再升高, 最后又降低的变化趋势, 明显不同于一般情况下弛豫峰随温度升高而逐渐降低的特征. 通过HN方程拟合得到的结果表明该异常变化对应于单羟基醇中德拜介电弛豫强度的异常变化, 即随着温度的升高, 德拜介电弛豫强度呈现出先减小、再增大、最后又降低的变化趋势. 分析得到的异丙醇和正丁醇的$ {\tau }_{{\mathrm{D}}} $和$ {\tau }_{{\mathrm{\alpha }}} $不仅整体上彼此比较接近, 而且在出现异常变化的温度区间内, 它们是十分接近的. 结合单羟基醇德拜介电弛豫的理论模型探讨了该异常变化产生的可能原因, 认为该异常变化是温度导致的德拜介电弛豫强度的减小与分子运动性变化引起的氢键分子链结构变化而导致的弛豫强度变化的共同结果. 通过对比分析表明单羟基醇中产生上述异常变化所要求的条件应比较苛刻, 但是分子中碳原子的多少以及分子结构影响氢键分子链的结构机制尚不清楚, 还有待于进一步研究. 本文研究不仅发现了单羟基醇中新的异常变化行为, 分析了可能的原因, 而且能够为单羟基醇的研究提供新的切入点和研究内容. 另外, 本文研究结果也表明仲醇中$ A $, $ D $和$ {\mathrm{l}}{\mathrm{g}}{\nu }_{0} $具有随着$ n $的增大而增大特征, 与伯醇中的规律类似, 可以为分子链长对单羟基醇动力学性质影响的研究提供参考.