首页
登录
注册
下载:
-
在量子场论中, 真空并非什么都没有, 而是存在不停的量子涨落(又被称为真空零点能涨落). 1948年, 荷兰物理学家Hendrik Casimir[1]提出了一种思想假设, 即真空中两块靠得很近的金属平板存在特定的、有限的电磁模式, 而金属平板外面存在无限的模式, 这种差异导致两金属平板存在相互吸引力[2]. 截至目前, 真空中Casimir效应产生的吸引力已被诸多精密实验所证实[3–6]. 此外, 特殊系统中Casimir斥力的研究也被相应报道[7], 包括超构材料系统[8,9]、拓扑绝缘体系统[10–12]以及复合溶液系统[13–15]等. Casimir效应引起的相互作用力(如吸引、排斥、扭转、牵引等)可作为驱动和操控微纳物体的有效手段[16–22].
近年来, 构建稳定的Casimir平衡点受到学术界的广泛关注[23–28]. 当两物体靠近时, Casimir效应表现为排斥力; 而当两物体距离较远时, Casimir效应表现为吸引力. 因此在特定距离下, 存在Casimir力为零的特殊点, 也被称为稳定的Casimir平衡点. 2019年, Zhao等[29]实验上观察到了一种基于Teflon涂层的稳定Casimir平衡点, 纳米级别厚度的金属薄片可稳定悬浮在溶液中. 随后, 人们对Casimir平衡点调控的研究也被不断报道[30–38]. 例如, 我们之前的研究工作发现利用相变材料二氧化钒, Casimir平衡点可通过温度进行调控[30]. 在电偏压的氧化铟锡[31]或石墨烯系统中[32], Casimir平衡点也可实现大范围的动态调控. 利用水溶液中离子浓度的改变, Casimir平衡点的调控也被报道[33]. Casimir平衡点的调控在光学谐振腔[34,35]、自组装[36–38]等领域中具有应用前景.
本文提出了一种基于双液体的可调控Casimir平衡点的设计. 我们以有机溶液(甲苯、苯或溴苯)和水组成的溶液系统为例子. 由于水与这些有机溶液不相溶的特性, 存在分层的现象. 密度低的在上层, 而密度高的在底层. 研究发现, 甲苯@水, 或者苯@水组成的双液体环境中, 金纳米薄膜存在稳定的Casimir平衡点. 此外, 倒置的溴苯@水系统中也存在Casimir平衡点. 这些稳定的Casimir平衡点的高度可通过水层的厚度改变实现调控. 最后, 我们研究了系统温度和水中离子浓度对稳定Casimir平衡点的影响. 我们发现, 水的离子浓度能较大地调控平衡点的高度范围.
-
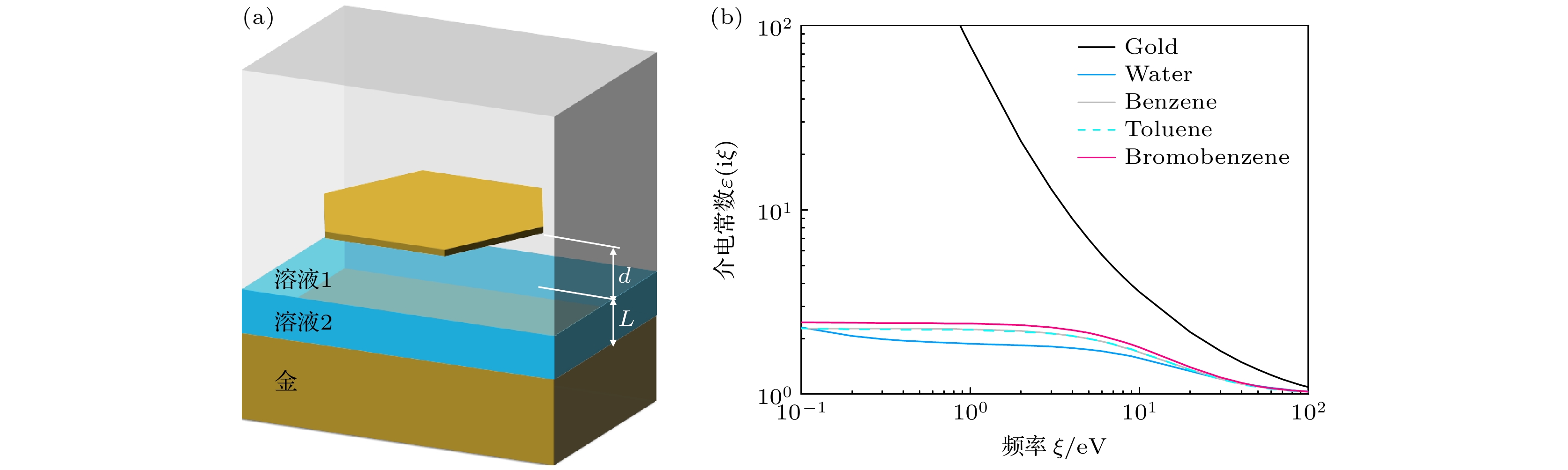
图1(a)展示了我们研究的两不相溶液体结构示意图. 悬浮在溶液1中的金纳米薄片厚度为L0, 距离液体分层界面为d. 溶液2紧挨金属衬底且具有厚度L. 双液体由水和有机溶液(甲苯、苯或溴苯)组成. 甲苯(C7H8)和苯(C6H6)是非极性有机溶液, 密度均小于水. 因此, 双液体的上层溶液1是甲苯或苯, 下层的溶液2则对应于水. 与此相反, 溴苯(C6H5Br)溶液的密度大于水. 在溴苯和水构成的双溶液环境中, 上层溶液1为水, 而下层溶液2为溴苯. 在计算Casimir压强过程中, 采用Lifshitz[39]的理论框架. 该理论不仅适用于真空环境, 在液体环境中也有效[25,40–43]. 假定金纳米薄片的水平面尺寸(例如10 μm级别[29])远大于距离d, 其受到的Casimir压强表达式为[33]
其中kB是玻尔兹曼常数; T是系统温度; 求和中符号 ' 表示n = 0项具有前因子1/2; k//是平行波矢量;
$ {{\boldsymbol{K}}_n} = \sqrt {{\boldsymbol{k}}_{/ /}^2 + {\varepsilon _{{\text{liq}}}}({\mathrm{i}}{\xi _n})\xi _n^2/{c^2}} $ 是垂直波矢量,$ c $ 是真空中的光速,$ {\varepsilon _{{\text{liq}}}}({\text{i}}{\xi _n}) $ 是用虚频$ \omega = {\text{i}}{\xi _n} $ 表示的液体(即溶液1)的介电常数,$ {\xi _n} = 2\pi {{{k_{\text{B}}}Tn} {/ } \hbar }{\text{ }}(n = 0, {\text{ }}1, {\text{ }}2, {\text{ }}3 \cdots ) $ 为离散的Matsubara频率,$ \hbar $ 是约化普朗克常数.$ r_{\text{t}}^\alpha $ 和$ r_{\text{b}}^\alpha $ 分别表示上层和下层层状结构的反射系数, 上标α = s和p分别对应横电波(TE)和横磁波(TM)极化. 反射系数下标t, b对应图1(a)的结构分别为悬浮金薄膜, 以及溶液2涂层@金衬底. 这些结构的反射系数可通过传输矩阵方法(transfer matrix method)数值计算[30], 也可通过下列解析形式给出[30]:其中l是薄膜的厚度; 垂直波矢表示为
$ {{\boldsymbol{k}}_{jz}} = \sqrt {{\boldsymbol{k}}_{/ /}^2 + {\varepsilon _j}({\mathrm{i}}\xi ){\xi ^2}/{c^2}} {, }\;j = 2 $ ;$ {\varepsilon _j}({\text{i}}\xi ) $ 是薄膜的介电常数; 反射系数$ r_{mn}^\alpha $ 下标表示光从介质m入射到n, 表达式为当考虑水具有离子浓度时(如添加少量的NaCl), (1)式中的n = 0项需要适当修正[33]. 零频率下水溶液中的垂直波矢量变为:
$ {k_z} = \sqrt {{\boldsymbol{k}}_{/ /} ^2 + {\kappa ^2}} $ , 其中κ = 1/λD, λD为水中离子的德拜屏蔽长度(Debye screening length), 德拜屏蔽长度是描述电解质溶液中静电屏蔽效应的一个重要参数, 其表达式为[33]式中,
$ \varepsilon $ 是溶液的静态相对介电常数,$ {\varepsilon _0} $ 是真空的介电常数,$ e $ 是电子电荷,$ {n_v} $ 是溶液中$ v $ 价离子的数密度. 通常λD的长度与距离d可比拟时, n = 0项的Casimir压强会受到明显的削弱, 但其他高阶项n > 0不受到影响[33]. 有机溶液溴苯、苯和甲苯是非极性溶剂, 不能有效地溶解极性离子, 它们的盐离子浓度在计算中为零. -
在计算反射系数过程中, 需要材料的介电常数. 我们展示金[44]、有机溶液(苯、甲苯和溴苯)[40]和水[45]的介电常数随虚频的变化如图1(b)所示. 结果显示, 宽频范围下金的介电常数最大, 有机溶液(溴苯、苯和甲苯)的介电常数大于水. 有机溶液中, 溴苯有更大的介电常数, 苯和甲苯的介电常数非常接近. 根据这些介电常数大小的比较, 可有助于判断Casimir压强的吸引和排斥特性.
-
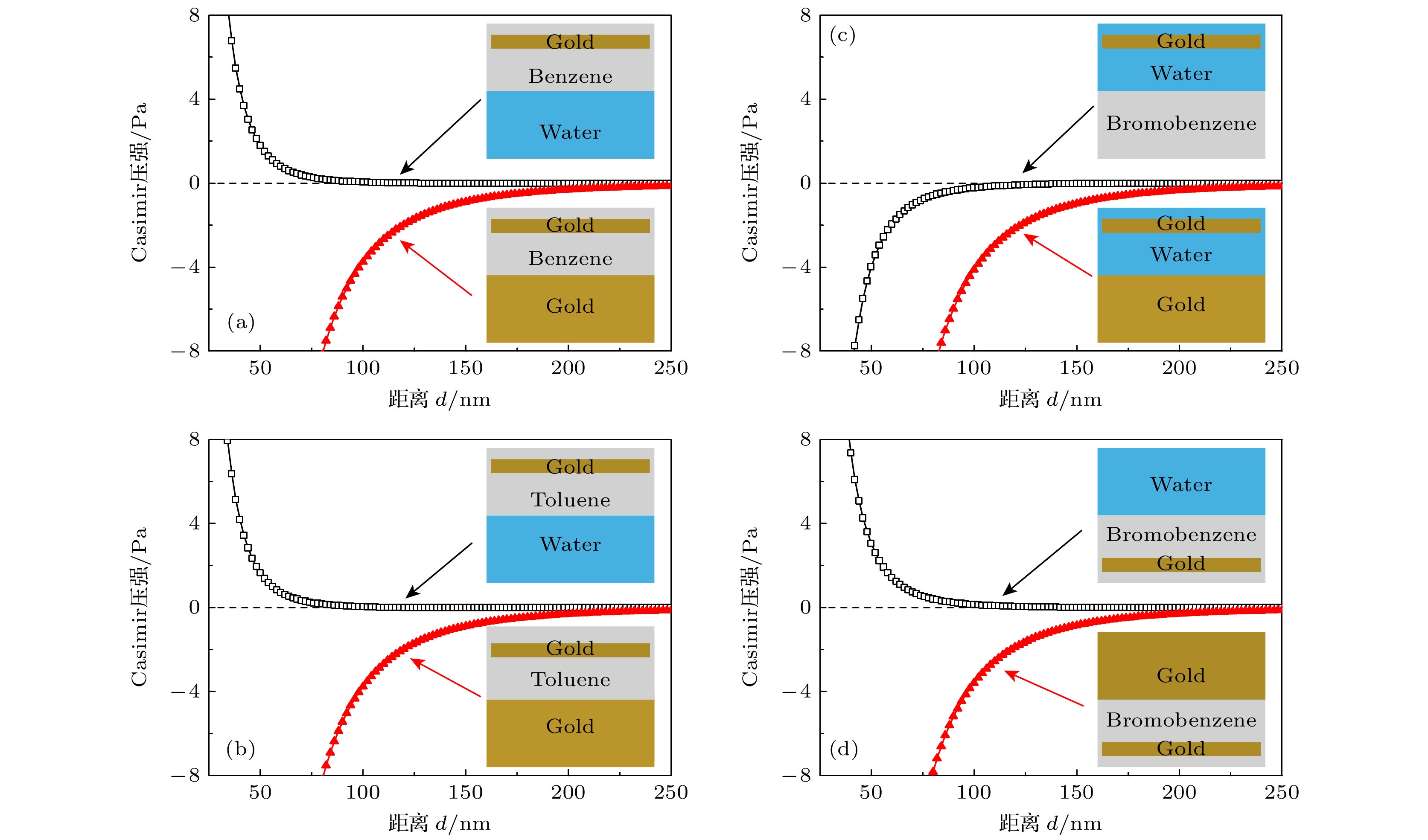
图2(a)展示了苯@水的双液体环境中Casimir力的计算结果, 隔离层的厚度取极限值. 当水的厚度L =
$ \infty $ 时, 悬浮在苯溶液中的金纳米片受到长程的Casimir排斥力. 这是由于层状系统的介电常数在宽频范围内满足排斥力的条件[42]:$ {\varepsilon }_{金}({\mathrm{i}}\xi ) > {\varepsilon }_{甲苯}({\mathrm{i}}\xi ) > {\varepsilon }_{水}({\mathrm{i}}\xi ) $ , 金对应的是悬浮金纳米薄片. 当水的厚度L = 0时, 金属纳米片的Casimir力表现为长程的吸引力. 这是由于两边金属的介电常数都大于甲苯的介电常数. 由于甲苯和苯的介电常数非常接近, 甲苯@水的双液体系统几乎与苯@水的Casimir压强曲线一致, 如图2(b)所示.在溴苯@水组成的双溶液系统中, 由于溴苯的密度大于水, 溴苯为隔离层在水层之下. 当溴苯的厚度L = 0或
$ \infty $ 时, 计算的Casimir压强为长程吸引力, 如图2(c)所示. 这是由于宽频范围内, 溴苯和金的介电常数都大于水, 无法满足产生Casimir排斥力的条件. 如果将图2(c)所示的结构倒置, 由于重力的作用, 水作为隔离层, 如图2(d)所示. 当水的厚度取无限大时, 悬浮在溴苯中的金纳米片与液体界面之间的Casimir压强表现为排斥力. 当水厚度L = 0时, 金属纳米薄片与金属衬底之间的Casimir力表现为吸引力. -
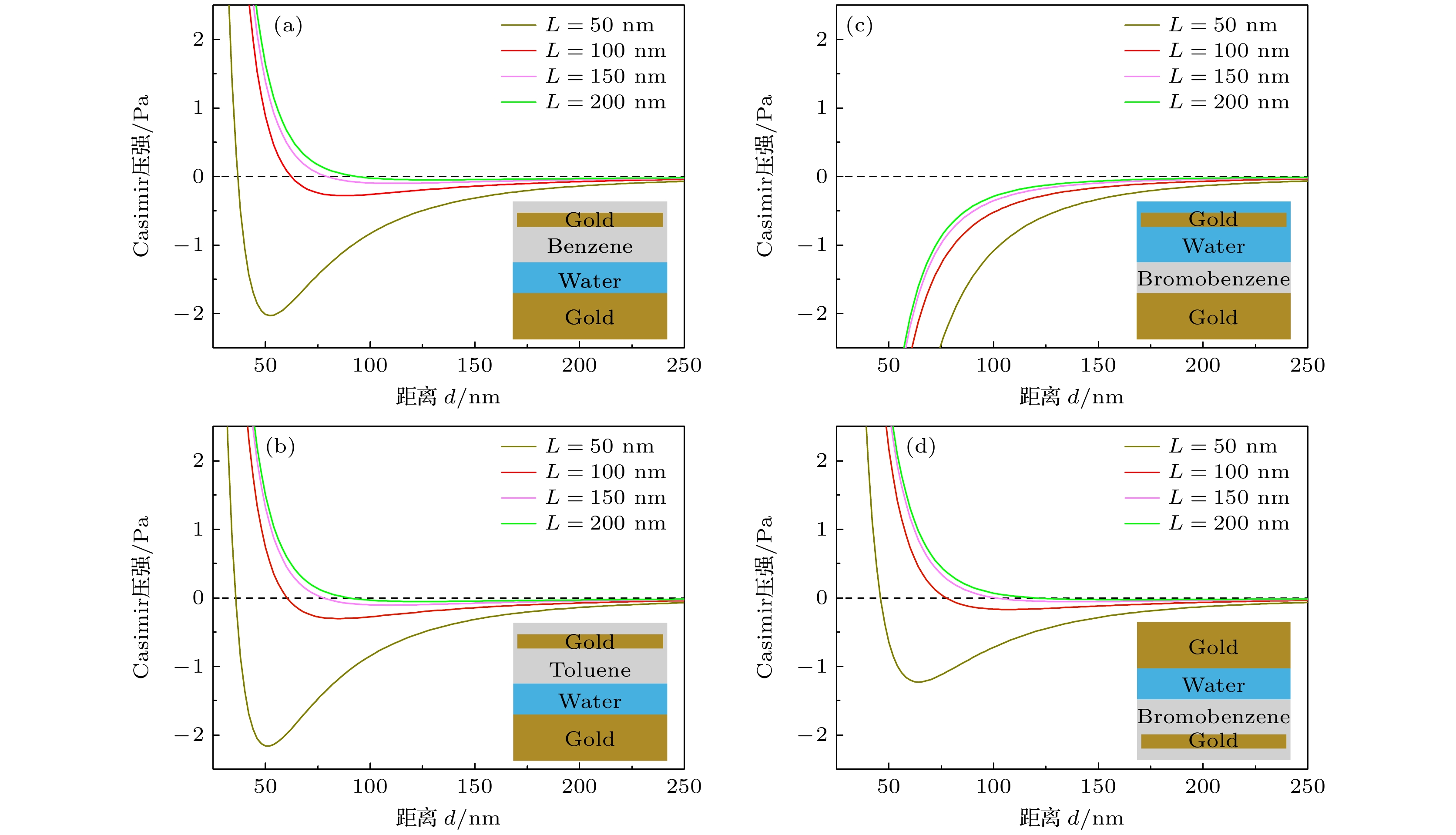
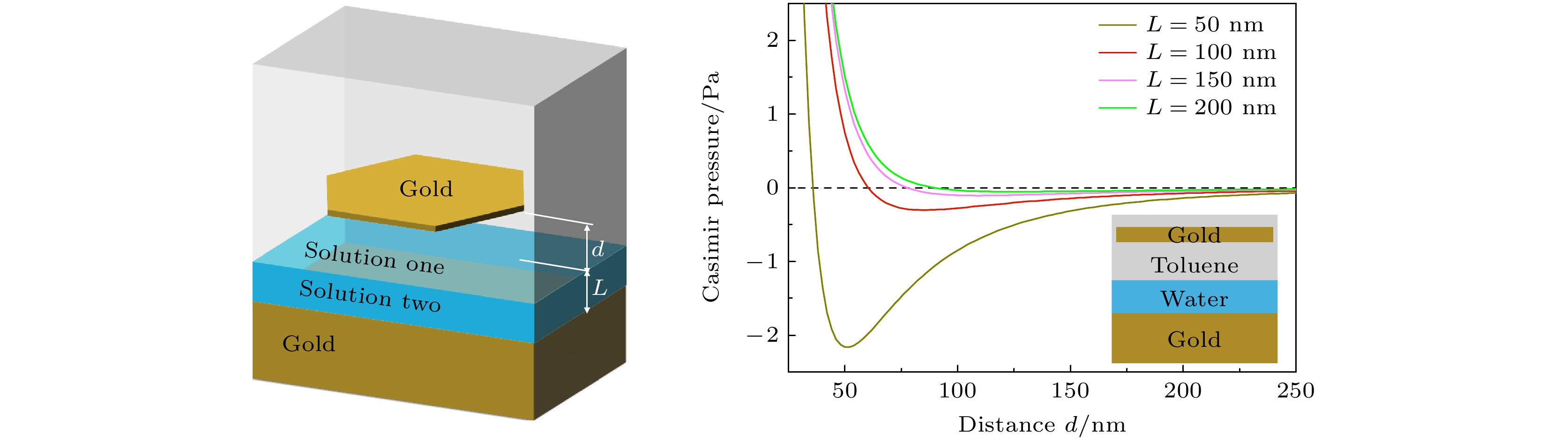
低折射率涂层薄膜覆盖金属衬底是构建Casimir平衡点的一种有效结构[29]. 受此启发, 我们设计水作为低折射率的涂层薄膜, 结构如图3(a)所示. 对于苯@水组成的双液体系统, 水作为隔离层, 金纳米薄片悬浮在苯液体中. 当金纳米薄片靠近液体分层界面时(例如距离d减小到30 nm), 受到Casimir排斥力. 这是由于金纳米薄片/甲苯/水之间的相互作用占主导, 金属纳米薄片受到Casimir斥力. 但当金纳米薄片远离分层界面时(例如距离d增大到100 nm), 金纳米薄片受到Casimir吸引力. 在特定距离下, 存在稳定的Casimir平衡点, 且该平衡点的特性与水的厚度密切相关. 当水的厚度为L = 200 nm时, 平衡点的位置d大约为100 nm, 且最大的吸引回复力较弱. 随着厚度L减小为100 nm (或者更薄的50 nm), 平衡点位置d降低, 且最大的吸引回复力增大为0.5 Pa (或者2 Pa). 因此, 利用水厚度的变化, 可实现对稳定Casimir平衡点的人工调控.
由于甲苯与苯具有相同的特性, 它们的折射率几乎一致, 且密度都小于水. 因此, 在甲苯@水构成的双液体环境中, Casimir压强曲线与苯@水系统的情况类似, 如图3(b)所示. 在溴苯@水组成的双溶液系统中, 溴苯作为隔离层且厚度有限. 金纳米薄片悬浮在水中, 且受到的Casimir压强如图3(c)所示. 计算表明Casimir压强始终是吸引, 无法实现稳定的Casimir平衡点. 当把该结构倒置时, 由于重力的作用, 液体分层情况如图3(d)所示. 此时, 液体隔离层为水溶液, 存在稳定的Casimir平衡点. 通过Casimir通过调控水溶液的厚度L, Casimir平衡点受到相应的调控, 与图3(a), (b)具有类似的特征.
-
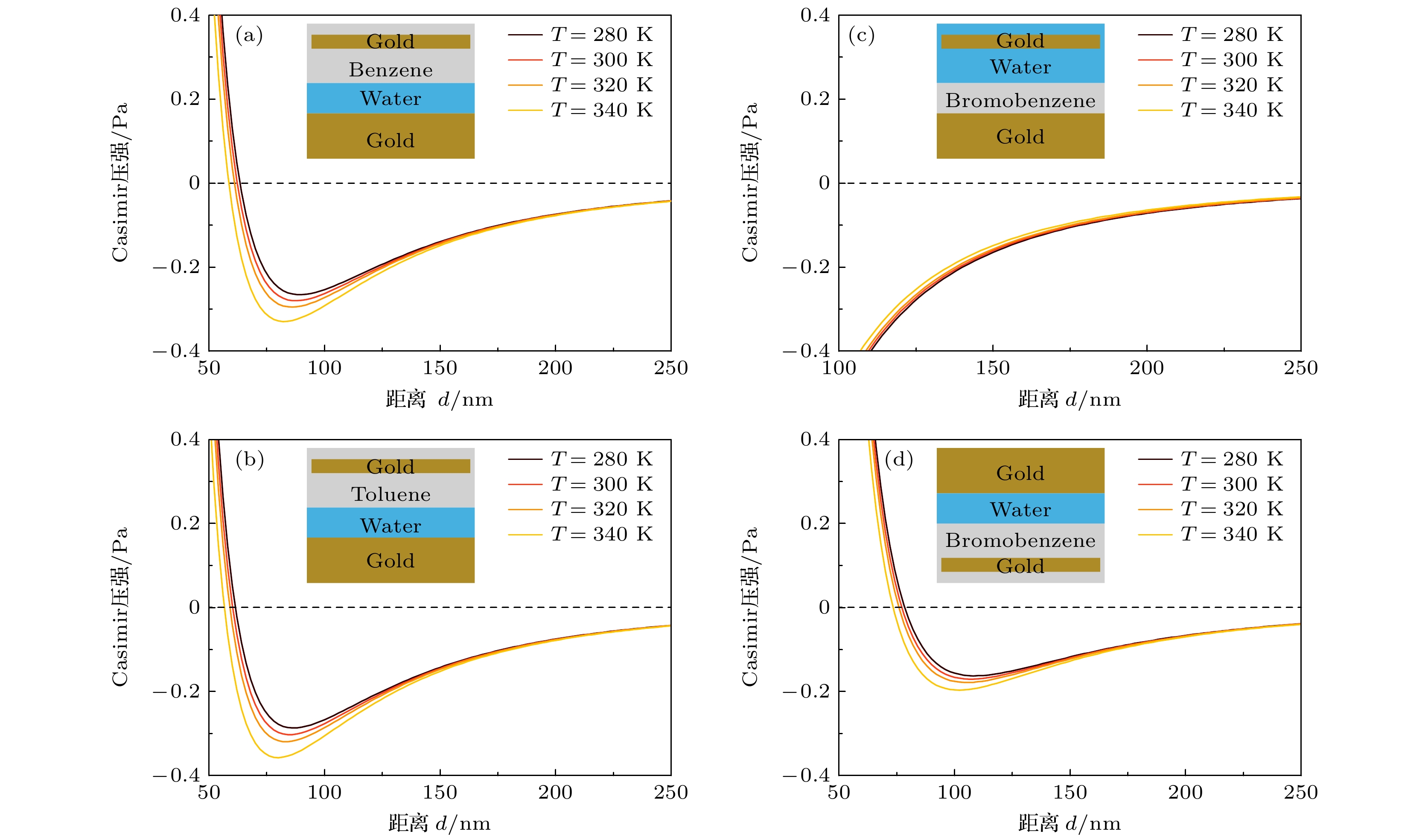
本文在计算Casimir压强时, 水和有机溶液需维持液体状态. 在标准大气压下, 苯的液体状态温度范围是279—351 K, 甲苯的液体状态温度范围是178—384 K, 溴苯的温度范围是242—429 K, 而水的液体状态温度范围是273—373 K. 我们假定金的介电常数在这些范围下保持不变, 有机液体在温度变化下的折射率改变约为10–4 /K, 因此其介电常数受温度的影响也可忽略不计[31]. 图4展示了双液体环境下, Casimir压强在不同温度下的变化曲线, 其中液体隔离层L = 100 nm. 在图4(a)—(c)双液体系统中, 温度增大时, Casimir平衡点对应的距离变小, 移动量为0.05—0.08 nm/K. 因此, 在本文考虑的参数范围下, 系统的Casimir平衡点具有良好的热稳定性.
-
水是一种极性分子, 通过添加一定的盐(例如NaCl), 水中离子浓度可被相应的调制. 由于离子电荷涨落, Casimir效应中的n = 0项会被部分屏蔽或者完全消除[33]. 对于纯水, 没有加入任何的盐, 水中的OH–和H+离子可形成的德拜屏蔽长度
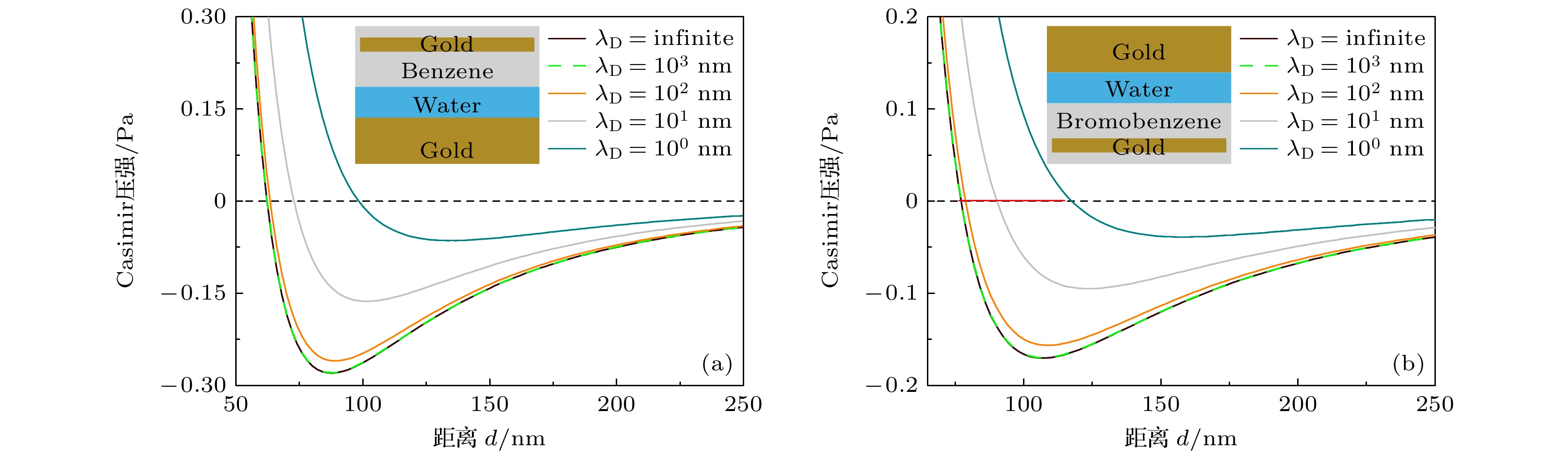
$ {\lambda _{\text{D}}} = 1000{\text{ nm}} $ [46]. 室温下, 当离子浓度从10–7 mol/L增大到10–3 mol/L时, 德拜屏蔽长度从1000 nm降低到10 nm. 双溶液系统下, 水中离子浓度可对Casimir力进行调制. 图5(a)为苯@水构成的双液体系统. 计算结果显示,$ {\lambda _{\text{D}}} = 1000 $ nm和$ {\lambda _{\text{D}}} = \infty $ (不考虑离子浓度)的Casimir压强曲线完全重叠, 说明此时离子电荷涨落对Casimir压强的影响可忽略. 但当λD从103 nm减少到100 nm过程中, Casimir压强受到调制变得明显, 平衡点的距离d逐渐约增大了35 nm. 虽然没有展示, 我们可知甲苯@水的双液体系统也有与图5(a)几乎完全一致的曲线特性. 倒置的溴苯@水系统的Casimir压强与λD的关系如图5(b)所示. 当λD从103 nm减少到100 nm过程中, 稳定Casimir平衡点移动了大约40 nm. 这些平衡点的移动有望通过光学F-P谐振腔的光谱进行探测[33]. -
本文提出了一种基于双液体的可调控Casimir平衡点的设计. 利用有机溶液(甲苯、苯或者溴苯)和水不相溶的特性, 结合金属衬底, 构成分层的双液体系统. 研究发现, 沉浸在甲苯或者苯溶液中的金属悬浮薄片具有稳定的Casimir平衡点, 由于甲苯和苯的介电常数十分接近, 这两种溶液中的金属薄片的Casimir平衡点相差只有约2 nm, 这对于Casimir平衡点的精细调控有一定的参考意义. 倒置的溴苯@水系统中的金属纳米薄片也具有Casimir平衡点. 这些Casimir平衡点距离液体分层界面的高度可通过水层的厚度人工调控. 最后, 讨论了系统温度和水中离子浓度对Casimir压强的影响, 发现离子浓度能较大范围内调控Casimir平衡点的高度. 在液体中, 悬浮的金纳米薄片(40 nm厚)所受的重力和浮力的总压强约为7 mPa[30], 对实际悬浮高度的影响很小, 相对于Casimir效应可忽略不计. 本文Casimir平衡点的调控方法可为微纳物体的“量子囚禁”, 以及微纳机电系统(MEMS)的实验提供理论指导.
双液体系统中的可调控Casimir平衡点
Tunable Casimir equilibria in dual-liquid system
-
摘要: 稳定的Casimir平衡点来源于Casimir能函数曲线在空间构成陷阱处的最小值. 本文提出了一种基于双液体的可调控Casimir平衡点. 在金属衬底上, 由于有机溶液和水之间的不相溶性, 形成分层液体体系. 密度低的溶液在上层, 而密度高的溶液在底层. 研究发现, 沉浸在甲苯或苯溶液中的金属悬浮薄片存在稳定的Casimir平衡点. 此外, 倒置的溴苯@水系统中也存在Casimir平衡点. 这些Casimir平衡点距离液体分层界面的高度可通过水层的厚度实现灵活调控. 最后, 还分析讨论了系统温度和水的离子浓度对Casimir平衡点的影响. 本文开辟了一种调控Casimir平衡点的新途径, 并对微纳尺度颗粒的“量子囚禁”具有重要意义.
-
关键词:
- Casimir平衡点 /
- 分层现象 /
- 悬浮 /
- 量子囚禁
Abstract: The Casimir effect, a macroscopic manifestation of quantum phenomena, arises from zero-point energy and thermal fluctuations. When two objects are brought into close proximity, the Casimir effect manifests as a repulsive force, while at greater separations, it transforms into an attractive force. There exists a specific distance at which the Casimir force vanishes, which is referred to as the stable Casimir equilibrium. Stable Casimir equilibrium arises from the curve minimum value of the Casimir energy, which can create spatial trapping. The manipulation of stable Casimir equilibrium provides promising applications in fields such as tunable optical resonators and self-assembly. This work presents a scheme for achieving tunable Casimir equilibrium in a dual-liquid system. The system comprises a multilayered stratified structure with a gold substrate. Above the gold substrate, a stratified liquid system is formed due to the immiscibility between organic solutions and water. The lower-density solution is at the top, while the higher-density solution is at the bottom. Our results suggest that a stable Casimir equilibrium for a suspended gold nanoplate can be realized, when the suspended gold nanoplate is immersed in organic solution of toluene or benzene. Moreover, the height of the suspended gold nanoplate, determined by the stable Casimir equilibrium, can be precisely tuned by changing the thickness of the water layer. The effects of finite temperature and ionic concentration on the Casimir equilibria are also analyzed in this work. The results suggest that the separation height of Casimir equilibrium decreases with the increase of temperature. Interestingly, when the Debye shielding length is comparable to or smaller than the separation length, the ion concentration in water significantly affects the Casimir pressure allowing for extensive modulations of Casimir equilibrium. This work opens up a new avenue for adjusting Casimir equilibrium and has important applications in “quantum trapping” of micro-nano particles.-
Key words:
- Casimir equilibria /
- stratification /
- suspensions /
- quantum trapping .
-
-
图 1 (a) 两不相溶液体中的Casimir悬浮示意图. 金纳米薄片距离液体分层界面为d. 溶液1的密度小于溶液2的密度; 而溶液2作为隔离层, 紧邻金属衬底且具有可调控厚度L. (b) 金、水、溴苯、苯和甲苯的介电常数随虚频率变化曲线
Figure 1. (a) Schematic diagram of Casimir suspension in two immiscible liquids. The distance between the gold nanoplate and the stratified liquid interface is d. The density of solution 1 is less than that of solution 2, while solution 2 acts as an isolation layer, close to the metal substrate and has a controllable thickness L. (b) Dielectric constants of gold, water, bromobenzene, benzene, and toluene change with the imaginary frequency.
图 2 悬浮金纳米薄片受到的Casimir压强 (a) 苯@水; (b) 甲苯@水; (c) 溴苯@水; (d)倒置的溴苯@水. 压力的正号表示排斥力, 负号表示吸引力. 金纳米薄片的厚度L0 = 40 nm, 系统温度T = 300 K
Figure 2. Casimir pressure acts on suspended metal nanoplates: (a) Benzene@water; (b) toluene@water; (c) bromobenzene@water; (d) tnverted bromobenzene@water. The positive sign of the pressure indicates repulsion, while the negative sign indicates attraction. Thickness of gold nanoplate L0 = 40 nm, and the temperature of system T = 300 K.
图 3 液体隔离层在有限厚度下, 双液体系统中金纳米薄片受到的Casimir压强 (a) 苯@水; (b) 甲苯@水; (c) 溴苯@水; (d) 倒置的溴苯@水
Figure 3. Casimir pressure acts on gold nanoplates in dual-liquid systems, where the layer thickness of liquid isolation is finite: (a) Benzene@water; (b) toluene@water; (c) bromobenzene@water; (d) inverted bromobenzene@water.
图 4 不同温度下的Casimir压强 (a) 苯@水; (b) 甲苯@水; (c) 溴苯@水; (d)倒置的溴苯@水. 液体隔离层L的厚度设定为100 nm
Figure 4. Casimir pressure at different temperatures: (a) Benzene@water; (b) toluene@water; (c) bromobenzene@water; (d) inverted bromobenzene@water. Thickness of the liquid isolation layer L is set to 100 nm.
图 5 不同德拜屏蔽长度下, Casimir压强随距离d的变化曲线 (a) 苯@水; (b) 倒置的溴苯@水. 液体隔离层L的厚度设定为100 nm, 系统温度T = 300 K
Figure 5. Casimir pressure changes with separation d under different Debye screening lengths: (a) Benzene@water; (b) inverted bromobenzene@water. Thickness of the liquid isolation layer L is set to 100 nm, and the system temperature T = 300 K.
-
[1] Casimir H B 1948 Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen (Vol. 51) p793 [2] 苗兵 2020 物理学报 69 080505 doi: 10.7498/aps.69.20200450 Miao B 2020 Acta Phys. Sin 69 080505 doi: 10.7498/aps.69.20200450 [3] Klimchitskaya G, Mohideen U, Mostepanenko V 2009 Rev. Mod. Phys. 81 1827 doi: 10.1103/RevModPhys.81.1827 [4] Lamoreaux S K 1997 Phys. Rev. Lett. 78 5 doi: 10.1103/PhysRevLett.78.5 [5] Mohideen U, Roy A 1998 Phys. Rev. Lett. 81 4549 doi: 10.1103/PhysRevLett.81.4549 [6] Garrett J L, Somers D A, Munday J N 2018 Phys. Rev. Lett. 120 040401 doi: 10.1103/PhysRevLett.120.040401 [7] Woods L, Dalvit D A R, Tkatchenko A, Rodriguez-Lopez P, Rodriguez A W, Podgornik R 2016 Rev. Mod. Phys. 88 045003 doi: 10.1103/RevModPhys.88.045003 [8] Rosa F S, Dalvit D A, Milonni P W 2008 Phys. Rev. Lett. 100 183602 doi: 10.1103/PhysRevLett.100.183602 [9] Song G, Zeng R, Al-Amri M, Xu J P, Zhu C J, He P F, Yang Y P 2018 Opt. Express 26 34461 doi: 10.1364/OE.26.034461 [10] Grushin A G, Cortijo A 2011 Phys. Rev. Lett. 106 020403 doi: 10.1103/PhysRevLett.106.020403 [11] Nie W J, Zeng R, Lan Y H, Zhu S Y 2013 Phys. Rev. B 88 085421 doi: 10.1103/PhysRevB.88.085421 [12] Chen L, Wan S L 2012 Phys. Rev. B 85 115102 doi: 10.1103/PhysRevB.85.115102 [13] Zhang Y C, Zhang H, Wang X X, Wang Y H, Liu Y C, Li S, Zhang T Y, Fan C, Zeng C G 2024 Nat. Phys. 20 1282 doi: 10.1038/s41567-024-02521-0 [14] Jiang Q D, Wilczek F 2019 Phys. Rev. B 99 125403 doi: 10.1103/PhysRevB.99.125403 [15] Hu Y, Wu X H, Liu H T, Ge W X, Zhang J H, Huang X Q 2024 ACS Photonics 11 1998 doi: 10.1021/acsphotonics.4c00129 [16] Gong T, Corrado M R, Mahbub A R, Shelden C, Munday J N 2020 Nanophotonics 10 523 doi: 10.1515/nanoph-2020-0425 [17] Bao F L, Shi K Z, Cao G J, Evans J S, He S L 2018 Phys. Rev. Lett. 121 130401 doi: 10.1103/PhysRevLett.121.130401 [18] Chen L, Chang K 2020 Phys. Rev. Lett. 125 047402 doi: 10.1103/PhysRevLett.125.047402 [19] Wang T B, Zhou Y, Mu H Q, Shehzad K, Zhang D J, Liu W X, Yu T B, Liao Q H 2022 Nanotechnology 33 245001 doi: 10.1088/1361-6528/ac59e6 [20] Yu T, You W, Wang T B, Yu T B, Liao Q H 2023 Results Phys. 52 106902 doi: 10.1016/j.rinp.2023.106902 [21] Wang L Q, Wu Y, Chen A X, Nie W J 2022 Results Phys. 41 105939 doi: 10.1016/j.rinp.2022.105939 [22] Wang Y P, Zhang Z C, Yu Y F, Zhang Z M 2019 Chin. Phys. B 28 014202 doi: 10.1088/1674-1056/28/1/014202 [23] Esteso V, Frustaglia D, Carretero-Palacios S, Míguez H 2024 Adv. Phys. Res. 3 2300065 doi: 10.1002/apxr.202300065 [24] Rodriguez A W, McCauley A P, Woolf D, Capasso F, Joannopoulos J D, Johnson S G 2010 Phys. Rev. Lett. 104 160402 doi: 10.1103/PhysRevLett.104.160402 [25] Ye Y Q, Hu Q, Zhao Q, Meng Y G 2018 Phys. Rev. B 98 035410 doi: 10.1103/PhysRevB.98.035410 [26] Liu X L, Zhang Z M 2016 Phys. Rev. Appl. 5 034004 doi: 10.1103/PhysRevApplied.5.034004 [27] Rahi S J, Kardar M, Emig T 2010 Phys. Rev. Lett. 105 070404 doi: 10.1103/PhysRevLett.105.070404 [28] Rong J N, Chen L, Chang K 2021 Chin. Phys. Lett. 38 084501 doi: 10.1088/0256-307X/38/8/084501 [29] Zhao R K, Li L, Yang S, Bao W, Xia Y, Ashby P, Wang Y, Zhang X 2019 Science 364 984 doi: 10.1126/science.aax0916 [30] Ge L X, Shi X, Xu Z J, Gong K 2020 Phys. Rev. B 101 104107 doi: 10.1103/PhysRevB.101.104107 [31] Ge L X, Shi X, Liu L, Gong K 2020 Phys. Rev. B 102 075428 doi: 10.1103/PhysRevB.102.075428 [32] Toyama H, Ikeda T, Iizuka H 2023 Phys. Rev. B 108 245402 doi: 10.1103/PhysRevB.108.245402 [33] Ge L X, Liu K P, Gong K, Podgornik R 2024 Phys. Rev. Appl. 21 044040 doi: 10.1103/PhysRevApplied.21.044040 [34] Esteso V, Carretero-Palacios S, Míguez H 2019 J. Phys. Chem. Lett. 10 5856 doi: 10.1021/acs.jpclett.9b02030 [35] Ge L X, Li B Z, Luo H, Gong K 2023 Phys. Rev. A 108 062814 doi: 10.1103/PhysRevA.108.062814 [36] Munkhbat B, Canales A, Kucukoz B, Baranov D G, Shegai T O 2021 Nature 597 214 doi: 10.1038/s41586-021-03826-3 [37] Krasnov M, Mazitov A, Orekhov N, Baranov D G 2024 Phys. Rev. B 109 195411 doi: 10.1103/PhysRevB.109.195411 [38] Küçüköz B, Kotov O V, Canales A, Polyakov A Y, Agrawal A V, Antosiewicz T J, Shegai T O 2024 Sci. Adv. 10 1825 doi: 10.1126/sciadv.adn1825 [39] Lifshitz E 1956 Sov. Phys. JETP-USSR 2 73 [40] Van Zwol P, Palasantzas G 2010 Phys. Rev. A 81 062502 doi: 10.1103/PhysRevA.81.062502 [41] Rodriguez A W, Woolf D, McCauley A P, Capasso F, Joannopoulos J D, Johnson S G 2010 Phys. Rev. Lett. 105 060401 doi: 10.1103/PhysRevLett.105.060401 [42] Munday J N, Capasso F, Parsegian V A 2009 Nature 457 170 doi: 10.1038/nature07610 [43] Dou M F, Lou F, Boström M, Brevik I, Persson C 2014 Phys. Rev. B 89 201407 doi: 10.1103/PhysRevB.89.201407 [44] Sehmi H S, Langbein W, Muljarov E A 2017 Phys. Rev. B 95 115444 doi: 10.1103/PhysRevB.95.115444 [45] Fiedler J, Bostrom M, Persson C, Brevik I, Corkery R, Buhmann S Y, Parsons D F 2020 J Phys. Chem. B 124 3103 doi: 10.1021/acs.jpcb.0c00410 [46] Wang Y F, Narayanan S R, Wu W 2017 ACS Nano 11 8421 doi: 10.1021/acsnano.7b04038 -
计量
- 文章访问数: 477
- HTML全文浏览数: 477
- PDF下载数: 2
- 施引文献: 0