高级搜索

不同相对湿度条件下复杂外混合气溶胶粒子群的光学特性

,  ,  , 

downloadPDF

上一篇

下一篇

王明军, 于记华, 白亮亮, 周熠铭. 不同相对湿度条件下复杂外混合气溶胶粒子群的光学特性[J]. 物理学报, 2025, 74(6): 064203-1. doi: 10.7498/aps.74.20241140
引用本文: 王明军, 于记华, 白亮亮, 周熠铭. 不同相对湿度条件下复杂外混合气溶胶粒子群的光学特性[J]. 物理学报, 2025, 74(6): 064203-1. doi: 10.7498/aps.74.20241140
shu
Mingjun WANG, Jihua YU, Liangliang BAI, Yiming ZHOU. Optical properties of ensemble of complex externally mixed aerosol particles under different relative humidity conditions[J]. Acta Physica Sinica, 2025, 74(6): 064203-1. doi: 10.7498/aps.74.20241140
Citation: Mingjun WANG, Jihua YU, Liangliang BAI, Yiming ZHOU. Optical properties of ensemble of complex externally mixed aerosol particles under different relative humidity conditions[J]. Acta Physica Sinica, 2025, 74(6): 064203-1. doi: 10.7498/aps.74.20241140
shu

不同相对湿度条件下复杂外混合气溶胶粒子群的光学特性

  • 1.

    西安理工大学自动化与信息工程学院, 西安　710048

  • 2.

    西安市无线光通信和网络研究重点实验室, 西安　710048

  • 3.

    陕西理工大学物理与电信工程学院, 汉中　723001

  • 4.

    新疆工程学院信息与工程学院, 乌鲁木齐　830091

    • 通讯作者: E-mail: yujh912@aliyun.com; 

  • 中图分类号: 42.25.Dd, 42.68.Mj, 92.60.Mt

Optical properties of ensemble of complex externally mixed aerosol particles under different relative humidity conditions

  • 1.

    School of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, China

  • 2.

    Xi'an Key Laboratory of Wireless Optical Communication and Network Research, Xi’an 710048, China

  • 3.

    School of Physics and Telecommunications Engineering, Shaanxi University of Technology, Hanzhong 723001, China

  • 4.

    School of Information Engineering, Xinjiang Institute of Engineering, Urumqi 830091, China

    • Corresponding author: E-mail: yujh912@aliyun.com.; 

  • MSC: 42.25.Dd, 42.68.Mj, 92.60.Mt

  • 摘要: 湿度环境下的气溶胶粒子群具有形状不一、成分不同、密度不等、复折射率多样、吸湿性参数不唯一、长短轴比不固定等复杂的微物理特性, 并且这些物理量会直接影响激光的传输和散射特性. 基于湿度环境下气溶胶粒子存在的各种可能性, 本文充分考虑了气溶胶粒子的形态(球形、扁椭球形、长椭球形、不规则形)、尺度谱、复折射率、密度、长短轴比及其分布模型、吸湿性参数等理化特性的多样性, 构建了一种复杂外混合气溶胶粒子群的光散射模型. 基于该光散射模型, 数值分析典型激光波长(0.78, 0.905, 1.064, 1.55, 2.1 μm)入射下不同混合比例和相对湿度对消光系数、单次散射反照率、不对称因子、散射相矩阵、后向散射系数、激光雷达比、线性退偏比等光学特性的影响. 结果表明: 消光系数、相函数P11对混合比例和相对湿度均表现出较强的敏感性, 且随着相对湿度的增大, 消光系数和相函数P11的前向散射也随之增大; 相比混合比例, 单次散射反照率、不对称因子对相对湿度更加敏感; 不同散射角处的线偏振、圆偏振特性对相对湿度和波长的敏感性差异显著; 后向散射系数和激光雷达比成反比, 且它们对混合比例和相对湿度均比较敏感, 相对湿度对线性退偏比的影响较大, 而混合比例的影响较弱. 本文所提出的复杂气溶胶光散射模型进一步丰富了气溶胶光学特性的研究, 为研究不同湿度环境下的大气物理、遥感探测、光通信等应用提供了理论支撑.
    Abstract: Microphysical quantities (particle shape, composition, size, density, complex refractive index, size distribution model, aspect ratio, hygroscopic parameter, etc.) of the ensemble of complex externally mixed aerosol particles vary greatly in humid environments (sea fog, water mist, haze, etc.). These microphysical quantities directly affect the transmission and scattering characteristics of laser. The optical properties (extinction coefficient, absorption coefficient, backscattering coefficient, phase function, etc.) of the ensemble of complex externally mixed aerosol particles directly determine the propagation properties of laser signals in the atmosphere, as well as the intensity and shape of echo signals. Therefore, studying the optical properties of the ensemble of complex externally mixed aerosol particles in humid environments is of significant importance for engineering applications such as autonomous driving, mapping, and remote sensing detection.Based on the various possibilities of aerosol particles existing in humid environments, the physicochemical properties of aerosol particles, including their shapes (sphere, oblate spheroid, prolate spheroid, and irregular), size distributions, complex refractive indices, densities, aspect ratios, their distribution models, and hygroscopicity parameters, are all taken into consideration in this work. Therefore, a scattering model of the ensemble of complex externally mixed aerosol particles is presented. Based on the presented complex aerosol scattering model, the influences of different mixing ratios (MR), and relative humidity (RH) on the optical properties, such as extinction coefficient, single scattering albedo, scattering phase matrix, asymmetry factor, backscattering coefficient, lidar ratio, and linear depolarization ratio, are numerically analyzed at typical incident laser wavelengths (0.78, 0.905, 1.064, 1.55, and 2.1 μm).In order to verify and demonstrate the rationality of the complex aerosol scattering model presented in this work, this model is compared with the scattering model of maritime pollution aerosol in optical properties of aerosols and clouds (OPAC). The results show that the optical properties of these two different aerosol scattering models vary similarly with wavelengths, although differences exist, but they are relatively small. Therefore, the influences of MR on the optical properties of the ensemble of complex internally mixed aerosol particles are analyzed. The influences of RH on the optical properties of the ensemble of complex internally mixed aerosol particles are also analyzed. The numerical results indicate that the extinction coefficient and phase function P11 exhibit strong sensitivity to both the MR and RH. As RH increases, the extinction coefficient and the forward scattering of P11 also increase. Compared with MR, single scattering albedo and asymmetry factor are more sensitive to RH. Significant differences in the sensitivity to RH and wavelength between linear and circular polarization properties are observed at different scattering angles. The backscattering coefficient is found to be inversely proportional to the lidar ratio, and the backscattering coefficient and the lidar ratio are both sensitive to MR and RH. It is observed that RH has a more pronounced effect on the linear depolarization ratio, while the influence of MR is weaker. The complex scattering model presented in this work further expands the study of aerosol optical properties and provides theoretical support for studying engineering applications involving lasers in different RHs environments. It is worth emphasizing that this work only focuses on external mixing. Therefore, the optical properties of the ensemble of complex internally mixed aerosol particles under different RHs will be discussed in the future.
  • 加载中

  • 图 1  气溶胶粒子形状　(a)球形; (b)扁椭球形; (c)长椭球形; (d)不规则形

    Figure 1.  Shapes of aerosol particles: (a) Sphere; (b) oblate spheroid; (c) prolate spheroid; (d) irregular.

    下载: 全尺寸图片 幻灯片

    图 2  椭球形气溶胶粒子　(a)长短轴比的示意图; (b)长短轴比的分布特征

    Figure 2.  Spheroid aerosol particles: (a) Diagram of aspect ratio; (b) distribution of aspect ratio.

    下载: 全尺寸图片 幻灯片

    图 3  比较不同气溶胶散射模型下的光学特性　(a)消光系数; (b)单次散射反照率; (c)不对称因子

    Figure 3.  Comparison of optical properties under different aerosol scattering models: (a) Extinction coefficient; (b) single scattering albedo; (c) asymmetry factor.

    下载: 全尺寸图片 幻灯片

    图 4  不同混合比例下的光学特性　(a)消光系数; (b)单次散射反照率; (c)不对称因子

    Figure 4.  Optical properties for different MRs: (a) Extinction coefficient; (b) single scattering albedo; (c) asymmetry factor.

    下载: 全尺寸图片 幻灯片

    图 5  入射波长为1.064 μm时不同混合比例下散射相矩阵随散射角的变化　(a) $ {P_{11}} $; (b) $ - {P_{12}}/{P_{11}} $; (c) $ {P_{22}}/{P_{11}} $; (d) $ {P_{33}}/{P_{11}} $; (e) $ {P_{34}}/{P_{11}} $; (f) $ {P_{44}}/{P_{11}} $

    Figure 5.  Scattering phase matrix vs. scattering angle for different MRs at λ = 1.064 μm: (a) $ {P_{11}} $; (b) $ - {P_{12}}/{P_{11}} $; (c) $ {P_{22}}/{P_{11}} $; (d) $ {P_{33}}/{P_{11}} $; (e) $ {P_{34}}/{P_{11}} $; (f) $ {P_{44}}/{P_{11}} $.

    下载: 全尺寸图片 幻灯片

    图 6  不同混合比例下的光学特性　(a)后向散射系数; (b)激光雷达比; (c)线性退偏比

    Figure 6.  Optical properties for different MRs: (a) Backscattering coefficient; (b) lidar ratio; (c) linear depolarization ratio.

    下载: 全尺寸图片 幻灯片

    图 7  典型激光波长入射下光学特性随相对湿度的变化　(a)消光系数; (b)单次散射反照率; (c)不对称因子

    Figure 7.  Changes of optical properties with RHs at typical laser wavelength incident: (a) Extinction coefficient; (b) single scattering albedo; (c) asymmetry factor.

    下载: 全尺寸图片 幻灯片

    图 8  入射波长为1.064 μm时不同相对湿度条件下散射相矩阵随散射角的变化　(a) $ {P_{11}} $; (b) $ - {P_{12}}/{P_{11}} $; (c) $ {P_{22}}/{P_{11}} $; (d) $ {P_{33}}/{P_{11}} $; (e) $ {P_{34}}/{P_{11}} $; (f) $ {P_{44}}/{P_{11}} $

    Figure 8.  Scattering phase matrix vs. scattering angle for different RHs at λ = 1.064 μm: (a) $ {P_{11}} $; (b) $ - {P_{12}}/{P_{11}} $; (c) $ {P_{22}}/{P_{11}} $; (d) $ {P_{33}}/{P_{11}} $; (e) $ {P_{34}}/{P_{11}} $; (f) $ {P_{44}}/{P_{11}} $.

    下载: 全尺寸图片 幻灯片

    图 9  RH为95%时典型激光波长入射下散射相矩阵随散射角的变化　(a) $ {P_{11}} $; (b) $ - {P_{12}}/{P_{11}} $; (c) $ {P_{22}}/{P_{11}} $; (d) $ {P_{33}}/{P_{11}} $; (e) $ {P_{34}}/{P_{11}} $; (f) $ {P_{44}}/{P_{11}} $

    Figure 9.  Scattering phase matrix vs. scattering angle at typical laser wavelength incident when RH is 95%: (a) $ {P_{11}} $; (b) $ - {P_{12}}/{P_{11}} $; (c) $ {P_{22}}/{P_{11}} $; (d) $ {P_{33}}/{P_{11}} $; (e) $ {P_{34}}/{P_{11}} $; (f) $ {P_{44}}/{P_{11}} $.

    下载: 全尺寸图片 幻灯片

    图 10  典型激光波长入射下光学特性随相对湿度的变化关系　(a)后向散射系数; (b)激光雷达比; (c)线性退偏比

    Figure 10.  Changes of optical properties with RHs at typical laser wavelength incident: (a) Backscattering coefficient; (b) lidar ratio; (c) linear depolarization ratio.

    下载: 全尺寸图片 幻灯片

    表 1  复杂外混合气溶胶粒子群的光散射模型

    Table 1.  Scattering model of the ensemble of complex externally mixed aerosol particles.

    Aerosol shape Aerosol density Hygroscopicity
    parameter    		 Aspect ratio Type of refractive
    index of aerosol    		 Log-normal distribution
    σ rmod
    Sphere 1.8 0.2 1 Water soluble 2.24 0.0212
    Spheroids 2.2 0.8 Ref. [16] Sea salt 2.03 0.209
    Spheroids 1.7 0.5 Ref. [17] Sulfate 2.03 0.0695
    Irregular 2.6 0 1.3 Mineral 2 0.5
    下载: 导出CSV
  • [1] Hess M, Koepke P, Schult I 1998 B. Am. Meteorol. Soc. 79 831 doi: 10.1175/1520-0477(1998)079<0831:OPOAAC>2.0.CO;2
    [2] 王莉 2022 硕士学位论文 (武汉: 武汉科技大学) Wang L 2022 M. S. Thesis (Wuhan: Wuhan University of Science and Technology
    [3] 赵佳佳, 顾芳, 张加宏, 崔芬萍 2020 光学学报 40 0501001 doi: 10.3788/AOS202040.0501001 Zhao J J, Gu F, Gu J H, Cui F P 2020 Acta Opt. Sin. 40 0501001 doi: 10.3788/AOS202040.0501001
    [4] Koepke P, Gasteiger J, Hess M 2015 Atmos. Chem. Phys. 15 5947 doi: 10.5194/acp-15-5947-2015
    [5] Tao Z M, Wang Z Z, Yang S J, Shan H H, Ma X M, Zhang H, Zhao S G, Liu D, Xie C B, Wang Y J 2016 Atmos. Meas. Tech. 9 1369 doi: 10.5194/amt-9-1369-2016
    [6] Lian W T, Dai C M, Chen S P, Zhang Y X, Wu F, Zhang C, Wang C, Wei H L 2024 Remote Sens. 16 770 doi: 10.3390/rs16050770
    [7] Petters M D, Kreidenweis S M 2007 Atmos. Chem. Phys. 7 1961 doi: 10.5194/acp-7-1961-2007
    [8] Zieger P, Fierz-Schmidhauser R, Weingartner E, Baltensperger U 2013 Atmos. Chem. Phys. 13 10609 doi: 10.5194/acp-13-10609-2013
    [9] Gasteiger J, Wiegner M 2018 Geosci. Model Dev. 11 2739 doi: 10.5194/gmd-11-2739-2018
    [10] 张学海, 戴聪明, 张鑫, 魏合理, 朱希娟, 马静 2019 红外与激光工程 48 0809002 doi: 10.3788/IRLA201948.0809002 Zhang X H, Dai C M, Zhang X, Wei H L, Zhu X J, Ma J 2019 Infrar. Laser Eng. 48 0809002 doi: 10.3788/IRLA201948.0809002
    [11] 战俊彤, 张肃, 付强, 段锦, 李英超, 姜会林 2020 红外与激光工程 49 20200057 doi: 10.3788/IRLA20200057 Zhan J T, Zhang S, Fu Q, Duan J, Li Y C, Jiang H L 2020 Infrar. Laser Eng. 49 20200057 doi: 10.3788/IRLA20200057
    [12] Shen C, Zhang S, Fu Q, Zhan J T, Duan J, Li Y C 2023 Front. Phys. 11 1266027 doi: 10.3389/fphy.2023.1266027
    [13] Wu S X, Gao X B, Dou X Q, Xie L 2024 J. Quant. Spectrosc. Radiat. Transfer 312 108808 doi: 10.1016/j.jqsrt.2023.108808
    [14] Gasteiger J, Wiegner M, Groß S, Freudenthaler V, Toledano C, Tesche M, Kandler K 2011 Tellus B: Chem. Phys. Meteorol. 63 725 doi: 10.1111/j.1600-0889.2011.00559.x
    [15] 张学海, 魏合理, 戴聪明, 曹亚楠, 李学彬 2015 物理学报 22 224205 doi: 10.7498/aps.64.224205 Zhang X H, Wei H L, Dai C M, Cao Y N, Li X B 2015 Acta Phys. Sin. 22 224205 doi: 10.7498/aps.64.224205
    [16] Dubovik O, Sinyuk A, Lapyonok T, Holben B N, Mishchenko M, Yang P, Eck T F, Volten H, Muñoz O, Veihelmann B, Van der Zande W J, Leon J F, Sorokin M, Slutsker I 2006 J. Geophys. Res. 111 D11208 doi: 10.1029/2005JD006619
    [17] Kandler K, Schütz L, Deutscher C, Ebert M, Hofmann H, Jäckel S, Jaenicke R, Knippertz P, Lieke K, Massling A, Petzold A, Schladitz B, Weinzierl A, Wiedensohler, Zorn S, Weinbruch1 S 2009 Tellus B 61 32 doi: 10.1111/j.1600-0889.2008.00385.x
    [18] Li L, Zheng X, Li Z Q, Li Z H, Dubovik O, Chen X F, Wendisch M 2017 Opt. Express 25 A813 doi: 10.1364/OE.25.00A813
    [19] 王明军, 吴振森, 李应乐, 张小安, 由金光 2006 红外与激光工程 35 66 doi: 10.3969/j.issn.1007-2276.2006.01.014 Wang M J, Wu Z S, Li Y L, Zhang X, You J G 2006 Infrar. Laser Eng. 35 66 doi: 10.3969/j.issn.1007-2276.2006.01.014
    [20] Wang M J, Yu J H, Ke X Z, Wu T 2018 Progress in Electromagnetics Research Symposium Toyama, Japan, August 1−4, 2018 p1141
    [21] Meng Z, Yang P, Kattawar G W, Bi L, Liou K N, Laszlo I 2010 J. Aerosol Sci. 41 501 doi: 10.1016/j.jaerosci.2010.02.008
    [22] Jung C H, Lee J Y, Um J, Lee S S, Yoon Y J, Kim Y P 2019 Appl. Sci. 9 1443 doi: 10.3390/app9071443
    [23] Castellanos P, Colarco P, Espinosa W R, Guzewich S D, Levy R C, Miller R L, Chin M, Kahn R A, Kemppinen O, Moosmüller H, Nowottnick E P 2024 Remote Sens. Environ. 303 113982 doi: 10.1016/j.rse.2023.113982
    [24] Liou K N, Yang P 2016 Light Scattering by Ice Crystals: Fundamentals and Applications (Cambridge: Cambridge University Press) pp100, 101
    [25] Akpootu D O, Bello G, Alaiyemola S R, Abdullahi Z, Aruna S, Umar M, Badmus T O, Isah A K, Abdulsalam M K, Aminu Z 2023 DUJOPAS 9 86 doi: 10.4314/dujopas.v9i2b.10
  • 加载中
图( 10) 表( 1)
计量
  • 文章访问数:  30
  • HTML全文浏览数:  30
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-15
  • 刊出日期:  2025-03-20

不同相对湿度条件下复杂外混合气溶胶粒子群的光学特性

    通讯作者: E-mail: yujh912@aliyun.com; 
  • 1. 西安理工大学自动化与信息工程学院, 西安　710048
  • 2. 西安市无线光通信和网络研究重点实验室, 西安　710048
  • 3. 陕西理工大学物理与电信工程学院, 汉中　723001
  • 4. 新疆工程学院信息与工程学院, 乌鲁木齐　830091
  • 收稿日期:  2024-08-15

摘要: 湿度环境下的气溶胶粒子群具有形状不一、成分不同、密度不等、复折射率多样、吸湿性参数不唯一、长短轴比不固定等复杂的微物理特性, 并且这些物理量会直接影响激光的传输和散射特性. 基于湿度环境下气溶胶粒子存在的各种可能性, 本文充分考虑了气溶胶粒子的形态(球形、扁椭球形、长椭球形、不规则形)、尺度谱、复折射率、密度、长短轴比及其分布模型、吸湿性参数等理化特性的多样性, 构建了一种复杂外混合气溶胶粒子群的光散射模型. 基于该光散射模型, 数值分析典型激光波长(0.78, 0.905, 1.064, 1.55, 2.1 μm)入射下不同混合比例和相对湿度对消光系数、单次散射反照率、不对称因子、散射相矩阵、后向散射系数、激光雷达比、线性退偏比等光学特性的影响. 结果表明: 消光系数、相函数P11对混合比例和相对湿度均表现出较强的敏感性, 且随着相对湿度的增大, 消光系数和相函数P11的前向散射也随之增大; 相比混合比例, 单次散射反照率、不对称因子对相对湿度更加敏感; 不同散射角处的线偏振、圆偏振特性对相对湿度和波长的敏感性差异显著; 后向散射系数和激光雷达比成反比, 且它们对混合比例和相对湿度均比较敏感, 相对湿度对线性退偏比的影响较大, 而混合比例的影响较弱. 本文所提出的复杂气溶胶光散射模型进一步丰富了气溶胶光学特性的研究, 为研究不同湿度环境下的大气物理、遥感探测、光通信等应用提供了理论支撑.

English Abstract

    全文HTML

    1.   引　言

    • 根据气溶胶粒子吸湿特征的强弱, 可将其分为非吸湿性气溶胶和吸湿性气溶胶, 其中吸湿性气溶胶包括水溶性(water soluble)、海盐性(sea salt)、硫酸盐性(sulfate)等粒子[1,2], 由于这些气溶胶粒子在湿度条件下能够吸收水分, 出现了吸湿增长现象, 导致粒子的物理和光学特性发生变化[3–5], 从而影响了激光的传输和散射. 毫无疑问, 湿度环境下(如海雾、水雾、雾霾等环境)下气溶胶粒子的种类不一, 成分复杂[6], 不可避免地对复杂混合气溶胶粒子群光学特性的模拟提出了挑战. 因此, 深入分析和量化相对湿度对气溶胶粒子群光学特性的影响, 这对于大气物理、遥感探测、光通信等领域具有重要的理论和实际意义.

      相对湿度、吸湿性参数、尺寸、密度、复折射率、形状、尺度分布模型等物理量对气溶胶光学特性影响的典型研究主要有: Hess等[1]基于Mie理论计算了气溶胶和云的光学特性(optical properties of aerosols and clouds, OPAC), 并提供了吸湿性气溶胶粒子在不同相对湿度(relative humidity, RH)下的复折射率, 基于OPAC可数值模拟吸湿性球形气溶胶粒子的光学特性. Petters和Kreidenweis [7]、Zieger等[8]分别基于$ \kappa $-Köhler理论和实地收集的大量数据, 提出了吸湿性气溶胶粒子的增长规律. 依据OPAC提供的气溶胶类型[1]. Gasteiger和Wiegner [9]数值分析了陆地型、沙漠型、海洋型、极地型吸湿性球形气溶胶的光学特性与相对湿度之间的变化关系. 张学海等[10]根据海盐气溶胶粒子在低、中、高湿度条件下的不同形态, 建立了不同的海盐气溶胶粒子光散射模型, 并采用离散偶极子近似(discrete dipole approximation, DDA)、Mie理论研究了相对湿度和粒子形态对海盐气溶胶光学特性的影响. 赵佳佳等[3]基于热力学、表面吸附理论分别建立了亲水性、疏水性气溶胶的吸湿增长模型, 并结合DDA数值计算了相对湿度为40%—90%范围内这两类气溶胶的光散射特性. 战俊彤等[11]比较和分析了不同湿度水雾环境下450, 532, 671 nm 线偏振光和圆偏振光的偏振特性, 表明偏振光的偏振度随水雾环境的湿度整体呈下降趋势. 王莉[2]根据亲水性、疏水性气溶胶的吸湿增长规律, 建立了气溶胶粒子的散射吸湿模型, 还进一步分析了不同相对湿度下气溶胶的辐射特性. Shen等[12]利用Mie理论、Monte Carlo法研究了不同相对湿度(0%, 10%, 40%, 95%)下油烟粒子的Mueller矩阵变化情况以及偏振特性. Wu等[13]在室内开展了不同相对湿度条件下激光在沙尘环境中的传输实验, 实验结果表明, 当相对湿度高于60%时, 沙尘粒子的吸湿增长对激光传输有明显的衰减作用. Lian等[6]根据不同湿度条件下海盐气溶胶粒子的各种形态和复折射率模型, 并结合对数正态尺度分布谱, 采用T矩阵计算了3种相对湿度(50%, 80%, 95%)条件下椭球形、圆柱形等海盐气溶胶粒子在波长1.06 μm处的光散射与偏振特性. 除了相对湿度、吸湿性参数、复折射率等物理量之外, 气溶胶的长短轴比及其分布特征对气溶胶光学特性的影响也不容忽视. 除了某一固定长短轴比之外[6,14,15], Dubovik等[16]、Kandler等[17]、Li等[18]基于大量的实测气溶胶数据, 提出了气溶胶的长短轴比分布(aspect ratio distribution)模型, 并分析了气溶胶的长短轴比及其分布模型对气溶胶光散射特性的影响. 王明军团队在复杂环境(如沙尘、烟雾、烟幕等复杂环境)下激光散射特性方面的研究也取得了不错的成果, 他们不仅计算了复杂目标在复杂环境下激光回波能量随不同观测角度和能见度的变化情况[19]; 还计算了长椭球型、扁椭球型雾霾粒子的激光散射特性, 给出了1.06 μm激光入射下稀薄随机分布雾霾气溶胶粒子的微分散射截面[20].

      然而, 上述研究成果所提出的不同相对湿度下气溶胶的光散射模型相对比较单一, 仅聚焦于一种或少数几种物理量的作用, 未能完全表征出不同湿度环境下气溶胶粒子的多样性. 为弥补这一不足, 本文提出了一种更为精细的复杂外混合气溶胶光散射模型, 其可精细地表征不同相对湿度条件下气溶胶粒子的多样性和复杂性(如气溶胶的形状、复折射率、密度、吸湿性参数等); 随后数值分析了典型激光波长入射下不同相对湿度、混合比例对复杂外混合气溶胶粒子群光学特性的影响, 这为研究极端恶劣环境下的激光工程应用提供了有价值的见解.

    2.   理论基础

      2.1.   气溶胶的吸湿增长模型

    • 根据$ \kappa $-Köhler理论以及实地收集的大量气溶胶, 相对湿度(RH)与吸湿性参数$ \kappa $、粒子尺寸之间的关系可表示为[7,8]

      式中, $ {r_{{\text{dry}}}} $为干燥时气溶胶粒子的尺寸, $ {r_{{\text{wet}}}}\left( {{\text{RH}}} \right) $为特定相对湿度下气溶胶粒子的尺寸. 由(1)式可知, 当RH大于0%且$ \kappa $大于0时, $ r_\text{wet} (\text{RH}) \gt r_\text{dry} $, 即气溶胶出现吸湿增长.

      • 2.2.   复杂外混合气溶胶粒子群的光散射模型

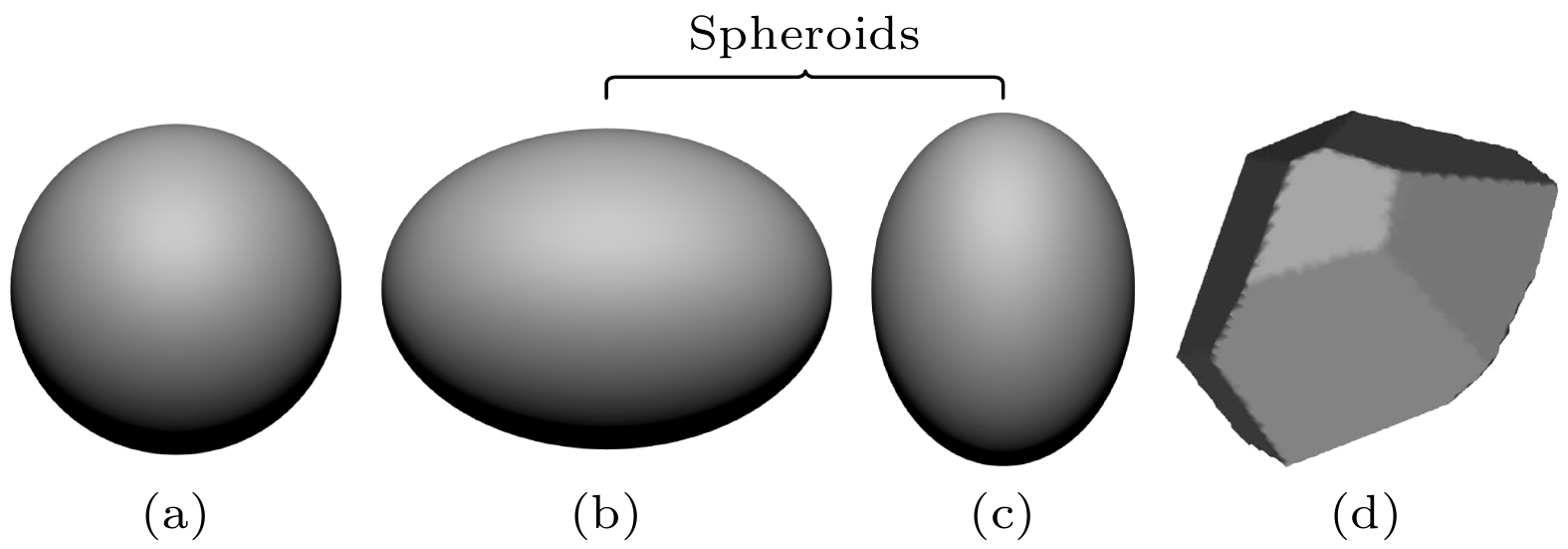
    • 气溶胶粒子的形状如图1所示, 本文考虑了球形(sphere)、扁椭球形(oblate spheroid)、长椭球形(prolate spheroid)、不规则形(irregular)这4种不同形状的气溶胶. 可以采用Mie理论、T矩阵、DDA分别数值计算球形、椭球形、不规则形粒子的光学特性, 它们在不同粒径、波长下的光散射特性具体可阅读文献[1,4,14,21]. 在获得单个粒子散射特性的基础上, 要完整地分析整个气溶胶粒子群的光学特性, 必须将所有尺寸的气溶胶考虑在内, 在实际的应用中, 普遍采用对数正态分布来表征气溶胶粒子的尺度分布特征[1,2,6,9],

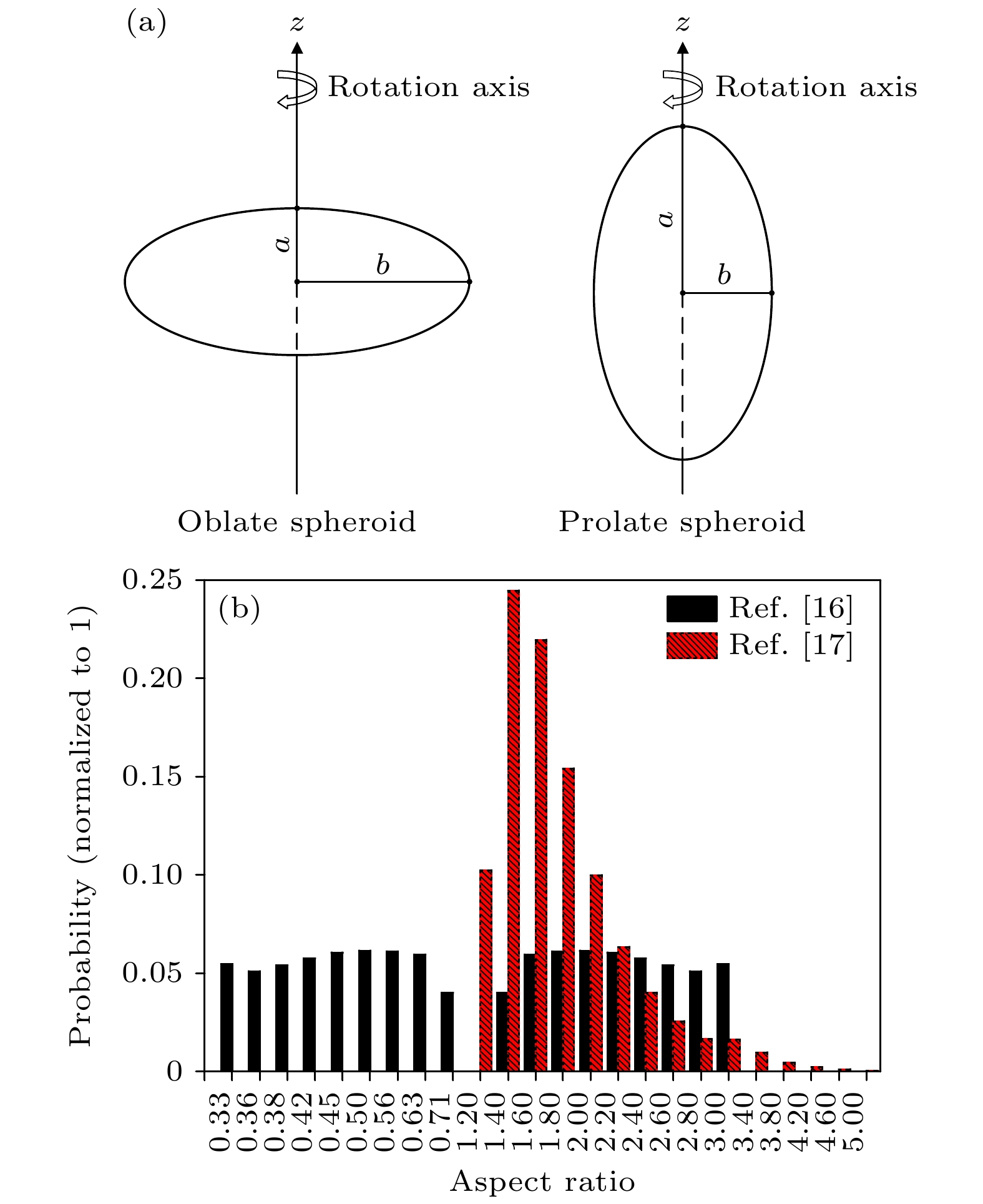
      式中, $ n\left( r \right) $为粒子尺度谱, $ {N_0} $为单位体积内的总数密度, σ为标准差, $ {r_{\text{mod} }} $为模态半径[1,6].

      除了气溶胶粒子的形状、对数正态分布模型之外, 本文还将不同的密度、不同吸湿性参数、不同复折射率、不同长短轴比及其分布模型等物理量考虑在内, 将这些物理量全部混合在一起, 就构成了如表1所列的复杂外混合气溶胶粒子群的光散射模型. 由表1可知, 本文提出了一种精细的复杂外混合气溶胶光散射物理模型, 该物理模型考虑了4种不同气溶胶粒子形状、具有4种不同参量的对数正态分布模型、4种不同密度、4种不同吸湿性参数、4种不同气溶胶类型(水溶性、海盐性、硫酸盐性、矿物性)的复折射率和4种不同的长短轴比(2种固定的长短轴比、由扁椭球和长椭球混合而成的椭球(spheroid)混合物分别使用2种不同的长短轴比分布模型(aspect ratio distribution)[16,17], 长短轴比的示意图和分布模型分别如图2(a), (b)所示, 其中z为旋转轴; $ a/b $表示为长短轴比, $ a/b > 1 $为长椭球, $ 0 < a/b < 1 $为扁椭球, $ a/b = 1 $为球形).

      在考虑多种气溶胶的类型、形状、复折射率、密度、吸湿性参数等物理量的基础上, 根据外混合方式, 按照每种成分的混合比例进行累加[22,23], 可得到复杂外混合气溶胶粒子群的消光系数$ {\beta _{{\text{ext}}}} $、散射系数$ {\beta _{{\text{sca}}}} $、单次散射反照率$ {\omega _0} $、不对称因子g、散射相矩阵P分别为

      式中r为粒子的等效半径; $ {r_{\max }} $和$ {r_{\min }} $分别为粒子的最大、最小半径; $ {C_{{\text{ext, }} j}} $和$ {C_{{\text{sca}}, j}} $分别为第j类气溶胶粒子的消光截面和散射截面; $ {n_j}\left( r \right) $为上文介绍的4种对数正态尺度分布模型, 如表1所列, 这4种对数正态分布的参量$ {N_0} $, $ {r_{\text{mod} }} $, σ的取值均不同; $ f\left( j \right) $为第j类气溶胶粒子的混合比例, 且$ \displaystyle\sum\nolimits_{j = 1}^J {f\left( j \right)} = 1 $; $ {g_j}\left( r \right) $为第j类气溶胶粒子的不对称因子; θ为散射角; 一般来说, 直接分析散射相矩阵P矩阵中的P11(相函数), P12, P22, P33, P43, P44这6个元素是很少见的. 在实际的应用中(如大气辐射传输等应用中), 常常分析$ {P_{11}} $, $ - {P_{12}}/{P_{11}} $, $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{34}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $随散射角的变化关系, 它们的物理含义分别为[6,23,24]: 相函数$ {P_{11}} $表示散射光在各个方向上的强度分布; $ - {P_{12}}/{P_{11}} $表示入射光为非偏振光时散射线偏振分量的偏振度; $ {P_{22}}/{P_{11}} $表示退偏振或交叉偏振的强度分量与总散射强度的比值; $ {P_{33}}/{P_{11}} $和$ {P_{44}}/{P_{11}} $分别表示当左旋圆偏振光、右旋圆偏振光入射时散射光的圆偏振特性; $ {P_{34}}/{P_{11}} $表示当入射光以–45°线性偏振时, 圆偏振光强与散射总光强的比值.

      基于外混合方式计算得到的消光系数$ {\beta _{{\text{ext}}}} $、单次散射反照率$ {\omega _0} $、散射相矩阵P这些光学特性, 可进一步得到复杂外混合气溶胶粒子群的后向 散射系数$ {\beta _{\text{b}}} $、激光雷达比S、线性退偏比$ {\delta _{\text{l}}} $分别 为[9,23]

    3.   数值结果与分析

      3.1.   与OPAC中海洋污染型气溶胶光散射 模型的对比

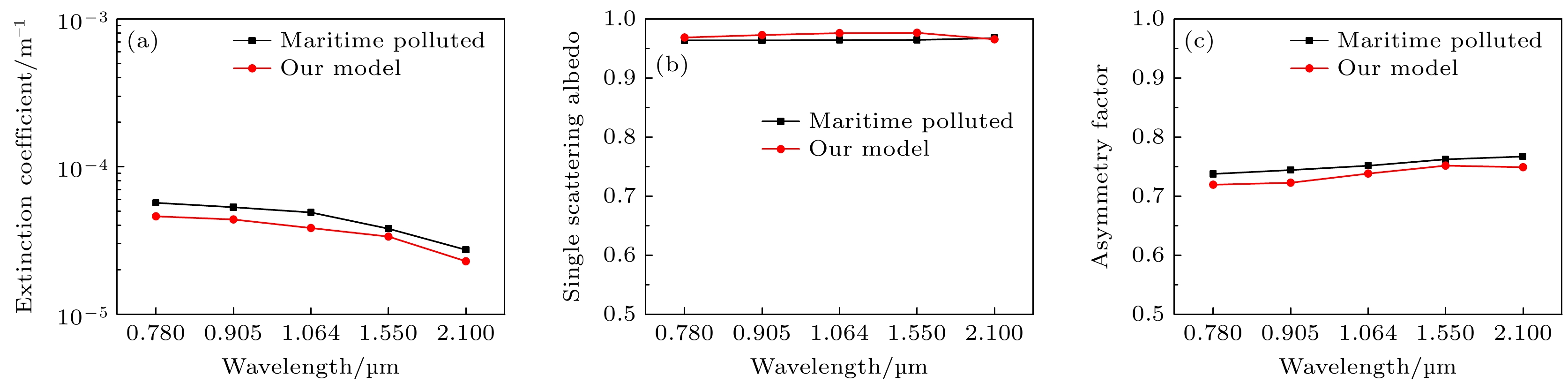
    • OPAC中的海洋污染型(maritime polluted)气溶胶光散射模型假定粒子形状为球形, 还将不同种类的气溶胶、相对湿度、吸湿性参数、密度等物理量囊括在内, 与本文应用场景很契合, 可用于验证和说明本文所提出的复杂外混合溶胶粒子群模型的合理性. 当采用体积V与平均投影面积A之比的等效半径$ {r_{V/A}} = 3 V/(4A) $时[14], 利用Mie理论、T矩阵、DDA可分别求得单个球形、椭球形、不规则形气溶胶粒子的光学特性. 在获得单个粒子散射特性的基础上, 结合(2)式表征的尺度谱和外混合方式下水溶性、海盐性、硫酸盐性、矿物性气溶胶粒子的混合比例(mixing ratio, MR)为38%∶2%∶51.8%∶8.2%时(将此混合比例记为MR1), 即可数值模拟第2节中所提出的复杂外混合气溶胶粒子群的光学特性.

      当相对湿度为70%时, 图3比较了典型激光波长(0.78, 0.905, 1.064, 1.55, 2.1 μm)入射下这两种不同气溶胶散射模型光学特性的差异. 由图3可知, 这两种不同气溶胶散射模型下消光系数、单次散射反照率、不对称因子随波长的变化很相似, 虽然存在着差异, 但总体来说差异较小. 值得强调的是, 海洋污染型气溶胶光散射模型是基于气溶胶粒子为球形的假设, 但这一设定忽略了气溶胶粒子通常呈现的非球形和不规则形态, 与实际情况不符. 而本文将非球形、不规则形的气溶粒子考虑在内, 恰好弥补了这一不足. 因此本文所提出的复杂外混合气溶胶光散射模型是一种更为精细的物理模型, 其可以精细地描述大气中气溶胶粒子的多样性和复杂性(如气溶胶的形状、尺度分布、复折射率、密度等), 从而提高复杂恶劣环境下光散射过程模拟的准确度.

      • 3.2.   混合比例对复杂外混合气溶胶粒子群光学特性的影响

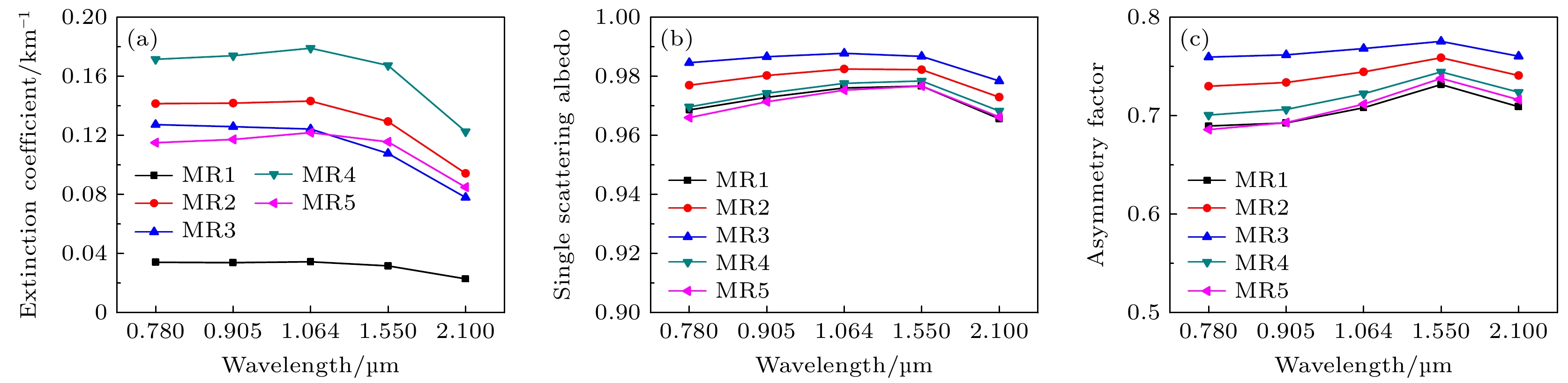
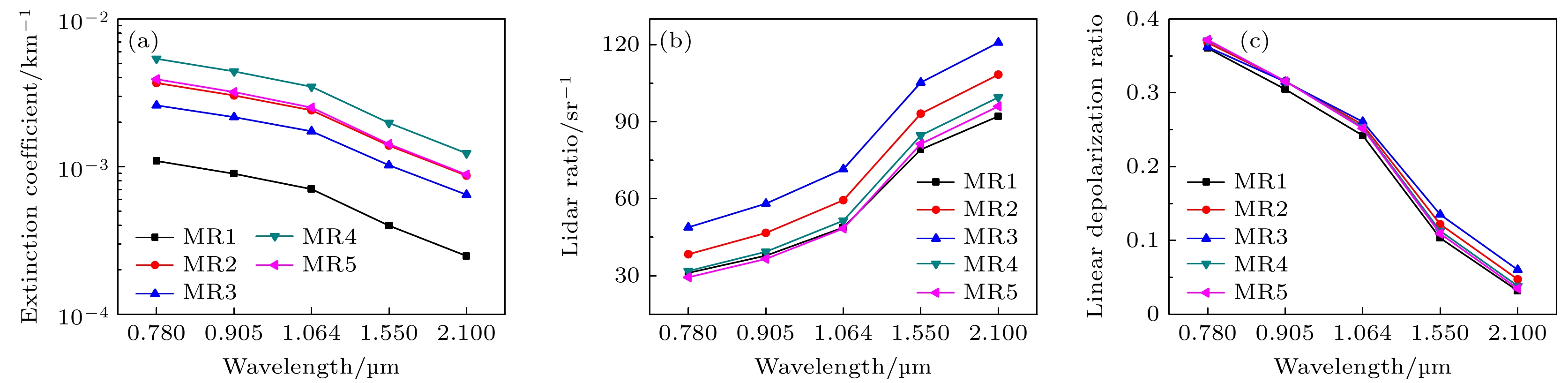
    • 除了使用图3给定的参数外, 另外再取其他4种混合比例25%∶25%∶25%∶25%, 20%∶30%∶35%∶15%, 10%∶20%∶30%∶40%, 40%∶10%∶30%∶20%, 并将它们分别记为MR2, MR3, MR4, MR5, 以进行混合比例对复杂外混合气溶胶粒子群光学特性的敏感性分析.

      图4(a)—(c)给出了不同混合比例下复杂外混合气溶胶粒子群的消光系数、单次散射反照率、不对称因子. 由图4(a)—(c)可知: 1)与消光系数相比, 单次散射反照率和不对称因子对混合比例的变化不敏感; 2)不同混合比例下复杂外混合气溶胶粒子群的光学特性表现出了明显差异, 尤其是不同波长下消光系数随混合比例的调整呈现出显著差异. 因此, 通过不断优化混合比例, 可以实现对光学特性(如消光系数)的有效调控, 从而满足特定应用场景对光散射特性模拟的需求.

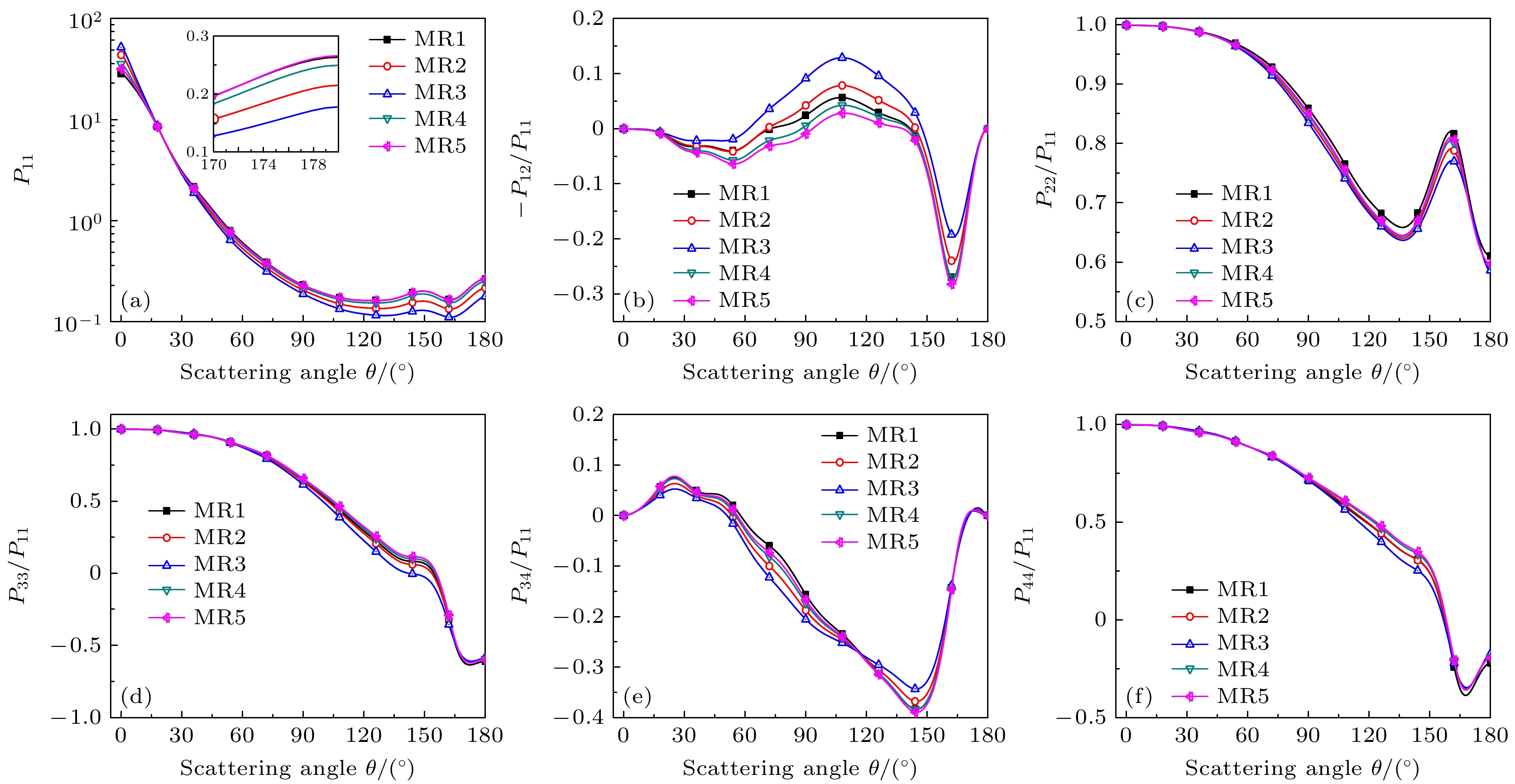
      当入射波长为1.064 μm时, 图5给出了不同混合比例下复杂外混合气溶胶粒子群的散射相矩阵元素$ {P_{11}} $(相函数), $ - {P_{12}}/{P_{11}} $, $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{34}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $随散射角的变化. 由图5(a)可知, 不同混合比例下$ {P_{11}} $的前向散射和后向散射均有明显的差异; 由图5(b)可知, 在60°—170°散射角范围内, $ - {P_{12}}/{P_{11}} $对混合比例比较敏感; 由图5(c)—(f)可知, 元素$ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{34}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $对混合比例均不敏感, 这是由于圆偏振特性主要受气溶胶形状和气溶胶自身的微物理性质主导, 混合比例对其影响较小. 综上, 散射相矩阵中的不同元素对混合比例的敏感性不同, 其中散射强度和偏振度对混合比例较为敏感, 而圆偏振特性表现出较小的差异.

      图6(a)—(c)给出了不同混合比例下复杂外混合气溶胶粒子群的后向散射系数、激光雷达比、线性退偏比. 由图6(a)—(c)可知: 1)不同混合比例下后向散射系数随波长的增大呈现逐渐下降的趋势, 但激光雷达比随波长的增大表现出逐渐上升的趋势, 这两幅图的曲线走势表明了激光雷达比(其定义为消光系数与后向散射系数之比[23])与后向散射系数成反比, 这一数值结果与物理意义完全自洽. 2)后向散射系数和激光雷达比对混合比例的变化较为敏感, 但混合比例对线性退偏比的影响较弱, 这表明线性退偏比主要由气溶胶粒子的形状和类型决定.

      • 3.3.   相对湿度对复杂外混合气溶胶粒子群光学特性的影响

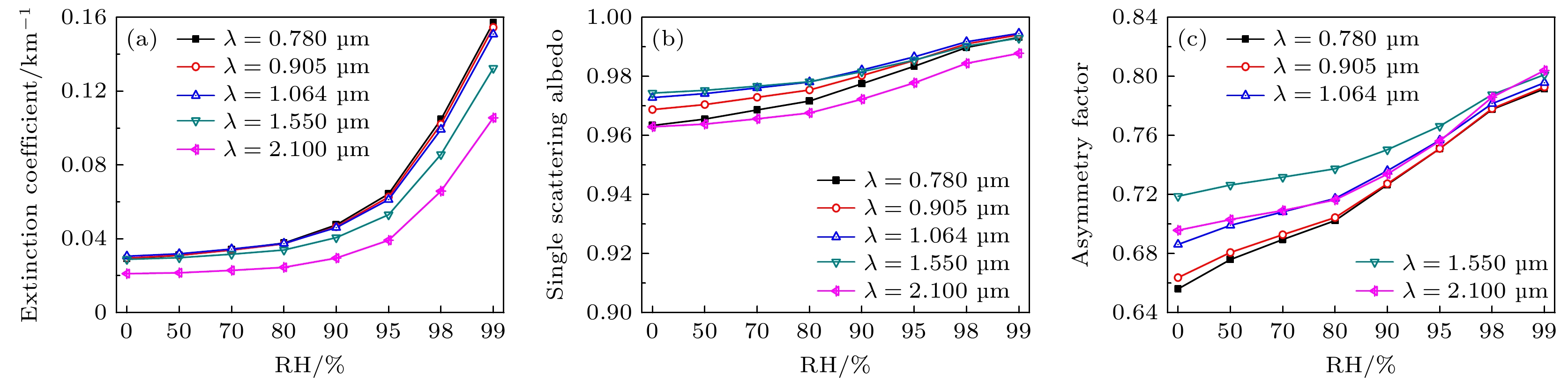
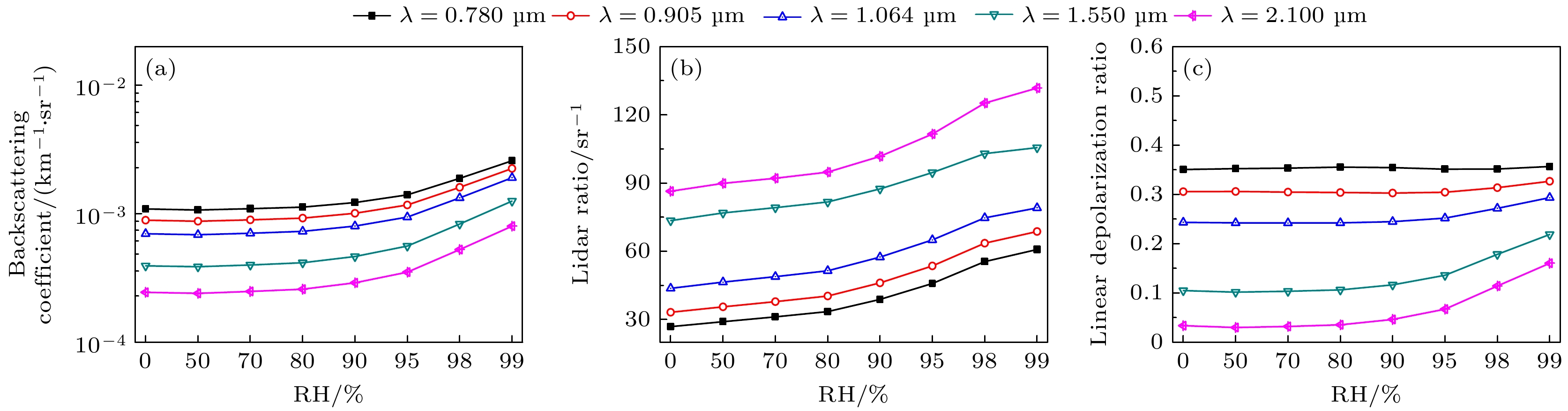
    • 除了使用图3给定的参数外, 结合OPAC提供的8种相对湿度(0%, 50%, 70%, 80%, 90%, 95%, 98%, 99%)以及这8种相对湿度条件下不同气溶胶类型的复折射率[1], 进一步数值分析典型激光波长入射下复杂外混合气溶胶粒子群的光学特性与相对湿度RH之间的变化关系.

      图7(a)—(c)给出了典型激光波长入射下复杂外混合气溶胶粒子群的消光系数、单次散射反照率、不对称因子随相对湿度的变化. 由图7(a)可知, 不同波长下消光系数的变化规律较为相似, 但短波长的消光系数略高于长波长. 当波长一定时, 随着相对湿度的增大, 消光系数也随之增大, 尤其相对湿度大于80%时, 消光系数呈指数增长, 这一现象与文献[25]中的结论一致, 但其仅考虑了球形吸湿性气溶胶粒子, 且所采用的光散射模型比较单一. 由图7(b)可知, 在整个相对湿度范围内, 各波长下的单次散射反照率随相对湿度的增大而略有增大, 且值始终保持在 0.96 以上. 其一是由于这些典型激光波长所对应气溶胶粒子复折射率的虚部较小, 即吸收作用较小, 衰减主要是由散射造成的; 其二是由于水分子折射率的虚部一般要比气溶胶折射率的虚部小[6], 气溶胶在湿度环境下发生了吸湿增长, 使其折射率的虚部进一步减小, 从而使单次散射反照率略微增大. 由图7(c)可知: 不对称因子随相对湿度的增大而增大, 这是由于吸湿增长使得粒子的尺寸增大, 从而使得前向散射随之增强. 在高湿度条件下(RH大于90%时), 2.1 μm波长下的不对称因子高于其他波长. 这是由于气溶胶粒子因吸湿膨胀而增长到与2.1 μm波长相近的尺寸, 导致前向散射显著增强, 使得该波长下的不对称因子显著增大.

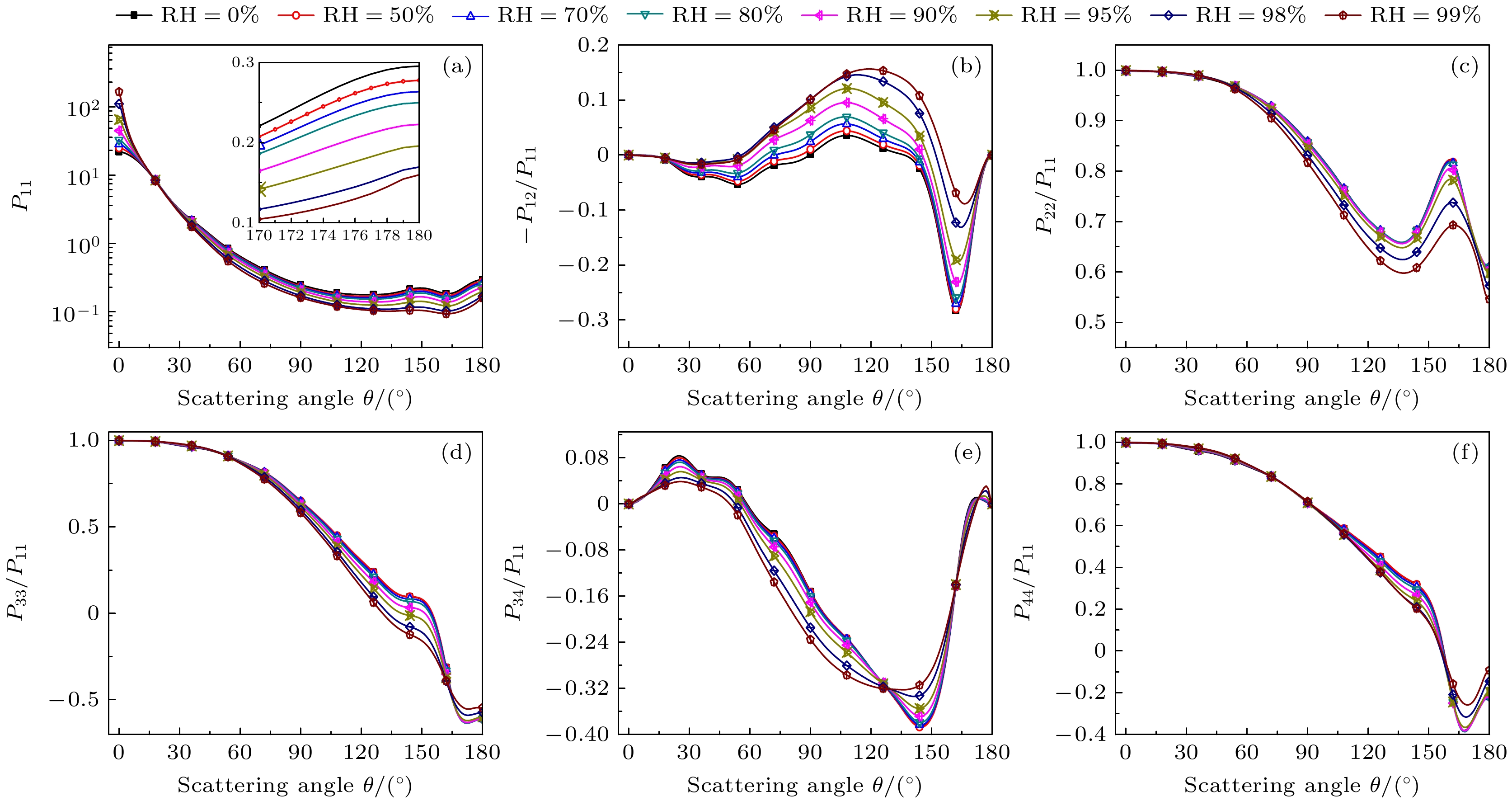
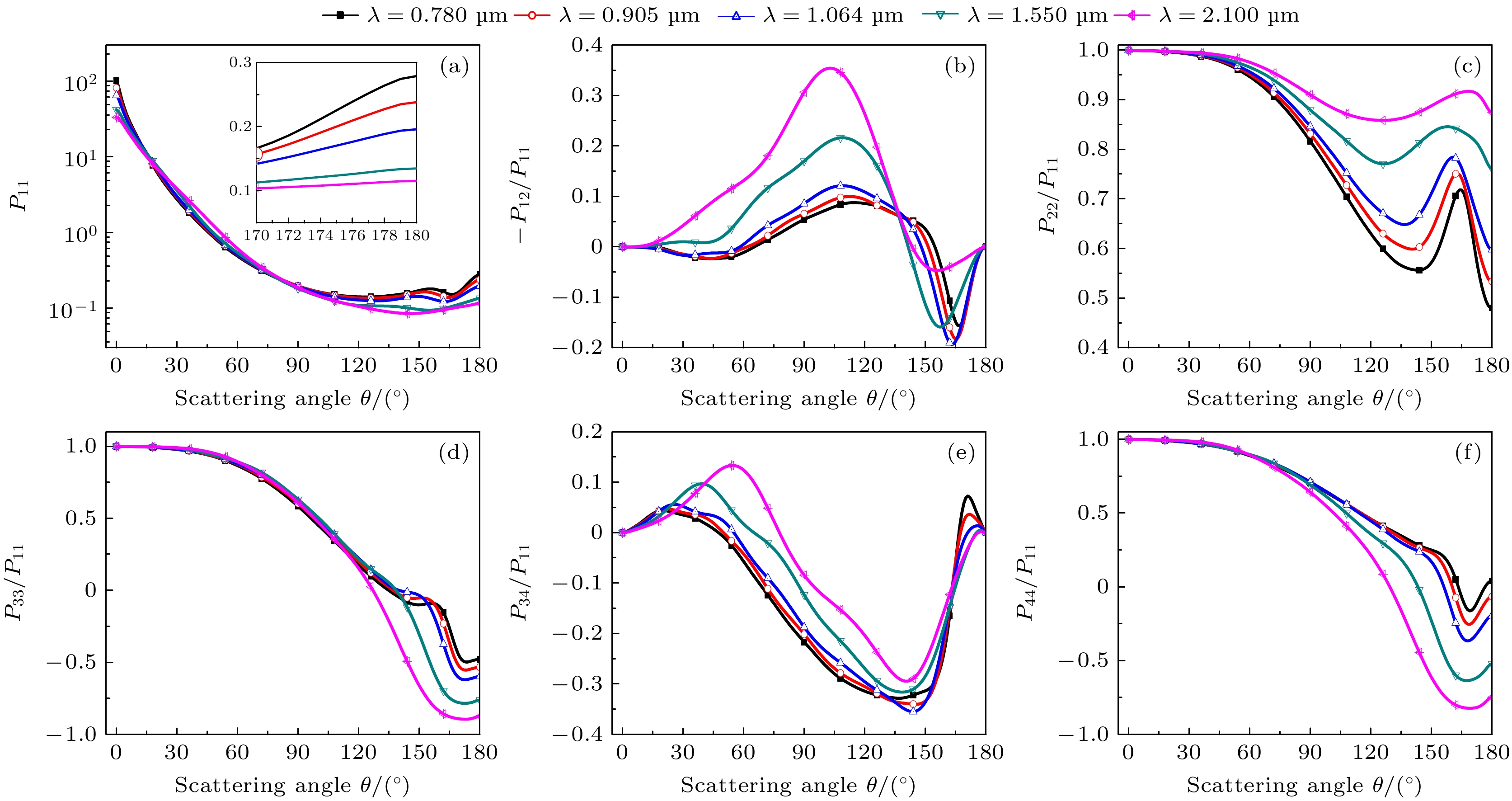
      当入射波长为1.064 μm时, 图8给出了不同相对湿度条件下复杂外混合气溶胶粒子群的散射相矩阵元素$ {P_{11}} $(相函数), $ - {P_{12}}/{P_{11}} $, $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{34}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $随散射角的变化. 由图8(a)可知, 不同湿度下相函数$ {P_{11}} $的前向散射较大, 后向散射较小, 且前向散射随着相对湿度的增大而增大, 表明了相对湿度增强了前向散射, 这与图7(c)的结论一致, 前后自洽. 由图8(b)可知, 不同湿度下偏振度$ - {P_{12}}/{P_{11}} $的变化规律很相似, 但在70°—170°散射角范围内, 相对湿度对偏振度的影响较为明显. 由图8(c)所示的$ {P_{22}}/{P_{11}} $, 图8(d)所示的$ {P_{33}}/{P_{11}} $和图8(f)所示的$ {P_{44}}/{P_{11}} $可知: 在0°—90°散射角范围内, $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $对相对湿度不敏感, 说明在前向散射区域$ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $几乎不受相对湿度的影响; 在后向散射区域(150°—180°散射角范围内), $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $对相对湿度均比较敏感. 由图8(e)可知, $ {P_{34}}/{P_{11}} $呈现出复杂的无规律波动, 且不同相对湿度下的波动幅度和位置均有所不同. 这主要归因于复杂外混合气溶胶粒子群的成分组成、分布特征、吸湿性参数等多种物理量之间的相互作用, 相较于单一成分的气溶胶粒子, 不同湿度下复杂外混合气溶胶粒子群表现出更复杂的圆偏振特性. 综上, 湿度环境下使得粒子的前向散射随之增强; 不同散射角处的偏振度、圆偏振度对相对湿度的敏感度存在着较大的差异.

      当RH为95%时, 图9给出了典型激光波长入射下复杂外混合气溶胶粒子群的散射相矩阵元素$ {P_{11}} $(相函数), $ - {P_{12}}/{P_{11}} $, $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{34}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $随散射角的变化. 由图9(a)可知, 不同波长下相函数$ {P_{11}} $的曲线走势很相似, 但在前向散射(0°)和后向散射(180°)方向上, 波长越长, 相函数$ {P_{11}} $的值略低且整体趋于更平滑. 由图9(b)可知, 偏振度$ - {P_{12}}/{P_{11}} $的曲线呈拱形, 且随入射激光波长的增大, 曲线的峰值有所上升. 由图9(c)所示的$ {P_{22}}/{P_{11}} $、图9(d)所示的$ {P_{33}}/{P_{11}} $、图9(f)所示的$ {P_{44}}/{P_{11}} $可知: 在0°—90°散射角范围内, $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $对波长不敏感, 说明在前向散射区域$ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $几乎不受波长的影响; 而在后向散射区域(150°—180°散射角范围内), $ {P_{22}}/{P_{11}} $, $ {P_{33}}/{P_{11}} $, $ {P_{44}}/{P_{11}} $对波长比较敏感, 具有明显的差异. 由图9(e)可知, $ {P_{34}}/{P_{11}} $呈现出复杂的无规律波动. 这主要是由于复杂外混合气溶胶粒子群中多个物理量的共同作用, 使光在通过气溶胶时经历多种物理过程(包括折射、衍射、反射和多次反射等), 从而导致出现了复杂的振荡. 综上, 不同散射角处的散射特性和偏振特性对波长的敏感性表现出显著差异.

      图10(a)—(c)给出了典型激光波长入射下复杂外混合气溶胶粒子群的后向散射系数、激光雷达比、线性退偏比随相对湿度的变化. 由图10(a)可知, 相对湿度一定时, 短波长的后向散射系数略高于长波长, 这是由于同等条件下短波长下的消光系数和$ {P_{11}}\left( {{{180}^\circ }} \right) $(如图9(a)所示)的值较大. 波长一定时, 后向散射系数随相对湿度的增大而增大, 这是由于湿度环境下消光系数出现了显著增长(如图7(a)所示). 结合图10(a), (b)进行分析可知, 不同波长下的激光雷达比(其定义为消光系数与后向散射系数之比[23])与后向散射系数成反比关系, 数值计算结果与其物理意义完全自洽, 验证了计算结果的正确性和可靠性. 由图10(c)可知, 相对湿度对长波长下的线性退偏比的影响较为显著, 且波长越长, 线性退偏比的值越小. 这是由于长波长入射下, 如图9(c)所示$ {P_{22}}/{P_{11}} $曲线的振荡幅度更大所致.

    4.   总　结

    • 除了气溶胶粒子的尺寸、密度、复折射率、形状、尺度谱分布等物理量之外, 相对湿度、吸湿性参数、长短轴比及其分布特征同样是影响气溶胶粒子光学特性的决定性参数. 为了全面表征不同湿度环境下气溶胶粒子存在的各种可能性, 本文将多种不同气溶胶的粒子形状、尺度谱、复折射率、密度、吸湿性参数、相对湿度、长短轴比及其分布模型等物理量进行外混合, 提出了一种精细的复杂外混合气溶胶粒子群光散射模型. 随后数值分析了典型激光波长(0.78, 0.905, 1.064, 1.55, 2.1 μm)入射下不同混合比例、相对湿度对该光散射模型光学特性(消光系数、单次散射反照率、散射相矩阵、不对称因子、后向散射系数、激光雷达比、线性退偏比)的影响.

      1)消光系数、相函数P11对混合比例的变化较为敏感.

      2)随着相对湿度的增大, 消光系数、相函数P11的前向散射、不对称因子呈增大趋势(尤其是相对湿度大于80%时, 消光系数呈指数增长); 这表明湿度环境增强了粒子群的前向散射.

      3)与混合比例相比, 不同散射角处的线偏振、圆偏振特性对相对湿度和波长的敏感性差异较大.

      4)后向散射系数和激光雷达比对混合比例和相对湿度均比较敏感; 然而, 相对湿度对线性退偏比的影响较大, 混合比例的影响则较弱.

      出现这些结论的根本原因就在于复杂外混合气溶胶粒子群的成分组成、分布特征、吸湿性参数、相对湿度、混合比例等多个物理量之间的共同作用, 这些复杂的相互作用导致了在不同湿度环境下, 气溶胶粒子发生吸湿增长、折射率变化以及水汽吸收等一系列复杂的物理现象. 然而, 本文仅仅是对不同湿度条件下不同类型气溶胶完全外混合的情况下进行了理论计算和数值分析, 鉴于文章篇幅有限, 暂没有将气溶胶的内混合考虑在内, 可以将其作为下一步研究工作的重点, 从而进一步丰富和完善不同湿度环境下气溶胶光学特性的研究.

    参考文献 (25)

目录

/

返回文章
返回