首页
登录
注册
-
1992年, Allen等[1]将宏观上的光场相位与微观上光子的轨道角动量(orbital angular momentum, OAM)相联系, 指出当光场相位中包含螺旋相位因子exp(i
$l\varphi $ )时, 光场中的每一光子的轨道角动量值为$ l\hbar $ , 其中$\varphi $ 是空间方位角,$ l$ 是拓扑荷数,$ \hbar $ 为约化普朗克常数. 这一发现引发了涡旋光束的研究热潮, 促使涡旋光束在光学探测、信息加密、光通信及量子信息等领域得到广泛应用[2-7]. 尤其是在光通信领域[8], OAM提供了一个新的高维可调谐自由度, 对经典和量子通信技术的进一步发展具有重要意义[9-12]. 由于OAM本征模式彼此正交且构成无穷维希尔伯特空间, 通过共轴传播不同OAM模式理论上可大大提高光通信系统信道容量, 进而解决当前通信资源紧缺的难题.当前OAM模式在光通信方面的应用机制主要有两种: 一是OAM键控通信(OAM-SK), 依据不同OAM本征模式的正交性与无穷性, 将信号编码为OAM模式, 每一个码元映射为一个特定的OAM模式[13,14]; 二是OAM复用(OAM-DM), 利用其正交性, 对不同OAM模式进行调制以实现多个信道的复用, 可与现有的波分复用技术(WDM)、时分复用技术(TDM)相兼容[15,16]. 而无论采用哪种应用方式, 均需要将多路OAM模式合为一路进行传输, 在光通信系统的接收端需将不同OAM模式进行有效解复用, 即OAM模式检测, 因此如何对光束携带的OAM模式进行有效识别、检测是推动OAM模式应用于大容量光通信系统的关键一环. 现有方法包括干涉测量[17]、衍射[18,19]、级联马赫-曾德尔干涉仪[20]、旋转多普勒效应[21,22]、深度学习[23-25]和光学几何变换[26]等. 其中涡旋光束的几何坐标变换技术具有器件无源、低能量损耗、结构紧凑、价格低廉等优势, 在基于OAM的光通信体制中有较大应用潜力. 虽然当前已有大量基于几何坐标变换技术的研究[26-30,15,28,31], 但都停留在改善其识别OAM模式的能力阶段, 鲜有将其应用于光通信系统进行数据传输的报道.
本文基于对数极坐标变换技术, 利用液晶聚合物材料设计并加工了一组OAM译码系统, 整个系统由一个坐标变换器件、一个相位校正器件和一个傅里叶变换透镜组成. 其中坐标变换器件用于将输入涡旋光束从极坐标系映射到直角坐标系, 并通过附加相位因子及相位校正器件将光束补偿为准直光束, 最后通过傅里叶变换透镜实现将不同OAM本征模式在不同空间位置的分离. 此外, 本文通过数值模拟分析不同器件参数对分束效果的影响, 在实验中利用坐标变换结构实现了–35—+31阶OAM模式的分束. 基于该OAM译码系统, 搭建了自由空间光数据传输演示系统, 尽管对数极坐标变换存在相邻模式发生混叠的缺陷[27,28], 但本工作仍通过一定的译码规则, 以OAM-SK方式实现了748934个码元的无误码传输, 这对坐标变换技术在 OAM 光通信系统中的应用有重要意义.
-
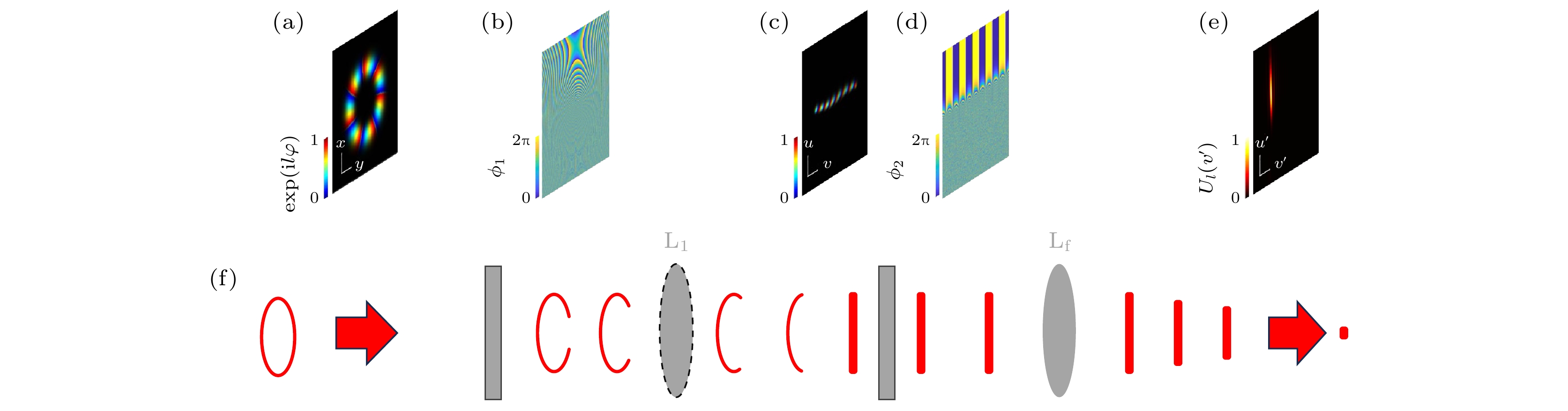
由于携带有横向梯度相位的平面光场在透镜的作用下将会聚于焦平面不同位置且聚焦位置由携带的梯度相位所决定, 可通过对数极坐标变换的方式先将涡旋光场转换为携带有横向梯度相位的矩形光场. 如图1所示, 原涡旋光束的模式阶次决定着转换后的横向梯度相位的梯度, 进而决定了转换后的矩形光场在通过透镜后的传播方向以及在透镜焦平面的聚焦位置. 不同阶次的 OAM 本征模式对应不同的传播方向, 即使是多模混合光束, 在经过坐标变换后也能在成像系统焦平面上完成分离.
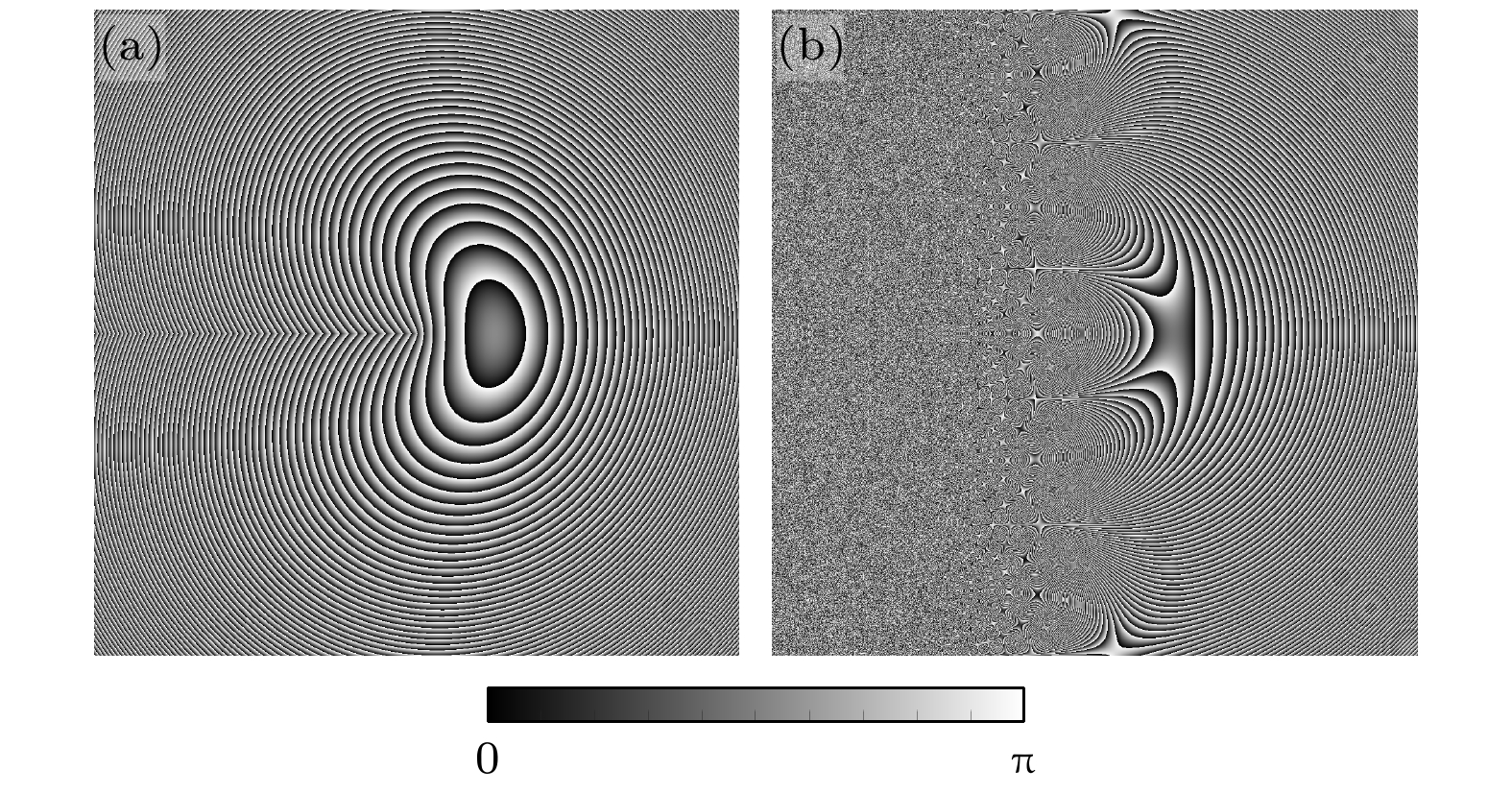
为实现上述过程, 需用到两个定制相位器件[26], 第1个为坐标变换器件, 如图1(b)所示, 用于通过对数极坐标变换实现涡旋光场向矩形光场的转换. 如图1(f) 所示, 涡旋光束受到该相位的调制并在随后经过第一透镜的衍射过程中, 环形光场逐渐展开, 原涡旋光场可以看作是无数个不同半径的圆形光场的叠加, 而不同的圆形光场因半径上的差异又导致新形成的直线形光场纵向位置的不同, 即不同半径的圆形光场与不同纵向位置的直线形光场一一对应, 最终使整个环形涡旋光场被映射为一个带有横向梯度相位的矩形光场, 如图1(c)所示. 然而因此引入的光程差导致了矩形光场存在一定相位失真, 需引入另一器件进行相位校正, 该校正器件的调制相位可根据坐标变换器件的相位通过静止相位近似方法求解[26], 如图1(d) 所示. 其中坐标变换器件和校正器件分别位于第一透镜的前后焦平面位置处, 同时校正器件位于第二透镜的前焦面处. 而实际上, 为简化系统结构, 可将第一透镜与坐标变换器件结构进行叠加[32], 两器件的调制相位为
其中
$ a $ 为对数极坐标变换映射过程的变换因子,$ b $ 可将变换后光场在$ u $ 方向上平移. 若以直线形光场各点的横向坐标作为横轴, 光场振幅作为纵轴, 则每一条直线形光场都可表示为带有横向梯度相位的门函数, 经焦距 f2 的傅里叶变换透镜后, 将会转换为 sinc 函数, 如图1(e)所示. 依据 sinc 函数的特点, 转换后光场的光强主要集中在中央主极大的位置, 且中央主极大的宽度与矩形光场的宽度满足反比关系. 此外, 中央主极大光斑最后呈现在透镜焦平面的位置由其携带的横向梯度相位决定, 且相位梯度与涡旋光阶次成正比. 0 阶涡旋光束分束后的条状光斑居于分束面的正中心, 高阶涡旋光束按照其阶次绝对值从小到大依次从内往外排布, 且相邻模式之间都是等间隔的. 环形涡旋光束经坐标变换后的携带横向梯度相位的矩形光场, 可以表示为$ {U_l}\left( v \right) = {{\text{e}}^{{\text{i}}lv/a}}{\text{rect}}\left[ {{v}/({{2{\text{π}}a}}}) \right] $ , rect(·) 即门函数, 门函数的宽度为2πa. 经傅里叶变换后的条状光场为$ {U_l}(v') = 2{\text{π}}a{\rm sinc} [ ({v' - {{\Delta }}l})/{\varDelta}] $ , 其中,$ {{\Delta }}l = {f_2}\lambda /({2{\text{π}}a} ) $ 为相邻模式间隔,$ \varDelta $ 是sinc函数主瓣的半宽,$ \left(u,v\right) $ 是坐标变换后的光场平面坐标,$ \left(u',v'\right) $ 是经傅里叶变换后的光场平面坐标. -
基于光束空间坐标变换方案所能识别的OAM模式范围存在一定限制[33]: 在解环过程中, 涡旋光场在平面
$(x, y)$ 上的每一点都与转换后平面$(u, v)$ 上的某点保持一一映射, 这将导致从不同点出射的光线具有不同的出射角$\tan \left( {{r {/ } L}} \right)$ , 其中r为解环元件上涡旋光束的半径, L为坐标变换器件与校正器件间距. 携带 OAM 的光束绝不是平面波, 由于其是坡印亭矢量的方位角分量, 使得这些光束在传播方向上具有角动量, 对于由螺旋相位项exp(i$l\varphi $ )描述的光束, 坡印亭矢量在方位角方向上的局部倾斜角可以表示为${\tan ^{ - 1}}\left( {{l {/ } {kr}}} \right)$ , 其中 l 为模式阶次, r 为光斑半径, k 为波数. 虽引入了校正相位对相位失真进行了补偿, 但方案仅在出射角较小, 即${r {/ } L}$ 与$\tan \left( {{r {/ } L}} \right)$ 近似相等时, 有较好的分束效果. 因此, 当输入模式阶次较大时, 由于光束坡印亭矢量在方位角方向的局部倾斜角过大, 导致不满足近似关系, 进而导致分束结果失真. 为减小这一因素带来的影响, 由解环元件带来的出射角偏折应该远大于涡旋光的局部倾斜角, 即:$ {l}/({{kr}}) \ll {D}/({{2 L}})$ . 也就是说, 最大可分束阶次由光束口径 D 、两定制相位器件间距L及入射光波长λ等因素决定. 其中光束口径 D 一般由调制元件的宽度所限制, 所以在实际的分束系统中其表示调制元件尺寸. 调制元件的菲涅耳数可以表示为$ F = {{{r^2}} {/ } {L\lambda }} $ , 所以最大可分束的模式阶次应满足$ l \ll 2{\text{π}}F $ , 即最大可分束的模式阶数只由调制元件的菲涅耳数所决定, 与其他参数无关. 当分束的模式阶数较大时, 可通过提高调制元件的菲涅耳数来解决, 比如可采用扩束系统增大入射的涡旋光束的半径、减小相位器件间距等手段. 根据上述分析, 设置器件参数为: a = 1/π, b = 4, f1 = 50 mm, λ = 1645 nm, 设计调制器件像元尺寸为4.8 μm × 4.8 μm, 像元数目为2101 × 2101. 利用液晶聚合物材料通过紫外激光直写方式加工器件[34], 由于其通过液晶单元的不同旋转角来引入几何相位, 实现偏振独立的相位调制, 因此所加工液晶分子的主轴排布应为所设计调制相位的一半, 即坐标变换器件主轴排布为$ {\alpha _1} = {{{\phi _1}} {/ } 2} $ , 校正器件主轴排布为$ {\alpha _2} = {{{\phi _2}} {/ } 2} $ , 相应的坐标变换器件及校正器件的液晶分子主轴排布如图2(a), (b)所示. -
实验搭建了OAM-SK数据传输系统, 评估了设计加工的OAM译码系统性能. 如图3(a) 所示, 采用中心波长1645 nm的Er:YAG连续输出激光器输出的水平线偏基模高斯光束入射空间光调制器, 以编码产生OAM态, 随后将产生的OAM态经4-f滤波后在自由空间进行1 m传输后输入OAM译码系统, 最后通过红外面阵探测器接收经过译码系统的聚焦透镜后焦面处光场. OAM译码系统样机实物图如图3(d)所示.
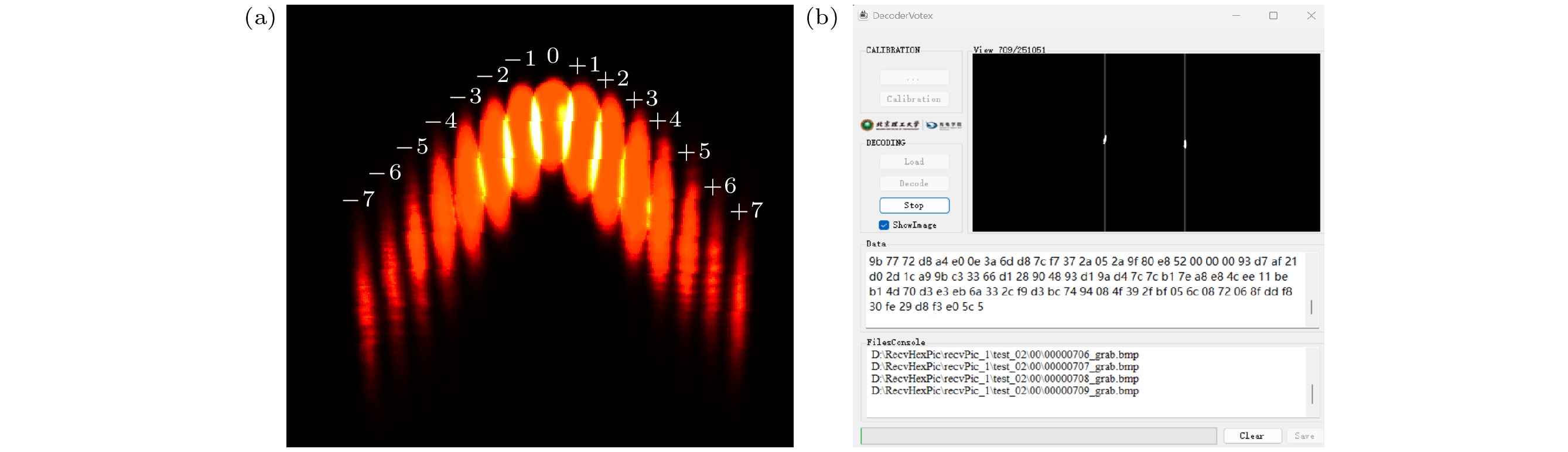
将模式范围–35—+35的OAM态输入译码系统, 经数值模拟与实验测试, 不同OAM态在分束面位置分布曲线如图4(a), (c)所示, 将分束面光场强度分布沿竖直方向求和后得到沿水平方向的归一化强度分布, 如图4(b), (d)所示. 通过以上结果可知, 随着模式阶次绝对值的增长, 所得分数面光斑旁瓣逐渐明显, 但以区域划分仍可识别出不同的模式. 值得注意的是, 实验中在模式本征值大于+31处出现异常, 该部分模式不在器件的正常识别范围内. 故系统实测表现为: 可识别OAM模式范围–35—+31. 实际测量模式范围与理论值存在一定差异, 这是由于实际加工中, 当相邻像元所对应液晶分子取向垂直时会出现分子断裂, 通常将其中一个方向的液晶分子少旋转5°, 导致器件实际相位调制深度为0—1.972π, 而实测可识别模式范围并不对称, 应为实验搭建时, 水平方向器件对准误差导致.
-
利用3.1节中搭建的系统, 通过OAM-SK方式进行编码数据传输, 由于通过液晶空间光调制器进行OAM态制备, 采用无需迭代即可利用纯相位光栅制备的OAM模式进行4位编码, 码元与OAM模式编码对应情况见表1. 在解码端采用OAM解复用系统, 如图5(a)所示, 根据不同单模OAM模式在分束面对应sinc函数主极大位置不同, 将分束面根据用于编码的单模OAM模式位置划分出不同区域, 通过这些区域内的强度响应情况即可完成译码. 实验根据上述方案编写了译码软件如图5(b) 所示. 通过3次实验, 每次传输748934个16进制码元, 这些码元经译码后未出现误码, 依据二项分布和泊松定理[35]可得本系统误比特率小于1×10–6.
一般来说, 采用对数极坐标变换方案进行OAM模式分束公认存在固有缺陷, 相邻模式在分束面会发生混叠, 进而导致模式识别出错, 产生误码. 但只要将划分区域依照sinc函数中心主极大位置为中心, 选取适当的半宽, 实际进行数据传输时, 并不会因混叠造成误码. 上述结果表明在实际的自由空间光通信链路中, 利用对数极坐标变换方式可实现低误码率的OAM模式译码. 此外, 值得注意的是, 该OAM-SK编码数据传输演示, 仅传输1 m. 随着传输距离的增大, 涡旋光束将受到湍流大气的影响, 导致螺旋相位畸变和OAM谱展宽, 这可能会导致识别OAM状态失准和误比特率(BER)的增加. 在这种情况下, 可通过自适应补偿方法改善这一问题.
-
本文首先通过分析基于对数极坐标变换OAM态分束原理, 从尽量支持较大模式分束范围的角度出发, 分析了最大可分束阶次与器件菲涅耳数的关系, 进而确定了坐标变换器件与校正器件参数. 然后利用液晶聚合物材料, 采用紫外激光直写手段加工器件, 搭建了OAM译码系统, 实现了–34—+31阶OAM模式分束. 最后通过自定义的混合编码策略完成了自由空间中OAM-SK编码数据传输演示实验, 实现了在使用了相邻OAM模式的情况下误比特率小于1×10–6. 该工作在分析分束系统的OAM态识别能力的基础上更进一步, 完成了数据传输译码测试, 译码实验表明尽管对数极坐标变换存在相邻模式混叠问题, 但在实际编码传输链路译码中, 仍有十分可靠的应用价值.
基于对数坐标变换的涡旋键控译码
Vortex key decoding based on logarithmic coordinate transformation
-
摘要: 光子轨道角动量(OAM)为光通信提供了新的高维自由度, 有望提高光信息传输系统信道容量, 解决当前通信资源紧张的问题. OAM键控(OAM-SK)是一种新型的信息传输机制, 其中, 对OAM模式的有效识别和检测是实现OAM-SK译码的核心技术之一. 本文提出了一种基于对数极坐标变换的OAM译码系统, 首先通过设计的坐标变换光栅进行映射, 再引入优化的相位校正光栅进行补偿, 最后采用一个傅里叶变换透镜实现了OAM模式的分离. 对系统在不同光栅参数下的分束效果进行数值评估, 在实验中成功实现了–35—+31阶轨道角动量模式的分束. 进一步地, 基于该OAM解复用系统, 搭建了自由空间光数据传输演示系统. 通过引入特定译码规则, 有效克服了对数极坐标变换存在的相邻模式混叠的问题, 实现了748934个码元的无误码传输. 本文结果为未来高容量光通信系统的发展提供了支持.Abstract: Orbital angular momentum (OAM), as a novel high-dimensional degree of freedom, shows great potential applications in optical communication in improving system channel capacity and solving the problem of scarce communication resources. However, the effective recognition and detection of OAM modes are the core challenges for achieving efficient communication in such systems. In this work, an OAM decoding system consisting of a designed coordinate transformation device, a phase corrector, and a Fourier transform lens is presented based on log-polar coordinate transformation. The coordinate transformation device fabricated by liquid crystal polymer is utilized to map the incident vortex beam from polar coordinates into Cartesian coordinates, followed by the phase corrector to compensate for phase distortions into a collimated beam. Finally, the Fourier transform lens is used to separate the OAM modes at different space positions in its rear focal plane. The performance of the system is numerically evaluated in several ablation studies, and the influence of various grating parameters on beam separation efficiency is analyzed. Experimentally, the system successfully achieves the decoding of OAM modes ranging from –35 to +31 orders. Furthermore, a free-space optical communication demonstration system is constructed based on this OAM decoding system. By introducing specifically designed decoding rules, the system effectively mitigates the adjacent mode crosstalk inherent in logarithmic polar coordinate transformation and successfully transmitted 748934 symbols without errors. These favorable results highlight the capabilities of the proposed OAM-based optical communication system and provide valuable insights for developing future high-capacity optical communication networks.
-
Key words:
- orbital angular momentum /
- state recognition /
- geometric coordinate transformation .
-
-
图 1 对数极坐标变换过程示意图 (a) 输入–7阶涡旋光束相位分布; (b)坐标变换调制相位; (c) –7阶涡旋光束对应的矩形光场相位分布; (d)校正相位; (e) –7阶涡旋光束对应的分束面光强分布; (f) 对数极坐标变换过程
Figure 1. Concept of the log-polar transformation: (a) The phase distribution of the incident beam with OAM state
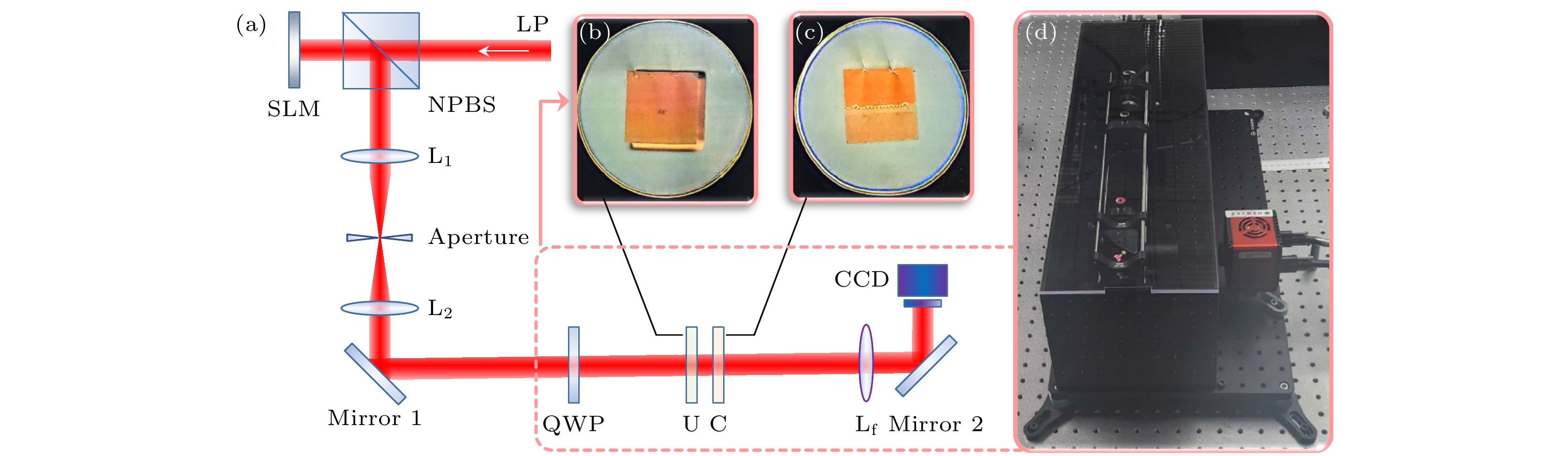
$|-7\rangle $ ; (b) the phase modulation of the coordinate transformation; (c) the phase distribution of the transformed rectangular light field corresponding to OAM state$|-7\rangle $ ; (d) the phase modulation of the phase correction; (e) the sorting plane intensity of the incident beam corresponding to OAM state$|-7\rangle $ ; (f) the convert sketch of a vortex beam via the log-polar transformation.
图 2 液晶分子主轴排布仿真效果 (a) 坐标变换器件; (b) 校正器件
Figure 2. Simulated main axis arrangement of the liquid crystal molecules: (a) The arrangement distribution of the coordinate transformation device; (b) the phase corrector.
图 3 OAM译码系统及数据传输演示装置 (a) 实验装置, 波长1645 nm的线偏振连续激光, 通过SLM后携带OAM模式, 经由透镜L1和L2构成的4-f滤波系统后在自由空间传输1 m后通过1/4波片输入OAM译码系统, 系统由坐标变换器件U、校正器件C和傅里叶变换透镜Lf组成, 最后分束面光场(傅里叶变换透镜后焦面处光场)由红外焦平面探测器CCD接收; (b) 坐标变换器件实物图; (c) 校正器件实物图; (d) OAM译码系统样机图
Figure 3. Experimental setup of the OAM decoding system for data transmission demonstration: (a) Experimental setup. The incident gaussian beam is a continuous-wave laser operating at 1645 nm, which is encoded by a SLM to generate the desired OAM mode. After passing through a 4-f system composed of lenses L1 and L2, the OAM mode is transmitted 1 m in free space and then incident the OAM decoding system, which is consist of a coordinate transformation device, a phase corrector and a Fourier transformation lens. Lastly, the sorted light field (Light field at the focal plane of Fourier transformation lens) is captured by a CCD. (b) The physical image of the coordinate transformation device. (c) The physical image of the phase corrector. (d) The physical image of the OAM decoding system prototype.
图 4 坐标变换分束效果 (a) 数值仿真不同OAM态在分束面的位置分布; (b) 数值仿真不同OAM态在分束面的水平方向归一化强度分布; (c) 实验测定不同OAM态在分束面的位置分布; (d) 实验测定不同OAM态在分束面的水平方向归一化强度分布
Figure 4. Sorting performance of the coordinate transformation: (a) The simulated position for sorting different OAM states along x-axis and y-axis in the sorting plane; (b) the overlaid line scans of the simulated intensity distributions of different OAM states along the horizontal direction; (c) the experimental position for sorting different OAM states along x-axis and y-axis in the sorting plane; (d) the overlaid line scans of the experimental intensity distributions of different OAM states along the horizontal direction.
图 5 OAM-SK数据传输译码过程 (a) OAM译码系统分束面; (b)译码软件界面
Figure 5. Data transmission decoding of OAM-shift keying: (a) The sorting plane of the OAM decoding system with OAM states
$| l\rangle $ , where l = –7–+7; (b) the decoding software interface.表 1 码元与OAM模式编码对应表
Table 1. Corresponding of symbols and OAM modes.
码元 0 1 2 3 4 5 6 7 OAM模式 — ±2 ±3 ±4 ±5 ±6 –6 –5 码元 8 9 A B C D E F OAM模式 –4 –3 –2 +2 +3 +4 +5 +6 
下载: 导出CSV
-
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185 doi: 10.1103/PhysRevA.45.8185 [2] Shen Y J, Wang X J, Xie Z W, Min C J, Fu X, Liu Q, Gong M L, Yuan X C 2019 Light Sci. Appl. 8 90 doi: 10.1038/s41377-019-0194-2 [3] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, Bao C, Li L, Cao Y, Zhao Z, Wang J, Lavery M P J, Tur M, Ramachandran S, Molisch A F, Ashrafi N, Ashrafi S 2015 Adv. Opt. Photon. 7 66 doi: 10.1364/AOP.7.000066 [4] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313 doi: 10.1038/35085529 [5] Fang X Y, Ren H R, Gu M 2020 Nat. Photonics 14 102 doi: 10.1038/s41566-019-0560-x [6] Erhard M, Fickler R, Krenn M, Zeilinger A 2017 Light Sci. Appl. 7 17146 doi: 10.1038/lsa.2017.146 [7] Wang J, Liu J, Li S, Zhao Y, Du J, Zhu L 2022 Nanophotonics 11 645 doi: 10.1515/nanoph-2021-0527 [8] Trichili A, Park K H, Zghal M, Ooi B S, Alouini M S 2019 IEEE Commun. Surv. Tutorials 21 3175 doi: 10.1109/COMST.2019.2915981 [9] Chen Y A, Zhang Q, Chen T Y, Cai W Q, Liao S K, Zhang J, Chen K, Yin J, Ren J G, Chen Z, Han S L, Yu Q, Liang K, Zhou F, Yuan X, Zhao M S, Wang T Y, Jiang X, Zhang L, Liu W Y, Li Y, Shen Q, Cao Y, Lu C Y, Shu R, Wang J Y, Li L, Liu N L, Xu F, Wang X B, Peng C Z, Pan J W 2021 Nature 589 214 doi: 10.1038/s41586-020-03093-8 [10] Qiu X, Guo H, Chen L 2023 Nat. Commun. 14 8244 doi: 10.1038/s41467-023-43950-4 [11] Vallone G, D’Ambrosio V, Sponselli A, Slussarenko S, Marrucci L, Sciarrino F, Villoresi P 2014 Phys. Rev. Lett. 113 060503 doi: 10.1103/PhysRevLett.113.060503 [12] Wang X L, Cai X D, Su Z E, Chen M C, Wu D, Li L, Liu N L, Lu C Y, Pan J W 2015 Nature 518 516 doi: 10.1038/nature14246 [13] Du J, Wang J 2015 Opt. Lett. 40 4827 doi: 10.1364/OL.40.004827 [14] Shang Z, Fu S Y, Hai L, Zhang Z, Li L, Gao C Q 2022 Opt. Express 30 34053 doi: 10.1364/OE.466353 [15] Wen Y, Chremmos I, Chen Y, Zhu G, Zhang J, Zhu J, Zhang Y, Liu J, Yu S 2020 Optica 7 254 doi: 10.1364/OPTICA.385590 [16] Wang J, Yang J Y, Fazal I M, Ahmed N, Yan Y, Huang H, Ren Y, Yue Y, Dolinar S, Tur M, Willner A E 2012 Nat. Photonics 6 488 doi: 10.1038/nphoton.2012.138 [17] Fu S Y, Zhai Y, Zhang J, Liu X, Song R, Zhou H, Gao C Q 2020 PhotoniX 1 19 doi: 10.1186/s43074-020-00019-5 [18] Fu S Y, Wang T W, Yan Gao Y, Gao C Q 2016 Chin. Opt. Lett. 14 080501 doi: 10.3788/COL201614.080501 [19] Zhao Q, Dong M, Bai Y H, Yang Y J 2020 Photon. Res. 8 745 doi: 10.1364/PRJ.384925 [20] Leach J, Padgett M J, Barnett S M, Franke-Arnold S, Courtial J 2002 Phys. Rev. Lett. 88 257901 doi: 10.1103/PhysRevLett.88.257901 [21] Zhou H L, Fu D Z, Dong J J, Zhang P, Chen D X, Cai X L, Li F L, Zhang X L 2016 Light Sci. Appl. 6 16251 doi: 10.1038/lsa.2016.251 [22] Lavery M P J, Speirits F C, Barnett S M, Padgett M J 2013 Science 341 537 doi: 10.1126/science.1239936 [23] Wang H, Zhan Z, Hu F, Meng Y, Liu Z, Fu X, Liu Q 2023 PhotoniX 4 9 doi: 10.1186/s43074-022-00079-9 [24] Wang J Q, Fu S Y, Shang Z J, Hai L, Gao C Q 2022 Opt. Lett. 47 1419 doi: 10.1364/OL.443726 [25] Zhou S Y, Li L, Gao C Q, Fu S Y 2023 Opt. Lett. 49 173 doi: 10.1364/OL.512147 [26] Berkhout G C G, Lavery M P J, Courtial J, Beijersbergen M W, Padgett M J 2010 Phys. Rev. Lett. 105 153601 doi: 10.1103/PhysRevLett.105.153601 [27] Mirhosseini M, Malik M, Shi Z, Boyd R W 2013 Nat. Commun. 4 2781 doi: 10.1038/ncomms3781 [28] Wen Y, Chremmos I, Chen Y, Zhu J, Zhang Y, Yu S 2018 Phys. Rev. Lett. 120 193904 doi: 10.1103/PhysRevLett.120.193904 [29] Cheng J, Wan C H, Zhan Q W 2022 Opt. Express 30 16330 doi: 10.1364/OE.455987 [30] Cheng J P, Sha X B, Zhang H, Chen Q M, Qu G Y, Song Q H, Yu S M, Xiao S M 2022 Nano Lett. 22 3993 doi: 10.1021/acs.nanolett.2c00572 [31] Li L, Guo Y C, Zhang Z C, Shang Z J, Li C, Wang J Q, Gao L L, Hai L, Gao C Q, Fu S Y 2023 Adv. Photonics 5 056002 doi: 10.1117/1.AP.5.5.056002 [32] Lavery M P J, Robertson D J, Berkhout G C G, Love G D, Padgett M J, Courtial J 2012 Opt. Express 20 2110 doi: 10.1364/OE.20.002110 [33] Lavery M P J, Robertson D J, Sponselli A, Courtial J, Steinhoff N K, Tyler G A, Wilner A E, Padgett M J 2013 New J. Phys. 15 013024 doi: 10.1088/1367-2630/15/1/013024 [34] Chen P, Wei B Y, Hu W, Lu Y Q 2020 Adv. Mater. 32 1903665 doi: 10.1002/adma.201903665 [35] Saber G, Gutiérrez-Castrejón R, Xing Z, Alam S, El-Fiky E, Ceballos-Herrera D E, Cavaliere F, Vall-Llosera G, Lessard S, Plant D V 2021 IEEE Photonics J. 13 1 doi: 10.1109/JPHOT.2021.3054240 -
计量
- 文章访问数: 37
- HTML全文浏览数: 37
- PDF下载数: 1
- 施引文献: 0