高级搜索

中子散射技术在Zintl相化合物热导率研究中的应用

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

张翠萍, 朱金峰, 沈晓玲, 舒明方, 任清勇, 马杰. 中子散射技术在Zintl相化合物热导率研究中的应用[J]. 物理学报, 2025, 74(1): 017301-1. doi: 10.7498/aps.74.20241163
引用本文: 张翠萍, 朱金峰, 沈晓玲, 舒明方, 任清勇, 马杰. 中子散射技术在Zintl相化合物热导率研究中的应用[J]. 物理学报, 2025, 74(1): 017301-1. doi: 10.7498/aps.74.20241163
shu
Cuiping ZHANG, Jinfeng ZHU, Xiaoling SHEN, Mingfang SHU, Qingyong REN, Jie MA. Application of neutron scattering to studying low lattice thermal conductivity of Zintl phase compounds[J]. Acta Physica Sinica, 2025, 74(1): 017301-1. doi: 10.7498/aps.74.20241163
Citation: Cuiping ZHANG, Jinfeng ZHU, Xiaoling SHEN, Mingfang SHU, Qingyong REN, Jie MA. Application of neutron scattering to studying low lattice thermal conductivity of Zintl phase compounds[J]. Acta Physica Sinica, 2025, 74(1): 017301-1. doi: 10.7498/aps.74.20241163
shu

中子散射技术在Zintl相化合物热导率研究中的应用

  • 1.

    上海交通大学物理与天文学院, 上海　200240

  • 2.

    散裂中子源科学中心, 东莞　523803

  • 3.

    中国科学院高能物理研究所, 北京　100049

  • 4.

    广东省极端条件重点实验室, 东莞　523803

    • 作者简介: 张翠萍. E-mail: zhangcuiping@sjtu.edu.cn .
    通讯作者: E-mail: jma3@sjtu.edu.cn.

  • 中图分类号: 73.50.Lw, 78.70.Nx

Application of neutron scattering to studying low lattice thermal conductivity of Zintl phase compounds

  • 1.

    School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China

  • 2.

    Spallation Neutron Source Science Center, Dongguan 523803, China

  • 3.

    Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China

  • 4.

    Guangdong Provincial Key Laboratory of Extreme Conditions, Dongguan 523803, China

    • Corresponding author: E-mail: jma3@sjtu.edu.cn.

  • MSC: 73.50.Lw, 78.70.Nx

  • 摘要: Zintl相化合物因为其独特的晶体结构和优异的输运性能, 在能源存储及转换领域尤其是热电材料应用中受到广泛关注. 为了理解Zintl相化合物优异热电性能起源, 科研工作者们利用中子散射技术结合分子动力学模拟, 对晶格热导和电声耦合效应展开研究, 取得了一系列成果. 本文系统总结了中子散射对一些Zintl相化合物的结构及其晶格动力学的相关研究工作, 按照零维A14MPn11型化合物、一维链状化合物、二维层状AB2X2型化合物和其结构变体AB4X3型化合物, 层状ZrBeSi结构Zintl相化合物的顺序依次梳理了其低晶格热导率的物理起源. 通过中子衍射技术探讨了晶体结构、原子位移参数等信息; 围绕中子非弹性散射实验, 探讨了声子态密度的测量方法及其对Zintl相化合物动力学性质的研究. 在深入认识Zintl相化合物的同时, 揭示了其微观结构和优化材料性能, 以期对设计新型热电功能材料具有一些启发.
    Abstract: Due to the unique crystal structures and excellent transport properties, the Zintl phase thermoelectric materials have aroused extensive interest in energy storage and conversion. To explore the origins of those excellent performances, a series of experimental and theoretical techniques have been applied, such as neutron scattering, thermal conductivity, and molecular dynamics simulations with machine learning. In this paper, the progress of neutron scattering research on the structure and dynamics of Zintl phase is summarized, for example A14MPn11 compounds with zero-dimensional (0D) substructures, 1D chains-based compounds, 2D layered A2BX2 compounds (including the binary Mg3Sb2) and their structural variants, as well as AB4X3, and ZrBeSi-type compounds. The underlying mechanisms of intrinsically low lattice thermal conductivity in those Zintl phase are discussed in detail. These compounds generally exhibit the following characteristics: 1) strong anharmonicity, which is characterized by strong atomic vibrations and anharmonic phonon-phonon scattering; 2) weak chemical bonding, which usually leads to low sound velocity and interatomic force constants, and corresponding to low-energy phonon branches; 3) intrinsic vacancy defect, which weakens the bond strengths, softens the lattice, and enhances anharmonic phonon-phonon scattering. Neutron diffraction is applied to studying crystal structures, lattice parameters, atomic occupancies, and atomic displacement parameters. Inelastic neutron scattering measures the lattice dynamics, and density of states, which are related to lattice thermal conductivity. Hence, the physical mechanisms of Zintl compounds are analyzed for optimizing material properties and designing new functional materials.
  • 加载中

  • 图 1  中子散射的三维示意图

    Figure 1.  Three-dimensional schematic of neutron scattering.

    下载: 全尺寸图片 幻灯片

    图 2  (a), (b) Yb14MnSb11的晶体结构和粉末X射线衍射谱[44]; (c) Yb14MnSb11的X射线吸收光谱[46]; (d) Cp/T随T 2的变化[46]

    Figure 2.  (a), (b) Crystal structure and rietveld refinement of powder X-ray diffraction of Yb14MnSb11[44]; (c) X-ray absorption near edge structure spectra of Yb14MnSb11[46]; (d) Cp/T vs. T 2 [46].

    下载: 全尺寸图片 幻灯片

    图 3  (a) Yb14MnSb11的动态结构因子[44]; (b) 将图(a)数据减去弹性峰并通过玻色-爱因斯坦因子修正后的动态结构因子[44]; (c), (d)声子态密度和约化声子态密度的温度依赖性[44]

    Figure 3.  (a) Dynamical structure factor of Yb14MnSb11[44]; (b) dynamical structure factor after subtracting the elastic line in panel (a) and correcting it by the Bose-Einstein factor[44]; (c), (d) temperature dependence of the phonon density-of-states and reduced phonon density-of-states[44].

    下载: 全尺寸图片 幻灯片

    图 4  (a) Eu14MnSb11, Yb14MnSb11和Zn4Sb3的元素特定核非弹性散射光谱[44]; (b) Eu14MnSb11中的分波和总声子态密度(上), Yb14MnSb11, Eu14MnSb11和Zn4Sb3中Sb的分波声子态密度(中)及约化后的分波声子态密度(下)[44]

    Figure 4.  (a) Element-specific nuclear inelastic scattering spectra measured in Eu14MnSb11, Yb14MnSb11, and Zn4Sb3[44]; (b) partial and total phonon density-of-states in Eu14MnSb11 (top), the partial phonon density-of-states (middle) and the reduced partial phonon density-of-states (bottom) in Yb14MnSb11, Eu14MnSb11, and Zn4Sb3[44].

    下载: 全尺寸图片 幻灯片

    图 5  (a), (b) Yb14MnSb11的动态结构因子[51]; (c), (d) Yb14MnSb11加权声子态密度和声子能带结构[51]; (e) Yb14MnSb11晶格热导率$ {\kappa }_{{\mathrm{L}}} $与双通道晶格动力学模拟值的比较[51–53], 其中$ {\kappa }_{{\mathrm{p}}{\mathrm{h}}} $和$ {\kappa }_{{\mathrm{d}}{\mathrm{i}}{\mathrm{f}}{\mathrm{f}}} $分别为声子-气体通道、扩散子通道

    Figure 5.  (a), (b) Dynamical structure factor of Yb14MnSb11[51]; (c), (d) phonon density-of-states and phonon band structure Yb14MnSb11[51]; (e) comparison of the lattice thermal conductivity of Yb14MnSb11 with the simulated values of dual channel lattice dynamics[51–53], $ {\kappa }_{{\mathrm{p}}{\mathrm{h}}} $, $ {\kappa }_{{\mathrm{d}}{\mathrm{i}}{\mathrm{f}}{\mathrm{f}}} $ represent phonon-gas and diffusion channel, respectively.

    下载: 全尺寸图片 幻灯片

    图 6  (a)—(c) TlInTe2的粉末X射线衍射分析和沿不同角度的晶体结构, 椭球尺寸代表所有原子的各向异性原子位移参数大小[60]; (d) Cp/T随T 2的变化[60]; (e) Cp/T 3随T的变化[60]; (f)吸收系数[60]

    Figure 6.  (a)–(c) Rietveld refinement of powder X-ray diffraction and crystal structure of TlInTe2, the anisotropic atomic displacement parameters of all the atoms plotted as ellipsoids[60]; (d) Cp/T vs. T 2 [60]; (e) Cp/T 3 vs. T[60]; (f) absorption coefficient[60].

    下载: 全尺寸图片 幻灯片

    图 7  (a) Tl原子的原子位移参数[63]; (b)—(d) TlInTe2的加权声子态密度、声子线宽和声子寿命[63]

    Figure 7.  (a) Atomic displacement parameters of Tl[63]; (b)–(d) neutron-weighted phonon density-of-states, phonon linewidth, and phonon lifetime of TlInTe2[63].

    下载: 全尺寸图片 幻灯片

    图 8  (a), (b) CaMg2Bi2的晶体结构和粉末X射线衍射[83]

    Figure 8.  (a), (b) Crystal structure and rietveld refinement of powder X-ray diffraction patterns of CaMg2Bi2[83].

    下载: 全尺寸图片 幻灯片

    图 9  (a), (b) CaZn2Sb2和YbZn2Sb2的晶格常数及各向同性原子位移参数[90]

    Figure 9.  (a), (b) Lattice constants and isotropic atomic displacements of CaZn2Sb2 and YbZn2Sb2[90].

    下载: 全尺寸图片 幻灯片

    图 10  (a), (b) Mg3Sb2的晶体结构和粉末X射线衍射[91]; (c) Mg3Sb2中3个化学键的约化密度梯度与sign(λ2)ρ的函数关系[100]; (d)晶格热导率[101,102]

    Figure 10.  (a), (b) Crystal structure and powder X-ray diffraction of Mg3Sb2[91]; (c) the noncovalent interaction analysis with reduced density gradient as a function of sign(λ2)ρ for the chemical bonds in Mg3Sb2[100]; (d) lattice thermal conductivity[101,102].

    下载: 全尺寸图片 幻灯片

    图 11  (a) Mg3Sb2和CaMg2Sb2的声子态密度[91]; (b), (c)动态结构因子[91]; (d) Mg3Sb2的分波声子态密度[91]; (e), (f)声子态密度的温度依赖性, 并与计算结果(黑色)进行比较[91]

    Figure 11.  (a) Phonon density-of-states of Mg3Sb2 and CaMg2Sb2[91]; (b), (c) neutron dynamical structure factor[91]; (d) calculated partial phonon density-of-states of Mg3Sb2[91]; (e), (f) temperature dependence of neutron density-of-states, and compared with the calculated results (black)[91].

    下载: 全尺寸图片 幻灯片

    图 12  (a), (b) RbCd2As2与RbCd4As3的晶体结构关系[111]; (c) NaCd4As3的粉末X射线衍射[111]; (d), (e) RbZn2As2与RbZn4As3的晶体结构关系[111]; (f) RbZn4As3的粉末X射线衍射[112]

    Figure 12.  (a), (b) Structural relationship between RbCd2As2 and RbCd4As3[111]; (c) rietveld refinement of powder X-ray diffraction patterns of NaCd4As3[111]; (d), (e) structural relationship between RbZn2As2 and RbZn4As3[111]; (f) rietveld refinement of powder X-ray diffraction patterns of RbZn4As3[112].

    下载: 全尺寸图片 幻灯片

    图 13  (a) RbZn4–xCuxAs3的总热导率和晶格热导率[112]; (b) Rb, Zn, As(1)和As(2)各向同性原子位移[112]

    Figure 13.  (a) Total thermal conductivity and lattice thermal conductivity of RbZn4–xCuxAs3[112]; (b) the isotropic atomic displacements of Rb, Zn, As(1), and As(2)[112].

    下载: 全尺寸图片 幻灯片

    图 14  (a), (b) SrCuSb的晶体结构和粉末中子衍射[123]; (c) ACuSb格林内森常数, 橙、深蓝和酒红色点分别代表CaCuSb, SrCuSb和BaCuSb[129]; (d) ACuSb中Ca, Sr和Ba原子的各向同性原子位移参数[129]; (e), (f) Eu2Zn0.98Sb2沿[103]方向的高角环形暗场扫描透射电子显微镜图像, 紫色、蓝色和橙色球体分别代表Eu, Sb和Zn[130]; (g) Eu2ZnSb2和EuAgSb的晶格热导率[131]; (h), (i) SrCuSb和Sr2ZnSb2的三声子和四声子散射率[[132]

    Figure 14.  (a), (b) Crystal structure and rietveld refinement of neutron powder diffraction of SrCuSb[123]; (c) Grüneisen parameter of ACuSb[129], the orange, dark blue and burgundy dots represent CaCuSb, SrCuSb and BaCuSb, respectively; (d) isotropic atomic displacements of Ca, Sr, and Ba atoms in ACuSb[129]; (e), (f) high-angle annular dark-field scanning transmission electron microscopy image along the [103] direction of Eu2Zn0.98Sb2[130], the purple, blue and orange spheres represent Eu, Sb and Zn, respectively; (g) lattice thermal conductivity of Eu2ZnSb2 and EuAgSb[131]; (h), (i) calculated three- and four-phonon scattering rates of SrCuSb and Sr2ZnSb2[132].

    下载: 全尺寸图片 幻灯片

    图 15  (a)—(c) Sr(Cu, Ag, Zn)Sb的动态结构因子[123]; (d)—(f) (110)平面的差分电荷密度[123]; (g)各向异性原子位移参数, 插图为Sr(Cu, Ag, Zn)Sb的晶体结构示意图, 椭圆体尺寸代表所有原子的各向异性原子位移参数大小[123]

    Figure 15.  (a)–(c) Dynamical structure factor of Sr(Cu, Ag, Zn)Sb[123]; (d)–(f) charge density differences projected in the (110) plane[123]; (g) the anisotropic atomic displacement parameters, insets show the schematic crystal structures of Sr(Cu, Ag, Zn)Sb with anisotropic atomic displacement parameters ellipsoids[123].

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Snyder G J, Toberer E S 2008 Nat. Mater. 7 105 doi: 10.1038/nmat2090
    [2] Rowe D M 2006 CRC Handbook of Thermoelectrics (Boca Raton: CRC/Taylor & Francis
    [3] Zintl E 1939 Angew. Chem. 52 1 doi: 10.1002/ange.19390520102
    [4] Laves F 1941 Naturwissenschaften 29 244 doi: 10.1007/BF01479157
    [5] Nesper R 1990 Prog. Solid State Chem. 20 1 doi: 10.1016/0079-6786(90)90006-2
    [6] Shuai J, Mao J, Song S W, Zhang Q Y, Chen G, Ren Z F 2017 Mater. Today Phys. 1 74 doi: 10.1016/j.mtphys.2017.06.003
    [7] Toberer E S, May A F, Snyder G J 2010 Chem. Mater. 22 624 doi: 10.1021/cm901956r
    [8] Zevalkink A, Pomrehn G, Takagiwa Y, Swallow J, Snyder G Y 2013 Chem. Sus. Chem. 6 2316 doi: 10.1002/cssc.201300518
    [9] Shi X, Song S W, Gao G H, Ren Z F 2024 Science 384 757 doi: 10.1126/science.adn7265
    [10] Kauzlarich S M, Brown S R, Snyder G J 2007 Dalton Trans. 21 2099 doi: 10.1039/B702266B
    [11] Kazem N, Kauzlarich S M 2016 Handbook on the Physics and Chemistry of Rare Earths (Vol. 50) (Holland: Elsevier) pp177–208
    [12] Liu K J, Zhang Z W, Chen C, Wei L H, He H L, Mao J, Zhang Q 2022 Rare Met. 41 2998 doi: 10.1007/s12598-022-02032-y
    [13] Kauzlarich S M, Devlin K P, Perez C J 2021 Thermoelectric Energy Conversion (Cambridge: Woodhead Publishing) pp157–182
    [14] He J, Tritt T M 2017 Science 357 eaak9997 doi: 10.1126/science.aak9997
    [15] Liu K F, Xia S Q 2019 J. Sol. State Chem. 270 252 doi: 10.1016/j.jssc.2018.11.030
    [16] Squires G L 2012 Introduction to the Theory of Thermal Neutron Scattering (Cambridge: Cambridge University Press
    [17] Fritzsche H, Huot J, Fruchart D 2016 Neutron Scattering and Othernuclear Techniques for Hydrogen in Materials (Cham: SpringerInternational Publishing
    [18] Wills B T M, Carlile C J 2009 Experimental Neutron Scattering (Oxford: Oxford University Press
    [19] Yamani Z, Ryan D H 2010 Can. J. Phys. 88 771 doi: 10.1139/P10-081
    [20] Bewley R I, Eccleston R S, McEwen K A, Hayden S M, Dove M T, Bennington S M, Treadgold J R, Coleman R L S 2006 Physics B (Amsterdam, Neth.) 385-386 1029 doi: 10.1016/j.physb.2006.05.328
    [21] Shirane G, Shapiro S M, Tranquada J M 2002 Neutron Scattering with a Triple-Axis Spectrometer: Basic Techniques (Cambridge University Press
    [22] Langel W 2023 ChemTexts 9 12 doi: 10.1007/s40828-023-00184-7
    [23] Chen M N, Wu J T, Huang Q, Jiao J, Dun Z L, Wang G H, Chen Z W, Lin G T, Rathinam V, Li C J, Pei Y Z, Ye F, Zhou H D, Ma J 2021 Front. Phys. 9 785801 doi: 10.3389/fphy.2021.785801
    [24] Ren Q Y, Gupta M K, Jin M, Ding J X, Wu J T, Chen Z W, Lin S Q, Fabelo O, Velamazan J A R, Kofu M, Nakajima K, Wolf M, Zhu J F, Wang J L, Cheng Z X, Wang G H, Tong X, Pei Y Z, Delaire O, Ma J 2023 Nat. Mater. 22 999 doi: 10.1038/s41563-023-01560-x
    [25] 王国华, 焦金龙, 马杰 2019 物理 48 715 doi: 10.7693/wl20191103 Wang G H, Jiao J L, Ma J 2019 Physics 48 715 doi: 10.7693/wl20191103
    [26] 马杰, 任清勇 2017 西北大学学报(自然科学版) 47 783 doi: 10.16152/j.cnki.xdxbzr.2017-06-001 Ma J, Ren Q Y 2017 J. Northw. Univ. (Nat. Sci. Ed.) 47 783 doi: 10.16152/j.cnki.xdxbzr.2017-06-001
    [27] 任清勇, 陈闽楠, 耿艳胜, 马杰, 童欣 2021 中国科学: 物理学 力学 天文学 51 123 Ren Q Y, Chen M N, Geng Y S, Ma J, Tong X 2021 Sci. Sin. Phys. Mech. Astron. 51 123
    [28] Ren Q Y, Qi J, Yu D H, Zhang Z, Song R Q, Song W L, Yuan B, Wang T H, Ren W J, Zhang Z D, Tong X, Li B 2022 Nat. Commun. 13 2293 doi: 10.1038/s41467-022-29997-9
    [29] Ren Q Y, Fu C G, Qiu Q Y, Dai S N, Liu Z Y, Masuda T, Asai S, Hagihala M, Lee S, Torri S, Kamiyama T, He L H, Tong X, Felser C, Singh D J, Zhu T J, Yang J, Ma J 2020 Nat. Commun. 11 3142 doi: 10.1038/s41467-020-16913-2
    [30] 任清勇, 王建立, 李昺, 马杰, 童欣 2025 物理学报 74 012801 doi: 10.7498/aps.74.20241178 Ren Q Y, Wang J L, Li B, Ma J, Tong X 2025 Acta Phys. Sin. 74 012801 doi: 10.7498/aps.74.20241178
    [31] Chen X, Weathers A, Carreys J, Mukhopadhyay S, Delaire O, Stewart D A, Mingo N, Girard S N, Ma J, Abernathy D L, Yan J, Sheshka R, Sellan D P, Meng F, Jin S, Zhou J, Shi L 2015 Nat. Commun. 6 6723 doi: 10.1038/ncomms7723
    [32] Wu J T, Lin Y F, Shu M F, Liu Y F, Ma Y P, Lin G T, Zhang C P, Jiao P F, Zhu F F, Wu Y, Ewings R A, Walker H C, Deng G C, Chi S X, Jiang S W, Baggioli M, Jin M, Wang H Z, Xie W W, Wei T R, Yang J, Shi X, Ma J 2024 Nat. Commun. 15 6248 doi: 10.1038/s41467-024-50249-5
    [33] Zhu J F, Shen X L, Ma J 2024 Innov. Energy 1 100049 doi: 10.59717/j.xinn-energy.2024.100049
    [34] Cordier G, Schäfer H, Stelter M 1984 Z. Anorg. Allg. Chem. 519 183 doi: 10.1002/zaac.19845191219
    [35] Holm A P, Olmstead M M, Kauzlarich S M 2003 Inorg. Chem. 42 1973 doi: 10.1021/ic020530r
    [36] Xia S Q, Bobev S 2007 Inorg. Chem. 46 874 doi: 10.1021/ic061958j
    [37] Xia S Q, Bobev S 2008 Inorg. Chem. 47 1919 doi: 10.1021/ic800242a
    [38] Suen N T, Wang Y, Bobev S 2015 J. Sol. State Chem. 227 204 doi: 10.1016/j.jssc.2015.03.031
    [39] Kim H, Condron C L, Holm A P, Kauzlarich S M 2000 J. Am. Chem. Soc. 122 10720 doi: 10.1021/ja002709b
    [40] Hu Y F, Cerretti G, Wille E L K, Bux S K, Kauzlarich S M 2019 J. Sol. State Chem. 271 88 doi: 10.1016/j.jssc.2018.12.037
    [41] Grebenkemper J H, Hu Y F, Barrett D, Gogna P, Huang C K, Bux S K, Kauzlarich S M 2015 Chem. Mater. 27 5791 doi: 10.1021/acs.chemmater.5b02446
    [42] Toberer E S, Cox C A, Brown S R, Ikeda T, May A F, Kauzlarich S M, Snyder G J 2008 Adv. Funct. Mater. 18 2795 doi: 10.1002/adfm.200800298
    [43] Justl A P, Ricci F, Pike A, Cerretti G, Bux S K, Hautier G, Kauzlarich S M 2022 Sci. Adv. 8 3780 doi: 10.1126/sciadv.abq3780
    [44] Mochel A, Sergueev I, Wille H C, Juranyi F, Schober H, Schweika W, Brown S R, Kauzlarich S M, Hermann R P 2011 Phys. Rev. B 84 184303 doi: 10.1103/PhysRevB.84.184303
    [45] Wang Y, Hu Y J, Firdosy S A, Star K E, Fleurial J P, Ravi V A, Chen L Q, Shang S L, Liu Z K 2018 J. Appl. Phys. 123 045102 doi: 10.1063/1.5013601
    [46] He A, Wille E L K, Moreau L M, Thomas S M, Lawrence J M, Bauer E D, Booth C H, Kauzlarich S M 2020 Phys. Rev. Mater. 4 114407 doi: 10.1103/PhysRevMaterials.4.114407
    [47] Hu M Y, Sturhahn W, Toellner T S, Mannheim P D, Brown D E, Zhao J Y, Alp E E 2003 Phys. Rev. B 67 094304 doi: 10.1103/PhysRevB.67.094304
    [48] Hermann R P, Grandjean F, Long G J 2005 Am. J. Phys. 73 110 doi: 10.1119/1.1783899
    [49] Ren F, Case E D, Sootsman J R, Kanatzidis M G, Kong H J, Uher C, Lara-Curzio E, Trejo R M 2008 Acta Mater. 56 5954 doi: 10.1016/j.actamat.2008.07.055
    [50] Jenkins J O, Rayne J A, and Ure R W 1972 Phys. Rev. B 5 3171 doi: 10.1103/PhysRevB.5.3171
    [51] Hanus R, George J, Wood M, Bonkowski A, Cheng Y Q, Abernathy D L, Manley M E, Hautier G, Snyder G J, Hermann R P 2021 Mater. Today Phys. 18 100344 doi: 10.1016/j.mtphys.2021.100344
    [52] Ribeiro R A, Hadano Y, Suekuni K, Avila M A, Takabatake T 2007 J. Phys. : Condens. Matter 19 376211 doi: 10.1088/0953-8984/19/37/376211
    [53] Toberer E S, Brown S R, Ikeda T, Kauzlarich S M, Snyder G J 2008 Appl. Phys. Lett. 93 062110 doi: 10.1063/1.2970089
    [54] Shi Q F, Yan Y L, Wang Y X 2014 Appl. Phys. Lett. 104 012104 doi: 10.1063/1.4860996
    [55] Zevalkink A, Toberer E S, Zeier W G, Larsenb E F, Snyder G J 2011 Energy Environ. Sci. 4 510 doi: 10.1039/C0EE00517G
    [56] Zevalkink A, Zeier W G, Pomrehn G, Schechtel E, Tremelb W, Snyder G J 2012 Energy Environ. Sci. 5 9121 doi: 10.1039/c2ee22378c
    [57] Pal K, Xia Y, Wolverton C 2021 npj Comp. Mater. 7 5 doi: 10.1038/s41524-020-00474-5
    [58] Wu M H, Huang Li 2019 Phys. Rev. B 100 075207 doi: 10.1103/PhysRevB.100.075207
    [59] Alekperov O Z, Nakhmedov E, Najafov A, Samedov O, Nadirova K, Gasymov V, Mahmudova G R 2020 J. Phys. D: Appl. Phys. 53 035103 doi: 10.1088/1361-6463/ab4ba5
    [60] Jana M K, Pal K, Warankar A, Mandal P, Waghmare U V, Biswas K 2017 J. Am. Chem. Soc. 139 4350 doi: 10.1021/jacs.7b01434
    [61] Cordier G, Schäfer H, Stelter M 1984 Zeitschrift für Naturforsch. B 39 727 doi: 10.1515/znb-1984-0605
    [62] Cordier G, Schäfer H, Stelter M 1987 Zeitschrift für Naturofsch. B 42 1268 doi: 10.1515/znb-1987-1011
    [63] Dutta M, Samanta M, Ghosh T, Voneshen D J, Biswas K 2021 Angew. Chem. Int. Ed. 60 4259 doi: 10.1002/anie.202013923
    [64] Lory P F, Pailhès S, Giordano V M, Euchner H, Nguyen H D, Ramlau R, Borrmann H, Schmidt M, Baitinger M, Ikeda M, Tomeš P, Mihalkovič M, Allio C, Johnson M R, Schober H, Sidis Y, Bourdarot F, Regnault L P, Ollivier J, Paschen S, Grin Y, Boissieu M D 2017 Nat. Commun. 8 491 doi: 10.1038/s41467-017-00584-7
    [65] Chen X X, Zhu J B, Qin D D, Qu N, Xue W H, Wang Y M, Zhang Q, Cai W, Guo F K, Sui J H 2021 Sci. China Mater. 64 1761 doi: 10.1007/s40843-020-1559-4
    [66] Xu Q, Zhao K P, Huang H R, Wang S, Ren Q Y, Hao X W, Wuliji H, Lei J D, Wei T R, Shi X 2024 Acta Mater. 274 120040 doi: 10.1016/j.actamat.2024.120040
    [67] Lei J D, Wuliji H, Ren Q Y, Hao X W, Chen H Y, Wei T R, Zhang J W, Qiu P F, Zhao K P, Shi X 2024 Energy Environ. Sci. 17 1416 doi: 10.1039/D3EE04164F
    [68] Luu S D N, Vaqueiro P 2016 J. Materiomics 2 131 doi: 10.1016/j.jmat.2016.04.002
    [69] Aydemir U, Zevalkink A, Ormeci A, Gibbs Z M, Bux S, Snyder G J 2015 Chem. Mater. 27 1622 doi: 10.1021/cm5042937
    [70] Aydemir U, Zevalkink A, Ormeci A, Bux S, Snyder G J 2016 J. Mater. Chem. A 4 1867 doi: 10.1039/C5TA07612A
    [71] Chanakian S, Weber R, Aydemir U, Ormeci A, Fleurial J P, Bux S, Snyder G J 2017 J. Electron. Mater. 46 4798 doi: 10.1007/s11664-017-5423-y
    [72] Kim S J, Kanatzidis M G 2001 Inorg. Chem. 40 3781 doi: 10.1021/ic010069n
    [73] Müller K H, Narozhnyi V N 2001 Rep. Prog. Phys. 64 943 doi: 10.1088/0034-4885/64/8/202
    [74] Canfield P C, Bud’ko S L 2010 Annu. Rev. Condens. Matter Phys. 1 27 doi: 10.1146/annurev-conmatphys-070909-104041
    [75] Ivanovskii A L 2011 Physics C 471 409 doi: 10.1016/j.physc.2011.04.009
    [76] Tan X Y, Tener Z P, Shatruk M 2018 Acc. Chem. Res. 51 230 doi: 10.1021/acs.accounts.7b00533
    [77] Kurosaki K, Uneda H, Muta H, Yamanaka S 2005 J. Appl. Phys. 97 053705 doi: 10.1063/1.1857061
    [78] Kurosaki K, Uneda H, Muta H, Yamanaka S 2005 J. Alloys Compd. 388 122 doi: 10.1016/j.jallcom.2004.06.086
    [79] Zhang H, Li S M, Li D D, Jin S F, Shen S J, Ying T P, Lin Z P, Li K K, Yuan D D, Zhao H Z 2015 Mater. Lett. 152 117 doi: 10.1016/j.matlet.2015.03.098
    [80] Lehr G J, Morelli D T, Jin H, Heremans J P 2015 J. Electron. Mater. 44 1663 doi: 10.1007/s11664-014-3509-3
    [81] Kunioka H, Kihou K, Kato D, Usui H, Iida T, Nishiate H, Kuroki K, Yamamoto A, Lee C H 2020 Inorg. Chem. 59 5828 doi: 10.1021/acs.inorgchem.9b02680
    [82] Gascoin F, Ottensmann S, Stark D, Haile S M, Snyder G J 2005 Adv. Funct. Mater. 15 1860 doi: 10.1002/adfm.200500043
    [83] May A F, McGuire M A, Singh D J, Custelcean R, Jellison G E 2011 Inorg. Chem. 50 11127 doi: 10.1021/ic2016808
    [84] Ang R, Khan A U, Tsujii N, Takai K, Nakamura R, Mori T 2015 Angew. Chem. 127 13101 doi: 10.1002/ange.201505517
    [85] Cao Q G, Zheng J, Zhang K, Ma G 2016 J. Alloys Compd. 680 278 doi: 10.1016/j.jallcom.2016.04.118
    [86] Peng W Y, Chanakian S, Zevalkink A 2018 Inorg. Chem. Front. 5 1744 doi: 10.1039/C7QI00813A
    [87] Shuai J, Geng H Y, Lan Y C, Zhu Z, Wang C, Liu Z, Bao J M, Chu C W, Sui J H, Ren Z F 2016 Proc. Natl. Acad. Sci. U. S. A 113 E4125 doi: 10.1073/pnas.1608794113
    [88] Shuai J, Liu Z, Kim H S, Wang Y M, Mao J, He R, Sui J H, Ren Z F 2016 J. Mater. Chem. A 4 4312 doi: 10.1039/C6TA00507A
    [89] Toberer E S, May A F, Melot B C, Larsend E F, Snyder G J 2010 Dalton Trans. 39 1046 doi: 10.1039/B914172C
    [90] May A F, McGuire M A, Ma J, Delaire O, Huq A, Custelcean R 2012 J. Appl. Phys. 111 033708 doi: 10.1063/1.3681817
    [91] Ding J X, Lanigan-Atkins T, Calderón-Cueva M, Banerjee A, Abernathy D L, Said A, Zevalkink A, Delaire O 2021 Sci. Adv. 7 1449 doi: 10.1126/sciadv.abg1449
    [92] Xin H X, Qin X Y, Jia J H, Song C J, Zhang K X, Zhang J 2009 J. Phys. D: Appl. Phys. 42 165403 doi: 10.1088/0022-3727/42/16/165403
    [93] Zhang K X, Qin X Y, Xin H X, Zhang J 2009 J. Alloys Compd. 484 498 doi: 10.1016/j.jallcom.2009.04.130
    [94] Bhardwaj A, Rajput A, Shukla A K, Pulikkotil J J, Srivastava A K, Dhar A, Gupta G, Auluck S, Misra D K, Budhani R C 2013 RSC Adv. 3 8504 doi: 10.1039/c3ra40457a
    [95] Bhardwaj A, Misra D K 2014 RSC Adv. 4 34552 doi: 10.1039/C4RA04889J
    [96] Shuai J, Wang Y M, Kim H S, Liu Z, Sui J H, Chen S, Sui J H, Ren Z F 2015 Acta Mater. 93 187 doi: 10.1016/j.actamat.2015.04.023
    [97] Tamaki H, Sato H K, Kanno T 2016 Adv. Mater. 28 10182 doi: 10.1002/adma.201603955
    [98] Song L R, Zhang J W, Iversen B B 2017 J. Mater. Chem. A 5 4932 doi: 10.1039/C6TA08316A
    [99] Zhang J W, Song L R, Pedersen S H, Yin H, Hung L T, Iversen B B 2017 Nat. Commun. 8 13901 doi: 10.1038/ncomms13901
    [100] Zhang J W, Song L R, Sist M, Tolborg K, Iversen B B 2018 Nat. Commun. 9 4716 doi: 10.1038/s41467-018-06980-x
    [101] Li A, Hu C L, He B, Yao M Y, Fu C G, Wang Y C, Zhao X B, Felser C, Zhu T J 2021 Nat Commun. 12 5408 doi: 10.1038/s41467-021-25722-0
    [102] Zhu Y F, Xia Y, Wang Y C, Sheng Y, Yang J, Fu C G, Li A R, Zhu T J, Luo J, Wolverton C, Snyder G J, Liu J J, Zhang W Q 2020 Research 2020 4589786 doi: 10.34133/2020/4589786
    [103] Maccioni M B, Farris R, Fiorentini V 2018 Phys. Rev. B 98 220301 doi: 10.1103/PhysRevB.98.220301
    [104] Kim S H, Kim C M, Hong Y K, Sim K I, Kim J H, Onimaru T, Takabatake T, Jung M H 2015 Mater. Res. Express 2 055903 doi: 10.1088/2053-1591/2/5/055903
    [105] Xin J, Li G, Auffermann G, Borrmann H, Schnelle W, Gooth J, Zhao X, Zhu T J, Felser C, Fu C G 2018 Mater. Today Phys. 7 61 doi: 10.1016/j.mtphys.2018.11.004
    [106] Jin M, Lin S Q, Li W, Zhang X Y, Pei Y Z 2021 Mater. Today Phys. 21 100508 doi: 10.1016/j.mtphys.2021.100508
    [107] Zhang J W, Song L R, Iversen B B 2019 npj Comp. Mater. 5 76 doi: 10.1038/s41524-019-0215-y
    [108] Peng W Y, Petretto G, Rignanese G M, Hautier G, Zevalkink A 2018 Joule 2 1879 doi: 10.1016/j.joule.2018.06.014
    [109] Pauling L 1960 The Nature of the Chemical Bond (Vol. 260) (Cornell University Press
    [110] Kanno T, Tamaki H, Yoshiya M, Uchiyama H, Maki S, Takata M, Miyazaki Y 2021 Adv. Funct. Mater. 31 2008469 doi: 10.1002/adfm.202008469
    [111] He H, Tyson C, Bobev S 2011 Inorg. Chem. 50 8375 doi: 10.1021/ic2009418
    [112] Ono K, Kihou K, Usui H, Kuroki K, Goto Y, Lee C H 2023 ACS Omega 8 42900 doi: 10.1021/acsomega.3c06021
    [113] Khatun M, Stoyko S S, Mar A 2013 Inorg. Chem. 52 3148 doi: 10.1021/ic302627n
    [114] Ishida J, Iimura S, Hosono H 2018 Inorg. Chem. 57 4997 doi: 10.1021/acs.inorgchem.8b00018
    [115] Yamashita A, Kihou K, Kunioka H, Nishiate H, Yamamoto A, Goto Y, Mizuguchi Y, Iida T, Takano Y, Lee C H 2020 J. Sol. State Chem. 291 121588 doi: 10.1016/j.jssc.2020.121588
    [116] Courteau B, Gvozdetskyi V, Lee S, Cox T, Zaikina J V 2022 Z. Anorg. Allg. Chem. 648 e202200095 doi: 10.1002/zaac.202200095
    [117] Gvozdetskyi V, Owens-Baird B, Hong S, Cox T, Bhaskar G, Harmer C, Sun Y, Zhang F, Wang C Z, Ho K M, Zaikina J V 2019 Chem. Mater. 31 8695 doi: 10.1021/acs.chemmater.9b02239
    [118] Ovchinnikov A, Bobev S 2019 J. Sol. State Chem. 270 346 doi: 10.1016/j.jssc.2018.11.029
    [119] Shuai J, Mao J, Song S W, Zhu Q, Sun J F, Wang Y M, He R, Zhou J W, Chen G, Singh D J, Ren Z F 2017 Energy Environ. Sci. 10 799 doi: 10.1039/C7EE00098G
    [120] Sangeeta, Kumar R, Singh M 2022 J. Mater. Sci. 57 10691 doi: 10.1007/s10853-022-06953-y
    [121] Bessas D, Sergueev I, Wille H C, Person J, Ebling D, Hermann R P 2012 Phys. Rev. B 86 224301 doi: 10.1103/PhysRevB.86.224301
    [122] Nielsen J W, Baenziger N C 1954 Acta Cryst. 7 132 doi: 10.1107/S0365110X5400031X
    [123] Zhu J F, Ren Q Y, Chen C, Wang C, Shu M F, He M, Zhang C P, Le M D, Torri S, Wang C W, Wang J L, Cheng Z X, Li L S, Wang G H, Jiang Y X, Wu M Z, Qu Z, Tong X, Chen Y, Zhang Q, Ma J 2024 Nat. Commun. 15 2618 doi: 10.1038/s41467-024-46895-4
    [124] Wilson D K, Saparov B, Bobev S 2011 Z. Anorg. Allg. Chem. 637 2018 doi: 10.1002/zaac.201100177
    [125] Li Y H, Zhang T, Zeng Z Y, Chen X R, Geng H Y 2022 J. Phys. : Condens. Matter 34 495701 doi: 10.1088/1361-648X/ac9722
    [126] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2006 Appl. Phys. Lett. 89 092108 doi: 10.1063/1.2339886
    [127] Feng Z Z, Fu Y H, Zhang Y S, Singh D J 2021 Phys. Rev. B 103 224101 doi: 10.1103/PhysRevB.103.224101
    [128] Zhang W M, Chen C, Yao H H, Xue W H, Li S, Bai F X, Huang Y F, Li X F, Lin X, Cao F, Sui J H, Wang S F, Yu B, Wang Y M, Liu X J, Zhang Q 2020 Chem. Mater. 32 6983 doi: 10.1021/acs.chemmater.0c02317
    [129] Zhou Z Z, Peng K L, Wu H X, Wang G Y, Zhou X Y 2021 Phys. Rev. Appl. 16 064034 doi: 10.1103/PhysRevApplied.16.064034
    [130] Chen C, Xue W H, Li S, Zhang Z W, Li X F, Wang X Y, Liu Y J, Sui J H, Liu X J, Cao F, Ren Z F, Chu C W, Wang Y M, Zhang Q 2019 Proc. Natl. Acad. Sci. U. S. A 116 2831 doi: 10.1073/pnas.1819157116
    [131] Chen C, Feng Z Z, Yao H H, Cao F, Lei B H, Wang Y M, Chen Y, Singh D J, Zhang Q 2021 Nat. Commun. 12 5718 doi: 10.1038/s41467-021-25483-w
    [132] Wang C, Wang Q, Zhang Q, Chen C, Chen Y 2022 Chem. Mater. 34 7837 doi: 10.1021/acs.chemmater.2c01430
    [133] Chanakian S, Peng W Y, Meschke V, Shawon A K M A, Adamczyk J, Petkov V, Toberer E, Zevalkink A 2023 Angew. Chem. Int. Ed. 62 e202301176 doi: 10.1002/anie.202301176
    [134] Dolyniuk J A, Owens-Baird B, Wang J, Zaikina J V, Kovnir K 2016 Mater. Sci. Eng. R 108 1 doi: 10.1016/j.mser.2016.08.001
    [135] Luo H, Krizan J W, Muechler L, Haldolaarachchige N, Klimczuk T, Xie W, Fuccillo M K, Felser C, Cava R J A 2015 Nat. Commun. 6 6489 doi: 10.1038/ncomms7489
  • 加载中
图( 16)
计量
  • 文章访问数:  784
  • HTML全文浏览数:  784
  • PDF下载数:  8
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-21
  • 刊出日期:  2025-01-05

中子散射技术在Zintl相化合物热导率研究中的应用

    通讯作者: E-mail: jma3@sjtu.edu.cn.
    作者简介: 张翠萍. E-mail: zhangcuiping@sjtu.edu.cn
  • 1. 上海交通大学物理与天文学院, 上海　200240
  • 2. 散裂中子源科学中心, 东莞　523803
  • 3. 中国科学院高能物理研究所, 北京　100049
  • 4. 广东省极端条件重点实验室, 东莞　523803
  • 收稿日期:  2024-08-21

摘要: Zintl相化合物因为其独特的晶体结构和优异的输运性能, 在能源存储及转换领域尤其是热电材料应用中受到广泛关注. 为了理解Zintl相化合物优异热电性能起源, 科研工作者们利用中子散射技术结合分子动力学模拟, 对晶格热导和电声耦合效应展开研究, 取得了一系列成果. 本文系统总结了中子散射对一些Zintl相化合物的结构及其晶格动力学的相关研究工作, 按照零维A14MPn11型化合物、一维链状化合物、二维层状AB2X2型化合物和其结构变体AB4X3型化合物, 层状ZrBeSi结构Zintl相化合物的顺序依次梳理了其低晶格热导率的物理起源. 通过中子衍射技术探讨了晶体结构、原子位移参数等信息; 围绕中子非弹性散射实验, 探讨了声子态密度的测量方法及其对Zintl相化合物动力学性质的研究. 在深入认识Zintl相化合物的同时, 揭示了其微观结构和优化材料性能, 以期对设计新型热电功能材料具有一些启发.

English Abstract

    全文HTML

    1.   引　言

    • 自20世纪80年代以来, 由于日益增长的能源消耗和环境污染问题, 人类开始寻找新的清洁且可再生能源, 并努力提高现有能源利用率. 热电转换材料具有能够将热能转化为电能的技术, 显示了其废热收集应用的潜力. 热电材料性能可以由无量纲的热电优值(ZT值)来描述, $ ZT={S}^{2}\sigma T/({\kappa }_{{\mathrm{L}}}+ {\kappa }_{{\mathrm{e}}}) $, 其中$ S $是塞贝克系数, $ \sigma $是电导率, T是绝对温度, $ {\kappa }_{{\mathrm{L}}} $是晶格热导率, $ {\kappa }_{{\mathrm{e}}} $是电子热导率[1]. 因此, 理想的热电材料需要具有优异的电学性能和低的热输运性质. 但是, 由于电子电导和热导具有强耦合, 仅通过电子调控实现高热电性能十分困难. 从热导率角度来看, 电子和晶格的贡献可以很好地解离: 电子热导率可以通过维德曼-弗朗茨定律$ {\kappa }_{{\mathrm{e}}}=L\sigma T $ (L是洛伦兹常数)估算得到, 而晶格热导率可以独立表示为$ {\kappa }_{{\mathrm{L}}}={1}/{3}{c}_{{\mathrm{v}}}{v}_{{\mathrm{g}}}l={1}/{3}{c}_{{\mathrm{v}}}{v}_{{\mathrm{g}}}^{2}\tau $, 其中$ {c}_{{\mathrm{v}}} $为定容热容, $ {v}_{{\mathrm{g}}} $为声子群速度, l为平均自由程, $ \tau $为声子寿命. 由此可见, 降低晶格热导率是一种直接提高热电优值的有效办法.

      随之而来, 科研工作者们提出了“电子晶体, 声子玻璃”思路[2], 即将材料的电子相关输运和晶格相关输运分为两个功能区域, 为独立调控电、晶格性能提供了设计空间. 作为一类以离子键和共价键共存为主要特征的金属间化合物, Zintl相化合物完美契合了这一概念[3,4]. 一方面, 阳离子可以复合阴离子或金属体的共价键网络提供利于电子迁移的通道, 从而使其具有“电子晶体”的特征; 另一方面, 阳离子还作为声子散射中心, 扮演“声子玻璃”的角色. 经过多年的发展, Zintl相化合物已经从二元相扩展到多元相, 而且相关的元素也从碱金属等扩充到过渡金属和稀土元素[5]. 同时, 一系列“离子键+共价键”的新化合物被不断合成, 这种具有新结构类型和原子结合模式的广义Zintl展现出各种有趣的物理性能, 大大丰富了热电材料的范畴. 在这些具有潜在热电应用的Zintl相化合物中, 根据其共价键框架的晶体结构性质, 可从维度的角度分为零维、一维、二维和三维Zintl相化合物[6–15]. 其中, 研究最广的材料主要有零维亚晶格的A14MPn11型化合物(如Yb14MnSb11, Yb14MgSb11, Ca14AlSb11等)[7]、一维链状A3BX3型化合物(如Sr3GaSb3, Ga3AlSb3, Sr3AlSb3等)[8]、二维层状AB2X2型化合物(如CaMg2Sb2, Mg3Bi2, Mg3Sb2等)[9,10]. 这些研究不仅改善了Zintl相的ZT值, 优化了其稳定性, 还衍生出了一些新的科学探索, 例如熵工程[9]、化学掺杂[11]、能带工程[13–15]等.

      作为热输运的主要贡献, 晶格热导率尽管是一个容易独立调控的物理量, 但受限于晶体生长和仪器测试技术, 与之密切相关的晶格动力学研究十分有限. 中子散射技术是研究晶体结构和晶格动力学的直接手段, 可以在全空间、全能量对结构及晶格动力学开展精细测量. 本文首先简要介绍中子散射技术的基本原理及其测试技术. 其次, 阐述中子散射技术在不同维度的Zintl相化合物研究中的应用实例, 对比中子散射技术和其他宏观物性测量的差别与联系, 并总结不同维度的Zintl相化合物低热导起源. 最后讨论目前Zintl相化合物研究存在的挑战和对未来发展的展望.

    2.   中子散射技术

    • 本节首先介绍中子散射基本原理和散射截面的概念, 然后简要概述中子衍射和非弹性中子散射技术原理[16–33].

      • 2.1.   中子散射基本原理

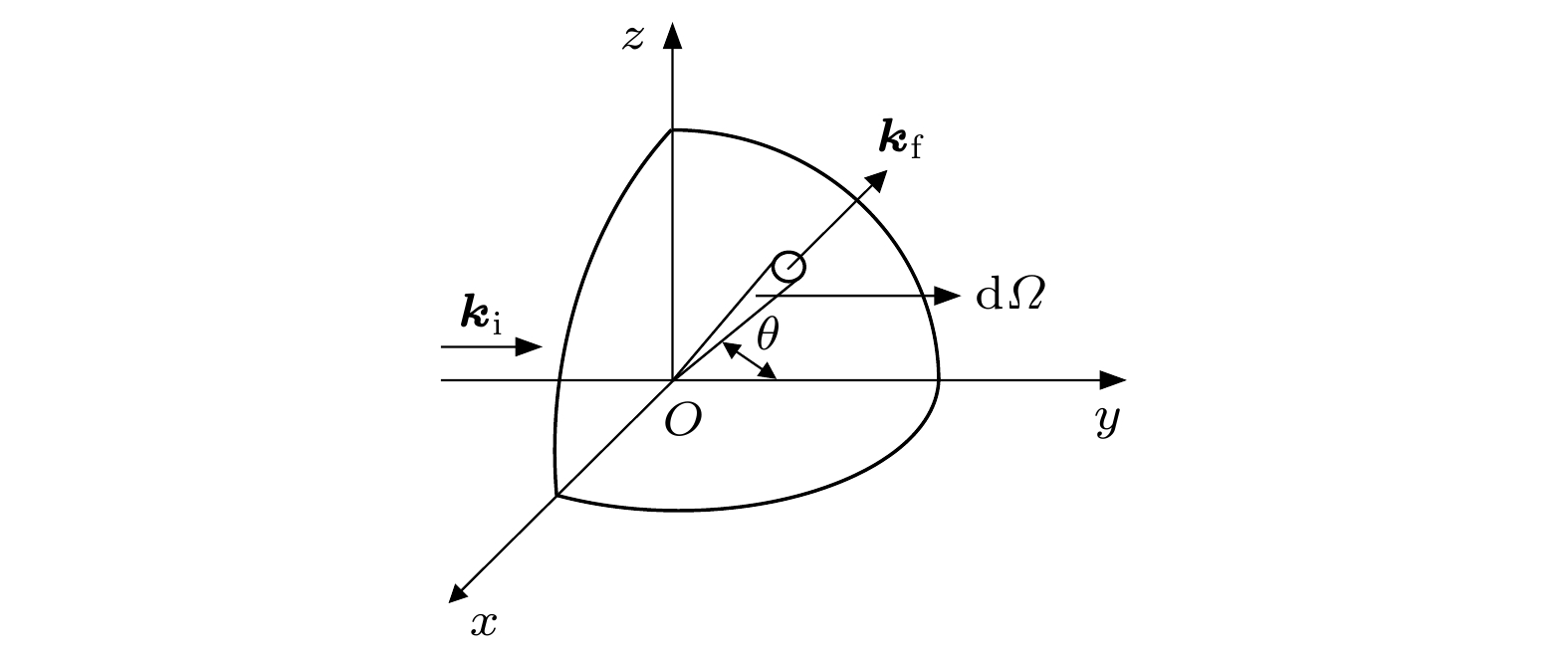
    • 中子散射技术如图1所示, 入射中子的波矢为ki, 与原子作用后的出射中子波矢为kf, 散射矢量为Q, 散射过程满足动量守恒和能量守恒定律:

      如果散射前后中子能量没有变化, 则为弹性散射; 如果中子能量有变化, 则为非弹性散射.

      散射过程中测试的物理量是微分散射截面, 即$ {{\mathrm{d}}}^{2}\sigma /\left({\mathrm{d}}\varOmega {\mathrm{d}}{E}_{{\mathrm{f}}}\right) $. 对应到中子散射实验中, 微分散射截面表示单位时间内探测器上接收到的中子数目, 探测器通过计算单位时间内散射到立体角$ {\mathrm{d}}\varOmega $内、能量在$ {E}_{{\mathrm{f}}} $到$ {E}_{{\mathrm{f}}}+{\mathrm{d}}{E}_{{\mathrm{f}}} $之间的中子数量来测量$ {{\mathrm{d}}}^{2}\sigma /\left({\mathrm{d}}\varOmega {\mathrm{d}}{E}_{{\mathrm{f}}}\right) $. 另一方面, 微分散射截面可以通过量子力学计算确定, 微分散射截面的一般表达式由van Hove导出[16], 称为van Hove散射函数或动态结构因子$ S\left(\boldsymbol{Q}, \omega \right) $:

      其中, 因子$ {A}_{{\boldsymbol{k}}_{{\mathrm{i}}}, {\boldsymbol{k}}_{{\mathrm{f}}}} $依赖于ki和kf, 这给实验数据和理论计算的定量比较提供了很大的方便.

      • 2.2.   中子衍射

    • 弹性中子散射也被称为中子衍射, 此时$ \boldsymbol{Q} $恰好为晶格倒格矢, 满足布拉格定律, 衍射图样中布拉格峰的强度取决于它的结构因子$ F\left(\boldsymbol{Q}\right) $, 对于理想晶体:

      其中b为散射长度, l是对单胞内的原子坐标求和, $ {{\bar b}_{l}} $为单胞内原子的散射长度的平均值, $ \left\langle{{U}^{2}}\right\rangle $是原子的均方位移. $ {\mathrm{e}}{\mathrm{x}}{\mathrm{p}}\left\langle{{U}^{2}}\right\rangle={\mathrm{e}}{\mathrm{x}}{\mathrm{p}}\left\langle{-2 W}\right\rangle $为德拜-沃勒(Debye-Waller)因子, 表示特定温度下, 由于原子热运动导致的弹性散射强度的衰减程度. 除了热运动, 原子振动通常也会受到晶格畸变与内应力的影响, 原子位移参数(atomic displacement parameter, ADP)是量化原子位移大小的物理量, 反映材料内部的原子键合环境. 中子衍射不仅可以用于研究物质的晶体结构, 得到晶格参数、原子占位、热振动等信息, 还可以通过变温实验给出这些参数随温度的变化趋势, 从而评估非谐性.

      • 2.3.   非弹性中子散射

    • 声子的能量和波矢之间的关系称为声子色散关系, 反映了晶格的动力学特征. 在晶体中, 中子的非弹性散射可视为中子与声子之间能量和动量交换的过程. 对于单晶样品, 能够提供声子色散谱的信息; 而在多晶样品中, 可以测量声子态密度. 在实验中, 可以通过分析声子色散关系的线宽来推导声子寿命, 并进一步判断声子谱的软化或硬化特性, 从而评估材料的非谐性. 结合理论计算, 解释与晶格动力学相关的物理现象.

    3.   中子散射技术在Zintl相化合物中的应用

    • Zintl相化合物由电负性差异较大的阴离子和阳离子构成, 阴离子之间通过共价键连接, 形成复杂的亚结构. Zintl相化合物的结构介于传统离子化合物和金属间化合物之间, 兼具离子键和共价键的特性. 这种独特结构使得Zintl相化合物符合“电子晶体-声子玻璃”概念: 阴离子基团通过共价键形成的亚结构, 有效提升了载流子的迁移率, 赋予其“电子晶体”特性; 阳离子基团则通过掺杂或元素替代来散射声子, 从而实现低晶格热导率的“声子玻璃”特性. 凭借这种结构优势, Zintl相化合物在热电材料的研究与应用中展现出重要潜力. 从维度出发, 可以将Zintl相化合物划分成: 1)零维孤立体系; 2)一维链状体系; 3)二维分层体系; 4)三维块状体系. 下面将围绕不同维度分别开展论述, 并应用中子衍射和对分布函数等技术分析其微观结构, 非弹性中子散射技术探讨声子色散谱和态密度, 并结合宏观输运性质测量及理论计算, 研究不同维度的Zintl相化合物低晶格热导率的物理起源.

      • 3.1.   零维孤立体系

    • Ca14AlSb11是首个被发现的零维亚晶格Zintl相化合物, 该体系的分子式为A14MPn11. 通常A是较重的碱土或二价稀土元素(Ca, Sr, Ba, Eu或Yb), M是主族元素或过渡金属(Al, Mn, Zn, Ga, Nb, In或Cd), 而Pn是碳族元素(P, As, Sb或Bi)[34–42]. A14MPn11型Zintl相化合物有3种类似的结构, 通过[MPn4]9–四面体的连接方式区分. 第1种连接方式是4个[MPn4]9–四面体通过边缘连接形成一个孤立的[M4Pn10]22–单元, 其中4个M原子在一条直线上[35,36]. 第2种方式是两个[MPn4]9–四面体通过边缘连接形成M2Pn6单元, 然后两个M2Pn6单元通过一个额外的Pn与单元内的一个Pn相连, 形成Pn—Pn键, 最终形成[M4Pn12]28–单元[37,38]. 第3种结构最常见, 它是在第2种连接类型中额外的Pn原子被另一个M4Pn11单元取代, 形成[M8Pn22]48–聚合物, 两个M4Pn11单元间通过Pn—Pn键连接[39–42]. 与其他Zintl相结构类型相比, A14MPn11是一种非常稳定的结构类型, 具有很大的灵活性. 对热电材料而言, 可以在很宽的范围内调节元素种类, 调控载流子浓度等各种性质. 典型的A14MPn11型Zintl相化合物包括Ca14AlSb11, Yb14MgSb11, Yb14MnSb11等.

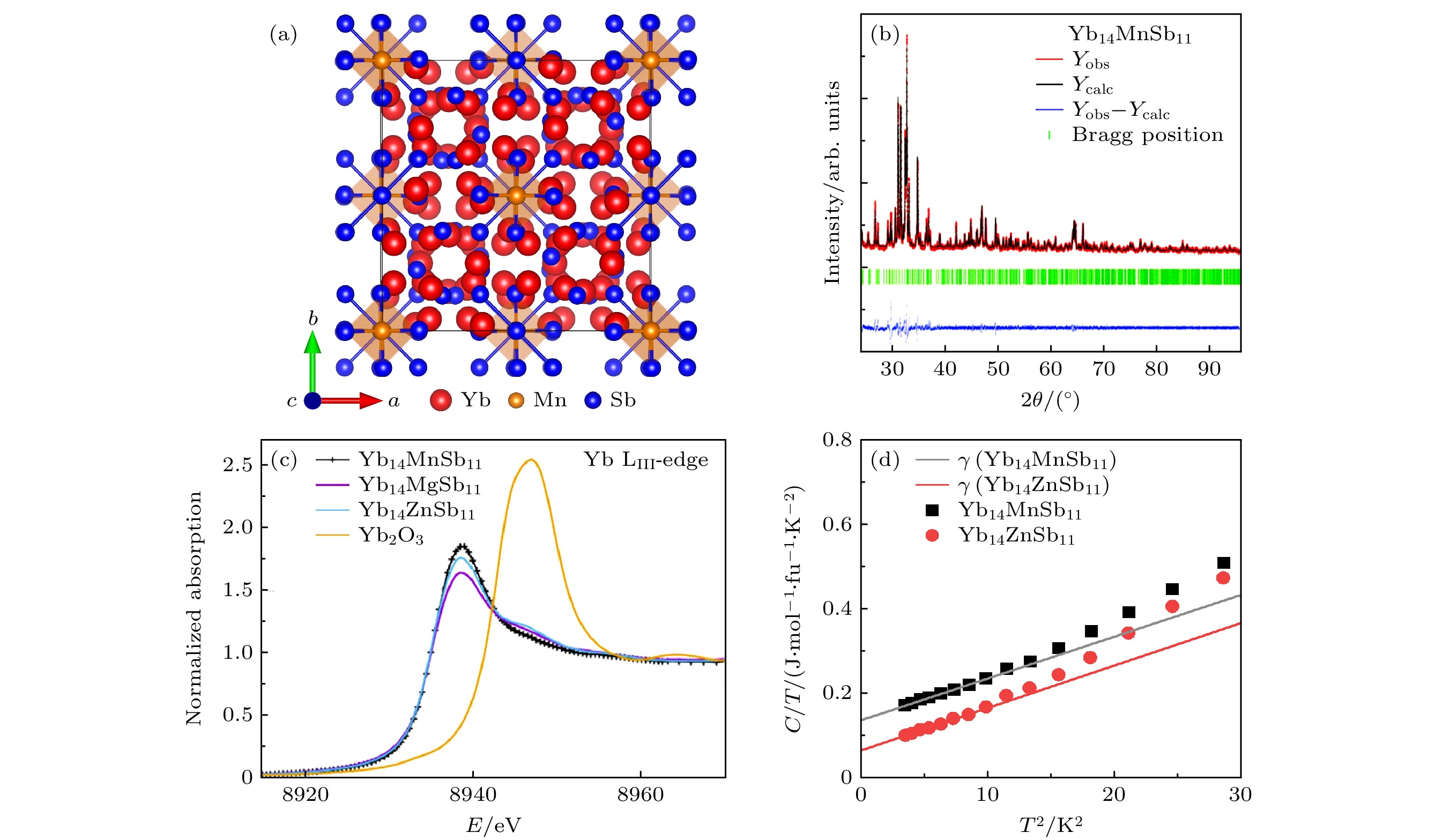
      长期以来, Yb14MnSb11是性能最好的p型热电Zintl相化合物之一, 其ZT值在1200 K时约达到1.2[43]. 如图2(a)所示, Yb14MnSb11的晶体结构(空间群: I41/acd)由[MnSb4]9–四面体和[Sb3]7–线性单元以及Sb3–阴离子和Yb2+阳离子构成, 图2(b)为Yb14MnSb11的粉末X射线衍射图谱[44]. Yb14MnSb11的晶胞内含有104个原子, 是一种大晶胞复杂结构材料, 室温下$ {\kappa }_{{\mathrm{L}}} $仅约为0.8 W/(m·K), 热导率在300—1200 K之间几乎不依赖于温度[42,43]. 这种低$ {\kappa }_{{\mathrm{L}}} $往往归因于重原子组成的大单元导致的结构复杂性, Wang等[45]通过第一性原理计算了Yb14MnSb11的声子谱, 表明低$ {\kappa }_{{\mathrm{L}}} $源于复杂晶体结构导致的强声子散射. 对热导率影响较大的低能区(0—3.39 THz)声子呈现出宽带, 这部分声子主要源于晶体结构中不同团簇的耦合. 此外, Mn原子的局域振动在较高频率处形成3个孤立的峰, 这种局域化的振动模式进一步增强了声子的散射, 从而减小了声子的平均自由程, 导致Yb14MnSb11的$ {\kappa }_{{\mathrm{L}}} $较低.

      除了考虑晶体结构对声子散射的影响外, 还需综合电子结构的影响. 2020年, He等[46]通过X射线吸收光谱(X-ray absorption near edge structure, XANES)实验分析了Yb14MnSb11中Yb的价态, 实验结果表明, Yb的价态为2+和3+之间的中间价态(图2(c)) (Yb2+的吸收峰低于8940 eV, Yb3+的吸收峰接近8944 eV). 这种价态波动会引入额外的散射机制, 从而增强了声子散射. 此外, 用公式$ C/T=\gamma +A{T}^{2} $拟合低温比热数据(图2(d)), 以分离电子比热($ \gamma T $)和晶格比热($ A{T}^{3} $)的贡献, 其中$ \gamma $为电子比热的线性系数(Sommerfeld系数), 直接反映了电子态密度的变化. 低温下电子比热有显著贡献, 也表明材料的热性能(低$ {\kappa }_{{\mathrm{L}}} $)与其Yb的价态波动密切相关.

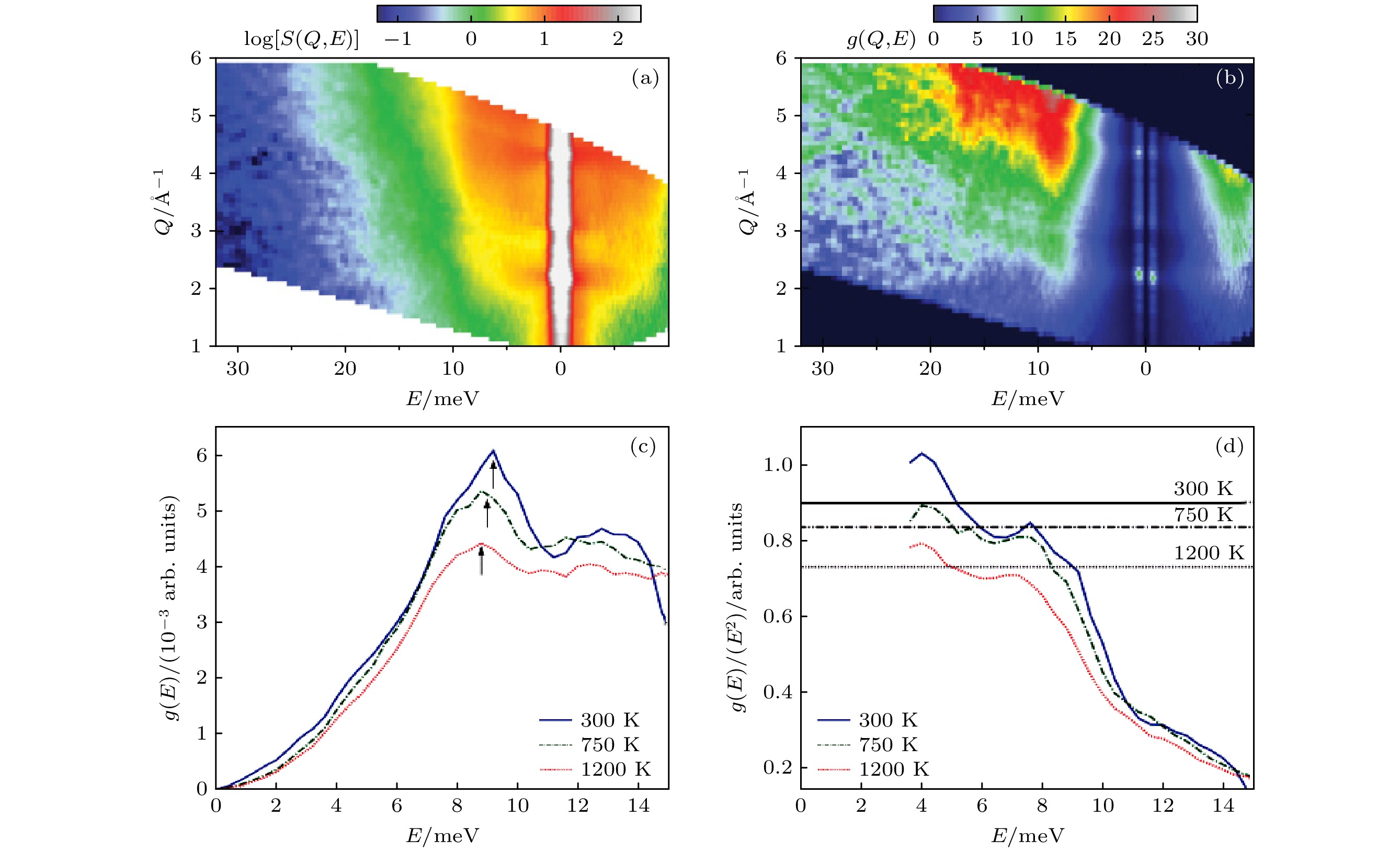
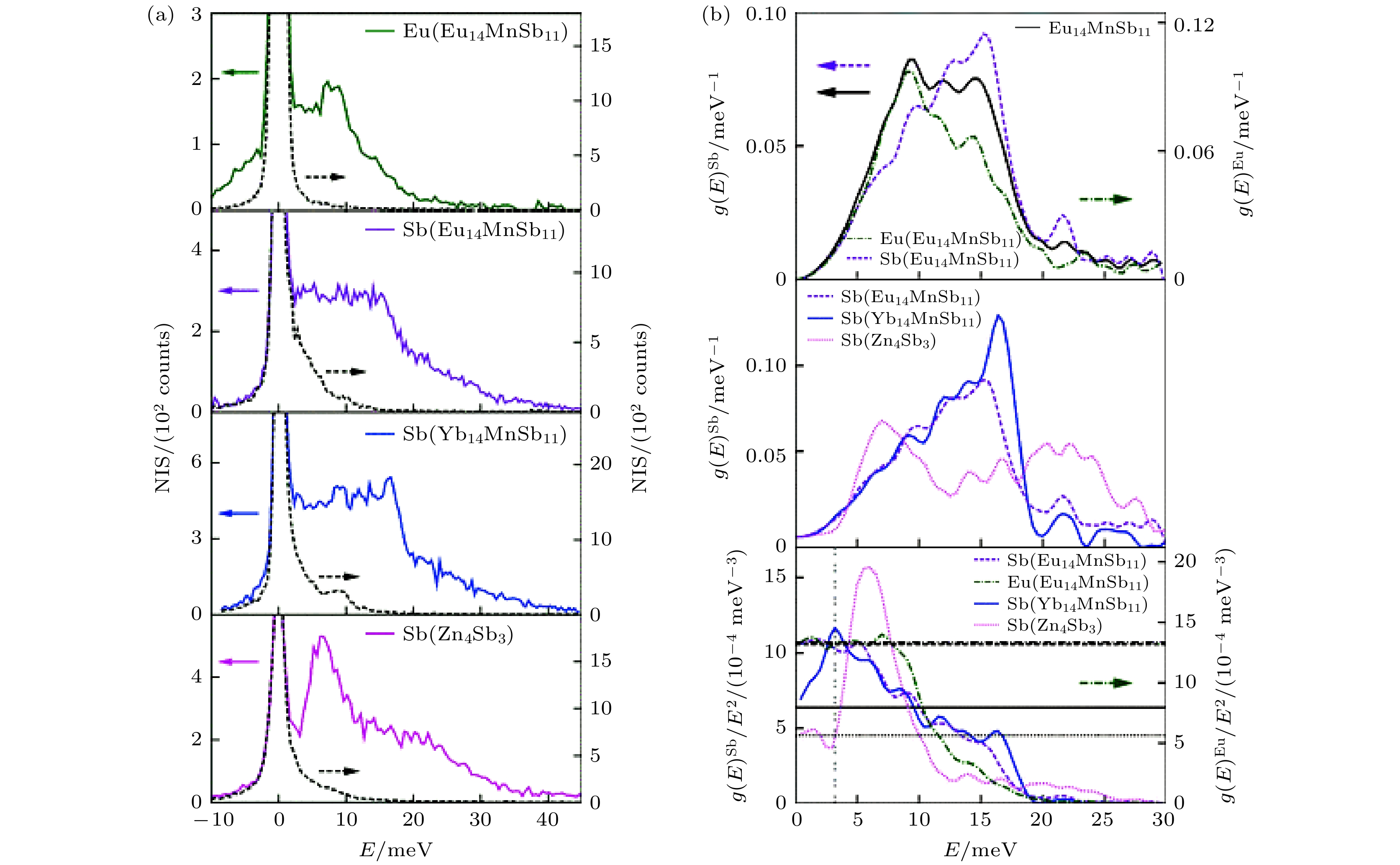
      2011年, Mochel等[44]利用非弹性中子散射技术直接测量声子谱, 从微观层面探讨了低声速是其低$ {\kappa }_{{\mathrm{L}}} $的重要原因. 为了检查变温后晶体结构变 化的影响, 他们首先通过非弹性中子散射数据的 弹性峰积分得到了中子衍射图, 没有观察到新的 第二相衍射峰. 图3(a), (b)展示了非弹性中子 散射的声子态密度数据, 所有的声子模式都低于25 meV, 在~10 meV处观察到一个相对尖锐的声子带, 在12—20 meV之间观察到一个宽频带. 在声子态密度的数据中可以观察到声子模式随温度 的展宽(图3(c), (d)), 约化后的数据显示德拜能级($ \underset{E\to 0}{{\mathrm{lim}}} [g(E)/{E}^{2}] $)随着温度的升高而降低, 表明声速随温度的升高而增加($ {\nu }_{{\mathrm{s}}}^{3} \sim 1/\left\{\underset{E\to 0}{{\mathrm{lim}}}[g(E)/{E}^{2}]\right\} $)[47], 然而由于中子信号背底扣除和归一化的问题, 声速变化需要进一步实验分析. 为研究这种低能光学模式的起源, 有必要对特定元素的分波声子态密度(partial phonon density-of-states, PDOS)进行分析.

      鉴于无法通过核非弹性散射(nuclear inelastic scattering, NIS)测量Yb的分波声子态密度, Mochel等[44]采用等结构化合物Eu14MnSb11中Eu的分波声子态密度作为替代, Eu14MnSb11, Yb14MnSb11的德拜温度和121Sb的分波声子态密度相似(图4(a)), 证明了Yb与Eu的声子模式非常相似. 此外, Mn原子质量较小, 声子模式处于较高的能量范围内, 且晶胞内Mn原子数量较少, 对晶格动力学的影响很小, 在此可忽略Mn对总声子态密度的贡献. 核非弹性散射测量的Eu的分波声子态密度分布(图4(b))在20 meV以下, 峰值在8 meV, 表明低能光学模式主要与Eu14MnSb11中的Eu和Yb14MnSb11中的Yb动力学有关. 结合理论计算[48], 可以得到Yb14MnSb11的声速为1880 (50) m/s, 与PbTe (1840 m/s)[49]和Bi2Te3 (1770 m/s)[50]的声速范围相当, 比Zn4Sb3 (2470 m/s)等其他锑化物低, 表明Yb14MnSb11的低$ {\kappa }_{{\mathrm{L}}} $与低声速有关. 根据非弹性中子散射技术测量到的声子谱, 声子模式分布在低能量范围内(图3(a), (b)), 低声速应与较低的力常数和软的化学键有关. 从分波声子态密度可以得到Sb原子的平均力常数为85 N/m, 显著低于其他锑化物(如Zn4Sb3的131 N/m), 表明Yb14MnSb11的化学键较软. 因此, 原子间的软化学键以及较大的晶胞体积被认为是Yb14MnSb11具有低声速(低$ {\kappa }_{{\mathrm{L}}} $)的重要原因.

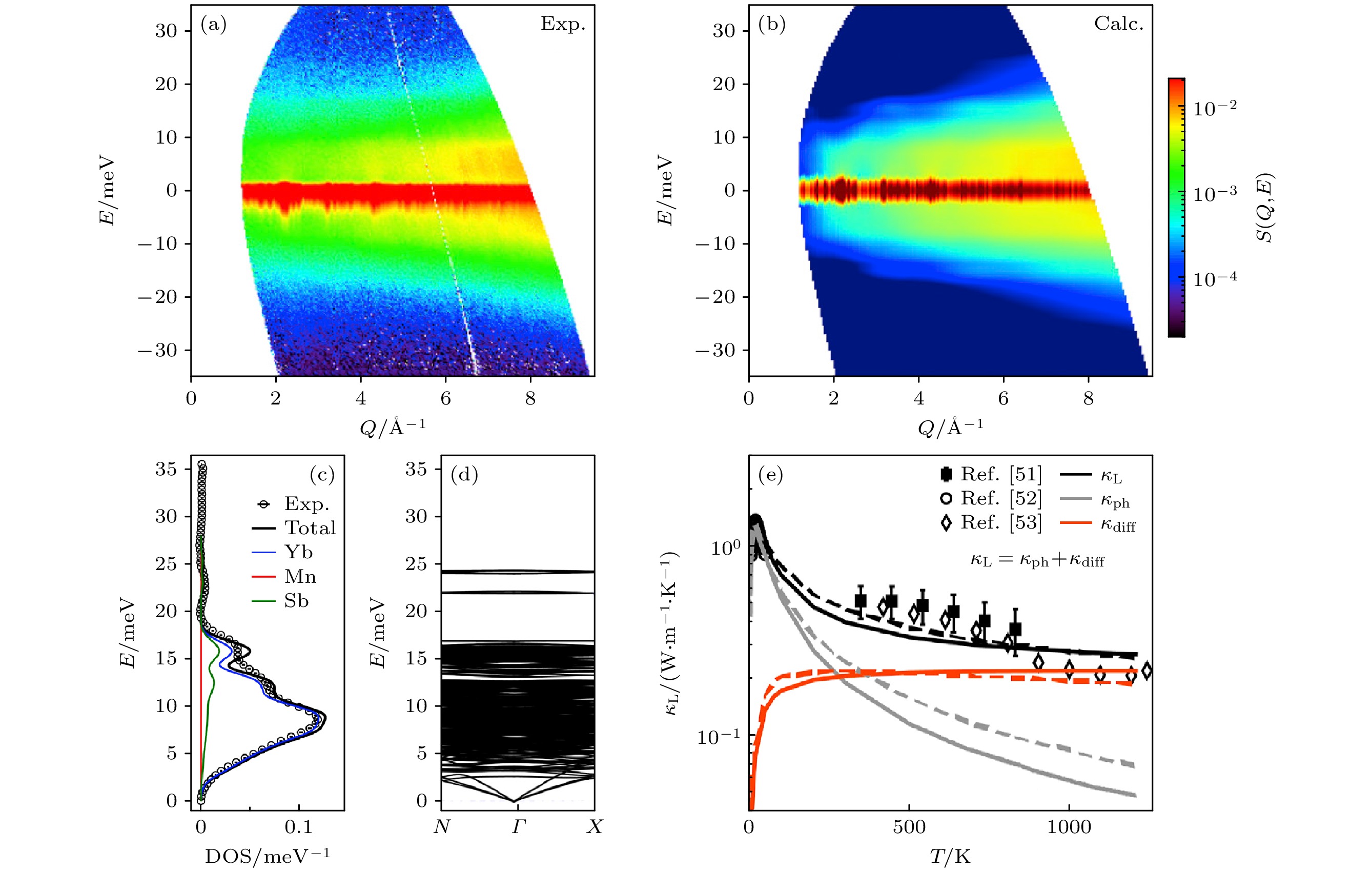
      虽然Yb14MnSb11的低$ {\kappa }_{{\mathrm{L}}} $与低声速有关, 但这并不能解释热导率在高温时弱温度依赖性. 由于Yb14MnSb11的热导率与玻璃在同一个数量级上, Hanus等[51]认为Yb14MnSb11晶体在室温以上导热与非晶体材料类似. 通过非弹性中子散射技术和双通道晶格动力学计算(同时考虑标准的声子气体通道和扩散子通道), 他们发现扩散子通道在300 K以上占主导地位, 从而揭示了热导率表现弱温度依赖性. 非弹性中子散射测量到的能量和动量传递的关系如图5(a)所示, 图5(b)显示了使用基于密度泛函理论的简谐振动模型模拟的中子散射强度. 结合理论计算, 在大约3—17 meV之间, 会出现许多能量非常接近的扁平分支. 在20 meV以下, 加权声子态密度与模拟结果(图5(c), (d))非常吻合, 由此可见, 这种非常平坦的声子支确实是存在的. 图5(e)为Yb14MnSb11的热导率测量与理论模拟图[51–53], 这里对声子-声子散射率(声子寿命$ \tau $的倒数)采用了两种分析形式: $ {\tau }_{{\mathrm{p}}{\mathrm{p}}}^{-1}=AT $ (图5(e)中的实线)和$ {\tau }_{{\mathrm{p}}{\mathrm{p}}}^{-1}=A'\omega T $ (图5(e)中的虚线), 其中$ A $和$ A' $参数通过拟合实验数据获得. 由于存在许多能量相近的光学声子, 晶格热导率的$ \omega $依赖性很弱, 表明高阶力常数(三阶和四阶)的影响有限. 因此, 声子-声子散射率的解析形式应为$ {\tau }_{{\mathrm{p}}{\mathrm{p}}}^{-1}=AT $, 在室温以上扩散子通道占主导地位[51].

      为了进一步探究这种能量相近的声子模式对热导率的影响, 可以在保持晶体结构和力常数不变的前提下, 仅改变Sb位点上的原子质量(将Sb位点上的原子替换为As和Bi), 计算了3种材料的热导率. 结果表明, 增大(减小) Sb位点上的原子质量会降低(增大)这些声子模式的能量, 进而与Yb主导的声子模式有更大(更小)的重叠, 导致更高(更低)的热导率. 与只考虑声子气体通道的预期不同, 原子质量的增大通常会导致热导率的降低, 因此这些大量能量相近声子模式导致了扩散子通道的显著作用, 从能量上将一个振动模式与其他模式隔离, 实现对热导率的调控.

      如上所述, 零维Zintl相化合物具有复杂晶体结构, 这种结构特性限制了声子的传播, 显著缩短了声子的平均自由程. X射线吸收光谱强调电子结构的变化(价态混合)引发了局域晶格无序, 间接降低热导率. 第一性原理计算和比热数据均量化 了低声速和低德拜温度, 中子散射实验不仅验证了低声速特性(表现为大量低能平坦的声子模式), 还进一步揭示了低能区域中高度重叠的光学声子模式, 突出了扩散子通道的关键作用, 这种类似于非晶材料的导热机制是零维材料体系晶格热导率的特点.

      • 3.2.   一维链状体系

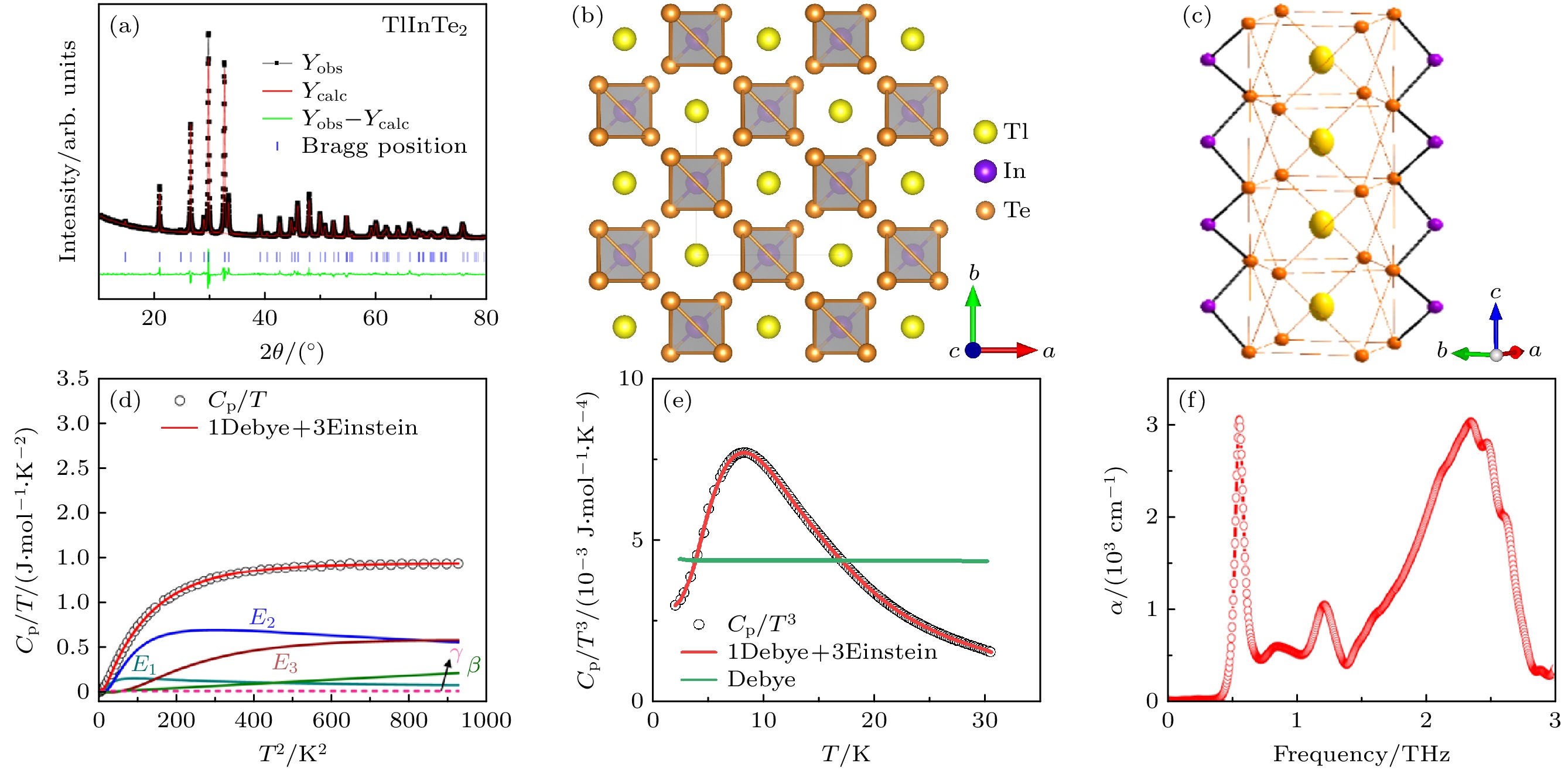
    • 一维链状结构Zintl相化合物的化学式是A3MPn3, 由MPn4四面体链连接构成, 其中A = Ca, Sr或Ba; M = Al, Ga或In; Pn = P, As或Sb. 这类材料往往有大晶胞和复杂结构[54–56], 本征晶格热导率较低, 具有较好的热电性能, 如Ca3AlSb3在1050 K时, $ {\kappa }_{{\mathrm{L}}} $为0.6 W/(m·K), ZT约为0.8[55]; Sr3GaSb3在1000 K时, $ {\kappa }_{{\mathrm{L}}} $为0.45 W/(m·K), ZT约为0.9[56].

      TlInTe2是一个典型的一维链状结构Zintl相化合物, 其空间群为I4/mcm, 在结构上类似于Ca3AlSb3和Sr3GaSb3, 如图6(b)所示, In原子与4个Te原子通过共价键形成InTe4四面体并沿着c轴延伸, 形成链状结构[57–59]. 相比于其他一维链状Zintl相化合物, 其晶体结构较简单, 具有极低的晶格热导率, 673 K时的$ {\kappa }_{{\mathrm{L}}} $为0.31 W/(m·K), 非常接近Cahill模型对TlInTe2的晶格热导率理论最小值(0.28 W/(m·K))[60], 其超低晶格导热率的起源需要进一步探索.

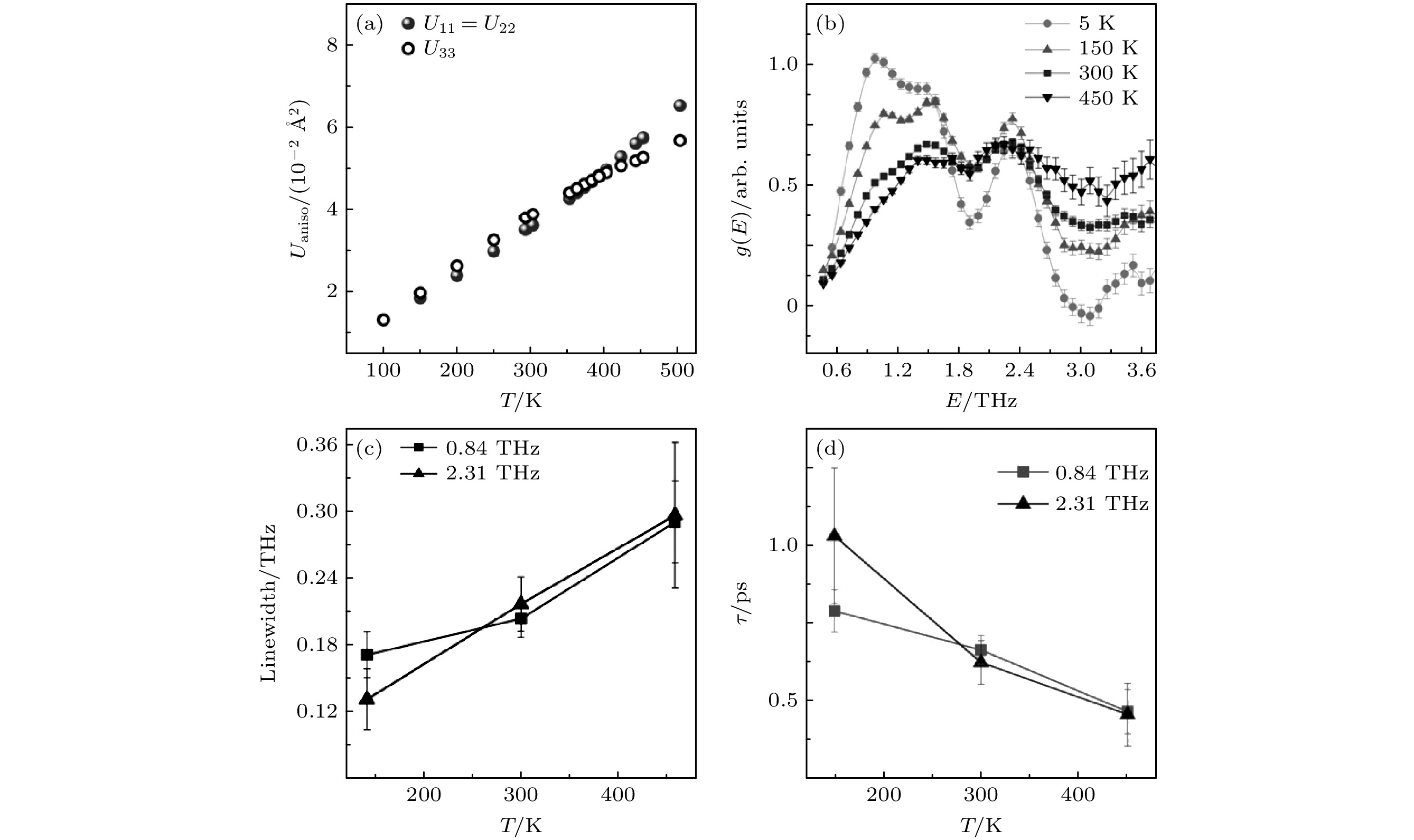
      Jana等[60]率先通过粉末X射线衍射和太 赫兹时域光谱技术研究了Tl原子的振动, 力图揭示低$ {\kappa }_{{\mathrm{L}}} $的起因. 从X射线衍射数据(图6(a))中提取的原子位移参数如图6(c)所示, Tl原子存在 很强的各向异性的振动(U11 = U22 = 0.027 Å2, U33 = 0.074 Å2), 沿c轴的原子位移参数非常大, 这与其他一维链状Zintl相化合物中小各向同性的原子位移参数形成鲜明对比(如Ca3AlSb3中Ca原子的各向同性原子位移参数约为0.0152 Å2 [61], 和Sr3GaSb3中Sr原子的各向同性原子位移参数约为0.0156 Å2 [62]). 使用德拜-爱因斯坦模型拟合TlInTe2的比热数据(图6(d)), 需要3个爱因斯坦模式(24.8, 44.5和79.8 K)才能很好地拟合. 同时, 在比热数据中观察到了类玻璃态的玻色峰(图6(e)). 结合第一性原理计算, Tl的原子振动产生的光学模式被认为是声子散射增强的原因, 继而导致了低$ {\kappa }_{{\mathrm{L}}} $. 为了验证这种低频光学模式的存在, TlInTe2的太赫兹时域光谱实验测量了室温下的吸收系数(图6(f)): 在1.5 THz以下观察到3个与比热数据中的爱因斯坦模式一致的激发(0.5, 0.9和1.2 THz)(偏差可能源于德拜-爱因斯坦模型未充分考虑晶格的非简谐性和实验分辨率的限制), 因此, Tl原子的振动与低$ {\kappa }_{{\mathrm{L}}} $密切相关.

      2021年, Dutta等[63]利用X射线对分布函数(pair distribution function, PDF)更详细地研究了TlInTe2中Tl原子的局域结构, 得到了不同于Jana等[60] X射线衍射的结果, 随着温度的升高, Tl的振动由各向同性逐渐变为各向异性[63]. 在393 K以上, Tl原子在a和b方向上的振动比c方向更强烈(图7(a)), 并将此归因于热膨胀(a和b方向的热膨胀比c方向高)导致Tl和Te之间的静电斥力减弱, 从而使Tl更容易沿a和b方向振动. 由于PDF分析同时使用了布拉格衍射和漫散射信号, 能够得到局域结构信息, 而X射线衍射数据仅能反映原子的平均振动. 因此, PDF得出的结论引起了很大的关注. 于是Dutta等[63]在不同温度下开展了非弹性中子散射测试, 研究了与Tl原子振动直接相关的声子模式, 为低晶格热导率的来源提供了确切的证据. 如图7(b)所示, 加权声子态密度在 5 K有3个独立的峰(0.84, 1.35和2.31 THz), 随温度的升高, 这3个声子模式急剧展宽(图7(c)). 因此, TlInTe2低能的声子模式存在强烈的声子散射和高度的非谐性. 对比声子寿命(图7(d)), TlInTe2的数值远低于很多成熟的热电材料(如PbTe, $ \tau \sim 2$ ps; AgSbTe, $ \tau \sim2.6$ ps)[64], 这也从另一方面表明了TlInTe2的强烈非谐性.

      由此可见, 一维Zintl相化合物结构相对来说较为简单, 原子键合较弱, X射线衍射和对分布函数分析揭示了键长分布的显著变化(体现为纵向声子)以及原子大幅度的局域振动. 第一性原理计算和比热数据间接表明与其相关的低能量光学声子模式的存在, 而非弹性中子散射实验则直接观测到了这些低能光学声子模式, 低能光学声子与声学声子之间的强耦合显著增加了声子散射. 此外, 中子数据展示了随着温度的升高, 声子线宽急剧增大(反映出高度的非谐性极大地抑制了声子寿命), 进一步验证了一维链状结构在该体系中起到了强烈声子散射中心的作用, 成为低热导率的关键.

      • 3.3.   二维层状体系

    • 相较于结构复杂的零维体系和电子迁移路径受限于链内的一维体系[15], 二维层状结构材料不仅有利于电子在层内自由迁移, 有效提高电子迁移率和金属状电导率, 还可利用层间较弱的相互作用有效阻碍声子传播降低了晶格热导率. 因此, 二维共价键子结构Zintl相材料较其他类型表现出更好的热电性能, 例如, 二维掺杂的Mg3Sb2基材料在773 K时的ZT值~1.81[65]远高于零维化合物Yb14MnSb11的ZT值~1.2 (1175 K)[43]和一维链状化合物Sr3GaSb3的ZT值~0.9 (1000 K)[56]. 目前, 二维层状Zintl相化合物作为具有较好的应用前景, 吸引了广大科研工作者的极大兴趣. 研究较多的二维层状结构Zintl体系主要有AB2X2型、AB4X3型和ABX型等, 下文将围绕这3类材料分别论述.

      • 3.3.1.   AB2X2型

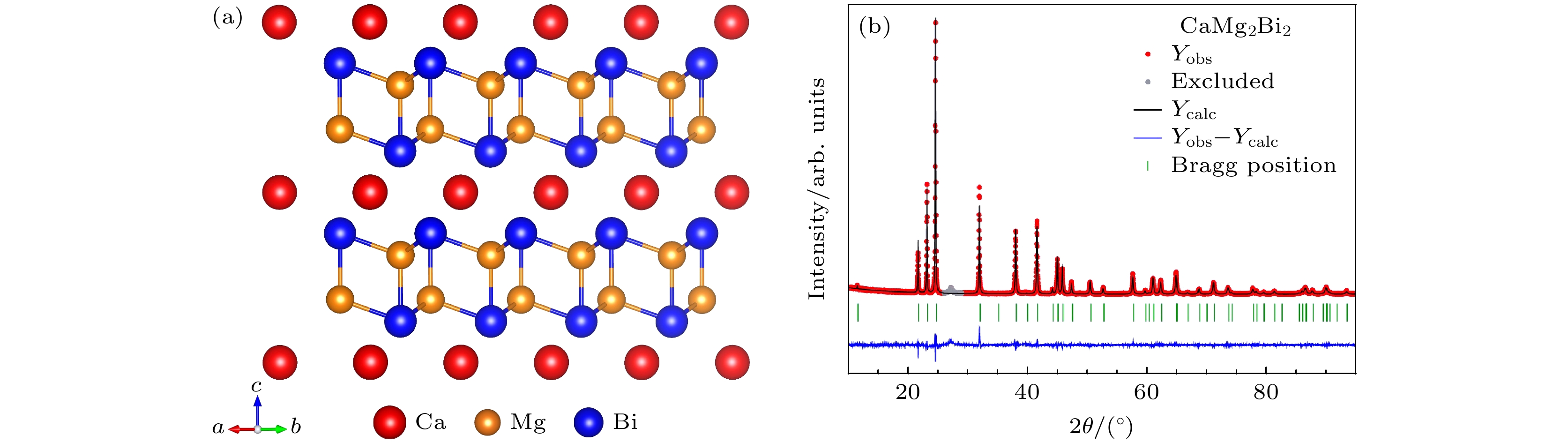
    • 二维层状AB2X2型Zintl相化合物具有组成元素多样, 电、热输运性质可调的特点. 从元素组成角度看, 该类材料中, A位是碱土或二价稀土元素, 如Ca, Ba, Yb或Eu; B位是d0, d5或d10族的过渡金属或主族元素, 如Mn, Zn, Cd或Mg; X位来自IVA或VA族, 如Sb或Bi[66,67]. 从晶体结构分析, 两种常见的化合物结构为: I4/mmm (ThCr2Si2型)和$ P\overline{3}m1 $(CaAl2Si2型)[68]. 此外, 当B位被三价元素(如Ga)时, 会形成完全不同的结构, 例如BaGa2Sb2, EuGa2As2和EuGa2Sb2会形成三维阴离子框架, 其中Ba和Eu离子形成一个管道面[68–72]. 由于ThCr2Si2型化合物具有的奇异磁性和超导性[73–76], 所以虽然该类化合物的热电性能相对较低[77–81], 如Ba0.97K0.03Cu2S2的ZT值为0.30 (773 K)[81], 但是仍引起了科研界的极大兴趣. 这里将主要关注三元CaAl2Si2结构材料和A = B的二元化合物Mg3Sb2.

      2005年, Gascoin等[82]合成了具有CaAl2Si2型结构的Zintl相化合物Ca1–xYbxZn2Sb2, 其ZT值高达约0.56. 由此, 许多其他CaAl2Si2型Zintl相热电材料被逐一发现[83–88]. 三元CaAl2Si2的晶体结构由Ca2+阳离子层与[Al2Si2]2–阴离子层交替组成, 其中Al和Si由于电负性相近形成具有共价键的[Al2Si2]2–阴离子层, Al原子与Si原子呈四面体配位, Ca原子与Si原子呈八面体配位. 图8展示了CaAl2Si2型Zintl相化合物CaMg2Bi2的晶体结构和X射线衍射图谱[83]. Bi基CaAl2Si2型化合物对环境友好, 近年来备受瞩目. 其中, (Eu0.5Yb0.5)1–xCaxMg2Bi2的ZT高达1.3 (873 K)[87]. Ca0.5Yb0.5Mg2Bi2, Eu0.5Ca0.5Mg2Bi2和Eu0.5Yb0.5Mg2Bi2的ZT值也高于1[87,88].

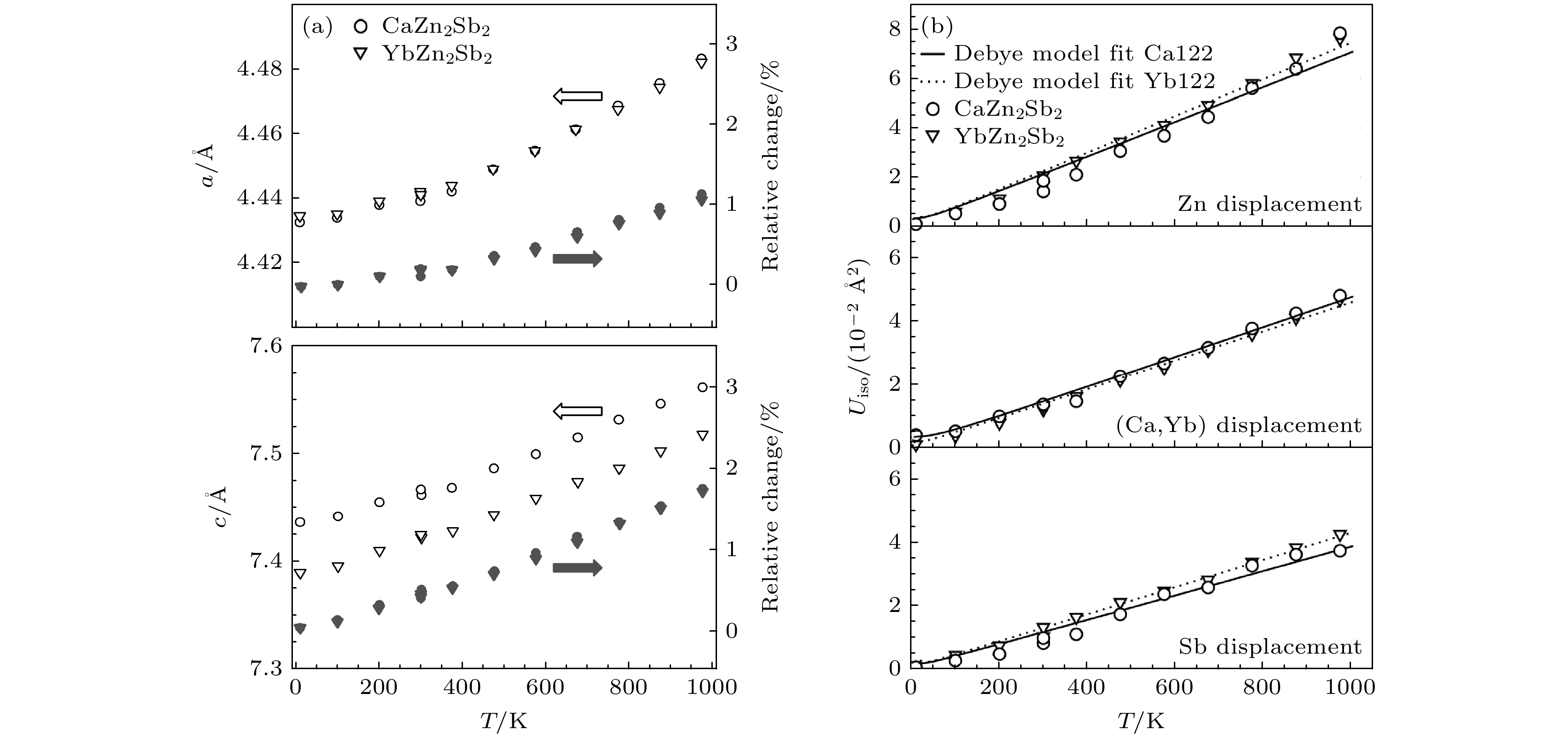
      一般来说, 良好的热电材料需要较高的电导率, 所以调控Zintl相化合物中的载流子迁移率是非常重要的. Toberer等[89]率先表征了AZn2Sb2 (A = Ca, Sr, Yb, Eu)的载流子迁移率, 发现YbZn2Sb2和EuZn2Sb2的载流子迁移率比CaZn2Sb2和SrZn2Sb2高. 拟合塞贝克系数与载流子浓度的依赖关系显示AZn2Sb2的有效质量相似(约为0.56me), 载流子迁移率差异主要归因于弛豫时间的变化. 随着温度升高, AZn2Sb2的载流子迁移率均呈下降趋势, 进而推测这种下降主要由散射效应引起, 散射强度的差异可能与A位离子对原子键合的影响有关. 为了进一步探究这种迁移率与结构间的联系, May等[90]利用粉末中子衍射技术研究了YbZn2Sb2和CaZn2Sb2的晶体结构, 发现随着温度升高, 尽管c轴的膨胀速度比a轴快(图9(a)), 但是各向同性原子位移参数(Uiso)非常相似(图9(b)). 通过德拜模型拟合Uiso:

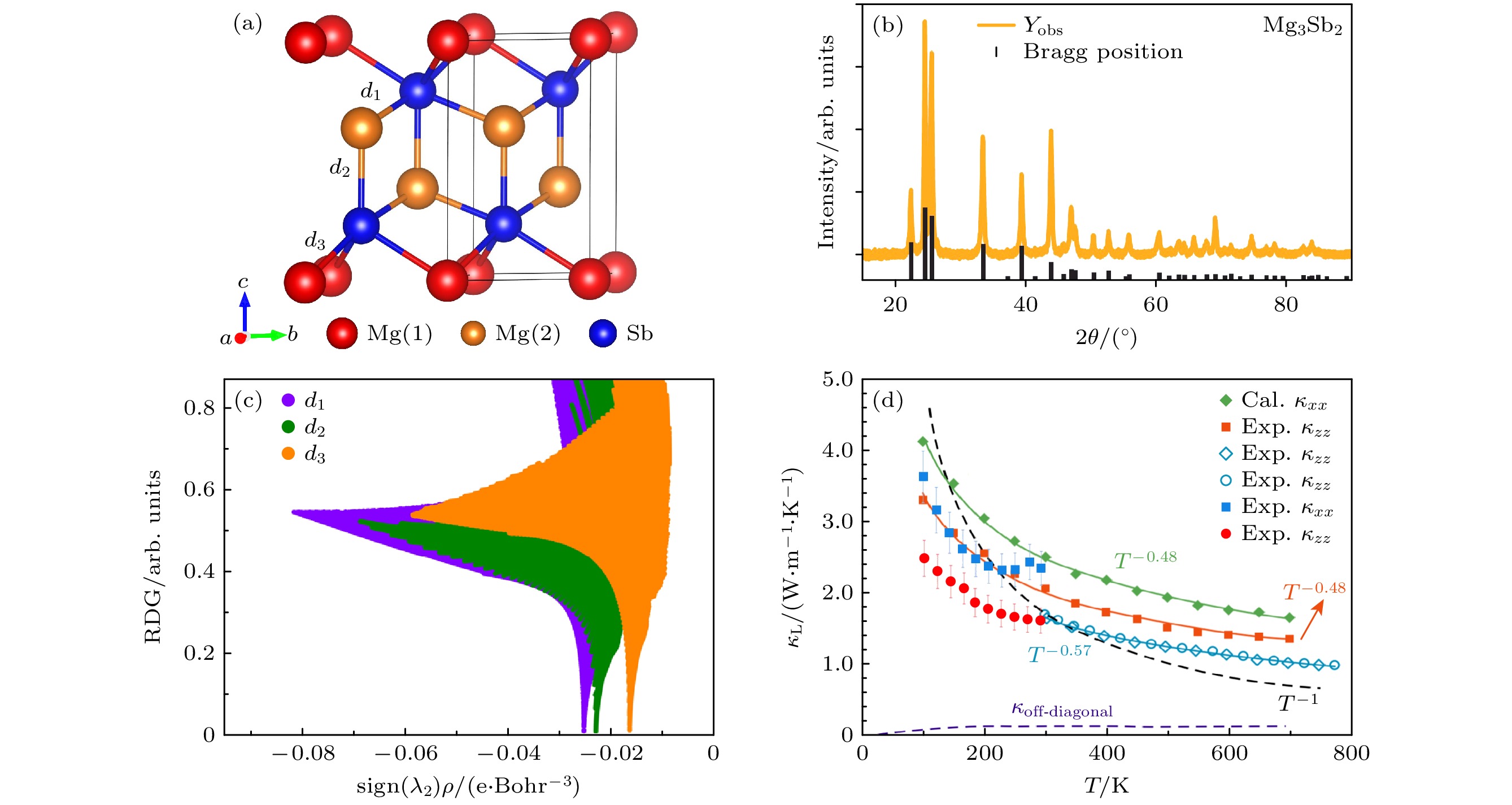
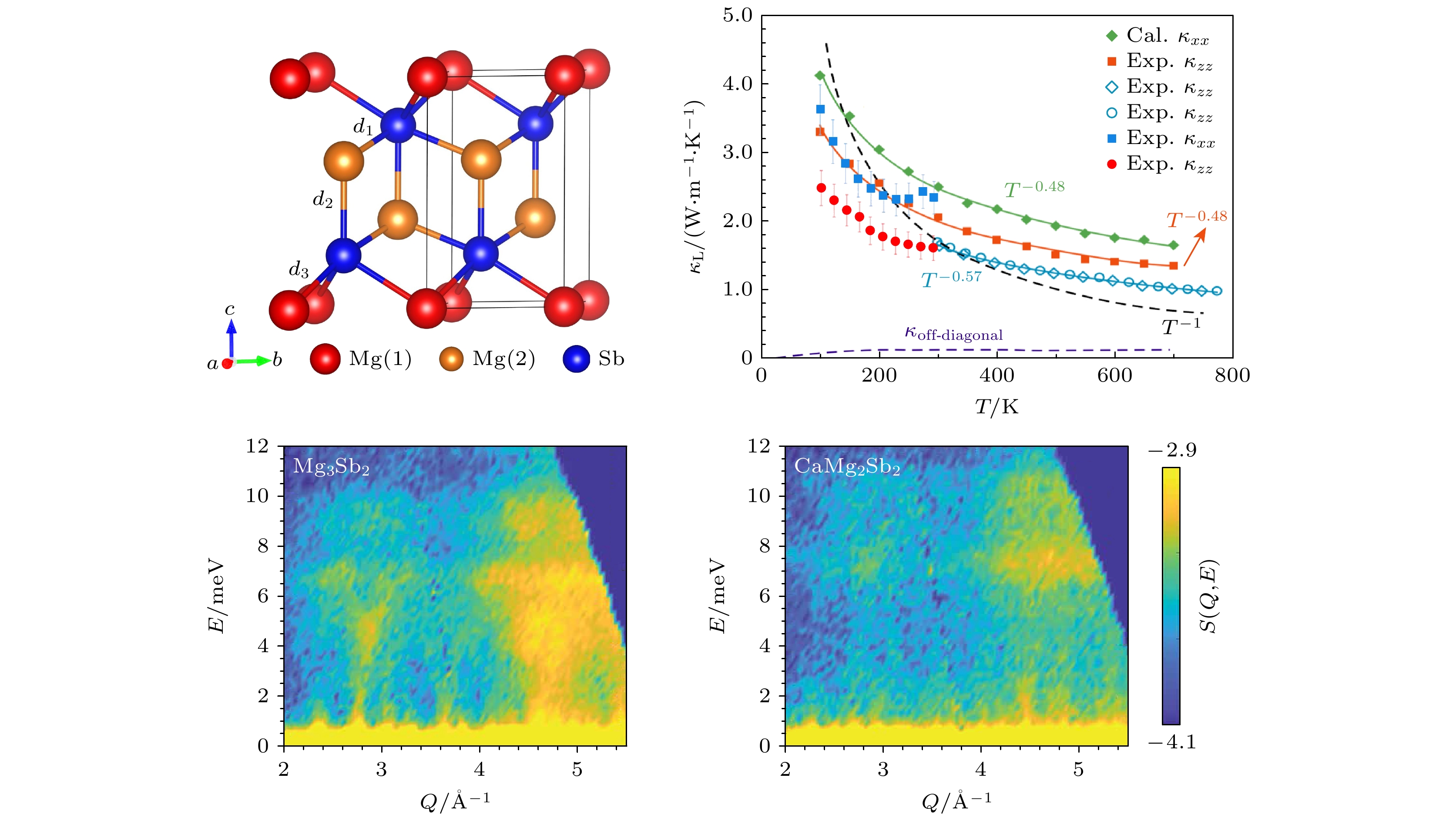
      其中, $ {\theta }_{{\mathrm{D}}} $是德拜温度, m是原子质量, NA是阿伏伽德罗常数, d是密度, νm是平均声速, M是分子量. 一方面, 德拜模型很好地描述了Uiso的温度依赖性; 另一方面, 拟合结果表明CaZn2Sb2比YbZn2Sb2有更大的德拜温度. 虽然两种化合物的m变化比例相当大(Ca和Yb的原子质量相差超过4倍), 但d/M比值变化不到5%, 仅凭原子质量的变化不足以解释$ {\theta }_{{\mathrm{D}}} $的变化. 因为$ {\theta }_{{\mathrm{D}}} $的变化代表了vm的变化, 所以CaZn2Sb2的声子速度远大于YbZn2Sb2. 结合声速与键能的关系, May等[90]认为本征缺陷是导致载流子迁移率降低的原因. 由此可见, 这种通过中子衍射实验将原子位移参数和迁移率关联了解局部键合的方法, 对理解材料的晶体结构和电子结构有很大的帮助.

      近年来, CaAl2Si2结构的Mg3Sb2作为一种极具应用前景的热电材料受到越来越多的关注. 对于这种A = B的二元化合物, 将A位(八面体配位)上的Mg原子称为Mg(1), B位(四面体配位)上的Mg原子称为Mg(2), 如图10(a)所示[91]. 图10(b)为Mg3Sb2的X射线衍射图谱[91]. 通常, 这种层状化合物不具有低热导率, 但二元Mg3Sb2具有不同于三元CaAl2Si2化合物的输运性质: 其晶格热导率很低(室温$ {\kappa }_{{\mathrm{L}}} $~1—1.5 W/(m·K)), 可与PbTe和Bi2Te3相比[92–95]. 尽管Mg3Sb2的功率因数较差, 但是通过化学掺杂、能带工程和结构工程可在700 K左右实现1.5的ZT值 [96–99].

      按照Zintl相的定义, 通常认为Mg3Sb2的阳离子层是通过离子键结合, 而阴离子层原子间通过共价键结合, 但Zhang等[100]通过电子密度的定量化学键分析发现Mg3Sb2拥有一个几乎各向同性的三维化学键网络, 层间相互作用主要是离子性(也具有部分极性的共价键性质), 与层内相互作用相当. 3个化学键的约化密度梯度(reduced density gradient, RDG)分布如图10(c)所示, 其中sign(λ2)ρ是电子密度Hessian矩阵的第2个特征值的符号. 层间的Mg(1)-Sb相互作用(d3)仅比倾斜的Mg(2)—Sb键(d1)和垂直的Mg(2)—Sb键(d2)略低. 对于层状材料而言, 层间散射效应更强, 往往层间的$ {\kappa }_{{\mathrm{L}}} $比层内更低. 然而图10(d)却清晰展示Mg3Sb2的层内$ {\kappa }_{{\mathrm{L}}} $略低于层间$ {\kappa }_{{\mathrm{L}}} $[101,102]. 目前普遍认为Mg3Sb2独特的成键结构是低层间$ {\kappa }_{{\mathrm{L}}} $的原因, 但是这种特征挑战了Zintl相的定义, 目前仍存在争议, 需要更深入的研究.

      已有多个研究小组报道了类似的$ {\kappa }_{{\mathrm{L}}} $值[101–106], 证实了低层间$ {\kappa }_{{\mathrm{L}}} $是Mg3Sb2的一个固有特征. 这种本征的低晶格热导率引起了极大的关注, 下文从计算和实验两个方面讨论Mg3Sb2低晶格热导率的起源.

      虽然大多数晶体材料在高温下的晶格热导 率遵循T –1温度依赖性的准则, 但Mg3Sb2中$ {\kappa }_{{\mathrm{L}}} $的温度依赖性比较弱. 理论计算得到的指数是T –0.48, 实验数据是T –0.57, 故该系统存在很强的声子非 谐性[102]. Maccioni等[103]利用第一性原理计算 了Mg3Sb2的晶格热导率, 认为晶界散射在对晶 格热导的影响很大, 而实验上测量的单晶和多 晶Mg3Sb2晶格热导率仅发现$ {\kappa }_{{\mathrm{L}}} $的微小差异(~15%)[94,104–106]. 因此, 晶界散射在声子输运中没有起到显著作用, 是否由声子-声子散射引起的固有低热导率需要深入探讨, 还要考虑声子散射相 空间的改变、四阶声子散射以及非对角线项的贡献[102,107]. Peng等[108]利用第一性原理计算了声子态密度, 将Mg3Sb2的反常热输运行为归因于Mg的原子尺寸太小(Mg(1)原子相较于八面体配位的其他离子太小). Pauling[109]提出的球型离子化合物成键模型中, 八面体配位的最小稳定阳离子与阴离子半径比为0.414, Mg3Sb2化合物的阳离子与阴离子半径比仅约为0.32, 远低于稳定性极限, 所以认为不稳定性的结构是导致弱层间键合及强非谐性的起源.

      为进一步研究Mg3Sb2晶体结构的不稳定性, Zhu等[102]进行了分子动力学模拟, 发现所有原子的原子位移近似各向同性, 只有Mg(2)原子沿z方向的运动更剧烈, 并且这种不对称性随着温度的升高而增强. 最终Mg(2)原子各向异性的热运动决定了不对称的势能分布, 导致$ {\kappa }_{{\mathrm{L}}} $偏离T–1温度依赖性.

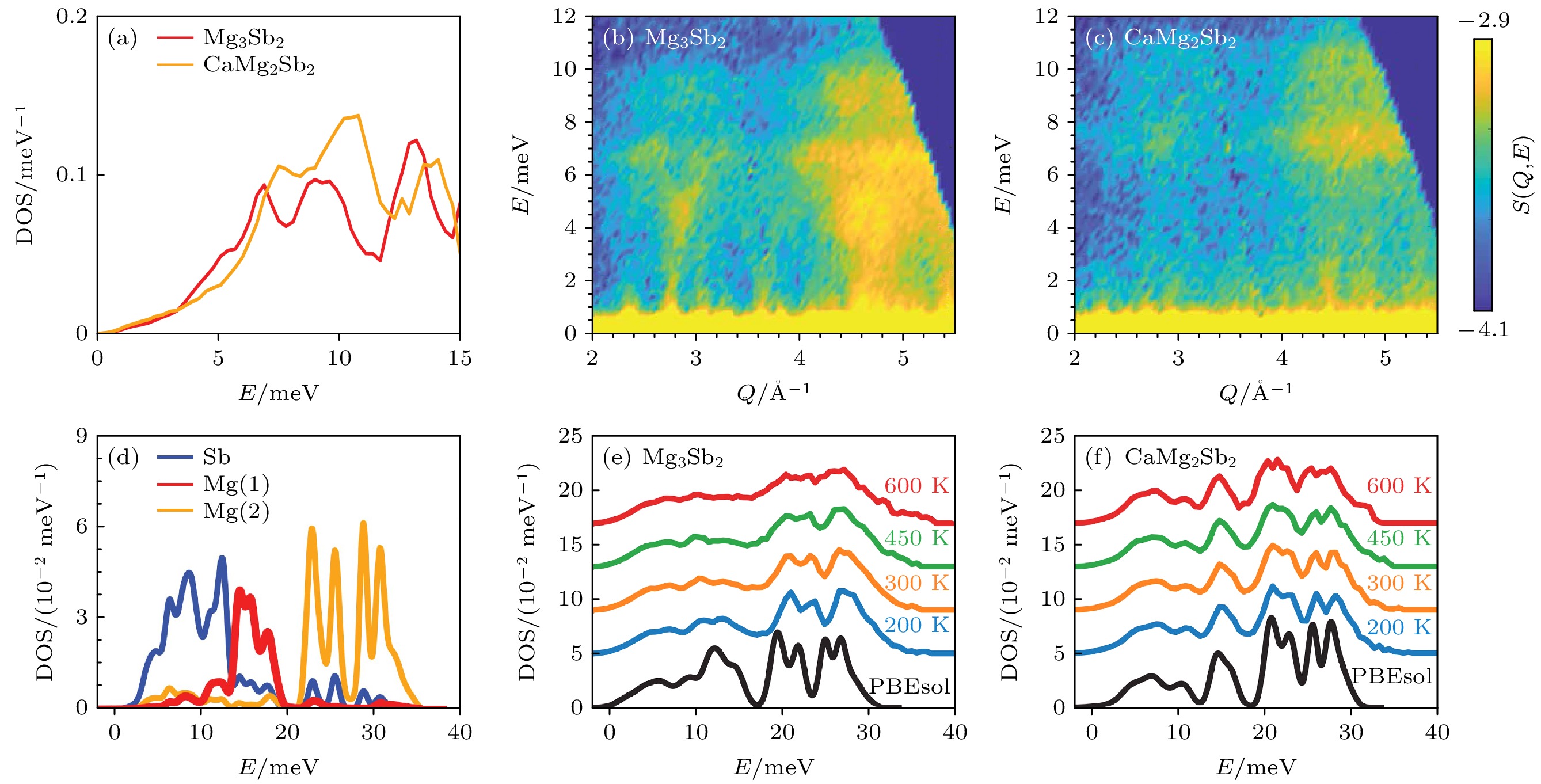
      尽管理论计算上已经表明Mg3Sb2的强非谐性导致了低$ {\kappa }_{{\mathrm{L}}} $, 为了探究这种非谐性的起源, 还需要对该材料的晶体结构和声子模式进行详细的实验分析. Ding等[91]利用非弹性中子散射技术测量了Mg3Sb2粉末样品及其类似化合物的声子态密度. 考虑到原子质量会直接改变声子频率, 在其他条件不变的情况下, 较重的原子应该表现出较低的声子能量, 但是当用Ca代替Mg(1)时, 在低于12 meV处观察到一个强烈的声子硬化(图11(a)—(c)), 这个现象在高Q处更明显, 表明Mg(1)的成键存在异常. 根据密度泛函理论计算出的分波声子态密度(图11(d)), Mg(2)原子的贡献主要在20 meV以上, Sb原子主要在10 meV以下, Mg(1)原子在中间区域占主导地位. 当用Ca取代的Mg(1)时, 能量大于20 meV的Mg(2)模式在实验和模拟中都几乎没有受到影响(图11(e), (f)), 所以该两种化合物中Mg(2)的局部环境和成键相对没有变化. 相较而言, 低能的声子硬化反映了Mg(1)-Sb相互作用的强烈变化. 随着温度的升高, 无论是Mg3Sb2还是CaMg2Sb2整个谱线都表现出了一定的展宽, 同时与理论计算可以完美的对应上. 由于只有在10—20 meV范围内的激发相对于理论计算有显著的展宽(图10(e)), Mg(1)的键合环境存在很强的非谐性. 理论计算出的二阶力常数表明, d3键的二阶力常数的模比d1和d2小得多. 因此, 可以认为弱Mg(1)—Sb键导致了声子软化, 增强了声子散射, 显著抑制了$ {\kappa }_{{\mathrm{L}}} $.

      与前面介绍的强调声子-声子非谐性散射作用的观点不同, Kanno等[110]通过X射线衍射和非弹性X射线散射技术测量, 认为Mg3Sb2存在大量的Frenkel缺陷, 并且这种额外的散射源是Mg3Sb2样品所特有的, 从而导致了低$ {\kappa }_{{\mathrm{L}}} $. Frenkel缺陷是指阳离子位点的负电荷的Mg空位和阳离子片附近的小四面体位点的正电荷的Mg间隙的成对缺陷, 这一缺陷模式在Mg3Sb2单晶X射线衍射数据分析中得到了证实. 在X射线衍射数据中没有观察到明显的漫散射信号, 进一步采用最大熵法分析X射线衍射数据, 在Sb原子附近发现了过剩电子密度, 证明间隙Mg原子的存在, 这表明Mg3Sb2单晶样品存在高浓度的缺陷. 相比之下, 没有在CaMg2Sb2中观察到任何间隙缺陷的痕迹. 为研究这种高浓度缺陷在Mg3Sb2中是如何稳定存在的, 微应变随温度的变化得到了进一步分析, 发现Mg3Sb2的微应变显著大于CaMg2Sb2, 并且表现出明显的各向异性, 表明缺陷导致的局部晶格畸变缓解了晶格不稳定性. 考虑到缺陷和局部晶格畸变对声子散射的影响, Kanno等[110]用非弹性X射线射测量了Mg3Sb2单晶的变温声子色散. 将实验数据与使用无缺陷晶体模型计算的声子色散对比, 两者基本一致, 表明缺陷并不会对声子能量产生影响. 而实验提取的纵向声学支的声子平均自由程与计算结果有显著差异(实验值明显比理论值小), 表明缺陷造成的结构无序主要作用是增强声子散射, 抑制声子平均自由程, 从而抑制了$ {\kappa }_{{\mathrm{L}}} $.

      • 3.3.2.   AB4X3型

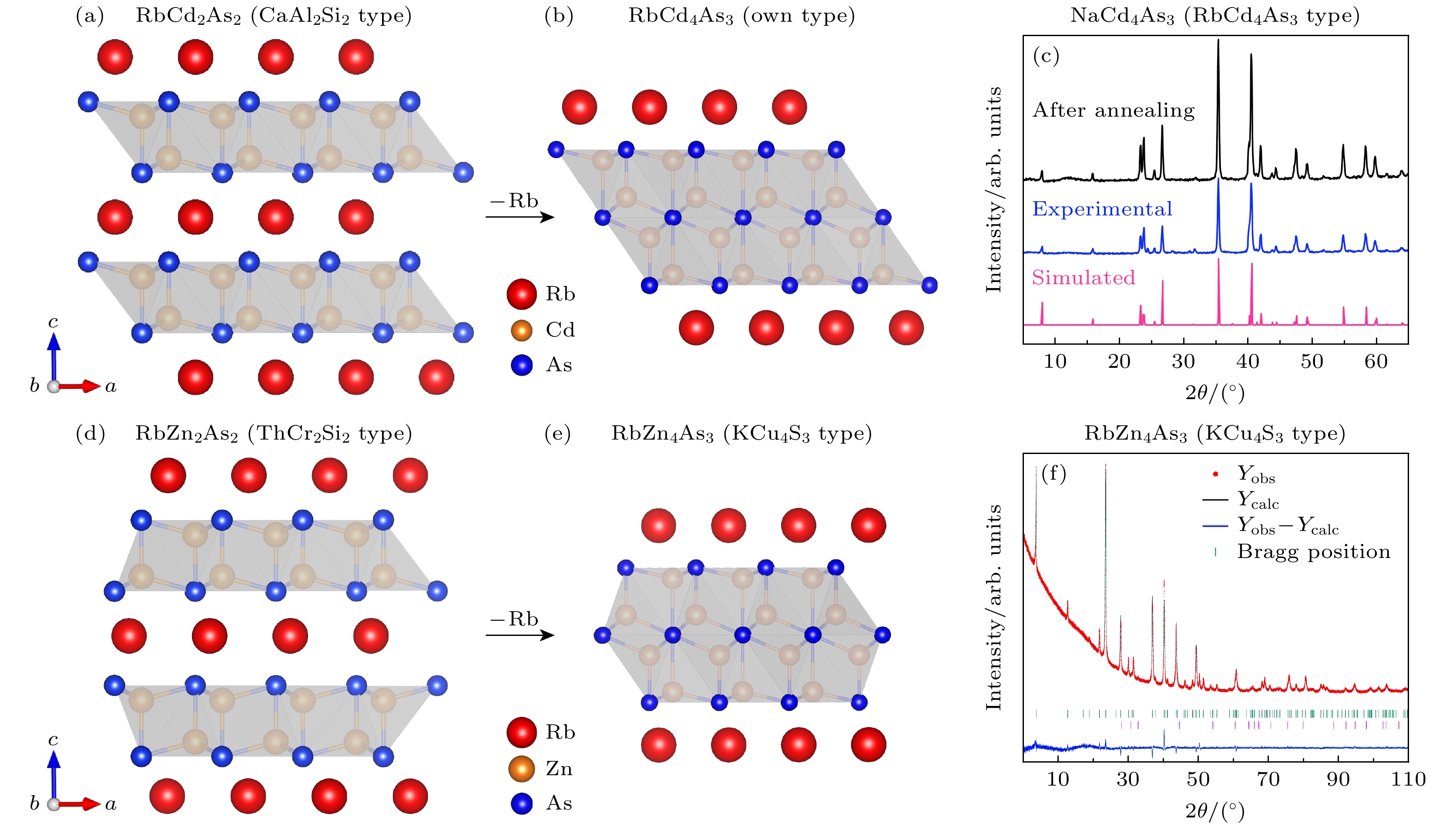
    • 二维层状AB2X2型Zintl相化合物可以通过堆叠层的组合转化成各种层状化合物, 而AB4X3型Zintl相化合物则是通过从每两个BX层去除一个A离子层而得到的化合物, 例如RbCd4As3和RbZn4As3 (图12)[111,112]. 其中RbCd4As3的合成过程中常伴随副产物生成, 由于副产物影响样品纯度, 难以获得高质量的X射线衍射数据[111]. 与此同时, Na和Rb的尺寸差异对晶体结构的影响很小, NaCd4As3的X射线衍射图谱能很好地匹配RbCd4As3的模拟数据[111], 故在此选择相同晶体结构且纯度更高的NaCd4As3的X射线衍射数据作为替代. 根据AB2X2型晶体结构的不同, 可以产生不同的变化, 主要可以得到两种类型的晶体结构, 分别是由三角的CaAl2Si2型和四方的ThCr2Si2型结构衍生而来的RbCd4As3型(空间群: $ R\overline{3}m $)结构和KCu4S3型(空间群: P4/mmm)结构 [111–114]. 如KZn4As3, CsZn4As3, RbZn4As3和RbZn4P3等化合物结晶于四方KCu4S3型, 而NaZn4Sb3, NaCd4As3, KCd4As3和KCd4P3等属于斜方RbCd4As3型晶体结构. 已经有研究小组报道了AB4X3型Zintl相化合物的热电性质[114–119], 其中NaZn4As3在室温下的ZT为0.067, $ {\kappa }_{{\mathrm{L}}} $ ~ 1.20—1.25 W/(m·K)[115]; NaZn4Sb3在室温下的ZT为1.4 × 10–3, $ {\kappa }_{{\mathrm{L}}} \sim 0.9 $ W/(m·K)[117]. 由于AB4X3型化合物的晶体结构与AB2X2型化合物的晶体结构密切相关, 因此它们也表现出明显较低的晶格热导率, 有望成为一类新型的高性能热电材料.

      Sangeeta等[120]通过第一性原理研究了RbZn4P3的晶格热导率(700 K时为0.56 W/(m·K)), 认为声子-声子非谐性散射在其中占主导作用. 由于计算出的声学声子与光学声子之间没有明显的能隙, 所以声学声子和光学声子之间可以存在较强耦合. 同时, 格林内森常数(1.42)较高, 与Bi2Te3相当[121], 表明RbZn4P3具有很强的非谐性, 这种非谐性会进一步增强声子散射并降低热导率.

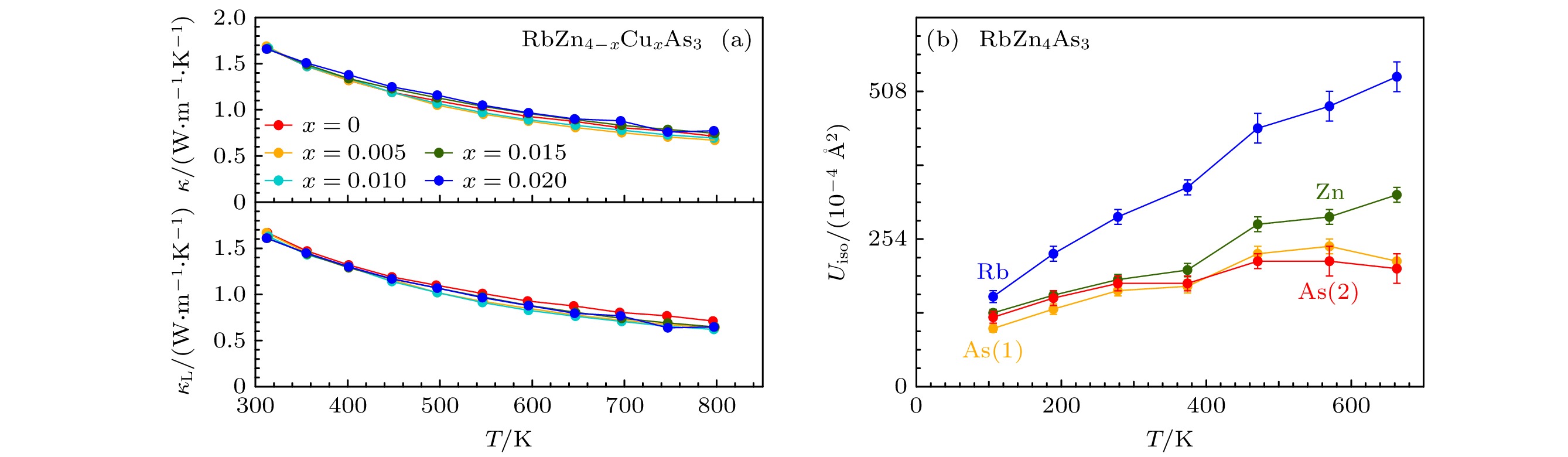
      前文的计算主要是从弹性模量这种宏观角度来说明材料的非谐性, Ono等[112]通过中子衍射分析揭示了RbZn4As3本征的低$ {\kappa }_{{\mathrm{L}}} $(312 K时为1.61 W/(m·K))源于Rb原子的非简谐振动. 通过测量一系列Cu掺杂的RbZn4As3样品, 发现样品的晶格热导率几乎与掺杂无关(图13(a)), 因此低$ {\kappa }_{{\mathrm{L}}} $是材料的一种固有特性, 而不是由掺杂引起. 对未掺杂的RbZn4As3样品进行变温中子衍射测量, 图13(b)展示了各向同性原子位移参数: 在106 K时, 所有原子的原子位移相似; 随着温度升高, Zn和As的原子位移参数以类似的速度增加, 而Rb的原子位移参数则以两倍的比例向上偏离. 尽管Rb原子的原子质量较大, 但它的原子位移参数却很大. 由此可见, Rb原子存在很强的非简谐振动, 引起了强烈的声子散射, 最终导致本征的低$ {\kappa }_{{\mathrm{L}}} $.

      • 3.3.3.   ABX型

    • ZrBeSi是一种半金属材料, 于1954年首次被发现[122], 一直是六角体系的代表结构, 被称为ZrBeSi结构(空间群: P63/mmc). ZrBeSi晶体由Zr原子沿c轴连接的蜂窝状的SiBe层形成的六角形晶体, 其中Si (Be)原子由6个Zr原子和3个Be (Si)原子配位. 典型的ZrBeSi结构材料有LaPdSb, SrCuSb, BaAgSb和EuCuSb等, 图14(a), (b)为SrCuSb的晶体结构和X射线衍射图谱[123]. ZrBeSi结构最显著的特点是其在金属位上容纳50%空位的能力, 由Wilson等[124]在研究A2ZnX2 (A = Sr或Eu, X = P, As, Sb或Bi)时首先注意到, 它们应该被视为具有ZrBeSi结构类型的ABX型的缺陷变体AB0.5X, 通常写作A2BX2. 虽然这类材料的磁性和拓扑性质研究较多, 但近年来, 科研工作者们对ZrBeSi结构Zintl相的热电性能开展了大量研究[124–129]. Sekimoto等[126]发现LaPdSb的电阻率(~10–4 Ω·cm)出乎意料的低, 而且室温时的ZT约为0.26. Feng等[127]发现KBaBi具有良好的热电性能, 在1000 K时ZT最大值为3. 这些研究揭示了ABX型Zintl相的热电输运性质, 丰富了其在热电材料领域的应用.

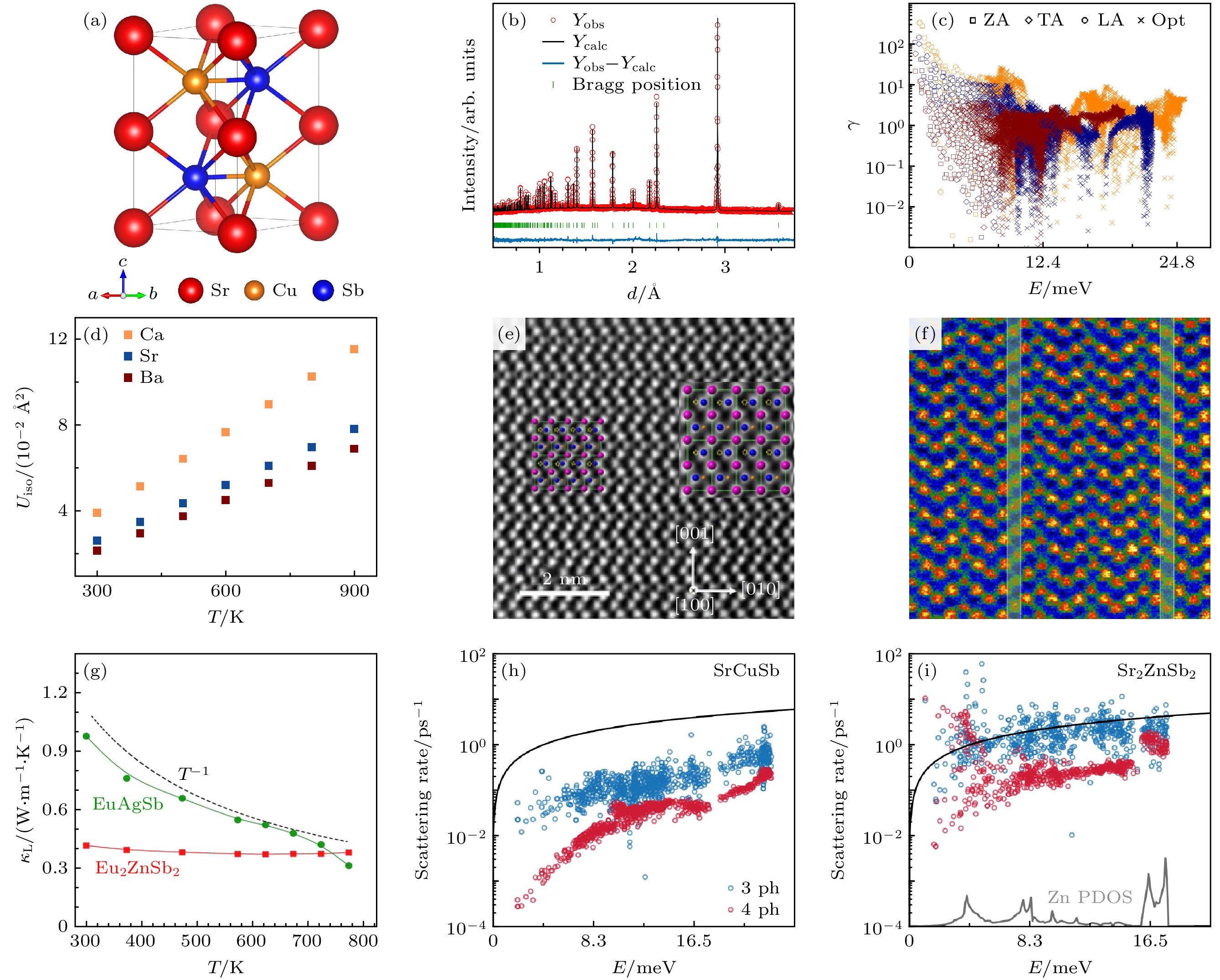
      Zhang等[128]研究了SrAgSb, EuAgSb以及EuCuSb的热电性能, 发现SrAgSb的原子质量虽然较小, 但其$ {\kappa }_{{\mathrm{L}}} $最低. 为了阐明这种异常热导率的起源, Zhou等[129]利用第一性原理计算研究了ACuSb (A = Ca, Sr和Ba)化合物的晶格振动和声子输运性质, 发现弱的层间相互作用有利于降低$ {\kappa }_{{\mathrm{L}}} $. 计算的晶格热导率表明用较轻的原子取代A位阳离子会产生较低的$ {\kappa }_{{\mathrm{L}}} $, 室温下的格林内森常数(图14(c))随着A位阳离子原子质量的增加而降低, 因此CaCuSb较低的$ {\kappa }_{{\mathrm{L}}} $源于强非谐性. 进一步通过原子位移参数来评估这3种ACuSb化合物的非谐性强弱, 发现Ca的原子位移参数比Sr和Ba的高(图14(d)), 并且随着温度的升高而增大得更快, 反映了Ca原子的强烈热振动, 这意味着CaCuSb中较弱的层间相互作用导致$ {\kappa }_{{\mathrm{L}}} $反向的质量趋势.

      上述ABX体系的SrAgSb, EuAgSb和EuCuSb的室温$ {\kappa }_{{\mathrm{L}}} $为2—4 W/(m·K)[128], 远高于A2BX2体系的Eu2ZnSb2 (室温~0.4 W/(m·K))[128], 其中不可忽略的因素是A2BX2晶体结构中存在着大量的本征空位. Chen等[130]通过高角环形暗场扫描透射电子显微镜(high-angle annular dark-field scanning transmission electron microscopy, HAADF-STEM)研究了Eu2Zn1–xSb2 (x = 0, 0.01, 0.02和0.04)的结构, 发现广泛分布的晶界平面缺陷是降低Eu2ZnSb2样品的$ {\kappa }_{{\mathrm{L}}} $主要因素. 图14(e)是Eu2Zn0.98Sb2沿[103]方向的高角环形暗场扫描透射电子显微镜图像, 其中一半的位置(黄色圆圈)没有被Zn原子占据, 证实了该晶体中Zn的占据率为50%. 同时, 可以观察到反相畴晶界平面缺陷的存在(图14(f)), 两个畴是通过边界处Sb位置的反转联系起来的. 使用实验测量的比热数据计算Eu2Zn1–xSb2的热导率, 随着缺陷浓度的增加(点缺陷散射增加), $ {\kappa }_{{\mathrm{L}}} $随之降低.

      考虑到Eu2ZnSb2中Zn的50%占据(这种部分占据很可能意味着无序), Chen等[131]通过第一性原理计算发现部分有序(Zn位点局部有序, 大尺度上无序)会形成本征纳米结构, 其纳米结构尺度可以有效散射声子降低热导率, 而不会影响电子输运. 实验测到的热导率数据显示, EuAgSb的$ {\kappa }_{{\mathrm{L}}} $随温度升高大幅下降(图14(g)). 相比之下, Eu2ZnSb2在低温范围内$ {\kappa }_{{\mathrm{L}}} $几乎与温度无关(图14(g)), 表明除了声子-声子非谐性散射之外还有额外的散射, 计算结果揭示了Zn位点无序对平均自由程的影响. 此外, 与具有高度随机无序的情况相比, Eu2ZnSb2保持了良好的迁移率.

      从强调声子-声子非谐性散射作用的角度, Wang等[132]通过第一性原理计算研究SrCuSb和Sr2ZnSb2的晶格动力学和热输运性质, 揭示了Zn空位对Sr2ZnSb2的$ {\kappa }_{{\mathrm{L}}} $显著抑制. 考虑到声子重整化, 图14(h), (i)展示了SrCuSb和Sr2ZnSb2的三声子和四声子散射率, 显然Sr2ZnSb2中的声子散射率大得多, 所以其具有更强的晶格非谐性. 同时, 在Zn主导的频率区域, 四声子散射率与三声子散射率相当甚至更大(图14(i)), 表明Zn原子导致了强非谐散射. 进一步结合分子动力学模拟声子重整化和准随机结构模型近似分析Zn空位对$ {\kappa }_{{\mathrm{L}}} $的影响[132], 表明高阶声子散射和Zn空位散射共同导致Sr2ZnSb2的$ {\kappa }_{{\mathrm{L}}} $降低.

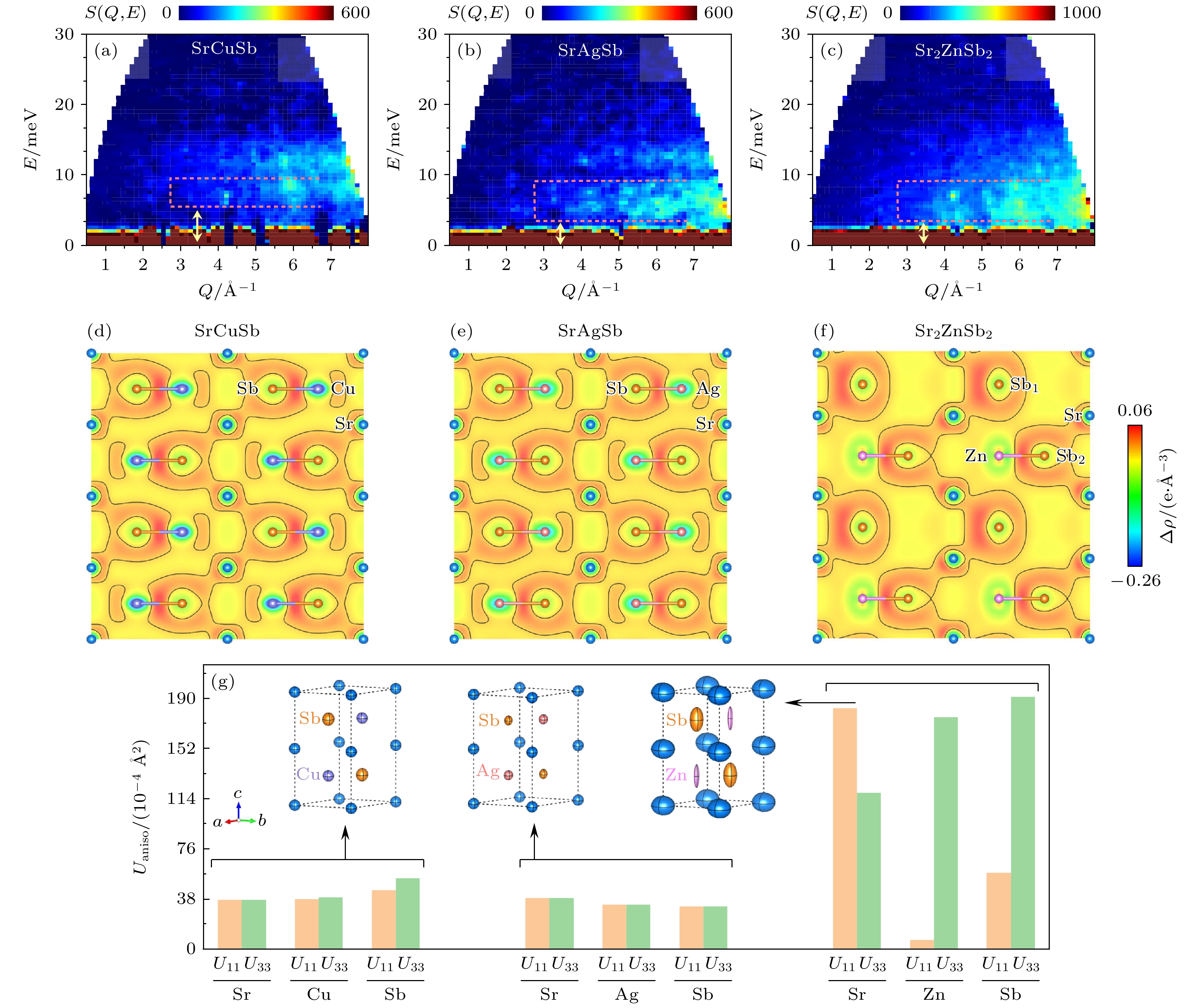
      综合实验测量和计算, 空位对抑制材料$ {\kappa }_{{\mathrm{L}}} $有重要影响, 还需进一步考虑不同空位浓度对$ {\kappa }_{{\mathrm{L}}} $的调控. Chanakian等[133]制备了不同空位浓度的EuCu1–xZn0.5xSb (0 ≤ x ≤1)样品, 并进行了X射线PDF分析. 通过比较PDF分析提取的不同空位浓度样品的原子位移参数, 发现随着空位浓度的增大, 所有原子的热振动普遍增强, 其中Sb比Cu/Zn表现更明显. 另外, Cu/Zn沿着c方向的热振动呈现出各向异性, 表明层间的键合环境发生了极大的变化. 此外, 基于PDF分析中提取的平均键长和晶胞体积随着x的增大而增大, 共振超声光谱探测了样品的弹性模量. 结果显示, x的增大对杨氏模量、体积模量和剪切模量下降的效应远大于晶胞体积增大2%的预期, 这种软化源于空位引起的层间相互作用减弱, 晶格变软. 更进一步, 室温下的$ {\kappa }_{{\mathrm{L}}} $曲线随着x的增大趋于平缓, 表明缺陷散射逐渐占据主导. 由此可见, 通过调整空位浓度, 可以影响晶格软化和缺陷散射, 实现了对$ {\kappa }_{{\mathrm{L}}} $的连续性调节.

      2024年, Zhu等[123]进一步探讨了空位效应, 通过对ZrBeSi结构化合物Sr(Cu, Ag, Zn)Sb的研究, 发现了空位在抑制晶格热导率方面的作用. 他们利用中子粉末衍射和非弹性中子散射技术, 结合分子动力学模拟, 揭示了空位对层间相互作用的弱化, 晶格非简谐性的增强, 从而导致$ {\kappa }_{{\mathrm{L}}} $的显著降低. 热输运测量表明, 尽管较重的Ag取代Cu后的$ {\kappa }_{{\mathrm{L}}} $下降了~51%, 但是用Zn取代Cu而产生的大量空位反而会产生更大的抑制. 为了探索空位抑制$ {\kappa }_{{\mathrm{L}}} $的内在机制, 他们进一步分析了从中子粉末衍射数据提取的总体各向同性原子位移参数. 基于德拜-爱因斯坦模型拟合, 得到SrCuSb, SrAgSb和Sr2ZnSb2化合物的德拜温度分别为279, 248和218 K, 表明SrAgSb和Sr2ZnSb2的晶格都表现出明显的软化. 随后, 用非弹性中子散射技术测量了Sr(Cu, Ag)Sb化合物的声子态密度, 以深入了解空位引起的软化对晶格动力学的影响. 图15(a)—(c)中粉色虚线标出的平坦声子带主要由远离布里渊区中心的声学支顶部和低能光学支组成, 其底部能量与弹性线(黄色箭头)之间有明显的间隙. 在SrAgSb和Sr2ZnSb2中, 该平带的能量较低, 其底部能量降至~3.5 meV, 表明SrAgSb和Sr2ZnSb2相对于SrCuSb都有很强的声子软化. 然而, 在SrAgSb化合物中可以清晰地追踪到3条尖锐的声子带, 低能声子带向较低能量的移动与中间声子带(以~13 meV为中心)形成了更清晰的间隙. 相比之下, 所有声子带在Sr2ZnSb2化合物中变得相当宽, 并且难以彼此区分. Sr2ZnSb2中的空位显著增强了晶格的非谐性, 导致整个声子谱大幅软化和宽化. 空位引起的声子非谐性, 加上缺陷散射, 使Sr2ZnSb2具有更小的$ {\kappa }_{{\mathrm{L}}} $.

      很显然, 存在空位缺陷的Sr2ZnSb2晶格动力学与SrAgSb和SrCuSb的晶格动力学不同. 为了解释Sr2ZnSb2的异常晶格动力学行为, Zhu等[123]计算了Sr(Cu, Ag, Zn)Sb化合物的差分电荷密度(图15(d)—(f)). 结果显示, Sr(Cu, Ag)Sb中Cu(Ag)-Sb的共用电子对在Sr2ZnSb2中从Zn转移到了Sb. 进一步量化Sr(Cu, Ag, Zn)Sb化合物的电荷转移, X射线光电子能谱数据揭示了Sr2ZnSb2中阳离子层Sr的电荷转移量远小于另外两种化合物的层间离子键削弱效应. 图15(g)展示了各向异性原子位移参数, 与Sr2ZnSb2相比, SrAgSb和SrCuSb的原子位移参数相近, Zn原子和Sb原子沿c轴的热振动显著增大, 这与化学键分析一致, 进一步证实了由于空位的引入导致晶格软化和层间相互作用减弱, 从而非谐性增强.

      对于二维Zintl相化合物, 第一性原理计算和电子密度分析表明, AB2X2型化合物层间键的强度较弱, 这导致声子模式的非简谐性, 热导率偏离了标准的T –1温度依赖性. 而非弹性X射线散射强调缺陷引起的晶格无序性显著限制了声子传输, 降低了晶格热导. 在此基础上, 非弹性中子散射揭示了与层间键相关的平坦的横向声子支的存在, 增加了声子的散射相空间, 同时低能量声子的软化会降低声子的群速度, 从而抑制热导率. 对于AB4X3型化合物, 第一性原理计算从弹性模量这种宏观角度来说明材料的非谐性(较高的格林内森常数), 通过中子衍射数据揭示了材料中不对称原子键的存在和原子非谐性振动的特征, 这为低热导率的物理起源提供了直接证据. 对于ABX化合物: 第一性原理计算发现弱的层间键合会显著增强晶格的非谐性, 表现出强的四声子散射, 这种高阶声子散射机制进一步降低了晶格热导率; 结合高角环形暗场扫描透射电子显微镜的研究, 发现空位(B位置空位)会引入局域结构无序性, 显示局部有序但整体无序的纳米结构特性, 这种局部无序显著增强声子的散射有助于降低热导率. 同时这种空位直接影响了晶格键合和振动特性, 非弹性中子散射数据揭示了整个声子谱的软化和展宽, 这些现象归因于空位引起的晶格键弱化, 是降低晶格热导的关键因素.

      • 3.4.   三维块状体系

    • 三维Zintl相化合物(如笼状化合物[134]和方钴矿[135]等)具备独特的三维共价键网络框架, 在这种三维网络中, 电子和声子可以自由传导, 使得三维Zintl相化合物表现出不同于低维Zintl相化合物的性质. 与低维Zintl相化合物相比, 三维Zintl相化合物的电子和声子传导机制更为复杂, 通常涉及到更多的耦合和多样的散射途径. 同时, 由于这种复杂性, 研究方法和热电性能优化策略也与低维Zintl相化合物有所区别. 因此, 三维Zintl相化合物已成为热电材料研究中一个独立且庞大的领域, 拥有自己特定的研究体系和应用方向. 出于篇幅限制以及内容聚焦的考量, 本文主要关注零维、一维和二维等低维Zintl相化合物, 详细探讨其结构特性、热电性能优化策略, 而未涉及到三维Zintl相化合物.

    4.   结　论

    • 本文总结了近年来利用中子散射技术研究低维Zintl相化合物的低晶格热导率物理起源方面的进展. 文中梳理了零维A14MPn11型化合物, 一维链状化合物, 二维层状AB2X2型化合物和其结构变体AB4X3型化合物, 存在本征空位的ABX型和A2BX2型化合物的研究进展, 还特别总结了A = B的二元AB2X2型化合物Mg3Sb2的研究现状. 综合分析, 不同维度的Zintl相化合物低晶格热导率的物理起源主要体现在以下几个方面.

      1) 零维Zintl相化合物的低热导率主要归因于复杂的晶体结构、强烈的声子散射以及局域晶格的无序性. 复杂的晶体结构限制了声子的传播, 显著缩短了声子自由程, 同时使声子模式高度复杂化, 从而增强了声子散射效应. 与此同时, 低能区域内高度重叠的光学声子模式突显了扩展子通道的作用, 这种类似无定形材料的导热机制进一步降低了晶格热导率. 此外, 局域晶格的无序性则导致了价态波动和扩散子通道的增强, 进一步加剧了材料热导率的下降.

      2) 一维Zintl相化合物的低热导率源于较弱的原子键合和高度非谐性. 由于原子键合较弱, 导致原子表现出大幅度的局域振动, 与之相关的低能光学声子模式与声学声子之间的强耦合, 这种耦合显著增强了声子散射. 此外, 随着温度升高, 声子模式展宽迅速加剧, 反映出高度非谐性振动特征, 这进一步增强了声子散射, 降低了热导率.

      3) 二维Zintl相化合物的低热导率主要源于其较弱的层间键合、结构无序性和高度非谐性. 较弱的层间键合导致了不对称原子键及原子非谐性振动, 在声子谱上体现为平坦的横向声学支的和显著声子软化, 增强了声子-声子非谐性散射. 同时存在本征空位等晶格缺陷, 使得晶格键合减弱和软化, 这种结构的无序进一步影响了整个声子谱的软化和展宽, 从而极大地增强了非谐性, 共同抑制了热导率.

      通过对低维Zintl相热电材料的研究发现, 化学键合、声子散射和非谐性在降低热导率方面发挥了关键作用, 为这类材料的研究提出展望: 1)调控材料的键合强度, 例如通过掺杂或结构调整优化键合层次性, 引入弱键合离子或大质量差异的元素, 结合中子衍射的键合分析, 探索不同化学键组合对材料性能的调控作用, 设计出更高性能的热电材料; 2)调控材料的非谐性, 例如引入缺陷和本征空位, 优化晶体结构的复杂性, 设计具有动态局域无序特性的材料, 从而增强原子的局域振动和声子-声子非谐性散射, 通过非弹性中子散射对声子谱的直接观测并结合理论计算, 优化声子模式的重叠与光学声子-声学声子耦合, 可进一步提升声子散射效率, 设计出更低热导率的热电材料.

      弹性中子散射技术, 即中子衍射, 不仅可以帮助理解材料的详细晶体结构信息, 包括晶格常数、化学键、原子位移参数、原子占位与分布等等, 还可以表征材料的无序和缺陷. 这些异常通常在衍射谱中显示出来, 例如晶体的无序性可能会表现为衍射峰的展宽或者出现大的鼓包; 原子的振动位移增大可能导致高Q衍射峰的展宽和强度降低. 非弹性中子散射技术可以通过测量声子及态密度, 得到声子寿命、群速度等信息, 相同的声子异常也可在声子色散关系和声子态密度上观察到. 例如, 声子散射的增强可能导致声子色散关系中声子分支的展宽和平带的出现, 声子态密度中声子带的展宽. 声子的非谐性增强可能表现为声子能量的降低, 而观察到的漫射信号的出现可能是扩散效应带来的. 另外, 随温度的变化谱图为晶体结构和声子特性提供了重要见解, 结合理论计算, 可以从局域振动模式、晶格无序性等角度, 确定材料的晶格动力学、缺陷散射、电声耦合、声子-声子相互作用等.

      综上所述, 中子散射技术结合理论计算对Zintl相化合物的深入研究, 不仅帮助科研工作者们更深入地理解材料的性质和晶格动力学, 对现有Zintl相化合物的性能优化提供科学依据, 还可以为筛选具有特定晶体结构和低热导率的Zintl相化合物, 从而加速新型高性能Zintl相热电材料的设计与开发.

    参考文献 (135)

目录

/

返回文章
返回