-
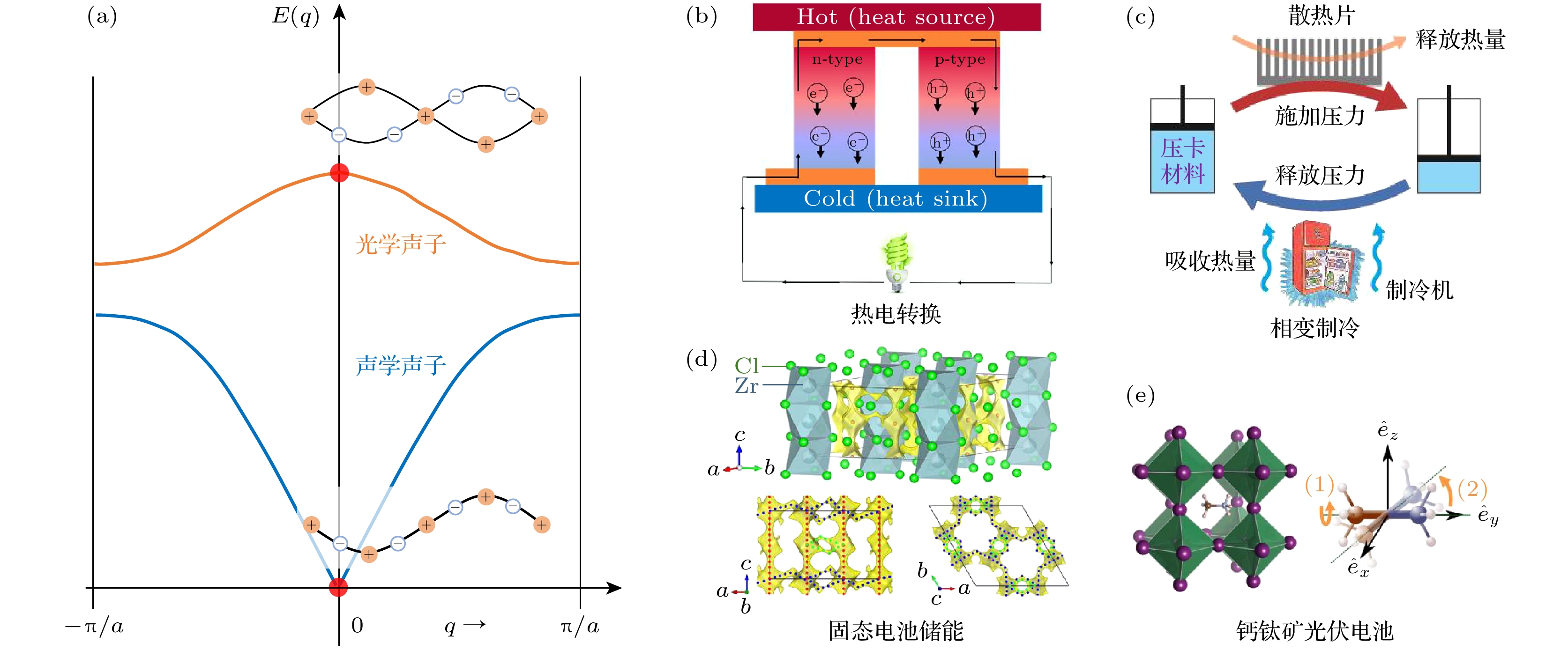
物质的微观结构是研究其宏观物理现象的基础, 然而许多物理现象无法仅通过晶体结构来完全解释. 根据量子力学与固体理论, 构成固态物质的原子、离子、分子等基元会在由周围其他基元构建的势场中进行振动, 且这些振动的能量具有量子化特征, 被称为声子准粒子; 而各基元之间形成的集体振动使声子的能量与动量呈现特定的依赖关系, 被称为声子色散谱或简称声子谱[1]. 声子蕴含着基元的动能与势能信息, 是理解物质热学性质的重要基础, 包括内能、比热、相变、热传导、热膨胀等[2]. 这些现象和性能构成了很多前沿能源材料的重要物理基础, 因此晶格动力学逐渐成为相变制冷与储能、热电转换、电池储能、光伏发电等能源材料的重要研究方向(见图1)[3–6].
以半导体热电材料为例, 好的性能需要同时具备良好的电输运性能和尽可能低的晶格热导率[7]. 在电输运方面, 影响载流子迁移率的多种散射势都与晶格振动密切相关, 包括声学声子形变势、光学声子形变势、压电散射和极化光学声子散射等[8]. 而在晶格热导方面, 声子是能量传输的载体, 其群速度、寿命或平均自由程以及态密度等因素决定了热导率的大小[9–12]. 因此, 深入研究晶格动力学对于热电材料的发展至关重要.
近年来, 能源材料的研究逐渐转向复杂的晶 体结构体系, 这些材料的晶格动力学也变得异常 复杂[12–16]. 大多数具有本征低热导的热电材料都具有非常复杂的晶体结构, 包括超大的晶胞[17–19]、大量的有序或无序空位缺陷[20,21]、局域畸变或无 序[22–24]、主客体原子或分子[25,26]、铁电或化学失稳、嵌套亚晶格等特征[27,28]. 与此同时, 晶体结构的复杂与多样化使得相关材料的声子谱也呈现出极端复杂性, 如具有超低的声学声子截止频率[18]、或很强的非谐性[29,30]、或明显的声子软化或过阻尼[31,32]、或布里渊区中心光学声子软化的“瀑布现象”[28,33]、或声学支与光学支之间的“避免交叉”等[25,34]. 在超离子固态电解质中, 部分亚晶格中的离子具有长程扩散行为, 而这些扩散行为与其他亚晶格的热振动密切关联[35–39]. 在光伏钙钛矿材料方面, 晶格中多面体表现出巨非谐性振动, 而有机分子则具有局域旋转运动行为, 这些复杂晶格动力学是驱动材料发生结构相变的重要物理基础, 同时也赋予相关材料高效的热载流子输运特性[3,40,41]. 在相变制冷或储能材料中, 晶格熵变是总熵变的一个重要贡献来源, 而分子的局域转动赋予晶格熵非常大的构型熵[42].
复杂的晶体结构与晶格动力学构成了许多新型能源材料的重要物理基础, 但同时也给相关材料物理机制的理解带来了巨大的挑战. 作为第一个被引入物理学的元激发准粒子, 晶格振动声子已有90多年的研究历史[43], 并发展了丰富的研究方法, 包括理论模拟和实验表征. 特别是在理论计算方面, 从密度泛函理论到机器学习分子动力学, 晶格动力学的模拟可以准确复现实验结果[12]. 然而, 随着能源材料晶体结构与晶格动力学的复杂化, 通过理论模拟来理解晶格动力学的研究思路面临着巨大挑战. 这些挑战不仅来自于理论模型的构建, 更源自对相关微观物理图像的准确把握的不足. 面对这些挑战, 利用实验手段直接表征晶格动力学变得至关重要. 表征晶格动力学的实验方法有很多, 包括拉曼、布里渊散射和中子散射等. 其中, 中子散射同时具有高的能量与动量分辨率, 是研究物质结构与晶格动力学最有效的方法之一. 近20年来, 基于中子散射技术的晶格动力学研究为许多能源材料的深入理解和性能优化提供了丰富而准确的信息[44,45].
本文就中子散射技术及其在能源材料微观结构与晶格动力学研究中取得的一些重要成果进行回顾和探讨. 首先介绍中子在功能材料微观结构解析、晶格动力学表征方面的关键技术与优势; 然后以超离子热电材料为例, 介绍中子散射技术在超低晶格热导率机制研究中取得的成功; 以固态电解质为例, 揭示离子扩散与晶格振动之间的关键作用机制; 以塑晶材料为例, 揭示塑晶态相变、构型熵与压卡制冷之间的内在关联; 最后介绍晶格振动与电荷、自旋等之间的相互作用, 为理解更多的能源材料提供基础.
-
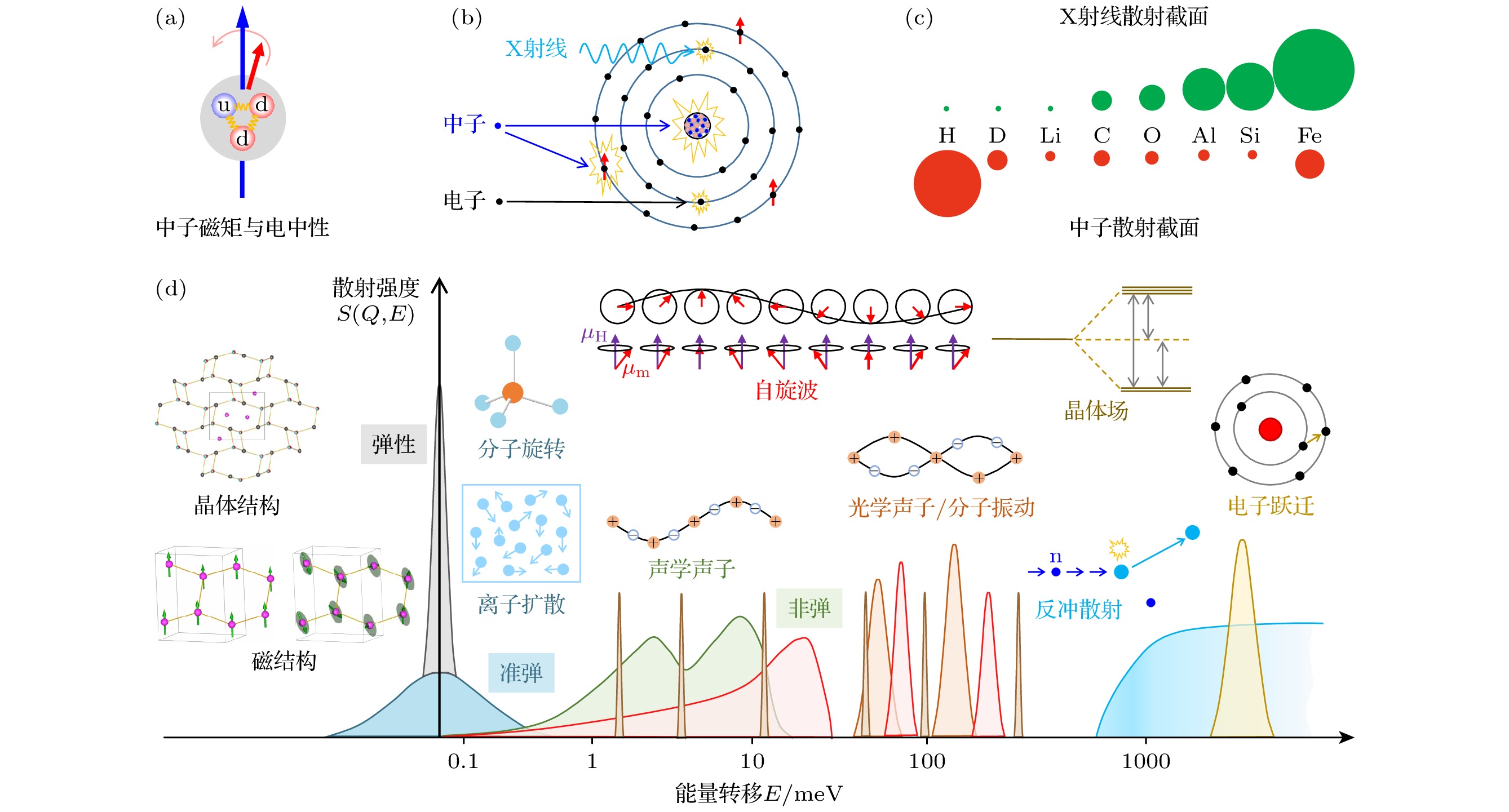
在物质结构和晶格动力学研究中, 中子散射技术之所以重要, 主要源于中子的特殊性质[46,47]. 1)中子为电中性粒子(图2(a)), 穿透深度大, 可以表征物质内部或体态信息, 开展材料无损检测, 同时便于加载各种极端样品环境, 包括超低温、极高温、强磁场、压力等, 满足各种测量需求. 2)中子主要与原子核发生散射作用, 不同于X射线或电子束, 后两者主要与原子核外电子云相互作用(图2(b)). 作用方式的不同决定了各元素的X射线或电子束的散射截面与原子序数成正比, 而中子散射截面则与原子序数无关, 且在相邻元素之间变化很大. 如图2(c)[47,48]所示, 中子可以测量轻元素, 如H, Li等, 这些都是能源材料中比较重要的元素; 同时, 中子能够区分原子序数相邻的元素和同位素, 与X射线形成很好的互补. 3)中子由一个上夸克和两个下夸克组成, 这种结构赋予中子一个自旋磁矩, 使其能够与核外未配对的电子发生磁散射, 在磁结构解析与自旋激发测量方面具有独特的优势. 4)中子的质量很大(约为1842个电子质量), 波长为原子尺度(埃米量级)的中子比相应的X射线的能量低很多, 与物质中的元激发能量相当. 中子散射(相比光散射)可以覆盖大的能量与动量范围, 并拥有相对较高的能量与动量分辨率, 因此是同时表征物质结构和测量晶格动力学的最佳手段之一, 可以用来研究离子扩散、分子旋转、晶格集体振动(声子)、晶体场等多种晶格动力学行为(图2(d))[49], 为材料物理性能的理解提供更直观的物理图像[44,45,50]; 这种低能量特性也使中子对物质的扰动接近于平衡态, 符合线性响应近似, 但在X射线散射实验中这种近似并不总是成立的.
根据费米黄金定则, 由中子散射实验直接获得的信息为双微分散射截面:
其中,
$ \sigma $ 为样品中元素的中子散射截面,$ {\boldsymbol{k}}_{{\mathrm{i}}} $ 和$ {\boldsymbol{k}}_{{\mathrm{f}}} $ 入射和散射中子波矢,$ N $ 为原子数.$ S\left(\boldsymbol{Q}, \omega \right) $ 被称为动力学结构因子, 向内从底层统计理论方面可以表达为式中,
$ G\left(\boldsymbol{r}, t\right) $ 为van Hove关联函数, 描述$ t=0 $ 时刻$ \boldsymbol{r} $ 位置的原子$ j $ 与$ t $ 时刻在$ {\boldsymbol{r}}'+\boldsymbol{r} $ 位置的原子$ i $ 之间的关联, 这里包含了时间与空间的关联. 向外到凝聚态物理层级,$ S\left(\boldsymbol{Q}, \omega \right) $ 可以描述为该式表示中子与样品发生能量转移并在样品中产生(+)或湮灭(–)一个声子的过程.
$ \boldsymbol{Q}={\boldsymbol{k}}_{{\mathrm{i}}}-{\boldsymbol{k}}_{{\mathrm{f}}} $ 为散射矢量,$ \boldsymbol{\tau } $ 为晶格倒格矢,$ \boldsymbol{q} $ 和$ \hslash \omega \left(\boldsymbol{q}\right) $ 为激发态准粒子的波矢与能量, 两个狄拉克δ函数分别对应(3)式中位置$ \boldsymbol{r} $ 与时间$ t $ 的傅里叶变换, 并约束散射事件遵守动量守恒与能量守恒[46,47,51]. εj(q)为声子简正模的极化矢量, 在实验测量中可以用来区分横波声子和纵波声子;${{\mathrm{e}}}^{-{\boldsymbol{Q}}^{2}\langle{u}^{2}\rangle} $ 为德拜-沃勒因子(Debye-Waller factor).根据中子与物质散射过程中是否发生能量转移, 即(4)式中
$ \hslash \omega \left(\boldsymbol{q}\right) $ 或$ {E}_{{\mathrm{f}}}-{E}_{{\mathrm{i}}} $ 是否为零, 中子散射可分类为弹性散射(elastic scattering)和非弹性散射(inelastic scattering) (图2(d)), 对应不同类型的谱仪与测量信息. 其中弹性散射包括中子衍射(diffraction)、全散射(total scattering)、漫散射(diffuse scattering)、小角中子散射(small angle neutron scattering, SANS)、中子反射(neutron reflection)等, 而非弹类包括有准弹性(quasi-elastic neutron scattering, QENS)与非弹性(inelastic neutron scattering, INS)散射. 下面将介绍相关谱仪的结构、功能和优缺点. -
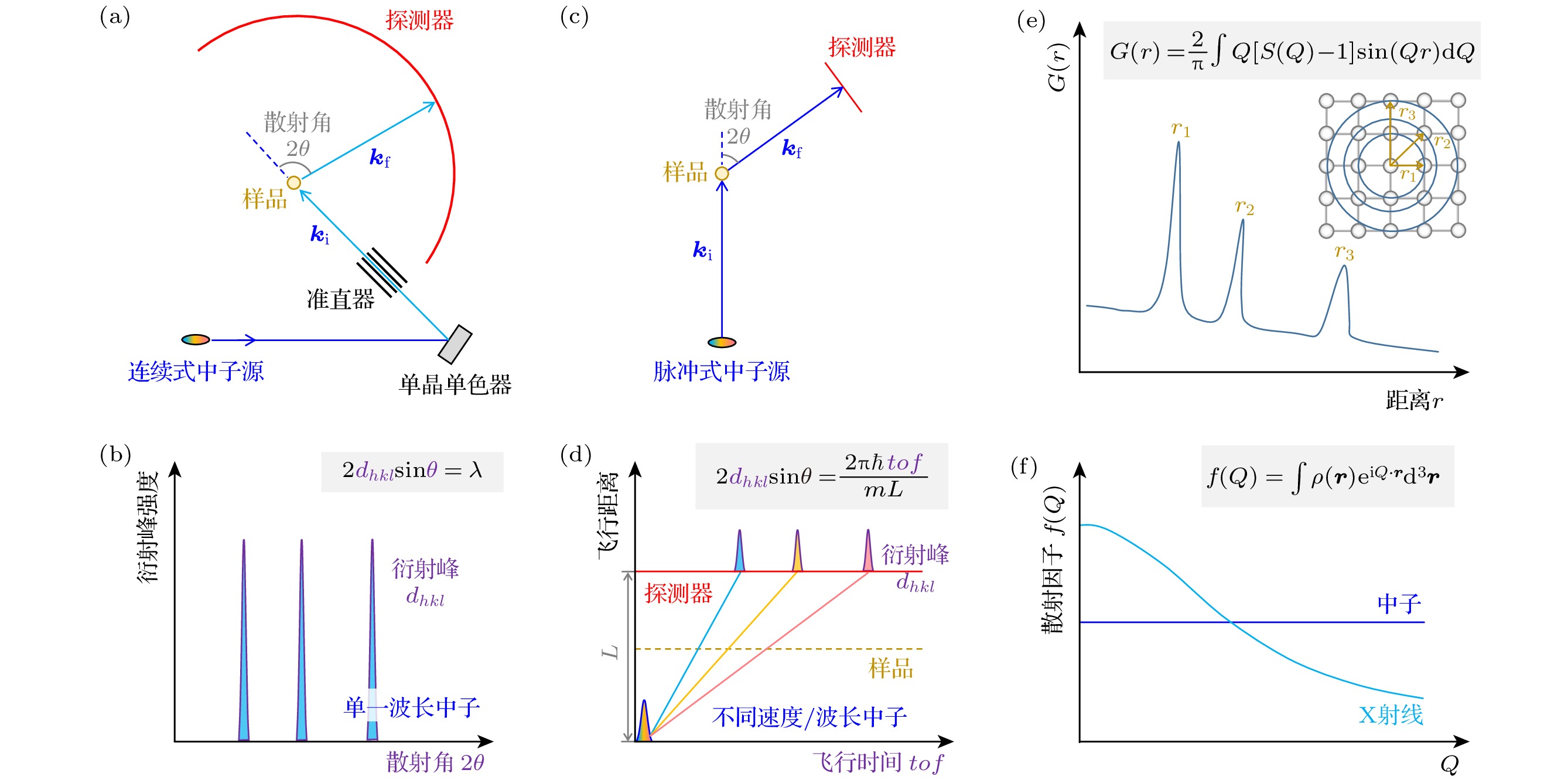
1)中子衍射谱仪与原理. 中子衍射是弹性散射技术中最常用的方法. 与X射线衍射和电子衍射类似, 中子衍射也是表征物质晶体结构的常用手段, 均遵循布拉格衍射定律. 目前主流的中子源有两种, 一种是连续式中子源(多为反应堆中子源, 如法国的ILL、美国的NIST和HFIR、德国的FRM II、澳大利亚的ANSTO以及我国的CMRR和CARR), 另一种为脉冲式中子源(多为散裂中子源, 如日本的J-PARC、美国的SNS、英国的ISIS以及中国的CSNS). 两种不同中子源的衍射谱仪结构和工作方式也有所不同. 反应堆中子源的衍射谱仪与传统X射线衍射谱仪类似, 采用单一波长的中子, 通过扫描不同的散射角2θ, 依次测量不同的衍射峰dhkl (图3(a)). 因此, 在这类固定波长的衍射实验中, 2θ和dhkl是布拉格公式中的两个主要变量(图3(b)). 脉冲式中子源的衍射谱仪则有不同的结构, 该类衍射谱仪的探测器角度固定, 慢化器(将高能质子打靶产生的高能中子的能量从MeV量级降低到meV量级的装置)与探测器之间的中子飞行距离固定(图3(c)), 通过测量中子的飞行时间 (time of flight, tof), 可得到中子的速度或波长或能量(图3(d)). 利用每个脉冲中不同速度或一定带宽的中子, 可以逐一测得不同的衍射峰. 因此, 脉冲中子衍射谱仪测量过程中的两个变量为tof和dhkl (图3(d)).
2)中子衍射技术的优势. 在能源材料的研究中, 掺杂、缺陷、无序占位、短程序、超大晶胞、低对称性等都是在结构表征中经常遇到的难点. 与电子和X射线不同, 中子可以探测轻元素、区分临近元素和同位素, 在掺杂和缺陷分析中优势明显. 另一方面, 超大晶胞和低对称性意味着更多更密的布拉格衍射峰, 准确的表征需要高的谱仪分辨率. 通量低和聚焦难度大决定了中子衍射谱仪的分辨率无法与X射线衍射谱仪相媲美, 尤其是同步辐射X射线衍射谱仪, 如英国Diamond光源的I11衍射仪的最佳分辨率可达Δd/d ~ 10–5. 但近年来, 基于散裂中子源和退耦合慢化器技术的发展, 使得高分辨率中子衍射谱仪成为可能, 如日本J-PARC的SuperHRPD衍射谱仪的分辨率可以达到Δd/d ~ 10–4量级, 能够满足大多数大晶胞和复杂结构体系的测量需求.
在晶体结构解析方面, 另一个重要参数是原子位移参数(atomic displacement parameters, ADP)或均方位移(mean-square displacement, MSD), 对应(4)式中的
$\langle{u}^{2}\rangle $ , 在衍射谱学上表现为原子振动对散射因子的影响, 即布拉格衍射峰强随Q的增大而发生系统性减弱的现象. 高质量、大Q范围的衍射谱采集可以获得精准的三维ADP, 为晶格动力学谱学的理解提供原子层级的实空间信息[21]. 正如前面内容所介绍的, 脉冲中子衍射谱仪的分辨率相对较高, 且容易获取大Q范围的衍射峰, 是分析ADP的最佳手段之一.3)短程序与无序结构表征. 弹性中子散射也为无序结构和短程序结构的解析提供了很多解决方案. 其中应用最广的是中子全散射谱仪, 此类谱仪借助对分布函数(pair distribution function, PDF)技术, 通过对倒空间中的结构因子S(Q)进行傅里叶变换实现对正空间中原子有序性的测量(图3(e)), 为局域无序、晶格畸变、非常规振动等提供不同视角的信息[22,52,53]. 脉冲中子衍射谱仪可以通过超宽带宽中子获得更大的Q (Q = 4πsinθ/λ)空间测量, 且中子的原子散射因子(atomic form factor)不随Q的增大而衰减(图3(f)), 因此在S(Q)的傅里叶变换与PDF分析方面比X射线更具优势. 在固态电解质材料的离子分布与扩散通道分析中, 一种有效的方法是中子衍射结合最大熵法(maximum entropy method, MEM). 这里应用信息熵最大化的基本原理, 可以克服传统晶体学的限制, 有效解析大范围内离子的无序排列[31,39,54]. 中子漫散射谱仪也为短程序或无序的表征提供了另外一种方案[55], 这种技术利用单晶样品, 可以观察到整个三维倒易空间中由短程序或无序引起的漫散信号, 进而利用逆蒙特卡罗方法还原实空间中原子的排列情况[56]. 此外, 单晶漫散射技术还衍生出了3维PDF技术[57].
除中子衍射、全散射和漫散射等, 弹性中子散射还包括有小角中子散射、中子反射、中子成像等技术. 小角中子散射可以表征纳米或更大尺度的不均匀结构和尺寸分布等, 如孔洞、缺陷、颗粒、内表面[58,59]; 中子反射谱仪可以用来分析薄膜的厚度、界面粗糙度、聚合物薄膜成分分布等信息[60,61]; 而中子成像可以分析亚微观尺度的器件结构等[62–64].
-
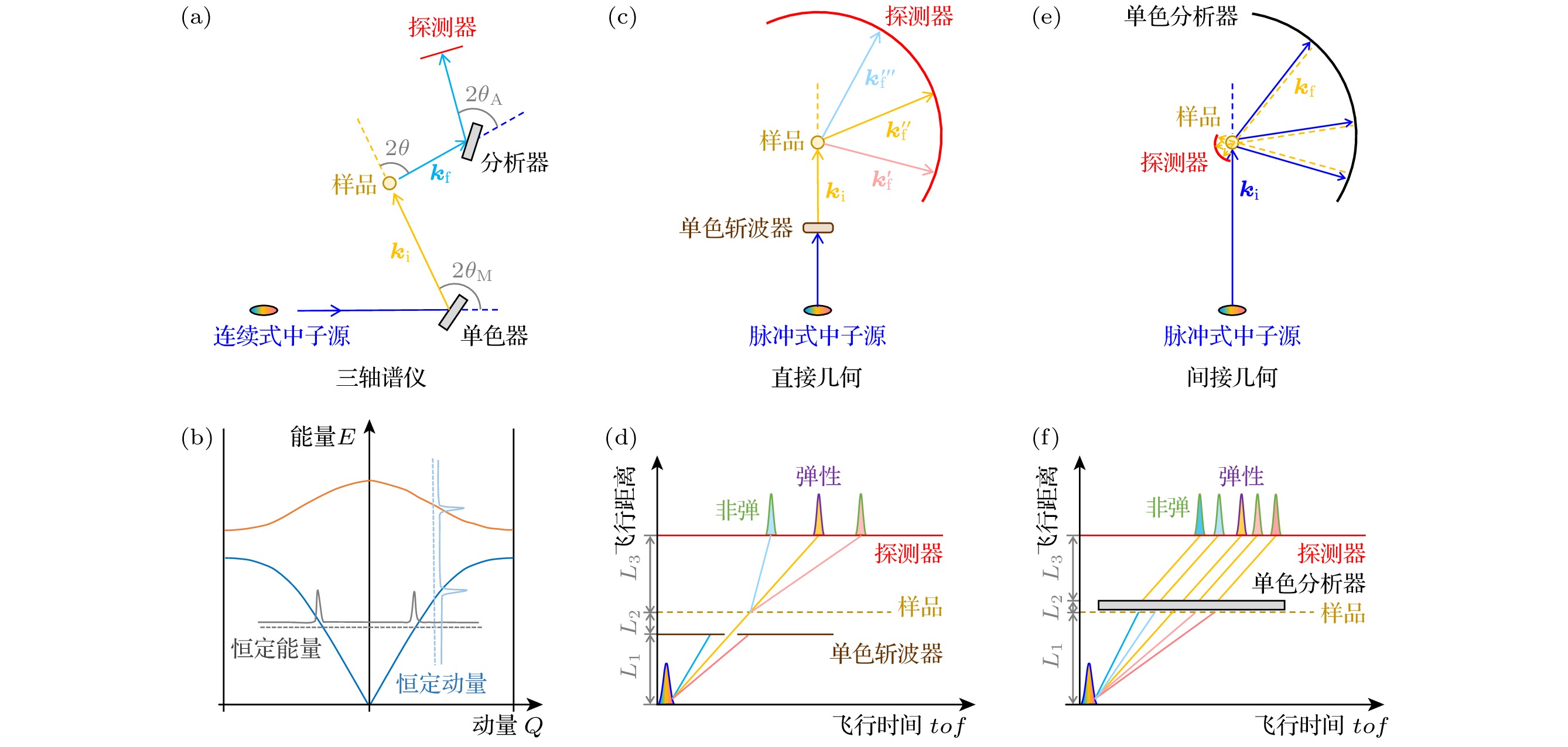
1)非弹性/准弹性中子散射谱仪与原理. 非弹性和准弹性中子散射过程同时涉及到动量和能量的转移, 并遵循动量与能量守恒定律. 动量转移Q决定于散射前后的中子波矢ki和kf以及二者之间的散射角2θ, 而能量转移则取决于散射前后的能量差值Ei-Ef. 散射角2θ由谱仪的几何结构所决定, 是较容易确定的参数. 但是, 中子探测器无法直接测量中子的能量, 需要借助其他方法. 中子能量的测定主要有两种方法. 第1种方法是利用布拉格衍射定律, 通过调整单晶衍射的角度, 来选择并确定中子的波长或能量. 这种方法常见于连续式中子源, 除了样品坐标上的转轴来确定散射角2θ外, 还需要在样品前后各放置一个转轴用来操作单色器单晶和分析器单晶的转角, 因此这类谱仪被称之为三轴谱仪(triple axis spectrometer), 见图4(a). 另外一种方法是利用固定距离L的中子飞行时间tof来确定中子的速度或能量, 这种方法常见于脉冲式中子源. 为了方便做能量减法, 需要Ei和Ef中的一个参数为单一数值. 具体的做法可以是在样品前放置一个单色斩波器使Ei变为单一数值, 也可以在样品后放置一个单色分析器, 使探测器测得的中子能量Ef为单一数值, 前者被称之为直接几何非弹谱仪(direct geometry), 见图4(c), (d), 后者被称之为间接几何或逆几何非弹谱仪(indirect/inverted geometry), 见图4(e), (f).
在色散谱的表征中, 三轴谱仪由于在样品前后都是单色能量, 因此需要沿着四维色散谱(3个动量维度和一个能量维度)中的某一条线进行扫描, 一般采用固定动量扫能量(constant-Q scanning)和固定能量扫动量(constant-E scanning)两种方式. 而脉冲式的直接几何与间接几何谱仪由于只需单色化一端的能量, 借助广角探测器和单晶样品旋转, 可以直接测绘出完整的四维色散谱. 因此, 在测量四维色散谱全谱方面, 脉冲式非弹谱仪比三轴谱仪的测试效率更高. 然而, 三轴谱仪可以沿着色散谱中某条固定的直线, 更加高效地追踪晶格动力学随温度场、磁场、应力场等的变化趋势[44].
2)能量分辨率. 能量分辨率是非弹性和准弹性中子散射谱仪的一个重要指标. 以直接几何谱仪为例, 能量分辨率与慢化器的能量展宽、慢化器到样品的距离、样品到探测器的距离、单色斩波器的频率、入射中子的能量、能量转移数值等相关[65]. 中子散射谱仪的能量分辨率一般由弹性散射位置的能量展宽与入射中子能量之间的比值, 即ΔE/Ei, 来描述. 大多数直接几何谱仪的能量分辨率都在3%—10%之间, 少数冷中子能量段的谱仪分辨率可以达到1%左右. 以日本J-PARC的冷非弹直接几何谱仪AMATERAS为例, 3.134 meV的入射中子能量的分辨率可以达到~1.7%, 分辨率绝对值为ΔE~53 μeV. 逆几何谱仪一般具有更长的中子飞行距离, 特别是样品到探测的飞行距离(见图4(e)), 可以提供更高的分辨率, 如美国SNS的BASIS谱仪的分辨率可以高达~0.1%, 其绝对值大约在3.5 μeV. 但是逆几何谱仪的探测器聚集于样品周围, 单位立体角内的覆盖面积很小, 以致其动量分辨率相较直接几何谱仪要低很多. 根据两种不同几何谱仪的分辨率特征, 直接几何谱仪一般用来测量声子色散谱与声子态密度, 而逆几何谱仪一般用来研究离子扩散、大分子振动等行为. 需要指出的是, 冷中子直接几何谱仪由于其较高的能量分辨率, 也经常被应用于离子扩散和大分子振动等动力学的测量.
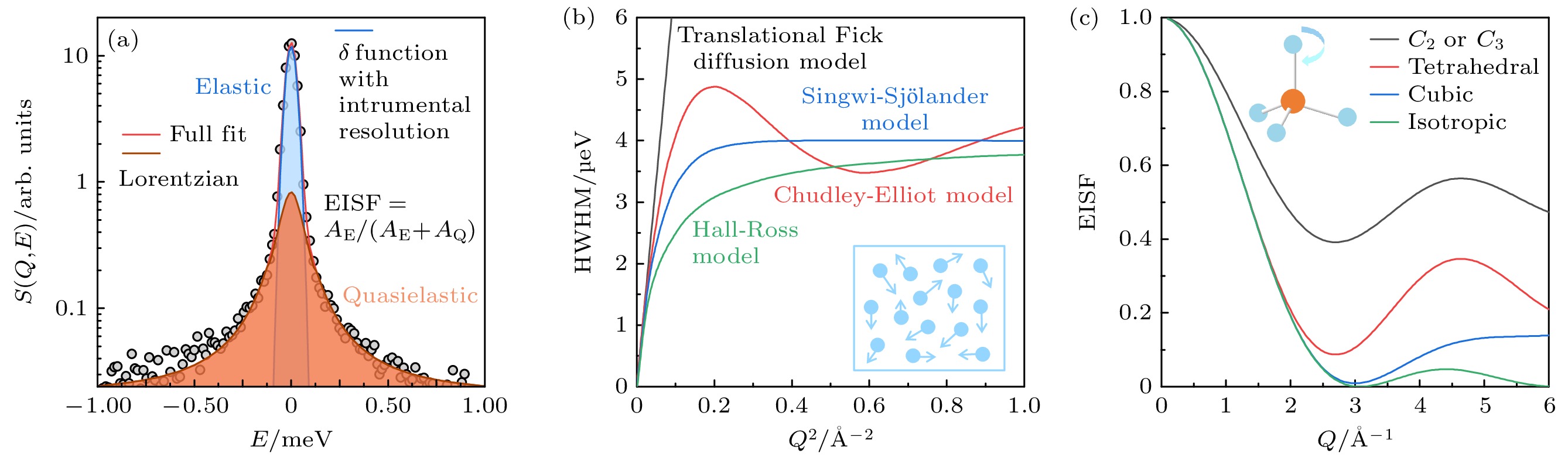
3)准弹性中子散射技术. 如图2(d)所示, QENS本质上是INS的一种极限情况. 但是, 有别于INS用来测量晶格中能量偏离弹性峰较远且具有量子化特征的动力学行为, QENS主要用来描述凝聚态物质中的扩散和旋转等非量子化的无序运动[66,67]. 中子与物质中无序运动原子之间的小的能量转移会给弹性峰带来多普勒展宽, 因此QENS一般包含两部分, 由δ函数卷积谱仪分辨率来描述的弹性散射部分和由洛伦兹峰描述的、紧贴弹性峰两边的准弹性部分(见图5(a)). 在能源材料研究中, 参与无序运动较多的H, Li, Cu和Ag等元素都具有较大非相干散射截面(incoherent cross-section)[46], 因此相关的QENS信号主要为非相干散射过程, 对应晶格中基元的自运动而非集体运动. 如图5(a)所示, 弹性信号
$ S\left(Q\right) $ 与原子振动的幅度$ \left\langle{{u}^{2}}\right\rangle $ (即均方位移)相关, 二者之间的具体关联可以由公式$ S\left(Q\right)\propto {\mathrm{e}}{\mathrm{x}}{\mathrm{p}}\left(-{Q}^{2}\left\langle{{u}^{2}}\right\rangle/3\right) $ 来描述[68]. 准弹性峰的展宽(half width at half maximum, HWHM)反映无序运动的特征时间, 根据HWHM的动量依赖曲线可以确定离子扩散的不同方式, 如长距离扩散的Fick模型, 扩散距离为某一常数的Chudley-Elliott模型和扩散距离具有一定分布方式的Hall-Ross模型等(图5(b))[69]. 而由弹性散射强度与总散射强度之间的比值构成的弹性非相干结构因子(elastic incoherent structure factor, EISF)则与扩散或分子转动的限域几何相关, 如铵基四面体沿C2/C3对称轴的旋转或在立方体的八个顶点之间旋转的Cubic模型等(图5(c))[70].4)其他非弹性散射技术. 在四维色散谱表征方面, 除了中子散射技术, 还可以采用布里渊光散射(Brillouin light scattering, BLS)[71,72]、非弹性X射线散射(inelastic X-ray scattering, IXS)[73,74]和四维电子损失谱散射(four-dimensional electron energy-loss spectroscopy, 4D-EELS)[75]等. 在样品制备方面, 相比中子散射对大块单晶样品的要求, 以上这3种技术对样品量的需求很小, 有的甚至不需要单晶样品. 在晶格动力学表征内容方面, BLS只能测量声学声子, 且可覆盖的能量范围很小(μeV量级), 而IXS和4D-EELS则与INS一样可以测量比较完整的色散谱. 在能量分辨率方面, IXS的分辨率一般在meV量级, 目前报道的最高值可以达到~0.75 meV左右[74], 但依然无法与INS媲美. 4D-EELS的分辨率则更差, 一般在14—16 meV, 因此该技术主要应用于声子谱结构比较简单且能量很高的材料[75]. 但是, 在这些非弹性散射技术中, 4D-EELS具有最高的空间分辨率, 可以实现对薄膜、表界面、局域缺陷等的声子谱表征. BLS, IXS和4D-EELS技术与三轴中子衍射谱仪类似, 在色散谱测量过程中都是沿着四维空间中的某一条线进行扫描的, 这与具有广角探测器的直接几何谱仪不同. 后者由于可以同时获得多个完整布里渊区的晶格动力学信息, 可以在使用粉末样品的情况下高效地获得带有中子权重(不同的原子核散射截面导致的)的声子态密度[21,76].
-
基于塞贝克效应和帕尔贴效应的热电材料, 可以通过温度梯度将热能转换为电能, 在余热回收、固态制冷、深空探测等领域展现出重要的应用前景[77,78]. 高性能的热电材料需要尽可能低的晶格热导率以保证器件在工作中能持续维系两端的温度梯度. 材料的晶格热导率可以由声子自由气模型
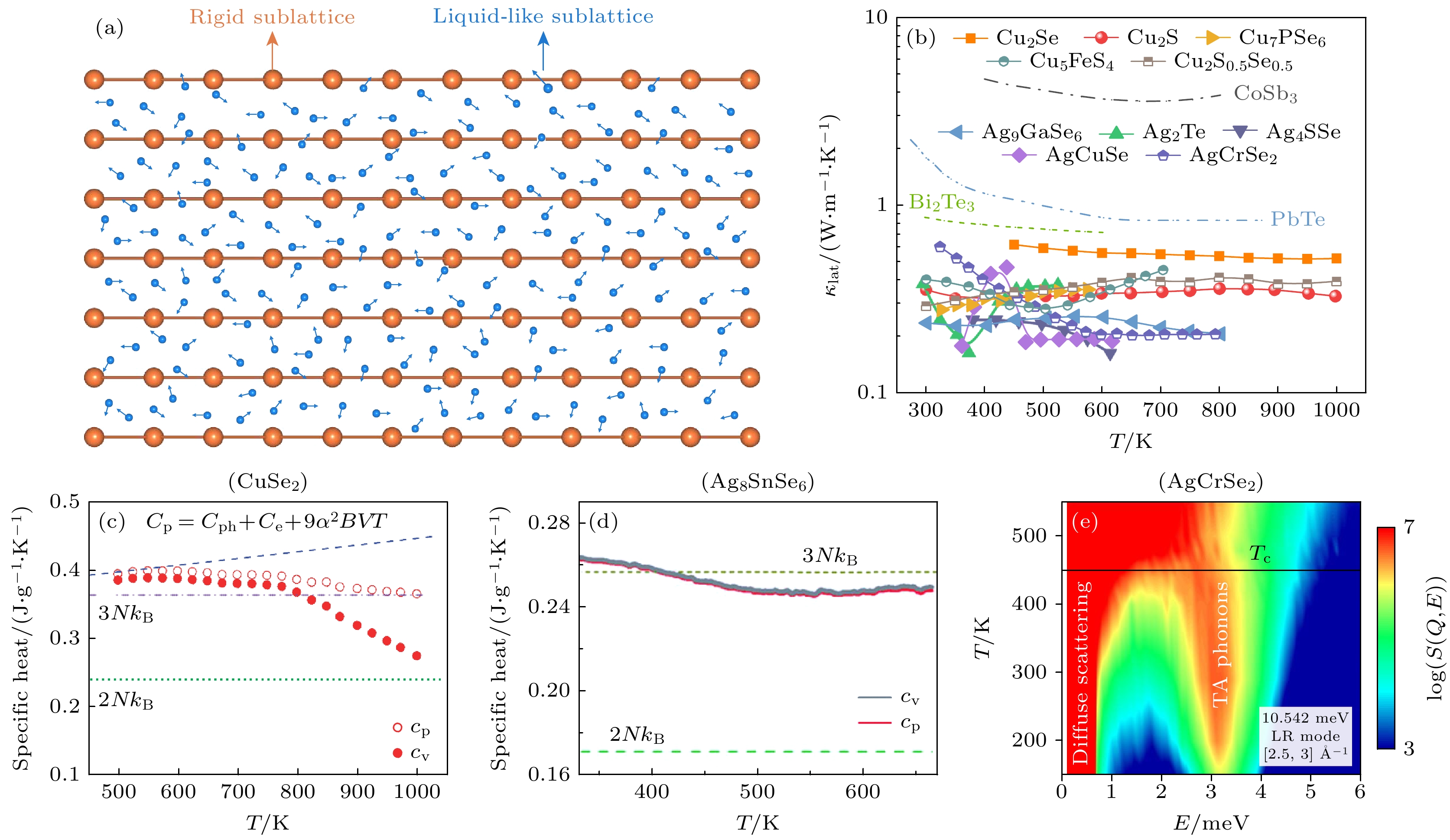
$ {\kappa }_{{\mathrm{l}}{\mathrm{a}}{\mathrm{t}}}=1/3 c{v}^{2}\tau =1/3 cvl $ 描述, 其中$ c,\; v,\; \tau $ 和$ l $ 分别代表比热、声子群速度、声子寿命和声子平均自由程[79]. 在这些参数中, 声子群速和晶格比热与原子质量、化学键强弱和晶胞尺寸等有关, 是材料的本征属性, 调控难度较大. 在热电材料开发中, 常用的抑制晶格热导率的办法是通过引入不同的散射机制来缩短声子寿命或减小其平均自由程, 具体方法有声子非谐、电-声子相互作用、0维点缺陷、1维位错、2维晶界散射和多尺度声子散射等[9,79,80]. 近年来, 一些新的抑制晶格热导率的方法被提出, 包括晶格应力工程、高熵法和类液态声子行为等[80–85]. 其中具有类液态声子行为的超离子(superionic)热电材料, 涉及到复杂晶体结构、离子迁移与结构稳定性、声子非谐以及横向声子模式的消失等问题, 是当下凝聚态物理和能源材料等领域的一个重要前沿研究.在微观晶格结构上, 这类超离子材料是由稳定的刚性亚晶格和可迁移的类液态亚晶格组成(图6(a))[85]. 在此类材料中, 刚性亚晶格可以保证良好的电学性能(电子晶体), 而类液态亚晶格被认为可以有效抑制晶格热导率(声子液体). 2012年, Liu等[23]提出了使用离子类液态行为来实现低晶格热导率的思路. 时至今日, 很多满足“声子液体-电子晶体”概念的超离子热电材料被发现和研究, 包Cu2–δ(S, Se, Te), Ag2(S, Se, Te), (Ag, Cu)CrSe2, Cu5FeS4和硫银锗矿基材料等[85]. 通过优化载流子浓度、控制晶格对称性、细化晶粒尺寸等方法, 这类材料的热电优值可以被提高到1.5左右, 甚至2.0以上, 为热电材料的研究开辟了一个新的领域[84,85].
相比传统热电材料, 超离子热电材料的最大优势是其具有极低的晶格热导率. 如图6(b)所示, 这类材料的晶格热导率一般都小于1 W/(m·K), 甚至可以低到0.1—0.2 W/(m·K), 这比传统热电材料的晶格热导率低1—2个数量级[84,85]. 但是, 有关这类材料中超低晶格热导率的微观物理起源存在很大争议[10,18,19,23,29,52,86–89].
一个流行的观点认为, 类液态亚晶格的振动没有剪切恢复力, 横向声子模式无法维系, 热量的有效传输通道减少, 从而导致材料的晶格热导率很低[80]. Liu等[23,87]发现Cu2Se和Cu8SnSe6超离子材料中的高温等容热容小于杜隆-珀蒂极限, 并利用该现象尝试证明该类材料中存在类液态声子行为(图6(c), (d)). 2018年, Li等[52]利用非弹性中子散射技术, 在CuCrSe2粉末样品中观测到3.2 meV左右的低频声子在超离子相变温度周围逐渐消失的现象, 并将该行为归结为横向声学声子(transverse acoustic phonon, TA)的软化及其向漫散射信号的融入, 从而尝试佐证类液态声子在超低晶格热导率中的重要作用(图6(e)).
尽管如此, 类液态声子模型很快便受到了挑战. 离子的扩散是否影响声子振动模取决于二者之间的时间尺度对比. 如果液体中原子或离子在邻近平衡位置之间的跳跃时间短于晶格振动周期, 那么声子振动模便会被破坏. 相反, 如果原子或离子停留的时间大于振动周期的话, 声子振动与传输不会受到影响[90]. 英国卢瑟福·阿普尔顿实验室的Voneshen等[29]首先发起了挑战, 他们使用QENS技术发现Cu2Se化合物中Cu的扩散跳跃时间尺度比一般TA声子的周期小很多, 只有0.4 meV以下的TA会被影响到. 2019年, Xie等[91]借助扫描投射电子显微镜在实空间中观察到AgCrSe2中的Ag原子在超离子相变温度之上存在固态无序行为, 而非液态行为. 鉴于此, 涌现出很多新的有关该类材料超低晶格热导率的解释, 包括低声子群速度[92]、低声学声子截止频率[18]、光学声子选择性破坏[86]、声子非谐性散射[29]以及晶格无序散射等[91].
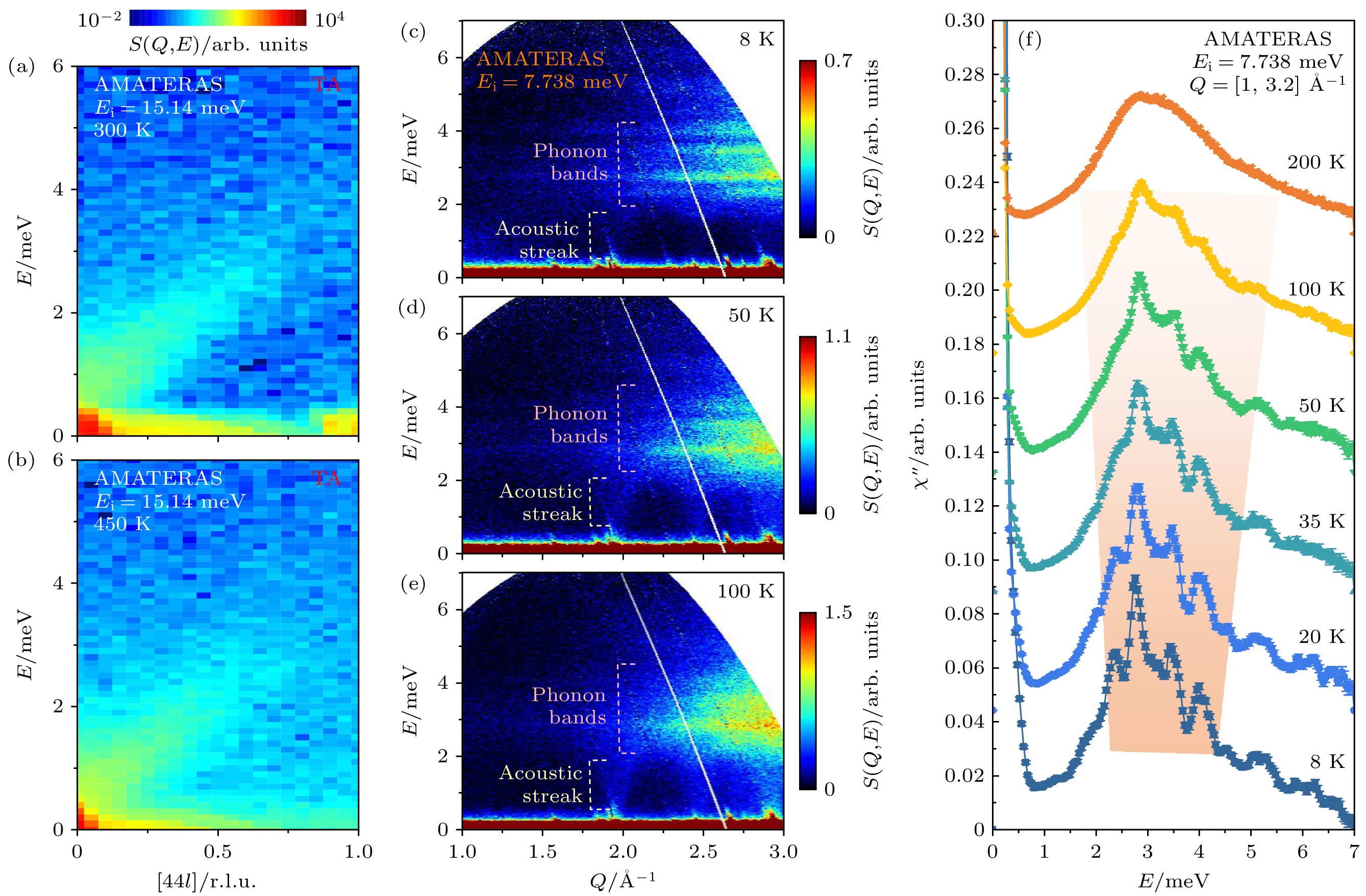
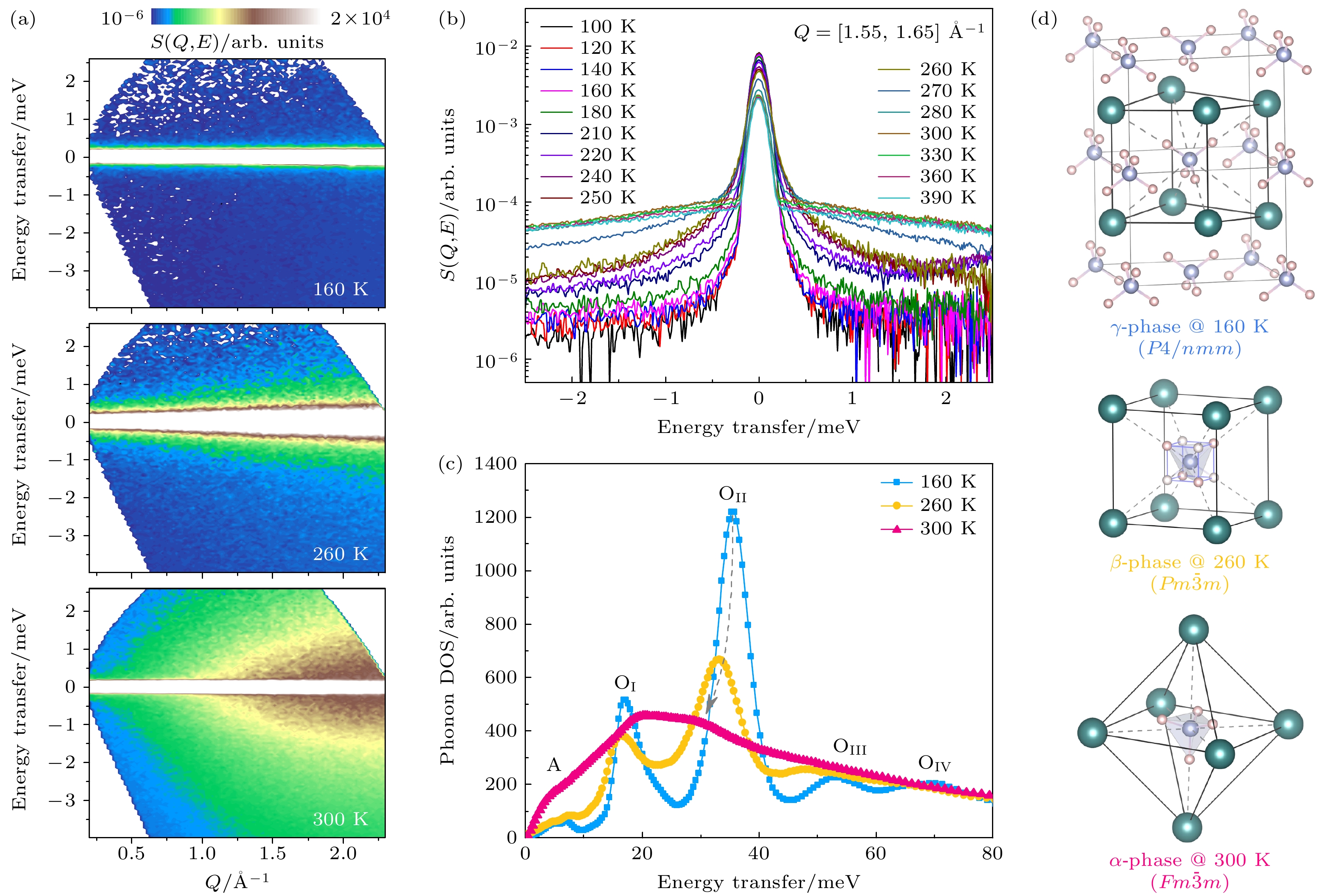
针对类液态声子模型是否是超离子化合物超低晶格热导率的物理起源的争议, 最简单直接的办法便是测量超离子相变前后的TA声子. 为此, Ren等[31]通过单晶样品生长和非弹性中子散射测量追踪了硫银锗矿基Ag8SnSe6样品在(440)布里渊区沿[00l]方向的TA声子的演化情况. 如图7(a), (b)所示, TA声子在300 K和450 K都被很清晰地测量到, 超离子相变并没有有效抑制TA声子振动. 该结果直接从声子谱表征方面否定了离子扩散抑制TA声子热导的类液态声子模型. 为了揭示Ag8SnSe6中超低晶格热导率的主要原因, 我们使用日本J-PARC的冷非弹谱仪AMATERAS (Ei为7.738 meV, ΔE ~ 0.223 meV)测量了Ag8SnSe6粉末样品在低温下的动力学结构因子S(Q, E). 在8 K极低温下, 2—4 meV之间具有很多无色散特增的低频光学声子(图7(c)). 但这些低频声子随温度的升高发生快速的宽化, 表现出极大的声子非谐性行为(图7(d)—(f)). 声子非谐性散射随温度快速增强的行为与Ag8SnSe6样品晶格热导率从20—50 K快速降低的趋势一致[31]. 微观晶格动力学与宏观输运性质高度一致, 这说明该材料中的极浅化学式能面与强声子非谐性是赋予该样品超低晶格热导率的主要物理机制[31,93].
-
在电池器件中, 电解质是一个重要的组成部分, 负责正负电极之间的离子传输, 从而使电池构成闭合的电流回路, 并有助于保持整个电池的电中性, 防止电荷失衡. 传统电池的电解质为液态材料, 存在泄漏、挥发和易燃等安全隐患. 为了克服这些缺点, 近年来固态电池概念被提出[94,95], 其与传统电池的本质区别是将液态电解质更换为固态电解质. 固态电池具有更高的能量密度、更好的安全性、更宽的工作范围、更长的循环寿命等优点, 是离子电池研究的一个重要方向, 而发展具有高离子电导率的固态电解质是核心研究内容之一[37]. 固态电解质的研究面临很多难点, 包括离子输运机理、电化学性质、机械性能等, 其中离子输运机理是最基本的科学问题[36,37,96,97].
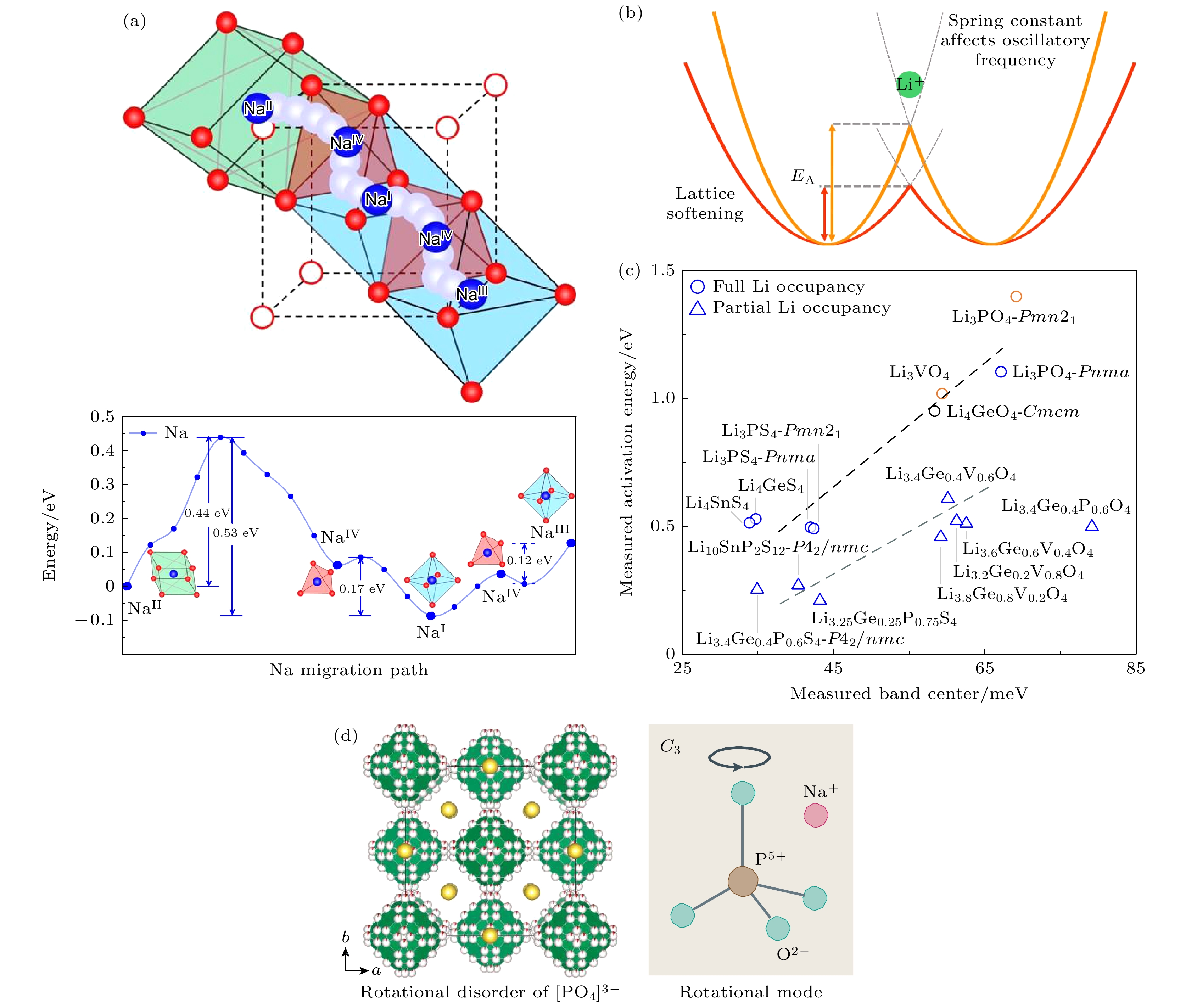
离子扩散通道与扩散势垒是目前理解不同固态电解质之间不同离子电导率的主要出发点, 如图8(a)[4,96,98]. 然而, 更加基础的物理理解需要同时考虑亚晶格之间的相互作用和晶格动力学行为. 2015年, Wang等[99]指出阴离子亚晶格和输运离子的性能密切相关, 且体心立方阴离子框架结构允许锂离子在相邻四面体位点之间直接跳跃, 因此是实现高离子电导率的最理想模型. 2017年, Kraft等[100]通过声速测量研究了Li6PS5X (X = Cl, Br, I)的晶格刚性(lattice stiffness), 发现晶格软化(lattice softening)可以有效降低扩散势垒(图8(b)). 2018年, Muy等[15]通过非弹性中子散射实验进一步发现低频光学声子的能量越低, 离子扩散的激活能也越低(图8(c)). 更有趣的是, 在一些材料中存在阴离子基团旋转带动阳离子扩散的现象, 被称之为“桨轮模型”(paddle-wheel), 如图8(d)所示[101]. 这些前期的研究工作说明晶体结构与晶格动力学表征是研究固态电解质离子输运机理的重要途径[102].
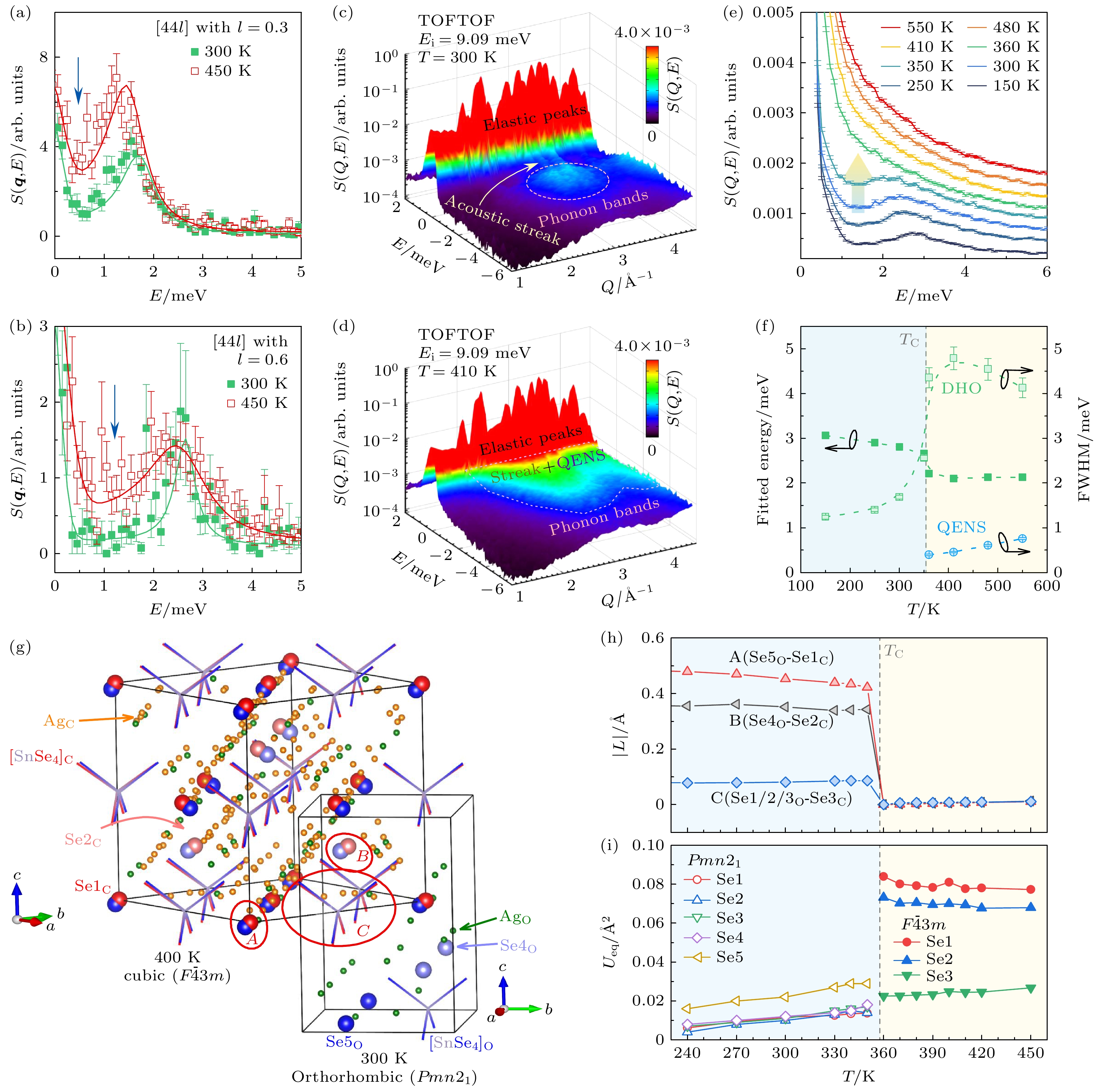
尽管晶格动力学在离子输运过程中的重要作用逐渐得到了重视, 但前期的研究比较宏观, 缺乏对各原子具体作用的理解, 而深入晶胞内部的研究对材料设计将更有帮助. Ren等[31]以Ag8SnSe6作为研究载体, 采用同步辐射XRD、中子衍射、非弹性中子散射INS和准弹性中子散射QENS等技术, 结合分子动力学模拟, 深入分析了硫银锗矿基化合物在超离子相变过程中的晶体结构、晶格动力学和离子扩散动力学的演化细节. 晶格动力学数据显示, 在超离子相变温度之上, 声子存在明显的过阻尼行为(phonon overdamping), 在色散谱上表现为声子峰与零能弹性峰之间的额外散射信号(如图9(a), (b)中箭头所指), 而在多晶数据上表现为~3 meV低频声子带的快速软化与宽化, 且其半高宽比声子中心能量还大(见图9(c)—(f)). 声子的这种过阻尼行为意味着某些晶格振动模不再需要任何能量便可被激活, 正好与代表离子扩散的QENS展宽同时出现, 说明在超离子相变过程中伴随着两个亚晶格之间关联作用的变化, 而这种协同变化可以被机器学习分子动力学模拟复现[31].
为了进一步揭示刚性亚晶格和超离子亚晶格之间关联作用的细节, 我们全面对比了相变前后的晶体结构. 如图9(g), (h)所示, Ag离子在超离子态下的分布变得更广, 同时A和B标记的Se原子发生了很大的位移, 但是由C标记的[SnSe4]四面体则在相变过程中变化不大(A对应低温相的Se5和高温相的Se1, B对应低温相的Se4和高温相的Se2). 该行为预示着A位置与B位置的Se原子在相变过程中扮演着关键作用. 为了验证这个推断, 通过分析同步辐射XRD衍射谱, 在图9(i)中对比了不同位置Se原子的各向同性原子位移参数Ueq在相变过程中的变化. 与图9(g), (h)的期待一样, A位置和B位置的Se原子在相变过程中的Ueq变化最大, 机器学习分子动力学模拟结果与该实验结果一致. 相关结果说明了A位置和B位置的Se原子在亚晶格相互作用中扮演着核心角色, 是该类材料作为固态电解质时调控离子电导率的重要修饰位置, 同时也是其作为热电材料提高器件化学稳定性的重要参考因素.
-
制冷在日常生活、工业生产过程中被广泛使用, 占全社会总能耗的25%以上[103]. 目前, 广泛应用的制冷设备主要基于气体压缩制冷技术, 其能效较低且会产生温室气体和臭氧破坏等环境问题[104,105]. 基于固态相变的热效应, 包括磁卡、电卡、弹卡和压卡效应等, 被认为是一类可以提高能效并降低环境影响的新型制冷技术[106–113]. 这些热卡效应具有共同的物理基础, 即相变过程中的总焓变或总熵变, 包括晶格熵和磁熵等. 因此, 在热卡材料的机理研究方面, 晶体结构与晶格动力学的表征是一条重要的途径[16,42,114,115].
压卡材料的研究是一个典型的例子. 压卡效应是通过压力来驱动相变并完成热能存储与释放的物理现象. 优秀的压卡材料需要尽可能大的相变熵、小的滞后损耗以及小的驱动压力. 在大相变熵的追求方面, 塑晶材料是一类优秀的候选材料[116–120]. 塑晶材料是一种由弱的长程作用力组合在一起的分子晶体, 兼具长程有序和短程无序的特征[16,101,121]. 与超离子材料中离子无序分布类型的平移对称性破缺不同, 塑晶材料中的短程无序为旋转对称性破缺, 即构成塑晶态料的分子基元的质心为长程有序, 但空间几何取向为无序. 分子的这种空间取向无序在相变过程中可以产生很大的构型熵, 是压卡制冷的理想载体.
研究塑晶态相变与压卡效应的常规方法有差示扫描量热法、XRD、原位拉曼等[119,122,123], 但中子散射技术能够提供更加全面的信息[42,120]. Li等[42]在一系列塑晶材料中发现了比传统材料高一个数量级的巨压卡效应, 并使用中子散射技术研究了新戊二醇(neopentylglycol, NPG)塑晶化合物的晶格动力学行为. 通过声子峰随温度的宽化揭示出该材料具有很大的晶格非谐性, 且这种晶格非谐性可赋予该类很大的可压缩性(compressibility). QENS数据和EISF的分析指出在塑晶态下NPG分子作为整体表现出各向同性的取向旋转, 为该材料提供极大的构型熵. 同时, 该研究工作利用原位加压QENS实验观测到了外加压力对分子取向旋转的抑制作用.
除了大的相变熵, 尽可能小的相变驱动压力也是压卡制冷的一个重要指标. Ren等[68]借助非弹性与准弹性中子散射技术系统研究了NH4I巨压卡化合物的相变与晶格动力学行为. 如图10(a), (b)所示, 该化合物的动态结构因子S(Q, E)随着温度的升高产生了明显的准弹性展宽, 说明[NH4]+四面体在中温相和高温相中存在转动行为, 但展宽程度的不同预示着两个相中的转动行为并不相同. 与此同时, 光学声子也发生了明显的非谐性软化与宽化, 特别是在中-高温相变附近声子峰宽化到无法再辨识(图10(c)). 晶格振动与分子取向旋转之间的这种协同变化说明分子与晶格骨架之间存在明显的耦合. ESIF和对称性分析进一步指出, [NH4]+四面体在中温相中具有二重空间取向自由度, 而在高温相具有六重自由度, 相关的晶体结构由图10(d)给出. 这里[NH4]+四面体分子空间取向自由度是指(相对)低对称的[NH4]+四面体在(相对)高对称的I–骨架亚晶格中由N—H···I氢键的成键情况和相对对称性决定的[NH4]+四面体的可以放置的、且能量简并的空间方位取向的数目. 在这里, 旋转几何的改变同时引起了[NH4]+和I–之间氢键数目的改变(1↔4), 而氢键数目的改变又进一步强化了晶格振动-分子取向旋转之间的耦合. 亚晶格之间的这种极强耦合使得NH4I中的塑晶态相变具有非常强的压力敏感性, 相变温度的压力依赖系数高达
$ \left|{\mathrm{d}}{T}_{{\mathrm{t}}}/{\mathrm{d}}P\right| $ ~0.79 K·MPa–1, 同时也赋予NH4I非常小的饱和可逆驱动压力(~40 MPa). -
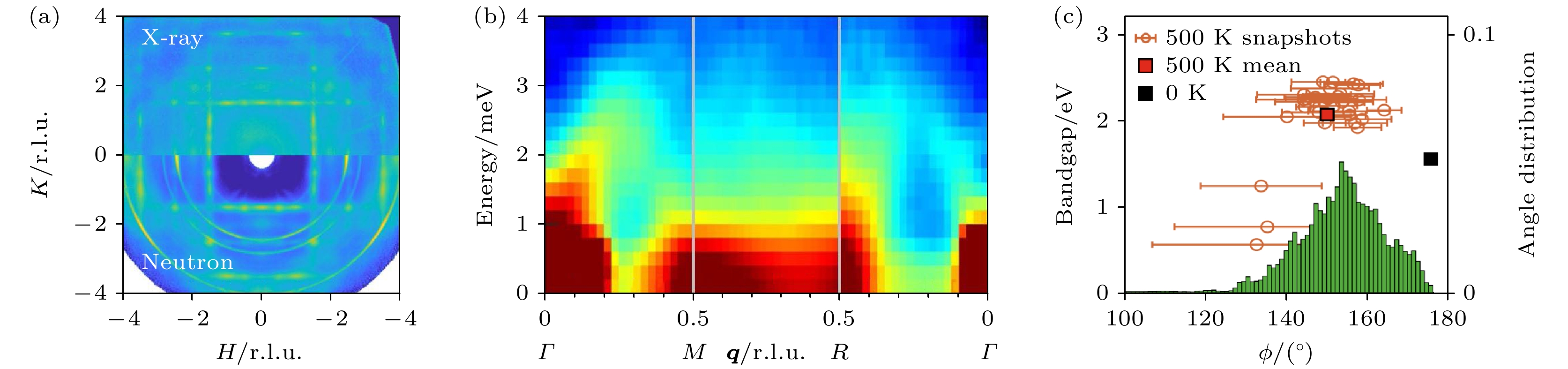
以上对超离子热电材料、固态电解质以及塑晶态压卡材料的晶格动力学研究都聚焦于亚晶格之间的相互作用, 但能源材料中的耦合效应远不止于此. 在卤素钙钛矿光电材料中, 晶格一般都有非常大的非谐性, 表现为低的热导率、大的热膨胀系数和大的原子位移参数等[124–126]. Lanigan-Atkins等[40]利用非弹性中子散射观测到CsPbBr3单晶在三维倒易空间中形成连续的网络状漫散射棒状带(图11(a)), 这些漫散信号是由[PbBr6]亚晶格主导的低能声子的阻尼行为引起的(图11(b)). 进一步研究发现晶格的这种巨非谐性振动会改变电子-声子耦合作用, 从而直接影响能隙的带边电子态并使该类材料中的热载流子有更长的寿命(图11(c))[40,127]. 电子-声子相互作用在热电材料中也扮演着重要的角色. Ren等[128]在ZrNiSn基半哈斯勒合金中发现, 载流子浓度的升高可以有效屏蔽极化光学声子振动造成的极化电场, 该极化电场可以提高纵波光学声子频率引起纵-横光学声子劈裂现象, 并会散射载流子并引起迁移率的降低. 载流子对极化光学声子的这种屏蔽作用甚至可以在NbFeSb基合金中造成光学声子的明显软化, 从而引起晶格热导率的大幅降低[34].
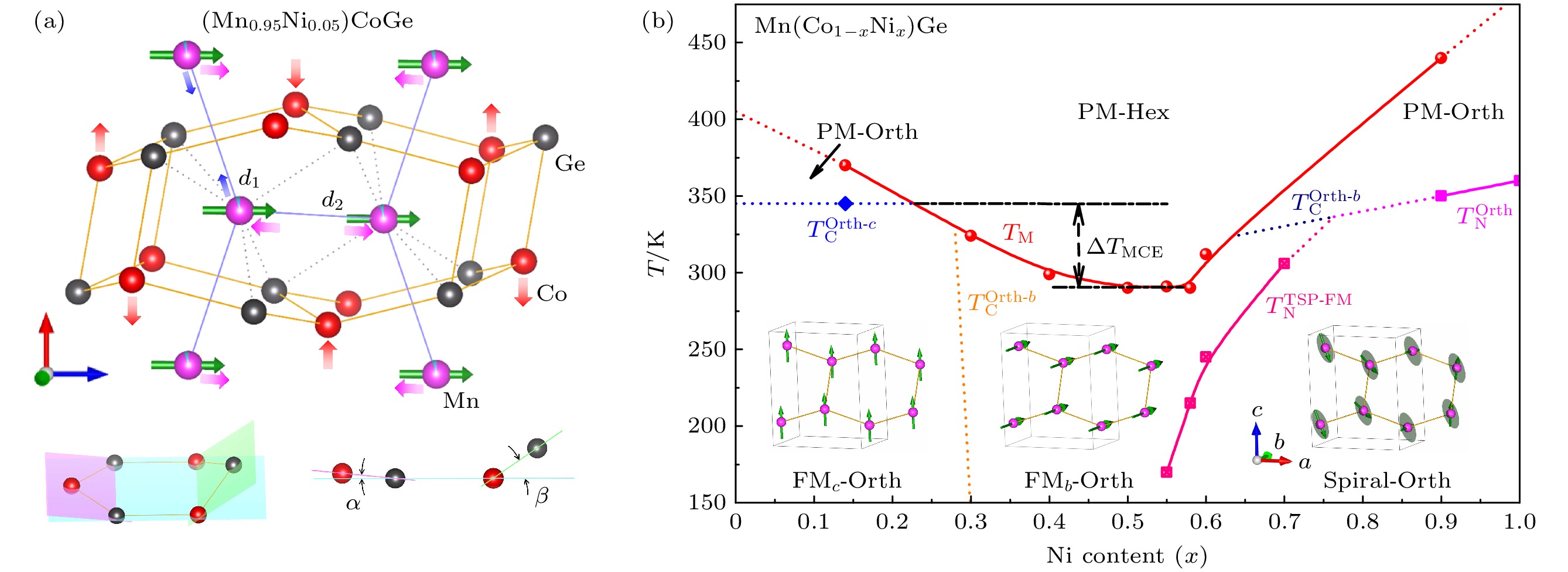
在磁卡制冷材料中, 一级磁-结构相变材料由于可以通过磁场同时诱发磁熵变和晶格熵变而备受关注[129–132]. MnCoGe基合金化合物具有相对稳定的磁相变温度和易调控的马氏体相变温度, 当磁相变与结构相变重合时会形成自旋-晶格耦合, 从而实现外场可驱动的磁-结构一级相变[133–137]. 理解并调控材料的一级磁-结构相变是MnCoGe基磁卡材料研究的重点. Ren等[138]借助原位变温和原位磁场中子衍射技术揭示出MnCoGe化合物的晶格对磁场的响应是通过Mn磁性亚晶格沿c轴方向的拉长(d1)和沿a轴方向的缩短(d2)而引起Co-Ge亚晶格骨架乃至整个晶体结构的改变(图12(a)). 在Co位置通过Ni掺杂引入额外的价电子, 可以明显改变MnCoGe合金化合物的马氏体相变温度TM, 从x = 0.18的~370 K逐渐减小到~290 K, 然后在x = 0.55处开始升高. Ni的掺入同时影响着低温正交相的磁结构, 低掺杂区的c轴铁磁结构首先发生自旋重取向转变为b轴方向的铁磁结构, 然后在x = 0.55处转变为非公度螺旋反铁磁结构(图12(b)). x = 0.55处的晶体结构和磁结构的协同变化可以通过价电子在Mn和Co-Ge亚晶格之间的转移与再分布得到很好的解释, 为调控此类合金化合物的自旋-晶格耦合和磁-结构相变提供新的思路[139,140].
-
通过前面5个经典案例不难发现, 微观晶体结构与晶格动力学是理解能源材料复杂物理机制的基础, 而中子散射技术因其较高的动量与能量分辨率是表征这些信息的重要谱学手段. 在超离子热电材料中, 相较于超离子相变与类液态声子模型, 巨声子非谐性散射对晶格热导率的抑制作用更为重要. 在硫银锗矿基固态电解质的离子输运过程中, 阳离子与刚性骨架亚晶格之间耦合作用的减弱以及随之而来的阳离子亚晶格的过阻尼振动构成离子扩散的重要动力学行为. 在塑晶态压卡材料中, 晶格非谐性随温度的加强可以解耦铵基分子和晶格骨架之间的氢键, 从而完成塑晶相变并带来大的构型熵变. 另一方面, 晶格与电荷之间的相互作用为提升光伏、热电材料的性能提供了可能, 而晶格与自旋之间的耦合则是设计磁卡制冷材料的重要思路. 可以看出, 晶格动力学在这些能源转换与存储材料中并不是独立存在的, 其在宏观物理性质中的复杂作用总是基于其特有的亚晶格嵌套结构, 结合与其他亚晶格、电荷、自旋等自由度之间的关联, 通过声子的非谐性演化来实现的.
尽管在能源材料复杂晶格动力学的中子散射研究方面已经取得了丰富的成果, 但仍有很多科学问题需要进一步深入认识. 如在超离子热电材料中, 非谐性声子散射是超低晶格热导率的主要物理起源已经逐渐成为共识[29,31,86], 但非谐性散射是如何具体影响这类材料中的声子输运目前还未得到充分研究. 另外, 超低晶格热导率材料通常还表现出非常规的温度依赖性[141–143]. 目前, 一种流行的解释是此类材料中的晶格热输运有两种通道, 一是常规声子波包的传输(propagons), 二是不同声子支之间的随机扩散(diffusons)[144–147]. 理论上该双通道模型分别对应声子的对角矩阵元和非对角矩阵元[146], 但是如何利用谱学技术从原子级动力学表征角度验证此模型, 目前尚无明确的方案. 在固态电解质离子扩散机制方面, 有理论分析指出多离子协同扩散模型中的扩散势垒比单离子扩散模型的要小[96], 但目前多粒子协同扩散的实验研究还很少. 在塑晶态压卡材料研究中, 声子非谐性在促进塑晶态相变的同时也会降低热输运, 阻碍材料在实际器件中的应用. 是否有可能将塑晶态相变与热输运进行解耦是一个重要的科学议题. 在磁卡制冷材料方面, 一级磁-结构相变对相变熵的正向作用是基于相变过程中晶格熵变与磁熵变是同方向吸热或放热的, 但两种熵变在不同的材料中是否都有同方向的贡献、各自贡献的比例是多少等, 都是材料设计过程中需要考虑的问题[115].
以上列举的能源材料物理机制研究中的一些新的科学问题, 对中子散射谱学技术与实验细节提出了新的挑战. 很多材料在结构上变得异常复杂, 存在超大晶胞、多重掺杂、高熵结构、有机-无机杂化、部分有序-部分无序、晶粒纳米化、微纳器件界面等情况. 这些材料体系往往难以获得大块单晶样品, 而在一些极端情况下即使能获得大块单晶也需要进行微区表征(如晶粒纳米化和微纳化器件应用等), 但是在当下有限的中子通量情况下开展微小样品测量甚至微纳器件测量变得异常困难. 尽管IXS和4D-EELS可以对毫米量级甚至更小的单晶样品进行晶格动力学表征, 但是这些技术的能量分辨率在大部分情况下满足不了复杂晶格动力学的表征需求. 因此, 声子态密度的中子散射表征变成了为数不多的可选项, 但色散谱中的很多有效信息都在“粉末平均”中被丢失. 在固态电解质的离子扩散机制研究方面, 如何区分相干与非相干散射截面、不同运动行为之间的准弹性信号(如离子扩散与聚阴离子旋转)等, 不仅急需发展极化非弹性中子散射技术(极化中子技术可以区分相干与非相干散射截面以及原子核与自旋磁矩散射), 同时对数据处理方法和物理模型分析提出了很高的挑战. 人工智能与机器学习可以自动发现隐藏在数据背后的规律, 据了解其在辅助电镜数据的处理与分析方面已经取得了明显的成功, 在复杂晶格动力学的中子散射数据分析方面引入人工智能与机器学习技术, 或许也可以为上述的测量与表征困难提供一些有效的解决路径.
如上所述, 中子散射技术特别是非弹性中子散射技术在功能材料的物理机理研究中具有重要的作用. 目前, 国内两个反应堆中子源(CARR和CMRR)以建成多台三轴谱仪, 散裂中子源(CSNS)建设有一台高能直接几乎非弹性中子散射飞行时间谱仪, 可以满足诸多科学研究需求. 尽管如此, 与国外中子源相比, 目前的谱仪布局还不够, 特别是在冷中子飞行时间谱仪方面目前尚属空白, 而该类谱仪因具有更高的能量分辨率, 在复杂晶格动力学谱学研究中被广泛使用. CSNS计划在“十四五”二期项目中建设两台新的处于冷能量波段的飞行时间谱仪, 预计2029年左右建成, 届时可以弥补与国外中子源的差异. 在中子通量方面, 散裂源二期项目会将功率从目前的~160 kW升级到~500 kW, 虽然还达不到J-PARC和SNS的功率水平, 但可以大幅提高实验效率. 在非弹性中子散射用户群方面, 目前国内在超导、量子磁性等领域已有多个非常专业的研究组, 但在能源材料与声子研究领域还很少. 借鉴国外经验, 定期举办非弹性中子散射技术与科学应用培训课程, 是快速扩大用户群体、提高用户专业水平、增加非弹性中子散射谱仪科研成果产出的重要途径. 期待经过10—20年的发展, 国内非弹性中子散射技术、用户群体和科研产出能够实现从“跟跑”欧美日到“并跑”的提升.
复杂晶格动力学与能源材料的中子散射研究
Neutron scattering studies of complex lattice dynamics in energy materials
-
摘要: 晶格动力学是众多前沿能源材料的重要物理基础. 许多优秀的能源材料具有亚晶格嵌套结构, 其晶格动力学非常复杂, 这给理解材料的物理机制带来了巨大挑战. 中子散射技术兼具高的能量和动量分辨率, 可以同时表征物质结构和复杂晶格动力学, 近年来在研究能源材料物理机制方面发挥了重要作用. 本文首先详细介绍了能源材料研究中常用的几种中子散射技术, 包括中子衍射、中子全散射、准弹性中子散射以及非弹性中子散射等. 然后, 综述了近年来以中子散射为主要表征方法在能源材料领域所取得的一些重要研究进展, 包括超离子热电材料中的超低晶格热导率、固态电解质中的离子扩散机制、压卡材料中的塑晶态相变与构型熵、光伏材料中的晶格非谐性与载流子输运以及磁卡制冷材料中的一级磁-结构相变等. 在这些能源转换与存储材料中, 晶格动力学并不是独立起作用的, 它们在宏观物理性质中的作用总是通过不同自由度如亚晶格、电荷、自旋等的复杂关联作用或相互耦合来实现的. 通过这些典型实例, 希望为能源材料与晶格动力学的进一步深入研究提供参考.Abstract:
Lattice dynamics play a crucial role in understanding the physical mechanisms of cutting-edge energy materials. Many excellent energy materials have complex multiple-sublattice structures, with intricate lattice dynamics, and the underlying mechanisms are difficult to understand. Neutron scattering technologies, which are known for their high energy and momentum resolution, are powerful tools for simultaneously characterizing material structure and complex lattice dynamics. In recent years, neutron scattering techniques have made significant contributions to the study of energy materials, shedding light on their physical mechanisms. Starting from the basic properties of neutrons and double differential scattering cross sections, this review paper provides a detailed introduction to the working principles, spectrometer structures, and functions of several neutron scattering techniques commonly used in energy materials research, including neutron diffraction and neutron total scattering, which characterize material structures, and quasi-elastic neutron scattering and inelastic neutron scattering, which characterize lattice dynamics. Then, this review paper presents significant research progress in the field of energy materials utilizing neutron scattering as a primary characterization method. 1) In the case of Ag8SnSe6 superionic thermoelectric materials, single crystal inelastic neutron scattering experiments have revealed that the “liquid-like phonon model” is not the primary contributor to ultra-low lattice thermal conductivity. Instead, extreme phonon anharmonic scattering is identified as a key factor based on the special temperature dependence of phonon linewidth. 2) Analysis of quasi-elastic and inelastic neutron scattering spectra reveals the changes in the correlation between framework and Ag+ sublattices during the superionic phase transition of Ag8SnSe6 compounds. Further investigations using neutron diffraction and molecular dynamics simulations reveal a new mechanism of superionic phase transition and ion diffusion, primarily governed by weakly bonded Se atoms. 3) Research on NH4I compounds demonstrates a strong coupling between molecular orientation rotation and lattice vibration, and the strengthening of phonon anharmonicity with temperature rising can decouple this interaction and induce plastic phase transition. This phenomenon results in a significant configuration entropy change, showing its potential applications in barocaloric refrigeration. 4) In the CsPbBr3 perovskite photovoltaic materials, inelastic neutron scattering uncovers low-energy phonon damping of the [PbBr6] sublattice, influencing electron-phonon coupling and the band edge electronic state. This special anharmonic vibration of the [PbBr6] sublattice prolongs the lifetime of hot carriers, affecting the material's electronic properties. 5) In MnCoGe magnetic refrigeration materials, in-situ neutron diffraction experiments highlight the role of valence electron transfer between sublattices in changing crystal structural stability and magnetic interactions. This process triggers a transformation from a ferromagnetic to an incommensurate spiral antiferromagnetic structure, expanding our understanding of magnetic phase transition regulation. These examples underscore the interdependence between lattice dynamics and other degrees of freedom in energy conversion and storage materials, such as sublattices, charge, and spin. Through these typical examples, this review paper can provide a reference for further exploring and understanding the energy materials and lattice dynamics. -
Key words:
- neutron scattering /
- thermoelectric materials /
- solid-state electrolytes /
- Caloric effects .
-

-
图 1 晶格动力学与能源材料 (a) 声学声子振动、光学声子振动及声子色散谱; (b) 热电转换材料与输运性质[5]; (c) 压卡相变制冷与相变熵[6]; (d) 固态电池之固态电解质与离子扩散动力学[4]; (e) 光伏电池与晶格振动[3]
Figure 1. Lattice dynamics and energy materials: (a) Lattice vibrations and phonon dispersion; (b) thermoelectric materials and transport properties[5]; (c) barocaloric effect and phase transition entropy change[6]; (d) solid-state electrolyte and ionic diffusion[4]; (e) solar cell and lattice vibrations in perovskites[3]
图 2 中子散射技术概述 (a) 由一个上夸克和两个下夸克组成的中子为电中性粒子, 并带一个磁矩; (b) 中子、电子和X射线与物质的作用方式; (c) 中子散射截面与X射线散射截面对比[47,48]; (d) 弹性、准弹性和非弹性中子散射技术覆盖的能量范围以及可测量的物理内容[49]
Figure 2. Overview of neutron scattering technology: (a) Neutron is a neutral particle with a magnetic moment; (b) the interactions of neutrons, electrons and X-rays with matter; (c) neutron and X-ray cross sections for some typical elements[47,48]; (d) the energy range spanned by the elastic, quasi-elastic and inelastic neutron scattering technologies and the typical physical contents in the energy range[49].
图 3 弹性中子散射谱仪 (a), (b) 基于连续式中子源的中子衍射谱仪结构及其测量原理. (c), (d) 基于脉冲式中子源的中子衍射谱仪结构及其“时间-距离飞行图”与测量原理. 两种不同类型衍射谱仪的布拉格公式中的变量不同, 由紫色字体给出, 图中蓝色线代表宽波段中子的飞行路线, 其他颜色代表单色中子飞行路线. (e) 中子全散射与对分布函数原理, 通过对结构因子S(Q)进行傅里叶变换, 可以测量实空间的分布函数G(r). (f) 原子散射因子f(Q)的对比, X射线的f(Q)随动量转移Q的增大迅速衰减, 而中子的几乎不变, 因此中子衍射更容易获得大Q处的布拉格衍射峰, 动量转移Q = ki-kf, ki表示入射中子波矢, kf表示散射中子波矢
Figure 3. Neutron diffraction spectrometers: (a), (b) Structure and measurement principle of a neutron diffraction spectrometer based on a continuous neutron source. (c), (d) Structure of a neutron diffraction spectrometer based on a pulsed neutron source and its time-distance diagram or measurement principle, the formats of the Bragg function for these two kinds of diffractometers are different and their variables are marked with purple color. The blue line in the figure represents the flight path of broadband neutrons, and other colors represent the flight paths of monochromatic neutrons. (e) The neutron total scattering and pair distribution function principle, through the Fourier transform of the structure factor S(Q), the real space distribution, G(r), could be measured. (f) Comparison of atomic scattering factor, f(Q), f(Q) for X-ray decays rapidly with momentum transfer Q, while f(Q) for neutron remains almost unchanged, so neutron diffraction is more easily to obtain Bragg diffraction peaks at large Q, the momentum transfer Q can be obtained by subtract scattered neutron wavevector kf from the incident neutron wavevector ki, Q = ki-kf.
图 4 非弹性中子散射谱仪 (a) 基于连续式中子源的三轴谱仪示意图, 具有3个可以独立转角的运动机构, 分别是单色器、样品台和分析器; (b) 三轴谱仪测量色散谱的两种方式, 恒定能量扫动量和恒定动量扫能量; (c) 基于脉冲式中子源的直接几何非弹性中子散射飞行时间谱仪(简称直接几何)示意图; (d) 直接几何非弹谱仪的“时间-距离飞行图”与工作原理, 脉冲式白光中子通过单色斩波器选出单一能量中子, 该单色中子与样品发生非弹性散射后, 能量和速度发生增减, 通过中子通过样品和探测器之间固定距离的飞行时间可以确定散射后的中子能量, 结合散射中子的角度和散射前的中子能量, 便可确定非弹性散射过程中的能量转移和动量转移; (e) 基于脉冲式中子源的间接几何非弹性中子散射飞行时间谱仪(简称间接几何或逆几何)示意图; (f) 间接几何非弹谱仪的“时间-距离飞行图”与工作原理, 该类型谱仪在样品前没有单色斩波器, 但在样品后放置单色分析器. 图中蓝色线代表宽波段中子的飞行路线, 其他颜色代表单色中子飞行路线
Figure 4. Inelastic neutron scattering spectrometer: (a) Schematic diagram of a triple-axis spectrometer based on a continuous neutron source, which has three independently rotating axis, corresponding to the monochromator, the sample stage, and the analyzer. (b) Two methods for a three-axis spectrometer to scan a dispersion, constant-energy scan and constant-momentum scan. (c) Schematic diagram of a direct-geometry inelastic neutron scattering time-of-flight spectrometer based on a pulsed neutron source. (d) The time-distance diagram or measurement principle of a direct geometry inelastic spectrometer, a bunch of single-energy neutrons are selected by a monochromatic chopper from the pulsed white beam. Then the single-energy neutrons will be inelastically scattered by the sample and their energy and speed will become larger or smaller; the neutron energy after scattering can be determined by the neutron flight time through a fixed distance between the sample and the detector; combined with the angle of the scattered neutron and the neutron energy before scattering, the energy transfer and momentum transfer during the inelastic scattering process can be determined. (e) Schematic diagram of an indirect geometry inelastic neutron scattering time-of-flight spectrometer based on a pulsed neutron source. (f) The “time-distance flight diagram” and working principle of the indirect geometry inelastic spectrometer, this type of spectrometer does not have a monochromator before the sample, but a monochromator analyzer is placed after the sample; the blue line in the figure represents the flight path of broadband neutrons, and other colors represent the flight paths of monochromatic neutrons.
图 5 准弹性中子散射数据分析方法 (a) 准弹性中子散射谱的拟合, 一般包括由δ函数卷积谱仪分辨率来描述的弹性散射部分和由洛伦兹峰描述的准弹性散射部分, 弹性峰面积AE与总面积AE+AQ之间的比例构成弹性非相干结构因子EISF[66]; (b) 准弹性散射的半高宽的动量依赖曲线可以用于研究不同的离子扩散模型[69]; (c) EISF与不同几何限域下的分子旋转模型[70]
Figure 5. Data analysis methods for QENS data: (a) A general discomposing of a QENS spectrum, comprising an elastic part described by a δ-function convoluted with instrumental resolution and a quasielastic part described with a Lorentzian profile, the ratio of the elastic area, AE, to the total area, AE+AQ, defines the elastic incoherent structure factor (EISF)[66]; (b) the Q-dependent width of QENS signal can be used to study different ionic diffusion models[69]; (c) molecular rotation models under different geometric confinements and corresponding EISF profiles[70] .
图 6 超离子热电材料与超低晶格热导率 (a) 超离子热电材料的晶体结构示意图, 包括刚性亚晶格和类液态亚晶格[85]; (b) 几种主要的超离子热电材料的晶格热导率及其与其他传统热电材料的对比[85]; (c)—(e) 通过比热测量和粉末样品非弹性中子散射实验尝试说明类液态声子的有效性[23,24,52]
Figure 6. Superionic thermoelectric materials and ultra-low lattice thermal conductivity: (a) Schematic diagram of the crystal structure of superionic thermoelectric materials, comprising a rigid sublattice and a liquid-like sublattice[85]; (b) lattice thermal conductivity of several main superionic thermoelectric materials and a comparison with that for other typical thermoelectric materials[85]; (c)–(e) the attempts to demonstrate the validity of the liquid-phonon models for the ultralow lattice thermal conductivity through specific heat measurements and inelastic neutron scattering measurements on powder samples[23,24,52] .
图 7 Ag8SnSe6硫银锗矿化合物的晶格动力学与超低晶格热导率[31] (a), (b) 300 K和450 K温度下, 在日本J-PARC的冷非弹谱仪AMATERAS上测得的Ag8SnSe6单晶样品在(440)布里渊区沿
$[00l] $ 方向的TA声子; (c)—(e) Ag8SnSe6粉末样品在8 K, 50 K和100 K温度下的动力学结构因子S(Q, E); (f) 声子态密度峰形随温度升高而快速宽化Figure 7. Lattice dynamics and ultra-low lattice thermal conductivity of Ag8SnSe6 argyrodite compounds[31]: (a), (b) TA phonons along the
$[00l]$ direction in the (440) Brillouin zone of the Ag8SnSe6 single crystal samples measured on the cold neutron spectrometer AMATERAS at J-PARC at 300 K and 450 K, respectively; (c)–(e) Dynamic structure factors S(Q, E) of the Ag8SnSe6 powder samples at 8 K, 50 K and 100 K; (f) the peaks in the phonon density of states become broad quickly with increasing temperature.图 8 固态电解质的离子扩散与晶格振动 (a) 离子扩散通道与扩散势垒示意图[98]; (b) 晶格软化对离子跳跃的影响示意图[100]; (c) 通过INS测得的LISICON和橄榄石型固态电解质中低频声子中心能量与离子扩散激活能之间的关系[15]; (d) γ-Na3PO4化合物中Na+离子输运的桨轮模型, 即[PO4]3–聚阴离子四面体旋转带动Na+离子的迁移[101]
Figure 8. Ion diffusion and lattice dynamics of solid-state electrolytes: (a) Schematic diagram of ion diffusion channels and diffusion barriers in Na3Zr2Si2PO12[98]; (b) schematic diagram of the effect of lattice softening on hopping of ions[100]; (c) relationship between low-frequency phonon center energies measured by INS and ion diffusion activation energies in LISICON and olivine-type solid-state electrolytes[15]; (d) paddle wheel model of Na+ ion transport in γ-Na3PO4 compounds, i.e., the rotation of [PO4]3– polyanion tetrahedron drives the migration of Na+ ions[101].
图 9 Ag8SnSe6超离子相变过程中的晶格动力学与亚晶格耦合行为[31] (a), (b) 在日本J-PARC中子源的AMATERAS谱仪测得的300 K和450 K温度下, [4 4 0.3]和[4 4 0.6] TA声子模的实验数据; (c), (d) 在德国FRM II中子源的TOFTOF直接几何谱仪测得的Ag8SnSe6多晶样品在300 K和410 K的动力学结构因子S(Q, E); (e) 在[2.0, 2.4] Å–1的动量Q范围内对S(Q, E)进行积分获得的动力学结构因子曲线; (f) 通过对图(e)中的曲线进行阻尼谐振子模型和洛伦兹模型拟合获得的声子能量、半高宽和QENS信号展宽; (g) 法国ILL中子源D9单晶中子衍射谱仪上获得的300 K和400 K下的正交结构(O)和立方结构(C)的对比; (h), (i) 通过精修原位XRD衍射谱获得的A, B, C位置的Se原子在超离子相变过程中的原子坐标位移|L|和各向同性原子位移参数Ueq的变化, A对应低温相的Se5和高温相的Se1, B对应低温相的Se4和高温相的Se2
Figure 9. Lattice dynamics and coupling of sublattices during the superionic phase transition of Ag8SnSe6[31]: (a), (b) Experimental data of [4 4 0.3] and [4 4 0.6] TA phonon modes at 300 K and 450 K measured on the AMATERAS spectrometer at the J-PARC spallation neutron source in Japan, respectively; (c), (d) dynamical structure factors, S(Q, E), of Ag8SnSe6 polycrystalline samples at 300 K and 410 K, respectively, measured on the TOFTOF direct-geometry spectrometer at the FRM II neutron source in Germany; (e) dynamical structure factor curves obtained by integrating S(Q, E) over the momentum Q range of [2.0, 2.4] Å–1; (f) phonon energy, phonon width and QENS broadening obtained by fitting the curve in panel (e) with the damped harmonic oscillator (DHO) and Lorentz profiles; (g) comparison of the orthorhombic structure (O) and cubic structure (C) at 300 K and 400 K obtained on the D9 single-crystal neutron diffractometer at the ILL neutron source in France; (h), (i) the changes in the atomic displacement |L| and isotropic atomic displacement parameters, Ueq, of Se atoms at positions A, B, and C during the superionic phase transition obtained by analyzing in situ XRD patterns, A corresponds to Se5 in the low-T phase and Se1 in the high-T phase, and B corresponds to Se4 in the low-T phase and Se2 in the high-T phase, respectively.
图 10 NH4I压卡材料中的塑晶态相变与晶格动力学行为[68] (a) 有非弹性中子散射测量获得的三个不同相变区间的动力学结构因子S(Q, E); (b) 通过在一定Q范围内对图(a)中的 S(Q, E)进行积分, 可获得不同相变区间的准弹性展宽信息; (c) 声子态密度随温度的软化与宽化行为; (d) 不同相变区间对应的晶体结构和铵基[NH4]–四面体的可能空间取向
Figure 10. Plastic-crystal phase transition and lattice dynamics in NH4I barocaloric material[68]: (a) Dynamic structure factors, S(Q, E), in three different phases measured by INS; (b) quasielastic broadening in different phases obtained by integrating S(Q, E) in (a) over a certain Q range; (c) softening and broadening processes of the phonon DOSs with temperature; (d) crystal structures in the three different phases and possible orientations of the [NH4]– tetrahedron.
图 11 CsPbBr3中晶格振动与能带之间的关系[40] (a) 433 K高温立方相中(H, K, L = 0.5)平面内的漫散射信号, 上半部分数据由XRD获得, 下半部分来自中子数据; (b) 419 K高温相中Γ-M-R-Γ方向的S(Q, E), 其中声子在布里渊区边界沿着M-R方向上有过阻尼行为; (c) 由分子动力学模拟获得的Pb-Br-Pb夹角分布及其与能带带隙之间的关系
Figure 11. Relationship between lattice vibration and energy band in CsPbBr3[40]: (a) Diffuse scattering signal in the (H, K, L = 0.5) plane in the high-temperature cubic phase at 433 K, the upper half of the data is obtained from XRD, and the lower half is from neutron data; (b) S(Q, E) along the Γ-M-R-Γ direction in the high-temperature phase at 419 K, where the phonons have overdamping behavior along the M-R direction at the Brillouin zone boundary; (c) Pb-Br-Pb angle distribution obtained by molecular dynamics simulation and its relationship with the energy band gap.
图 12 MnCoGe基磁卡材料中的磁-结构相变 (a) 通过原位中子衍射实验分析得到的Mn0.95Ni0.05CoGe化合物中Mn磁性亚晶格和Co-Ge骨架亚晶格对外加磁场的响应[138]; (b) 以Ni含量或价电子数目(Co: 3d74s2, Ni: 3d84s2)和温度为参数的Mn(Co1–xNix)Ge化合物磁-结构相图[139]
Figure 12. Magneto-structural transitions in MnCoGe-based magnetocaloric materials: (a) Response of the Mn magnetic sublattice and Co-Ge skeleton sublattice in the Mn0.95Ni0.05CoGe compound to an applied magnetic field obtained by in situ neutron diffraction experiments[138]; (b) magnetic structural phase diagram of the Mn(Co1–xNix)Ge compound with Ni content or valence electron number (Co: 3d74s2, Ni: 3d84s2) and temperature[139].
-
[1] 黄昆, 韩汝琦 1988 固体物理学 (北京: 高等教育出版社) Huang K, Han R Q 1988 Solid State Physics (Beijing: Higher Education Press [2] Ashcroft N W, Mermin N D 1976 Solid State Physics (Holt, Rinehart and Winston [3] Leguy A M, Frost J M, McMahon A P, Sakai V G, Kochelmann W, Law C, Li X, Foglia F, Walsh A, O'Regan B C, Nelson J, Cabral J T, Barnes P R 2015 Nat. Commun. 6 7124 doi: 10.1038/ncomms8124 [4] Wang K, Ren Q Y, Gu Z Q, Duan C M, Wang J Z, Zhu F, Fu Y Y, Hao J P, Zhu J F, He L H, Wang C W, Lu Y Y, Ma J, Ma C 2021 Nat. Commun. 12 4410 doi: 10.1038/s41467-021-24697-2 [5] Kortshagen Group Thermoelectrics https://kortshagen.umn. edu/research/thermoelectrics [6] Pressure Makes Best Cooling https://j-parc.jp/en/topics/2019/190329.html [2019-3-29] [7] He J, Tritt T M 2017 Science 357 1369 doi: 10.1126/science.aak9997 [8] 叶良修 2007 半导体物理学 (北京: 高等教育出版社) Ye L X 2007 Semiconductor Physics (Beijing: Higher Education Press [9] Chen Z W, Zhang X Y, Pei Y Z 2018 Adv. Mater. 30 1705617 doi: 10.1002/adma.201705617 [10] Qiu W, Xi L, Wei P, Ke X, Yang J, Zhang W 2014 Proc. Natl. Acad. Sci. U. S. A. 111 15031 doi: 10.1073/pnas.1410349111 [11] Fu C G, Wu H J, Liu Y T, He J Q, Zhao X B, Zhu T J 2016 Adv. Sci. 3 1600035 doi: 10.1002/advs.201600035 [12] Qian X, Zhou J W, Chen G 2021 Nat. Mater. 20 1188 doi: 10.1038/s41563-021-00918-3 [13] Wei B, Sun Q Y, Li C, Hong J W 2021 Sci. China Phys. Mech. Astron. 64 117001 doi: 10.1007/s11433-021-1748-7 [14] Akkerman Q A, Manna L 2020 ACS Energy Lett. 5 604 doi: 10.1021/acsenergylett.0c00039 [15] Muy S, Bachman J C, Giordano L, Chang H H, Abernathy D L, Bansal D, Delaire O, Hori S, Kanno R, Maglia F, Lupart S, Lamp P, Shao-Horn Y 2018 Energy Environ. Sci. 11 850 doi: 10.1039/C7EE03364H [16] Cazorla C 2019 Nature 567 470 doi: 10.1038/d41586-019-00974-5 [17] 沈家骏, 方腾, 傅铁铮, 忻佳展, 赵新兵, 朱铁军 2019 无机材料学报 34 260 doi: 10.15541/jim20180320 Shen J J, Fang T, Fu T Z, Xin J Z, Zhao X B, Zhu T J 2019 J. Inorg. Mater. 34 260 doi: 10.15541/jim20180320 [18] Lin S Q, Li W, Li S S, Zhang X Y, Chen Z W, Xu Y D, Chen Y, Pei Y Z 2017 Joule 1 816 doi: 10.1016/j.joule.2017.09.006 [19] Li W, Lin S Q, Weiss M, Chen Z W, Li J, Xu Y D, Zeier W G, Pei Y Z 2018 Adv. Energy Mater. 8 1800030 doi: 10.1002/aenm.201800030 [20] Xia K Y, Hu C L, Fu C G, Zhao X B, Zhu T J 2021 Appl. Phys. Lett. 118 140503 doi: 10.1063/5.0043552 [21] Zhu J F, Ren Q Y, Chen C, Wang C, Shu M F, He M, Zhang C P, Le M D, Torri S, Wang C W, Wang J L, Cheng Z X, Li L S, Wang G H, Jiang Y X, Wu M Z, Qu Z, Tong X, Chen Y, Zhang Q, Ma J 2024 Nat. Commun. 15 2618 doi: 10.1038/s41467-024-46895-4 [22] Li X Y, Liu P F, Zhao E Y, Zhang Z G, Guidi T, Le M D, Avdeev M, Ikeda K, Otomo T, Kofu M, Nakajima K, Chen J, He L H, Ren Y, Wang X L, Wang B T, Ren Z F, Zhao H Z, Wang F W 2020 Nat. Commun. 11 942 doi: 10.1038/s41467-020-14772-5 [23] Liu H L, Shi X, Xu F F, Zhang L L, Zhang W Q, Chen L D, Li Q, Uher C, Day T, Snyder G J 2012 Nat. Mater. 11 422 doi: 10.1038/nmat3273 [24] Li L, Liu Y, Dai J Y, Hong A J, Zeng M, Yan Z B, Xu J, Zhang D, Shan D, Liu S L, Ren Z F, Liu J M 2016 J. Mater. Chem. C 4 5806 doi: 10.1039/C6TC00810K [25] Christensen M, Abrahamsen A B, Christensen N B, Juranyi F, Andersen N H, Lefmann K, Andreasson J, Bahl C R, Iversen B B 2008 Nat. Mater. 7 811 doi: 10.1038/nmat2273 [26] Koza M M, Johnson M R, Viennois R, Mutka H, Girard L, Ravot D 2008 Nat. Mater. 7 805 doi: 10.1038/nmat2260 [27] Lee S, Esfarjani K, Luo T F, Zhou J W, Tian Z T, Chen G 2014 Nat. Commun. 5 3525 doi: 10.1038/ncomms4525 [28] Delaire O, Ma J, Marty K, May A F, McGuire M A, Du M H, Singh D J, Podlesnyak A, Ehlers G, Lumsden M D, Sales B C 2011 Nat. Mater. 10 614 doi: 10.1038/nmat3035 [29] Voneshen D J, Walker H C, Refson K, Goff J P 2017 Phys. Rev. Lett. 118 145901 doi: 10.1103/PhysRevLett.118.145901 [30] Li C W, Hong J, May A F, Bansal D, Chi S, Hong T, Ehlers G, Delaire O 2015 Nat. Phys. 11 1063 doi: 10.1038/nphys3492 [31] Ren Q Y, Gupta M K, Jin M, Ding J, Wu J, Chen Z W, Lin S Q, Fabelo O, Rodríguez-Velamazán J A, Kofu M, Nakajima K, Wolf M, Zhu F, Wang J L, Cheng Z, Wang G, Tong X, Pei Y Z, Delaire O, Ma J 2023 Nat. Mater. 22 999 doi: 10.1038/s41563-023-01560-x [32] Delaire O, Marty K, Stone M B, Kent P R C, Lucas M S, Abernathy D L, Mandrus D, Sales B C 2011 Proc. Natl. Acad. Sci. U. S. A. 108 4725 doi: 10.1073/pnas.1014869108 [33] Li C W, Hellman O, Ma J, May A F, Cao H B, Chen X, Christianson A D, Ehlers G, Singh D J, Sales B C, Delaire O 2014 Phys. Rev. Lett. 112 175501 doi: 10.1103/PhysRevLett.112.175501 [34] Han S, Dai S N, Ma J, Ren Q Y, Hu C L, Gao Z H, Duc Le M, Sheptyakov D, Miao P, Torii S, Kamiyama T, Felser C, Yang J, Fu C G, Zhu T J 2023 Nat. Phys. 19 1649 doi: 10.1038/s41567-023-02188-z [35] Bachman J C, Muy S, Grimaud A, Chang H H, Pour N, Lux S F, Paschos O, Maglia F, Lupart S, Lamp P, Giordano L, Shao-Horn Y 2015 Chem. Rev. 116 140 doi: 10.1021/acs.chemrev.5b00563 [36] Gao Y R, Nolan A M, Du P, Wu Y F, Yang C, Chen Q L, Mo Y F, Bo S H 2020 Chem. Rev. 120 5954 doi: 10.1021/acs.chemrev.9b00747 [37] Famprikis T, Canepa P, Dawson J A, Islam M S, Masquelier C 2019 Nat. Mater. 18 1278 doi: 10.1038/s41563-019-0431-3 [38] Kamaya N, Homma K, Yamakawa Y, Hirayama M, Kanno R, Yonemura M, Kamiyama T, Kato Y, Hama S, Kawamoto K, Mitsui A 2011 Nat. Mater. 10 682 doi: 10.1038/nmat3066 [39] Kato Y, Hori S, Saito T, Suzuki K, Hirayama M, Mitsui A, Yonemura M, Iba H, Kanno R 2016 Nat. Energy 1 16030 doi: 10.1038/nenergy.2016.30 [40] Lanigan-Atkins T, He X, Krogstad M J, Pajerowski D M, Abernathy D L, Xu G, Xu Z, Chung D Y, Kanatzidis M G, Rosenkranz S, Osborn R, Delaire O 2021 Nat. Mater. 20 977 doi: 10.1038/s41563-021-00947-y [41] Li B, Kawakita Y, Liu Y, Wang M, Matsuura M, Shibata K, Ohira-Kawamura S, Yamada T, Lin S Q, Nakajima K, Liu S F 2017 Nat. Commun. 8 16086 doi: 10.1038/ncomms16086 [42] Li B, Kawakita Y, Ohira-Kawamura S, Sugahara T, Wang H, Wang J L, Chen Y, Kawaguchi S I, Kawaguchi S, Ohara K, Li K, Yu D, Mole R, Hattori T, Kikuchi T, Yano S I, Zhang Z, Zhang Z, Ren W, Lin S Q, Sakata O, Nakajima K, Zhang Z 2019 Nature 567 506 doi: 10.1038/s41586-019-1042-5 [43] 谢梦祥, 任捷 2022 物理 51 855 doi: 10.7693/wl20221205 Xie M X, Ren J 2022 Wuli 51 855 doi: 10.7693/wl20221205 [44] 任清勇, 陈闽楠, 耿艳胜, 马杰, 童欣 2021 中国科学: 物理学 力学 天文学 51 087332 doi: 10.1360/SSPMA-2021-0016 Ren Q Y, Chen M N, Geng Y S, Ma J, Tong X 2021 Sci. Sin. : Phys. Mech. Astron. 51 087332 doi: 10.1360/SSPMA-2021-0016 [45] 马杰, 任清勇 2017 西北大学学报 (自然科学版) 47 783 Ma J, Ren Q Y 2017 J. Northwestern Uni. (Nat. Sci. Ed. ) 47 783 [46] Squires G L 1978 Introduction to the Theory of Thermal Neutron Scattering (Cambridge: Cambridge University Press [47] Furrer A, Mesot J, Strässle T 2009 Neutron Scattering in Condensed Matter Physics (Vol. 4) (Singapore: World Scientific [48] Sears V F 1992 Neutron News 3 26 doi: 10.1080/10448639208218770 [49] Berrod Q, Lagrené K, Ollivier J, Zanotti J M 2018 EPJ Web Conf. 188 05001 doi: 10.1051/epjconf/201818805001 [50] 王延绪, 龚武, 苏玉华, 李昺 2024 金属学报 60 1001 doi: 10.11900/0412.1961.2024.00063 Wang Y X, Gong W, Su Y H, Li B 2024 Acta Metall. Sin. 60 1001 doi: 10.11900/0412.1961.2024.00063 [51] Delaire O A, Stassis C 2012 Phonon Studies (John Wiley & Sons [52] Li B, Wang H, Kawakita Y, Zhang Q, Feygenson M, Yu H L, Wu D, Ohara K, Kikuchi T, Shibata K, Yamada T, Ning X K, Chen Y, He J Q, Vaknin D, Wu R Q, Nakajima K, Kanatzidis M G 2018 Nat. Mater. 17 226 doi: 10.1038/s41563-017-0004-2 [53] Božin E S, Malliakas C D, Souvatzis P, Proffen T, Spaldin N A, Kanatzidis M G, Billinge S J L 2010 Science 330 1660 doi: 10.1126/science.1192759 [54] Sakata M, Sato M 1990 Acta Crystallogr. Sec. A 46 263 doi: 10.1107/S0108767389012377 [55] Keen D A, Goodwin A L 2015 Nature 521 303 doi: 10.1038/nature14453 [56] Neder R B, Proffen T 2008 Diffuse Scattering and Defect Structure Simulations: A Cook Book Using the Program DISCUS (Vol. 11) (OUP Oxford [57] Weber T, Simonov A 2012 Zeitschrift für Kristallographie 227 238 doi: 10.1524/zkri.2012.1504 [58] Cai G L, Li Y H, Fu Y, Yang H, Mei L, Nie Z Y, Li T F, Liu H, Ke Y B, Wang X L, Brédas J L, Tang M C, Chen X K, Zhan X W, Lu X H 2024 Nat. Commun. 15 2784 doi: 10.1038/s41467-024-47052-7 [59] Jeffries C M, Ilavsky J, Martel A, Hinrichs S, Meyer A, Pedersen J S, Sokolova A V, Svergun D I 2021 Nature Reviews Methods Primers 1 70 doi: 10.1038/s43586-021-00064-9 [60] Skoda M W A 2019 Current Opinion in Colloid & Interface Science 42 41 doi: 10.1016/j.cocis.2019.03.003 [61] Combet S, Cousin F, Fadda G, Schirò G 2020 EPJ Web Conf. 236 04001 doi: 10.1051/epjconf/202023604001 [62] Aswal D K, Sarkar P S, Kashyap Y S 2022 Neutron Imaging: Basics, Techniques and Applications (Springer [63] Strobl M, Manke I, Kardjilov N, Hilger A, Dawson M, Banhart J 2009 J. Phys. D: Appl. Phys. 42 243001 doi: 10.1088/0022-3727/42/24/243001 [64] Kardjilov N, Manke I, Hilger A, Strobl M, Banhart J 2011 Mater. Today 14 248 doi: 10.1016/S1369-7021(11)70139-0 [65] Luo W, Feng Y, Liu X Z, Wang M, Zhu D H, Gao W, Geng Y S, Ren Q Y, Shen J Y, Sun Y, Zhang X Y, Xia Y G, Zuo T S, Zheng Y, Tong X 2023 Nucl. Instrum. Methods Phys. Res., Sect. A 1046 167676 doi: 10.1016/j.nima.2022.167676 [66] Embs J P, Juranyi F, Hempelmann R 2010 Z. Phys. Chem. 224 5 doi: 10.1524/zpch.2010.6090 [67] Bee M 1988 Quasielastic Neutron Scattering : Principles and Applications in Solid State Chemistry, Biology, and Materials Science (Bristol, England; Philadelphia: Adam Hilger [68] Ren Q Y, Qi J, Yu D H, Zhang Z, Song R Q, Song W L, Yuan B, Wang T H, Ren W J, Zhang Z D, Tong X, Li B 2022 Nat. Commun. 13 2293 doi: 10.1038/s41467-022-29997-9 [69] Jobic H, Theodorou D N 2007 Microporous Mesoporous Mater. 102 21 doi: 10.1016/j.micromeso.2006.12.034 [70] Verdal N, Udovic T J, Rush J J, Skripov A V 2015 J. Alloys Compd. 645 S513 doi: 10.1016/j.jallcom.2014.12.070 [71] Merklein M, Kabakova I V, Zarifi A, Eggleton B J 2022 Appl. Phys. Rev. 9 041306 doi: 10.1063/5.0095488 [72] Wolff C, Smith M J A, Stiller B, Poulton C G 2021 J. Opt. Soc. Am. B 38 1243 doi: 10.1364/JOSAB.416747 [73] Baron A Q 2015 arXiv: 1504.01098 [cond-mat.mtrl-sci] [74] Ishikawa D, Ellis D S, Uchiyama H, Baron A Q 2015 J. Synchrotron. Radiat. 22 3 doi: 10.1107/S1600577514021006 [75] Wu M, Shi R C, Qi R S, Li Y H, Du J L, Gao P 2023 Ultramicroscopy 253 113818 doi: 10.1016/j.ultramic.2023.113818 [76] Delaire O, May A F, McGuire M A, Porter W D, Lucas M S, Stone M B, Abernathy D L, Ravi V A, Firdosy S A, Snyder G J 2009 Phys. Rev. B 80 184302 doi: 10.1103/PhysRevB.80.184302 [77] Shi X, He J 2021 Science 371 343 doi: 10.1126/science.abf3342 [78] Mao J, Chen G, Ren Z F 2021 Nat. Mater. 20 454 doi: 10.1038/s41563-020-00852-w [79] Toberer E S, Zevalkink A, Snyder G J 2011 J. Mater. Chem. 21 15843 doi: 10.1039/c1jm11754h [80] Wei P C, Liao C N, Wu H J, Yang D, He J, Biesold-McGee G V, Liang S, Yen W T, Tang X, Yeh J W, Lin Z, He J H 2020 Adv. Mater. 32 e1906457 doi: 10.1002/adma.201906457 [81] Hanus R, Agne M T, Rettie A J E, Chen Z W, Tan G, Chung D Y, Kanatzidis M G, Pei Y Z, Voorhees P W, Snyder G J 2019 Adv. Mater. 31 1900108 doi: 10.1002/adma.201900108 [82] Wu Y X, Chen Z W, Nan P F, Xiong F, Lin S Q, Zhang X Y, Chen Y, Chen L D, Ge B H, Pei Y Z 2019 Joule 3 1276 doi: 10.1016/j.joule.2019.02.008 [83] Jiang B B, Yu Y, Cui J, Liu X X, Xie L, Liao J C, Zhang Q H, Huang Y, Ning S C, Jia B H, Zhu B, Bai S Q, Chen L D, Pennycook S J, He J Q 2021 Science 371 830 doi: 10.1126/science.abe1292 [84] Zhang Z X, Zhao K P, Wei T R, Qiu P F, Chen L D, Shi X 2020 Energy Environ. Sci. 13 3307 doi: 10.1039/D0EE02072A [85] Zhao K P, Qiu P F, Shi X, Chen L D 2019 Adv. Funct. Mater. 30 1903867 doi: 10.1002/adfm.201903867 [86] Niedziela J L, Bansal D, May A F, Ding J, Lanigan-Atkins T, Ehlers G, Abernathy D L, Said A, Delaire O 2019 Nat. Phys. 15 73 doi: 10.1038/s41567-018-0298-2 [87] Jiang B B, Qiu P F, Eikeland E, Chen H Y, Song Q F, Ren D D, Zhang T S, Yang J, Iversen B B, Shi X, Chen L D 2017 J. Mater. Chem. C 5 943 doi: 10.1039/C6TC05068A [88] Ding J, Niedziela J L, Bansal D, Wang J L, He X, May A F, Ehlers G, Abernathy D L, Said A, Alatas A, Ren Y, Arya G, Delaire O 2020 Proc. Natl. Acad. Sci. U. S. A. 117 3930 doi: 10.1073/pnas.1913916117 [89] Xie L, Feng J H, Li R, He J Q 2020 Phys. Rev. Lett. 125 245901 doi: 10.1103/PhysRevLett.125.245901 [90] Trachenko K 2008 Phys. Rev. B 78 104201 doi: 10.1103/PhysRevB.78.104201 [91] Xie L, Wu D, Yang H L, Yu Y, Wang Y F, He J Q 2019 J. Mater. Chem. C 7 9263 doi: 10.1039/C9TC03235E [92] Li W, Lin S Q, Ge B H, Yang J, Zhang W Q, Pei Y Z 2016 Adv. Sci. 3 1600196 doi: 10.1002/advs.201600196 [93] de Boissieu M 2023 Nat. Mater. 22 931 doi: 10.1038/s41563-023-01605-1 [94] Janek J, Zeier W G 2016 Nat. Energy 1 16141 doi: 10.1038/nenergy.2016.141 [95] Zhao Q, Stalin S, Zhao C Z, Archer L A 2020 Nat. Rev. Mater. 5 229 doi: 10.1038/s41578-019-0165-5 [96] He X F, Zhu Y Z, Mo Y F 2017 Nat. Commun. 8 15893 doi: 10.1038/ncomms15893 [97] Zou Z Y, Li Y J, Lu Z H, Wang D, Cui Y H, Guo B K, Li Y J, Liang X M, Feng J W, Li H, Nan C W, Armand M, Chen L Q, Xu K, Shi S Q 2020 Chem. Rev. 120 4169 doi: 10.1021/acs.chemrev.9b00760 [98] Zhu L, Wang Y W, Chen J C, Li W L, Wang T T, Wu J, Han S Y, Xia Y H, Wu Y M, Wu M Q, Wang F W, Zheng Y, Peng L M, Liu J J, Chen L Q, Tang W P 2022 Sci. Adv. 8 eabj7698 doi: 10.1126/sciadv.abj7698 [99] Wang Y, Richards W D, Ong S P, Miara L J, Kim J C, Mo Y, Ceder G 2015 Nat. Mater. 14 1026 doi: 10.1038/nmat4369 [100] Kraft M A, Culver S P, Calderon M, Böcher F, Krauskopf T, Senyshyn A, Dietrich C, Zevalkink A, Janek J, Zeier W G 2017 J. Am. Chem. Soc. 139 10909 doi: 10.1021/jacs.7b06327 [101] Zhang Z, Nazar L F 2022 Nat. Rev. Mater. 7 389 doi: 10.1038/s41578-021-00401-0 [102] Muy S, Schlem R, Shao-Horn Y, Zeier W G 2021 Adv. Energy Mater. 11 2002787 doi: 10.1002/aenm.202002787 [103] The Royal Society 2021 https://royalsociety.org/topics [104] United Nations Environmental Programme https://ozone.unep.org/ites/default/files/2019 [2018-5] [105] Peters T 2018 Technical Report. https://www.birmingham.ac.uk/Documents/college [106] Hou H, Qian S, Takeuchi I 2022 Nat. Rev. Mater. 7 633 doi: 10.1038/s41578-022-00428-x [107] Chen Y L, Wang Y, Sun W, Qian S X, Liu J 2022 The Innovation 3 100205 [108] Aprea C, Greco A, Maiorino A, Masselli C 2019 Climate 7 115 doi: 10.3390/cli7090115 [109] Maier L M, Corhan P, Barcza A, Vieyra H A, Vogel C, Koenig J D, Schäfer-Welsen O, Wöllenstein J, Bartholomé K 2020 Commun. Phys. 3 186 doi: 10.1038/s42005-020-00450-x [110] Aprea C, Greco A, Maiorino A, Masselli C 2020 Energy 190 116404 doi: 10.1016/j.energy.2019.116404 [111] Lloveras P, Zhang Z, Zeng M, Barrio M, Kawakita Y, Yu D, Lin S Q, Li K, Moya X, Tamarit J L, Li B 2023 Colossal Barocaloric Plastic Crystals (IOP Publishing) p7-1-7-30 [112] Zhang K, Zhang Z, Pan H L, Wang H Y, Zhao X T, Qi J, Zhang Z, Song R Q, Yu C Y, Huang B H, Li X J, Chen H C, Yin W, Tan C L, Hu W J, Wübbenhorst M, Luo J S, Yu D H, Zhang Z D, Li B 2024 The Innovation 5 100577 doi: 10.1016/j.xinn.2024.100577 [113] 李昺, 张志东 2021 中国科学: 物理学 力学 天文学 51 067505 doi: 10.1360/SSPMA-2020-0333 Li B, Zhang Z D 2021 Sci. Sin. Phys. Mech. Astron. 51 067505 doi: 10.1360/SSPMA-2020-0333 [114] Qian X, Han D, Zheng L, Chen J, Tyagi M, Li Q, Du F, Zheng S, Huang X, Zhang S, Shi J, Huang H, Shi X, Chen J, Qin H, Bernholc J, Chen X, Chen L Q, Hong L, Zhang Q M 2021 Nature 600 664 doi: 10.1038/s41586-021-04189-5 [115] 郝嘉政, 胡凤霞, 尉紫冰, 沈斐然, 周厚博, 高怡红, 乔凯明, 梁文会, 张丞, 王晶, 孙继荣, 沈保根 2021 中国科学: 物理学 力学 天文学 51 067520 doi: 10.1360/SSPMA-2020-0328 Hao J Z, Hu F X, Wei Z B, Shen F R, Zhou H B, Gao Y H, Qiao K M, Liang W H, Zhang C, Wang J, Sun J R, Shen B G 2021 Sci. Sin.: Phys. Mech. Astron. 51 067520 doi: 10.1360/SSPMA-2020-0328 [116] Aznar A, Lloveras P, Barrio M, Negrier P, Planes A, Manosa L, Mathur N D, Moya X, Tamarit J L 2020 J. Mater. Chem. A 8 639 doi: 10.1039/C9TA10947A [117] Li J, Dunstan D, Lou X, Planes A, Manosa L, Barrio M, Tamarit J L, Lloveras P 2020 J. Mater. Chem. A 8 20354 doi: 10.1039/D0TA05399F [118] Li F B, Li M, Xu X, Yang Z C, Xu H, Jia C K, Li K, He J, Li B, Wang H 2020 Nat. Commun. 11 4190 doi: 10.1038/s41467-020-18043-1 [119] Lloveras P, Aznar A, Barrio M, Negrier P, Popescu C, Planes A, Manosa L, Stern-Taulats E, Avramenko A, Mathur N D, Moya X, Tamarit J L 2019 Nat. Commun. 10 1803 doi: 10.1038/s41467-019-09730-9 [120] Zhang Z, Li K, Lin S Q, Song R, Yu D, Wang Y, Wang J L, Kawaguchi S, Zhang Z, Yu C, Li X, Chen J, He L, Mole R, Yuan B, Ren Q Y, Qian K, Cai Z, Yu J, Wang M, Zhao C, Tong X, Zhang Z, Li B 2023 Sci. Adv. 9 eadd0374 doi: 10.1126/sciadv.add0374 [121] Staveley L A K 1962 Annu. Rev. Phys. Chem. 13 351 doi: 10.1146/annurev.pc.13.100162.002031 [122] Seo J, Ukani R, Zheng J, Braun J D, Wang S, Chen F E, Kim H K, Zhang S, Thai C, McGillicuddy R D, Yan H, Vlassak J J, Mason J A 2024 J. Am. Chem. Soc. 146 2736 doi: 10.1021/jacs.3c12402 [123] Yu Z B, Zhou H B, Hu F X, Liu C, Yuan S K, Wang D H, Hao J Z, Gao Y H, Wang Y X, Wang B J, Tian Z Y, Lin Y, Zhang C, Yin Z, Wang J, Chen Y Z, Li Y L, Sun J R, Zhao T Y, Shen B G 2022 NPG Asia Mater. 14 96 doi: 10.1038/s41427-022-00448-7 [124] Sakata M, Harada J, Cooper M J, Rouse K D 1980 Acta Crystallogr. Sec. A 36 7 doi: 10.1107/S0567739480000022 [125] Songvilay M, Giles-Donovan N, Bari M, Ye Z G, Minns J L, Green M A, Xu G, Gehring P M, Schmalzl K, Ratcliff W D, Brown C M, Chernyshov D, van Beek W, Cochran S, Stock C 2019 Phys. Rev. Mater. 3 093602 doi: 10.1103/PhysRevMaterials.3.093602 [126] Lee W, Li H, Wong A B, Zhang D, Lai M, Yu Y, Kong Q, Lin E, Urban J J, Grossman J C, Yang P 2017 Proc. Natl. Acad. Sci. U. S. A. 114 8693 doi: 10.1073/pnas.1711744114 [127] Li W, Vasenko A S, Tang J, Prezhdo O V 2019 J. Phys. Chem. Lett. 10 6219 doi: 10.1021/acs.jpclett.9b02553 [128] Ren Q Y, Fu C G, Qiu Q Y, Dai S N, Liu Z Y, Masuda T, Asai S, Hagihala M, Lee S, Torri S, Kamiyama T, He L H, Tong X, Felser C, Singh D J, Zhu T J, Yang J, Ma J 2020 Nat. Commun. 11 3142 doi: 10.1038/s41467-020-16913-2 [129] de Campos A, Rocco D L, Carvalho A M, Caron L, Coelho A A, Gama S, da Silva L M, Gandra F C, dos Santos A O, Cardoso L P, von Ranke P J, de Oliveira N A 2006 Nat. Mater. 5 802 doi: 10.1038/nmat1732 [130] Krenke T, Duman E, Acet M, Wassermann E F, Moya X, Manosa L, Planes A 2005 Nat. Mater. 4 450 doi: 10.1038/nmat1395 [131] Liu J, Gottschall T, Skokov K P, Moore J D, Gutfleisch O 2012 Nat. Mater. 11 620 doi: 10.1038/nmat3334 [132] Choe W, Pecharsky V K, Pecharsky A O, Gschneidner Jr K A, Young Jr V G, Miller G J 2000 Phys. Rev. Lett. 84 4617 doi: 10.1103/PhysRevLett.84.4617 [133] Ren Q Y, Hutchison W D, Wang J L, Cobas R, Cadogan J M, Campbell S J 2015 Hyperfine Interactions 231 75 doi: 10.1007/s10751-014-1101-0 [134] Ren Q Y, Hutchison W D, Wang J L, Studer A J, Campbell S J 2017 J. Alloys Compd. 693 32 doi: 10.1016/j.jallcom.2016.09.169 [135] Ren Q Y, Hutchison W D, Wang J L, Studer A J, Din M F M, Pérez S M, Cadogan J M, Campbell S J 2016 J. Phys. D: Appl. Phys. 49 175003 doi: 10.1088/0022-3727/49/17/175003 [136] Ren Q Y, Hutchison W D, Wang J L, Muñoz Pérez S, Cadogan J M, Campbell S J 2014 Phys. Status Solidi A 211 1101 doi: 10.1002/pssa.201330561 [137] Liu E K, Wang W H, Feng L, Zhu W, Li G J, Chen J L, Zhang H W, Wu G H, Jiang C B, Xu H B, de Boer F 2012 Nat. Commun. 3 873 doi: 10.1038/ncomms1868 [138] Ren Q Y, Hutchison W, Wang J L, Studer A, Wang G, Zhou H B, Ma J, Campbell S J 2019 ACS Appl. Mater. Interfaces 11 17531 doi: 10.1021/acsami.9b02772 [139] Ren Q Y, Hutchison W D, Wang J L, Studer A J, Campbell S J 2018 Chem. Mater. 30 1324 doi: 10.1021/acs.chemmater.7b04970 [140] Landrum G A, Hoffmann R, Evers J, Boysen H 1998 Inorg. Chem. 37 5754 doi: 10.1021/ic980223e [141] Zhu Y F, Xia Y, Wang Y C, Sheng Y, Yang J, Fu C G, Li A R, Zhu T J, Luo J, Wolverton C, Snyder G J, Liu J J, Zhang W Q 2020 Research 2020 4589786 doi: 10.34133/2020/4589786 [142] Lin S Q, Li W, Pei Y Z 2021 Mater. Today 48 198 doi: 10.1016/j.mattod.2021.01.007 [143] Wang Y X, Lin R X, Zhu P C, Zheng Q H, Wang Q J, Li D Y, Zhu J 2018 Nano Lett. 18 2772 doi: 10.1021/acs.nanolett.7b04437 [144] Bernges T, Hanus R, Wankmiller B, Imasato K, Lin S Q, Ghidiu M, Gerlitz M, Peterlechner M, Graham S, Hautier G, Pei Y Z, Hansen M R, Wilde G, Snyder G J, George J, Agne M T, Zeier W G 2022 Adv. Energy Mater. 12 2200717 doi: 10.1002/aenm.202200717 [145] Luo Y X, Yang X L, Feng T L, Wang J Y, Ruan X L 2020 Nat. Commun. 11 2554 doi: 10.1038/s41467-020-16371-w [146] Simoncelli M, Marzari N, Mauri F 2019 Nat. Phys. 15 809 doi: 10.1038/s41567-019-0520-x [147] Mukhopadhyay S, Parker D S, Sales B C, Puretzky A A, McGuire M A, Lindsay L 2018 Science 360 1455 doi: 10.1126/science.aar8072 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: