首页
登录
注册
-
点衍射干涉测量法[1–5]是近年来为满足光刻领域超精检测需求而发展起来一种新方法, 该方法通过微米尺寸小孔衍射, 产生近似理想的球面波作为参考面构成干涉测量系统, 摆脱了实物参考镜对其测量精度的限制, 理论上可达到亚纳米级检测精度[6,7]. 依据衍射小孔的不同, 常分为光纤点衍射干涉仪[8,9]和小孔点衍射干涉仪[10]两种. 小孔点衍射干涉仪中的小孔衍射板是用石英玻璃作为基底, 在玻璃基底上镀铬金属反射膜, 再刻蚀出微米级的衍射小孔, 因此具有衍射精度高、衍射范围大等优点[11,12], 是目前主流研究方向. 国外对于小孔点衍射干涉仪的研究起步较早[13,14], 目前已有成型设备; 而国内对于小孔点衍射干涉测量的研究多处于实验室阶段[15–19]. 在实际小孔点衍射干涉仪构建中, 经汇聚透镜聚焦入射至小孔板上的光斑是否与衍射小孔精确对准将直接影响衍射波面精度以及后续光路构建. 因此, 要推动点衍射干涉仪仪器化, 衍射小孔的对准技术将是亟待解决的问题.
目前传统的干涉仪例如斐索干涉仪都配备有可视对准装置, 但是由于干涉仪的测量原理不同, 无法适用于点衍射干涉测量光路, 为此需要结合点衍射干涉仪的光路特点, 设计一种专门的可视对准光路. 2001年Ota等[20]提出一种具有小孔对准系统的点衍射干涉仪, 该系统可以监测入射光束光斑与衍射小孔两者位置关系, 但系统中使用的四象限探测器受目标光斑大小和光斑能量分布影响大, 对实验光路的设计要求更高, 增加了光路构建的复杂性. 2019年Zhao等[21]提出一种基于图像信息的点衍射干涉仪精密光路对准系统, 在光路中加入了光功率计测量了反射和衍射光束的强度, 以此提高图像对比度, 但该系统的操作方法、搭建过程以及后续处理较为复杂.
本文提出借助电荷耦合器件(charge coupled device, CCD)对小孔衍射板反射图像进行监控, 小孔衍射板反射光斑经过分光棱镜后再次反射, 经过辅助对准光路后被CCD接收, 通过监控对准状态、分析对准精度, 对小孔衍射板进行调整, 达到精确对准的目的. 其中, 衍射小孔通过离子束刻蚀具有高精度, 并且系统结构简单、后续处理容易、实现成本低. 本文将可视对准技术及图像处理算法相结合, 为实用小孔点衍射干涉仪的发展奠定技术基础.
-
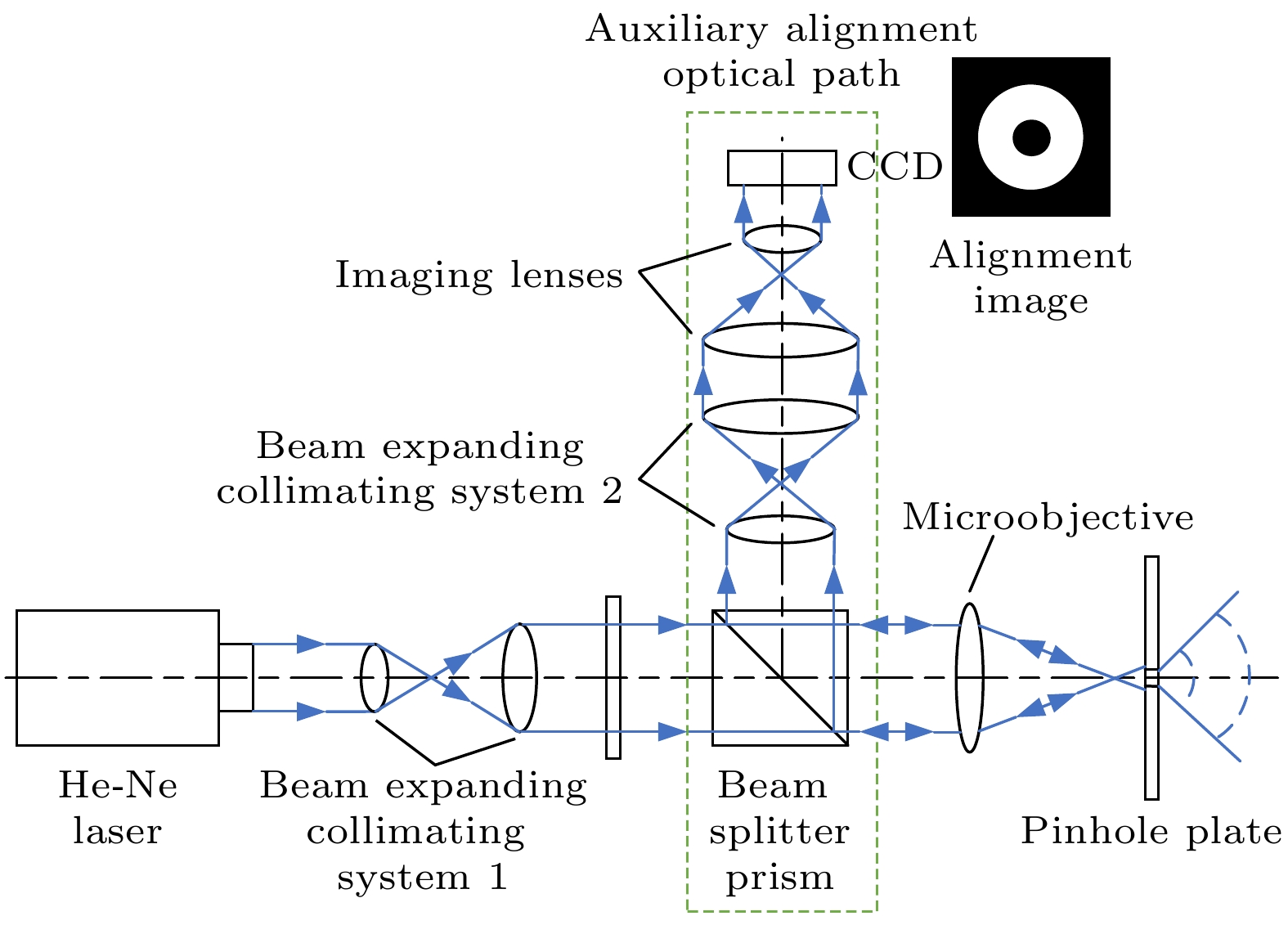
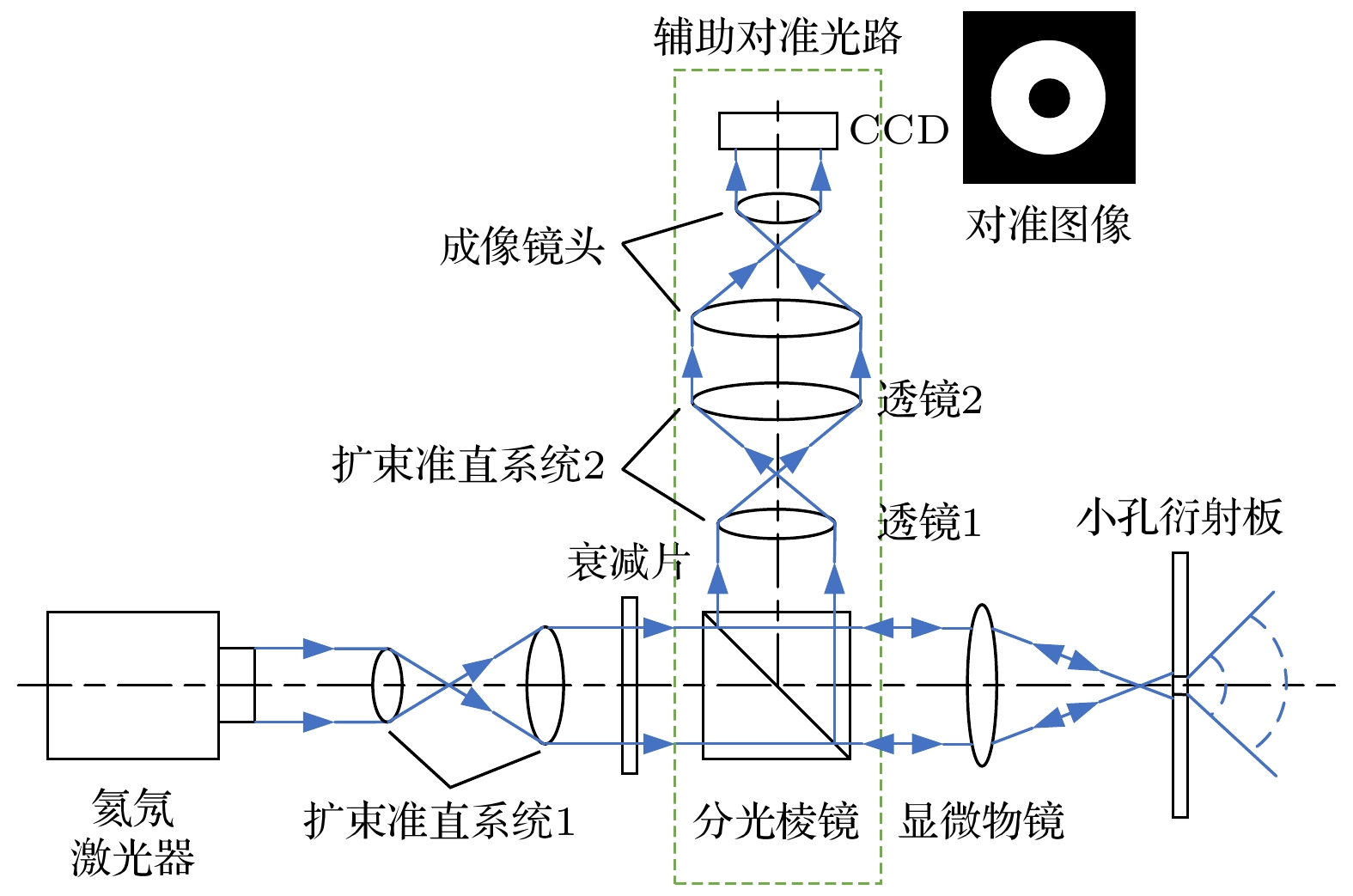
图1是可视对准光路的原理示意图, 整体光路由小孔点衍射光路以及辅助对准光路构成. 对准原理是在小孔点衍射干涉测量系统中的点衍射光路中加入分光棱镜引出辅助对准光路, 从而实现小孔可视对准.
由氦氖激光器发出的光束依次经过扩束准直系统1、衰减片、分光棱镜后由显微物镜汇聚至小孔衍射板上. 汇聚到小孔衍射板上的光束一部分穿过小孔发生衍射, 产生理想球面波, 构成点衍射光路; 另一部分由小孔衍射板表面沿原路反射回来. 而反射回来的光束也可以分为两路: 一部分返回至激光器入射口, 另一部分经分光棱镜再次反射. 再次反射的光束经扩束准直系统2和成像镜头, 最后由CCD进行采集, 构成辅助对准光路. 由于小孔衍射板上刻蚀掉的小孔部分几乎不反射光束, 因此在小孔精确对准的情况下CCD上获得的对准图像将是中央暗外圈亮的同心光斑, 中央暗斑对应衍射小孔图像, 外圈亮斑对应显微物镜汇聚光斑图像. 通过对采集到的对准图像进行处理, 即可得出汇聚光斑与衍射小孔在像方的中心偏移距离, 通过调节实验仪器实现精确对准的目的.
-
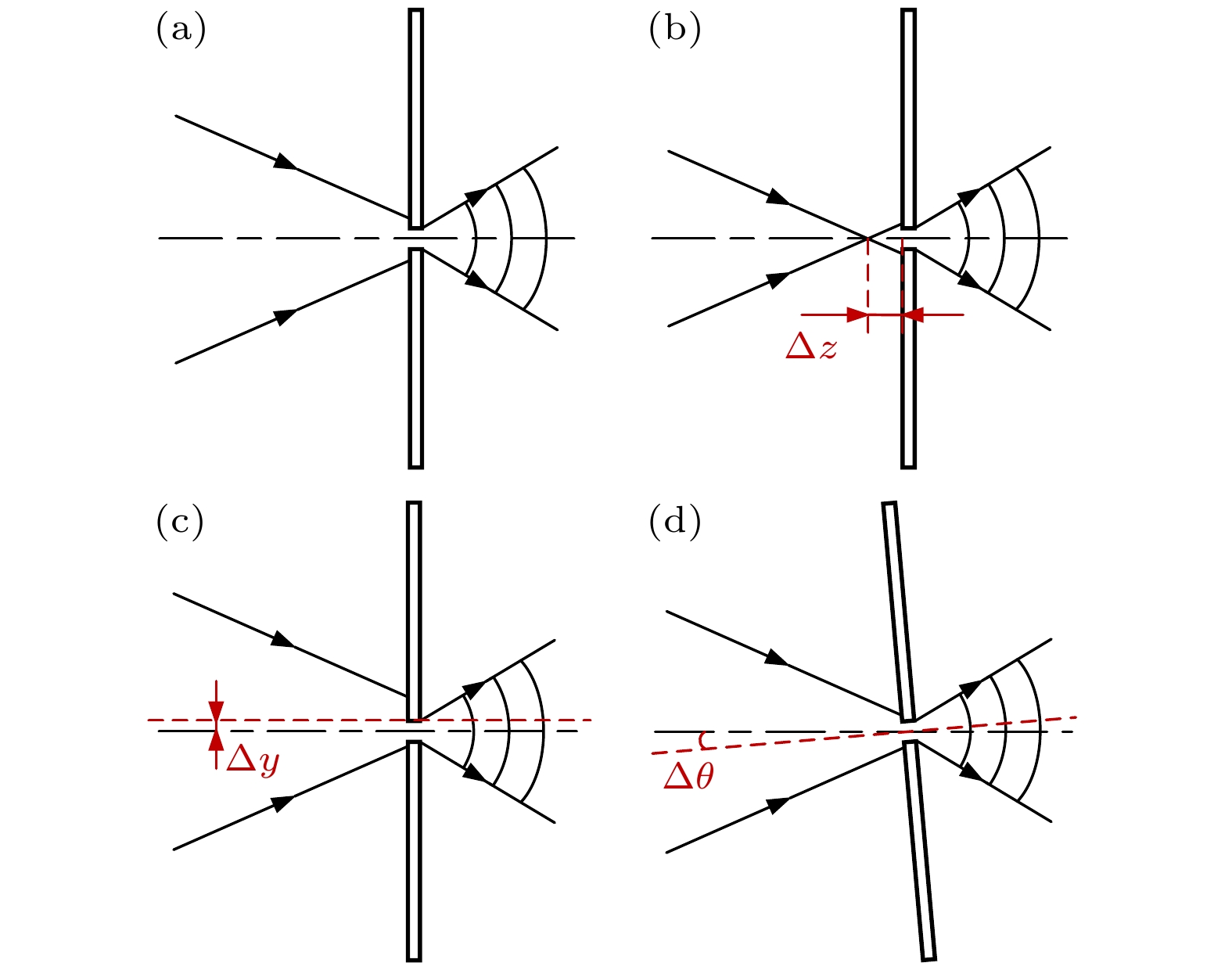
在实际光路搭建中, 小孔衍射板的调校过程可能会产生离焦、平移、倾斜变化, 图2为衍射小孔与汇聚光斑完全对准时以及以上三种对准状态的示意图, 图3为不同对准状态下对应的可视图像示意图. 根据不同对准误差下的小孔衍射波面误差分析结果[22]可知, 平移对准误差对衍射波面精度影响最大, 且对准误差以不超过小孔直径的1/10为宜. 为实现减小对准误差从而指导实验精确对准的目的, 需要利用算法进行对准图像处理从而求出物方对准偏移量, 该过程则需要对汇聚光斑-衍射小孔不同对准状态下的物像关系进行推导.
首先对小孔衍射板产生离焦偏离以及平移偏离进行讨论: 离焦会让光斑的大小发生变化, 但由于光轴水平通过小孔衍射板中心, 因此光斑中心不发生改变. 光轴相对于小孔衍射板发生平移时光斑中心发生偏移, 假设物平面上光斑和小孔中心偏移量为Δy, 整体光路物像放大倍率为k1, 则此时光斑中心和小孔中心在实际采集时水平偏移k1Δy.
接下来对小孔衍射板俯仰产生的偏离进行讨论: 根据图1所示辅助对准光路, 设光轴相对于小孔衍射板俯仰角度为θ、经过显微物镜中心的光线被小孔衍射板反射后到达显微物镜时, 光斑中心与显微物镜中心相距设为x1, 成像镜头两侧物距为l, 像距为l', 设激光器发出的光线到达透镜1时光斑中心与透镜中心相距x2, 成像镜头与分光棱镜中心相距L1, 透镜1与分光棱镜相距L2, 显微物镜焦距为f'. 根据光线在光路中的传播关系得到:
此时可以计算得到x2, 即
设显微物镜放大倍率β, 激光器发出的光线经过显微物镜后与光轴夹角为α, d1为过透镜2在成像镜头方向上的焦点且平行于透镜2到成像镜头方向传播光线的辅助线与透镜2相交的点与透镜2中心的距离, 设透镜1焦距
$f_1' $ , 光线到达透镜2时光斑中心与透镜中心相距距离为x3, 透镜1与透镜2相距L3. 此时可以计算x3的值, 根据光线在光路中传播关系得到:此时可以计算得到x3, 推导得(4)式:
假设激光器发出的光线到达成像镜头时, 光斑中心与透镜中心相距距离为x4, 光线经过透镜2后与光轴夹角θ2, 透镜2与成像镜头相距距离L4, 透镜2焦距
${f}_{2}' $ , d2为透镜2上的光斑中心在成像镜头平面上的投影和成像镜头上的光斑中心的距离. 根据光线在光路中传播关系得到(5)式:此时可以计算得到x4的值:
设小孔衍射板发生俯仰后接收端光斑中心与CCD靶面中心相距Δx, 成像镜头放大倍率为k2, 则Δx = k2x4. 综上, 对准图像经过辅助光路后到达CCD靶面上时横向偏移距离为k1Δy, 纵向偏移距离为Δx, 相机靶面上整体偏移距离
$ D = \sqrt {{{\left( {{k_1}\Delta y} \right)}^2} + \Delta {x^2}} $ . -
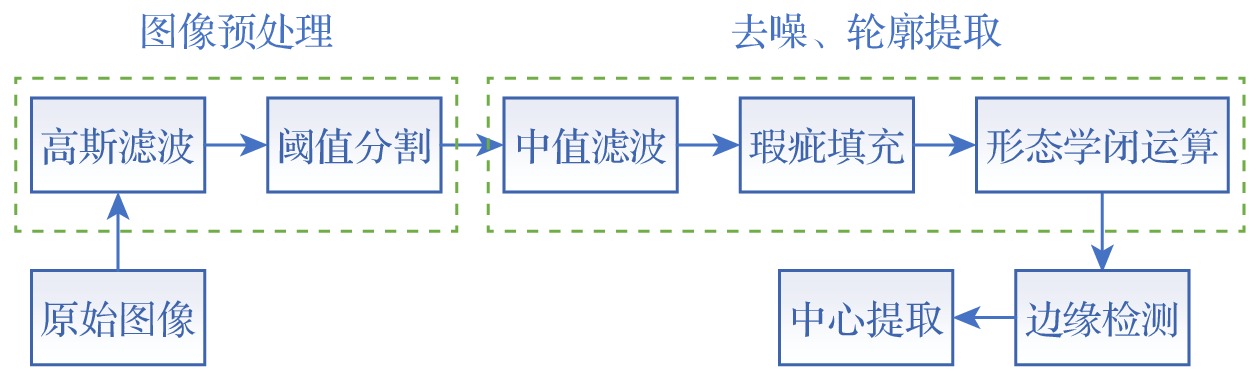
仿真不同情况的对准图像并且基于仿真图像进行对准图像处理算法分析及验证: 对仿真图像采用Matlab软件分别对小孔中心以及汇聚光斑中心进行提取, 判断偏离程度. 对原始图像的处理要考虑到实验环境的影响和实际采集到的图像边缘处不完整的影响, 图4是对准图像处理过程图.
高斯滤波可以将环境噪声滤去, 起到图像平滑作用. 阈值分割根据设置的阈值, 将图像中的物体以像素级分割出来, 能凸显出感兴趣的目标的轮廓. 中值滤波对孤立的噪声像素即椒盐噪声、脉冲噪声具有良好的滤波效果. 瑕疵填充可以填补图像分割后物体中的空洞. 边缘检测选择Sobel算子边缘检测算法, Sobel算子具备一阶算子算法简单、处理速度快的优点, 同时由于使用了加权平均算法, 因此对图像中的一些噪声具有一定的抑制能力. 二值化用来突出图像轮廓, 预处理可以对图像进行图像滤波和阈值分割, 边缘检测后将数据记录, 利用求质心的原理提取光斑和小孔图像中心, 中心提取也是对准图像处理算法中的重点, 其提取精度将直接影响对准误差计算精度.
本文图像中心提取算法原理主要基于几何学中的曲线或多边形的面积和重心的关系. 根据几何原理, 对于一个多边形, 可以将其分割成若干个三角形, 多边形的重心可以通过将每个三角形的面积乘以其重心坐标再求和得到, 最终的结果即为整个多边形的质心坐标. 基于以上原理: 在直角坐标系中, 设三角形的三个顶点为A(x1, y1), B(x2, y2), C(x3, y3), 则三角形面积S可以通过向量积计算:
则每个三角形的重心坐标可以表示为
将每个三角形的面积S乘以其重心坐标(Cx, Cy), 再将结果相加, 即可得到所求多边形的质心坐标.
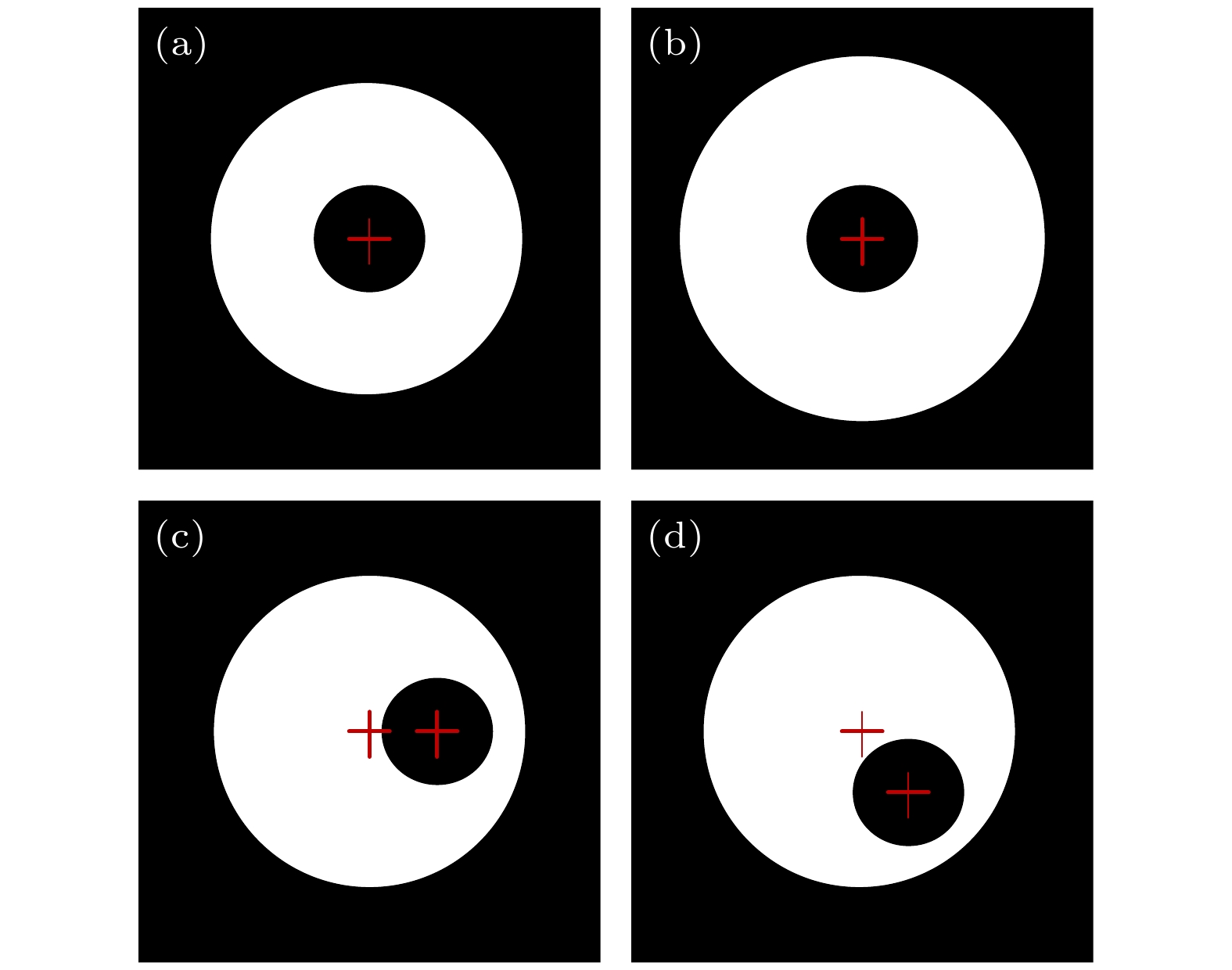
基于高斯光束的光场分布以及夫琅禾费圆孔衍射原理仿真得到小孔中心三种不同程度不同方向偏离光斑中心的对准图像, 图5(a)表示光斑中心和小孔中心同心, 且不偏离画面中心, 图5(b)和图5(c)分别表示小孔中心不同程度不同方向偏离光斑中心的仿真图像.
表1列出了仿真时规定小孔中心像素坐标和光斑中心像素坐标, 其中(x0, y0)为光斑像素坐标值, (x1, y1)为小孔中心像素坐标值.
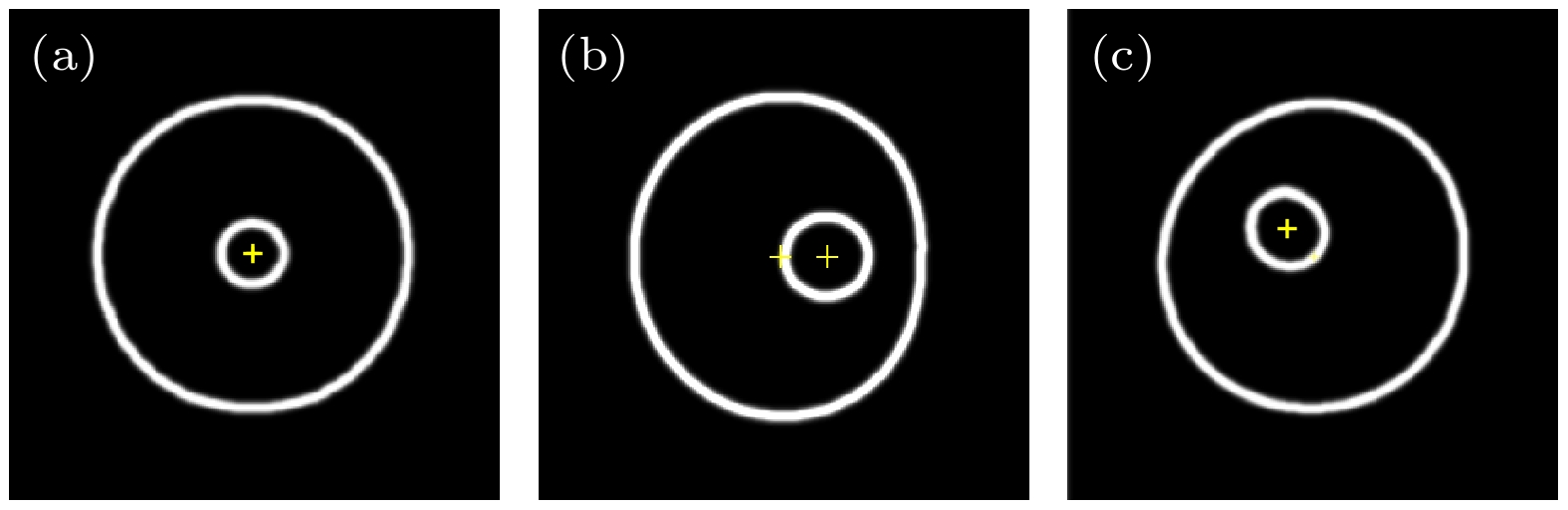
根据图4中的图像处理算法分别对三种不同偏离情况下的仿真图像进行处理, 中心提取结果如图6所示. 表2列出了提取到的光斑中心和小孔中心像素坐标.
根据两点间距离公式:
式中, D为两点间距, 根据已知像素坐标得图像处理算法中心提取误差精度满足精度要求0.1 μm.
-
根据图1所示的辅助对准光路方案搭建实际实验系统, 如图7所示. 实验采用DH-HN250 P单模氦氖激光器作为光源, 工作波长为632.8 nm, 激光器出射光束直径0.7 mm, 功率稳定性≤±2.5%; 显微物镜数值孔径0.25, 物方孔径为6 mm, 放大倍率为10×; 衍射小孔直径为2.5 μm, 对应的衍射全角约35°, 可用于测试光路的有效数值孔径NAtest不超过0.152; 扩束准直系统1采用10×扩束; 衰减片使用波段是400—700 nm; 分光棱镜透射率与反射率均为50%; 实验时, 为排除汇聚光斑边缘光束反射汇聚形成光点对对准误差分析产生影响, 设置离焦量29.5 μm. 扩束准直系统2由两个平凸透镜组合而成, 使光束经过扩束准直系统2后放大2.5×; 成像镜头是整体式远心成像镜头, 倍率为0.16×; CCD感光面尺寸为6.5 mm×4.8 mm, 像素数为782 pixel×582 pixel. 根据上述参数核算得到: 实验中实际小孔直径为2.5 μm, 汇聚光斑直径约为15 μm; CCD接收时小孔直径约为0.4 mm, 汇聚光斑直径约为2.4 mm.
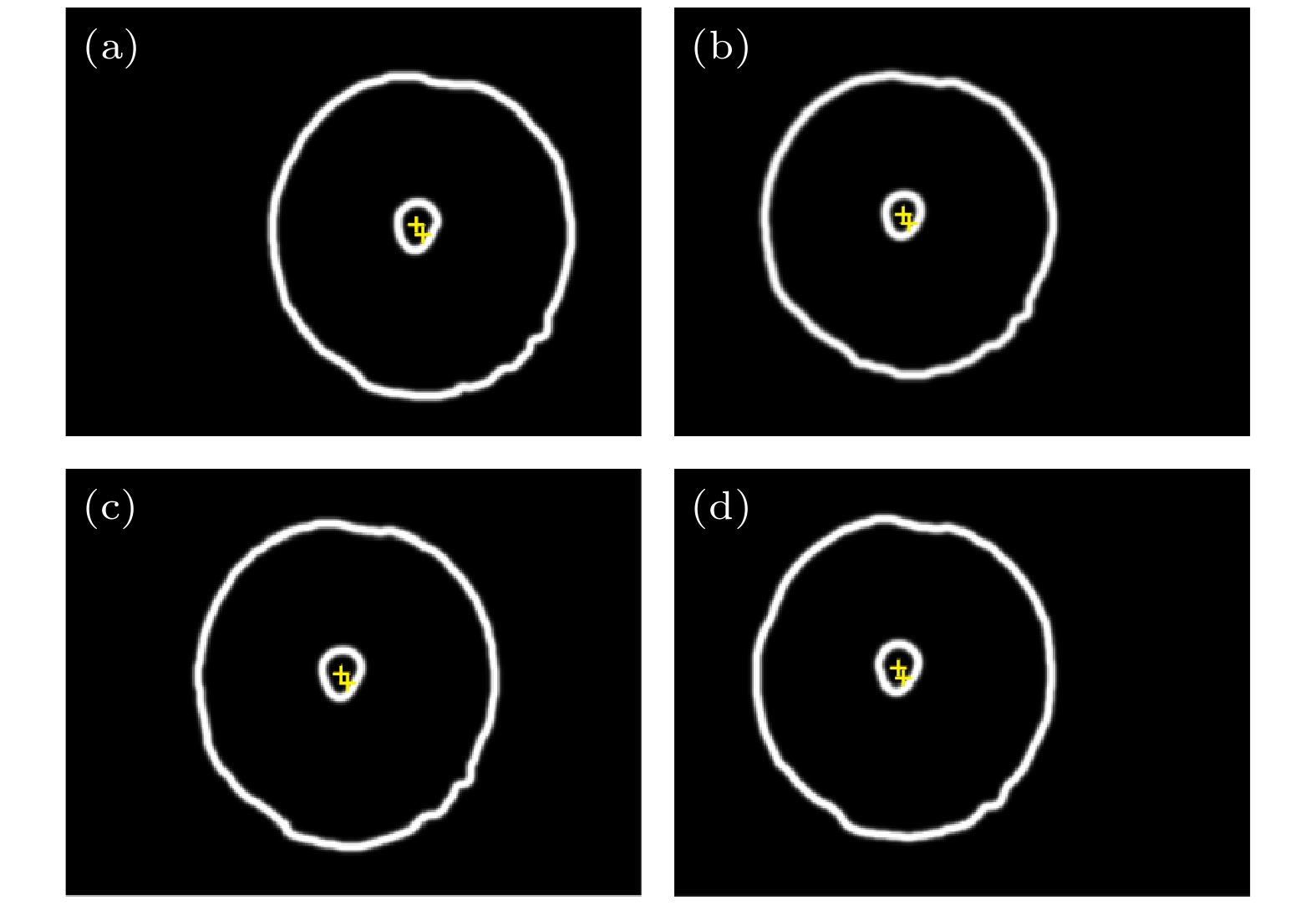
光路搭建过程中CCD摆放位置对准十分重要, 在实际实验中通过在分光棱镜对面引入辅助激光器进行光路调校和定位, 确保小孔衍射板反射光斑与辅助激光器出射光斑入射点相同, 实现CCD位置对准, 搭建完成后移除辅助激光器. 根据图7搭建的光路进行对准图像的采集, 采集时可以在扩束准直系统1和分光棱镜之间加入可调光阑滤除杂散光, 实际采集到对准图像如图8所示.
根据图4流程设计的图像处理算法对图像进行处理, 边缘检测提取了小孔图像和光斑图像边缘线条, 接着对边缘检测后的图像进行小孔和光斑中心点的提取, 中心点提取后图像如图9所示.
对实验采集图像进行图像处理、中心提取后得到光斑和小孔图像中心点像素坐标, 表3为实验图像中心点像素坐标. 其中(x0, y0)为光斑像素坐标值, (x1, y1)为小孔中心像素坐标值.
根据实验选用的芯片尺寸1/2 in德国Basler的acA780-75 gm工业相机, 其感光面尺寸为6.5 mm×4.8 mm, 像素数为782 pixel×582 pixel. 将像素坐标换算为相机感光面上位置坐标, 表4为实验图像中心点相机靶面坐标.
根据两点间距离公式计算光斑中心与小孔中心在相机靶面上的偏移距离得
结合表4中的坐标, 计算得Da = 0.136 mm, Db = 0.130 mm, Dc = 0.139 mm, Dd = 0.139 mm. 根据实际实验器件参数核算后, 实际对准图像相对于CCD靶面上接收到的对准图像放大160×, 因此实际小孔中心和光斑中心偏移距离应为D/160. 因此实际偏移距离da = 0.850 μm, db = 0.815 μm, dc = 0.868 μm, dd = 0.868 μm, 平均偏移距离d ≈ 0.850 μm. 根据表3计算得到水平方向像素坐标偏差平均值约为8.75 pixel, 竖直方向像素坐标偏差平均值约为13.75 pixel, 光斑与小孔中心之间平均像素数约为16.30 pixel, 结合平均偏移距离d, 可得对准精度约为0.05 μm.
根据不同对准误差下的小孔衍射波面误差分析结果[22]可知, 小孔对准误差以不超过小孔直径的1/10为宜, 本文采用直径2.5 μm的衍射小孔, 因此对准误差应小于0.25 μm. 综上所述, 本文研究的可视对准方案对准精度达到0.05 μm, 满足对准精度要求.
-
本文基于小孔点衍射干涉测量原理, 提出借助CCD对小孔点衍射干涉仪中衍射小孔的可视对准光路方案进行研究. 基于仿真图像进行对准图像处理算法研究, 并对算法正确性以及精度进行验证. 根据光线在光路中的传播原理, 对不同对准状态下的可视图像物像关系进行了公式推导, 为小孔衍射板的精确调校提供理论依据. 根据理论设计的光路进行实际实验搭建, 对实验图像进行了采集和处理, 提取了光斑和小孔图像中心坐标并且计算中心偏移距离. 结果表明, 本文提出的辅助光路对准方案和对准图像中心提取处理算法可行, 对准精度达到0.05 μm. 根据不同对准状态下的物像关系, 再结合汇聚光斑和衍射小孔中心偏离量, 通过调节实验仪器达到指导实验精确对准的目的.
本文对小孔点衍射干涉仪中衍射小孔的可视对准技术进行了研究, 但受到时间和实验条件的限制, 目前仅通过原理性实验对所提方法的可行性进行了验证, 要依据小孔移动量与对准图像之间的关联模型, 实现衍射小孔的自动对准, 还需从硬件以及软件方面对本系统进行优化提升及进一步实验. 硬件方面, 本系统缺少高精度电控位移设备, 后续可以通过结合支撑结构, 在小孔衍射板上加入二维高精度电控位移台辅助小孔位置精密对准. 软件方面, 为将来能实现小孔的长时间自动精准对准, 必须配以上位机自动控制软件, 需实现两方面的功能: 一方面自动获取对准系统中CCD采集的图像, 结合相关算法计算出对准位置及偏离; 另一方面连接带动小孔移动的二维压电陶瓷相移器(piezoe-lectric transducer, PZT), 依据监测的对准位置及偏离进行反馈控制, 上述两方面工作将另文探讨.
小孔点衍射干涉仪中衍射小孔的可视对准技术
Visual alignment technology of diffraction pinhole in pinhole point diffraction interferometer
-
摘要: 为解决小孔点衍射干涉仪构建中, 显微物镜汇聚光斑与衍射小孔之间对准误差对波前误差、衍射强度、干涉条纹对比度产生影响, 而导致实际测量精度降低的问题, 本文提出一种衍射小孔可视对准方法, 借助电荷耦合器件和分光棱镜在小孔衍射前端搭建辅助对准光路, 通过对小孔衍射板反射图像进行采集及处理来监测小孔对准状态并计算对准误差. 文中设计了可视精密对准光路方案, 仿真分析了平移、倾斜以及离焦三种典型对准偏差下对准图像的视觉表现, 构建了对准图像与对准误差之间物像关系数学模型, 研究了对准图像处理算法. 经原理性验证实验表明, 本文所提辅助光路对准方法和对准图像处理算法可行, 对准精度可达到0.05 μm. 研究成果有利于提高点衍射干涉仪的对准效率和精度, 可为实用点衍射干涉仪开发奠定一定的技术基础.Abstract: In the construction of the pinhole point diffraction interferometer, the alignment error between the convergent spot of the microscopic objective lens and the diffraction hole in the front end of the pinhole diffraction will lead to problems such as diffraction wavefront error, diffraction intensity reduction, and interference fringe contrast reduction, which will affect the actual measurement accuracy. In order to solve the problem of inaccurate alignment between the convergent spot of the microscopic objective lens and the diffraction hole, a diffraction hole visual alignment method based on the auxiliary optical path is proposed in this work. An auxiliary alignment optical path is built at the front end of the pinhole diffraction, and the beam reflected by the pinhole diffraction plate is mainly reflected by the beam splitter prism, and then received by a charge coupled device (CCD). By collecting and processing the spot image reflected by the small hole diffraction plate, the alignment state of the small hole is monitored and the alignment error is calculated. In this work, a visual-precision optical path alignment scheme is designed, and the visual performance of the alignment image under three typical alignment deviations of translation, tilt and defocus is simulated and analyzed. The mathematical model of the object-image relationship between the alignment image and the alignment error is constructed, and the alignment image error measurement and processing algorithm is studied. The experimental results show that the auxiliary optical path alignment method and the alignment image processing algorithm proposed in this work are feasible, and the alignment accuracy can reach 0.05 μm. The research results are helpful in improving the alignment efficiency and accuracy of point diffraction interferometer, and can lay a certain technical foundation for the development of practical point diffraction interferometer.
-
Key words:
- point diffraction interferometer /
- diffraction pinhole /
- visual alignment /
- alignment error .
-
-
图 1 辅助对准光路原理示意图
Figure 1. Schematic diagram of the principle of auxiliary alignment optical path.
图 2 不同对准状态示意图 (a)完全对准; (b)离焦; (c)平移; (d)倾斜
Figure 2. Schematic diagram of different alignment states: (a) Fully aligned; (b) defocused; (c) translation; (d) inclination
图 3 不同对准状态下的可视图像示意图 (a)完全对准; (b)离焦; (c)平移; (d)倾斜
Figure 3. Visual images in different alignment states: (a) Fully aligned; (b) defocus; (c) translation; (d) inclination.
图 5 不同偏离情况下的仿真图像 (a)同心; (b)右偏; (c)左偏
Figure 5. The simulation images under different deviations: (a) Concentric; (b) right-deviated; (c) left-deviated.
图 6 对准图像中心提取结果 (a)同心; (b)右偏; (c)左偏
Figure 6. The center extraction results of alignment image: (a) Concentric; (b) right-deviated; (c) left-deviated.
表 2 仿真图像中心提取像素坐标
Table 2. Pixel coordinates extracted from the center of the simulation image.
下载: 导出CSV
-
[1] Patrick P N, Kenneth A G, Sang H L 1999 Appl. Opt. 38 7252 doi: 10.1364/AO.38.007252 [2] 王同盟, 高芬, 李兵 2024 光学精密工程 32 208 doi: 10.37188/OPE.20243202.0208 Wang T M, Gao F, Li B 2024 Opt. Precis. Eng. 32 208 doi: 10.37188/OPE.20243202.0208 [3] 张金鹏, 高芬, 李兵 2022 光子学报 51 0412004 doi: 10.3788/gzxb20225104.0412004 Zhang J P, Gao F, Li B 2022 Acta Photonica Sin. 51 0412004 doi: 10.3788/gzxb20225104.0412004 [4] Shan M G, Yin Z Y, Zhong Z, Liu B, Yu L, Liu L 2024 Phys. Scr. 99 065118 doi: 10.1088/1402-4896/ad491f [5] Zheng D H, Ma Z Y, Zhang Z, Hu C H 2023 Appl. Opt. 62 745 doi: 10.1364/AO.479044 [6] Yang X, Guo R H, Tang X, Yin Z Y, Liu C X, Li J X 2021 Appl. Opt. 60 10988 doi: 10.1364/AO.441563 [7] 毛姗姗, 李艳秋, 刘克, 刘丽辉, 郑猛, 闫旭 2019 红外与激光工程 48 0814002 doi: 10.3788/IRLA201948.0814002 Mao S S, Li Y Q, Liu K, Liu L H, Zheng M, Yan X 2019 Infrared Laser Eng. 48 0814002 doi: 10.3788/IRLA201948.0814002 [8] 张宇, 金春水, 马冬梅, 王丽萍 2012 红外与激光工程 41 3384 Zhang Y, Jin C S, Ma D M, Wang L P 2012 Infrared Laser Eng. 41 3384 [9] Feng P, Tang F, Wang X Z, Lu Y J, Xu J H, Guo F D, Zhang G X 2020 Appl. Opt. 59 3093 doi: 10.1364/AO.387540 [10] 郑东晖, 李金鹏, 陈磊, 朱文华, 韩志刚, 乌兰图雅, 郭仁慧 2016 物理学报 65 114203 doi: 10.7498/aps.65.114203 Zheng D H, Li J P, Chen L, Zhu W H, Han Z G, Wulan T Y, Guo R H 2016 Acta Phys. Sin. 65 114203 doi: 10.7498/aps.65.114203 [11] Nicolás D, Ali N B, Marc D, Myers R M 2022 Appl. Opt. 61 4160 doi: 10.1364/AO.439569 [12] Lu J S, Li B, Zhao Z, Geng L Q 2022 Opt. Lett. 47 4877 doi: 10.1364/OL.465189 [13] Smartt R N, Steel W H 1985 Appl. Opt. 24 1402 doi: 10.1364/AO.24.001402 [14] Otaki K, Yamamoto T, Fukud Y, Ota K, Nishiyama I, Okazaki S 2002 J. Vac. Sci. Technol., B 20 295 doi: 10.1116/1.1445161 [15] 卢毅伟, 骆永洁, 刘维, 孔明, 王道档 2023 红外与激光工程 52 20220593 doi: 10.3788/IRLA20220593 Lu Y W, Luo Y J, Liu W, Kong M, Wang D D 2023 Infrared Laser Eng. 52 20220593 doi: 10.3788/IRLA20220593 [16] Sun Y, Shen H, Li X, Li J, Gao J M, Zhu R H 2019 Appl. Opt. 58 1253 doi: 10.1364/AO.58.001253 [17] 冯鹏, 李中梁, 王向朝, 步扬, 卢云君, 郭福东, 李思坤 2022 中国激光 49 2104001 doi: 10.3788/CJL202249.2104001 Feng P, Li Z L, Wang X C, Bu Y, Lu Y J, Guo F D, Li S K 2022 Chin. J. Lasers 49 2104001 doi: 10.3788/CJL202249.2104001 [18] Gao F, Jiang Z D, Zhao Z, Li B 2015 Opt. Eng. 54 014102 doi: 10.1117/1.OE.54.1.014102 [19] Geng L Q, Li B, Zhao Z, Lu J S 2024 Opt. Laser Eng. 178 108198 doi: 10.1016/j.optlaseng.2024.108198 [20] Ota K, Yamamoto T, Fukuda Y, Otaki K, Nishiyama I, Okazaki S 2001 Proc. SPIE 4343 543 doi: 10.1117/12.436686 [21] Zhao Z, Li B, Kang X Q, Chen L, Wei X 2019 Appl. Opt. 58 3703 doi: 10.1364/AO.58.003703 [22] 高芬, 蒋庄德, 李兵 2014 光学学报 34 0812004 doi: 10.3788/AOS201434.0812004 Gao F, Jiang Z D, Li B 2014 Acta Opt. Sin. 34 0812004 doi: 10.3788/AOS201434.0812004 -
计量
- 文章访问数: 65
- HTML全文浏览数: 65
- PDF下载数: 1
- 施引文献: 0