超声悬浮是地面条件下模拟空间无容器环境的一种重要实验方法^[1–10]. 它利用高强声场产生的声辐射压力来平衡物体的重力, 从而实现物体的稳定悬浮. 与电磁悬浮、静电悬浮等其他悬浮技术相比, 超声悬浮具有悬浮和加热独立控制的特点, 且对样品的电学和磁学性质没有限制, 因而可以处理金属材料、陶瓷材料等不同类型的材料. 在过冷态液体的热物理性质测定^[11–15]、凝固过程动力学^[16–22]、液体运动规律研究^[23]等领域^[24,25]具有广泛的应用.

超声悬浮方法是研究过冷液体形核和结晶规律的一种重要方法^[26,27]. Trinh等^[6]使用声悬浮技术实现了低熔点金属(In, Ga, Sn)以及非金属(o-terthyenyl)的过冷与凝固, 并观察到晶体的形核和生长始于表面. Ohsaka与Trinh^[28]在声悬浮条件下完成了丁二腈的熔化和凝固, 发现形核首先从液滴的表面开始, 并以枝晶的方式生长. Lü等^[20]使用声悬浮技术实现了大体积水的深过冷快速凝固, 并利用统计的方法得到了两个声压幅值下水的过冷度分布, 发现声压的增强不利于水的过冷.

上述研究工作主要针对金属和非金属单质, 且实验缺少对超声场的调控, 只研究了在极大和极小声压幅值下金属和非金属单质的凝固规律, 所以对于不同声场条件下合金液滴的液态过冷能力以及结晶规律尚不清晰, 有待进一步研究. 因此, 本文采用超声悬浮方法, 实现了丁二腈-樟脑(SCN-DC)透明合金的快速凝固, 同时借助高速CCD和红外热像仪, 对凝固过程中液滴的温度变化和晶体生长过程进行记录, 分析了不同径厚比下SCN-DC合金的过冷能力和晶体生长规律, 揭示了超声悬浮对合金的液态过冷能力以及结晶过程的影响机制.

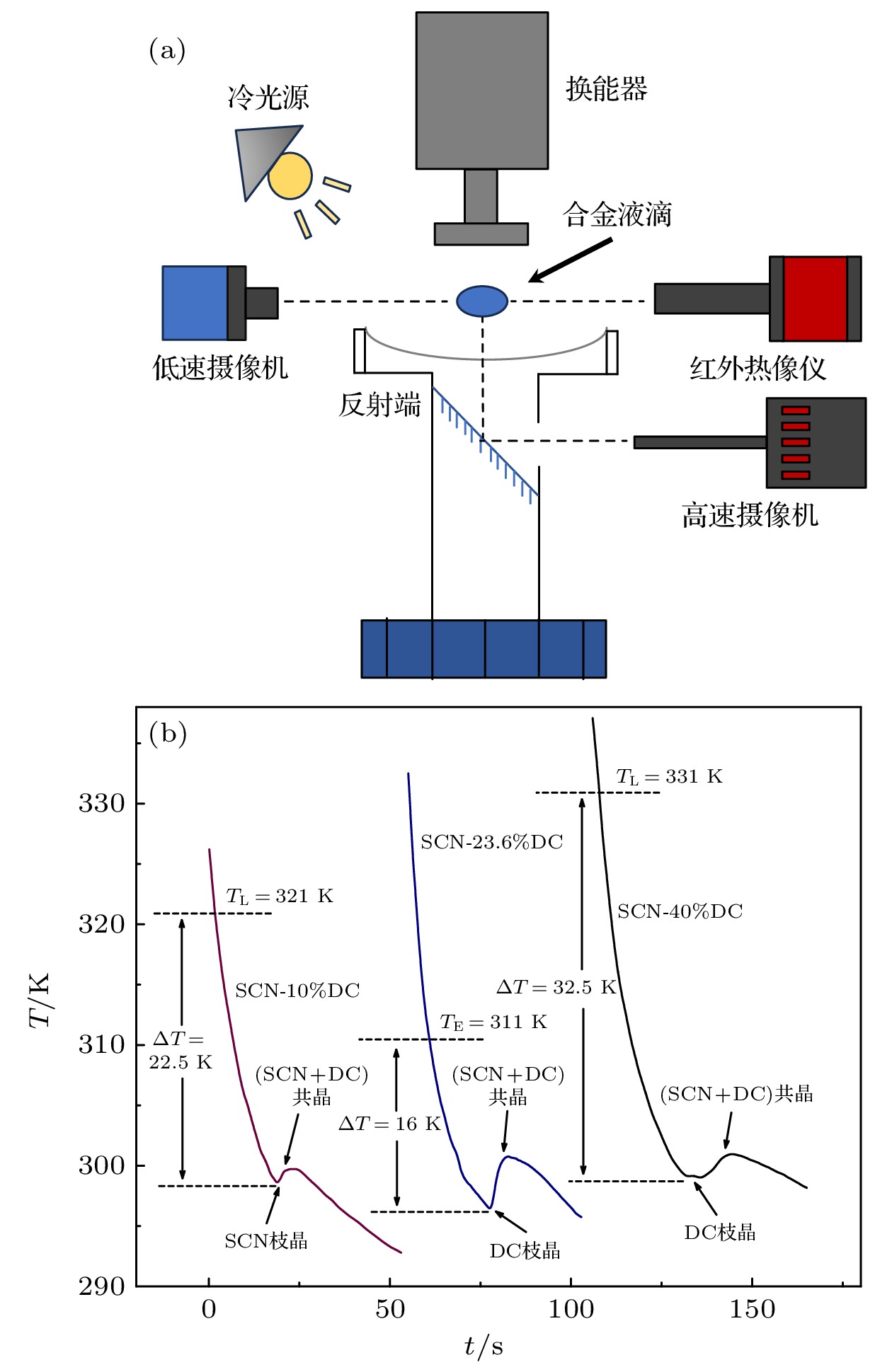
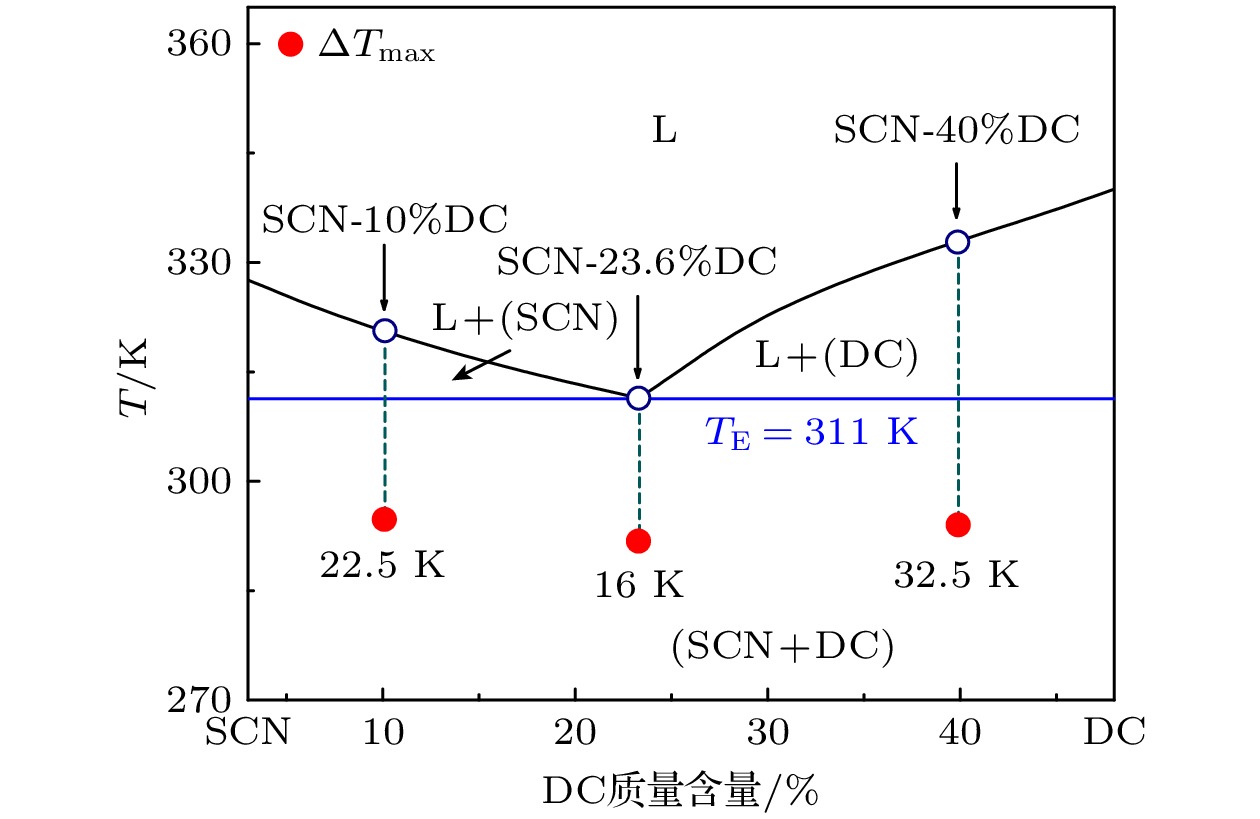
二元SCN-10%DC亚共晶合金、SCN-23.6%DC共晶合金和SCN-40%DC过共晶合金的母合金, 均由纯度为99%的丁二腈和97%的樟脑在323 K下低温排气烘干后按照一定比例在试管中水浴加热制成. 三种合金在相图中位置如图1所示^[29]. 水浴温度高于合金液相线大约10 K并保温1 min, 在保温过程中轻微摇晃试管. 保温完成后将液滴加热至353 K用于超声悬浮实验. 使用单轴式超声悬浮装置进行实验. 图2(a)是本文所用的单轴式超声悬浮装置的结构示意图, 主要由超声波发生系统、悬浮控制系统和成像系统组成, 声悬浮的工作频率为22 kHz. 反射端使用一个等厚光学玻璃, 反射端下方支架处的反射镜以45°放置, 并在样品斜上方使用LED冷光源进行照明以提高成像质量. 使用高速CCD (Photron FASTCAM Mini UX100, Japan) 对合金液滴的结晶过程进行实时记录, 高速CCD的拍摄速率为500 f/s. 使用一个低速摄像机(SunTime T240C)对合金液滴侧面轮廓信息进行记录, 用于计算合金液滴的径厚比, 低速摄像机拍摄速率为30 f/s. 使用红外热像仪(InfraTec IR5300, Germany)监测合金液滴结晶过程中温度的变化. 热像仪的拍摄速率为50 f/s. 图2(b)是红外热像仪记录的温度曲线, 对于SCN-10%DC亚共晶合金, 两次拐点对应SCN枝晶和(SCN+DC)共晶的生长, 对于SCN-23.6%DC共晶和SCN-40%DC过共晶合金, 温度曲线的拐点对应DC枝晶和(SCN+DC)共晶的生长. 实验中使用移液枪吸取30 μL合金液滴, 将其悬浮在声压节点处, 然后调节发射端反射端间距使其稳定.

本文采用有限元方法, 通过求解Helmholtz方程并耦合Navier-Stokes (N-S)方程计算合金液滴内外的声流分布. 计算模型中, 发射端半径为12 mm, 反射端半径为20 mm, 反射端端面曲率半径为40 mm, 且发射端反射端间距为34.5 mm. 采用四面体网格剖分, 共包含约180000个单元, 合金液滴内部网格最大和最小单元尺寸分别为0.25 mm和0.1 mm, 液滴外部采用预定义的较细化网格. 样品表面采用阻抗边界条件, 发射端端面法向振幅为15 μm, 反射端表面为硬声场边界, 整个声场的外边界采用柱面波辐射条件.

样品表面的声辐射压$ {{P}}_{\text{r}} $表示为^[23]

式中, $ {p} $是声压; $ {\rho}_{0}{\mathrm{是}} $空气密度; $ {{c}}_{0} $是空气声速; $ \boldsymbol{v} $表示介质中粒子的速度; $ \left\langle{\cdots }\right\rangle $表示时间平均.

静态条件下由超声场引起的气相中声流分为两部分, 即黏性边界层内部声流和外部声流. 其中黏性边界层内部声流的稳态极限速度$ {\boldsymbol{v}}_{\text{a}} $定义为^[3]

式中, $ { \omega } $是角频率; $ {{\boldsymbol{P}}} $为投影算符; $ {{ \varGamma }}_{\text{d}} $为液滴表面; $ {\boldsymbol{v}}_{\text{g}} $为速度$ \boldsymbol{v} $的幅值. 将$ {\boldsymbol{v}}_{\text{a}} $作为黏性边界层外部声流稳态极限速度$ {\boldsymbol{v}}_{\text{d}} $的切向滑移条件代入, 可得

$ {{R}}_{\text{s}} $为液滴的等效半径. $ {\eta}_{\text{L}} $是合金黏度, $ {\eta}_{0} $是空气黏度. 将$ {\boldsymbol{v}}_{\text{a}} $和$ {\boldsymbol{v}}_{\text{d}} $分别带入N-S方程求解分别获得外部声流和内部声流. 计算模拟过程中所使用的具体参数详列于表1.

超声悬浮液滴由于受到重力及不均匀声辐射压力而呈扁球状或圆饼状, 液滴变形程度可以由径厚比γ (γ = d/δ)表示, 其中d表示液滴赤道直径, δ表示液滴厚度. King的理论表明, 声场中液滴所受声压的非线性项的时间平均称为声辐射压$ {{P}}_{\text{r}} $. 基于球形波函数, 声辐射压由以下公式给出^[29]:

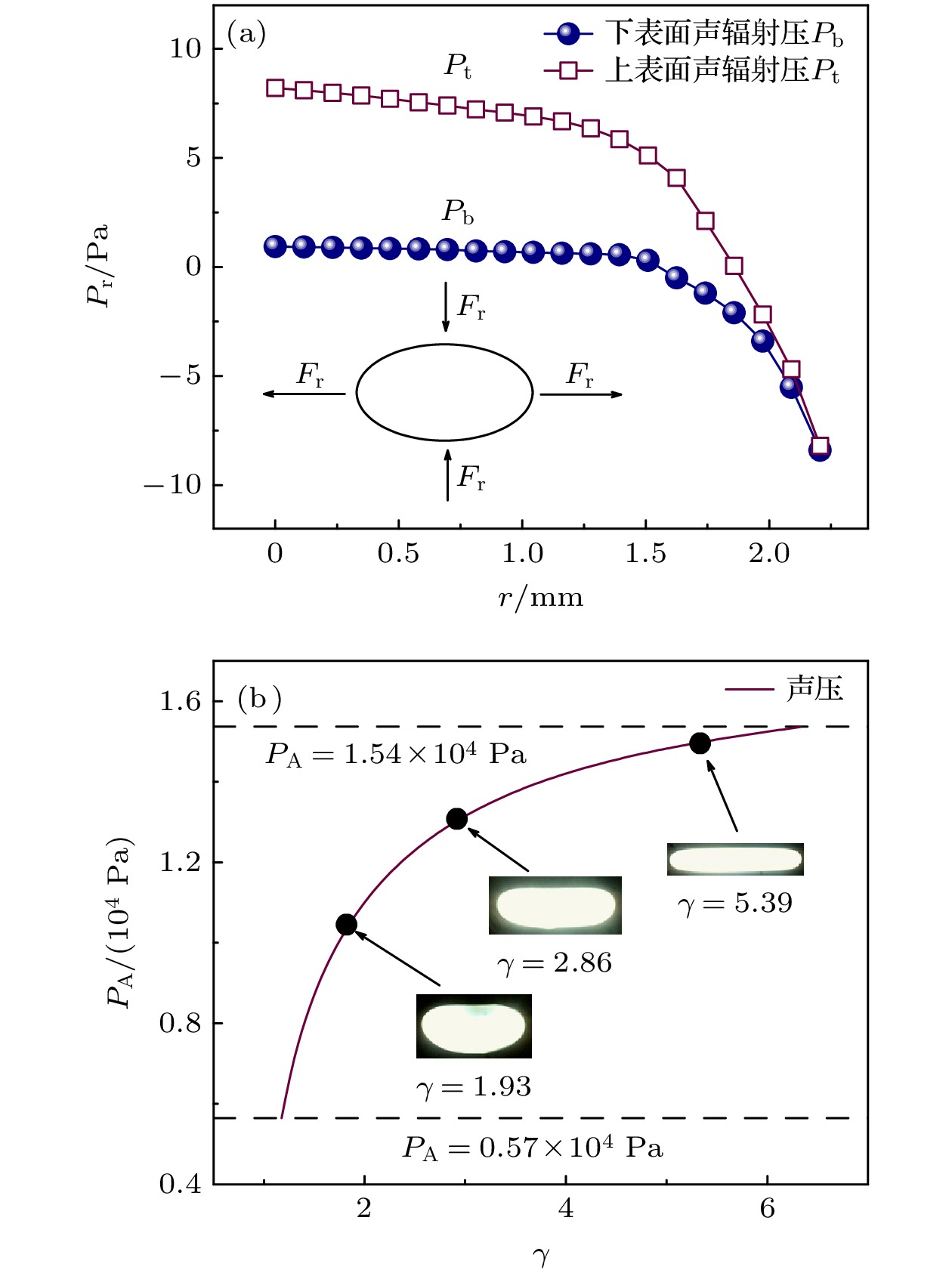
式中, $ {{P}}_{\text{A}} $是声压幅值, $ {k} $是波数, $ {x} $是悬浮液滴的纵坐标, $ {{R}}_{\text{s}} $是液滴的等效半径, $ {r} $是液滴表面的径向位置. (5)式决定液滴最终的形状, 它关于液滴上下表面是对称的. (6)式对液滴悬浮起决定作用. 通过(4)式计算得到样品上下表面声辐射压分布, 如图3(a)所示. 通过计算可以得到γ = 2时合金液滴上下表面中心处的声辐射压分别为0.94 Pa和8.21 Pa, 边缘处的声辐射压幅值大小为8.3 Pa. 由于声辐射压的作用, 合金液滴克服重力, 以椭球形稳定悬浮在空气中.

Marston利用线性无黏理论计算了声辐射压对可压缩球体的影响, 给出了超声悬浮液滴的平衡形状与声压的关系^[30]:

式中, $ {{r}}_{\text{s}} $是液滴表面到液滴中心的距离; $ \theta$是极角; $\sigma $是液滴的表面张力. 由(7)式可知超声悬浮液滴形状由声压幅值$ {{P}}_{\text{A}} $决定.

在超声悬浮条件下, 对于一个特定的合金, 声压幅值$ {{P}}_{\text{A}} $满足$ {{P}}_{\text{m}}\leqslant {{P}}_{\text{A}}\leqslant {{P}}_{\text{M}} $, 其中$ {{P}}_{\text{m}} $是可以悬浮此合金的最小声压幅值, $ {{P}}_{\text{M}} $是确保合金稳定悬浮的最大声压幅值. Danilov和Mironov给出了临界声压幅值$ {{P}}_{\text{m}} $和$ {{P}}_{\text{M}} $的表达式^[30,31]:

式中, $ {\rho }_{\text{s}} $是合金的密度. 对于SCN-23.6%DC共晶合金, $ {{P}}_{\text{m}}= 0.565 \times{10}^{4} $Pa, $ {\text{}{P}}_{\text{M}}={1.536}\times{10}^{4} $ Pa, SCN-23.6%DC合金的热物理性质参数以及计算所需物理参数由表1给出.

由(7)式, 可以得到径厚比γ$ ={{r}}_{\text{s}}\left(\text{π}/2\right)\text{/}{{r}}_{\text{s}}\text{(0)} $. 使用表1的参数计算得到液滴变形程度与声压的关系如图3(b)所示. 由图3(b)发现, 合金的径厚比随声压的增加而逐渐变大, 液滴形状由近球形变为扁球形, 最后变为圆饼状, 此时, 合金液滴顶部和底部中心处从凸面变为凹面.

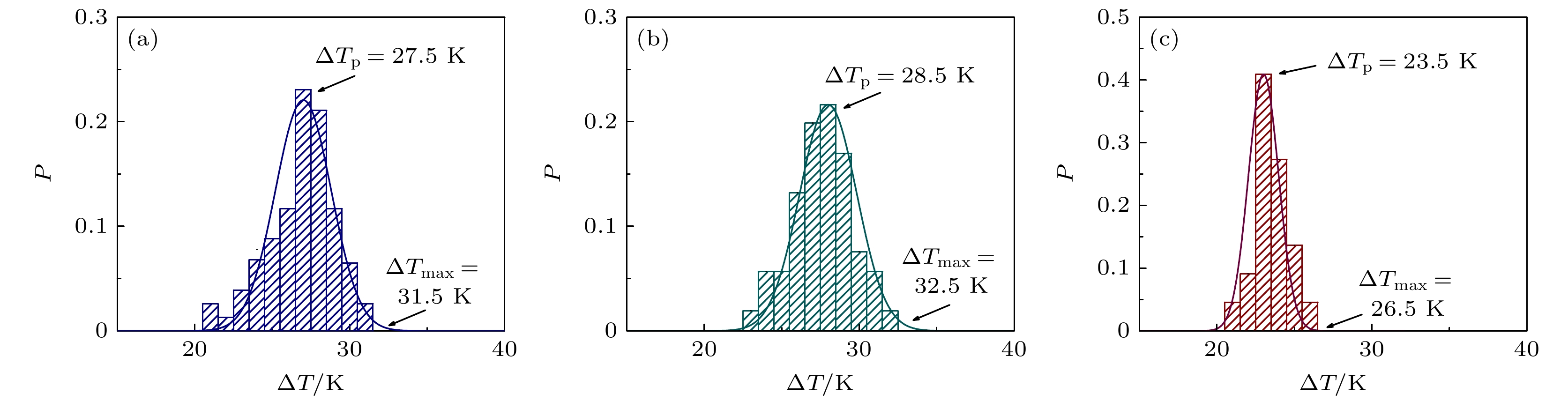
在超声悬浮条件下, 声场的作用直接影响合金的液态过冷. 实验发现SCN-10%DC亚共晶、SCN-23.6%DC共晶和SCN-40%DC过共晶获得的最大过冷度分别为22.5 K, 16 K和32.5 K.

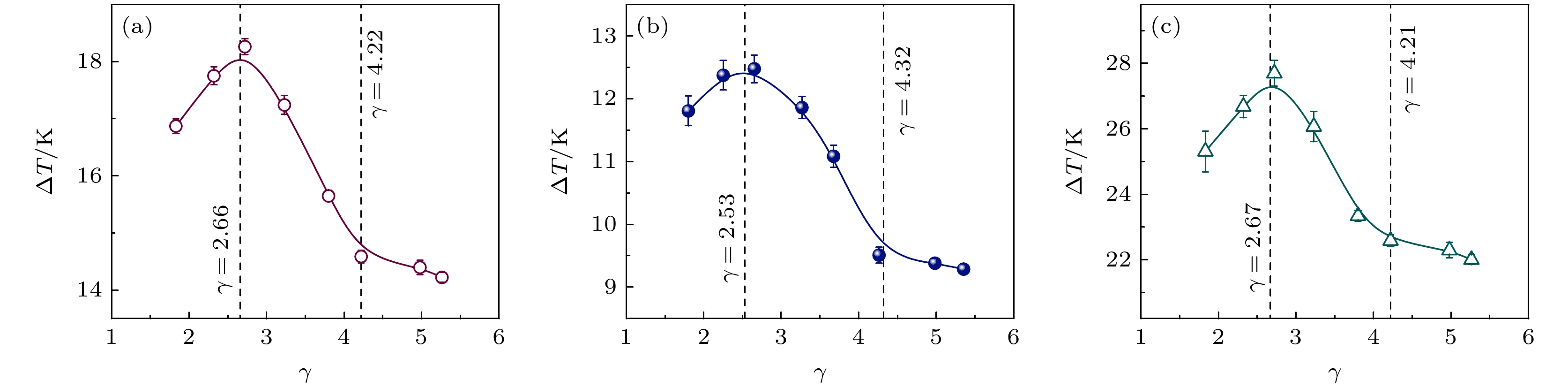
图4是合金液滴过冷度随径厚比γ的变化曲线. 每个合金成分分别进行357, 386和378次实验. 图4中的每一个点均是30—50个数据点的平均值, 每个点的数据范围为[$ \gamma -0.1, \text{}\gamma +0.1 $].

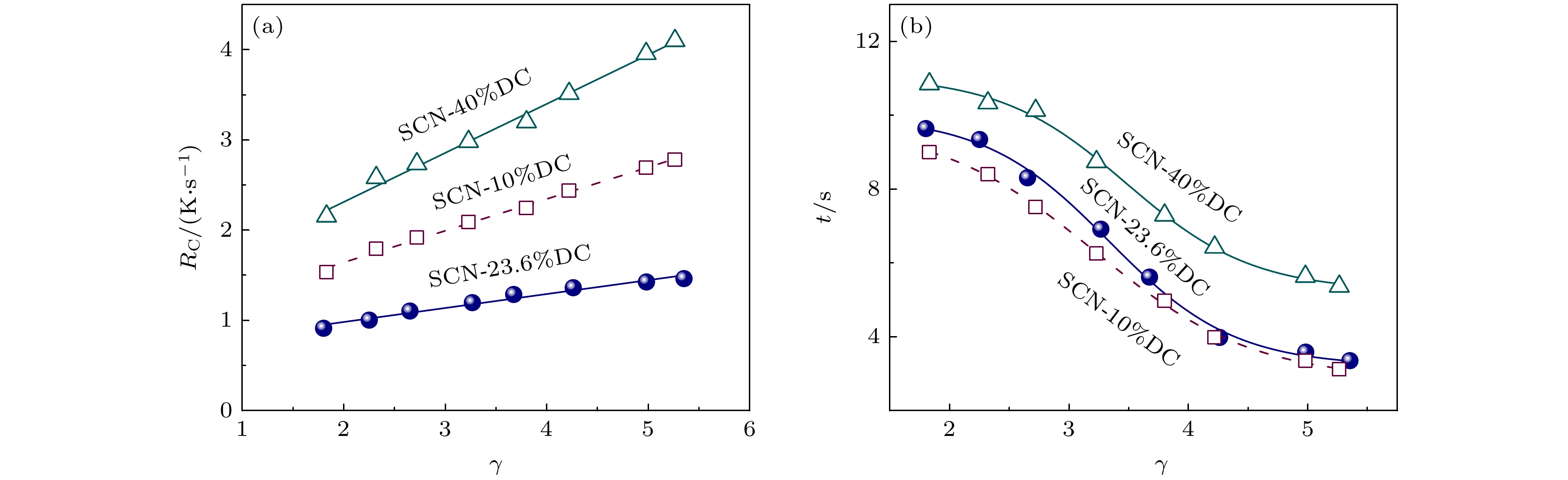
从过冷度分布来看, SCN-10%DC亚共晶、SCN-23.6%DC共晶和SCN-40%DC过共晶平均过冷度分布在14—18 K, 9—12.5 K和22—28 K之间. 从过冷度变化趋势来看, 随着液滴径厚比$ \gamma $的增加, SCN-10%DC亚共晶合金、SCN-23.6%DC共晶合金和SCN-40%DC过共晶合金的过冷度都呈现先增加后减小最后基本不变的趋势. 对于SCN-10%DC亚共晶合金, 当$ \gamma $ < 2.66时液滴的平均过冷度随径厚比的增加逐渐变大, 2.66 < $ \gamma $ < 4.22时液滴平均过冷度随径厚比的增加而逐渐减小, $ \gamma $ > 4.22时合金液滴平均过冷度逐渐趋于稳定. 对于SCN-23.6%DC共晶合金, $ \gamma $ < 2.53时液滴的平均过冷度随径厚比的增加逐渐变大, 2.53 < $ \gamma $ < 4.32时液滴的平均过冷度随径厚比的增加而逐渐减小, $ \gamma $ > 4.32时, 液滴的平均过冷度逐渐趋于稳定. 对于SCN-40%DC过共晶合金, $ \gamma $ < 2.67时液滴的平均过冷度随径厚比的增加逐渐变大, $ 2.67\text{ < }\gamma \text{ < }4.21 $时液滴的平均过冷度随径厚比的增加而逐渐减小, $ \gamma $ > 4.21时, 液滴的平均过冷度逐渐趋于稳定.

鉴于合金液滴过冷度随径厚比γ变化呈现出特定规律, 为揭示其背后成因, 计算了合金液滴平均冷却速率和形核孕育时间随径厚比$ \gamma $的变化关系, 如图5所示. 将实验中获得的最小过冷度液滴的形核温度记为$ {{T}}_{\text{N}} $, 从333 K降温到$ {{T}}_{\text{N}} $所需要的时间为$ {{t}}_{\text{n}} $, 定义冷却速率为$ {{R}}_{\text{c}}=\left(333-{{T}}_{\text{N}}\right)\text{/}{{t}}_{\text{n}} $. 对于SCN-10%DC亚共晶合金, $ {{T}}_{\text{N}}=309\text{}\text{ K} $; 对于SCN-23.6%DC共晶合金, $ {{T}}_{\text{N}}=304\text{}\text{ K} $; 对于SCN-40%DC, $ {{T}}_{\text{N}}=312\text{}\text{ K} $. 将合金液滴从液相线$ {{T}}_{\text{L}} $降温到开始结晶经历的时间记为形核孕育时间t_ges. 发现合金液滴的冷却速率随径厚比$ \gamma $的增加呈上升趋势, 而形核孕育时间随径厚比$ \gamma $增加而逐渐降低. 以SCN-40%DC为例, 当$ \gamma $ < 2.67时, 合金液滴冷却速率随径厚比$ \gamma $的增加而逐渐增大, 而形核孕育时间几乎保持不变. 所以过冷度随径厚比$ \gamma $的增加而逐渐变大, 此时冷却速率的增加是提高合金液滴过冷度的主要因素. 当2.67 < γ < 1时, 合金液滴的冷却速率随径厚比γ的增加而进一步增大, 形核孕育时间随径厚比γ的增加呈下降趋势, 但形核孕育时间下降产生的过冷度减小要大于冷却速率升高促使的过冷度增加. 这是因为随着声场的增强, 合金液滴表面积逐渐增大, 而表面形核率与表面积成正比, 所以表面形核率也逐渐增大. 且声场增强导致液滴表面产生振动, 也会成为异质形核的位点, 所以合金液滴过冷度逐渐下降. 当γ > 4.21时, 液滴的冷却速率仍随径厚比γ的增加而逐渐增大, 形核孕育时间随径厚比$ \gamma $的增加呈下降趋势, 但是下降的趋势变缓. 这是因为在强声场条件下, 声场会给处于过冷态的合金熔体提供克服形核势垒的能量, 此时通常也会伴随着合金液滴的剧烈振动, 这会使合金液滴提前进入形核阶段, 极大地抑制深过冷的获得. 一旦合金液滴过冷到一定程度, 会立即形核. 这导致了液滴过冷度在径厚比γ > 4.21时趋于不变. 基于以上分析发现, 合金液滴径厚比较小时, 冷却速率增加是影响其过冷度的主要因素, 随着径厚比的增大, 表面形核率的增加以及液滴的振动抑制了深过冷的获得, 随着径厚比的进一步增加, 合金液滴的剧烈振动使其过冷度逐渐趋于不变.

为了进一步探究超声悬浮条件下合金液滴的形核规律, 对合金液滴在不同过冷度下的形核概率(液滴在某个过冷度下的形核事件数目与总形核事件数目之比)进行统计. 合金液滴的形核过程遵循一定的统计规律, 因此合金液滴的过冷度分布也具有一定的统计规律. 由于SCN-40%DC合金液滴过冷度分布范围较广, 且数据分布较为平均, 所以选取此合金液滴统计形核概率分布. 计算了平均径厚比$ \gamma $ = 2.3, 3.2, 4.1时, 合金液滴的形核概率与过冷度的关系, 每个径厚比$ \gamma $都有80—90个数据点, 数据范围为[$ \gamma -0.2, \text{}\gamma +0.2 $]. 图6为SCN-40%DC合金液滴在平均径厚比$ \gamma $ = 2.3, 3.2, 4.1时过冷度分布规律.

在所有的形核温度中均统计单位温度间隔内的形核事件数目, 纵轴形核概率P指的是在$ [{T}-{0.5, }\;{T}+0.5] $的温度间隔内形核事件的数目$ {{N}}_{\text{n}} $与总的形核事件的数目$ {{N}}_{\text{t}} $之比, 即$ {P}\text{[}{T}-{0.5, } {T}+{0.5]}={{N}}_{\text{n}}\text{/}{{N}}_{\text{t}} $. 统计结果表明, 当径厚比$ \gamma $ = 3.2时, 合金液滴的形核分布比较分散, 覆盖的温度区间为20—32 K. 当径厚比$ \gamma $ = 4.1时, 合金熔体的形核分布较窄, 覆盖的温度区间为20—26 K.

由于在$ \left[{\Delta }{T}, \text{}{\Delta }{T}{+\text{δ}}{T}\right] $过冷度间隔内的形核概率为^[20]

根据经典形核理论, $ { \omega }{(\Delta }{T}) $为如下表达形式:

式中, A和B是两个独立参数, 其中

N表示单位形核区域内SCN-DC分子的数目, h是Plank常量, D是形核区域尺寸. 将(11)式代入(10)式并对实验数据进行拟合可得径厚比γ = 2.3, 3.2, 4.1时, A的值分别为1.08×10⁶, 1.23×10⁶, 1.88×10⁶, B的值分别为8.62×10⁴, 8.36×10⁴, 6.23×10⁴. 参数A是一个与形核区域尺寸相关的参数, 可以发现当径厚比γ从2.3变为3.2再变为4.1时, 表面积分别增加了1.12倍和1.5倍. 而参数A的值分别增加了1.14和1.74倍. 这就说明当合金液滴径厚比γ较小时, 形核主要集中在合金液滴表面. 当合金液滴径厚比γ越来越大, 近表面区域也会成为一个形核区域. 参数B实际上度量了形核激活能的大小, 随着液滴径厚比γ越来越大, B的值越来越小, 这表明高强度声压引起的合金液滴振动能够显著降低形核激活能, 使形核更容易发生.

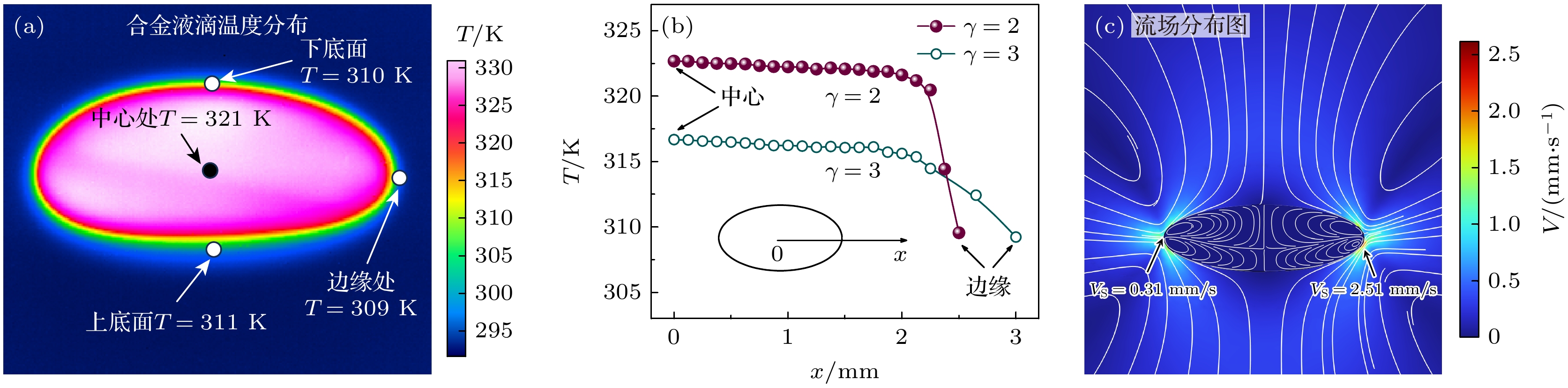
为了进一步解释合金液滴的表面形核, 对合金液滴的温度场与流场进行了分析. 通过分析不同径厚比$ \gamma $的合金液滴沿纵截面上的温度分布, 如图7(a)和图7(b)所示, 发现赤道面表面处温度最低, 中心温度最高. 近表面区域的温度梯度较大, 且随着径厚比$ \gamma $的增加, 边缘区域和中心区域的温差逐渐减小. 由于合金液滴表面的温度总是低于内部温度, 所以形核总是发生在表面.

图7(c)是Comsol软件计算的γ = 3时合金液滴内外部流场分布. 合金液滴内部赤道面边缘处的流速较大, 中心处流速较慢, 最大流速为0.31 mm/s. 合金液滴外部声流也是近赤道面处较大, 而极点处较小, 最大流速为2.51 mm/s. 随着径厚比$ \gamma $的增加, 合金液滴内外部流速都会增大. 所以在超声悬浮条件下: 一方面, 合金液滴周围空气流动随径厚比γ的增加逐渐加剧, 空气和合金液滴表面之间的对流换热逐渐加强, 表面温度降低变快. 另一方面, 合金液滴近表面处液相流动速度较快, 会将热量迅速的带到液滴表面向周围环境释放. 而内部的热量要通过合金液滴表面向周围环境释放, 于是在合金液滴径向方向形成温度梯度. 且随着径厚比γ的增加, 因为液滴形状逐渐变扁, 内部液体流动速度以及外部空气流动的速度变得越来越快, 温度梯度就会越来越小. 所以当径厚比γ较大时, 合金液滴近表面区域也会成为一个的形核区域.

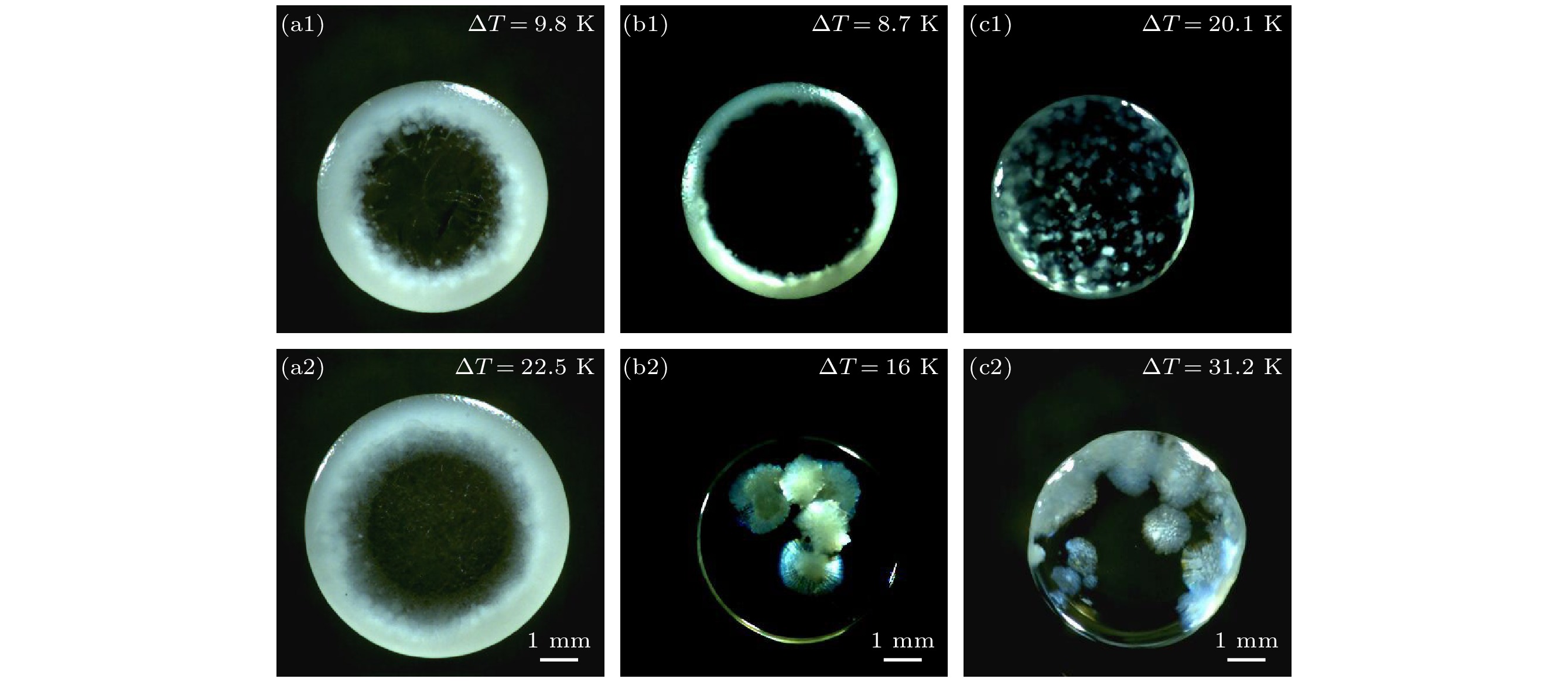
使用红外热像仪以及高速CCD分别记录合金液滴冷却结晶时温度的变化和液固界面迁移的 过程. 图8(a)是过冷度ΔT = 9.8 K和22.5 K时SCN-10%DC亚共晶合金凝固组织, 可以发现过冷度ΔT＜18.6 K时, 初生SCN枝晶总是从边缘往中间凝固, 随着过冷度的增加, SCN枝晶逐渐细化. 当过冷度ΔT＞18.6 K时, SCN枝晶会在过冷熔体的表面随机形核, 不再具有生长方向性. 图8(b)是过冷度ΔT = 8.7 K和16 K时SCN-23.6%DC共晶合金凝固组织, 当过冷度ΔT＜12.6 K时, 形核总是发生在液滴边缘, 并以相同的速度向中心生长, 直至完全凝固. 当过冷度ΔT＞12.6 K时, DC枝晶优先形核生长, (SCN+DC)共晶依附在枝晶上生长. 图8(c)是过冷度ΔT = 20.1 K和31.2 K时SCN-40%DC过共晶合金凝固组织, 当ΔT = 20.1 K时, 初生DC枝晶形核呈现一定的随机性, 但是边缘处的形核概率要明显大于中心处. 枝晶生长界面较为尖锐, 各向异性强. 当过冷度ΔT = 31.2 K时, DC枝晶的形核率明显下降, 枝晶生长界面较为平滑, 可以认为DC枝晶生长的各向异性明显减弱.

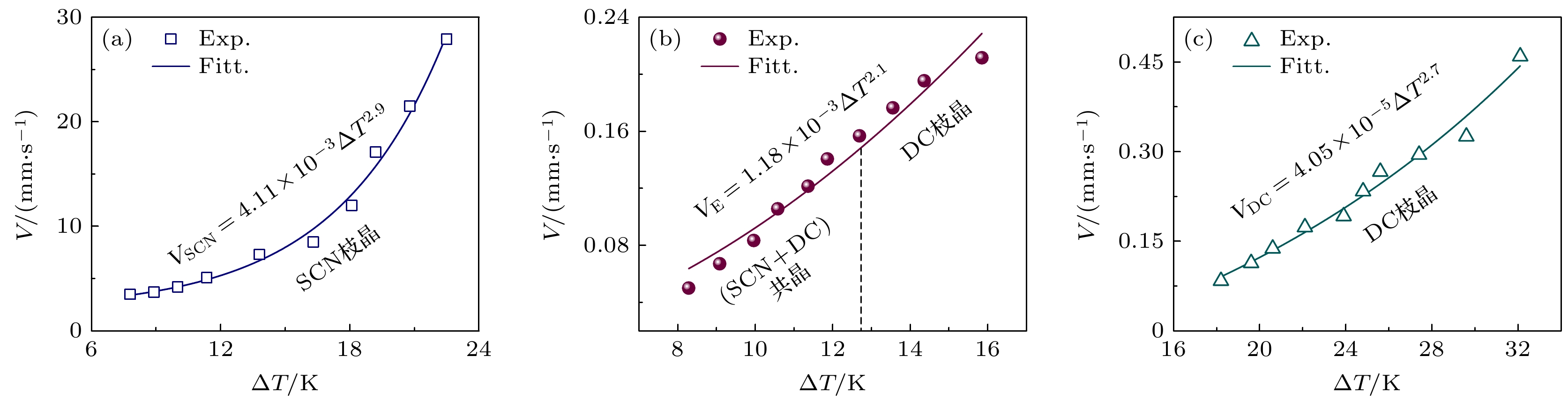
枝晶和共晶生长速度$ {V}\text{}=\text{}{D}{\text{/}{t}}_{\text{r}} $, D是合金液滴尺寸, $ {{t}}_{\text{r}} $是第一次再辉时间. SCN枝晶、(SCN+DC)两相共晶和DC枝晶的生长速度与过冷度ΔT之间的关系分别为

图9是SCN-10%DC亚共晶合金SCN枝晶生长速度、SCN-23.6%DC共晶合金(SCN+DC)共晶生长速度以及SCN-40%DC过共晶合金DC枝晶生长速度随过冷度变化曲线. 结果表明, SCN枝晶、(SCN+DC)两相共晶和DC枝晶的生长速度都随着过冷度的增加而单调增大, SCN枝晶的最大生长速度为$ {{V}}_{\text{SCN}} $= 27.91 mm/s, 对应的过冷度为22.5 K. (SCN+DC)两相共晶最大生长速度$ {{V}}_{\text{E}} $ = 0.21 mm/s, 对应的过冷度为16 K. DC枝晶的最大生长速度为$ {{V}}_{\text{DC}} $= 0.45 mm/s, 对应的过冷度为32.5 K.

在超声悬浮无容器状态下, 实现了SCN-DC透明合金的快速凝固. 结合高速CCD和红外热像仪, 对不同径厚比γ的合金液滴过冷度分布以及结晶规律进行了研究, 得出以下结论.

1) 超声悬浮条件下, 随着声压的增强, 液滴径厚比γ会逐渐增大. 随着径厚比γ的增大, 冷却速率的增加可以提高液滴的过冷度, 而表面形核率的提高和液滴振荡抑制了合金过冷度升高. 这三个因素的耦合作用导致了合金液滴的过冷度随径厚比γ的增加呈现先增大后减小最后基本不变的趋势.

2) 当合金液滴径厚比γ较小时, 形核主要集中在液滴表面. 随着合金液滴径厚比γ的增加, 近表面区域也会成为形核区域. 分析表明, 声流作用和高强度的声压是产生这个现象的主要原因.

3) SCN-10%DC亚共晶、SCN-23.6%DC共晶和SCN-40%DC过共晶合金所获得的最大液态过冷度分别为22.5 K, 16 K和32.5 K, 相应的晶体生长速度为27.91 mm/s, 0.21 mm/s和0.45 mm/s. 随着过冷度的增加, SCN-10%DC亚共晶中SCN枝晶由边缘形核转变为随机形核, SCN-23.6%DC共晶合金中DC枝晶优先形核生长, (SCN+DC)共晶依附在枝晶上生长, SCN-40%DC过共晶中DC枝晶的生长界面由尖锐逐渐变为光滑.