高级搜索

力学约束对锂离子电池双层电极中锂扩散和应力的影响

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

张凯, 徐鹏, 关学锋, 杜玉群, 王轲杰, 陆勇俊. 力学约束对锂离子电池双层电极中锂扩散和应力的影响[J]. 物理学报, 2025, 74(2): 020201-1. doi: 10.7498/aps.74.20241275
引用本文: 张凯, 徐鹏, 关学锋, 杜玉群, 王轲杰, 陆勇俊. 力学约束对锂离子电池双层电极中锂扩散和应力的影响[J]. 物理学报, 2025, 74(2): 020201-1. doi: 10.7498/aps.74.20241275
shu
Kai ZHANG, Peng XU, Xuefeng GUAN, Yuqun DU, Kejie WANG, Yongjun LU. Influence of mechanical constraints on Li diffusion and stress in bilayer electrode of lithium-ion batteries[J]. Acta Physica Sinica, 2025, 74(2): 020201-1. doi: 10.7498/aps.74.20241275
Citation: Kai ZHANG, Peng XU, Xuefeng GUAN, Yuqun DU, Kejie WANG, Yongjun LU. Influence of mechanical constraints on Li diffusion and stress in bilayer electrode of lithium-ion batteries[J]. Acta Physica Sinica, 2025, 74(2): 020201-1. doi: 10.7498/aps.74.20241275
shu

力学约束对锂离子电池双层电极中锂扩散和应力的影响

  • 1.

    中北大学工程力学系, 太原　030051

  • 2.

    中北大学应用化学系, 太原　030051

  • 3.

    西北工业大学工程力学系, 西安　710129

    • 通讯作者: E-mail: kzhang222@163.com.;  E-mail: luyongjun@mail.nwpu.edu.cn.

  • 中图分类号: 02.60.Cb, 82.47.Aa, 82.80.Fk, 46.05.+b

Influence of mechanical constraints on Li diffusion and stress in bilayer electrode of lithium-ion batteries

  • 1.

    Department of Engineering Mechanics, North University of China, Taiyuan 030051, China

  • 2.

    Department of Applied Chemistry, North University of China, Taiyuan 030051, China

  • 3.

    Department of Engineering Mechanics, Northwestern Polytechnical University, Xi’an 710129, China

    • Corresponding authors: E-mail: kzhang222@163.com.;  E-mail: luyongjun@mail.nwpu.edu.cn.

  • MSC: 02.60.Cb, 82.47.Aa, 82.80.Fk, 46.05.+b

  • 摘要: 锂离子电池中的电极总是处于特定的约束当中, 这些约束既包括电池内部不可避免的被动结构约束, 又包括一些新兴技术应用场景可能赋予的外部主动约束. 本文主要利用化学-力学双向耦合的基本假设建立描述双层电极结构的理论模型, 考虑4种不同强弱的理想化变形约束作为其边界条件, 并通过数值求解研究在充电过程中这些外部约束对双层电极中Li扩散和应力的影响. 从力学的角度, 所研究的双层电极结构存在侧向伸缩和弯曲变形两个自由度, 弱化的约束条件能够部分或完全激活这些应力释放机制, 从而降低电极结构整体的应力水平, 并提升结构的力学稳定性. 然而, 从电化学的角度, 电极结构的正向弯曲变形所产生的应力梯度会阻碍嵌Li过程, 强化的约束能够部分或完全抑制电极的正向弯曲, 使活性层内Li浓度更加均匀, 从而提高活性层的容量利用率. 这些结果不仅为进一步理解双层电极在更加真实或极端服役条件下的化学-力学响应提供理论参考, 还从设计的角度表明折中的外部约束有利于平衡电极的结构耐久性和电化学性能.
    Abstract: Lithium-ion batteries (LIBs) are widely used in portable electronic devices, electric vehicles, and other fields. With the rapid development of its application fields, there is an urgent need to further improve its energy density and safety. In the charging/discharging process of the LIBs, the diffusion of Li will cause local volumetric change in the electrode material. The degradation and damage of the electrode material structure caused by diffusion-induced deformation is a major obstacle to the development of LIBs. Generally speaking, the electrode materials in LIBs are always subject to specific external constraints, including both inevitable passive structural constraints within the battery and external active constraints that may be imposed by emerging technology application scenarios, which can also affect the mechanical properties of the electrode materials. Therefore, a more in-depth understanding of the diffusion-induced stress and Li concentration changes in the electrode material is an engineering requirement for developing new material design paradigms to improve the overall performance of LIBs. In this work, a two-way diffusion-stress coupling model is used to discuss the effects of the four different levels of idealized deformation constraints on the Li concentration and stress in the bilayer plate electrode in the charging process through the numerical solution. From a mechanical perspective, the bilayer plate electrode structure has two degrees of freedom: lateral expansion and bending deformation. Weakened constraint conditions can partially or completely activate these stress release mechanisms, thereby reducing the overall stress level of the electrode structure and improving its mechanical stability. However, from an electrochemical perspective, the stress gradient generated by the forward bending deformation of the electrode structure can hinder the Li intercalation process. Enhanced constraints can partially or completely suppress the forward bending of the electrode, making the Li concentration in the active layer more uniform and thus improving the capacity utilization efficiency of the active layer. These results not only provide theoretical references for further understanding the chemical-mechanical response of the bilayer electrodes under more realistic or extreme service conditions, but also indicate from a design perspective that compromised external constraints are beneficial for balancing the structural durability and electrochemical performance of electrodes.
  • 加载中

  • 图 1  (a)活性层与集流体构成的双层电极横截面示意图(1, 2分别代表活性层和集流体); (b)四种电极的约束情况

    Figure 1.  (a) Schematic diagram of the cross-section of a bilayer electrode composed of active layer and current collector (1 and 2 represents the active layer and the current collector); (b) four electrode constraint situations.

    下载: 全尺寸图片 幻灯片

    图 2  恒流(${\bar J_0} = 0.5$)充电过程活性层中不同时刻浓度场的解析解与数值解

    Figure 2.  Analytical and numerical solutions of concentration field in the active layer at different time under constant current (${\bar J_0} = 0.5$) charging.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 充电过程中双层电极内无量纲曲率随时间的变化情况; (b) 活性层中不同时刻无量纲锂浓度沿活性层厚度的分布情况

    Figure 3.  (a) Variations of dimensionless curvature with time in the bilayer electrodes under charging; (b) distribution of dimensionless Li concentration at different time in the active layer.

    下载: 全尺寸图片 幻灯片

    图 4  充电过程中无量纲通量沿活性层厚度方向的分布情况. 扩散和弯曲应力诱导通量　(a) $ \bar t = 0.1 $, (b) $ \bar t = 1.2 $; 总通量 (c) $ \bar t = 0.1 $, (d) $ \bar t = 1.2 $

    Figure 4.  Distribution of dimensionless flux along the thickness of the active layer under charging. Diffusion and bending stress-induced flux: (a) $ \bar t = 0.1 $; (b) $ \bar t = 1.2 $. Total flux: (c) $ \bar t = 0.1 $; (d) $ \bar t = 1.2 $.

    下载: 全尺寸图片 幻灯片

    图 5  充电过程中双层电极中无量纲应力沿电极厚度方向的分布情况　(a) $ \bar t = 0.1 $; (b) $ \bar t = 1.2 $. (c)活性层与集流体界面以及(d)活性层表面处无量纲应力随时间的变化情况

    Figure 5.  Distribution of dimensionless stress along the thickness direction of the bilayer electrode during charging process: (a) $ \bar t = 0.1 $; (b) $ \bar t = 1.2 $. (c) The variation of dimensionless stress over time at the interface between the active layer and the current collector, as well as at (d) the surface of the active layer.

    下载: 全尺寸图片 幻灯片
  • [1] Zhang H, Li C M, Eshetu G G, et al. 2020 Angew. Chem. Int. Ed. 59 534 doi: 10.1002/anie.201913923
    [2] Mukhopadhyay A, Sheldon B W 2014 Prog. Mater. Sci. 63 58 doi: 10.1016/j.pmatsci.2014.02.001
    [3] 张俊乾, 吕浡, 宋亦诚 2017 力学季刊 38 14 Zhang J Q, Lü B, Song Y C 2017 Chin. Q. Mech. 38 14
    [4] Zhao Y, Stein P, Bai Y, Al-Siraj M, Yang Y, Xu B X 2019 J. Power Sources 413 259 doi: 10.1016/j.jpowsour.2018.12.011
    [5] de Vasconcelos L S, Xu R, Xu Z, et al. 2022 Chem. Rev. 122 13043 doi: 10.1021/acs.chemrev.2c00002
    [6] Yang F 2024 J. Energy Storage 75 109634 doi: 10.1016/j.est.2023.109634
    [7] Haftbaradaran H, Gao H, Curtin W A 2010 Appl. Phys. Lett. 96 091909 doi: 10.1063/1.3330940
    [8] Vanimisetti S K, Ramakrishnan N 2012 Proc. IMechE Part C: J. Mech. Eng. Sci. 226 2192 doi: 10.1177/0954406211432668
    [9] Lu B, Ning C Q, Shi D X, Zhao Y F, Zhang J Q 2020 Chin. Phys. B 29 026201 doi: 10.1088/1674-1056/ab6841
    [10] Li J, Dozier A K, Li Y, Yang F, Cheng Y T 2011 J. Electrochem. Soc. 158 A689 doi: 10.1149/1.3574027
    [11] Chew H B, Hou B, Wang X, Xia S 2014 Int. J. Solids Struct. 51 4176 doi: 10.1016/j.ijsolstr.2014.08.008
    [12] Xie H, Zhang Q, Song H, Shi B, Kang Y 2017 J. Power Sources 342 896 doi: 10.1016/j.jpowsour.2017.01.017
    [13] Li D, Wang Y, Hu J, Lu B, Cheng Y T, Zhang J 2017 J. Power Sources 366 80 doi: 10.1016/j.jpowsour.2017.09.004
    [14] Sethuraman V A, Chon M J, Shimshak M, Srinivasan V, Guduru P R 2010 J. Power Sources 195 5062 doi: 10.1016/j.jpowsour.2010.02.013
    [15] Pharr M, Suo Z, Vlassak J J 2013 Nano Lett. 13 5570 doi: 10.1021/nl403197m
    [16] Guo Z S, Zhang T, Zhu J, Wang Y 2014 Comput. Mater. Sci. 94 218 doi: 10.1016/j.commatsci.2014.04.019
    [17] 宋旭, 陆勇俊, 石明亮, 赵翔, 王峰会 2018 物理学报 67 140201 doi: 10.7498/aps.67.20180148 Song X, Lu Y J, Shi M L, Zhao X, Wang F H 2018 Acta Phys. Sin. 67 140201 doi: 10.7498/aps.67.20180148
    [18] Lu Y, Che Q, Song X, Wang F, Zhao X 2018 Scr. Mater. 150 164 doi: 10.1016/j.scriptamat.2018.03.023
    [19] Zhang J, Lu B, Song Y, Ji X 2012 J. Power Sources 209 220 doi: 10.1016/j.jpowsour.2012.02.104
    [20] Yang B, He Y P, Irsa J, Lundgren C A, Ratchford J B, Zhao Y P 2012 J. Power Sources 204 168 doi: 10.1016/j.jpowsour.2012.01.029
    [21] Hao F, Fang D 2013 J. Power Sources 242 415 doi: 10.1016/j.jpowsour.2013.05.098
    [22] Song Y, Shao X, Guo Z, Zhang J 2013 J. Phys. D: Appl. Phys. 46 105307 doi: 10.1088/0022-3727/46/10/105307
    [23] He Y L, Hu H J, Song Y C, Guo Z S, Liu C, Zhang J Q 2014 J. Power Sources 248 517 doi: 10.1016/j.jpowsour.2013.09.118
    [24] Song Y, Li Z, Zhang J 2014 J. Power Sources 263 22 doi: 10.1016/j.jpowsour.2014.04.007
    [25] Zhang X Y, Hao F, Chen H S, Fang D N 2015 Mech. Mater. 91 351 doi: 10.1016/j.mechmat.2015.04.016
    [26] Ji L, Guo Z, Du S, Chen L 2017 Int. J. Mech. Sci. 134 599 doi: 10.1016/j.ijmecsci.2017.10.048
    [27] Liu D, Chen W, Shen X 2017 Compos. Struct. 165 91 doi: 10.1016/j.compstruct.2017.01.011
    [28] Yin J, Shao X, Lu B, Song Y, Zhang J 2018 Appl. Math. Mech. 39 1567 doi: 10.1007/s10483-018-2386-6
    [29] Pouyanmehr R, Hassanzadeh-Aghdam M K, Ansari R 2020 Mech. Mater. 145 103390 doi: 10.1016/j.mechmat.2020.103390
    [30] Zhang A, Wang B, Li G, Wang J, Du J 2020 Eng. Fract. Mech. 235 107189 doi: 10.1016/j.engfracmech.2020.107189
    [31] Gao C, Guan L, Shi Y, Zhou J, Cai R 2022 Acta Mech. 233 5265 doi: 10.1007/s00707-022-03379-0
    [32] Zhang P, Wang Q, Qiu W, Feng L 2023 J. Electrochem. Soc. 170 050508 doi: 10.1149/1945-7111/acced7
    [33] Crank J 1979 The Mathematics of Diffusion (London: Oxford University Press) p61
    [34] Prussin S 1961 J. Appl. Phys. 32 1876 doi: 10.1063/1.1728256
    [35] Zhang X, Shyy W, Sastry A M 2007 J. Electrochem. Soc. 154 A910 doi: 10.1149/1.2759840
    [36] He Y, Hu H, Huang D 2016 Mater. Des. 92 438 doi: 10.1016/j.matdes.2015.12.085
    [37] Xia X, Afshar A, Yang H, Portela C M, Kochmann D M, Di Leo C V, Greer J R 2019 Nature 573 205 doi: 10.1038/s41586-019-1538-z
    [38] Qiu W, Zhang J, Su D, Zhang Y, Zhang P, Wang Q, Feng L 2023 Int. J. Mech. Sci. 248 108231 doi: 10.1016/j.ijmecsci.2023.108231
    [39] Berg S, Akturk A, Kammoun M, Ardebili H 2017 Extreme Mech. Lett. 13 108 doi: 10.1016/j.eml.2017.02.007
    [40] Shi Y, Xu C, Weng L, Wei Y, Chen B, Wang Y, Zhou J, Cai R 2021 Mech. Mater. 161 104024 doi: 10.1016/j.mechmat.2021.104024
    [41] Kim S, Choi S J, Zhao K, Yang H, Gobbi G, Zhang S, Li J 2016 Nat. Commun. 7 10146 doi: 10.1038/ncomms10146
    [42] Johannisson W, Harnden R, Zenkert D, Lindbergh G 2020 Proc. Natl. Acad. Sci. U. S. A. 117 7658 doi: 10.1073/pnas.1921132117
    [43] Carlstedt D, Runesson K, Larsson F, Jänicke R, Asp L E 2023 J. Mech. Phys. Solids 179 105371 doi: 10.1016/j.jmps.2023.105371
    [44] Zhou W 2015 Electrochim. Acta 185 28 doi: 10.1016/j.electacta.2015.10.097
    [45] Xuan F Z, Shao S S, Wang Z, Tu S T 2008 J. Phys. D: Appl. Phys. 42 015401
    [46] Zhu Z, Hu H, He Y, Tao B 2018 Compos. Struct. 204 822 doi: 10.1016/j.compstruct.2018.08.020
    [47] Zhu Z, Wan J, Wu T, Huang P 2022 Acta Mech. 233 2471 doi: 10.1007/s00707-022-03229-z
    [48] Song X, Lu Y, Wang F, Zhao X, Chen H 2020 J. Power Sources 452 227803 doi: 10.1016/j.jpowsour.2020.227803
    [49] Peng Y, Hao F 2023 J. Energy Storage 57 106195 doi: 10.1016/j.est.2022.106195
    [50] Shi Y, Xu C, Chen B, Zhou J, Cai R 2023 Appl. Math. Mech. 44 189 doi: 10.1007/s10483-023-2920-7
    [51] Guan L, Shi Y, Gao C, Wang T, Zhou J, Cai R 2023 Electrochim. Acta 440 141669 doi: 10.1016/j.electacta.2022.141669
    [52] Geng S, Zhang K, Zheng B, Zhang Y 2024 Acta Mech. 235 191 doi: 10.1007/s00707-023-03726-9
    [53] Zhuang Y, Zou Z Y, Lu B, Li Y J, Wang D, Avdeev M, Shi S Q 2020 Chin. Phys. B 29 068202 doi: 10.1088/1674-1056/ab943c
    [54] 张静, 冯露, 仇巍 张鹏飞 2021 应用力学学报 38 2306 Zhang J, Feng L, Qiu W, Zhang P F 2021 Chin. J. Appl. Mech. 38 2306
    [55] Yang S, Lu Y, Liu B, Che Q, Wang F 2023 Int. J. Hydrogen Energy 48 12461 doi: 10.1016/j.ijhydene.2022.12.107
    [56] Freud L B 1993 J. Cryst. Growth 132 341 doi: 10.1016/0022-0248(93)90280-A
    [57] 陆勇俊, 杨溢, 王峰会, 楼康, 赵翔 2016 物理学报 65 098102 doi: 10.7498/aps.65.098102 Lu Y J, Yang Y, Wang F H, Lou K, Zhao X 2016 Acta Phys. Sin. 65 098102 doi: 10.7498/aps.65.098102
    [58] Purkayastha R, McMeeking R 2013 Comput. Mater. Sci. 80 2 doi: 10.1016/j.commatsci.2012.11.050
    [59] Sethuraman V A, Srinivasan V, Bower A F, Guduru P R 2010 J. Electrochem. Soc. 157 A1253 doi: 10.1149/1.3489378
    [60] Yang F 2013 J. Power Sources 241 146 doi: 10.1016/j.jpowsour.2013.04.103
    [61] Haftbaradaran H, Xiao X, Verbrugge M W, Gao H 2012 J. Power Sources 206 357 doi: 10.1016/j.jpowsour.2012.01.097
    [62] Yang F 2011 J. Power Sources 196 465 doi: 10.1016/j.jpowsour.2010.06.082
  • 加载中
图( 5)
计量
  • 文章访问数:  327
  • HTML全文浏览数:  327
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-10
  • 刊出日期:  2025-01-20

力学约束对锂离子电池双层电极中锂扩散和应力的影响

    通讯作者: E-mail: kzhang222@163.com.; 
    通讯作者: E-mail: luyongjun@mail.nwpu.edu.cn.
  • 1. 中北大学工程力学系, 太原　030051
  • 2. 中北大学应用化学系, 太原　030051
  • 3. 西北工业大学工程力学系, 西安　710129
  • 收稿日期:  2024-09-10

摘要: 锂离子电池中的电极总是处于特定的约束当中, 这些约束既包括电池内部不可避免的被动结构约束, 又包括一些新兴技术应用场景可能赋予的外部主动约束. 本文主要利用化学-力学双向耦合的基本假设建立描述双层电极结构的理论模型, 考虑4种不同强弱的理想化变形约束作为其边界条件, 并通过数值求解研究在充电过程中这些外部约束对双层电极中Li扩散和应力的影响. 从力学的角度, 所研究的双层电极结构存在侧向伸缩和弯曲变形两个自由度, 弱化的约束条件能够部分或完全激活这些应力释放机制, 从而降低电极结构整体的应力水平, 并提升结构的力学稳定性. 然而, 从电化学的角度, 电极结构的正向弯曲变形所产生的应力梯度会阻碍嵌Li过程, 强化的约束能够部分或完全抑制电极的正向弯曲, 使活性层内Li浓度更加均匀, 从而提高活性层的容量利用率. 这些结果不仅为进一步理解双层电极在更加真实或极端服役条件下的化学-力学响应提供理论参考, 还从设计的角度表明折中的外部约束有利于平衡电极的结构耐久性和电化学性能.

English Abstract

    全文HTML

    1.   引　言

    • 可充电锂离子电池作为一项先进的储能技术已经在全球范围内被广泛用于驱动诸如智能手机、平板和笔记本电脑以及数码照相机等便携式电子产品, 开创了可移动的人类现代文明新纪元. 不仅如此, 它的应用也已经并将持续渗透到电动交通工具以及电网固定储能等大规模储能领域, 展现出广阔的应用前景. 锂离子电池的基本结构主要由3个活性部件——阳极、阴极和电解质构成, 其工作原理是由锂离子通过电解质在阳极和阴极之间来回穿梭而实现化学能与电能的互换[1]. 从材料科学的角度看, 电化学循环过程中电极活性材料为锂离子的存取提供了基本的结构框架, 锂离子的嵌入/脱出过程使得电极内部化学物质的数量和分布发生变化, 同时诱发电极材料产生变形、应力甚至破坏等一系列力学现象[2,3]. 这些过程相互耦合, 不仅是构成商用电池性能退化的重要原因, 还是阻碍电池材料更新换代的关键科学问题[4,5].

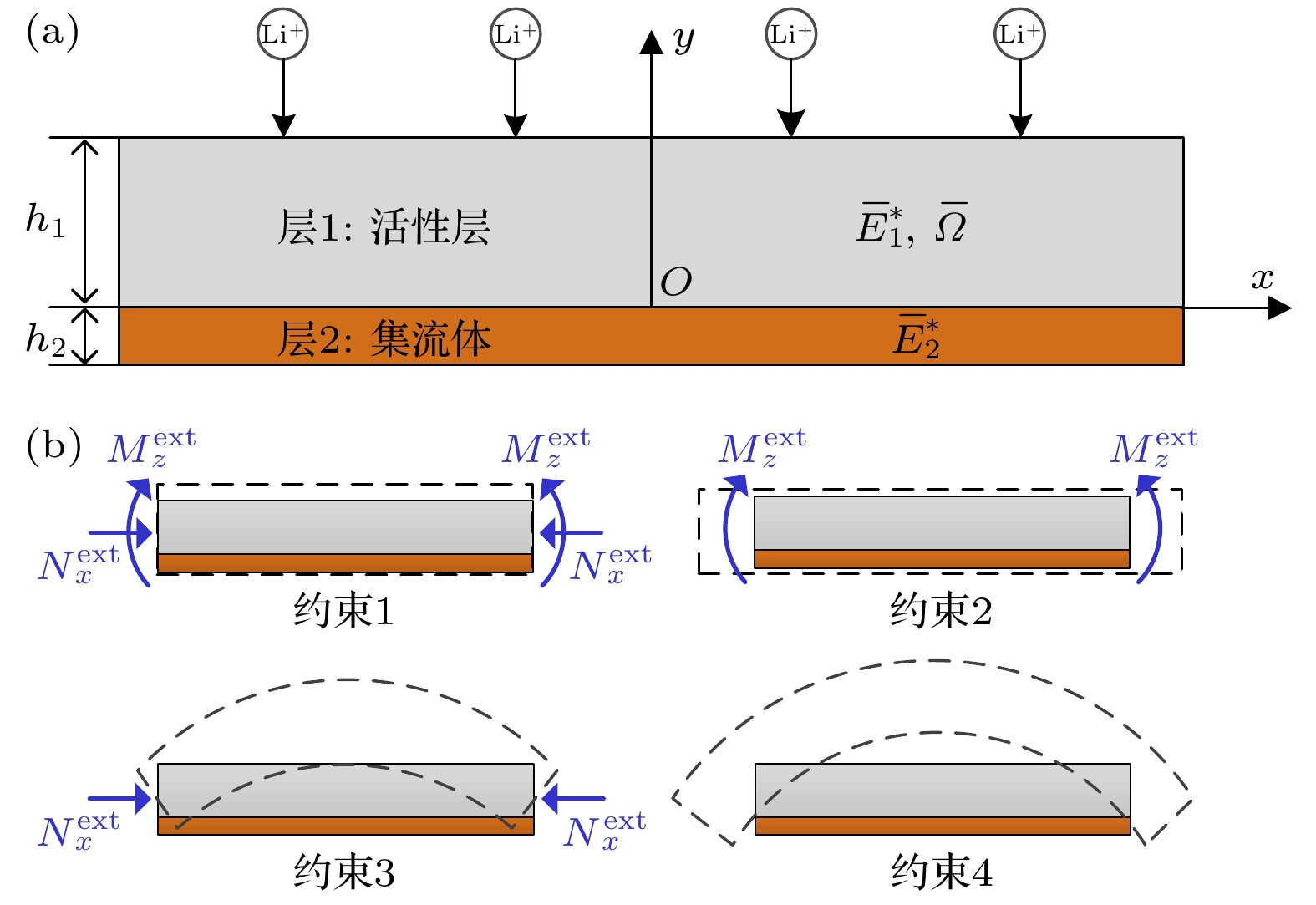
      电极材料的化学-力学耦合响应与其几何结构和约束条件紧密相关[6]. 为了实现结构和功能的完整性, 实际中的电极部件通常由活性材料与非活性组分(粘结剂、导电剂和集流体等)构成一个多层级的复合结构. 根据问题研究的需要, 在不同层次上可以抽象出不同的结构形式, 其中板状构型是一类典型的形式, 且至少体现在以下3个方面: 1)在微观层次上看, 一些活性存储颗粒可近似为板状结构[7,8]; 2)在宏观层次上看, 电极结构本身就是由活性材料层涂敷在金属集流体表面而形成的多层系统[9], 只不过商用电极中的活性层多为包含活性颗粒的多孔复合结构, 但也存在活性层为均质活性材料薄膜构型的情况[10,11]; 3)在实验测试领域, 薄膜-基底构型的电极系统被广泛地用于光学曲率测试技术, 用以探究电极材料在电化学过程中的应力、变形等关键力学行为[12–15]. 本文主要关注多层平板结构类型的电极系统.

      基于理论建模的方法研究和分析多层平板电极中的化学-力学耦合问题及其相关的结构和材料设计策略在过去的十多年受到了广泛关注[16–32]. 这些建模分析方法通常可分为两种类型, 其中一类方法假设单向的化学-力学耦合, 即忽略应力对扩散的影响, 利用经典的Fick定律描述电极材料中Li的物质传输, 由此获得的不均匀Li分布以变形失配的方式直接耦合到力学方程中. 由于Fick扩散问题在特定物理或几何简化条件下存在封闭的解析解[33], 从而能够获得相应条件下电极材料中的变形和应力的解析解, 基于这一方法描述的扩散诱导应力完全相似于固体中的热应力[34]. 在早期研究中, Zhang等[19]运用该类方法分析了由活性材料层和集流体构成的双层结构电极在不同充电条件下的扩散诱导应力, 并给出了基于力学原理的电极结构和材料设计策略. 另一类方法则假设双向的化学-力学耦合, 其与单向耦合的主要区别在于将Fick定律所规定的扩散驱动力——浓度梯度拓展为更加广义的应力有关的化学势梯度, 从而引入了应力梯度对扩散的驱动作用[35,36]. 由于扩散和力学控制方程形成了相互耦合的偏微分方程系统, 通常需要通过数值方法求解. 例如, Yang等[20]基于该类方法研究了纳米Si-Cu双层结构阳极在嵌/脱Li过程的Li扩散和应力演化, 并着重探讨了浓度有关的弹性模量、有限浓度效应和结构弯曲变形对这些过程的影响. 然而, 早期这些关于双层电极板的研究工作无论采用哪一类方法均只考虑各层材料间的相互约束[22], 基本上忽略了电极结构整体与周围介质的相互作用.

      事实上, 锂离子电池作为一个天然的多尺度复合系统, 其构成部件无论是微尺度的活性材料还是宏观尺度的电极结构都必然处于某种特定的约束当中. 不仅如此, 最近发展的一些基于平板电极构型的新兴技术概念和应用场景, 例如, 可重构架构化电极[37,38]、薄膜或柔性电池[39,40]、电化学驱动的机械能俘能器[41]、电化学致动或传感器件[42,43]等对(主动或被动)约束作用下的结构和性能可靠性提出了更高要求. 在这些不同的情况中, 外部约束通常会诱导多层电极结构在服役过程产生不同的应力和变形行为, 不同的应力状态反过来又会对活性层中的Li扩散产生不同的影响[44,45], 因此研究不同约束条件下双层板状电极的化学-力学响应对于优化电极性能具有重要意义. 在最近的研究中, Zhu等[46,47]详细分析了端部受横向压缩约束的3层对称薄板电极结构在各种因素, 例如结构和材料参数、电化学条件以及制造工艺等影响下的结构稳定性问题. Song等[48]通过建立描述全固态多层薄膜结构锂离子电池的电化学-力学全耦合模型, 研究了电池在指定变形约束下的力-电-化响应. 基于相似的方法, 这一研究还被进一步拓展到了具有不同界面和材料行为的柔性固态多层电池体系受变形约束的情况[49–51]. 此外, Geng等[52]分析了双层电极结构在外部(弯矩)载荷约束下的Li扩散和应力分布. Zhuang等[53]使用多尺度方法研究了新型无阳极电池不同金属集流体中的Li扩散机制, 并揭示了锂化诱导的合金膨胀对Li扩散的正向促进作用. 然而, 这些研究所考虑的约束情况较为单一, Qiu等[38]和Zhang等[54]针对三维架构微结构电极中的多层活性材料微单元应力建模分析中, 确实考虑了框架结构对多层微单元的不同柔韧性约束, 但遗憾的是他们的研究方法主要基于单向的化学-力学耦合假设, 因此未能反映出不同约束条件对活性材料中Li扩散的影响.

      最近, Yang等[55]利用化学-力学双向耦合的假设, 研究了不同变形约束下多层平板结构燃料电池由于阴极中氧传输诱导的变形和应力演化, 这一现象实际上与当前研究的锂离子电池多层结构电极的充放电过程具有物理上的相似性, 因此启发作者在本文中将先前关于无约束双层电极结构的化学-力学双向耦合模型[17]进一步拓展到有约束的情况. 通过揭示不同强弱的约束条件对双层电极结构在充电过程中Li扩散和应力的影响规律, 将进一步深化我们对电极结构在更加真实或极端服役环境下的化学-力学退化机理的理解.

    2.   物理模型

      2.1.   基本假设

    • 考虑由厚度为h1的活性层和厚度为h2的集流体组成的一个双层板状电极结构, 其任意的横截面如图1(a)所示. 建立空间笛卡尔坐标系O-xyz使得y轴沿板厚方向指向活性层表面, x-z平面位于活性层与集流体的界面. 为了简化建模的复杂性, 一些合理的假设已经在之前的研究中被很好地阐述[17,19], 其主要包括: 1)系统为平面几何体, 即厚度尺寸远小于平面内尺寸, 且面内x与z方向尺度相当; 2)双层结构界面为完美粘结, 变形过程维持位移连续; 3) Li仅在活性层上表面发生嵌/脱反应, 并沿着厚度y轴方向扩散; 4)活性层Li含量变化仅引起较小的各向同性局部化学膨胀, 不诱导材料的相变行为; 5)集流体和活性层均为各向同性线弹性材料, 且不随Li含量变化.

      当Li嵌入活性层, 将引起材料内部不均匀的局部体积膨胀, 加之集流体的限制作用, 结构将发生弯曲变形. 对于实际情况而言, 电极还将处于复杂的约束环境: 一方面, 电池内部固有的多尺度结构不可避免地使电极处于被动的结构约束; 另一方面, 一些新兴的技术应用场景, 例如柔性电池, 可能额外赋予电极主动的外部约束. 然而, 大多数以前的相关研究总是考虑电极板无外部约束的基本假设, 本文的主要创新点正是围绕着约束条件开展研究. 基于双层电极的变形特点, 为了简化对约束的分析同时又能揭示其一般规律, 本文将考虑如图1(b)所示的4种理想化的变形约束:

      约束1—电极既不发生弯曲变形, 也不发生面内伸缩变形;

      约束2—电极不发生弯曲变形, 仅可沿面内自由伸缩;

      约束3—电极可自由地弯曲变形, 但不发生面内伸缩变形;

      约束4—电极可自由地弯曲和伸缩.

      约束1和4分别对应了约束强弱的两种极限情况, 约束2和3则表示两种中间约束状态. 这些约束将作为边界条件在2.4节进行详细论述.

      • 2.2.   电极结构的变形和应力

    • 根据上述基本假设, Li在进入活性层后形成的不均匀分布诱导系统内部的变形失配, 并使得板状电极处于平面应力状态[56], 面内正应力满足:

      且其余应力分量为0. 由于固体材料的弹性变形速度远快于原子的扩散, 电极的变形可视为准静态过程, 此时力学平衡方程为$\sigma_{ij, i}=0 $. 于是, 电极系统的力学问题中所有变量仅为y的函数.

      相应地, 仅考虑物质扩散与弹性变形间的耦合, 面内正应变满足小变形情况的加法分解:

      其中上标“el”表示弹性贡献; c为活性层中Li的物质的量浓度; Ω为Li嵌入活性材料晶格中的偏摩尔体积, 相似于热膨胀系数, 系数$ {\varOmega {/ } 3} $表示(Vegard)化学膨胀系数.

      另一方面, 根据经典的Euler–Bernoulli弯曲变形假设或小变形理论中的变形协调条件[19], 可得双层系统的正应变沿厚度方向线性变化:

      其中ε0为界面处(y = 0)的正应变或参考应变; $ \kappa $为电极弯曲变形的曲率.

      联立(1)式—(3)式以及广义Hooke定律, 可以得到双层电极中耦合扩散和弹性的本构关系:

      其中$ {E^*} = {E {/ } {\left( {1 - \nu } \right)}} $为双轴模量, E为材料弹性模量, ν为泊松比. 此时, 若给定Li浓度分布, 系统中的应力将完全由几何参数ε0和κ决定, 而这两个参数可通过边界条件求解[57].

      不失一般性, 考虑结构受边界约束作用, 相应的边界平衡为

      其中${N}_{x}^{\text{ext}} $和${M}_{z}^{\text{ext}} $表示边界约束等效施加的外加轴力和外加力(偶)矩. 需注意的是, ${N}_{x}^{\text{ext}} $相对于界面y = 0通常会附加一个额外的力矩, 上述力矩平衡中将其视为${M}_{z}^{\text{ext}} $的一部分, 无需单独处理. 将方程(4)代入上述边界方程, 并可整理为如下线性方程系统:

      其中

      式中Ci (i = 1, 2, 3)表示抵抗相应变形的结构刚度; Nx和Mz可以理解为由活性材料中的化学应变以及外部边界约束共同作用下的载荷(轴力和力矩). 这5个参数共同决定了双层电极结构的变形行为:

      • 2.3.   活性层中的锂扩散动力学

    • 由于Li从活性层表面进入后沿厚度方向扩散, 其扩散通量J仅存在y-坐标分量Jy, 且满足质量守恒律:

      其中t为扩散时间. 根据Gibbs热力学原理, 化学势(μ)梯度构成了物质运动的热力学驱动力, 相应的动力学关系为[35]

      其中M为原子迁移率, 通常被假设为关于扩散物质浓度的线性函数[58]:

      其中$ {M_0} = {{{D_0}} {/ } {\left( {RT} \right)}} $, D0为与浓度无关(稀溶液)的扩散率, R为气体常数, T为绝对温度; cmax为电极材料的饱和嵌锂浓度. (10)式考虑了嵌Li晶格点的饱和效应, 即当Li浓度达到材料可容纳极限时, Li的扩散运动将消失.

      根据Larché-Cahn理论以及前述假设, Li嵌入电极固溶体中的化学势可采用如下简单形式[59]:

      式中右边第1项μ0作为化学势的参考值表示理想焓的贡献, 第2项为理想二元固溶体混合熵的贡献, 第3项代表了嵌锂诱导的纯体积弹性能的贡献, 其中σh为平均应力

      将方程(11)和方程(12)代入方程(9)即可获得Li的扩散通量, 为了便于后续的结果分析, 将Li的扩散通量分解为浓度梯度诱导和弯曲诱导的两部分:

      其中

      可知, $J_y^{\text{c}} $和$J_y^{\text{b}} $均包含了应力梯度对扩散的驱动作用. 而且, 当电极结构发生正向曲率弯曲κ > 0, $J_y^{\text{b}} >0$指向y轴正向, 从而阻碍Li向活性层内部扩散; 反之κ < 0, 则促进Li向内部的扩散.

      • 2.4.   初始、边界条件和无量纲化

    • 假设初始时刻电极活性层处于无Li状态, 即c(y, 0) = 0. 考虑恒流充电条件, 即在活性层上表面处存在沿法线方向恒定的扩散通量, Jy(h1, t) = –J0; 下表面与集流体相接, 无物质交换, Jy(0, t) = 0.

      假设平板电极结构无初始变形, 考虑图1(b)所示的4种由强到弱的理想约束情况.

      • 2.4.1.   约束1

    • 电极结构受到完全约束, 使得电极板在嵌Li过程既不发生(x-z)面内的侧向伸缩, 也不产生面外弯曲, 这一约束等效于将集流体视为刚性基底的情况[6,60]. 相应的变形和边界载荷总结为

      此时电极本构方程(4)直接退化为

      • 2.4.2.   约束2

    • 电极结构(等效于)受到上下表面光滑接触面约束, 使得电极在嵌Li过程仅可在(x-z)面内自由伸缩, 而不产生面外弯曲, 这一约束相似于三层对称夹心结构电极[19]. 相应的变形和边界载荷总结为

      此时, 参考正应变根据方程(6)1得到:

      相应地, 电极本构方程(4)退化为

      • 2.4.3.   约束3

    • 电极结构受到侧边固定铰支座约束, 使得电极在嵌Li过程可以自由弯曲但不能沿侧向伸缩, 这一约束相似于可重构架构化电极中[37]的约束. 相应的变形和边界载荷总结为

      此时, 变形曲率根据方程(6)2得到:

      相应地, 电极本构方程(4)退化为

      • 2.4.4.   约束4

    • 电极结构处于完全自由状态, 不存在外部约束. 相应的变形和边界载荷总结为

      此时, 结构的变形和本构关系仍由方程(4)和方程(7)决定.

      至此, 完成了建立受约束双层电极板在充放电过程应力和浓度场演变的初始边值问题. 方程(7)、方程(8)和方程(12)共同构成了描述电极板扩散-变形耦合的控制方程组, 虽然这些方程组最终退化为单一的扩散控制方程, 但由于具有高度非线性而难以获得一般解析解, 因此将通过数值方法求解. 为了便于数值计算并揭示系统的基本物理规律, 引入如下无量纲参数以消除材料和结构参数的影响:

      此时, 可得扩散方程(8)对应的无量纲形式:

      上述方程可由COMSOL通用有限元平台的PDE模块直接实现数值求解.

    3.   结果与分析

    • 考虑一个特定双层电极系统的充电过程作为数值算例, 其典型的参数选取自我们之前的研究[17], 主要包括结构参数${\bar h_2} = 0.1$, 以及材料参数${\bar E^ * } = 0.154$, $\bar E_1^ * = 45.2$, $\bar \varOmega = 0.11$. 充电速率设为$ {\bar J_0} = 0.36 $, 当活性层表面Li浓度达到饱和时停止充电.

      • 3.1.   数值有效性

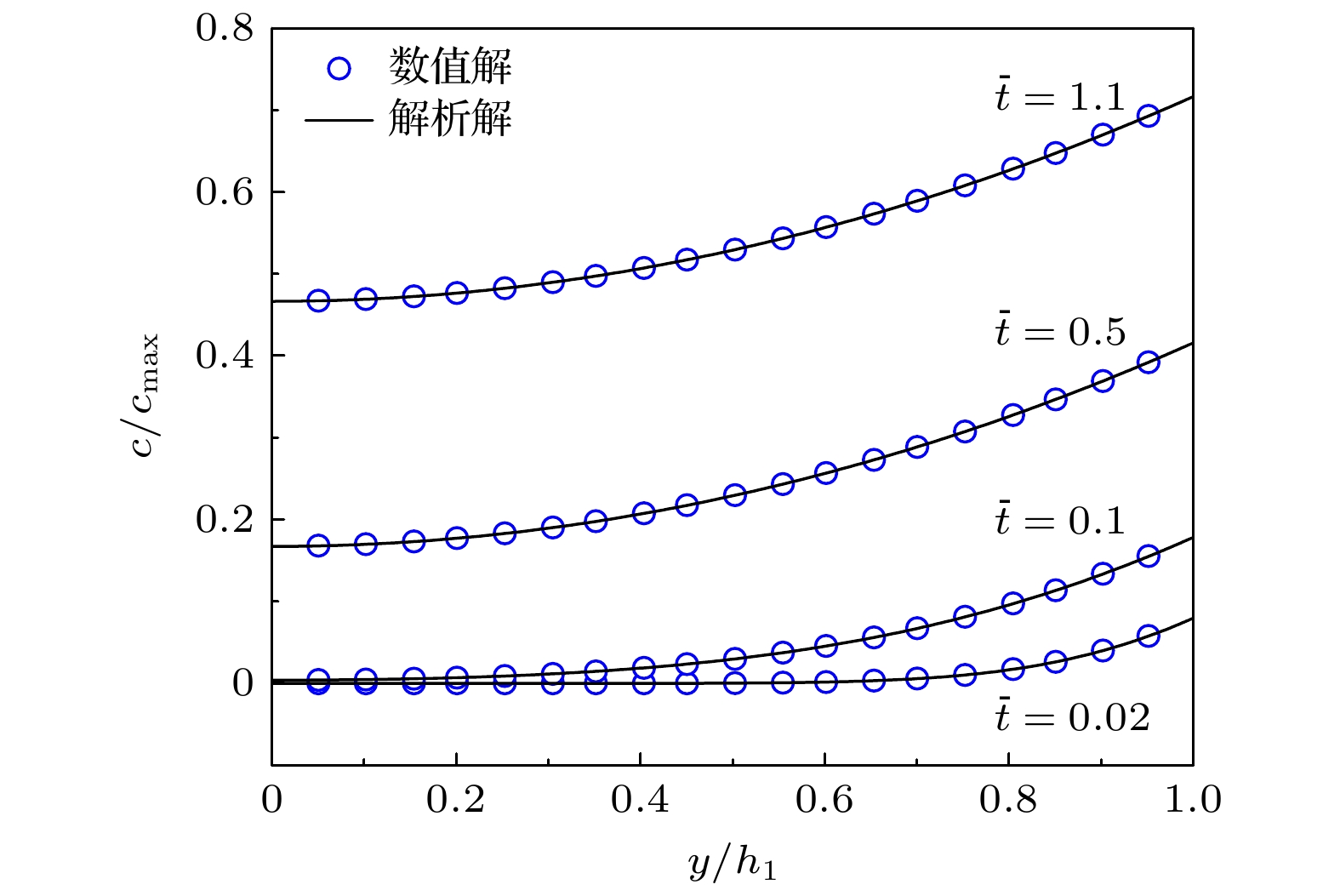
    • 在进行结果分析之前, 首先论证数值计算的有效性. 忽略应力作用, 考虑Li在活性层中的运动为纯浓度驱动的扩散过程, 则方程(8)和方程(25)退化为经典的Fick扩散方程. 此时, 运用求解温度分布的类似方法, 可得恒流边界作用下活性层中浓度分布的解析表达[33]:

      其中${\bar c_0}$为初始浓度; ${\bar J_0}$为边界通量, 且当${\bar J_0} > 0$表示Li从上表面嵌入电极, 反之则迁出电极.

      在${\bar c_0} = 0$, ${\bar J_0} = 0.5$条件下, 活性层中浓度场的解析解和数值解在图2中给出, 在不同时刻下解析解和数值解均符合较好, 从而证实了数值求解的可靠性.

      • 3.2.   浓度和曲率演变

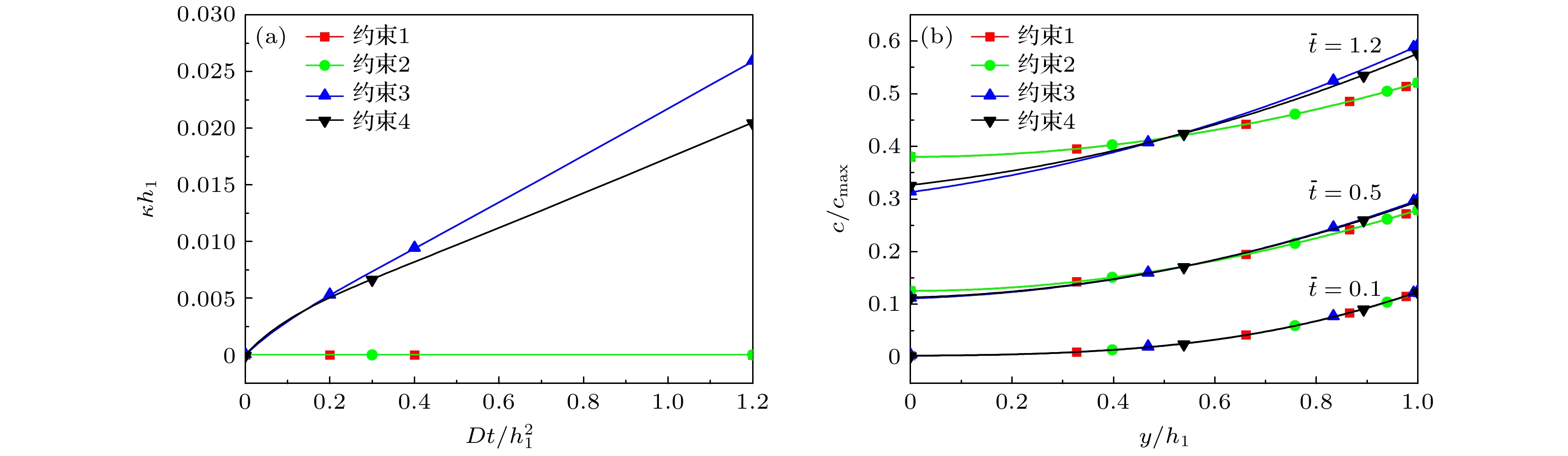
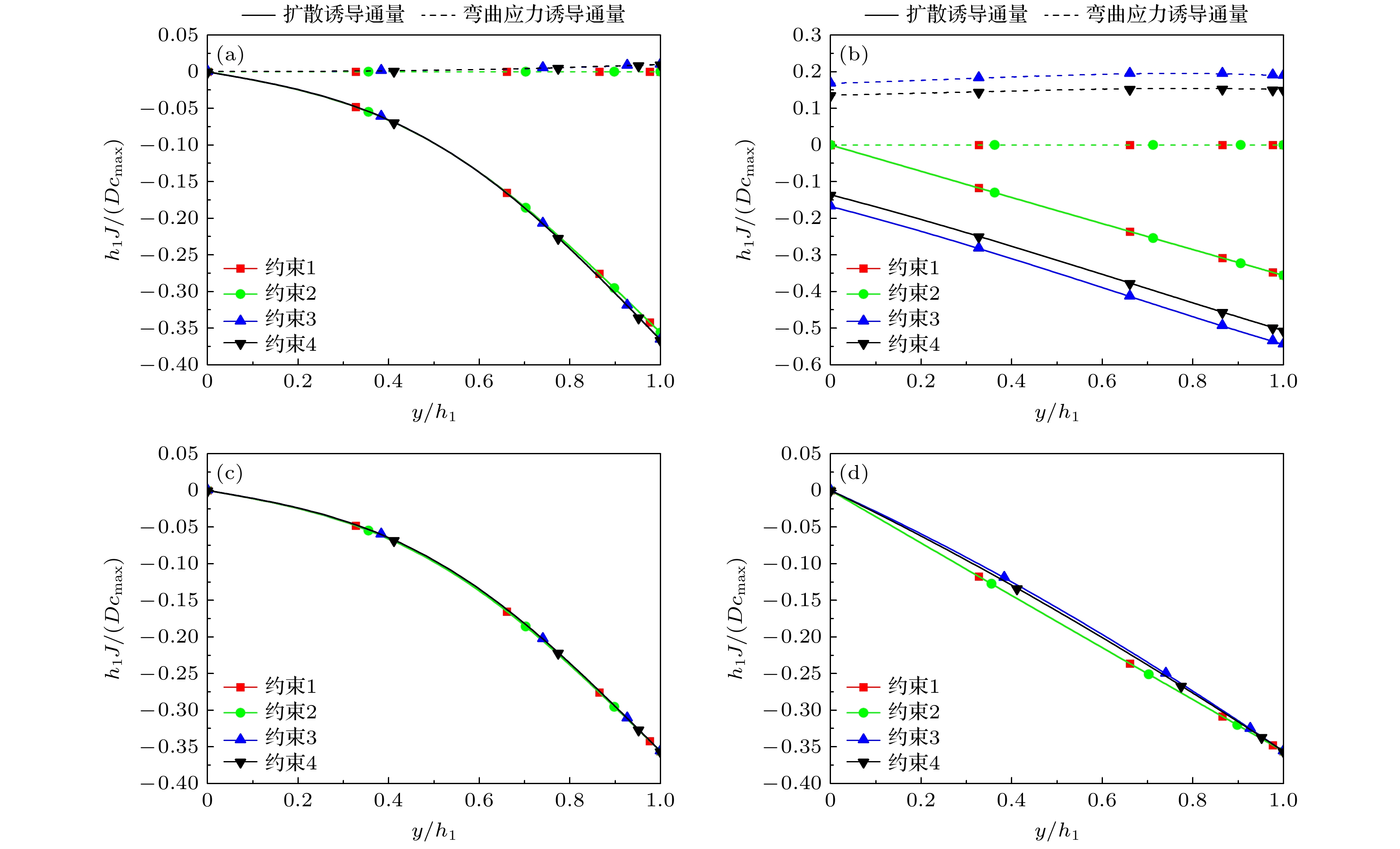
    • 图3(a)为双层电极在充电过程中的曲率变化情况, 其中约束1和约束2条件下电极不发生弯曲($\bar\kappa $ = 0). 电极受约束3作用下的曲率总是大于约束4 (自由状态), 这是由于当电极不能发生侧向伸缩时, 需要产生更大的弯曲变形来释放扩散诱导的不对称应力. 图3(b)为充电过程中活性层内Li浓度沿厚度方向的演化情况, 可以看到, 约束1和约束2对应的Li浓度分布在整个充电过程中始终保持一致, 表明电极板的侧向约束不影响锂浓度分布; 而约束3和约束4对应的浓度分布仅在充电初期($\bar t = 0.1$)与前述分布重合, 并随着时间增加逐渐出现分离, 表明弯曲变形是影响锂浓度分布的主要因素. 经过足够的充电后($\bar t = 1.2$), 所有情况相比, 约束1和约束2的浓度分布最均匀, 约束3的浓度分布最陡峭.

      上述不同约束情况引起的浓度分布差异性完全归结为本文所采用的化学-力学双向耦合假设, 即考虑了应力梯度驱动的扩散效应, 这正是本文与之前研究[38,54]的重要不同之处. 为了更直观地理解和阐述这种差异性, 考虑方程(13)关于Li扩散通量的分解: 浓度梯度诱导通量$\bar J_y^{\mathrm{c}} $和弯曲变形诱导通量$\bar J_y^{\mathrm{b}} $, 应力梯度对扩散的驱动作用则以不同的形式隐含在这两部分通量贡献中. 显然, 不同的外部约束仅仅通过影响弯曲曲率($\bar\kappa $)的方式影响通量$\bar J_y^{\mathrm{b}} $, 并最终影响浓度分布, 这一影响机制实际上等同于Song等[22]所考虑的多层电极内部结构约束对扩散的影响. 图4给出了不同约束对应的活性层内Li通量在不同时刻的分布. 无弯曲的约束1和约束2不产生任何弯曲通量$\bar J_y^{\mathrm{b}} $ = 0, 因此二者的总通量保持相等, 从而解释了图3(b)中相应浓度分布相同的现象. 如图4(a)和图4(b), 约束3和约束4由于使电极产生正向弯曲(图3(a)), 相应地产生正向弯曲通量$\bar J_y^{\mathrm{b}} >0$, 从而阻碍Li向活性层内部的扩散运动, 造成更大的浓度梯度; 比较而言, 约束3使电极产生更大的曲率(图3(a)), 因此其对应的浓度梯度也更大(图3(b)). 事实上, 由于活性层内Li沿厚度方向存在浓度梯度, 导致Li在嵌入活性层中时活性层表面区域受压, 活性层内远离表面的区域受拉, 由此产生的应力梯度将进一步促进锂向活性层中扩散. 但是当集流体发生弯曲变形后, 活性层内应力得到释放, 从而导致应力梯度减小而使得应力梯度对Li扩散的促进效果减弱, 造成Li在活性层内的浓度梯度比无弯曲时大. 值得一提的是, 虽然未体现在本文所研究的约束条件, 一些外部的主动约束可能会导致电极产生负向弯曲[48,52], 这种情况将有利于充电过程的Li扩散, 产生更加均匀的浓度分布.

      从电化学的角度, 这些不同约束条件产生的差异化浓度分布对于电极性能的优化设计具有一定的指导意义. 这是因为对于恒流充电情况, 当活性层外表面处达到浓度饱和时即终止充电, 那么基于以上讨论, 更强的外部约束(例如约束1和约束2)通过抑制电极的弯曲变形甚至使其不发生弯曲(图3(a)), 使活性层内产生更加均匀的Li浓度(图3(b)), 从而有效地增加充电时间, 提高活性层的容量利用率. 然而, 从力学的角度, 这些不同的约束对电极中的应力及结构可靠性的影响还需要进一步讨论.

      • 3.3.   应力演变

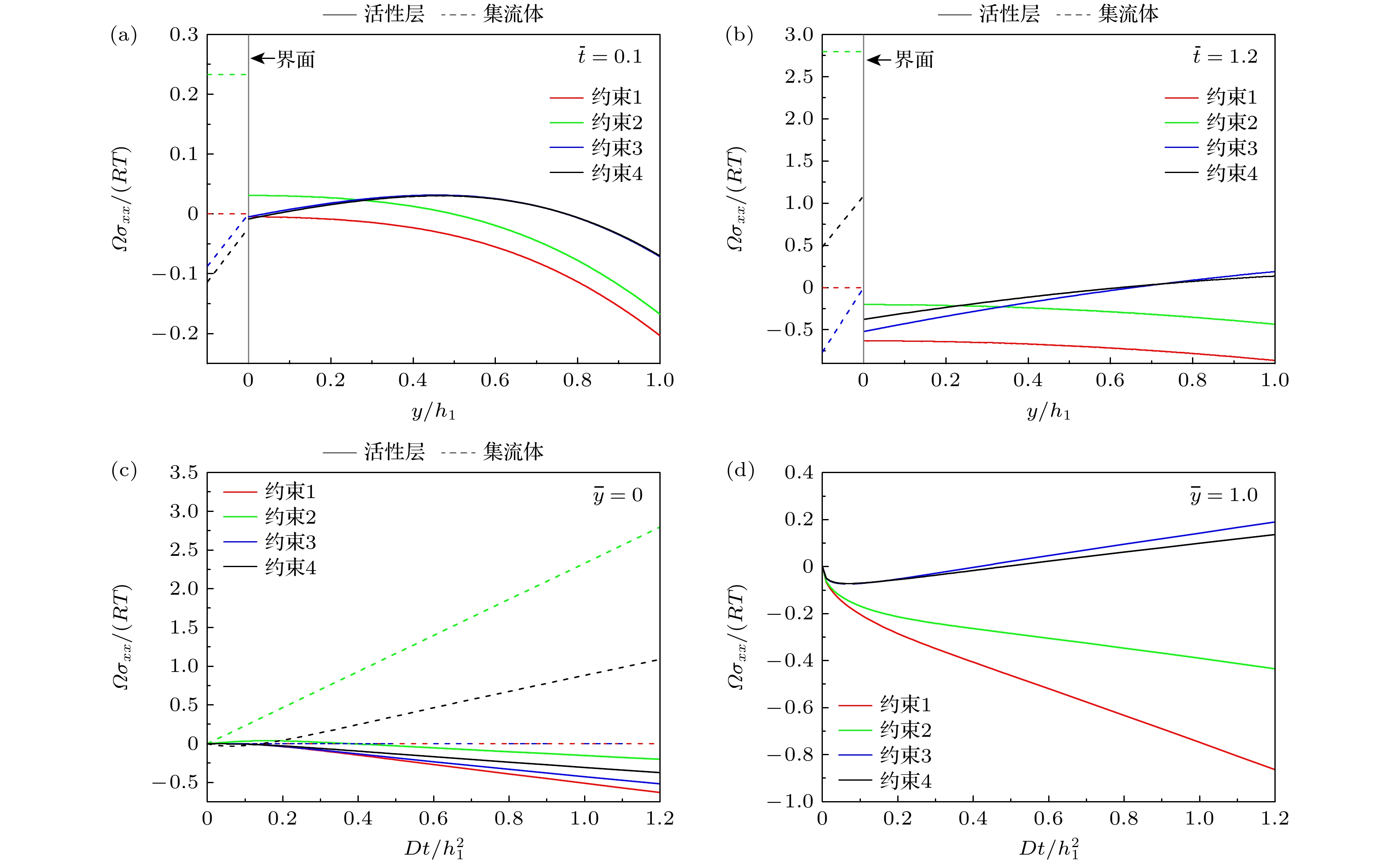
    • 双层电极结构在不同时刻的等轴应力分布如图5(a)和图5(b)所示, 不同的约束作用导致明显不同的应力分布, 和前述浓度分布一样, 这些应力的差异性与结构的弯曲变形程度密切相关. 双层电极在约束1和约束2作用下无弯曲变形, 表现出与三层对称电极完全相似的变形行为[19], 因此二者约束下的应力分布也具有相似性, 即集流体中的应力为均匀分布, 活性层中的应力为浓度梯度诱导的形式. 区别在于, 约束1等价于集流体为刚性的极限情况, 因而其内部应力为0, 且对活性层施加了最强约束, 导致活性层具有较大的压缩应力; 相比之下, 约束2考虑集流体为有限刚度的可变形体, 通过允许电极自由地侧向伸缩作为一种应力释放机制, 极大地缓解了活性层中的压缩应力, 但同时在集流体中产生较大的拉伸应力. 同样地, 在约束3和约束4作用下双层电极发生弯曲变形, 作为另一种应力释放机制, 使得活性层和集流体中的应力同时得到松弛. 但需要注意, 在充电早期($\bar t = 0.1$), 约束3和约束4对应的电极曲率较小且相等(图3(a)), 此时活性层中的应力由浓度梯度主导, 活性层表面区域为受压状态, 且二者几乎保持相等. 随着更多的Li被嵌入到活性层($\bar t = 1.2$), 约束3和约束4对应的电极曲率逐渐变大(图3(a)), 使得活性层中的应力由弯曲变形主导, 活性层表面区域也因此转变为受拉状态; 相比之下, 约束3由于产生更大的曲率(图3(a)), 其对应的表面拉应力更大.

      整体上看, 电极中的应力水平通常随充电量的增加而增大, 而且经过充电初期的应力波动后, 电极结构中的应力将保持单调的变化趋势(图5(b)), 因此, 拉伸或压缩峰值应力总是出现在电极中的界面或活性层表面位置, 从而可能造成这些位置出现塑性变形[17]、微裂纹、脱粘或屈曲[61,62]等力学失效现象. 为了更好地可视化双层电极中的应力变化情况, 图5(c)和图5(d)分别显示了活性层-集流体界面两端和活性层表面位置应力随时间的演化过程. 由图5(c)可知, 在整个充电过程, 所有约束相比, 约束1作用下活性层位于界面处的压缩应力总是最大, 约束2在集流体位于界面位置产生的拉伸应力总是最大, 而约束3和约束4对应的界面两端应力水平则相对较低. 在图5(d)中, 约束1在活性层表面处产生的压缩应力总是最大, 约束2次之; 约束3和约束4使得活性层表面发生应力反转现象, 即由充电初期的压应力逐渐转变拉应力, 并且可理解为浓度梯度和弯曲变形两种不同应力诱导机制竞争的结果[19]. 综合上述分析, 从力学的角度, 更弱的外部约束(例如约束3和约束4)通过允许更多的应力释放途径, 能有效地降低双层电极整体的应力水平, 从而提升电极结构的力学可靠性.

    4.   结　论

    • 本文通过建立化学-力学双向耦合的双层电极结构理论模型, 讨论了锂离子电池中常见的4种不同强弱的理想化变形约束情况. 由于引入了应力梯度对Li扩散的影响, 变形约束将通过影响电极板内扩散诱导应力的释放来反向影响固相内Li的扩散行为. 首先, 电极的正向弯曲变形可以很好地释放电池内的扩散诱导应力, 但会阻碍Li向电极内扩散, 从而降低电极的储Li能力; 而侧向约束不会影响电极内Li的扩散行为. 其次, 对电极施加外部约束会影响电极内扩散诱导应力的释放, 从而导致双层电极的集流体和活性层内应力的增加, 进而影响电极结构的稳定性. 最后, 被外部约束限制了弯曲变形的电极, 由于缺少正向弯曲变形应力对Li扩散的阻碍作用, 可以使得更多的Li进入到活性层中, 最终提高了电池的最大容量. 综上所述, 考虑到电极结构的力学可靠性和电极的储Li能力, 在锂电池的设计过程中需要选取合适的外部电极约束方式. 本文的研究结论有望为多层平板结构类型电极系统的设计提供参考.

    参考文献 (62)

目录

/

返回文章
返回