在无相互作用的系统中引入足够强的随机无序, 将会破坏波函数的遍历性, 导致系统经历Anderson局域化^[1-3], 从延展相转变到局域相. 作为局域化理论中的一个核心概念, 迁移率边^[4]是指能谱中将延展本征态和局域本征态分隔开的临界能量. 经过几十年的发展, 人们基于不同的实验平台 (例如冷原子^[5-8]和光子系统^[9-12]), 对这种局域化现象进行了充分的研究. 通常来说, 迁移率边被认为出现于三维系统中^[13]. 而在一维和二维系统中, 随机无序的引入将会使得所有本征态局域化, 此时能谱中不会存在迁移率边. 然而, 若将确定性的准周期无序引入到一维系统中, 研究表明延展本征态与局域本征态可以在特定条件下共存^[14-18]. 一维Aubry-André-Harper (AAH) 模型^[19]作为一个标志性的准周期晶格模型, 是能展现出Anderson局域化相变的最简单模型之一. 由于AAH模型中包含自对偶对称性^[19], 标准AAH模型中的局域化相变是能量无关的, 也就是说能谱中没有迁移率边的存在. 令人感兴趣的是, 若加入一些破坏自对偶对称性的额外条件, 迁移率边就会出现在这些广义AAH模型中^[17,20-26].

另一方面, 由于天文学观测能力的限制, 对弯曲时空下量子效应^[27-29]的量子模拟引发了广泛的兴趣, 也催生了一系列相关实验^[30-33]. 近几年来, 人们逐渐开始关注弯曲时空下晶格模型的凝聚态物理^[34-39], 其中包括弯曲时空下的AAH模型^[39]. 在弯曲时空下, AAH模型中的局域相和延展相被临界格点分隔, 形成所谓的相分离现象. 在弯曲时空AAH模型能谱中, 会出现共存的局域相、延展相和摇摆相. 其中在摇摆相中, 不同准周期调制相位下, 本征态的表现将在局域化和延展化之间摇摆, 从而导致摇摆的迁移率边. 目前, 仅有少数弯曲时空晶格模型得以在实验中实现, 例如基于光波导实现的黑洞附近量子行走实验^[40,41]. 然而在光波导中动态调制晶格参数难度较大, 限制了其在实验中制备和观测量子态的能力. 而在超冷原子系统中, 丰富的调控工具使得其有希望成为弯曲时空晶格模型量子模拟的理想实验平台.

在超冷原子系统中, 研究者利用光学晶格^[24,42,43]和动量态晶格^[25,26]均分别实现了一维AAH模型及其广义模型. 在这些由超冷原子实现的一维广义AAH链中, 迁移率边的性质得到了广泛的研究^[24-26]. 同时, 超冷原子系统中的模拟黑洞实验^[30,31]也展现了其研究弯曲时空下物理的前景. 考虑到上述优势, 本文提出可以在超冷原子系统中基于动量态晶格实现弯曲时空的AAH模型, 为实验实现并研究类似的弯曲时空晶格模型铺平了道路.

本文基于超冷原子动量态晶格系统提出了弯曲时空AAH链的实验实现方案. 动量态晶格哈密顿量的数值计算结果表明, 处于弯曲时空的AAH链会出现理论预测的相分离现象. 在相分离临界格点两边, 波包会分别表现出局域化和延展化的演化过程. 根据波包演化数据, 还可以解析出对应参数下的相分离临界格点. 此外, 通过对时空弯曲参数进行调制, 本文提出了一种弯曲时空AAH链的本征态制备方案. 进一步地, 通过不同准周期调制相位下制备得到的本征态, 可以解析出能谱中不同本征能量的分形维数, 识别出了共存的局域相、摇摆相以及延展相, 这也表明其中存在摇摆的迁移率边.

基于此前研究^[35,39], 在一维量子晶格模型中, 如果跃迁强度具有幂律格点位置依赖的特性, 其低能动力学可以与 (1+1) 维Jackiw-Teitelboim引力影响下的Dirac场建立联系, 从而能够模拟事件视界附近的凝聚态物理. 因此, 弯曲时空下的一维对角AAH模型的哈密顿量可以表示为

其中, $ {\hat c}_{n}^{\dagger} $和$ {\hat c}_{n} $分别是第n个格点上的产生和湮灭算符. $ J_n = J \cdot \big[{n}/({L-1)}\big]^{\sigma} $是幂律格点位置依赖的最近邻跃迁, 这里σ表示时空弯曲程度. $ V_n = \lambda {\rm{cos}} \left(2 \pi b n + \phi\right) $是准周期调制的格点能量, 其中λ表示格点能量调制强度, 无理数b是调制频率, ϕ则是调制相位. 当$ \sigma=0 $时, 此时所有跃迁强度均为J, 哈密顿量对应的时空将退回平坦时空, 如图1(a)所示. 而当$ \sigma \geqslant 1 $时, 在热力学极限$ L \to \infty $下, 可知$ J_1 \to 0 $, 这时系统在格点$ 1 $上将会出现类似事件视界的表现, 如图1(b)所示. 为了方便起见, 同时也不失一般性, 本文在后续的讨论中都将格点能量调制频率设为一个典型的无理数$ b = \lim\limits_{n \to \infty} \left(F_{n-1}/F_n\right) = \left(\sqrt{5}-1\right)/2 $, 其中$ F_n $是第n个Fibonacci数.

基于Li等^[39]的理论, 可以通过一种分割方法分析接近热力学极限下弯曲时空AAH链的局域化性质. 该分割方法以两条标准AAH子链相连组成的总链为起点, 并逐步扩展到热力学极限下由$ L-1 $条标准AAH子链相连组成的总链, 最终将其对应到弯曲时空AAH链. 基于分割法的理论分析表明, 弯曲时空AAH链中将会出现相分离现象: 整条链通过一个临界格点边界$ n_{\rm{c}} $分为两部分, 其中$ n < n_{\rm{c}} $的子链是局域化的, 而$ n > n_{\rm{c}} $的区域则属于延展相. 这表明局域相和延展相会在实空间中被完全分隔开. 该相分离的临界格点可表示为

这里$ \left\lfloor\cdots\right\rfloor $是向下取整函数. 直接观察(2)式的形式可以发现, 弯曲时空AAH链中临界格点的相对位置由$ \lambda/J $和σ共同决定. 这表明, 相分离现象是由弯曲时空和准周期格点能量调制共同引发的.

作为表征局域化性质和研究迁移率边最重要的指标之一, 分形维数可以写为如下形式^[44,45]:

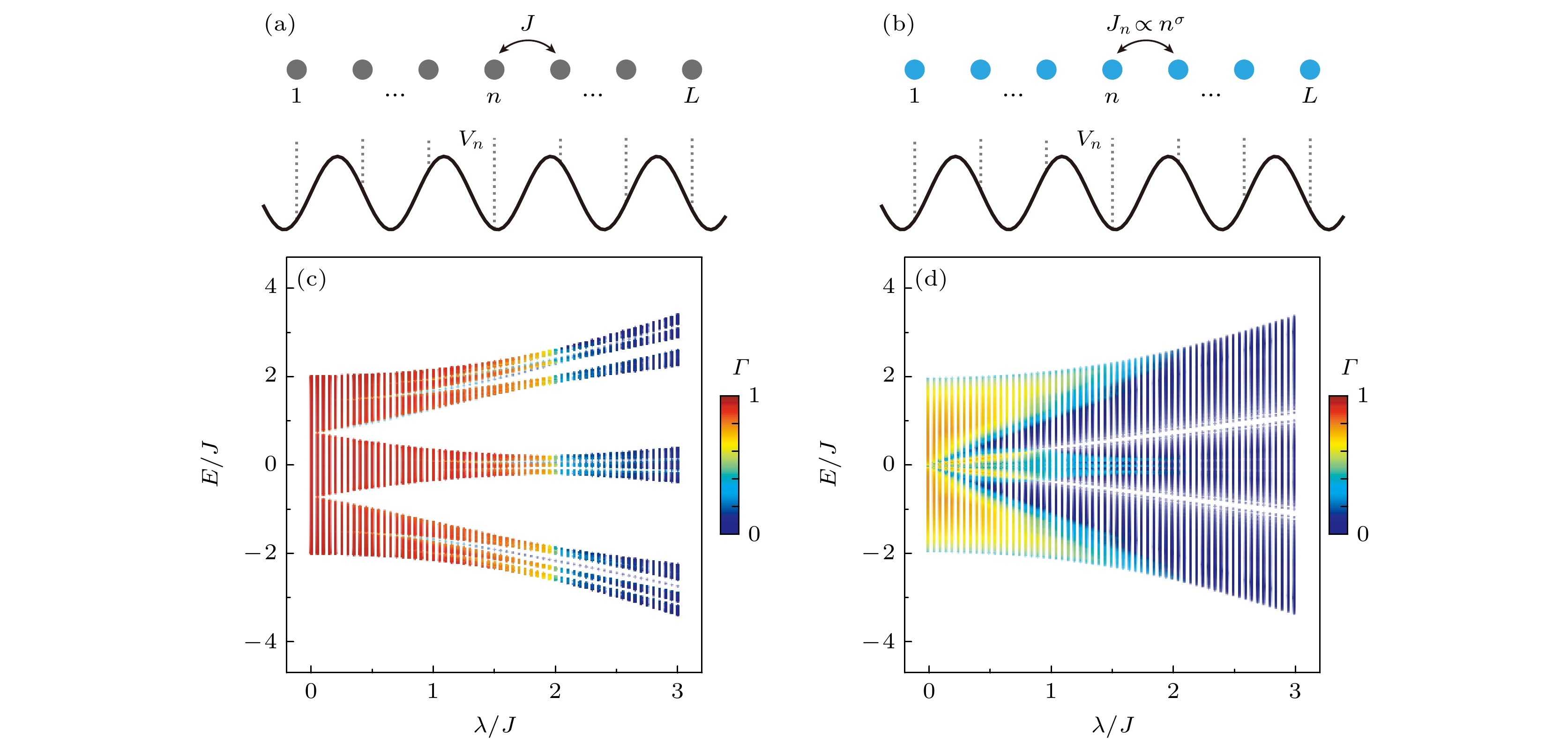
其中逆参与率$ {\rm{IPR}}_n = \displaystyle\sum\nolimits _{j=1}^{L} \left| \psi_{n, j} \right|^4 $, $ \psi_{n} $为第n个 本征态. 当本征态局域分布在几个格点上时, 有$ {\rm{IPR}} \to 1 $, 也即$ \varGamma \to 0 $; 延展本征态则趋于均匀分布在整条链上, 有$ {\rm{IPR}} \to 1/L $, 也即$ \varGamma \to 1 $; 对于两者间的临界态, 则有$ 0 < \varGamma < 1 $. 对于标准AAH链, 其局域化相变由一个临界调制强度$ \lambda/J = 2 $来刻 画^[19], 这一临界点清晰地体现在图1(c)中. 当$ \lambda/J < 2 $时, 所有本征态均处于延展相. 随着λ逐渐增大越过临界点$ \lambda/J=2 $, 系统经历相变进入局域相. 如图1(d)所示, 在弯曲时空下的AAH链中, 系统呈现出更为复杂的物理^[39]. 当$ \lambda/J=0 $时, 系统整体处于延展相. 随着$ \lambda/J $逐渐增大, 能谱中心出现延展相和局域相的混合相, 这种混合相被称作摇摆相. 摇摆相中, 本征态随调制相位ϕ的变化将在延展相和局域相之间摇摆, 而不是固定于单一的相. 进一步增大$ \lambda/J $, 系统中延展相、摇摆相和局域相将共存. 直到$ \lambda/J $增大到超过临界值$ 2 $, 系统将整体进入到局域相. 理论研究表明, 通过分析由相分离临界格点分隔的局域子链与延展子链的能谱, 可以获得弯曲时空AAH链的相图. 此外, 还可以利用标度分析方法来分辨不同的相^[39].

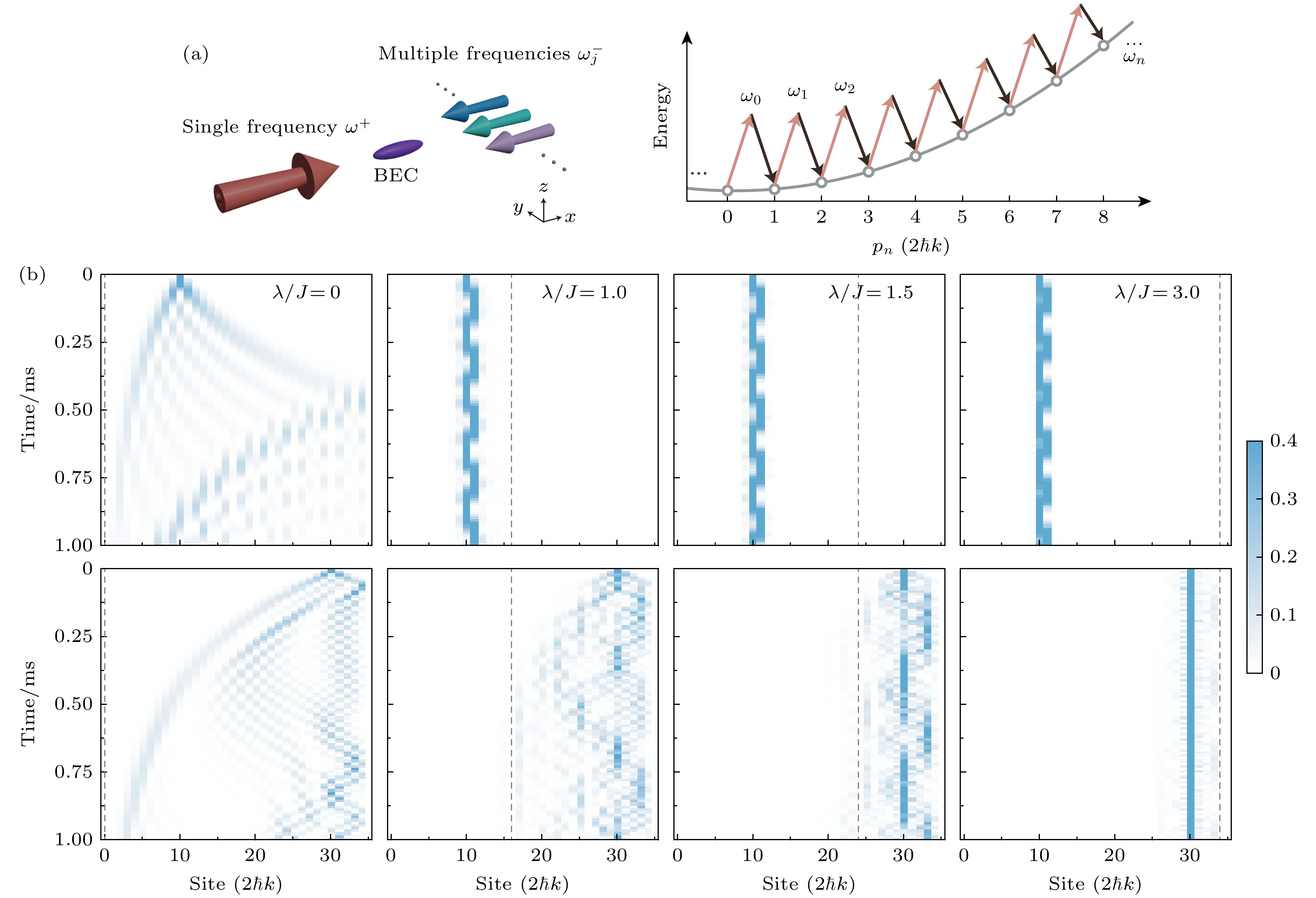
动量态晶格作为近年来出现的人造晶格技术, 为超冷原子实验提供了强大的晶格调制能力以及单格点分辨的探测能力. 在动量态晶格中, 可以轻松实现不同结构的一维晶格并引入各种无序^[46-49]. 动量态晶格本质上是一系列互相耦合的离散动量态组成的晶格, 而其中的离散动量态是由双光子过程中的动量守恒限制确定的. 如图2(a)所示, 在实验中, 用两束对打的远失谐激光照射玻色爱因斯坦凝聚体 (BEC) 原子团, 可以形成由原子动量态组成的一维晶格. 其中, 沿x轴正向传播的光场包含单一频率$ E^+\left(x, t\right) = E^+ {\rm{cos}}\left(k^+ x- \omega^+ t + \phi^+\right) $, 而反向传播的光场则由多频率成分组成, $ E^-\left(x, t\right) = \displaystyle\sum\nolimits _j E_j^- {\rm{cos}}\left(k_j^- x- \omega_j^- t + \phi_j^-\right) $. 这里所有光场被设定为近似单色的, 因此波矢$ k^+ \approx k_j^- \approx k = 2\pi/l $, 其中l是激光的波长. 本文中无需在耦合项中引入相位, 为了简单起见在后续的讨论中设置$ \phi^+ = \phi_j^- = 0 $. 若囚禁势阱对原子团的能级结构没有明显修饰, 则原子遵循自由粒子的二次型能量动量色散关系, 结合双光子过程中的动量守恒限制, 可以定义一系列离散的动量态$ |n\rangle = |n \cdot 2\hbar k\rangle $以及其对应能级$ E_n = (2n\hbar k)^2/(2M) = 4 n^2 E_{\rm{r}} $, 其中$ E_{\rm{r}} = \hbar^2 k^2/ \left(2 M\right) $是激光对原子的反冲能量, M为原子质量. 单频光场分别与多频光场中的各个频率成分组成双光子对$ \{\omega^+, \omega_j^-\} $, 对应的双光子能量$ \hbar \omega_j = \hbar\left(\omega^+ - \omega_j^-\right) $. 设定第j组双光子对相对耦合$ |n\rangle \leftrightarrow $ $|n+1\rangle $的失谐为$ \delta_{n, j} $, 则双光子能量$ \hbar \omega_j = 4 (2 n+ 1) E_{\rm{r}} + \hbar\delta_{n, j} $. 基于动量态晶格理论, 可以写出相互作用表象下的系统哈密顿量^[50,51]

其中$ \varOmega_j $是第j组双光子对的有效Rabi频率. 若近似条件$ \hbar \varOmega_j \ll 8 E_{\rm{r}} $和$ \hbar \delta_{j, j} \ll 8 E_{\rm{r}} $得到满足, 则(4)式的哈密顿量能够写成如下的有效哈密顿量:

其中$ \varepsilon_{n_i} = 0 $以及$ \varepsilon_{n \neq n_i} = \displaystyle \sum\nolimits _{m=n_i}^{n-1} \hbar \delta_{m, m} $, 这里$ n_i $是动量态晶格的起始格点. 选择实验参数使得$ \hbar\varOmega_n/2 = J_n $以及$ \varepsilon_{n_i+n-1} = V_n - V_{1} $, 就可以在动量态晶格中实现(1)式中的哈密顿量.

在本文的实验方案中, 选取⁷Li超冷原子系统作为实验平台. 根据文献[52], 可以通过Feshbach共振精确调控原子间相互作用. 由于本文中无需原子相互作用, 考虑处于$ | F = 1, m_F = 1 \rangle $内态的BEC原子团, 原子数$ N \approx 10^4 $以及囚禁势阱频率$ (\omega_x, \omega_y, \omega_z) = 2\pi (710, 710, 78) $ Hz, 则可以在520 G (1 G = 10^–4 T)的偏置磁场下得到接近于0的散射长度, 从而尽可能排除原子相互作用的影响. 在未来的 研究中, 还可以通过调节偏置磁场来研究系统在相互作用影响下的物理. 将对打激光的波长选定在$ 1064 $ nm, 可得反冲能量$ E_{\rm{r}} \approx 2\pi\hbar \times 25.119 $ kHz. 注意到要满足近似条件, 所有强度都要远小于$ 8 E_{\rm{r}} = 2\pi\hbar \times 200.952\; {\mathrm{kHz}} $, 因此本文中设定基准跃迁强度$ J = 2\pi\hbar \times 8\; {\mathrm{kHz}} $以及格点能量调制强度范围$ 0 \leqslant \lambda/J \leqslant 3 $. 通过一束包含单个频率的$ 1064 $ nm激光和一束反向传播的包含33个频率的$ 1064 $ nm激光对打照射⁷Li的BEC原子团, 就可构建链长$ L= F_9=34 $的弯曲时空AAH动量态链. 由于任何时候在初始时间原子都处于零动量态, 只能通过改变动量态链的初始和末尾动量态, 以相对地改变在整条链中注入初态的格点位置. 为了方便理解, 同时为了能与(1)式中的格点指标对应, 在后续的讨论中都会将整条链的格点指标固定为1—34.

考察波包在链中的演化过程, 可以揭示对应参数下AAH链的局域化性质. 在图2(b)中, 展示了$ 1 $ ms内不同格点能量调制强度$ \lambda/J $下的波包演化过程. 随着$ \lambda/J $逐渐增大, 理论预测的相分离临界格点$ n_{\rm{c}} $会从0开始扫过整条链, 直到超过最右端的格点34. 在此过程中, 由弯曲时空和准周期格点能量调制所共同确定的AAH链局域化区域逐渐增大, 而延展区域被逐渐压缩直至完全消失. 当$ \lambda/J = 0$时, 系统退化为弯曲时空下的普通晶格模型. 无论波包从初始格点$ n_0=10 $还是$ n_0=30 $开始演化, 都会扩散到几乎整条链. 当波包的左侧边界接近模拟事件视界的格点1时, 其扩散速度会持续减缓, 与平坦时空下普通晶格中波包对称扩散的现象形成鲜明对比. 当$ \lambda/J = 1.0 $和$J = 1.5 $时, 初始格点$ n_0=10 $位于临界格点左侧的局域区域中, 对应的演化动力学表现出了局域现象; 初始格点$ n_0=30 $则位于临界格点右侧的延展区域中, 波包在演化过程中扩散到了整个区域, 且几乎未越过对应的临界格点. 而当$ \lambda/J = 3 $时, 系统整体进入局域相, 从初始格点$ n_0=10 $和$ n_0=30 $出发的波包都会被局域在初始位置附近.

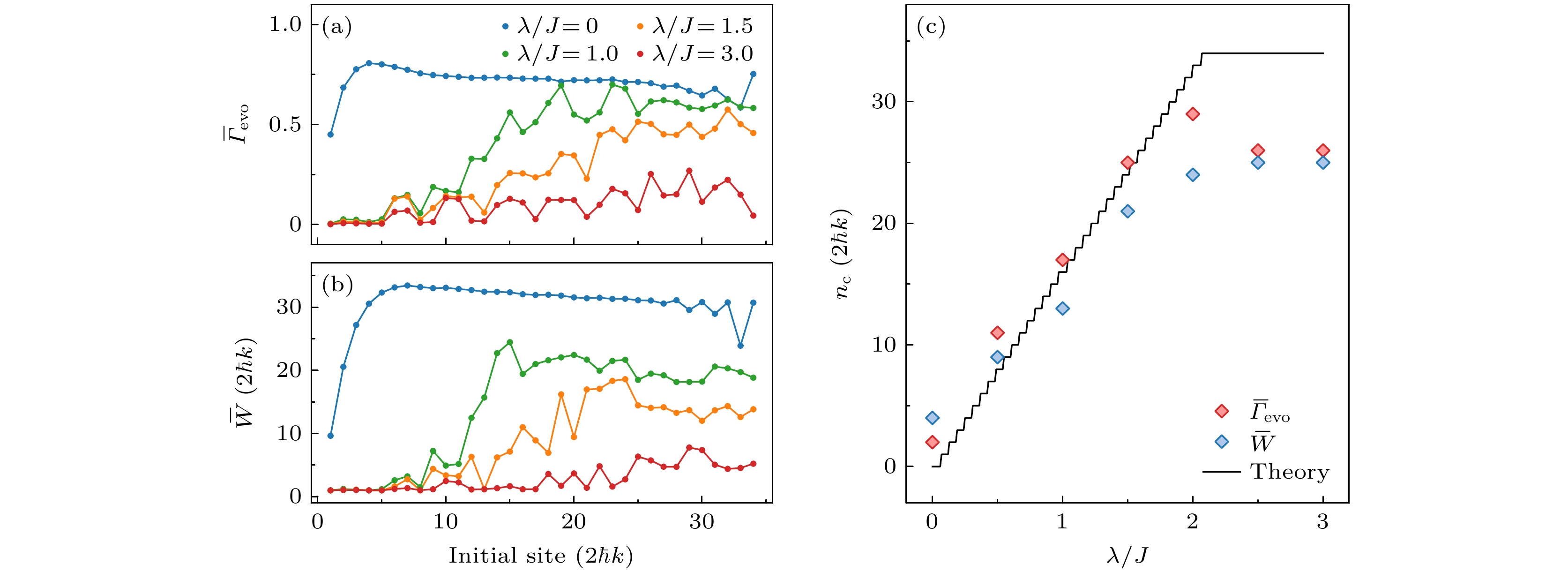
为了进一步定量表征弯曲时空下AAH链的局域化性质, 本文提出了通过波包演化数据提取的两个可观测量: 演化分形维数$ \varGamma_{\rm{evo}} $和波包宽度W. 定义t时刻的演化分形维数以及波包宽度如下:

其中$ P\left(t\right) $是t时刻波包的比例分布, 而$ {\rm{Index}}[P(t)\geqslant P_{\rm{Th}}] $是t时刻波包比例分布中大于阈值$ P_{\rm{Th}} $的格点指标. 图3(a)和图3(b)分别展示了在不同格点能量调制强度$ \lambda/J $下时间平均的演化分形维数$ \overline{\varGamma}_{\rm{evo}} $和时间平均的波包宽度$ \overline{W} $作为波包初始格点的函数, 其中波包宽度的阈值设定为$ P_{\rm{Th}} = 0.01 $. 随着$ \lambda/J $的增大, 表现出局域化的演化过程的波包初始格点逐渐变多, 局域化和非局域化的初始格点边界逐渐右移.

对于一个集合$ \left\{X_n \middle| n \in [1, L] \cap \mathbb{Z}\right\} $, 定义第n个点与后续点的平均值差值$ D_n = M_n - \dfrac{1}{L-n + 1} \times \displaystyle\sum\nolimits _{j=n}^{L} X_j $. 当$ 1 < n < L $时$ M_n =\！ \dfrac{1}{3}\displaystyle\sum\nolimits _{j=n-1}^{n+1} X_j $, $ M_1 = \dfrac{1}{2}\displaystyle\sum\nolimits _{j=1}^{2} X_j $, 以及$ M_L = \dfrac{1}{2}\displaystyle\sum\nolimits _{j=L-1}^{L} X_j $. 将集合$ \left\{D_n \geqslant 0\right\} $中第一个元素的指标定义为转变点, 对于$ \overline{\varGamma}_{\rm{evo}} $和$ \overline{W} $来说, 这个转变点就是可观测的相分离临界格点$ n_{\rm{c}} $. 图3(c)给出了不同格点能量调制强度$ \lambda/J $下从$ \overline{\varGamma}_{\rm{evo}} $和$ \overline{W} $解析出的临界格点$ n_{\rm{c}} $. 可以看到, 在$ \sigma=1 $的情况下, 当$ \lambda/J $增大, $ n_{\rm{c}} $随之接近线性地增大. 直到$ \lambda/J $超过临界值$ 2 $, $ n_{\rm{c}} $几乎不再变化. 从$ \overline{\varGamma}_{\rm{evo}} $和$ \overline{W} $解析出的临界格点, 与根据(2)式计算出的理论值较为符合, 其中$ n_{\rm{c}} \to L $附近的偏差主要来源于系统的尺寸效应.

研究不同能量本征态的局域化性质, 可以得到能谱中不同的相, 以及其中的迁移率边. 在弯曲时空AAH链中, 当时空弯曲参数σ足够大时, 所有本征态都会趋于极端局域化并分布在几乎单个格点上, 这正好符合动量态晶格中分布在零动量态的初始波包. 基于上述特性, 本文提出可以通过调制时空弯曲参数σ来制备能谱中的所有本征态. σ的调制曲线设定如下:

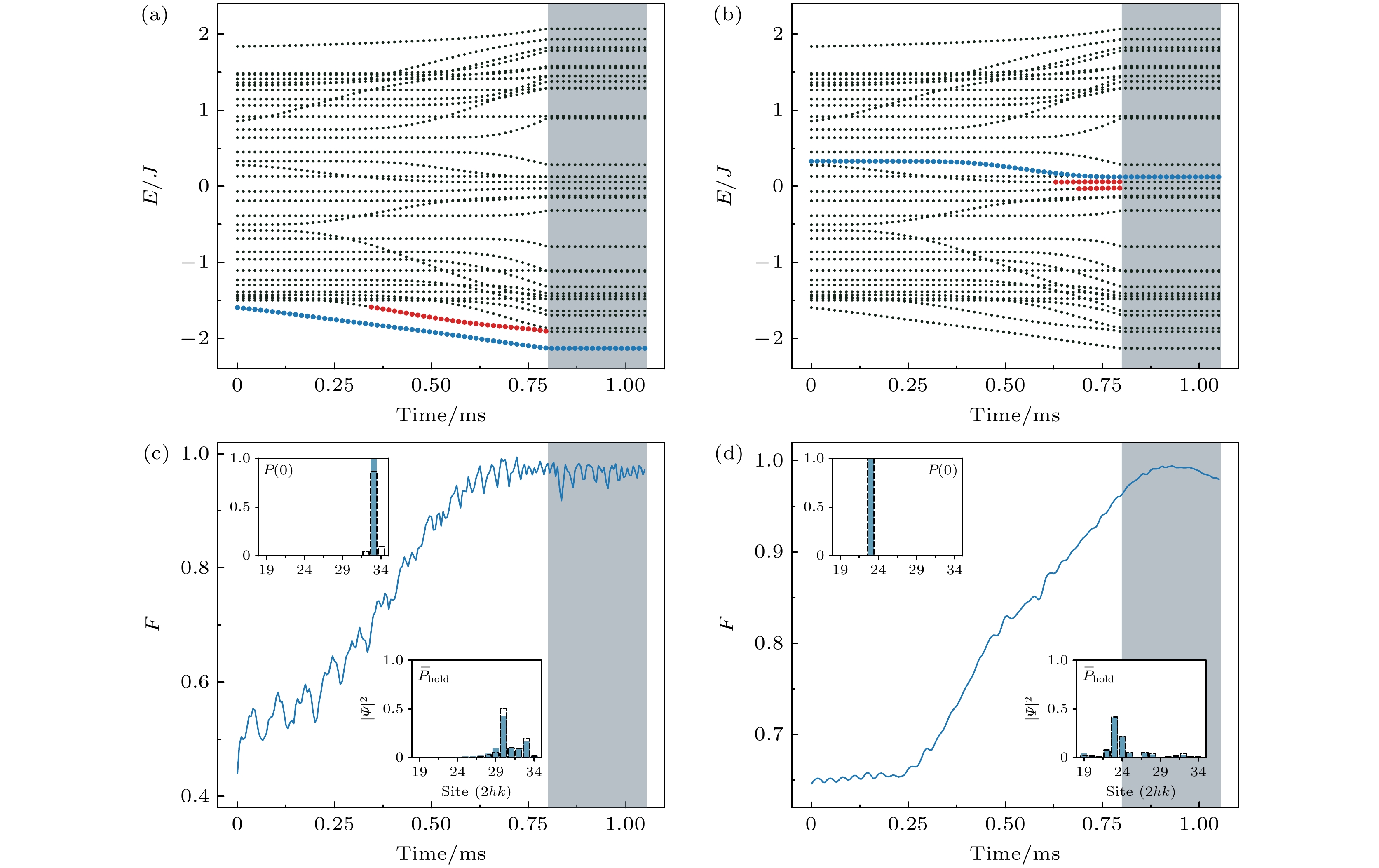
其中α是调制参数, $ t_{\rm{evo}} $和$ t_{\rm{hold}} $分别是演化阶段和保持阶段的时间, $ \sigma_{\rm{i}} $和$ \sigma_{\rm{e}} $则分别是$ \sigma\left(t\right) $的初始值和目标值. 从不同的初始格点出发, 依据(8)式的曲线调制σ, 就能最终演化到对应的本征态. 定义制备保真度

其中$ P^{\rm{eig}} $是目标本征态的概率分布. 针对不同的初始格点, 在固定保持时间$ t_{\rm{hold}} = 0.25\;{\mathrm{ms }} $的条件下, 对演化时间$ t_{\rm{evo}} \in [\text{0.1 ms}, \text{0.8 ms}] $和参数$ \alpha \in [1, 15] $下的制备过程进行数值计算. 以保持阶段保真度几何平均值最大为准则, 选取优化的制备参数. 图4分别演示了从初始格点$ n_0 = 33 $和$ n_0 = 23 $出发制备本征态的过程. 对于含时哈密顿量$ H(t) $中的本征态$ |\psi_n\rangle $, 绝热参数$ A = |\langle\psi_m|\dot{H}|\psi_n\rangle|/\varDelta_{mn}^2 \ll 1 $是其绝热演化的条件. 其中$ |\psi_{m \neq n}\rangle $是除去目标本征态的其他本征态, $ \varDelta_{mn} $是本征态$ |\psi_m\rangle $与$ |\psi_n\rangle $之间的能量差. 在图4中, 仅有少数本征态在短时间内与目标本征态之间的绝热参数$ A > 0.1 $. 在整个本征态制备过程中, 绝大部分时间内初态是沿着设计的制备路径绝热地进行演化的. 在制备过程的初始时刻, 初始格点为$ 23 $的波包对应的本征态也完全分布在格点$ 23 $上; 初始格点为$ 33 $的波包对应的本征态则有很小部分还分布在相邻的格点. 随着时间的演化, 从两个初始格点出发的制备保真度随之增大, 最后在保持阶段基本达到$ 0.95 $以上. 将保持阶段的波包分布做时间平均, 可以观察到其比例分布与理论预测的本征态概率分布十分一致. 结果表明, 这种制备方案具有较高的有效性.

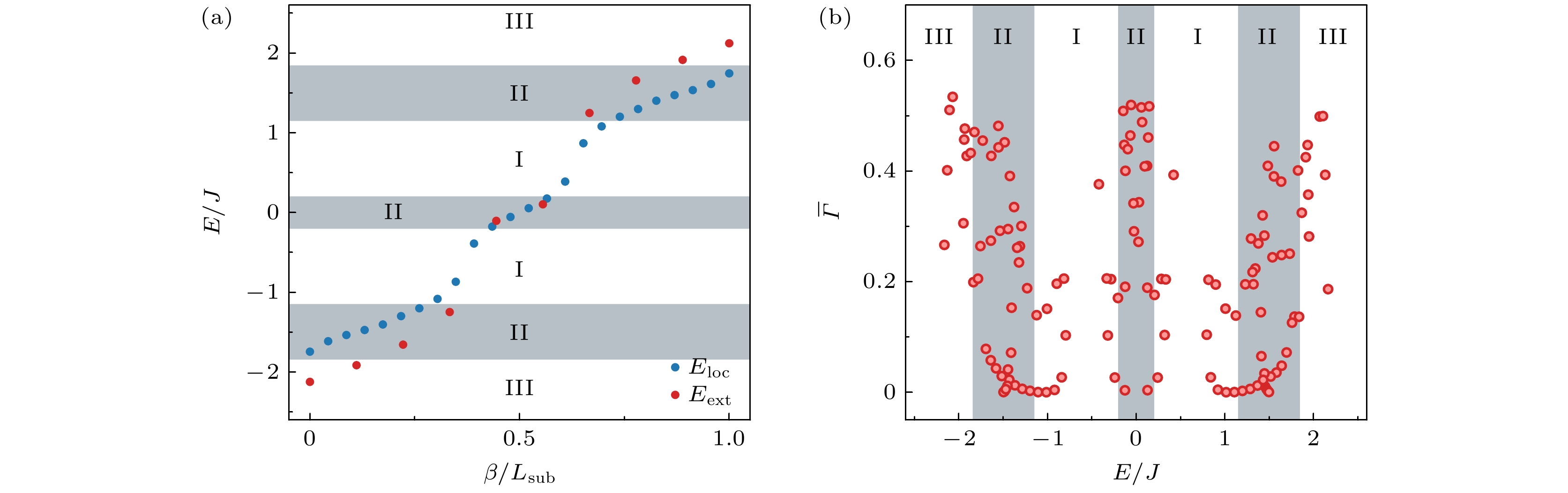
图5(a)展示了被相分离临界格点$ n_{\rm{c}}= 24 $分隔的两条子链对应的理论能谱. 为了标记出摇摆相, 对101个不同相位ϕ下的计算结果进行了平均处理. 为了便于比较, 能级指标β根据各自子链的链长进行了归一化. 在图中, 属于局域子链的本征能量单独出现的区域标记为局域相I; 两条子链共存的能量区域标记为摇摆相II; 而属于延展子链的本征能量单独出现的区域标记为延展相III.

接着, 基于上述的本征态制备方案, 就可以实现能谱中所有本征态的制备. 通过获取各本征能量对应的本征态, 可以直观分析其局域化性质, 并解析出能谱中不同本征能量对应的相. 如图5(b)所示, 在四种不同相位设置下, 通过动量态晶格分别制备了能谱中的所有本征态, 并根据保持阶段时间平均的波包比例分布$ \overline{P}_{\rm{hold}} $计算得到了对应的分形维数$ \overline{\varGamma} = - \ln{\displaystyle \sum\nolimits _{j=1}^{34} \overline{P}_{{\rm{hold}}, j}^2} / \ln{34} $. 不难发现, 在理论给出的摇摆相区域II内, $ \overline{\varGamma} $的范围从$ 0 $到$ 0.5 $跨度相当大, 这表明局域本征态和延展本征态共存, 符合理论预期. 在局域相理论区域I内, 除去个别点$ \overline{\varGamma} $基本都小于$ 0.2 $, 本征态表现出局域化的特性. 而在延展相理论区域III内, 除去个别点$ \overline{\varGamma} $都大于$ 0.25 $, 也就是本征态表现出延展化的特性. 数值仿真结果表明, 在能谱中出现了共存的I局域相、II摇摆相和III延展相, 且存在调制相位ϕ依赖的摇摆迁移率边. 注意到, 在足够长的弯曲时空AAH链中, 理论分析指出$ E=0 $附近的摇摆相II中会分出多个局域相和摇摆相^[39], 而图5中$ E=0 $附近的简单结构主要是由尺寸效应所导致的.

本文提出了在超冷原子动量态晶格中编辑幂律位置依赖的耦合强度$ J_n \propto n^{\sigma} $实现弯曲时空AAH链的实验方案. 基于动量态晶格的数值模拟结果, 展示了相分离临界格点两边不同局域性质的波包演化过程, 并根据演化动力学数据得到了随准周期调制强度线性变化的相分离临界格点. 另外, 利用对时空弯曲参数的调制, 提出了制备弯曲时空AAH链的本征态的方案. 最后, 从制备的本征态中分析了能谱中的局域化性质, 并确认了在能谱中共存的局域相、摇摆相和延展相. 本文为弯曲时空下的AAH模型提供了可行的实验方案, 特别是基于时空弯曲程度调制的本征态制备方案, 可以进一步应用于类似的弯曲时空晶格模型的研究中. 此外, 这种本征态制备方案还可能被用在标准AAH模型的本征态制备中, 为相关的研究提供了新的工具^[25,26].