首页
登录
注册
下载:
-
里德伯原子指的是主量子数很大(n＞10)的高激发态原子. 里德伯原子的原子轨道半径较大, 结合能较小, 对外场敏感, 原子寿命较长, 电极化率较大, 是一种很好的电磁场传感器. 基于里德伯原子的电磁波探测技术是利用量子效应来实现电场的测量和探测, 不受限于电子学探测器的经典极限, 其能达到的最优指标取决于量子极限, 因此在灵敏度、带宽、抗干扰等方面有望超越基于电子学的电磁波探测器. 随着量子精密测量技术的发展, 近年来基于里德伯原子的电磁波传感器的研究取得了巨大进展. 利用里德伯原子电磁诱导透明(electromagnetically induced transparency, EIT)和AT(Autler-Townes)分裂效应[1–4], 已实现可溯源电场探头[1,5]、功率传感器[6]、电压测量[7,8]、到达角检测[9]和通信信号接收[10–14]. 为提升原子传感器的灵敏度, Jing等[15]在微波频段实现了里德伯原子超外差探测方案, 灵敏度达55 nV/(cm·Hz1/2), 并且该方法可实现频谱分析功能[16–19].
太赫兹波是指频率在0.1—10 THz范围内的电磁波, 这部分波段介于微波和红外波之间, 太赫兹具有穿透力强、指向性好、光子能量低等特点, 在成像、通信、材料检测、安检等领域具有广泛应用前景. 但由于人们对太赫兹波的研究起步较晚, 产生和探测难度较高, 并且该波段尚未被开发, 因此常被人成为“太赫兹间隙”. 里德伯原子在太赫兹频段仍然具有较大的电偶极矩, 将原子传感器用于探测太赫兹波也会具有极高的灵敏度. 最早Chen等[20]将里德伯原子用于探测太赫兹场[20]和高速高灵敏太赫兹成像[21,22]. 国内, 陈志文等[23]同样将原子传感技术拓展至太赫兹频段, 实现了可溯源太赫兹电场强度精密测量, 并演示了用原子接收机实现太赫兹无线通信[24]. 进一步实现了太赫兹频段的原子超外差探测[25], 探测器的等效噪声功率已优于现有电子学探测器.
太赫兹优异的穿透性特点在工业测厚方面具有极佳的应用前景, 适用的材料包括木材、纸张、陶瓷、塑料以及多种复合材料. 并且无需接触样品表面, 非接触测量更易于工业自动化集成, 而其不具有电离辐射的特点对操作的人员提供了安全保障. 太赫兹测厚是材料科学和工业检测中的重要技术, 利用太赫兹的传播特性实现厚度测量, 主要包括太赫兹光谱法和成像法. 光谱法基于飞行时间原理, 发出太赫兹波作用在样品上, 太赫兹波具有穿透性能够到达每一个界面层, 然后在每个界面产生相应的反射信号, 通过分析每个界面的反射太赫兹信号即可对被测材料的厚度实现检测[26–30]. 成像法利用太赫兹在材料表面的近场分布来获取厚度信息. 受限于太赫兹源的有限功率和太赫兹探测器的灵敏度, 传统太赫兹测厚技术有待进一步提升和完善. 由于原子超外差太赫兹探测具有优于传统探测器的灵敏度, 因此有望提升材料测厚的精确度, 并扩展太赫兹测厚技术的应用范围, 例如更厚的有机材料、超导金属薄膜等.
本文在实现室温原子超外差太赫兹高灵敏 探测的基础上, 将该技术应用于材料的厚度测量上. 该室温原子超外差太赫兹探测场强灵敏度为5.76 μV/(cm·Hz1/2), 线性动态范围达到60 dB. 将待测样品放置于太赫兹信号场内, 通过原子超外差探测信号的强度变化测出样品的太赫兹透射率, 根据标准样片的厚度和透射率, 可以计算得到待测样品的厚度值. 本文实验测量了蓝宝石晶体材料和聚四氟乙烯有机材料的厚度, 而且由太赫兹透射信号可以清晰地分辨出单层石墨烯与少层石墨烯. 甚至对于厚度达到1 μm的超导金属铌薄膜也可以探测到微弱的太赫兹透射信号, 这都得益于原子超外差太赫兹探测器的高灵敏度.
-
在原子超外差中, 太赫兹信号的全部信息被编码在太赫兹缀饰里德伯暗态的一阶能量转移中. 强共振的局域太赫兹场导致两个缀饰态
$ \left| \pm \right\rangle $ , 在能量上被$\hbar \varOmega_{\rm L}$ 隔开, 其中$\hbar $ 是普朗克常数. 这两个态分别对应25S1/2和25P3/2两个里德伯能级的对称与反对称叠加, 使得本征能量以余弦形式微扰振荡, 表达式为其中, 幅值与演化的相位分别由±
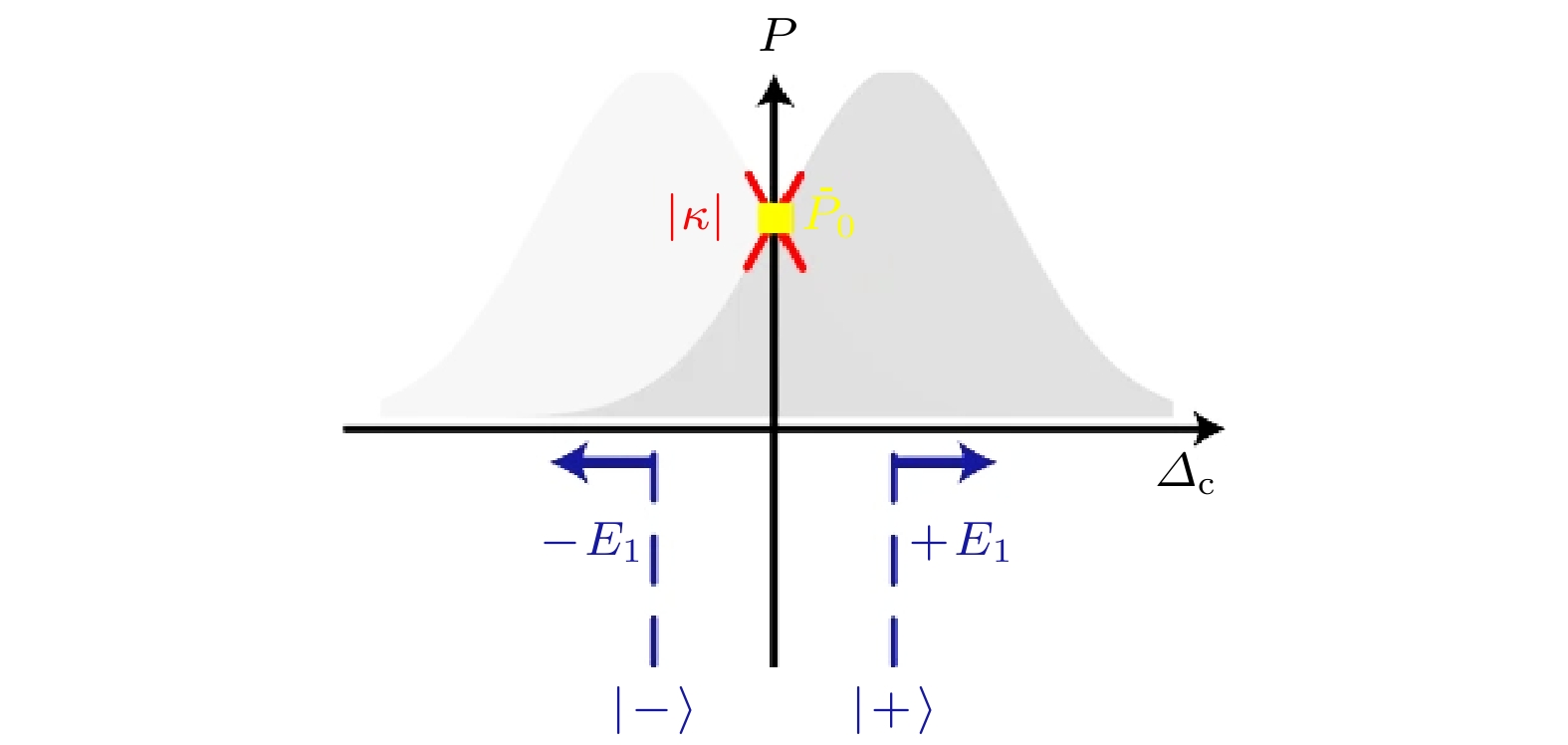
$\hbar $ ΩSig/2, Φ(t)决定. 根据投影到探测光的共振透射光谱, 如图1所示. 以本征能量为中心的浅灰色和深灰色包络分别表示系统耗散导致太赫兹缀饰里德伯暗态的光谱, 由此将本征能级的微扰振荡±E1转换为探测光的透射光强, 转换效率正比于光谱线型的斜率|κ|. 因此调节本振场太赫兹拉比频率的大小, 可以实现对光谱特性的调节, 从而使得共振位置$ {\bar P_0} $ 处光谱线型斜率最大, 即本征能级$ \left| \pm \right\rangle $ 扰振荡斜率最大, 此时探测光透射率最大, 表明这一系统参量下原子外差系统对外场响应最灵敏. 同时根据上述推理, 也证明了在原子外差系统中, 本振太赫兹场作为频率和相位的参考, 与待测信号场相互干涉, 从而利用其产生的中频信号解码信号太赫兹场的相位和频率信息.因此, 原子超外差探测技术以里德伯原子作为混频器, 将对太赫兹信号场的高频测量转换为低频差频(fIF = δ)信号的测量, 通过光学探测读出. 探测光强度表达式为
其中
$ {\overline P_0} $ 表示探测光的平均透射强度, κ表示系统总的内禀增益系数. 由表达式可以分析出, 探测光透射强度可线性响应太赫兹信号场的电场强度, 且可以同时获得信号场与本振场的相对频率和相位信息. 对于振荡信号的测量可以通过傅里叶变换实现:式中, |P(δ)|表示对P(t)进行傅里叶变换后频域的探测光强度, 在频率为δ处, 单边傅里叶频谱|P(f)|的幅值为
根据上述公式可以推导出, 外差测量中待测场的绝对电场强度为
其中μ表示里德伯能级跃迁偶极矩. 由于参量|κ|和|P(δ)|都是直接从光谱中导出, 可以将太赫兹电场强度测量简化为光学频率测量, 因此原子外差探测方法具有可溯源性. 将光电探测器探测到的光强振荡信号进行傅里叶变换后, 用频谱上差频信号的强度来进行太赫兹电场强度的测量, 极大地提高了探测灵敏度, 特别是在太赫兹频段.
材料对电磁波响应可以由多种函数来描述[31], 对于特别厚的材料, 如果吸收很小, 例如本文中测量的蓝宝石晶体和聚四氟乙烯有机材料, 材料的折射率nj可近似为实数. 将厚度为d的均匀介质样品放置在空气中, 空气折射率为ni, 则透射率可以由通过样品后传输的电磁波电场强度Es的大小得出, 其表达式为
其中, ω为太赫兹频率, Er为无样品、空气中传输时的电磁波电场强度大小. 根据菲涅耳透射系数tij和反射系数rij, 传播因子
$ \exp ({\text{i}}n\omega d/c) $ 以及描述材料内部多重反射的Fabry-Perot项Fiji, 可以直接得出该介质的透射率, 表达式为其中, 下标i和j分别表示自由空间和材料样品, c是光速. 正入射时:
其中, Fabry–Perot项的上限p是由材料内部反射次数决定的, 对于较厚的材料, p可取为0. 在原子超外差太赫兹测厚的实验中, 采用的是固定频点(频率为338.7 GHz)的太赫兹信号测量材料样品的透射率, 因此(7)式可简化为
由于材料透射率与厚度d呈指数关系, 因此在已知标准样品的厚度前提下, 通过测量和比较待测样品与标准样品的太赫兹透射率, 可计算得到待测样品的厚度, 表达式如下:
其中, ds和dr分别表示待测样品与标准样品的厚度, Ts和Tr分别表示样品对应的透射率.
-
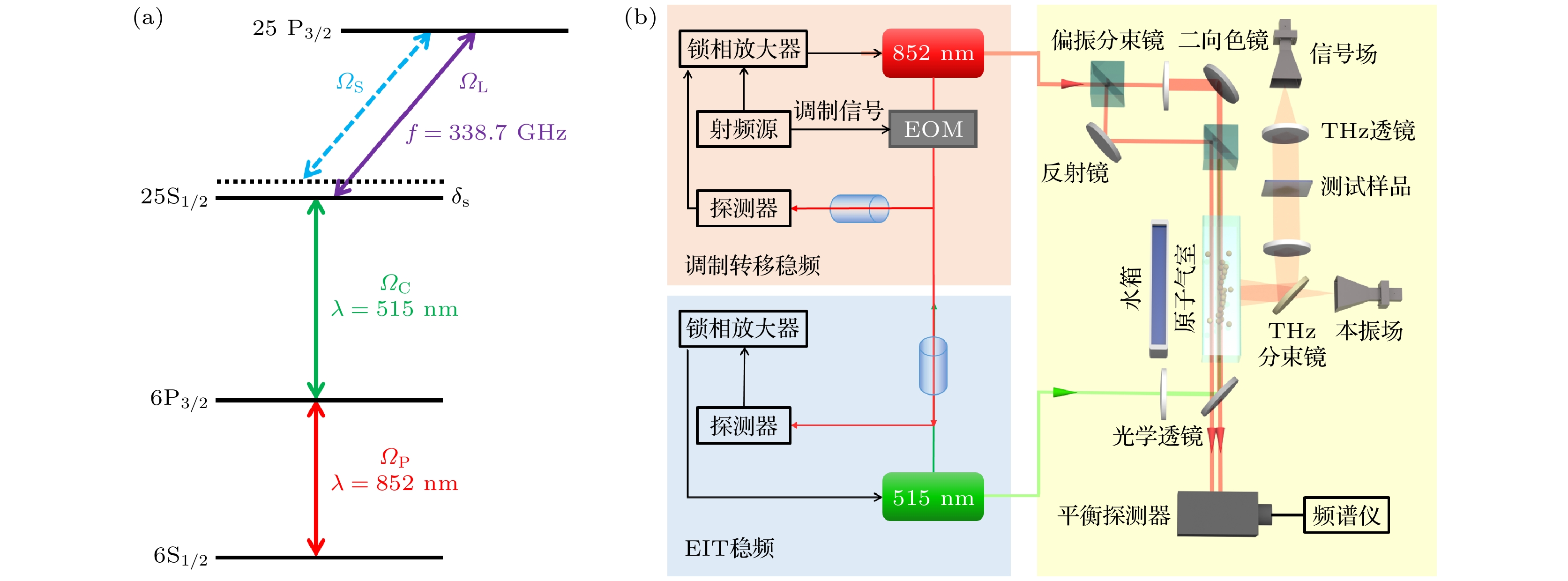
如图2(a)所示, 在室温铯原子气室中, 通过双光子激发实现里德伯原子的制备. 探测光852 nm与原子能级跃迁6S1/2→6P3/2耦合, 耦合光515 nm激光将6P3/2态的原子耦合至里德伯态25S1/2. 实验中将电光相位调制器(EOM)作为外部调制器为852 nm激光器提供调制信号, 通过调制转移稳频的方式实现激光频率稳定. 为使其与515 nm激光器同步, 在电光相位调制器后分出一束光与部分耦合光相互作用于原子, 实现EIT稳频, 如图2(b)所示. 实验采用外部调制的锁频方式, 以达到降低系统频率噪声的目的. 将852 nm探测光分为两束, 一束作为参考光, 一束作为探测光, 采用平衡探测器(PDB)进行探测以减小背景抖动的影响. 测厚时需增强太赫兹波束与待测样品的相互作用, 以提升测量精度, 因此采用柱面镜将激光束整形为2 mm宽的光片, 以增大原子与太赫兹波束的相互作用面积. 耦合光与探测光对向入射进入10 mm×10 mm×60 mm的长方体原子气室. 探测光功率为 256 μW, 拉比频率为Ωp/(2π) = 19.72 MHz. 耦合光功率为 11 mW, 拉比频率为Ωc/(2π) = 1.79 MHz. 太赫兹本振场(LO)与25S1/2→25P3/2能级跃迁共振, 频率为338.7 GHz, 径向电偶极矩513ea0. 信号场(SIG)与本振场固定差频为δS = 250 kHz. 实验利用焦距为50 mm的太赫兹透镜对信号场进行准直, 使太赫兹均匀平行穿透样品. 然后由焦距为150 mm的透镜将太赫兹信号场聚焦于原子气室. 利用水对太赫兹的强吸收, 将水槽放置于原子气室后方用以吸收穿透原子气室的太赫兹波, 避免反射太赫兹波对探测信号的干扰.
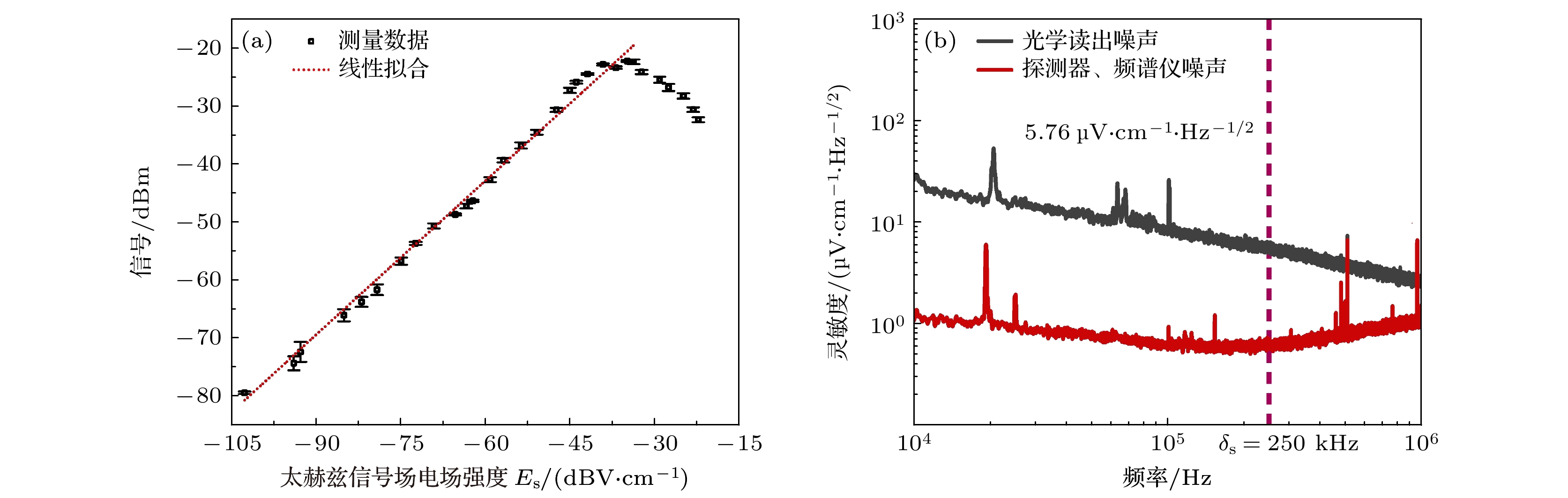
根据图2所示实验方案, 利用里德伯原子作为混频器, 可将太赫兹信号下转换为δS = 250 kHz的中频信号. 中频信号强度与待测场电场幅值在一定范围内呈线性变化, 由频谱分析仪测量, 如图3(a)所示. 由于太赫兹倍频源功率是非线性改变的, 为校准线性动态范围, 首先在EIT Autler-Townes分裂(ATS)线性区域内测得两个点的电场强度值, 然后利用衰减片逐步减弱太赫兹功率, 以确认另外两个点的电场强度值, 然后通过降低太赫兹固态倍频源的微波基频的功率, 使其在原子处的电场强度与衰减后两点的电场强度一致. 反复进行以上操作, 最终完成整个线性范围的校准. 当信噪比(SNR)为1时, 获得能够测量的最小电场为7.88 µV/cm (探测时间为1 s), 最大线性动态范围为70 dB左右. 此外, 实验还采集并分析了系统的噪声频谱, 包括PDB和频谱分析仪光学读出噪声、激光频率噪声和原子传输噪声, 如图3(b)所示. 所测得的灵敏度S是中频信号频率δS的函数, 频谱中红色虚线处频率为δS = 250 kHz, 与黑色曲线相交处表示系统灵敏度为5.76 μV/(cm·Hz1/2). 噪声频谱得出的灵敏度与线性动态范围校准得出的1 s探测时间的最小可探测电场一致.
-
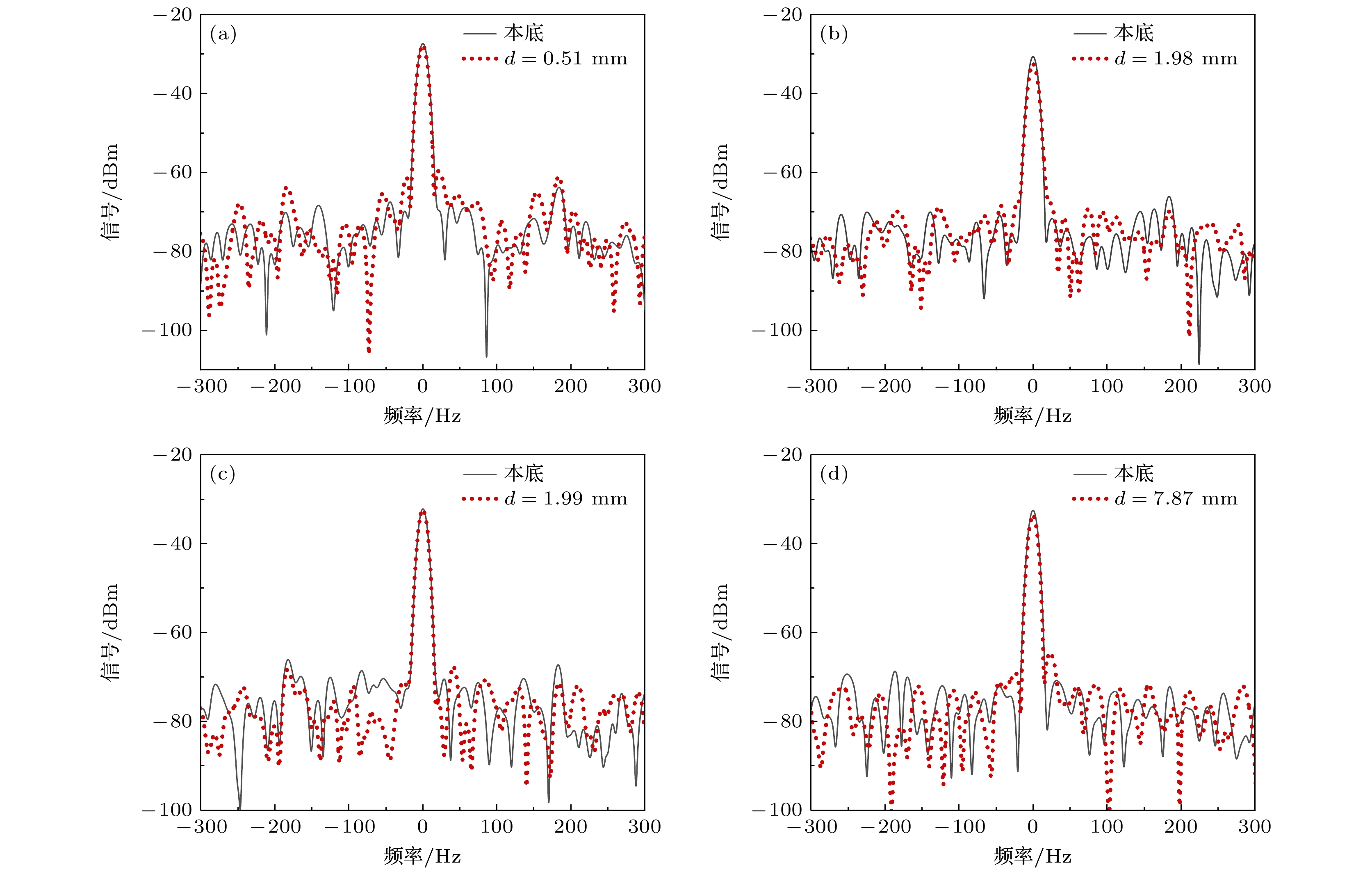
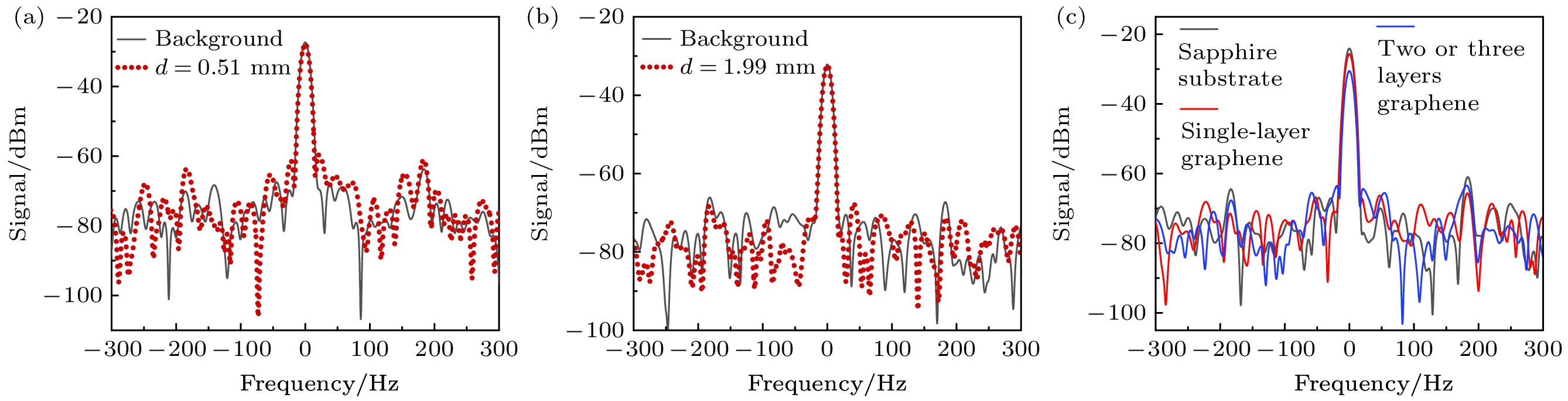
太赫兹对非金属材料具有很好的穿透性, 实验选取了两种不同固体材料进行太赫兹测厚验证. 首先是蓝宝石晶体材料, 如图4(a), (b)所示, 以厚度为0.51 mm的蓝宝石片为标准样品, 测得超外差中频信号强度为(–27.72±0.07) dBm, 对比未加样品时的信号强度(–27.21±0.07) dBm, 得到透射率约为89%. 将待测蓝宝石片放入太赫兹信号场中, 测得加样品前后的外差中频信号强度值(–30.52±0.07) dBm和(–32.41±0.03) dBm, 获得透射率约为64.7%. 对比待测样品与标准样品的透射率, 由于材料透射率与材料厚度呈指数关系, 计算得到待测蓝宝石片厚度为1.91 mm, 与游标卡尺测量的厚度值1.98 mm一致. 其次是聚四氟乙烯有机材料, 如图4(c), (d)所示, 以1.99 mm厚度的聚四氟乙烯为标准样品, 测得外差中频信号强度为(–32.73±0.51) dBm, 对比未加样品的信号强度(–32.45±0.53) dBm, 获得透射率约为93.7%. 实验将聚四氟乙烯待测样品放入太赫兹信号场中, 对比加样品前后的外差中频信号强度值(–32.24±0.08) dBm和(–33.42±0.12) dBm, 获得透射率约为76.3%, 根据理论计算获得待测样品厚度为8.27 mm, 与游标卡尺测量得到的厚度值7.87 mm一致. 由以上结果可知, 对于晶体和有机材料, 太赫兹虽然具有良好的穿透性, 但根据原子超外差探测的透射信号, 仍然可以计算得到待测样品的准确厚度.
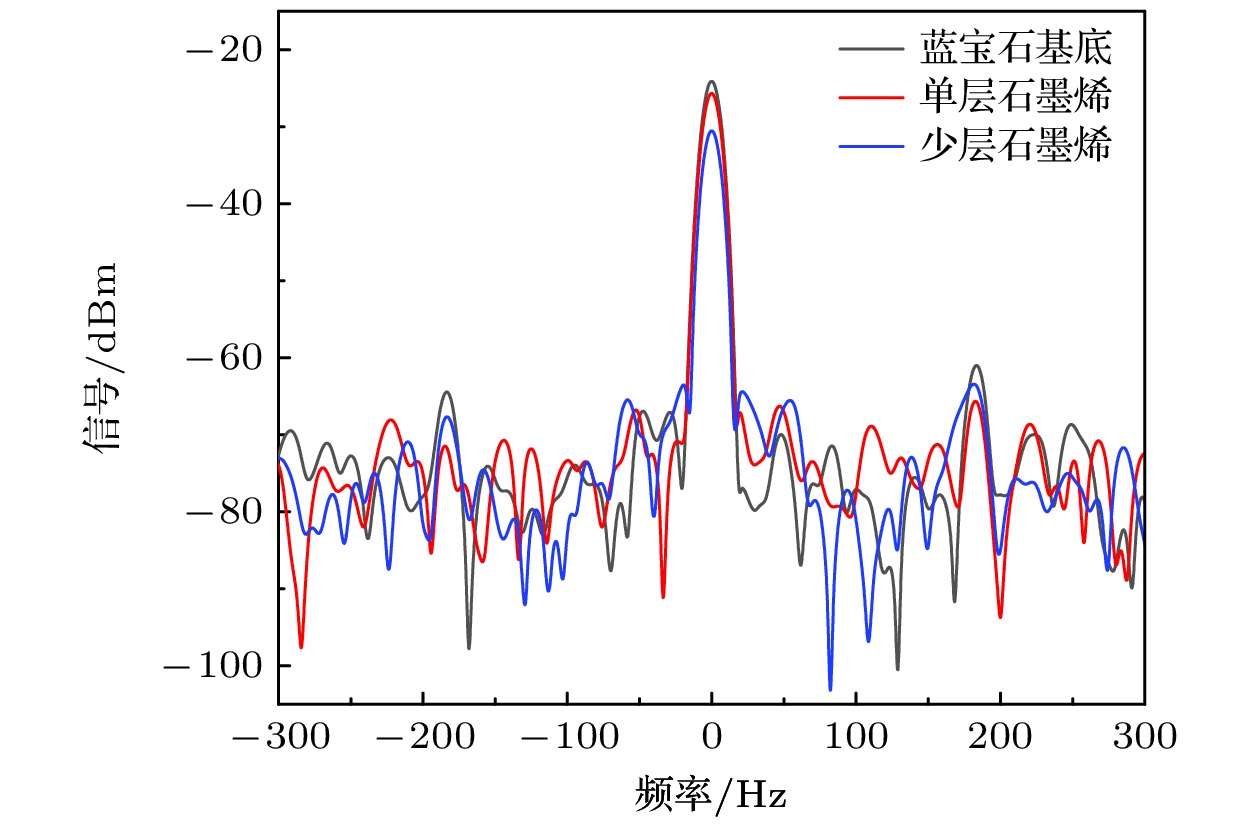
对于厚度小于1 μm的薄膜材料, 不满足(11)式的条件, 但仍然可以由原子超外差探测到的太赫兹信号透射率的差别来区分该种材料的不同厚度甚至不同层数. 石墨烯是二维碳材料, 具有优异的光学、电学、力学特性, 在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景, 被认为是一种未来革命性的材料. 实验选取了蓝宝石基底的石墨烯作为测试样品, 分别测量了蓝宝石基底、以蓝宝石为基底的单层石墨烯和少层石墨烯的太赫兹透射信号, 如图5所示. 通过对比加样品前后的外差中频信号强度值, 获得蓝宝石基底的透射率为76.2%(黑色曲线). 未加入蓝宝石基底的单层石墨烯样品的中频信号强度为(-23.36±0.35) dBm, 加入样品后为(–25.748±0.42) dBm (红色曲线), 则单层石墨烯材料的透射率约为57.7%. 少层石墨烯材料的层数为双层或三层, 加样品前后的外差中频信号强度值为(–27.61±0.23) dBm和(–30.34±0.18) dBm(蓝色曲线), 获得透射率约为53.3%. 分析实验结果获得, 原子太赫兹测厚方法能够清楚地分辨出单层石墨烯与少层石墨烯透射信号的差异, 说明原子超外差太赫兹探测对石墨烯的层数分辨具有很高的灵敏度.
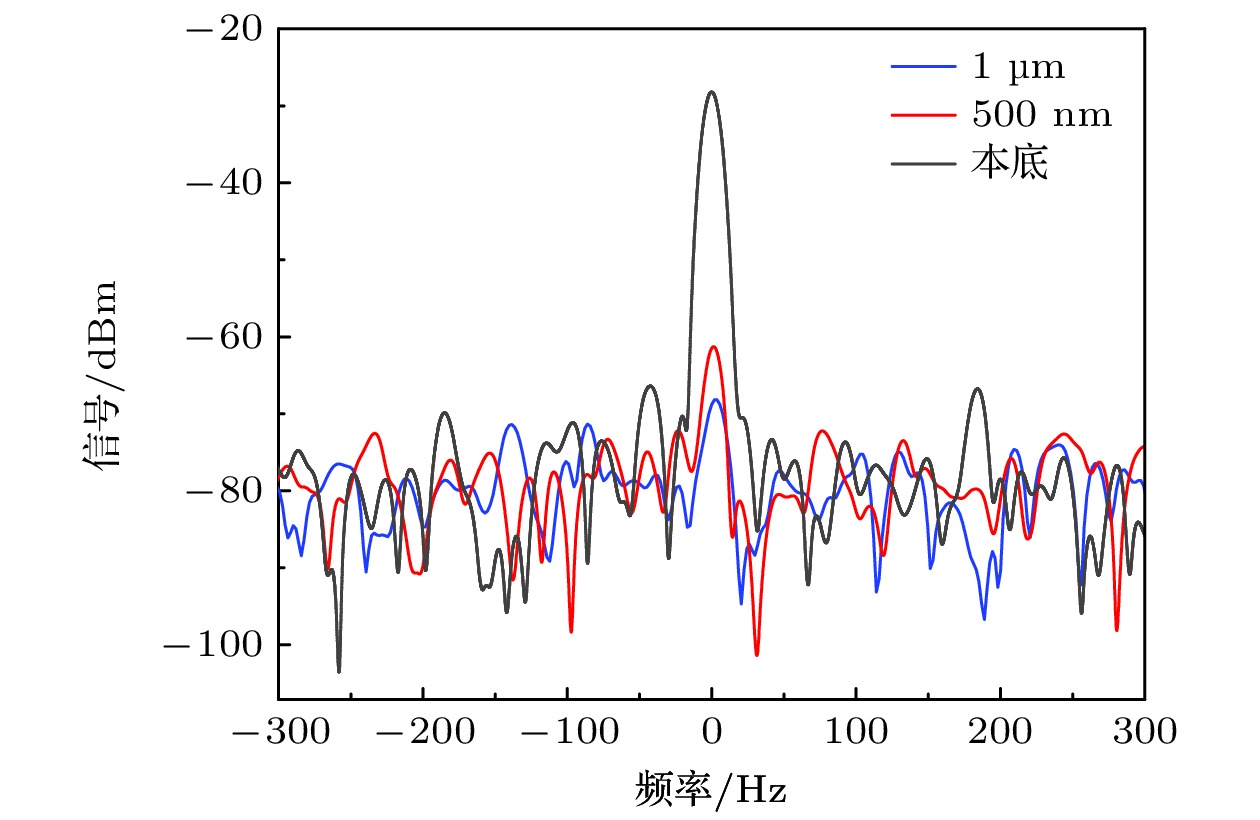
基于原子超外差太赫兹探测的高灵敏以及大线性动态范围的优势, 实验进一步验证其对金属薄膜材料的厚度测量, 测试样品为以430 μm厚的蓝宝石为基底的超导铌膜, 实验结果如图6所示. 加样品前的外差中频信号强度(–24.435±0.193) dBm(黑色曲线), 加入500 nm厚的铌膜后信号强度为(–61.474±0.385) dBm(红色曲线), 1 μm薄膜的外差中频信号强度值为(–68.494±0.337) dBm(蓝色曲线). 对比加入样品前后信号强度值, 500 nm薄膜的太赫兹透射率约为1.98×10–4, 1 μm薄膜的透射率约为4.7×10–5. 由实验结果可以验证, 对于金属薄膜材料原子外差太赫兹探测器仍然可以通过太赫兹透射信号分辨出薄膜的厚度差别.
-
本文基于原子太赫兹超外差探测方法, 在室温条件实现了5.76 μV/(cm·Hz1/2)的太赫兹电场强度测量的灵敏度, 线性动态范围可达60 dB, 并利用这些优点将其应用于材料厚度测量. 首先, 通过测量太赫兹信号场对蓝宝石晶体材料、聚四氟乙烯有机材料的透射率, 从而计算获得材料厚度, 证明了原子超外差太赫兹测厚的高准确度. 进一步, 原子超外差太赫兹测厚系统可以由透射信号的差异, 灵敏地分辨出单层石墨烯与少层石墨烯. 由于原子超外差系统具有较大的线性动态范围和极高的灵敏度, 可探测到微弱的穿透厚度为1 μm的超导金属薄膜材料的太赫兹透射信号. 基于原子超外差探测器的太赫兹测厚方法不仅可以应用于固体材料、二维材料的测量, 还可以实现金属薄膜材料的厚度检测, 在太赫兹测厚、无损检测等应用领域具有广阔的应用前景.
基于原子超外差探测的太赫兹测厚
Terahertz thickness measurement based on atomic superheterodyne detection
-
摘要: 基于室温原子的超外差太赫兹电场探测, 场强灵敏度可达5.76 μV/(cm·Hz1/2), 线性动态范围优于60 dB. 原子超外差太赫兹探测具有极高的灵敏度, 可用于精确测量材料的透射率, 实现对材料厚度的高精度测量. 本文实验测量了蓝宝石晶体材料和聚四氟乙烯有机材料的厚度, 而且由太赫兹透射信号可以清晰地分辨出单层石墨烯与少层石墨烯. 甚至对于厚度达到1 μm的超导金属铌薄膜也可以探测到微弱的太赫兹透射信号, 这都得益于原子超外差太赫兹探测器的高灵敏度. 总之, 本文采用的基于原子超外差探测太赫兹测厚技术, 在有机材料缺陷检测、涂层材料测厚及二维材料参数测量等方面都具有重要的应用价值.Abstract: Terahertz thickness measurement is very important in materials research and industrial test. And it can beused to measure various materials such as wood, paper, ceramics, plastics, and composite materials. Atomic superheterodyne terahertz detector has extremely high sensitivity. The sensitivity of terahertz electric field strength measurement can reach 5.76 μV/(cm·Hz1/2). Simultaneously, the linear dynamic range is better than 60 dB. So, it can be used to precisely measure the thickness of materials through the terahertz transmission efficiency. The experiments in this work demonstrate the thickness measurement of sapphire crystal and organic materials PTFE. The terahertz signal is shown in Fig. (a) sapphire material and Fig. (b) PTFE material. The thickness can be calculated from the transmittance, and the result is consistent with the result measured directly with a vernier caliper. Furthermore, single-layer graphene and few-layer graphene can be clearly distinguished from terahertz transmission signals as shown in Fig. (c) graphene material. Even for niobium meta thin films with thickness of 1 μm, very weak terahertz signal can be well distinguished due to the high sensitivity of atomic superheterodyne terahertz detector. In summary, the technology developed for terahertz thickness measurement based on atomic superheterodyne detection is very important for detecting defects, checking coating, and measuring the parameters of materials.
-
Key words:
- Rydberg atom /
- atomic heterodyne detection /
- terahertz thickness measurement .
-
-
图 2 实验方案 (a) 实验能级图; (b) 实验装置示意图
Figure 2. Experimental programme: (a) Energy diagram; (b) experimental setup.
图 3 原子超外差探测器线性区域和灵敏度
Figure 3. Linear dynamical range and sensitivity of the atomic heterodyne detector.
图 4 固体材料厚度测量 (a) 0.49 mm厚蓝宝石材料透射光谱; (b) 2 mm厚蓝宝石材料透射光谱; (c) 2 mm厚聚四氟乙烯材料透射光谱; (d) 8 mm厚聚四氟乙烯材料透射光谱
Figure 4. Solid material thickness measurements: (a) Transmission spectrum of 0.49 mm thick sapphire material; (b) transmission spectrum of 2 mm thick sapphire material; (c) transmission spectrum of 2 mm thick PTFE material; (d) transmission spectrum of 8 mm thick PTFE material.
-
[1] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819 doi: 10.1038/nphys2423 [2] Holloway C L, Gordon J A, Jefferts S, Schwarzkopf A, Anderson D A, Miller S A, Raithel G 2014 IEEE T. Antenn. Propag. 62 6169 doi: 10.1109/TAP.2014.2360208 [3] 焦月春, 赵建明, 贾锁堂 2018 物理学报 67 073201 doi: 10.7498/aps.67.20172636 Jiao Y C, Zhao J M, Jia S T 2018 Acta Phys. Sin. 67 073201 doi: 10.7498/aps.67.20172636 [4] 吴逢川, 安强, 姚佳伟, 付云起 2023 物理学报 72 047401 doi: 10.7498/aps.72.20222091 Wu F C, An Q, Yao J W, Fu Y Q 2023 Acta Phys. Sin. 72 047401 doi: 10.7498/aps.72.20222091 [5] Gordon J A, Holloway C L, Schwarzkopf A, Anderson D A, Miller S, Thaicharoen N, Raithel G 2014 Appl. Phys. Lett. 105 024104 doi: 10.1063/1.4890094 [6] Holloway C L, Simons M T, Kautz M D, Haddab A H, Gordon J A, Crowley T P 2018 Appl. Phys. Lett. 113 094101 doi: 10.1063/1.5045212 [7] Daschner R, Kübler H, Löw R, Baur H, Frühauf N, Pfau T 2014 Appl. Phys. Lett. 105 041107 doi: 10.1063/1.4891534 [8] Holloway C L, Prajapati N, Kitching J, Sherman J A, Teale C, Rufenacht A, Norrgard E B 2021 arxiv: 2110.02335 [9] Robinson A K, Prajapati N, Senic D, Simons M T, Holloway C L 2021 Appl. Phys. Lett. 118 114001 doi: 10.1063/5.0045601 [10] Song Z F, Liu H P, Liu X C, Zhang W F, Zou H Y, Zhang J, Qu J F 2019 Opt. Express 27 8848 doi: 10.1364/OE.27.008848 [11] Holloway C L, Simons M T, Gordon J A, Novotny D 2019 IEEE Antenn. Wirel. Pr. 18 1853 doi: 10.1109/LAWP.2019.2931450 [12] Cox K C, Meyer D H, Fatemi F K, Kunz P D 2018 Phys. Rev. Lett. 121 110502 doi: 10.1103/PhysRevLett.121.110502 [13] Anderson D A, Sapiro R E, Raithel G 2020 IEEE T Antenn. Propag. 69 2455 [14] Otto J S, Hunter M K, Kjærgaard N, Deb A B 2021 J. Appl. Phys. 129 154503 doi: 10.1063/5.0048415 [15] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911 doi: 10.1038/s41567-020-0918-5 [16] Meyer D H, Kunz P D, Cox K C 2021 Phys. Rev. Appl. 15 014047 doi: 10.1103/PhysRevApplied.15.014047 [17] Yang B W, Yan Y H, Li X J, Xiao L, Li X L, Chen L Q, Deng J L, Cheng H D 2024 Phys. Rev. Appl. 21 L031003 doi: 10.1103/PhysRevApplied.21.L031003 [18] Zhang L H, Liu Z K, Liu B, Zhang Z Y, Guo G C, Ding D S, Shi B S 2022 Phys. Rev. Appl. 18 014033 doi: 10.1103/PhysRevApplied.18.014033 [19] Liu X H, Liao K Y, Zhang Z X, Tu H T, Bian W, Li Z Q, Zheng S Y, Li H H, Huang W 2022 Phys. Rev. Appl. 18 054003 doi: 10.1103/PhysRevApplied.18.054003 [20] Chen S, Reed D J, Mac Kellar A R, Downes L A, Almuhawish N F, Jamieson M J, Weatherill K J 2022 Optica 9 485 doi: 10.1364/OPTICA.456761 [21] Wade C G, Šibalić N, De Melo N R., Kondo J M, Adams C S, Weatherill K J 2017 Nat. Photonics 11 40 doi: 10.1038/nphoton.2016.214 [22] Downes L A, Mac Kellar A R, Whiting D J, Bourgenot C, Adams C S, Weatherill K J 2020 Phys. Rev. X 10 011027 [23] 陈志文, 佘圳跃, 廖开宇, 黄巍, 颜辉, 朱诗亮 2021 物理学报 70 060702 doi: 10.7498/aps.70.20201870 Chen Z W, She Z Y, Liao K Y, Huang W, Yan H, Zhu S L 2021 Acta Phys. Sin. 70 060702 doi: 10.7498/aps.70.20201870 [24] Lin Y Y, She Z Y, Chen Z W, Li X Z, Zhang C X, Liao K Y, Zhang X D, Chen J H, Huang W, Yan H, Zhu S L 2023 Fundamental Research https://doi.org/10.1016/j.fmre.2023. 02.019 [25] She Z Y, Zhu X J, Lin YY, Li X Z, Yang X L, Shang Y F, Teng Y Q, Tu H Q, Liao K Y, Zhang C X, Liu X H, Chen J H, Huang W 2024 Chin. Phys. Lett. 41 084201 doi: 10.1088/0256-307X/41/8/084201 [26] Ospald F, Zouaghi W, Beigang R, Matheis C, Jonuscheit J, Recur B, Vandewal M 2014 Opt. Eng. 53 031208 [27] Yasui T, Yasuda T, Sawanaka K I, Araki T 2005 Appl. Optics 44 6849 doi: 10.1364/AO.44.006849 [28] Iwata T, Yoshioka S, Nakamura S, Mizutani Y, Yasui T 2013 J. Infrared Millim. Te. 34 646 doi: 10.1007/s10762-013-0015-2 [29] 张洪桢, 何明霞, 石粒力, 王鹏騛 2020 光谱学和光谱分析 40 3066 Zhang H Z, He M X, Shi L L, Wang P F 2020 Spectrosc. Spect. Anal. 40 3066 [30] 林玉华, 何明霞, 赖慧彬, 李鹏飞, 马文鹤 2017 光谱学和光谱分析 37 3332 Lin Y H, He M X, Lai H B, Li P F, Ma W H 2017 Spectrosc. Spect. Anal. 37 3332 [31] James L H, Jeon T I 2012 J. Infrared Millim. Te. 33 871 doi: 10.1007/s10762-012-9905-y -
图( 7)
计量
- 文章访问数: 275
- HTML全文浏览数: 275
- PDF下载数: 2
- 施引文献: 0