首页
登录
注册
-
快中子多重性测量技术主要用于核材料的质量衡算, 特别是铀和钚等裂变材料, 以确保核不扩散和核材料的安全管理, 在军控核查领域中发挥着重要作用. 快中子多重性测量是一种基于中子探测和事件统计分析的技术, 与热中子多重性测量技术不同, 其采用闪烁体探测器直接对裂变中子进行探测, 无需中子慢化过程, 再通过时间关联分析方法分析中子时间序列, 确定中子多重计数率, 最后代入方程求解核材料的质量, 在核材料属性认证上具有独特的优势[1–3]. 国内外众多研究机构对其开展了研究, 取得了较大进展[4–6], Zhang等[7,8]推导了钚材料的高阶快中子多重性测量方程和铀材料的有源快中子多重性方程, 针对快中子测量中存在的散射串扰现象, 还引入了串扰系数进行修正并推导了新方程[9]. 点模型是快中子多重性方程建立过程中的一条重要假设, 即假设所有中子是从同一点产生的. 对于公斤级样品, 裂变中子的空间增殖非均匀性更加明显, 不满足该假设条件, 对测量结果造成较大偏差[10]. 为修正测量偏差, Li等[11]提出了基于增殖系数修正的测量方法, Liu等[12]提出了一种双参数迭代的方法对增殖系数进行修正. 除此之外, 还有基于增殖系数和α系数拟合修正的方法[13], 以及人工智能的方法[14,15]. Burward-Hoy 等[16]针对中子多重性测量技术进行了大量研究, 建立了加权点模型方程, 对热中子多重性方法进行了修正, 该方法通过对大量不同质量、形状的样品进行模拟计算, 得到权重因子与泄漏增殖系数的拟合经验公式, 通过该公式得到权重因子的具体数值, 再将权重因子代入方程, 实现对公斤级钚样品质量的求解. 这种方法虽然在一定程度上修正了测量偏差, 但权重因子都是通过大量的仿真计算后得到的经验值, 且加权点模型方程的提出并未给出具体推导过程和思路, 缺乏充分的理论分析, 计算量大, 难以推广. 而快中子多重性测量中存在的质量求解偏差问题仍未得到有效解决, 相关模型仍存在较大偏差. 因此, 本文拟对快中子多重性点模型方程进行修正, 通过分析中子的空间增殖效应, 得到中子泄漏增殖系数的变化特性, 在此基础上提出n阶增殖系数的修正因子, 推导快中子多重性加权点模型方程, 并通过Geant4进行仿真验证, 以期实现公斤级钚样品质量的精准求解.
-
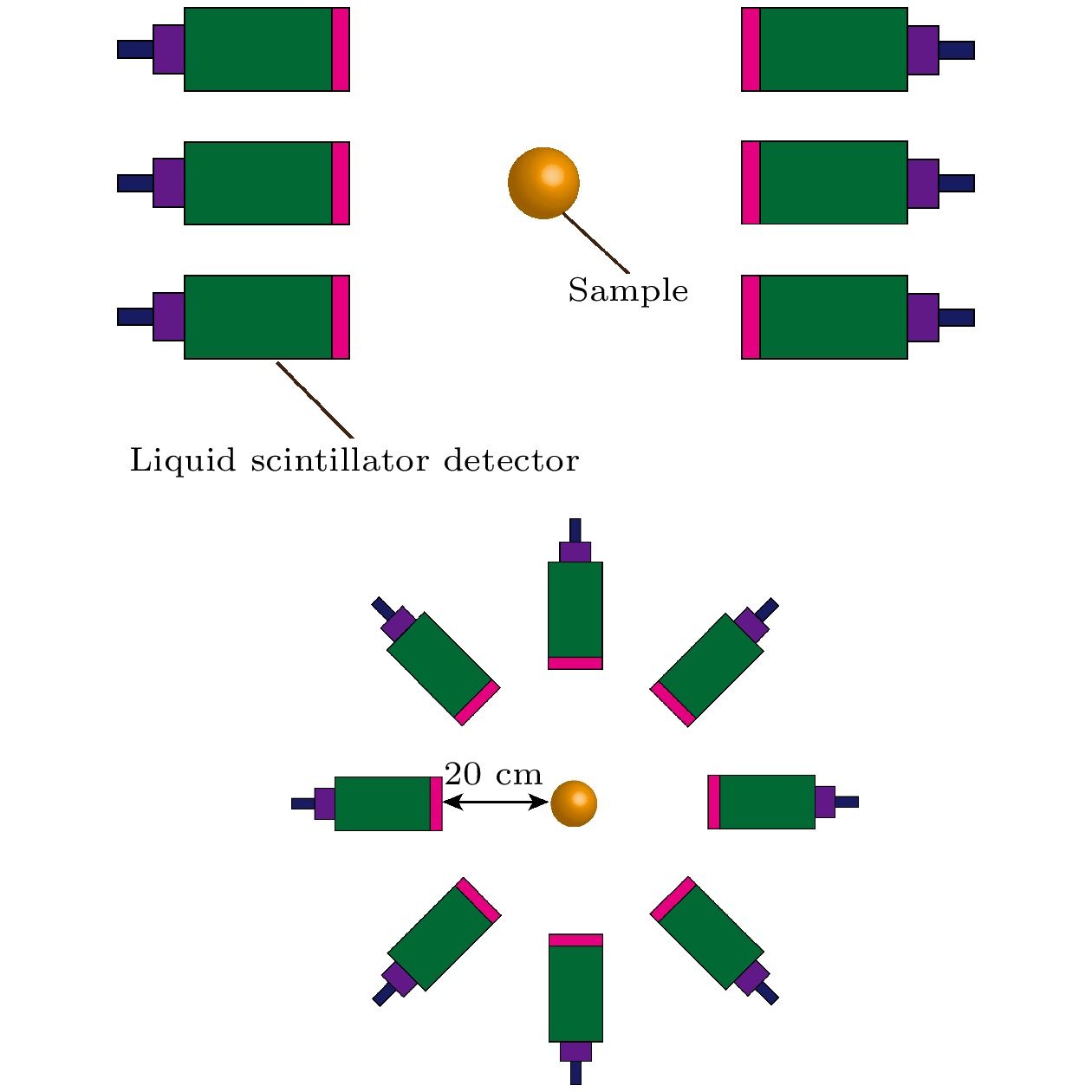
本文涉及模拟验证, 为完成相关内容, 还需搭建快中子多重性测量模型. 快中子多重性测量的模拟主要包含两个部分: 一是探测过程模拟, 对核材料裂变、粒子输运、探测响应等物理过程进行模拟; 二是计数过程模拟, 对探测的中子信号进行处理, 提取相关信息. 其中, 第1部分主要通过Geant4实现, 主要包括探测模型的搭建、物理过程的构建、探测过程的设置. 对于探测模型的构建, 本文采用Geant4搭建出一套井型测量系统进行模拟研究[17,18]. 该测量系统由24个液闪探测器组成, 共3层, 每层均匀排列分布8个BC501A液闪探测器, 闪烁体密度为0.874 g/cm3. 单个探测器的几何尺寸为
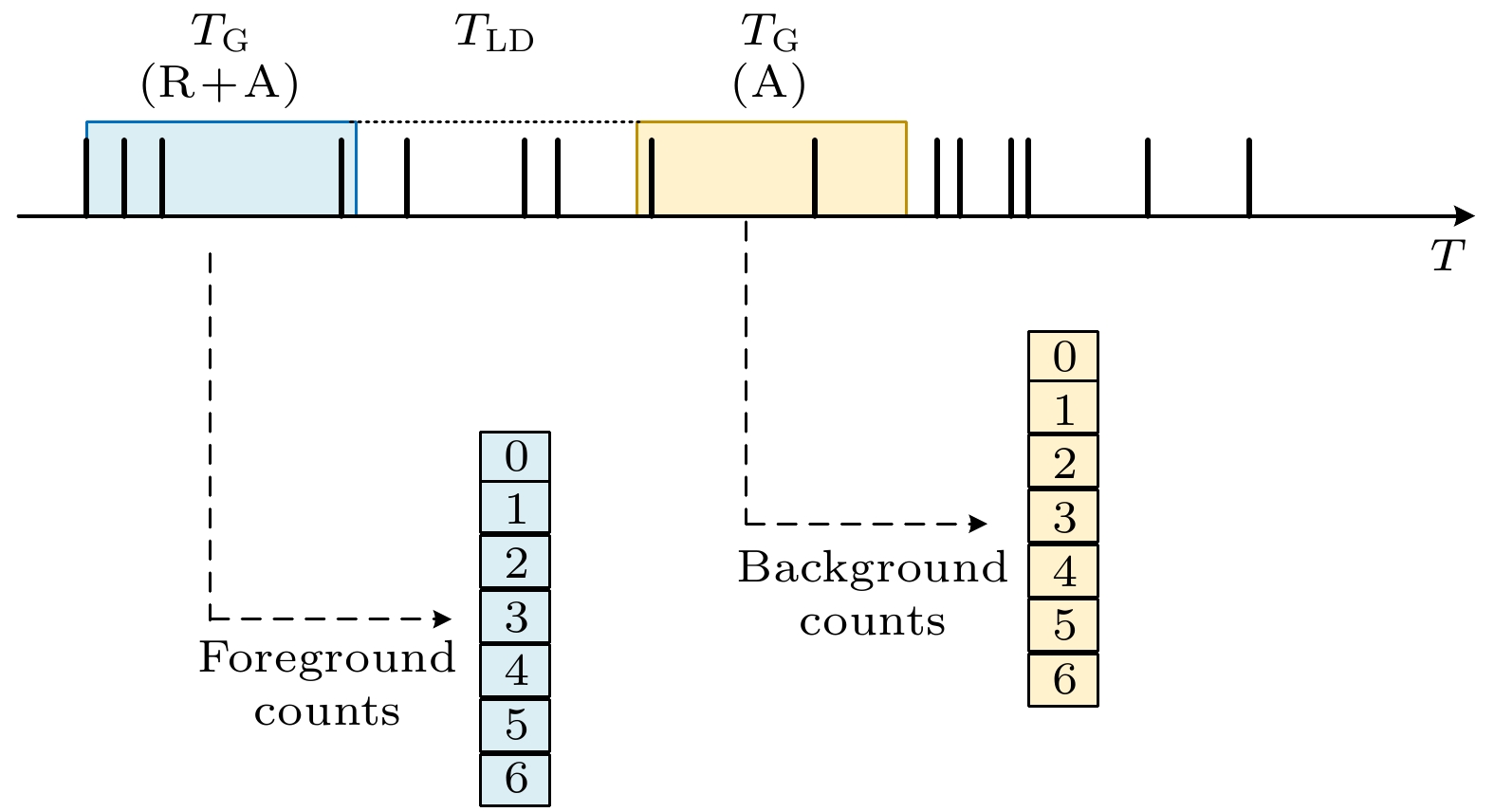
$ \phi $ 120 mm$ \times $ 60 mm, 探测器前端面距离探测系统的中心轴20 cm, 探测阵列的垂直高度为42 cm, 探测系统的几何中心设置待测样品, 空腔填充空气. 系统布局结构如图1所示. 其中, Geant4模型所采用的数据库为G4NDL中子数据库(根据 ENDF/B-VII.1评价核数据库制作而成). 物理过程的构建主要包括粒子的衰变、中子散射、诱发裂变、粒子输运等, 采用Geant4内置的G4HadronElasticProcess、G4NeutronInelasticProcess、 G4HadronCaptureProcess、G4HadronFissionProcess模型. 通过闪烁体探测器记录中子时间信息, 生成list-mode数据文件[19].第2部分的模拟主要通过Matlab来实现, 通过编程构建一个虚拟的多重性移位寄存器. 多重性移位寄存器原理如图2所示, 每个探测到的中子信号作为一个触发信号, 触发信号后TG时间内的中子信号个数为前景重数, 每次计数结束后使前景重数对应的前景计数器加1. TLD是为保证不会有与触发信号相关的计数设置的长延时, TLD后TG时间内的中子信号个数为背景重数, 每次计数使背景重数对应的背景计数器加1. 分析第1部分模拟得到的中子脉冲序列, 设置符合门宽为100 ns, 提取前景计数以及背景计数, 根据多重性分布与前景、背景计数的等量关系[20], 求得多重计数率
$ {\text{Singles}}(S), {\text{Doubles}}(D), {\text{Triples}}(T) $ . -
中子多重性测量是基于点模型, 其意义表示样品整个空间体积内的增殖效应相同. 但在实际测量过程中由于中子通量分布、诱发裂变密度等差异, 样品空间体积内中子的增殖效应会随着位置发生变化. 通常情况下, 泄漏增殖系数会随着样品质量的增大而增大, 泄漏增殖系数高估会导致样品质量偏小. 因此, 中子泄漏增殖系数的准确性对测量结果至关重要. 本节主要对样品空间体积内的中子增殖效应进行分析, 定义中子产生量为
$ P(r) $ , 中子吸收量为$ A(r) $ , 中子增长量为$ N(r) $ , r代表该点在样品体积内的位置. 通过(1)式和(2)式可计算得到材料空间体积内的中子净增殖量$ {N_{{\text{tot}}}} $ :在求得中子净增殖量的基础上, 根据泄漏增殖系数的定义, 材料的中子泄漏增殖系数可表示为
其中,
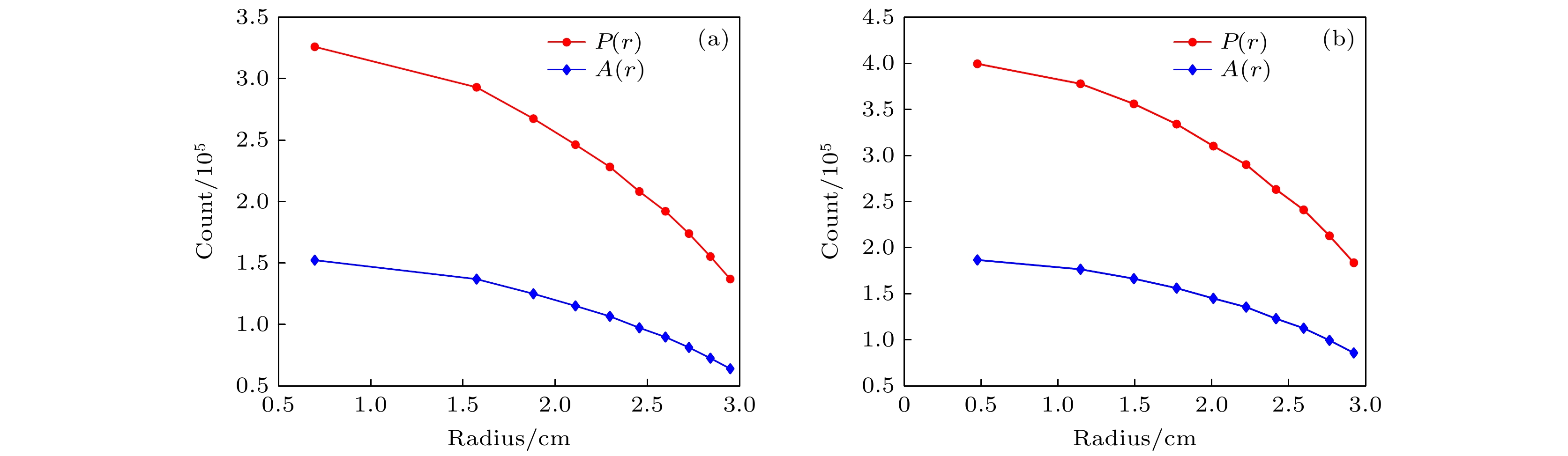
$ {N_\alpha } $ 为(α, n)反应产生中子数, F为自发裂变率,$ {v_{{\text{sf1}}}} $ 为单次裂变平均释放中子数.为分析中子的空间增殖效应, 采用第2节中搭建的闪烁体探测模型对两种不同形状的纯金属钚材料进行测量: 球体(r = 3 cm)和圆柱体(h = 6 cm, r = 3 cm), 密度为19.8 g/cm3, 丰度占比f240 = 10%, f239 = 90%, 质量分别为2238.192 g和3357.288 g. 钚材料在空间体积内均匀分布, 以球体样品的球心为中心, 沿半径将球体分成质量相等的10个球壳, 每个壳层约重223.82 g, 包含22.38 g的240Pu; 对于圆柱体样品, 保持轴向高度不变, 沿径向将圆柱体样品分成质量相等的10个壳层, 每个壳层约重335.73 g, 包含33.57 g的240Pu. 记录每个壳层的中子产生量
$ P(r) $ 和吸收量A(r), 中子产生量是指来自本壳层的诱发裂变产生中子数, 中子吸收量是指本壳层诱发裂变吸收中子数, 也可理解为本壳层发生的诱发裂变次数. 在此基础上, 根据(1)式和(2)式得到每个壳层的中子净增殖量$ {N_{{\text{tot}}}} $ , 结果如图3和表1所示.从图3 可以看出, 无论球体还是圆柱体, 材料空间体积内的中子产生量与吸收量会随着空间位置发生改变, 内层的中子产生量和吸收量均高于外层, 这主要是因为在材料内部中子会不断与重核发生散射, 导致内层的中子通量密度更高, 诱发裂变概率更大, 从而导致中子的产生量和吸收量更大. 而且这种空间分布上的差异会导致各个壳层的中子净增殖量不同, 如表1所示, 内层的中子净增殖量明显高于外层. 中子的净增殖量是影响中子泄漏增殖系数的重要因素, 如(3)式所示, 在保证核材料均匀分布且各壳层的质量相等的情况下, 各壳层的初级行为产额
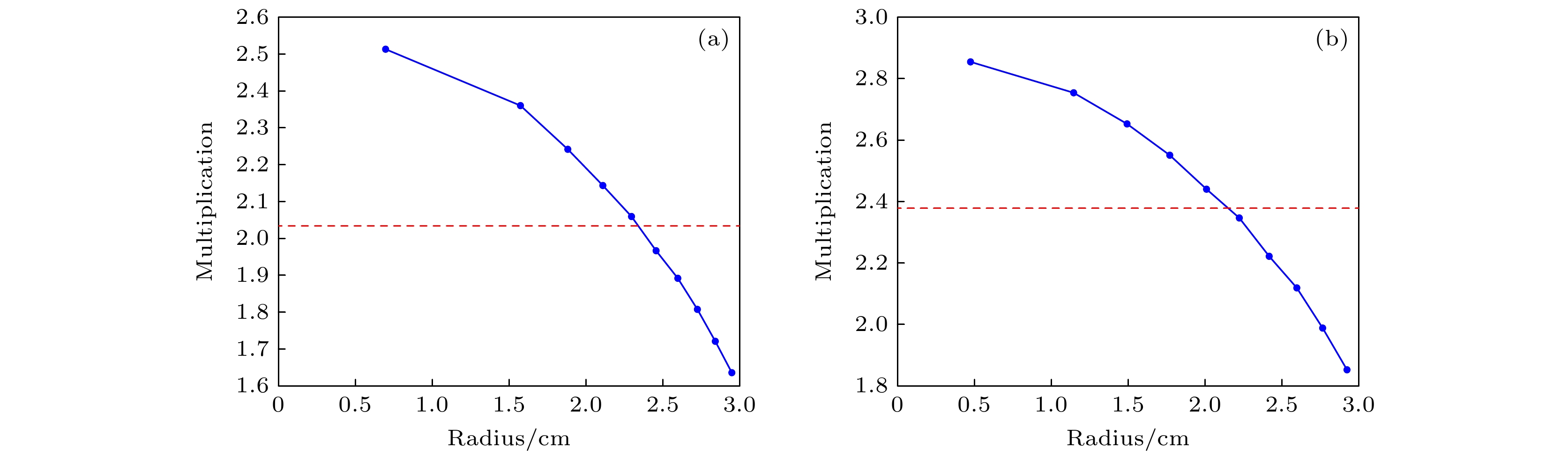
$ F{v_{{\text{sf1}}}} + {N_\alpha } $ 会保持相同, 泄漏增殖系数的计算取决于中子净增殖量$ {N_{{\text{tot}}}} $ . 通过该式可以得到不同壳层的中子泄漏增殖系数, 如图4所示.图4中红线为该材料的平均中子泄漏增殖系数, 蓝线为不同壳层的中子泄漏增殖系数. 与中子净增殖量一样, 泄漏增殖系数会随着半径的增大而逐渐减小, 内层的中子泄漏增殖系数高于平均值, 外层低于平均值. 与点模型假设相反, 图4的结果表明中子泄漏增殖系数并不是固定的, 会随空间位置的变化发生改变, 而点模型方程假定核材料空 间体积内的中子增殖效应是相同的、泄漏增殖系数是恒定的, 这种理想条件下求解的泄漏增殖系数往往大于实际值, 从而导致求解的质量偏小. 为修正该偏差, 本文通过模拟计算得到材料空间各位置的中子泄漏增殖系数, 提出修正因子进行修正, 并推导方程.
-
本节主要对中子的空间增殖系数进行修正, 从物理过程出发, 利用概率母函数和阶乘矩对快中子多重性加权点模型方程进行推导. 中子的来源主要包含3个方面: 自发裂变、诱发裂变、(α, n)反应. 在点模型、超裂变等基本假设下, 待求解参数可以简化成自发裂变率F、(α, n)反应系数α、泄漏增殖系数ML. 其中, 定义α系数为(α, n)反应中子数与自发裂变中子数之比, 如(4)式所示.
$ {N_{{\text{sf}}}} $ 为自发裂变释放中子数.由于(α, n)反应一次只能放出一个中子, 初级事件的总反应率为
$ {P_{{\text{sf}}}}{(}v{)} $ 为自发裂变的中子多重性分布, 自发裂变和(α, n)反应释放中子的多重性分布为$ {\delta _{{\text{1v}}}} $ 为Kronecker 符号, 在超裂变假设的基础上, 可以将自发裂变中子、(α, n)反应中子、诱发裂变中子视为同时出射, 满足多重性分布$ P(v) $ .$ P(v) $ 与对应的多重性阶乘矩$ {v_n} $ 满足如下关系:根据参考文献[20], 出射中子多重性分布的第一、第二、第三阶乘矩与各项参数满足如下关系:
其中,
$ {v_{{\text{sf}}n}} $ 为自发裂变多重性的阶乘矩,$ {v_{{\text{i}}n}} $ 为诱发裂变多重性的阶乘矩, 数据均可从核数据库中查阅[21].$ \varepsilon $ 表示中子探测效率,$ k $ 为一重散射串扰率, 与探测系统布局紧密相关, 可提前通过标准源刻度求得. 本文研究中所采用的测量模型的探测效率和一重散射串扰率均通过模拟计算获得.根据上述分析, 出射中子多重性分布P(v)与阶乘矩
$ {v_n} $ 满足(7)式, 且在点模型假设的基础上, P(v)不会随位置发生改变, 中子空间增殖效应会保持一致. 但第3节的研究结果表明, 在测量材料的空间体积内, 中子的空间增殖效应并不相同, 会随位置发生改变. 相应的出射中子的阶乘矩也会随位置发生变化, 应进行如下修正:根据(8)式—(10)式中泄漏增殖系数ML与中子多重性阶乘矩的关系, 将(8)式—(10)式分别代入(11)式, 可以得到
其中,
$ \overline {{M_{\text{L}}}} = \displaystyle\frac{1}{V}\int {{M_{\text{L}}}(r)} {\text{d}}V $ ,$ \overline {M_{\text{L}}^n} = \displaystyle\frac{1}{V}\int {M_{\text{L}}^n(r)} {\text{d}}V $ . 在点模型假设的条件下, 可认为$ \overline {M_{\text{L}}^n} = {(\overline {{M_{\text{L}}}} )^n} $ , 但根据图4计算结果, 泄漏增殖系数并不恒定, 不满足该等式关系. 因此, 提出空间增殖系数修正因子为将该修正因子代入点模型快中子多重性方程, 最终建立起加权点模型测量方程, 如(16)式—(18)式所示:
与点模型测量方程的求解方法相似, 该方程的求解同样使用牛顿迭代法, 通过(16)式—(18)式的合理迭代, 消去F和α得到泄漏增殖系数ML的五阶多项式, 先求解泄漏增殖系数ML, 再求解自发裂变率F和α系数, 如(19)式、(20)式所示, 其中
$ a, b, c, d $ 分别为对应泄漏增殖系数n阶多项式的系数, 由已知参量构成: -
采用第2节中搭建的快中子多重性测量模型分别对第3节的两种材料进行模拟测量, 求解各壳层对应的泄漏增殖系数, 分别通过(21)式、(22)式计算球体、圆柱体的n阶泄漏增殖系数的平均值, 再通过(15)式计算修正因子
$ {g_n} $ , 结果如表2所示.从表2可以看出, 随着泄漏增殖系数的幂增大,
$ \overline {{M^n}} $ 和$ \langle \overline M { \rangle ^n} $ 的差距也在逐渐增大, 从而导致$ {g_n} $ 不断增大. 因此在高阶方程中, 这种偏差会放大, 导致最终求解结果偏差不断增大. 将测得的修正因子代入测量方程得到公式, 便可得到快中子多重性加权点模型方程.通过快中子加权点模型求解泄漏增殖系数与材料质量, 并与点模型方程的求解结果进行比较, 结果如表3所示.
分析表3的测量结果可以发现, 点模型方程求解的泄漏增殖系数往往高于真实值, 偏差较大, 导致的测量偏差接近于30%. 修正后求解的泄漏增殖系数更加接近实际值, 测量偏差明显缩小, 充分证明了该方法的有效性, 可应用于公斤级钚样品的快中子多重性测量.
-
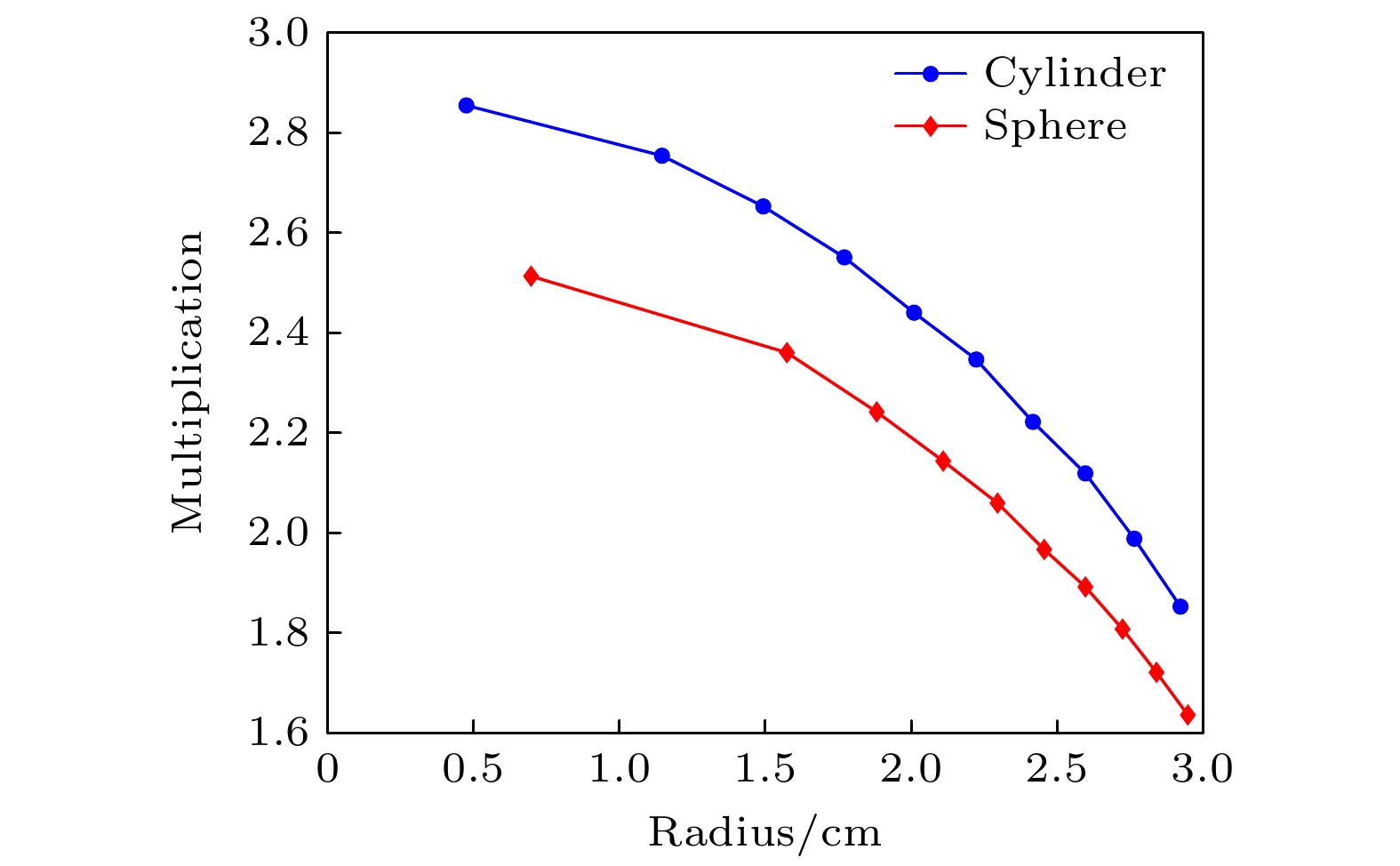
一般来说, 离散数据越多, 样品的分层也越多, 得到的修正因子更贴切, 测量结果会更加精确. 但也会极大的降低计算效率. 为实现精度与效率 的平衡统一, 保证测量结果的准确性, 本文将各壳层求得的泄漏增殖系数与对应半径进行拟合, 得 到泄漏增殖系数与半径之间的函数关系式, 如图5所示.
得到拟合函数关系如(23)式、(24)式所示, 球体和圆柱体的拟合关系式的拟合精度分别高达99.97%和99.96%. 拟合系数与测量对象的性质有关, 包括材料种类、体积、密度等:
通过该函数关系式在材料空间体积上进行积分, 如(25)式、(26)式所示, 得到平均泄漏增殖系数
$ {\overline M _{{\text{sphere}}}} = 2.0284 $ ,$ {\overline M _{{\text{cylinder}}}} = 2.3744 $ .同理, 对n阶泄漏增殖系数进行积分, 得到拟合修正因子, 结果如表4所示.
将表4得到的修正因子代入快中子多重性方程, 求解泄漏增殖系数和材料质量, 并与离散修正的结果进行比较, 结果如表5所示.
从表5 可以看出, 拟合修正得到的测量结果与离散修正的测量结果相比, 测量精度有小幅度的提升, 更贴合于实际值.
-
快中子多重性测量方法作为一种无损检测技术在国际核保障监督以及军控核查领域扮演着重要作用. 其中点模型假设对于快中子多重性测量方程的建立至关重要, 但该理想化假设不可避免地会对测量结果造成系统偏差. 本文通过对中子的空间增殖效应进行分析, 测量了不同壳层的中子产生量、吸收量和净增长量, 得到了不同壳层的泄漏增殖系数. 通过出射中子多重性阶乘矩的表达式, 将这种空间特异性转移到了泄漏增殖系数M上, 并提出了基于n阶泄漏增殖系数的权重因子, 代入点模型方程, 推导了快中子多重性加权点模型方程. 通过Geant4搭建的测量模型进行仿真验证, 测量结果显示, 对于公斤级的球形钚样品, 点模型方程的求解偏差为28%, 而修正后的测量偏差缩小至6%以内, 证实了该方法的有效性. 此项研究, 修正了快中子多重性点模型方程, 实现了公斤级钚材料的精准测量, 对核查技术的发展具有现实意义.
基于空间增殖系数修正的钚材料快中子多重性测量
Fast neutron multiplicity measurement of plutonium material based on spatial multiplication coefficient correction
-
摘要: 快中子多重性测量技术是军控核查领域一项重要的无损检测技术, 可用于核材料的质量衡算. 但该方法是基于点模型假设建立的, 会造成系统偏差. 为修正偏差提升测量精度, 本文对两种不同形状的样品进行了快中子多重性模拟测量, 得到了材料空间体积内中子产生、吸收和净增长随位置的变化关系, 发现了中子泄漏增殖系数的空间变化规律. 根据中子多重性阶乘矩与待测参数间的函数关系, 提出了一种基于空间增殖系数修正的方法, 通过引入修正因子$ {g_n} $, 推导了快中子多重性加权点模型方程. 为验证该方法的准确性, 本文通过Geant4搭建了一套测量模型, 对球体和圆柱体两种形状的公斤级钚样品进行了模拟测量. 结果表明, 快中子多重性加权点模型方程的测量精度高于点模型方程, 测量偏差缩小至6%以内, 提供了一种求解公斤级钚样品质量的优化方法, 推动了快中子多重性测量技术向前发展.Abstract: Fast neutron multiplicity measurement technology is an important non-destructive testing technology in the field of arms control verification. In the technique, the liquid scintillation detector is used to detect the fission neutron and combined with the time correlation analysis method to extract multiplicity counting rates from the pulse signals. This technique is commonly used to measure the mass of nuclear materials, however, it is based on the point model that assumes that the neutron multiplication coefficient keeps constant in the whole spatial volume, which will lead to overestimation of the multiplication coefficient and result in system deviation. To correct the deviation and improve the measurement accuracy, the fast neutron multiplicity simulation measurements are carried out on spherical and cylindrical samples in this work. The relationship among the position of neutron generation, absorption and net growth in the space volume of the material is obtained. According to the definition of the leakage multiplication coefficient, the leakage multiplication coefficients at different positions in the space volume of the material are calculated. On this basis, a method based on spatial multiplication coefficient correction is proposed according to the functional relationship between neutron multiplicity factorial moments and the unknown parameters. In this method, the n-order multiplication coefficient is modified by introducing a weight factor $ {g_n} $, and the fast neutron multiplicity weighted point model equation is derived. To verify the accuracy of this method, a set of fast neutron multiplicity detection model is built by Geant4, and the fast neutron multiplicity simulation measurement is carried out on the spherical and cylindrical samples. The results show that the solution accuracy of the weighted point model equation is higher than that of the standard point model equation, and the measurement deviation is reduced to less than 6 %. This work provides an optimization method for solving plutonium samples with several kilograms in mass, and promotes the development of the fast neutron multiplicity measurement technology.
-
-
图 3 中子产生量和吸收量 (a)球体; (b)圆柱体
Figure 3. neutron production and absorption: (a) Sphere; (b) cylinder.
图 4 中子泄漏增殖系数空间分布 (a)球体; (b)圆柱体
Figure 4. Spatial distribution of neutron multiplication coefficient: (a) Sphere; (b) cylinder.
表 1 中子净增殖量
Table 1. Net increase of neutron.
样品 第1层 第2层 第3层 第4层 第5层 第6层 第7层 第8层 第9层 第10层 球体 173663 156111 142509 131236 121585 110940 102358 92682 82744 72978 圆柱体 212847 201300 189675 177980 165286 154546 140224 128419 113419 97833 
下载: 导出CSV
表 2 离散修正因子
Table 2. Discrete correction factor.
样品 $ \overline {M_{\text{L}}^n} $ $ {(\overline {{M_{\text{L}}}} )^n} $ $ {g_n} $ $ \overline {{M_{\text{L}}}} $ $ \overline {M_{\text{L}}^{2}} $ $ \overline {M_{\text{L}}^{3}} $ $ \overline {M_{\text{L}}^{4}} $ $ \overline {M_{\text{L}}^{5}} $ $ {(\overline {{M_{\text{L}}}} )^1} $ $ {(\overline {{M_{\text{L}}}} )^2} $ $ {(\overline {{M_{\text{L}}}} )^3} $ $ {(\overline {{M_{\text{L}}}} )^4} $ $ {(\overline {{M_{\text{L}}}} )^5} $ $ {g_1} $ $ {g_2} $ $ {g_3} $ $ {g_4} $ $ {g_5} $ 球体 2.03 4.21 8.87 18.97 41.24 2.03 4.14 8.42 17.13 34.84 1 1.017 1.053 1.107 1.184 圆柱体 2.38 5.76 14.16 35.36 89.52 2.38 5.66 13.45 31.99 76.09 1 1.017 1.052 1.105 1.176
下载: 导出CSV
表 3 离散修正效果
Table 3. discrete correction effect.
泄漏增殖系数 计算质量 计算偏差/% 球体 圆柱体 球体 圆柱体 球体 圆柱体 修正前 2.16 2.51 161.05 243.06 –28.04 –27.6 修正后 2.07 2.40 236.03 344.30 5.5 2.6
下载: 导出CSV
表 4 拟合修正因子
Table 4. Fitting correction factor.
样品 $ \overline {M_{\text{L}}^n} $ $ {(\overline {{M_{\text{L}}}} )^n} $ $ {g_n} $ $ \overline {{M_{\text{L}}}} $ $ \overline {M_{\text{L}}^{2}} $ $ \overline {M_{\text{L}}^{3}} $ $ \overline {M_{\text{L}}^{4}} $ $ \overline {M_{\text{L}}^{5}} $ $ {(\overline {{M_{\text{L}}}} )^1} $ $ {(\overline {{M_{\text{L}}}} )^2} $ $ {(\overline {{M_{\text{L}}}} )^3} $ $ {(\overline {{M_{\text{L}}}} )^4} $ $ {(\overline {{M_{\text{L}}}} )^5} $ $ {g_1} $ $ {g_2} $ $ {g_3} $ $ {g_4} $ $ {g_5} $ 球体 2.03 4.18 8.76 18.64 40.22 2.03 4.11 8.35 16.93 34.34 1 1.016 1.049 1.101 1.171 圆柱体 2.37 5.74 14.08 35.09 88.61 2.37 5.64 13.39 31.78 75.47 1 1.017 1.052 1.104 1.174
下载: 导出CSV
表 5 拟合修正效果
Table 5. Fitting correction effect.
泄漏增殖系数 计算质量 计算偏差/% 球体 圆柱体 球体 圆柱体 球体 圆柱体 离散修正 2.07 2.40 236.03 344.30 5.45 2.55 拟合修正 2.08 2.39 231.24 343.02 3.32 2.13
下载: 导出CSV
-
[1] Fulvio A D, Shin T H, Jordan T, Sosa C, Ruch M L, Clarke S D, Chichester D L, Pozzi S A 2017 Nucl. Instrum. Meth. A 855 92 doi: 10.1016/j.nima.2017.02.082 [2] Li S F, Qiu S Z, Zhang Q H 2016 Appl. Radiat. Isot. 110 53 doi: 10.1016/j.apradiso.2015.12.064 [3] Stewart J, Menlove H, Mayo D, Geist W, Carrillo L, Herrera G D 2000 The Ephithermal Neutron Multiplicity Counter Design and Performance Manual: More Rapid Plutonium and Uranium Inventory Verifications by Factors of 5–20 (United States: Los Alamos National Lab) p168 [4] Piau V, Litaize O, Chebboubi A, Oberstedt S, Gook A, Oberstedt A 2023 Phys. Lett. B. 837 137648 doi: 10.1016/j.physletb.2022.137648 [5] Clark A, Mattingly J, Favorite J 2020 Nucl. Sci. Eng. 194 308 doi: 10.1080/00295639.2019.1698267 [6] Fraïsse B, Bélier G, Méot V, Gaudefroy L, Francheteau A, Roig O 2023 Phys. Rev. C 108 014610 doi: 10.1103/PhysRevC.108.014610 [7] Zhang Q H, Yang J Q, Li X S, Li S F, Hou S X, Su X H, Zhou M, Zhuang L, Lin H T 2019 Appl. Radiat. Isot. 152 45 doi: 10.1016/j.apradiso.2019.06.022 [8] 黎素芬, 李凯乐, 张全虎, 蔡幸福 2022 物理学报 71 091401 doi: 10.7498/aps.71.20211653 Li S F, Li K L, Zhang Q H, Cai X F 2022 Acta Phys. Sin. 71 091401 doi: 10.7498/aps.71.20211653 [9] Shin T H, Hutchinson J, Bahran R 2019 Nucl. Sci. Eng. 193 663 doi: 10.1080/00295639.2018.1560758 [10] Croft S, Alvarez E, Chard P, McElroy R, Philips S 2007 48th INMM Annual Meeting (Tucson) p89 [11] Li S F, Li K L, Zhang Q H, Cai X F 2022 Nucl. Instrum. Meth. A 1027 166314 doi: 10.1016/j.nima.2022.166314 [12] Liu X B, Chen L G 2021 Nucl. Instrum. Meth. A 1016 165779 doi: 10.1016/j.nima.2021.165779 [13] Zhang Q H, Su X H, Hou S X, Li S F, Yang J Q, Hou L J, Zhuang L, Huo Y G, Li J J 2020 J. Nucl. Sci. Technol. 57 678 doi: 10.1080/00223131.2020.1715898 [14] Li K L, Li S F, Zhang Q H 2021 AIP Adv. 11 165 [15] Enqvist A, Pázsit I, Avdic S 2010 Nucl. Instrum. Meth. A 615 62 doi: 10.1016/j.nima.2010.01.022 [16] Burward-Hoy J M, Geist W H, Krick M S, Mayo D R 2004 Achieving Accurate Nuetron-Multiplicity Analysis of Metals and Oxides with Weighted Point Model Equations (United States: Los Alamos National Lab) p132 [17] Fulvio A D, Shin T H, Basley A, Swenson C, Sosa C, Clarke S D, Sanders J, Watson S, Chichester D L, Pozzi S A 2018 Nucl. Instrum. Meth. A 907 248 doi: 10.1016/j.nima.2018.05.049 [18] Zhang Q H, Li S F, Zhuang L, Huo Y G, Lin H T, Zuo W M 2018 Appl. Radiat. Isot. 135 92 doi: 10.1016/j.apradiso.2018.01.022 [19] Bai H Y, Xiong Z H, Zhao D S, Su M, Gao F, Xia B Y, Li C G, Pang C G, Mo Z H, Wen J 2023 Nucl. Instrum. Meth. A 1056 168652 doi: 10.1016/j.nima.2023.168652 [20] Böhnel K 1985 Nucl. Sci. Eng. 90 75 doi: 10.13182/NSE85-2 [21] Brown D A, Chadwick M B, Capote R 2018 Nucl. Data Sheets 148 142 -
图( 5) 表( 5)
计量
- 文章访问数: 233
- HTML全文浏览数: 233
- PDF下载数: 1
- 施引文献: 0