高级搜索

基于定向声源的局域型声学斯格明子模式的选择性激发

,  ,  ,  , 

downloadPDF

上一篇

下一篇

张孝悦, 徐华锋, 陈婉娜, 周农, 吴宏伟. 基于定向声源的局域型声学斯格明子模式的选择性激发[J]. 物理学报, 2025, 74(5): 054301-1. doi: 10.7498/aps.74.20241286
引用本文: 张孝悦, 徐华锋, 陈婉娜, 周农, 吴宏伟. 基于定向声源的局域型声学斯格明子模式的选择性激发[J]. 物理学报, 2025, 74(5): 054301-1. doi: 10.7498/aps.74.20241286
shu
Xiaoyue ZHANG, Huafeng XU, Wanna CHEN, Nong ZHOU, Hongwei WU. Selective excitation of localized acoustic skyrmion modes based on directional sound sources[J]. Acta Physica Sinica, 2025, 74(5): 054301-1. doi: 10.7498/aps.74.20241286
Citation: Xiaoyue ZHANG, Huafeng XU, Wanna CHEN, Nong ZHOU, Hongwei WU. Selective excitation of localized acoustic skyrmion modes based on directional sound sources[J]. Acta Physica Sinica, 2025, 74(5): 054301-1. doi: 10.7498/aps.74.20241286
shu

基于定向声源的局域型声学斯格明子模式的选择性激发

  • 1.

    安徽理工大学力学与光电物理学院, 淮南　232001

  • 2.

    安徽理工大学基础物理研究中心, 淮南　232001

    • 作者简介: 张孝悦.E-mail: zxy1913486877@163.com .
    通讯作者: E-mail: xhfeng716@126.com.;  E-mail: hwwu@aust.edu.cn.

  • 中图分类号: 43.55.+p, 43.35.+d, 43.40.+s

Selective excitation of localized acoustic skyrmion modes based on directional sound sources

  • 1.

    School of Mechanics and Photoelectric Physics, Anhui University of Science and Technology, Huainan 232001, China

  • 2.

    Center for Fundamental Physics, Anhui University of Science and Technology, Huainan 232001, China

    • Corresponding authors: E-mail: xhfeng716@126.com.;  E-mail: hwwu@aust.edu.cn.

  • MSC: 43.55.+p, 43.35.+d, 43.40.+s

  • 摘要: 声学斯格明子模式是一种在声学结构表面产生的速度场矢量拓扑纹理结构, 这种受保护的矢量分布为声音信息处理、传输和数据存储提供了新的机遇. 本文结合声学波导和亚波长阿基米德螺旋结构设计了一种组合结构, 利用定向声源激发波导模式传输, 进而实现对局域型声学斯格明子模式的选择性激发. 通过理论分析和数值仿真, 研究了自旋声源、Huygens声源、Janus声源在此结构中激发的压力场分布以及速度场分布, 展示了组合结构中声表面波的定向传输性质和选择性激发的声学斯格明子模式. 这种由定向声源选择性激发声学斯格明子模式的方式为设计先进声学信息处理功能器件提供了新的途径.
    Abstract: Acoustic skyrmion modes are topological texture structures of velocity field vectors generated on the surface of acoustic structures. This protected vector distribution provides new opportunities for processing sound information, transmission, and data storage. In this study, a combined structure of waveguides and spiral structures is designed by using directional acoustic sources to excite waveguide mode transmission, thereby achieving selective excitation of localized acoustic skyrmion modes. Through theoretical analysis and numerical simulations, the pressure field distribution and velocity field distribution excited by spin acoustic sources, Huygens acoustic sources, and Janus acoustic sources in this structure are investigated, demonstrating the directional transmission properties of acoustic surface waves and the selectively excited acoustic skyrmion modes in the combined structure. Numerical calculations reveal that when the spin acoustic source excites acoustic surface waves propagating along the waveguide, the acoustic skyrmion modes in the helical structure in the direction corresponding to the propagation are selectively excited. When the Huygens source excites acoustic surface waves propagating along the waveguide, the acoustic skyrmion modes in the right or left direction are selectively excited. However, when the Janus source excites acoustic surface waves propagating along the waveguide, the acoustic skyrmion modes in the upward or downward direction are selectively excited. This selective excitation of acoustic skyrmion modes by a directional acoustic source provides a new way to design advanced acoustic information processing functional devices.
  • 加载中

  • 图 1  (a) 组合结构示意图; (b) 不同波导宽度$ {\mathrm{Q}}{\mathrm{U}}{\mathrm{O}}{\mathrm{T}}{\mathrm{E}}{\mathrm{W}}{\mathrm{W}} $的色散关系曲线; (c)螺旋结构示意图; (d) 声学skyrmion模式图

    Figure 1.  (a) Schematic diagram of combination structure; (b) dispersion relation curves for different waveguide widths $ W $; (c) schematic diagram of spiral structure; (d) acoustic skyrmion pattern diagram.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 顺时针旋转的自旋声源激发声表面波沿波导定向传播示意图; (b) 声表面波沿上方波导向右传播的声压强度变化曲线图; (c) 声表面波沿波导前后向传输比随频率变化的曲线图; (d) 声表面波沿下方波导向左传播的声压强度变化曲线图

    Figure 2.  (a) Schematic diagram of the directional propagation of surface acoustic waves along a waveguide excited by a clockwise rotating spin acoustic source; (b) graph of the variation of sound pressure intensity of surface acoustic waves propagating to the right along the upper waveguide; (c) graph of the ratio of forward and backward transmission of surface acoustic waves along the waveguide as a function of frequency; (d) graph of the variation in sound pressure intensity of surface acoustic waves propagating to the left along the lower waveguide.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 顺时针旋转的自旋声源激发的组合结构中压力场分布; (b) 顺时针旋转的自旋声源激发的组合结构中的声学skyrmion模式; (c) 逆时针旋转的自旋声源激发的组合结构中的压力场分布; (d) 逆时针旋转的自旋声源激发的组合结构中的声学skyrmion模式

    Figure 3.  (a) Pressure field distribution in a combined structure excited by a clockwise rotating spin source; (b) acoustic skyrmion modes in combinatorial structures excited by clockwise rotating spin sources; (c) pressure field distribution in a combined structure excited by a counterclockwise rotating spin source; (d) acoustic skyrmion modes in combinatorial structures excited by counterclockwise rotating spin sources.

    下载: 全尺寸图片 幻灯片

    图 4  (a) 声学表面波沿波导向1号方向传播的示意图; (b) 螺旋结构中的声学skyrmion模式; (c) 声学表面波沿波导向2号方向传播; (d) 螺旋结构中的声学skyrmion模式; (e) 声学表面波沿波导向3号方向传播; (f) 螺旋结构中的声学skyrmion模式; (g) 声学表面波沿波导向4号方向传播; (h) 螺旋结构中的声学skyrmion模式

    Figure 4.  (a) Schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.1; (b) acoustic skyrmion modes in helical structures; (c) schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.2; (d) acoustic skyrmion modes in helical structures; (e) schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.3; (f) acoustic skyrmion modes in helical structures; (g) schematic diagram of acoustic surface waves propagating along the waveguide in the direction of No.4; (h) acoustic skyrmion modes in helical structures.

    下载: 全尺寸图片 幻灯片

    图 5  (a) 前向的Huygens声源激发的组合结构中的压力场分布; (b) 前向的Huygens声源激发的组合结构中的声学skyrmion模式; (c) 后向的Huygens声源激发的组合结构中的压力场分布; (d) 后向的Huygens声源激发的组合结构中的声学skyrmion模式

    Figure 5.  (a) Pressure field distribution in the combined structure excited by a forward Huygens sound source; (b) acoustic skyrmion modes in the composite structure excited by forward Huygens sound sources; (c) pressure field distribution in the combined structure excited by a backward Huygens sound source; (d) acoustic skyrmion modes in composite structures excited by backward Huygens acoustic sources.

    下载: 全尺寸图片 幻灯片

    图 6  (a) 向上的Janus声源激发的组合结构中的压力场分布; (b) 向上的Janus声源激发的组合结构中的声学skyrmion模式; (c) 向下的Janus声源激发的组合结构中的压力场分布; (d) 向下的Janus声源激发的组合结构中的声学skyrmion模式

    Figure 6.  (a) Pressure field distribution in a combined structure excited by an upward Janus source; (b) acoustic skyrmion modes in combinatorial structures excited by upward Janus sources; (c) pressure field distribution in a combined structure excited by a downward Janus source; (d) acoustic skyrmion modes in combinatorial structures excited by downward Janus sources.

    下载: 全尺寸图片 幻灯片

    图 7  (a) 向上的Janus声源激发的组合结构中的压力场分布; (b) 向上的Janus声源激发的组合结构中的声学skyrmion模式; (c) 向下的Janus声源激发的组合结构中的压力场分布; (d) 向下的Janus声源激发的组合结构中的声学skyrmion模式

    Figure 7.  (a) Pressure field distribution in a combined structure excited by an upward Janus source; (b) acoustic skyrmion modes in combinatorial structures excited by upward Janus sources; (c) pressure field distribution in a combined structure excited by a downward Janus source; (d) acoustic skyrmion modes in combinatorial structures excited by downward Janus sources.

    下载: 全尺寸图片 幻灯片
  • [1] Skyrme T H R 1962 Nucl. Phys. 31 556 doi: 10.1016/0029-5582(62)90775-7
    [2] Adkins G S, Nappi C R, Witten E 1983 Nucl. Phys. 228 3
    [3] Khawaja U AI, Stoof H 2001 Nature 411 918 doi: 10.1038/35082010
    [4] Su S W, Liu I K, Tsai Y C, Liu W M, Gou S C 2012 Phys. Rev. A 86 023601 doi: 10.1103/PhysRevA.86.023601
    [5] Fukuda J I, Zumer S 2011 Nat. Commun 2 246 doi: 10.1038/ncomms1250
    [6] Duzgun A, Selinger J, Saxena A 2018 Phys. Rev. E 97 062706 doi: 10.1103/PhysRevE.97.062706
    [7] Robler U K, Bogdanov A N, Pfleiderer C 2006 Nature 442 7104
    [8] Tokura Y, Kanazawa N 2021 Chem. Rev. 121 5
    [9] Muhlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, Georgii R, Boni P 2009 Science 323 5916
    [10] Yu X Z, Koshibae W, Tokunaga Y, Shibata K, Taguchi Y, Nagaosa N, Tokura Y 2018 Nature 564 95 doi: 10.1038/s41586-018-0745-3
    [11] 陈崇, 马铭远, 潘峰, 宋成 2024 物理学报 73 058502 doi: 10.7498/aps.73.20231908 Chen C, Ma M Y, Pan F, Song C 2024 Acta Phys. Sin. 73 058502 doi: 10.7498/aps.73.20231908
    [12] Zhang X C, Xia J, Zhou Y, Wang D W, Liu X X, Zhao W S, Ezawa M 2016 Phys. Rev. B 94 094420 doi: 10.1103/PhysRevB.94.094420
    [13] Zhang S L, Kronast F, Van der Laan G, Hesjedal T 2018 Nano Lett. 18 2
    [14] Bhukta M M M, Mishra A, Pradhan G, Mallick S, Singh B B, Bedanta S 2018 arXiv: 1810: 08262
    [15] Kezsmarki I, Bordacs S, Milde P, et al. 2015 Nat. Mater. 14 1116 doi: 10.1038/nmat4402
    [16] Nayak A K, Kumar V, Ma T, Werner P, Pippel E, Sahoo R, Damay F, Robler U K, Felser C, Parkin S S P 2017 Nature 548 561 doi: 10.1038/nature23466
    [17] Gilbert D A, Maranville B B, Balk A L, et al. 2015 Nat. Commun. 6 8462 doi: 10.1038/ncomms9462
    [18] Xia J, Zhang X C, Ezawa M, Tretiakov O A, Hou Z P, Wang W H, Zhao G P, Liu X X, Diep H T, Zhou Y 2020 Appl. Phys. Lett. 117 012403 doi: 10.1063/5.0012706
    [19] Nagaosa N, Tokura Y 2013 Nat. Nanotechnol. 8 899 doi: 10.1038/nnano.2013.243
    [20] Fert A, Reyren N, Cros V 2017 Nat. Rev. Mater. 2 17031 doi: 10.1038/natrevmats.2017.31
    [21] Du L P, Yang A P, Zayats A V, Yuan X C 2019 Nat. Phys. 15 650 doi: 10.1038/s41567-019-0487-7
    [22] Davis T J, Janoschka D, Dreher P, Frank B, Meyer zu Heringdorf F J, Giessen H 2020 Science 368 6489
    [23] Tsesses S, Ostrovsky E, Cohen K, Gjonaj B, Lindner N H, Bartal G 2018 Science 361 6406
    [24] Bai C Y, Chen J, Zhang Y X, Zhang D W 2020 Opt. Express 28 10320 doi: 10.1364/OE.384718
    [25] Bliokh K Y, Rodriguez-Fortuno F J, Nori F, Zayats A V 2015 Nat. Photonics 9 796 doi: 10.1038/nphoton.2015.201
    [26] Shi P, Du L P, Yuan X C 2020 Nanophotonics 9 4619 doi: 10.1515/nanoph-2020-0430
    [27] Karnieli A, Tsesses S, Bartal G, Arie A 2021 Nat. Commun. 12 1092 doi: 10.1038/s41467-021-21250-z
    [28] Deng Z L, Shi T, Krasnok A, Li X P, Alu A 2022 Nat. Commun. 13 1
    [29] Li X H, Liu L L, Zhou Z X, Shen J R, Zhang Y R, Han G D, Li Z 2022 Adv. Opt. Mater. 10 15
    [30] Shi C Z, Zhao R K, Long Y, Yang S, Wang Y, Chen H, Ren J, Zhang X 2019 Natl. Sci. Rev. 6 4
    [31] Burns L, Bliokh K Y, Nori F, Dressel J 2020 New. J. Phys. 22 053050 doi: 10.1088/1367-2630/ab7f91
    [32] Long Y, Zhang D M, Yang C W, Ge J M, Chen H, Ren J 2020 Nat. Commun. 11 4716 doi: 10.1038/s41467-020-18599-y
    [33] Bliokh K Y, Nori F 2019 Phys. Rev. B 99 020301
    [34] Bliokh K Y, Nori F 2019 Phys. Rev. B 99 174310 doi: 10.1103/PhysRevB.99.174310
    [35] Weiner M, Ni X, Alu A, Khanikaev A B 2022 Nat. Commun. 13 6332 doi: 10.1038/s41467-022-34072-4
    [36] Long Y, Ge H, Zhang D M, Xu X Y, Ren J, Lu M H, Bao M, Chen H, Chen Y F 2020 NSR 7 6
    [37] Sun Q L, Peng Y G, Gao F, Li B, Zhu X F 2023 Phys. Rev. Appl. 20 024025 doi: 10.1103/PhysRevApplied.20.024025
    [38] Ge H, Xu X Y, Liu L, Xu R, Lin Z K, Yu S Y, Bao M, Jiang J H, Lu M H, Chen Y F 2021 Phys. Rev. Lett. 127 144502 doi: 10.1103/PhysRevLett.127.144502
    [39] Hu P, Wu H W, Sun W J, Zhou N, Chen X, Yang Y Q, Sheng Z Q 2023 Appl. Phys. Lett. 122 022201 doi: 10.1063/5.0131777
    [40] Cselyuszka N, Secujski M, Engheta N, Crnojevic-Bengin V 2016 New. J. Phys. 18 103006 doi: 10.1088/1367-2630/18/10/103006
    [41] Zhu J, Chen Y Y, Zhu X F, Garcia-Vidal F J, Yin X B, Zhang W L, Zhang X 2013 Sci. Rep. 3 1728 doi: 10.1038/srep01728
    [42] Jia H, Lu M H, Ni X, Bao M, Li X D 2014 J. Appl. Phys. 116 124504 doi: 10.1063/1.4895990
    [43] Ooi K, Okada T, Tanaka K 2011 Phys. Rev. B 84 115405 doi: 10.1103/PhysRevB.84.115405
    [44] Xie P X, Sheng Z Q, Huang Z X, Hu P, Wu H W 2023 Appl. Phys. Lett. 122 222202 doi: 10.1063/5.0151926
    [45] Morse P, Ingard K 1986 Theoretical Acoustics (Princeton: Princeton University Press
    [46] 张孝悦, 徐华锋, 陈婉娜, 周农, 孙文军, 吴宏伟 2024 物理学报 73 144301 doi: 10.7498/aps.73.20240484 Zhang X Y, Xu H F, Chen W N, Zhou N, Sun W J, Wu H W 2024 Acta Phys. Sin. 73 144301 doi: 10.7498/aps.73.20240484
  • 加载中
图( 7)
计量
  • 文章访问数:  73
  • HTML全文浏览数:  73
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-12
  • 刊出日期:  2025-03-05

基于定向声源的局域型声学斯格明子模式的选择性激发

    通讯作者: E-mail: xhfeng716@126.com.; 
    通讯作者: E-mail: hwwu@aust.edu.cn.
    作者简介: 张孝悦.E-mail: zxy1913486877@163.com
  • 1. 安徽理工大学力学与光电物理学院, 淮南　232001
  • 2. 安徽理工大学基础物理研究中心, 淮南　232001
  • 收稿日期:  2024-09-12

摘要: 声学斯格明子模式是一种在声学结构表面产生的速度场矢量拓扑纹理结构, 这种受保护的矢量分布为声音信息处理、传输和数据存储提供了新的机遇. 本文结合声学波导和亚波长阿基米德螺旋结构设计了一种组合结构, 利用定向声源激发波导模式传输, 进而实现对局域型声学斯格明子模式的选择性激发. 通过理论分析和数值仿真, 研究了自旋声源、Huygens声源、Janus声源在此结构中激发的压力场分布以及速度场分布, 展示了组合结构中声表面波的定向传输性质和选择性激发的声学斯格明子模式. 这种由定向声源选择性激发声学斯格明子模式的方式为设计先进声学信息处理功能器件提供了新的途径.

English Abstract

    全文HTML

    1.   引　言

    • 斯格明子(Skyrmion)是一种拓扑保护的准粒子, 由英国物理学家Skyrme[1]于1962年在核物理学中首次提出, 用于描述介子的相互作用. 此后, skyrmion的概念, 即以拓扑整数 (称为skyrmion数) 表征矢量场结构特征的拓扑稳定性, 已在许多学科中得到关注, 例如核子[2]、玻色-爱因斯坦凝聚 体[3,4]、液晶[5,6]和磁性材料[7–11]. 特别是在磁性材料中, skyrmion已经发展成一个庞大的研究领域, 根据不同的拓扑结构也衍生出各种拓扑纹理, 例如Neél型、Bloch型、反型、skyrmionium、bimeron和bimeronium[12–18]. 丰富多样的skyrmion模式结构为高级信息处理、高密度数据存储和传输等方面的应用提供了巨大的可调自由度[19,20]. 光作为重要的信息载体, 迫切需要操纵磁场和电场的矢量纹理. 为此, 人们通过在特殊形状的表面等离子激元结构中构建衰逝电磁场分布[21–23], 在光波中通过三维电矢量结构模拟skyrmion拓扑保护的准粒子性质. 随后, 人们也构建了各种矢量场来实现光学skyrmion, 为操控光信息处理提供新的维度, 如电和磁矢量[24]、自旋[21,25,26]和合成赝自旋矢量[27]. 最近, 一种熟悉的亚波长空间卷曲超结构也被提出来, 其构建出具有多频带的skyrmion纹理[28,29].

      众所周知, 电磁波是横波, 从逻辑上来说光学skyrmion是容易实现的. 然而, 声波长期以来被认为是无旋的标量波. 直到最近, 这一传统观点才得到更新, 例如, 在自由空间中垂直传播的两个声波的干涉中, 或在沿超材料波导传播的导模衰减场中, 人们观察到由局部速度矢量旋转定义的声自旋[30–34]. 与光学系统中的横向自旋角动量的产生方式相类似, 有人利用自旋动量锁定, 通过创建可允许声表面波传播的超表面波导, 实现了声自旋源产生的声波定向传播特性[32,35]. 在此基础上, Long等[36]通过使用具有独特近场分布的声源(如自旋声源、Huygens声源和Janus声源)来激发超表面波导, 然后对结构和声源进行对称性选择, 从而产生定向声表面波传输特性. 通过各种声源配置对不同方向的声表面波进行激发和控制, 为微粒子的操纵提供了一个更优异的平台. 此后Sun等[37]受III型Dirac点独特性质的启发, 利用不同声波传播方向区域的混合声学Dirac晶格来对Plaquette状态进行操控. 其概念的提出, 为讨论声学skyrmion提供了机会. 近年来, Ge等[38]设计了一种六边形声学超表面来捕获表面声波并形成动态声速场的skyrmion晶格图案; 课题组[39]也利用亚波长阿基米德螺旋结构, 从理论上研究并实验证明了局域型声学skyrmion结构. 声学skyrmion拓扑结构可能为声波信息的存储和处理提供一个理想平台.

      本文基于一种波导和螺旋结构的组合结构, 通过理论分析和模拟仿真, 研究了自旋声源、Huygens声源、Janus声源在此结构中激发的压力场分布以及速度场分布, 展示了组合结构中声表面波的定向传输性质和选择性激发的声学skyrmion模式. 这些研究结果将有助于新颖的声学波导器件的开发, 可用于局域型声学skyrmion模式的调控.

    2.   结　果

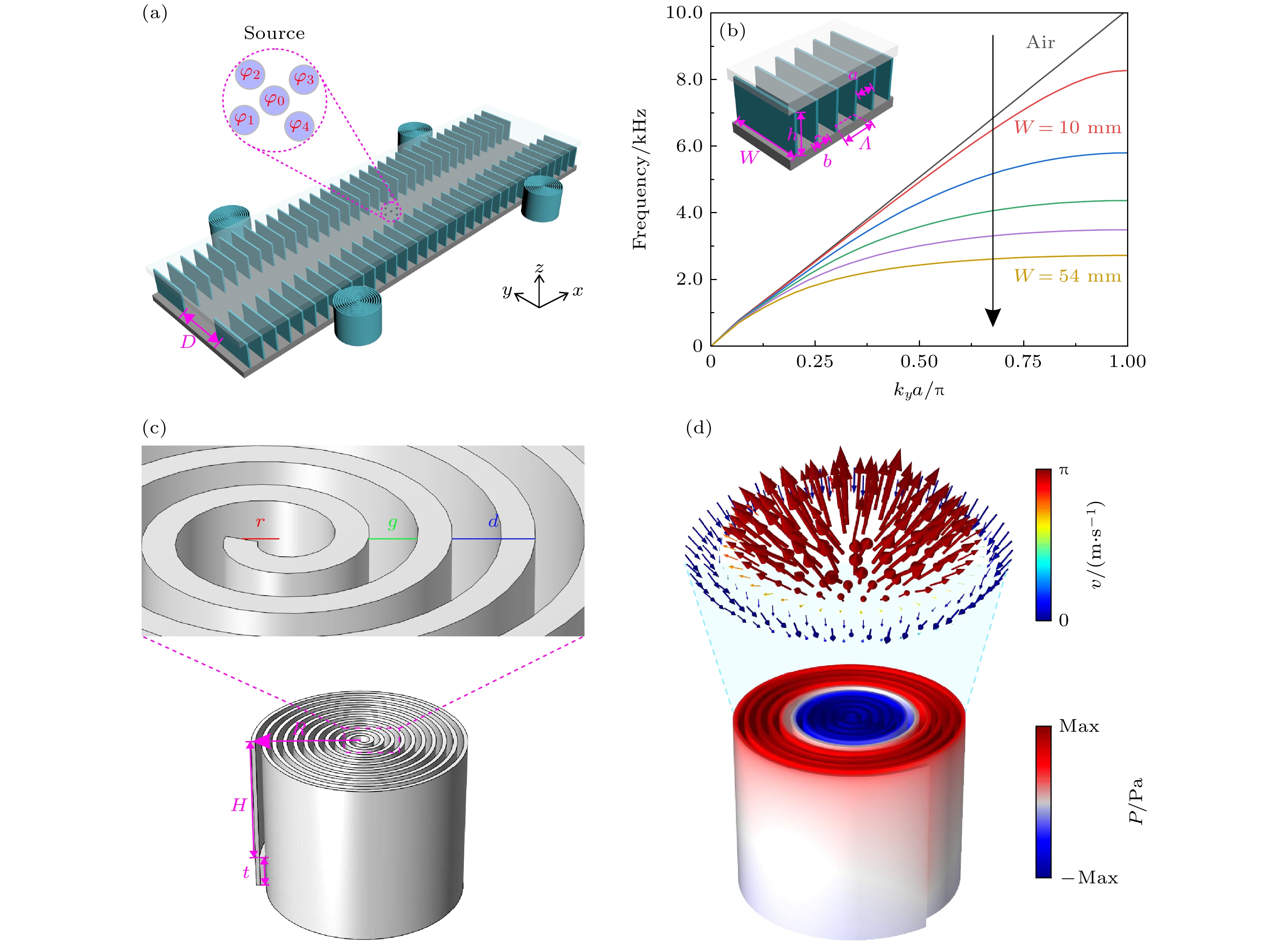
    • 利用周期性刚性小片设置了两条声学波导, 如图1(a)所示, 这些小片之间的间隔距离为$ a=1.5\;{\mathrm{c}}{\mathrm{m}} $, 周期为$ \varLambda =a+b $, $ b=0.2\;{\mathrm{c}}{\mathrm{m}} $, b是小片的厚度, 小片的宽度为$ W=5.4\;{\mathrm{c}}{\mathrm{m}} $, 高度为$ h= 3.2\;{\mathrm{c}}{\mathrm{m}} $, 两条波导之间的通道宽度为$ D=6.0\;{\mathrm{c}}{\mathrm{m}} $. 与人工表面等离激元性质相类似[40–42], 由周期性布置的刚性小片组成的这种声学波导也可以产生沿波导传播的声表面波, 并且可以描述其色散关系为[43,44]

      式中, k 是声表面波的波矢, $ {k}_{0} $是声音在空气中传播的波矢. 通过计算, 我们得到了波导宽度 W 变化时波导的色散关系曲线, 如图1(b)所示, 当$ W= 1.0\;{\mathrm{c}}{\mathrm{m}} $时, 此波导结构的声学波导的截止频率为8.271 kHz, 在其宽度增大到5.4 cm时, 截止频率则降低为2.721 kHz.

      采用基于阿基米德螺旋线形的螺旋结构实现声学 skyrmion 模式, 结构示意图如图1(c)所示. 结构细节如下: 间隙宽度$ g=0.145\;{\mathrm{c}}{\mathrm{m}} $, 螺旋螺距$ d=0.245{\mathrm{ }}\;{\mathrm{c}}{\mathrm{m}} $, 外半径$ R=2.55{\mathrm{ }}\;{\mathrm{c}}{\mathrm{m}} $, 内半径$ r= 0.1{\mathrm{ }}\;{\mathrm{c}}{\mathrm{m}} $, 壁厚为$ 0.1{\mathrm{ }}\;{\mathrm{c}}{\mathrm{m}} $, 凹槽深度为$ H=3.25{\mathrm{ }}\;{\mathrm{c}}{\mathrm{m}} $, 底座高度为$ t=0.8{\mathrm{ }}\;{\mathrm{c}}{\mathrm{m}} $, 螺旋旋转数$ n=10 $. 将4个螺旋结构放置在波导结构的两端, 呈现对称布置, 组合成一个整体结构. 图1(d)显示了在一阶 skyrmion 模式下单个螺旋结构上的声学压力场和速度场分布, 特征频率为$ f=2.431{\mathrm{ }}\;\;{\mathrm{k}}{\mathrm{H}}{\mathrm{z}} $, 结构中的颜色标记压力场分布, 而结构上方的颜色矢量表示速度场的结构. 从矢量方向可以看出, 速度场矢量在中心处向上, 而随着半径的增大, 速度场的方向逐渐翻转, 最终在结构边缘向下. Skyrmion模式的拓扑性质可以用skyrmion数S来表征: $ S= \displaystyle\frac{1}{4{\mathrm{\pi }}}\iint \boldsymbol{n} \cdot \left(\frac{\partial \boldsymbol{n}}{\partial x} \times \frac{\partial \boldsymbol{n}}{\partial y}\right){\mathrm{d}} x {\mathrm{d}}y $, 其中, $ \boldsymbol{n} = \dfrac{Re\left(\boldsymbol{v}\right)}{\left|Re\left(\boldsymbol{v}\right)\right|} $[39].

      根据声辐射理论[45], 声源可以看作是声单极子、声偶极子的叠加, 一般形式为

      式中, $ {\boldsymbol{Q}}_{{\mathrm{s}}} $表示声源的矢量声场; $ M $, $ D $分别表示声单极子、声偶极子; $ \boldsymbol{\alpha } $, $ \boldsymbol{\beta } $分别为单极极化率与偶极极化矢量. 为了实现有趣的声源-波导耦合现象, 根据近场声学的几何和对称特性引入3个近场源[36]: 声学自旋源 $ {\boldsymbol{Q}}_{{\mathrm{Spin}}}={D}_{x}\pm {{\mathrm{i}}D}_{y} $; 声学Huygens源$ {\boldsymbol{Q}}_{{\mathrm{H}}{\mathrm{u}}{\mathrm{y}}{\mathrm{g}}{\mathrm{e}}{\mathrm{n}}{\mathrm{s}}} = M \pm {{\mathrm{i}}D}_{x} $; 声学Janus源 $ {\boldsymbol{Q}}_{{\mathrm{J}}{\mathrm{a}}{\mathrm{n}}{\mathrm{u}}{\mathrm{s}}} = M \pm {D}_{y} $.

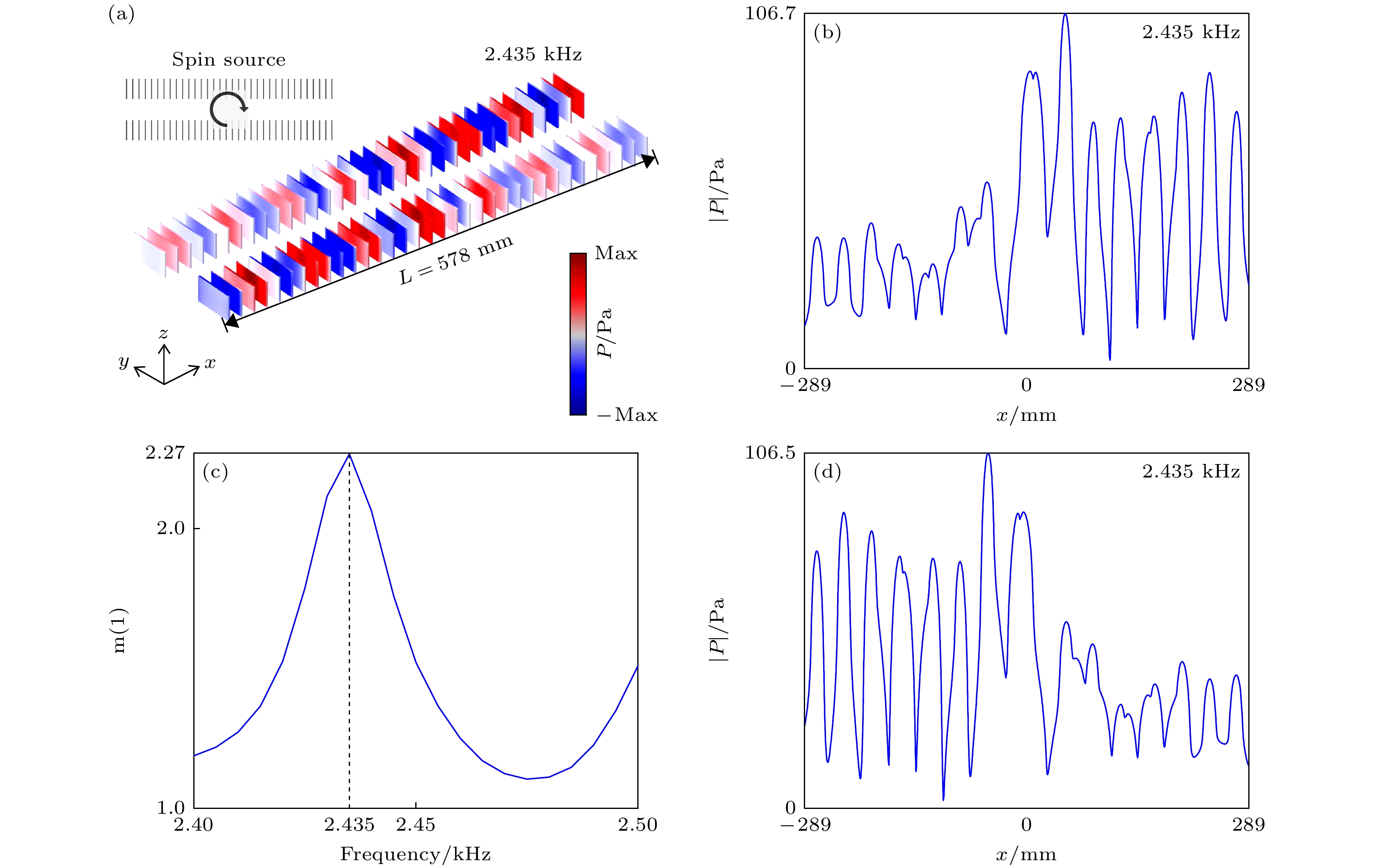
      首先, 将一个声学自旋源放置在组合结构的中心, 如图1(a)所示, 设置$ {\varphi }_{1},\; {\varphi }_{2},\;{ \varphi }_{3},\; {\varphi }_{4} $ 4个单极点源来实现自旋声源[46], 此时$ {\varphi }_{0} $处于禁用状态, 以特定的相位设置来激发它们. 当设置$ {\varphi }_{1}= {{\mathrm{\pi }}}/{2},\; {\varphi }_{2}= 0,\;{\varphi }_{3} = {3{\mathrm{\pi }}}/{2},\; {\varphi }_{4}={\mathrm{\pi }} $时, $ {\boldsymbol{Q}}_{{\mathrm{Spin}}} = {D}_{x}-{{\mathrm{i}}D}_{y} $, 可以实现顺时针自旋声源, 当设置$ {\varphi }_{1}=3{\mathrm{\pi }}/2, {\varphi }_{2}=0, \;\varphi _{3}= {\mathrm{\pi }}/2, {\varphi }_{4}={\mathrm{\pi }} $时, $ {\boldsymbol{Q}}_{{\mathrm{S}}{\mathrm{p}}{\mathrm{i}}{\mathrm{n}}}={D}_{x}+{{\mathrm{i}}D}_{y} $, 可以实现逆时针自旋声源.

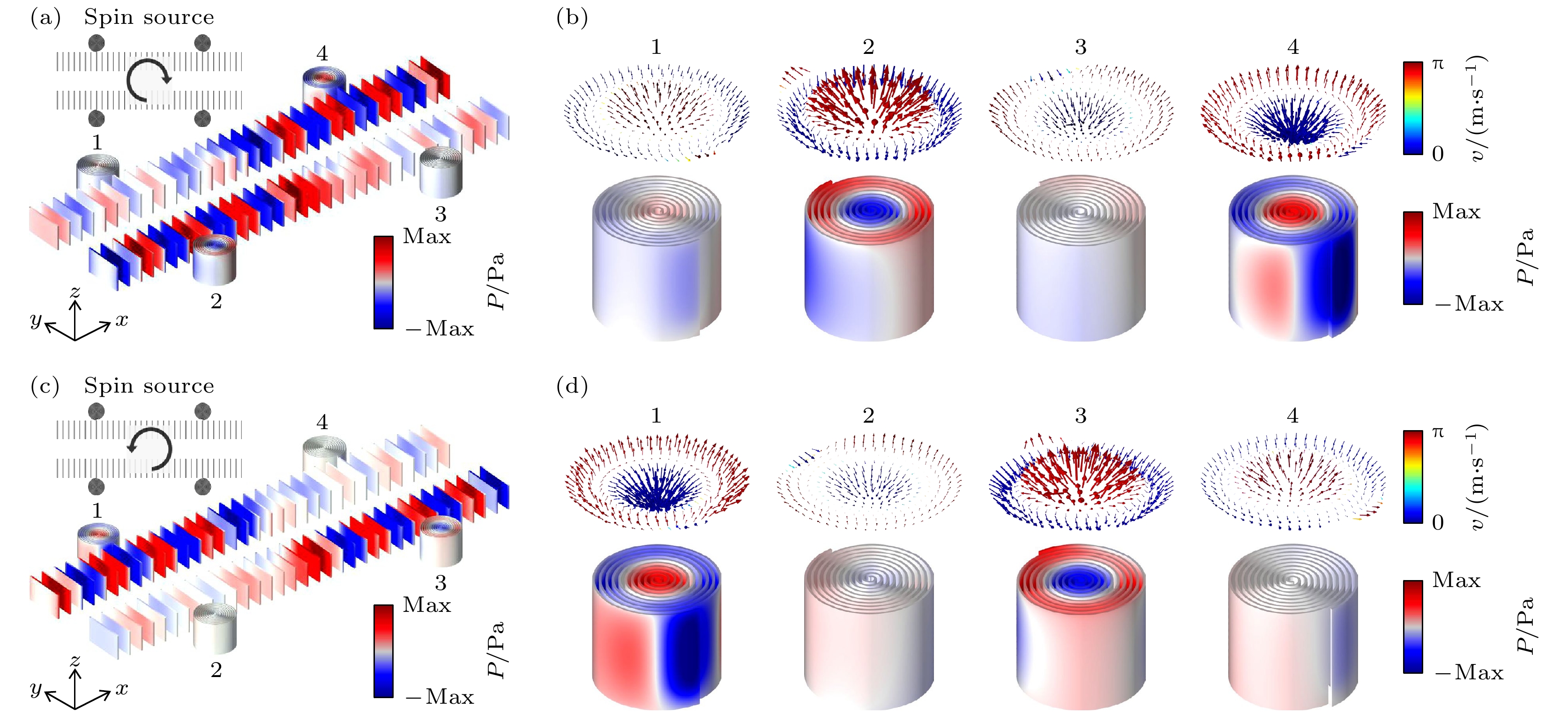
      下文将先研究声表面波在波导结构中的传播现象, 将一个顺时针旋转的声学自旋源放置在波导结构的中心, 如图2(a)所示, 通过有限元仿真软件COMSOL Multiphysics的压力声学模块模拟计算了声学波导中的压力场分布. 在模拟中, 波导片的区域设置为内部硬声场边界[46]; 周围的材料设置为空气, 空气密度$ {\rho }_{0}=1.21\;{\mathrm{k}}{\mathrm{g}}/{{\mathrm{m}}}^{3} $, 声速$ v= 343\;{\mathrm{m}}/{\mathrm{s}} $, 将包含波导和自旋源的区域四周设置为球面波辐射边界条件. 图2(c)所示为顺时针旋转的自旋声源定向激发声学表面波沿波导前后向传输比随频率变化的曲线图, 可以发现当频率$ f= 2.435{\mathrm{ }}\;{\mathrm{k}}{\mathrm{H}}{\mathrm{z}} $时, 前后向传输比最高. 接下来, 设定自旋声源的激发频率$ f=2.435{\mathrm{ }}\;{\mathrm{k}}{\mathrm{H}}{\mathrm{z}} $, 计算波导空间压力场分布如图2(a)所示, 计算结果发现顺时针旋转的自旋声源可以定向激发声学表面波沿波导传播. 图2(b)所示为顺时针旋转的自旋声源定向激发声学表面波沿上方波导向右传播的声压强度分布曲线图, 可以发现其中的声压强度变化与声压场图相互吻合, 在上方波导结构右侧声压强度很高, 而在左侧的声压强度很低. 图2(d)所示为顺时针旋转的自旋声源定向激发声学表面波沿下方波导向左传播的声压强度分布曲线图, 在下方波导结构左侧声压强度很高, 而在右侧的声压强度很低. 上述计算结果验证了声表面波在此波导结构中的定向传播行为.

      接下来, 利用定向声源激发波导模式传输进而实现对局域型声学skyrmion模式的选择性激发. 为此在波导的4个端口位置放置编号为1, 2, 3, 4号的阿基米德螺旋结构, 如图3(a)所示, 顺时针旋转的声自旋源激发声表面波沿波导定向传播, 激发频率为$ f=2.435{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}\;{\mathrm{k}}{\mathrm{H}}{\mathrm{z}} $, 通过计算可以得到在忽略声学波导中的损耗时, 此组合结构的空间声压力场分布. 通过计算可以发现, 顺时针旋转的声自旋源可以激发声学表面波沿波导向着2号和4号方向传播, 并且选择性地激发2号和4号螺旋结构 的声学skyrmion模式, 2号和4号的skyrmion数分别为$ {S}_{2}=0.95 $和$ {S}_{4}=-0.97 $, 接近理论值$ \pm 1 $. 组合结构中具体每一个螺旋结构的声压力场分布和声速度场分布如图3(b)所示, 可以发现2号和4号的压力场分布和速度场分布明显大于1号和3号. 然后, 当我们设置声自旋源为逆时针旋转 时, 如图3(c)所示, 可以发现, 在组合结构中, 将会激发声学表面波沿波导向着1号和3号方向传输, 并且选择性地激发1号和3号螺旋结构的声学skyrmion模式, 1号和3号的skyrmion数分别为$ {S}_{1}=-0.95 $和$ {S}_{3}=0.99 $, 接近理论值$ \pm 1 $. 由上述结果分析, 当$ {\boldsymbol{Q}}_{{\mathrm{S}}{\mathrm{p}}{\mathrm{i}}{\mathrm{n}}}={D}_{x}-{{\mathrm{i}}D}_{y} $时, 为顺时针的声自旋源, 它将会激发声表面波在波导中沿着右上和左下方向传播; 当$ {\boldsymbol{Q}}_{{\mathrm{S}}{\mathrm{p}}{\mathrm{i}}{\mathrm{n}}}={D}_{x}+{{\mathrm{i}}D}_{y} $时, 为逆时针的声自旋源, 它将会激发声表面波在波导中沿着向左上和右下方向传播, 并且实现了组合结构中的局域型声学skyrmion模式的选择性激发.

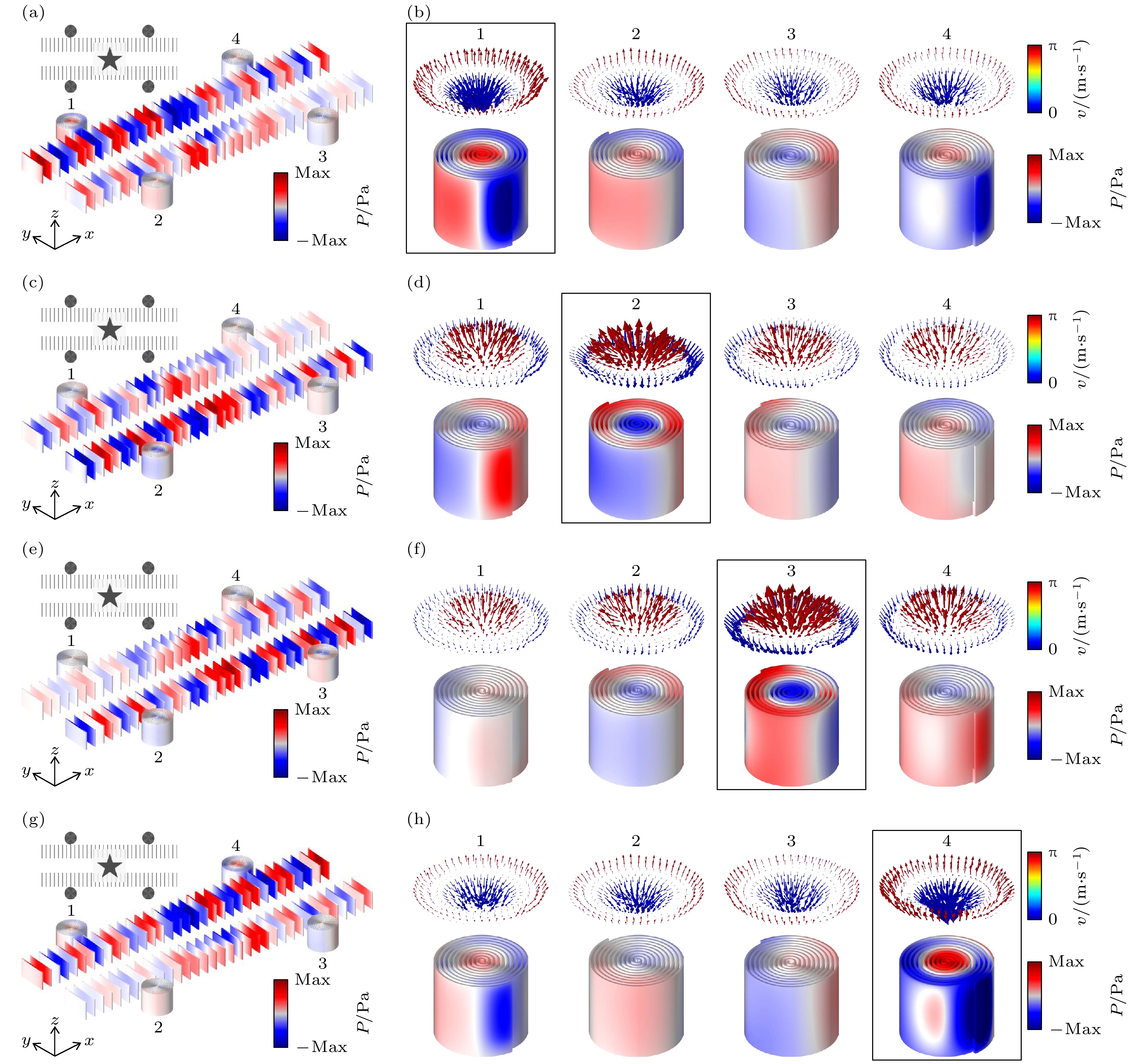
      进一步地, 利用选择性地激发单向单侧表面波进而实现对单个螺旋结构的声学skyrmion模式的激发. 通过设置$ {\varphi }_{1},\; {\varphi }_{2},\;{ \varphi }_{3},\; {\varphi }_{4} $ 4个单极点源以 特定的相位设置来激发它们, 从而实现单向单侧 激励的声源. 将一个单向单侧激励的声源放置在 组合结构的中心, 激发频率$ f=2.435\;{\mathrm{kHz}} $, 通过计算可以得到组合结构的空间声压力场分布. 当设 置$ {\varphi }_{1}= 3{\mathrm{\pi }}/2,\; {\varphi }_{2}=0 $时, 计算结果发现可以激发声学表面波沿波导向1号方向传播, 如图4(a)所示, 并且选择性地激发1号螺旋结构的声学skyrmion模式, 1号的skyrmion数为$ {S}_{1}=-0.91 $, 接近理论值$ -1 $. 组合结构中具体每一个螺旋结构的声压 力场分布和声速度场分布如图4(b)所示, 可以发现1号的压力场分布和速度场分布的场强大于2号, 3号和4号. 同样, 当设置$ {\varphi }_{1}={\mathrm{\pi }}/2,\; {\varphi }_{4}={\mathrm{\pi }} $时, 如图4(c)所示, 在波导中将激发声学表面波 沿波导向着2号方向传输, 激发2号螺旋结构的 声学skyrmion模式, 2号的skyrmion数为$ {S}_{2}= 0.97 $, 接近理论值$ 1 $. 当设置$ {\varphi }_{3}={\mathrm{\pi }}/2,\; {\varphi }_{4}={\mathrm{\pi }} $时, 如图4(e)所示, 在波导中将激发声学表面波沿波导向着3号方向传输, 并且激发3号螺旋结构的声学skyrmion模式, 3号的skyrmion数为$ {S}_{3}=0.94 $, 接近理论值$ 1 $. 当设置$ {\varphi }_{2}=0,\; {\varphi }_{3}=3{\mathrm{\pi }}/2 $时, 如 图4(g)所示, 在波导中将激发声学表面波沿波导向着4号方向传输, 同时激发4号螺旋结构的声学skyrmion模式, 4号的skyrmion数为$ {S}_{4}=-0.98 $, 接近理论值$ -1 $. 由上述结果表明利用单向单侧激励的声源可以在波导系统中实现单个声学skyrmion模式的激发.

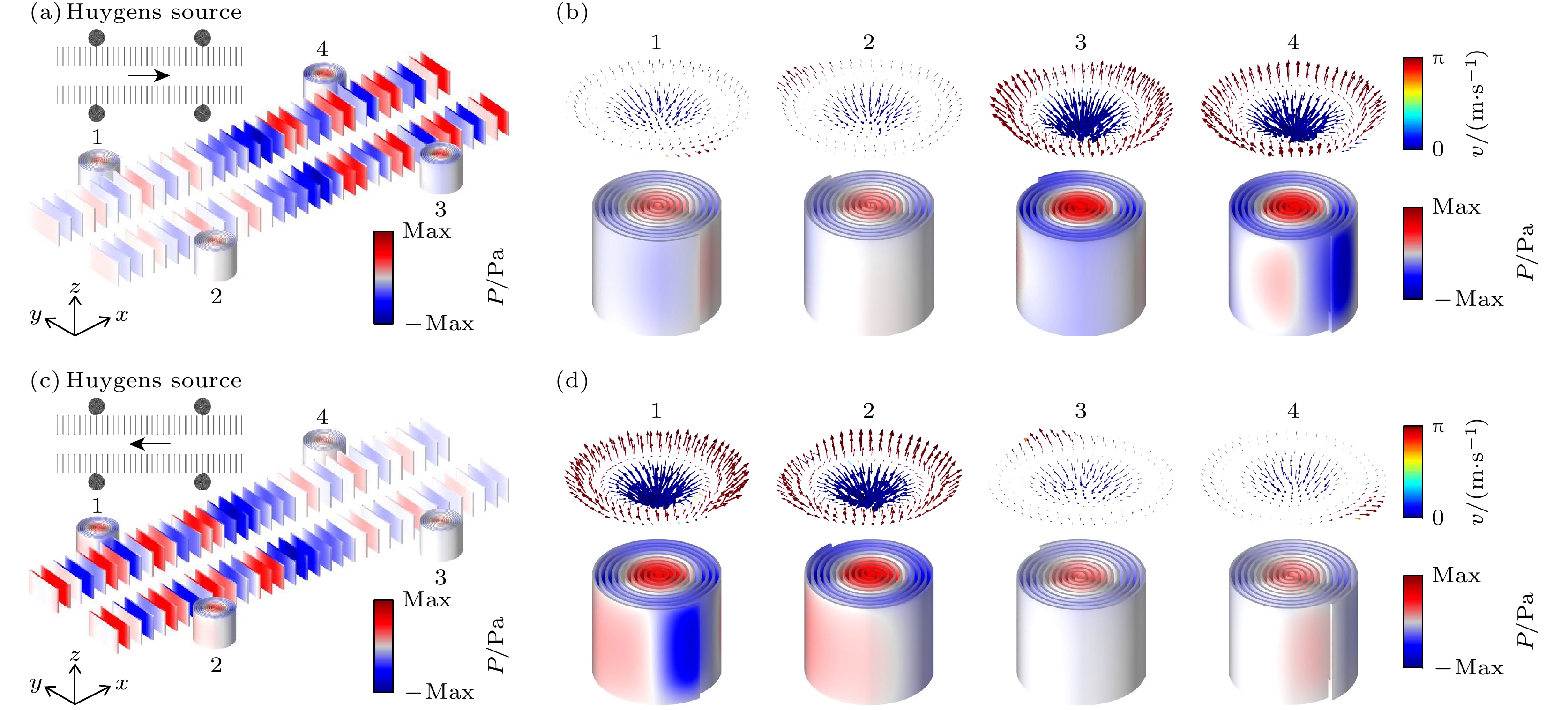
      进一步将一个Huygens声源放置在组合结构的中心, 如图1(a)所示, 我们设置$ {\varphi }_{1},\; {\varphi }_{0},\;{ \varphi }_{3} $ 3个单极点源来实现Huygens声源, 此时$ {\varphi }_{2},\;{ \varphi }_{4} $处于禁用状态, 以特定的相位设置来激发它们. 当设置$ {\varphi }_{1} = {\mathrm{\pi }}/2,\; {\varphi }_{0} = 0,\;{ \varphi }_{3} = 3{\mathrm{\pi }}/2 $时, $ {\boldsymbol{Q}}_{{\mathrm{H}}{\mathrm{u}}{\mathrm{y}}{\mathrm{g}}{\mathrm{e}}{\mathrm{n}}{\mathrm{s}}}=M+{{\mathrm{i}}D}_{x} $, 可以实现前向的Huygens声源, 当设置$ {\varphi }_{1}=3{\mathrm{\pi }}/2, {\varphi }_{0}=0,\;{ \varphi }_{3}={\mathrm{\pi }}/2 $时, $ {\boldsymbol{Q}}_{{\mathrm{H}}{\mathrm{u}}{\mathrm{y}}{\mathrm{g}}{\mathrm{e}}{\mathrm{n}}{\mathrm{s}}}=M-{{\mathrm{i}}D}_{x} $, 可以实现后向的Huygens声源.

      将一个前向的Huygens声源放置在组合结构的中心, 如图5(a)所示, 激发频率为$ f=2.435~\;{\mathrm{kHz}} $, 通过计算可以得到组合结构的空间声压力场分布, 结果发现前向的Huygens声源可以激发声学表面波沿波导向3号和4号方向传播, 并且选择性地激发3号和4号螺旋结构的声学skyrmion模式, 3号和4号的skyrmion数分别为$ {S}_{3}=-0.94 $和$ {S}_{4}=-0.99 $, 接近理论值$ -1 $. 组合结构中具体每一个螺旋结构的声压力场分布和声速度场分布如图5(b)所示, 可以发现3号和4号的压力场分布和速度场分布都呈现对称模式, 且他们的场强明显大于1号和2号. 同样, 如果将Huygens声源设置为后向时, 如图5(c)所示, 在波导中将激发声学表面波沿波导向着1号和2号方向传输, 并且选择性地激发1号和2号螺旋结构的声学skyrmion模式, 1号和2号的skyrmion数分别为$ {S}_{1}= -1.06, $$ {S}_{1}= -1.06, $和$ {S}_{2}=-0.91 $, 接近理论值$ -1 $. 由上述结果表明利用前向和后向的Huygens声源可以通过波导系统选择性地激发局域型声学skyrmion模式.

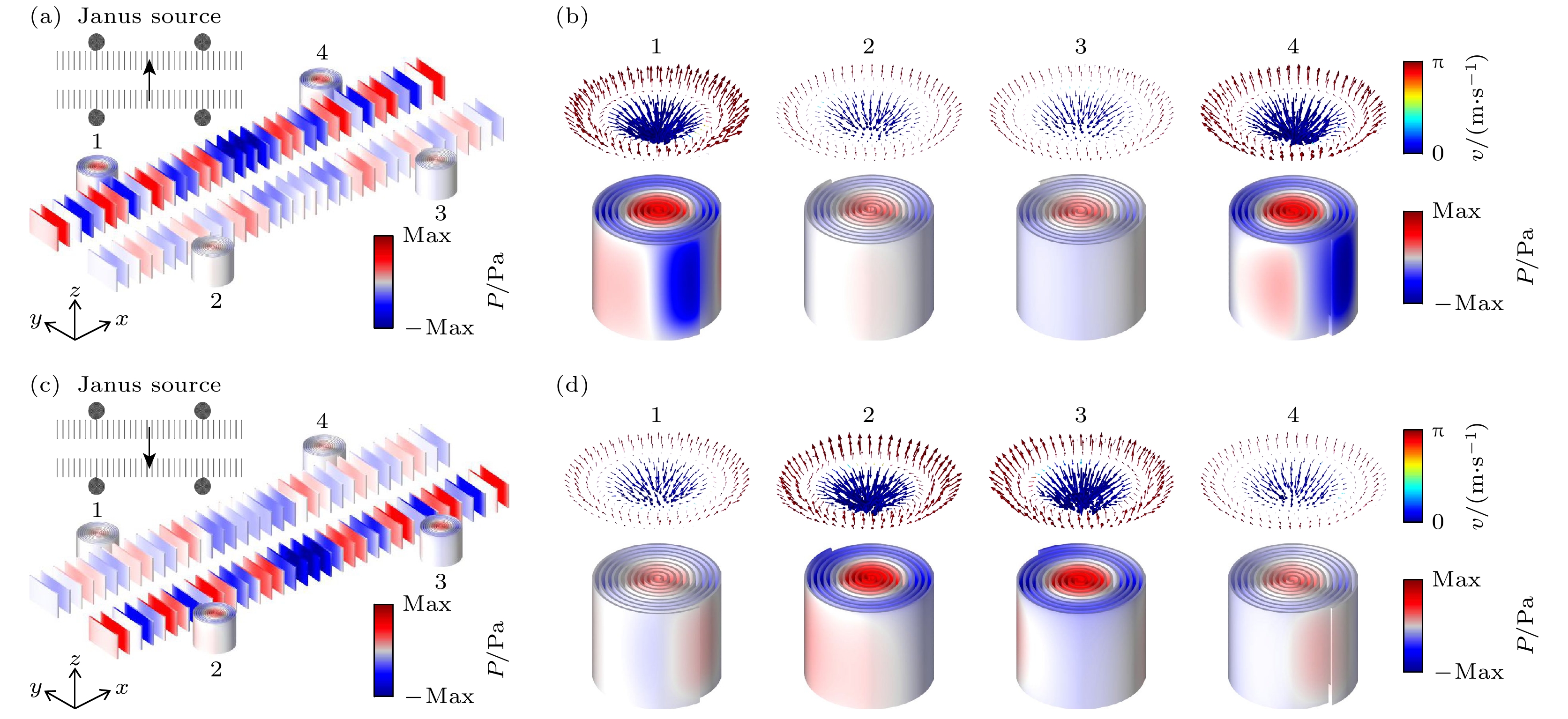
      最后研究了Janus声源对skyrmion模式的选择性激发. 如图1(a)所示, 设置$ {\varphi }_{2},\; {\varphi }_{0},\;{ \varphi }_{4} $ 3个单极点源来实现 Janus 声源, 此时$ {\varphi }_{1},\;{ \varphi }_{3} $处于禁用状态, 以特定的相位设置来激发它们. 当设置$ {\varphi }_{2}=0, {\varphi }_{0}=0,\;{ \varphi }_{4}={\mathrm{\pi }} $时, $ {\boldsymbol{Q}}_{{\mathrm{J}}{\mathrm{a}}{\mathrm{n}}{\mathrm{u}}{\mathrm{s}}}=M+{D}_{y} $, 可以实现向上的Janus声源, 当设置$ {\varphi }_{2}={\mathrm{\pi }},\; {\varphi }_{0}=0,\;{ \varphi }_{4}=0 $时, $ {\boldsymbol{Q}}_{{\mathrm{J}}{\mathrm{a}}{\mathrm{n}}{\mathrm{u}}{\mathrm{s}}}=M-{D}_{y} $, 可实现向下的Janus声源.

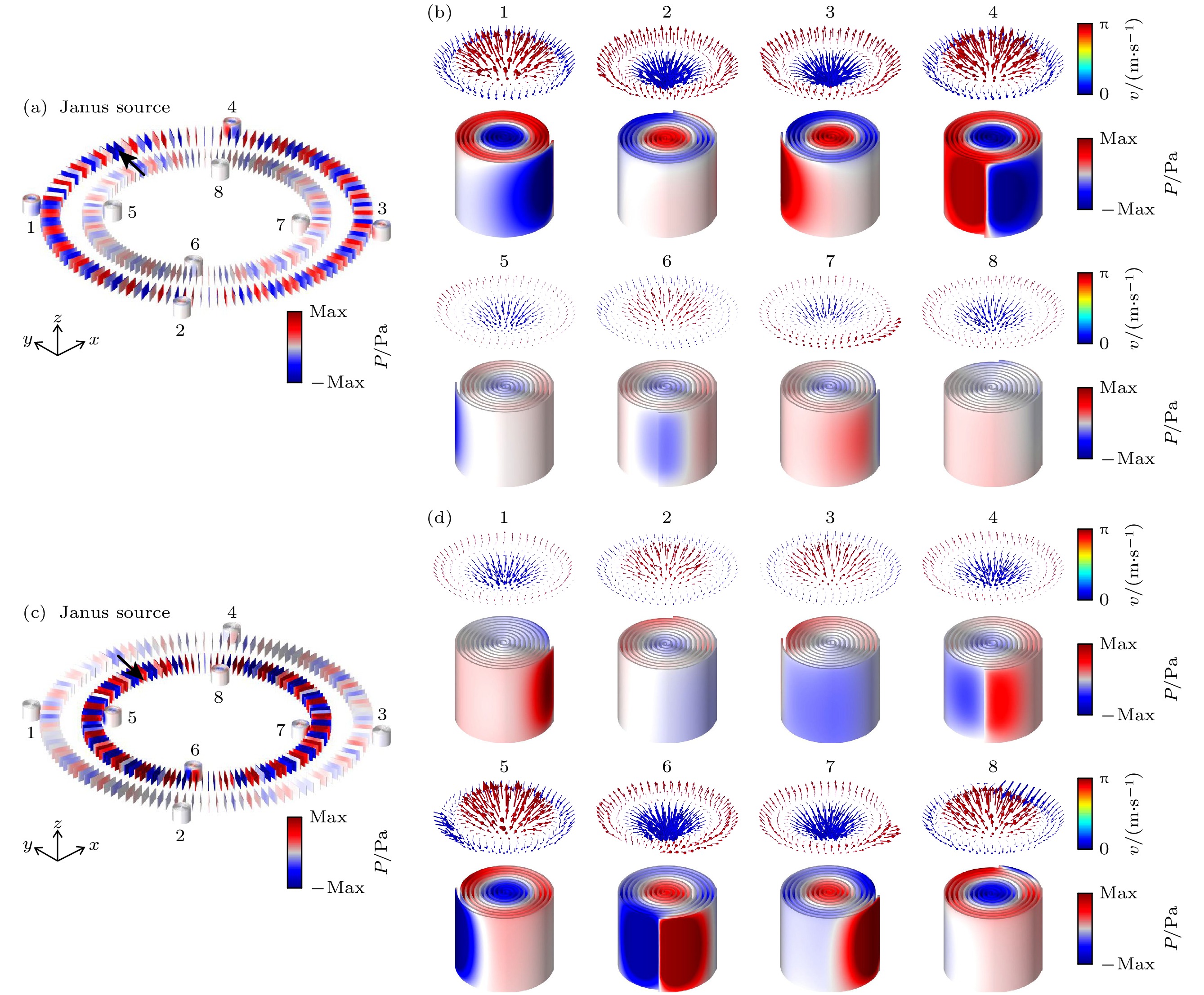
      将一个向上的Janus声源放置在组合结构中心, 如图6(a)所示, 激发频率依然为$ f = 2.435{\mathrm{ }}\;{\mathrm{kHz}} $, 通过计算可以得到组合结构的空间声压力场分布, 结果发现向上的Janus声源可以激发声学表面波沿上波导传输且选择性地激发1号和4号螺旋结构的声学skyrmion模式, 理论计算发现1号和4号skyrmion数分别为$ {S}_{1}=-1.03 $和$ {S}_{4}= -1.02 $, 接近理论值$ -1 $. 组合结构中具体每一个螺旋结构的声压力场分布和声速度场分布如图6(b)所示, 然而, 当将Janus声源设置为向下时, 如图6(c)所示, 在组合结构的波导中将激发2号和3号螺旋结构的声学skyrmion模式, 2号和3号的skyrmion数分别为$ {S}_{2} = -0.96 $和$ {S}_{3} = -0.92 $, 接近理论值 $ -1 $, 具体每一个螺旋结构的声压力场分布和声 速度场分布如图6(d)所示, 可以发现2号和3号的压力场分布和速度场分布都呈现对称模式, 且其场强明显大于1号和4号. 因此, 我们从理论和 仿真计算中证明了Janus声源可选择性地激发 不同位置的阿基米德螺旋结构中的声学skyrmion模式.

      进一步地, 将波导结构围成环形, 如图7(a), (c)所示, 在环形波导结构的外圈位置放置编号为1, 2, 3, 4号的阿基米德螺旋结构, 在环形波导结构的内圈位置放置编号为5, 6, 7, 8号的阿基米德螺旋结构. 将一个Janus声源放置在如图7(a)所示的位置上, 此时声源指向径向外侧, 设置激发频率$ f=2.335{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}\;{\mathrm{k}}{\mathrm{H}}{\mathrm{z}} $, 通过计算可以得到组合结构的空间声压力场分布, 结果发现向外的Janus声源可以激发声学表面波沿外圈波导传输且激发1, 2, 3, 4号螺旋结构的声学skyrmion模式, 具体每一个螺旋结构的声压力场分布和声速度场分布如图7(b)所示. 然而, 当Janus声源指向径向内侧时, 设置激发频率$ f=2.390\;{\mathrm{kHz}} $, 如图7(c)所示, 在组合结构的波导中将激发内圈的5, 6, 7, 8号螺旋结构的声学skyrmion模式, 具体每一个螺旋结构的声压力场分布和声速度场分布如图7(d)所示. 由上述结果表明, 利用Janus声源可以在环形波导结构系统中实现外圈或内圈所有螺旋结构中声学skyrmion模式的激发.

    3.   结　论

    • 本文设计了一种波导和螺旋结构的组合结构, 研究了自旋声源、Huygens声源、Janus声源在此结构中激发的压力场分布以及速度场分布, 展示了组合结构中声表面波的定向传输性质和4个螺旋结构中选择性激发的声学skyrmion模式. 这种波导激发方式是一种激发声学skyrmion模式的新手段, 使得声学skyrmion模式的激发更加灵活. 并且这种波导激发的方式在更复杂和更大规模的声学系统中有着重要的应用潜力, 这些研究结果将在设计新颖的声学器件方面提供应用价值, 例如声学加密设备, 声学天线和声学传感器等.

    参考文献 (46)

目录

/

返回文章
返回