高精度微小角度测量技术在小角度测量应用外, 还可以用于厚度、平面度、直线度的测量^[1,2], 不仅在医疗、军事、航空航天等领域^{[3, 4]}有着极大需求, 在芯片制造^[5]、硅晶圆生产等半导体行业关键性技术领域也日益重要^{[6, 7]}. 采用位置敏感探测器 (PSD)^[8,9]、CCD^[10]等进行光电转换和位置测量，具有精度更高、动态测量能力和测量分辨力更好，并融合图像处理算法^[11–14]的微小角度测量技术成为当前研究的重点^[15–17].

文献[18]采用Tolansky干涉为微小角度测量提供了一种新颖的技术方案, 其利用分光镜的反射与折射形成两路光, 通过两个反射镜形成各自的虚拟相干点光源, 在观察位置产生同心圆环结构的干涉图形. 当任意反射镜偏转时, 所产生的同心圆环的圆心会随之发生偏转, 进而通过干涉圆心的移动情况来反推反射镜转动的微小角度大小与方向. 由于采用了系列同心圆环的定圆心方式, 这种测角方式可以提高定中瞄准精度. 根据两个反射镜的相互动静和位置关系情况, 这种技术可以衍生出前静后动、前动后静、单臂共程、双臂异路等结构类型^[18,19]. 经研究, 这种技术方案不仅能实现微小角度的测量, 而且在端面厚度、平行度和直线度的测量方面具有潜在作用^[20]. 但是文献[18]中的方案在拓展应用方面存在被测量依赖动镜测量臂长的问题. 为了解决此问题, 本文提出了一种双臂Tolansky干涉自准直仪的方案, 巧妙地将这种干涉测角与自准直测角相结合, 使之具有自准直测量结果的直观性强、适用范围广和操作便捷等优点, 同时兼具光学干涉测量的精度高、测量范围广以及光电自动化等优点.

研究发现, 这种新型自准直仪中分光镜厚度及其折射率会影响仪器测角准确度. 为此, 本文利用文献[21]中的方法对此进行理论分析, 建立包含分光镜厚度和折射率的圆心偏移量与偏转角之间的关系, 通过理论、仿真及实体实验相结合的方式, 详细考察了分光镜参数的影响, 为这种新型自准直仪的深度研究和开发提供了重要的指导.

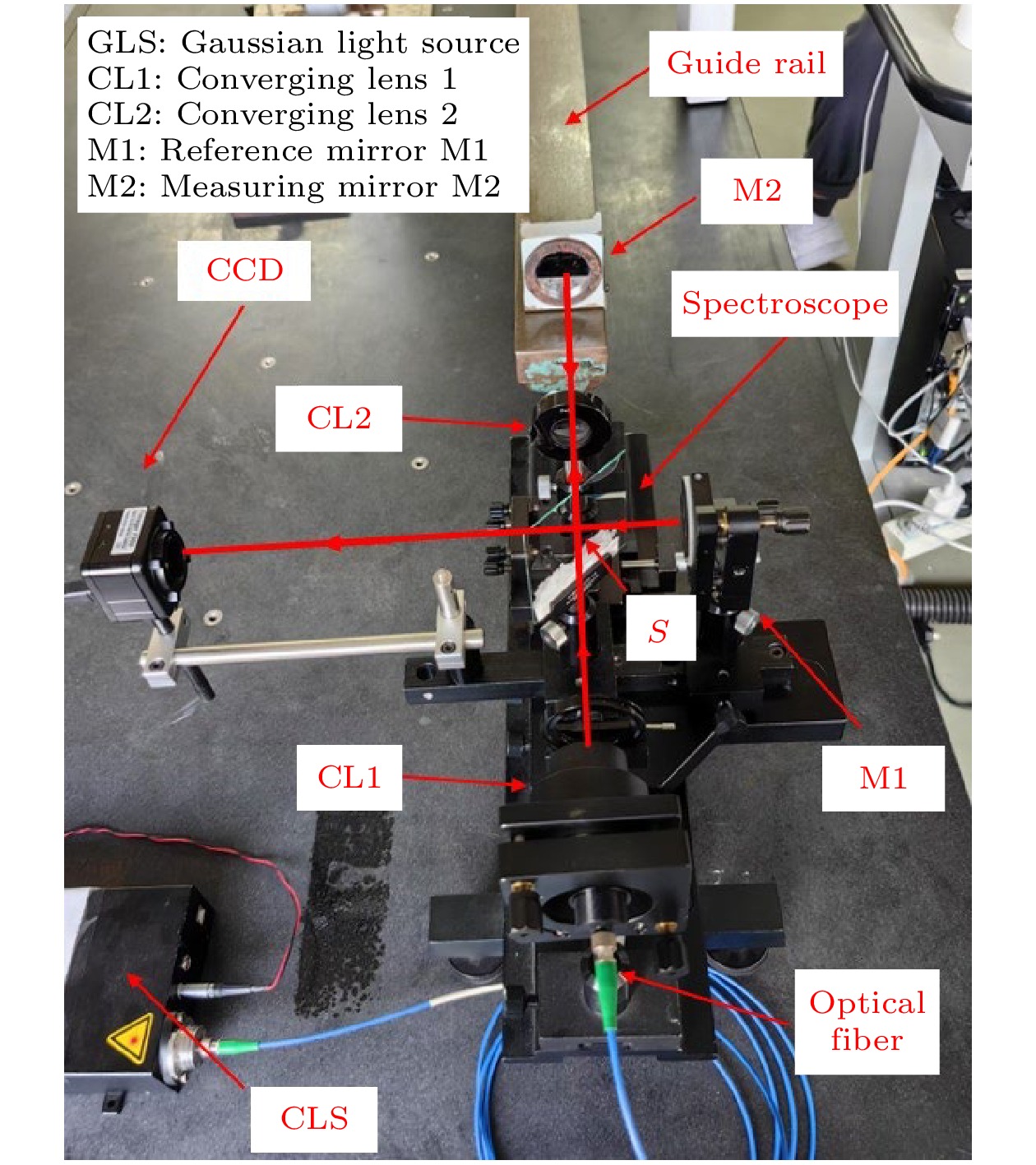
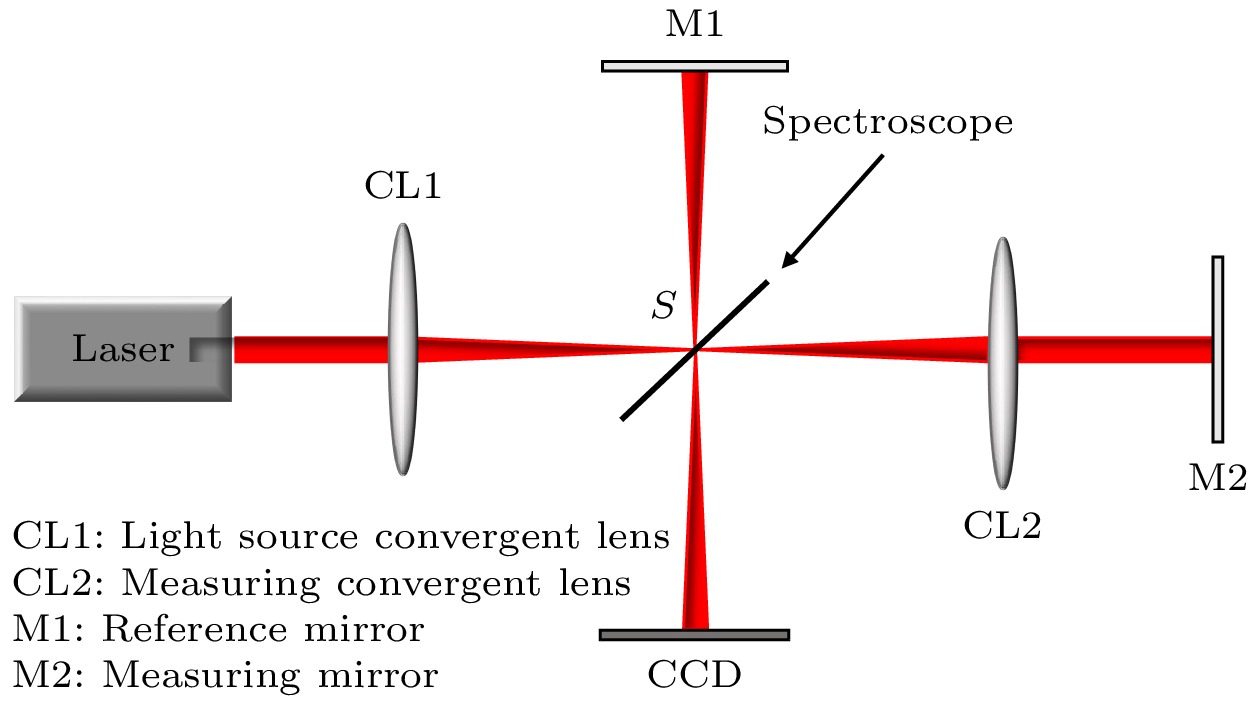
双臂Tolansky干涉测角系统结构如图1所示, 其中M1为参考反射镜, 静止不动; M2为测量反射镜, 会产生偏转, 其功能类似与传统自准直仪的桥板反射镜. 激光器发出的光经过光源会聚透镜CL1作用后在分光镜的前表面形成点光源S, 随后经分光镜的反射及折射分成参考光和测量光, 其中参考光垂直入射至参考反射镜M1, 并原路返回; 测量光经过测量会聚透镜CL2后入射至测量反射镜M2, 并原路返回. 两束原路返回的激光束再次通过分光镜融合后共路传播, 在空间中相干叠加形成干涉同心圆环, 使用CCD面阵相机采集干涉图像, 如图2所示.

本文的双臂Tolansky干涉测角系统是在文献[16]的系统基础上发展起来的, 主要的改进是在测量光路中加入了一个会聚透镜CL2, 点光源S正好位于CL2的焦点上. 这样, 经过CL2后的光束呈平行状态. 平行光束原路返回后会聚点仍在焦点处. 当M2发生偏转时, 这个会聚点始终于CL2的焦平面上移动. 如此, 会聚透镜CL2和反射镜M2构成了光杠杆结构, 这就既保持了Tolansky干涉的功能, 又融合了光杠杆原理, 使Tolansky干涉测角不再受限于测量镜的测量臂臂长.

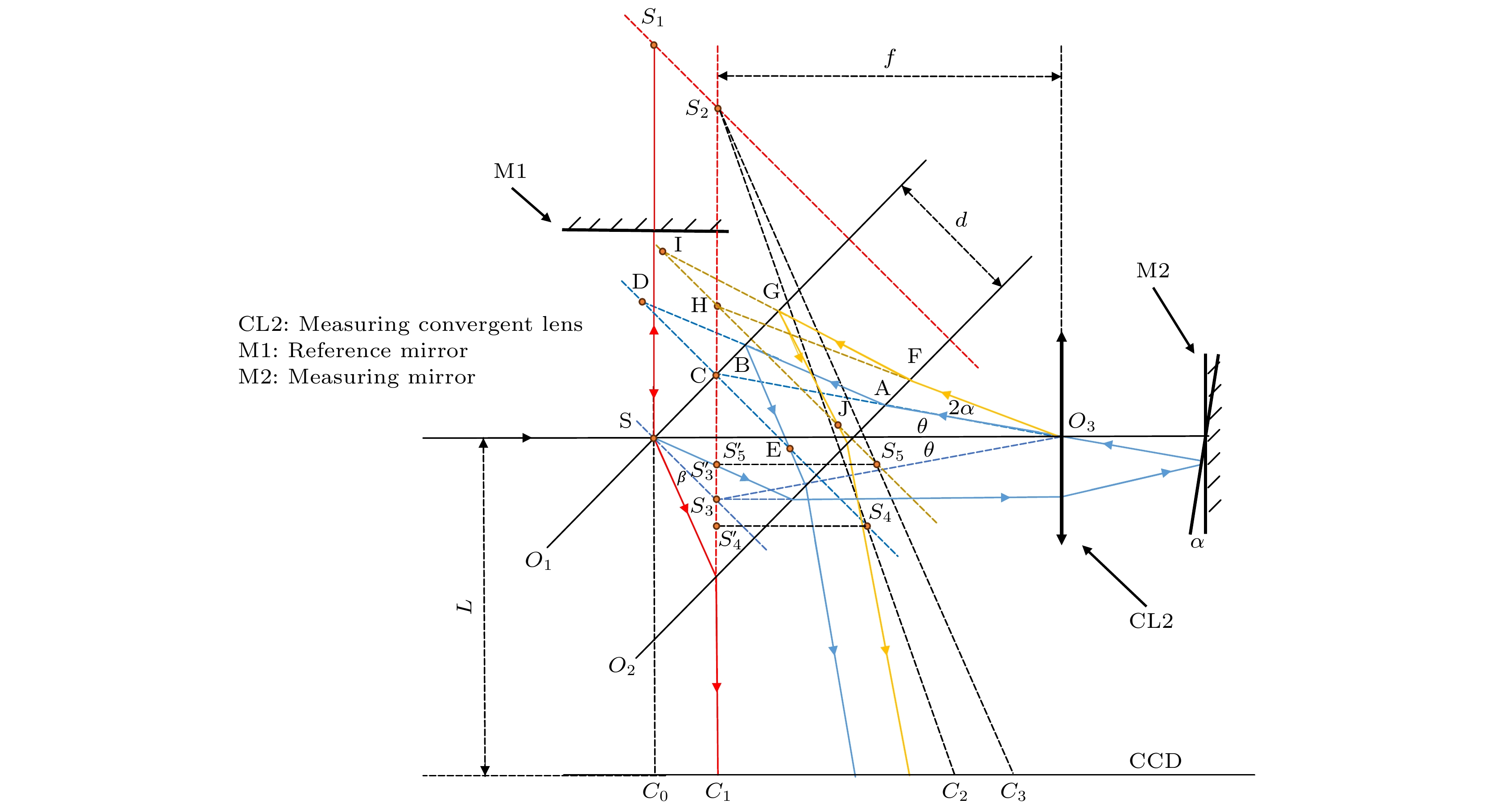
为了详细分析分光镜的影响, 将分光镜视为具有一定厚度的平行玻璃板, 其局部放大后整个系统光路结构如图3所示. 参考臂返回的中心光线与光源光束中心光线均以45°角入射分光镜; 设点光源S至M1反射面的距离为$ {D}_{1} $, 至CCD面阵相机接收面的距离为$ L $, 至CL2的距离为$ {D}_{2} $; 测量会聚透镜CL2为薄透镜, 其中心$ {{\mathrm{O}}}_{3} $位于Z轴上, 焦距为$ f $; 空气折射率为$ {n}_{0} $ , 玻璃板内折射率为$ n $, 分光镜玻璃厚度为d, 前表面记为$ {O}_{1} $, 且镀有一层50%的分光膜, 后表面记为$ {O}_{2} $, 镀有一层全透膜, 膜层厚度不计. 整个系统的符号遵从左负右正、上正下负的原则.

双臂Tolansky干涉自准直仪中形成干涉同心圆环的两个虚拟点光源的产生过程如下.

1) 参考点光源$ {S}_{2} $. 如图3中红色线所示, 点光源S依次经过分光镜前表面$ {O}_{1} $反射, 参考反射镜M1反射, 分光镜前表面折射, 分光镜后表面折射后, 成像为点光源$ {S}_{2} $, 期间由像点$ {S}_{1} $进行过渡, 如图3红色线所示. 参考光束通过参考反射镜M1所形成的虚像为$ {S}_{1} $, 经M1反射后在S点入射分光镜, 出射后交CCD面阵相机接收面于$ {C}_{1} $点, 由平行平板成像原理和单折射球面物像关系可知: 虚像$ {S}_{1} $发出的光经过平行玻璃板折射后, 其光轴为过$ {S}_{1} $点垂直于$ {O}_{1} $的虚线; 反向延长出射光线交光轴于$ {S}_{2} $点, 得到参考点光源$ {S}_{2} $, 其相对虚像$ {S}_{1} $的轴向偏移量为$ {S}_{1}{S}_{2} $.

2) 测量反射镜M2未偏转时的测量点光源$ {S}_{4} $. 如图3中蓝线所示, 测量臂光束从S点出发, 经分光镜面$ {O}_{1}, {O}_{2} $面两次折射后, 于$ {O}_{2} $面水平射出, 由平行平板成像原理和单折射球面物像关系可知: 点光源S发出的光线经过$ {O}_{1} $面时, 光轴为过S点垂直于$ {O}_{1} $面的虚线, 此时反向延长出射光线交光轴于$ {S}_{3} $点, 得到出射光线的点光源$ {S}_{3} $, 其相对点光源S的轴向偏移量为$ S{S}_{3} $. 点光源S的光线以45°角入射$ {O}_{1} $面, 折射角记作$ \beta $, 由折射定律可得(1)式和(2)式:

光线经过分光镜平行平板效应的轴向位移$ \Delta {L}' $见表达式(3)式和(4)式:

故上文提到的$ S{S}_{3} $的长度可表示为(5)式, 且根据图中几何数学关系可以推得$ {S}_{1}{S}_{2}=S{S}_{3} $; 进一步可得$ S_2 $距点光源S的轴向距离也为$ \Delta L′$. 由于测量会聚透镜CL2的透镜中心$ {O}_{3} $位于主光轴上(Z轴), 与入射光轴不重合, 所以水平入射的光线经过CL2透镜中心后形成的平行光束与主光轴呈$ \theta $夹角. 测量会聚透镜CL2的焦平面为过$ {S}_{3} $点垂直于主光轴的虚线, 即虚线$ {S}_{2}{S}_{3} $. 测量反射镜M2反射回的光线经过CL2的透镜中心$ {O}_{3} $交焦平面于C点, 得到测量臂返回光束的会聚焦点C. 在测量反射镜未偏转的时, 返回光线经过CL2的透镜中心$ {O}_{3} $且与主光轴呈$ \theta $夹角, 所以C点与$ {S}_{3} $点相对主光轴对称, 线段$ SC, S{S}_{3} $存在$ SC= S{S}_{3} $的关系, 由此可得(5)式:

单折射球面公式为: $ \dfrac{{n}'}{{l}'}-\dfrac{n}{l}=\dfrac{{n}'-n}{r} $. 当折射面为平面时, 曲率半径$ r $取无限大, 故等式右边为零, 得到单折射球面变形公式, 见(6)式:

返回光线交分光镜后表面$ {O}_{2} $于A点, 发生折射后光线交$ {O}_{1} $面于B点, 于B点反射后再次通过$ {O}_{2} $面折射后出射. 由平行平板成像原理和单折射球面物像关系可知, 返回光焦点为C点时, 其光轴为过C点且垂直于$ {O}_{2} $的虚线. 此时返回光束的焦点C为$ {O}_{2} $面入射的物, 此处$ {CO}_{2}=-d $, 将数据代入单折射球面变形公式(6)可得(7)式:

计算得到$ {DO}_{2}=-{nd}/{{n}_{0}} $ , 得到光轴上的像点D, 且$ {DO}_{2}=DC+{CO}_{2} $ . 光线经$ {O}_{1} $面反射后得到像点E, 长度上$ DC=CE=d\cdot \left({n}/{{n}_{0}}-1\right) $. 之后光线从$ {{{O}}}_{2} $面出射, E点视为出射光线的物, 将数据代入单折射球面变形(7)式可得到光线从$ {O}_{2} $面出射的表达式(8), 其中$ E{O}_{2}=C{O}_{2}-CE $:

计算得到$ {O}_{2}{S}_{4}=d\cdot \left(1 - {2{n}_{0}}/{n}\right) $, 可在光轴上找到出射光线的像点$ {S}_{4} $. 所以$ {S}_{4} $点为考虑分光镜厚度且测量反射镜M2未偏转时的测量点光源.

3)测量反射镜M2偏转时的测量点光源$ {S}_{5} $. 如图3中黄线所示, 点光源S的光线经过分光镜前表面$ {O}_{1} $以及后表面$ {O}_{2} $折射后, 出射光线路径与蓝线一致, 此时测量反射镜M2存在一个大小为$ \alpha $的偏转角, 所以经测量反射镜M2反射后, 经过CL2透镜中心的返回光线与主光轴呈$ \theta +2\alpha $的夹角; 与上文分析相同, 此时返回光束的焦点位于H点, 过H点做垂直于$ {O}_{2} $的虚线, 该虚线为此次折射的光轴. H点为入射$ {O}_{2} $面的物点, H点距$ {O}_{2} $面的距离$ H{O}_{2} $可表示为:

I点为光线入射$ {O}_{2} $面的像点, I点位置可将$ H{O}_{2} $数值代入单折射球面变形(6)式计算得到, 像点计算公式为:

计算得到I点的位置,

之后光线经过$ {O}_{1} $面反射后得到像点J, 几何关系可知$ {O}_{1}J=I{O}_{2}-\left(-d\right) $, 所以$ {O}_{1}J $可以表示为:

且$ J{O}_{2}=-d-{O}_{1}J $, 故

光线再次从$ {O}_{2} $面出射, 点J为此次折射的物, 由单折射球面变形(6)式可以得到得光线由J点从$ {O}_{2} $面出射的表达式:

将$ J{O}_{2} $的数值代入表达式计算, 得到$ {O}_{2}{S}_{5}= \Big(1-\dfrac{2{n}_{0}}{n}\Big) d + \dfrac{\sqrt{2}}{2}\Delta {L}' \cos \dfrac{{\mathrm{\pi }}}{4}-\dfrac{\sqrt{2}}{2}f \tan (\theta + 2\alpha ) $. 在黄色光线对应的光轴上取距离$ {O}_{2} $面为$ {O}_{2}{S}_{5} $的点$ {S}_{5} $, $ {S}_{5} $即为测量反射镜M2偏转时的测量点光源.

由文献[19]可知, Tolansky干涉形成的同心圆环的圆心处于两个虚拟点光源的连线上, 因此, 在上述相干点光源位置分析基础上, 连接参考点光源$ {S}_{2} $点与测量点光源$ {S}_{4} $点, 交CCD面阵相机接收面于$ {C}_{2} $点, 得测量反射镜发生偏转前干涉圆环圆心点$ {C}_{2} $; 连接$ {S}_{2} $与$ {S}_{5} $点, 交CCD面阵相机接收面于$ {C}_{3} $点, 得测量反射镜发生偏转后干涉圆环圆心点$ {C}_{3} $. 线段$ {C}_{2}{C}_{3} $的值则为测量反射镜M2发生偏转角$ \alpha $前后干涉同心圆环的圆心偏转量X. 这个偏转量与M2偏角$ \alpha $之间的关系式推导如下.

过$ {S}_{4} $点做水平线交$ {{C}_{1}S}_{2} $线于$ {S}_{4}' $点, 在$ \Delta {S}_{2}{C}_{1}{C}_{2} $中, 由三角形比例关系可得

其中

$ {C}_{1}{C}_{2} $的表达式为

同理过$ {S}_{5} $点做水平线交$ {{C}_{1}S}_{2} $线于$ {S}_{5}' $点, 在$ \Delta {S}_{2}{C}_{1}{C}_{3} $中, 由三角形比例关系可得

其中$ {S}_{5}{S}_{5}' = \sqrt{2}\left(1-{{n}_{0}}/{n}\right)d $, $ {S}_{2}{S}_{5}' = {S}_{5}'H+ H{S}_{2}= 2{D}_{1} - f \tan (\theta + 2\alpha )+\sqrt{2}\left(1 - {{n}_{0}}/{n}\right)d $, $ {S}_{2}{C}_{1} = 2{D}_{1} + L-\Delta {L}'\cdot {\mathrm{c}}{\mathrm{o}}{\mathrm{s}} ({{\mathrm{\pi }}}/{4}) $, $ {C}_{1}{C}_{3} $表达式为

干涉圆环圆心的偏移量$ X $可表示为$ X={C}_{1}{C}_{3}- {C}_{1}{C}_{2} $, $ X $的表达式为

将$ \tan (\theta +2\alpha ) = \dfrac{ \tan \theta + \tan2\alpha }{1 - \tan\theta \cdot \tan2\alpha } $和$ \tan\theta = \Delta L' \cos (\text{π}/4)/f$ 代入(17)式, 可得含厚度因素

在不考虑分光镜厚度时, 即d = 0, (18)式可进一步简化得到不含厚度因素(19)式. 其中, 为了与(18)式有所区分, 此处将偏移量改为$ {X}_{0} $:

(18)式和(19)式非常清晰地显示考虑分光镜厚度与否, 圆心偏移量和偏角之间关系的不同.

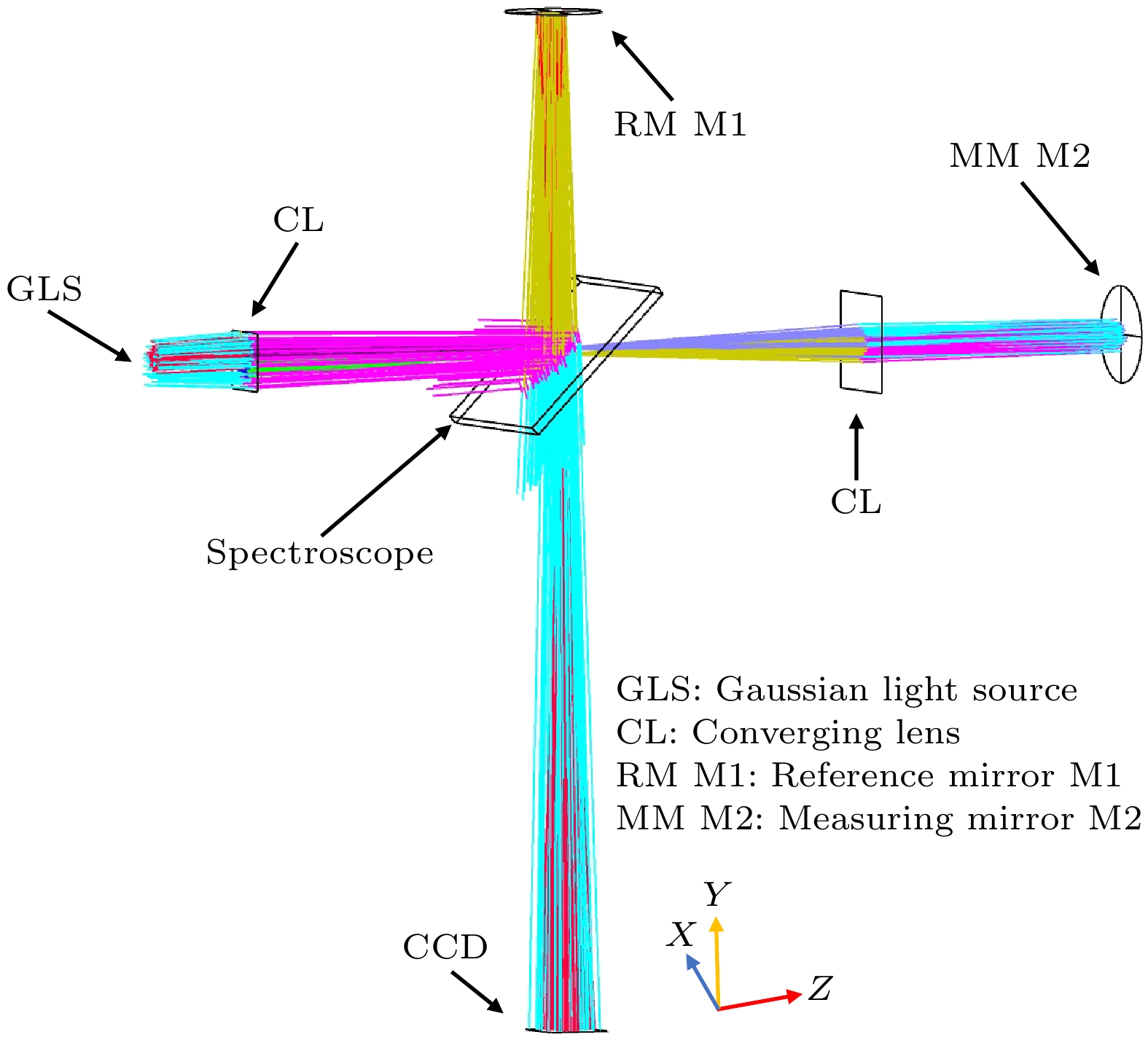
对应与图1的Zemax仿真模型如图4所示, 相关仿真参数如表1所示. 其中坐标结构如下: 以激光器为起始点和坐标原点, 垂直于纸面向里为X轴正方向, 竖直向上为$ Y $轴正方向, 水平向右为$ Z $轴正方向.

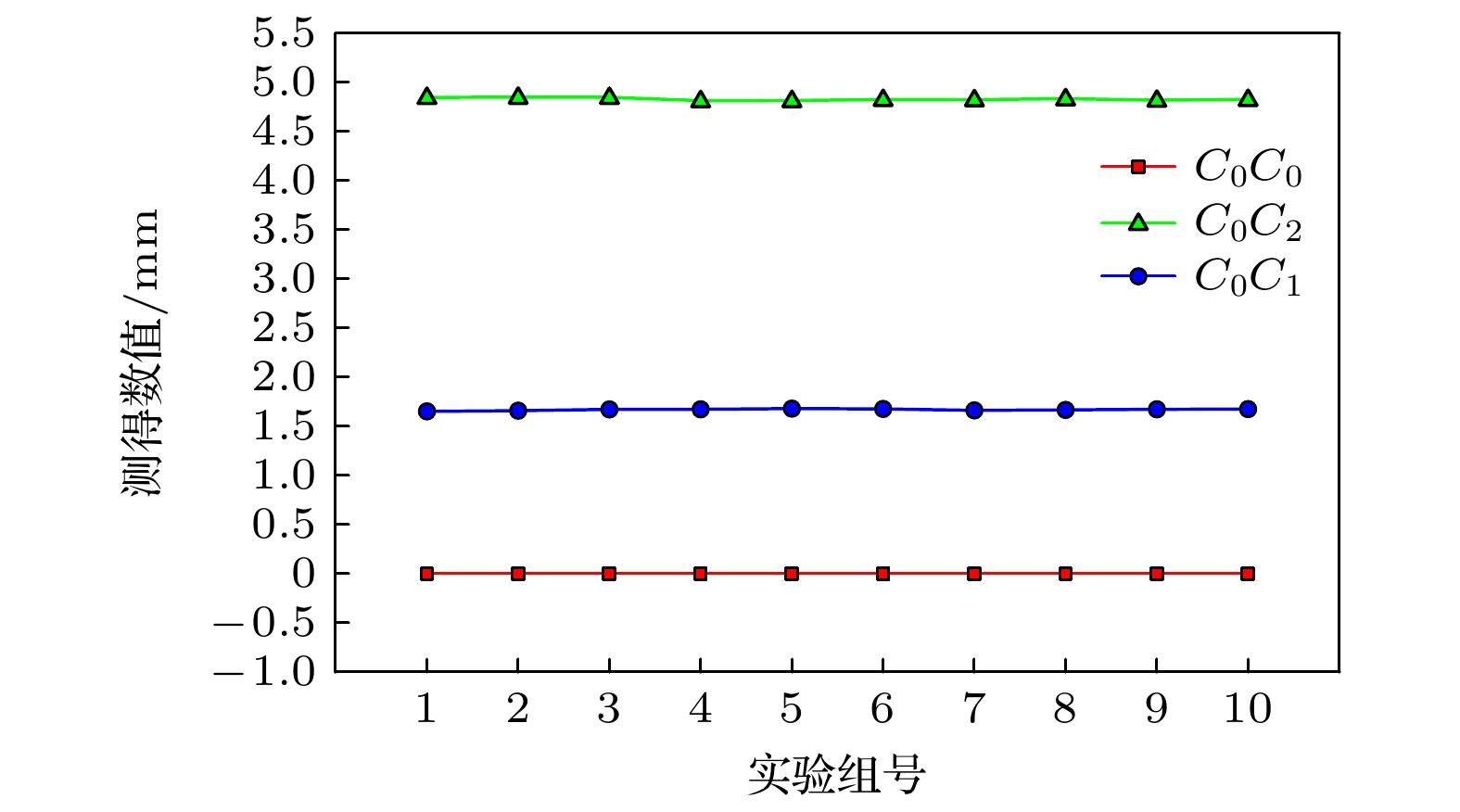
上文分析显示, 分光镜厚度的考虑与否会使干涉图形的圆心发生变动, 如图3的$ {C}_{0} $, $ {C}_{1} $, $ {C}_{2} $等点所示. 为此, 通过3个对照组仿真实验对圆心受分光镜厚度的影响进行研究: 实验组一验证分光镜玻璃板无厚度时的圆心位置$ {C}_{0} $点; 实验组二验证考虑分光镜玻璃板厚度且不对测量会聚透镜CL2位置进行侧移量调整; 实验组三验证考虑分光镜玻璃板厚度且对测量会聚透镜CL2位置进行侧移量调整. 3组对照组均保持测量反射镜M2不发生偏转. 3组实验中, 先提取实验组一干涉圆环圆心$ {C}_{0} $的位置; 实验组二引入分光镜玻璃板厚度厚, 提取干涉圆环圆心$ {C}_{2} $的位置, 圆心偏移量$ {C}_{0}{C}_{2} $的计算公式见(4)式和(14)式; 实验组三圆心偏移量$ {C}_{0}{C}_{1} $见(4)式, 除表1之外的其他相关参数如表2所示. 3个对照组各自进行10次仿真实验, 数据结果见图5.

由图5可得, 仿真实验测得的干涉圆环圆心$ {C}_{1}$和${C}_{2} $相对$ {C}_{0} $点的偏移量与理论圆心偏移量的数值均与图3中推导的$ {C}_{0}, {C}_{1}, {C}_{2} $的圆环圆心位置相吻合, 验证了理论分析和关系建模的正确性. 由于对仿真实验图片的进行图像圆心识别会存在一定误差, 所以仿真实验测得数值围绕真值略有上下波动.

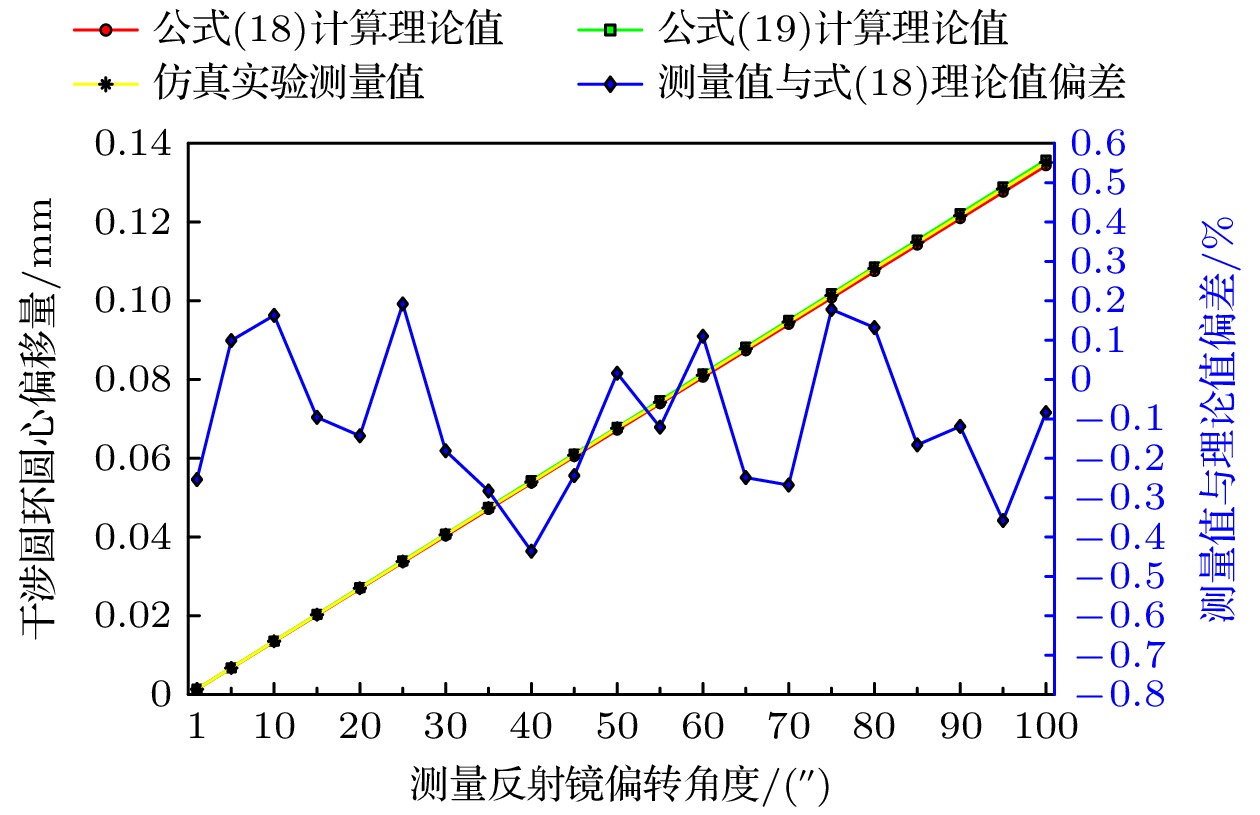
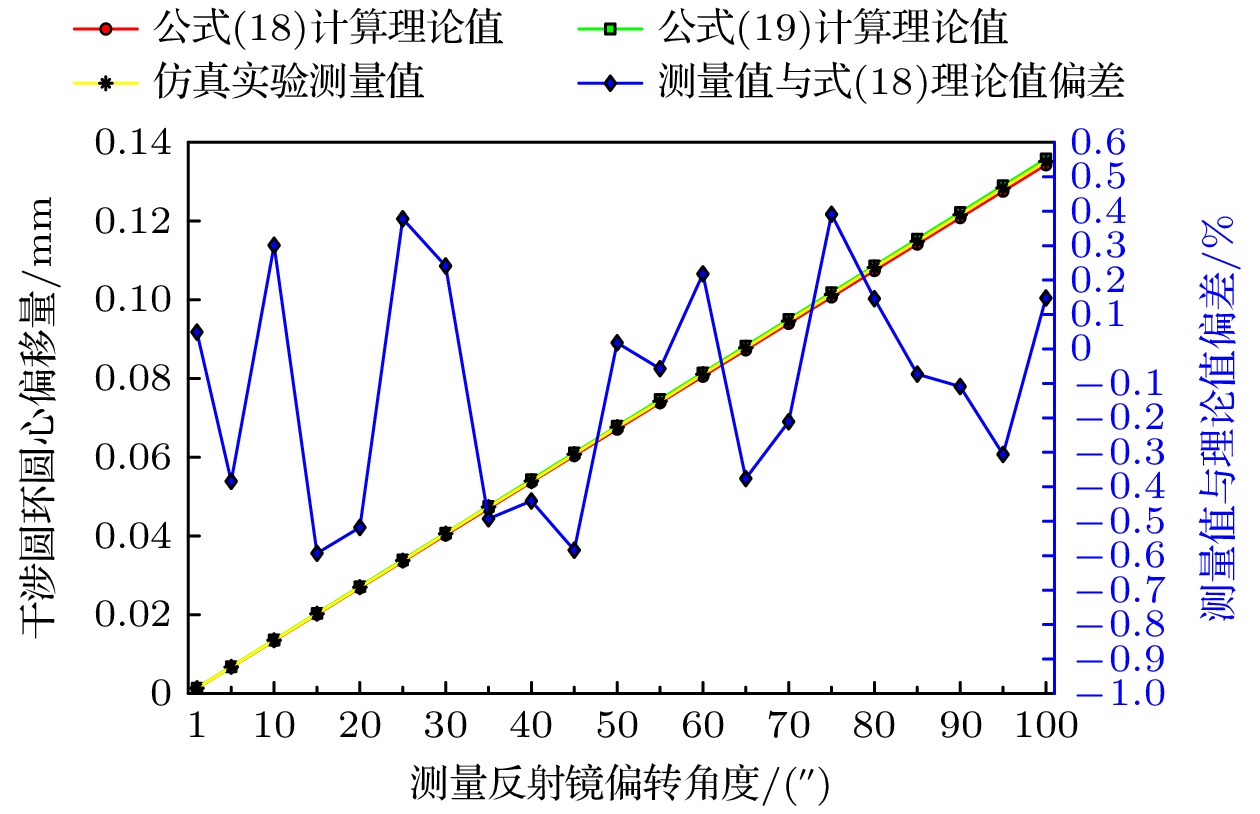
测量反射镜以X轴(正方向)为轴心顺时针偏转, 偏转角度从1'' 增大至100'', 每隔5'' 取一个测量点. 偏转角度归零时干涉圆环圆心所在坐标位置为$ {C}_{2} $, 各偏转角度下干涉圆环圆心所在坐标位置为$ {C}_{3} $, 则仿真实验干涉圆环圆心偏移量大小为$ {C}_{2}{C}_{3} $, 用$ {X}_{5} $表示. 同理, 测量反射镜以y轴(正方向)为轴心顺时针偏转实验. 除表1之外的其他相关参数如表3所示.

记录仿真实验各组干涉图像, 利用图像识别算法和软件^[22,23]提取其中的干涉圆环圆心坐标, 得到仿真实验的圆环圆心偏移量$ {X}_{5} $. 将偏转角度代入(18)式与(19)式, 计算干涉圆环圆心的理论偏移量$ {X}_{0}{\mathrm{与}}X $. 将仿真实验测得的圆环圆心偏移量与对应角度下所求关系式的理论偏移量做数据对比, 分析结果制成折线图, 测量反射镜两个方向的测量数据结果见图6和图7.

从图6和图7可看出, 无论测量反射镜以X轴或Y轴为轴心偏转, 随着分光镜厚度的增大, 含厚度因素的(18)式与不含厚度因素的(19)式之间的差值会逐渐增大, 而仿真测量数据结果与(18)式的理论值相对偏差在±0.5%以内.

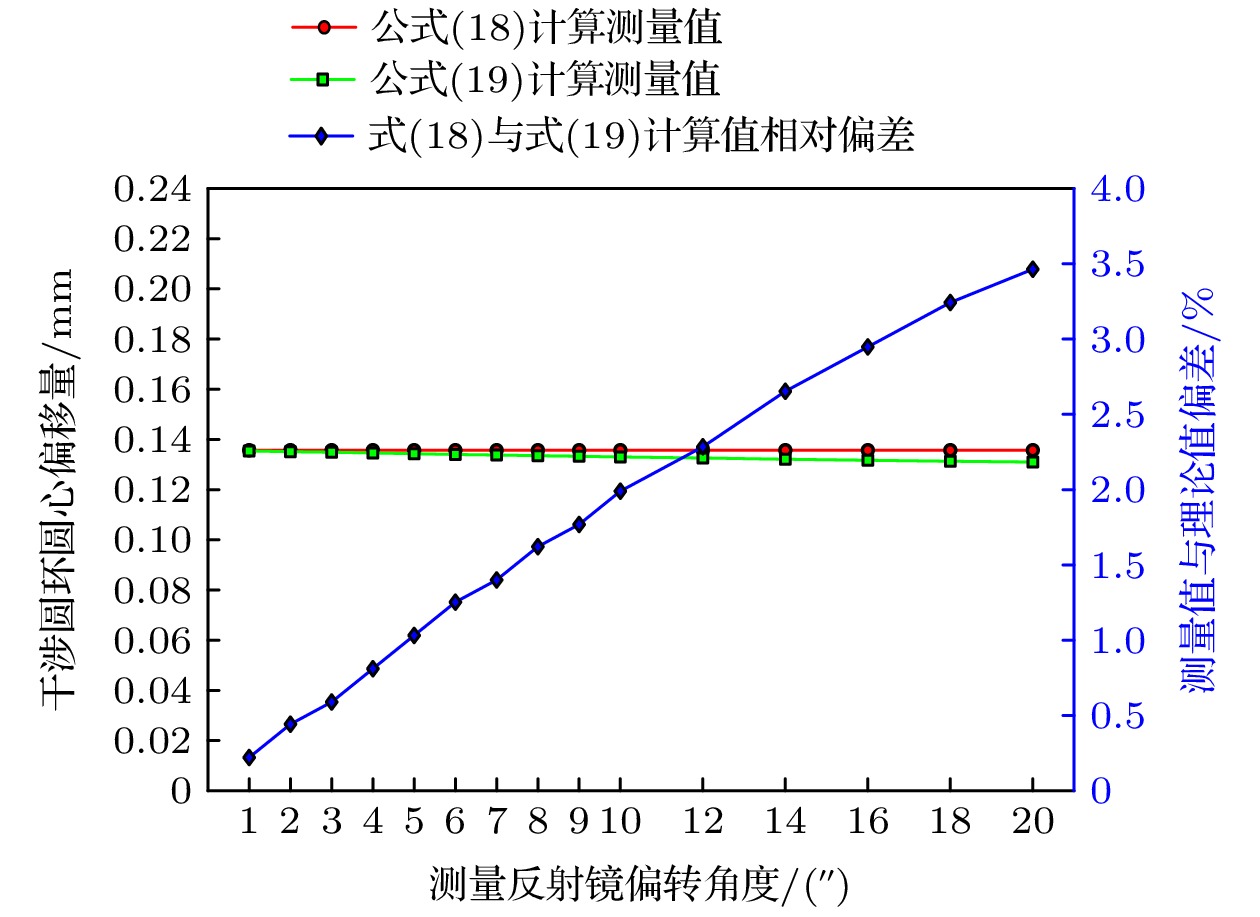
上文充分论述并验证了推导的含厚度因素(18)式比不含厚度因素(19)式更能贴合测量真值. 在实体仪器中, 分光镜存在物理厚度是不可避免的, 故需要寻找合适的厚度区间, 使其带来的测量偏差降至最低. 在其他参数条件不变的情况下, 控制测量反射镜偏转角固定为100'', 改变分光镜厚度自1 mm增大到20 mm, 考察含厚度因素(18)式和不含厚度因素(19)式对应的干涉圆环圆心偏移量对比情况, 见图8.

由图8可得, 在同样的角度下, 随着分光镜厚度的增大, 含厚度因素的(18)式和不含厚度因素的(19)式之间的差值会逐渐增大. 为了减小厚度的影响, 分光镜玻璃厚度应越小越好.

基于图1和虚拟仿真实验搭建了实体仪器, 见图9所示.

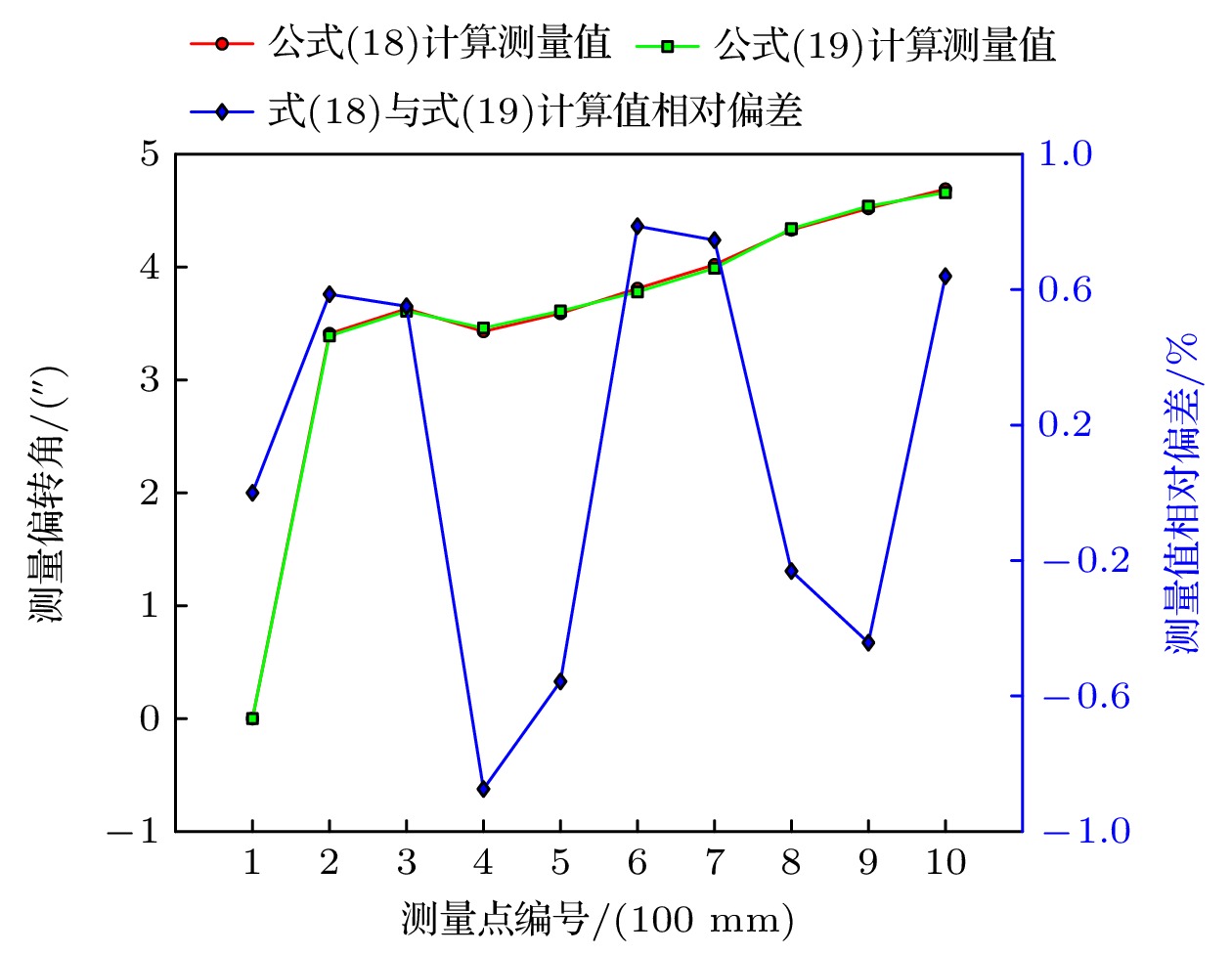
双臂 Tolansky 干涉自准直仪的测量反射镜更换为自准直仪的桥板反射镜(底板长度为100 mm), 且置于一根平直导轨上. 首先通过已标定的自准直仪完成对平直导轨各测量点多次测量, 获得各测量点处稳定的偏转角, 以此作为双臂 Tolansky 干涉自准直仪反射镜的偏角输入值. 调试完仪器后, 提取各测量点的圆心偏移量, 代入含厚度因素的关系(18)式计算各个偏转角并与自准直仪测量结果进行对较, 见图10.

从图10可以看出, 在1 mm的分光镜厚度下, 对总量程为1000 mm的10个测量点进行测量, 双臂 Tolansky 干涉自准直仪的测量数据与已标定自准直仪的测量数据的相对偏差在±0.9%内. 这与图8所示现象一致, 即在分光镜厚度为1 mm的条件下, 含厚度因素的(18)式与不含厚度因素(19)式的计算数值相对偏差仅为0.22%.

论文分析了一种双臂Tolansky干涉自准直测角方案的原理, 通过理论推导、虚拟仿真和实验验证交叉互印的方式分析了其中分光镜厚度对测角准确性的影响, 建立了不用于分光镜厚度近似为零的测角关系式. 结果显示, 分光镜的厚度不仅影响测角准确性, 而且还能影响干涉同心圆环的圆心位置. 因此, 在实际使用时应尽量选用厚度小的分光镜. 这为后续改进Tolansky干涉进行微小角度测量提供了理论及实验参考.