半导体激光器(SL)在光纤通信中的应用及其广泛, 是最常用的光源设备之一, 具有结构简单、质量轻、体积小、耗电少、工作寿命长和易于集成等诸多优点. 普遍认为, SL在受到外部扰动时, 可以表现出复杂的非线性动力学行为. 通过合理的选择和控制参数, 能够高效地实现高维、宽带、复杂的混沌输出, 可以广泛应用于混沌保密通信^[1-5]、压缩感知^[6]、混沌雷达^[7]、储备池计算^[8–13]、神经计算^[14–18]和高速物理随机数生成^[19–21]等领域.

在混沌通信中, 小幅度信息嵌入到混沌载波中并传送到接收端, 而接收端激光器利用混沌同步和混沌滤波效应又再现混沌载波, 最后通过传输信号与接收端激光器输出的差异正确恢复信息^[22]. 因此, 混沌同步是混沌通信的必备条件. 混沌同步在光通信、保密通信、随机数生成以及混沌信号处理^[23]等领域中具有重要的应用潜力. 由于混沌激光器对初始条件和系统参数的高度敏感性, 可以产生复杂而难以预测的混沌信号, 这为加密通信提供了一种高效的解决方案. 在混沌激光通信系统中, 通过实现多个激光器之间的同步, 可以确保不同信号通道之间的独立性与安全性. 截至目前, 有关混沌同步的研究集中在不同的激光器上^[24–26]. 例如, Zhang等^[24]从理论上研究了两个相互耦合的垂直腔面发射激光器(VCSEL)的偏振切换(PS)动力学和同步性能, 发现足够强的偏振选择性注入可以抑制PS, 若考虑频率失谐, 则偏振选择性相互注入的影响将减弱. Wang等^[25]证明了两个自由运行的VCSEL产生的偏振混沌可以在相互耦合的配置中实现同步, 详细研究了平行注入和正交注入两种情况下偏振混沌的同步质量和稳健性. Li等^[26]还以数值方式研究了主从配置中混沌同步的特性, 在所研究的耦合模式中, 采用全局注入方案, 两个混沌半导体环形激光器(SRL)模式之间的同步性能更好. 然而, 随着通信系统对小型化、高效性和稳定性的要求不断提高, NL^[27–29]因其体积小、功耗低和响应速度快, 逐渐成为混沌通信领域的新兴研究方向.

在混沌保密通信中, 当多个SLs之间信号同时传输时, 信号间的相互干扰势必会对系统的同步性能有所影响, 具有一定的局限性. Rontani等^[30]提出一种基于主被动分解法(APD)的双路混沌光信号复用系统, 该方法通过合理设计系统参数, 使得多个激光器(例如主激光器和从激光器)之间能够实现高品质的混沌同步, 从而实现光信号的复用和解复用. 在此方案的基础上, 陆续有学者对混沌复用通信的频谱利用问题进行了研究^[31,32]. El-Azab等^[32]针对混沌复用系统提高信道传输速率为4 Gbit/s. Flunkert和 Schöll ^[31]对互耦SL系统中耦合相位对混沌同步性能的影响进行了研究. 此外, Liu和Feng^[33]研究了开环SL混沌通信系统的系统增益和参数失配对通信性能的影响. 赵跃鹏等^[34]在光注入Fabry-Perot系统中完成了高速光时分复用(OTDM)的全光解复用研究. Jing等^[35]提出并演示了一种基于同步混沌谱相位加密和解密的新型物理、安全高速光通信方案, 将原始消息加密为类噪声信号, 并且原始消息的定时时钟有效地隐藏在加密信号中. 文献[36]基于类似的系统结构, 对混沌信号的正交性进行了初步讨论. 在理想情况下, 要想实现基于APD的混沌复用, 两路混沌信号必须满足正交性, 即完全不相关, 这意味着两个信号可以被完全分离(复用和解复用过程无干扰), 任何一个信号的存在都不会影响另一个信号, 因此是理想状态. 但是两路激光器之间存在相互耦合的现象, 无法实现完全正交性. 因此, 我们发现在无法实现完全正交性的情况下, 存在一种“伪正交性”, 即相关性很低, “伪正交性”是对完全正交性的一种近似, 它允许信号之间有微弱的相关性, 而非完全为零. 在实际系统中, 由于激光器间存在耦合、噪声和系统非理想性, 信号无法完全正交, 但其相关性可以降到很低. 虽然文献[37]分析了两个主激光器参数失配及参数选择对混沌同步性能的影响, 并对其复用系统的安全性能和频谱性能进行了研究, 但其只能在较小的范围内实现“伪正交性”. 相较于传统的SL, NL响应速度高、频谱利用效率高且具有较高的参数可调性, 有助于提升系统的传输速率以及优化混沌信号的同步性能, 更加适合研究高速复用通信. 同时, NL体积小, 耦合性弱, 其间的相互干扰比传统激光器更低, 有助于实现更接近理想状态的“伪正交性”, 这为高质量混沌同步提供了稳定的物理基础. 因此, 我们选择NL来研究基于APD的微纳激光混沌系统的复用同步.

本文主要研究了基于NL的双路激光混沌复用系统的同步性, 相较于传统的SL, 效果要好得多, 能够在较大参数范围内实现两主激光器间保持较低的相关性. 并且, 详细分析了系统参数、单个参数及多个参数同时失配对该复用系统同步性能的影响. 本文的结构如下: 第2节构建了双路激光混沌复用系统的理论模型和相应的速率方程; 第3节对得到的数值结果进行分析; 最后, 在第4节给出相应的结论.

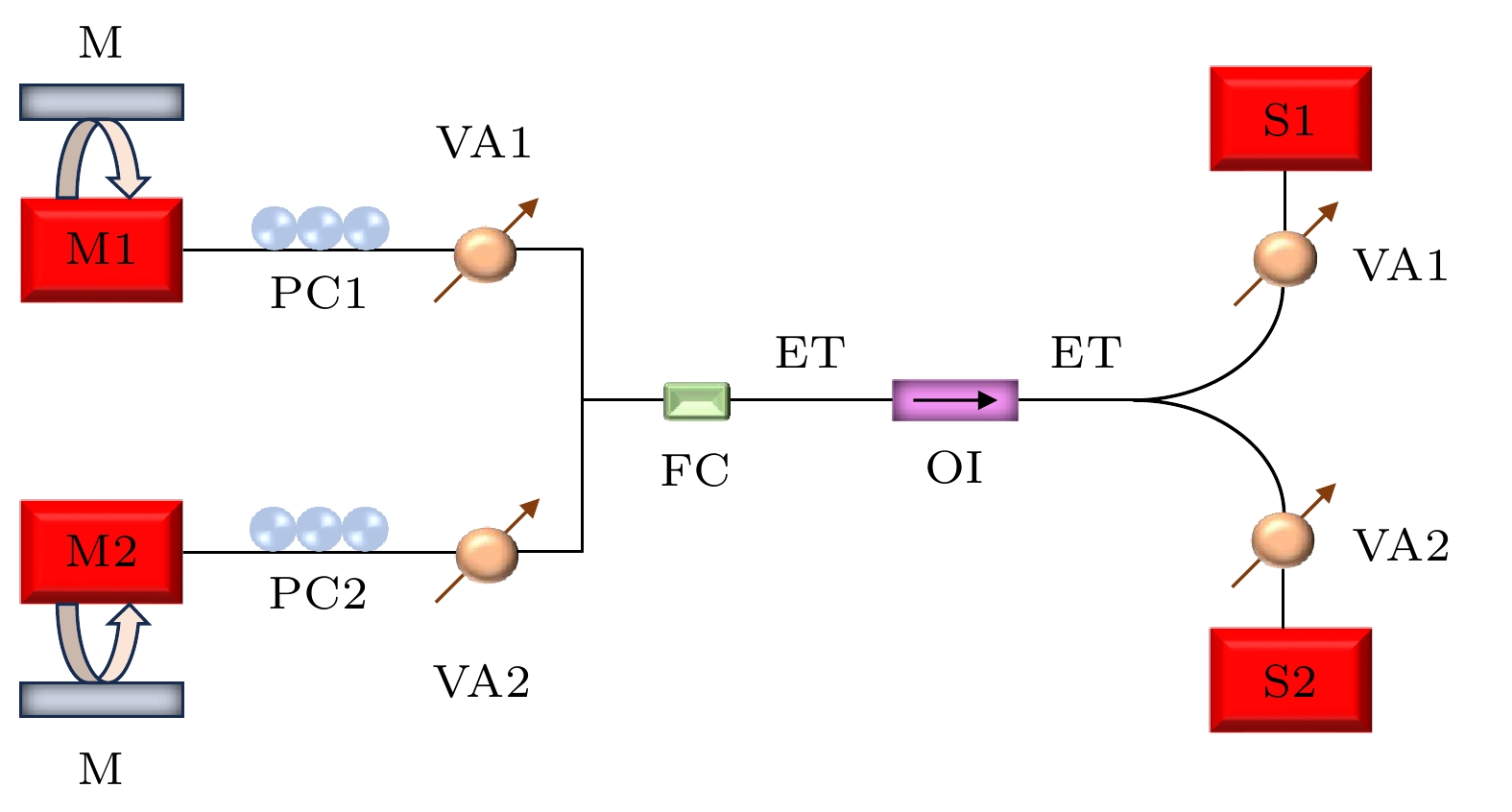
基于NL的双路激光混沌复用系统的结构模型如图1所示. 该系统中有4个NLs, 包括两个主激光器和两个从激光器. 在发送端, 主激光器1 (M1)和主激光器2 (M2)之间相互耦合, 它们各自接收两个信号: 一个是其自身的反馈信号, 另一个是来自互耦合NL的信号. 两个主激光器输出的复用混沌信号(ET)经过偏振控制器(PC)和光衰减器(VA)后由光纤耦合器(FC)合并到同一链路. 最后, ET经过光隔离器(OI)和VA单向传送到接收端的从激光器1 (S1)和从激光器2 (S2), 使得两个从激光器也产生混沌信号. 值得注意的是, M1/S1和M2/S2相互配对, 基于APD原理, 两配对激光器之间能实现高质量的混沌同步.

图1中M1为主激光器1, M2为主激光器2, S1为从激光器1, S2为从激光器2, PC为偏振控制器, VA为光衰减器, FC为光纤耦合器, M为反射镜, ET为两主激光器输出的复用混沌信号, OI为光隔离器.

所提出系统的速率方程为^[38–40]

在上述速率方程(1)—(5)中, 下标“${{\text{M}}_{1, 2}}$”和“${{\text{S}}_{1, 2}}$”分别代表主激光器M1和M2以及从激光器S1和S2. 其中, $S\left( t \right)$是相位密度, $\phi \left( t \right)$是相位, $N\left( t \right)$是载流子密度. 在该模型中$F$是Purcell因子, $\beta $是自发辐射耦合因子, $\varGamma $为约束因子, ${\tau _{\text{n}}}$和${\tau _{\text{p}}}$分别是辐射载流子寿命和光子寿命. ${g_{\text{n}}}$为考虑群速度影响的差分增益, ${N_0}$为透明载流子密度, $\varepsilon $为增益饱和因子, $\alpha $为线宽增强因子. $I$为直流偏置电流, ${I_{{\text{th}}}}$是与$F$和$\beta $相关的阈值电流, ${V_{\text{α }}}$为活性区体积, $e$为电子电荷, ${N_{{\text{th}}}}$为阈值载流子密度. 方程(6)—(9)中, $2{\text{π}}{f_{{{\text{M}}_{{\text{1, 2}}}}}}$和$2{\text{π}}{f_{{{\text{M}}_{{\text{2, 1}}}}}}$是M1和M2之间的角频率失谐, 其中$\Delta f_{{\text{21, 12}}}^{\text{M}} = {f_{{{\text{M}}_{{\text{2, 1}}}}}} - {f_{{{\text{M}}_{{\text{1, 2}}}}}}$, 而$\Delta f_{{\text{21, 12}}}^{\text{C}}$则表示主从激光器间的频率失谐.

值得注意的是, 相互配对的主从激光器之间要想实现完全同步, 需要设置合理的注入参数和反馈参数. 方程(1)和(4)的最后一项表示注入项, 该项包括注入延迟(${\tau _{\text{r}}}$)和注入强度(kr), kr的计算公式为^[38]

其中, $R$表示NL的腔面反射率, ${R_{{\text{inj}}}}$表示注入比, $c$为光在自由空间中的速度, $n$代表折射率, $L$表示NL反馈腔的长度.

同样, 在方程(1)和(4)中, 倒数第2项表示反馈项, 在该项中, 包含了反馈延迟(${\tau _{\text{d}}}$)和反馈强度(${{kd}}$). 这里, ${R_{{\text{ext}}}}$为外镜的功率反射率, f为反馈耦合分数, 即反射光场重新注入激光模式的分数. ${{kd}}$的表达式表示为^[40]

假设4个激光器的内部参数都是相同的, 并且在仿真中忽略噪声对该系统带来的影响. 众所周知, 在注入系统中, ${\tau _{\text{r}}}$对激光器输出的动态特性的影响是最小的. 因此, 在接下来的研究中, 假设${\tau _{\text{r}}} = 0$. 表1列出了仿真中一些关键参数的数值.

本文主要分析的是该系统激光器混沌输出的同步性能, 利用互相关函数(CCF)来量化M1/S1和M2/S2之间的同步质量, 定义的CCF为^[42]

其中, $i$和$j$分别表示为M1/M2和S1/S2. $\Delta t$是两个混沌时间序列之间的位移, $\langle {~} \rangle $表示强度时间序列的平均值. 值得注意的是, $\left| C \right| = 1$表示相互配对的主从激光器间实现了完全的混沌同步, $\left| C \right| = 0$则表示两个激光器之间没有任何相关性. 在本文认为当$ \left|C\right|>0.95 $时, 两激光器之间混沌信号实现了高质量的混沌同步.

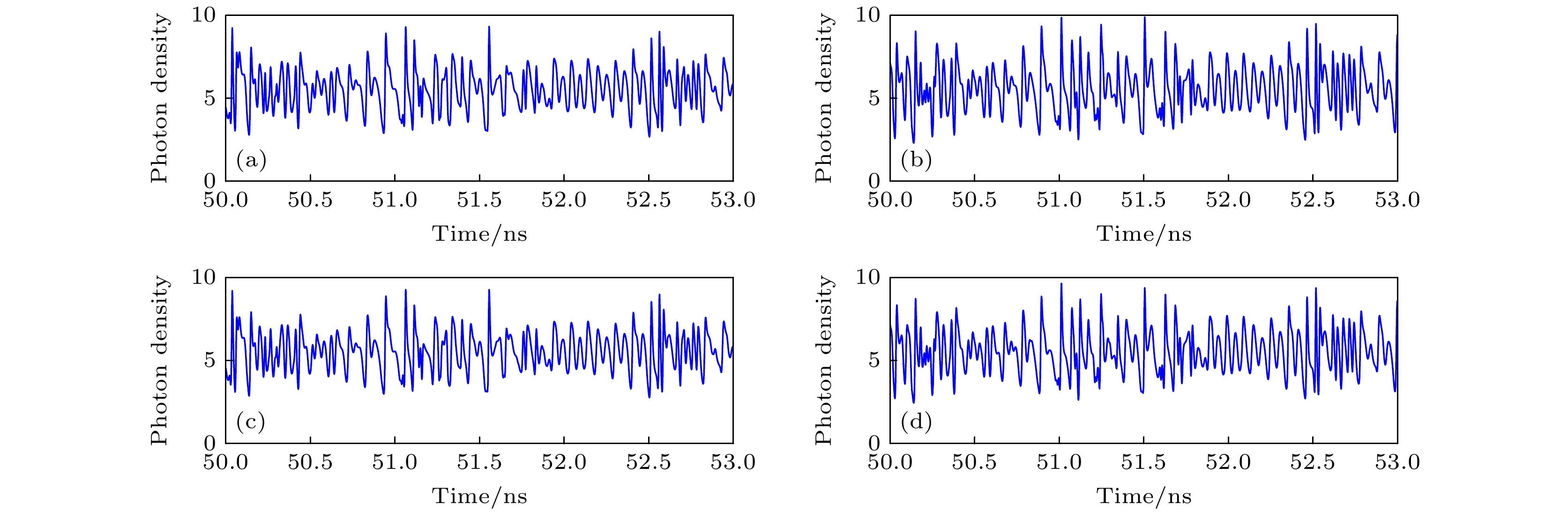
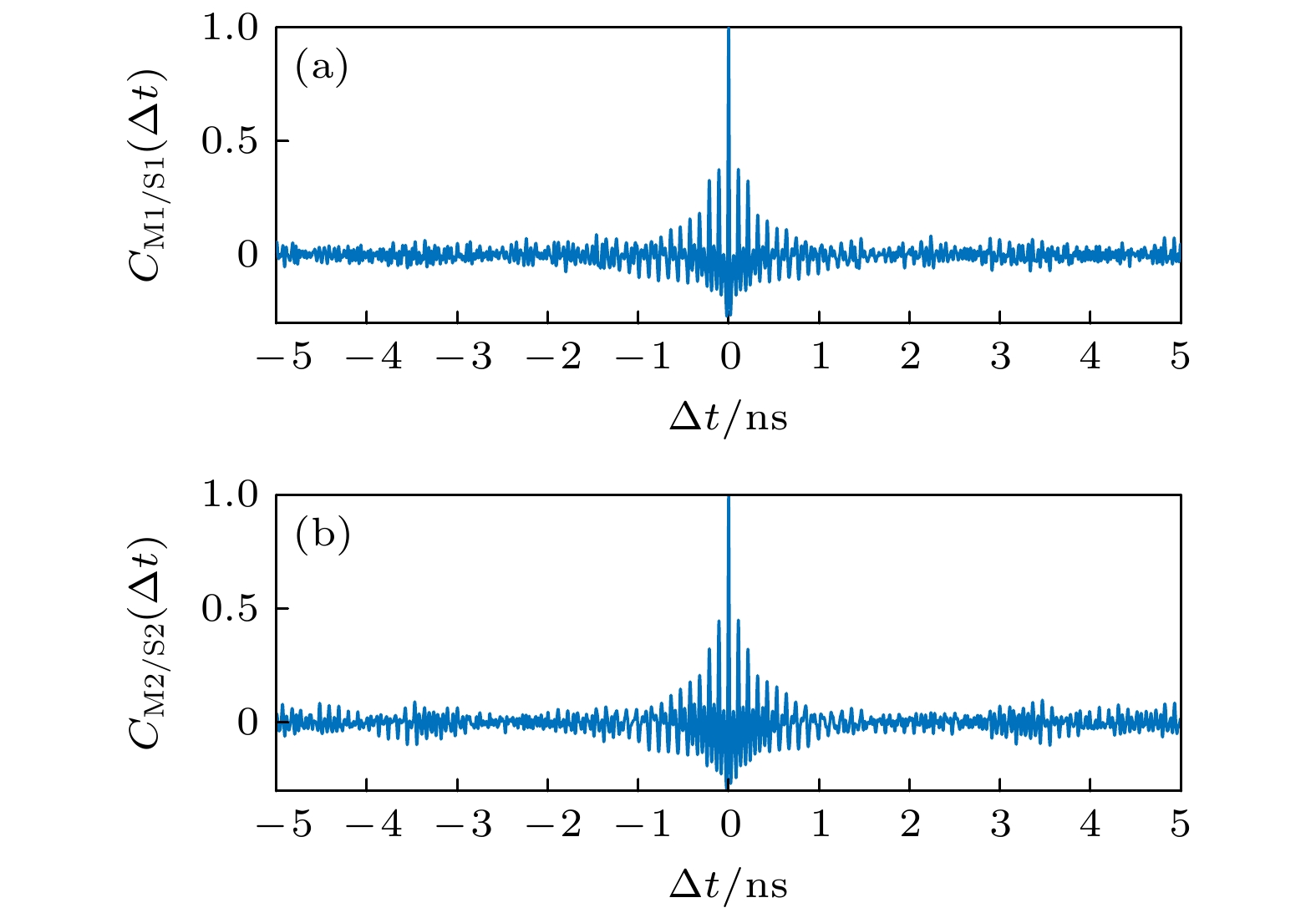
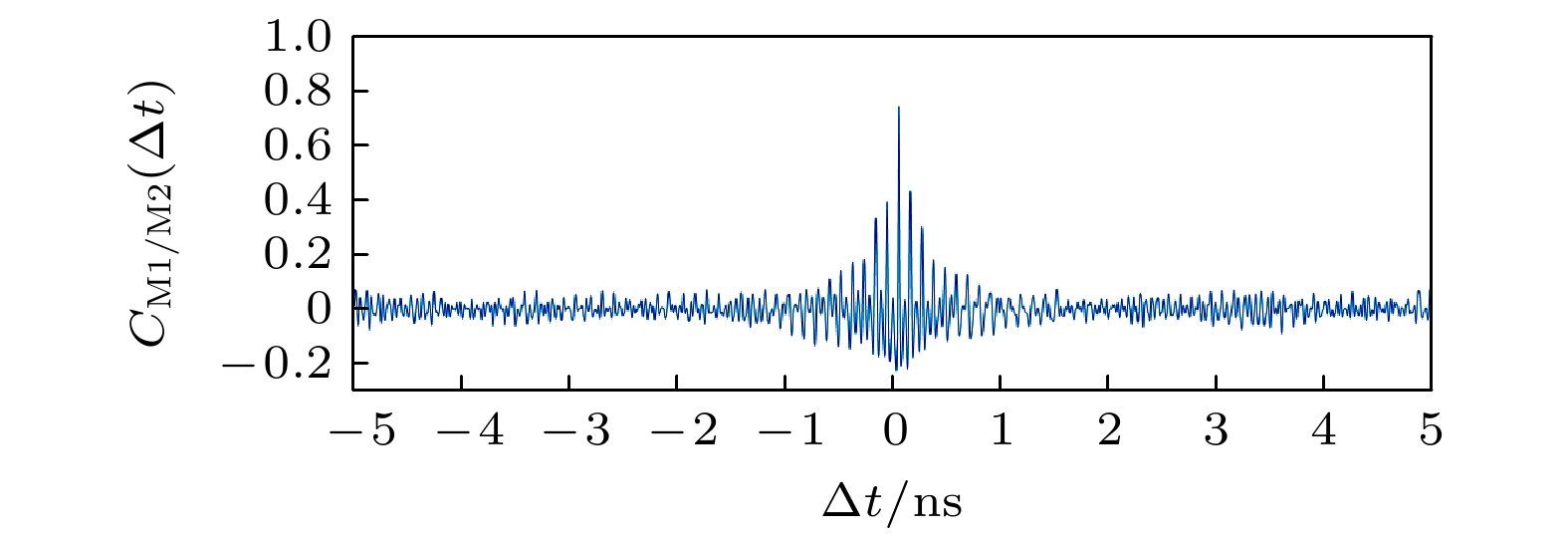
本节采用四阶Runge-Kutta算法对上述混沌复用系统的速率方程进行数值模拟, 分析该系统的混沌同步特性, 探究关键参数及参数失配对同步性能的影响. 通过数值仿真, 实现了M1/S1和M2/S2之间的完全同步. 图2所示为M1, M2, S1和S2的时域输出波形, 由此可以看出所有激光器都工作在混沌状态. 图3(a), (b)分别为M1/S1和M2/S2的互相关曲线. 从图3(a)可以发现, M1和S1输出之间的相关函数曲线关于$\Delta t = 0$对称, 且在该点相关性为1, 这说明M1和S1同步且同步延迟为0. 同理, 从图3(b)中可得出相同结论.

在M1/S1和M2/S2之间达到完全同步、实现各路独立信息同时传输的同时, 为了保证信息的安全传输, 信道间的串扰问题需要得到解决. 如引言所述, 要想实现基于APD的混沌复用, M1和M2输出的混沌载波必须满足“伪正交性”, 即两者之间相关性较低. 图4为主激光器间的互相关曲线, 可以发现M1和M2间的最大相关系数为0.7. 这表明, 各配对激光器之间虽然能实现高质量的混沌 同步, 但是主激光器之间不满足“伪正交性”. 由于主激光器间存在的高相关性, 在主激光器M1输出的混沌载波中加载有用信息, 那么部分有用信息就可能被M2和S1恢复, 从而降低了该混沌复用系统的安全性. 若M1和M2同时加载两个完全独立有用信息, 则会出现信道串扰问题, 导致信息恢复不准确. 但是, 相比于传统SL仅能在小范围内实现“伪正交性”, 基于NL的混沌复用系统能够在广泛的参数范围内实现, 并且在较大的参数范围内保持其互相关系数在0.4以下, 这保证了两路有用信息的加密与解密. 为了在实现混沌同步的同时, 还能保证M1/M2输出的混沌信号满足“伪正交性”, 我们将详细研究相关参数对该系统实现同步的 影响.

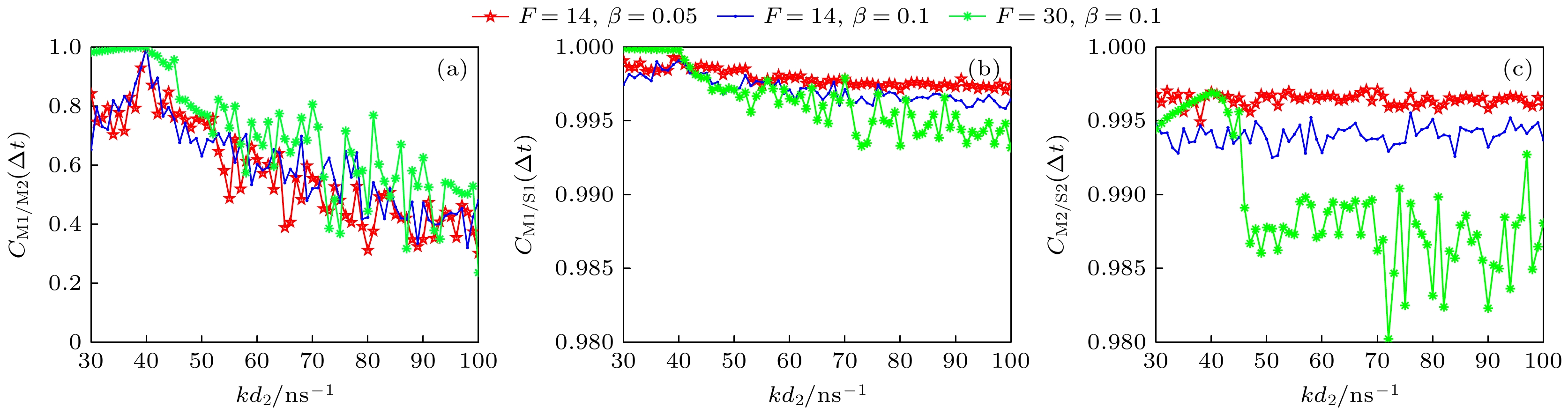
对于NL来说, 有两个重要的物理因子, 即Purcell因子$F$和自发辐射耦合因子$\beta $^[43,44], 对混沌同步的影响具有重要意义, Purcell因子$F$反映了光学腔对自发辐射速率的增强效应, 通过精确调控, 能够显著提高光子发射速率和系统的非线性响 应能力; 而自发辐射耦合因子$\beta $则表示进入受激辐射过程的自发辐射比例, $\beta $越大, 激光器的自发辐射对输出光场的贡献越显著, 通过调节$F$和$\beta $, NL系统可以在更广泛的反馈强度和频率失谐范围内维持高品质的混沌输出, 这显著优于传统激光器系统的能力. 因此, 接下来, 分析了$F$和$\beta $对M1/M2, M1/S1和M2/S2同步性能的影响, 结果如图5所示. 从图5(a)可以看出, ${{{kd}}_2}$的增大对主激光器之间互相关函数的影响是非线性的. 在不同$F$和$\beta $的组合下, M1和M2之间的最大相关系数${C_{12}}$随${{{kd}}_2}$的增大, 呈现先增大后减小的趋势. 这说明适中的反馈增强了激光器之间的相关性, 而过强的反馈则可能引入了不稳定性和噪声, 使得互相关函数呈现下降趋势, 这种趋势反映了激光器在${{{kd}}_2}$变化下从同步态到混沌态的过渡. 相较于$F = 14$, $\beta = 0.1$和$F = 30$, $\beta = 0.1$, 当$F = 14$, $\beta = 0.05$时, M1和M2之间的相关性更低. 同时, 图5(b), (c)分别为不同参数组合下M1/S1和M2/S2的互相关曲线, 根据结果显示, 不同$F$和$\beta $取值下已配对的激光器均可以实现高质量同步. 其中$F = 14$, $\beta = 0.05$时, M1/S1和M2/S2的相关系数最高. 根据之前的研究我们发现^[45], 较小的$F$和$\beta $可以使时延能够在较大范围内实现隐藏. 因此, 在后续的研究中选择$F = 14$, $\beta = 0.05$是合适的.

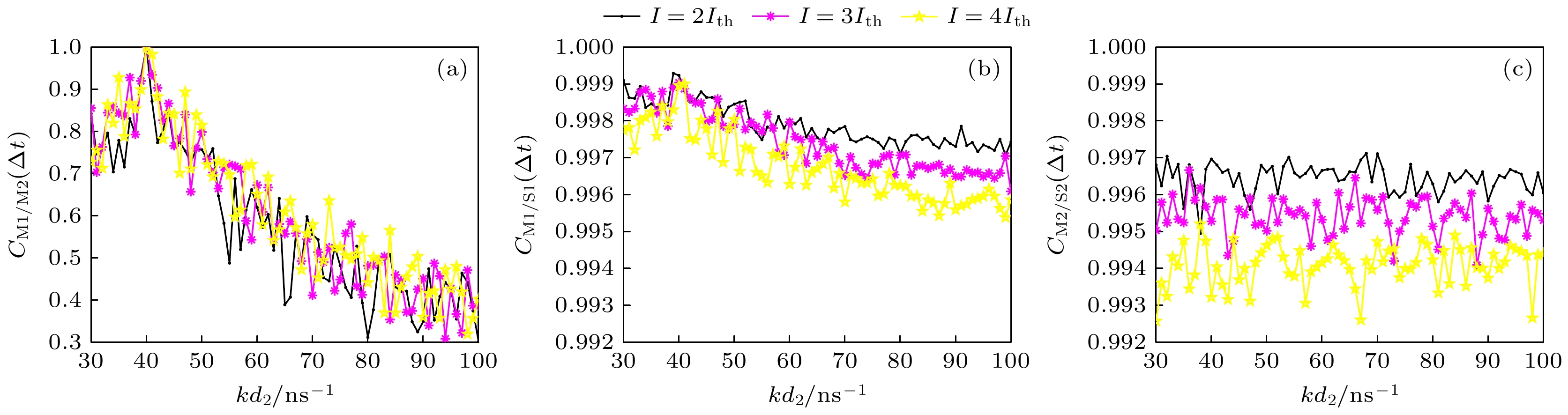
注入电流是决定激光器输出特性的重要外部参数之一, 并且对混沌系统的同步性具有显著的调控作用. 因此, 有必要研究激光器注入电流对系统混沌同步的影响. 所以接下来将$F = 14$和$\beta = 0.05$固定, 然后研究不同$q$值, 即注入电流比对系统同步的影响. 图6(a)—(c)分别为M1/M2, M1/S1和M2/S2的最大相关系数随${{{kd}}_2}$变化的示意图. 在图6(a)中可以发现, 随着${{{kd}}_2}$的增大, 不同$q$取值下M1和M2之间的最大相关系数都呈现出先增大后减小的趋势, 并且对主激光器M1和M2之间的最大相关系数的影响相似. 然而, 对于M1/S1和M2/S2的同步情况, 3种电流表示出不同的结果. 从图6(b), (c)可以看出, 虽然M1/S1和M2/S2在3种电流下都能实现较好的同步, 但是, 随着注入电流的增大, M1/S1和M2/S2的最大相关系数${C_{13}}$和${C_{24}}$的数值则下降. 由此可得到, 较小的注入电流, 即工作电流$I = 2{I_{{\text{th}}}}$, 能够使配对的激光器实现更高质量的混沌同步. 其中, 该系统所设定的阈值电流${I_{{\text{th}}}} = 1.1$ mA, 在该系统中${I_{{\text{th}}}}$是调整$I$的基准, 将激光器的$I$保持在略高于${I_{{\text{th}}}}$的水平, 可以使其维持稳定的输出, 这对于系统之间同步的动态特性和稳定性至关重要. 因此, 为了保证M1/S1和M2/S2的高质量同步, 选择$I = 2{I_{{\text{th}}}}$能够更好地进行后续的研究.

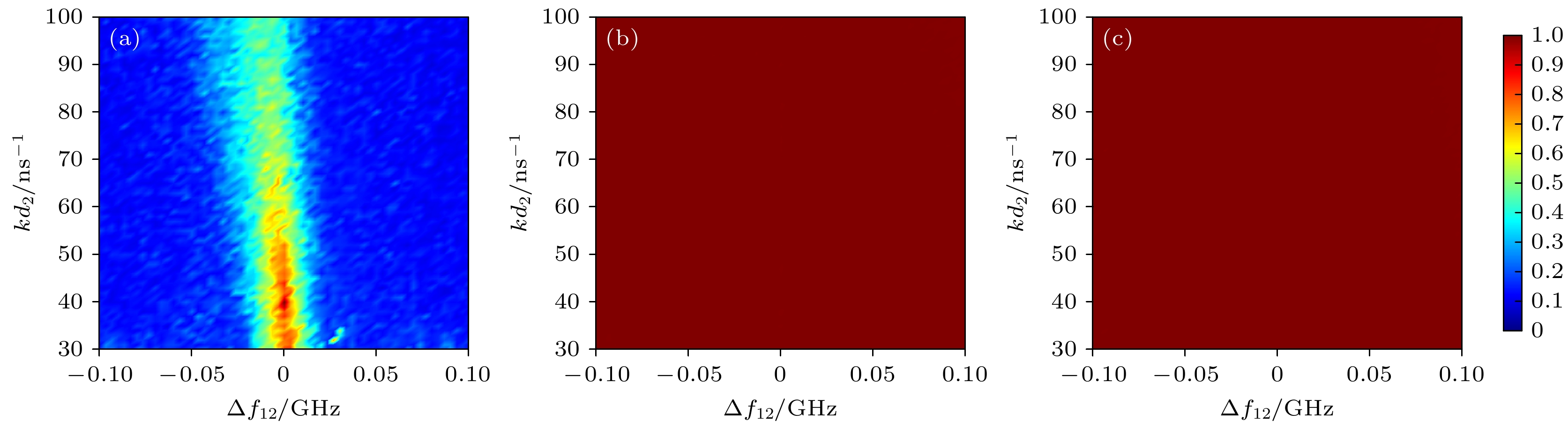
众所周知, 反馈强度和频率失谐是影响混沌系统动态特性的重要因素. 下面讨论反馈强度${{{kd}}_2}$和频率失谐$\Delta f_{{12}}^{\text{M}}$对此复用系统的混沌同步性能的影响. 图7给出了当${{{kd}}_2}$和$\Delta f_{{12}}^{\text{M}}$同时变化时, 激光器间最大相关函数的变化趋势, 图7(a)—(c)分别对应M1/M2, M1/S1和M2/S2的结果. 从图7(b), (c)可以看出, M1/S1和M2/S2在整个参数平面内都实现了混沌同步, 表明这两个参数对它们的同步性能并无明显影响. 然而, 从图7(a)可以发现, 反馈强度和频率失谐对主激光器间同步性能具有明显影响. 相较于反馈强度对同步性能的影响, 频率失谐对其影响更为显著. 具体来说, 当频率失谐在–10—10 GHz范围内时, ${C_{12}}$的值均大于0.4. 并且, 当$ {{kd}}_{2}<50 $ ns^–1时, ${C_{12}}$值甚至超过了0.8. 说明M1和M2在$\Delta f_{{12}}^{\text{M}}$=[–10 GHz, 10 GHz]范围内不能满足两个激光器的“伪正交性”. 但是, 相较于基于传统SL双路混沌系统, 该NL系统能够在更广泛的参数范围内保证主激光器具有较差的同步性能, 即当$ \Delta {f}_{12}^{\text{M}}<-10 $ GHz和$ \Delta {f}_{12}^{\text{M}}>10 $ GHz时满足系统两个主激光器“伪正交性”的要求. 进一步证明了本文所提出的系统能够在更大程度上实现降低两个主激光器之间相关系数, 进而保证两路独立信息的加密与解密.

参数失配在实际应用中是不可避免的, 尤其在复杂的混沌系统中, 它会对系统的同步性能产生显著影响. 因此, 我们探究了关键参数失配对该系统同步性能的影响. 在这里, M1和S1之间的参数以及M2和S2之间的参数保持一致. 并且, 设置M1和S1的注入强度为40 ns^–1, M2和S2之间的注入强度为50 ns^–1. 假定M1的参数固定不变, 调节M2的关键参数, 来定量分析两个激光器之间的同步性能. 定义参数失配率如下^[43]:

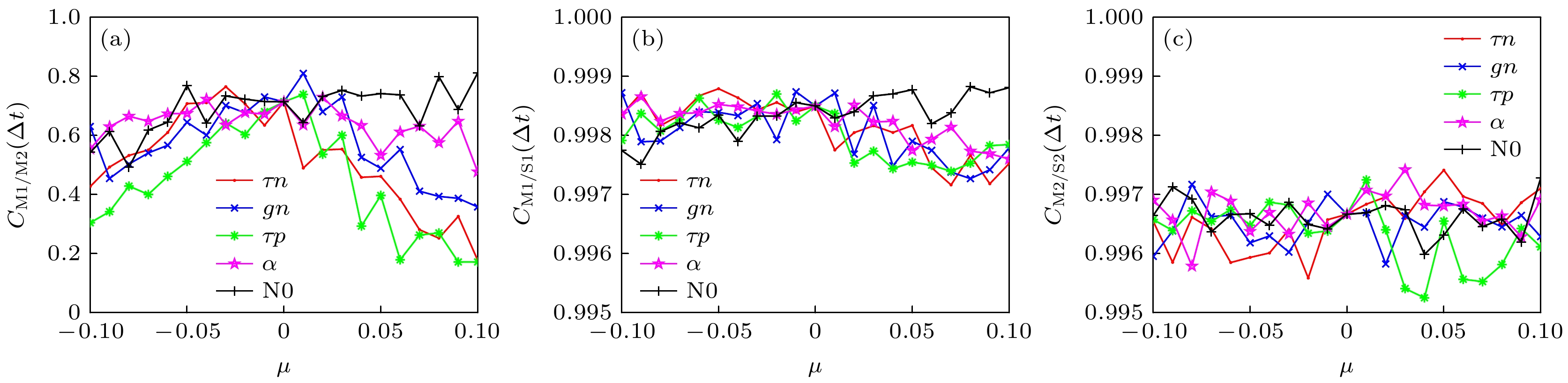
其中, $\varPi $表示参数包括载流子寿命${\tau _{\text{n}}}$、差分增益系数${g_{\text{n}}}$、光子寿命${\tau _{\text{p}}}$、线宽增强因子$\alpha $和透明载流子密度${N_0}$.

图8所示为单个参数失配时, M1/M2, M1/S1和M2/S2的最大相关系数随参数失配率的变化. 通过观察图8(a)可发现, 不同参数对M1/M2的同步性能有不同程度的影响. 其中, ${\tau _{\text{p}}}$, ${\tau _{\text{n}}}$, ${g_{\text{n}}}$在较大的参数失配率下可以使主激光器的最大相关系数保持在0.4以下, 而其他参数对主激光器的同步性能影响较小, 无法保证它们之间的弱相关性, 且这些参数的失配不会明显改变激光器之间的同步状态, 这说明该混沌系统对这些参数并不敏感. 图8(b), (c)分别展示了单个参数失配对M1/S1和M2/S2同步性能的影响, 可以发现在参数失配的整个范围内, 各配对激光器之间的互相关函数值总是大于0.995, 可以实现高品质的混沌同步. 因此, 单个参数失配并不会对配对激光器的同步性能有较大影响.

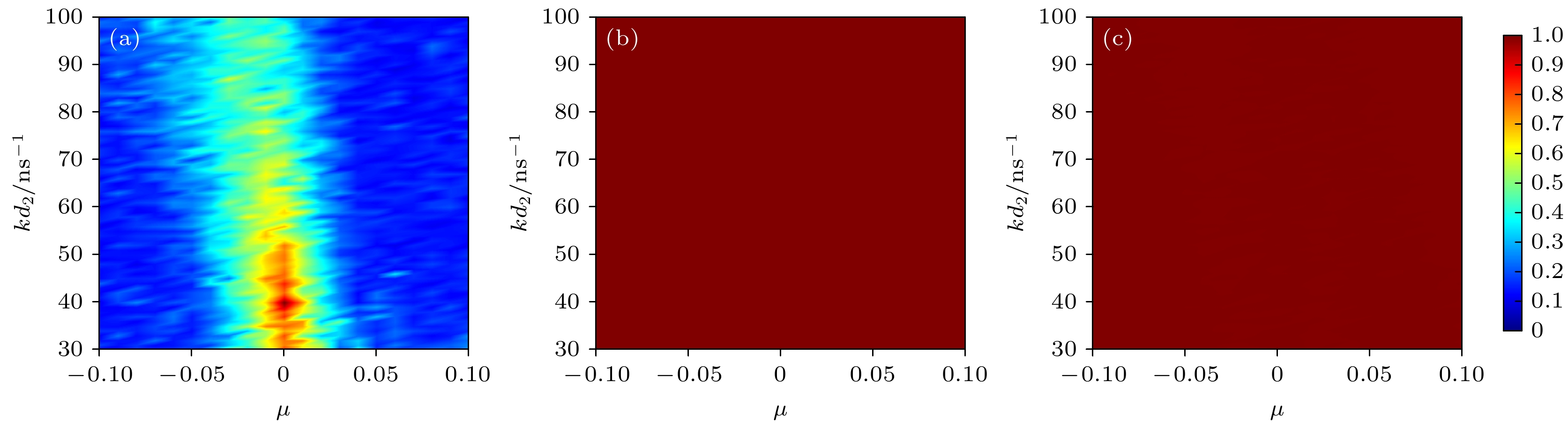
当多个参数同时失配时, 可能会对混沌系统的同步性能产生更复杂和显著的影响, 所以接下来, 又继续研究了多个参数同时失配对该系统同步性能的影响. 为了减少$\Delta f_{12}^{\text{M}}$的影响, 在接下来的数值模拟中, 设置$\Delta f_{{12}}^{\text{M}} = 0$. 图9所示为当$\Delta f_{{12}}^{\text{M}} = 0$时, 最大相关系数随参数失配率$\mu $和${{{kd}}_2}$变化的结果. 图9(a)—(c)对应M1/M2, M1/S1和M2/S2的结果. 由图9(a)可以看出, 仅在$ -0.03<\mu <0.03 $范围内, 主激光器间的最大互相关系数大于0.4, 在参数失配率$\mu = 0$左右且反馈强度$ {{kd}}_{2}<50 $ ns^–1范围内的最大相关系数接近于1. 然而, 在广泛的参数失配范围内可以保证M1/M2具有较差的同步性能, 即当$ \mu < -0.03 $或$ \mu > 0.03 $时, 满足系统两个主激光器混沌输出的“伪正交性”的要求, 可以在更大的参数失配范围内确保每个通道独立传输信息而不会互相干扰, 增强了系统的保密性和抗干扰能力.

以上结果说明, 合理选择频率失谐和参数失配的值, 可以保证M1/M2之间具有较弱的相关性, 并且, 各配对的激光器之间总是能够实现高质量的混沌同步. 同时, 论证了本文所提出的基于NL的激光混沌复用系统的可行性.

本文对基于纳米激光器的双路激光混沌复用系统的同步性进行了详细研究. 在建立理论模型和相关速率方程的基础上, 讨论了$F$和$\beta $、系统参数、单个参数失配以及多个参数同时失配对混沌同步的影响. 研究结果表明, 该系统在合理选择激光器参数和系统参数的情况下, 可以保证主激光器之间的相关性较低且各配对激光器之间能够实现高品质的混沌同步. 在此基础上, 我们发现单个参数失配并不会对配对激光器的同步性能有较大影响, 而当多个参数同时失配时, 在广泛的参数范围内可以保证M1/M2具有较差的同步性能, 满足系统两个主激光器混沌输出的“伪正交性”的要求. 因此, 这项研究为基于纳米激光器的混沌同步技术提供了理论支持, 也为构建安全、稳定和高效的光通信系统提供了新的思路.