-
量子纠缠作为量子力学最显著的特征之一, 已经成为量子信息处理领域的重要资源[1–3]. 迄今为止, 纠缠态的制备和操纵不仅在微观系统而且在宏观系统中也得到了验证. 在微观系统中利用各类型光学系统, 比如利用四波混频系统[4–6]、光学参量振荡器[7,8]和光学参量放大器[9,10]实现多组分纠缠, 以及大尺度纠缠的制备[11,12]. 而由光子与机械振子通过辐射压力非线性耦合而形成的腔光力学(cavity optomechanics, COM), 为宏观量子纠缠的实现提供了新的途径, 并在理论和实验方面取得了显著的进展[13–15], 包括实现机械振子与电磁场之间的纠缠[16], 两个机械振子之间的纠缠[17], 机械运动的量子压缩[18]等. 与腔光力系统类似, 腔磁力学(cavity magnomechanics, CMM)也引起了人们对宏观量子效应的极大兴趣[19,20]. 在过去的十年里, 基于磁子的复合体系结构在量子信息处理、量子传感和量子网络中具有广阔的应用前景. 尤其是, 磁子与微波或光学光子之间的耦合为光学控制、设计、检测和传输磁子态提供了可能性[21–28], 当利用压缩光驱动腔模时还可以为系统获得量子纠缠或者导引, 以及其他更丰富的性质. 近年来, 有研究者关注利用非经典光驱动腔模的研究, 比如在腔磁系统中获得磁-磁纠缠与导引[29], 增强稳态量子效率和增强两个磁子模式之间的纠缠和高斯导引并且提高纠缠对于温度的鲁棒性[30]. COM和CMM结合, 磁振子色散地耦合到磁致伸缩诱导的振动声子模式, 磁力位移经由辐射压力耦合到光学腔, 磁振子模式通过磁偶极相互作用进一步耦合到微波腔模式, 形成腔光磁力(opto-magnomechanics, OMM)系统[31–33]. 这样的系统提供了更丰富的非线性相互作用来支持量子协议, 在量子信息处理和量子网络中展示了潜在的应用.
本文提出利用OMM系统同时制备微波-声子以及光-磁子纠缠的理论模型. 将电光装置产生的微波-光纠缠源注入腔光磁力系统, 作为内腔场. 通过蓝失谐微波场驱动磁振子模式激活的磁力参量下转换相互作用, 产生磁振子-声子纠缠. 同时红失谐激光驱动光学腔模式激活光力分束器相互作用, 再结合微波-磁子之间的磁偶极相互作用, 纠缠最终被分配到微波力学以及磁光子系统中. 利用对数负性(logarithmic negativity)研究了微波-声子以及光-磁量子纠缠特性. 该系统是基于磁振子的混合量子系统的一种构型, 为在宏观尺度上产生量子纠缠开辟了一条新的途径, 并在量子信息处理和通信中具有潜在的应用价值.
-
我们提出的OMM模型如图1(a)和图1(b)所示, 由YIG晶体中的磁振子模、磁致伸缩引起的振动声子模以及超低噪声电光装置产生的纠缠的微波腔模和光学腔模组成. 其中一对纠缠的光-微波光束(利用超低噪声腔电光装置[34,35]在连续变量域[36]通过自发参量下转换过程[37]产生), 作为内腔场, 在腔内振荡. 磁振子模式通过YIG晶体中大量自旋的集体运动(自旋波)来体现, 并且通过将晶体置于均匀偏置磁场中并施加其磁分量垂直于偏置场的微波驱动场来激活. 磁振子模通过磁偶极相互作用与微波腔模耦合, 磁力位移通过辐射压力与光学腔模耦合. 机械模式在系统中具有最低的谐振频率, 通常以兆赫兹为单位, 并且在低温下也是高热度填充. 所以, 把机械模式冷却到基态是在系统中制备量子态的必要条件[38]. 为了满足这一要求, 我们利用红失谐激光场驱动光学腔模, 这样就可以激活光力反斯托克斯散射并且能在分辨带宽极限
$ {\omega _{\text{b}}} \gg {\kappa _{\text{c}}} $ 处显著地冷却机械模, 如图1(c)所示.系统的哈密顿量由下式给出:
其中
$a({a^\dagger })$ ,$ c({c^\dagger }) $ ,$ m({m^\dagger }) $ 分别表示微波腔模, 光学腔模以及磁振子模的湮灭(产生)算符, 并且满足$ \left[ {o, {o^\dagger }} \right] = 1(o = a, {\text{ }}c, {\text{ }}m) $ ; q和p是机械振子模式的无量纲位置和动量, 满足$ \left[q,p\right]=\mathit{\mathit{i}} $ ;$ {\omega }_{\text{a}}(\kappa {}_{\text{a}}) $ ,$ {\omega }_{\text{c}}(\kappa {}_{\text{c}}) $ ,$ {\omega }_{\text{m}}(\kappa {}_{\text{m}}) $ 和$ {\omega _{\text{b}}} $ ($ {\gamma _{\text{b}}} $ )分别是微波腔模、光学腔模、磁振子模和机械振子模的本征频率(耗散率);$ {g_{{\text{cb}}}} $ ($ {g_{{\text{mb}}}} $ )表示单光(磁)力耦合强度,$ {g_{{\text{am}}}} $ 表示微波-磁子之间的磁偶极相互作用强度. (1b)式表示驱动项哈密顿量, 其中$ {E_{1(2)}} = \sqrt {2{\kappa _{{\text{c}}({\text{a}})}}{P_{{\text{l}}(0)}}/\hbar {\omega _{{\text{l}}(0)}}} $ 表示光学(微波)腔模与激光(微波)驱动场之间的耦合强度, 激光功率(频率)为$ {P}_{\text{l}}({\omega }_{\text{l}}) $ , 微波功率(频率)为$ {P}_{0}({\omega }_{0}) $ . Rabi频率$ {\varOmega _{\text{d}}} = \dfrac{{\sqrt 5 }}{4}\gamma \sqrt {{N_{\text{d}}}} {B_{\text{d}}} $ [27]表示磁振子模与振幅为$ {B_{\text{d}}} $ , 频率为$ {\omega _0} $ 的微波驱动场之间的耦合强度, 其中$ \gamma $ 是旋磁比, Nd是YIG晶体中的自旋数. 需要注意的是, 假设磁振子处于低激发极限$ \langle {m^\dagger }m\rangle \ll 2{N_{\text{d}}}s $ ,$ s = {5}/{2} $ 是基态Fe3+在YIG中的自旋数[38]. 这证实了自旋的玻色描述, 这样系统可以很好地被描述成谐振子[39].该方案使用了实验上可行参数[19,20,32,38,40]:
$ \omega_{\text{b}}/2\pi=40\text{ }\rm{M}\rm{H}\text{z} $ ,$ {\omega _{\text{m}}}{\text{/}}2\pi = 10{\text{ G}}{\rm H}{\text{z}} $ ,$ {\omega _{\text{a}}} = {\omega _{\text{m}}} $ ,$ {\omega _{\text{c}}} = 2\pi c/{\lambda _{\text{l}}} $ ,$ {\lambda _{\text{l}}} = 1550{\text{ nm}} $ ,$ {\kappa _{\text{m}}}/2\pi = 1{\text{ }}{\rm MHz} $ ,$ {\kappa _{\text{c}}} = 1.5{\text{ MHz}} $ ,$ {\gamma _{\text{b}}}/2{\text{π}} = 100{\text{ }}{\rm H}{\text{z}} $ ,$ {\kappa _{\text{m}}} = {\kappa _{\text{a}}} $ ,$ {G_{\text{c}}}/2\pi = 4{\text{ }}{\rm M}{\rm H}{\text{z}} $ ,$ {G_{\text{m}}}/2{\text{π}} = 1.5{\text{ }}{\rm M}{\rm H}{\text{z}} $ ,$ {g_{{\text{am}}}}/2\pi = 4{\text{ }}{\rm M}{\rm H}{\text{z}} $ ,$ {\varDelta _{\text{a}}} = - {\omega _{\text{b}}} $ ,${\tilde \varDelta _{\text{m}}} = - {\omega _{\text{b}}}$ ,${\tilde \varDelta _{\text{c}}} = {\omega _{\text{b}}}$ ,$ T = 10{\text{ m}}{\rm K} $ ,$ r = 0.2 $ ,$ \theta = \pi /2 $ .通过考虑每个模式的耗散和输入噪声, 在相互作用绘景中我们得到系统的朗之万方程(QLEs), 由下式给出:
其中
$ {\varDelta _{{\text{m}}({\text{a}})}} = {\omega _{{\text{m}}({\text{a}})}} - {\omega _0} $ ,$ {\varDelta _{\text{c}}} = {\omega _{\text{c}}} - {\omega _{\text{l}}} $ . 输入噪声$ {K_{{\mathrm{in}}}}(t) $ ($ K = m, b $ )的平均值为零, 满足相关方程:$ \xi (t) $ 是作用在机械振荡器上的布朗噪声算符, 满足相关方程$\left\langle {\xi (t)\xi (t') + \xi (t')\xi (t)} \right\rangle /2 \cong {\gamma _{\text{b}}}[2{N_{\text{b}}}({\omega _{\text{b}}}) + 1]\delta (t - t')$ .$ {N_{K, j}}({\omega _{K, j}}) = [\exp (\hbar {\omega _{K, j}}/{\left. {{k_{\text{B}}}T) - 1} \right]^{ - 1}} $ 表示在浴温T下各个模式的平均热激发数, kB是玻尔兹曼常数. 如图1(a)所示, 将双模压缩微波-光场注入腔内, 使得微波腔与光学腔模式的噪声算符量子相关. 双模压缩场的输入噪声相关方程为其中
$ N = {\sinh ^2}r $ ,$ M = \sinh r \cdot \cosh r $ , r为双模压缩场的压缩参数.在系统中产生例如纠缠的强量子关联, 需要足够强的光力和磁力相互作用强度. 为此, 我们使用强激光(微波)场驱动光学腔(磁振子)模, 这就会导致
$ \left| {\left. {\langle c\rangle } \right|, \left| {\left. {\langle m\rangle } \right| \gg 1} \right.} \right. $ . 因此, 可以通过在稳态解 附近忽略小的二阶起伏项来线性化非线性光力动力学和磁力动力学, 这一过程通过将每个模式算 符写成其经典平均值和量子涨落算符的和来实现, 即$ o = \left\langle o \right\rangle + \delta o $ ,$ {{q}} = \left\langle q \right\rangle + \delta q $ ,$ p = \left\langle p \right\rangle + \delta p $ . 为了研究宏观子系统之间的量子关联, 专注于量子涨落的动力学(稳态平均值附近). 描述量子涨落的线性化QLEs为$ \left( {\delta {X_{\text{a}}}, \delta {Y_{\text{a}}}, \delta {X_{\text{c}}}, \delta {Y_{\text{c}}}, \delta {X_{\text{m}}}, \delta {Y_{\text{m}}}, \delta q, \delta p} \right) $ . 其中$ \delta {X_o} = (\delta o + \delta {o^\dagger })/\sqrt 2 $ 和$ \delta {Y_o} = {\mathrm{i}}\left( {\delta {o^\dagger } - \delta o} \right)/\sqrt 2 $ ($ o = a, {\text{ }}c, {\text{ }}m $ )分别表示相应模式的正交振幅和正交位相的起伏量. 之后将线性化QLEs写成如下的矩阵形式:其中
$ {\boldsymbol{u}} = {(\delta {X}_{\text{a}}, \delta {Y}_{\text{a}}, \delta {X}_{\text{c}}, \delta {Y}_{\text{c}}, \delta {X}_{\text{m}}, \delta {Y}_{\text{m}}, \delta q, \delta p)}^{{\mathrm{T}}} $ ,$ {\boldsymbol{n}}(t) $ =$(\sqrt {2{\kappa _{\text{a}}}} \delta X_{\text{a}}^{{\text{in}}}, \sqrt {2{\kappa _{\text{a}}}} \delta Y_{\text{a}}^{{\text{in}}}, \sqrt {2{\kappa _c}} \delta X_{\text{c}}^{{\text{in}}}, \sqrt {2{\kappa _{\text{c}}}} \delta Y_{\text{c}}^{{\text{in}}}, \sqrt {2{\kappa _{\text{m}}}} \delta $ $ X_{\text{m}}^{{\text{in}}},\sqrt {2{\kappa _{\text{m}}}} \delta Y_{\text{m}}^{{\text{in}}}, 0, \xi , )^{\text{T}} $ . 同时得到漂移矩阵为其中
$ {G_{\text{c}}} = {\mathrm{i}}\sqrt 2 {g_{{\text{cb}}}}\left\langle c \right\rangle $ ,$ {G_{\text{m}}} = {\mathrm{i}}\sqrt 2 {g_{{\text{mb}}}}\left\langle m \right\rangle $ 分别是有效光力耦合强度和有效磁力耦合强度.$ {\tilde \varDelta _{\text{c}}} = {\varDelta _{\text{c}}} - {g_{{\text{cb}}}}\left\langle q \right\rangle $ ,$ {\tilde \varDelta _{\text{m}}} = {\varDelta _{\text{m}}} + {g_{{\text{mb}}}}\left\langle q \right\rangle $ 分别是光学腔模式和磁振子模式的有效失谐量. 并且本文计算的所有纠缠都由漂移矩阵的负本征值保证其处于稳定状态.由于系统的动力学方程已经被完全线性化, 并且输入噪声是高斯的, 所以系统在任何给定时刻的状态都是高斯的, 可以由8×8的协方差矩阵V来表征. 当系统稳定时, V可以通过求解李雅普诺夫方程得到:
扩散矩阵D的表达形式如下:
其中,
$ {\kappa ^ + } = \sqrt {{\kappa _{\text{a}}}{\kappa _{\text{c}}}} (M + {M^*}) $ ,$ {\kappa ^ - } = {\mathrm{i}}\sqrt {{\kappa _{\text{a}}}{\kappa _{\text{c}}}} ( - M + {M^*}) $ . 计算得到协方差矩阵V后, 利用对数负性[41,42]方法来量化任意两个子系统之间的纠缠, 其定义为其中
$ {\eta ^ - } \equiv {2^{ - 1/2}}{[\varSigma - {({\varSigma ^2} - 4 \times \det {{\boldsymbol{V}}_4})^{1/2}}]^{1/2}} $ ,$ {{\boldsymbol{V}}_4} = [{{\boldsymbol{V}}_e}, {{\boldsymbol{V}}_{ef}};{\boldsymbol{V}}_{ef}^{\text{T}}, {{\boldsymbol{V}}_f}] $ 是包含模式e和f (e, f = a, c, m, b)二体子系统4×4的协方差矩阵,$ \varSigma \equiv \det {{\boldsymbol{V}}_e} + \det {{\boldsymbol{V}}_f} - 2\det {{\boldsymbol{V}}_{ef}} $ . -
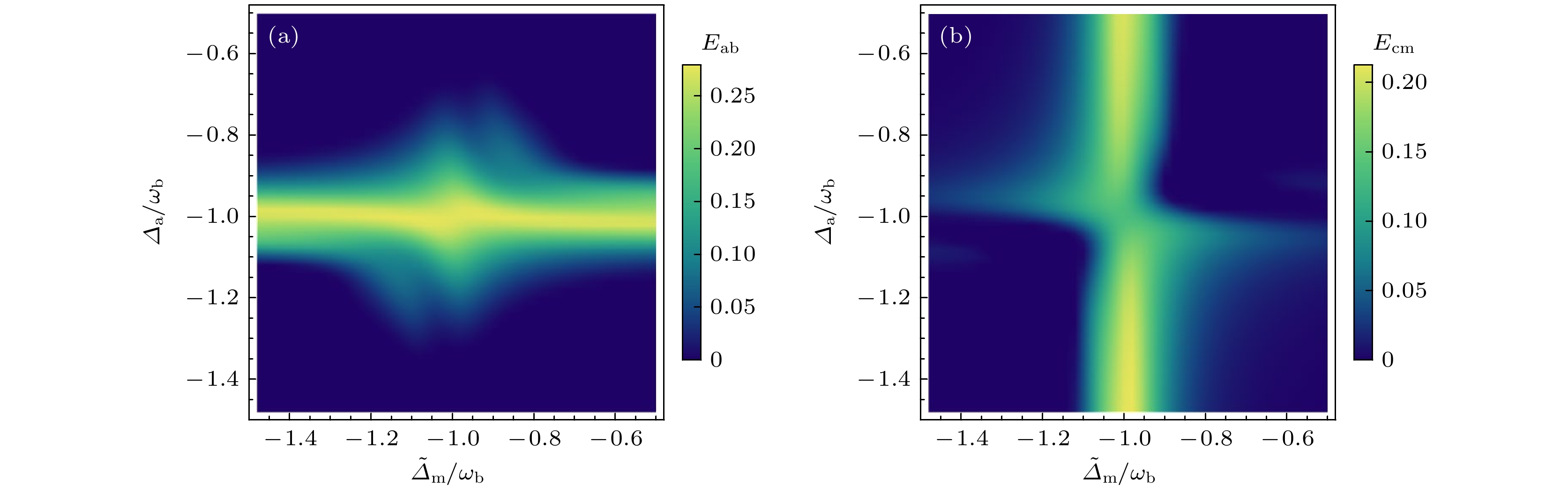
系统首先通过注入超导电光装置产生的微波-光纠缠源, 即Eac. 利用微波-磁子之间的状态交换相互作用以及光力分束器相互作用, 将纠缠转移到了微波力学以及磁光子系统中, 可以产生微波-声子纠缠Eab以及光-磁纠缠Ecm. 此外, 用蓝失谐微波场驱动YIG晶体中的磁振子模式, 利用微波-磁子之间的状态交换相互作用以及光力分束器相互作用, 也会产生微波-声子纠缠Eab以及光-磁纠缠Ecm. 稳态纠缠Eab和Ecm随磁子模式和微波光子模式有效失谐量变化密度图如图2(a)和图2(b)所示. 从图2(a)和图2(b)中还可以看出纠缠Eab集中在
$ {\varDelta _{\text{a}}} = - {\omega _{\text{b}}} $ 附近, 纠缠Ecm集中在${\tilde \varDelta _{\text{m}}} = - {\omega _{\text{b}}}$ 附近.从整个过程来看, 纠缠作为一种有限的量子资源, 最初存在于微波-光与磁振子-声子之间, 之后通过光力分束器相互作用以及微波-磁子状态交换相互作用, 纠缠最终转移到微波力学以及磁光子系统中.
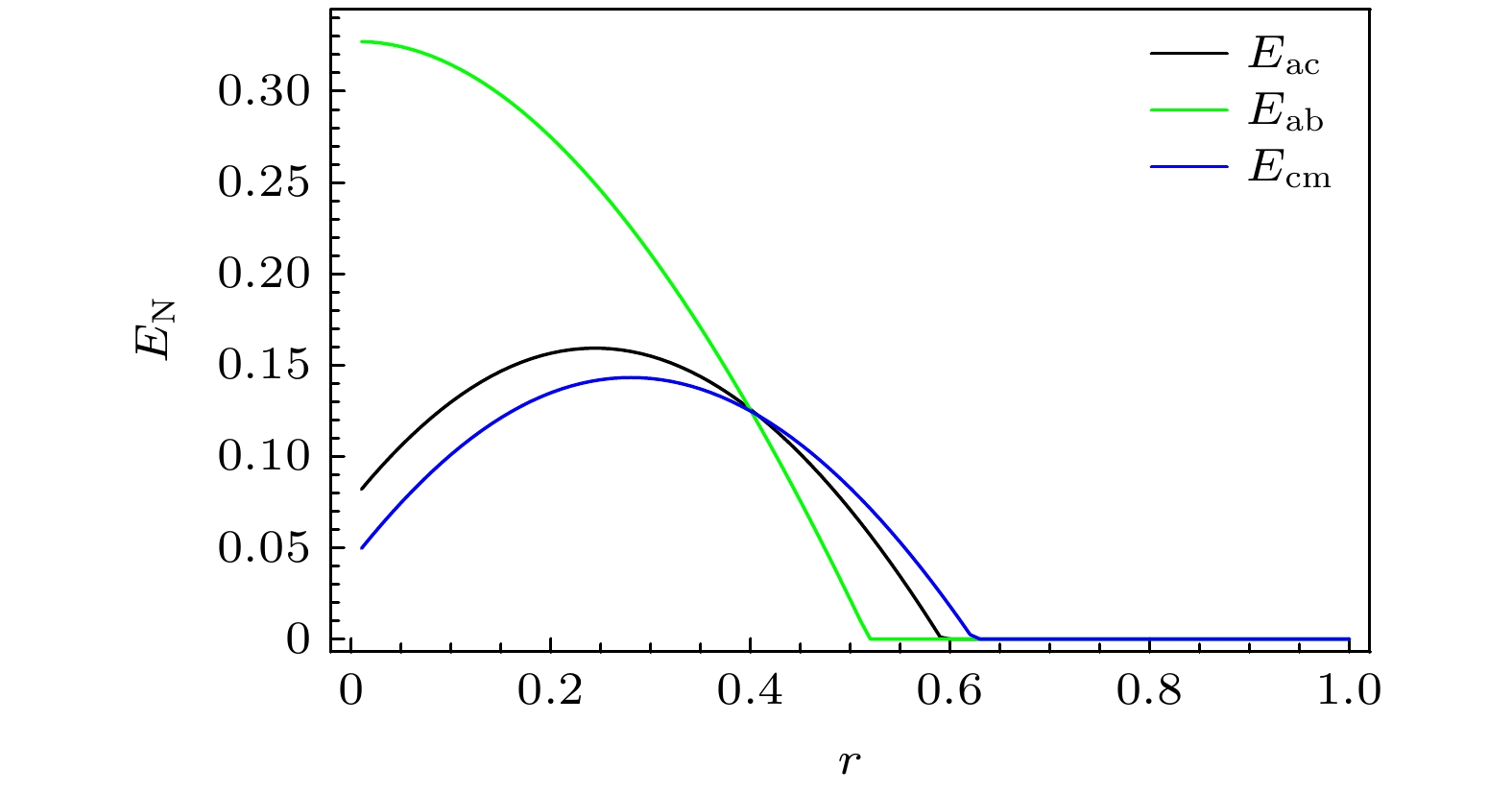
之后, 我们研究了压缩参数r对系统中二体纠缠的影响, 如图3所示. 光-微波纠缠Eac随r的变大先增强后减弱, 且r在0.2附近存在最佳值. 由于光与微波的纠缠也是实现量子计算等的重要资源, 因此在本文结果计算中我们采取r = 0.2.
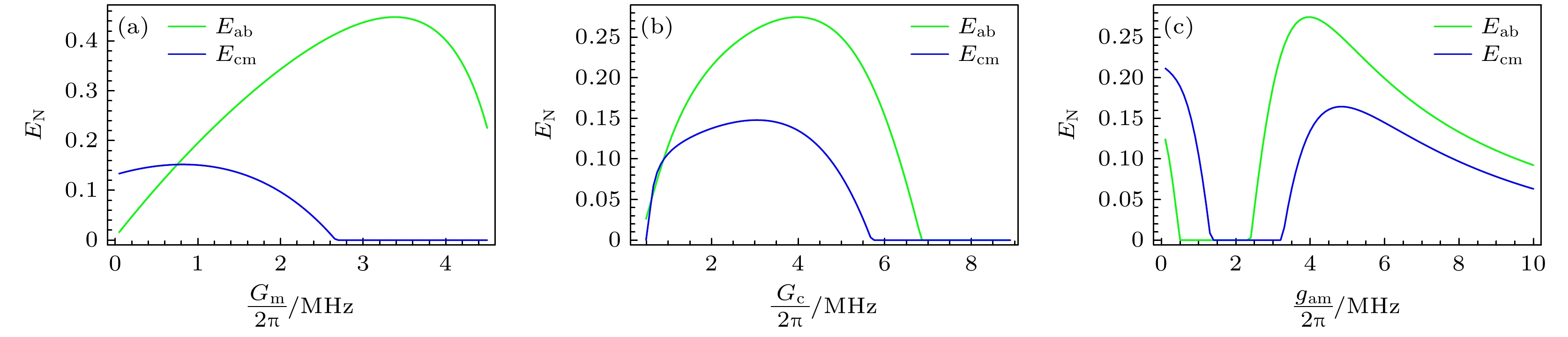
系统耦合强度对纠缠态的产生是非常重要的. 因此, 在图4中分析了微波-声子以及光-磁纠缠Eab和Ecm分别随磁力耦合强度Gm、光力耦合强度Gc、以及微波-磁子之间磁偶极相互作用强度gam的变化趋势. 图4(a)中纠缠Eab和Ecm随Gm的增强而先增加后减小. 其原因为随着Gm增强, 除本身的微波-光纠缠源Eac外, 由磁致伸缩产生的纠缠增加, 通过微波-磁子状态交换相互作用以及光力分束器作用转移到微波力和磁光子系统中, 从而在一定参数范围内纠缠Eab与Ecm随Gm增加. 但是随着Gm继续增强, 大部分的磁子与声子发生相互作用, 影响纠缠转移, 从而导致纠缠Ecm与Eab开始减小. 图4(b)中随着Gc变大, 纠缠Eab与Ecm先增加后减小. 其原因为, 开始时光-微波和磁致伸缩产生的纠缠会通过微波-磁子状态交换相互作用以及光力分束器相互作用转移到微波力学以及磁光子系统中, 从而在一定参数范围内纠缠Eab与Ecm随Gc增强而增加. 但是当Gc继续增强时, 光学光子尽可能与声子发生相互作用, 从而导致纠缠源减小, 进而导致纠缠Ecm与Eab开始减小. 从图4(c)中发现随gam增强时, 纠缠Eab和Ecm变化趋势一致, 都是随着gam的增强而先减小至0, 之后又随着gam增强而先增加后减小. 其原因是, 开始时微波-磁子状态交换相互作用与光力分束器作用相互竞争, 但并未起到转移纠缠的作用, 因此纠缠Eab和Ecm先减小直到为0. 之后随着gam继续变大, 微波-磁子状态交换相互作用以及光力分束器相互作用开始转移两个纠缠源, 从而导致纠缠Eab和Ecm开始增加. 但是随着gam继续增强, 大部分微波光子与磁子发生作用, 导致与光学光子作用的微波光子变少以及与声子作用的磁子变少, 即纠缠源Eac和Ecm减少, 进而导致纠缠Eab和Ecm又开始减少. 相较于系统中微波与光本身不纠缠的情况[33], 本文系统中产生的纠缠Eab和Ecm既可以同时存在也可以单独存在. 尤其是当gam=0时, 纠缠Eab和Ecm依旧存在.
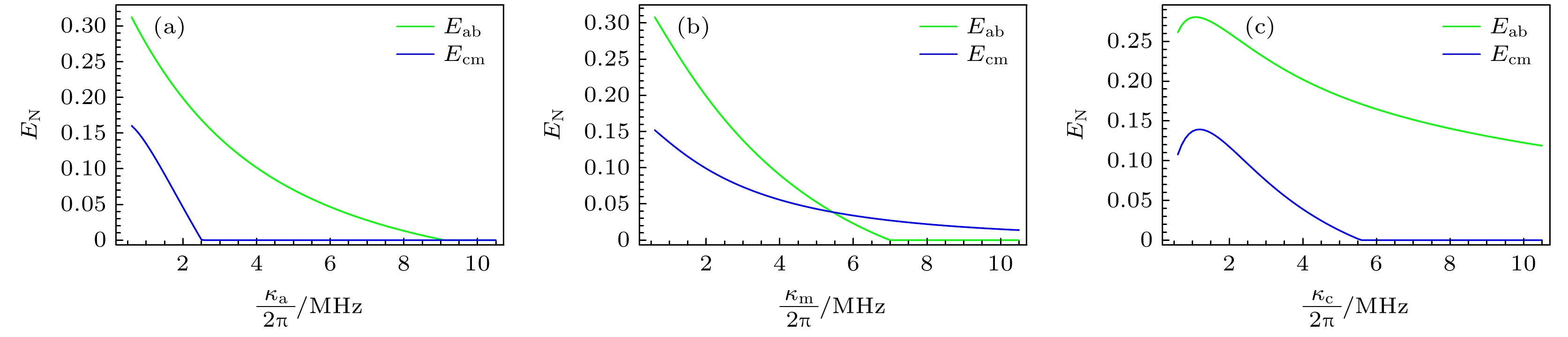
图5给出了不同模式耗散率对纠缠的影响. 通过结果发现, 微波-声子以及光-磁纠缠Eab和Ecm随着微波腔模式耗散率
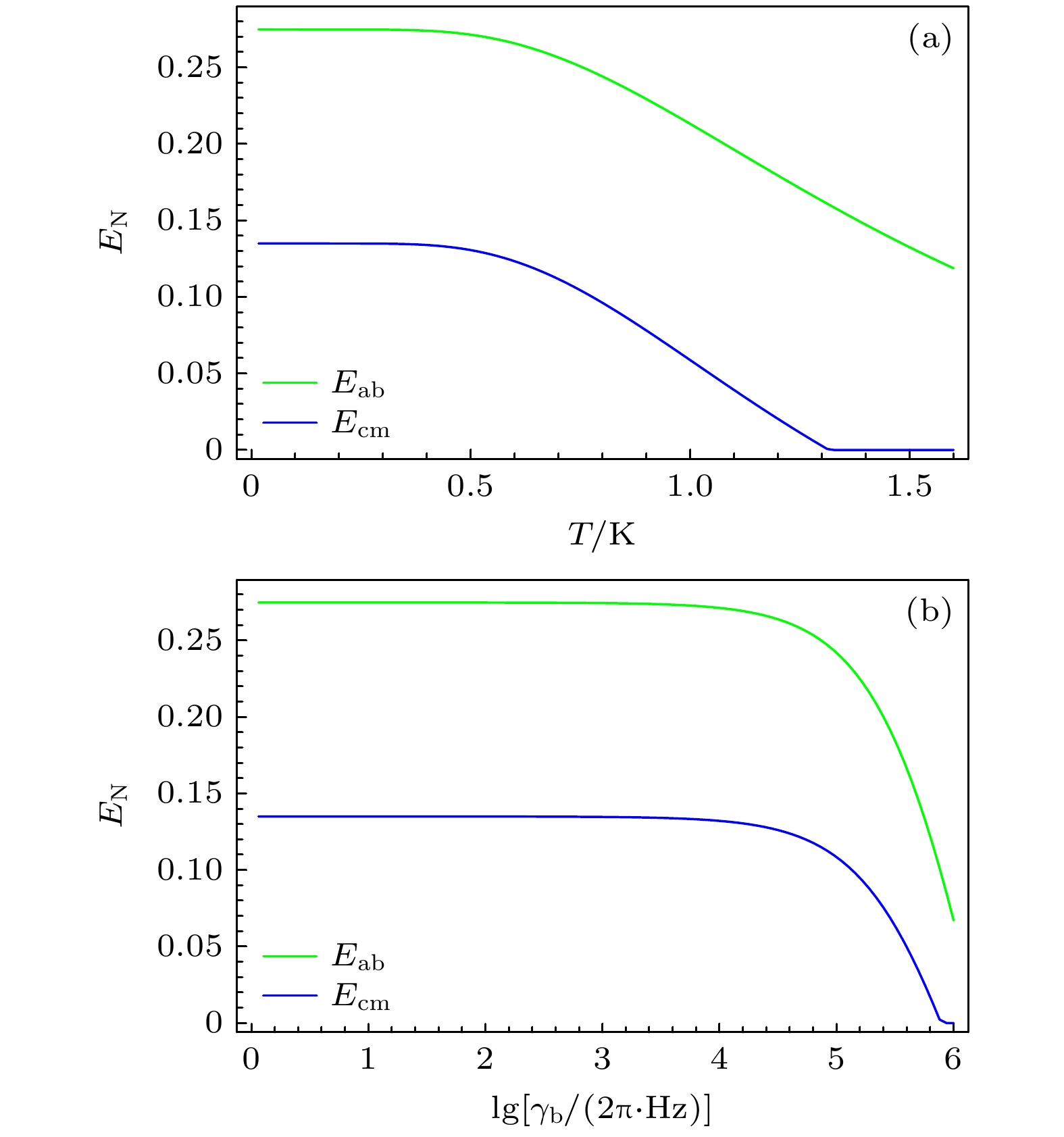
$ {\kappa _{\text{a}}} $ 以及磁子模式耗散率$ {\kappa _{\text{m}}} $ 的增强而减小, 但是随着光学腔模式耗散率$ {\kappa _{\text{c}}} $ 的增强而先增加后减小. 当$ {\kappa _{\text{a}}} $ 增强时, 与磁子和光学光子发生作用的微波光子变少, 导致两纠缠源通过磁偶极相互作用转移的过程受到影响, 从而导致纠缠Ecm和Eab减小. 同理, 当$ {\kappa _{\text{m}}} $ 增强时, 与微波和声子作用的磁子变少, 两纠缠源通过磁偶极相互作用转移的过程受到影响, 从而导致纠缠Ecm和Eab减小. 并且通过对比图5(a)和图5(b)可以发现纠缠Eab对磁子模式耗散率$ {\kappa _{\text{m}}} $ 更敏感, 而纠缠Ecm则对微波模式耗散率$ {\kappa _{\text{a}}} $ 更敏感. 物理上可以这样解释: 尽管纠缠Eab与纠缠Ecm产生的来源是相同的, 都可以由注入的微波-光纠缠以及磁声耦合产生. 但结合图3与图4(a)可以看到, 压缩参数r对纠缠Eab主要起抑制作用, 而有效磁力耦合强度Gm对纠缠Eab起先促进后抑制的作用, 表明纠缠Eab的产生主要来源于磁声耦合. 同理, 有效磁力耦合强度Gm对纠缠Ecm主要起抑制作用, 而压缩参数r对纠缠Ecm起先促进后抑制的作用, 表明纠缠Ecm的产生主要来源于注入的微波-光纠缠. 而当$ {\kappa _{\text{c}}} $ 增强时, 光学光子逸出通过耗散机制[43]与微波光子耦合产生纠缠, 这一过程会使纠缠Eac增加, 所以通过Eac转移产生的纠缠Eab和Ecm会先增加, 但是当超过最佳值时, 会导致系统退相干效应, 破坏系统纠缠. 可以看出, 虽然损耗通常被视为量子纠缠的负面影响因素, 但在某些情况下, 耗散过程可以用来产生和维持量子纠缠. 同时,$ {\kappa _{\text{c}}} $ 增强还会使与声子作用的光学光子变少, 影响纠缠Eac和Emb通过光力分束器相互作用的转移过程, 导致纠缠Ecm和Eab减小.最后研究了温度对系统中微波-声子以及光-磁纠缠Eab和Ecm的影响. 相较于注入不纠缠的微波与光[44]的系统, 我们的方案会显著地提升纠缠对于温度的鲁棒性. 如图6(a)所示, 纠缠Ecm和Eab在1.3 K的温度下仍然存在. 同时, 如图6(b)所示, 在
${\gamma }_{\text{b}}$ 约为$ 2\pi \times 5.8\times {10}^{5} $ 时, 纠缠Ecm与Eab仍然存在, 表明该系统制备的纠缠Eab和Ecm对声子耗散率也同样具有鲁棒性. -
我们提出了一种在OMM系统中获得微波-声子以及光-磁之间稳态纠缠的可行方案, 并利用负对数性研究了系统中纠缠特性以及对相关参数的依赖关系. 该方案中, 纠缠首先由微波-光以及磁子-声子产生, 之后通过光力分束器相互作用以及微波-磁子状态交换相互作用, 最终被转移到微波力学以及磁光子系统中. 研究表明微波-声子和光-磁纠缠可以在同一系统中同时产生, 并且该方案对环境温度以及声子耗散率具有很强的鲁棒性. 纠缠的微波-声子以及光-磁振子可以作为量子网络中的节点, 实现不同量子系统之间的连接, 这对于构建大规模的量子网络至关重要, 将在量子信息处理和量子网络中具有潜在的应用价值.
微波-声子与光-磁纠缠态的产生
Generation of microwave-phonon and magnon-optics entangled states
-
摘要: 量子纠缠是量子计算和量子通信网络的核心资源. 本文提出了一种在腔光磁力系统中同时获得微波-声子和光-磁纠缠的理论模型. 该模型基于磁振子的混合量子系统, 注入由超导电光装置产生的光-微波纠缠光束作为内腔场, 并且用蓝失谐微波场激发磁振子模式产生磁振子-声子纠缠. 通过光力分束器及微波-磁子状态交换相互作用转移纠缠, 最终可以获得微波-声子和光-磁纠缠. 理论上从系统哈密顿量和量子郎之万方程出发, 得到漂移矩阵A, 由漂移矩阵的负本征值保证文章计算的纠缠处于稳定状态. 再利用对数负性分析研究了系统中量子纠缠的特性与相关参数的依赖关系. 研究表明, 该系统可同时获得微波-声子以及光-磁之间稳态纠缠, 并且在系统中直接注入纠缠的微波与光可以显著地提升纠缠对温度的鲁棒性. 该研究将在量子网络和混合量子系统的量子信息处理方面奠定基础.Abstract: Quantum entanglement is a key resource for performing quantum computing and building quantum communication networks. By injecting a microwave-optical dual-mode entanglement field into the system, as well as pumping the optical and microwave cavities, and by appropriately choosing the detuning relationship between the pumping field and the modes, it is shown in this work that microwave-phonon entanglement Eab and magnon-optics entanglement Ecm can be generated simultaneously in the cavity opto-magnomechanic system, and the entanglement can be in a steady state. Specifically, the model is based on a hybrid quantum system of magnons, where a microwave-light entanglement generated by an optically pulsed superconducting electro-optical device through spontaneous parametric down-conversion process is injected as the intracavity field, and a blue-detuned microwave field is used to excite the magnon modes to produce magnon-phonon entanglement. Through the interaction between an optomechanical beam splitter and microwave-magnon state-swap, steady microwave-phonon entanglement Eab and magnon-optics entanglement Ecm are successfully realized. The entanglement Eab and Ecm in the system are analyzed using the logarithmic negativity. The effects of several parameters of the system, such as environment temperature, coupling strength and dissipation rate, on the degree of entanglement are investigated. In particular, the entanglement Eab and Ecm generated in this system can exist both simultaneously and individually. Especially when gam = 0, the entanglement Eab and Ecm still exist. Moreover, directly injecting entangled microwave-light into the system can significantly enhance the robustness of the entanglement against temperature, which will have broad application prospects in quantum information processing in quantum networks and hybrid quantum systems. Notably, the entanglement Eab and Ecm exist even at a temperature of 1.3 K. Our research has potential value for applications in the fields of quantum information processing and quantum networks.
-
Key words:
- quantum entanglement /
- opto-magnomechanics /
- two-mode squeezing .
-

-
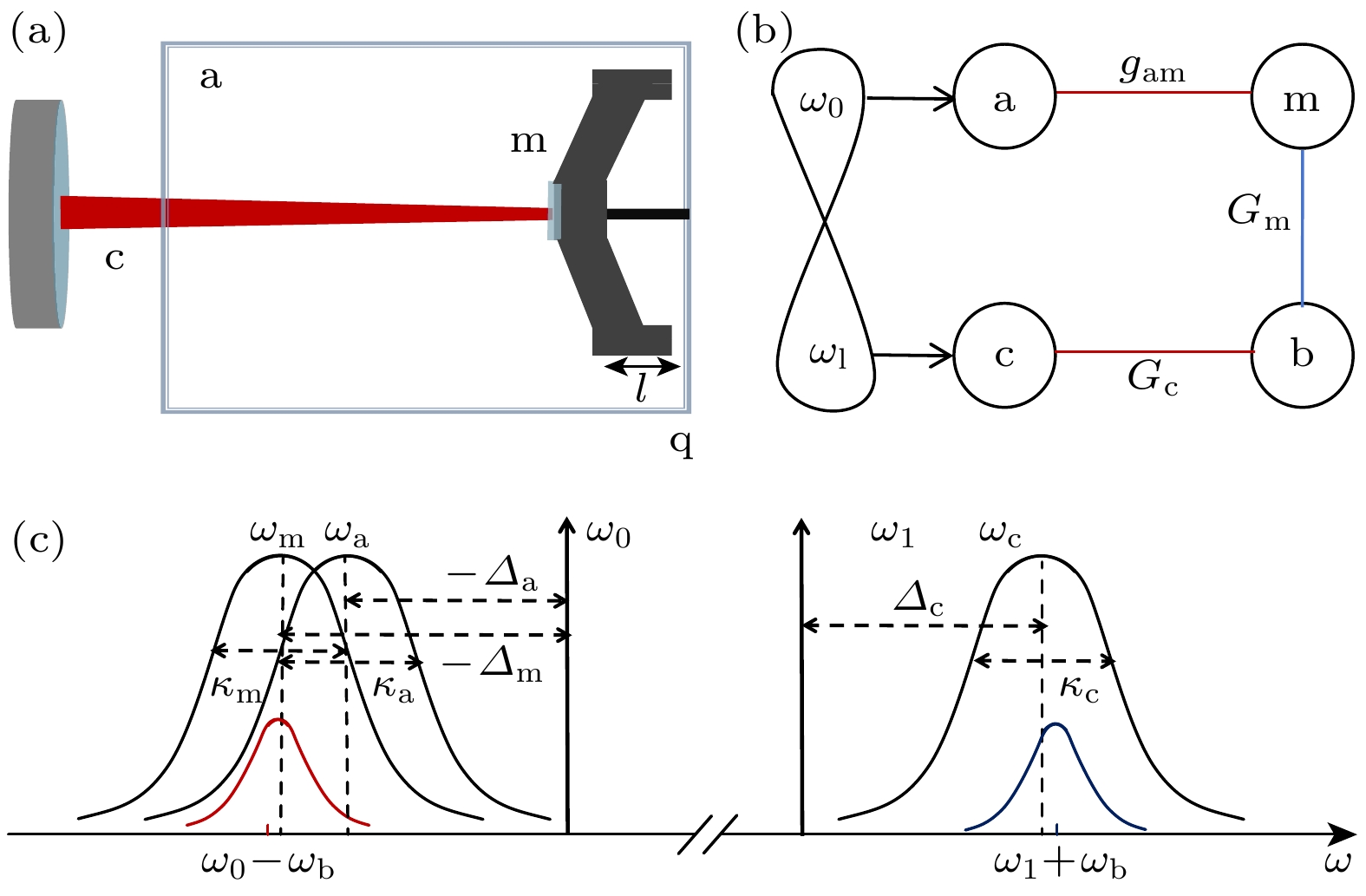
图 1 (a), (b) OMM系统示意图. YIG晶体中的磁振子模式m耦合到微波腔模a并且通过磁致伸缩引起振动声子b耦合到光学腔模c. 图(b)中蓝色(红色)线表示参量下转换(分束器)相互作用; (c)模型采用的模式频率和带宽. 当光学腔模与驱动激光场的反斯托克斯边带(蓝色)在频率为(
$ {\omega _{\text{l}}} + {\omega _{\text{b}}} $ )处共振, 并且磁子模和微波腔模同时与微波驱动场的斯托克斯边带(红色)在频率为($ {\omega _0} - {\omega _{\text{b}}} $ )处共振, 可以建立微波-声子以及光-磁子之间的稳态纠缠Eab和EcmFigure 1. (a), (b) OMM system scheme. A magnon mode m in a YIG crystal couples to a microwave cavity mode a and to an optical cavity mode c via the mechanical vibration b induced by the magnetostriction. The blue (red) line in Figure (b) denotes the effective parametric down-conversion (beam-splitter) interaction; (c) mode frequency and bandwidth used adopted in the protocol. When the optical cavity is resonant with the (blue) anti-Stokes sideband of the driving laser at frequency (
$ {\omega _0} - {\omega _{\text{b}}} $ ), and the magnon and microwave cavity modes are resonant with the (red) Stokes sideband of the microwave drive field at frequency ($ {\omega _{\text{l}}} + {\omega _{\text{b}}} $ ), microwave-mechanics entanglement Eab and magnon-optics entanglement Ecm can be generated at steady state.图 4 光-磁和微波-声子之间纠缠随有效耦合强度变化 (a)有效光力耦合强度Gc; (b)有效磁力耦合强度Gm; (c)微波-磁子耦合强度gam
Figure 4. Stationary magnon-optics entanglement Ecm and microwave-mechanics entanglement Eab versus effective coupling strength: (a) The effective optomechanical coupling strength Gc; (b) the effective magno-mechanical coupling strength Gm; (c) the microwave-magnon coupling rate gam.
图 5 微波-声子以及光-磁之间纠缠随不同模式耗散率变化 (a) 微波腔模耗散率
$ {\kappa _{\text{a}}} $ ; (b) 磁振子模耗散率$ {\kappa _{\text{m}}} $ ; (c) 光学腔模耗散率$ {\kappa _{\text{c}}} $ Figure 5. Stationary microwave-mechanics entanglement Eab and magnon-optics entanglement Ecm versus dissipation rates: (a) Microwave cavity mode dissipation rate
$ {\kappa _{\text{a}}} $ ; (b) magnon mode dissipation rate$ {\kappa _{\text{m}}} $ ; (c) optical cavity mode dissipation rate$ {\kappa _{\text{c}}} $ . -
[1] Tang J F, Hou Z B, Shang J W , Zhu H J, Xiang G Y, Li C F, Guo G C 2020 Phys. Rev. Lett. 124 060502 doi: 10.1103/PhysRevLett.124.060502 [2] Konrad T, De Melo F, Tiersch M, Kasztelan C, Aragão A, 2008 Buchleitner A Nat. Phys. 4 99 doi: 10.1038/nphys885 [3] Aspelmeyer M, Böhm H R, Gyatso T, Jennewein T, Kaltenbaek R, Lindenthal M, Molina-Terriza G, Poppe A, Taraba M, Ursin R, Walther P, Zeilinger A 2003 Science 301 621 doi: 10.1126/science.1085593 [4] 杨荣国, 张超霞, 李妮, 张静, 郜江瑞 2019 物理学报 68 094205 doi: 10.7498/aps.68.20181837 Yang R G, Zhang C X, Li N, Zhang J, Gao J R 2019 Acta Phys. Sin. 68 094205 doi: 10.7498/aps.68.20181837 [5] Liang Y Y, Yang R G, Zhang J, Zhang T C 2023 Opt. Express 31 11775 doi: 10.1364/OE.486260 [6] Zhang K, Wang W, Liu S H, Pan X Z, Du J J, Lou Y B, Yu S, Lü S C, Treps N, Fabre C, Jing J T 2020 Phys. Rev. Lett. 124 090501 doi: 10.1103/PhysRevLett.124.090501 [7] 郝景晨, 杜培林, 孙恒信, 刘奎, 张静, 杨荣国, 郜江瑞 2024 物理学报 73 074203 doi: 10.7498/aps.73.20231630 Hao J C, Du P L, Sun H X, Liu K, Zhang J, Yang R G, Gao J R 2024 Acta Phys. Sin. 73 074203 doi: 10.7498/aps.73.20231630 [8] 闫智辉, 贾晓军, 谢常德, 彭堃墀 2012 物理学报 61 014206 doi: 10.7498/aps.61.014206 Yan Z H, Jia X J, Xie C D, Peng K C 2012 Acta Phys. Sin. 61 014206 doi: 10.7498/aps.61.014206 [9] Liu K, Cui S Z, Yang R G, Zhang J X, Gao J R 2012 Chin. Phys. Lett. 29 060304 doi: 10.1088/0256-307X/29/6/060304 [10] 刘奎, 马龙, 苏必达, 李佳明, 孙恒信, 郜江瑞 2020 物理学报 69 124203 doi: 10.7498/aps.69.20200107 Liu K, Ma L, Su B D, Li J M, Sun H X, Gao J R 2020 Acta Phys. Sin. 69 124203 doi: 10.7498/aps.69.20200107 [11] Yang R G, Zhang J, Klich I, González-Arciniegas C, Pfister O 2020 Phys. Rev. A 101 043832 doi: 10.1103/PhysRevA.101.043832 [12] Du P L, Wang Y, Liu K, Yang R G, Zhang J 2023 Opt. Express 31 479420 [13] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391 doi: 10.1103/RevModPhys.86.1391 [14] Liu X M, Yang R G, Zhang J, Zhang T C 2023 Opt. Express 31 30005 doi: 10.1364/OE.496528 [15] 罗均文, 吴德伟, 苗强, 魏天丽 2020 物理学报 69 054203 doi: 10.7498/aps.69.20191735 Luo J W, Wu D W, Miao Q, Wei T L 2020 Acta Phys. Sin. 69 054203 doi: 10.7498/aps.69.20191735 [16] Palomaki T A, Teufel J D, Simmonds R W, Lehnert K W 2013 Science 342 710 doi: 10.1126/science.1244563 [17] Riedinger R, Wallucks A, Marinkovi´c I, Löschnauer C, Aspelmeyer M, Hong S, Gröblacher S 2018 Nature 556 473 doi: 10.1038/s41586-018-0036-z [18] Wollman E E, Lei C U, Weinstein A J, Suh J, Kronwald A, Marquardt F, Clerk A A, Schwab K C 2015 Science 349 952 doi: 10.1126/science.aac5138 [19] Zhang X F, Zou C L, Jiang L, Tang H X 2016 Sci. Adv. 2 e1501286 doi: 10.1126/sciadv.1501286 [20] Shen R C, Li J, Fan Z Y, Wang Y P, You J Q 2022 Phys. Rev. Lett. 129 123601 doi: 10.1103/PhysRevLett.129.123601 [21] Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003 doi: 10.1103/PhysRevLett.111.127003 [22] Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603 doi: 10.1103/PhysRevLett.113.083603 [23] Bai L, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201 doi: 10.1103/PhysRevLett.114.227201 [24] Osada A, Hisatomi R, Noguchi A, Tabuchi Y, Yamazaki R, Usami K, Sadgrove M, Yalla R, Nomura M, Nakamura Y 2016 Phys. Rev. Lett. 116 223601 doi: 10.1103/PhysRevLett.116.223601 [25] Zhang X F, Zhu N, Zou C L, Tang H X 2016 Phys. Rev. Lett. 117 123605 doi: 10.1103/PhysRevLett.117.123605 [26] Osada A, Gloppe A, Hisatomi R, Noguchi A, Yamazaki R, Nomura M, Nakamura Y, Usami K 2018 Phys. Rev. Lett. 120 133602 doi: 10.1103/PhysRevLett.120.133602 [27] Zhu N, Zhang X, Han X, Zou C L, Zhong C, Wang C H, Jiang L, Tang H X 2020 Optica 7 1291 doi: 10.1364/OPTICA.397967 [28] Haigh J A, Nunnenkamp A, Ramsay A J 2021 Phys. Rev. Lett. 127 143601 doi: 10.1103/PhysRevLett.127.143601 [29] Yang Z B, Liu X D, Yin X Y, Ming Y, Liu H Y, Yang R C 2021 Phys. Rev. Appl. 15 024042 doi: 10.1103/PhysRevApplied.15.024042 [30] Yin X Y, Yang Z B, Huang Y M, Wan Q M, Yang R C, Liu H Y 2023 Ann. Phys. 535 2200603 doi: 10.1002/andp.202200603 [31] Fan Z Y, Shen R C, Wang Y P, Li J, You J Q 2022 Phys. Rev. A 105 033507 doi: 10.1103/PhysRevA.105.033507 [32] Fan Z Y, Qian H, Li J 2023 Quantum Sci. Technol. 8 015014 doi: 10.1088/2058-9565/aca3cf [33] Fan Z Y, Qiu L, Gröblacher S, Li J 2023 Laser Photonics Rev. 17 2200866 doi: 10.1002/lpor.202200866 [34] Rueda A, Hease W, Barzanjeh S, Fink J M 2019 npj Quantum Inf. 5 108 doi: 10.1038/s41534-019-0220-5 [35] Hease W, Rueda A, Sahu R, Wulf M, Arnold G, Schwefel H G L, Fink J M 2020 PRX Quantum 1 020315 doi: 10.1103/PRXQuantum.1.020315 [36] Andersen U L, Gehring T, Marquardt C, Leuchs G 2016 Phys. Scr. 91 053001 doi: 10.1088/0031-8949/91/5/053001 [37] Sahu R, Qiu L, Hease W, Arnold G, Minoguchi Y, Rabl P, Fink J M 2023 Science 380 718 doi: 10.1126/science.adg3812 [38] Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601 doi: 10.1103/PhysRevLett.121.203601 [39] Lachance-Quirion D, Tabuchi Y, Gloppe A, Usami K, Nakamura Y 2019 Appl. Phys. Express 12 070101 doi: 10.7567/1882-0786/ab248d [40] Heyroth F, Hauser C, Trempler P, Geyer P, Syrowatka F, Dreyer R, Ebbinghaus S G, Woltersdorf G, Schmidt G 2019 Phys. Rev. Appl. 12 054031 doi: 10.1103/PhysRevApplied.12.054031 [41] Vidal G, Werner R F 2002 Phys. Rev. A 65 032314 doi: 10.1103/PhysRevA.65.032314 [42] Plenio M B 2005 Phys. Rev. Lett. 95 090503 doi: 10.1103/PhysRevLett.95.090503 [43] Tan H T, Deng W W, Li G X 2017 Phys. Rev. A 95 053842 doi: 10.1103/PhysRevA.95.053842 [44] Luo Y X, Cong L J, Zheng Z G, Liu H Y, Ming Y, Yang R C 2023 Opt. Express 31 34764 doi: 10.1364/OE.500854 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: