首页
登录
注册
-
随着载人登月、火星探索以及小行星采样星际返回等深空探测国家重大任务的推进, 飞行器呈现速度更快、时间更长、气动布局更复杂、设计余量更小等突出特点, 高焓非平衡飞行环境的精细化气动热预测与调控技术已成为制约新一轮高超声速飞行器研制的关键共性技术. 飞船返回舱等飞行器在大气层中超高速飞行时, 头部激波层内高温导致气体组分发生振动激发、离解甚至电离等物理化学现象, 流场中原子、离子将在壁面催化效应下发生复合反应, 具体体现在催化复合作用改变壁面附近各组分的质量分数梯度分布, 进而引起流场中输运特性的改变, 最终显著改变壁面气动热载荷的分布[1].
壁面催化效应的表征通常以边界条件的形式给出, 完全催化壁(fully catalytic wall, FCW)、有限催化壁(partially catalytic wall, PCW)和非催化壁(non-catalytic wall, NCW)是高温热化学非平衡气动热环境预示中最常用的三种催化边界条件, 且国内外学者已开展了大量的研究[2,3]. 其中, Davide等[4]针对高焓激波/边界层干扰流场, 建立了考虑多种壁面催化条件的非平衡流场计算方法. 结果表明, 壁面催化模型影响高焓分离区流场的准确预测. Yu等[5]研究了不同壁面催化条件下返回舱等离子体鞘套电磁参数分布影响, 揭示壁面催化对组分分布影响机制. 周凯等[6]在膨胀管风洞中进行了超高速再入速度条件下标准球头模型气动热测量实验. 结果表明, 完全催化壁(Cu涂层)比非催化壁(Al2O3涂层)的驻点热流率高出53.93%. 为精确预测壁面热流密度、组分分布, 现阶段的研究多集中在有限催化边界条件, 以反映真实的壁面催化效应.
催化复合反应速率常数计算是有限催化边界计算模型的关键, 特定催化效率模型相对简单, 且有大量防热材料催化系数实验数据支撑, 得到了广泛应用[7]. 对于此模型关键在于催化复合系数的取值, 当前多采用取为常数的催化复合系数进行研究. 例如苗文博、程晓丽等[8,9]成体系开展固定催化效率的SRE模型(specified reaction efficiency model)的相关研究. 针对RAM-CII气动外形, Ma∞ = 25.9, H = 71 km的来流条件下, 完全催化壁热流峰值比非催化壁高约40%, 原子复合放热将提高近壁面温度梯度, 改变近壁面组分分布. 2021年, 莫凡等[10]建立了考虑辐射平衡壁温下有限催化的数值计算方法, 依托LENS系列激波风洞标模返回舱实验数据, 验证了SRE特定催化效率模型的合理性.
新型热防护机制的发展是满足下一代高超声速飞行器对热防护需求的关键[11]. 磁控热防护技术是磁流体动力(magnetohydrodynamic, MHD)控制在热防护领域的应用, 该技术具备结构外形/尺寸适应性强、服役环境广、降热/冷却能力优异等特点, 近年来引起广泛关注[12,13]. 陈刚等[14]数值研究了不同磁场配置对二维基准外形弹道式再入飞行器表面热流分布的影响, 给出了流动的不同区域, 磁场空间分布应遵循的一般性原则. 丁明松等[15]分析了电导率模型对高焓等离子体流场磁控效果影响, 结果表明, 不同等离子体电导率模型计算结果相差可达数倍, 严重影响了高焓流场磁流体力、热控制效果. Heather与Nikos[16]进一步分析了多组分热化学非平衡模型对高焓钝体、双锥流场结构MHD控制机制, 指出化学反应模型、电导率模型的选择影响高焓流场MHD控制效率. 滕子昂等[17]基于多组分、热力学平衡模型分析了典型实验工况下化学反应对磁控激波/热防护效果影响机制.
可以看出, 高温流场MHD控制技术涉及流体场、热场、化学反应及电磁场等多方面的研究. 物理化学反应方面, 采用能够精确描述组分产生、消亡, 以及其碰撞、运动、能量转化过程机理的高温非平衡物理化学模型, 模拟多场、多组分、多过程复杂带电流体的流动, 是实现评估高温流场调控效果和效率的前提和基础. 从目前已有的研究结果来看, 壁面催化效应改变激波层内的组分分布及壁面温度梯度, 直接影响高温热化学非平衡流场MHD控制效果, 其内在机理及影响机制需要进一步分析. 本文主要针对常见等离子体空气热化学气体模型, 开展热化学非平衡气体高焓等离子体电磁流动数值分析, 系统地探讨壁面催化效应等对高温非平衡流场及其MHD控制效果的影响.
-
高温非平衡流数值研究中较为常用组元模型为7组元和11组元模型, 针对电离反应较为显著的超高速再入流动, 涉及更多电离反应的11组元(N2, O2, NO, N, O, NO+, N+, O+, N
${}_2^+ $ , O${}_2^+ $ , e–)模型更适合. 化学反应方程式及相应反应速率常数由Gupta模型[18]给出, 温度模型选用Park双温度模型. 热化学非平衡流的输运系数主要涉及热传导系数${k_i}$ ,${k_v}$ ,$k$ , 黏性系数${\mu _i}$ ,$\mu $ 及组元的扩散系数${D_i}$ , 主要采用半经验公式拟合[19-21]求出. 表1列举了高温空气里主要发生的反应表达式及正逆反应控制温度[22], 其中的M被称为中性粒子碰撞体. 对于分子离解反应, 其正向反应由平动、振动温度共同作用, 控制温度如下所示: -
壁面催化效应会影响表面附近等离子体电离复合, 进而影响等离子体组分、温度分布. 因此, 本文主要考虑壁面催化模型对热化学非平衡流场热流预测及MHD控制效果影响. 完全催化和非催化壁面边界处理方法参考李鹏等[25]的文献, 对于有限催化壁面(主要考虑氮原子和氧原子复合反应), 一般通过求解壁面附近质量守恒方程的方法构建, 表达式为
其中
$ {k_s} $ 为化学反应速率常数;$ {\dot m_{s, {\text{w}}}} $ 表示组分s在壁面处的质量通量;$ {D_s} $ 为组分s扩散系数;$ {c_s} $ 为组分s质量分数. SRE模型中${k_s}$ 的求解可以转换为催化复合系数${\gamma _s}$ 与碰撞速率的乘积[26], 即式中,
$ {M_s} $ 为组分s的摩尔质量;$ {T_{\text{w}}} $ 为壁面温度;$ \Re $ 为普适气体常数. 壁面催化复合系数${\gamma _s}$ 表示壁面发生催化复合的原子数与入射到壁面总原子数之比[27], 取值来源于材料实验数据. -
低磁雷诺数假设下, 耦合电磁场的双温度、多组分热化学非平衡流动控制方程[28]为
其中
${\boldsymbol{U}}$ 为守恒变量;$ \boldsymbol{F}, \boldsymbol{G}, \boldsymbol{H} $ 分别为$ x, y, z $ 方向对流通量项;$ {\boldsymbol{F}}_{v}, {\boldsymbol{G}}_{v}, {\boldsymbol{H}}_{v} $ 分别为$ x, y, z $ 方向黏性通量项; W为化学反应源项矢量;$ {{\boldsymbol{S}}_{{\text{MHD}}}} $ 表示电磁源项.式中,
${\rho _i}$ 为组元 i 密度,$\rho $ 为混合气体密度;${\dot \omega _i}$ 代表组元 i 质量生成率;$p$ 为混合气体压力;${e_{\text{t}}}$ ,${e_{\text{v}}}$ 分别代表单位质量混合气体总能、振动能;${S_{\text{v}}}$ 为振动能量源项;${h_{\text{t}}}$ 为混合气体的总焓.${{\boldsymbol{u}}}$ 为速度矢量,${\boldsymbol B}$ 磁场强度矢量,${\boldsymbol{E}}$ 为电场强度矢量,${\boldsymbol{J}}$ 为电流密度矢量,$ {\gamma _{{\text{ev}}}} $ 表征不同非平衡模式间的电磁能量分配, 称为电磁能量分配比, 取$ {\gamma _{{\text{ev}}}} $ = 0.1.外加磁偶极子磁场表达式为
引入广义欧姆定律, 绝缘壁面条件下, 霍尔效应可忽略. 该假设下, 电磁能量源项
$ {\boldsymbol{J}} \cdot {\boldsymbol{E}} = {0} $ , 电流密度矢量${{\boldsymbol{J}}}$ 如下所示:$\sigma $ 为流场电导率, 可以由(16)式求出, 即其中电子质量
${m_{\text{e}}} = 9.11 \times {10^{ - 31}}{\text{ kg}}$ ; 电子电量$e = 1.6022 \times {10^{ - 19}}{\text{ C}}$ ;${n_{\text{e}}}$ 为电子数密度, 单位为m–3;$v_{{\text{e}}, s}^{}$ (单位Hz)代表电子与其他粒子的有效碰撞频率, 具体表达式参考Luo等[28]的文献.应力张量各分量如(17)式所示:
其中
$ \mu $ 为黏性系数, 可以由Sutherland公式求出.组元的质量生成率
$ {\dot \omega _s} $ 表达式为式中,
$ nr $ 为化学反应方程数;$ {\alpha _{r, s}} $ ,$ {\beta _{r, s}} $ 分别为化学反应当量系数;$ {R_{{\text{f}}, r}} $ ,$ {R_{{\text{b}}, r}} $ 分别为正向反应及逆向反应速率系数.本文流场计算区域包括远场/入口边界、出口边界、对称边界以及壁面边界. 远场/入口边界给定为自由来流条件:
${\varPhi _{{\text{in}}}} = {\varPhi _\infty } $ ; 出口边界一般位于超声速区域, 采用线性外插法:${\varPhi _N} = 2{\varPhi _{N1}} - {\varPhi _{N2}}$ ; 对称面边界, 采用零梯度对称条件:$\dfrac{{\partial \varPhi }}{{\partial n}} = 0 $ ; 其中,$\varPhi $ 为原始变量,${\varPhi _{{\text{in}}}}$ 为远场/入口边界原始变量,${\varPhi _\infty } $ 为自由流原始变量,${\varPhi _{N1}}$ 和${\varPhi _{N2}}$ 分别为第一层和第二层虚拟网格原始变量.壁面边界具体包括速度无滑移条件:
$ {u_{{\text{Wall}}}} = {v_{{\text{Wall}}}} = {w_{{\text{Wall}}}} = 0 $ ; 等温壁条件:$ {T_{\text{w}}} = {T_{v, {\text{w}}}} = {T_{{\text{Const}}}} $ ; 边界层零压力梯度条件:$ \dfrac{{\partial p}}{{\partial n}} = 0 $ .控制方程(4)的求解基于有限差分法, 黏性项采用中心差分离散, 对流项采用AUSMPW差分格式, 隐式离散方程采用LU-SGS方法求解, 具体求解方式参考李开等[29]的研究结果. Doihara与Nishida[30]研究指出低轨道再入飞行工况下的辐射热流量不到对流热流的1/20, 故考虑热化学非平衡效应后, 由于温度模型和组分扩散项的存在, 基于能量平衡关系壁面总热流主要包括由温度梯度产生的平动、振动传导热流和组分扩散热流项, 如(19)式所示:
其中
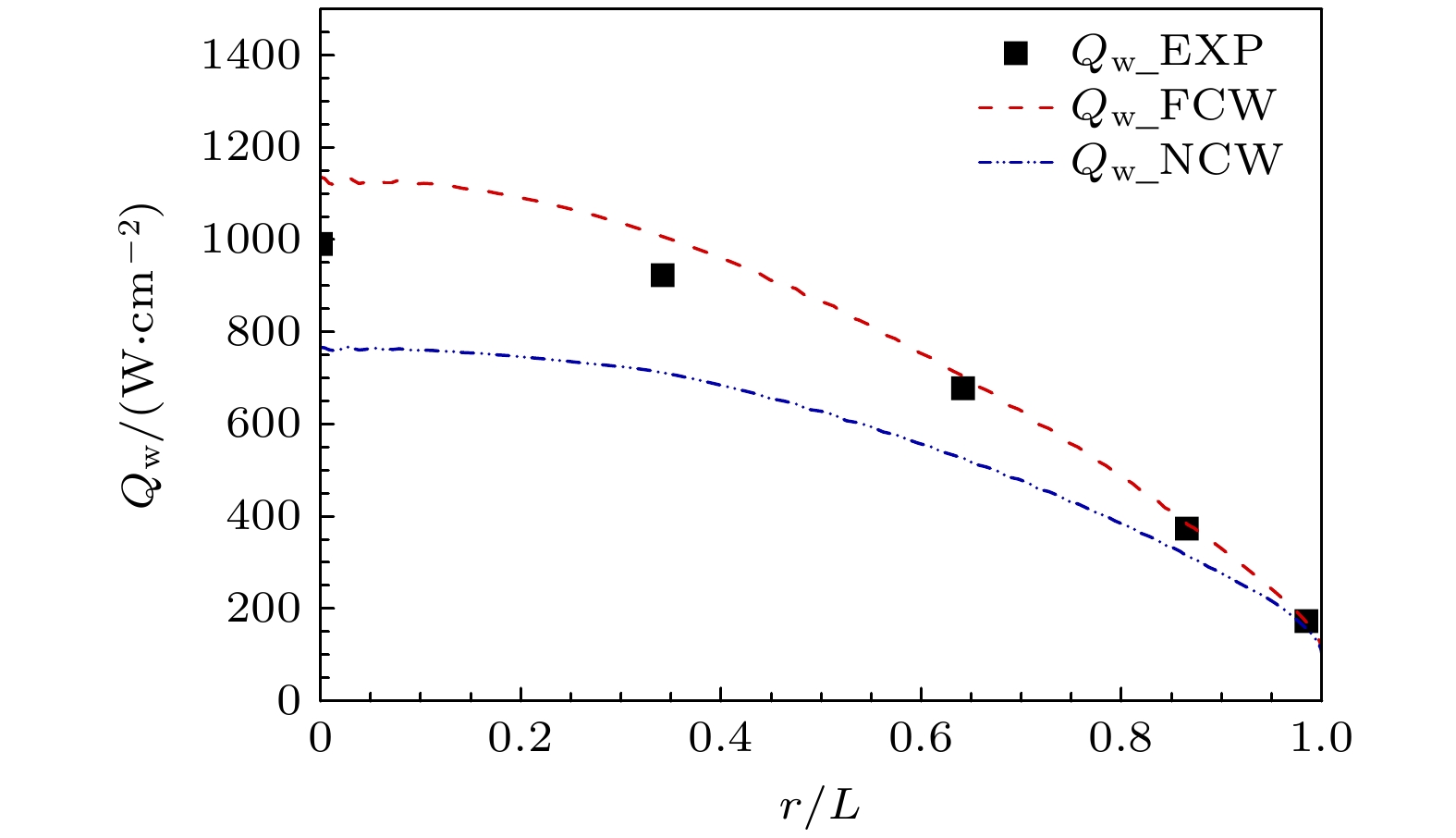
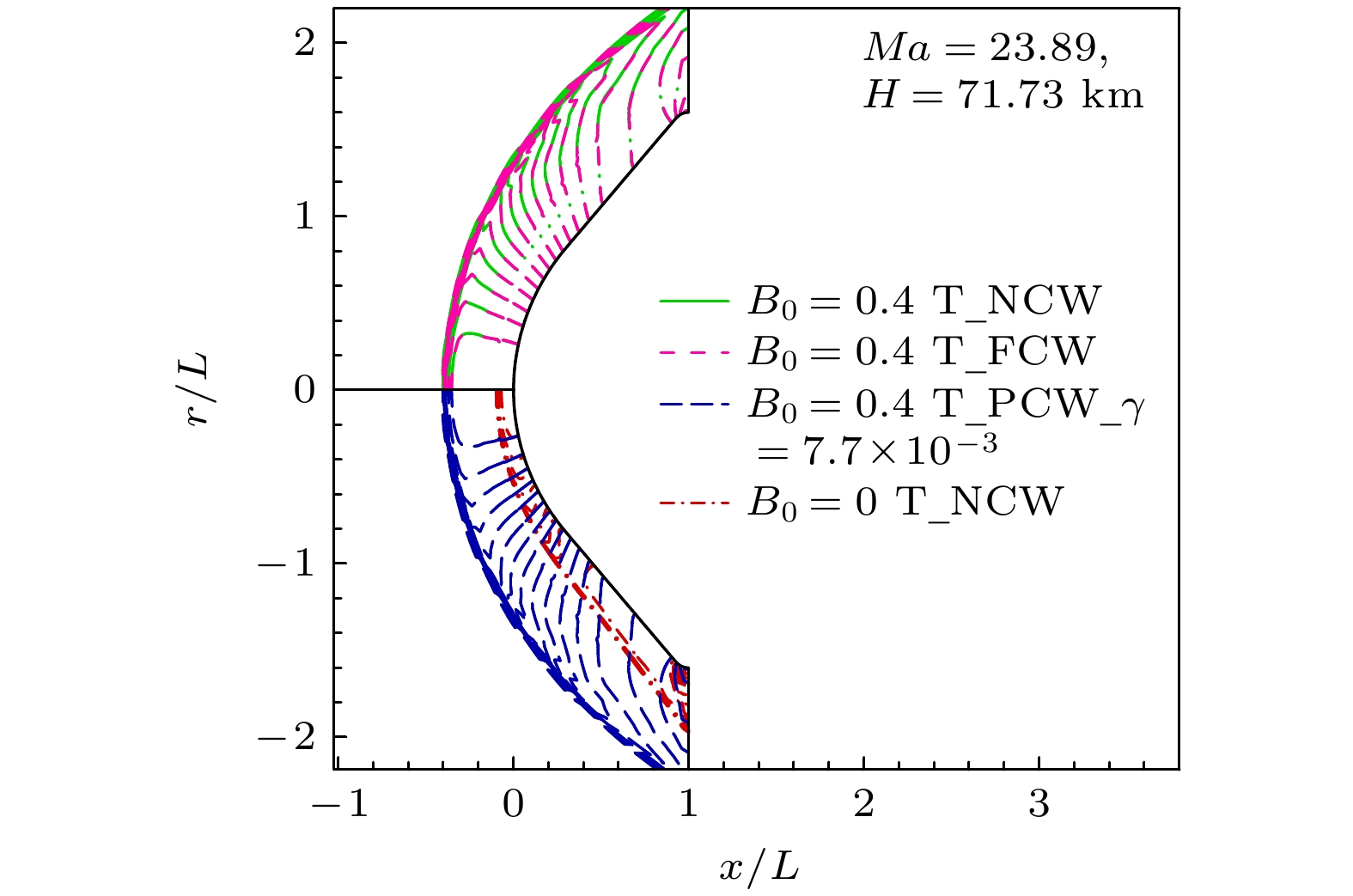
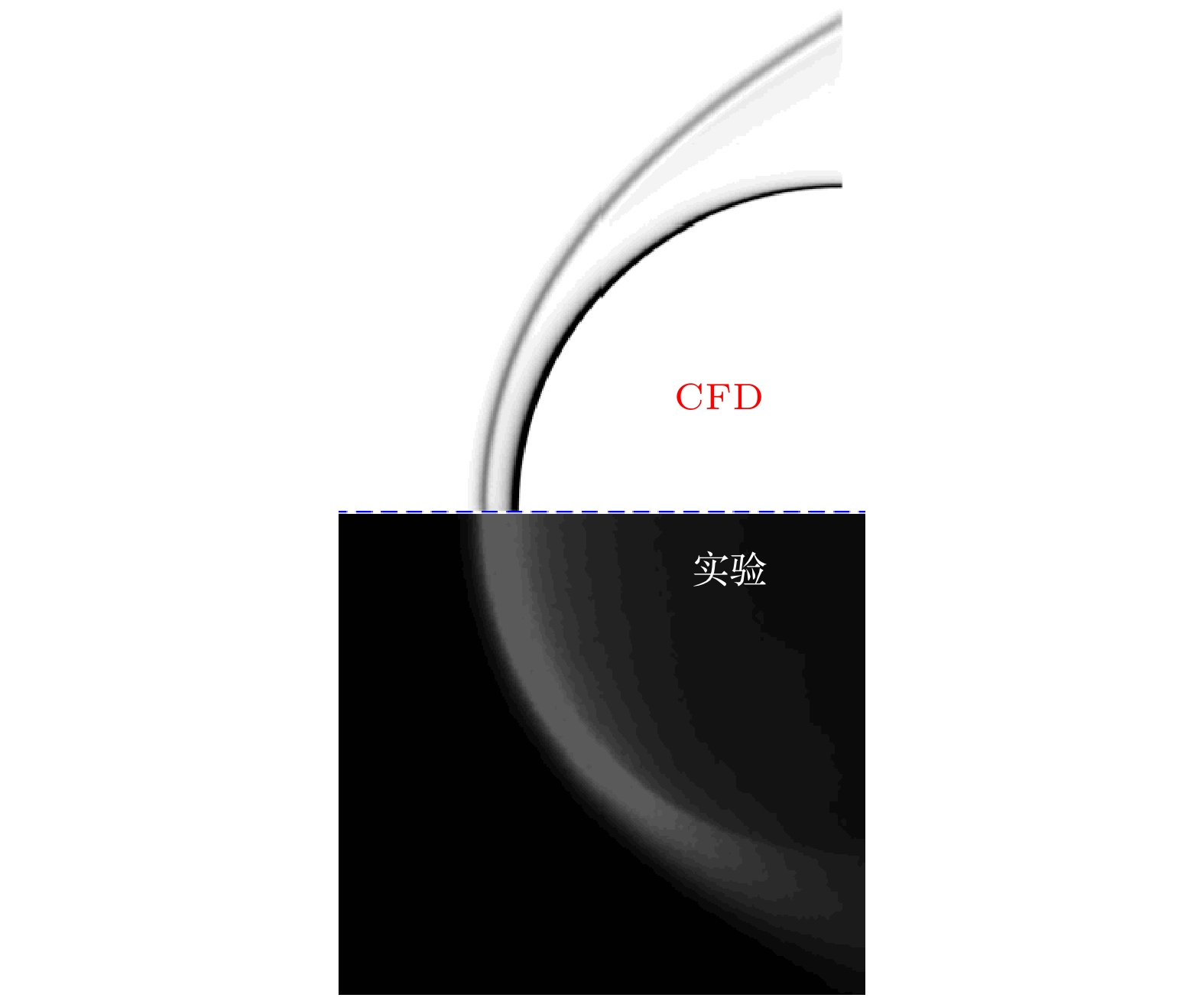
${q_n}$ 为总热流密度n方向分量;$T$ ,${T_{\text{v}}}$ 分别代表平动温度及振动温度;$ns$ 为化学反应方程数;${D_i}$ ,${h_i}$ ,${c_i}$ 分别为组元i扩散系数、单位质量静焓及质量分数.在以往的工作中, 作者所在研究团队对耦合电磁场的高超声速流动控制方程求解进行了较为广泛的研究, 验证了完全气体磁流体湍流[31]、耦合磁场的热化学非平衡流动[32]等多个计算模块的可靠性. 本节主要是针对高温热化学非平衡壁面催化效应方面的校验. 选取高焓膨胀管风洞实验流场为验证工况, 如表2所列. 实验模型为直径25 mm球头, 依托高速相机及同轴热电偶传感器, 分别测得该工况下脱体激波形状及壁面热流分布. 图1和图2分别为实验结果与程序计算结果对比, 从图中可以清晰地看到, 数值预测的半圆球脱体激波外轮廓与实验结果接近, 常壁温(Tw = 300 K)条件下, 壁面热流值实验结果介于非催化、完全催化壁计算结果之间, 驻点区域与实验结果存在一定差距, 主要是由于传感器测量误差及壁面催化计算边界条件的不同导致.
-
国内外学者针对再入飞行器(orbital reentry experiment, OREX)[33]返回舱模型进行了一系列的数值及实验研究. 其中, OREX飞行器前体的几何构型分为三部分, 分别为球头、锥体(半锥角50°)、肩部. 飞行器头部半径为1350.0 mm, 头部顶点到肩部顶点轴向距离L = 1013.9 mm. 采用热化学非平衡模型开展高温钝体流场数值模拟, 计算工况选用再入飞行时间在7441.5—7501.5 s之间的7个来流条件, 具体参数如表3所列, 壁面温度条件为等温壁.
-
网格分布, 特别是壁面法向第一层网格高度对气动热仿真结果影响较大[34]. 为考核不同催化壁面条件下非平衡流场热流计算网格无关性, 采用了来流网格雷诺数
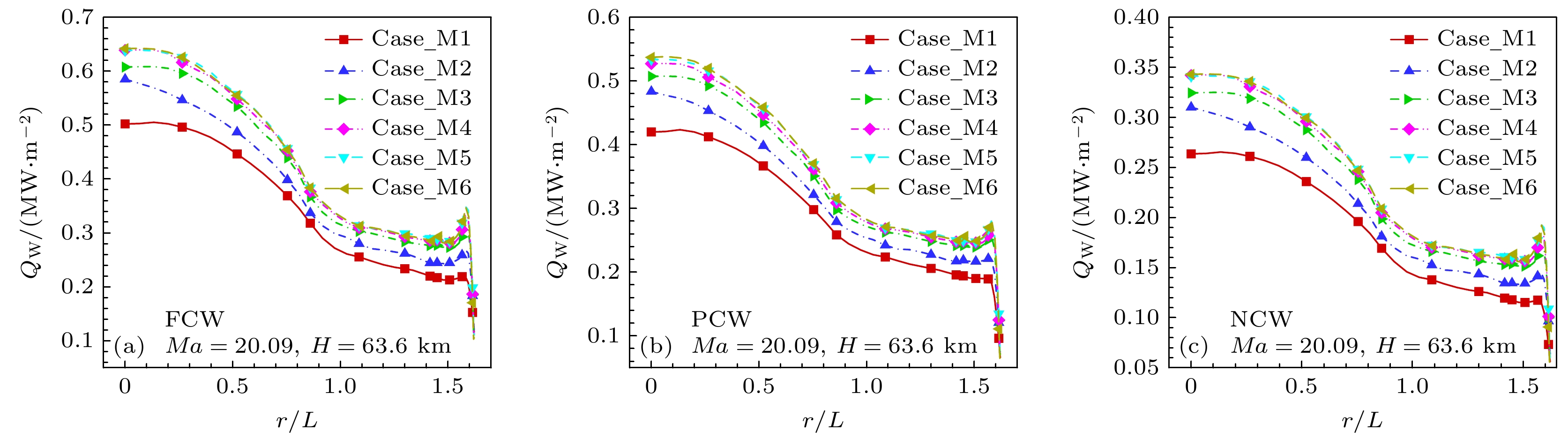
$R{e_{\Delta n, \infty }} = {{{\rho _\infty }{u_\infty }\Delta n} {/ } {{\mu _\infty }}}$ 作为判定准则, 其中,${\rho _\infty }$ ,${u_\infty }$ ,${\mu _\infty }$ 分别为来流密度、速度和黏性系数,$\Delta n$ 为壁面法向第一层网格高度. 基于上述准则, 共划分了六套网格, 具体参数如表4所列. 图3给出了基于热化学非平衡模型, OREX飞行器C3工况, 三类壁面催化条件下不同网格表面热流分布, 横轴表示无量纲法向距离, 参考长度为OREX头部顶点到肩部顶点轴向距离L. 结果表明, 不同催化壁面条件下, 非平衡热流计算网格收敛趋势基本一致, 固定壁面温度条件,$R{e_{\Delta n, \infty }} \leqslant 1$ 时, 非平衡表面热流变化不大(误差2%以内), 后续选用Case_M5网格开展计算分析. -
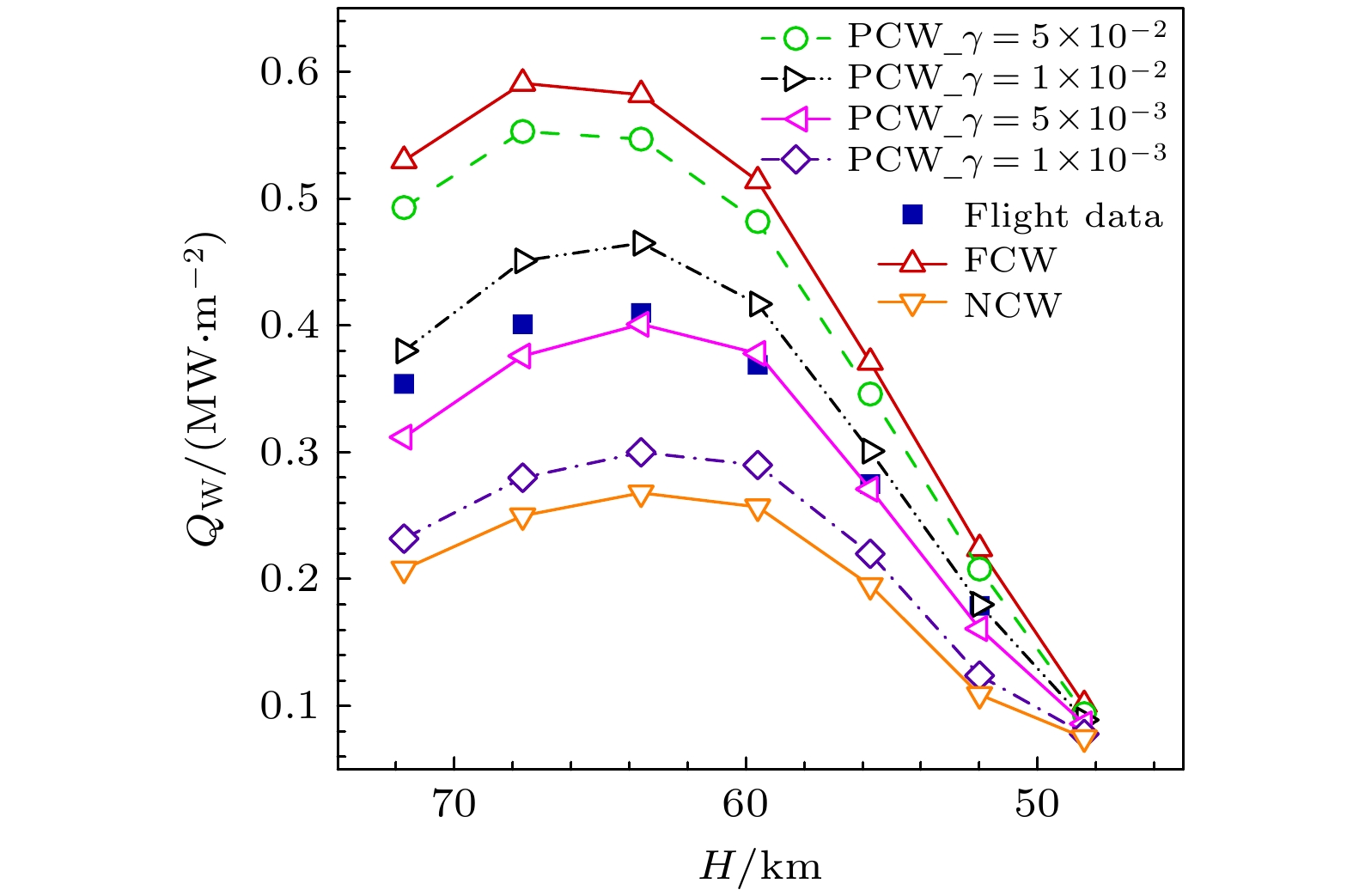
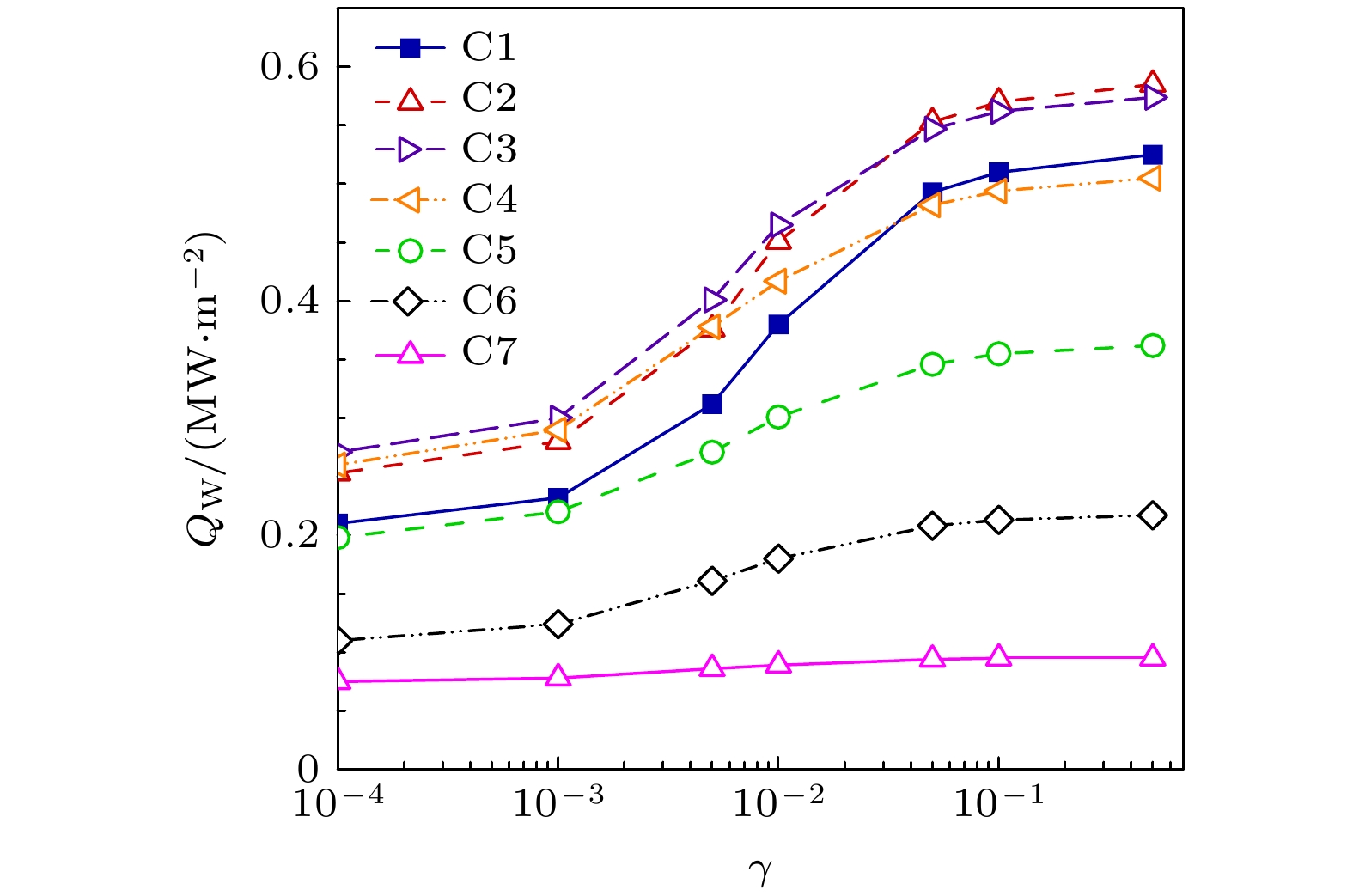
首先, 为研究壁面催化对高温非平衡热流的影响, 以OREX返回舱为对象开展数值分析, 计算工况为表3中7个飞行工况. 图4给出了驻点热流随飞行高度的变化曲线, 并与Doihara和Nishida[30]文献中飞行实验数据结果进行了对比分析. 由图4可以看出, 催化效应对返回舱驻点热流影响较大, 热流随飞行高度变化规律与飞行实验测量结果基本一致, 即随飞行高度的降低, 返回舱驻点热流呈现先增加后降低的趋势. 飞行高度63.6 km以上高空空气密度较低, 粒子碰撞概率较低, 大部分原子运动到壁面才由壁面催化效应作用完成复合, 具体表现为驻点热流受催化边界条件影响较大; 飞行高度63.6 km以下, 飞行实验数据与γ = 5×10–3有限催化模型表面热流计算结果符合较好(热流偏差低于2%), 一定程度验证了本文程序热化学非平衡流场有限催化计算模块的有效性. 图5为各飞行工况驻点热流随壁面催化复合系数γ取值变化计算结果. 由图5可以看出, 再入过程中, 驻点热流随催化复合系数变化曲线呈单调递增分布, 趋势与Doihara和Nishida[30]拟合结果一致.
表5给出了OREX飞行器C1—C7工况计算结果与驻点热流实验数据拟合得到的有效催化复合系数. 由表5可以看出, OREX飞行器低轨道弹道式再入条件下, 有效催化复合系数随飞行高度的降低呈现先减小(C4工况γ最低)后增加的趋势. 值得注意的是, 有效催化复合系数与壁面温度、压力等参数密切相关, 文中所述有效催化复合系数随飞行高度变化规律可能并不具有普适性, 需要后续进一步深入研究.
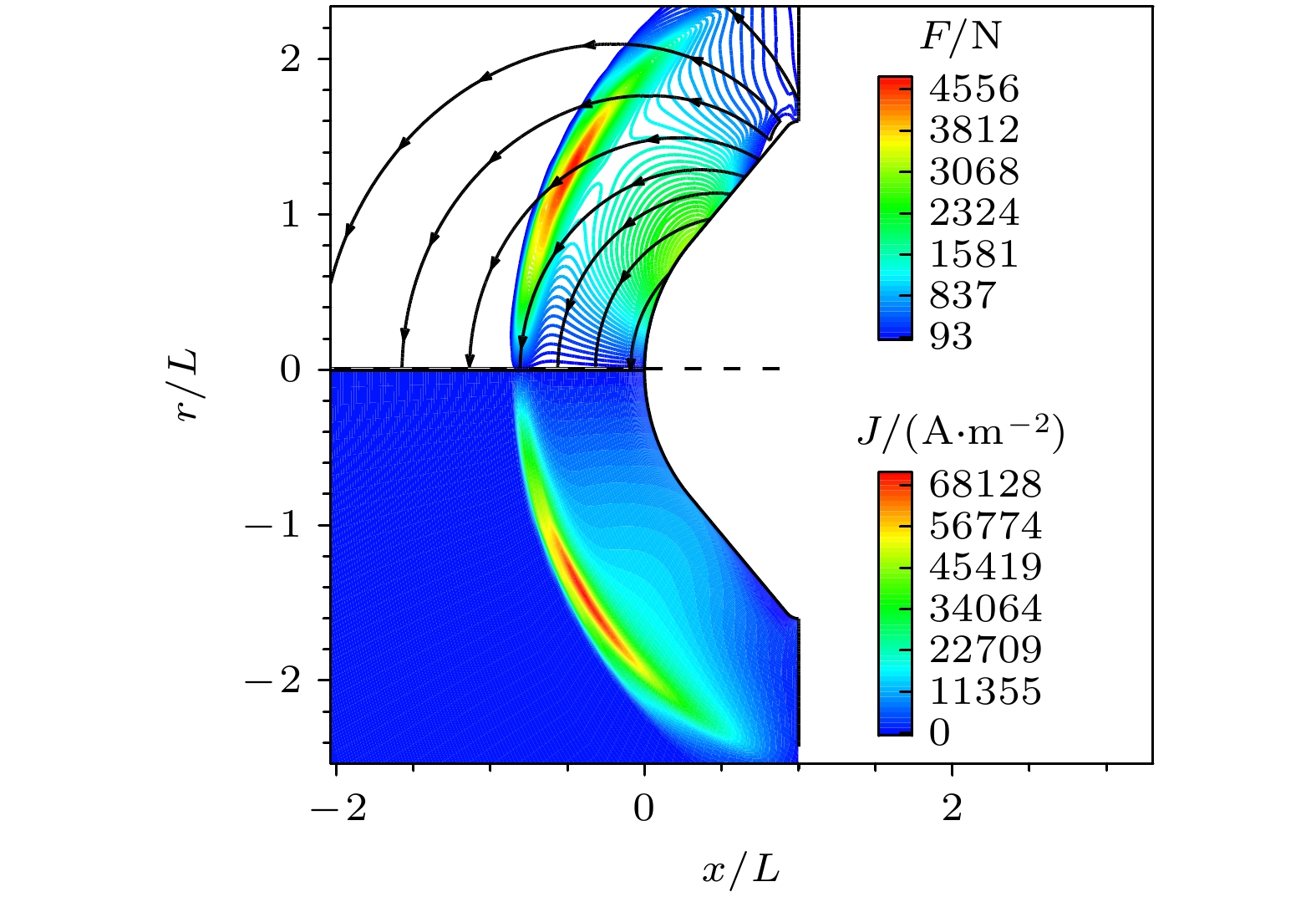
为分析壁面催化效应对大钝头飞行器高温 流场MHD控制效果, 选取高焓流场电离程度较 高的OREX返回舱C1工况进行磁控效果计算 分析. 外加磁场强度B0 = 0—1.20 T, 有限催化 壁条件采用SRE模型, 参考表5拟合结果, 给定 γ = 7.7×10–3. 图6表示磁场0.4 T作用下激波层内洛伦兹力及电流密度分布情况, 电流密度、洛伦兹力峰值区域集中在激波层外侧. 图7给出
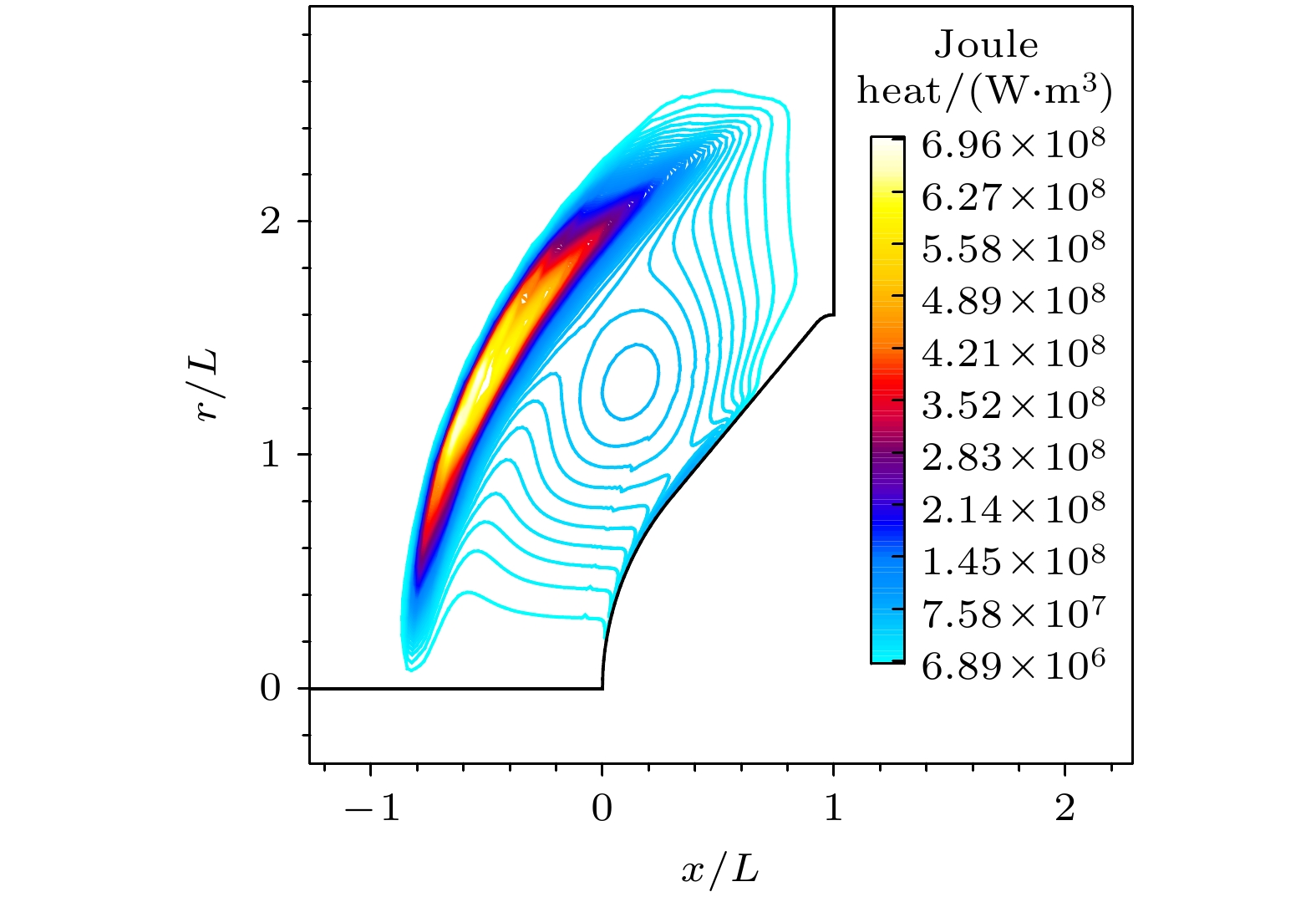
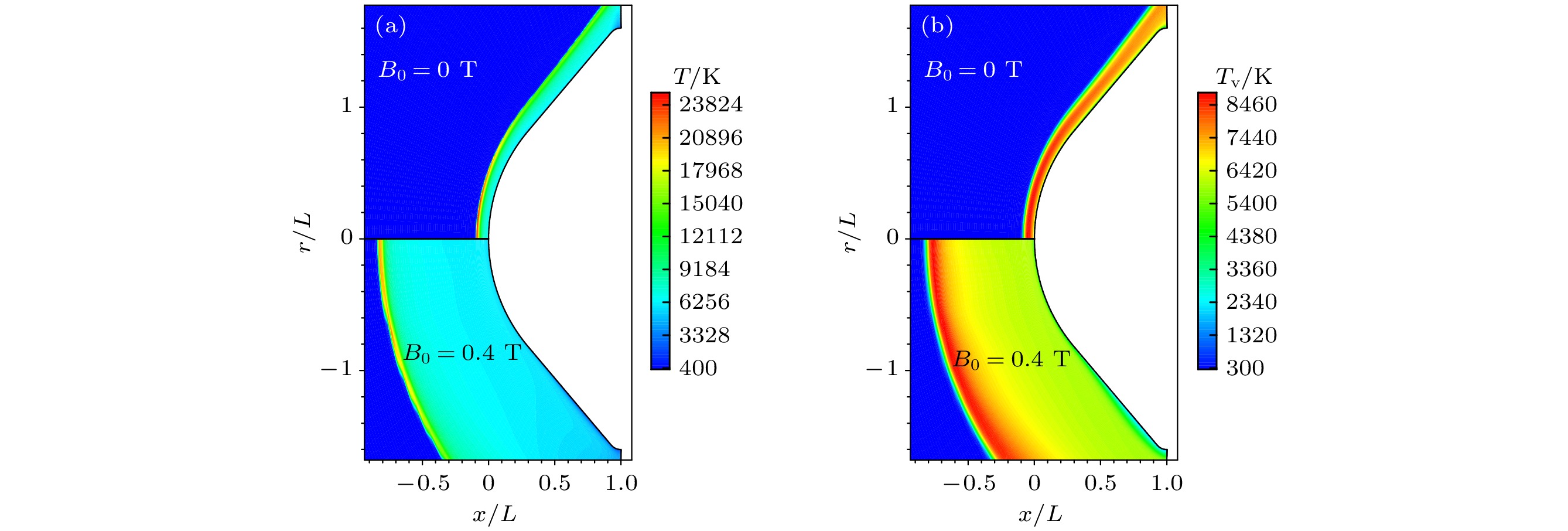
$ {\gamma _{{\text{ev}}}} $ = 0.1时振动焦耳热源项分布, 可以看出, 激波间 断附近焦耳热较大, 将一定程度影响激波层内振动温度分布.图8表示全催化壁面外加磁场对流场平动温度、振动温度分布的影响. 流场经激波压缩后形成高温区, 外加磁场作用下, 流场激波层内平动、振动温度峰值基本无变化, 激波面外推, 热力学平衡区域明显增大. 图9表示不同壁面催化条件、磁场条件下驻点线平动、振动温度分布. 由图9可以看出, 原子复合放热将提高近壁面温度梯度, 其中, B0 = 0 T时, 壁面催化条件改变壁面附近平动温度, 振动温度影响较小, 距驻点x = 5 mm位置, 完全催化壁平动温度比非催化壁平动温度增大20%; B0 = 0.4 T时, MHD相互作用下壁面附近平动、振动温度梯度明显低于无磁场工况.
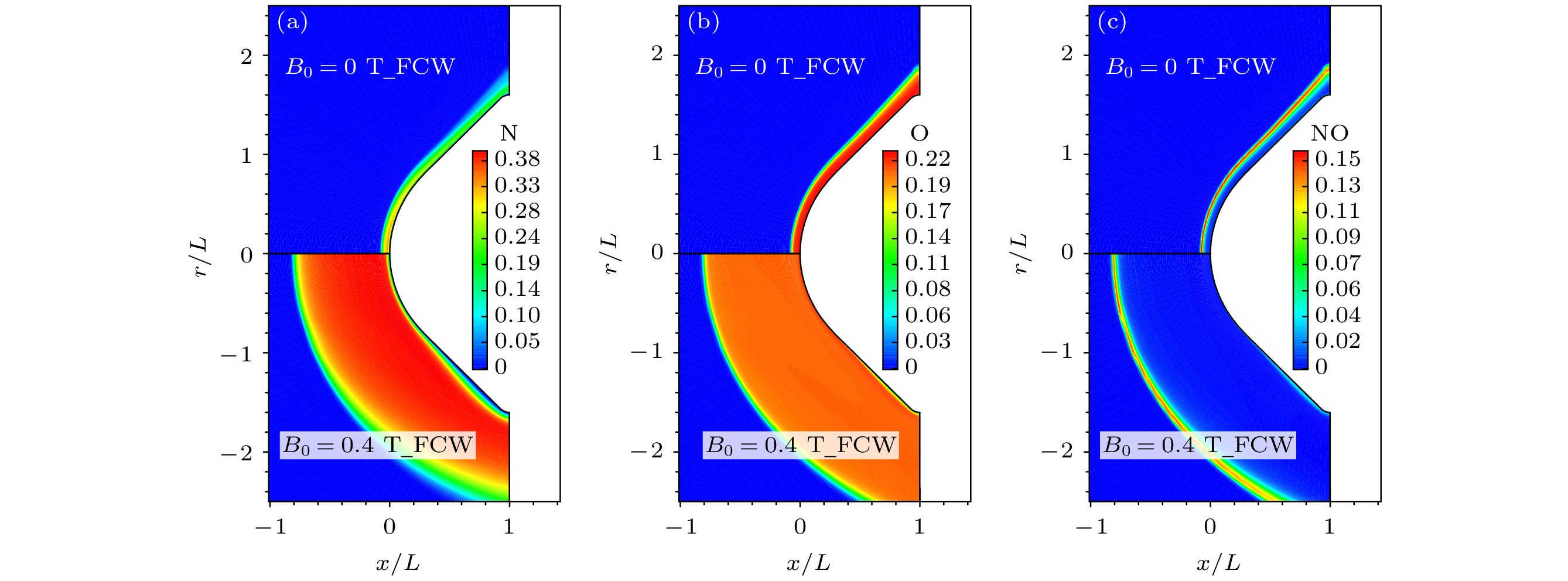
图10给出了不同外加磁场全催化壁面条件下激波层内组元质量分数分布云图, 磁场与流场相互作用产生的外推洛伦兹力使激波脱体距离增大, 流场高温区增大, 这意味着流场中化学高温离解反应有效时间更长, 氮气离解程度更大, 流场中氮原子的质量分数峰值更高; 而氧气由于离解温度较低, 部分区域在无磁场作用时就离解得较为完全, 因此氧原子质量分数峰值受MHD影响相对较小.
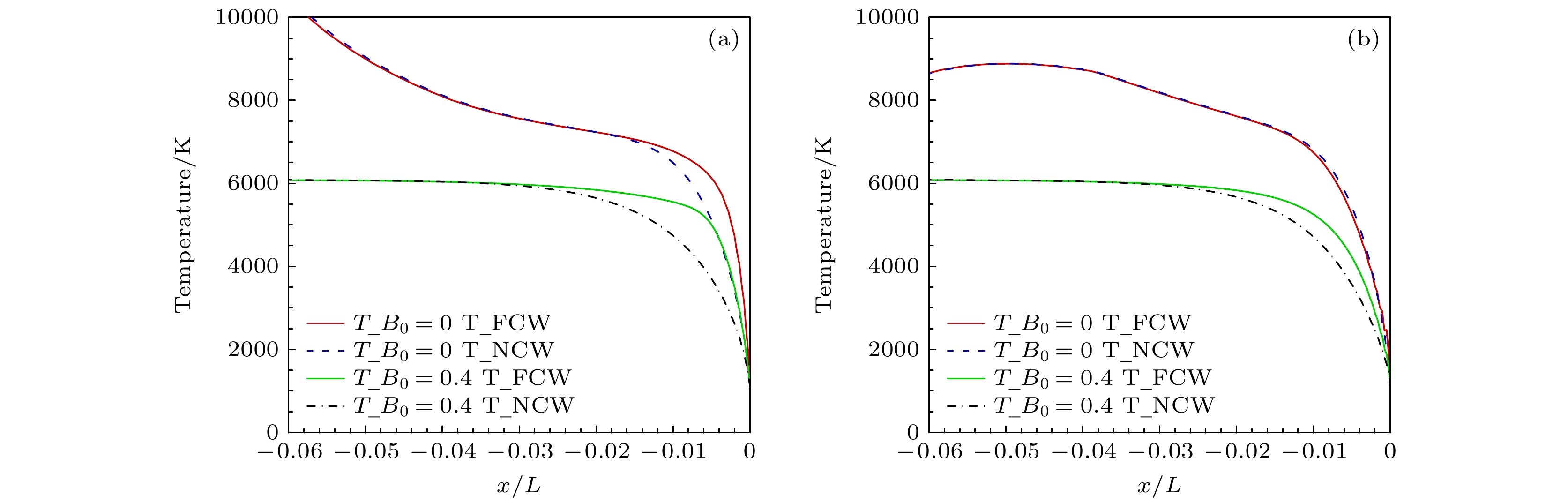
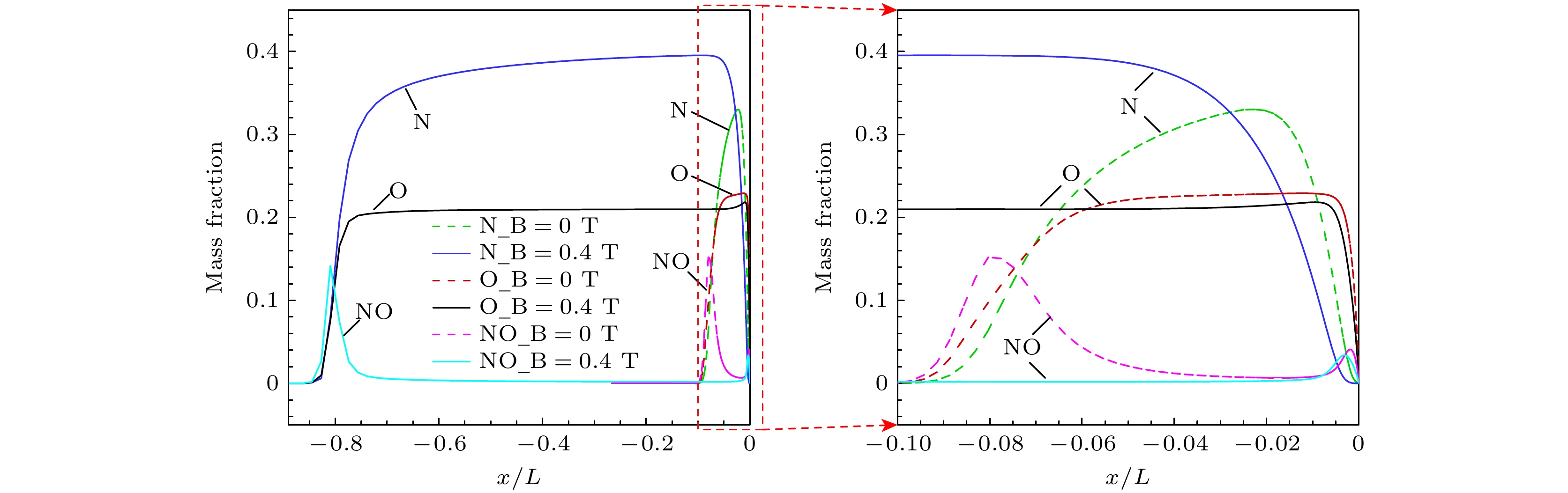
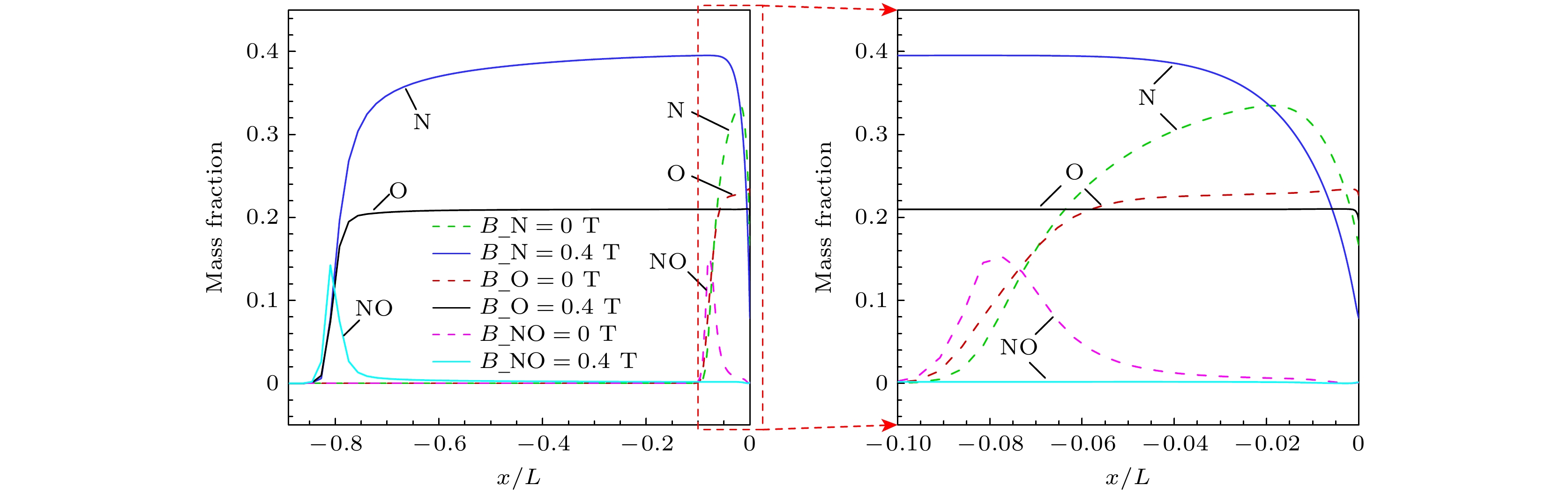
图11和图12给出了完全催化条件及部分催化条件下(γ = 7.7×10–3)驻点线氮原子、氧原子和NO分子质量分数. 由图11可见, 完全催化壁面条件下, NO分子质量分数峰值位置远离飞行器表面, 该组分是流动中化学反应的有效标志物, 表明洛伦兹力导致热力学平衡区域增大, 而壁面附近由于强复合反应, 有/无磁场作用氮原子和氧原子均无堆积. 从图12可以看出, 在催化复合系数较低(γ = 7.7×10–3)时, 由于壁面催化复合反应速率相对较慢, 壁面处氧原子、氮原子来不及复合, 有较大程度的堆积; 外加磁场作用下, 壁面氧原子、氮原子质量分数均低于无磁场工况. 此外, 不同催化壁面激波脱体距离增大均导致氧原子和氮原子扩散梯度降低.
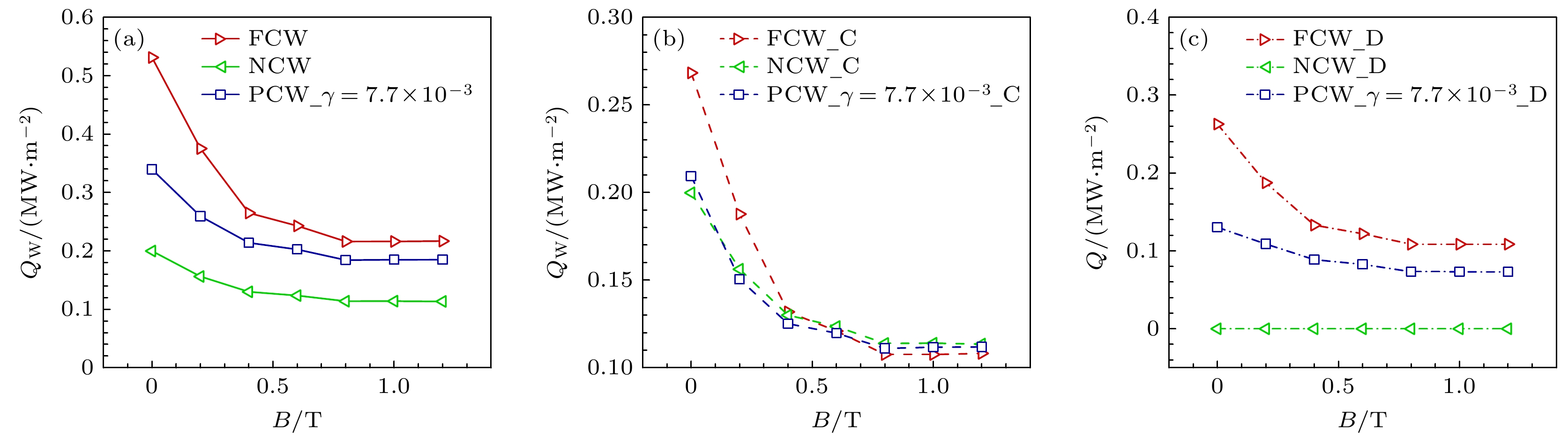
图13表示不同壁面催化条件下MHD流场压力分布轮廓图, 壁面催化复合过程对激波脱体距离MHD控制效果无影响. 图14给出了完全催化、有限催化及非催化壁面条件下驻点热流密度随磁场强度变化情况. 由图14(a)可知, 不同壁面催化条件驻点热流随磁场强度变化趋势一致, 再入工况Ma∞ = 25.9, H = 71 km条件, 外加磁场强度大于0.8 T时, “磁控饱和”现象明显, 即随着外加磁场强度的增加, 热流降低幅度减小, 逐步趋于稳定, 从经济高效的角度考虑, 外加磁场强度不宜过大. “磁控饱和”状态时, MHD控制效果从强至弱依次是全催化、有限催化、非催化壁面, 相对于无磁场工况驻点热流密度分别降低了59%, 46%, 43%. 由图14(b), (c)可知, “磁控饱和”状态下, 完全催化壁面, 驻点传导热流相对MHD控制前总热流下降的百分率为30.2%, 驻点扩散热流相对MHD控制前总热流下降的百分率为28.8%; 非催化壁面驻点传导热流相对MHD控制前总热流下降的百分率为43%; 有限催化壁面(γ = 7.7×10–3), 驻点传导热流相对MHD控制前总热流下降的百分率为29.1%, 驻点扩散热流相对MHD控制前总热流下降的百分率为16.9%. 综上所述, 磁控热防护机理方面, 与真实情况更接近的有限催化壁模型下, 外加磁场导致壁面氮原子、氧原子堆积量减少, 激波面外推导致氧原子、氮原子扩散梯度降低及壁面温度梯度降低, 进而同时降低壁面传导热流、扩散热流, 综合表现为MHD相互作用使壁面总热流密度降低.
-
本文综合考虑气体分子热力学激发、空气化学反应、壁面催化复合及电磁效应, 通过数值求解耦合磁场的高温热化学非平衡控制方程和壁面处能量、质量平衡关系, 分析了壁面催化条件对流场热流及MHD控制效果.
1) 考核结果表明, 来流网格雷诺数
$R{e_{\Delta n, \infty }} \leqslant 1$ 可以作为不同壁面催化条件下高温热化学非平衡热流计算的网格收敛判据. 此外, 分别基于膨胀管风洞实验流场球头算例、OREX返回舱飞行工况算例进行了数值校验与对比分析, 热化学非平衡流场气动热环境数值模拟结果与风洞地面实验结果、文献报道的飞行实验结果符合较好, 验证了本文程序各类催化模型下表面热流数值计算结果具有较高的可信度.2) 针对OREX返回舱外形, 分析了表面催化特性差异对不同飞行条件下气动热环境的影响规律. 低轨道弹道式再入条件下, 表面热流随催化复合系数的增加呈单调递增分布, 随飞行高度的降低, 再入飞行器驻点热流呈现先增加后降低的趋势.
3) 再入飞行器表面热流MHD作用效果与壁面催化效应密切相关, “电磁冷却”能力从大到小依次是全催化、有限催化、非催化壁面. 要定量分析磁控热防护效果, 须考虑壁面材料的有限催化特性, 结合焦耳热、洛伦兹力对温度传导热流、组分扩散热流影响程度, 共同研判飞行器总热流密度变化趋势.
壁面催化对高温非平衡流场磁控效果影响分析
Analysis of wall catalytic effects on magnetohydrodynamic control of high-temperature non-quilibrium flow field
-
摘要: 以轨道再入实验飞行器为研究对象, 采用热化学非平衡磁流体动力学模型对高超声速飞行器的表面热流进行数值模拟, 分析了不同飞行工况下壁面催化条件对气动热环境影响规律, 研究了外加磁场条件对热化学非平衡流场影响机制. 结果表明: 再入过程中, 表面热流随催化复合系数的增加呈单调递增分布, 壁面催化条件显著影响磁流体动力学控制效果, 总热流密度与壁面附近原子组分堆积量、扩散梯度及温度梯度密切相关. 外加磁场作用下, 壁面附近氧原子、氮原子组分堆积量减少; 洛伦兹力导致激波脱体距离增大, 组分扩散梯度、壁面温度梯度降低. 磁控热防护系统“电磁冷却”能力从大到小依次为全催化、有限催化、非催化壁面.Abstract: In the re-entry process of the vehicle into the atmosphere, the high-temperature environment, induced by the compression of the strong shock wave and viscous retardation, is created around the head of a vehicle. These generate a conductive plasma flow field, which provides a direct working environment for the application of magnetohydrodynaimic (MHD) control technology. Numerical simulations based on thermochemical non-equilibrium MHD model are adopted to analyze the surface heat flux of an orbital reentry experiment (OREX) vehicle. The influences of wall catalytic conditions on the aerothermal environment under different flight conditions are discussed. In addition, the control mechanism of an external magnetic field on high-temperature thermochemical non-equilibrium flow field is analyzed. The results show that the distribution of surface heat flux monotonically increases with the catalytic recombination coefficient increasing, and the surface heat flux rises and then drops with the flight altitude decreasing. Moreover, the wall catalytic properties significantly affect the efficiency of MHD control technology, and the total heat flux is closely related to the accumulation of atomic components, diffusion gradient and temperature gradient near the wall region. With an external magnetic field applied, the accumulation of oxygen atoms and nitrogen atoms near the wall can be reduced. Moreover, the Lorentz force can increase the shock standoff distance, and then reduce the component diffusion gradient and wall temperature gradient. Under three different wall catalytic conditions, the ability to control the surface heat flux MHD is ranked from strong to weak as fully catalyzed, partially catalyzed and non-catalyzed.
-
Key words:
- thermochemical non-equilibrium /
- magnetohydrodynamic /
- catalytic effect /
- numerical simulation .
-
-
图 1 高焓膨胀管球头脱体激波实验图像与计算结果对比
Figure 1. Comparison between high enthalpy expansion tube experimental images and calculated results of ball head detached shock wave.
图 2 不同催化壁面条件热流计算结果与实验结果对比
Figure 2. Comparison between calculated heat flux under different catalytic wall conditions and experimental results.
图 3 不同壁面催化条件下热流分布 (a) 完全催化; (b) 部分催化; (c) 非催化
Figure 3. Heat flux distribution under different wall catalytic conditions: (a) Full catalysis; (b) partially catalysis: (c) non-catalysis.
图 4 不同壁面催化模型OREX算例驻点热流计算与实验结果的比较
Figure 4. Comparison of computed stagnation point heat flux with OREX experimental results under different wall catalytic models.
图 5 OREX各工况驻点热流随壁面催化复合系数的变化曲线
Figure 5. Variation of stagnation point heat flux along wall catalytic recombination coefficient under various OREX conditions.
图 6 外加磁场对流场洛伦兹力及感应电流分布的影响(FCW)
Figure 6. Lorentz force and annular electric current distribution with an external magnetic field applied (FCW).
图 7 外加磁场对流场振动焦耳热源项分布的影响(FCW)
Figure 7. Vibrational Joule heat energy source term distribution with an external magnetic field applied (FCW).
图 8 全催化壁面外加磁场对流场温度分布的影响
Figure 8. Temperature contour distribution under fully catalytic wall conditions with an external magnetic field applied.
图 9 不同壁面催化条件、磁场条件对驻点线温度分布的影响 (a) 平动温度; (b) 振动温度
Figure 9. Temperature distribution along stagnation point line under different wall catalytic conditions with an external magnetic field applied: (a) Translational temperature; (b) vibrational temperature.
图 10 不同磁场强度作用下组元质量分数分布云图(FCW)
Figure 10. Species contour structure under different imposed magnetic field strengths (FCW).
图 11 不同磁场强度作用下驻点线组元质量分数分布(FCW)
Figure 11. Mass fraction of the species along stagnation point line under different imposed magnetic field strengths (FCW).
图 12 不同磁场强度作用下驻点线组元质量分数分布(PCW, γ = 7.7×10–3)
Figure 12. Mass fraction of the species along stagnation point line under different imposed magnetic field strengths (PCW, γ = 7.7×10–3)
图 13 不同壁面催化条件下MHD流场压力分布轮廓图
Figure 13. MHD flow field pressure profiles under different wall catalytic conditions.
图 14 不同壁面催化条件下驻点总热流密度随磁场强度的变化情况 (a) 总热流; (b) 传导热流; (c) 扩散热流
Figure 14. Variation of heat flux at stagnation point along magnetic field strength under different wall catalysis conditions: (a) Total heat flux; (b) conductive heat flux; (c) diffusion heat flux.
表 1 高温空气里主要发生的反应类型及正逆反应控制温度[22]
Table 1. Main types of reactions in high temperature air and control temperature of forward and reverse reactions[22].
反应类型 反应表达式 控制温度 离解反应 $ {\text{AB}} + {\text{M}} \rightleftarrows {\text{A}} + {\text{B}} + {\text{M}} $ $ 正向 : {T}_{\text{f}} = {T}^{\alpha }{T}_{v}^{1-\alpha };\text{ }逆向 : {T}_{\text{b}} = T $ 交换反应 $ \begin{array}{c} {\text{AB}} + {\text{C}} \rightleftarrows {\text{A}} + {\text{BC}} \\ {\text{A}}{{\text{B}}^ + } + {\text{C}} \rightleftarrows {{\text{A}}^ + } + {\text{BC}} \end{array} $ $ 正向 : {T}_{\text{f}} = T;\text{ }逆向 : {T}_{\text{b}} = T $ 一般电离反应 $ \begin{array}{c} {\text{A}} + {\text{B}} \rightleftarrows {\text{A}}{{\text{B}}^ + } + {{\mathrm{e}}^ - } \\ {\text{AB}} + {\text{M}} \rightleftarrows {\text{A}}{{\text{B}}^ + } + {{\mathrm{e}}^ - } + {\text{M}} \\ {{\text{A}}_2} + {{\text{B}}_2} \rightleftarrows {\text{A}}{{\text{B}}^ + } + {\text{AB}} + {{\mathrm{e}}^ - } \end{array} $ $ 正向 : {T}_{\text{f}} = T;\text{ }逆向 : {T}_{\text{b}} = {T}_{v} $ 电子碰撞电离反应 $ {\text{A}} + {{\mathrm{e}}^ - } \rightleftarrows {{\text{A}}^ + } + {{\mathrm{e}}^ - } + {{\mathrm{e}}^ - } $ $ 正向 : {T}_{{\mathrm{f}}} = {T}_{v};\text{ }逆向 : {T}_{\text{b}} = {T}_{v} $ 
下载: 导出CSV
表 2 高焓球头实验流场参数
Table 2. Flow field parameters of high enthalpy ball head experiment.
参数 符号 值 速度/(km·s–1) ${V_\infty }$ 7.99 来流温度/K T∞ 345 总焓/(MJ·kg–1) ${H_0}$ 32 来流密度/(kg·m–3) ρ∞ 1.77×10–4
下载: 导出CSV
算例 飞行时间 H/km ${\rho _\infty }$ /(kg·m–3)Ma ${T_\infty }$ /KC1 7441.5 71.73 6.489×10–5 23.89 214.98 C2 7451.5 67.66 1.143×10–4 22.22 225.99 C3 7461.5 63.60 1.960×10–4 20.09 237.14 C4 7471.5 59.60 3.255×10–4 17.55 248.12 C5 7481.5 55.74 5.203×10–4 14.71 258.74 C6 7491.5 51.99 8.065×10–4 11.80 268.20 C7 7501.5 48.40 1.253×10–3 9.06 270.65
下载: 导出CSV
表 4 OREX飞行器计算网格
Table 4. Computational grid for OREX vehicle.
网格 $\Delta n$ /(10–6 m)$R{e_{\Delta n, \infty }}$ Case_M1 252.00 20 Case_M2 126.00 10 Case_M3 50.00 4 Case_M4 25.00 2 Case_M5 7.20 0.6 Case_M6 3.60 0.3
下载: 导出CSV
表 5 OREX各工况与实验数据拟合得到的驻点有效催化复合系数
Table 5. Effective recombination coefficient at stagnation point in accordance with experimental data under various OREX conditions.
工况 H /km 驻点热流实验结果 $ Q_{\text{w},\exp}/(\text{MW}{\cdot}\text{m}^{-2}) $ 实验数据
拟合有效
催化系数
γ/10–3C1 71.73 0.354 7.7 C2 67.66 0.401 6.3 C3 63.60 0.410 5.5 C4 59.60 0.369 4.2 C5 55.74 0.275 5.5 C6 51.99 0.179 9.6 C7 48.40 0.093 36.0
下载: 导出CSV
-
[1] 罗仕超, 张志刚, 柳军, 龚红明, 胡守超, 吴里银, 常雨, 庄宇, 李贤, 黄成扬 2023 力学学报 55 2439 doi: 10.6052/0459-1879-23-196 Luo S C, Zhang Z G, Liu J, Gong H M, Hu S C, Wu L Y, Chang Y, Zhuang Y, Li X, Huang C Y 2023 Chin. J. Theor. Appl. Mech. 55 2439 doi: 10.6052/0459-1879-23-196 [2] Cui Z L, Zhao J, Yao J 2022 Chin. J Aeronaut. 35 56 doi: 10.1016/j.cja.2021.11.025 [3] Bonelli F, Pascazio G, Colonna G 2021 Phys. Rev. Fluids 6 033201 doi: 10.1103/PhysRevFluids.6.033201 [4] Davide N, Francesco B, Gianpiero C 2022 Acta Astronaut. 201 247 doi: 10.1016/j.actaastro.2022.09.017 [5] Yu M H, Qiu Z Y, Takahashi Y 2023 Phys. Fluids 35 056106 doi: 10.1063/5.0149660 [6] 周凯, 彭俊, 欧东斌 2020 中国科学: 技术科学 50 1095 doi: 10.1360/SST-2019-0396 Zhou K, Peng J, Ou D B 2020 Sci. Sin. Technol. 50 1095 doi: 10.1360/SST-2019-0396 [7] 丁明松, 董维中, 高铁锁, 江涛, 刘庆宗 2018 航空学报 39 121588 Ding M S, Dong W Z, Gao T S, Jiang T, Liu Q Z 2018 Acta Aeronaut. Astronaut. Sin. 39 121588 [8] 苗文博, 程晓丽, 艾邦成 2011 空气动力学学报 29 476 doi: 10.3969/j.issn.0258-1825.2011.04.013 Miao W B, Cheng X L, Ai B C 2011 Acta Aerodyn. Sin. 29 476 doi: 10.3969/j.issn.0258-1825.2011.04.013 [9] 苗文博, 程晓丽, 艾邦成, 沈清 2013 宇航学报 34 442 Miao W B, Cheng X L, Ai B C, Sheng Q 2013 J. Astronaut. 34 422 [10] 莫凡, 王锁柱, 高振勋 2021 气体物理 6 1 Mo F, Wang T Z, Gao Z X 2021 Phys. Gases 6 1 [11] 梁伟, 金华, 孟松鹤, 杨强, 曾庆轩, 许承海 2021 宇航学报 42 409 doi: 10.3873/j.issn.1000-1328.2021.04.002 Liang H, Jing H, Meng S H 2021 J. Astronaut. 42 409 doi: 10.3873/j.issn.1000-1328.2021.04.002 [12] 罗凯, 汪球, 李逸翔, 李进平, 赵伟 2021 力学学报 53 1515 Luo K, Wang Q, Li J Y, Li J P, Zhao W 2024 Chin. J. Theor. Appl. Mech. 53 1515 [13] Peng S, Jin K, Zheng X 2022 AIAA J. 60 6536 doi: 10.2514/1.J061968 [14] 陈刚, 张劲柏, 李椿萱 2008 力学学报 40 752 Chen G, Zhang J B, Li C X 2008 Chin. J. Theor. Appl. Mech. 40 752 [15] 丁明松, 江涛, 刘庆宗, 董维中, 高铁锁, 傅杨奥骁 2019 航空学报 40 123009 Ding M S, Jiang T, Liu Q Z, Dong W Z, Gao T S, Fuyang O X 2019 Acta Aeronaut. Astronaut. Sin. 40 123009 [16] Heather A M, Nikos N 2021 Phys. Fluids 34 107114 [17] 滕子昂, 周志峰, 张智超, 许珂, 高振勋 2024 气动研究与试验 2 86 Teng Z A, Zhou Z F, Zhang Z C, Xu K, Gao Z X 2024 Aerodynamic Research & Experiment 2 86 [18] Gupta R N, Yos J M, Thompson R, Lee K P 1990 NASA RP-1232 [19] Shang J J S, Yan H 2020 Adv. Aerodyn. 2 19 doi: 10.1186/s42774-020-00041-y [20] Candler G V 2019 Annu. Rev. Fluid Mech. 51 379 doi: 10.1146/annurev-fluid-010518-040258 [21] Zhang W, Zhang Z, Wang X 2022 Adv. Aerodyn. 4 38 doi: 10.1186/s42774-022-00125-x [22] 蒋浩, 车学科, 张天天, 龚陟阳, 柴振霞, 柳军 2023 空天技术 3 40 Jiang H, Che X K, Zhang T T, Gong Z Y, Chai Z X, Liu J 2023 Aerosp. Technol. 3 45 [23] Park C, Griffith W 1991 Phys. Today 44 98 [24] Gnoffo P A, Gupta R N, Shinn J L 1989 NASA/TP–2867 [25] 李鹏, 陈坚强, 丁明松, 梅杰, 何先耀, 董维中 2021 航空学报 42 726400 doi: 10.7527/S1000-6893.2021.25718 Li P, Cheng J Q, Ding M S, Mei J, He X Y, Dong W Z 2021 Acta Aeronaut. Astronaut. Sin. 42 726400 doi: 10.7527/S1000-6893.2021.25718 [26] MacLean M, Marineau E, Parker R, Dufrene A, Holden M, DesJardin P 2013 J. Spacecraft Rockets 50 470 doi: 10.2514/1.A32327 [27] 莫凡, 高振勋, 蒋崇文, 李椿萱 2021 中国科学: 物理学 力学 天文学 51 104703 doi: 10.1360/SSPMA-2021-0110 Mo F, Gao Z X, Jiang C W, Li C X 2021 Sci. Sin. Phys. Mech. Astron. 51 104703 doi: 10.1360/SSPMA-2021-0110 [28] Luo S C, Wu L Y, Chang Y 2023 Aerosp. Sci. Technol. 132 108041 doi: 10.1016/j.ast.2022.108041 [29] 李开 2017 博士学位论文 (长沙: 国防科技大学) Li K 2017 Ph. D. Dissertation (Changsha: National University of Defense Technology [30] Doihara R, Nishida M 2002 Shock Waves 11 331 doi: 10.1007/s001930200119 [31] 罗仕超, 吴里银, 常雨 2022 物理学报 71 214702 doi: 10.7498/aps.71.20220941 Luo S C, Wu L Y, Chang Y 2022 Acta Phys. Sin. 71 214702 doi: 10.7498/aps.71.20220941 [32] 罗仕超, 胡守超, 柳军, 吴里银, 孔小平, 常雨, 吕明磊 2024 中国科学: 物理学 力学 天文学 54 274711 doi: 10.1360/SSPMA-2023-0356 Luo S C, Hu S C, Liu J, Wu L Y, Kong X P, Chang Y, Lü M L 2024 Sci. Sin. Phys. Mech. Astron. 54 274711 doi: 10.1360/SSPMA-2023-0356 [33] Fujino T, Shimosawa Y 2016 J. Spacecraft Rockets 53 1 doi: 10.2514/1.A33545 [34] 张智超, 高振勋, 蒋崇文, 李椿萱 2015 北京航空航天大学学报 41 594 Zhang Z C, Gao Z X, Jiang C W. Li C X 2015 J. Beijing Univ. Aeronaut. Astronaut. 41 594 -
计量
- 文章访问数: 305
- HTML全文浏览数: 305
- PDF下载数: 1
- 施引文献: 0