首页
登录
注册
下载:
-
引力波的直接探测开启了研究宇宙的崭新窗口, 对推动多信使天文学等学科的发展以及深入理解宇宙起源和演化具有重要的科学意义. 由于宇宙各种天文事件产生的引力波类型各异, 其频段跨度较大, 可覆盖10–16—104 Hz[1]. 针对不同波段, 探测方法也不同: 基于迈克耳孙干涉仪的地基引力波探测, 主要探测频段在10 Hz—10 kHz[2–4]; 基于太空干涉仪的空间引力波探测, 主要探测频段在1×10–4 —1 Hz[5–7]; 基于脉冲星计时阵列的脉冲星探测, 主要探测频段在1×10–9—1×10–7 Hz[8,9]. 其中, 地基引力波探测装置在2015年人类首次观测到双黑洞合并事件GW150914的引力波信号后[10], 已经探测到数百个引力波信号.
地基引力波探测都采用大型激光干涉仪对引力波进行精密测量, 下一代地基引力波探测计划, 比如ET (Einstein telescope)[11], CE (cosmic explorer)[12]以及国内谛听计划[13,14], 都将通过一系列如压缩降噪[15]、低温系统新技术以及高真空系统[16], 增大探测灵敏度从而探测到更加微弱的信号, 进一步探索宇宙的奥秘[17,18]. 但因其测量灵敏度直接受激光光源强度噪声的影响, 想要进一步增大探测灵敏度必须先抑制激光强度噪声. aLIGO探测装置中, 对高功率1064 nm波段激光相对强度噪声要求为≤2.0×10–9 Hz–1/2@10 Hz, 4.0×10–9 Hz–1/2@20 Hz, ≤4.0×10–7 Hz–1/2@10 kHz[19]. 为了能准确评估相应频段激光相对强度噪声, 需要构建噪声低于上述指标的激光光源强度噪声评估系统以便进一步进行噪声抑制.
2004年, Rollins等[20]通过主动反馈将10 W输入的全固态激光器相对强度噪声在10 Hz处抑制到10–8 Hz–1/2; 2009年, Patrick等[21]将相对强度噪声在10 Hz处抑制到2.4×10–9 Hz–1/2; 2017 年, Jonas等[22]实现在百kHz频段内2.6×10–9 Hz–1/2的噪声抑制. 随着精密测量精度的提升, 对激光光源的更低噪声需求与日俱增, 同时需要保证噪声测量评估准确性及提升光电反馈增益性能, 这也就需要研发更低本底噪声的测试系统进行噪声评价与表征. 在强度噪声激光强度噪声评估方面, 2022年山西大学郑耀辉团队采用了对数轴功率谱密度(Logarithmic frequency axis Power Spectral Density, LPSD[23])估计算法, 在空间引力波探测频段内实现了评估流程架构[24]. 在地基引力波方面, 2022年Fabian和 Benno[25]提出10 Hz—10 kHz范围内激光相对强度噪声评估系统, 在100 Hz处本底噪声达到 2×10–9 Hz–1/2.
本文基于极低噪声的光电探测器与FFT分析仪进行噪声信号采集, 并使用LabVIEW编写仪器控制系统, 将其与基于MATLAB编写的谱线拼接程序集成打包生成应用程序, 构建起应用于地基引力波10 Hz—10 kHz探测频段的噪声评估系统, 并对其中的仪器本底噪声、光电探测器电子学噪声以及自由运转下的激光强度噪声进行噪声评估测试. 实验结果表明: 前置放大器以及动态信号分析仪的整体电子学噪声为3.8×10–9 Hz–1/2@(10 Hz—10 kHz); 在20 Hz—10 kHz频段范围内满足aLIGO指标需求; 光电探测器电子学噪声为
$ 1.4 \times {10^{ - 8}} \;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 Hz &$ 8.1 \times {10^{ - 9}} \;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 kHz; 进一步通过对标准信号源及多个商用激光器的激光强度噪声进行评估测量, 使用本系统对商用NKT激光器测试得到其相对强度噪声为1.2×10–6 Hz–1/2@10 Hz & 4.2×10–7 Hz–1/2@10 kHz, 验证了该套评估系统的准确性及通用性, 说明了该噪声评估系统具有准确度高、操作性强、实时处理效率高等优点, 可为地基引力波探测中激光强度噪声评估提供重要的探测方法及测试系统, 也为后续进行主动反馈强度噪声抑制提供了软硬件基础. -
激光强度噪声测试评估系统包括低噪声光电探测、低噪声前置放大、动态信号分析以及上位机软件操控算法编程, 其主体架构如图1所示. 首先, 包含激光的实时功率信息的光信号通过光电二极管转化为光电流信号, 通过跨阻电路, 将光电二极管得到的光电流信号转化为电压信号并进行放大, 再使用减法器将其与基准电压源提供的基准信号进行减法运算提取出误差信号, 通过低噪声前置放大对高频成分进行滤波放大, 之后通过商用动态信号分析仪(SR760)以及自研算法进行相应数据处理及噪声评估.
光电探测器作为激光强度噪声转换的首要器件, 其电子学噪声及增益特性直接影响激光强度噪声的评估. 光电探测器中光电二极管的响应度记为Res, 入射激光二极管的光功率为P, 则产生的光电流I为
光电流信号I的散粒噪声极限可由其谱密度
$ {I_{{\text{snl}}}} $ 表征:其中e为单电子电荷量. 光电流经过跨阻放大(TIA)电路进行电流-电压转换, 设跨阻阻值为R, 此时可以计算电压信号为
此时,
$ {V_{{\text{out}}}} $ 包含激光功率信号的直流项和交流噪声项, 可记为因为, 地基引力波探测中要求激光噪声非常小,
$ \Delta V $ 需达到10–9量级, 一般商用仪器等评估手段无法直接进行测量和评估, 所以需要利用滤波放大电路或者低噪前置放大器将直流信号滤除, 并放大交流信号, 记放大倍数为G1, 则放大器输出电压信号$ V_{{\text{out}}}^{{\text{BW}}} $ 为其中N1为前置放大器引入的额外噪声, 一般情况下需要G1足够大, 以便忽略N1影响. 经过放大后的信号噪声水平远大于动态信号分析仪的电子学噪声, 故可以直接通过动态信号分析仪采集数据, 得到电压信号功率密度谱结果, 之后除以G1, 得到噪声项
$ \Delta V $ 的功率密度谱.激光相对强度噪声(RIN)定义为激光功率波动与激光平均功率之比:
激光相对强度噪声的谱密度通常定义为其时域的傅里叶变换. 激光相对强度噪声通常用噪声谱密度进行表征:
由于光电流散粒噪声与光电流大小成反关联关系, 因此选择具有较高饱和光功率特性的光电二极管以及高饱和电压的光电探测电路, 避免所探测的激光相对强度噪声受散粒噪声的限制. 自研探测器选用Hamamatsu G12180-130 A光电二极管, 暗电流0.8 nA (Max), 响应度1.1 A/W@1550 nm, 响应范围900—1670 nm.
由于频段跨度大, 需要在对数轴上绘制图像, 传统频谱分析仪测量结果中数据点在频率轴上为线性分布, 导致对数轴上频段跨度越大谱线拖尾现象越严重, 影响噪声准确评估[26], 而在本文测试方法中, 将分析频率10 Hz—10 kHz分成3个子分析频率段, 分别为10—100 Hz, 100—1000 Hz以及1—10 kHz, 针对每段分析频率, 每段固定采集400个点, RBW分别为0.4 Hz, 3.9 Hz, 31.25 Hz. 之后根据算法将三段分析频率的噪声结果按(8)式
进行拼接[27,28], 可以减轻拖尾现象的影响. 这里,
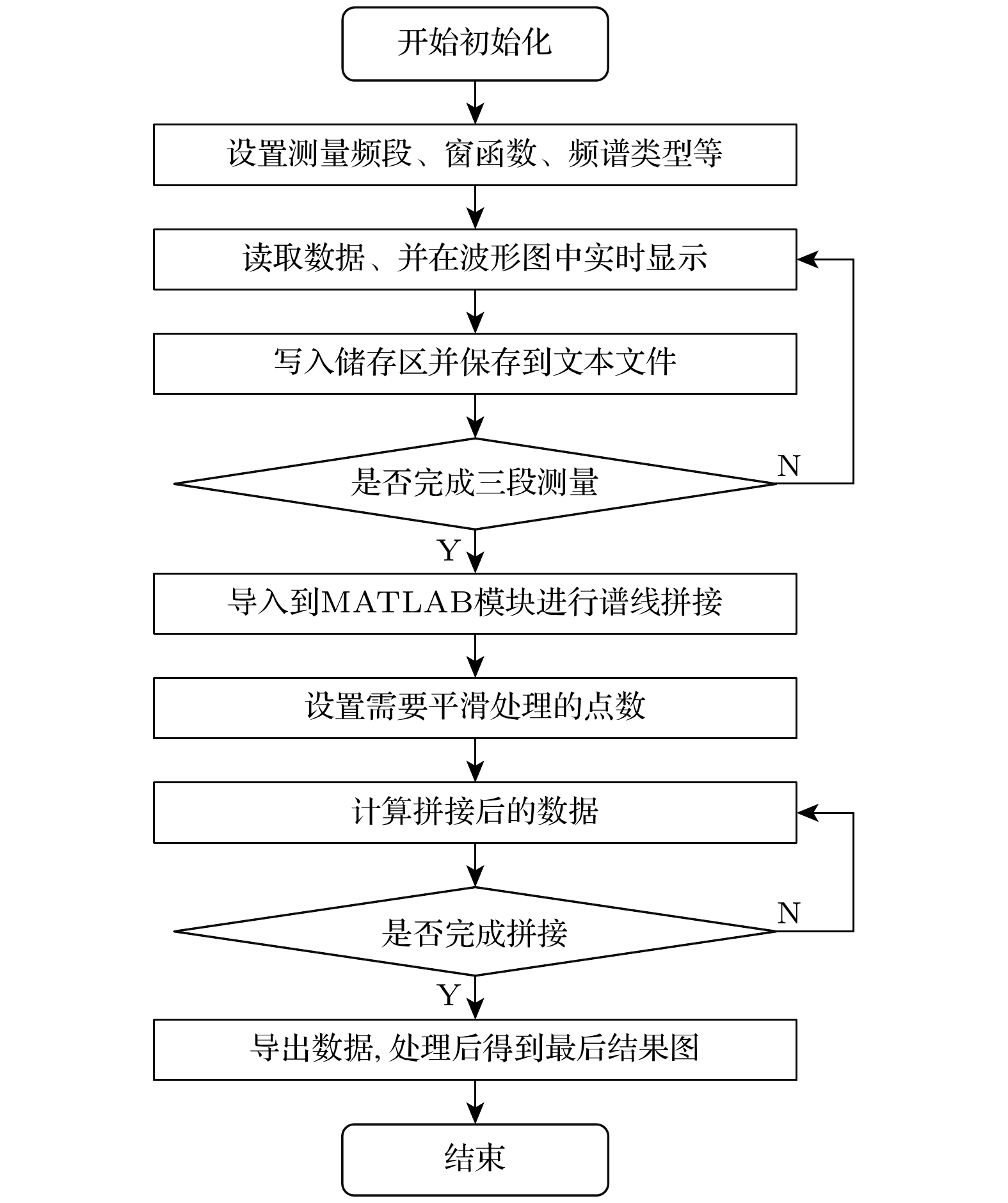
$f_{\rm max} $ 与$f_{\rm min} $ 分别为两段频谱交叠区域频率的最大值与最小值,$S_{\rm H}(f) $ 与$S_{\rm L}(f) $ 分别为两段频谱交 叠区域幅值的最大值与最小值, f为拼接后的频 率. 此外, 此研究需要软件对仪器进行实时交互, 从而进行控制及数据采集导出. 基于IEEE488.2协议使用LabVIEW并集成MATLAB包编写程序, 制作成应用程序, 采用通用接口总线(GPIB)将仪器与上位机链接, 从而做到使用计算机进行远程多仪器操控. 图2为LabVIEW程序流程图, 首先进行GPIB初始化及选址, 设置默认地址, 然后在 LabVIEW前面板上设置好采集频段、窗函数、频谱类型等参数后便可以进行数据采集与存储, 每次采集到的数据可在前面板波形图上实时显示, 并存储到缓存区. 重复以上过程并采集到3组或以上的数据段后程序结束. 之后将缓存的数据导入到内置MATLAB脚本中进行频谱拼接.以3份数据段举例, 将信号功率谱(power spectral density , PSD)谱分为1—100 Hz, 100—1000 Hz, 1—10 kHz进行采集, 然后采用(8)式进行光滑处理, 最后进行拼接, 并且集成为一个MATLAB程序, 使用Origin软件进行绘图. 这为地基引力波噪声评估系统提供了一套具有方便快捷、通用性强的仪器控制程序.
通过LabVIEW算法实现内存中数据组的分析, 包括实时滚动显示、极值分析、平均值及方差估算等时域上的数据分析; 与此同时将数据以及采样时间进行文本保存, 做好数据备份操作; 如果采集数据点达到设置的数据总量N, 则时域数据采集及分析结束, 否则继续采集数据; 在达到数据总量N基础上, 将全部数据传送到频域数据处理程序模块, 进行频域分析, 从而形成一套具有通用性、高精度、操作简易、实时处理等优势的激光噪声探测及评估系统.
-
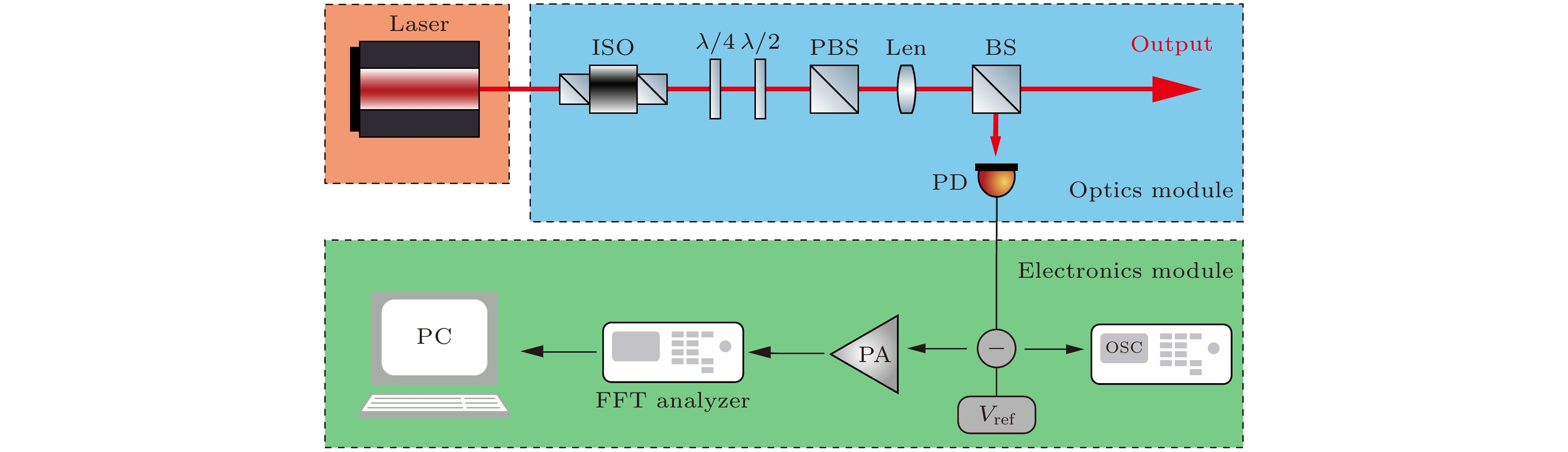
面向第三代地基引力波探测, 我们正在研制低噪声百瓦级1550 nm波段激光系统, 其中低噪声种子源是实现大功率激光系统的基础. 利用构建的激光强度噪声测试评估系统对不同1550 nm种子激光进行噪声测试与评估. 实验装置如图3所示. 首先, 激光器输出自由空间传播的1550 nm激光, 经准直头和两个1550 nm高反镜准直光束后, 通过λ/4, λ/2波片和一个偏振分光棱镜进行偏振纯化及功率调节, 调整λ/2波片角度可以进行主光束功率调节. 经透镜聚焦后, 再通过分束镜分光, 使得激光由透镜聚焦到光电探测器的光电二极管光敏面上, 并进行光电转换. 光电二极管光敏面与激光入射方向呈约60°夹角, 并用吸收片吸收光敏面的微弱反射光, 防止光敏面背向反射光发生散射影响探测准确性. 将探测器输出的电压信号输入到示波器中测量得到探测器的直流电压; 设置基准源电压与探测器直流电压相同, 通过减法器进行减法运算后得到交流噪声信号, 之后将交流噪声信号输入到测试仪器中并通过上位机控制处理, 得到最终结果.
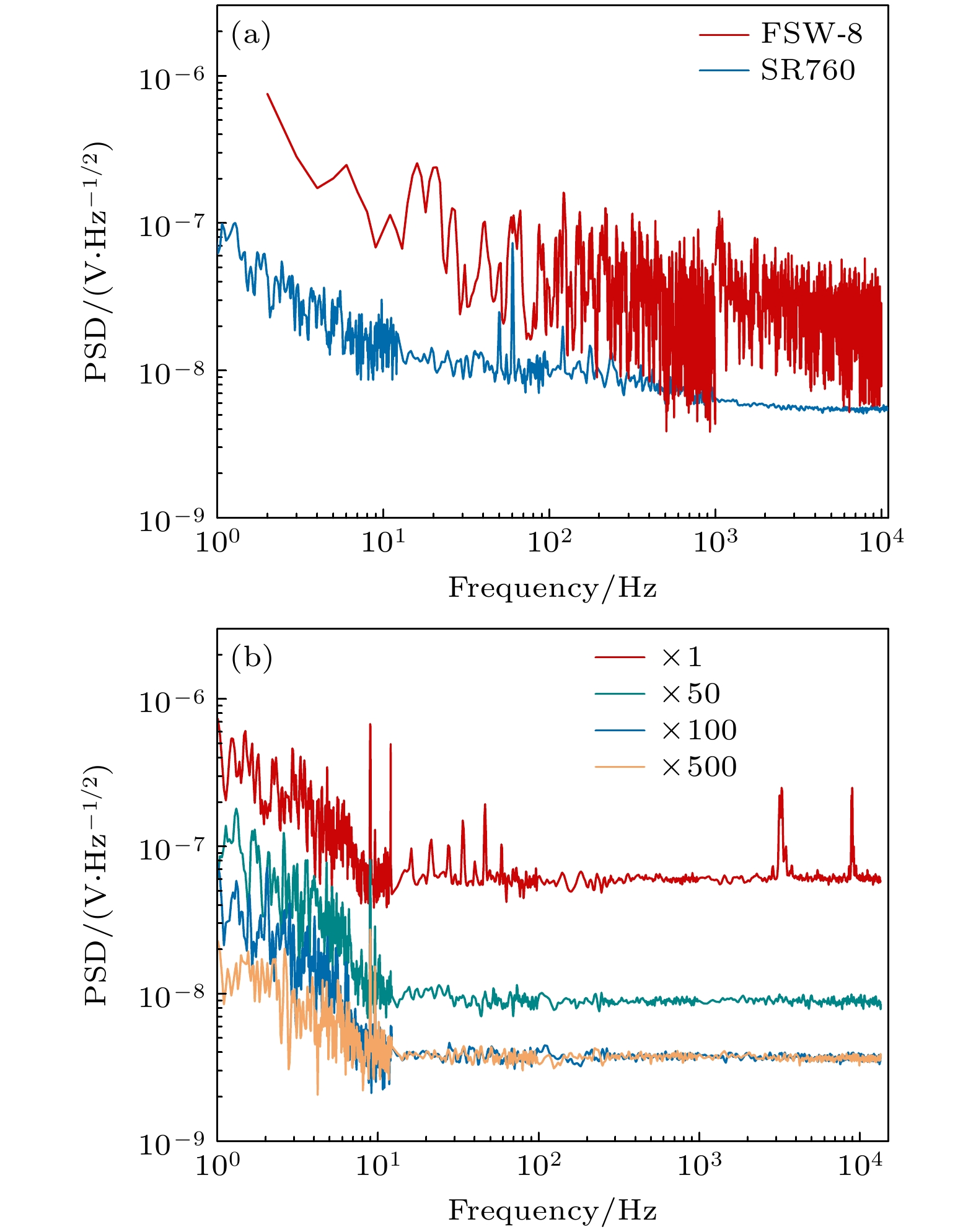
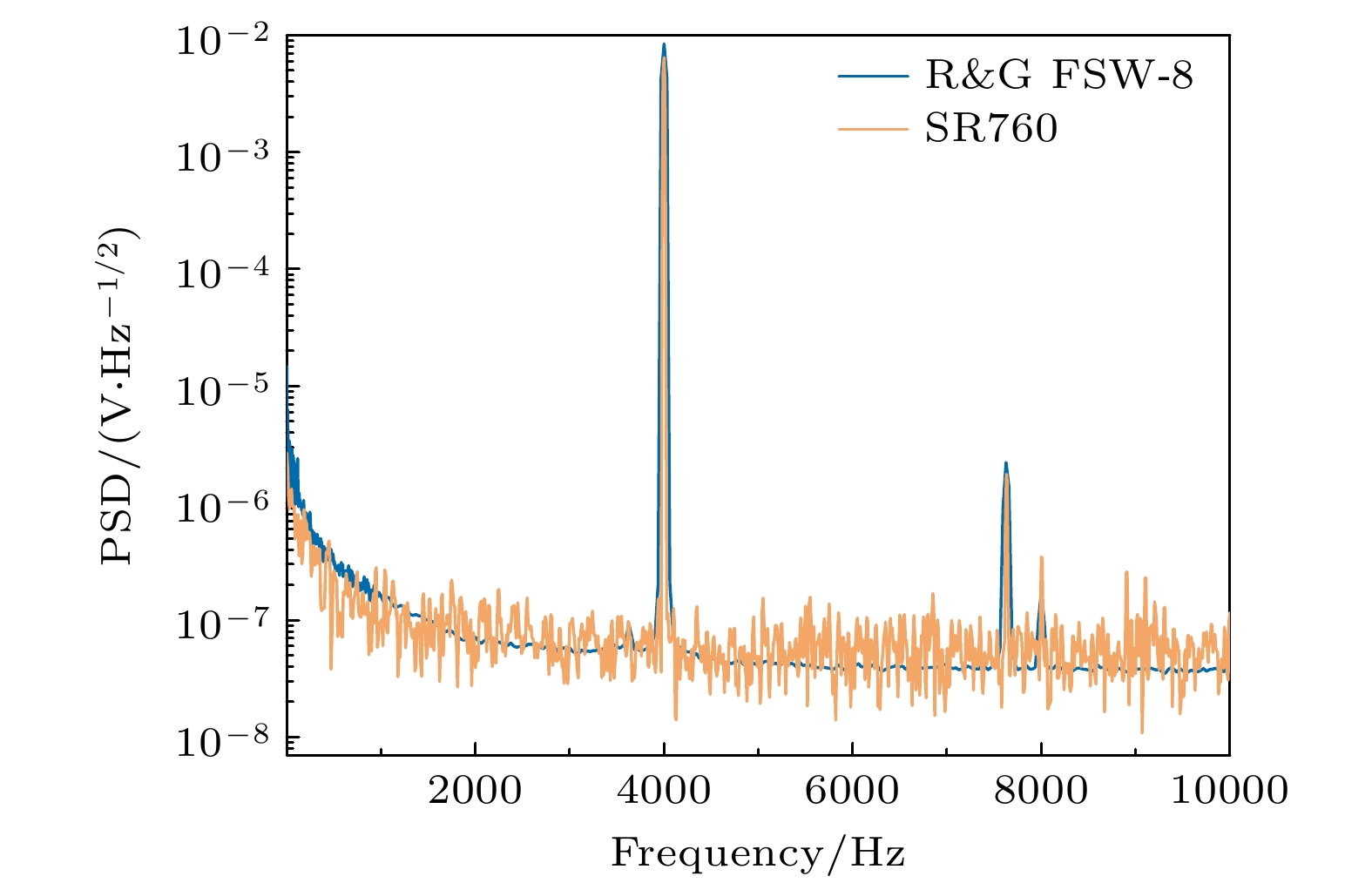
为保证地基引力波频段激光强度噪声测试结果的准确性, 首先对比测量了频谱分析仪(Rohde & Schwarz FSW Singal & Spectrum Analyzer FSW-8)以及傅里叶分析仪(Stanford, SR760)的电子学噪声, 判断噪底是否会对测试结果产生影响. 使用50 Ω短接环(Thorlabs FT500 50 Ω)分别将FSW-8和SR760信号输入口进行短接, 运行测试得到仪器电子学噪声. 实验结果见图4(a). 可以看到, SR760本底噪声的绝对值为
$ 1.5 \times {10^{ - 8}} \;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 Hz以及$ 5.6 \times {10^{ - 9}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 kHz, 而谱仪噪声明显高于SR760本底噪声, 所以我们利用SR760进行后续测量. 根据(5)式, 在SR760前加前置放大器SR560, 由于前置放大器不能设置连续倍数, 只能设置数个倍数值(1倍、50倍、100倍、500倍), 所以在各个倍数下, 改变前置放大器倍数, 并进行电子学噪声测量, 实验结果如图4(b)所示. 结果表明, 测试经过100倍放大后本底噪声可以在10 Hz以上达到最优值, 为3.8×10–9 Hz–1/2@10 Hz—10 kHz, 在20 Hz以上可以满足地基引力波激光相对强度噪声所要求的2×10–9 Hz–1/2@10 Hz & 10–7 Hz–1/2@1 kHz[19].为进一步验证本文评估系统的准确性, 使用标准信号源对本文系统进行验证. 将信号源输出的频率为4 kHz、幅值为1 mV的标准正弦信号, 放大100倍后用以上系统进行测试. 图5为测试结果. 为保证绝对值的准确性, 选择不加窗函数, 发现在4 kHz处有一峰值, 数值为9×10–3 Hz–1/2, 经计算与输入信号幅值基本一致, 即可以验证本文系统的准确性.
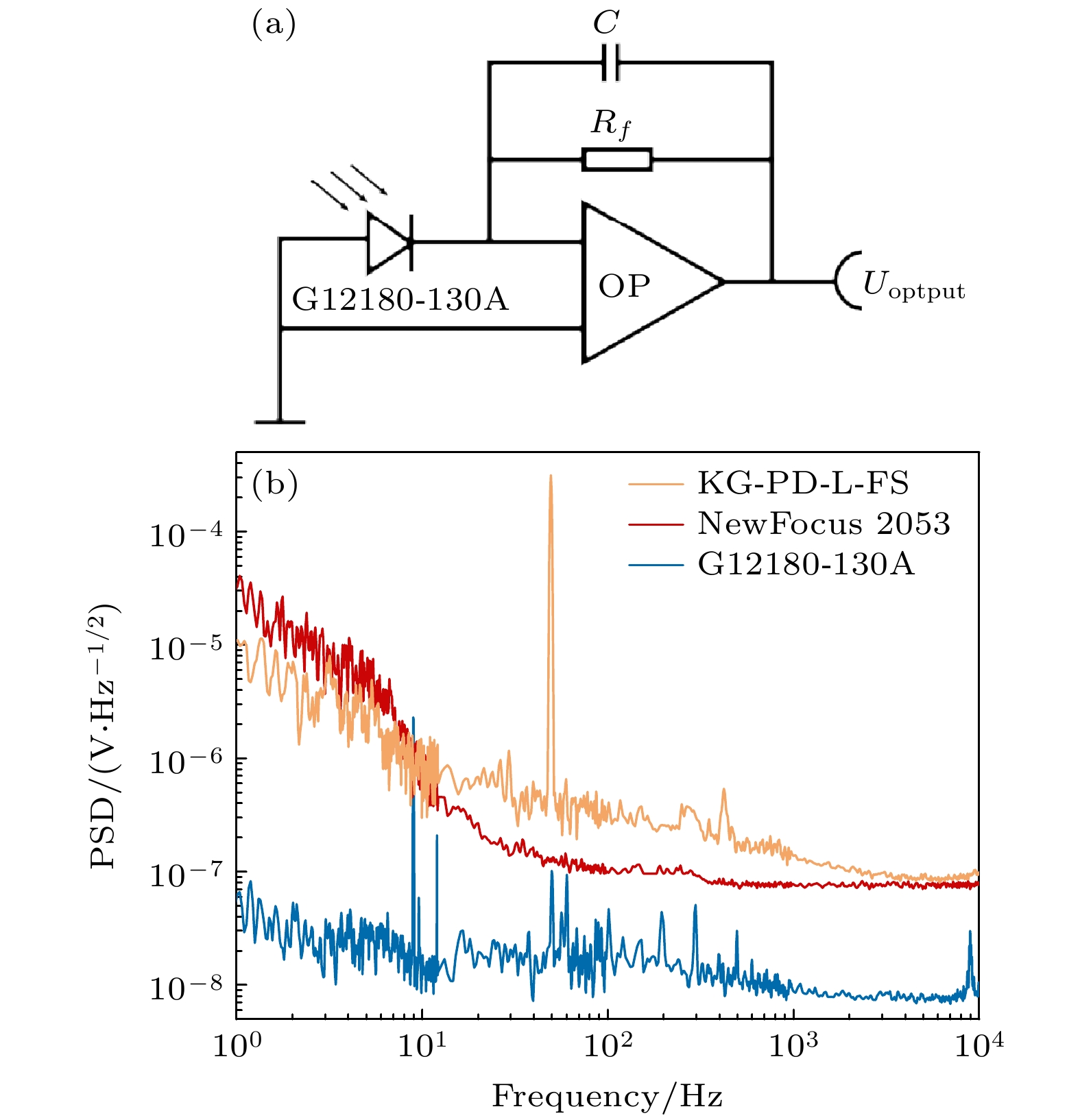
在此基础上进行光电探测器电子学噪声测试, 影响光电探测器电子学噪声主要有反向偏压、光电二极管类型、跨阻芯片、供电电压等[21], 原理图如图6(a)所示. 最终, 我们选择G12180-130A光电二极管, 跨阻运放选择AD797芯片[29,30], 无反向偏压的结构进行光电探测器的研发, 并对其电子学噪声进行测量, 测试时将激光器关闭并对光电二极管光敏面挡光, 供电采用±15 V低噪声镍氢电池, 将信号输入进SR760中进行分析, 得到结果如图6(b)所示.
经测试自研G12180-130 A探测器电子学噪声为
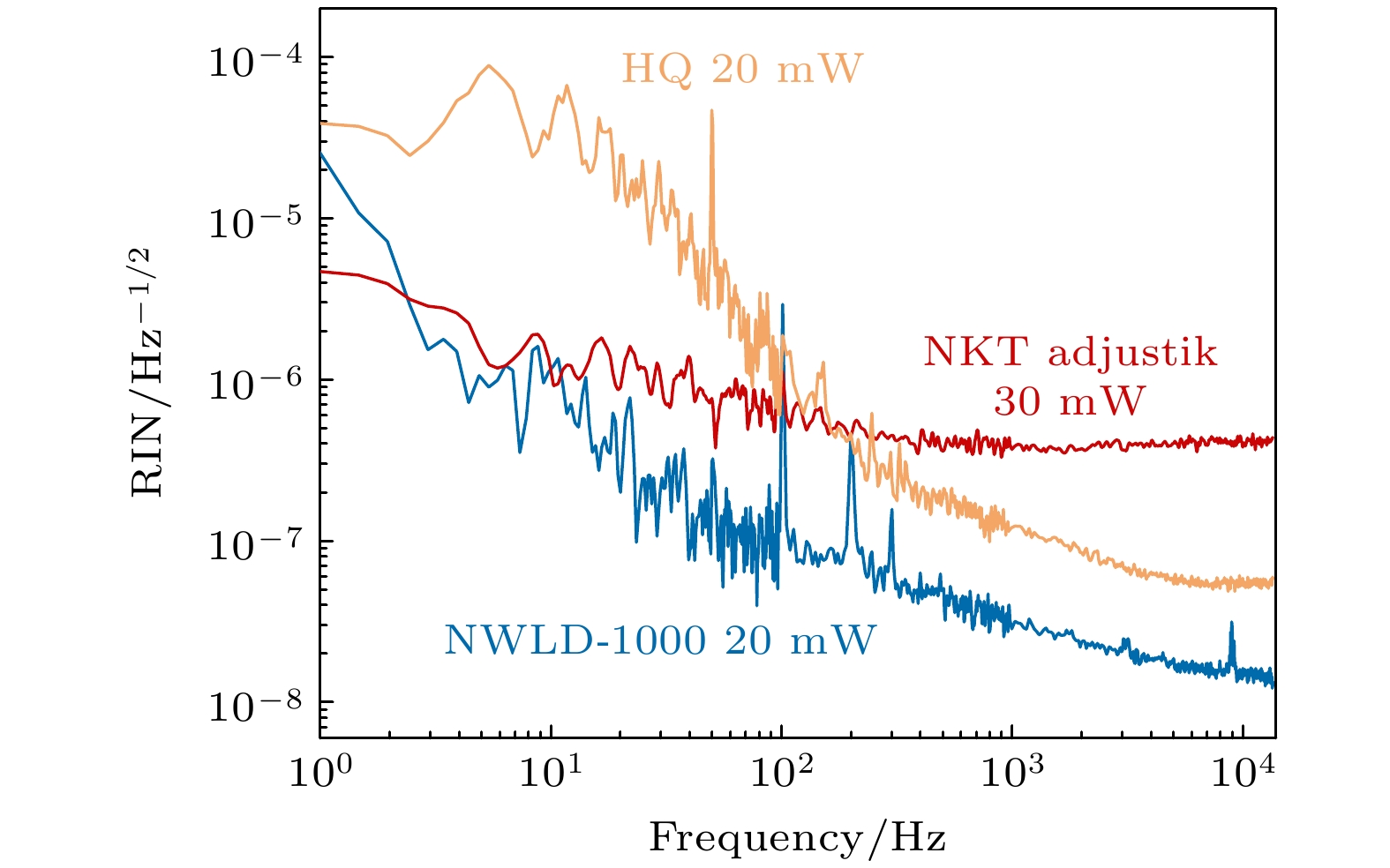
$ 1.4 \times {10^{ - 8}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 Hz &$ 8.1 \times {10^{ - 9}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 kHz. 作为对比, 将商用NewFocus 2053-FS-M和康冠KG-PD探测器在同等情况下进行电子学噪声测试, 结果如图6(b)中红色及橙色线, NewFocus2053-FS-M电子学噪声为$ 9.1 \times {10^{ - 7}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 Hz &$ 8.1 \times {10^{ - 8}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 kHz, KG-PD电子学噪声为$ 8.5 \times {10^{ - 7}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 Hz &$ 9.5 \times {10^{ - 8}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 kHz, 并且在50 Hz处有一尖峰, 这是由于商用探测器采用市电供电, 受到50 Hz工频干扰. 自研探测器的噪声远低于同等饱和光功率下的商用探测器噪声, 虽然已经采用了锂电池供电, 仍然在几处频段也有噪声尖峰, 这可能是受到工频干扰和环境中杂散电磁波耦合. 将来为了抑制百瓦级高功率单频激光器强度噪声[21], 仍需进一步研制多光电管阵列高功率探测系统[21,31–33], 并利用增加滤波电容、更改供电、更换屏蔽线、加装坡莫合金网等设计进一步降低探测系统噪声, 提高高功率激光噪声评估准确性.最后利用自研的评估系统对不同商用激光器在自由运转情况下10 Hz—10 kHz频段内的强度噪声进行表征. 分别对丹麦NKT Adjustik E15激光器输出30 mW、武汉光谷互连科技公司NWLD-1000输出20 mW、深圳横琴东辉科技公司HQ种子激光器输出20 mW激光进行测试. 测试结果如图7所示. 可以发现测试NKT Adjustik E15激光器相对强度噪声水平在1.2×10–6 Hz–1/2@10 Hz & 4.2×10–7 Hz–1/2@10 kHz; 武汉光谷互连科技公司NWLD-1000相对强度噪声水平为8.5×10–7 Hz–1/2@10 Hz & 1.2×10–8 Hz–1/2@10 kHz; 深圳横琴东辉科技公司HQ种子激光器相对强度噪声为4.2×10–5 Hz–1/2@10 Hz & 5.7×10–8 Hz–1/2@10 kHz; 同时, 将NKT激光器由本套系统测得的相对强度噪声与官方所给数据(–120 dBm/Hz@10 Hz—10 kHz)进行对比验证, 发现测得数据基本一致, 也可以验证本套系统的准确性.
-
本文基于低噪声高饱和功率光电探测模块、傅里叶分析仪SR760、前置放大器SR560等构建了面向地基引力波频段激光强度噪声的评估表征系统, 结合LabVIEW及MATLAB算法编程进行仪器控制和数据处理, 并对3种商用1550 nm激光器的相对强度噪声进行了测试评估. 实验结果表明, 前置放大器以及动态信号分析仪的整体电子学噪声为3.8×10–9 Hz–1/2@(10 Hz—10 kHz); 光电探测器电子学噪声为
$ 1.4 \times {10^{ - 8}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 Hz &$ 8.1 \times {10^{ - 9}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ @10 kHz; 可测得商用NKT激光器自由运转时相对强度噪声为1.2×10–6 Hz–1/2@10 Hz & 4.2×10–7 Hz–1/2@10 kHz; 进一步, 可以通过光电反馈控制[34]等技术抑制激光强度噪声, 并可利用此低噪声评估系统对光电反馈控制环路中各个器件进行噪声评估并做进一步改进. 此外, 本文系统地提供了地基引力波评估表征系统详细的理论推导、提供了相应测试手段, 并为整套系统配置了上位机控制程序兼具了操作简便及通用性, 为地基引力波探测频段激光强度噪声抑制提供了实验基础.
面向地基引力波探测频段的超低噪声激光强度噪声评估系统
Ultra-low-noise laser intensity noise evaluation system in Hz frequency band for ground-based gravitational wave detection
-
摘要: 引力波的直接探测打开了认识宇宙的新窗口, 开辟了多信使天文学, 各种天文事件产生引力波的频段涵盖范围较大, 不同频段引力波的探测机理及方案不尽相同. 目前, 正在运行的地基引力波探测装置的探测频段主要集中在10 Hz—10 kHz范围, 为达到探测灵敏度需求, 要对激光强度噪声进行准确评估并通过光电反馈将其抑制到≤2.0×10–9 Hz–1/2@10 Hz以及≤4.0×10–7 Hz–1/2@10 kHz. 本文基于激光噪声机理分析, 通过探究极小噪声评估方案, 研发低噪声光电探测器, 对比前置放大器不同放大倍数对信号的噪声耦合, 编写上位机操控及数据处理程序, 从而构建了低噪声高精度集成化激光强度噪声评估系统. 实验结果表明, 前置放大器以及动态信号分析仪的整体电子学噪声为3.8×10–9 Hz–1/2@(10 Hz—10 kHz); 光电探测器电子学噪声为$ 1.4 \times {10^{ - 8}} \;{\text{V}}/\sqrt {{\text{Hz}}} $@10 Hz &$ 8.1 \times {10^{ - 9}} \;{\text{V}}/\sqrt {{\text{Hz}}} $@10 kHz, 通过标准正弦信号进行校准等措施, 检验了评估系统的准确性. 相关研究结果为制备高功率低噪声激光光源及引力波探测等领域提供了实验基础.Abstract: The direct detection of gravitational waves has opened up a new window for understanding the universe and trailblazed multi-messenger astronomy. The frequency bands of gravitational waves generated by various astronomical events can cover a broadband range, and the detection mechanisms and schemes for gravitational waves in different frequency bands are different. For example, the ground-based gravitational wave detection has a frequency band ranging from 10 Hz to 10 kHz, which is based on Michelson interferometer. The space gravitational wave detection has a frequency band in a range of 0.1 mHz–1 Hz , which is based on space interferometer. The pulsar gravitational wave detection has a frequency band ranging from 1×10–9 Hz to 1×10–7 Hz, which is based on pulsar timing array. The next-generation ground-based gravitational wave project requires higher sensitivity to detect faint signals, necessitating an assessment system with minimal background noise to accurately measure the laser relative intensity noise. At present, the detection frequency band of ground-based gravitational wave detection devices in operation is mainly concentrated in a range of 10 Hz–10 kHz. To satisfy the detection sensitivity requirements, the laser relative intensity noise should be accurately evaluated and suppressed to ≤2.0×10–9 Hz–1/2 at 10 Hz and ≤4.0×10–7 Hz–1/2 at 10 kHz by photoelectric feedback. In this work, an evaluation and characterization system is constructed for ground-based gravitational wave band laser intensity noise, which is based on low noise and high sensitivity photoelectric detection device and combined with LabVIEW and MATLAB algorithm programming for instrument control and data processing. This low noise evaluation system is used to test the background noise of fast Fourier transform (FFT) analyzer SR760, preamplifier SR560, photoelectric detector electronic noise and intensity noise of homemade optical fiber amplifier, and then the data extraction and image processing are carried out by LabVIEW and MATLAB algorithms, and finally the ground-based gravitational wave frequency band system is evaluated. The experimental results show that the electronic noises for the preamplifier SR560 and the FFT analyzer SR760 are lower than 3.8×10–9 Hz–1/2@(10 Hz–10 kHz). The electronic noise for the photodetector is lower than $ 1.4 \times {10^{ - 8}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ at 10 Hz and $ 8.1 \times {10^{ - 9}}\;{\text{V}}/\sqrt {{\text{Hz}}} $ at 10 kHz, and the accuracy of the system is calibrated and tested by the standard sinusoidal signal. Finally, the noise of commercial laser is evaluated and compared with the factory data to verify the accuracy of the evaluation system. Related research, device and system development provide hardware, software and theoretical basis for preparing high-power low-noise laser light source and gravitational wave detection, and also provide the theoretical basis and evaluation criteria for detecting the ground-based gravitational wave .
-
-
图 1 地基引力波探测频段激光强度噪声测试评估系统架构
Figure 1. Architecture of laser intensity noise measurement and evaluation system.
图 2 地基引力波探测频段激光强度噪声评估系统程序流程图
Figure 2. Program flow chart of laser intensity noise evaluation system for ground-based GW detection.
图 4 高精度测试仪器本底噪声表征 (a) FFT分析仪测试结果; (b)外加前置放大器后电子学噪声测试结果
Figure 4. Electronic noise characterization of high precision instruments: (a) The test result of FFT; (b) the electronic noise characterization of pre-amplifier.
图 3 地基引力波探测频段激光强度噪声评估系统实验装置示意图, 其中Laser为激光器; ISO为光隔离器; λ/4为λ/4波片; λ/2为λ/2波片; PBS为偏振分束棱镜; BS为分束棱镜; len为f = 50 mm透镜; PD为光电探测器; PA为前置放大器; FFT analyzer为傅里叶分析仪; OSC为示波器; Vref为参考电压源; PC为计算机
Figure 3. Evaluation system for laser intensity noise at ground-based gravitational wave detection frequency band, where Laser is soild state laser, ISO is isolator, λ/4 is λ/4 waveplate, λ/2 is λ/2 waveplate, PBS is polarization beam splitter, BS is beam splitter, len is f = 50 mm len, PD is photodetector, PA is pre-amplifier, FFT analyzer is SR760, OSC is oscilloscope, Vref is voltage reference, PC is computer.
图 6 (a)光电探测器原理图; (b)不同探测器性能对比测试
Figure 6. (a) Schematic diagram of PD; (b) the contrast test of different PD’s performance.
-
[1] Sathyaprakash B S, Schutz B F 2009 Living Rev. Relativ. 12 2 doi: 10.12942/lrr-2009-2 [2] Schmidt P 2019 J. Phys. Conf. Ser. 1468 012218 doi: 10.1088/1742-6596/1468/1/012218 [3] Patrick K 2010 Ph. D. Dissertation (Hannover: Vom Fachbereich Physik der Universiät Hannover [4] Anza S 2005 Classical Quant. Grav. 22 S125 doi: 10.1088/0264-9381/22/10/001 [5] Rer N 2005 Ph. D Dissertation (Hannover: Vom Fachbereich Physik der Universiät Hannover [6] Armano M, et al. (LIGO Scientific and Virgo Collaboration) 2016 Phys. Rev. Lett. 116 231101 doi: 10.1103/PhysRevLett.116.231101 [7] 王在渊, 王洁浩, 李宇航, 柳强 2023 物理学报 72 054205 doi: 10.7498/aps.72.20222127 Wang Z Y, Wang J H, Li Y H, Liu Q 2023 Acta Phys. Sin. 72 054205 doi: 10.7498/aps.72.20222127 [8] Ran D 2024 J. Cosmol. Astropart. Phys. 2 16 doi: 10.1088/1475-7516/2024/02/016 [9] Daniel J, Andrew Z, Ryan M, Valentina D 2022 Astrophys. J. Lett. 1 L7 doi: 10.3847/2041-8213/acdd02 [10] Abbott B P, et al. (LIGO Scientific and Virgo Collaboration) 2016 Phys. Rev. Lett. 116 061102 doi: 10.1103/PhysRevLett.116.061102 [11] Antonino C 2023 EPJ Web of Conferences RICAP-22 280 03003 doi: 10.1051/epjconf/202328003003 [12] Hofacker C 2020 Aerospace Am. 58 10 [13] 李庆回, 李卫, 孙瑜, 王雅君, 田龙, 陈力荣, 张鹏飞, 郑耀辉 2022 物理学报 71 164203 doi: 10.7498/aps.71.20220552 Li Q H, Li W, Sun Y, Wang Y J, Tian L, Chen L R, Zhang P F, Zheng Y H 2022 Acta Phys. Sin. 71 164203 doi: 10.7498/aps.71.20220552 [14] 李卫, 谢超帮, 李庆回, 鞠明健, 武志学, 郑耀辉 2023 量子光学学报 29 040201 doi: 10.3788/JQO20232904.0201 Li W, Xie C B, Li Q H, Ju M J, Wu Z X, Zheng Y H 2023 J. Quantum Optics 29 040201 doi: 10.3788/JQO20232904.0201 [15] Gao L, Zheng L A, Lu B, Shi S P, Tian L, Zheng Y H 2024 Light Sci. Appl. 13 294 doi: 10.1038/s41377-024-01606-y [16] 郭禧庆, 周静, 王晨曦, 秦琛, 郭成哲, 李刚, 张鹏飞, 张天才 2024 物理学报 73 050401 doi: 10.7498/aps.73.20231462 Guo X Q, Zhou J, Wang C X, Qin C, Guo C Z, Li G, Zhang P F, Zhang T C 2024 Acta Phys. Sin. 73 050401 doi: 10.7498/aps.73.20231462 [17] Vahlbruch H, Wilken D, Mehmet M 2018 Phys. Rev. Lett. 121 173601 doi: 10.1103/PhysRevLett.121.173601 [18] Acernese F, Agathos M. 2019 Phys. Rev. Lett. 123 2311081 doi: 10.1103/PhysRevLett.123.231108 [19] Benno W, Peter K, Rick S, Peter F 2011 Pre-Stabilized Laser Design Requirements LIGO-T050036-v4 [20] Rollins J, Ottaway D, Zucker M, Weiss R, Abbott R 2004 Opt. Lett. 29 1876 doi: 10.1364/OL.29.001876 [21] Patrick K, Benno W, Karsten D 2009 Opt. Lett. 34 2912 doi: 10.1364/OL.34.002912 [22] Jonas J, Patrick O, Benno W 2017 Opt. Lett. 42 755 doi: 10.1364/OL.42.000755 [23] 李番, 王嘉伟, 高子超, 李健博, 安炳南, 李瑞鑫, 白禹, 尹王保, 田龙, 郑耀辉 2022 物理学报 71 209501 doi: 10.7498/aps.71.20220841 Li F, Wang J W, Gao Z C, Li J B, An B N, Li R X, Bai Y, Yin W B, Tian L, Zheng Y 2022 Acta Phys. Sin. 71 209501 doi: 10.7498/aps.71.20220841 [24] Michael T, Gerhard H 2006 Measurement 39 12 doi: 10.1016/j.measurement.2005.10.005 [25] Fabian M, Benno W 2022 Instruments 15 1 doi: 10.1103/PhysRevLett.129.121103 [26] Cooley J W, Tukey J W 1965 Math. Comput. 19 297 doi: 10.1090/S0025-5718-1965-0178586-1 [27] Welch P D 1967 IEEE Trans. Audio Electroacoust. 15 70 doi: 10.1109/TAU.1967.1161901 [28] 张骥, 魏珊珊, 刘昊炜, 刘元煌, 姚波, 毛庆和 2021 中国激光 48 0301002 doi: 10.3788/CJL202148.0301002 Zhang J, Wei S S, Liu H W, Liu Y H, Yao B, Mao Q H 2021 Chin. J. Lasers 48 0301002 doi: 10.3788/CJL202148.0301002 [29] 郑立昂, 李番, 王嘉伟, 李健博, 高丽, 贺子洋, 尚鑫, 尹王保, 田龙, 杨文海, 郑耀辉 2023 光学学报 52 0552220 doi: 10.3788/gzxb20235205.0552220 Zheng L A, Li F, Wang J W, Li J B, Gao L, He Z Y, Shang X, Yin W B, Tian L, Yang W H, Zheng Y H 2023 Acta Photonica Sin. 52 0552220 doi: 10.3788/gzxb20235205.0552220 [30] Goßler S, Bertolini A, Born M, Chen Y, Dahl K, Gering D, Gräf C, Heinzel G, Hild S, Kawazoe F, Kranz O, Kühn G, Lück H, Mossavi K, Schnabel R, Somiya K, Strain K A, Taylor J R, Wanner A, Westphal T, Willke B, Danzmann K 2010 Classical Quant. Grav. 27 084023 doi: 10.1088/0264-9381/27/8/084023 [31] Patrick K, Frank S, Benno W, Karsten D 2007 Rev. Sci. Instrum. 78 073103 doi: 10.1063/1.2754400 [32] Frank S, Patrick K, Michèle H, Benno W, Karsten D 2006 Opt. Lett. 13 2000 doi: 10.1364/OL.31.002000 [33] Jennrich O, Newton G, Skeldon K D, Hough J 2002 Opt. Com. 205 405 doi: 10.1016/S0030-4018(02)01368-8 [34] 刘骏杨, 韩逸凡, 陈力荣, 赵琴, 武延鹏, 李林, 王雅君, 郑耀辉 2025 量子光学学报 31 040201 doi: 10.3788/JQO20253104.0201 Liu J Y, Han Y F, Chen L R, Zhao Q, Wu Y P, Li L, Wang Y J, Zheng Y H 2025 J. Quantum Opt. 31 040201 doi: 10.3788/JQO20253104.0201 -
图( 7)
计量
- 文章访问数: 47
- HTML全文浏览数: 47
- PDF下载数: 0
- 施引文献: 0