-
受激布里渊散射(stimulated Brillouin scattering, SBS)在光纤传感技术中应用广泛, 包括对温度[1–4]、应变[5–7]、弯曲[8]及声阻抗[9]等参量的测量. 其中, 布里渊频移(Brillouin frequency shift, BFS)与布里渊增益谱(Brillouin gain spectrum, BGS)对光纤所受温度及应力变化极为敏感, 因此, 通过BGS的精确测量, 可准确传感温度、应力等参数变化, 在传感器领域显得尤为关键. 通常在单模光纤[10–12]中BGS为单峰谱, 对同时进行多性能同步传感具有局限性, 且单模光线的传输容量接近有限[13], 数据传输能力已达瓶颈. 近年来, 国内外专家学者进行多模光纤(multi-mode fibers, MMFs)布里渊传感研究[14,15], 发现其BGS表现出多峰特性, 与单模相比, 可支持多模态传输, 布里渊散射参数随模式的变化而调整. 因此, 研究不同传输模式下布里渊散射特性是极为重要的, 通过分析各种光模式和声模式的耦合重叠, 可对任意特定设计的光纤进行BGS数值计算.
在光纤波导中, 纤芯材料特性的差异会导致不同的布里渊散射频移和增益值波动, 甚至激发高阶声模[16], 典型的新型布里渊媒介材料有铌酸锂[17,18]、硅[19,20]、氮化硅[21–23]、硫化砷[24,25]、硒化砷[26]以及砷化镓[27]等, 研究人员发现由这些材料制成光纤的布里渊增益系数远高于普通二氧化硅光纤. 铌酸锂(LiNbO3)号称“光学硅”, 相关研究表明, 作为一种具有较高折射率的综合性能优异的多功能晶体材料, LiNbO3光纤较于硅光纤在芯材与包层材料之间的折射率差异更高, 可激发强烈的光子-声子相互作用, 显著增强光纤波导对光场的约束能力[28], 从而实现较大布里渊增益, 有效提升SBS效率; 此外, 其优异的强电光效应(在1500 nm处最大r33 = 27 pm/V)、宽透明波长(400 nm—5 μm)[29]、稳定的物理化学特性等天然优势, 有利于增强光与物质的相互作用, 激发强光子-声子相互作用[30]. 这些优良性能使LiNbO3光纤在布里渊光纤通信传感器件中具有广阔的应用前景, 对铌酸锂多模光纤(lithium niobate multimode fiber, LiNbO3-MMF)的不同传输模式下布里渊散射特性的研究也显得极为重要.
本文对LiNbO3光纤中后向布里渊散射过程中光学模式与声学模式之间的耦合机制进行研究, 利用COMSOL软件有限元方法仿真分析直径为3 μm的LiNbO3光纤内前5阶相位匹配条件下的模内相互作用, 分析该光纤所支持的光学模式与声学模式及声光耦合规律. 通过分析计算, 布里渊增益最大值达到了13.503 m–1·W–1, 与普通硅材料结构光纤相比增益有显著提升, 这种微米量级的LiNbO3多模光纤有望成为下一代光纤传感系统通用光纤.
-
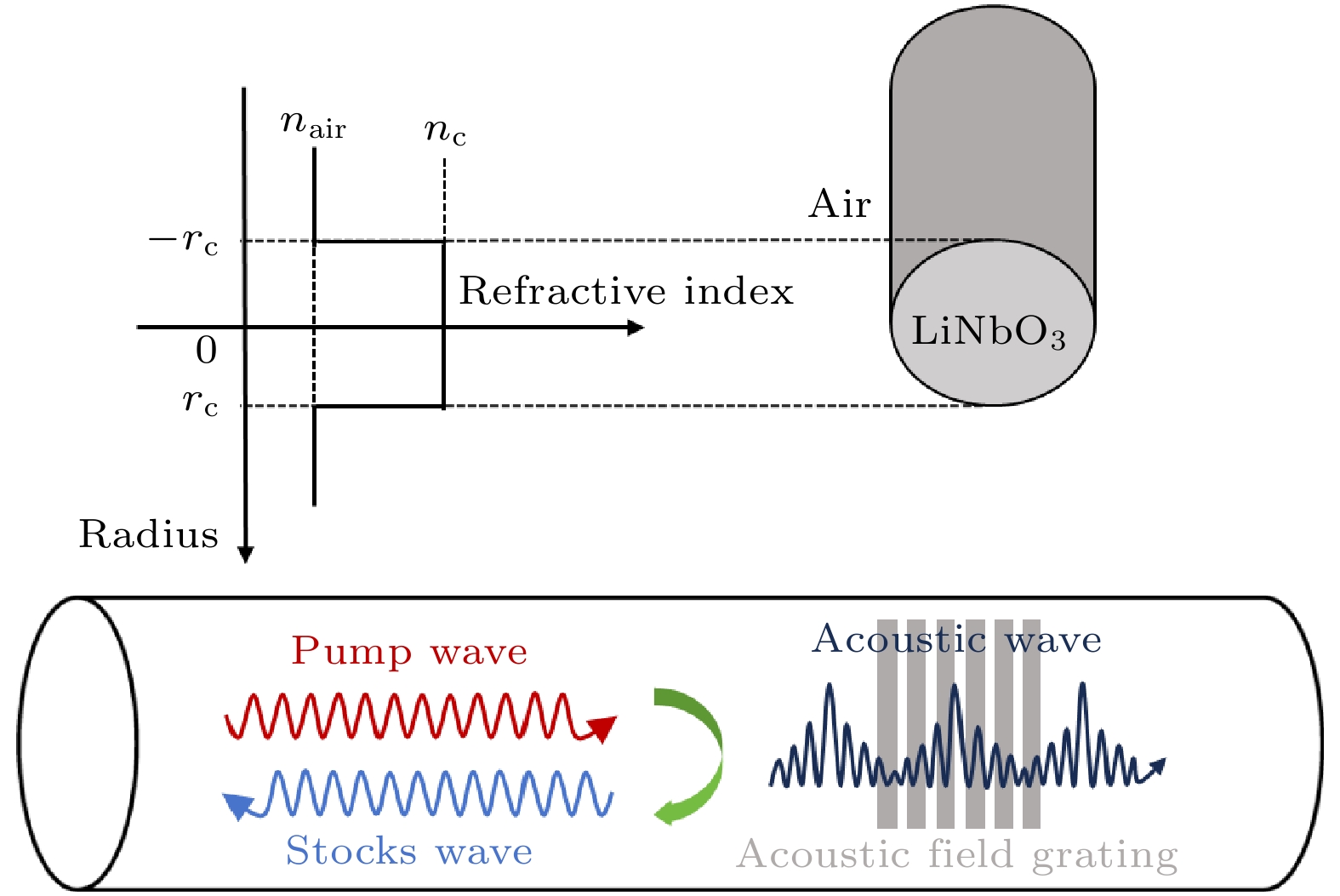
后向受激布里渊散射(backward stimulated Brillouin scattering, BSBS)是光纤中一种重要的3阶非线性光学现象, 如图1所示, 由电致伸缩效应(一种介质密度周期变化的物理现象)[31,32]引起, 需满足一定的相位匹配条件, 即动能守恒条件:
式中,
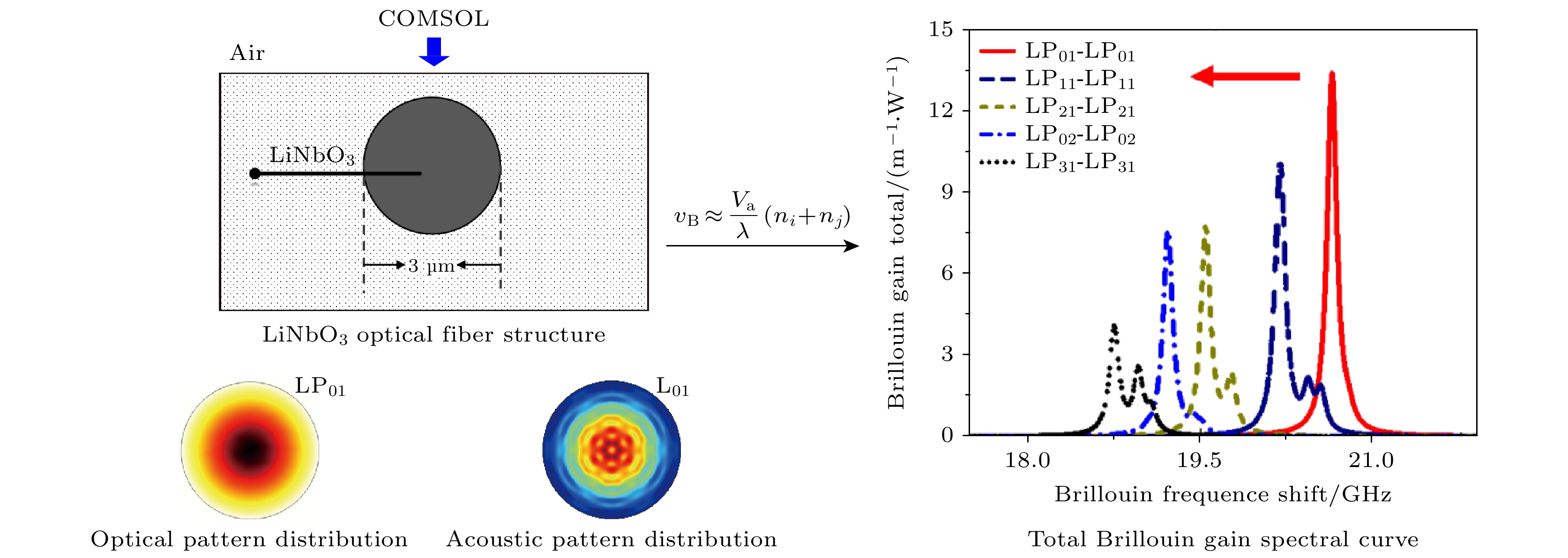
$ {{\boldsymbol{k}}_{\text{p}}} $ ,$ {{\boldsymbol{k}}_{\text{s}}} $ ,$ {{\boldsymbol{k}}_{\text{a}}} $ 以及${\omega _{\text{p}}}$ ,${\omega _{\text{s}}}$ ,${\omega _{\text{a}}}$ 分别为泵浦光、斯托克斯光、声波的波矢量和角频率.结合微米光纤具有的较低耦合损耗、大百分比倏逝场、高折射率差的强限制光场以及灵活的色散特性等优点, 设计了一种以铌酸锂为芯材的3 μm圆形阶梯折射率微米光纤(图2(a)), 利用有限元分析研究光学模式(图2(b))与声学模式(图2(c))之间相互耦合对后向布里渊散射的贡献. 微米光纤的包层一般为空气或者水等低折射率介质, 纤芯和包层之间的高折射率差使得强光场约束能够增强SBS, 模拟中使用的结构和材料参数如表1所列.
在该结构中, 由于芯材和包层材料之间的相对折射率差较大, 已经不能利用弱导近似方法, 需通过柱对称介质麦克斯韦方程组计算, 为简化分析, 使用线偏振(LP)模式的精确公式. 多模传输的模式数由其归一化频率V决定, 阶跃式多模归一化频率V的表达式为
式中,
$\lambda $ 为入射光的波长;$a$ 为光纤芯半径; NA为数值孔径,${{NA}} = \sqrt {n_i^2 - n_j^2} $ . 归一化频率V是表征模式传输特性的重要参数. V越大, 允许存在的导模就越多, 反之亦然. 当V < 2.405时, 只允许存在一种模态(HE11), 其中模态个数$M = {V^2}/2$ . 由该式计算可知, 在设计结构中存在将近300种光学模式, 但当关注布里渊散射的声场分布变化时, 高阶模式存在强度较弱, 因此只分析相互作用中最强的前5种光学模式, 分别为LP01, LP11, LP21, LP02和LP31.不同声模的BGS具有不同的增益, 其BFS表达式为
式中,
${\nu _{\text{B}}}$ 为声波频率,${n_{i\left( j \right)}}$ 和${\lambda _{i\left( j \right)}}$ 分别为第$i\left( j \right)$ 模的有效折射率和波长,${V_{\text{a}}}$ 为声模速度. 在波长为1550 nm, 有效折射率为2.213, 声速为7318 m/s时, 计算得到的${\nu _{\text{B}}}$ 约为21 GHz.光纤中存在多个声学模式, 通过研究特征频率可以得出不同声学模式的模场分布和声模频率等参数, 声场的频率和位移分布可以利用包含电致伸缩力的弹性动力学方程表示:
式中,
${u_i}$ 表示在i方向上的位移分量;${u_{k, l}}$ 为模式数;${c_{ijkl}}$ 为弹性矩阵;$T_{ij}^{{\text{es}}}$ 为电伸缩应力张量,$ T_{ij}^{{\text{es}}} = - {\varepsilon _0}{\chi _{klij}}\left[ {{E_k}E_l^*} \right] $ , 其中${E_k}E_l^*$ 是电场的并向矢量,${x_{klij}}$ 为4阶极化张量,${\chi _{klij}} = {\varepsilon _{km}}{\varepsilon _{ln}}{p_{mnij}}$ ,$ {\varepsilon _0} $ 为真空介电常数,${\varepsilon _{km(ln)}}$ 为介质的介质张量,${p_{mnij}}$ 为四阶弹光张量. 较大折射率对比度的光纤在其边界上会产生强大的光力, 而较小的尺寸会导致更强的移动边界效应[33], 所以在研究布里渊增益(${g_{\text{B}}}$ )时需考虑光弹效应(photoelastic effect, PE)和移动边界散射(moving boundary, MB)对光纤的影响[18,34]:将相同模式对下所有声模态相加,
${\varOmega _m}$ 为不考虑声损失的第m个声模态的特征频率; 声光有效重叠面积是表征声光耦合效率的重要参数,$A_m^{{\text{ao}}}$ 指声光模在光纤横截面上模场分布的交叠情况;${f_{{\text{PE}}}}$ 指PE对光纤的力, 为面积的重叠积分;${f_{{\text{MB}}}}$ 指MB对光纤的力, 是线的重叠积分. 各声模的布里渊增益为洛伦兹函数, 布里渊散射增益系数定义为式中,
${Q_m}$ 为机械能质量因子;${V_{{\text{gp}}}}\left( {{V_{{\text{gs}}}}} \right)$ ,$\varepsilon $ ,$\rho $ 分别为Pump光(Stokes光)的群速度、电导率、密度;$ {E_{\text{p}}} $ 和$ {E_{\text{s}}} $ 分别为Pump光和Stokes光的电场强度;$f$ 为Pump光和Stokes光的光力之和;${u_m}$ 是第m个声模的位移向量. -
基于上述理论, 利用有限元仿真模拟了以铌酸锂晶体为纤芯时可以实现多模式的BSBS. LP01, LP11, LP21, LP02和LP31这5种模式对应的有效折射率分别为2.1785, 2.1332, 2.0639, 2.0305和1.9797, 有效折射率随着光学模式阶数的增加而递减.
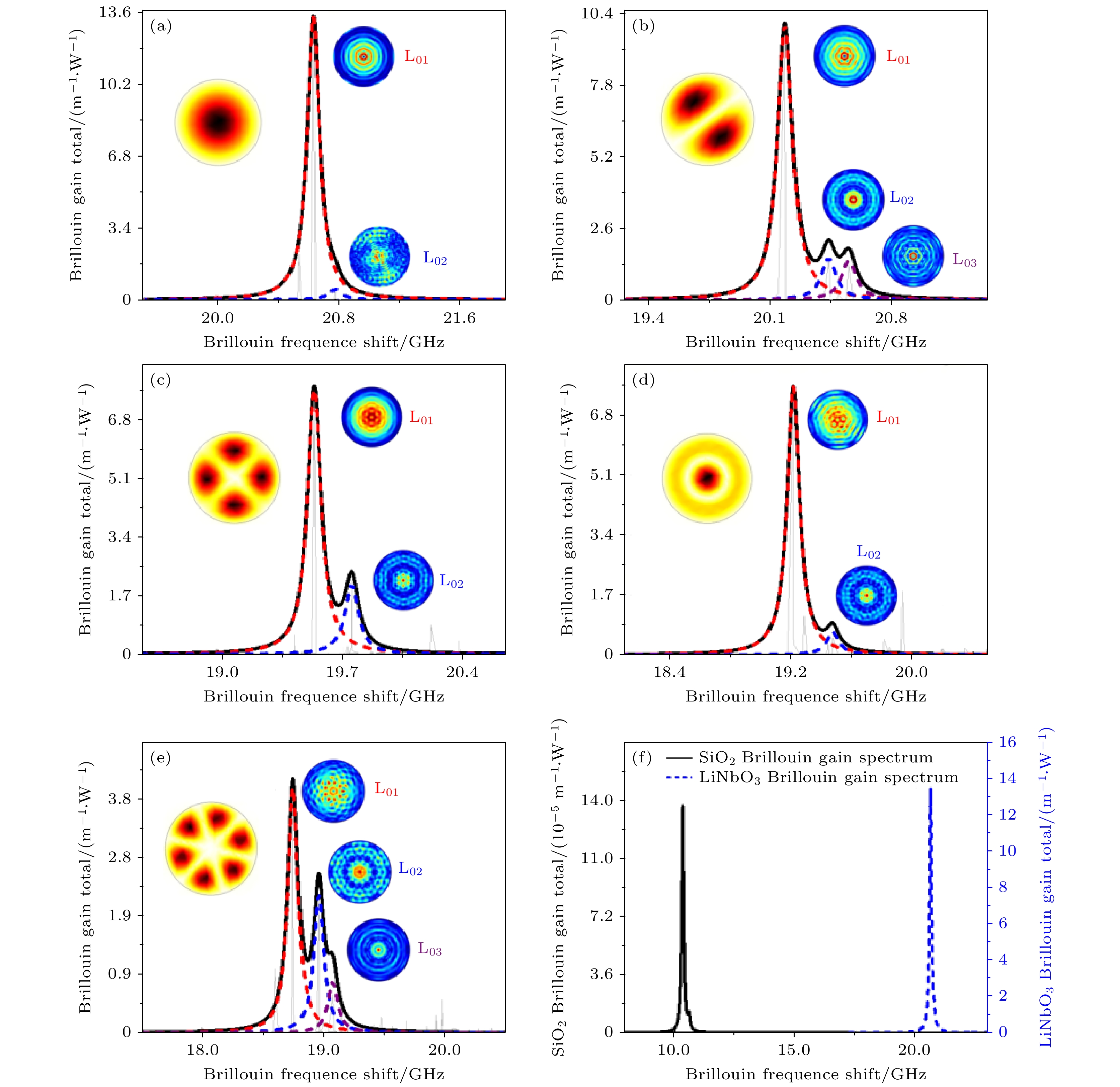
图3(a)—(e)分别为LP01-LP01, LP11-LP11, LP21-LP21, LP02-LP02和LP31-LP31对应Pump-Stokes模式对BSBS的BGS模拟结果. 结合声波形状的指数衰减, 用洛伦兹曲线对BGS中的每个峰进行拟合, 其中, 每条曲线对应一个声模Lmn. 仿真结果显示, 每个BGS可拟合不同数量(1—3条)的洛伦兹曲线, 对于所有模式对的BGS, 以L0n声模(m = 0)为主导, 这是由于这些声学模式在模内BSBS中呈现对称结构; 且因为LP01模式的声光耦合效率更高, 所有最大峰值的声学模态都为L01模式, 对应BSBS的最大增益. 同一模型相同条件下, LiNbO3光纤相较于普通SiO2光纤其增益有显著提升, 如图3(f), 以LP01-LP01模式为例, 作LiNbO3光纤与SiO2光纤的增益谱对比图, SiO2光纤的最大增益在10–4量级, 而LiNbO3光纤的最大增益则达到了13.503 m–1·W–1, 有利于提升SBS效率.
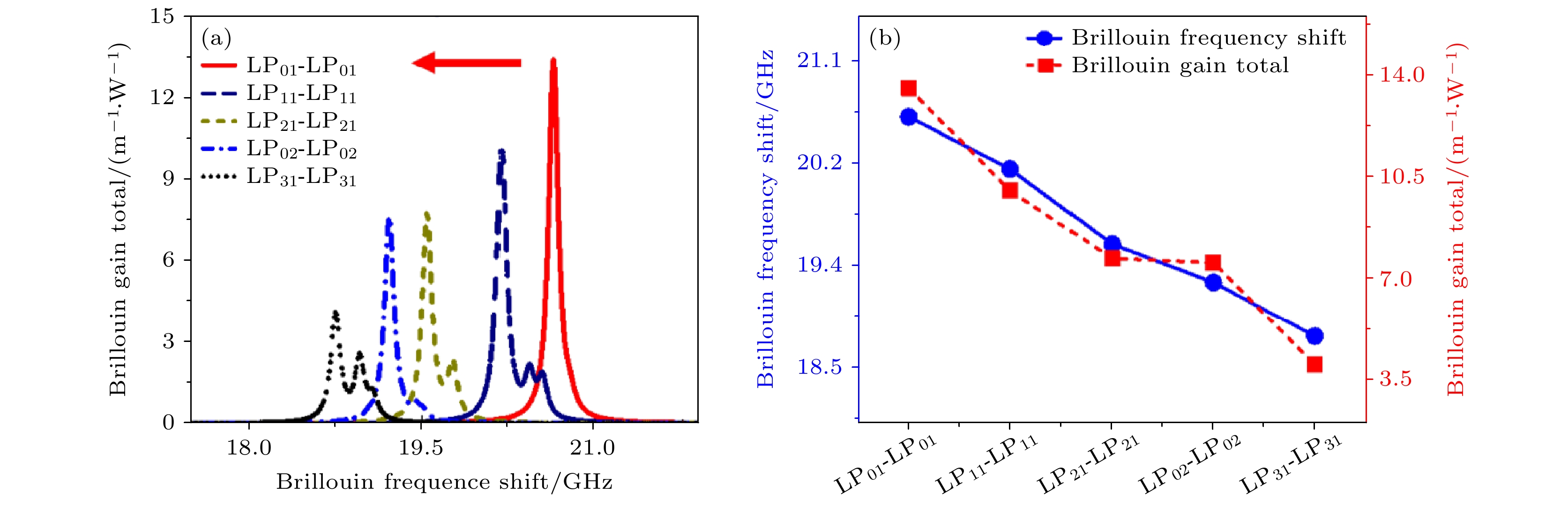
图4所示为仿真中5个LPmn-LPmn的Pump-Stokes模式对相互作用的BGS的总洛伦兹曲线 和布里渊频移及相对增益关系. 图4(a)中, 芯径为 3 μm铌酸锂微米光纤在前5阶光模式下, 峰值BFS在18.747 (LP31-LP31)—20.63( LP01-LP01) GHz范围内; 布里渊增益系数在LP01-LP01光模式最大, 为13.503 m–1·W–1, 结合图4(b)发现, 在模内BSBS情况下, 随着模式阶数的增大, 不止峰值BFS产生红移, 布里渊增益系数也随之递减.
将
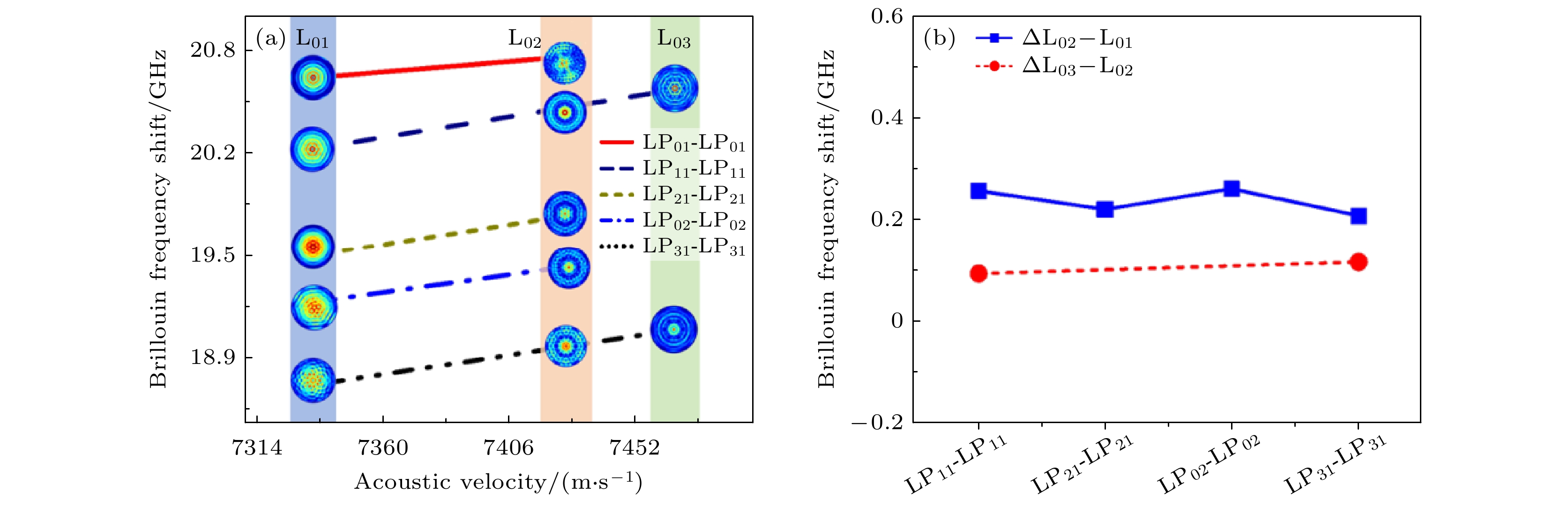
${n_i}$ 和${n_j}$ 以及模拟计算的BFS代入(4)式得到声模速度, 图5(a)为声模速度与BFS的关系, 其中, 每种颜色线条代表一个LPmn-LPmn光模对, 蓝色、橘色、绿色色块分别代表L01声模、L02声模、L03声模. 通过对比可以发现, 在相同声模(Lmn)下, 尽管低阶光模对应较大的频移值, 但不同光模对(LPmn-LPmn)下对应相同声模(L0n)的声速一致. 这是由于随着模式阶数的变化, 频移值与有效折射率都在减小, 而不同光模对(LPmn-LPmn)下L0n声模之间的频率差大致相等(如图5(b)所示)则导致了其呈线性增长. -
本文设计了直径3 μm的以新型光电材料LiNbO3为纤芯的光纤波导, 模拟计算了前5阶Pump-Stokes模式对在LiNbO3光纤中的布里渊散射特性. 详细分析了Pump-Stokes模式对中的L0n声学模: 与传统的SiO2光纤不同, 掺LiNbO3光纤的增益可达到13.503 m–1·W–1, 布里渊散射频移在18.747—20.63 GHz范围内, 其增益至少提升了5个数量级, 本研究成果为具有电光特性的铌酸锂材料光纤传感器奠定了基础.
铌酸锂微米光纤模内后向布里渊散射特性
Intra-mode backward stimulated Brillouin scattering in lithium niobate micron fibers
-
摘要: 多模光纤的布里渊传感技术因其能够同时进行温度、应变等多参量的模态传输, 具备更高的信息容量 和传输效率而备受关注. 此外, 铌酸锂材料凭借其优异的电光特性, 在传感领域展现出潜在应用价值, 有望 提供更高灵敏度和精度. 然而, 受工艺成熟度影响, 目前光纤传感的研究多集中于硅基材料, 以铌酸锂为纤芯材料的研究相对较少, 其应用潜力被普遍低估. 本文针对铌酸锂光纤中的布里渊散射效应的理论研究, 通过有限元仿真技术, 模拟微米量级铌酸锂光纤中各阶数模式的后向布里渊散射特性, 分析光纤中前5个LP模(LP01, LP11, LP21, LP02和LP31)的模内受激布里渊散射特性, 以探明铌酸锂微米光纤模态内后向布里渊散射特性. 结果表明, 铌酸锂光纤的有效折射率(2.1785—1.9797)、布里渊散射频移(20.63—18.747 GHz)以及增益(4.0115—13.503 m–1·W –1)均随着模式阶数的增高而减小. 模拟结果进一步表明, 与普通硅结构光纤相比, 铌酸锂光纤结构的布里渊增益有显著提高, 预示其在传感方面的灵敏度也会更高.Abstract:
The Brillouin sensing technology in multimode optical fibers has received much attention due to its ability to simultaneously transmit multiple parameters, such as temperature and strain, and its higher information capacity and transmission efficiency. Additionally, lithium niobate possesses excellent electro-optical properties, so it shows potential application value in the sensing field and is expected to provide higher sensitivity and precision. Owing to the maturity of manufacturing processes, current research on fiber optic sensing focuses on silicon-based materials, however, there are fewer studies of fibers in which lithium niobate is used as the core material, thereby underestimating its application potential. In this work, the Brillouin scattering effects in lithium niobate optical fibers are investigated numerically. We simulate the intra-mode backward Brillouin scattering characteristics of the first five orders of LP modes in micrometer-sized lithium niobate fibers by means of finite-element simulation to explore its intrinsic law. First of all, the relationship between the Brillouin frequency shift and gain for the first five optical mode interactions is analyzed in detail. The results show that in the case of intra-mode backward stimulated Brillouin scattering, the peak of Brillouin frequency shift exhibits a significant redshift ranging from 20.63 GHz to 18.747 GHz. The Brillouin gain coefficient decreases from 13.503 m–1·W–1 to 4.0115 m–1·W–1 with the increase of mode order, in which mode LP01 having the strongest gain intra modal interaction means the best sensing sensitivity. In addition, compared with ordinary silica fiber, the lithium niobate fiber has Brillouin gain increased by about 5 orders of magnitude, which means that fibers with lithium niobate as the core can have higher sensing sensitivity. In addition, it is found that although there are significant differences in the Brillouin frequency shift values of each optical mode under intra modal interactions, the sound velocity of their corresponding acoustic modes is always consistent under the same acoustic mode. In data processing, it is noticed that this is because as the mode order changes, the corresponding effective refractive index decreases to ensure that each acoustic mode of the material always has the same sound velocity. These findings provide a foundation for further studying the lithium niobate fiber sensors with electro-optic properties. -
Key words:
- stimulated Brillouin scattering /
- lithium niobate /
- micron fibers /
- simulation .
-

-
图 2 LiNbO3光纤结构原理图及光学声学模式分布图 (a) LiNbO3光纤结构原理图; (b) 光学模式分布图; (c) 声学模式分布图
Figure 2. Schematic diagram of LiNbO3 optical fiber structure and distribution diagram of optical acoustic mode: (a) Schematic diagram of LiNbO3 optical fiber structure; (b) optical pattern distribution; (c) acoustic pattern distribution.
图 3 不同模式内布里渊增益谱以及SiO2光纤与LiNbO3光纤增益谱对比图 (a) LP01-LP01模式; (b) LP11-LP11模式; (c) LP21-LP21模式; (d) LP02-LP02模式; (e) LP31-LP31模式; (f) SiO2光纤与LiNbO3光纤增益谱对比图
Figure 3. Gain spectrum within Brillouin in different modes and comparison of gain spectra between SiO2 and LiNbO3 fibers: (a) LP01-LP01 mode; (b) LP11-LP11 mode; (c) LP21-LP21 mode; (d) LP02-LP02 mode; (e) LP31-LP31 mode; (f) comparison of gain spectra between SiO2 and LiNbO3 fibers.
图 4 5个LPmn-LPmn的Pump-Stokes模式对相互作用的BGS的总洛伦兹曲线以及BFS和相对增益关系 (a) BGS的总洛伦兹曲线; (b) Pump-Stokes模式对中最高峰对应的BFS和增益关系
Figure 4. Total Lorentz curves of BGS for the interaction of the pump-Stokes mode pairs of 5LPmn-LPmn as well as the BFS and relative gain relationship: (a) Total Lorentz curves of BGS; (b) the BFS and gain relationship for the highest peak of the pump-Stokes mode pairs.
图 5 声模速度与BFS的关系以及声模频率差关系 (a) 5个pump-Stokes模式对之间BFS与声速的关系; (b)模态间的频率差关系
Figure 5. Relationship between the velocity of the sound model and the BFS and the relationship between the frequency difference of the sound mode: (a) BFS and sound velocity between five Pump-Stokes mode pairs; (b) frequency difference relationship between modalities.
表 1 光纤结构和材料参数[29]
Table 1. Fiber structure and material parameters.
Parameters Values Core Clading Radius/μm 3 — Refractive index 2.213 1 Mass density/(kg·m–3) 4700 1.29 Longitudinal acoustic
velocity/(m·s–1)7318 340 Photo-elastic coefficients p11 = –0.02, p12 = 0.08,
p44 = 0.12Transmission loss at
1550 nm /(dB·cm–1)0.89 -
[1] Hayashi N, Mizuno Y, Nakamura K, Zhang C, Jin L, Set S Y, Yamashita S 2020 Jpn. J. Appl. Phys. 59 088002 doi: 10.35848/1347-4065/aba157 [2] Wang L, Zhou B, Shu C, He S L 2013 IEEE Photonics J. 5 6801808 doi: 10.1109/JPHOT.2013.2287557 [3] Catalano E, Vallifuoco R, Zeni L, Minardo A 2022 IEEE Sens. J. 22 6601 doi: 10.1109/JSEN.2022.3150075 [4] Zeng Z, Peng D, Zhang Z Y, Zhang S J, Ni G M, Liu Y 2020 IEEE Photonics Tech. L. 32 995 doi: 10.1109/LPT.2020.3008749 [5] Coscetta, A, Minardo A, Zeni L 2020 Sensors 20 5629 doi: 10.3390/s20195629 [6] Gao S, Wen Z R, Wang H Y, Baker C, Chen L, Cai Y J, Bao X Y 2023 J. Lightwave Tech. 41 4359 doi: 10.1109/JLT.2022.3184109 [7] Peng J Q, Lu Y G, Zhang Z L, Wu Z N, Zhang Y Y 2021 IEEE Photonics Tech. L. 33 1217 doi: 10.1109/LPT.2021.3112761 [8] Ba D X, Chen C, Fu C, Zhang D Y, Lu Z W, Fan Z G, Dong Y K 2018 IEEE Photonics J. 10 1 doi: 10.1109/JPHOT.2017.2783956 [9] Liu P K, Lu Y A, Zhang W J, Zhu M 2024 Opt. Commun. 563 130571 doi: 10.1016/j.optcom.2024.130571 [10] Ippen E P, Stolen R H 1972 Appl. Phys. Lett. 21 539 doi: 10.1063/1.1654249 [11] Kobyakov A, Sauer M, Chowdhury D 2009 Adv. Opt. Photonics 2 1 doi: 10.1364/AOP.2.000001 [12] Hill K O, Kawasaki B S, Johnson D C 1976 Appl. Phys. Lett. 28 608 doi: 10.1063/1.88583 [13] Essiambre R J, Kramer G, Winzer P J, Foschini G J, Goebel B 2010 J. Lightwave Technol. 28 662 doi: 10.1109/JLT.2009.2039464 [14] Dong Y K 2021 Photonic Sens. 11 69 doi: 10.1007/s13320-021-0616-7 [15] Feng C, Schneider T 2021 Sensors 21 1881 doi: 10.3390/s21051881 [16] Eggleton B J, Poulton C G, Pant R 2013 Adv. Opt. Photonics 5 536 doi: 10.1364/AOP.5.000536 [17] Yang Y H, Wang J Q, Zhu Z X, Xu X B, Zhang Q, Lu J J, Zeng Y, Dong C H, Sun L Y, Guo G C, Zou C L 2024 Sci. China Phys. Mec. 67 214221 doi: 10.1007/s11433-023-2272-y [18] Rodrigues C C, Zurita R O, Alegre T P, Wiederhecker S G 2023 J. Opt. Soc. Am. B 40 56 doi: 10.1364/JOSAB.482656 [19] Otterstrom N T, Behunin R O, Kittlaus E A 2018 Science 360 1113 doi: 10.1126/science.aar6113 [20] Kittlaus E A, Shin H, Rakich P T 2016 Nat. Photonics 10 463 doi: 10.1038/nphoton.2016.112 [21] Gyger F, Liu J Q, Yang F, He J J, Raja A S, Wang R N, Bhave S A, Kippenberg T J, Thevenaz L 2020 Phys. Rev. Lett. 124 013902 doi: 10.1103/PhysRevLett.124.013902 [22] Xiang C, Guo J, Jin W, Wu L, Peters J, Xie W Q, Chang L, Shen B Q, Wang H M, Yang Q F, Kinghorn D, Paniccia M, Vahala K J, Morton P A, Bowers J E 2021 Nat. Commun. 12 6650 doi: 10.1038/s41467-021-26804-9 [23] Botter R, Ye K X, Klaver Y, Suryadharma R, Daulay O, Liu G J, van den Hoogen J, Kanger L, van der Slot P, Klein E, Hoekman M, Roeloffzen C, Liu Y, Marpaung D 2022 Sci. Adv. 8 2196 doi: 10.1126/sciadv.abq2196 [24] Morrison B, Casas-Bedoya A, Ren G, Vu K, Liu Y, Zarifi A, Nguyen T G, Choi D Y, Marpaung D, Madden S J, Mitchell A, Eggleton B J 2017 Optica 4 847 doi: 10.1364/OPTICA.4.000847 [25] Choudhary A, Morrison B, Aryanfar I, Shahnia S, Pagani M, Liu Y, Vu K, Madden S, Marpaung D, Eggleton B J 2017 J. Lightwave Tech. 35 846 doi: 10.1109/JLT.2016.2613558 [26] Florea C M, Bashkansky M, Dutton Z, Sanghera J, Pureza P, Aggarwal I 2006 Opt. Express 14 12063 doi: 10.1364/OE.14.012063 [27] Balram K C, Davanço M I, Song J D, Srinivasan K 2016 Nat. Photonics 10 346 doi: 10.1038/nphoton.2016.46 [28] Kim Y H, Song K Y 2021 Sensors 21 2168 doi: 10.3390/s21062168 [29] Feng L Y, Liu Y, He W J, You Y J, Wang L Y, Xu X, Chou X J 2022 Applied Sciences 12 6476 doi: 10.3390/app12136476 [30] Lin J, Bo F, Cheng Y, Xu J J 2020 Photonics Res. 8 1910 doi: 10.1364/PRJ.395305 [31] Eggleton B J, Poulton C G, Rakich P T, Steel M J, Bahl G 2019 Nat. Photonics 13 664 doi: 10.1038/s41566-019-0498-z [32] Cao M, Huang L, Tang M, Mi Y A, Ren W H, Ning T G, Pei L, Ren G B 2022 Opt. Commun. 507 127612 doi: 10.1016/j.optcom.2021.127612 [33] Florez O, Jarschel P F, Espinel Y A V, Cordeiro C M B, Alegre T P M, Wiederhecker G S, Dainese P 2016 Nat. Commun. 7 11759 doi: 10.1038/ncomms11759 [34] Rakich P T, Reinke C, Camacho R, Davids P, Wang Z 2012 Phys. Rev. X. 2 011008 doi: 10.1103/PhysRevX.2.011008 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: