在${\boldsymbol{E}} \times {\boldsymbol{B}}$的放电装置中, 与电场E垂直的磁场B被用来约束电子, 从而使工质气体能够在较低的气压下发生电离并产生等离子体. 在这些装置中, 外加磁场能够保证电子磁化, 离子非磁化, 即${\rho _{\text{e}}} \ll L$, ${\rho _{\text{i}}} \gg L$. ${\rho _{\text{e}}}$, ${\rho _{\text{i}}}$, $L$分别是电子、离子拉莫尔半径和等离子体区域的特征长度. 在霍尔推力器中, 电子在${\boldsymbol{E}} \times {\boldsymbol{B}}$的作用下沿着角向漂移维持放电, 而离子由于不受磁场的影响(较大的${\rho _{\text{i}}}$), 因此能够在电场作用下沿着轴向被加速喷出, 从而产生推力. 尽管霍尔推力器以及霍尔等离子体源已得到了广泛的应用, 但这些装置中存在的一些现象目前还不能给出明确的解释, 如电子反常输运^[1,2]、湍流加热^[3]、连续模结构^[4,5]等. 电子的反常输运表现为实验上测得的横越磁力线的电子迁移率比用经典碰撞理论计算得到的迁移率大2—3个数量级^[6,7]. 目前认为导致这一现象的原因是等离子体不稳定性, 特别是电子漂移不稳定性(EDI)^[8], 以及由密度梯度和磁场梯度驱动的长波长不稳定性^[9–12].

电子的${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移, 等离子体密度、温度、磁场梯度, 离子通量, 以及碰撞效应是激发霍尔推力器中不稳定性的诱因^[8,13–16]. Ducrocq等^[17]利用色散关系研究表明, 当满足条件$\omega - {k_y}{\upsilon _{\text{E}}} = n{\omega _{{\text{ce}}}}$时EDI将变得不稳定. $\omega $为模式的本征值, ${k_y}$为角向波数, ${\upsilon _{\text{E}}}$为电子的角向漂移速度, ${\omega _{{\text{ce}}}}$为电子的回旋频率, $n$为整数. Lafleur等^[18]研究表明, 在非线性湍流作用下, EDI将转变为离子声波不稳定性, 这与光散射实验结果一致. Boeuf和Garrigues ^[8]采用二维轴向-角向的粒子模型研究了不同电离率对EDI的影响, 结果表明当电离率较小时EDI引起的角向电场扰动不足以引起电子横越磁力线的运动, 模式转变离子声波不稳定性. Tavant等^[19]和Taccogna等^[20]的研究结果表明, EDI引起的径向电子加热将会导致二次电子发射系数增大, 增加的二次电子会使EDI引起的反常电子迁移率减小20%. Mandal等^[21]研究表明由于波粒相互作用, 电子从EDI中获得能量, 使垂直于磁场方向的温度升高, $ {T_{{\text{e}} \bot }}/{T_{/ /}} \approx 4 $, 从而增强电子横越磁力线的输运. Chen等^[22]采用一维粒子模型研究了不同类型工质下EDI的增长机制及其特征, 结果表明由于朗道阻尼, EDI不稳定性最终将达到饱和. 采用轻原子质量的工质时, EDI的振荡幅值将显著的减小, 线性增长率、频率、相速度都将增大, 但是工质种类不会对电子迁移率产生显著影响.

此外, 由密度、温度、磁场梯度引起的不稳定性在霍尔推力器实验中也被发现^[9,23]. Frias等^[24]利用三场流体模型研究了存在磁场、密度和温度梯度时的长波长不稳定性, 结果表明由于有限电子温度扰动, 电子压缩效应将对非均匀磁场中不稳定性的判据和特征产生修正, 由密度梯度和磁场梯度驱动的长波长不稳定性的频率满足${\omega _{\text{r}}}\sim - (k_ \bot ^2/{k_y}){\omega _{{\text{ci}}}}{(l_{\text{N}}^{{{ - 1}}} - 2 l_{\text{B}}^{{{ - 1}}})^{ - 1}}$, ${l_{\text{N}}}$和${l_{\text{B}}}$分别表示密度和磁场梯度的特征长度. Romadanov等^[13]采用包含电子惯性、电场、磁场, 以及等离子体密度的非局域模型对梯度漂移不稳定性进行了研究. 在角向波数${k_y}$较小时, 非局域模型能够在局域模型所预测的稳定区间中驱动不稳定性; ${k_y}$较大时, 非局域模型与局域模型的结果一致, 但在局域模型预测的稳定区间仍存在不稳定性. Lakhin等^[14]推导了包含有限拉莫尔半径效应时, 由密度梯度和磁场梯度驱动、沿垂直于磁场方向传播、频率介于离子回旋频率和电子回旋频率之间的不稳定性色散关系. 结果表明, 电子惯性和有效拉莫尔半径效应对短波长不稳定性有稳定作用. Marusov等^[15]研究了磁场梯度和密度梯度对梯度漂移不稳定性的影响, 结果表明根据不稳定模式的特点, 沿着轴向可以将霍尔推力器的放电通道分为3个区间: 1)以角向长波长不稳定性占主导的近阳极区; 2)轴向短波长模式占主导的加速区; 3)以倾斜的短波长占主导的羽流区.

需要说明的是, 目前利用色散关系对霍尔推力器中漂移不稳定性的研究主要是在理想的双流体模型下开展. 研究中假定物理量不随轴向位置发生变化. 实际上, 霍尔推力器中等离子体密度、电场、磁场的空间分布是关于轴向位置的函数. 采用能够详细描述各物理量在空间精确分布的二维或三维动理学模型进行研究, 则需要较长的计算时间. 基于此, 本文将在考虑推力器放电通道中各物理量轴向分布的情况下, 利用包含电子漂移、电子碰撞, 以及磁场和密度梯度的色散关系对霍尔推力器中的稳定性进行研究.

参照Smolyakov等^[6]和Lakhin等^[14]的工作给出基于流体理论的色散关系的推导过程. 放电通道中磁场、电势等物理量的分布参考Marusov等^[15]工作中给出的分布. 需要说明的是, 文献[15]中关于电势的分布表达式存在笔误, 下文将给出合适的表达式. 霍尔推力器中, 由于离子的质量远大于电子的质量, 使得离子的拉莫尔半径${\rho _{\text{i}}}$通常大于系统的长度$L$, 离子的回旋频率${\omega _{{\text{ci}}}}$小于振荡频率$\omega $. 这一特征可以在描述离子运动中忽略磁场对离子的作用. 忽略磁场的作用后, 离子的连续性方程和动量方程满足如下的形式:

式中, ${n_{\text{i}}}$是离子的密度, ${{\boldsymbol{\upsilon }}_{\text{i}}}$是离子的速度, $\phi $是空间电势, e为点电荷, ${m_{\text{i}}}$为离子质量. 假定扰动满足$\sim \exp ({\text{i}}{\boldsymbol{k}} \cdot {\boldsymbol{\hat x}} - {\text{i}}\omega t)$, k为波矢, ${\boldsymbol{\hat x}}$为单位方向矢量, $\omega $为振荡频率. 线性化处理后离子的扰动密度$\tilde n$与平衡密度${n_0}$满足关系:

其中, $ {{\boldsymbol{\upsilon }}_{{\text{0 i}}}} $是平衡时的离子速度, ${\tilde \upsilon _{\text{i}}} = {({\text{e}}\tilde \phi /{m_{\text{i}}})^{1/2}}$是离子的扰动速度. 考虑电子惯性和有效拉莫尔半径效应, 则电子的动量方程和连续性方程为^[6,25]

式中, ${m_{\text{e}}}$, ${n_{\text{e}}}$分别表示电子质量和电子密度, 在准中性假设下有${n_{\text{e}}} = {n_{\text{i}}}$. ${{\boldsymbol{\upsilon }}_{\text{e}}} = {{\boldsymbol{\upsilon }}_{/ /{\text{e}}}} + {{\boldsymbol{\upsilon }}_{ \bot {\text{e}}}}$为电子的速度, 包含平行速度${{\boldsymbol{\upsilon }}_{/ /{\text{e}}}}$和垂直速度${{\boldsymbol{\upsilon }}_{ \bot {\text{e}}}}$ (相对于磁场的方向). B为外加磁场, ${p_{\text{e}}}$为电子压强, $\varPi $为黏性张量, ${\nu _{{\text{en}}}}$为电子与中性原子的碰撞频率. 假定扰动频率远小于电子的回旋频率, 即${\text{d/d}}t \ll {\omega _{{\text{ce}}}}$, 则电子的黏性张量为无碰撞的回旋黏性张量${\varPi _{\text{g}}}$, 即可以忽略电子沿磁场方向的速度. 假定电子的速度变化率小于电子的回旋频率${\omega _{{\text{ce}}}}$, 则电子的速度可以写成^[6]:

其中, ${{\boldsymbol{\upsilon }}_{\text{E}}} = c{\boldsymbol{b}}/{B_0} \times {\nabla _ \bot }\phi $是电子的${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移速度, $c$为光速, b为沿着磁场方向的单位矢量, ${B_0}$是磁感应强度. ${{\boldsymbol{\upsilon }}_{{\text{pe}}}} = - {\boldsymbol{b}}/({\text{e}}n{B_0}) \times {\nabla _ \bot }{p_{\text{e}}}$是抗磁性漂移速度, $ {{\boldsymbol{\upsilon }}_{\text{I}}} = - {\boldsymbol{b}}/{\omega _{{\text{ce}}}} \times ({\text{d}}{{\boldsymbol{\upsilon }}_{\text{E}}}{\text{/d}}t + {\text{d}}{{\boldsymbol{\upsilon }}_{{\text{pe}}}}{\text{/d}}t) $是与惯性相关的漂移速度. $ {{\boldsymbol{\upsilon }}_\nu } = \nu {\boldsymbol{b}}/{\omega _{{\text{ce}}}} \times ({{\boldsymbol{\upsilon }}_{\text{E}}} + {{\boldsymbol{\upsilon }}_{{\text{pe}}}}) $是碰撞引起的电子漂移速度; $ {{\boldsymbol{\upsilon }}_{{\varPi _{\text{g}}}}} = - c{\boldsymbol{b}}/({\text{e}}n{B_0}) \times \nabla \cdot {{\boldsymbol{\varPi }}_{\text{g}}} $是与回旋黏性张量相关的漂移速度. 考虑回旋抵消作用, 电子速度可以写成${{\boldsymbol{\upsilon }}_{{\text{e}} \bot }} = {\boldsymbol{\upsilon }}_{\text{e}}^{(0)} + {\boldsymbol{\upsilon }}_{\text{e}}^{(1)}$:

式中, ${\boldsymbol{\upsilon }}_{\text{e}}^{(0)}$表示电子速度的零阶量, 包含电子的${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移速度和抗磁性漂移速度, ${\boldsymbol{\upsilon }}_{\text{e}}^{(1)}$为电子速度的一阶量, 包含电子惯性项以及电子的回旋黏滞效应对电子速度的修正. 电子的密度扰动可以写成如下的形式:

忽略平衡电子流${{\boldsymbol{\upsilon }}_{\text{E}}}$的剪切效应以及密度的高阶导数, 电子密度的扰动则满足如下的形式:

其中, ${\omega _0} = {\boldsymbol{k}} \cdot {\boldsymbol{\upsilon }}_{\text{E}}^{0}$是平衡电子流引起的漂移频率, $\rho _{\text{e}}^{2} = c{T_{\text{e}}}/(e{B_0}{\omega _{{\text{ce}}}})$是电子的拉莫尔半径, ${T_{\text{e}}}$是电子的温度. 需要说明的是(10)式中假定磁场是均匀的, 即流体为不可压缩流体. 考虑非均匀磁场引起的抗磁性漂移速度修正$\nabla \cdot (n{{\boldsymbol{\upsilon }}_{{\text{pe}}}})\sim 2 n{{\boldsymbol{\upsilon }}_{{\text{pe}}}} \cdot \nabla \ln B$后, 包含电子惯性, 回旋黏滞, 密度梯度和磁场梯度的色散关系可写成如下的形式^[6]:

假设电场沿着轴向${\boldsymbol{\hat x}}$, 磁场沿着径向${\boldsymbol{\hat z}}$, 则${\omega _*} = {k_y}{\upsilon _*}$, ${\omega _{\text{D}}} = {k_y}{\upsilon _{\text{D}}}$, ${\omega _0} = {k_y}{\upsilon _{\text{E}}}$分别表示密度梯度、磁场梯度引起的沿着角向的抗磁性漂移频率和 多普勒漂移频率. 其中${\upsilon _*} = - c{T_{\text{e}}}{\kappa _{\text{n}}}/({\text{e}}B)$和${\upsilon _{\text{D}}} = - 2 c{T_{\text{e}}}{\kappa _{\text{B}}} /(eB)$分别表示由于密度和磁场梯度引起的漂移速度, ${{\boldsymbol{\upsilon }}_{\text{E}}} = - cE\hat y{\text{/}}B$是电子的漂移速度^[15]. ${\kappa _{\text{N}}} = \partial \ln n(x)/\partial x$为密度梯度, ${\kappa _{\text{B}}} = \partial \ln B(x)/\partial x$为磁场梯度, $k_ \bot ^2 = k_x^2 + k_y^2$. $\omega = {\omega _r} + {\text{i}}\gamma $, ${\omega _{\text{r}}}$和$\gamma $分别代表频率和增长率. $ c_{\text{s}}^{2} = {T_{\text{e}}}/{m_{\text{i}}} $为离子声速. ${\omega _{{\text{lh}}}} = {\omega _{{\text{pi}}}}{(1 + \omega _{{\text{pe}}}^{2}/\omega _{{\text{ce}}}^{2})^{ - 1/2}}$为低杂波频率, ${\omega _{{\text{p(e, i)}}}} = \sqrt {4{\text{π}}n{e^2}/{m_{{\text{(e, i)}}}}} $为电子和离子等离子体振荡频率.

对于典型的霍尔推力器, 磁场沿着轴向满足如下的表达式^[15]:

式中, $d$为放电通道长度, ${B_{\text{m}}}$为推力器放电通道 出口处的磁感应强度, ${\vartheta _1}$为调节磁场剖面的系数. 等离子体密度与磁场具有相似的分布, 只是密度的最大值与磁场的最大值不在同一位置^[26]. 等离子体密度分布满足^[15]:

式中, ${l_1}$为密度峰值${n_{\text{m}}}$所对应的位置, 位于放电通道出口上游位置, 即${l_1} \lt d$. ${\vartheta _2}$为调节密度剖面的系数. 则磁场梯度和密度梯度可以表示为

其与梯度特征长度满足关系${l_{\text{n}}} = 1/{\kappa _{\text{N}}}$, ${l_{\text{b}}} = 1/{\kappa _{\text{B}}}$. 平衡时的电势分布为

式中, ${l_2}$为电势在轴向方向上变化最大的点, 即电场强度最大的位置, 与密度峰值位置${l_1}$之间的关系为${l_1} \lt {l_2}$. ${\vartheta _3}$为调节电势剖面的系数, ${\alpha _1} = 1{\text{/}}\left[ {\arctan ( - {\vartheta _3}) - {\alpha _2}} \right]$, ${\alpha _2}$为推力器放电通道出口下游电势的最小值. 则沿着轴向的电场分布为^[15]

其中${E_{\text{m}}} = - {\varPhi _{\text{m}}}{\alpha _1}{\vartheta _3}/{l_2}$. 则离子的沿着轴向的速度为

电子温度沿着轴向的分布为^[15]

式中, ${l_3}$为电子温度峰值$T_{\text{e}}^{{\text{max}}}$所对应的轴向位置, 其与${l_1}$, ${l_2}$之间满足关系${l_1} \lt {l_2} \lt {l_3}$. $T_{\text{e}}^{{\text{min}}}$为推力器出口下游的最小电子温度, ${\vartheta _4}$为调节温度剖面的参数.

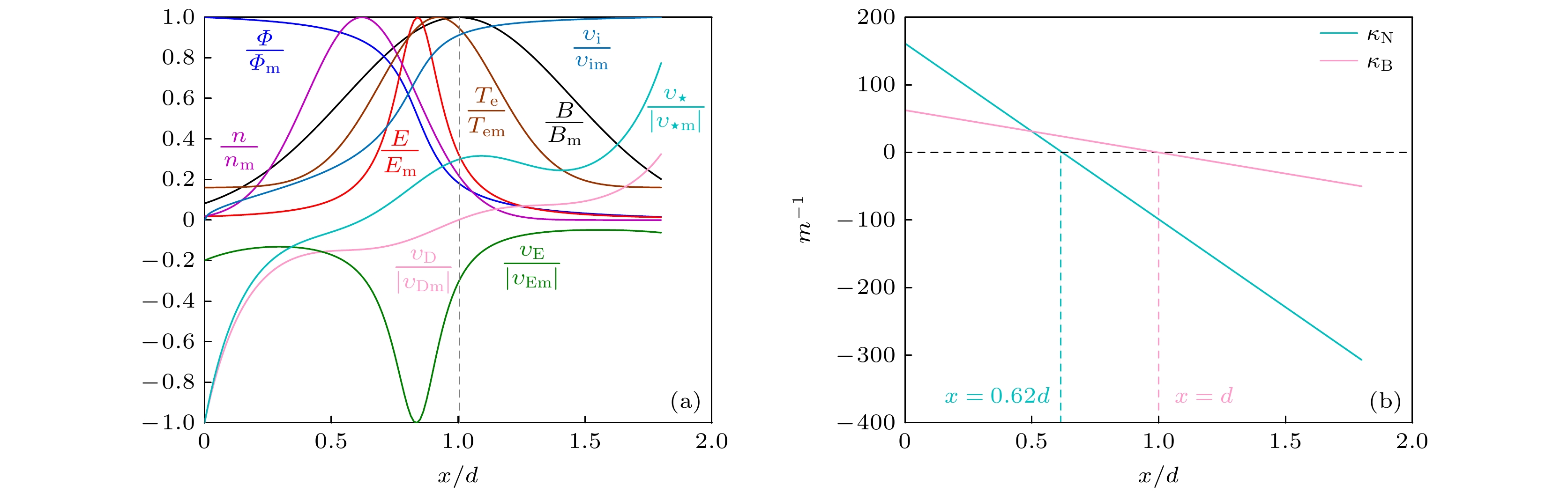
计算中磁场、等离子体密度、电势、电场、温度剖面所中涉及的参数如表1所示. 根据磁场、等离子体密度、电势、电子的${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移速度以及梯度表达式计算得到的电势$\varPhi $、等离子体密度$n$、磁感应强度$B$、电场强度$E$、离子速度${\upsilon _{\text{i}}}$、电子温度${T_{\text{e}}}$、电子漂移速度${\upsilon _{\text{E}}}$, 以及密度和磁场梯度引起的抗磁性漂移速度${\upsilon _{\text{D}}}$和${\upsilon _*}$沿着轴向的分布如图1(a)所示. 图中各物理量用其最大值进行归一化. 磁场梯度${\kappa _{\text{B}}}$和密度梯度${\kappa _{\text{N}}}$引起的漂移速度的符号与对应梯度的符号相反, 即沿着轴向, 抗磁性漂移速度${\upsilon _{\text{s}}}$和${\upsilon _{\text{d}}}$从“–”变为“+”, 而密度梯度和磁场梯度的符号变化则与之相反, 如图1(b)所示. 另外, 结合磁场和密度剖面可知: ${\kappa _{\text{N}}} \gt 0$($x \lt 0.62 d$)和${\kappa _{\text{B}}} \gt 0$($x \lt d$)意味着磁场和密度大小沿着轴向距离的增大而增大; ${\kappa _{\text{N}}} \lt 0$和${\kappa _{\text{B}}} \lt 0$则意味着磁场和密度大小沿着轴向距离的增大而减小.

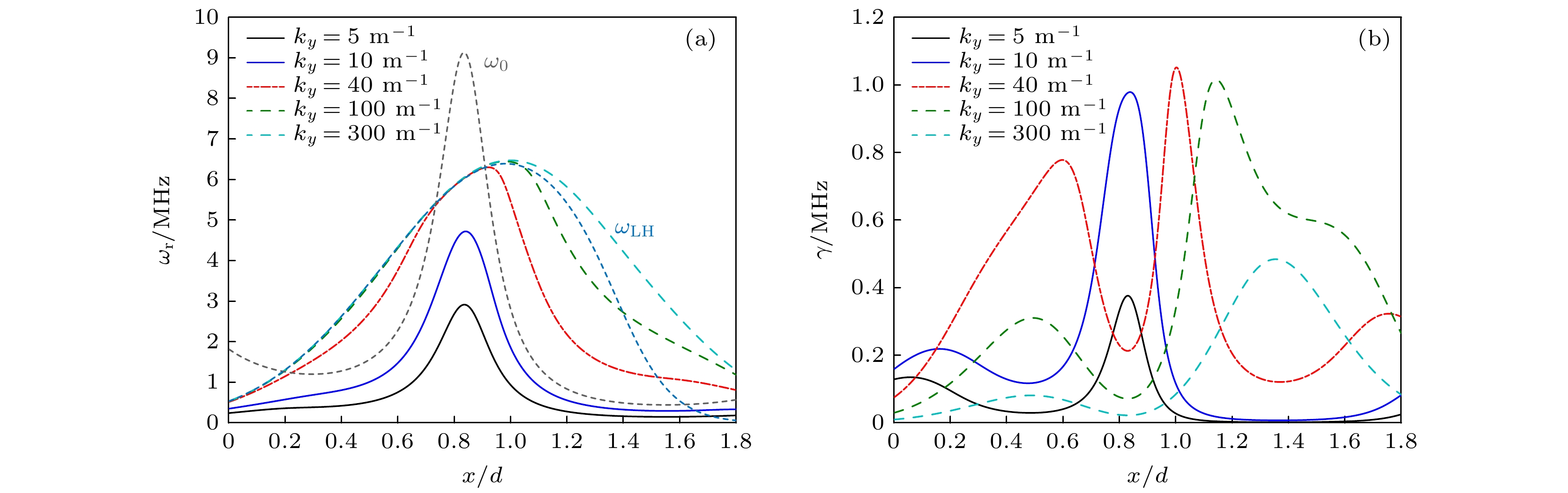
Litvak和Fisch ^[27]研究表明, 即使不存在密度梯度和磁场梯度时, 沿着${\boldsymbol{E}} \times {\boldsymbol{B}}$方向漂移电子流的碰撞效应也能够激发沿着角向传播的静电低杂波不稳定性和电磁的阿尔芬波不稳定性. 不存在密度梯度时, 包含电子惯性、电子碰撞效应, 以及平衡电子流时的色散关系为^[6]

对(10)式求解得到的不稳定性频率和增长率沿着轴向的变化如图2所示. 计算中${\nu _{{\text{en}}}} = 1.3~{\text{MHz}}$, 且激发的不稳定性完全沿着角向传播, 即${k_x} = {k_z} = 0$.

从图2可以看出, 模式的本征值沿着轴向的变化依赖于角向波矢${k_y}$的大小, 且随着${k_y}$的增大, 模式频率和增长率在轴向发生显著的变化. 图2(a)中的灰色点线为${k_y} = 15 {{\text{ m}}^{{{ - 1}}}}$时电子${\boldsymbol{E}} \times {\boldsymbol{B}}$的漂移频率, 其大小与${k_y}$成正比. 当${k_y} \lt 40 {{\text{ m}}^{{{ - 1}}}}$时, 模式的频率${\omega _{\text{r}}}$沿着轴向呈现高斯分布, 在$x = 0.8375 d$处达到最大值${\omega _{\text{r}}}_{\max }$, 且${\omega _{\text{r}}}_{\max }$随着${k_y}$的增大而增大, 如图2(a)中实线所示. 模式的增长率$\gamma $沿着轴向存在两个峰值, 且第1个峰值${\gamma _{\max 1}}$所对应的位置随着${k_y}$的增大而增大, 第2个峰值${\gamma _{\max 2}}$对应的位置不随${k_y}$改变, 与${\omega _{\text{r}}}_{\max }$所对应的位置相同. 此外, 位于两个峰值增长率之间的最小增长率${\gamma _{\min }}$所对应的位置也不随${k_y}$变化. 相较于${k_y} \lt 40 {{\text{ m}}^{{{ - 1}}}}$, 在${k_y} = 40 {{\text{ m}}^{{{ - 1}}}}$时, ${\omega _{\text{r}}}$和$\gamma $沿着轴向都发生了显著的变化. 在${k_y} = 40 {{\text{ m}}^{{{ - 1}}}}$时${\omega _{\text{r}}}_{\max }$所对应的位置向放电通道出口移动, 且${\omega _{\text{r}}}$峰值的半高宽有明显的增大. 沿着轴向$\gamma $仍存在两个峰值, 但峰值所对应的位置向放电通道出口移动. 具体而言, ${k_y} = 40 {{\text{ m}}^{{{ - 1}}}}$时的第1个峰值${\gamma _{\max 1}}$位置接近于${k_y} \lt 40 {{\text{ m}}^{{{ - 1}}}}$时${\gamma _{\min }}$所对应的位置, 第2个峰值${\gamma _{\max 2}}$位置位于$x = d$处. 位于${\gamma _{\max 1}}$和${\gamma _{\max 2}}$之间的${\gamma _{\min }}$所对应的位置与${k_y} \lt 40 {{\text{ m}}^{{{ - 1}}}}$时${\gamma _{\max 2}}$的位置相同, 如图2(b)中红线所示. 当${k_y} \gt 40 {{\text{ m}}^{{{ - 1}}}}$时, ${\omega }_{\rm r\max }$的位置进一步向通道出口移动, 直至$x = d$时${\omega _{\rm r\max }}$的位置不再随${k_y}$的增大而变化, 如图2(a)中的虚线所示. 与${k_y} \lt 40 {{\text{ m}}^{{{ - 1}}}}$相比, 当${k_y} \gt 40 {{\text{ m}}^{{{ - 1}}}}$时$\gamma $沿着轴向有相反的分布, 即${k_y} \lt 40 {{\text{ m}}^{{{ - 1}}}}$时增长率峰值的位置为${k_y} \gt 40 {{\text{ m}}^{{{ - 1}}}}$时${\gamma _{\min }}$的位置, 如图2(b)中虚线所示. 另一方面, ${k_y} \gt 40 {{\text{ m}}^{{{ - 1}}}}$时${\gamma _{\max 1}}$和${\gamma _{\max 2}}$随着${k_y}$的增大而减小, 且${\gamma _{\max 2}}$对应的位置随着${k_y}$的增大进一步向放电通道出口下游移动, 但其他峰值和峰谷所对应的位置不再随${k_y}$的变化而变化. 根据图中${\omega _{\text{r}}}$和$\gamma $的变化可知, 随着${k_y}$的增大, 模式的动力学行为会发生显著的变化, 这一点可以从(${\omega _{\text{r}}}$, $\gamma $)在相空间的变化得到进一步证实.

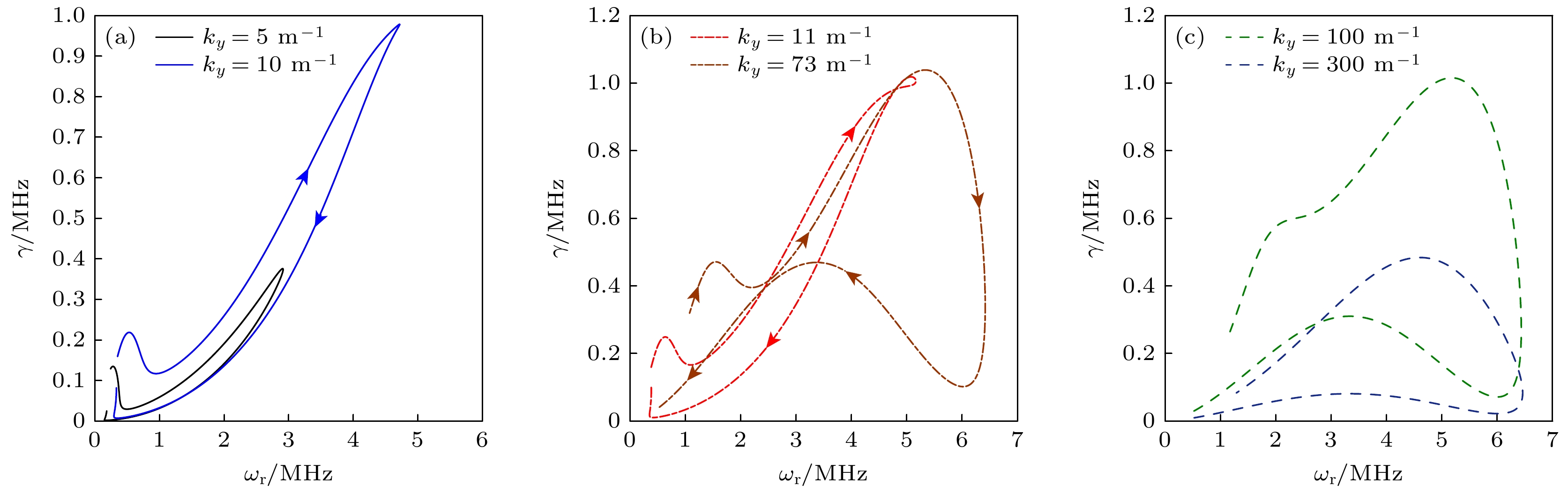
图3所示为不同${k_y}$下${\omega _{\text{r}}}$和$\gamma $在相空间上的变化. 图中的箭头代表轴向位置从推力器阳极区向羽流区的变化. 在$ {k_y} \lt 10 {{\text{ m}}^{{{ - 1}}}} $时${\omega _{\text{r}}}$和$\gamma $呈线性关系, 即$\gamma $随着${\omega _{\text{r}}}$的增大而增大, 在${\omega _{\text{r}}}$达到最大值后, $\gamma $随着${\omega _{\text{r}}}$的减小而减小, 如图3(a)所示. 在$11 {{\text{ m}}^{{{ - 1}}}} \lt {k_y} \lt 73 {{\text{ m}}^{{{ - 1}}}}$时, $\gamma $与${\omega _{\text{r}}}$在相空间中存在交点(${\omega _{{\text{rc}}}}$, ${\gamma _c}$), 且交点处所对应的(${\omega _{{\text{rc}}}}$, ${\gamma _{\text{c}}}$)值随着${k_y}$的增大而减小. 值得注意的是, 当${\omega _{\text{r}}} \lt {\omega _{{\text{rc}}}}$时, $\gamma $与${\omega _{\text{r}}}$的依赖关系与$ {k_y} \lt 10 {{\text{ m}}^{{{ - 1}}}} $时的关系相同. 当${\omega _{\text{r}}} \gt {\omega _{{\text{rc}}}}$时, $\gamma $随${\omega _{\text{r}}}$的增大而减小, 在达到最小值后随着${\omega _{\text{r}}}$的减小而增大, 直至达到最大值后又随着${\omega _{\text{r}}}$的减小而减小, 如图3(b)所示. 当${k_y} \gt 73 {{\text{ m}}^{{{ - 1}}}}$时$\gamma $与${\omega _{\text{r}}}$在相空间中不存在交点, $\gamma $与${\omega _{\text{r}}}$的依赖关系与图3(b)中${\omega _{\text{r}}} \gt {\omega _{{\text{rc}}}}$时依赖关系一致, 如图3(c)所示. 图3的结果表明, 随着${k_y}$的增大模式的本征值在相空间中由顺时针旋转变为逆时针旋转, 不稳定性从一种模式转变为另一种模式. 根据低杂波不稳定性满足的特点: ${\omega _{{\text{ci}}}} \lt {\omega _{\text{r}}} \lt {\omega _{{\text{ce}}}}$, $k_y^2\rho _{\text{e}}^{2} \leqslant 1$, $k_y^2\rho _{\text{i}}^{2} \geqslant 1$可知, 在${k_y} \lt 11 {{\text{ m}}^{{{ - 1}}}}$时模式为碰撞引起的低杂波不稳定性^[27]. ${\omega _{{\text{ci}}}}$为离子回旋频率, ${\rho _{\text{i}}}$为电子拉莫尔半径. 随着${k_y}$的增大, 在${k_y} \gt 73 {{\text{ m}}^{{{ - 1}}}}$时, 模式则转变为离子声波不稳定性. 在沿着磁场方向的波数${k_z} = 0$时, 低杂波不稳定性可以转变为离子声波不稳定性^[28]. 当$11 {{\text{ m}}^{{{ - 1}}}} \lt {k_y} \lt 73 {{\text{ m}}^{{{ - 1}}}}$时则属于两种不稳定模式的共存区间.

假定模式的频率小于电子沿着${\boldsymbol{E}} \times {\boldsymbol{B}}$方向的漂移频率, 即${\omega _{\text{r}}} \ll \left| {{\omega _0}} \right|$, 则色散关系(20)式的解满足如下的形式^[29]:

模式的增长率为

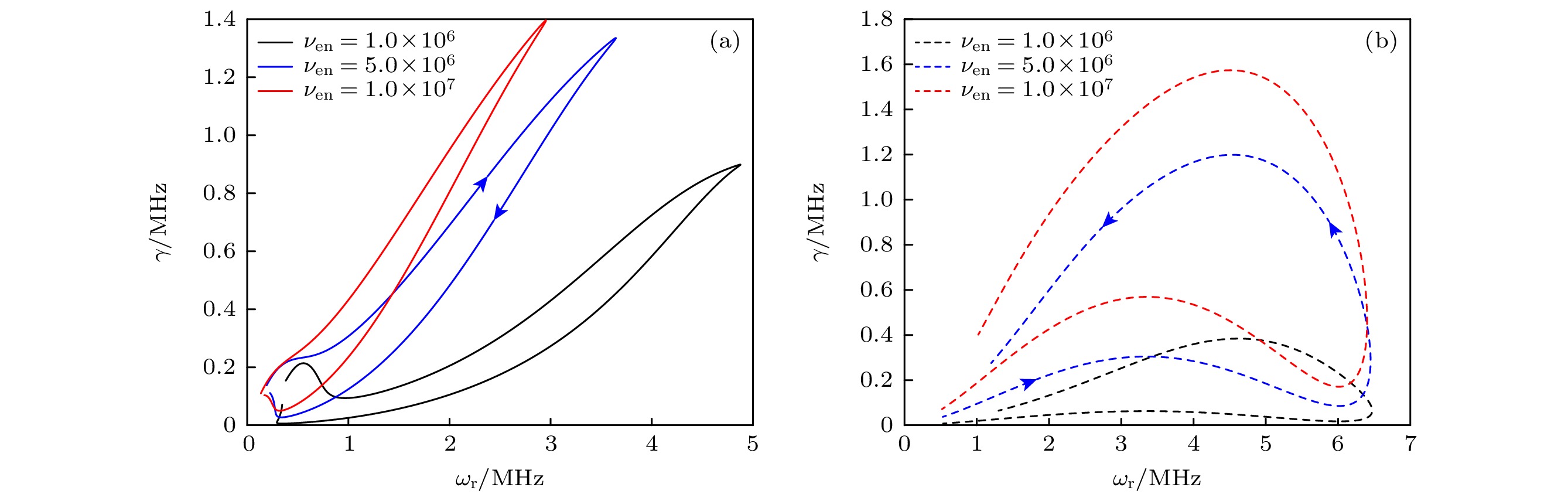
需要说明的是上述的解是基于$\omega \ll\left| {{\omega _0}} \right|$的假设下得到的. 在典型的霍尔推力器几何参数和电参数下, 当角向波矢${k_y}$较小时, 低杂波的频率${\omega _{{\text{LH}}}}\sim {\text{MHz}}$, 与${\omega _0}$的量级相同, 则由(22)式可知不稳定模式的增长率$\gamma \sim {\nu _{{\text{en}}}}$, 如图2(b)中的实线所示. 当${k_y}$较大时, 则$\gamma $与${k_y}$成反比, 如图2(b)中的虚线所示.

图4为不同碰撞频率下${k_y} = 10 {{\text{ m}}^{{{ - 1}}}}$(图4(a))和${k_y} = 300 {{\text{ m}}^{{{ - 1}}}}$时(图4(b))不稳定模式的本征值在相空间中的变化. ${k_y}$一定时$\gamma \propto {\nu _{{\text{en}}}}$, 但${\omega _{\text{r}}}$与${\nu _{{\text{en}}}}$的关系依赖于${k_y}$的大小. 当${k_y} = 10 {{\text{ m}}^{{{ - 1}}}}$时, 最大增长率${\gamma _{\max }}$对应频率${\omega _{\text{r}}}$随着${\nu _{{\text{en}}}}$的增大而减小; 当${k_y} = 300 {{\text{ m}}^{{{ - 1}}}}$时, 与${\gamma _{\max }}$对应的频率${\omega _{\text{r}}}$, 以及${\omega _{{\mathrm{r}}\max }}$几乎不随${\nu _{{\text{en}}}}$的变化而变化. 这是因为在$k_y^2\rho _{\text{e}}^{2}$较大时, 电子的响应从麦克斯韦分布变为玻尔兹曼分布, 模式由低杂波不稳定性转化为离子声波不稳定性^[6]. 上述结果表明: 1)模式的转换由角向波矢${k_y}$的改变引起; 2) ${\nu _{{\text{en}}}}$在较大的变化范围 (1.0×10⁶—1.0×10⁷ s^–1) 内改变, 不会对模式的动力学行为产生影响; 3)不依赖于$ {k_y} $的大小, 由碰撞激发的不稳定模式的增长率随着碰撞频率的增大而增大.

前面计算中忽略了等离子体的密度梯度, 事实上在无碰撞情况下, 等离子体的密度梯度也可以激发不稳定性. 本节同时考虑密度梯度、电子碰撞效应对不稳定性模式的影响, 则色散关系可以写成如下的形式:

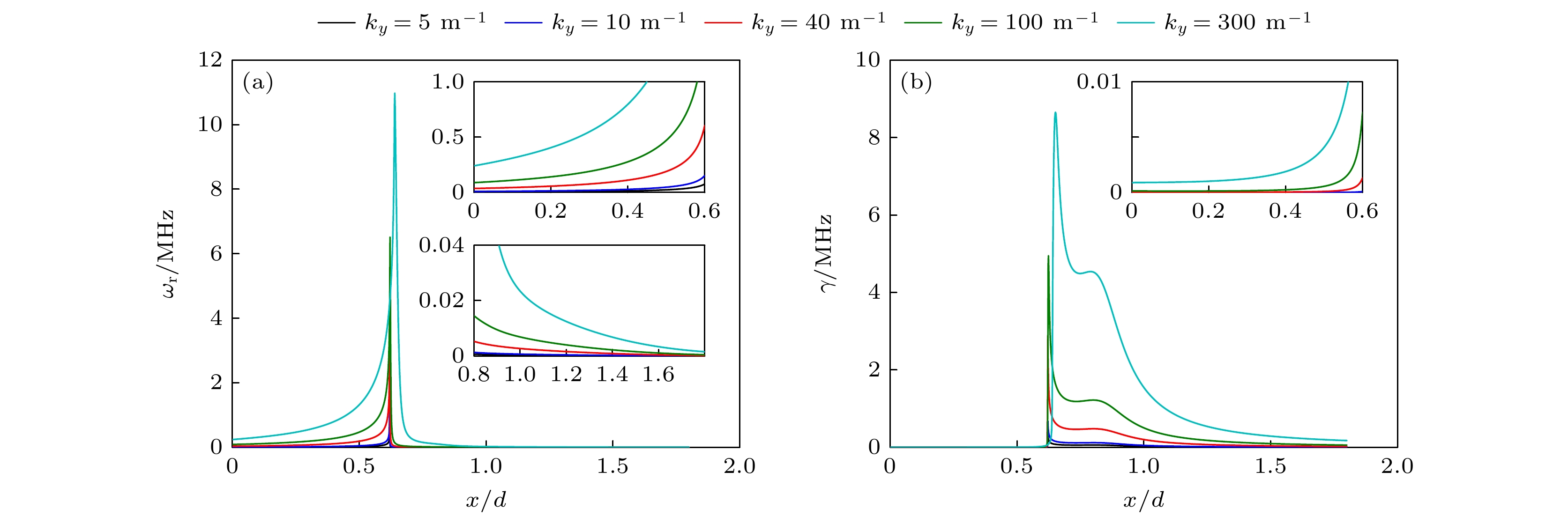
式中${\omega _*}$为密度梯度引起的抗磁性漂移频率.

图5为同时包含了碰撞效应和等离子体密度梯度时激发的不稳定性. 与图2相比, 在包含了密度梯度后, 模式的本征值发生了显著的变化. 模式的本征值在$x = 0.62 d$附近达到最大值. 由图1可知, 在$x = 0.62 d$处等离子体密度达到最大值, 密度梯度${\kappa _{\text{N}}}\sim 0$, 则相应的由密度梯度引起的漂移频率${\omega _{\text{s}}} = 0$. 此时, 模式的本征值与不包含密度梯度时计算得到的本征值相同, 如图2所示. 此外, 模式的本征值在$x = 0.62 d$两侧有相反的变化趋势. 在$x \lt 0.62 d$时, ${\omega _{\text{r}}}$和$\gamma $的随着$x$的增大而增大; 当$x \gt 0.62 d$时, ${\omega _{\text{r}}}$和$\gamma $随着$x$增大而减小. 这是因为在$x = 0.62 d$两侧由密度梯度引起的漂移频率${\omega _{\text{s}}}$的符号发生了变化. 当$x \lt 0.62 d$时${\omega _{\text{s}}} \lt 0$, 且$\left| {{\omega _{\text{s}}}} \right|$随着$x$的增大而减小; 当$x \gt 0.62 d$时${\omega _{\text{s}}} \gt 0$, 且$\left| {{\omega _{\text{s}}}} \right|$随着$x$的增大而增大, 如图1(a)中的${\upsilon _*}/\left| {{\upsilon _{*{\text{m}}}}} \right|$的分布. 比较图2和图5可知, 相较于碰撞激发的不稳定性: 当$ \omega_{{\mathrm{a}}} $与${\omega _{\text{r}}}$反向时密度梯度对不稳定性的激发有削弱作用($x \lt 0.62 d$); 当${\omega _{\text{s}}}$与${\omega _{\text{r}}}$同向时密度梯度对不稳定性的激发有增强作用($x \gt 0.62 d$). 另一方面, 不同于碰撞引起的不稳定性的本征值与${k_y}$的依赖关系, 包含密度梯度时${\omega _{\text{r}}}, \gamma \propto {k_y}$, 这意味着在同时包含碰撞和密度梯度效应时, 密度梯度占主导作用.

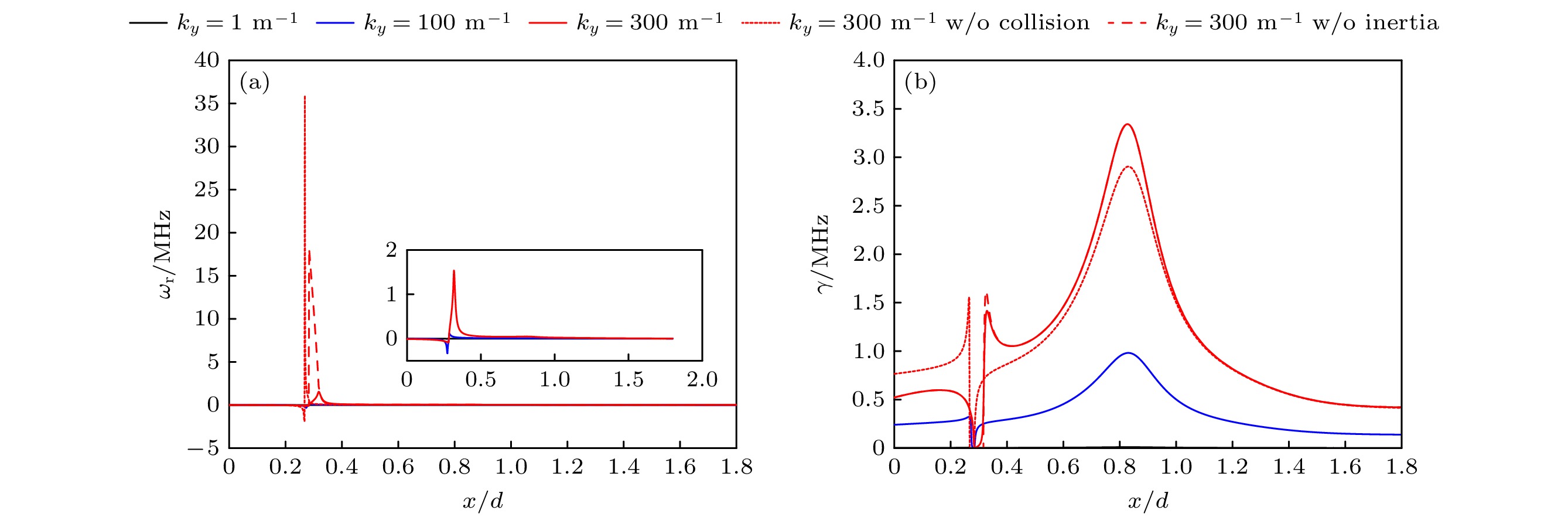
Frias等^[24]在忽略电子惯性和径向波数${k_z} = 0$的情况下, 研究了不同霍尔推力器中磁场梯度和密度梯度引起的不稳定性, 结果表明, 由磁场梯度和密度梯度引起的不稳定性在不同的霍尔推力器中具有相同的特征: 沿着推力器放电通道轴向, 梯度漂移不稳定性出现在近阳极区和羽流区两个分离的区域, 在加速区中不存在不稳定性. 本节同时考虑包含磁场和密度梯度、电子碰撞, 以及电子惯性时所激发的不稳定性. 此时, 色散关系满足如下的形式:

图6所示为同时包含了密度和磁场梯度以及电子碰撞和电子惯性时${\omega _{\text{r}}}$和$\gamma $沿着轴向的分布. 为了比较电子碰撞和电子惯性对不稳定性的影响, 图中同时给出了${k_y} = 300 {{\text{ m}}^{{{ - 1}}}}$时无电子碰撞(图中红色虚线)和无电子惯性(图中红色点线)时${\omega _{\text{r}}}$和$\gamma $沿着轴向的变化. 从图6可以看到: 1)包含碰撞和电子惯性作用时, 沿着放电通道$\gamma \gt 0$, 在$x = 0.28 d$附近$\gamma \sim 0$; 当不包含碰撞作用时, 在$0.28 d— 0.32 d$的区间内$\gamma = 0$, 其余位置处$\gamma \gt 0$; 当不包含电子惯性作用时, 在区间$0.26 d—0.28 d$上$\gamma = 0$, 其余位置处$\gamma \gt 0$. 上述结果表明, 电子惯性和碰撞效应有轻微的去稳作用. 不包含电子惯性和碰撞效应时, 将出现稳定窗; 2)模式的本征值与${k_y}$成正比, 模式的频率除了在临界稳定点附近较大外, 其余区域模式的频率都较小. 在不包含碰撞和电子惯性时的色散关系可以写成如下的形式:

(25)式的解为

系统具有不稳定性的条件为

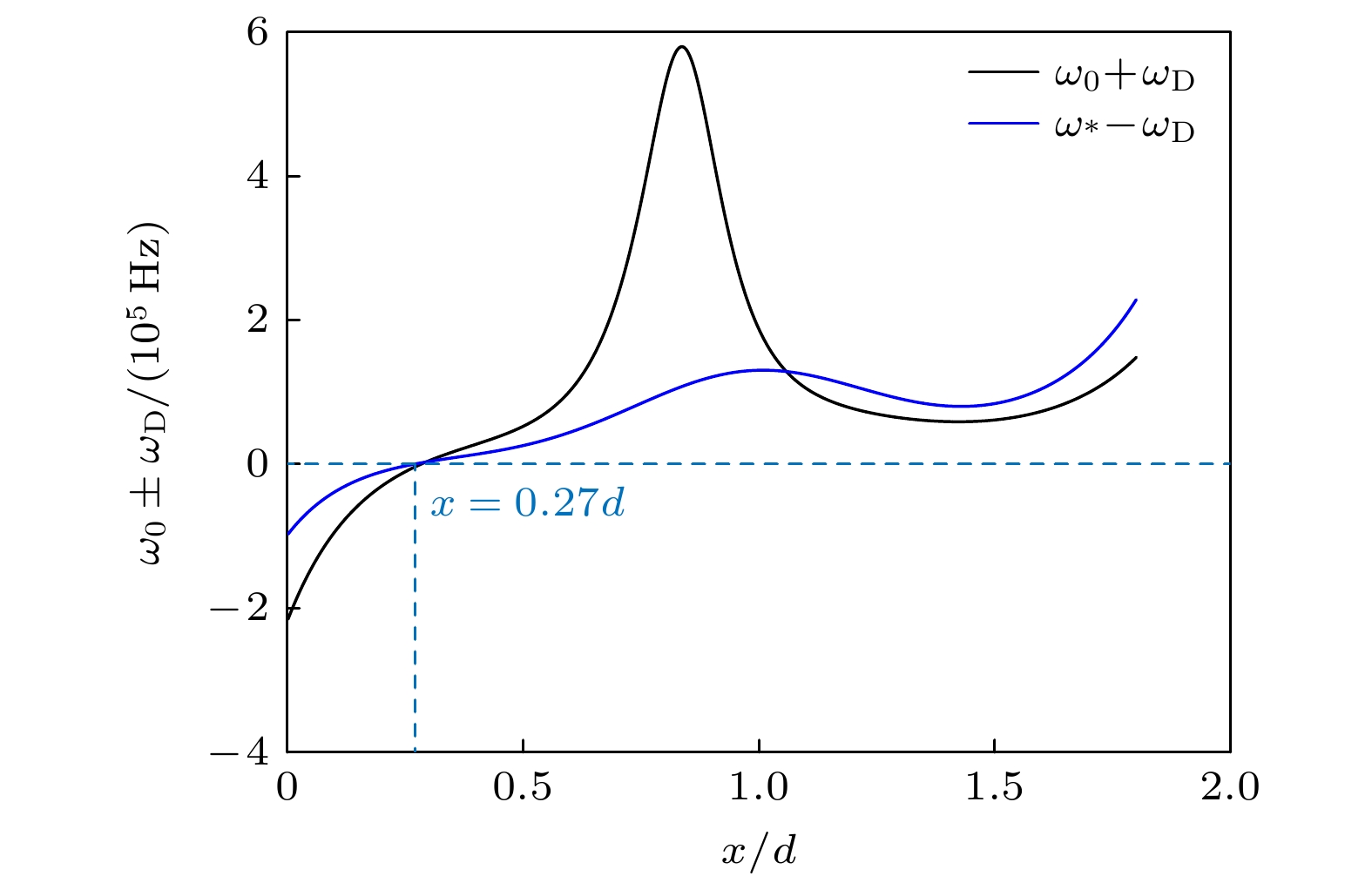
即$\Im = k_ \bot ^2 c_{\text{s}}^{2}/({\omega _*} - {\omega _{\text{D}}})$和$ \Re = \Im - 4({\omega _0} + {\omega _{\text{D}}}) $具有相反的符号($\Im \gt 0$时$\Re \lt 0$, 或$\Im \lt 0$时$\Re \gt 0$). 换句话说, 是否存在不稳定模式取决于${\omega _*}$, ${\omega _{\text{D}}}$以及${\omega _0}$的相对大小. 图7所示为${k_y} = 1 {{\text{ m}}^{{{ - 1}}}}$时${\omega _0} + {\omega _{\text{D}}}$, ${\omega _*} - {\omega _{\text{D}}}$轴向的分布. 从图7可以看到, 由于沿着轴向${\omega _0} \gt 0$, ${\omega _*}$和${\omega _{\text{D}}}$的大小依赖于密度和磁场分布, 因此沿着放电通道${\omega _0} + {\omega _{\text{D}}}$和${\omega _*} - {\omega _{\text{D}}}$的符号将发生变化. 1) 当$\Im \gt 0$时, ${\omega _*} - {\omega _{\text{D}}} \gt 0$, $x \gt 0.2687 d$, 存在不稳定性的条件为$ \Im - 4({\omega _0} + {\omega _{\text{D}}}) \lt 0 $, 意味着$ {\omega _0} + {\omega _{\text{D}}} \gt \Im /4 $, 对应$x \gt 0.285 d$, 即存在不稳定性的区域为$x \gt 0.285 d$; 2) 当$\Im \lt 0$时, ${\omega _*} - {\omega _{\text{D}}} \lt 0$, $x \lt 0.2687 d$, 存在不稳定性的条件为$ \Im - 4({\omega _0} + {\omega _{\text{D}}}) \gt 0 $, 意味着$\Im /4 \gt {\omega _0} + {\omega _{\text{D}}}$, 对应$x \lt 0.285 d$, 即存在不稳定性的区域为$x \lt 0.2687 d$; 3) 当$x\sim 0.27 d$时, $\Im \to \infty $, ${\omega _*} - {\omega _{\text{D}}} \to 0$, $\Im \times \Re \to + \infty $, 意味着不存在不稳定模式, 即$\gamma = 0$, 且${\omega _{\text{r}}}$在$x\sim 0.27 d$附近将出现尖峰, 如图6所示.

上述结果与Smolyakov等^[6]和Frias等^[24]的研究定性一致. 对于由磁场和密度梯度驱动的不稳定性, 频率满足${\omega _{\text{r}}}\sim - (k_ \bot ^2/{k_y}){\omega _{{\text{ci}}}}{({\kappa _{\text{N}}} - 2{\kappa _{\text{B}}})^{ - 1}}$^[26]. 当只考虑密度梯度时, 模式频率${\omega _{\text{r}}}\sim - k_ \bot ^2{\omega _{{\text{ci}}}}/ ({\kappa _{\text{N}}}{k_y})$^[6]. 由于本文只考虑了沿着角向传播的不稳定性, 即${\omega _{\text{r}}}\sim \left| {{k_y}{\omega _{{\text{ci}}}}/{\kappa _{\text{N}}}} \right|$, 因此${\omega _{\text{r}}}\sim | {k_y}{\omega _{{\text{ci}}}}/ {\kappa _{\text{N}}} |$; 考虑密度和磁场梯度时${\omega _{\text{r}}}\sim | {k_y}{\omega _{{\text{ci}}}}({\kappa _{\text{N}}} - 2{\kappa _{\text{B}}})^{ - 1} |$. 当${\kappa _{\text{N}}} \to 0$或者${\kappa _{\text{N}}} - 2{\kappa _{\text{B}}} \to 0$时, 模式的频率将出现尖峰, 如图5和图6所示. 此外, 根据图2可知, 对于${\kappa _{\text{N}}} - 2{\kappa _{\text{B}}} \to 0$的情况, 只能发生在$x \lt 0.62 d$的位置处, 即$x = 0.28 d$附近. 需要说明的是图5和图6中的频率峰值~MHz, 但模式并非EDI, 这是因为EDI的激发需要满足共振条件${k_y}{\upsilon _{\text{E}}} = n{\omega _{{\text{ce}}}}$, 其沿着角向和径向的振荡频率与离子等离子体振荡频率接近.

值得说明的是, 早期的研究结果表明, 电子与中性原子的碰撞作用会使得线性增长的EDI达到饱和, 并且在波对离子的捕获作用下使EDI转化为声波不稳定性^[30]. 而低杂波不稳定性作为一种特殊的EDI^[17,31–33], 能够被电子碰撞效应激发, 且随着${k_y}$的增大转化为离子声波不稳定性. 与仅由碰撞激发的低杂波不稳定性相比, 在包含密度梯度和磁场梯度后模式的行为发生了显著的变化, 即在同时包含电子碰撞和密度、磁场梯度效应时, 梯度效应在不稳定性的激发中起主导作用. 上述结果意味着, 相较于梯度效应, 电子碰撞和电子惯性对EDI有更加直接的影响. 这是因为, 轴向电场分布通过电子迁移率受电子与中性原子碰撞效应的影响, 而轴向电场的改变则会对电子的漂移速度产生影响, 进而对EDI产生影响. 此外, 电子惯性对高频、短波长模式的耦合有重要的影响, 而梯度驱动的长波长不稳定性则通常是在忽略电子惯性的情况下得到. 当电子的角向漂移速度小于电子的热速度时则可以忽略电子惯性^[34], 此时EDI满足离子声波色散关系, 且在离子的朗道阻尼作用下达到饱和^[17].

本文基于两场流体模型下的色散关系, 结合霍尔推力器中的各物理量沿着轴向的分布, 研究了电子与中性原子的碰撞效应, 电子惯性、密度梯度、磁场梯度对霍尔推力器中沿着角向传播的不稳定性的影响, 得到以下结果.

1) 在无磁场梯度和密度梯度的情况下, 电子与中性原子之间的碰撞能够激发不稳定性. 在${k_y} \lt 10 {{\text{ m}}^{ - 1}}$时为碰撞激发的低杂波不稳定性, ${k_y} \gt 70 {{\text{ m}}^{{{ - 1}}}}$为离子声波不稳定性, $11 {{\text{ m}}^{{{ - 1}}}} \lt {k_y} \lt 70 {{\text{ m}}^{{{ - 1}}}}$为两种不稳定性的共存区间. 随着${k_y}$的增大, 从阳极到羽流区, 模式本征值在相空间中从沿顺时针旋转变为逆时针旋转. 此外, 在${k_y} \ne 0$, ${k_x} = {k_z} = 0$的情况下模式的增长率随着碰撞频率的增大而增大, 这一趋势不依赖于${k_y}$的大小.

2) 在包含密度梯度、碰撞、以及电子惯性时, 密度梯度对不稳定性的激发起主导作用, 模式的频率和增长率随着${k_y}$的增大而增大, 但模式的动力学行为在相空间中不会随${k_y}$变化. 当${\omega _{\text{s}}}$与${\omega _{\text{r}}}$反向时密度梯度对不稳定性的激发有削弱作用($x \lt 0.62 d$); 当${\omega _{\text{s}}}$与${\omega _{\text{r}}}$同向时密度梯度对不稳定性的激发有增强作用($x \gt 0.62 d$).

3) 在考虑密度梯度、磁场梯度、电子惯性和碰撞效应时, 模式本征值的变化依赖于电子的${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移频率, 密度梯度以及磁场梯度引起的抗磁性漂移频率三者的相对大小. 当 ${\omega _*} - {\omega _{\text{D}}} \gt 0$时不稳定模式存在的区域为$x \gt 0.285 d$; 当 ${\omega _*} - {\omega _{\text{D}}} \lt 0$时不稳定模式存在的区域为$x \lt 0.2687 d$; 当 ${\omega _*} - {\omega _{\text{D}}}\sim 0$时不存在不稳定模式, 即$\gamma = 0$.

后续, 我们将在自洽计算各物理量的基础上, 研究有限电子拉莫尔半径、三维效应, 以及离子速度对霍尔推力器中不稳定性的影响.