首页
登录
注册
下载:
-
第三代稀土永磁材料NdFeB由于其优异的磁性能为人们广泛应用和研究, 然而, Nd/Pr的大量消耗导致了大量廉价的高丰度稀土(如La, Ce, Y等)的积压. 利用这些高丰度廉价稀土制备成高性能高熵永磁合金是解决这一问题的有效方法. 高熵合金技术由于其独特的扩散机制和鸡尾酒效应为稀土永磁体提供了新的机遇[1,2], 有望在降低成本的同时提高样品性能. 高熵稀土永磁材料是一种新型的磁性材料, 它由多种稀土元素(RE)组成, 这些元素具有相似的原子半径并逐渐占据4f轨道, 赋予其丰富的光学、电学和磁学性质[3]. 研究表明高熵组分对提高样品磁性能有较大帮助, 例如高熵永磁材料Fe2CoNiAlCu0.4Ti0.4在铸态矫顽力达到1078 Oe (1 Oe =79.58 A/m), 已具备强的硬磁性, 与AlCoFeNi的软磁性有较大不同[4]. 有研究表明, (La13Ce24Pr7Nd28Y28)16FebalM0.7B6 (M = Al, Cu, Ga, Zr, Nb, 含量为原子百分比)高熵合金的磁能积可达到33.48 MGOe (1 MGOe = 7.96 kJ/m3), 这为制备高性价比的磁体提供了一种思路[5]; (La0.25Pr0.25Nd0.25Sm0.25)2Co17高熵合金在5 K时的磁矩高达39.81μB, 大于Pr2Co17, Nd2Co17和Sm2Co17化合物的最大值[6]. 这些优势使得高熵稀土永磁材料在各种应用中具有巨大的潜力. 因此, 它们被认为是一类重要的高熵材料, 正处于快速发展的前沿.
高丰度廉价稀土虽然有可能制备出低成本较高磁性能的高熵永磁体, 但是高丰度稀土对矫顽力带来的下降是不可忽视的[7], 而较大的矫顽力对磁体反磁化机理的研究至关重要, 所以为得到高性能的永磁体, 在高熵组分中添加重稀土元素就显得尤为重要. 对于高性能的高熵稀土永磁材料, 高磁能积(BH)max和反磁化机理研究是重中之重. 目前NdFeB磁体的最大磁能积已经达到理论值的90%以上, 但实际矫顽力数值与其理论值仍有较大差距. 我们知道(BH)max的最大值由剩磁Mr决 定, 在保证一定方形度的情况下, 矫顽力与剩磁值应该满足Hc≈4πMr. 目前众多实验研究表明与剩磁相比, 矫顽力Hc对于(BH)max的影响更为关 键. 对于具有优异磁性能表现的如纳米复合相、 取向烧结单相NdFeB磁体, 科研人员对其反磁 化过程和矫顽力机理开展了大量的理论和实验研究[8–12]. 然而高熵稀土永磁体的磁性机理以及反磁化机理仍不清楚, 其反磁化机理到底是形核模型或是钉扎模型亦或是自钉扎机制[13,14]仍然需要进一步讨论.
除了反磁化机理研究, 磁黏滞系数S的研究有助于进一步理解高熵稀土永磁材料独特的性质[15]和提高其磁性能. 磁黏滞性是一种材料在磁场变化下的磁化率变化的现象. 在固定磁场中磁化强度随时间的变化可以描述为:
$M(t) = A+S\ln (t + t_0) $ , 其中t是外加恒定磁场的时间, 磁黏滞系数S和t0是常数. 这是由于磁性材料中存在的亚稳态相在外加磁场作用下发生磁矩翻转, 从而导致材料的整体磁化率发生变化. 研究表明[10,16], NdFeB磁体的磁黏滞系数与其微观结构, 特别是与晶粒大小和形状, 以及晶粒间的交互作用密切相关. 对于复合纳米NdFeB磁体, 其磁黏滞系数会受到硬磁相和软磁相的比例的影响[8,17–19]. 磁黏滞系数可以反映材料的磁滞损耗, 从而决定其在电机和发电机等设备中的利用效率.本文制备了(La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88和(La0.2Pr0.2Nd0.2Gd0.2 Tb0.2)11.76Fe82.36B5.88高熵永磁合金. 除了添加高丰度廉价稀土La和轻稀土Sm以外, 还分别添加了重稀土Gd, Dy和Tb. 这些重稀土往往能提升永磁体的矫顽力. 我们测试了样品的X射线衍射(XRD)图谱、M-H和M-T曲线, 并研究样品的Henkel曲线和磁黏滞系数S以进一步理解高熵对高熵稀土永磁体的反磁化过程和矫顽力机理的影响.
-
在高纯氩气条件下, 通过真空电弧熔炼技术反复熔炼3次得到Nd11.76Fe82.36B5.88, (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88 (样品A)和(La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88 (样品B)合金铸锭, 本实验所选用的稀土元素和过渡族元素的纯度均大于99.9%. 鉴于稀土元素沸点较低, 熔炼过程中易挥发, 所以配料过程中多加入5%的稀土元素作为补偿, 其中Sm多加15%作为补偿. 每个样品的配比质量为10 g. 熔炼完成后将铸锭进行Ar气封管, 将封管后的试样进行热处理, 退火温度为1050 ℃, 保温7 d后炉冷. 退火完成后使用熔融旋甩快淬法得到快淬合金薄带, 铜锟转速为20 m/s.
用XRD(SmartLab, Rigaku, Cu Kα)确定样品的物相组成, 扫描速率为2 (°)/min, 扫描范围为25°—60°. 采用超导量子干涉仪(SQUID)测量了条带样品在500 Oe磁场下的M-T热磁曲线, 温度范围为300—650 K, 变温速率为5 K/min, 居里温度点由求导得出. 在300 K测量条带样品的M-H磁滞回线, 其中所用的最大外场为40 kOe. 测量回复曲线时, 通过周期性改变起始磁化曲线和退磁曲线上的外加磁场, 在外加磁场达到目标值后将磁场降为零, 测量得到目标磁场下的剩磁, 并以目标磁场与饱和磁场下的矫顽力之比为x轴, 目标磁场下的剩磁与饱和磁场下的剩磁之比为y轴, 得到起始磁化曲线和退磁曲线下的回复曲线. 在逐渐递增外场至37 kOe所测量的磁滞回线中, 统计从每个周期磁场中测得剩磁和矫顽力, 进而得到矫顽力和剩磁与最大外场H的关系. Henkel-plot曲线由公式
$\delta m = [M_{\mathrm{d}}(H) - M_{\mathrm{r}} + 2 M_{\mathrm{r}}(H)]/M_{\mathrm{r}}$ 获得, 其中剩磁Mr(H)是在施加磁场 H 后并随后移除得到的; Md(H)是在单一方向上直流饱和后, 随后施加并移除反方向的磁场 H 后得到的. 测量用样品的形状为长约5 mm、宽约1.5 mm. 为减小退磁效应, 测量方向选择为条带样品的长轴方向. -
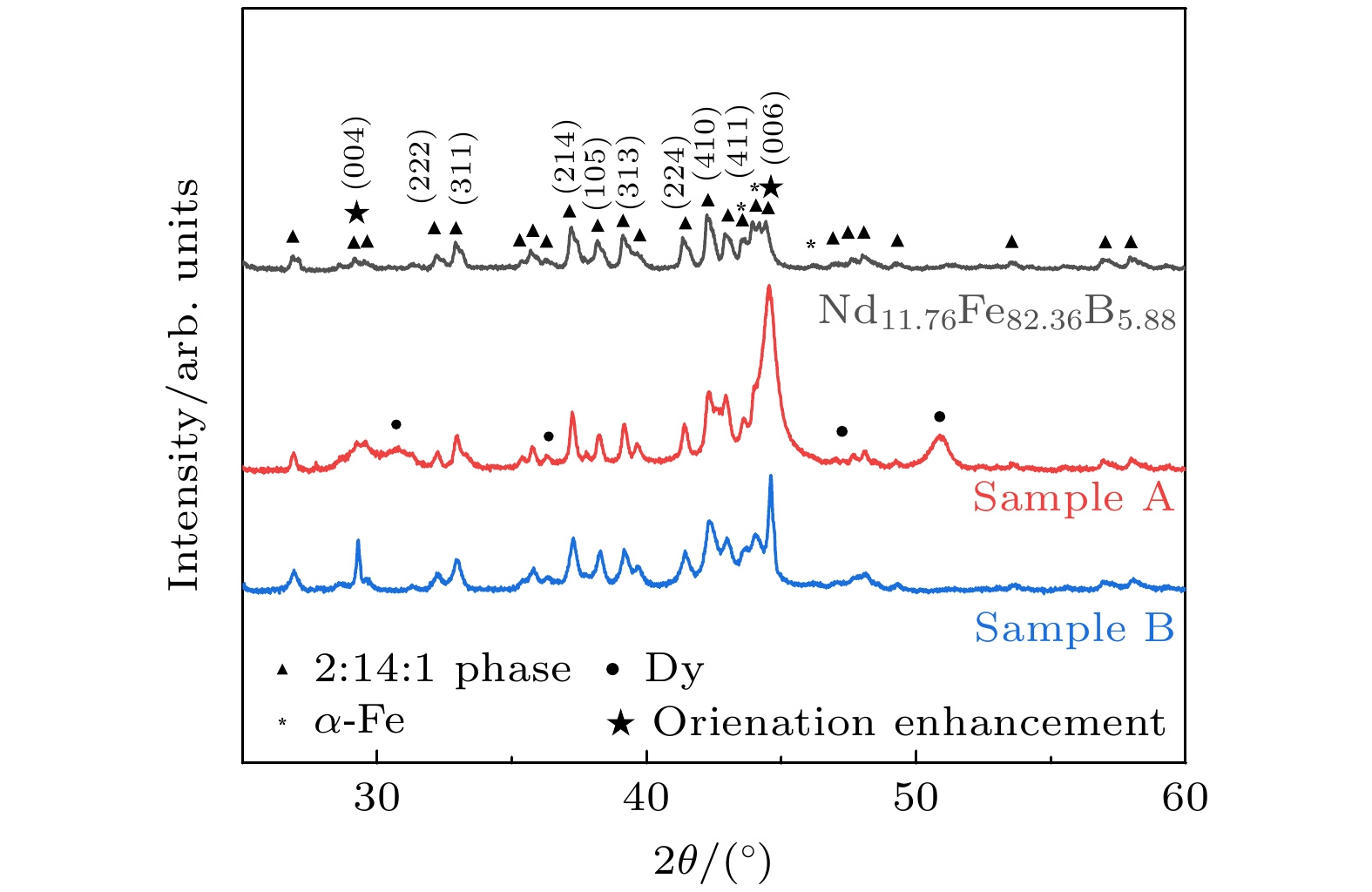
图1给出了样品Nd11.76Fe82.36B5.88, (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88 (样品A)和(La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88 (样品B) 的 XRD图谱. 由图1可以看出Nd11.76Fe82.36B5.88样品除了2∶14∶1主相以外, 存在少量α-Fe相. 样品A中除了存在少量Dy单相, 主要由2∶14∶1相构成. 样品B主要由2∶14∶1相构成, 无明显杂相, 样品A和B均在[001]方向上出现织构.
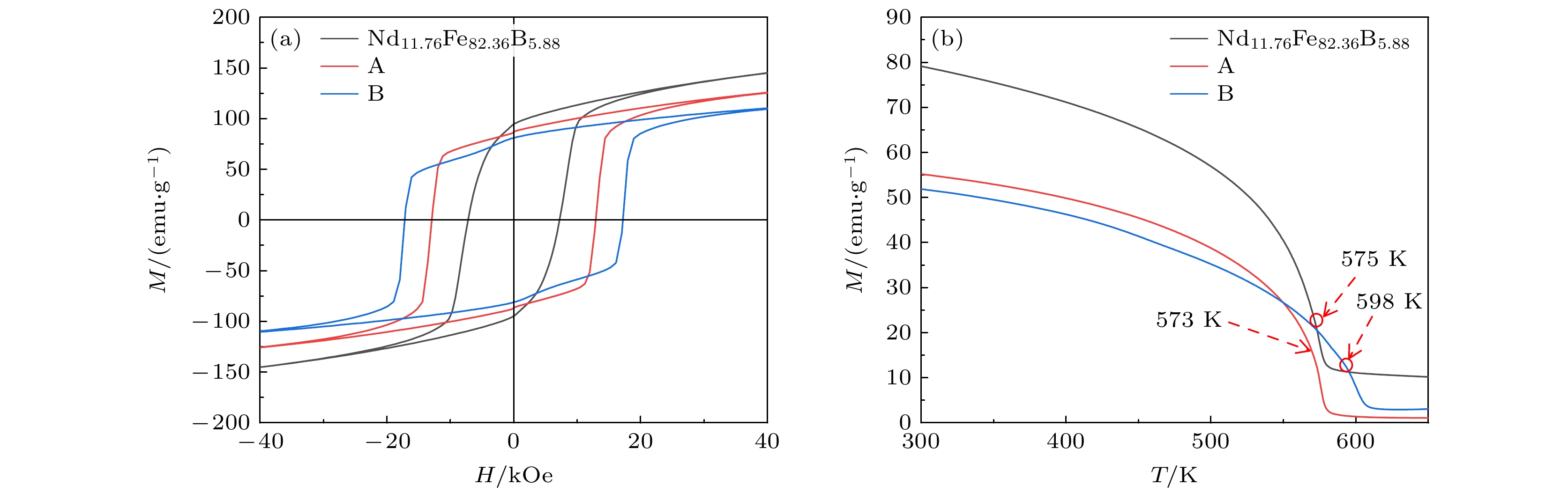
图2(a), (b)分别为纯NdFeB, 样品A, B在室温下的磁滞回线(M-H)和热磁(M-T)曲线. 从图2(a)可看出, 纯NdFeB、样品A和样品B表现为单一硬磁相. 纯NdFeB的矫顽力Hc = 7.18 kOe, 饱和剩磁Mr = 94.12 emu/g; 样品A的矫顽力Hc = 12.94 kOe, 饱和剩磁Mr = 87.11 emu/g; 样品B的矫顽力Hc = 17.5 kOe, 饱和剩磁Mr = 81.17 emu/g. 从图2(b)可以进一步看出, 纯NdFeB在达到居里温度时, 样品磁矩不为零, 说明样品中存在少量α-Fe相; 样品A和样品B在达到居里温度后磁矩基本为0, 表明样品中α-Fe含量较少. 所研究的高熵样品与纯NdFeB相比, 高熵样品在具有较大矫顽力的同时剩磁并没有降低太多, 且成相过程中α-Fe相含量较低.
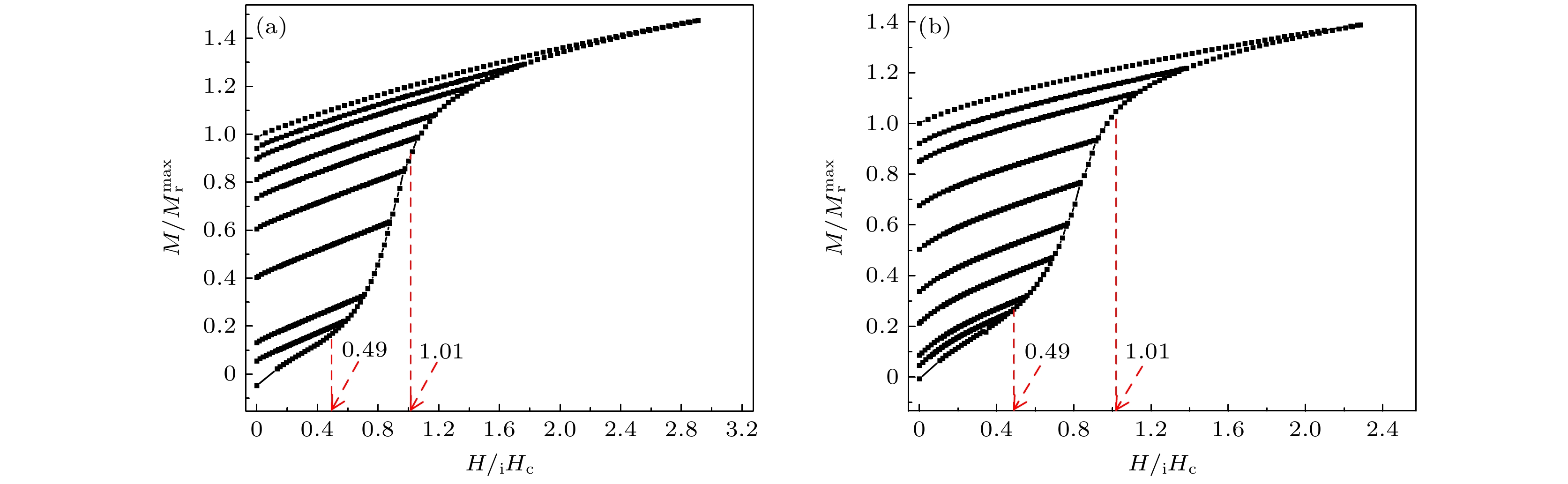
为了进一步研究样品的反磁化机理, 图3(a), (b)分别为样品A和样品B的起始磁化曲线和至零场的回复曲线. 其中M是磁化强度, Mr是剩余磁化强度,
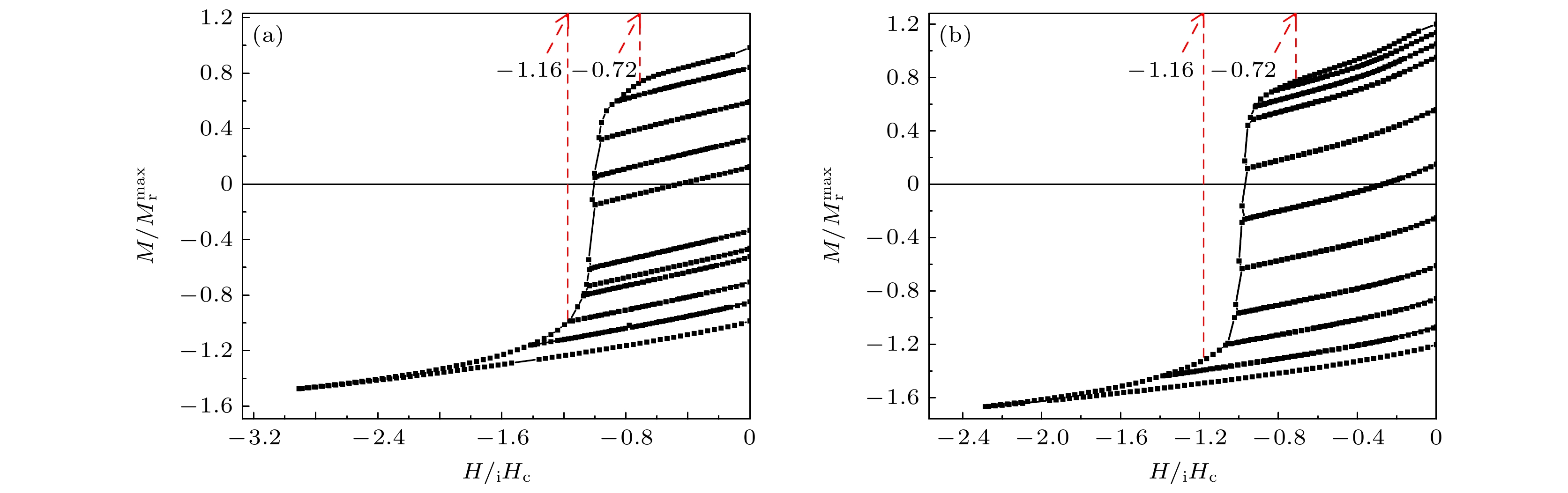
$ M_{\text{r}}^{{\text{max}}} $ 是饱和剩磁值. 当两样品的H/iHc < 0.49时, 磁化曲线具有较强的可逆性, 磁化率和剩磁值较低; 当H/iHc > 0.49时, 磁化率迅速提高, 剩磁值迅速增大, 在此过程中, 不可逆性变得尤为明显. 如图3(a)所示, 对于样品A, 当H/iHc = 1.01时, 即H > iHc, 其剩磁M/$ M_{\text{r}}^{{\text{max}}} $ = 0.94; 如图3(b)所示, 对于样品B, 当H/iHc = 1.01时, 即H >iHc, 其剩磁M/$ M_{\text{r}}^{{\text{max}}} $ = 1.04, 即当外加磁场大于内禀矫顽力时, 两样品的剩磁均达到了饱和剩磁值[15]. 而对于钉扎模型, 起始磁化曲线具有较低的磁化率, 剩磁无法快速达到饱和剩磁值. 由此得知, 可以排除样品的反磁化机理为钉扎模型的可能, 所以可以推论出该样品的矫顽力机理为形核模型. 本样品在低磁场表现出较低的磁导率是因为磁体从初始状态开始逐步磁化的过程中, 磁畴壁偏离最小畴壁能的位置比较困难, 磁畴壁难以移动. 当磁场进一步升高时, 由于高熵合金独特的扩散机制, 晶体内部成分比较均匀, 在永磁体中, 晶粒内部对磁畴壁移动的阻碍作用比较小, 这使得磁晶各向异性势垒降低, 技术反磁化的过程中这些晶粒很容易达到磁化饱和, 所以磁化率升高, 由形核模型主导[8]. 但研究发现矫顽力并没有下降, 这可能是由于均匀化使得交换耦合长度变大所导致.图4(a), (b)分别为样品A和样品B的退磁曲线和退磁过程中的回复曲线. 两样品在H/iHc <0.72时, 磁矩翻转较慢, 当0.72 < H/iHc < 1.16时, 磁矩迅速翻转之后达到饱和. 与上述分析一致.
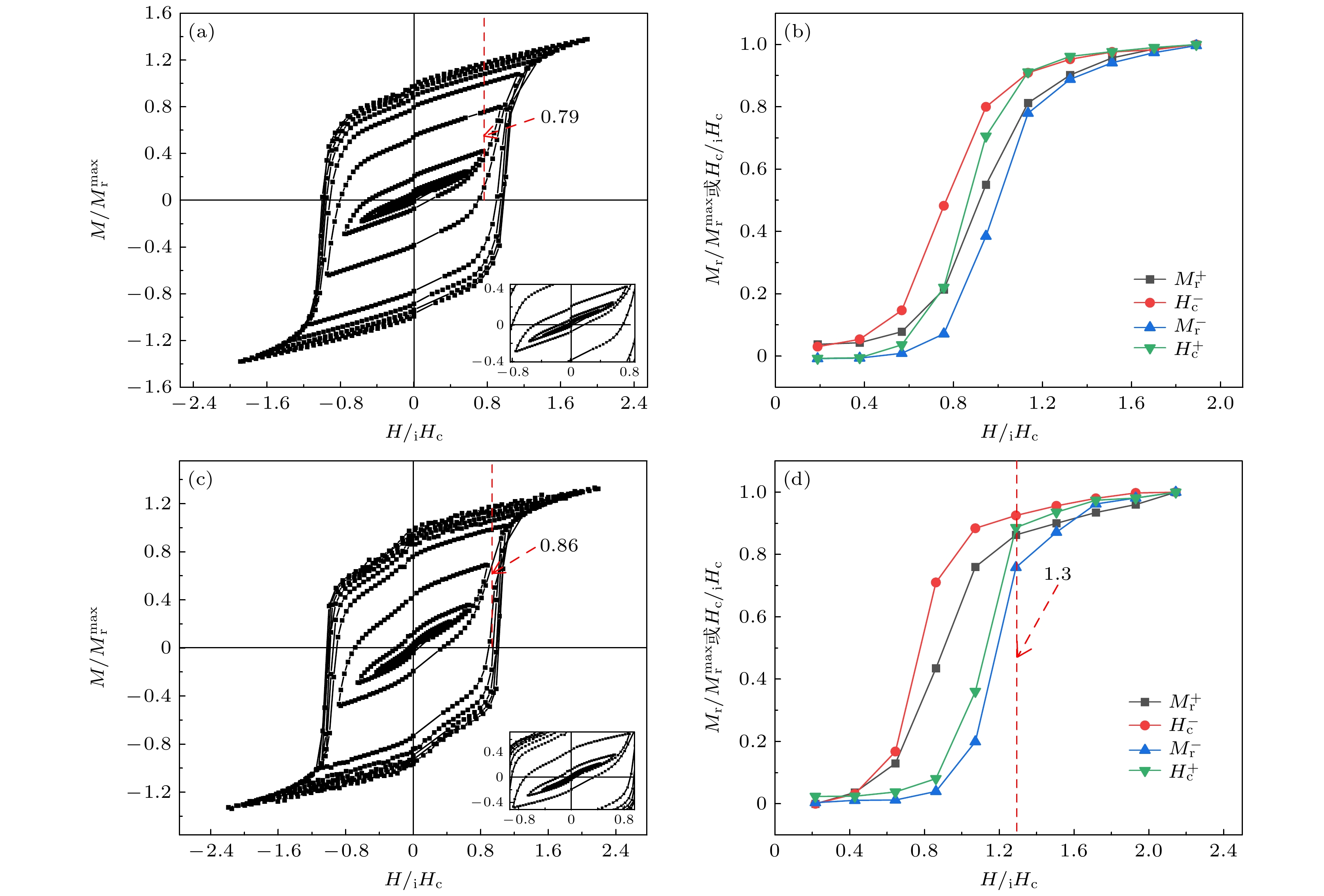
图5(a), (c)分别为样品A和样品B逐渐递增外场至37 kOe所测量的磁滞回线, 图5(b), (d)为样品A和样品B由图5(a), (c)得到的矫顽力和剩磁与最大外场H的关系. 由图5(a)可以看出, 在H/iHc <0.79时, 回线表现出严重的不对称性. 在图5(c)中, 在H/iHc < 0.86时, 也出现了同样的不对称现象, 这是由于当外磁场相对较小时, 磁畴壁不能移动, 磁体的磁化强度变化十分缓慢, 使得第二象限的矫顽力和剩磁数值大于第四象限. 样品A在H/iHc > 0.79时, 矫顽力和剩磁快速增大, 小回线趋于对称, 样品B在H/iHc > 0.86时也表现出相同的性质, 两样品均对应形核控制的反磁化机理. 在此之前, 张宏伟等[9]通过研究Pr8Fe74B起始磁化曲线和退磁曲线的回复曲线, 证明了其矫顽力机理为以钉扎为主, 但不同于传统的钉扎模型. 图5(b), (d)为矫顽力和剩磁与最大外场H的关系, 可以看出样品在低场下曲线斜率较小, 磁导率较低, 这是由于钉扎效应导致磁晶各向异性势垒较高, 磁畴壁难以移动, 当磁场进一步增大后, 曲线斜率变大, 磁导率迅速提高, 晶粒磁化过程迅速达到饱和, 这进一步证明了样品中低磁场下钉扎主导, 高磁场下形核主导的反磁化机制, 其中钉扎和成核中心存在着一些联系, 这一结论与自钉扎机制有一定相似之处. 在H/iHc = 1时, 矫顽力基本达到饱和值的80%, 剩磁在H/iHc = 1.1时才基本达到饱和值的80%, 矫顽力趋近饱和的速率明显大于剩磁, 矫顽力直接反映了材料抵抗磁化反转的能力, 而形核是这个过程的起点. 剩磁则是材料在外界磁场撤去后的剩余磁性, 涉及形核后的磁畴扩展和重新排列, 因而相对较慢. 这是形核模型的主要特征, 同时说明以剩磁为判据可以更好地判断样品的技术饱和磁化程度. 从图5(a), (b)中可以看出, 样品A的矫顽力和剩磁在磁场逐渐升高时, 对应曲线变化率基本一致, 但在H/iHc > 1.3时样品B的矫顽力和剩磁才基本趋于一致.
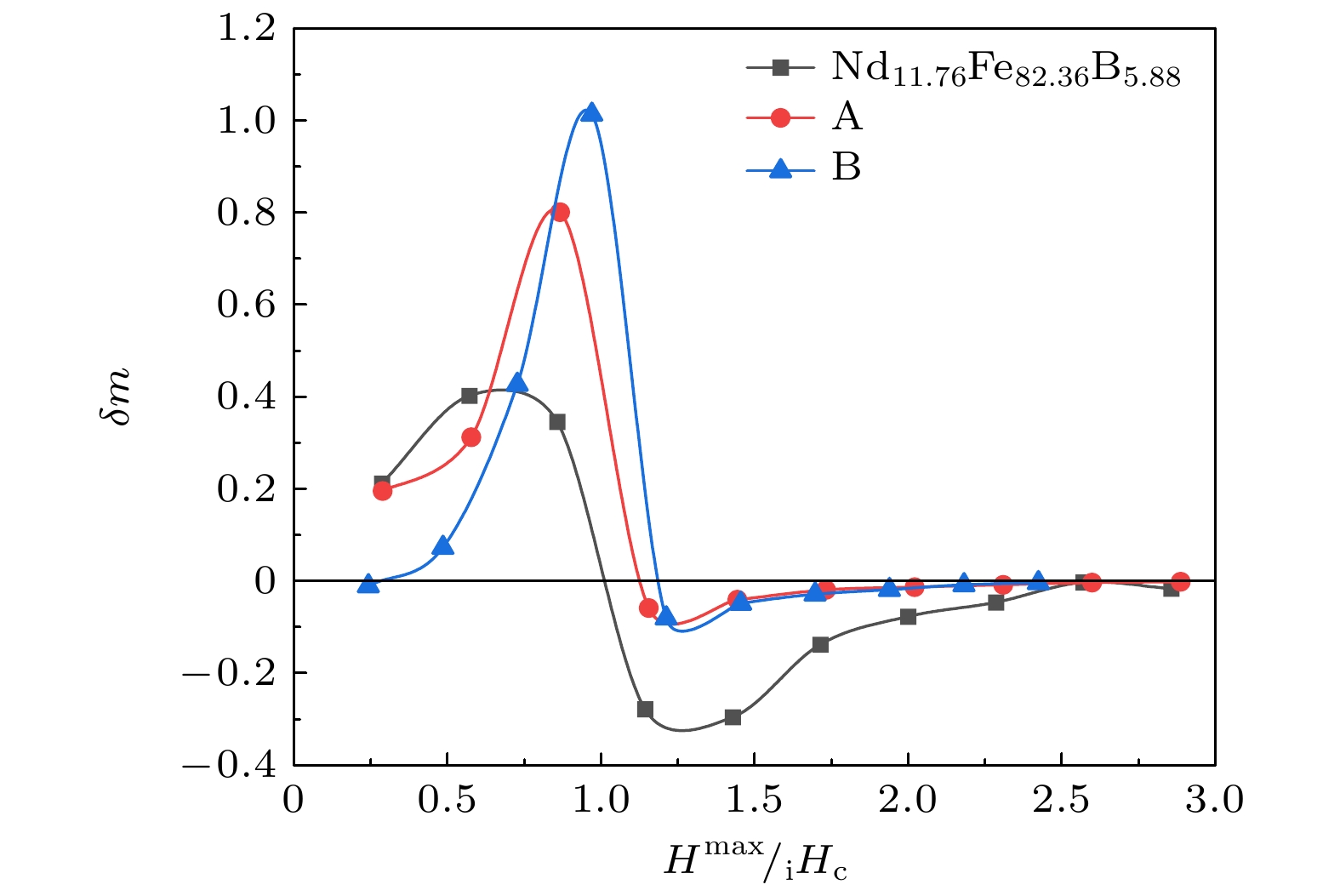
Henkel曲线是衡量样品晶间交换耦合(IGEC)的一种有效方式[8]. 图6是样品A, B以及纯NdFeB样品的Henkel图, 正δm值是由系统的IGEC引起的[15]. 如图6所示, 当Hmax < iHc时, 纯NdFeB和样品A的δm均为正值, 随着磁场的增大先增大后减小, 样品B的δm随着磁场的增大单调增大, 并在矫顽力iHc附近达到最大值后迅速减小. 样品A和样品B的–δm最大值为–0.05和–0.08, 数值相近, 说明样品中退磁有关的偶极相互作用相近, 这是由于高熵样品独特的磁晶间扩散作用使得样品均匀化导致. 纯NdFeB –δm最大值为–0.31, 远大于高熵样品, 这表明高熵稀土永磁材料的晶粒尺寸分布更加均匀. 对于正的δm最大值, 样品A和样品B的δm最大值分别为0.8和1.01, 是纯NdFeB的一倍. 样品B由于其较大的矫顽力, 所以δm最大, IGEC最强. 因此高熵组分样品的IGEC大于纯NdFeB样品, 即高熵掺杂明显使样品中IGEC增强.
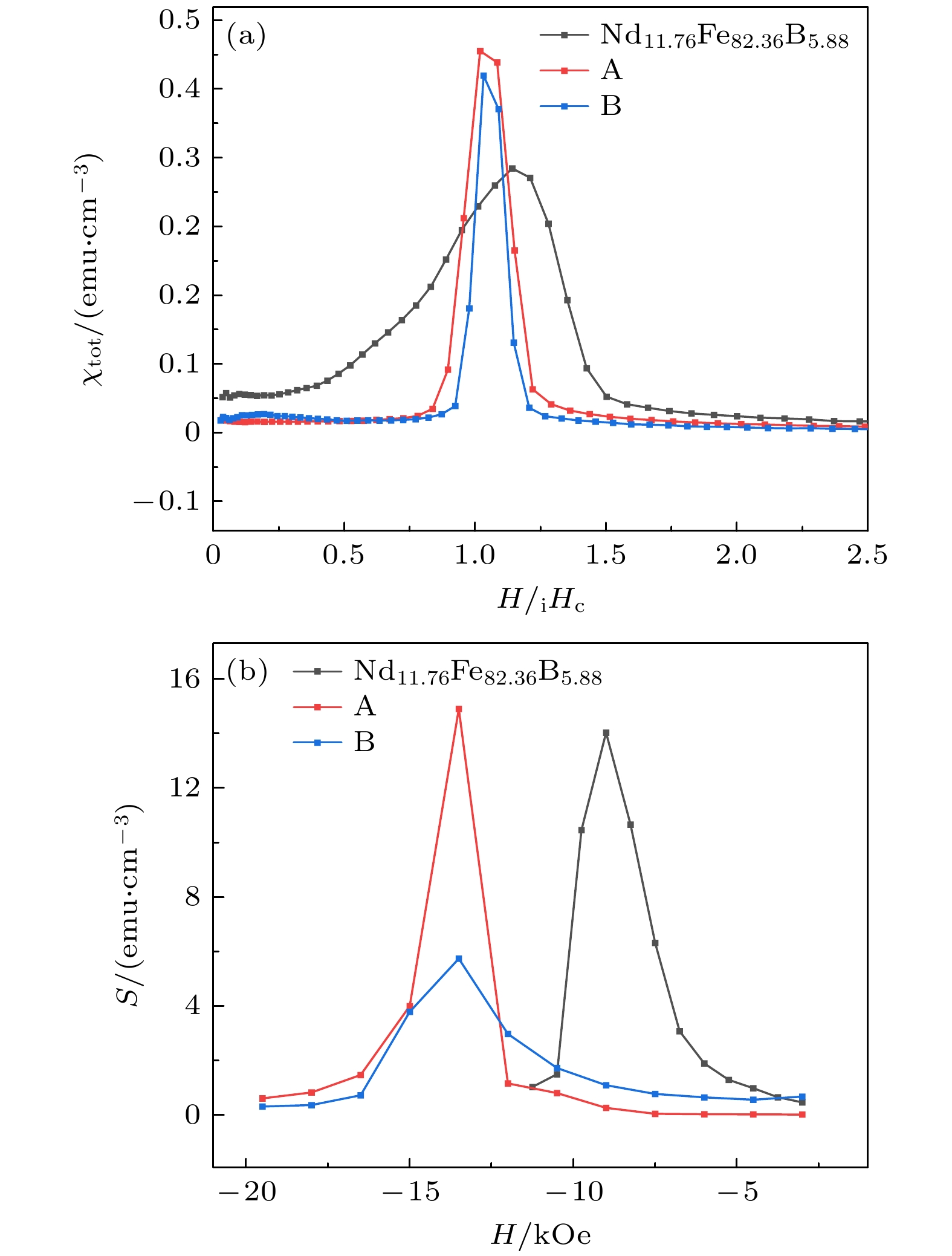
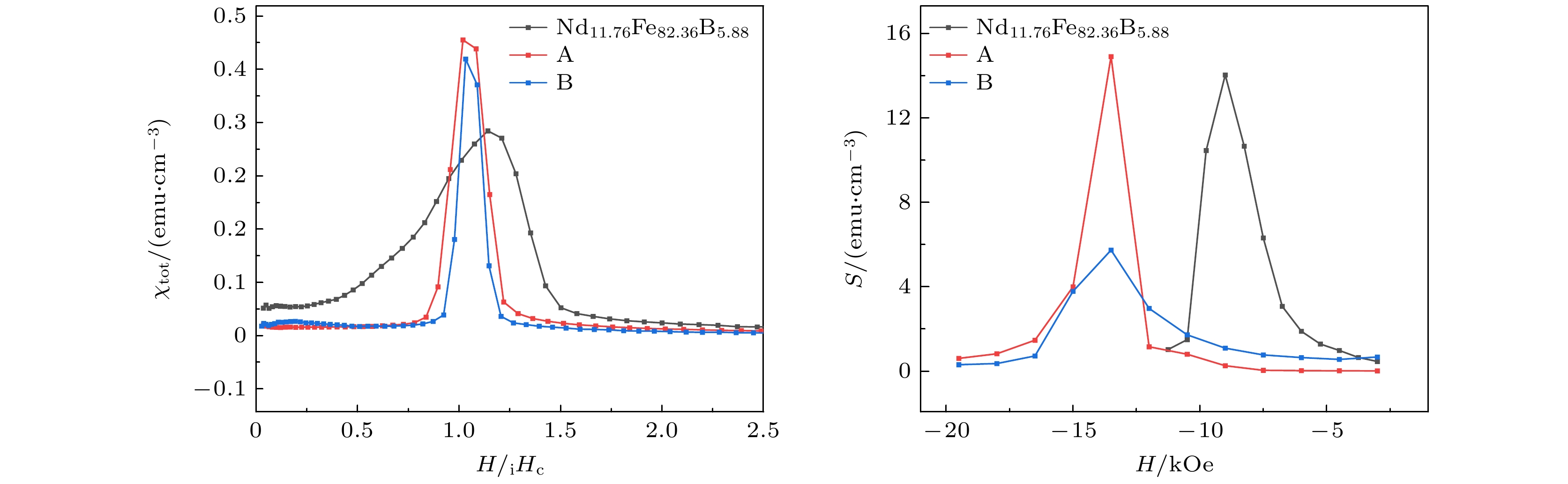
图7所示为样品A, B室温下的总磁化率χtot与外场H的关系(图7(a))以及纯NdFeB、样品A和样品B的磁黏滞系数S (图(b)). 室温下总磁化率χtot通过对退磁曲线局部求导得到, 即χtot = dM/dH. 磁黏滞系数S由公式
$M(t) = A+S\ln(t + t_0) $ 求得[20-22]. 从图7(a)可以看出, 样品A和样品B的最大磁化率均大于纯NdFeB. 对于纯NdFeB, 该样品的矫顽力为7.15 kOe, 从图7(b)可以看出, 纯NdFeB的磁黏滞系数S在–9 kOe时取得最大值13.87 emu/cm3. 对于样品A, 在外场值达到矫顽力附近磁黏滞系数S出现最大值14.72 emu/cm3, S的变化规律与图7(a)中χtot相同, 这种现象与纳米复合材料中因硬磁相反转所导致磁黏滞性的现象相同, 这可能是由于样品A中Dy单质的存在所导致. 而样品B则在外场小于矫顽力时达到最大S, 与图7(a)中样品B在矫顽力附近达到最大χtot不同, 这可能是由于样品B在外场小于磁晶各向异性场时, 硬磁相反转, 但是由于高熵合金独特的扩散机制, 此时磁晶间耦合作用并未达到最强所导致. -
本文研究了(La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88和(La0.2Pr0.2Nd0.2Gd0.2 Tb0.2)11.76Fe82.36B5.88高熵永磁合金的反磁化过程和矫顽力机理. 对比分析了重稀土掺杂的高熵永磁样品(La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88和(La0.2Pr0.2Nd0.2Gd0.2 Tb0.2)11.76Fe82.36B5.88. XRD表明两样品主要由2∶14∶1相构成, 两个样品均在[001]方向上出现织构; 在M-T曲线中, 当高熵样品温度达到居里温度时磁矩基本为0, 证明样品中基本没有α-Fe, 高熵掺杂对样品成相有一定帮助; (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88和(La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88的磁化机理为低磁场下钉扎主导, 高磁场下形核主导, 这与纯NdFeB的磁化机理不同, 与自钉扎机制有一定相似之处, 同时得益于高熵合金独特的扩散机制, 使得样品均匀化, 降低了钉扎作用, 使得硬磁相晶粒反磁化畴形核; 高熵组分样品的晶间交换耦合作用大于纯NdFeB样品, 而磁偶极相互作用小于纯NdFeB样品, 但矫顽力提高, 这说明高熵样品在降低了磁晶各向异性场势垒的同时, 提高了磁晶耦合长度; (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88中磁黏滞系数变化规律与χtot相同, 但(La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88在外场值小于矫顽力时磁黏滞系数达到最大, 与纯NdFeB和纳米复合材料与有一定区别, 这可能是由于高熵合金独特的扩散机制, 在硬磁相完全反转时磁晶间耦合作用并未达到最强所导致, 这表明该永磁体由于磁黏滞系数较低, 温升较慢, 在长时间使用时饱和磁化强度变化较小.
2:14:1型高熵稀土永磁材料的反磁化机理
Mechanism of magnetization reversal of 2∶14∶1 high-entropy rare-earth permanent magnets
-
摘要: 稀土元素具有相似的基态电子性质, 其独特的镧系收缩效应可以降低高熵材料中稀土元素的混合焓, 这对于制备廉价且高性能的高熵稀土金属间化合物至关重要. 本文在分析磁化和反磁化曲线的基础上, 辅以Henkel曲线和磁黏滞系数S计算, 研究了Nd11.76Fe82.36B5.88(NdFeB), 以及高熵稀土永磁合金化合物(La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88和(La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88等快淬条带的反磁化机理. 研究结果发现, 与纯NdFeB相比, 高熵稀土永磁材料的晶间耦合作用显著增强, 而磁偶极相互作用减弱. 这表明, 含重稀土的高熵材料中元素扩散机制在使样品均匀化的同时, 其矫顽力有大幅度提高, 矫顽力机制为硬磁相晶粒中的反磁化畴形核. (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88的磁黏滞系数大于纯NdFeB, (La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88由于硬磁相反转与磁晶间耦合作用不同步, 导致样品在具有较大各向异性场的同时, 磁黏滞系数较小. 这表明高熵稀土永磁材料的反磁化机理与传统稀土永磁材料显著不同, 值得进一步深入研究.Abstract: Rare-earth elements share similar ground-state electronic properties, and their unique lanthanide contraction effect can lower the mixing enthalpy of rare-earth elements in high-entropy materials, which is of great significance for fabricating low-cost and high-performance high-entropy rare-earth intermetallic compounds. In this work, the magnetization reversal mechanisms of rapidly quenched ribbons such as Nd11.76Fe82.36B5.88 (NdFeB) and the relevant high-entropy rare-earth permanent magnet alloy compounds (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88 and (La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88 are studied by analyzing the magnetization and demagnetization curves, supplemented by Henkel curves and magnetic viscosity coefficient S. Compared with the pure NdFeB sample, the high-entropy rare-earth permanent magnet has the inter-grain exchange coupling significantly enhanced and the magnetic dipole interaction weakened, indicating that the element diffusion mechanism in heavy rare-earth containing high-entropy material homogenizes the sample, and significantly increases the coercivity. The mechanism of the coercivity is the nucleation of magnetization reversal domains in the grains of the hard magnetic phase. The magnetization mechanism is dominated by pinning at low magnetic fields and by nucleation at high magnetic fields, which is different from the magnetization mechanism of pure NdFeB and has some similarities with the self-pinning mechanism. The magnetic viscosity coefficient of (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88 is larger than that of pure NdFeB. Due to the asynchrony of hard magnetic phase reversal and intergranular magnetic coupling in (La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88, the magnetic viscosity coefficient is small but the anisotropy field is large. This indicates that high-entropy sample reduces the magnetocrystalline anisotropy field barrier but increases the magnetocrystalline coupling length. This suggests that the magnetization reversal of high-entropy rare-earth permanent magnet material is significantly different from that of conventional rare earth permanent magnet material and it is worthy of further in-depth research.
-
-
图 2 样品在室温下的磁滞回线 (a)和M-T曲线 (b)
Figure 2. (a)The magnetic hysteresis loops and (b) the temperature-dependent magnetization (M-T) curves of all the samples.
图 3 样品A (a)和B (b)的起始磁化曲线和相应至零场的回复曲线
Figure 3. The initial magnetization curves and corresponding recovery curves to zero field of samples A (a) and B (b).
图 4 样品A(a)和B(b)的退磁曲线和退磁过程中的回复曲线
Figure 4. The demagnetization curves and recovery curves during demagnetization of samples A (a) and B (b).
图 5 逐渐递增外场至37 kOe所测量的样品A(a)和样品B(c)磁滞回线; (b), (d)由(a)和(c)得到的矫顽力和剩磁与最大外场H的关系, +为第2象限值, –为第4象限值
Figure 5. Magnetization hysteresis loops measured for sample A (a) and sample B (c) with the external field gradually increased up to 37 kOe; (b), (d) the relationship between the coercivity and remanence obtained from (a) and (c) with the maximum external field H, “+” represents a value in the second quadrant, “–” represents a value in the fourth quadrant.
图 6 Nd11.76Fe82.36B5.88、样品A、样品B的Henkel曲线
Figure 6. The Henkel curves of Nd11.76Fe82.36B5.88, sample A and sample B.
图 7 室温下总磁化率χtot (a)和磁黏滞系数S (b)与外场H的关系
Figure 7. (a)The total susceptibility (χtot) and (b) magnetic viscosity coefficient(S ) of the samples measured at 300 K.
-
[1] Balaji V, Xavior M A 2024 Heliyon 10 e26464 doi: 10.1016/j.heliyon.2024.e26464 [2] Zhao H C, Qiao Y L, Liang X B, Hu Z F, Chen Y X 2020 Rare Metal Mat. Eng. 49 1457 [3] Fu H, Jiang Y, Zhang M Z, Zhong Z Y, Liang Z, Wang S Y, Du Y P, Yan C H 2024 Chem. Soc. Rev. 53 2211 doi: 10.1039/D2CS01030E [4] Chen H Y, Gou, J M, Jia W T, Song X, Ma T Y 2023 Acta Mater. 246 118702 doi: 10.1016/j.actamat.2023.118702 [5] Zhou C, Liu Y, Li J 2023 Mater. Lett. 347 134534 doi: 10.1016/j.matlet.2023.134534 [6] 董霄鹏, 赵兴, 殷林瀚, 彭思琦, 王京南, 郭永权 2023 物理学报 72 107501 doi: doi:10.7498/aps.72.20221995 Dong X P, Zhao X, Yin L H, Peng S Q, Wang J N, Guo Y 2023 Acta Phys. Sin. 72 107501 doi: doi:10.7498/aps.72.20221995 [7] Li Z, Li Y Q, Liu W Q, Wu D, Chen H, Xia W X, Yue M 2021 Rare Metals 40 180 doi: 10.1007/s12598-020-01556-5 [8] 陈允忠, 贺淑莉, 张宏伟, 陈仁杰, 荣传兵, 孙继荣, 沈保根 2005 物理学报 54 5890 doi: 10.3321/j.issn:1000-3290.2005.12.066 Chen Y Z, He S L, Zhang H W, Chen R J, Rong C B, Sun J R, Shen B G 2005 Acta Phys. Sin. 54 5890 doi: 10.3321/j.issn:1000-3290.2005.12.066 [9] 张宏伟, 荣传兵, 张健, 张绍英, 沈保根 2003 物理学报 52 718 doi: 10.7498/aps.52.718 Zhang H W, Rong C B, Du X B, Zhang J, Zhang S Y, Shen B G 2003 Acta Phys. Sin. 52 718 doi: 10.7498/aps.52.718 [10] 彭懿, 赵国平, 吴绍全, 斯文静, 万秀琳 2014 物理学报 63 167505 doi: 10.7498/aps.63.167505 Peng Y, Zhao G P, Wu S Q, Si W J, Wan X L 2014 Acta Phys. Sin. 63 167505 doi: 10.7498/aps.63.167505 [11] 李柱柏, 李赟, 秦渊, 张雪峰, 沈保根 2019 物理学报 68 177501 doi: 10.7498/aps.68.20190364 Li Z B, Li Y, Qin Y, Zhang, X F, Shen B G 2019 Acta Phys. Sin. 68 177501 doi: 10.7498/aps.68.20190364 [12] 高汝伟, 姜寿亭, 李华, 丘梅影, 郭贻诚 1989 物理学报 38 439 doi: 10.7498/aps.38.439 Gao R W, Jiang S T, Li H, Qiu M Y, Kuo Y C 1989 Acta Phys. Sin. 38 439 doi: 10.7498/aps.38.439 [13] Zhao G P, Wang X L, Yang C, Xie L H, Zhou, G 2007 J. Appl. Phys. 101 09K102 doi: 10.1063/1.2711404 [14] 鲜承伟, 赵国平, 张庆香, 徐劲松 2009 物理学报 58 3509 doi: 10.7498/aps.58.3509 Xian C W, Zhao G P, Zhang Q X, Xu J S 2009 Acta Phys. Sin. 58 3509 doi: 10.7498/aps.58.3509 [15] Zhang H W, Rong C B, Du X B, Zhang J, Zhang S Y, Shen B G 2003 Appl. Phys. Lett. 82 4098 doi: 10.1063/1.1576291 [16] 孙亚超, 朱明刚, 韩瑞, 石晓宁, 俞能君, 宋利伟, 李卫 2018 金属学报 54 457 doi: 10.11900/0412.1961.2017.00211 Sun Y C, Zhu M G, Han R, Shi X N, Yu N J, Song L W, Li W 2018 Acta Metall. Sin. 54 457 doi: 10.11900/0412.1961.2017.00211 [17] 李维丹, 谭晓华, 任科智, 刘洁, 徐晖 2016 金属学报 52 561 doi: 10.11900/0412.1961.2015.00517 Li W D, Tan X H, Ren K Z, Liu J, Xu H 2016 Acta Metall. Sin. 52 561 doi: 10.11900/0412.1961.2015.00517 [18] 邓晨华, 于忠海, 王宇涛, 孔森, 周超, 杨森 2023 物理学报 72 027501 doi: 10.7498/aps.72.20221479 Deng C H, Yu Z H, Wang Y T, Kong S, Zhou C, Yang S 2023 Acta Phys. Sin. 72 027501 doi: 10.7498/aps.72.20221479 [19] 张宏伟, 荣传兵, 张绍英, 沈保根 2004 物理学报 53 4347 doi: 10.7498/aps.53.4347 Zhang H W, Rong C B, Zhang S Y, Shen B G 2004 Acta Phys. Sin. 53 4347 doi: 10.7498/aps.53.4347 [20] Feutrill E H, McCormick P G, Street R 1996 J. Phys. D Appl. Phys. 29 2320 doi: 10.1088/0022-3727/29/9/014 [21] Street R, Woolley J C 1949 Proc. Phys. Soc. 62 562 doi: 10.1088/0370-1298/62/9/303 [22] Crew D C, McCormick P G, Street R 1996 Ieee T. Magn. 32 4356 doi: 10.1109/20.538867 -
计量
- 文章访问数: 248
- HTML全文浏览数: 248
- PDF下载数: 2
- 施引文献: 0