首页
登录
注册
下载:
-
里德伯原子具有较大原子尺度、高极化率和电偶极矩, 对外部电场敏感, 适用于电场的精密测量[1,2], 其丰富的能级结构结合电磁诱导透明(EIT)效应[3–6], 以及共振电场作用下的奥特勒-汤斯效应(Autler-Townes effect, AT)[7]、非共振电场作用下的斯塔克效应(Stark effect)[8,9], 可实现DC—THz频率范围内的电场测量. 里德伯原子传感器大多是玻璃材质的气室, 对被测电场无畸变影响, 且传感器尺寸与被测电场波长无关, 可小型化. 特别是, 基于里德伯原子外场效应得到的光谱特征量与场强的关系可溯源至普朗克常数, 可实现自校准的电场测量. 目前, 基于里德伯原子电磁诱导透明和奥特勒-汤斯(EIT-AT)效应的微波(主要在GHz以上频段)电场测量研究已在基础物理领域取得巨大突破, 并拓展至军事国防[10]、航空航天[11]、生物医疗[12]、微电子[13]等应用领域, 测量性能备受好评. 但是对于GHz以下非共振低频电场测量的研究相对滞后, 而此频段电场在医疗、各工业等领域普遍存在, 近年来对其进行精密测量的需求也日益突出[14–16].
GHz以下低频电场与里德伯原子系统作用产生Stark效应, 即高里德伯态原子在电场作用下发生能级偏移, 宏观表现为所对应的光谱发生频移. 早期研究中, 基于基本原理推导出光谱频移量与场强平方成正比[17]. 但是随后研究者发现, 非氢里德伯原子存在量子亏损, 在高场强作用下出现能级抗交叉, 频移量与场强呈现出复杂的非线性关系[18]. 继而相关实验研究发现, 外电场作用除了使EIT峰值位置移动, 还伴随着光峰展宽压低、单峰分裂为多峰(对应精细能级态)等现象, 与此同时光峰频移和形态随着时变电场动态变化[19].
测量场景的环境因素和系统参数设置都会影响基于里德伯原子的电场测量的准确性. 阎晟等[20]发现, 随着温度的升高, 原子的热运动加剧, 进而引起EIT谱峰的形态变化, 混淆外场对原子的作用效果. 王延正等[21]发现, 激光功率会影响EIT光谱的宽度和不对称度, 对测量结果产生极大影响, 并在此基础上探索量子测量技术的最佳实验条件, 为基于里德伯原子的电场测量精度提供了实验依据. Noah等[22]研究发现引入强磁场可以增大里德伯原子对于微弱电场测量的能力. Sedlacek等[23]研究发现电场的矢量方向同样会影响EIT光谱的特征. Bao等[24]通过使用不同性质的激光(线性偏振光、右旋圆偏振光和左旋圆偏振光)对里德伯原子作用, 分析其对Rydberg-EIT光谱的影响, 结果发现Rydberg-EIT光谱依赖于激光的相对偏振组合. 本团队研究发现, 线偏振的探测光与耦合光之间不同的偏振方向也会影响EIT-Stark光谱, 从而影响外部电场的测量.
本文首先建立低频外电场与里德伯原子作 用的理论模型, 阐述EIT和Stark效应的物理机制, 其中将Stark频率代入激光与碱金属原子作用的密度矩阵, 直接仿真EIT-Stark光谱; 其次, 基于理论模型阐释探测光和耦合光偏振方向的匹配需求. 最后, 构建测量系统, 实验获得不同偏振方向配置下的Stark频移量, 以验证对电场测量的 影响.
-
基于微扰理论建模体现弱电场对里德伯态原子的作用, 其中哈密顿量可表示为
式中, H0为里德伯原子在无电场时的哈密顿量,
$H' $ 为考虑电场势能的哈密顿量. 本征矢和本征能量进行微扰展开, 得式中,
$ {\psi _n}\left( \lambda \right) $ 为主量子数为n的本征矢,$ \psi _n^{\left( i \right)} $ 为本征矢的i阶微扰,$ {W_n}\left( \lambda \right) $ 为主量子数为n的本征能量,$ W_n^{\left( j \right)} $ 为本征能量的j阶微扰, λ为示踪系数, 用于分析系统在受到小扰动时的行为:通常情况下, 高阶微扰对能量修正的贡献会逐渐减小, 1—2阶微扰所得到的能量修正已经足够精确地反映电场对系统的影响. 本文考虑到二阶微扰, 可实现电场对系统的整体扰动进行有效描述.
计算零阶微扰即无外场的原子能量时, 只需要考虑微扰展开指数为0的部分:
计算一阶微扰时, 只需要考虑计算一阶微扰修正能量:
因为外场势能哈密顿量为奇函数, 求得(5)式一阶微扰修正能量为0. 同理, 计算二阶微扰修正能量:
其中将里德伯原子视作一对电偶极子, 因此外场势能哈密顿量可表示为
式中, e为电荷数常数, Ez为跃迁矩阵元方向(定义为z轴)的电场强度,
$ \left\langle {n, l, j, {m_j}} \right|z\left| {n', l', j', {m_j}'} \right\rangle $ 为能级间跃迁的矩阵元素, 其中z为位移算符,$ \left| {n, l, j, {m_j}} \right\rangle $ 为量子态, n为主量子数、l是轨道角量子数、j为总角量子数, mj为磁量子数;$\sigma_{mj, mj'}, \sigma_{l, l+1}$ 为选择定则, 分别为磁量子数在电场作用下的变化符合Δmj = 0, ±1以及轨道角量子数Δl = ±1;$ \left\langle {n, l, j} \right|r\left| {n', l', j'} \right\rangle $ 为$ \left\langle {n, l, j} \right| $ 到$ \left| {n', l', j'} \right\rangle $ 的径向跃迁矩阵元素;$ \left\langle {{l, 1/2, {m_l}, {m_j} - {m_l}}} \mathrel{\left | {\vphantom {{l, 1/2, {m_l}, {m_j} - {m_l}} {j, {m_j}}}} \right. } {{j, {m_j}}} \right\rangle $ 为从轨道角动量l和自旋角动量1/2耦合得到总角动量j和磁量子数mj的波函数投影.分析(7)式可知, 激光偏振方向的变化会导致原子系统中在z轴方向的改变, 从而影响电场在z轴上的分量, 进而影响原子系统对电场的感知和响应. 综上可知, 一阶微扰修正为0, 电场强度的二次方与二阶修正成正比. 此外, 在确定里德伯态的主量子数、角量子数、磁量子数后, 各阶本征能量与本征矢量都是常数.
因此, 电场强度与里德伯原子能级能量之间的表达式为
里德伯原子能级能量与频率关系为
式中, Δf为频移量, h为普朗克常数. 在原子中, 主量子数决定能级的大小, 角量子数决定能级的角动量性质, 而磁量子数则描述能级在外场下的取向. 联立(8)式和(9)式, 可整理为
式中, α为里德伯原子在电场下的极化率.
由(10)式可知, 将外电场作用于某里德伯态(具有特定的主量子数n、角量子数j、磁量子数m)下的原子, 测量光谱的频移量Δf, 就可换算出电场强度值.
-
采用布洛赫方程来描述激光光场与原子系统的作用及动态演化:
式中, ρ为密度矩阵, H为系统哈密顿量, L(ρ)为Lindblad超算符.
设激光场为
式中, k为激光沿着z轴元方向传输的真空波矢, ω为激光角频率, 电磁场沿x轴方向极化,
$ {\boldsymbol{\delta }} $ 为偏振方向单位矢量. 考虑不同激光偏振方向, 激光场强关系式为式中, μ12(32)为探测光和耦合光作用能级间的跃迁偶极矩, I0p(c)为射入气室的探测光(耦合光)光强.
${{\boldsymbol{\delta }}_{{\text{p(c)}}}}$ 分别为探测光和耦合光的偏振方向单位矢量. 因此, 对于阶梯型三能级系统, 哈密顿量H为式中, ћ为约化普朗克常数, Δp和Δc分别为探测光和耦合光的失谐量.
本文将外部电场引起的Stark效应能级偏移等效为耦合光与跃迁频率间的失谐量, 并耦合入系统哈密顿量中, 将(14)式修正为
将(15)式代入(11)式, 并令dρ/dt = 0求解稳定响应, 其中反映探测光特性的矩阵元ρ21表示为
进一步求解该量可得复极化率χ, 从而表征铯原子系综在探测光作用下的光学响应:
式中, N为里德伯原子密度, ε0为自由空间的介电常数, I0p为入射激光的初始强度. χ的虚部χ''反映出原子对探测光的吸收特性, 亦可用于描述EIT-Stark光谱. 综上可推导出χ''的表达式:
式中, θ为探测光与耦合光偏振方向之间的夹角. 由(18)式可知, 当探测光和耦合光之间的偏振方向一致时χ''的值最大, 当探测光和耦合光之间的偏振方向不一致时χ''的值减小, 且χ''随夹角呈周期变化, 周期为90°.
探测光经过原子气室后透射出的光强Ip可表示为
式中, I0p是入射光的初始光强, L是原子气室的长度, λp是探测光的波长.
-
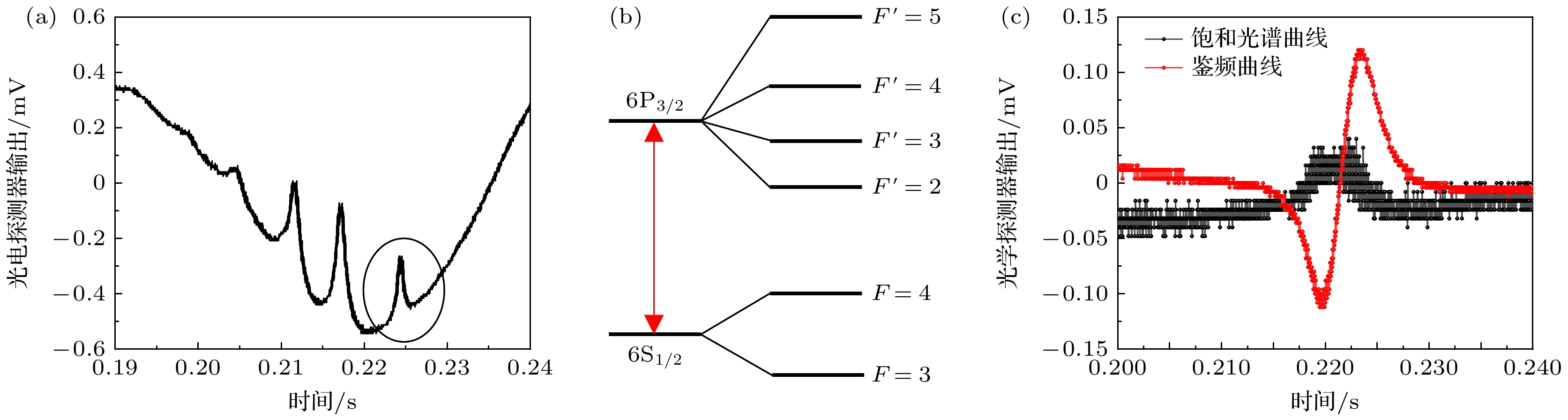
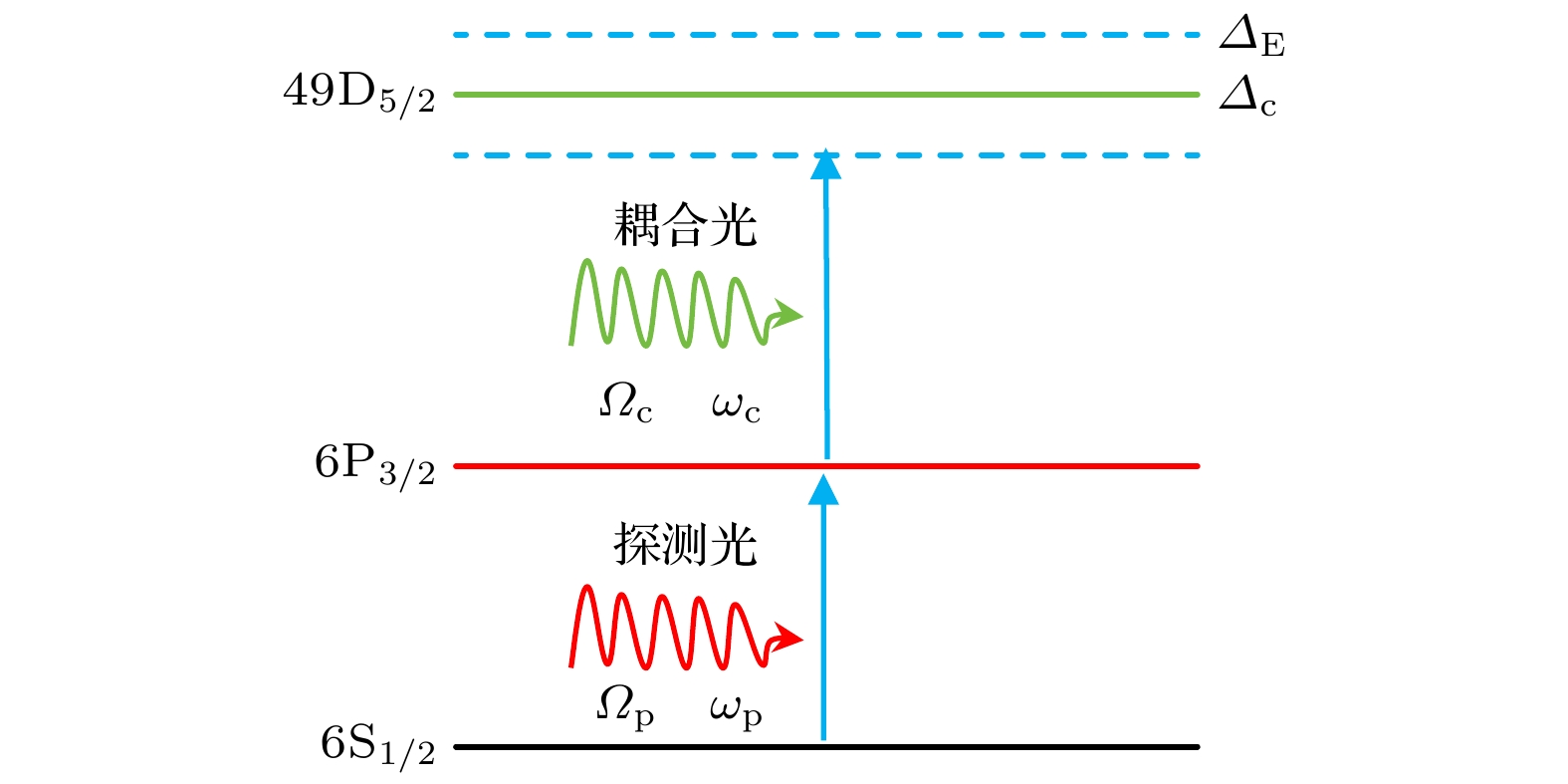
本文采用的测量系统能级结构如图1所示, 将探测光和耦合光反方向重叠射入铯原子气室. 其中, 852.347 nm探测光将铯原子从基态6S1/2激发到中间态6P3/2, Ωp为探测光的拉比频率, ωp为从基态6S1/2激发到中间态6P3/2的跃迁频率. 509.539 nm耦合光进一步将其激发到里德伯态49D5/2, 其中Ωc为耦合光的拉比频率, ωc为从中间态6P3/2激发到里德伯态49D5/2的跃迁频率. Δc为耦合光的频率失谐量, ΔE为电场作用下的频率失谐量.
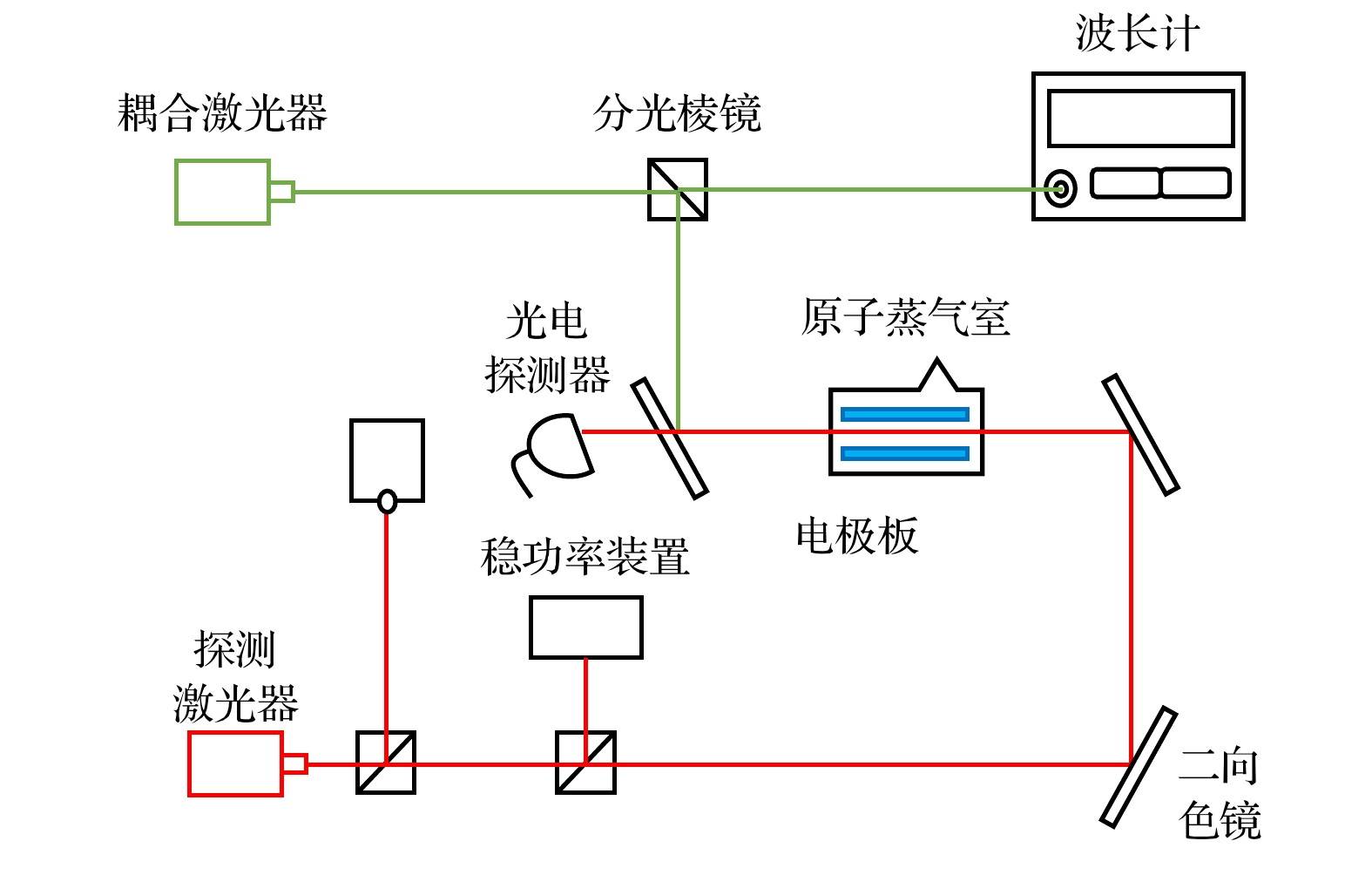
试验装置构成如图2所示. 探测光首先经过隔离器后经分束镜分束, 一部分进入饱和光谱进行锁频, 另一束光进入声光调制器实现稳定功率, 最后一部分通入原子蒸气室, 将铯原子从基态激发为第一激发态(6S1/2→6P3/2). 耦合光(509 nm)通入原子蒸气室, 将铯原子从第一激发态激发为里德伯态(6P3/2→49D3/2). 完成里德伯原子的制备后, 将光信号通过光电转换器转化为电信号, 并输入到示波器中显示EIT光谱.
-
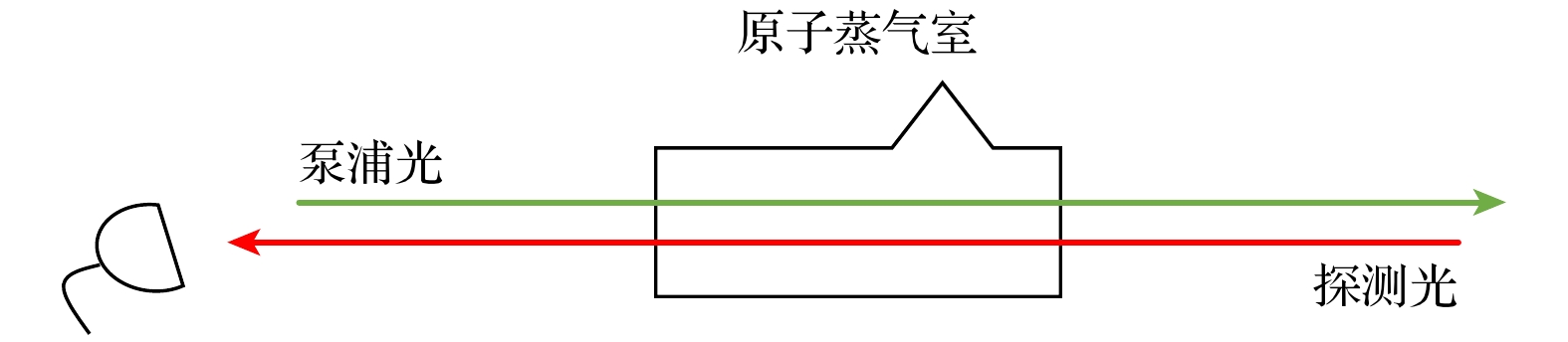
稳频装置采用饱和光谱稳频法, 基本原理如图3所示, 首先分光棱镜将一束激光分为一束光强较强的泵浦光和一束光强较弱的探测光, 通过光学器件引导, 共线方向引入到原子蒸气室中.
扫描激光频率会获得如图4(a)的饱和光谱, 图中的凹陷是多普勒背景, 是由原子热运动导致. 在一个扫描周期内存在多个小峰, 其中不同的峰值对应的频率代表碱金属原子的一个精细能级, 如图4(b)所示. 通过将扫描周期固定到一个精细能级附近, 对其进行处理, 反馈出鉴频曲线作用到激光器上, 实现激光的稳频, 如图4(c)所示. 经测试, 激光经过锁频模块后频率稳定度可达到10–10量级.
-
经过分束的另一束光进入声光调制器(AOM)及光电探测器实现稳定功率, 如图5所示. 具体地, 将一部分激光功率引入到光电探测器中, 光电探测器将光功率转换为电信号. 然后, 光电探测器的电信号传送到控制电路, 用于监测激光功率的变化. 最后, 将调制信号施加到AOM上, 调节压电换能器的输出声波频率, 从而改变通过AOM的激光功率, 使其保持在一个稳定的值. 经测试, 激光在功率稳定模块作用下功率稳定度可达到±0.3%.
-
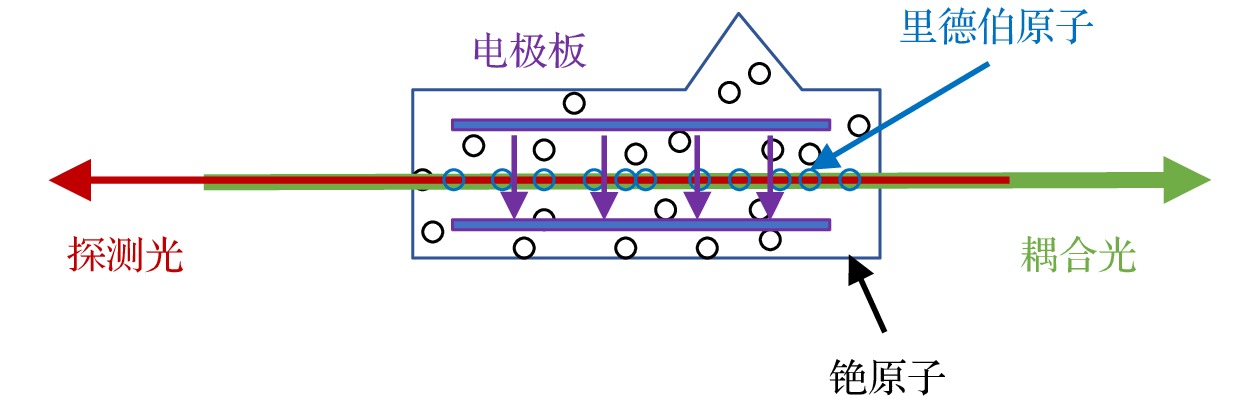
加载较低频率的电场时, 一部分碱金属原子会附着在原子蒸气室内壁上, 对待测场造成屏蔽, 进而导致激发的里德伯原子并未感知到电场, 电场传感失效. 为了解决上述问题, 本文采用内置极板的方法, 把电极板加载到原子蒸气室内部, 可以从根本上避免碱金属附着所导致的影响, 结构如图6所示.
-
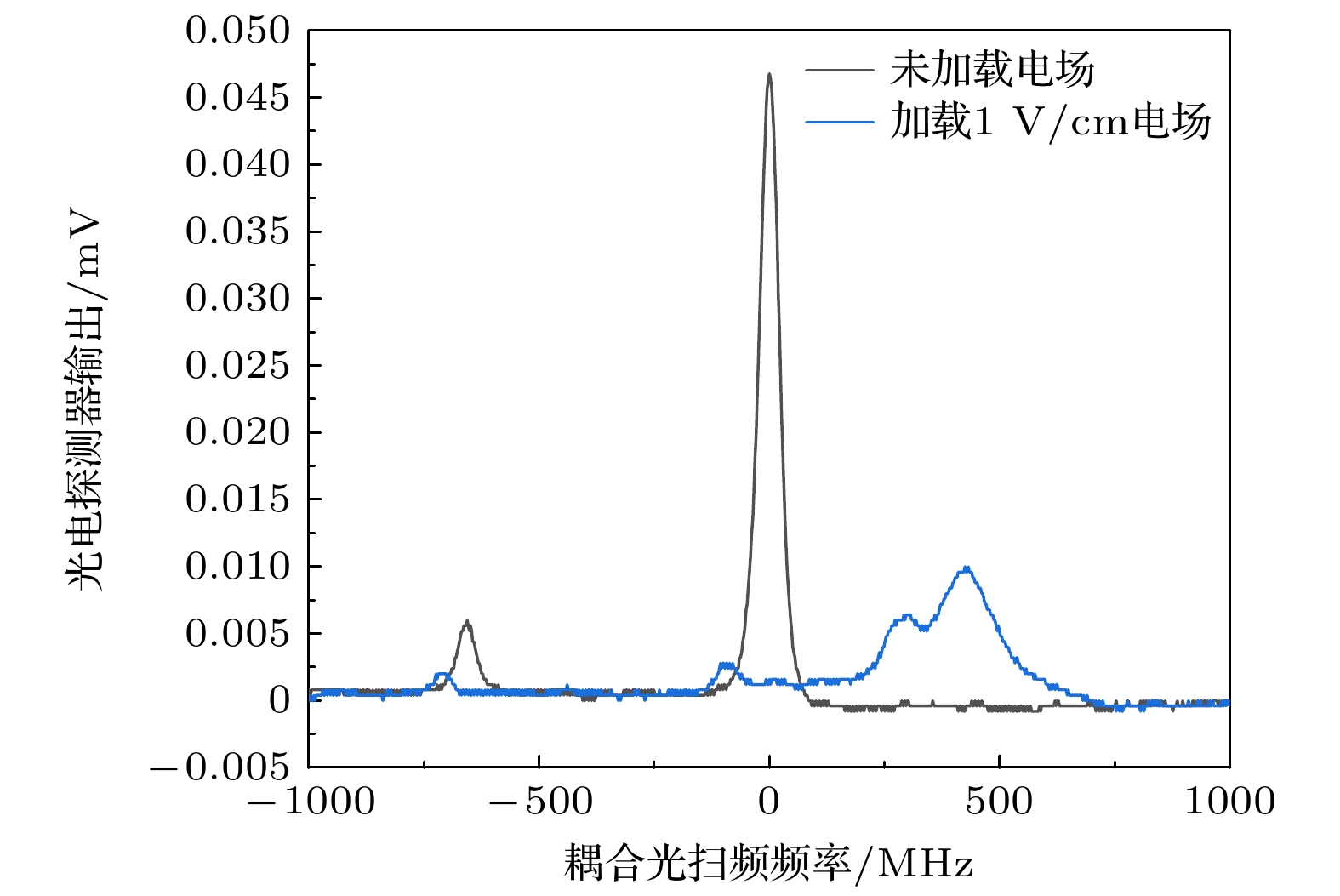
首先, 原子通过和探测光和耦合光作用发生 EIT效应, 通过检测从原子蒸气室透射出来的探 测光的光谱变化可以实现对电场的测量. 在测量电场之前需要用标准源产生一个标准场, 加载到原子蒸气室两端, 对电场测量装置进行校准并计算, 结果见图7. 加载标准源产生1 V/cm, 测量EIT光谱的频移量, 拟合(10)式, 计算极化率 α(njm)为362.0682 MHz/(V/cm)2.
-
由于半导体激光器输出光通常为高质量的线偏振光, 本文通过调整半波片来调节激光的偏振角度, 如图8所示. 通过观察探测光与耦合光在不同夹角下的EIT光谱, 分析夹角变化对EIT光谱的影响规律.
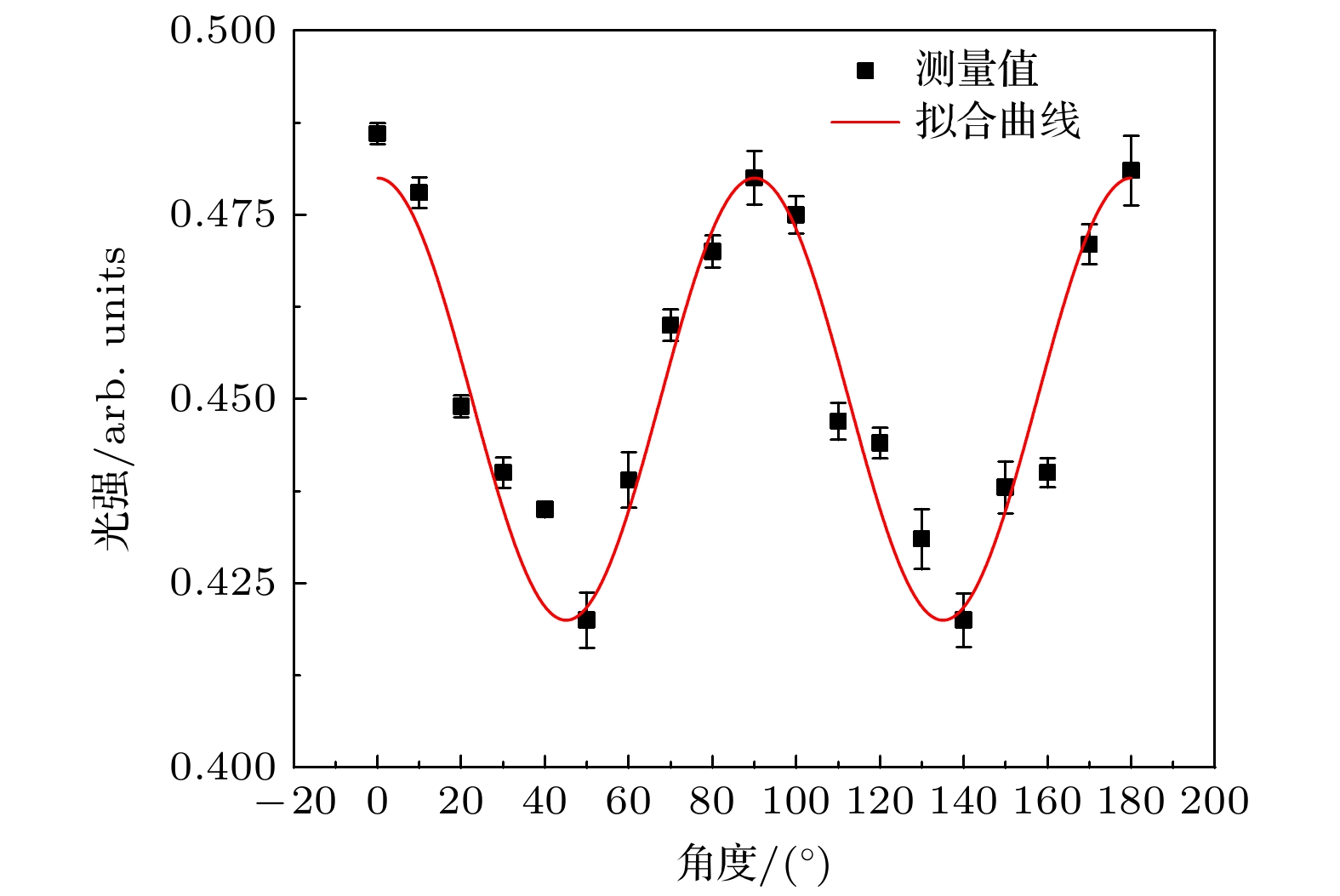
图9展示了不同探测光和耦合光夹角对EIT光谱峰值的影响. 可知, 随着两束激光的增加, EIT光谱的峰值呈周期性变化, 变化周期为90°; 当夹角为0°时, EIT光谱峰值最大, 夹角为45°时, EIT光谱峰值最小. 与(18)式分析结果一致. 系统的测量误差不超过5%, 主要是功率稳定度、温漂和噪声等因素所造成的.
-
在磁场作用下, 会与原子能级作用产生塞曼效应, 这首先会导致EIT谱峰发生频移和分裂, 这混淆电场对原子的Stark效应. 其次, 能级的分裂也会导致原子布局的改变. 同时, 不同塞曼子能级间的CG系数不同, 也会影响不同能级之间的跃迁概率, 破坏量子相干效应.
在磁场作用下, 能级会发生频移, 表达式为
式中, gJ为朗德因子, mJ为磁量子数, μB为玻尔磁子, B为外加磁场的强度, h为普朗克常数. 对于D5/2态原子, 考虑背景磁场(B = 0.1 mT)能级频移表达式可进一步表达为
计算由于磁场导致的能量偏移(MHz量级)远远小于电场作用下的能量偏移(百MHz量级), 因此本文忽略背景磁场对于原子能级的作用.
-
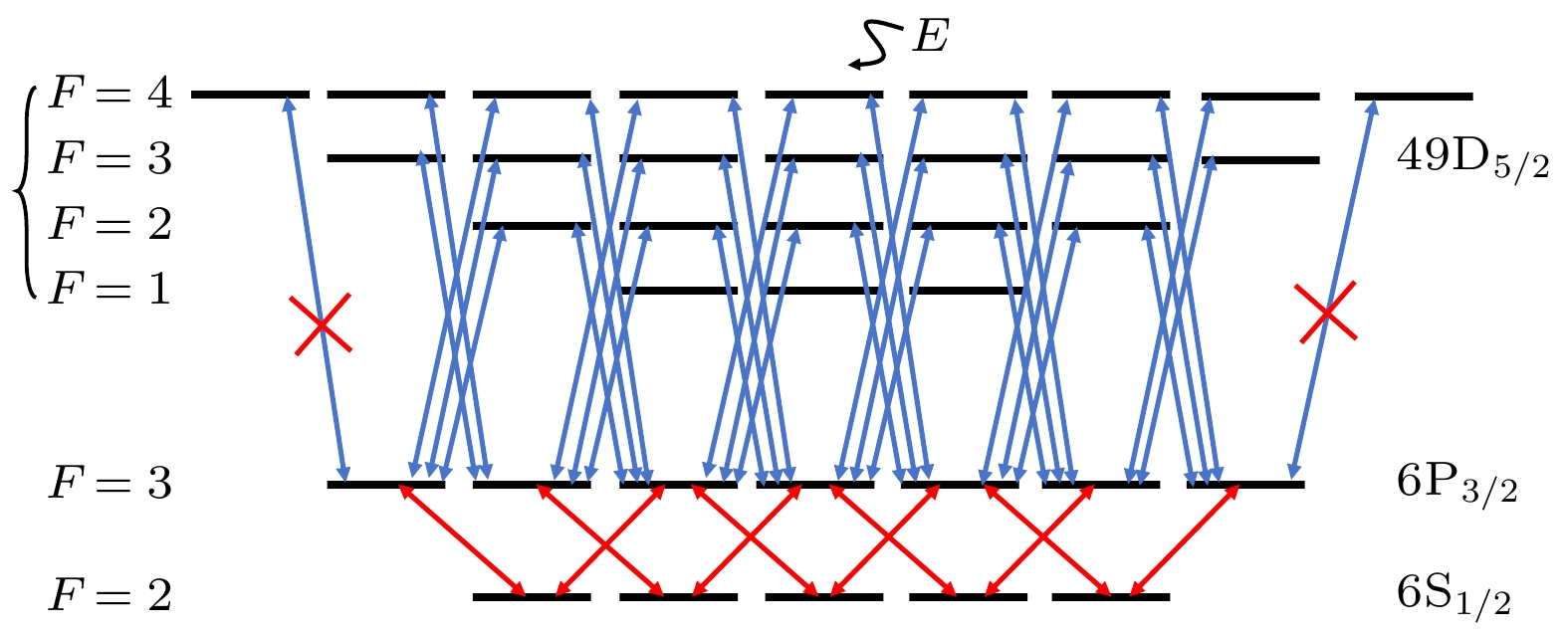
考虑精细能级后, 实验所涉及的全部36种可能状态的能级图如图10所示. 其中F为超精细量子数, 用于描述原子能级中由于原子核自旋与电子自旋的相互作用引起的能级分裂, 而相同F下可进一步分裂为不同的mf能级, mf是F的磁量子数, 其取值范围是–F到+F. 值得注意的是, 原子态的精细能级在无外加电场的情况下处于简并态, 因此无法观察到探测光与耦合光偏振失配所带来的影响. 必须在施加电场、消除能级简并的条件下, 分析探测光与耦合光偏振方向对原子能级激发的影响.
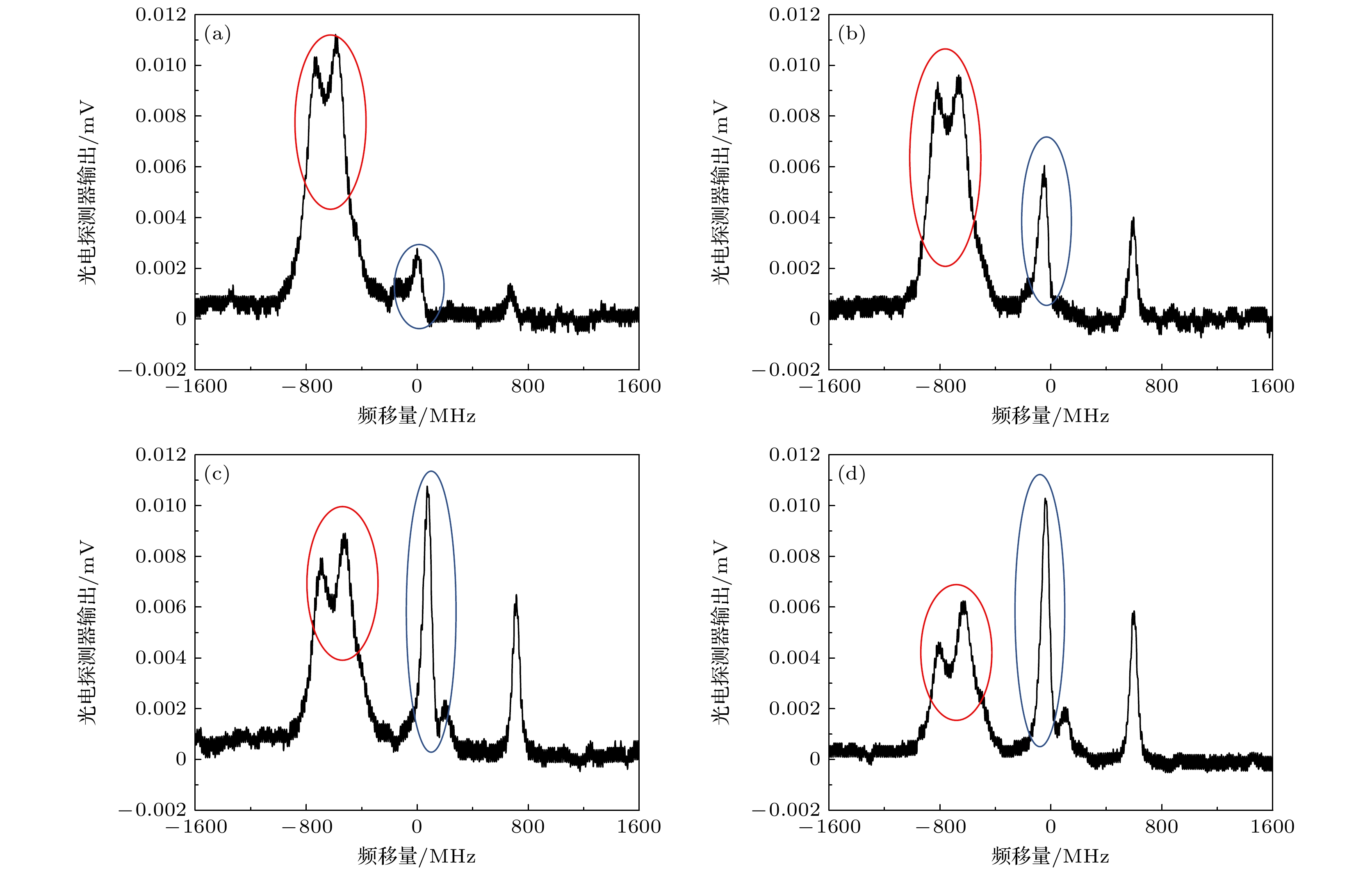
当探测光与耦合光偏振方向相同时, 激发通道会全部打开, 当探测光与耦合光偏振方向不同时, 不同的激光偏振方向会影响精细能级的激发通道, 影响电场与能级之间的相互作用, 进而增加测量误差. 加载相同电场下, 调控探测光和耦合光之间的夹角, 测量结果如图11所示. 分析图11可知, 加载电场时, EIT光谱不仅会在Stark效应的作用下发生频移, 还会伴随发生分裂、峰值降低以及展宽的现象. 不仅如此, 当调控探测光和耦合光偏振方向夹角时, 不同谱峰的形态也会相应发生变化. 当探测光和耦合光的偏振方向平行时, 图11蓝色圆圈内的谱峰峰值相较红色圆圈内的谱峰较小(图中蓝色圆圈和红色圆圈内从左到右依次为mj = 1/2, mj = 3/2, mj = 5/2能级对应的透射峰). 随着探测光与耦合光偏振方向夹角的增大, 该谱峰所对应的精细能级通道的激发比例增加, 导致谱峰峰值上升. 与之相反, 图11红色圆圈内的谱峰所对应的精细能级通道激发比例则会减小, 因此谱峰峰值也随之下降.
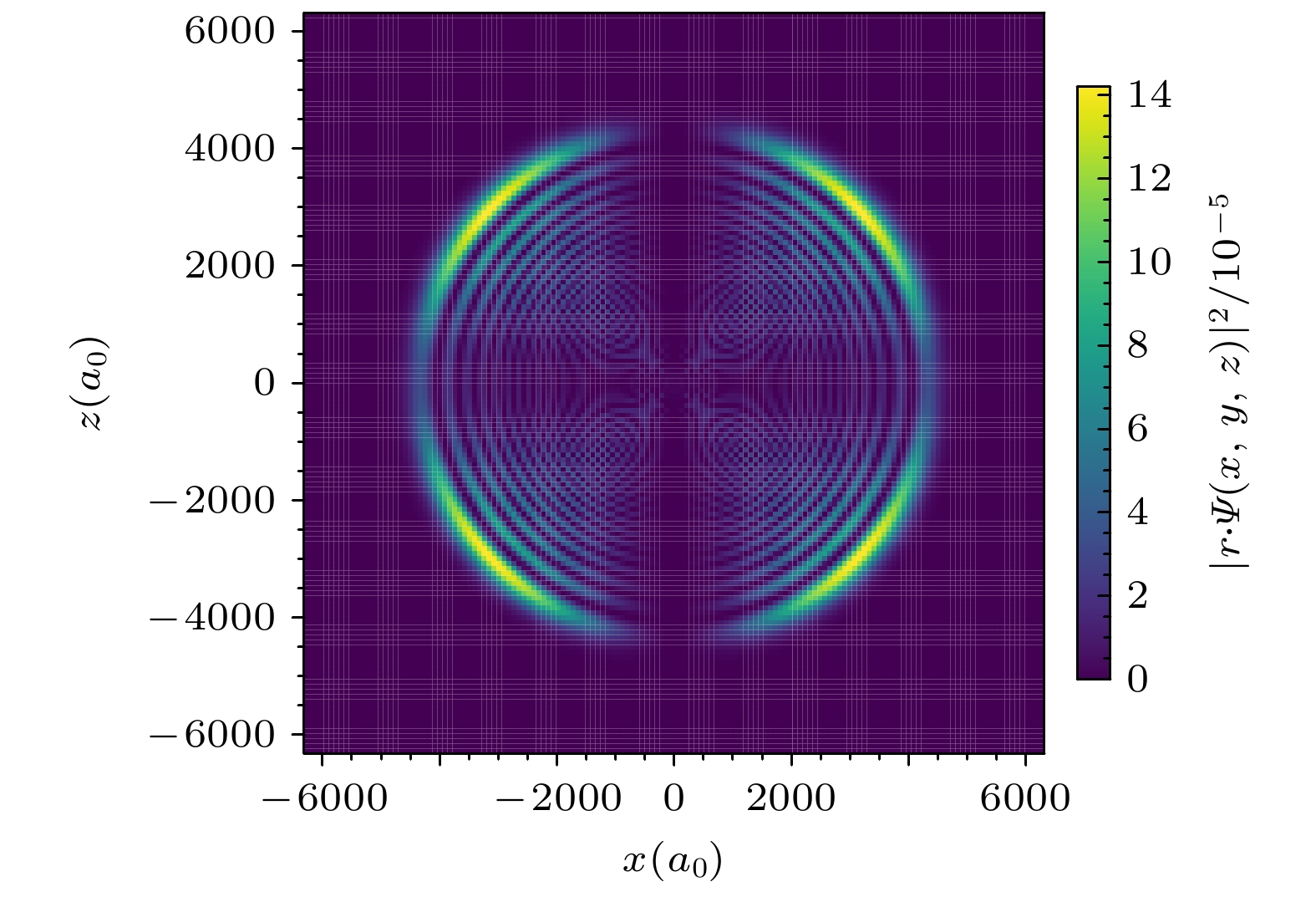
为了进一步研究探测光和耦合光之间偏振失配对电场的影响, 由(10)式可知, 极化率与电场方向与原子波函数有关, 计算D态原子波函数的轨道如图12所示. 分析图12可知, D态里德伯原子呈四叶草形状, 其空间分布反映了电子在原子核周围的概率密度分布. 由于其对称性, D态轨道的极化方向可以分为4个主要方向, 每个方向对应一个叶片的取向. 在不同的激发条件下, 会导致原子极化方向与电场方向发生改变, 进而影响里德伯原子对电场的传感性. 当电场方向与极化方向一致时, 原子对电场的Stark效应最为敏感; 随着极化方向与电场夹角从0°增大至45°, 原子对电场的感应强度逐渐减弱. 然而, 当夹角继续增大至45°—90°之间时, 由于偶极选择规则, 接近垂直的极化方向反而增强了对电场的感知.
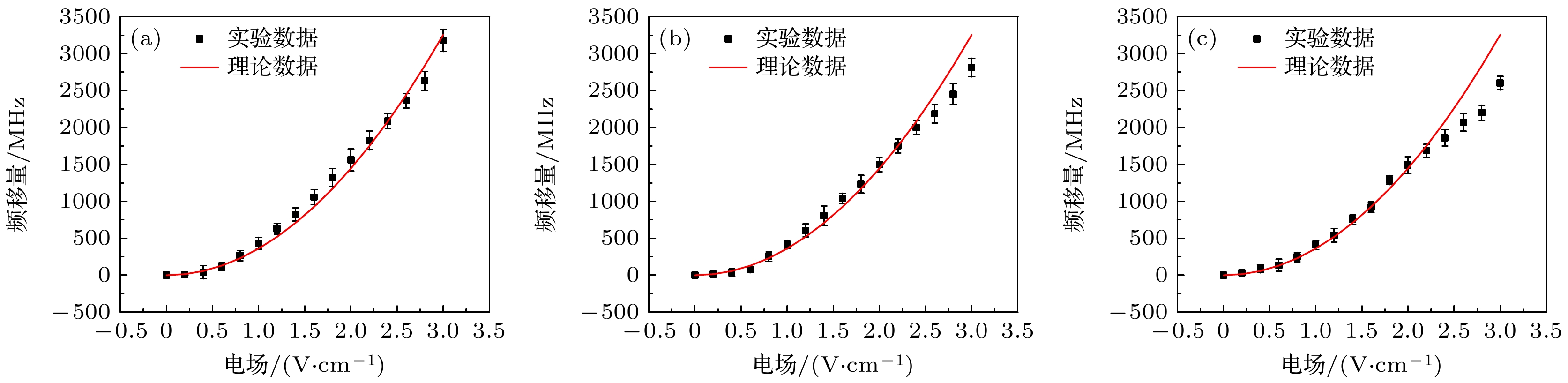
图13为测量探测光和耦合光不同偏振方向夹角下电场的测量结果, 其中黑色数据点为测量数据, 按照4.1节的极化率标定, 理论曲线(红色曲线)的计算公式为
分析图13可知, 随着电场的增大, 当探测光和耦合光偏振方向相互平行时, 测量参数与理论数据误差最小, 最大相对误差为1.67%. 此时偏振方向最匹配. 随着两束激光的偏振方向夹角度数的增大, 对电场测量结果误差逐渐升高. 当探测光和耦合光偏振方向相互夹角为22.5°时, 最大相对误差为6.67%. 当探测光和耦合光偏振方向相互夹角为45°时, 测量参数与理论数据误差最大, 最大相对误差为10.24%, 此时偏振失配程度最大. 此外, 该系统的测量误差不超过1%. 上述实验结果与理论计算的误差主要是激光偏振的不匹配会显著影响精细能级之间跃迁通道的耦合强度, 部分跃迁通道可能被抑制或关闭, 使光谱特征发生改变, 从而增加测量误差. 此外, 温漂和噪声等因素也会引入统计误差.
-
1)本文首先通过微扰法求解薛定谔方程, 推导出能量偏移量与电场强度的函数关系. 然后, 将能量偏移量与电场强度的函数关系代入密度矩阵方程求解, 推导并分析探测光和耦合光偏振方向对EIT-Stark数学模型的影响.
2)搭建实验平台, 采用内置极板的方法, 消除碱金属原子附着所导致的屏蔽效应, 实现电场的有效加载. 通过施加标准源, 测量EIT光谱的频移量, 来实现里德伯态极化率的标定.
3)通过调控激光的偏振方向, 研究激光偏振失配对EIT光谱以及电场测量结果的影响. 实验数据显示, 探测光和耦合光激光偏振方向互为平行时, 为激光最匹配的偏振方向, EIT光谱峰值最大, 电场测量最大相对误差为1.67%. 探测光和耦合光激光偏振夹角互为45°时, 激光偏振失配程度最严重, EIT光谱峰值最小, 电场测量最大相对误差为10.24%.
基于里德伯原子电场量子测量方法及激光偏振影响分析
Rydberg atom electric field based quantum measurement method and polarization influence analysis
-
摘要: 电场与里德伯态能级互相作用产生Stark效应可以通过EIT光谱的频移量进行量子探测, 利用频移量与电场之间的函数关系, 能够实现电场的测量. 但是当探测光与耦合光偏振方向失配时会导致频移量的测量结果出现误差, 进而影响电场的准确测量. 本文首先求解密度矩阵方程进而推导EIT-Stark数学模型, 分析探测光和耦合光偏振方向对模型的影响. 其次, 本文采用内置极板的方法避免了由于碱金属原子附着在原子蒸气室表面对加载电场所造成的屏蔽作用. 最后, 通过调控激光偏振方向, 验证了偏振失配对EIT光谱以及电场测量结果的影响. 实验数据显示, 探测光和耦合光偏振方向互为平行时, 为激光最匹配的偏振方向, EIT光谱峰值最大, 电场测量最大相对误差为1.67%. 探测光和耦合光偏振方向夹角为45°时, 激光偏振失配程度最严重, EIT光谱峰值最小, 电场测量最大相对误差为10.24%.Abstract: The interaction between an electric field and the energy levels of Rydberg states results in the Stark effect, which can be used for quantum detection by measuring the frequency shift in electromagnetically induced transparency (EIT) spectra. By using the functional relationship between the frequency shift and the electric field, it is possible to measure the electric field in question. However, the mismatch between the probe laser and the polarization direction of the coupled laser leads to errors in the measurement of the frequency shift, affecting the accurate measurement of the electric field. In this work, the Schrödinger equation is solved by perturbation method to derive the functional relationship between the energy offset and the electric field strength. Then, the functional relationship between the energy offset and the electric field strength is brought into the solution of the density matrix equation, and the influences of the polarization direction of the detected light and coupled light on the EIT-Stark mathematical model are analyzed. Then an internal electrode method is used to prevent shielding effects caused by alkali metal atoms adhering to the surface of the atomic vapor cell, thereby enabling the application of the electric field. The calibration of the Rydberg state polarisation rate is achieved by using a standard source and measuring the frequency shift of the EIT spectrum. Finally, the effects of polarisation mismatch on the measurement results of EIT spectrum and the electric field are verified by modulating the laser polarization direction. The experimental data show that when the polarization directions of the probe laser and coupled laser are parallel to each other, it is the most matched polarization direction for the lasers, the peak value of the EIT spectrum is the largest, and the maximum relative error of the electric field measurement is 1.67%. When the angle between the polarisation directions of the probe light and the coupled light laser is 45°, the laser polarisation mismatch is the most severe, the EIT spectral peak is the lowest and the maximum relative error of the electric field measurement is 10.24%.
-
-
图 3 饱和光谱法稳频结构图
Figure 3. Structural diagram of frequency stabilisation by saturation spectroscopy.
图 4 饱和光谱法锁频原理图 (a) 饱和光谱图; (b) 精细能级结构; (c) 饱和光谱及其鉴频曲线
Figure 4. Schematic diagram of frequency locking by saturation spectroscopy: (a) Saturation spectrum; (b) fine structure levels; (c) saturation spectrum and its frequency discrimination curve.
图 9 EIT光谱峰值随双光子偏振夹角增加变化曲线
Figure 9. Variation curve of EIT spectral peak with increasing two-photon polarisation pinch angle.
图 11 激光偏振方向对EIT光谱的影响 (a)探测光和耦合光偏振方向平行; (b) 探测光和耦合光偏振方向夹角20°; (c) 探测光和耦合光偏振方向夹角45°; (d) 探测光和耦合光偏振方向垂直
Figure 11. Effect of laser polarisation direction on EIT spectra: (a) Polarization directions of the probe light and coupling light are parallel; (b) the polarization directions of the probe light and coupling light form an angle of 20°; (c) the polarization directions of the probe light and coupling light form an angle of 45°; (d) the polarization directions of the probe light and coupling light are perpendicular.
图 13 测量结果 (a)探测光和耦合光偏振方向平行; (b)探测光和耦合光偏振方向夹角22.5°; (c)探测光和耦合光偏振方向夹角45°
Figure 13. Measurement results: (a) Parallelism between the direction of polarisation of the probe and coupled laser; (b) 22.5° angle between the direction of polarisation of the probe and coupled laser; (c) 45° angle between the direction of polarisation of the probe and coupled laser.
-
[1] Holloway C L, Prajapati N, Simons M T, Artusio-Glimpse A 2022 IEEE Microw. Mag. 23 44 doi: 10.1109/MMM.2022.3148705 [2] 张学超, 乔佳慧, 刘瑶, 苏楠, 刘智慧, 蔡婷, 何军, 赵延霆, 王军民 2024 物理学报 73 073201 doi: 10.7498/aps.73.20231778 Zhang X C, Qiao J H, Liu Y, Su N, Liu Z H, Cai T, He J, Zhao Y T, Wang J M 2024 Acta Phys. Sin. 73 073201 doi: 10.7498/aps.73.20231778 [3] 夏刚, 张亚鹏, 汤婧雯, 李春燕, 吴春旺, 张杰, 周艳丽 2024 物理学报 73 104203 doi: 10.7498/aps.73.20240233 Xia G, Zhang Y P, Tang J W, Li C Y, Wu C W, Zhang J, Zhou Y L 2024 Acta Phys. Sin. 73 104203 doi: 10.7498/aps.73.20240233 [4] Hao L, Xue Y, Fan J, Bai J, Jiao Y, Zhao J 2020 Chin. Phys. B 29 033201 doi: 10.1088/1674-1056/ab6c49 [5] 张淳刚, 李伟, 张好, 景明勇, 张临杰 2021 光子学报 50 0602001 doi: 10.3788/gzxb20215006.0602001 Zhang C G, Li W, Zhang H, Jing M Y, Zhang L J 2021 Acta Photon. Sin. 50 0602001 doi: 10.3788/gzxb20215006.0602001 [6] 李伟, 张淳刚, 张好, 景明勇, 张临杰 2021 激光与光电子学进展 58 1702002 doi: 10.3788/LOP202158.1702002 Li W, Zhang C G, Zhang H, Jing M Y, Zhang L J 2021 Laser Optoelectron. Prog. 58 1702002 doi: 10.3788/LOP202158.1702002 [7] Hu J L, Li H Q, Song R, Bai J X, Jiao Y C, Zhao J M, Jia S T 2022 Appl. Phys. Lett. 121 014002 doi: 10.1063/5.0086357 [8] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030 doi: 10.1063/1.5095633 [9] Amy K R, Nikunjkumar P, Senic D 2021 Appl. Phys. Lett. 118 114001 doi: 10.1063/5.0045601 [10] 阮伟民, 张映昀, 冯志刚, 周亚东, 宋振飞, 屈继峰 2024 计量学报 45 97 doi: 10.3969/j.issn.1000-1158.2024.01.14 Ruan W M, Zhang Y Y, Feng Z G, Zhou Y D, Song Z F, Qu J F 2024 Acta Metrol. Sin. 45 97 doi: 10.3969/j.issn.1000-1158.2024.01.14 [11] 张映昀, 阮伟民, 冯志刚, 屈继峰, 宋振飞 2023 计量学报 44 1438 doi: 10.3969/j.issn.1000-1158.2023.09.18 Zhang Y Y, Ruan W M, Feng Z G, Qu J F, Song Z F 2023 Acta Metrologica Sinca 44 1438 doi: 10.3969/j.issn.1000-1158.2023.09.18 [12] 李可, 田建飞, 张好, 景明勇, 张临杰 2023 光子学报 52 0902001 doi: 10.3788/gzxb20235209.0902001 Li K, Tian J F, Zhang H, Jing M Y, Zhang L J 2023 Acta Photon. Sin. 52 0902001 doi: 10.3788/gzxb20235209.0902001 [13] 刘修彬, 贾凤东, 周飞, 俞永宏, 张剑, 谢锋, 钟志萍 2023 宇航计测技术 43 5 doi: 10.12060/j.issn.1000-7202.2023.03.02 Liu X B, Jia F D, Zhou F, Yu Y Y, Zhang J, Xie F, Zhong Z P 2023 J. Astron. Metrol. Measurem. 43 5 doi: 10.12060/j.issn.1000-7202.2023.03.02 [14] Cai M H, Xu Z S, You S H, Liu H P 2022 Photonics 9 250 doi: 10.3390/photonics9040250 [15] 蔡德成, 胡星, 吴海洋, 吕健双 2023 电力大数据 26 90 doi: 10.19317/j.cnki.1008-083x.2023.05.011 Cai D C, Hu X, Wu H Y, Lü J S 2023 Power Syst. Big Data 26 90 doi: 10.19317/j.cnki.1008-083x.2023.05.011 [16] 张缘圆, 辛明勇, 冯起辉, 祝健杨 2023 电力大数据 26 69 doi: 10.19317/j.cnki.1008-083x.2023.03.009 Zhang Y Y, Xin M Y, Feng Q H, Zhu J Y 2023 Power Syst. Big Data 26 69 doi: 10.19317/j.cnki.1008-083x.2023.03.009 [17] Liu W, Zhang L, Wang T 2023 Chin. Phys. B 32 053203 doi: 10.1088/1674-1056/aca6db [18] Zhao S S, Gao W, Cheng H, You L, Liu H P 2018 Phys. Rev. Lett. 120 063203 doi: 10.1103/PhysRevLett.120.063203 [19] 韩玉龙, 刘邦, 张侃, 孙金芳, 孙辉, 丁冬生 2024 物理学报 73 113201 doi: 10.7498/aps.73.20240355 Han Y L, Liu B, Zhang K, Sun J F, Sun H, Ding D S 2024 Acta Phys. Sin. 73 113201 doi: 10.7498/aps.73.20240355 [20] 阎晟, 肖冬萍, 石筑鑫, 张淮清, 刘卫华 2024 电工技术学报 39 2953 doi: 10.19595/j.cnki.1000-6753.tces.230395 Yan S, Xiao D P, Shi Z X, Zhang H Q, Liu W H 2024 Transactions of China Electrotechnical Society 39 2953 doi: 10.19595/j.cnki.1000-6753.tces.230395 [21] 王延正, 武博, 付运起, 安强 2025 激光与光电子学进展 62 0302001 Wang Y Z, Wu B, Fu Y Q, An Q 2025 Laser Optoelectron. Prog. 62 0302001 [22] Noah S, Andrew P R, Alexandra B A, Nikunjkumar P, Samuel B, Dangka S, Matthew T S, Christopher L H 2024 Phys. Rev. A 109 L021702 doi: 10.1103/PhysRevA.109.L021702 [23] Sedlacek J A, Schwettmann A, Kubler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001 doi: 10.1103/PhysRevLett.111.063001 [24] Bao S X, Zhang H, Zhou J, Zhang L J, Zhao J M, Xiao L T, Jia S T 2016 Phys. Rev. A 94 043822 doi: 10.1103/PhysRevA.94.043822 -
计量
- 文章访问数: 178
- HTML全文浏览数: 178
- PDF下载数: 2
- 施引文献: 0