-
水下光学成像技术在海洋资源勘探、水下生态环境监测、海底地形探测等领域有着广阔的应用前景[1–3]. 然而, 水下环境中无处不在的粒子产生的“帷幔效应”影响了成像质量[4]. 因此, 从总光强中提取有价值的目标光信息, 降低后向散射光干扰是水下成像领域的重大挑战.
在各种水下成像方法中[5–8], 偏振成像是利用不同光的偏振特性差异, 降低介质散射影响, 获得清晰水下成像结果的最有效方法之一[9–11]. Schechner等[12]基于大退化模型, 利用免靶区域以计算后向散射光信息. 在此基础上, 考虑多种偏振特性的目标, Huang等[13]额外引入参数表征不同偏振特性的目标信息光, 实现了多偏振特性目标的去散射. Hu等[14]提出了透射率校正的偏振成像, 取得了较好的去散射效果. Wei等[15]基于深度信息的水下Lambertian反射模型, 实现了被动成像色彩校正, 取得了较好的彩色成像效果. 在深海场景中, Treibitz和Schechner[16]采用主动偏振光源建立了水下主动偏振成像模型. 在此基础上, Wei等[17]基于独立成分分析提出了一种针对目标表面非均匀偏振特性的解决方案. 然而, 以上方法均依赖于免靶区域计算后向散射光信息, 而实际场景中相机捕获的场景往往不存在免靶区域. 这意味着需要全空间的解析目标信息光和后向散射光信息, 所以以上方法在实际应用中可能难以适应.
针对以上方法依靠免靶区域可能导致实际场景中难以适应的问题. 本文结合主动偏振成像和透射率去散射模型, 提出一种不依赖于免靶区域的水下偏振去散射方法. 首先, 将相机视场内的总光强分解为具有偏振信息和无偏振信息的部分, 具有偏振信息的部分采用主动偏振成像模型进行计算. 其中, 基于后向散射光偏振角为零计算全空间的目标信息光偏振度; 基于全局估计以计算后向散射光偏振度. 无偏振信息的部分采用Stokes矢量转换的最小强度图像计算. 最后, 结合透射率去散射原理得到水下场景. 实验和真实场景的成像结果表明, 无论是否存在免靶区域, 本文方法均能有效去除大部分后向散射光, 并提升了图像的对比度和熵. 同时, 具有一定速率优势, 能够助力实时复杂水下的成像技术.
-
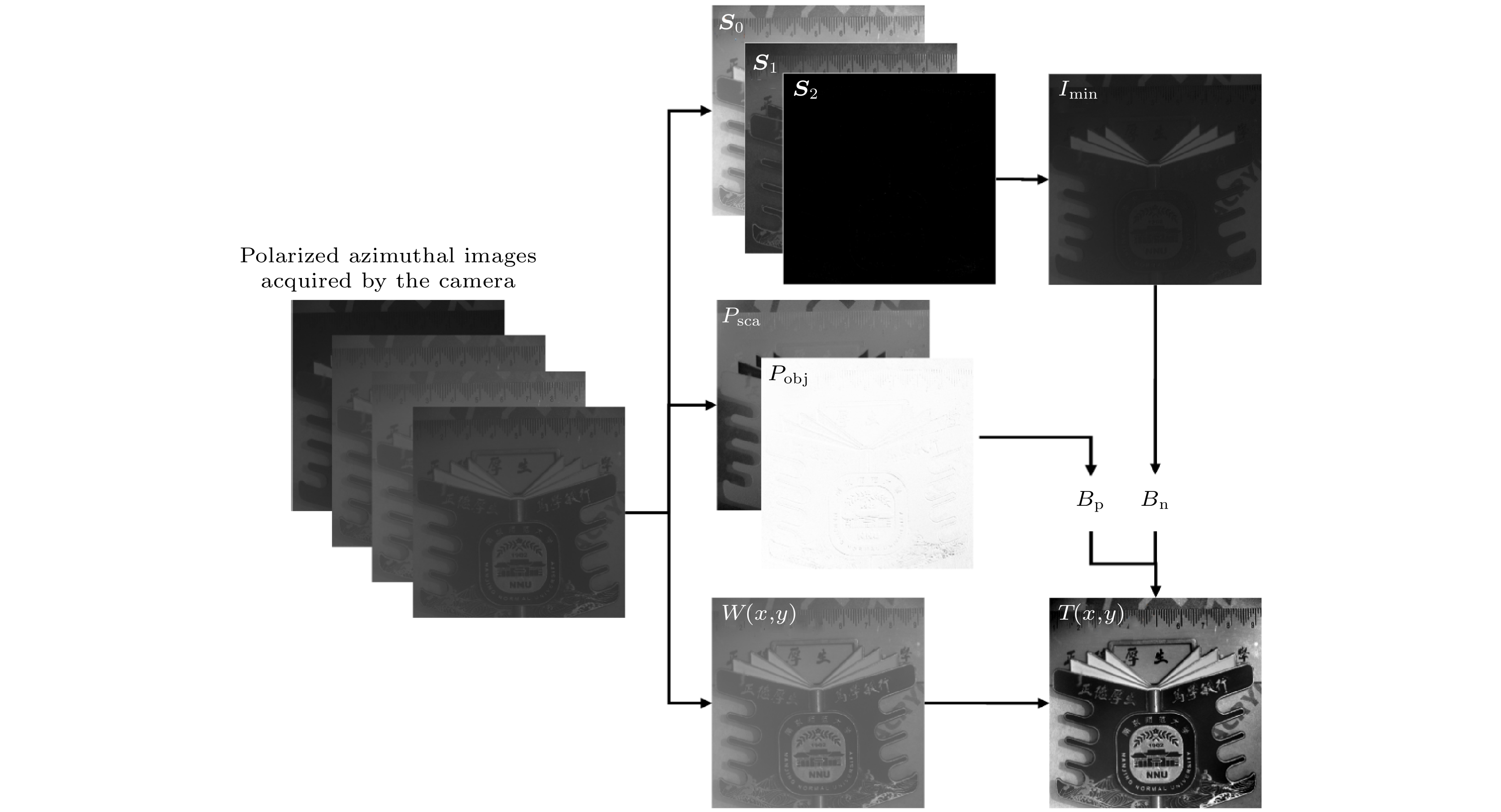
在水下成像过程中, 相机接收到的图像可以认为是目标信息光、后向散射光和前向散射光非相干叠加的结果. 水下成像质量下降主要源于后向散射光的影响, 因此一般忽略前向散射光. 相机探测到的总光强可表示为[13]
其中
$W(x, y)$ 表示成像设备采集到的像素$(x, y)$ 处的光照强度值,$T$ 表示目标信息光的强度, 即清晰的目标场景图像.$B$ 是后向散射光强度. 采用线偏振光源照射, 考虑到目标信息光和后向散射光往往是部分偏振的, 因此方程(1)应当更新为[18]其中
$ {T_{\text{p}}} $ 和$ {B_{\text{p}}} $ 为具有偏振信息的目标信息光和后向散射光; 而$ {T_{\text{n}}} $ 和$ {B_{\text{n}}} $ 是无偏振的目标信息光和后向散射光. 根据方程(2), 清晰的目标场景如(3)式所示:由于光在水下传输时会发生衰减, 结合目标信息光与背景散射光偏振特性差异, 根据透射率去散射原理[9,12,14], 方程(3)应当修改为
其中, 分母体现了散射介质对场景光的衰减作用.
$ k $ 为调节参数, 采用如下方式计算:其中,
$ \eta \left( l \right) $ 是指在整个图像中, 灰度值为$ l $ 的像素所占的比例.$ M $ 和$ N $ 分别表示图像的行数和列数.$ \rho \left[ {T(x, y) = l} \right] $ 为指示函数, 当$ T(x, y) = l $ 时值为1, 否则为0. 由于不包含偏振信息的后向散射光强度${B_{\text{n}}}(x, y)$ 与偏振方位角无关, 根据Stokes矢量转换的最小偏振强度图像进行计算:基于主动偏振成像模型,
${B_{\text{p}}}(x, y)$ 可以表示为[16]其中
$ {p_{{\text{obj}}}} $ 和$ {p_{{\text{scat}}}} $ 为目标信息光和后向散射光的偏振度.$ {I_{\max }} $ 和$ {I_{\min }} $ 为最大偏振强度图像和最小偏振强度偏振图像, 可以基于Stokes矢量得到. 由于目标的复杂性[13,17]和后向散射光的非均匀性[19], 需要全局计算后向散射光偏振度, 因此$ {p_{{\text{obj}}}} $ 和$ {p_{{\text{scat}}}} $ 应当更新为$ {P_{{\text{obj}}}}\left( {x, y} \right) $ 和$ {P_{{\text{scat}}}}\left( {x, y} \right) $ . 基于全局估计[20],$ {P_{{\text{scat}}}}\left( {x, y} \right) $ 可以表示为其中
$\hat B\left( {x, y} \right)$ 为估计的后向散射光强度. 根据散射光在图像上表现为低频分量[21], 可使用高斯低通滤波器估计$\hat B\left( {x, y} \right)$ [22]. 考虑到后向散射光的偏振角为零[23], 目标表面每个像素点的偏振度表示为其中,
$ {{\boldsymbol{S}}_0} $ ,$ {{\boldsymbol{S}}_1} $ 和$ {{\boldsymbol{S}}_2} $ 为Stokes矢量,$ P $ 为偏振度. 本文方法步骤如图1所示. -
由于后向散射光的偏振度主要受散射角的 影响, 对入射光的偏振角不敏感[24], 采用图2所示的设置进行了实验. 白光LED光源通过偏振片, 照亮淹没在浑浊水中的目标. 使用像素偏振相机 (BFS-U3-51S5P-C)获取原始4幅共计两对正交偏正方位角图像, 曝光时间为80—100 ms. 在实验中, 将4 L清水与全脂牛奶混合配制成浑浊水溶液模拟水下环境. 其中, 全脂牛奶蛋白质含量为3.2 g/100 mL, 脂肪含量为3.8 g/100 mL作为散射介质.
-
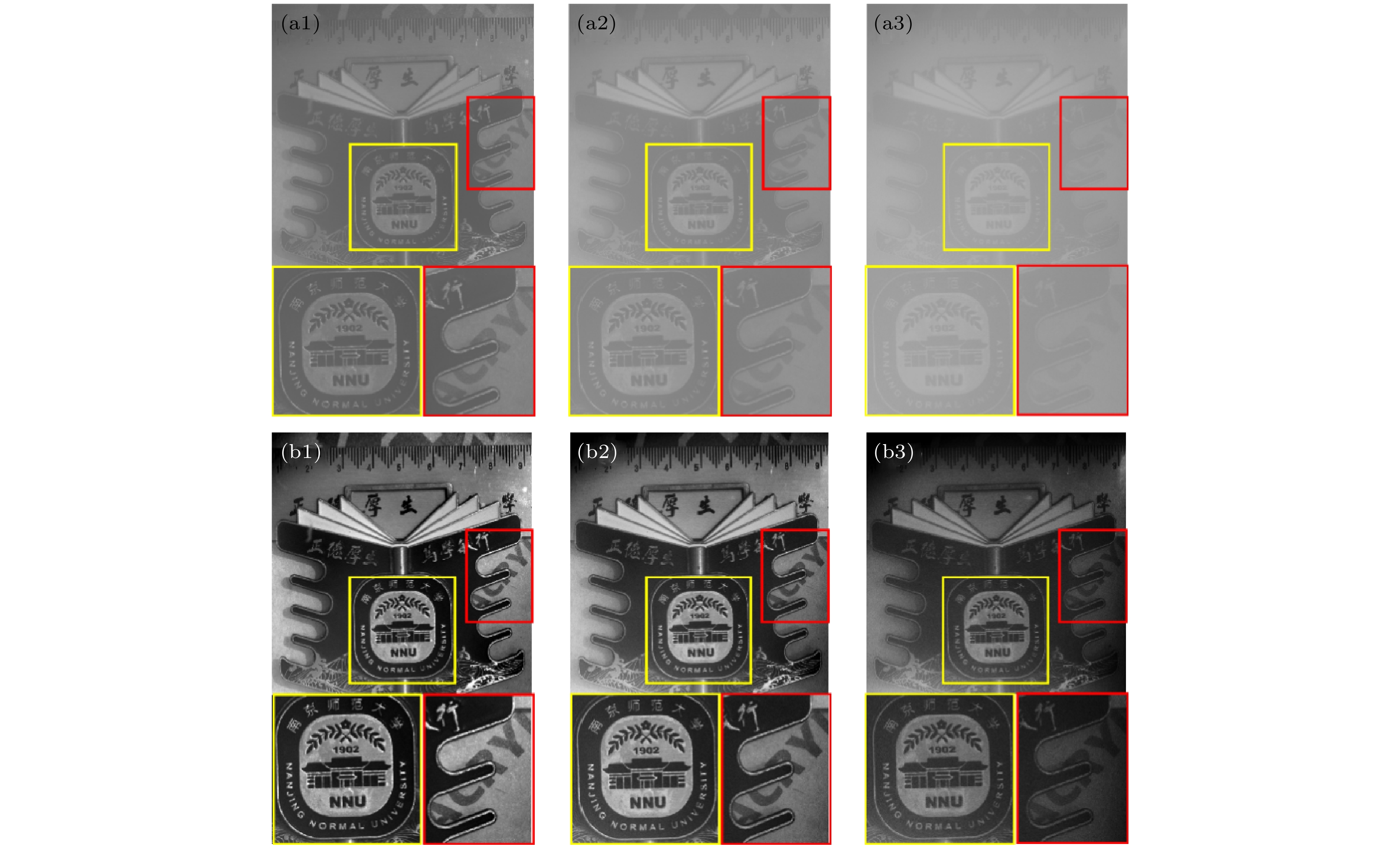
相机视场内的目标选择木板、钢尺以及奖牌, 且无免靶区域. 向清水中倒入牛奶, 浑浊度设置为25 NTU, 35 NTU和58 NTU. 相机获取的强度图像如图3(a1)—(a3), 本文方法成像结果如图3(b1)—(b3). 图像中的细节采用黄色和红色矩形框标记. 可见, 随着浑浊度的不断提升, 粒子造成的后向散射光逐渐增强, 强度成像对比度和清晰度显著下降. 本文方法将相机接收到的总光强分解为具有偏振信息和无偏振信息的部分, 而不是简单认为相机接收到的总光强完全具有偏振信息. 进而分别计算了具有偏振信息的后向散射光强度和无偏振信息的后向散射光强度. 其中, 考虑到目标的复杂性和后向散射光的非均匀性, 在主动偏振成像模型中结合了全局估计方法. 因此能够去除大部分后向散射光, 可轻松识别目标表面的细节信息, 验证了文中提出方法的可行性.
-
在主动照明条件下, 使用偏振相机在大鹏湾记录的以珊瑚和鱼类为主的真实水下场景[25]. 如图4所示, 该场景不存在无目标的免靶区域. 将我们所提出的方法与其他4种方法进行比较, 分别是强度成像、Schechner的方法[6]、CLAHE[26]、PDS[25], 共5种方法成像结果如图4(a1)—(e1)所示. 红色和黄色矩形框内所取局部图像分别对应于图4(a2)—(e2)和图4(a3)—(e3). 红色矩形框内所选取的是以珊瑚为主的局部场景, 黄色矩形框内所选取的是以沙石颗粒为主的局部场景. 由于两处目标的材质有明显差异, 它们的反射光偏振特性亦不同, 同时比较全场景和局部场景以充分比较各种方法成像效果. 因受到粒子散射的影响, 强度成像结果质量劣化明显. Schechner的方法对后向散射光的去除具有一定的效果, 但是其假设后向散射光和目标信息光为常数, 难以适应于具有复杂偏振特性目标信息光的场景. 因此, 图4(b1)—(b3)整体和局部均存在大量的暗区, 存在细节丢失. CLAHE是目前广泛应用的图像处理方法, 但是该方法难以去除后向散射光, 成像结果受“帷幔效应”影响严重. 因此, 在图4(c1)—(c3)整体和局部均泛白, 对比度较低. PDS是Shen等[25]提供的方法, 该方法对散射光的去除效果和细节表现较好, 但其采用的是被动偏振成像模型, 认为目标信息光是完全非偏振的, 而事实上目标信息光也会存在部分偏振的特性. 所以最终的成像效果可能有待提升. 本文采用主动偏振成像模型并计算了全局的目标信息光偏振度以及后向散射光强度和偏振度, 在有效去除后向散射光的同时保留了细节信息.
为了进一步证实本文方法的有效性, 文中选择了存在免靶区域的场景进行成像并与其他方法进行比较, 对比结果如图5所示. 红色和黄色矩形框分别选择远场和近场场景. 由于所选远场景具有大景深平缓性质且目标信息少, 因此该区域可以作为免靶区域计算散射光信息. 而所选取的近场场景 区域受到目标的遮挡, 辐照度较低. 选择该区域以比较各种方法对于非均匀光照条件下的成像效果. 综合比较图5(a1)—(e3)各种成像结果, 本文方法成像结果具有较高的整体清晰度和细节信息识别度.
为了能更好地定量分析成像结果, 文中进一步选择多种场景进行研究, 结果如图6及表1所示. 由于单一的评价指标往往难以全面的评价图像质量, 选择图像熵[27]和对比度[28]作为成像结果的客观评价指标. 图像熵的值越高表明图像中有效信息越丰富, 但难以评价整体清晰程度. 对比度的值越高说明图像整体越清晰, 但难以评价图像中尤其是人眼能够获得的信息量. 因此, 需要综合考量这两个评价指标. 如表1所示, 最佳值采用加粗标注, 次之采用*标注. 综合比较两个评价指标可见, 本文方法成像质量综合表现较优. 值得注意的是, 在一台搭载Intel Core i5-9300 h处理器的便携式计算机上进行成像实验, 单次成像平均时间在表2列出. 由于CLAHE图像处理方法原理是直方图拉伸, 难以去除场景中的后向散射光, 因此该方法单次成像平均时间未列入比较范围. 未采用计算机并行计算时, 本文方法单次成像的平均时间为1.78 s. 相比PDS成像方法, 所需时间仅为其13.98%; 相比Schechner的方法, 所需时间仅为其32.46%. 由此可见, 文中方法更能助力实时复杂条件下的水下成像技术.
-
本文基于主动偏振成像模型提出了一种不依赖于免靶区域的水下偏振去散射方法. 将主动偏振成像模型与透射率校正原理相结合, 将相机接收到的总光强分解为具有偏振信息和无偏振信息的部分分别计算. 实验结果表明, 本文方法的有效性. 本文方法不仅对比度和图像熵的综合表现较优, 而且成像速率方面存在优势. 综上所述, 若采用并行计算和更强大的硬件系统, 相信本文提出的方法能够实现实时复杂水下偏振去散射成像需求并应用于水下资源勘探和研究等领域.
感谢西北工业大学自动化学院赵永强教授团队开源的实验原始数据和方法.
基于无免靶区域的水下偏振去散射成像
Underwater polarization de-scattering imaging independent of target-free region
-
摘要: 偏振成像技术在去除后向散射光方面是有效的. 针对该技术依赖免靶区域以计算后向散射光信息限制其适用范围和实时成像能力的问题, 本文提出了无免靶区域的偏振成像方法. 该方法结合主动偏振成像和透射率去散射模型, 将相机接收到的图像分解为具有偏振信息和无偏振信息的部分, 具有偏振信息的部分采用主动成像模型计算, 而无偏振信息的部分基于Stokes矢量计算. 同时, 结合透射率校正原理实现去散射. 实验和真实世界水下成像结果表明, 本文方法能够有效去除大部分后向散射光, 且具有速率优势, 能够助力实时复杂条件下的水下成像技术, 在海底资源探测与研究等领域具有广阔的应用前景.Abstract:
Underwater optical imaging technology possesses broad application prospects in fields such as marine resource exploration, underwater ecological environment monitoring, and seabed topography detection. The technology employs the polarization characteristics of light, particularly those of the background and target, to achieve a clear image. However, the traditional methods rely on target-free regions to compute the backscattered light information, which is infrequently present in the actual scene captured by the camera. Then the full-space resolution of target information light and backscattered light information are required. At this time, the traditional methods may be difficult to adapt in practical application. In this work, an underwater polarization de-scattering method independent of target-free regions is proposed by combining active polarization imaging and transmittance de-scattering model. Initially, the total light intensity within the camera’s field of view is decomposed into its polarized and unpolarized components. By removing the backscattered light with polarized and unpolarized information from the total light intensity, a clear underwater target can be obtained. Based on the active polarization imaging model, the backscattered light with polarization information is calculated, in which the polarization angle of the backscattered light is considered to be zero in the full-space. Thus, the polarization degree of the target information light occupying the camera’s entire field of view can be derived. According to the polarization correlation, the polarization degree of the backscattered light can be characterized, and the intensity of the backscattered light with polarization information in the camera’s entire field of view can also be obtained. Then the unpolarized component is calculated using the minimum intensity image with Stokes vector transformation. Finally, the underwater scene is obtained by combining the transmittance de-scattering principle and introducing adjustment parameters. Experimental and real-world underwater imaging results demonstrate that the proposed method can effectively remove the majority of the backscattered light and improve the image contrast and entropy, regardless of whether there are target-free regions. Additionally, this method possesses a certain rate advantage, which can facilitate the real-time complex underwater imaging technology. -
Key words:
- target-free regions /
- underwater polarization imaging /
- de-scattering /
- transmittance correction .
-

-
图 3 水下偏振成像实验结果 (a1)—(a3) 强度成像结果, 环境浑浊度为25 NTU, 35 NTU和58 NTU; (b1)—(b3) 本文方法成像结果, 黄色和红色矩形框内展示图像细节
Figure 3. Results of underwater polarization imaging experiments: (a1)–(a3) The intensity imaging results with ambient turbidity of 25 NTU, 35 NTU and 58 NTU; (b1)–(b3) the imaging results of the proposed method in this paper, the yellow and red rectangles show the imaging details.
图 4 无免靶区域不同方法成像结果比较 (a1)—(a3) 强度成像; (b1)—(b3) Schechner的方法; (c1)—(c3) CLAHE方法; (d1)—(d3) PDS方法; (e1)—(e3) 本文方法
Figure 4. Comparison of imaging results using different methods independent of target-free regions: (a1)–(a3) The intensity imaging; (b1)–(b3) Schechner’s method; (c1)–(c3) CLAHE method; (d1)–(d3) PDS method; (e1)–(e3) the proposed method in this paper.
图 5 存在免靶区域不同方法成像结果比较 (a1)—(a3) 强度成像; (b1)—(b3) Schechner的方法; (c1)—(c3) CLAHE方法; (d1)—(d3) PDS方法; (e1)—(e3) 本文方法
Figure 5. Comparison of imaging results using different methods in the presence of target-free regions: (a1)–(a3) The intensity imaging; (b1)–(b3) Schechner’s method; (c1)–(c3) CLAHE method; (d1)–(d3) PDS method; (e1)–(e3) the proposed method in this paper
图 6 各种场景不同方法成像结果比较 (a1)—(e1) 强度成像; (a2)—(e2) Schechner的方法; (a3)—(e3) CLAHE方法; (a4)—(e4) PDS方法; (a5)—(e5) 本文方法
Figure 6. Comparison of imaging results using different methods in various scenes: (a1)–(e1) The intensity imaging; (a2)–(e2) Schechner’s method; (a3)–(e3) CLAHE method; (a4)–(e4) PDS method; (a5)–(e5) the proposed method in this paper.
表 1 图6成像结果定量分析与比较, 最佳值采用加粗标注, 次之采用*标注
Table 1. Quantitative analysis and comparison of imaging results from Fig.6, the best values are highlighted in bold, and the second-best values are marked in *.
Figures Evaluation Intensity Schechner CLAHE PDS Our (a1)—(a5) Entropy 7.0835 5.2074 7.1600 6.3775 6.9319* Contrast 0.2933 –∞ 0.3620 0.7076 0.4968* (b1)—(b5) Entropy 7.1815 7.2357 7.2334 7.0689 7.3007 Contrast 0.3495 –∞ 0.4143 0.6053 0.5608* (c1)—(c5) Entropy 6.6501 6.8566 7.3142 6.0976 6.9915* Contrast 0.1996 0.7476 0.3625 0.3573 0.4523* (d1)—(d5) Entropy 6.6219 6.0931 7.1348 6.5029 6.7891* Contrast 0.1947 –∞ 0.3249 0.4311 0.4566 (e1)—(e5) Entropy 6.8163 6.2458 7.1551 6.9662 7.1863 Contrast 0.2249 –∞ 0.2909 0.3916 0.3725* -
[1] Bailey G, Flemming N 2008 Quat. Sci. Rev. 27 2153 doi: 10.1016/j.quascirev.2008.08.012 [2] Ji T T, Wang G Y 2015 J. Ocean Univ. China 14 255 doi: 10.1007/s11802-015-2426-2 [3] Panetta K, Gao C, Agaian S 2016 IEEE J. Oceanic Eng. 41 541 doi: 10.1109/JOE.2015.2469915 [4] Li X B, Han Y L, Wang H Y, Liu T G, Chen S C, Hu H F 2022 Front. Phys. 10 815296 doi: 10.3389/fphy.2022.815296 [5] McLean E A, Burris H R, Strand M P 1995 Appl. Opt. 34 4343 doi: 10.1364/AO.34.004343 [6] Jaffe J S 2005 Opt. Express 13 738 doi: 10.1364/OPEX.13.000738 [7] Gong W L, Han S S 2011 Opt. Lett. 36 394 doi: 10.1364/OL.36.000394 [8] Le M N, Wang G, Zheng H B, Liu J B, Zhou Y, Xu Z 2017 Opt. Express 25 22859 doi: 10.1364/OE.25.022859 [9] Schechner Y Y, Karpel N 2005 IEEE J. Oceanic Eng. 30 570 doi: 10.1109/JOE.2005.850871 [10] 管今哥, 朱京平, 田恒, 侯洵 2015 物理学报 64 224203 doi: 10.7498/aps.64.224203 Guan J G, Zhu J P, Tian H, Hou X 2015 Acta Phys. Sin. 64 224203 doi: 10.7498/aps.64.224203 [11] 韩平丽, 刘飞, 张广, 陶禹, 邵晓鹏 2018 物理学报 67 054202 doi: 10.7498/aps.67.20172009 Han P L, Liu F, Zhang G, Tao Y, Shao X P 2018 Acta Phys. Sin. 67 054202 doi: 10.7498/aps.67.20172009 [12] Schechner Y Y, Narasimhan S G, Nayar S K 2003 Appl. Opt. 42 511 doi: 10.1364/AO.42.000511 [13] Huang B J, Liu T G, Hu H F, Han J H, Yu M X 2016 Opt. Express 24 9826 doi: 10.1364/OE.24.009826 [14] Hu H F, Zhao L, Huang B J, Li X B, Wang H, Liu T G 2017 IEEE Photonics J. 9 1 doi: 10.1109/JPHOT.2017.2698000 [15] 卫毅, 刘飞, 杨奎, 韩平丽, 王新华, 邵晓鹏 2018 物理学报 67 184202 doi: 10.7498/aps.67.20180692 Wei Y, Liu F, Yang K, Han P L, Wang X H, Shao X P 2018 Acta Phys. Sin. 67 184202 doi: 10.7498/aps.67.20180692 [16] Treibitz T, Schechner Y Y 2009 IEEE Trans. Pattern Anal. Mach. Intell. 31 385 doi: 10.1109/TPAMI.2008.85 [17] Wei Y, Han P L, Liu F, Liu J P, Shao X J 2021 Chin. Opt. Lett. 19 111101 doi: 10.3788/COL202119.111101 [18] Wei Y, Han P L, Liu F, Shao X P 2021 Opt. Express 29 22275 doi: 10.1364/OE.433072 [19] Hu H F, Zhao L, Li X B, Wang H, Liu T G 2018 IEEE Photonics J. 10 6900309 doi: 10.1109/JPHOT.2018.2791517 [20] 封斐, 吴国俊, 吴亚风, 苗宇宏, 刘博 2020 光学学报 40 2111002 doi: 10.3788/AOS202040.2111002 Feng F, Wu G J, Wu Y F, Miao Y H, Liu B 2020 Acta Opt. Sin. 40 2111002 doi: 10.3788/AOS202040.2111002 [21] Liu F, Cao L, Shao X P, Han P L, Bin X L 2015 Appl. Opt. 54 8116 doi: 10.1364/AO.54.008116 [22] Deng J, Zhu J, Li H, Zhang X, Guo F, Hou X 2023 Opt. Lasers Eng. 169 107721 doi: 10.1016/j.optlaseng.2023.107721 [23] Fang M, Cai Y X, Zhang J R 2024 Opt. Express 32 19801 doi: 10.1364/OE.523180 [24] Wang J J, Wan M J, Cao X Q, Zhang X J, Gu G H, Chen Q 2022 Opt. Express 30 46926 doi: 10.1364/OE.474026 [25] Shen L H, Reda M, Zhang X, Zhao Y Q, Kong S G 2024 IEEE Trans. Geosci. Remote Sens. 62 4202615 doi: 10.1109/TGRS.2024.3358828 [26] Pour A M, Seyedarabi H, Jahromi S H A, Javadzadeh A 2020 IEEE Access 8 136668 doi: 10.1109/ACCESS.2020.3005044 [27] Coifman R R, Wickerhauser M V 1992 IEEE Trans. Inform. Theory 38 713 doi: 10.1109/18.119732 [28] Yang L M, Liang J, Zhang W F, Ju H J, Ren L Y, Shao X P 2019 Opt. Commun. 438 96 doi: 10.1016/j.optcom.2018.12.022 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: