首页
登录
注册
-
传统的光学成像技术是通过探测器获取视野范围内的场景并进行成像. 随着激光成像技术的快速发展和探测器精度的提高, 非视域(non-line-of-sight, NLOS)成像技术实现了对视线外隐藏物体进行光学探测和可视化, 打破了光沿直线传播的固有物理约束, 在医学、军事、自动驾驶、智慧医疗等领域具有广阔的应用前景. 近年来, 非视域成像技术在国内外均取得了不错的研究进展. 非视域成像概念在2008年被首次提出后, 引发了广泛的研究. 2009年Kirmani等[1]证明了非视域成像可用于恢复隐藏的平面物体的可行性. 随后, Velten等[2]提出了椭球反投影(back-projection, BP)算法, 使用条纹相机完成了隐藏物体的三维重建. Victor等[3]利用光子到达的飞行时间和总距离之间的相关性, 提出了快速反投影非视域成像算法, 使得重建速度提升了3个数量级. 2018年, O’Toole等[4]使用收发同轴的方法, 提出的基于光锥变换(the light-cone transform, LCT)的共焦非视域成像方法, 简化了成像模型, 以物理模型贴合度高、成像模型 简单、计算方式高效等优势促进了非视域成像的发展. 其后, 涌现出了更多表现优异的算法, 如频率-波数偏移(frequency-wavenumber, F-K)算法[5]、基于费马流的非视域成像算法[6]、相量场虚拟波(phasor-field virtual wave, V-W)算法[7]、定向光锥变换方法(directional light cone transform, D-LCT)[8] , 也有学者引入深度学习进行非视域成像处理[9–12]. 此外, 在提高重建质量和效率方面也有不少研究, 如对捕获的飞行时间信息进行滤波处理[13]、通过捕获中频域信息估计隐藏场景的功率密度噪信比[14]、引入空间复用检测[15]等. 2021年, Wang等[16]构建了基于短激光脉冲泵浦技术的红外端上转换单光子探测器(up-conversion single-photon detector, UCSPD)实现室温探测, 提高了探测器时间分辨率, 实现了1.43 km的非视域成像[17]. 2023年Liu等[18]引入贝叶斯推断, 提出基于虚拟共焦补偿的信号与物体联合先验(confocal complemented signal-object collaborative regularization, CC-SOCR)重建方法, 实现了任意中介面形态下的准确成像.
由于非视域成像过程中光子的多次漫反射, 致使大量信号损失, 且目标信息极易淹没在环境噪声中, 如何提高目标信号的信噪比成为了非视域成像领域的主要难点. 门控单光子雪崩二极管(single-photon avalanche diode, SPAD)凭借在弱光环境中出色的探测能力, 在非视域领域的发展中发挥了重要作用. 近年来, 不少学者在非视域探测和成像中引入了门控控制, Laurenzis和Velten[19]使用可门控强化电荷耦合装置相机和照明装置组成的激光门控选通(laser-gated viewing, LGV)系统进行数据采集. Buttafava等[20]使用SPAD进行飞行时间信息采集, 减小了成像系统尺寸、降低了器件成本, 并指出提高门控SPAD的有效动态范围有利于降低一次回波信号对目标回波信号的干扰. Zhu等[21]展示了一套具有10 ps时间门控上转换检测的非视域成像和定位系统, 使用非线性频率转换生成的皮秒门控单光子探测器, 可以实现皮秒单光子时间选通, 同时抑制了背景噪声. Zhao等[22]提出了一种梯度门控技术并结合开发的SPAD阵列实现了非视域目标重构, 减少了非视域成像数据采集过程中光子堆积问题.
然而, 在这些工作中, 实际使用门控SPAD进行目标信号探测时, 通常需要手动调整门位置和宽度, 并依赖于操作经验. 同时, 在非视域成像数据采集过程中, 现有方法多需要结合中介面信息、隐藏目标范围等先验知识进行门宽位置预设, 且需采集中介面所有扫描点信息进行校准. 由于每个扫描点的最优门控宽度、位置不同, 预设的门宽位置存在不能完全去除非目标信号干扰或目标信号丢失等问题, 因此如何准确、高效进行门控设置亟待进一步研究. 本文利用三角定位原理[23]和少量特征点回波信息, 提出了一种对门控SPAD的自适应控制方法, 实现了门控参数调节自动化, 有效减少了对中介面信息、目标隐藏范围等先验知识的需求, 避免非目标信号干扰. 搭建基于门控SPAD的非视域成像系统, 验证了自适应门控控制算法对目标信号位置、门宽识别的有效性, 定量分析了门控SPAD对目标信号信噪比和成像质量的作用, 并对主流的非视域成像算法重建质量进行了客观评价.
-
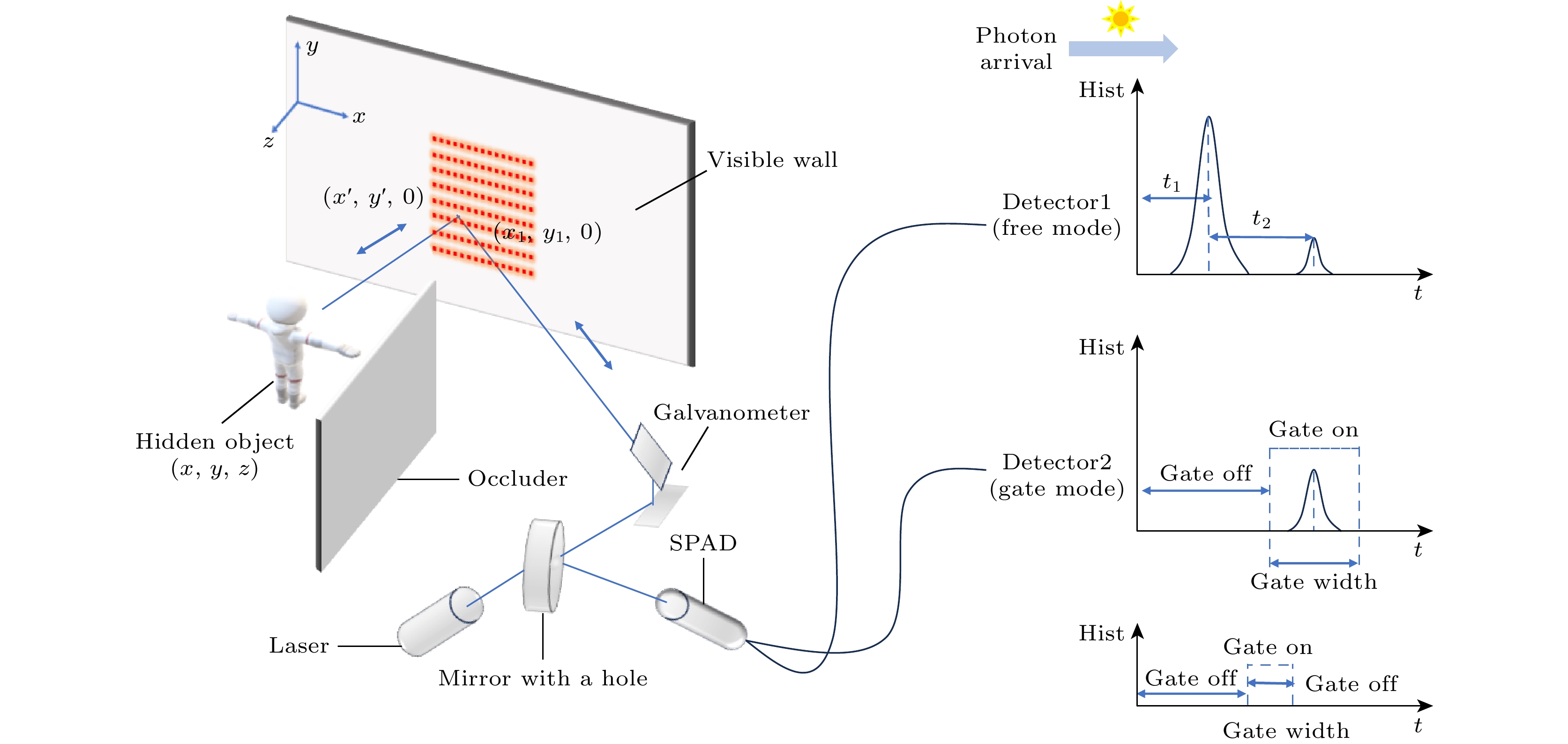
激光器向视线内的中介墙面发射脉冲激光, 发生第1次漫反射, 随后散射到整个隐藏空间中, 由隐藏空间内的目标发生第2次漫反射, 其中一部分光子反射到了中介墙面, 经过第3次漫反射后由探测器捕获, 通过对捕获到的目标信号处理分析, 实现隐藏物体重构. 成像原理图如图1(左)所示.
以中介墙面为基础建立直角坐标系, 使得探测点
$ (x', y') $ 和激光点$ ({x_1}, {y_1}) $ 均在中介面$ z = 0 $ 平面上, 则非视域成像的模型可表示为式中,
$ c $ 表示光速,$\rho (x, y, z)$ 表示隐藏物体表面$\varOmega $ 每个点的反射率, 探测点到隐藏物体某点的距离表示为${r_1} = \big[{{(x' - x)}^2} + {{(y' - y)}^2} + {z^2}\big]^{1/2} $ , 激光点与隐藏目标某点距离表示为${r_2} = \big[{{({x_1} - x)}^2} + {{({y_1} - y)}^2} + {z^2}\big]^{1/2} $ . 在共焦光路中, 探测点与激光点相同, 均为$ (x', y') $ , 从而成像模型可表示为式中,
$r$ 表示探测点与隐藏目标间距离,$\delta $ 为由${x^2} + {y^2} + {z^2} = {\left( {{{tc} {/ } 2}} \right)^2}$ 给出的时空四维超圆锥表面.通过对成像模型进行求解, 得到隐藏物体表面各点反射率, 实现非视域目标重建. 本文搭建了基于门控SPAD的共焦非视域成像系统, 对目标回波信号进行采集, 并运用主流的非视域图像重构算法完成隐藏目标重构.
-
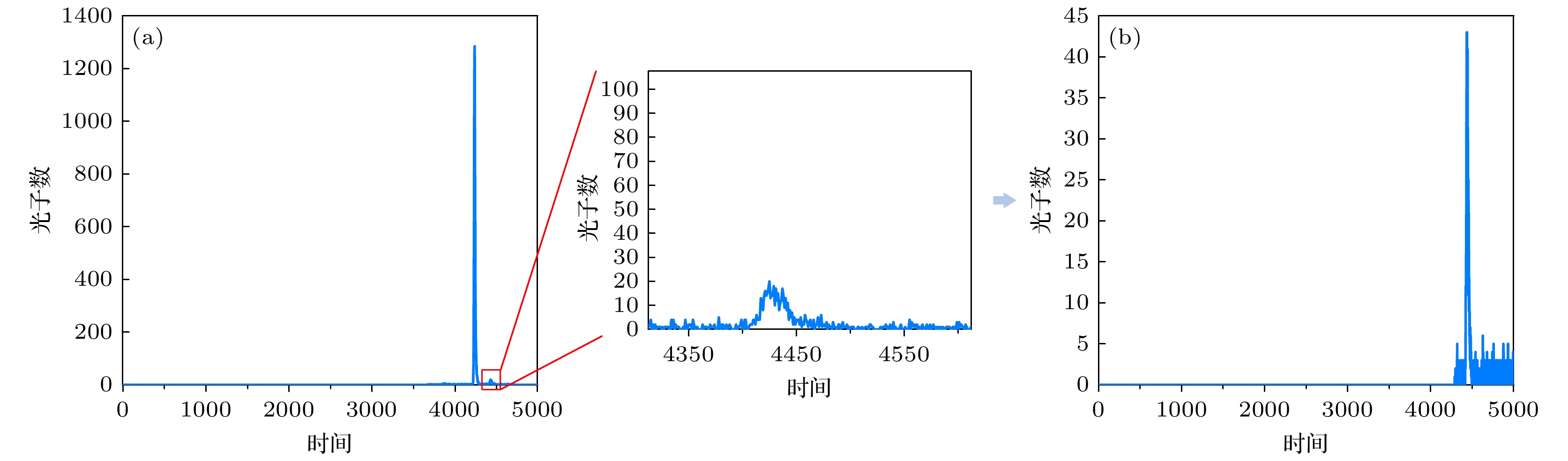
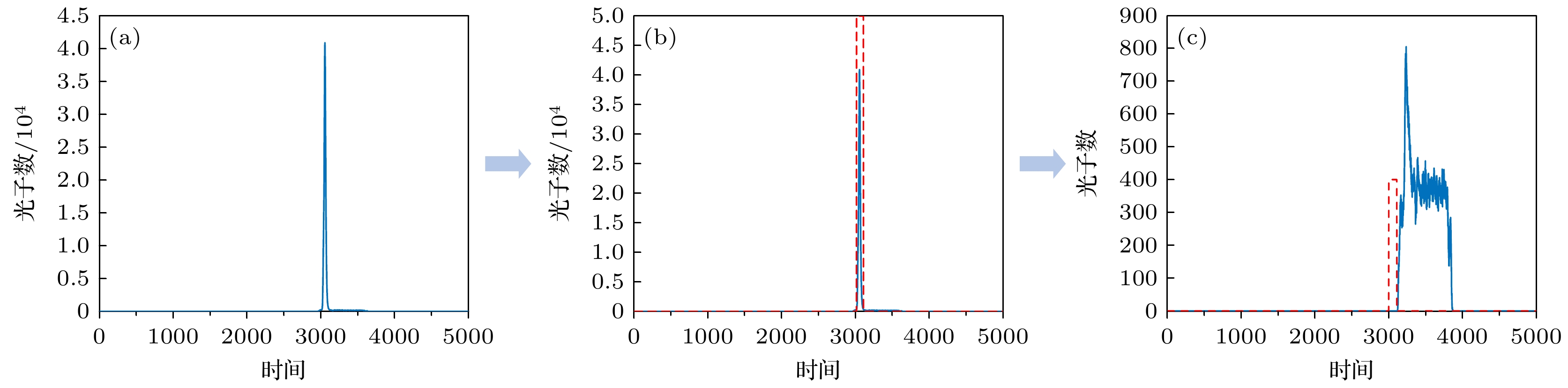
门控SPAD具有单光子级别的探测灵敏度和皮秒级的时间分辨率, 使其在低信噪比环境具备出色的探测能力. 通过在特定时间窗口内启用或关闭探测器, 可以有效滤除无关信息, 保留目标信号, 如图1所示. 信号输入后, 探测器的门控模块和探测模块将对信号进行识别探测. 自由模式下, 信号被检测后转换输出; 门控模式下, 当信号在特定时间窗口内时, 信号才能被门控输入并进行检测转换输出. 当信号处于非特定时间窗口时, 门控输出为0, 探测器转换输出也为0. 即只有当光子信号在特定时间窗口内输入时, 才能被探测器检测并输出. 门控SPAD实际效果如图2所示, 图2(a)为自由模式下获取的回波信号, 图2(b)为门控模式下获取的目标回波信号.
-
在进行非视域目标探测时, 探测器最先收到的往往是中介面直接返回的回波(中介面回波). 由于中介面回波(一次回波)只经过一次散射, 其回波能量远大于经过三次散射的目标回波能量, 所以会形成一个极大的峰值, 从而对目标回波信号识别造成严重影响. 因此, 使用门控SPAD获取信号的关键在于避开非目标信息的干扰, 尤其是中介面回波信号.
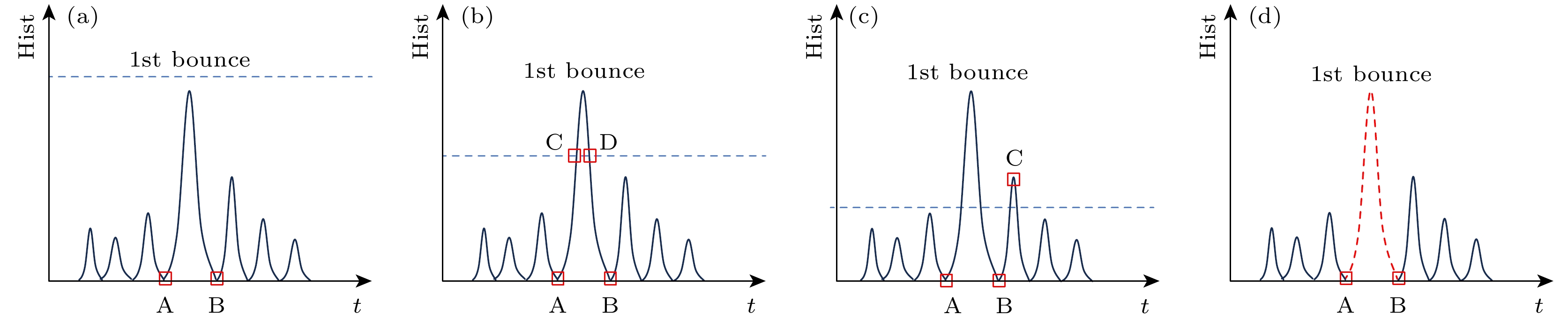
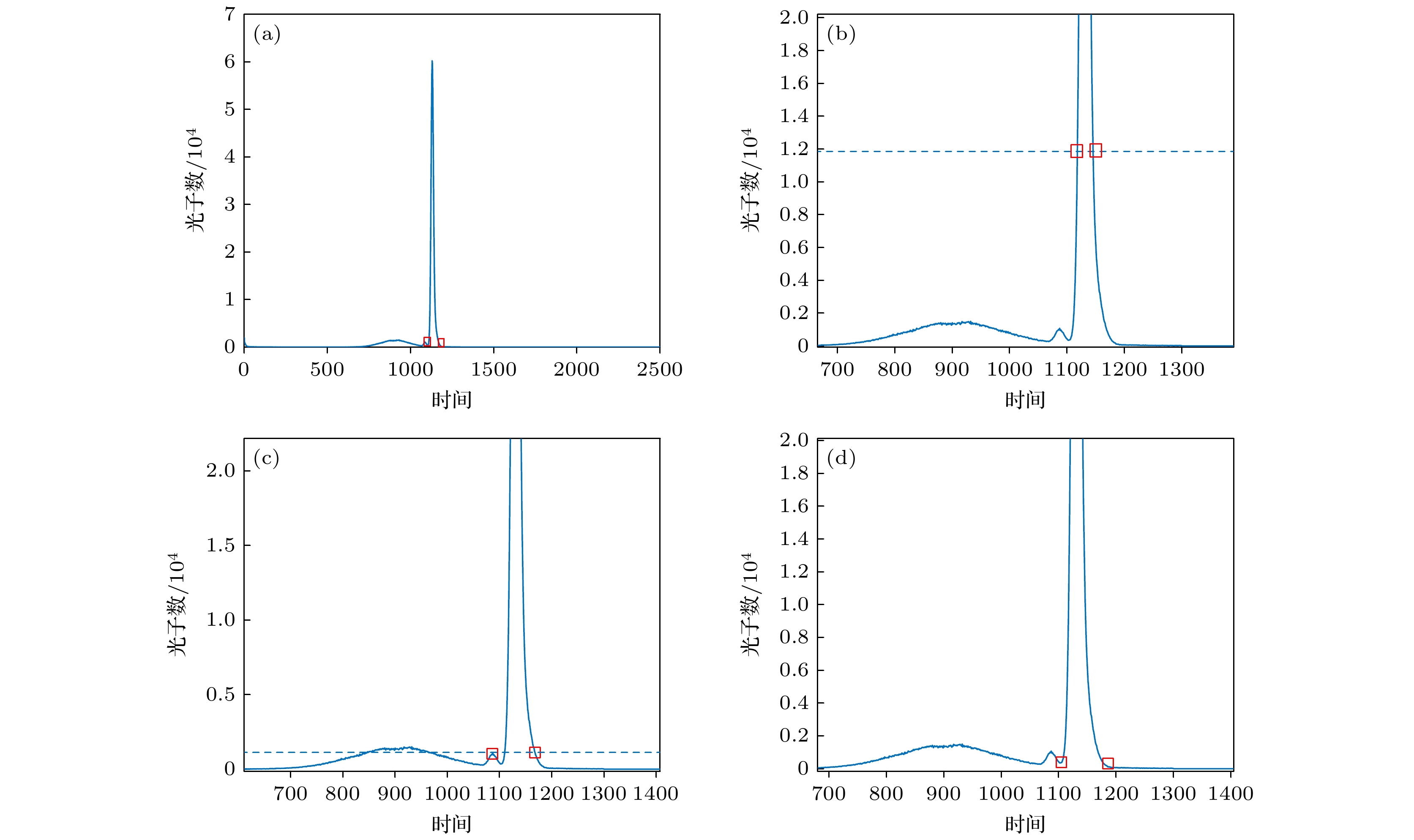
常规方法中通过设置一定阈值进行中介面回波信号抑制时, 多选用取中介面回波信号峰值的一定比例或者噪声均方根倍数作为阈值, 该方法存在以下问题: 阈值设定范围需要人工干预设置. 首先, 当阈值设置高于中介面回波峰值时, 存在无法抑制中介面回波信号的可能, 此时光子堆积现象可能致使单光子探测器饱和, 即探测器进入死时间, 导致目标回波信噪比降低, 如图3(a)所示. 其次, 如果将中介面信号小于阈值的左右两个bin作为中介面信号的起点与终点, 则与中介面回波信号实际的起点与终点不符, 无法完全抑制中介面回波信号, 如图3(b)所示. 再次, 当阈值设置过低时, 极易受到凸起的噪声信号干扰, 并将噪声峰值误认为中介面回波信号峰值, 导致目标与中介面间的飞行时间识别产生偏差, 如图3(c)所示. 因此, 设置阈值进行中介面回波信号抑制, 容易误判中介面回波信号起点、终点位置信息, 难以完全抑制中介面回波信号.
针对门控SPAD门控设置中需要手动调整且门宽位置预设对先验信息依赖等问题, 本文提出了一种自适应门控参数计算方法, 可以全自动辨识出中介面回波的区域并加以抑制, 如图3(d)所示. 自适应门控参数计算方法根据中介面回波信号能量极大的特点, 借助中介面回波信号峰值信息, 将中介面回波信号循环位移至信号中间, 随后将循环位移信号分为左右两半. 以左半信号为例, 经过其起点和终点作一条辅助直线, 左半信号上各点与辅助直线两端点构成一个三角形. 为了完全抑制中介面回波信号, 其起点与终点需要完全包含中介面波形, 因此起点、终点应该是中介面边界的最低点, 即距离辅助直线最远. 利用三角形顶点到底边距离最大的原理, 就能实现对中介面回波信号的识别, 如图4(b)—(d)所示, 进而完成采集信号自适应门控参数计算, 可以更加准确、稳定地抑制中介面回波信号, 并实时反馈中介面回波信号的起点、终点、峰值位置.
算法具体步骤如下: 首先找到采集信号中的回波信号的峰值, 再对信号进行循环位移, 使其位于信号中间, 将信号从峰值处分为左右两半, 分别在两半信号的起点和终点作一条辅助直线, 计算每个点到辅助直线的距离, 将左半信号中距离最大的位置作为中介面回波信号的起点, 右半信号中距离最大的位置作为中介面回波信号的终点, 计算公式为
式中,
$ {p_{\text{l}}} $ 表示循环位移后的信号回波起点,$ {p_{\text{T}}} $ 为循环位移后的信号峰值位置,$ {p_{\text{r}}} $ 表示循环位移后的信号回波终点,$p$ 表示信号离散点数的自变量,$S$ 表示采集信号离散总点数.${D_{\text{l}}}(p)$ 和${D_{\text{r}}}(p)$ 分别为左半信号、右半信号到辅助直线的距离函数, 其计算公式为式中,
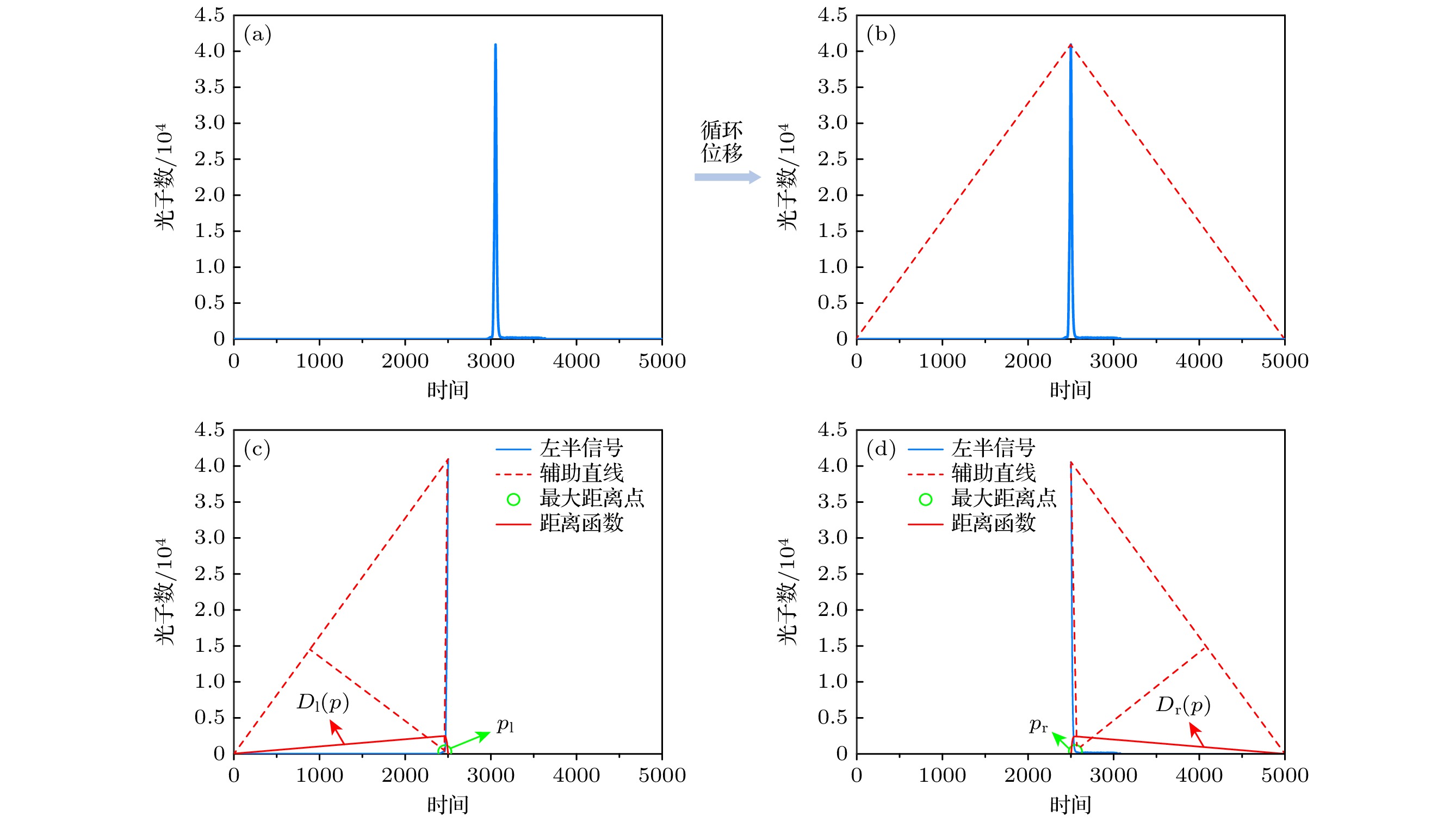
$ {G_{\text{l}}}(p) $ 表示左半信号,$ {G_{\text{l}}}(0) $ 表示$ p = 0 $ 处的左半信号幅值信息,$ {G_{\text{l}}}({p_{\text{T}}}) $ 表示$ p = {p_{\text{T}}} $ 处的左半信号幅值.$ {G_{\text{r}}}(p) $ 表示右半信号,$ {G_{\text{r}}}(S) $ 表示$ p = S $ 处的右半信号幅值信息,$ {G_{\text{r}}}({p_{\text{T}}}) $ 表示$ p = {p_{\text{T}}} $ 处的右半信号幅值. 分别计算出循环位移后中介面回波信号的起点与终点$ {p_{\text{l}}} $ 与$ {p_{\text{r}}} $ . 利用三角定位方法获取中介面回波信号位置过程如图4所示, 图4(a)为使用门控SPAD采集的某点回波信号, 图4(b)为对回波信号进行循环位移后结果, 图4(c)为左半信号的处理结果, 图4(d)为右半信号的处理结果.然后将信号进行反向循环位移回原来坐标系,
$ {p_{\text{l}}} $ 反向循环位移后即为中介面回波信号回波起点位置(用${s_{\text{b}}}$ 表示),$ {p_{\text{r}}} $ 反向循环位移后即为中介面回波信号终点位置(用${s_{\text{e}}}$ 表示),$ {p_{\text{T}}} $ 反向循环位移后即为中介面回波信号峰值位置(用${s_{\text{m}}}$ 表示), 则中介面回波信号宽度$ w $ 的计算公式为式中,
$\text{mod} $ 表示求余函数.为了抑制中介面回波, 理论上门控参数应设置为中介面回波的反向, 即将中介面回波终点作为门控参数的起点, 并将非中介面回波的宽度作为门控的宽度. 因此, 门控SPAD参数设置为: 起点
$ k{s_{\text{e}}} $ , 宽度$ k\left( {S - w} \right) $ ,$k$ 表示采集信号时间和离散点之间的换算系数. -
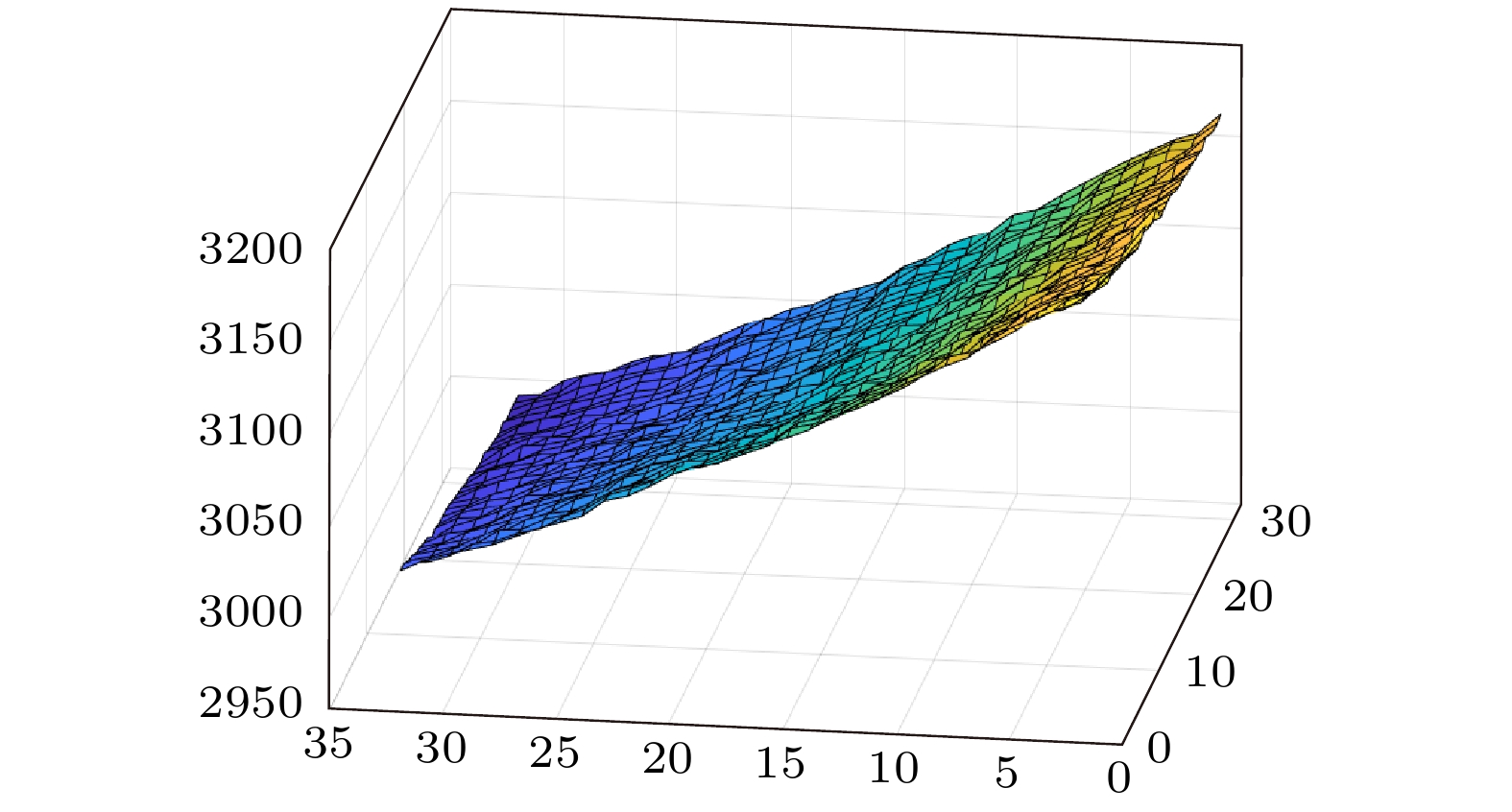
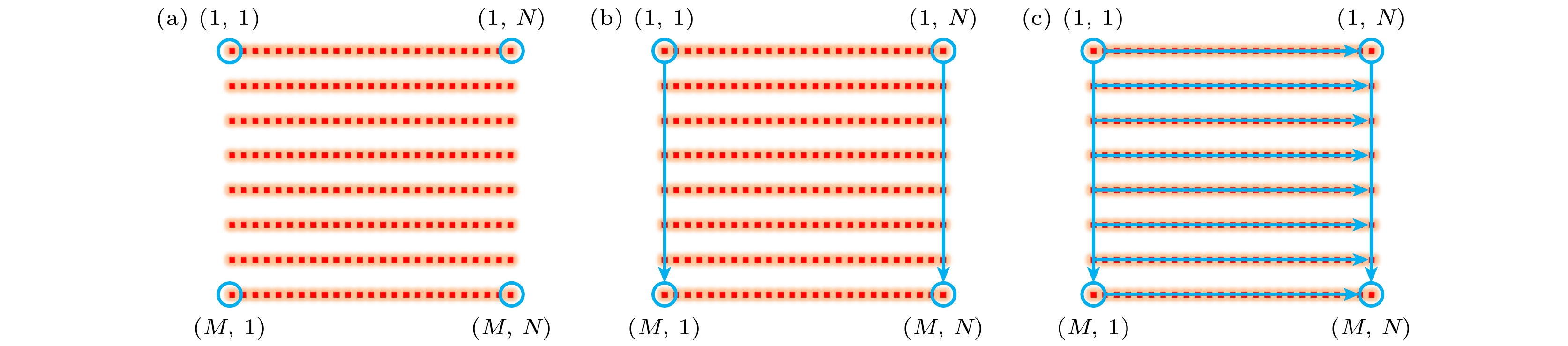
在非视域成像数据采集过程中, 除采集目标回波信号外, 还需要获取中介面回波信号, 从而得到目标与中介面间的相对位置关系. 为了获取更强的回波信号, 使用门控SPAD固定门控模式进行数据采集时, 每个采集点都需要采集两次: 首先用自由模式采集中介面回波信号, 获取中介面回波信息, 再用门控模式抑制中介面回波采集目标信号, 进而得到中介面回波信号与目标回波信号的相对位置关系. 因此, 门控SPAD数据采集量和耗时会比常规方法增加一倍. 而且每个场景的门宽位置设置对应不同的最佳参数, 如果参数设置不佳, 就会导致探测器饱和、目标回波信号采集受限等问题. 由于扫描点的位置呈线性变化, 因此可以通过某些特征点的回波信号来计算所有扫描点的位置, 扫描面上各采集点回波信号位置变化示意图如图5所示.
因此, 本文提出一种自适应门控控制算法, 以扫描区域的4个顶点作为特征点, 实现所有扫描点的门控参数计算. 与固定门控模式相比, 本文方法只需进行一次逐点数据采集, 并采集扫描区域4个顶点的信息, 从而有效提高信号采集的效率, 扫描面各扫描点位置推导示意图如图6所示. 进行非视域成像数据采集时, 多选用
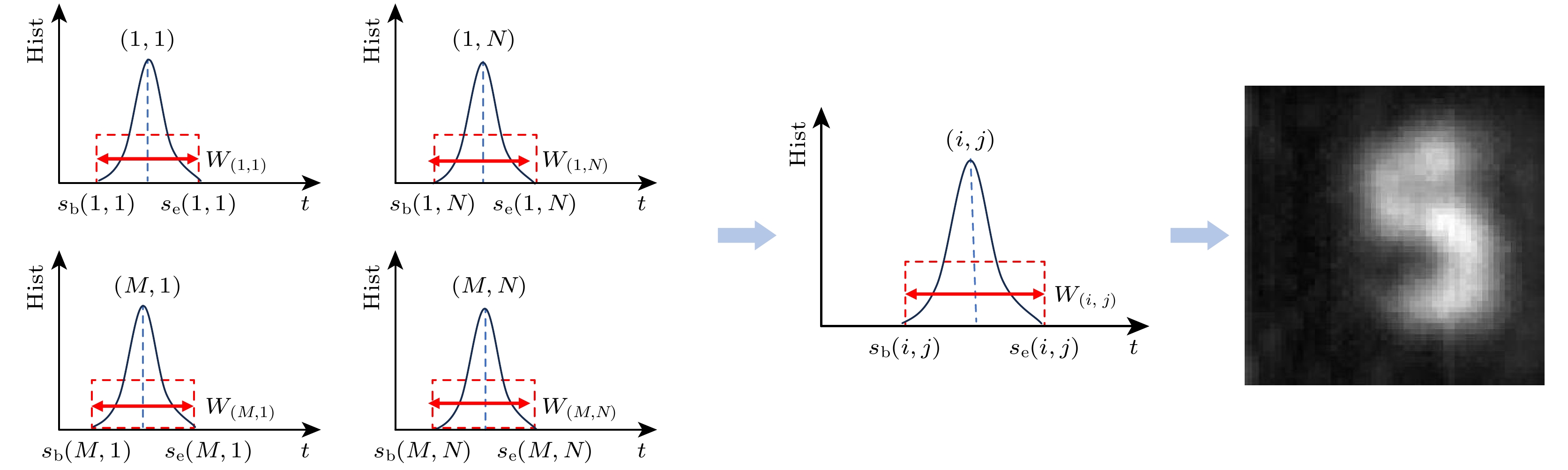
$ M \times N $ 的阵列扫描方式, 而扫描点的位置呈线性变化, 扫描阵列如图6(a)所示, 利用4个顶点信息实现整个扫描面的示意图如图6(b), (c)所示.使用自适应门控控制算法进行所有扫描点的门控参数计算具体步骤如下: 假设扫描区域为
$ M \times N $ 的矩阵, 首先利用上节方法得到左上、右上、左下、右下顶点的中介面回波起点位置$ {s_{\text{b}}}(1, 1) $ ,$ {s_{\text{b}}}(1, N) $ ,$ {s_{\text{b}}}(M, 1) $ ,$ {s_{\text{b}}}(M, N) $ , 中介面回波终点位置$ {s_{\text{e}}}(1, 1) $ ,$ {s_{\text{e}}}(1, N) $ ,$ {s_{\text{e}}}(M, 1) $ ,$ {s_{\text{e}}}{(}M, N) $ , 中介面回波峰值位置$ {s_{\text{m}}}(1, 1) $ ,$ {s_{\text{m}}}(1, N) $ ,$ {s_{\text{m}}}(M, 1) $ ,$ {s_{\text{m}}}(M, N) $ . 则扫描点$ (i, j) $ ,$ i $ 为横向扫描点序数,$ j $ 为纵向扫描点序数,$ i = 1, {\text{ }}2, \cdots , M, {\text{ }}j = 1, {\text{ }}2, \cdots , {\text{ }}N $ 中介面回波起点位置$ {s_{\text{b}}}(i, j) $ 的第$ i $ 行起点位置$ {s_{\text{b}}}(i, 1) $ 计算公式为第
$ i $ 行终点位置$ {s_{\text{b}}}(1, N) $ 计算公式为则扫描点
$ (i, j) $ 中介面回波起点位置$ {s_{\text{b}}}(i, j) $ 计算公式为令
则扫描点
$(i, j)$ 中介面回波起点位置$ {s_{\text{b}}}(i, j) $ 可以表示为同理, 扫描点
$ (i, j) $ 中介面回波终点位置$ {s_{\text{e}}}(i, j) $ 计算公式为扫描点
$ (i, j) $ 中介面回波峰值位置$ {s_{\text{m}}}(i, j) $ 计算公式为扫描点
$ (i, j) $ 中介面回波宽度$ {w_{(i, j)}} $ 计算公式为则扫描点
$ (i, j) $ 门控SPAD参数设置为: 起点$ k{s_{\text{e}}}(i, j) $ , 宽度$ k\left[ {S - w(i, j)} \right] $ .综上, 使用自适应门控控制算法进行非视域目标成像详细步骤如下:
1)使用门控SPAD的自由模式或固定门控模式采集4个顶点的回波信号;
2)利用上述回波信号, 使用自适应门控参数计算方法, 根据(3)式—(5)式计算各个特征点的门控参数;
3)通过上述特征点的门控参数, 使用自适应门控控制算法, 根据(8)式—(11)式计算所有扫描点的门控参数;
4)根据所有扫描点的门控参数, 自适应设置门控SPAD的参数, 采集所有扫描点的回波信号;
5)利用所有扫描点的回波信号, 完成非视域目标成像.
自适应门控控制算法进行非视域目标成像示意图如图7所示.
-
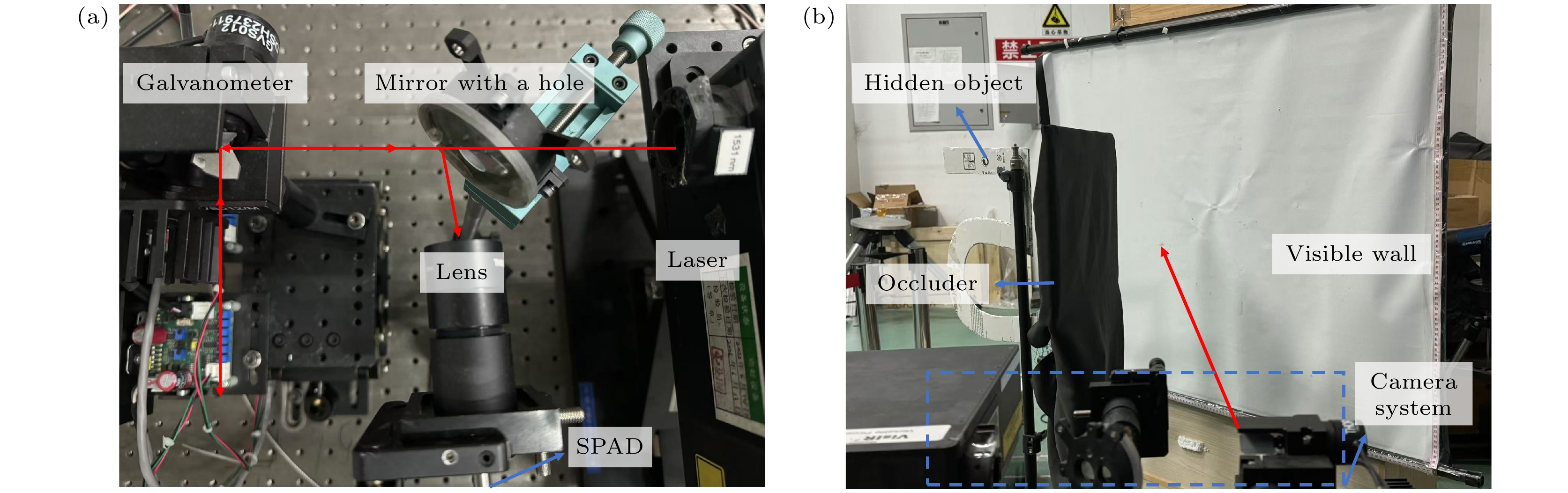
为了验证自适应门控控制算法的有效性, 并定量探究门控SPAD对于回波信号信噪比的影响, 搭建了如图8所示的实验系统. 系统的主要组件为1530 nm激光光源(功率375 mW, 脉冲宽度70 ps, 重复频率20 MHz)、振镜(Thorlabs GVS012)、门控SPAD (ID Qube, 抖动200 ps, 探测器的死时间为100 ns, 上升降沿为0.84 ns)、时间相关单光子计数器、穿孔反射镜、透镜、信号发生器和不同的隐藏目标. 此外, 使用穿孔反射镜替换掉共焦非视域系统中的分束镜, 有效减少了对激光信号的损失, 有助于提高信号信噪比.
-
为验证自适应门控参数较常规方法的优势, 对中介面回波信号进行采集分析, 采集数据如图9所示, 图9(a)为采集信号; 图9(b), (c)为使用常规方法进行中介面信号抑制示意图; 图9(d)为使用三角定位方法进行中介面信号抑制示意图. 具体指标和结果在表1和表2列出. 实验结果表示, 使用自适应门控参数计算方法较常规方法而言, 可以有效识别中介面回波信号, 并完成抑制.
为验证自适应门控参数计算方法抑制中介面回波信号的有效性, 采集某点回波信号, 使用自适应门控参数计算方法对该点中介面回波信号进行了位置与宽度计算, 并将计算结果返回控制端, 完成对中介面回波信号的抑制, 实验结果如图10所示, 图10(a)为该点回波信号的原始数据, 图10(b)为使用自适应门控参数计算方法对中介面回波信号位置与宽度的计算结果, 图10(c)为根据计算结果设置门控抑制中介面回波后的目标回波信号. 实验结果表明, 使用自适应门控参数计算方法可以有效抑制中介面回波信号.
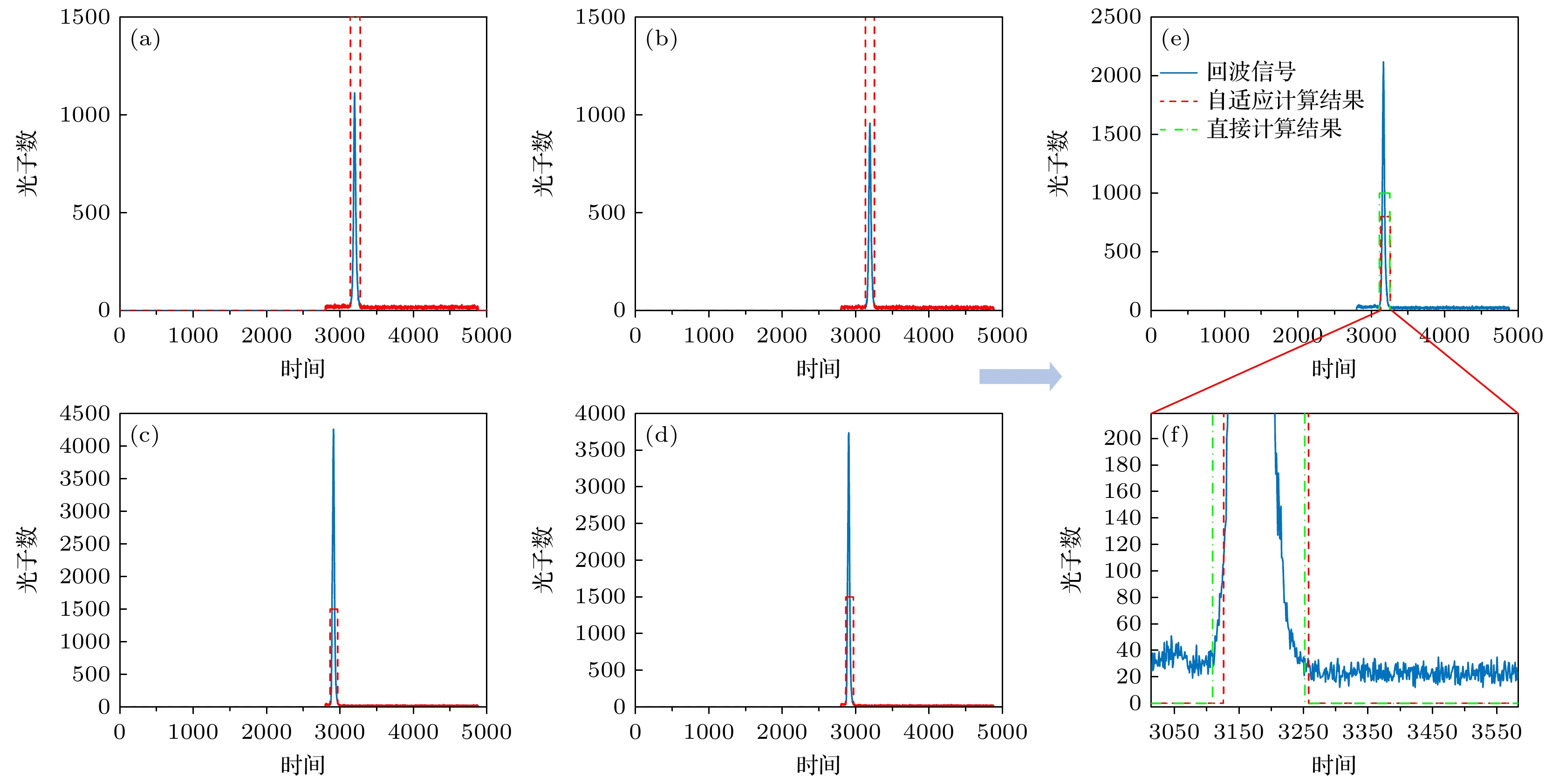
另外, 为验证通过特征点计算所有扫描点结果的准确性, 首先采集扫描区域4个顶点回波信息, 并对各顶点进行了中介面回波信号位置与宽度计算, 采集信号与计算结果如图11(a)—(d)所示. 随后使用自适应门控控制算法, 对某点中介面回波信号进行位置与宽度计算, 计算结果如图11(e), (f)红色虚线所示. 最后采集该点实际回波信号如图11(e), (f)蓝色实线所示, 并对该点中介面回波信号位置与宽度进行直接计算, 结果如图11(e), (f)绿色虚线所示. 表3列出了对比结果.
如表3所示, 利用特征点回波信号自适应计算出该点的中介面回波起点位置为3127, 中介面回波终点位置为3257, 中介面回波信号宽度为1.31 ns. 通过实际采集信号直接计算出该点的中介面回波信号起点位置为3110, 中介面回波信号终点位置为3251, 中介面回波信号宽度为1.41 ns. 其中, 中介面回波起点位置偏差0.17 ns, 中介面回波终点位置偏差0.06 ns, 中介面回波宽度偏差0.11 ns. 由于该门控SPAD自身抖动为0.2 ns, 上述偏差均小于抖动, 故可认为计算结果可靠. 综上, 本文提出的自适应门控参数计算方法可以充分利用回波信息, 有效抑制中介面回波; 使用自适应门控控制算法可通过特征点回波信号实现各个扫描点的位置与宽度计算, 从而大幅减少中介面信息采集时间, 提高处理效率和准确性.
-
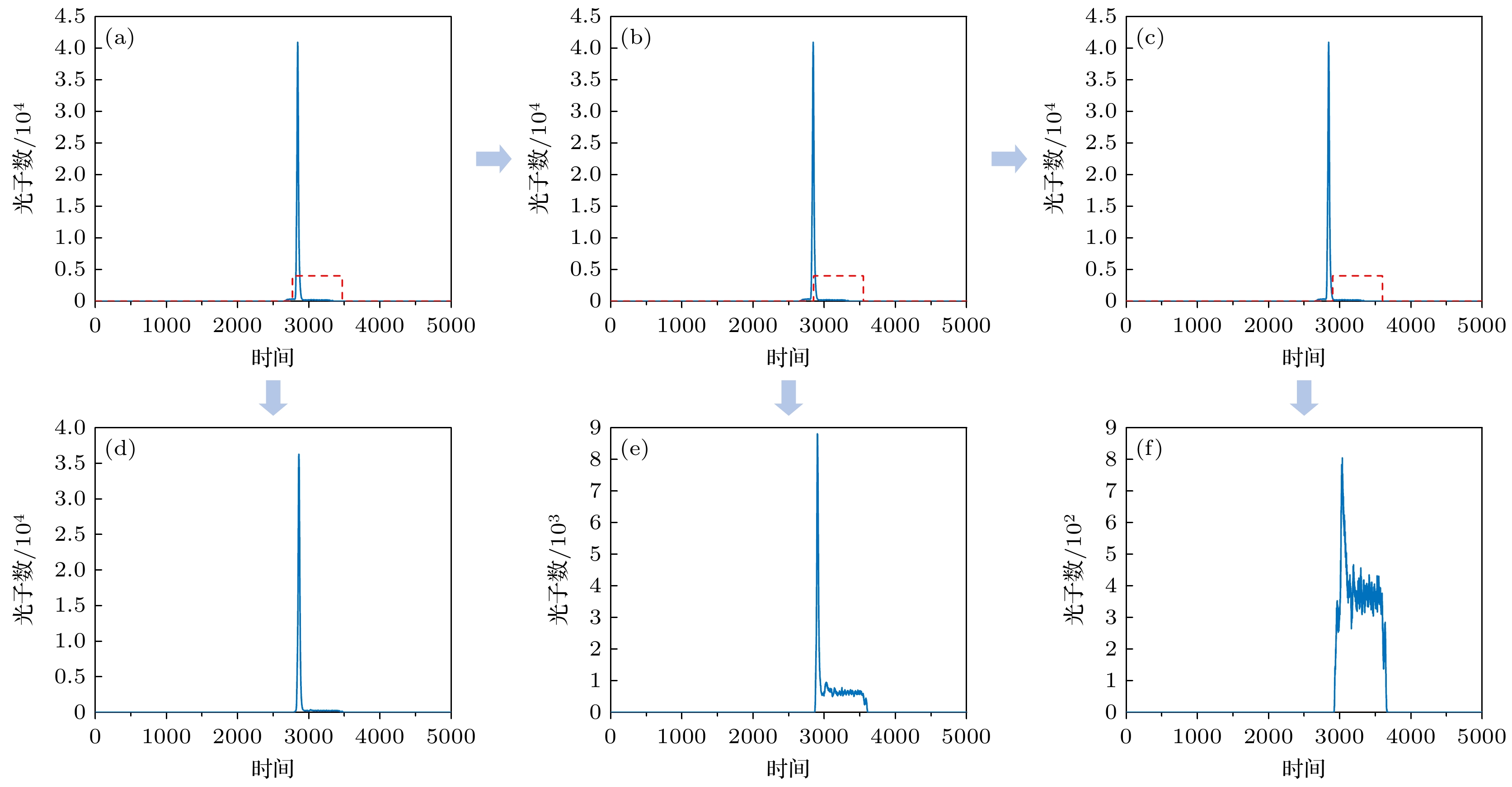
为验证抑制中介面回波信号对目标回波信号作用, 以0.1 ns为间隔进行门位置移动, 采集了逐渐抑制一次回波信号的实验数据. 回波信号如图12所示: 图12(a)—(c)为门位置移动示意图, 图12(d)为未抑制一次回波的回波信号图, 图12(e)为抑制一半一次回波的回波信号图, 图12(f)为完全抑制一次回波的回波信号图. 表4为抑制中介面回波信号对目标信号信噪比的影响. 由图12和表4可知, 随着门位置的移动, 一次回波信号强度逐渐降低, 目标回波信号强度不断增大, 目标信号的信噪比逐渐提高. 即抑制中介面回波信号可显著提升目标回波信号信噪比.
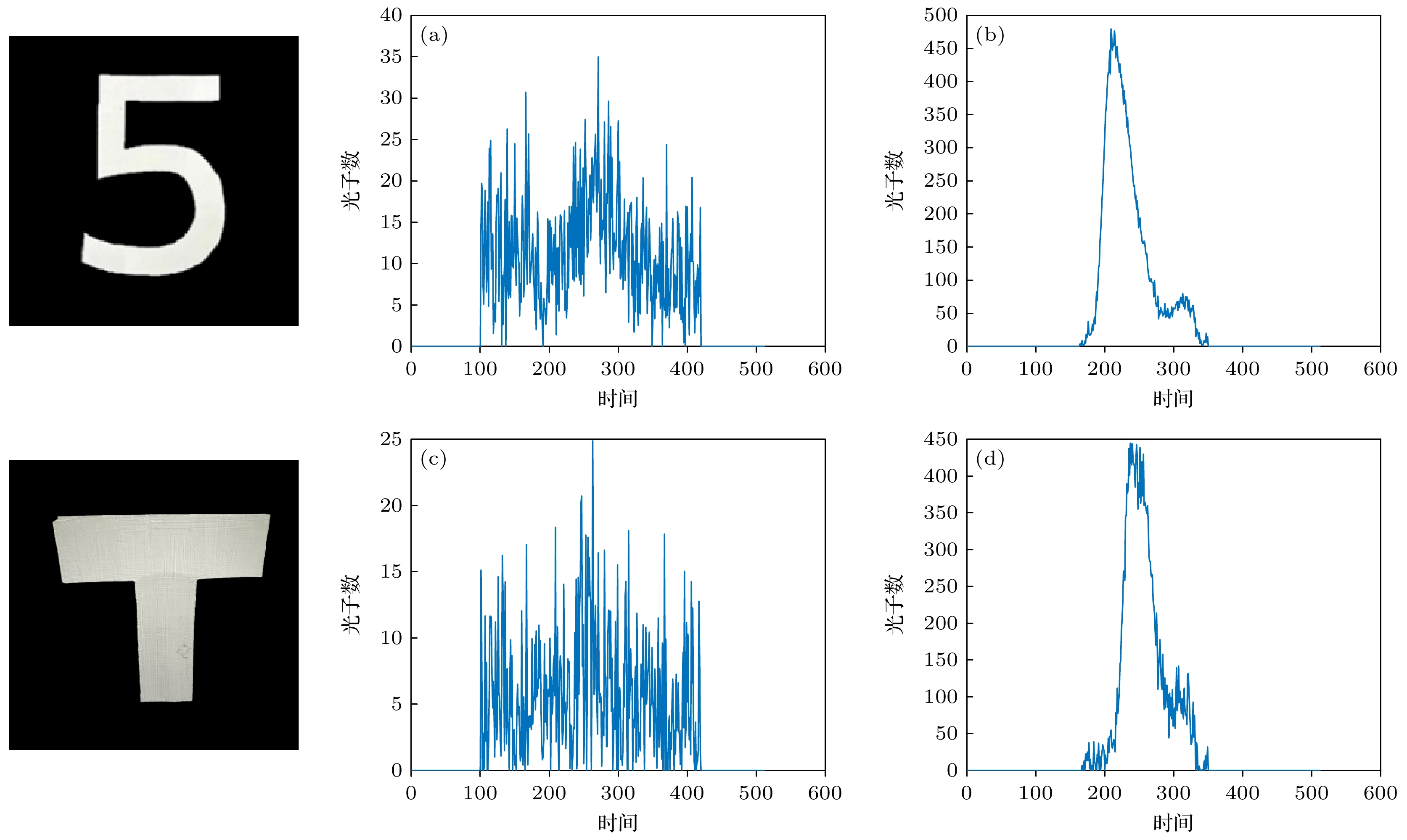
为进一步验证门控SPAD对目标信号的作用, 使用不同模式对不同隐藏目标进行数据采集, 回波信号如图13所示. 图13(a)为自由模式下的隐藏目标5的回波信号, 图13(b)为门控模式下的隐藏目标5的回波信号, 图13(c)为自由模式下的隐藏目标T的回波信号, 图13(d)为门控模式下的隐藏目标T的回波信号. 表5为门控SPAD对目标信号的定量分析. 由图13和表5可知, 自由模式下获取的目标回波信号, 信号质量较差, 噪声影响显著. 门控模式下完全抑制一次回波信号后, 目标回波信号强度显著提升, 即使用门控SPAD可有效提高对目标回波信号的探测能力.
综上, 使用门控SPAD可以显著提升目标回波信号信噪比, 在完全抑制一次回波信号后, 目标回波信号强度较自由模式下信号强度可提高10—20倍, 目标回波信号信噪比可提升3—4倍, 目标回波信号的可观测性大幅提升.
-
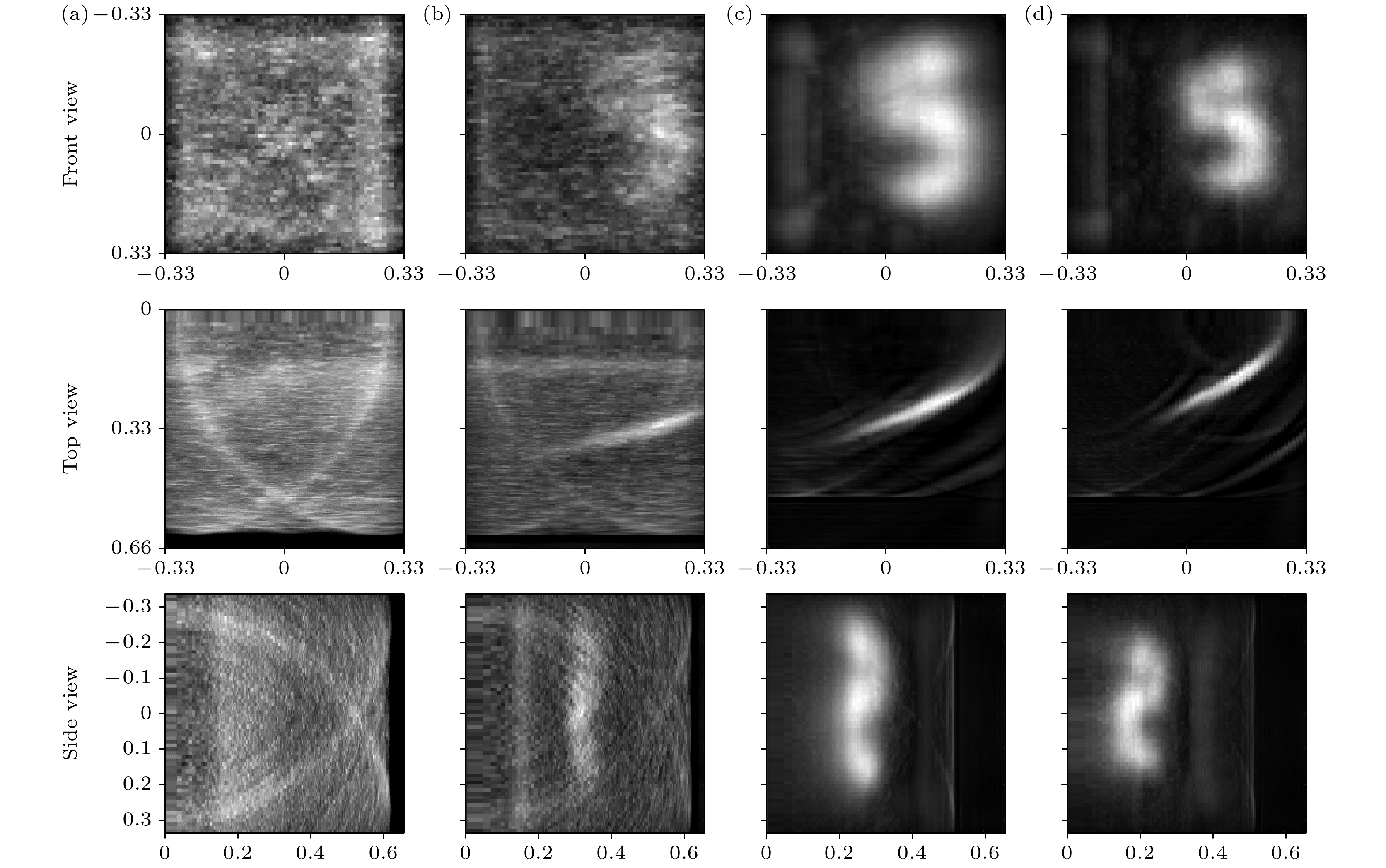
为验证门控SPAD、自适门控控制算法对目标成像质量的影响, 搭建了如图8所示的实验场景图, 中介面扫描范围为66 cm×66 cm, 采集阵列为64×64, 分别在自由模式和门控模式下对隐藏目标进行了光子飞行时间信息捕获, 并对隐藏目标进行了成像处理, 如图14所示. 图14(a)为自由模式下目标重构结果, 图14(b)为固定门宽时未抑制一次回波的目标重构结果, 图14(c)为固定门宽时抑制一次回波的目标重构结果, 图14(d)为使用自适应门控控制算法的目标重构结果. 由于自适应计算方法可以有效避免每个扫描点单独采集计算的随机误差, 因此理论上可以提升成像质量. 表6为数据采集量、耗时情况对比; 表7为对隐藏目标成像质量的定量分析.
由于本实验在白天强环境光和强噪声干扰条件下开展, 自由模式下重构结果无法识别目标轮廓. 使用固定门宽未抑制一次回波信号的重构结果可见目标轮廓. 使用固定门宽抑制一次回波信号和本文方法的重构结果均可清晰看见目标轮廓. 由表5可知, 自适应门控控制计算方法可以限制提高数据采集效率, 减少数据采集量; 由表6可知, 使用门控SPAD进行目标重构, 即使采用固定门宽, 其相关系数较自由模式下也能提升80倍, 结构相似度提升0.25, 成像质量远高于自由模式下的重构结果; 如果使用本文提出的自适应门控控制算法, 重构效果还能进一步提升: 其相关系数较自由模式下提升了92.7倍, 结构相似度提升了0.28.
为了进一步验证门控SPAD采集信号的有效性, 使用多个主流的非视域成像方法对不同隐藏目标进行成像. 如图15(a)—(e)所示, 图15(a)为固定门宽的BP算法重构结果, 图15(b)为固定门宽的F-K算法重构结果, 图15(c)为固定门宽的V-W算法重构结果, 图15(d)为固定门宽的LCT算法重构结果, 图15(e)为本文提出的自适应门控的LCT算法重构结果. 同时使用峰值信噪比、相关系数等评价指标对不同方法的重构质量进行了定量分析, 结果列于表8.
由实验结果可知, 使用门控SPAD采集的不同隐藏目标均能实现成像: BP算法成像结果模糊, F-K算法的成像结果噪点较多, 虚拟波算法和LCT算法的成像质量更好. 与固定门控参数方法相比, 本文提出的自适应门控控制算法能进一步提升非视域目标重构质量. 相较于固定门控参数的LCT算法, 本文方法成像质量峰值信噪比平均提升了0.2094, 结构相似度平均提升了0.011, 相关系数平均提升了0.0165. 因此, 本文提出的自适应门控控制算法不仅可以提高数据采集效率, 还能提升非视域目标成像质量.
-
门控SPAD可以通过调整门控宽度去除非目标信号干扰, 在非视域成像领域发挥了重要作用. 本文针对使用门控SPAD门宽位置预设存在非目标信号干扰和目标信号丢失等问题, 提出了自适应门控控制算法, 此算法充分利用了回波信号信息, 可仅通过采集少量特征点回波信息, 实现所有扫描点的门宽和位置设定. 该算法有效减少了非视域成像中对中介面先验知识的依赖, 在提高数据采集效率的同时, 进一步提升了目标成像质量. 通过对比分析自由模式和门控模式下的回波信息, 发现随着一次回波信号强度的降低, 目标回波信号强度显著增加, 故门控SPAD在提升目标信号强度上具有显著效果. 并且去除非目标信息干扰后的目标回波信号强度可提升10—20倍, 目标回波信号信噪比可提升3—4倍, 成像质量评价指标均正向上升, 目标成像质量显著提高. 基于门控SPAD的非视域成像系统在低信噪比的环境中表现优异, 具有低探测率高成像质量的性能, 对目标信号的信噪比、探测器的探测效率要求更低, 有望实现更远距离非视域成像.
自适应门控低信噪比非视域成像
Adaptive gating for low signal-to-noise ratio non-line-of-sight imaging
-
摘要: 非视域成像技术是对视域外隐藏目标进行光学成像的新兴技术. 由于历经多次漫反射, 信号回波微弱, 门控单光子雪崩二极管(single-photon avalanche diode, SPAD)在低信噪比环境中探测信号发挥了重要作用. 然而, 实际使用门控SPAD进行目标信号探测时, 现有方法多需要借助先验信息进行门宽位置预设, 无法完全避免非目标信号干扰和信号丢失, 并且存在数据采集量大、耗时长等问题. 针对上述问题, 本文利用三角定位原理和少量特征点信息, 提出一种自适应门控算法, 该算法可自动识别回波信号并计算其宽度, 无需额外先验信息或人工干预, 降低数据采集量, 提高处理效率等功能. 同时, 搭建了基于门控SPAD的共焦非视域成像系统, 对提出的算法进行验证. 此外, 本文就门控SPAD对目标信号提升效果和目标成像质量进行了定量评估, 并对比了主流的非视域图像重构算法成像质量. 实验结果表明, 自适应门控算法可以有效识别回波信号, 实现门控参数的自动调节, 并在减少数据采集量、提升处理效率的同时, 提高目标成像质量.Abstract: Non-line-of-sight (NLOS) imaging is an emerging optical imaging technique used for detecting hidden targets outside the line of sight. Due to multiple diffuse reflections, the signal echoes are weak, and gated single-photon avalanche diode (SPAD) plays a pivotal role in signal detection under low signal-to-noise ratio (SNR) conditions. However, when gated SPAD is used for detecting a target signal, existing methods often depend on prior information to preset the gate width, which cannot fully mitigate non-target signal interference or signal loss. Additionally, these methods encountered some problems such as large data acquisition volumes and lengthy processing times. To address these challenges, an adaptive gating algorithm is proposed in this work based on the principle of maximizing the distance from the vertex of a triangle to its base. The algorithm possesses advantages of the linear variation in scan point positions and the echo information from specific feature points. It can automatically identify echo signals and compute their widths without additional prior information or manual intervention. This method reduces the amount of data collected, improves processing efficiency, and has other benefits. Moreover, a confocal NLOS imaging system based on gated SPAD is developed to validate the proposed algorithm. The work further quantitatively evaluates the enhancement of target signal detection and image quality achieved by gated SPAD, and compares its imaging performance with leading NLOS image reconstruction algorithms. Experimental results demonstrate that the adaptive gating algorithm can effectively identify echo signals, facilitate automatic adjustment of gating parameters, and significantly improve target imaging quality while reducing data acquisition volume and enhancing processing efficiency.
-
Key words:
- non-line-of-sight imaging /
- adaptive gating /
- signal-to-noise ratio .
-
-
图 1 非视域成像与门控工作原理
Figure 1. Working principle of non-line-of-sight imaging and gate control.
图 2 门控SPAD探测效果 (a) 自由模式下回波信号信息; (b) 门控模式下目标回波信号信息
Figure 2. Detection performance of gated SPAD: (a) Echo signal information in free mode; (b) echo signal information for the third signal in gated mode.
图 3 中介面回波信号抑制设置示意图 (a)中介面回波信号示意图; (b), (c)常规方法; (d)三角定位方法
Figure 3. Schematic diagram of intermediate echo signal suppression settings: (a) Schematic diagram of the intermediates echo signal; (b), (c) conventional methods; (d) triangulation method.
图 4 中介面回波信号处理过程 (a) 使用门控SPAD采集的某点回波信号; (b) 该回波信号循环位移后的结果; (c) 左半信号处理结果; (d) 右半信号处理结果
Figure 4. Signal processing procedure for the interface echo signal: (a) Echo signal acquired using gated SPAD at a certain point; (b) result after cyclic shift of the echo signal; (c) result of processing the left half of the signal; (d) result of processing the right half of the signal.
图 5 扫描面各采集点回波位置变化示意图
Figure 5. Schematic diagram of the change of echo position at each point of the scanning surface.
图 6 扫描面各扫描点位置推导示意图 (a)扫描阵列示意图; (b), (c)利用特征点计算各扫描点示意图
Figure 6. Schematic diagram of the position of each scan point on the scanning surface: (a) Schematic diagram of the scanning array; (b), (c) schematic diagram of calculating each scanning point using characteristic points.
图 8 实际搭建系统 (a)基于SPAD的共焦非视域成像系统; (b)搭建的非视域成像场景
Figure 8. Actual system setup: (a) Confocal non-line-of-sight imaging system based on SPAD; (b) constructed non-line-of-sight imaging scene.
图 9 中介面信号实际抑制示意图 (a)实际采集中介面回波信号; (b), (c)常规方法; (d)三角定位方法
Figure 9. Schematic diagram of the actual suppression of the intermediary signal: (a) Actual collection of intermediates echo signals; (b), (c) conventional approach; (d) triangulation method.
图 10 中介面回波信号抑制结果 (a)某点中介面回波信号; (b)某点中介面回波信号识别结果; (c)抑制中介面回波信号后的目标回波信号
Figure 10. Suppression results of intermediate surface echo signal: (a) Echo signal for the intermediate interface midpoint; (b) result of identifying the echo signal of an intermediary surface at a certain point; (c) target echo signal after suppressing the intermediate interface echo signal.
图 11 中介面回波信号位置与宽度计算结果 (a)左上顶点中介面回波信号位置与宽度计算结果; (b)右上顶点中介面回波信号位置与宽度计算结果; (c)左下顶点中介面回波信号位置与宽度计算结果; (d)右下顶点中介面回波信号位置与宽度计算结果; (e)自适应计算结果和直接计算结果对比图; (f)计算结果细节图
Figure 11. Results of the adaptive gated control algorithm: (a) Calculated position and width of the interface echo signal at the top-left vertex; (b) calculated position and width of the interface echo signal at the top-right vertex; (c) calculated position and width of the interface echo signal at the bottom-left vertex; (d) calculated position and width of the interface echo signal at the bottom-right vertex; (e) comparison of adaptive algorithm results and direct calculation results; (f) detailed plot of the calculated results.
图 12 一次回波对目标信号作用 (a)—(c)移动门位置示意图; (d)未抑制一次回波的回波信号图; (e)抑制一半一次回波的回波信号图; (f)完全抑制一次回波的回波信号图
Figure 12. Effect of single echo on the target signal: (a)–(c) Schematic diagram of the moving gate position; (d) echo signal diagram without suppressing the single echo; (e) diagram of the echo signal with half of the single echo suppressed; (f) diagram of the echo signal with the single echo completely suppressed.
图 13 门控SPAD对目标回波信号影响 (a)自由模式下隐藏目标5回波信号; (b)门控模式下隐藏目标5回波信号; (c)自由模式下隐藏目标T回波信号; (d)门控模式下隐藏目标T回波信号
Figure 13. Impact of gated SPAD on target echo signals: (a) Hidden target 5 echo signal in free-running mode; (b) hidden target 5 echo signal in gated mode; (c) hidden target T echo signal in free-running mode; (d) hidden target T echo signal in gated mode.
图 14 不同模式重建结果对比 (a)自由模式下目标重构结果; (b)固定门宽未抑制一次回波的目标重构结果; (c)固定门宽抑制一次回波的目标重构结果; (d)本文自适应门控控制算法目标重构结果
Figure 14. Comparison of different mode reconstruction results: (a) Reconstruction result under free mode; (b) reconstruction result without suppressing the first echo with fixed gate width; (c) reconstruction result with fixed gate width suppressing the first echo; (d) reconstruction result using the proposed adaptive gate control algorithm in this paper.
图 15 不同方法重建结果 (a) BP算法; (b) F-K算法; (c) V-W算法; (d) LCT算法; (e)本文自适应门控的LCT算法
Figure 15. Reconstruction results using different methods: (a) BP algorithm; (b) F-K algorithm; (c) V-W algorithm; (d) LCT algorithm; (e) adaptive LCT algorithm in this work.
表 1 不同方法中介面位置的对比
Table 1. Comparison of the results of different method.
采集信号 常规方法
抑制常规方法
抑制三角定位法
抑制起点 1103 1118 1090 1105 终点 1181 1145 1170 1178 宽度/ns 0.78 0.27 0.8 0.73 
下载: 导出CSV
表 2 不同方法对中介面回波信号抑制结果偏差对比
Table 2. Comparison of the deviation in suppression results of interface echo signals using different methods.
起点 终点 宽度/ns 常规方法抑制情形一 15 36 0.51 常规方法抑制情形二 13 9 0.02 三角定位法抑制 2 3 0.05
下载: 导出CSV
表 3 自适应计算机果和直接计算结果对比
Table 3. Comparison of adaptive algorithm results and direct calculation results
起点 终点 宽度/ns 自适应计算 3127 3257 1.31 实际采集计算 3110 3251 1.41 偏差/ns 0.17 0.06 0.11
下载: 导出CSV
表 4 一次回波对目标回波信号的影响
Table 4. Impact of primary echo on the target echo signal.
未抑制一次
回波信号抑制一半一次
回波信号完全抑制一次
回波信号一次回波峰值 36190 8811 0 目标回波峰值 372 952 805 信号信噪比 16.79 19.48 28.75 主观 目标信号被淹没 目标信号可见 目标信号突出
下载: 导出CSV
表 5 门控SPAD对目标回波信号的影响
Table 5. Impact of gated single-photon avalanche diode on the target echo signal.
目标5信号
(自由模式)目标5信号(门控模式) 目标T信号
(自由模式)目标T信号
(门控模式)目标回波峰值 35 480 25 445 信号信噪比 6.79 25.54 6.15 23.21 主观 目标波形可见 目标波形清晰 目标波形可见 目标波形清晰
下载: 导出CSV
表 6 不同方法采集数据量、耗时对比
Table 6. Comparison of data collection volume and time consumption across different methods.
数据采集量 耗时/T 自由模式 一次逐点扫描 1 未抑制中介面回波信号 一次逐点扫描 1 抑制中介面回波信号 两次逐点扫描 2 自适应门控控制算法 一次逐点扫描+
四个特征点≈1
下载: 导出CSV
表 7 不同模式下成像质量对比
Table 7. Comparison of imaging quality under different modes.
自由模式 未抑制中介面
回波信号抑制中介面
回波信号自适应门控
控制算法峰值
信噪比6.94 9.52 10.70 11.4932 结构
相似度0.56 0.73 0.81 0.8466 相关系数 0.007 0.31 0.56 0.64885 主观 无法识别
目标可见目标
轮廓目标轮廓
清晰目标轮廓
清晰
下载: 导出CSV
表 8 不同目标重构质量对比
Table 8. Reconstruction quality comparison of different objects.
评价指标 BP F-K V-W LCT 本文 目标5 峰值信噪比 7.0311 10.15 8.9784 10.7017 11.4932 结构相似度 0.6443 0.7873 0.7408 0.8107 0.8466 相关系数 0.4545 0.5098 0.5315 0.5703 0.6489 主观 目标模糊 可见目标轮廓 目标轮廓清晰 目标轮廓清晰 目标轮廓清晰 目标L 峰值信噪比 7.1744 9.543 8.4819 11.179 11.3109 结构相似度 0.6689 0.7781 0.7825 0.8535 0.8621 相关系数 0.386 0.4459 0.5093 0.6014 0.6587 主观 目标模糊 可见目标轮廓 目标轮廓清晰 目标轮廓清晰 目标轮廓清晰 目标H 峰值信噪比 8.8224 9.4324 9.4568 10.1954 10.558 结构相似度 0.7477 0.8071 0.8163 0.8417 0.8564 相关系数 0.6077 0.4839 0.5092 0.6017 0.6275 主观 目标模糊 可见目标轮廓 目标轮廓清晰 目标轮廓清晰 目标轮廓清晰 目标Plane 峰值信噪比 9.8436 11.6533 11.4687 12.2066 11.9239 结构相似度 0.7745 0.8545 0.8465 0.8533 0.8608 相关系数 0.6019 0.5541 0.6223 0.6524 0.6325 主观 目标模糊 可见目标轮廓 目标轮廓清晰 目标轮廓清晰 目标轮廓清晰 目标T 峰值信噪比 7.9285 11.1673 11.2831 12.7401 12.604 结构相似度 0.6883 0.8106 0.8328 0.8812 0.877 相关系数 0.6566 0.6714 0.7388 0.7102 0.7696 主观 目标模糊 可见目标轮廓 目标轮廓清晰 目标轮廓清晰 目标轮廓清晰
下载: 导出CSV
-
[1] Kirmani A, Hutchison T, Davis J, Raskar R 2009 IEEE 12th International Conference on Computer Vision Kyoto, Japan, September 29–October 2, 2009 p159 [2] Velten A, Willwacher T, Gupta O, Veeraraghavan A, Bawendi M G, Raskar R 2012 Nat. Commun. 3 745 doi: 10.1038/ncomms1747 [3] Victor A, Diego G, Adrian J 2017 Opt. Express 25 11574 doi: 10.1364/OE.25.011574 [4] O’Toole M, Lindell D B, Wetzstein G 2018 Nature 555 338 doi: 10.1038/nature25489 [5] Lindell D B, Wetzstein G, O’Toole M 2019 ACM T. Graphic. 38 116 [6] Xin S, Nousias S, Kutulakos K N, Sankaranarayanan A C, Narasimhan S G, Gkioulekas I 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Long Beach, CA, USA, June 15–19, 2019 p6793 [7] Liu X C, Guillén I, La Manna M, Nam J H, Reza S A, Huu Le T, Jarabo A, Gutierrez D, Velten A 2019 Nature 572 620 doi: 10.1038/s41586-019-1461-3 [8] Young S I, Lindell D B, Girod B, Taubman D, Wetzstein G 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Seattle, WA, USA, June 14–19, 2020 p1404 [9] Chen X J, Li M Y, Chen T T, Zhan S Y 2023 Photonics 10 25 doi: 10.3390/photonics10010025 [10] Plack M, Callenberg C, Schneider M, Hullin M B 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) Waikoloa, HI, USA, January 2–7, 2023 p3066 [11] Shen S Y, Wang Z, Liu P, Pan Z Q, Li R Q, Gao T, Li S Y, Yu J Y 2021 IEEE T. Pattern Anal. 43 2257 doi: 10.1109/TPAMI.2021.3076062 [12] 吴嘉伟 2021 硕士学位论文 (长沙: 湖南大学) Wu J W 2021 M. S. Thesis (Changsha: Hunan University [13] 任禹, 罗一涵, 徐少雄, 马浩统, 谭毅 2021 光电工程 48 84 Ren Y, Luo Y H, Xu S X, Ma H T, Tan Y 2021 Opto-Electron. Eng. 48 84 [14] 唐佳瑶, 罗一涵, 谢宗良, 夏诗烨, 刘雅卿, 徐少雄, 马浩统, 曹雷 2023 物理学报 72 014210 doi: 10.7498/aps.72.20221600 Tang J Y, Luo Y H, Xie Z L, Xia S Y, Liu Y Q, Xu S X, Ma H T, Cao L 2023 Acta Phys. Sin. 72 014210 doi: 10.7498/aps.72.20221600 [15] 郑海洋, 罗一涵, 李泰霖, 唐佳瑶, 刘雅卿, 夏诗烨, 吴琼雁, 谢宗良 2023 光电工程 50 101 Zheng H Y, Luo Y H, Li T L, Tang J Y, Liu Y Q, Xia S Y, Wu Q Y, Xie Z L 2023 Opto-Electron. Eng. 50 101 [16] Wang B, Zheng M Y, Han J J, Huang X, Xie X P, Xu F H, Zhang Q, Pan J W 2021 Phys. Rev. Lett. 127 053602 doi: 10.1103/PhysRevLett.127.053602 [17] Wu C, Liu J J, Huang X, Li Z P, Yu C, Ye J T, Zhang J, Zhang Q, Dou X K, Goyal V K, Xu F H, Pan J W 2021 PNAS 118 e2024468118 doi: 10.1073/pnas.2024468118 [18] Liu X T, Wang J Y, Xiao L P, Shi Z Q, Fu X, Qiu L Y 2023 Nat. Commun. 14 3230 doi: 10.1038/s41467-023-38898-4 [19] Laurenzis M, Velten A 2014 J. Electron. Imag. 23 063003 doi: 10.1117/1.JEI.23.6.063003 [20] Buttafava M, Zeman J, Tosi A, Eliceiri K, Velten A 2015 Opt. Express 23 20997 doi: 10.1364/OE.23.020997 [21] Zhu S Y, Sua Y M, Rehain P, Huang Y P 2021 Opt. Express 29 40865 doi: 10.1364/OE.441764 [22] Zhao J X, Gramuglia F, Keshavarzian P, Toh E H, Tng M, Lim L 2024 IEEE J. Sel. Top. Quant. 30 8000110 doi: 10.1109/JSTQE.2023.3283150 [23] Luo Y H, Xie Z L, Xu S X, Ma H T, Ren Y, Cao L 2020 China Patent CN202010742670.6 [2020-06-28] -
计量
- 文章访问数: 117
- HTML全文浏览数: 117
- PDF下载数: 2
- 施引文献: 0