高级搜索

J-TEXT托卡马克锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响

,  ,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

丁肖冠, 赵开君, 谢耀禹, 陈志鹏, 陈忠勇, 杨州军, 高丽, 丁永华, 温思宇, 胡莹欣. J-TEXT托卡马克锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响[J]. 物理学报, 2025, 74(4): 045201-1. doi: 10.7498/aps.74.20241364
引用本文: 丁肖冠, 赵开君, 谢耀禹, 陈志鹏, 陈忠勇, 杨州军, 高丽, 丁永华, 温思宇, 胡莹欣. J-TEXT托卡马克锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响[J]. 物理学报, 2025, 74(4): 045201-1. doi: 10.7498/aps.74.20241364
shu
Xiaoguan DING, Kaijun ZHAO, Yaoyu XIE, Zhipeng CHEN, Zhongyong CHEN, Zhoujun YANG, Li GAO, Yonghua DING, Siyu WEN, Yingxin HU. Effects of turbulence spreading and symmetry breaking on edge shear flow during sawtooth cycles in J-TEXT tokamak[J]. Acta Physica Sinica, 2025, 74(4): 045201-1. doi: 10.7498/aps.74.20241364
Citation: Xiaoguan DING, Kaijun ZHAO, Yaoyu XIE, Zhipeng CHEN, Zhongyong CHEN, Zhoujun YANG, Li GAO, Yonghua DING, Siyu WEN, Yingxin HU. Effects of turbulence spreading and symmetry breaking on edge shear flow during sawtooth cycles in J-TEXT tokamak[J]. Acta Physica Sinica, 2025, 74(4): 045201-1. doi: 10.7498/aps.74.20241364
shu

J-TEXT托卡马克锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响

  • 1.

    东华理工大学核科学与工程学院, 南昌　330013

  • 2.

    华中科技大学电气与电子工程学院, 磁约束聚变与等离子体国际合作联合实验室, 强电磁技术全国重点实验室, 武汉　430074

    • 作者简介: 丁肖冠. E-mail: 844203458@qq.com .
    通讯作者: E-mail: kjzhao@ecut.edu.cn.; 

  • 中图分类号: 52.35.Ra, 52.25.Gj, 52.30.-q, 52.35.-g

Effects of turbulence spreading and symmetry breaking on edge shear flow during sawtooth cycles in J-TEXT tokamak

  • 1.

    School of Nuclear Science and Engineer, East China University of Technology, Nanchang 330013, China

  • 2.

    State Key Laboratory of Advanced Electromagnetic Technology, International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China

    • Corresponding author: E-mail: kjzhao@ecut.edu.cn.; 

  • MSC: 52.35.Ra, 52.25.Gj, 52.30.-q, 52.35.-g

  • 摘要: 锯齿振荡引起热脉冲和湍流脉冲可以传播到边缘等离子体中增强边缘剪切流并诱发低约束模到高约束模的转换. 在J-TEXT托卡马克上观测了锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响. 采用快速往复静电探针阵列测量了边缘等离子体湍流和剪切流等, 观测到锯齿崩塌后, 芯部的热脉冲和湍流传播至边缘等离子体, 且湍流脉冲快于热脉冲. 本文发现了锯齿崩塌后在边缘等离子体中引起湍流对称性破缺, 湍流传播和对称性破缺可以增强湍流雷诺协强, 从而驱动剪切流. 这些结果阐明了锯齿崩塌对边缘湍流和剪切流的增强作用过程.
    Abstract: The effect of sawteeth on plasma performance and transport in the plasma of tokamak is an important problem in the fusion field. Sawtooth oscillations can trigger off heat and turbulence pulses that propagate into the edge plasma, and thus enhancing the edge shear flow and inducing a transition from low confinement mode to high confinement mode. The influences of turbulence spreading and symmetry breaking on edge shear flow with sawtooth crashes are observed in the J-TEXT tokamak. The edge plasma turbulence and shear flow are measured using a fast reciprocating electrostatic probe array. The experimental data are analyzed using some methods such as conditional average and probability distribution function. After sawtooth crashes, the heat and turbulence pulses in the core propagate to the edge, with the turbulence pulse being faster than the heat pulse. The attached figures (a)–(e) show the core electron temperature, and the edge electron temperature, turbulence intensity, turbulence drive and spreading rates, Reynolds stress and its gradient, and shearing rates, respectively. After sawtooth crashes, the edge electron temperature increases and the edge turbulence is enhanced, with turbulence preceding temperature. The enhanced edge turbulence is mainly composed of two parts: the turbulence driven by local gradient and the turbulence spreading from core to edge. The development of the estimated turbulence spreading rate is prior to that of the turbulence driving rate. The increase in the turbulence intensity can cause the turbulent Reynold stress and its gradient to increase, thereby enhancing shear flows and radial electric fields. Turbulence spreading leads the edge Reynolds stresses to develop and the shear flow to be faster than edge electron temperature. The Reynolds stress arises from the symmetry breaking of the turbulence wave number spectrum. After sawtooth collapses, the joint probability density function of radial wave number and poloidal wave number of turbulence intensity becomes highly skewed and anisotropic, exhibiting strong asymmetry, which can be seen in attached figures (f) and (g). The development of turbulence spreading flux at the edge is also prior to the particle flux driven by turbulence, indicating that turbulent energy transport is not simply accompanied by turbulent particle transport. These results show that the turbulence spreading and symmetry breaking can enhance turbulent Reynolds stress, thereby driving shear flows, after sawtooth has crashed.
  • 加载中

  • 图 1  静电探针结构图

    Figure 1.  Structure of electrostatic probe array.

    下载: 全尺寸图片 幻灯片

    图 2  等离子体放电参数　(a)等离子体电流; (b)线积分电子密度; (c)环向磁场; (d) $ r/a=0.01 $处的电子温度; (e) $ r/a=0.88 $处的悬浮电位; (f)探针位移

    Figure 2.  Plasma discharge parameters: (a) Plasma current; (b) line integrated electron density; (c) toroidal magnetic field; (d) electron temperature at $ r/a=0.01 $; (e) floating potential at $ r/a=0.88 $; (f) probe positions.

    下载: 全尺寸图片 幻灯片

    图 3  不同径向位置处的电子温度和湍流相对强度

    Figure 3.  Electron temperature and relative intensities of turbulence at various radial positions, respectively.

    下载: 全尺寸图片 幻灯片

    图 4  (a) $ r/a=0.01 $处的电子温度; (b) $ r/a=0.90 $处的电子温度; (c) $ r/a=0.90 $处的悬浮电位; (d) $ r/a=0.90 $处的湍流强度; (e) $ r/a=0.90 $处的$ \boldsymbol{E}\times \boldsymbol{B} $极向速度; (f) $ r/a=0.90 $处的剪切率; (g) $ r/a=0.90 $处的电子温度和湍流强度的李萨如图; (h) $ r/a=0.90 $处锯齿崩塌前后悬浮电位的自功率谱

    Figure 4.  (a) Electron temperature at $ r/a=0.01 $; (b) electron temperature at $ r/a=0.90 $; (c) floating potential at $ r/a=0.90 $; (d) turbulence intensity at $ r/a=0.90 $; (e) $ \boldsymbol{E}\times \boldsymbol{B} $ poloidal velocity at $ r/a=0.90 $; (f) shearing rate at $ r/a=0.90 $; (g) trajectory of electron temperature and turbulence intensity at $ r/a=0.90; $ (h) auto-power spectra of the floating potential before and after sawtooth collapse at $ r/a=0.90 $.

    下载: 全尺寸图片 幻灯片

    图 5  (a) $ r/a=0.01 $处的电子温度; (b) $ r/a=0.90 $处的湍流强度; (c) $ r/a=0.90 $处的湍流驱动率; (d) $ r/a=0.90 $处的湍流传播率

    Figure 5.  (a) Electron temperature at $ r/a=0.01 $; (b) turbulence intensity at $ r/a=0.90 $; (c) turbulence drive rates at $ r/a=0.90 $; (d) turbulence spreading rates at $ r/a=0.90 $.

    下载: 全尺寸图片 幻灯片

    图 6  (a) $ r/a=0.01 $的电子温度; (b) $ r/a=0.90 $处的湍流传播通量; (c) $ r/a=0.90 $处的湍流粒子通量; (d) $ r/a= $$ 0.90 $处的湍流传播平均射流速度; (e) $ r/a=0.90 $处的粒子输运速度

    Figure 6.  (a) Electron temperature at $ r/a=0.01 $; (b) turbulence spreading flux at $ r/a=0.90 $; (c) turbulence particle flux at $ r/a=0.90 $; (d) mean jet velocity of turbulence spreading at $ r/a=0.90; $ (e) particle transport velocity at $ r/a=0.90 $.

    下载: 全尺寸图片 幻灯片

    图 7  (a) $ r/a=0.01 $处的电子温度; $ ({\mathrm{b}})\;r/a=0.90 $处的径向电场强度; (c) $ r/a=0.90 $处的压强梯度; (d) $ r/a=0.90 $处的极向流对径向电场的贡献

    Figure 7.  (a) Electron temperature at $ r/a=0.01 $; (b) radial electric fields intensity at $ r/a=0.90 $; (c) contributions of the pressure gradient at $ r/a=0.90; $ (d) poloidal flows to the radial electric field at $ r/a=0.90 $.

    下载: 全尺寸图片 幻灯片

    图 8  (a) $ r/a=0.01 $处的电子温度; (b) $ r/a=0.90 $处的电子温度; (c) $ r/a=0.90 $处的雷诺协强; (d) $ r/a=0.90 $处的雷诺协强梯度; (e) $ r/a=0.90 $处的雷诺功; (f) $ r/a=0.90 $处的剪切率

    Figure 8.  (a) Electron temperature at $ r/a=0.01 $; (b) electron temperature at $ r/a=0.90 $, (c) Reynolds stress at $ r/a=0.90 $; (d) gradient of Reynolds stress at $ r/a=0.90 $; (e) Reynolds power at $ r/a=0.90; $ (f) shearing rate at $ r/a=0.90 $.

    下载: 全尺寸图片 幻灯片

    图 9  $ r/a=0.90 $处锯齿崩塌前(a)和崩塌后(b)的湍流径向和极向波数联合几率密度分布

    Figure 9.  Joint probability density function of radial and poloidal wave numbers of turbulence intensity before (a) and after (b) sawtooth collapse at $ r/a=0.90 $.

    下载: 全尺寸图片 幻灯片
  • [1] Hastie R J 1997 Astrophys. Space Sci. 256 177 doi: 10.1023/A:1001728227899
    [2] Von Goeler S, Stodiek W, Sauthoff N 1974 Phys. Rev. Lett. 33 1201 doi: 10.1103/PhysRevLett.33.1201
    [3] Wanger F, Fussmann G, Grave T, Keilhacker M, Kornherr M, Lackner K, McCormick K, Müller E R, Stäbler A, Becker G, Bernhardi K, Ditte U, Eberhagen A, Gehre O, Gernhardt J, Gierke G V, Glock E, Gruber O, Haas G, Hesse M, Janeschitz G, Karger F, Kissel S, Klüber O, Lisitano G, Mayer H M, Meisel D, Mertens V, Murmann H, Poschenrieder W, Rapp H, Röhr H, Ryter F, Schneider F, Siller G, Smeulders P, Söldner F, Speth E, Steuer K H, Szymanski Z, Vollmer O 1984 Phys. Rev. Lett. 53 1453 doi: 10.1103/PhysRevLett.53.1453
    [4] Ido T, Kamiya K, Miura Y, Hamada Y, Nishizawa A, Kawasumi Y 2002 Phys. Rev. Lett. 88 055006 doi: 10.1103/PhysRevLett.88.055006
    [5] Martin Y R, Team TCV 2004 Plasma Phys. Controlled Fusion 46 A77 doi: 10.1088/0741-3335/46/5A/008
    [6] Moyer R A, Burrell K H, Carlstrom T N, Coda S, Conn R W, Doyle E J, Gohil P, Groebner R J, Kim J, Lehmer R, Peebles W A, Porkolab M, Rettig C L, Rhodes T L, Seraydarian R P, Stockdale R, Thomas D M, Tynan G R, Watkins J G 1995 Phys. Plasmas 2 2397 doi: 10.1063/1.871263
    [7] Burrell K H 1997 Phys. Plasmas 4 1499 doi: 10.1063/1.872367
    [8] Manz P, Xu M, Thakur S C, Tynan G R 2011 Plasma Phys. Controlled Fusion 53 095001 doi: 10.1088/0741-3335/53/9/095001
    [9] Zhao K J, Cheng J, Diamond P H, Dong J Q, Yan L W, Hong W Y, Xu M, Tynan G, Miki K, Huang Z H, Itoh K, Itoh S I, Fujisawa A, Nagashima Y, Inagaki S, Wang Z X, Wei L, Song X M, Lei G J, Li Q, Ji X Q, Liu Y, Yang Q W, Ding X T, Duan X R, HL-2A Team 2013 Nucl. Fusion 53 123015 doi: 10.1088/0029-5515/53/12/123015
    [10] Zhao K J, Nagashima Y, Guo Z B, Dong J Q, Yan L W, Itoh K, Itoh S I, Li X B, Li J Q, Fujisawa A, Inagaki S, Cheng J, Xu J Q, Kosuga Y, Sasaki M, Wang Z X, Zhang H Q, Chen Y Q, Cao X G, Yu D L, Liu Y, Song X M, Xia F, Wang S 2022 Plasma Sci. Technol. 25 015101 doi: 10.1088/2058-6272/ac7c60
    [11] Zhang J Y, Zhao K J, Yang Z J, Chen Z P, Guo Z B, Dong J Q, Itoh K, Chen Z Y, Shi Y J, Ding Y H, Li J Q, Xie Y Y, Zhang H Q, Chen Y Q, Li R, Cao X G, Du J J, Jiang J M, Zhang G S, Cheng J, Xu J Q, Xiang L, Wang N C, Wang L, Liang Y F, J-TEXT team 2023 Phys. Plasmas 30 082305 doi: 10.1063/5.0153055
    [12] Grenfell G, Van Milligen B PH, Losada U, Ting W, Liu B, Silva C, Spolaore M, Hidalgo C, TJ-II Team 2019 Nucl. Fusion 59 016018 doi: 10.1088/1741-4326/aaf034
    [13] Long T, Diamond P H, Ke R, Chen Z P, Xu X, Tian W J, Hong R J, Cao M Y, Liu Y M, Xu M, Wang L, Yang Z J, Yuan J B, Zhou Y K, Yan Q H, Yang Q H, Shen C S, Nie L, Wang Z H, Hao G Z, Wang N C, Chen Z Y, Li J Q, Chen Wei, Zhong W L 2024 Nucl. Fusion 64 066011 doi: 10.1088/1741-4326/ad3e15
    [14] Long T, Diamond P H, Ke R, Chen Z P, Cao M Y, Xu X, Xu M, Hong R J, Tian W J, Yuan J B, Liu Y M, Yan Q H, Yang Q H, Shen C S, Guo W X, Wang L, Nie L, Wang Z H, Hao G Z, Wang N C, Chen Z Y, Pan Y, Li J Q, Chen W, Zhong W L 2024 Nucl. Fusion 64 064002 doi: 10.1088/1741-4326/ad40c0
    [15] Ding Y H, Wang N C, Chen Z Y, Xia D H, Yang Z J, Chen Z P, Zheng W, Yan W, Li D, Zhou S, Xu X, Zhang X Y, Mao F Y, Fang J G, Ren Z K, Chen X X, Zhang J L, Zhang X B, He Y, Zhang Q, Li Y, Bai W, Mou L K, Li F, Long T, Ke R, Gao L, Shi P, Shen C S, Liu J X, Guo W X, Wang L, Li H H, Jiang Z H, Zhang X Q, Li J C, Rao B, Cheng Z F, Zhu P, Liu M H, Xu T, Ma S X, Yang Y, Li C, Wang Z J, Zhang M, Yu K X, Hu X W, Liang Y, Yu Q, Gentle K W, Pan Y, the J-TEXT Team 2024 Nucl. Fusion 64 112005 doi: 10.1088/1741-4326/ad336e
    [16] Liang Y F, Wang N C, Ding Y H, Chen Z Y, Chen Z P, Yang Z J, Hu Q M, Cheng Z F, Wang L, Jiang Z H, Rao B, Huang Z, Li Y, Yan W, Li D, Liu H, Zeng L, Huang Y, Huang D W, Lin Z F, Zheng W, Hu F R, Zhao K J, Jiang M, Shi Y J, Zhou H, Peng S T, Guo W X, Gao L, Wang Z J, Zhang M, Yu K X, Hu X W, Yu Q, Zhuang G, Gentle K W, Pan Y, the J-TEXT Team 2019 Nucl. Fusion 59 112016 doi: 10.1088/1741-4326/ab1a72
    [17] Zhao K J, Lan T, Dong J Q, Yan L W, Hong W Y, Yu C X, Liu A D, Qian J, Cheng J, Yu D L, Yang Q W, Ding X T, Liu Y, Pan C H 2006 Phys. Rev. Lett. 96 255004 doi: 10.1103/PhysRevLett.96.255004
    [18] Xie Y Y, Zhao K J, Yang Z J, Chen Z P, Dong J Q, Chen Z Y, Shi Y J, Tan M Z, Gao L, Ding Y H, Chen Y Q, Zhang H Q, Li R, Cao X G, Du J J, Jiang J M, Zhang G S, Cheng J, Xu J Q, Zhang J Y, Xiang L, Wang N C, Wang L, Liang Y F 2025 Plasma Phys. Controlled Fusion 67 015008 doi: 10.1088/1361-6587/ad95ba
    [19] Manz P, Ribeiro T T, Scott B D, Birkenmeier G, Carralero D, Fuchert G, Müller S H, Müller H W, Stroth U, Wolfrum E 2015 Phys. Plasmas 22 022308 doi: 10.1063/1.4908272
    [20] Wu T, Diamond P H, Nie L, Xu M, Yu Y, Hong R J, Chen Y H, Xu J Q, Long T, Zhang Y, Yan Q H, Ke R, Cheng J, Li W, Huang Z H, Yan L W, Chu X, Wang Z H, Hidalgo C 2023 Nucl. Fusion 63 126001 doi: 10.1088/1741-4326/acf5d9
    [21] Long T, Diamond P H, Ke R, Nie L, Xu M, Zhang X Y, Li B L, Chen Z P, Xu X, Wang Z H, Wu T, Tian W J, Yuan J B , Yuan B D, Gong S B, Xiao C Y, Gao J M, Hao Z G, Wang N C, Chen Z Y, Yang Z J, Gao L, Ding Y H, Pan Y, Chen W, Hao G Z, Li J Q, Zhong W L, Duan X R 2021 Nucl. Fusion 61 126066 doi: 10.1088/1741-4326/ac36f2
    [22] Gürcan Ö D, Diamond P H, Hahm T S 2006 Phys. Plasmas 13 052306 doi: 10.1063/1.2180668
    [23] Hahm T S, Diamond P H 2018 J. Korean Phys. Soc. 73 747 doi: 10.3938/jkps.73.747
    [24] Wolf R C 2003 Plasma Phys. Controlled Fusion 45 R1 doi: 10.1088/0741-3335/45/1/201
    [25] Zhao K J, Chen Z P, Shi Y J, Diamond P H, Dong J Q, Chen Z Y, Ding Y H, Zhuang G, Liu Y B, Zhang H Q, Chen Y Q, Liu H, Cheng J, Nie L, Rao B, Cheng Z F, Gao L, Zhang X Q, Yang Z J, Wang N C, Wang L, Li J Q, Jin W, Xu J Q, Yan L W, Liang Y F, Xie Y Y, Liu B 2020 Nucl. Fusion 60 106030 doi: 10.1088/1741-4326/abadad
    [26] Diamond P H, Kim Y B 1991 Phys. Fluids B 3 1621 doi: 10.1063/1.859681
    [27] Xu Y H, Yu C X, Luo J R, Mao J S, Liu B H, Li J G, Wan B N, Wan Y X 2000 Phys. Rev. Lett. 84 3867 doi: 10.1103/PhysRevLett.84.3867
    [28] Diamond P H, Kosuga Y, Gürcan Ö D, McDevitt C J, Hahm T S, Fedorczak N, Rice J E, Wang W X, Ku S, Kwon J M, Dif-Pradalier G, Abiteboul J, Wang L, Ko W H, Shi Y J , Ida K, Solomon W, Jhang H, Kim S S, Yi S, Ko S H, Sarazin Y, Singh R, Chang C S 2013 Nucl. Fusion 53 104019 doi: 10.1088/0029-5515/53/10/104019
  • 加载中
图( 9)
计量
  • 文章访问数:  226
  • HTML全文浏览数:  226
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-27
  • 刊出日期:  2025-02-20

J-TEXT托卡马克锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响

    通讯作者: E-mail: kjzhao@ecut.edu.cn.; 
    作者简介: 丁肖冠. E-mail: 844203458@qq.com
  • 1. 东华理工大学核科学与工程学院, 南昌　330013
  • 2. 华中科技大学电气与电子工程学院, 磁约束聚变与等离子体国际合作联合实验室, 强电磁技术全国重点实验室, 武汉　430074
  • 收稿日期:  2024-09-27

摘要: 锯齿振荡引起热脉冲和湍流脉冲可以传播到边缘等离子体中增强边缘剪切流并诱发低约束模到高约束模的转换. 在J-TEXT托卡马克上观测了锯齿振荡期间湍流传播和对称性破缺对边缘剪切流的影响. 采用快速往复静电探针阵列测量了边缘等离子体湍流和剪切流等, 观测到锯齿崩塌后, 芯部的热脉冲和湍流传播至边缘等离子体, 且湍流脉冲快于热脉冲. 本文发现了锯齿崩塌后在边缘等离子体中引起湍流对称性破缺, 湍流传播和对称性破缺可以增强湍流雷诺协强, 从而驱动剪切流. 这些结果阐明了锯齿崩塌对边缘湍流和剪切流的增强作用过程.

English Abstract

    全文HTML

    1.   引　言

    • 锯齿振荡, 又称锯齿不稳定性或锯齿崩塌, 是磁约束等离子体中常见的一类宏观不稳定性[1], 自1974年在ST托卡马克上发现后[2], 一直是聚变界一个活跃研究的领域. 锯齿振荡具体表现为等离子体芯部的扰动导致芯部温度和密度等参数周期性地快速崩塌和缓慢重建. 与此同时, 芯部的粒子和能量向外快速输运, 导致外部等离子体温度和密度等参数周期性地突然上升又缓慢下降, 呈反锯齿状.

      目前人们已在ASDEX[3], JFT-2M[4]和TCV[5]等多个装置上观测到, 锯齿可以触发低约束模(low confinement mode, L模)到高约束模(high confinement mode, H模)的转换. 研究表明, 在L-H模转换过程中, 托卡马克边缘剪切流增强, 湍流被显著地抑制, 压强梯度迅速增大并形成边缘输运垒, 等离子体输运水平降低, 约束性能大幅提高[6,7]. 剪切流可以由湍流自组织产生, 且通过剪切退相关湍流, 并从湍流中获取能量[8].

      锯齿振荡可以产生密度、热以及湍流脉冲从芯部传播至边缘等离子体, 从而改变边缘密度、温度和湍流来影响等离子体剪切流. 在HL-2A[9,10], J-TEXT[11]装置上发现锯齿崩塌后, 边缘等离子体流和湍流显著地增强. 等离子体湍流既可以由局域的梯度驱动, 也可以由远大于其相关长度的径向距离位置的湍流传播. 在TJ-II[12]和J-TEXT[13–15]装置上观测到湍流驱动和传播对边缘湍流强度和空间分布的影响. 然而, 锯齿振荡期间, 湍流传播如何影响边缘等离子体湍流的时间演化和剪切流的产生机制等问题还有待进一步研究.

      本文采用快速往复静电探针阵列在J-TEXT托卡马克上研究了锯齿振荡期间, 湍流传播和对称性破缺对边缘湍流和剪切流的影响. 研究结果对理解等离子体的约束和输运具有重要意义. 第2节描述实验安排, 第3节分析锯齿振荡对边缘湍流和剪切流的影响, 以及湍流传播和对称性破缺对它们的作用, 第4节对全文进行总结.

    2.   实验安排

      2.1.   实验装置

    • J-TEXT是中型的托卡马克装置, 其大半径和小半径分别为$ R=1.05\;{\mathrm{m}} $和$ a=0.255\;{\mathrm{m}} $[16]. 本文中的实验在限制器位形下欧姆放电的氢等离子体中展开, 采用脉冲送气加料方式. 放电等离子体参数为等离子体电流$ {I}_{{\mathrm{p}}}\text{= 190 kA} $、中心线积分密度$ {n}_{{\mathrm{e}}}^{{\mathrm{L}}{\mathrm{I}}}=1-1.7\times 1{0}^{19}\;{{\mathrm{m}}}^{-2} $、环向磁场$ {B}_{{\mathrm{t}}}=1.7\;{\mathrm{T}} $以及边界安全因子$ {q}_{{\mathrm{a}}}=2.7 $.

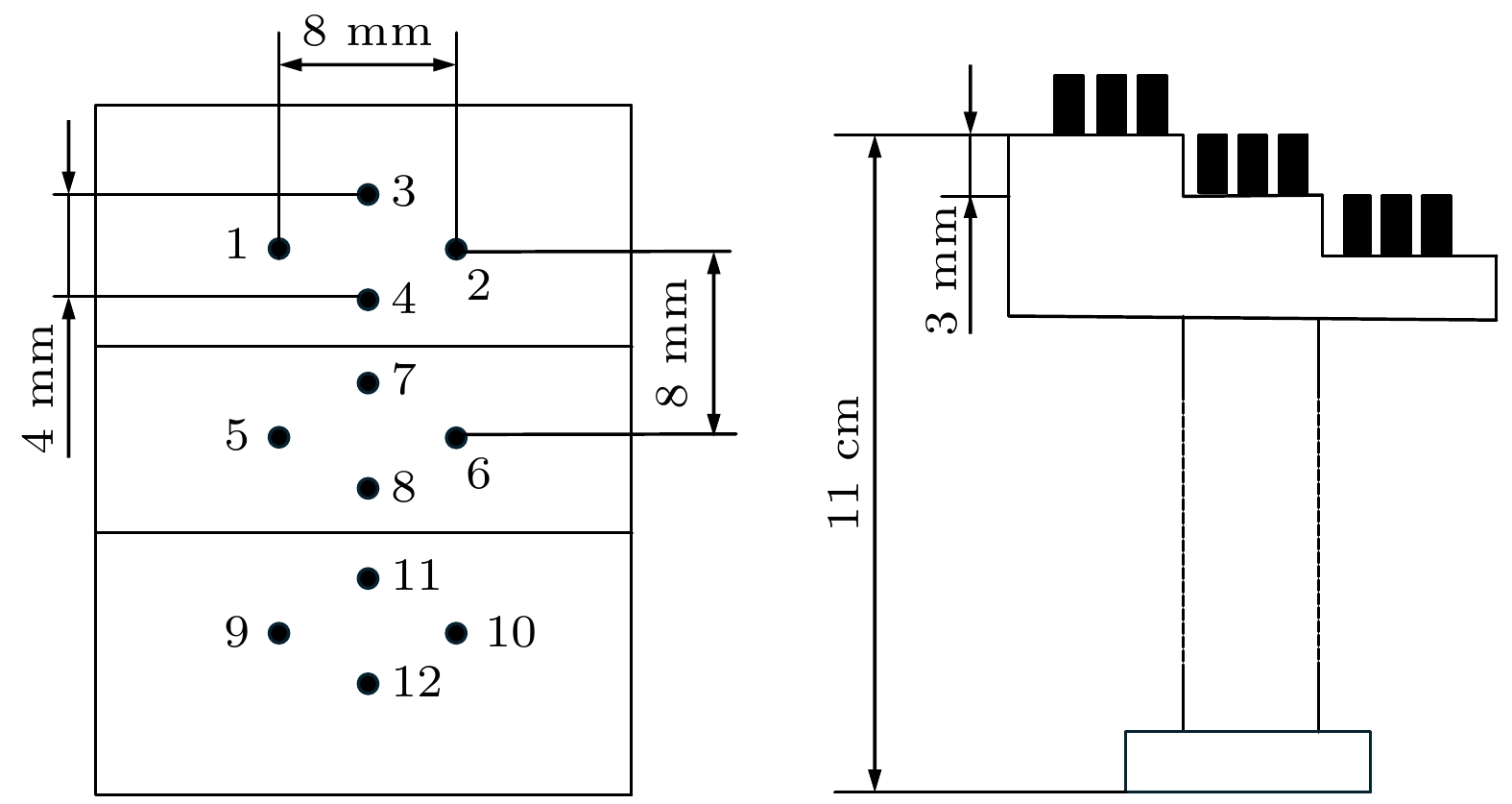
      采用24道电子回旋辐射系统(electron cyclotron emission, ECE)观测芯部等离子体电子温度. ECE系统的采样率为$ \text{1 MHz} $. 采用快速往复静电探针阵列观测边缘等离子体参数. 探针阵列安装在J-TEXT装置的顶部, 且径向方向可移动$ \text{5 cm} $. 静电探针阵列由3个台阶组成, 每个台阶均有4个探针, 其结构如图1所示. 所有探针的长度均为$ \text{3 mm} $, 直径为$ \text{2 mm} $. 探针3和4, 7和8, 以及11和12的极向距离均为$ d_{\theta}=4\text{ mm} $, 远小于湍流极向相关长度$ 1—3\text{ cm} $; 相邻台阶的径向距离为$ {d}_{{\mathrm{r}}}= 3\text{ mm} $, 远小于湍流的径向相关长度$ 1—2\text{ cm} $[17]. 正偏压$ {V}_{+} $由探针1, 5和9测量, 负偏压$ {V}_{-} $由探针2, 6和10测量, 其余探针测量悬浮电位$ {V}_{{\mathrm{f}}} $. 通过三台阶探针阵列, 可以观测等离子体局部电子温度、电子密度、等离子体电位、极向电场和径向电场等参数. 电子温度$ {T}_{{\mathrm{e}}}=\left({V}_{+}-{V}_{{\mathrm{f}}}\right)/{\ln 2} $, 离子饱和流$ {I}_{{\mathrm{S}}}=\left({V}_{+}-{V}_{-}\right)/{R}_{{\mathrm{S}}} $, 其中$ {R}_{{\mathrm{S}}} $是分流电阻, 电子密度$ {n}_{{\mathrm{e}}}={I}_{{\mathrm{s}}}/0.49 e{A}_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}}({T}_{{\mathrm{e}}}/{m}_{{\mathrm{i}}}{)}^{1/2} $, 其中$ {A}_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $为电流有效收集面积, $ {m}_{{\mathrm{i}}} $为离子质量. 等离子体电位$ {V}_{{\mathrm{p}}}={V}_{{\mathrm{f}}}+\alpha {T}_{{\mathrm{e}}} $, $ \alpha $的取值为2.5. 极向电场由探针阵列同一台阶的悬浮电位极向梯度可得$ {E}_{\theta }= ({V}_{{\mathrm{f}}}^{{\theta }_{i}}-{V}_{{\mathrm{f}}}^{{\theta }_{i+1}})/{d}_{\theta } $, i为3, 7或11号探针. 径向电场由相邻两个台阶的等离子体电位径向梯度可得$ {E}_{{\mathrm{r}}}=({V}_{{\mathrm{p}}}^{{r}_{j}}-{V}_{{\mathrm{p}}}^{{r}_{j+1}})/{d}_{\mathrm{{r}}} $, $ j $为第1个或第2个台阶. 径向$ \boldsymbol{E}\times \boldsymbol{B} $速度为$ {V}_{{\mathrm{r}}}={E}_{\theta }/{B}_{{\mathrm{t}}} $, 极向$ E\times B $速度为$ {V}_{\theta }= {E}_{{\mathrm{r}}}/{B}_{{\mathrm{t}}} $. 探针的采样率为$ \text{2 MHz} $, 对应的奈奎斯特频率为$ \text{1 MHz} $.

      • 2.2.   分析方法

    • 条件平均方法可以识别出信号中的相干结构, 并且抑制信号噪声. 采用条件平均方法分析数据时, 首先需要选择参考信号. 在本实验中, 锯齿崩塌是参考信号, 并通过ECE信号在$ r/a=0.01 $处的时间导数计算得到. 在每个锯齿周期内, 定义导数极小值处的时刻$ t=0\ \mathrm{ms} $. 锯齿的平均周期为2.5 ms, 选择$ t= -1.25 — 1.25\;{\mathrm{m}}{\mathrm{s}} $为时间窗, 提取每段信号序列. 将所有提取的序列进行叠加求平均, 即可得到信号的条件平均结果. 这里总共提取了25个锯齿数据进行条件平均分析.

    3.   实验结果与讨论

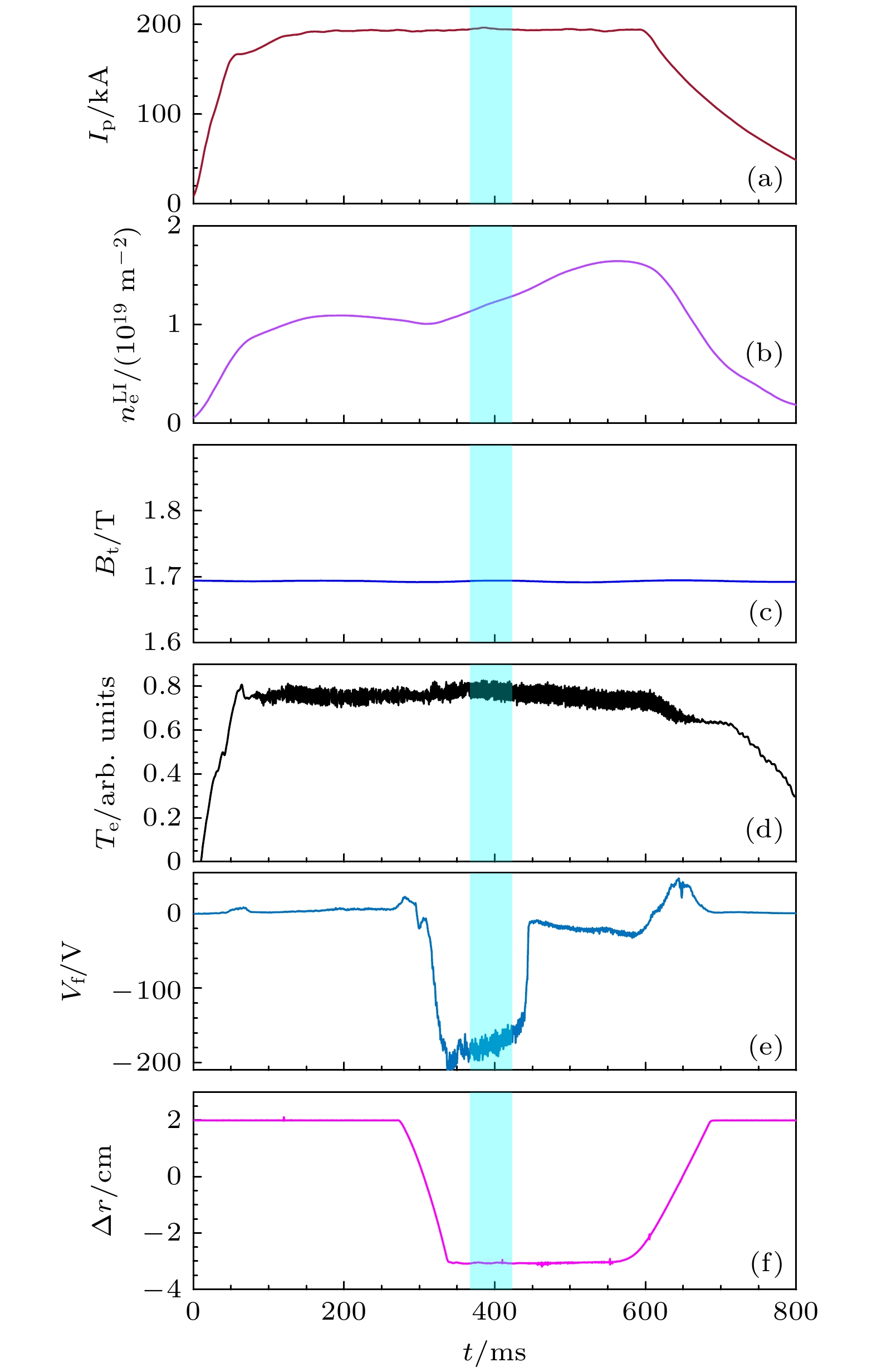
    • 本次分析采用#1063158炮的实验数据. 图2(a)—(c)分别表示等离子体电流$ {I}_{{\mathrm{p}}} $、线积分电子密度$ {n}_{{\mathrm{e}}}^{{\mathrm{L}}{\mathrm{I}}} $、环向磁场$ {B}_{{\mathrm{t}}} $. 图2(d)为利用电子回旋辐射诊断系统测量的$ r/a=0.01 $处的电子温度, 单位为任意单位. 目前, J-TEXT装置上的电子回旋辐射诊断只进行了相对定标, 并不能给出实际温度. 图2(e)和图2(f)分别为$ r/a=0.88 $处的悬浮电位和探针位移的时间演化, 其中$ \Delta r $表示最后闭合磁面(last closed flux surface, LCFS)与探针测量位置之间的距离, 负号表示在LCFS内部. $ t= 270\;{\mathrm{m}}{\mathrm{s}} $时, 探针开始插入等离子体中直至$ t=340\;{\mathrm{m}}{\mathrm{s}} $时刻停止运动, 停留在闭合磁面内约3 cm位置, 悬浮电位约为–170 V. 阴影部分时间段为$ t=367 — 423\;{\mathrm{m}}{\mathrm{s}} $, 以下对该时间段内的探针数据进行详细分析.

      • 3.1.   等离子体的湍流传播

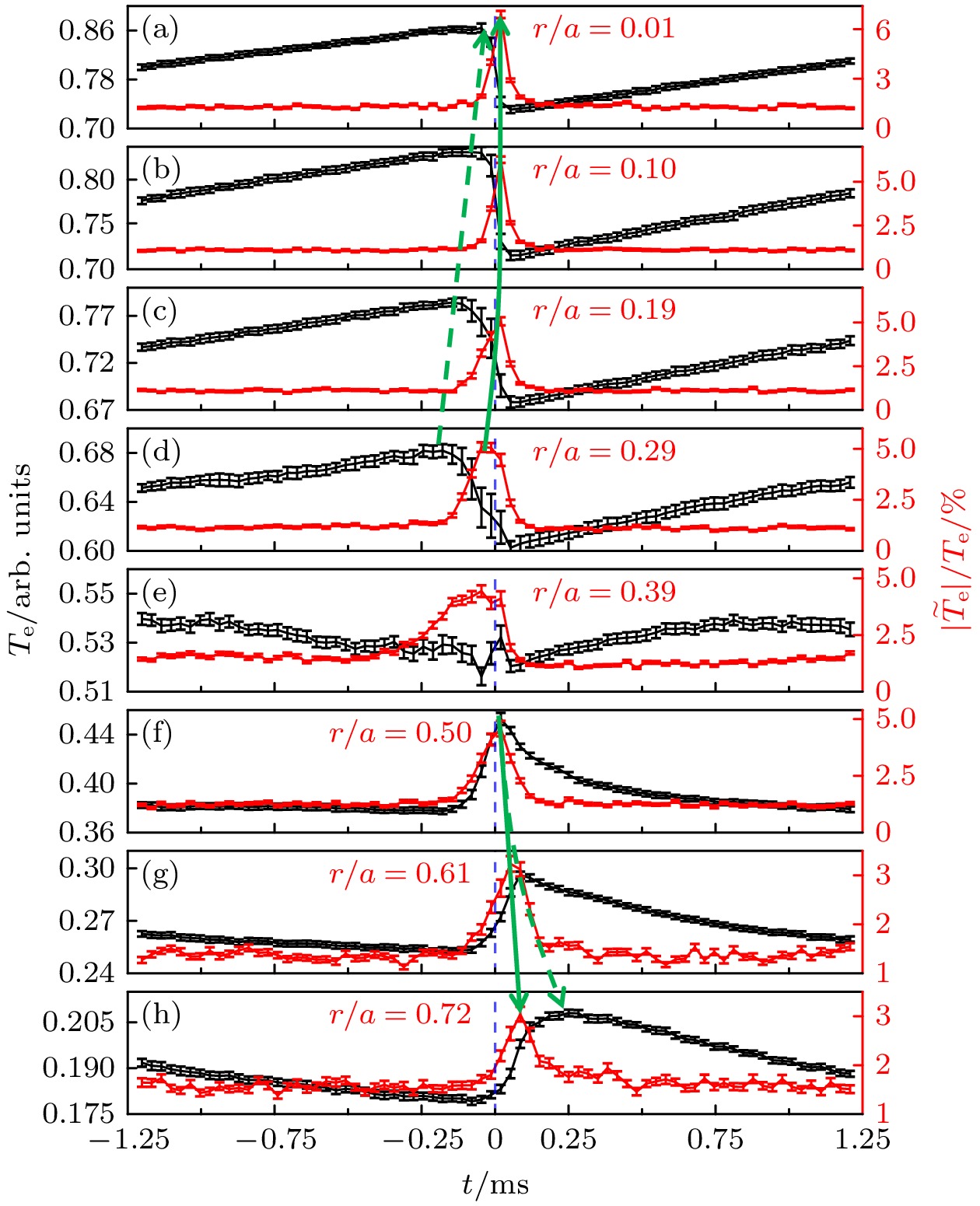
    • 锯齿崩塌后, 热脉冲和湍流脉冲从反转半径处向外传播至边缘等离子体. 图3(a)—(h)分别给出不同径向位置处的电子温度和湍流相对强度. 这里的电子温度涨落$ \tilde{{T}_{{\mathrm{e}}}} $由ECE信号推导得出, 相应的频段为10—50 kHz. 从ECE信号中提取湍流信号的方法详细介绍在文献[11,18]. 图中误差棒由条件平均对应信号的标准差给出, 蓝色虚线表示$ t= 0\;{\mathrm{m}}{\mathrm{s}} $, 对应$ r/a=0.01 $处锯齿崩塌时刻, 绿色实线和虚线分别连接湍流相对强度和电子温度的峰值, 箭头代表传播方向. 由图3可见, 反转半径在$ r/a= 0.39 $左右. 反转半径以内, 锯齿崩塌和湍流脉冲均向内传播, $ r/a=0.29, 0.19, 0.10{\mathrm{和}}0.01 $处湍流相对强度分别上升257%, 378%, 442%和381%. 反转半径以外的热脉冲和湍流脉冲向外传播, $ r/a= 0.5, 0.61{\mathrm{和}}0.72 $处电子温度分别上升18%, 16%和16%, 湍流相对强度分别上升219%, 122%和90%, 且湍流脉冲快于热脉冲传播, 速度分别为0.6 km/s和0.2 km/s.

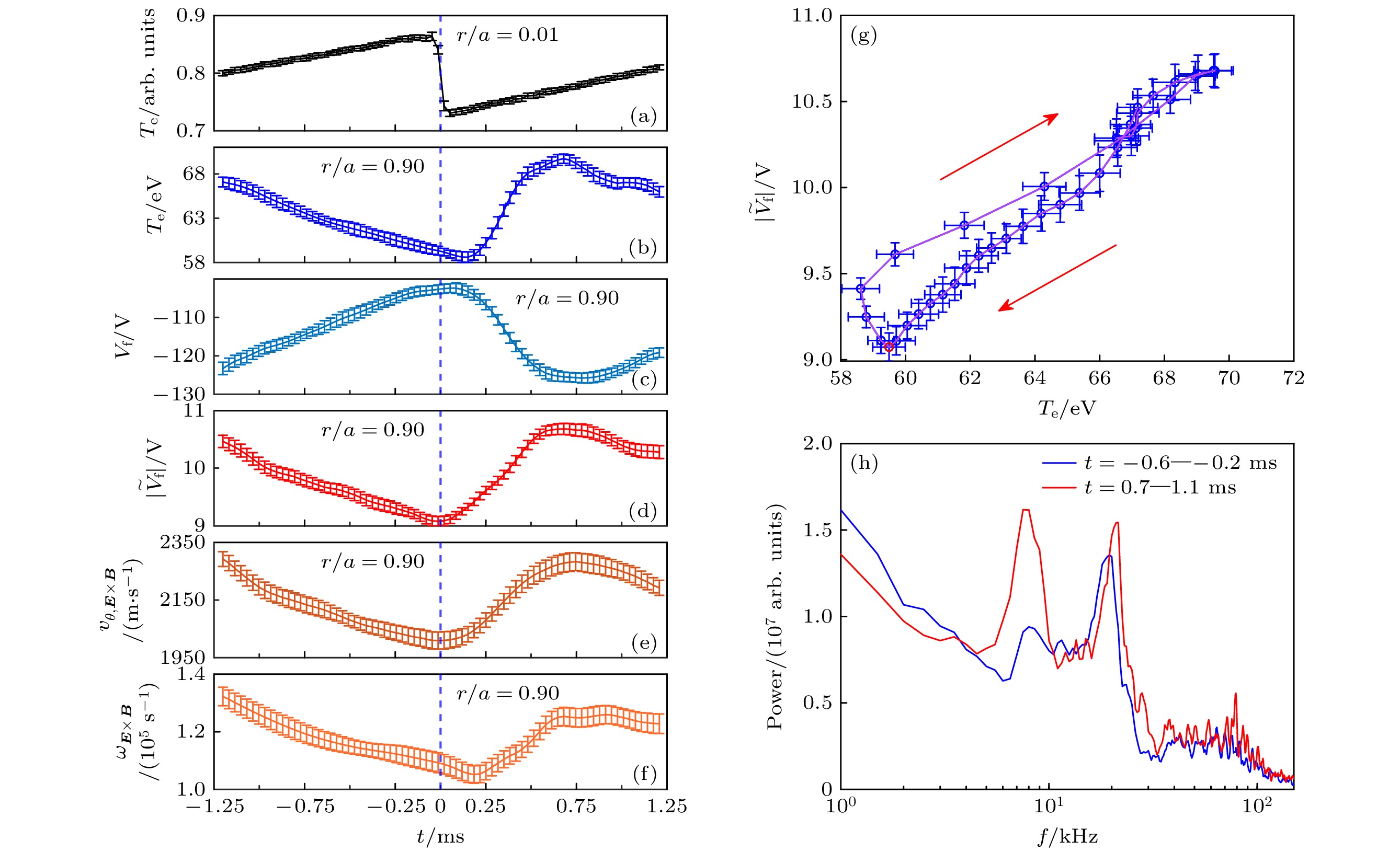
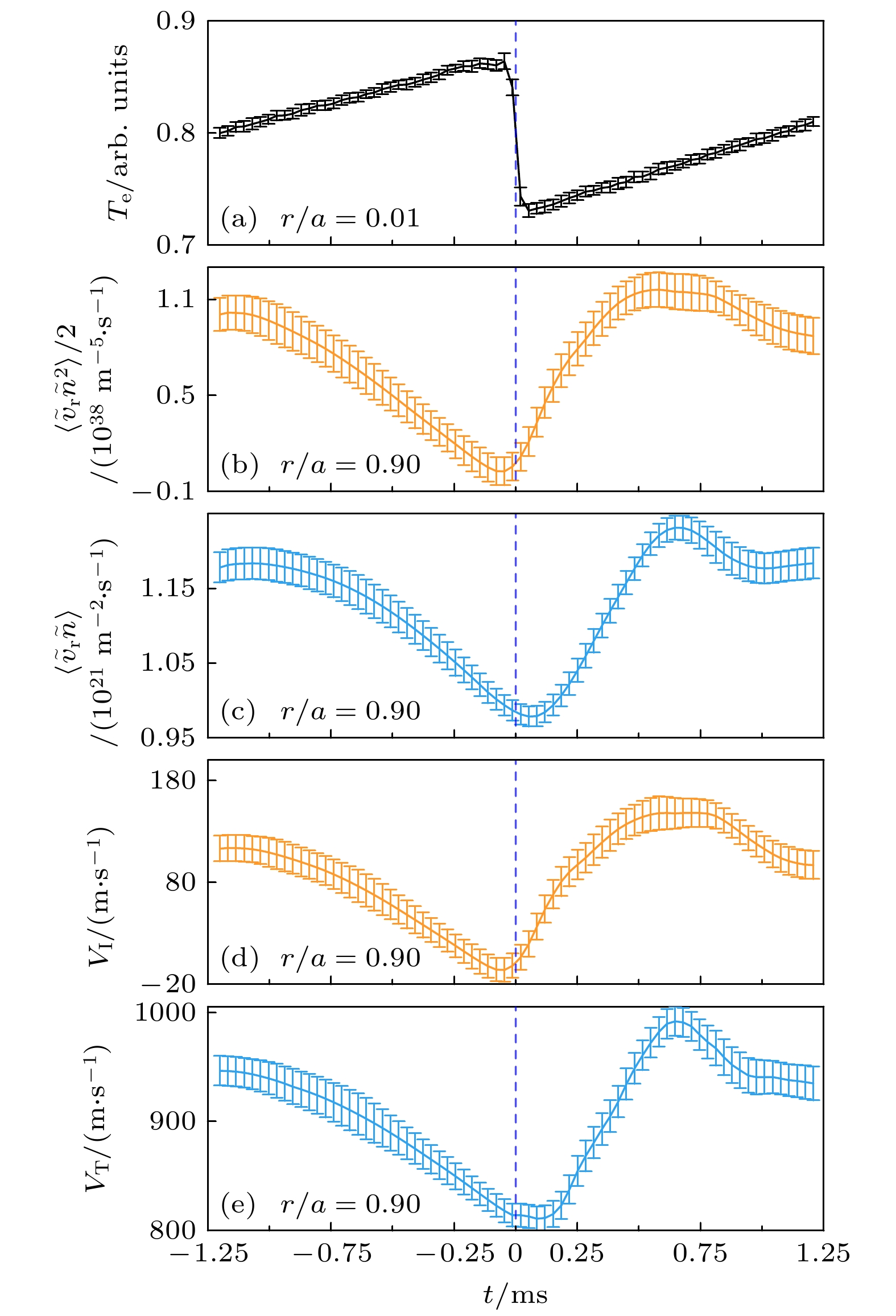
      图4(a)—(d)分别给出$ r/a=0.01 $处的电子温度、$ r/a=0.90 $处电子温度、悬浮电位和湍流强度. 这里的边缘湍流强度由悬浮电位的绝对涨落$ |\tilde{{V}_{{\mathrm{f}}}}| $给出, 涨落量由对应信号的边缘湍流频段(30—150 kHz)滤波得出. 由图4(a)—(d)可知, 锯齿崩塌0.7 ms后, 边缘电子温度上升20%到最大值, 悬浮电位下降20%到最小值. 边缘湍流强度在锯齿崩塌0.6 ms后增加20%到最大值. 图4(g)给出$ r/a=0.90 $处电子温度和湍流强度的李萨如图, 其中红色箭头表示轨迹的旋转方向, 红色圆点表示$ r/a=0.01 $处锯齿崩塌时刻. 如图4(g)所示, 轨迹整体沿顺时针旋转, 锯齿崩塌后, 边缘湍流的发展快于电子温度, 并率先达到最大值. 这表明锯齿崩塌后, 从芯部传播至边缘的湍流脉冲快于热脉冲, 且热脉冲延迟时间约0.1 ms.

      图4(h)给出锯齿崩塌前后$ r/a=0.90 $处悬浮电位的自功率谱. 由图可见, $ f= 30—150\;{\mathrm{k}}{\mathrm{H}}{\mathrm{z}} $为湍流频段, 测地声模(geodesic acoustic mode, GAM)的频率在18 kHz, 8 kHz的谱峰为撕裂模. 锯齿崩塌后, 湍流明显增强, 其驱动的GAM也增强, 且峰值频率从18 kHz上升至21 kHz, 撕裂模不稳定性也增加.

      湍流通过非线性相互作用可以自组织产生剪切流. 图4(e)和图4(f)分别给出$ r/a=0.90 $处的$ \boldsymbol{E}\times \boldsymbol{B} $极向速度及其剪切率. 可以看出, 锯齿崩塌后, 随着湍流强度增强, 边缘$ \boldsymbol{E}\times \boldsymbol{B} $极向速度从2 km/s增大至2.3 km/s, 增加约15%, 极向$ \boldsymbol{E}\times \boldsymbol{B} $流剪切率从1.0×105 s–1增加至1.2×105 s–1. 一般地, 较强的剪切流有助于改善约束.

      锯齿崩塌后, 边缘增强的湍流主要包含两部分, 即边缘局域梯度驱动的湍流和从芯部传播至边缘的湍流. 通过Manz 等[19]对湍流能量的演化研究, 我们可以识别这两类不同来源的湍流. 忽略横越磁场耦合和阻尼以及背景流的影响, 并考虑垂直于磁场的平面内不可压缩湍流, 可以从连续性方程的径向部分推导出湍流能量演化方程:

      式中, $ \left\langle{\cdots }\right\rangle $表示在远大于湍流相关时间的时间间隔上的平均值. 等式左边第一项表示湍流自由能的时间演化, $ \tilde{n} $为密度涨落. 等式右边第一项与局域梯度对湍流的驱动有关, $ \left\langle{{\tilde{v}}_{\mathrm{{r}}} \tilde{n}}\right\rangle $表示粒子输运, $ {\tilde{v}}_{\mathrm{{r}}} $为径向速度涨落. 等式右边第二项为非局域非线性的湍流传播项. 采用局域湍流振幅$ \langle {\tilde{n}}^{2}\rangle $进行归一化处理, 得到局域密度梯度驱动的湍流驱动率:

      湍流传播率则表示为

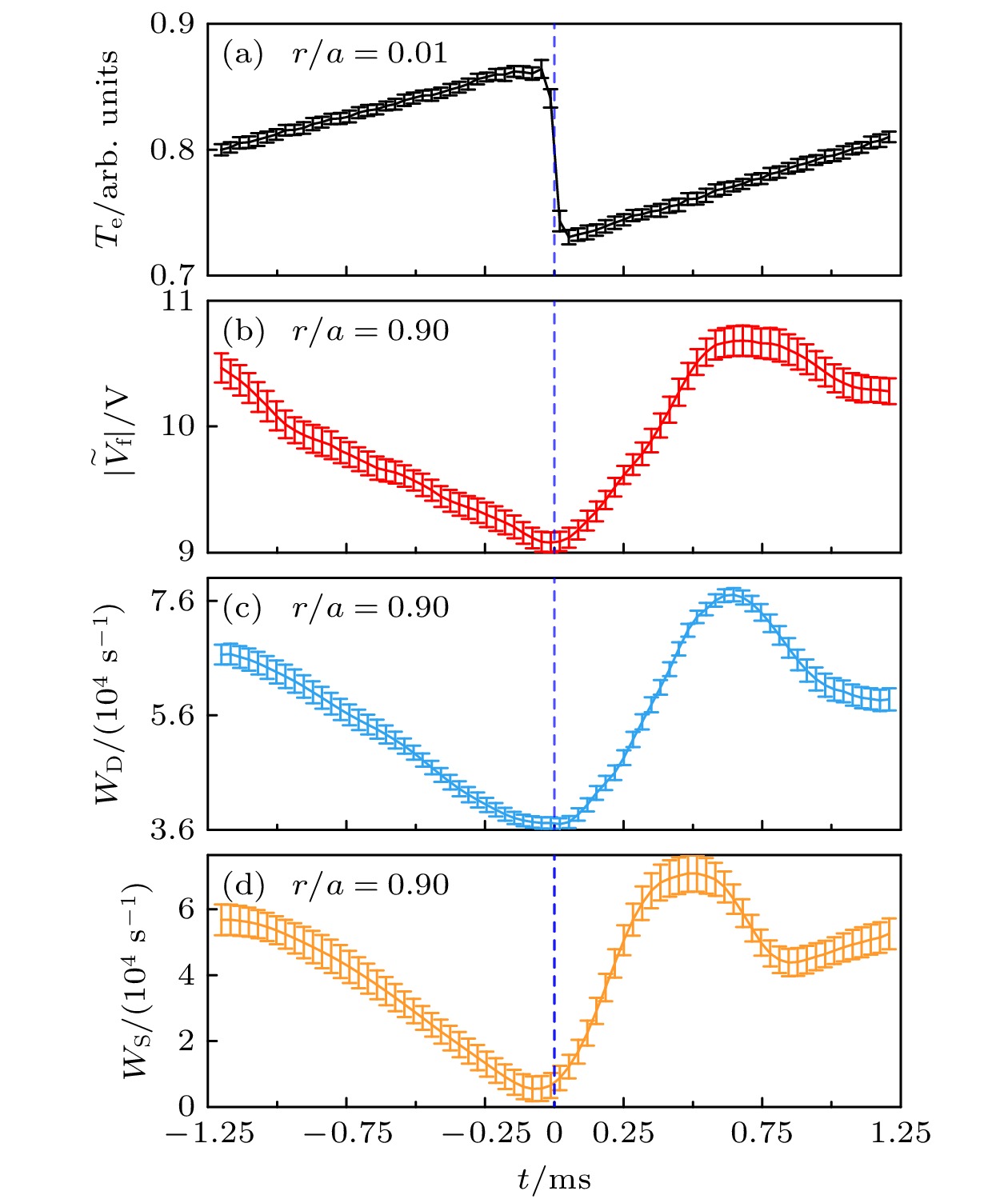
      图5(a)—(d)分别给出$ r/a=0.01 $处的电子温度、$ r/a=0.90 $处湍流强度、湍流驱动率以及湍流传播率. 由图5可知, 锯齿崩塌0.7 ms后, 湍流驱动率达到最大值7.6×104 s–1. 锯齿崩塌0.6 ms后, 湍流传播率达到最大值7.0×104 s–1. 湍流传播率的增加比驱动率大约快0.1 ms. 该结果与湍流脉冲快于热脉冲的结果一致, 这表明边缘湍流脉冲快于热脉冲是由于湍流传播引起的. 由此可知, 锯齿崩塌0.6 ms后, 从反转半径处向外传播的湍流脉冲比热脉冲率先达到边缘, 增强边缘湍流. 湍流传播来源于湍流的非线性相互作用, 一般地, 湍流强度的增加将导致湍流非线性相互作用增强, 从而湍流传播也增强. 锯齿崩塌0.7 ms后, 当热脉冲到达边缘时, 影响边缘局域梯度分布, 湍流驱动率随着局域梯度变陡而增加. 这是因为湍流线性驱动主要来自于梯度. 此外, 锯齿崩塌后, 湍流驱动率和湍流传播率达到最大值的数值相近, 这说明边缘局域梯度驱动的湍流和从芯部传播至边缘的湍流对边缘湍流增强均可能发挥重要作用.

      湍流传播是指由于非线性相互作用而导致的湍流强度或能量的空间传播. 湍流能量由湍流内能和动能组成. 对于湍流内能, $ \langle {\tilde{v}}_{\mathrm{{r}}} {\tilde{n}}^{2}\rangle \langle {C}_{{\mathrm{s}}}^{2}\rangle /(2{\langle n\rangle }^{2}) $是相关的通量, $ {C}_{{\mathrm{s}}} $是离子声速. 对于湍流动能, $ \langle {\tilde{v}}_{\mathrm{{r}}} {\tilde{v}}_{\perp }^{2}\rangle /2 $是相关通量, $ {\tilde{v}}_{\perp }^{} $是垂直速度涨落. 一般, 在实验中观测到的动能通量比内能通量约小2个数量级[20,21], 因此在本次计算中可以忽略不计. 为了简化, 湍流传播通量可以由$ \langle {\tilde{v}}_{{\mathrm{r}}}{\tilde{n}}^{2}\rangle /2 $计算. 这种计算方法在理论和模拟中也得到了应用[22,23]. 为进一步了解湍流传播的特征, 计算了湍流平均射流速度$ {V}_{{\mathrm{I}}}= \langle {\tilde{v}}_{\mathrm{{r}}} {\tilde{n}}^{2}\rangle /\langle {\tilde{n}}^{2}\rangle $. 湍流传播平均射流速度表示湍流内能在空间上传播的特征速度. 由图6(b)和图6(d)可见, 锯齿崩塌0.6 ms后, 湍流传播通量和湍流传播平均射流速度都达到最大值, 与图5(d)中湍流传播率的变化相符. 为比较湍流传播通量与湍流驱动通量, 还计算了湍流粒子通量$ \langle {\tilde{v}}_{{{\mathrm{{r}}}}}{\tilde{n}}^{}\rangle $ 以及粒子输运速度$ {V}_{{\mathrm{T}}}=\langle {\tilde{v }}_{\mathrm{{r}}} \tilde{n}\rangle /\langle {\tilde{n}}^{2}{\rangle }^{1/2} $. 粒子输运速度可以看作是湍流粒子通量输运的特征速度. 由图6(c)和图6(e)可见, 锯齿崩塌0.7 ms后, 湍流粒子通量和粒子输运速度均达到最大值, 与图5(c)中湍流驱动率的变化相符. 分析表明锯齿崩塌后湍流传播通量达到最大值的时间快于湍流粒子通量约0.1 ms. 这说明湍流能量输运并不是简单的伴随湍流粒子输运. 此外, 锯齿振荡期间, 粒子输运和湍流传播平均射流速度分别估计可达990 m/s和150 m/s, 这与龙婷等[14]报道的结果类似.

      • 3.2.   锯齿振荡对径向电场的影响

    • $ \boldsymbol{E}\times \boldsymbol{B} $流源于径向电场$ {E}_{{\mathrm{r}}} $和环向磁场$ {B}_{{\mathrm{t}}} $引起的$ \boldsymbol{E}\times \boldsymbol{B} $漂移. 径向电场通过径向力平衡方程可以分解成3项[24]:

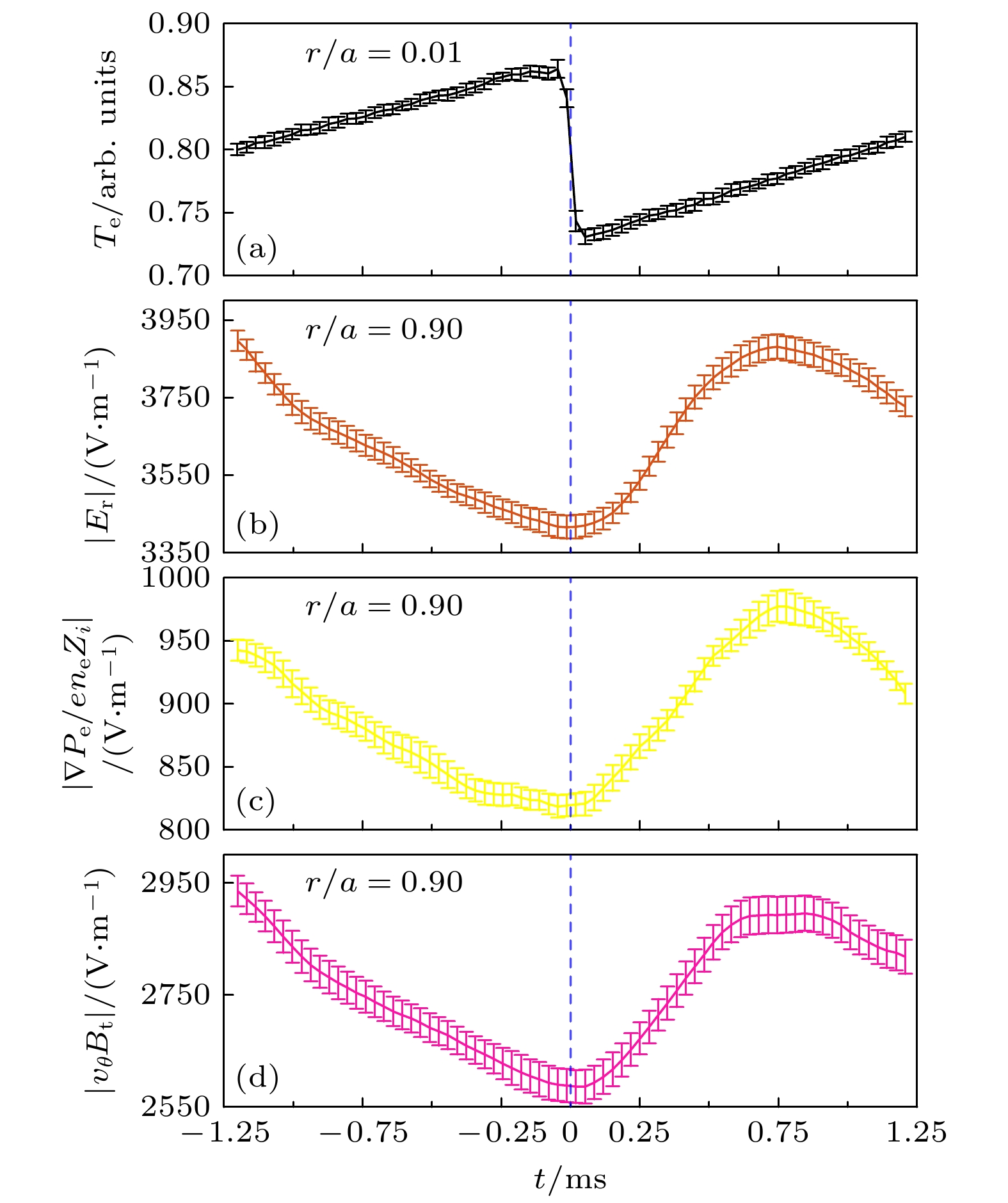
      等式右边第一项表示离子压强梯度驱动的平均流对径向电场的贡献, $ \nabla {P}_{{\mathrm{i}}}, {n}_{{\mathrm{i}}} $和$ {Z}_{{\mathrm{i}}} $分别为离子压强梯度、离子密度和离子核电荷数. 在边缘等离子体中, 假设$ {T}_{{\mathrm{e}}}\approx {T}_{{\mathrm{i}}} $ 以及等离子体准中性条件$ {n}_{{\mathrm{e}}}\approx {n}_{{\mathrm{i}}} $ 得$ {P}_{{\mathrm{e}}}\approx {P}_{{\mathrm{i}}} $. 等式右边第二项表示极向流对径向电场的贡献, $ {v }_{\theta } $为极向速度, $ {B}_{{\mathrm{t}}} $为环向磁场强度. 等式右边第三项表示环向流对径向电场的贡献, $ {v }_{\phi } $为环向速度, $ {B}_{\theta } $为极向磁场强度. 在托卡马克中, 一般极向磁场比环向磁场小一个量级, 且J-TEXT装置上L模放电时, 边缘环向流速与极向流速接近[25], 因此, 综合极向磁场和环向流速考虑, 可忽略环向流对径向电场的贡献. 径向力平衡方程可简化为$ {E}_{{\mathrm{r}}}=\nabla {P}_{{\mathrm{e}}}/e{n}_{{\mathrm{e}}}{Z}_{{\mathrm{i}}}-{v }_{\theta }{B}_{{\mathrm{t}}} $. 图7(a)—(d)分别给出$ r/a=0.01 $处的电子温度、$ r/a=0.90 $处径向电场强度、压强梯度以及极向流对径向电场的贡献. 由图7可见, 锯齿崩塌后0.6 ms后, 极向流的贡献增加16%. 锯齿崩塌0.7 ms后, 径向电场强度增强约16%, 压强梯度的贡献增加13%. 其中压强梯度和极向流对径向电场的贡献占比分别为25%和75%. 该结果说明锯齿振荡期间, 极向流对径向电场的贡献起主要作用, 且锯齿崩塌后, 极向流增加要快于压强梯度.

      • 3.3.   锯齿振荡对边缘湍流雷诺协强的影响

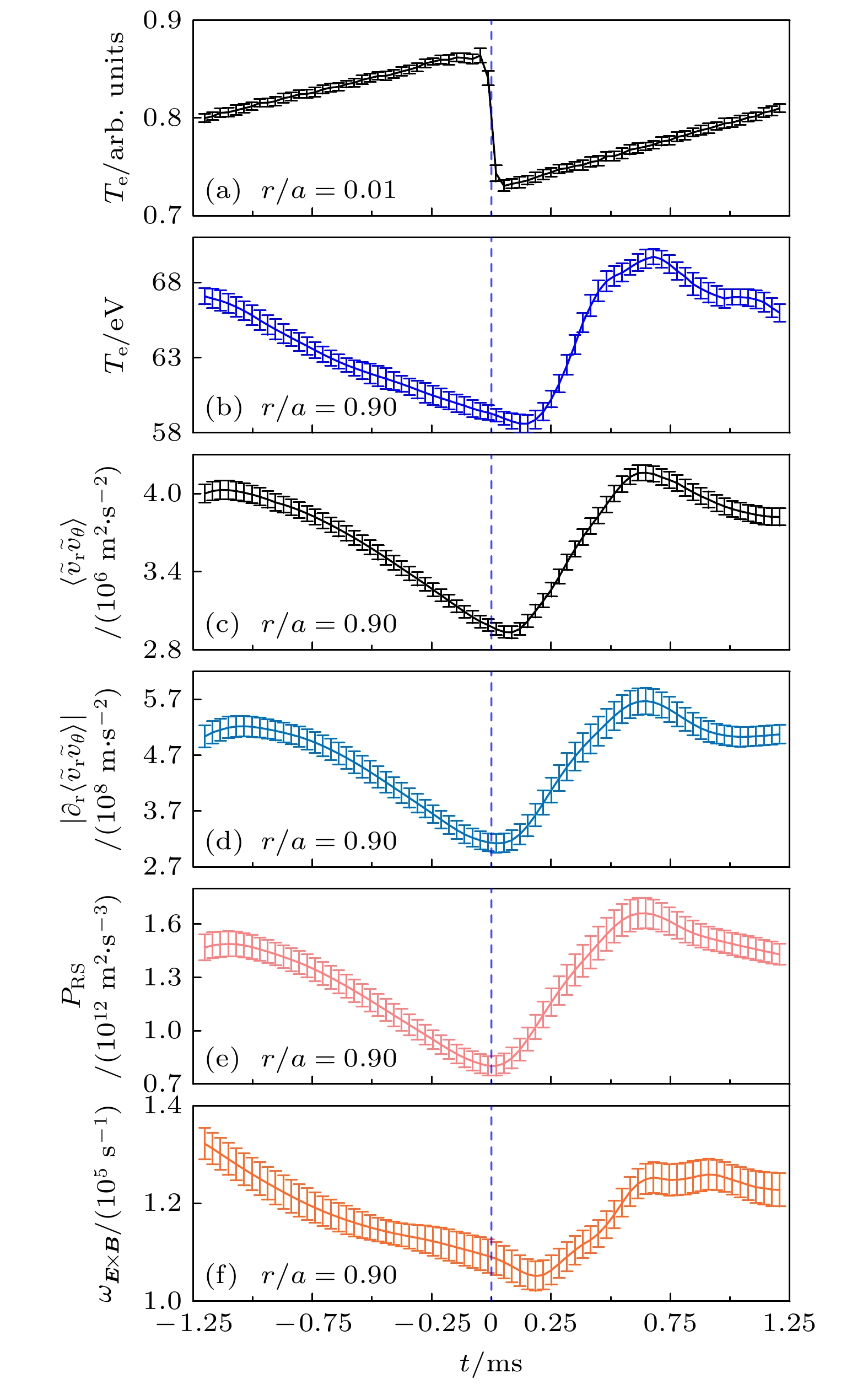
    • 欧姆放电中, 极向流主要源于湍流雷诺协强[26]. 雷诺协强可由$ \langle {\tilde{v}}_{\mathrm{{r}}} {\tilde{v}}_{\theta }\rangle $计算, $ {\tilde{v}}_{\theta } $为极向速度涨落. 雷诺协强的径向梯度可以引起极向动量的再分布, 从而产生极向流剪切[27]. 湍流通过雷诺协强向极向流能量转换的功率被称为雷诺功$ {P}_{\rm RS}= -\langle {\tilde{v}}_{\mathrm{{r}}} {\tilde{v}}_{\theta }\rangle \partial \langle {v}_{\theta }\rangle /\partial r $. 图8(c)—(e)分别给出$ r/a=0.90 $处雷诺协强、雷诺协强梯度绝对值和雷诺功, 可见锯齿崩塌0.6 ms后, 雷诺协强、雷诺协强梯度以及雷诺功都增强到最大值. 比较图8(b)、图8(d)和图8(f), 锯齿崩塌后, 雷诺协强梯度和剪切流达到最大值的时间要快于边缘电子温度达到最大值的时间, 约0.1 ms, 且与边缘湍流传播率的延迟时间相符. 这表明湍流传播对边缘雷诺协强及其梯度起到重要作用, 从而影响边缘极向剪切流.

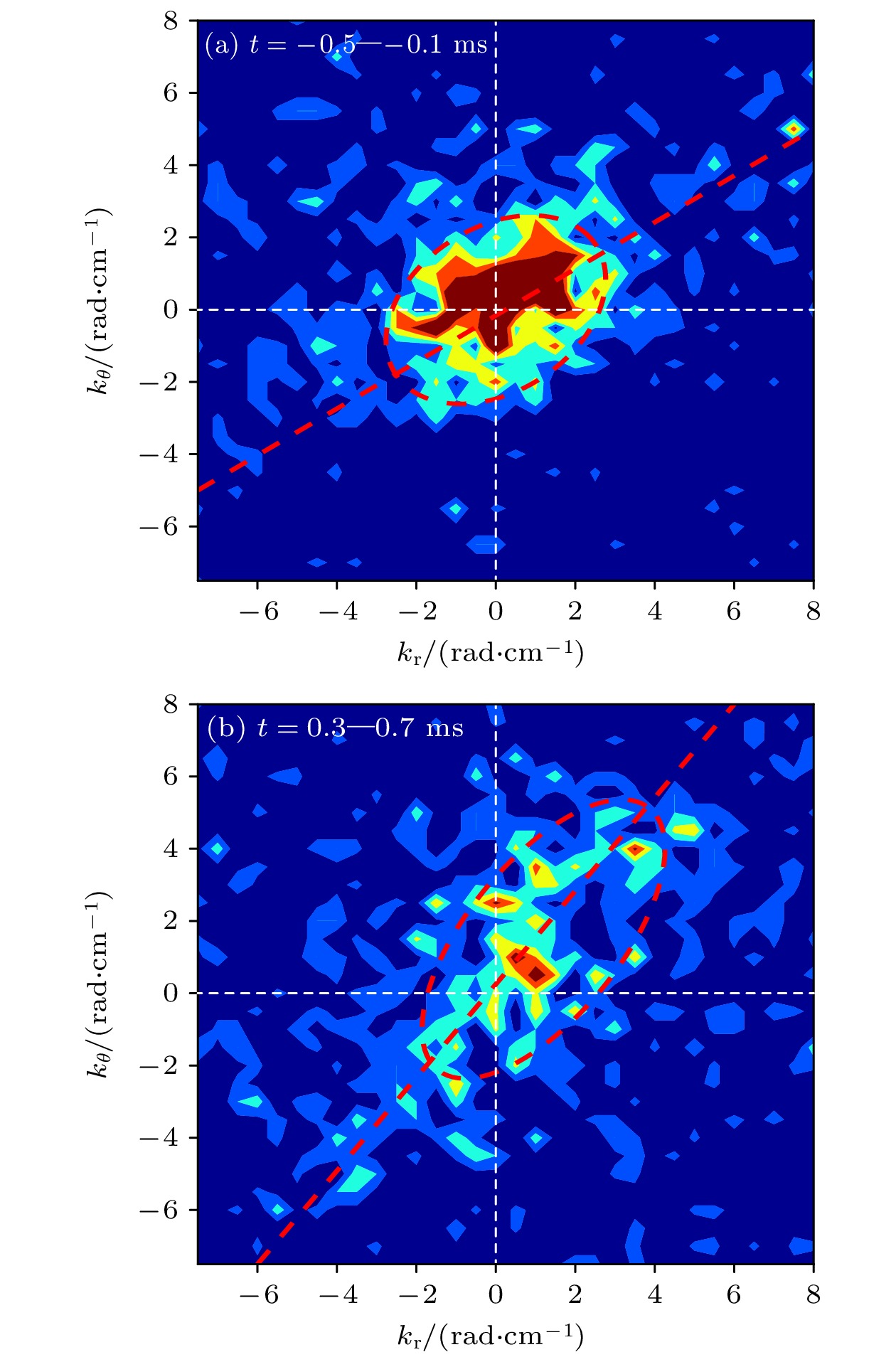
      湍流雷诺协强源于湍流波数谱的对称性破缺[28]. 雷诺协强$ \langle {\tilde{v}}_{\mathrm{{r}}} {\tilde{v}}_{\theta }\rangle \propto \langle {k}_{\theta }{k}_{{\mathrm{r}}}\rangle |\tilde{\phi }{|}^{2}/{B}^{2} $, $ {k}_{{\mathrm{r}}} $和$ {k}_{\theta } $分别为径向和极向波数, $ \tilde{\phi } $为电位涨落, B为磁场强度. 由公式可知, 当湍流涡旋几何结构对称时, 即$ \langle {+k}_{\theta }\rangle =\langle {-k}_{\theta }\rangle $时, 产生的雷诺协强为0. 当湍流涡旋的对称性几何被破坏, 即$ \langle {+k}_{\theta }\rangle \ne \langle {-k}_{\theta }\rangle $时, $ \langle {k}_{{\mathrm{r}}}{k}_{\theta }\rangle =\underset{}{{\displaystyle\sum }_{\boldsymbol{k}}}{k}_{{\mathrm{r}}}{k}_{\theta }|{\tilde{\phi }}_{\boldsymbol{k}}{|}^{2} \Big/{{\displaystyle\sum }_{\boldsymbol{k}}|{\tilde{\phi }}_{\boldsymbol{k}}{|}^{2}}_{}\ne 0 $, 才能产生非零的雷诺协强. 为研究雷诺协强的产生机制, 计算了湍流$ {k}_{{\mathrm{r}}} $和$ {k}_{\theta } $联合几率密度谱分布$ P\left({k}_{{\mathrm{r}}}, {k}_{\theta }\right)= {N}_{{k}_{{\mathrm{r}}}{k}_{\theta }}/{N}_{0} $, $ {N}_{{k}_{{\mathrm{r}}}{k}_{\theta }} $为落在($ {k}_{{\mathrm{r}}}, {k}_{{\mathrm{r}}}+\Delta {k}_{{\mathrm{r}}} $)和($ {k}_{\theta }, {k}_{\theta }+ \Delta {k}_{\theta } $)区间的事件数, $ {N}_{0} $为总事件数. 如图9(a)和图9(b)所示, 锯齿崩塌前, $ P\left({k}_{{\mathrm{r}}}, {k}_{\theta }\right) $沿径向方向伸长, 倾斜角度为30°, 更接近对称分布. 锯齿崩塌后, $ {k}_{\theta } $主要分布范围从$ -2—2\;{\mathrm{r}}{\mathrm{a}}{\mathrm{d}}{\cdot} {\text{cm}}^{-1} $变为$ -2—4\;{\mathrm{r}}{\mathrm{a}}{\mathrm{d}}{\cdot}{\text{cm}}^{-1} $, $ P\left({k}_{{\mathrm{r}}}, {k}_{\theta }\right) $沿极向方向伸长, 倾斜角度为50°, 主要在第一象限和第三象限分布, 且谱总体向正$ {k}_{{\mathrm{r}}} $方向移动. $ P\left({k}_{{\mathrm{r}}}, {k}_{\theta }\right) $变得高度倾斜且各向异性, 展示了强的不对称性. 这与锯齿崩塌后湍流产生更强的雷诺协强的结果一致.

    4.   总　结

    • 锯齿对磁约束边缘等离子体的约束性能和输运水平的影响一直是聚变领域的重要问题. 之前的研究主要集中在锯齿产生的温度、密度和梯度的传播. 事实上, 锯齿还可以诱发湍流脉冲传播至边缘, 影响边缘等离子体湍流和剪切流. 本文采用快速往复静电探针阵列首次观测了锯齿振荡期间湍流传播和对称性破缺对边缘湍流和剪切流的影响, 实验结果如下.

      1)锯齿振荡期间, 热脉冲和湍流脉冲从芯部传播至边缘等离子体, 且湍流在边缘的传播快于热脉冲. 锯齿崩塌后, 边缘湍流增强主要由边缘局域梯度驱动的湍流和从芯部传播至边缘的湍流脉冲两部分组成, 湍流传播快于驱动是湍流在边缘的发展快于热脉冲的重要原因. 湍流传播通量在边缘的发展同样快于湍流驱动的粒子通量, 这表明湍流能量的输运并不是简单的伴随湍流粒子输运.

      2)锯齿崩塌后, 边缘增强的湍流有助于剪切流的形成. 边缘径向电场的发展主要由极向流贡献. 极向流主要由湍流雷诺协强产生, 锯齿崩塌后, 湍流雷诺协强及其梯度都增强, 且它们的发展快于热脉冲, 表明湍流传播在其中起重要作用. 锯齿崩塌后, 湍流联合几率密度谱分布展示了强的不对称性, 这表明锯齿崩塌后湍流对称性破缺可以产生雷诺协强. 这一研究结果阐明湍流传播和对称性破缺对边缘等离子体流和湍流的作用过程. 该研究对理解等离子体约束和输运具有重要意义, 并为未来聚变堆的设计和运行提供参考.

    参考文献 (28)

目录

/

返回文章
返回