首页
登录
注册
-
量子密钥分发(quantum key distribution, QKD)的安全性建立在量子力学基本原理之上, 理论上具有无条件安全性[1–4]. 自首个QKD协议(BB84协议)提出以来, 研究人员在系统性能和系统复杂度等方面开展了广泛研究, 旨在推动其实用化进程. 系统性能通常以密钥生成率与传输距离的关系来衡量, 而系统复杂度则强调“越低越好”. 为此, 许多技术手段被相继提出, 以提高性能并简化系统, 例如诱骗态方法有效解决了光子数分离攻击[5,6], 测量设备无关QKD协议一次性关闭了所有针对探测端的攻击[7,8], 双场QKD协议可以使得密钥率以信道衰减的平方根线性下降, 从而进一步提升了密钥分发距离[9–13], 测量后配对QKD协议通过经典后处理实现时间复用以构建双光子贝尔态, 大大降低双场QKD系统的严格要求[14,15].
在QKD协议中, 后处理是影响协议安全密钥率的关键环节. 由于量子态制备不完美、参考系失谐、窃听者攻击等实际因素的存在, 导致双方的筛后密钥中不可避免地存在比特错误. 随着通信距离的增大, 系统的比特误码率也会显著上升. 在高误码率的情况下, 若直接进行纠错操作, 因大量密钥的消耗, 常常难以生成安全密钥. 为解决此问题, 优势提纯(advantage distillation, AD)方法通过将原始密钥分割成若干小块, 从中提取出高关联性的比特对, 从而降低误码率和提升安全密钥率. 该方法最初应用于经典密码中[16], Renner[17]将其引入QKD协议并进行了安全性分析. 此后, AD方法被应用于多种QKD协议以提升系统性能[18–21], 例如参考系无关QKD、测量设备无关QKD以及双场QKD等. 值得注意的是, AD方法主要在远距离通信中展现出显著的密钥增益, 而在密钥率低于10–10 bit/pulse量级的情况下, 相关数据的实验测量难度较大, 因此亟需高速且鲁棒的实验系统进行验证.
BB84协议是当前实用化程度最高的QKD协议, 相关研究已实现远距离[22]、高速率[23]及片上集成[24]的技术突破. 本文基于SiO2的非对称马赫-曾德尔干涉仪搭建了一套高速率实验平台, 验证了结合优势提纯的三强度诱骗态BB84协议. 与传统的光纤器件或块状光学器件相比, 基于SiO2的光子集成电路具有尺寸小、灵活性高、可实现大规模生产等优势, 且SiO2光波导芯片与光纤耦合损耗小、波导传输损耗低, 非常适合用于构建QKD系统[25–27]. 最终, 在50 km和105 km的传输距离下, 系统分别实现了104 kbits/s和59 bits/s的实时密钥率. 实验结果表明, 优势提纯方法显著提升了QKD系统在远距离下的密钥生成率. 这不仅验证了优势提纯的实验可行性, 也为该方法在更多QKD协议及应用场景中的推广奠定了坚实基础.
-
本节以信息论方法介绍加入优势提纯步骤后的协议安全性证明. 为此, 首先构建一个基于纠缠的等价协议, 在该等价协议中, Alice制备量子态
$ \left| {{\phi _0}} \right\rangle $ 并通过量子信道将第2个量子比特发送给Bob. Alice和Bob通过在Z基或X基下对量子比特进行测量获取密钥. 经过量子信道传输后, Alice和Bob最终共享的量子态为其中, 系数
${\lambda _i}$ 满足$ \displaystyle\sum\nolimits_{i = 0}^3 {{\lambda _i}} = 1 $ ;$ \left| {{\phi _0}} \right\rangle $ ,$ \left| {{\phi _1}} \right\rangle $ ,$ \left| {{\phi _2}} \right\rangle $ 和$ \left| {{\phi _3}} \right\rangle $ 是4种贝尔态,显然, Z基和X基的比特误码率分别满足
$ {\lambda _2} + {\lambda _3} = e_1^{\text{Z}} $ 和$ {\lambda _1} + {\lambda _3} = e_1^{\text{X}} $ 的约束关系. 最终, Alice和Bob共享的安全密钥率为其中
$ S({\text{A|E}}) = S({{{\mathrm{A}}, {\mathrm{E}}}}) - S({\text{E}}), {\text{ }}H({\text{A|B}}) = H({{{\mathrm{A}}, {\mathrm{B}}}}) - H({\text{B}}) $ ,$ S $ 和$ H $ 分别表示冯⋅诺依曼熵函数和二元香农熵函数.下面介绍优势提纯方法. 优势提纯能够从弱关联性的比特对中提取强关联性的比特对, 进而降低筛后密钥的比特误码率和提升安全密钥率.
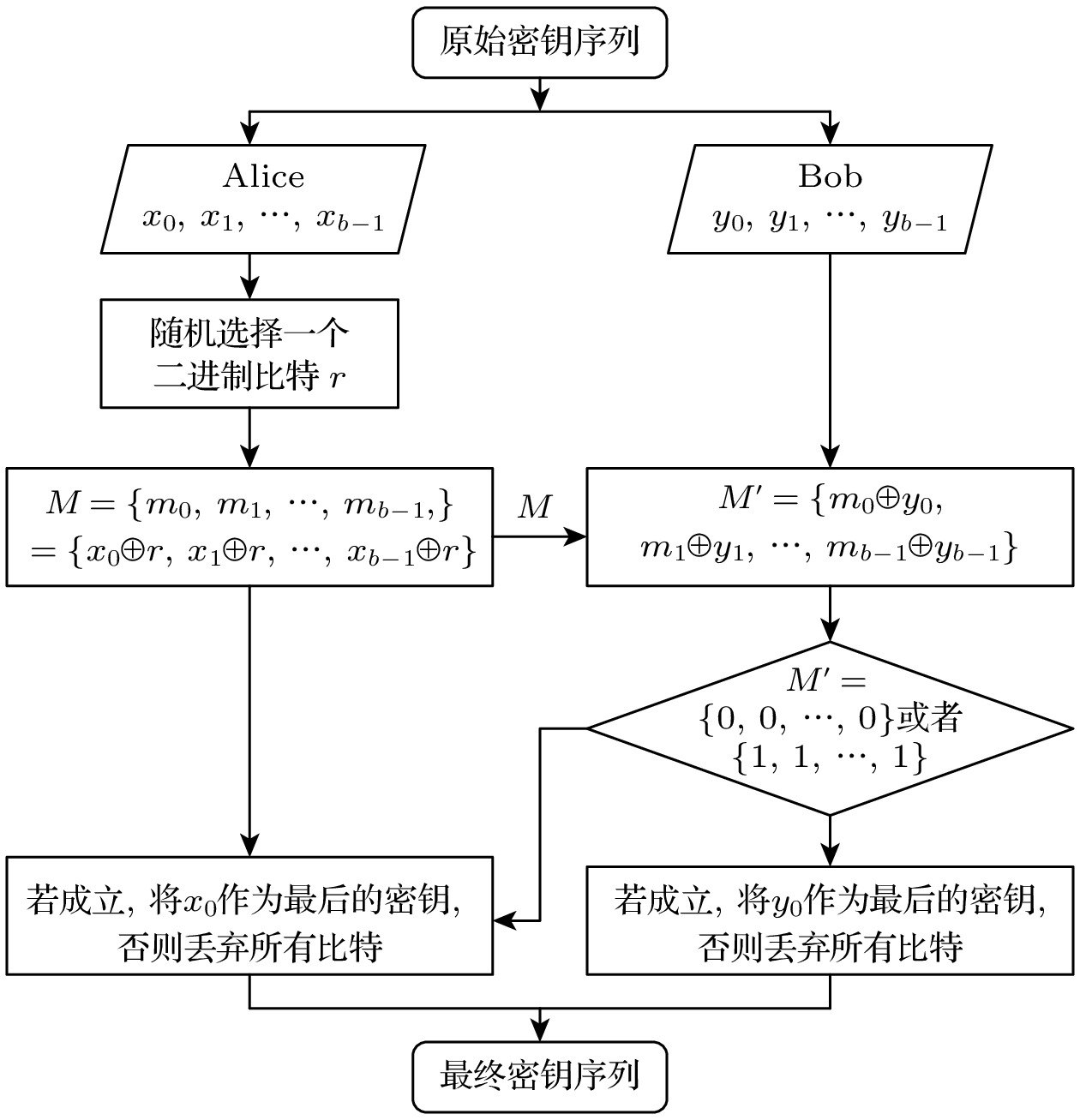
优势提纯方法的流程图如图1所示, 其核心思想为: 首先, Alice和Bob分别将自身的比特串划分为长度为
$b$ 的比特串, 分别定义为$ \{ {x_0}, {x_1}, \cdots {x_{b - 1}} \} $ 和$ \left\{ {{y_0}, {y_1}, \cdots {y_{b - 1}}} \right\} $ . 然后, Alice随机独立选择二进制比特$r$ 计算$ m = \left\{ {{m_0}, {m_1}, \cdots {m_{b - 1}}} \right\} = ( {x_0} \oplus r, \cdots {x_{b - 1}} \oplus r ) $ , 并将其发送给Bob; Bob接收到消息$m$ 后计算$ \left\{ {{m_0} \oplus {y_0}, {m_1} \oplus {y_1}, \cdots , {m_{b - 1}} \oplus {y_{b - 1}}} \right\} $ 的结果. 当且仅当该比特串为全0或全1时, Bob通知Alice此轮优势提纯成功, 双方仅保留$ {x_0} $ 和$ {y_0} $ 作为最终的密钥, 否则双方丢弃该段比特串.经过优势提纯后, Alice和Bob最终共享的量子态为
此时的安全密钥率为
对于(5)式可以这样解释: 由于量子信道可以由Eve控制, 因此她可以选择最优参数
${\lambda _i}$ 来降低密钥率; 而Alice和Bob可以通过优势提纯, 即选择最优参数$b$ 尽可能提升密钥率.对于使用相位随机化的弱相干源的三强度诱骗态BB84协议, 加入优势提纯后的安全密钥率为
其中的变量满足以下约束关系:
其中
$ Q_u^{\text{Z}} $ 为信号态的计数率,$ E_u^{\text{Z}} $ 为量子比特错误率,$ Y_1^{{\text{Z}}, L} $ 是单光子计数率的下界,$ e_1^{{\text{X}}, U} $ 是X基中的单光子误码率上界, 它们都可以通过诱骗态技术进行准确估计, 计算公式如下所示:式中,
$u$ 为信号态强度,$v$ 为诱骗态强度,${e_0}$ 为真空态的误码率, 一般取值0.5,${Y_0}$ 为暗计数率, 系统的整体效率可表示为$\eta = {\eta _{\text{d}}}{10^{ - \alpha L/10}}$ , 其中${\eta _{\text{d}}}$ 为探测效率,$\alpha $ 代表信道损耗系数,$L$ 是信道长度. -
为了验证优势提纯方法的可行性, 我们搭建了基于SiO2的非对称马赫-曾德尔干涉仪(asymmetric Mach-Zehnder interferometers, AMZI)的实验平台, 图2为其装置结构. Alice端使用中心波长为1550 nm的分布式反馈激光器产生相位随机化的弱相干脉冲, 激光器工作频率为625 MHz, 脉冲宽度为200 ps. 之后, 激光通过强度调制器(intensity modulator, IM)调制为不同强度的诱骗态信号. 调制后的光脉冲经过非对称马赫-曾德尔干涉仪进行相位编码, 并通过可调衰减器将光强衰减至单光子水平, 最终通过光纤量子信道发送到Bob端.
在Bob端, 量子信号首先进入具有相同臂长差的AMZI进行解调, 解调后的光信号由雪崩光电二极管探测器(avalanche photodiode detector, APD)进行探测. APD工作在门控模式, 探测效率为20%, 暗计数率为
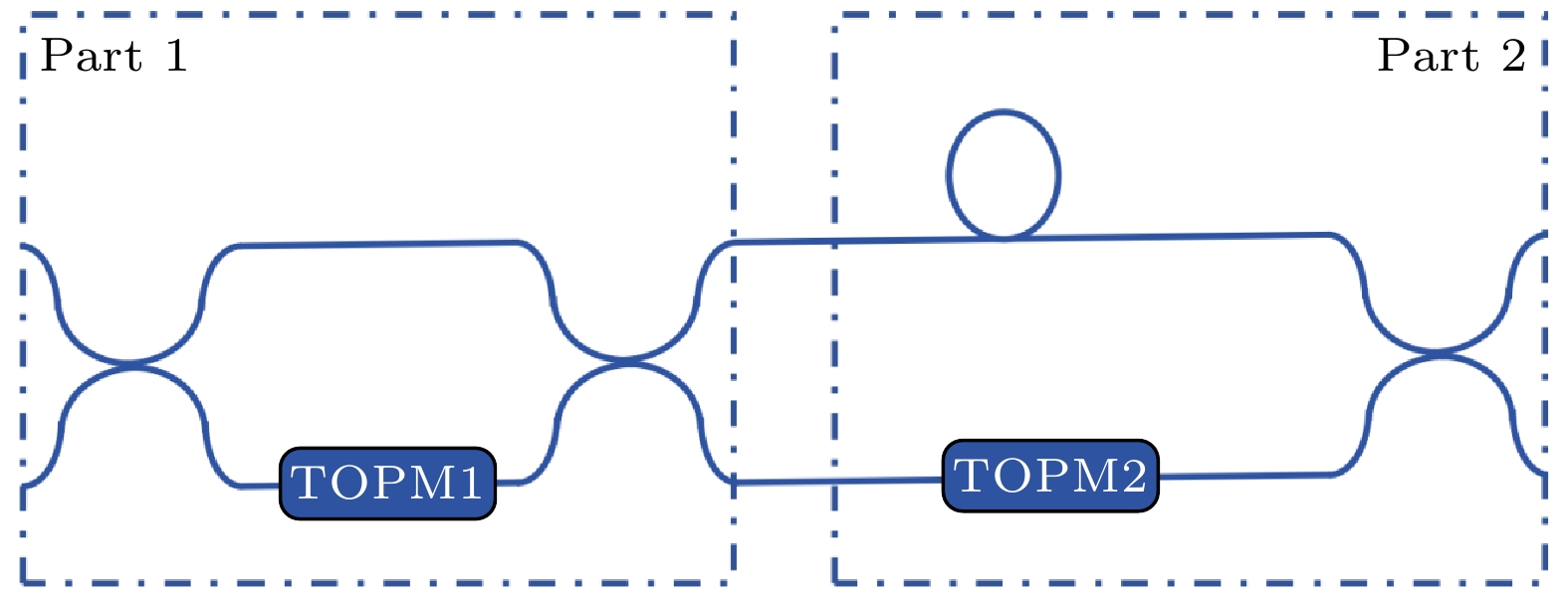
$ 3.2\times {10}^{-6} $ . APD将接收到的光信号转换为电信号, 并将其输出至时间数字转换器(time-to-digital converter, TDC)进行时间记录. 在整个实验过程中, 采用同一台任意波形发生器同步驱动激光器、强度调制器、APD以及TDC, 以确保实验信号的时序准确.AMZI芯片的结构如图3所示, 主要由等臂MZI和非等臂MZI两部分组成. 前者通过可调定向耦合器来实现光功率的平衡, 其中一臂配备有热光相位调制器(TOPM1), 用于补偿非等臂MZI中延迟线引入的附加损耗, 以确保输出的双脉冲功率达到平衡状态. 非等臂MZI部分则由一条由弯曲波导组成的长臂与一条直波导组成的短臂构成, 长臂用于产生400 ps的延迟, 短臂设有热光相位调制器2 (TOPM2), 用于相位调制, 实现量子态编码.
AMZI模块的实物图如图4所示, 其尺寸为
$ 30\;{\mathrm{ }}{\mathrm{m}}{\mathrm{m}}\times 7.8\;{\mathrm{ }}{\mathrm{m}}{\mathrm{m}} $ . 在测试过程中, 收发两端的AMZI都置于保温箱中, 以隔绝外部温度变化的干扰. 接收端(偏振控制器、AMZI模块、耦合头等)的整体损耗为6.2 dB. 二氧化硅PLC AMZI模块上的TOPM1和TOPM2电极通过电线连接到印刷电路板的垫片上. 引线由一个直流稳压电源供电, 以调节TOPM1和TOPM2的电压. -
系统参数总脉冲
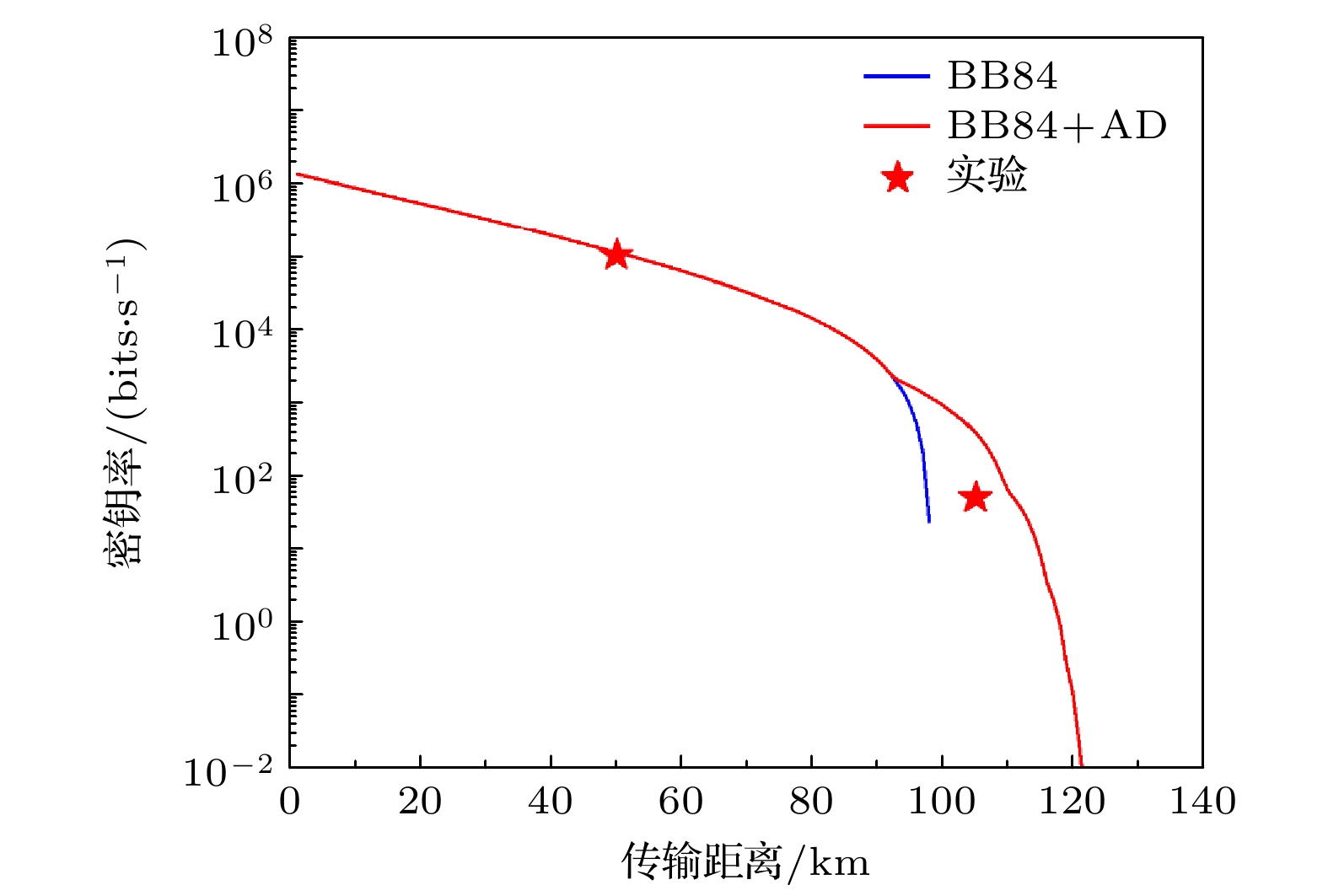
$N$ 为1011, 系统重复频率$f$ 为625 MHz, 衰减系数$\alpha $ 为0.2 dB/km, 本底误码${e_{\text{d}}}$ 为0.01, 探测效率${\eta _{\text{d}}}$ 为20%, 暗计数率${Y_0}$ 为$ 3.2\times {10}^{-6} $ , 纠错效率${f_{\text{e}}}$ 为1.16. 表1分别给出了在50 km和105 km传输距离下的理论数据以及实验数据. 通过对比可以看出, 在50 km传输距离下, 实验数据与理论数据基本上吻合, 说明系统性能在该距离下能够很好地预测理论数值. 然而, 在105 km传输距离下, 实验中测得的误码率略高于理论值, 因此导致最终密钥率较理论值有所降低. 这种差异主要源于长距离传输过程中光信号的衰减和系统噪声的累积, 导致量子比特误码率有所上升, 从而影响了密钥生成效率. 尽管在105 km时实验数据低于理论值, 但实验结果仍然证明了优势提纯技术在远距离量子密钥分发中的有效性, 为进一步优化QKD系统提供了宝贵的实验依据.图5为三强度BB84协议的理论仿真与实验密钥率的对比曲线. 其中, 蓝色实线代表原始BB84协议的密钥率曲线, 红色实线则代表加入优势提纯方法后的密钥率曲线, 而红色五角星则为实验结果. 可以看出, 在近距离处, 蓝色实线与红色实现基本重合, 表明在这种距离, 优势提纯方法并未提升密钥率. 50 km处的实验数据也与理论数值十分吻合, 验证了系统的可靠性. 然而, 随着传输距离的增加, 尤其在90 km之后, 原始BB84协议已经无法产生密钥, 而加入优势提纯方法后的BB84协议依然能够生成密钥, 且成码距离延长了约20 km. 在105 km的传输距离下, 密钥率达到了59.3 bits/s, 虽然略低于理论值, 但相比未使用优势提纯方法的情况(无法生成密钥), 实验结果清楚地展示了优势提纯方法在远距离量子密钥分发中提升密钥率的显著作用.
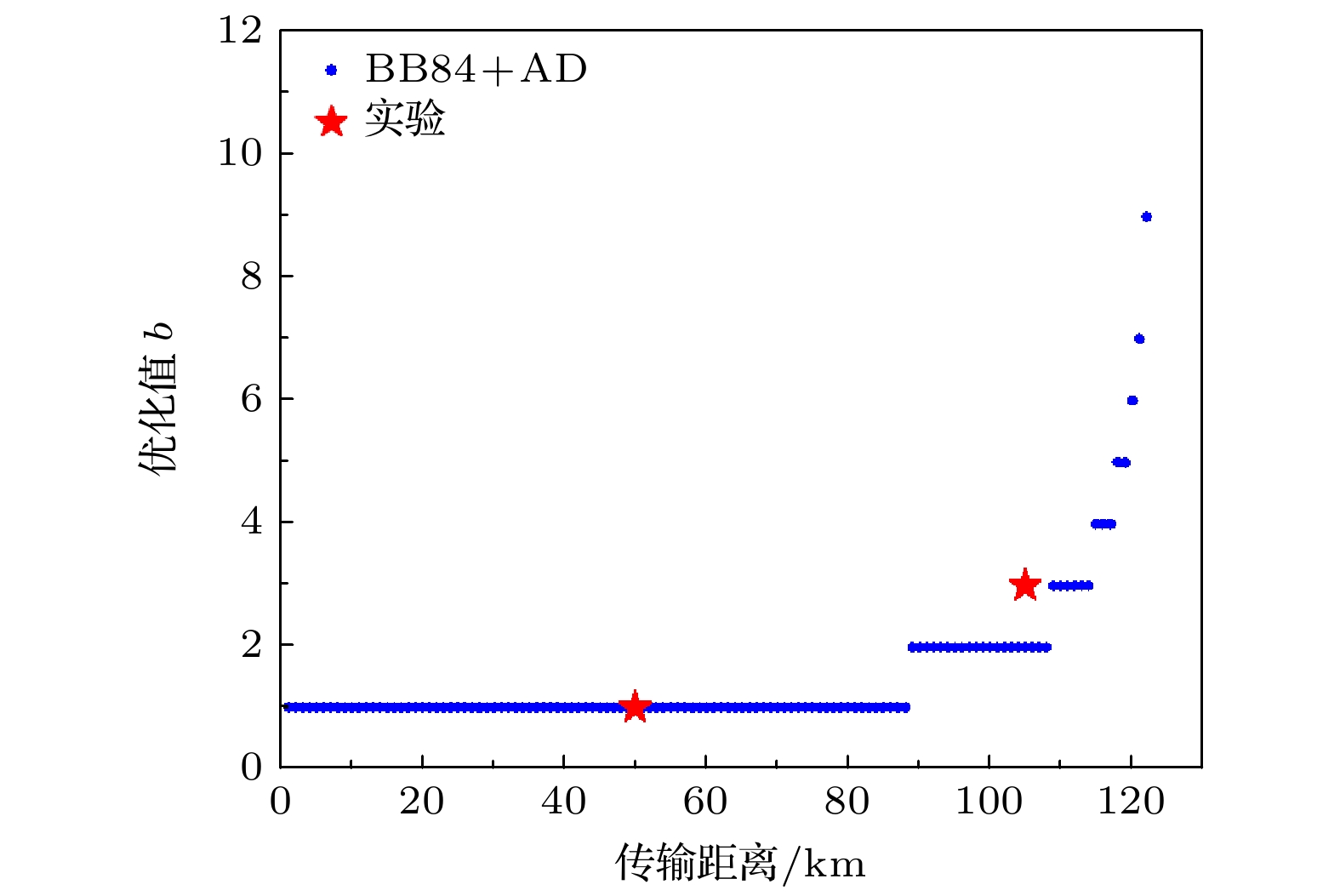
图6为在不同传输距离下最优参数b的变化趋势. 需要注意的是, 在105 km处, 基于实验数据优化得到的b值为3, 而理论仿真结果中的最优值为2. 该差异主要归因于远距离传输时信噪比的下降, 导致实际测得的比特误码率高于理论预期. 因此, 为了从弱相关性比特对中提取出高度相关的密钥信息, 实验中需要更大的比特序列长度b, 即从更多的比特中提取出有效的关联信息.
-
本文基于二氧化硅AMZI芯片搭建了BB84-QKD系统, 成功验证了优势提纯方法在实际QKD系统中的可行性. 通过对比分析50 km和105 km传输距离下的理论数据与实验数据, 我们发现, 优势提纯方法有效提高了三强度诱骗态BB84协议在远距离传输中的密钥生成率, 显著改善了系统的传输性能. 尤其是在105 km的长距离条件下, 尽管误码率略高于理论预期, 优势提纯方法仍然展现出了其提升密钥质量的显著效果. 此外, 得益于二氧化硅AMZI芯片的高集成度、低耦合损耗和低传输损耗等优势, 该系统在未来有望应用于大规模BB84-QKD网络中, 推动量子通信技术的实际部署与发展.
基于优势提纯技术的片上量子密钥分发实验验证
Experimental verification of on-chip quantum key distribution based on advantage distillation
-
摘要: 优势提纯提供了一种从弱关联性比特对中提取强关联性比特对的有效方法, 已被广泛应用于多种量子密钥分发协议. 然而, 该方法的增益效果主要体现在远距离密钥传输中, 目前在实验系统中尚未得到充分验证. 本文将优势提纯方法应用于三强度诱骗态BB84协议, 并基于SiO2的非对称马赫-曾德尔干涉仪构建实验平台进行验证. SiO2光波导芯片具有低耦合损耗和低波导传输损耗的优点. 实验结果表明, 在105 km的传输距离下, 系统安全密钥率达到了59 bits/s, 充分证明了优势提纯方法在提升量子密钥分发系统性能方面的重要作用.Abstract: Quantum key distribution (QKD) has been extensively studied for practical applications. Advantage distillation (AD) represents a key technique to extract highly correlated bit pairs from weakly correlated ones, thus improving QKD protocol performance, particularly in large-error scenarios. However, its practical implementation remains under-explored. In this study, the AD is integrated into the three-intensity decoy-state BB84 protocol and its performance is demonstrated on a high-speed phase-encoding platform. The experimental system employs an asymmetric Mach-Zehnder interferometer (AMZI) fabricated on a silicon dioxide optical waveguide chip for phase encoding, which is benefited from its low coupling loss and minimum waveguide transmission loss. Phase-randomized weak coherent pulses, generated by a distributed feedback laser at 625 MHz, are modulated into decoy states of varying intensities. The signals are encoded via an AMZI and attenuated to single-photon levels before transmission. At the receiver, another AMZI demodulates the signals detected by avalanche photodiodes in gated mode. Experiments conducted at 50 km and 105 km demonstrate secure key rates of 104 kbits/s and 59 bits/s, respectively. The results at shorter distances closely match theoretical predictions, while slight deviations at 105 km are attributed to signal attenuation and noise. Despite these challenges, the results obtained at 105 km highlight the effectiveness of AD in enhancing secure key rates in the large-error scenario. This study confirms the potential of AD in extending secure communication range of QKD. By leveraging the high integration and scalability of silicon dioxide photonic chips, the proposed system lays a foundation for large-scale QKD deployment, paving the way for developing advanced protocols and real-world quantum networks.
-
Key words:
- quantum key distribution /
- advantage distillation /
- optical waveguide chip /
- decoy-state .
-
-
图 2 BB84 QKD系统实验装置结构示意图, 其中Laser为激光器模块, IM为强度调制器, AMZI为非对称马赫-曾德尔干涉仪, APD为探测器模块, TDC为时间数字转换器
Figure 2. Schematic diagram of the experimental setup for BB84 QKD system, where Laser is the laser module, IM is the intensity modulator, AMZI is the low-loss unbalanced Mach-Zehnder interferometer chip, APD denotes the avalanche photodiode detector module, and TDC is the time-to-digital converter.
图 3 非对称马赫-曾德尔干涉仪原理图
Figure 3. Schematic diagram of the asymmetric Mach-Zehnder interferometer.
图 4 非对称马赫-曾德尔干涉仪实物图
Figure 4. Physical picture of the asymmetric Mach-Zehnder interferometer.
图 5 基于AD技术的BB84协议的理论与实验密钥率对比图
Figure 5. Comparison between theoretical and experimental key rates of BB84 protocol based on AD technology.
图 6 基于AD技术的BB84协议的理论与实验最优值
$ b $ Figure 6. Theoretical and experimental optimal values
$ b $ of BB84 protocol based on AD technology.表 1 实验数据
Table 1. Experimental data.
50 km (10 dB) 105 km (21 dB) 类型 理论数值 实验数据 理论数值 实验数据 $u$ 0.66653 0.64151 $v$ 0.04537 0.07259 ${P_u}$ 0.97000 0.94795 ${P_v}$ 0.02190 0.03627 $ Q_{u} $ $ 7.195\times {10}^{-4} $ $ 7.1084\times {10}^{-4} $ $ 5.692\times {10}^{-5} $ $ 5.2736\times {10}^{-5} $ $ Q_{v} $ $ 8.006\times {10}^{-5} $ $ 7.5179\times {10}^{-5} $ $ 1.714\times {10}^{-5} $ $ 1.6844\times {10}^{-5} $ $ E_{u} $ $ 0.01403 $ $ 0.01220 $ $ 0.06510 $ $ 0.085985 $ $ E_{v} $ $ 0.04623 $ $ 0.05180 $ $ 0.1930 $ $ 0.2109 $ $ Y_{1} $ $ 9.481\times {10}^{-4} $ $ 8.756\times {10}^{-4} $ $ 7.719\times {10}^{-5} $ $ 7.7438\times {10}^{-5} $ $ e_{1} $ $ 0.02064 $ $ 0.02562 $ $ 0.0715 $ $ 0.0974 $ $ R $ $ 115700 $ $ 104260 $ $ 389.0636 $ $ 59.3501 $ 
下载: 导出CSV
-
[1] Bennett C H, Brassard G 2014 Theoret. Comput. Sci. 560 7 doi: 10.1016/j.tcs.2014.05.025 [2] Lo H K, Chau H F 1999 Science 283 2050 doi: 10.1126/science.283.5410.2050 [3] Shor P W 2000 Phys. Rev. Lett. 85 441 doi: 10.1103/PhysRevLett.85.441 [4] Mayers D 2001 Journal of the ACM 48 3 doi: 10.1145/382780.382781 [5] Wang X B 2005 Phy. Rev. Lett. 94 230503 doi: 10.1103/PhysRevLett.94.230503 [6] Lo H K, Ma X F, Chen K 2005 Phy. Rev. Lett. 94 230504 doi: 10.1103/PhysRevLett.94.230504 [7] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503 doi: 10.1103/PhysRevLett.108.130503 [8] Braunstein S L, Pirandola S 2012 Phys. Rev. Lett. 108 130502 doi: 10.1103/PhysRevLett.108.130502 [9] Lucamarini M, Yuan Z L, Dynes J F, Shields A 2018 Nature 557 400 doi: 10.1038/s41586-018-0066-6 [10] Wang X B, Yu Z W, Hu X L 2018 Phys. Rev. A 98 062323 doi: 10.1103/PhysRevA.98.062323 [11] Cui C, Yin Z Q, Wang R, Chen W, Wang S, Guo G C, Han Z F 2019 Phys. Rev. Appl. 11 034053 doi: 10.1103/PhysRevApplied.11.034053 [12] Curty M, Azuma K, Lo H K 2019 npj Quantum Inf. 5 64 doi: 10.1038/s41534-019-0175-6 [13] Ma X F, Zeng P, Zhou H Y 2018 Phys. Rev. X 8 031043 doi: 10.1103/PhysRevX.8.031043 [14] Zeng P, Zhou H Y, Wu W, Ma X 2022 Nat. Commun. 13 3903 doi: 10.1038/s41467-022-31534-7 [15] Xie Y M, Lu Y S, Weng C X, Yin H L, Chen Z B 2022 PRX Quantum 3 020315 doi: 10.1103/PRXQuantum.3.020315 [16] Maurer U M 1999 IEEE Trans. Inf. Theory 39 733 doi: 10.1109/18.256484 [17] Renner R 2008 Int. J. Quantum Inf. 6 1 doi: 10.1142/S0219749908003256 [18] Li H W, Zhang C M, Jiang M S, Cai Q Y 2022 Commun. Phys. 5 53 doi: 10.1038/s42005-022-00831-4 [19] Wang R Q, Zhang C M, Yin Z Q, Li H W, Wang S, Chen W, Guo G C, Han Z F 2022 New J. Phys. 24 073049 doi: 10.1088/1367-2630/ac8115 [20] Li H W, Wang R Q, Zhang C M, Cai Q Y 2023 Quantum 7 1201 doi: 10.22331/q-2023-12-06-1201 [21] Zhang K, Liu J, Ding H, Zhang C H, Wang Q 2023 Entropy 25 1174 doi: 10.3390/e25081174 [22] Boaron A, Boso G, Rusca D, Vulliez C, Autebert C, Caloz M, Perrenoud M, Gras G, Bussiѐres F, Li M J, Nolan D, Martin A, Zbinden H 2018 Phys. Rev. Lett. 121 190502 doi: 10.1103/PhysRevLett.121.190502 [23] Yuan Z, Plews A, Takahashi R, Doi K, Tam W, Sharpe A, Dixon A, Lavelle E, Dynes J, Murakami A, Kujiraoka M, Lucamarini M, Tanizawa Y, Sato H, Shields A 2018 J. Light. Technol. 36 3427 doi: 10.1109/JLT.2018.2843136 [24] Li W, Zhang L K, Tan H, Lu Y C, Liao S K, Huang J, Li H, Wang Z, Mao H K, Yan B Z, Li Q, Liu Y, Zhang Q, Peng C Z, You L X, Xu F H, Pan J W 2023 Nat. Photonics 17 416 doi: 10.1038/s41566-023-01166-4 [25] Zhang G W, Chen W, Fan-Yuan G J, Zhang L, Wang F X, Wang S, Yin Z Q, He D Y, Liu W, An J M, Guo G C, Han Z F 2022 Sci. China Inf. Sci. 65 200506 doi: 10.1007/s11432-022-3514-3 [26] Wu D, Zhang C X, Zhang J S, Wang Y, Chen W, Wu Y D, An J M 2024 Opt. Commun. 564 130597 doi: 10.1016/j.optcom.2024.130597 [27] Zhu J L, Zhou X Y, Ding H J, Liu J Y, Zhang C H, Li J, An J M, Wang Q 2025 Phys. Rev. A 111 012608 doi: 10.1103/PhysRevA.111.012608 -
图( 6) 表( 1)
计量
- 文章访问数: 89
- HTML全文浏览数: 89
- PDF下载数: 0
- 施引文献: 0