首页
登录
注册
-
半导体激光器自20世纪60年代问世以来, 经过了数十年的快速发展, 目前已得到广泛应用. 集成光电子技术的发展使得激光器能够与其他光电元件集成在同一芯片上, 提升了系统的整体性能和可靠性. 与其他激光源相比, 半导体激光器具有更小的尺寸、更低的成本、更紧凑的结构以及更稳定的性能. 在基于半导体激光的科学和应用研究中, 分布式反馈半导体激光器(DFB- SL)的线性和非线性动力学研究正在快速发展, 线性动力学主要集中在模式耦合和相干光谱特性方面; 而非线性动力学研究则聚焦于激光器产生的混沌行为、增益饱和效应以及多模态特性的优化, 这些研究结果也推动了激光器在复杂信息处理中的应用. 此外, 随着光通信、激光传感、生物医学等领域的发展, DFB-SL激光器的非线性动力学特性进一步引起了科学家的重视.
外部信号注入会对DFB-SL产生干扰, 使其产生丰富的非线性动力学态. 使DFB-SL产生非线性动力学态的主要结构有: 光反馈、电反馈、外部光注入、噪声引导等. 其中, 光反馈结构中可以通过激光器的输出延迟反馈回自身, 干扰激光器的输出, 引发稳态、多稳态以及混沌等多种非线性动力学态, 当反馈光达到一定强度后, 激光器各模式发生激烈的相互作用而导致相干崩塌, 激光器光谱、频谱演化为连续谱[1–3]. Lang和Kobayashi[4]提到当引入额外的自由度, 例如外部光反馈、外部光注入或外部光电反馈等时, DFB-SL能够产生复杂、高维和宽带的混沌输出, 从外腔结构的SL输出特性出发, 提出了差分速率方程理论模型. 对该速率方程模型的仿真能重现实验观察结果中的主要特征, 为后来研究添加附加自由度后激光器的动态特性奠定了坚定的理论基础. Soriano等[5]在通过引入附加自由度实现混沌信号输出的几种方法中, 选用外光反馈的半导体激光器, 因其结构相对简单且所需的元件较少, 因此被广泛应用. Saboureau等[6]提出了一种结合光电反馈和光注入的方法来控制半导体激光器(SL)动态输出的稳定性. 研究结果表明, 在适当的光反馈范围内可以显著扩大光注入锁定区域, 光电正反馈能够放大并稳定由光注入产生的皮秒脉冲序列. 通过调节SL的偏置电流和频率失谐, 可以有效控制脉冲的重复速率. Tang和Liu[7]对光电正反馈条件下的半导体激光器进行了理论和实验研究, 探讨了其多种动态特性. 结果表明激光器输出的动态行为与反馈延时密切相关, 载流子的弛豫振荡与光电反馈之间的相互作用是导致不同输出状态的主要原因. 此外, 在不同的光电反馈条件下, 激光器的输出可以从准周期振荡转变为混沌状态. 光反馈和电反馈在激光器产生非线性动力学态过程中扮演着至关重要的角色, 但二者工作机制并不相同, 目前多为对光、电反馈分别研究, 往往忽略二者之间的竞争关系对DFB-SL输出结果的影响. Hizanidis等[8]尝试用全光反馈和光电反馈相结合的方案组成的激光器系统, 达到了隐藏时延结构的目的并保证了系统的安全性. Chen等[9]采用了光电混合反馈的形式, 通过实验手段研究了光电共同反馈的DFB激光器产生单一频率的微波光子信号. 目前关于光电共同反馈的DFB激光器的研究大多依赖于实验数据, 研究重点多为其产生某一特定动力学态的应用, 缺乏相应的理论框架来解释这些现象. 这使得我们在理解光与电反馈如何共同作用于DFB-SL的非线性动力学时面临挑战. 理论模型的缺乏不仅限制了我们对激光器行为的预测能力, 也使得我们在设计和优化激光器时缺乏必要的指导.
本文对半导体激光器在外光反馈、电反馈作用下的各种非线性动力学行为进行数值模拟, 通过光谱和频谱对不同反馈强度下的非线性动态特征进行系统的观察与分析, 获得了输出特性随反馈强度变化的动力学态分布图. DFB-SL内部的非线性效应主要体现在激光器的工作状态和输出信号的特征上. 当激光器的工作点接近其阈值时, 激光输出的功率和输入电流之间的关系会呈现出复杂的非线性特性. 反馈强度和延迟时间的变化对激光器的输出特性有显著影响, 尤其是在电反馈强度、电反馈延迟时间和偏置电流等关键因素的作用下, 激光器的输出状态和性能会发生明显变化. 这些非线性现象的研究, 不仅可以帮助我们更深刻地理解激光器的物理机制, 也为其在实际应用中的优化与改进提供了理论基础.
-
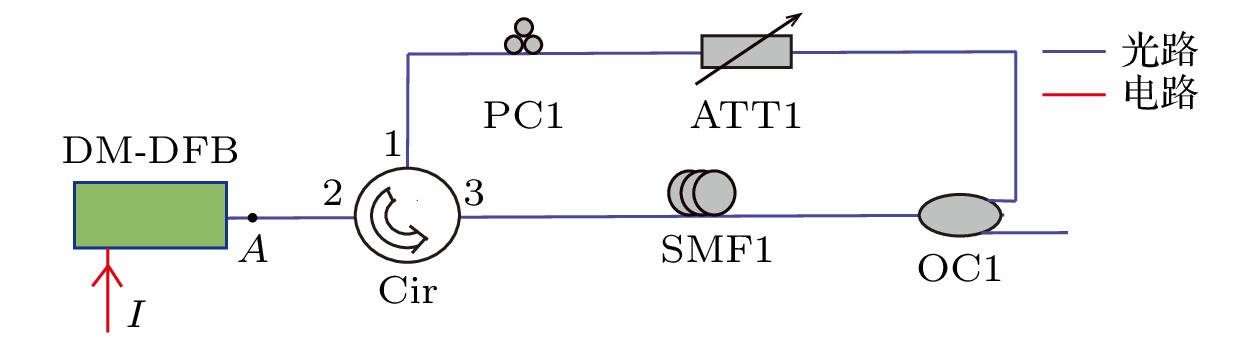
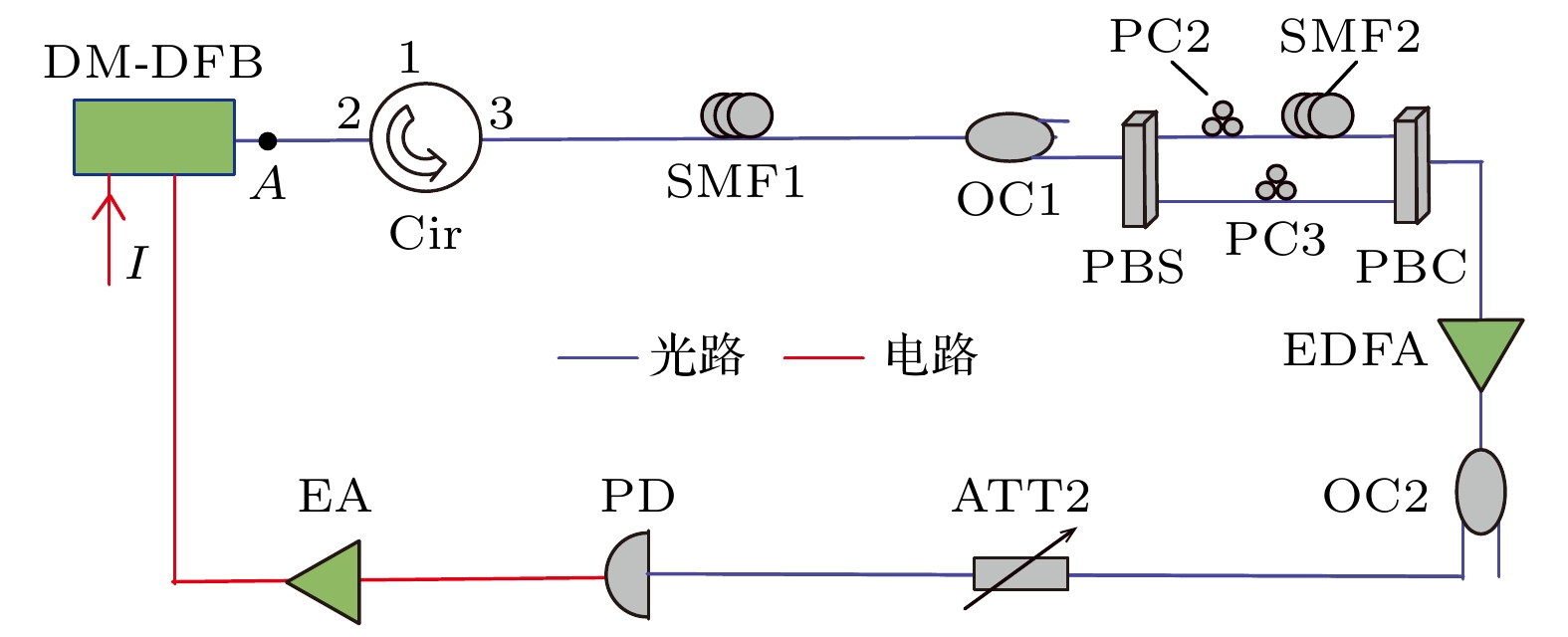
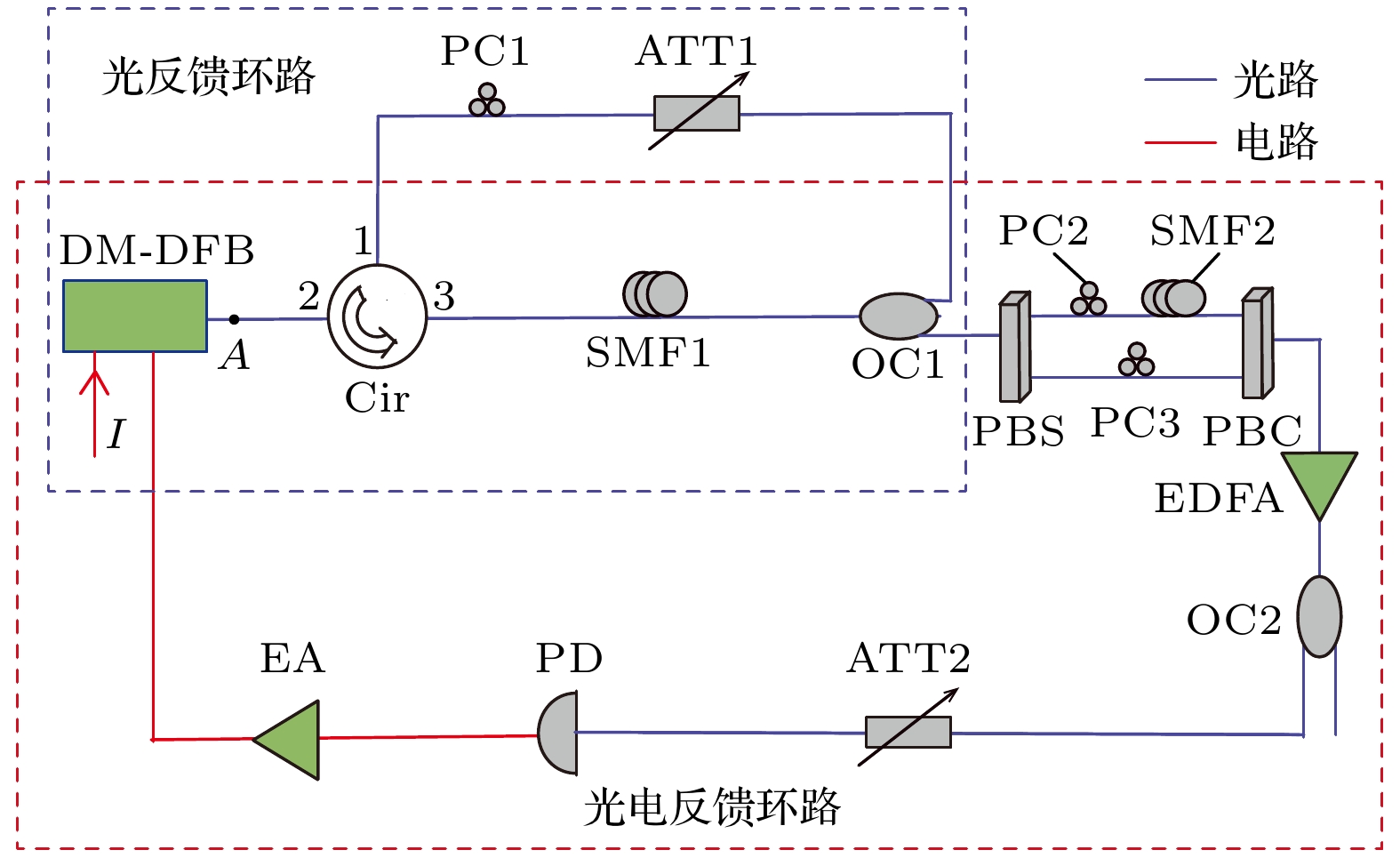
本文研究方案如图1所示, 主要包括全光结构与光电反馈回路两部分. DFB-SL是产生非线性动力学态的核心器件; 光纤环形器(Cir)用于构建自反馈环路与电反馈环路; 单模光纤(SMF)用于改变环长; 光耦合器(OC)用于构建光反馈和电反馈回路; 可变光衰减器(ATT)用于微调光功率, 改变耦合系数; 偏振控制器(PC)用于调整光场偏振; 偏振分束器(PBS)用于将入射光束分成两束正交偏振态的光; 偏振合束器(PBC)用于将两束正交偏振态的光耦合成一束光; 掺铒光纤放大器(EDFA)用于补偿信号衰减与信号放大; 光电探测器(PD)用于光电转换; 电吸收调制器(EA)用于提供电反馈增益.
在光电反馈条件下, 半导体激光器的动力学行为可由下列关于光子数
$ S\left( t \right) $ 、载流子数$ N\left( t \right) $ 、反馈光相位$ \varPhi \left( t \right) $ 随时间变化的方程组描述:式中
$\kappa $ 为光反馈强度, 表示图1中A点的反馈光强度与激光器出射光强度的分贝比;$\zeta $ 为电反馈强度, 是多个元件共同作用的结果, 其可以表示为:$\zeta = \mu \vartheta \chi \delta $ , 其中$\mu , \vartheta , \chi , \delta $ 分别为光纤损耗、EDFA的光增益、PD的光电转化效率、EA的电增益;$ \tau $ ,${\tau _{{\text{oe}}}}$ 分别为光、电反馈时间, 由光纤长度决定;$ I $ 为激光器偏置电流; 关于饱和增益因子、限制因子、自发辐射因子、激光器的中心频率和线宽增强因子等参数值主要来源于文献[2,6,7], 这些参数值涵盖了在实际应用中所需的典型商用器件的参数值范围; 微分增益、透明载流子数、阈值光子数和激光腔内反馈时间等参数值是基于本实验室使用的商用DFB激光器的规格说明书中获得的; 模型方程中用到的物理常数均为教材中通用数值; 式中的参数名称及其对应的取值在表1中列出.在上述方程组中, (1)式描述了光子数
$ S\left( t \right) $ 随时间的变化率, 第1项$ \varGamma \dfrac{{{G_{\text{N}}}\left[ {N\left( t \right) - {N_0}} \right]}}{{1 + \varepsilon S\left( t \right)}}S\left( t \right) $ 包括了由载流子增益和光子反馈引起的变化, 当载流子浓度高于阈值时, 会增加光子数, 而当光子数过多时, 会因为饱和效应而减小增益; 第2项$ - {{S\left( t \right)}}/{{{\tau _{\text{p}}}}} $ 表示光子的消耗; 第3项$ {{\varGamma \beta N\left( t \right)}}/{{{\tau _{\text{e}}}}} $ 表示载流子转化为光子的过程; 第4项$ 2\dfrac{\kappa }{{{\tau _{{\text{in}}}}}}\sqrt{S(t)S (t-\tau)} \cos [\theta (t)] $ 为延迟注入光与此时腔内光子的耦合. (2)式描述载流子数$ N\left( t \right) $ 随时间的变化率, 第1项$ {I}/{{\text{e}}} $ 表示注入偏置电流引起的载流子数的增加; 第2项$ \dfrac{I}{{\text{e}}}\dfrac{{\zeta S\left( {t - {\tau _{{\text{oe}}}}} \right)}}{{{S_0}}} $ 表示载流子数随时间的变化率受到光电延迟的影响, 当DFB-SL出射光强较大时, 延迟反馈光经光电转换后增强了反馈电流, 也即增加了注入的载流子数; 第3项$ - {{N\left( t \right)}}/{{{\tau _{\text{e}}}}} $ 表示载流子寿命引起的衰减; 第4项$ - \dfrac{{{G_{\text{N}}}\left[ {N\left( t \right) - {N_0}} \right]}}{{1 + \varepsilon S\left( t \right)}}S\left( t \right) $ 表示载流子因受激辐射而减小. (3)式描述了相位的变化率, 它与光子的增益和损耗有关, 相位的改变会影响激光器的干涉效果和输出光的波动特性. 当光子数增多(即增益大于损耗)时, 相位会变化得更快; 反之, 当光子数量减少时, 相位变化速度也会减慢.为了分析光电反馈下DFB-SL的各种动力学态, 用4阶龙格-库塔算法求解述微分方程组.
-
首先讨论只有光反馈的情况, 此时只有光的反馈影响. 通过观察时间序列、光子数与载流子数的关系图及相应的功率谱, 讨论激光器内部的机理; 再讨论只有光电反馈的情况(图中OC1上环路断开), 探究电注入对激光器的影响; 最后是光反馈和电反馈共同存在时的情况, 讨论光反馈与光电反馈的竞争机制.
-
图1中OC1下环路断开, 此时只有光反馈的回路, 如图2所示. 此时(2)式中光电反馈强度
$\zeta = 0$ . -
固定以下参数值:
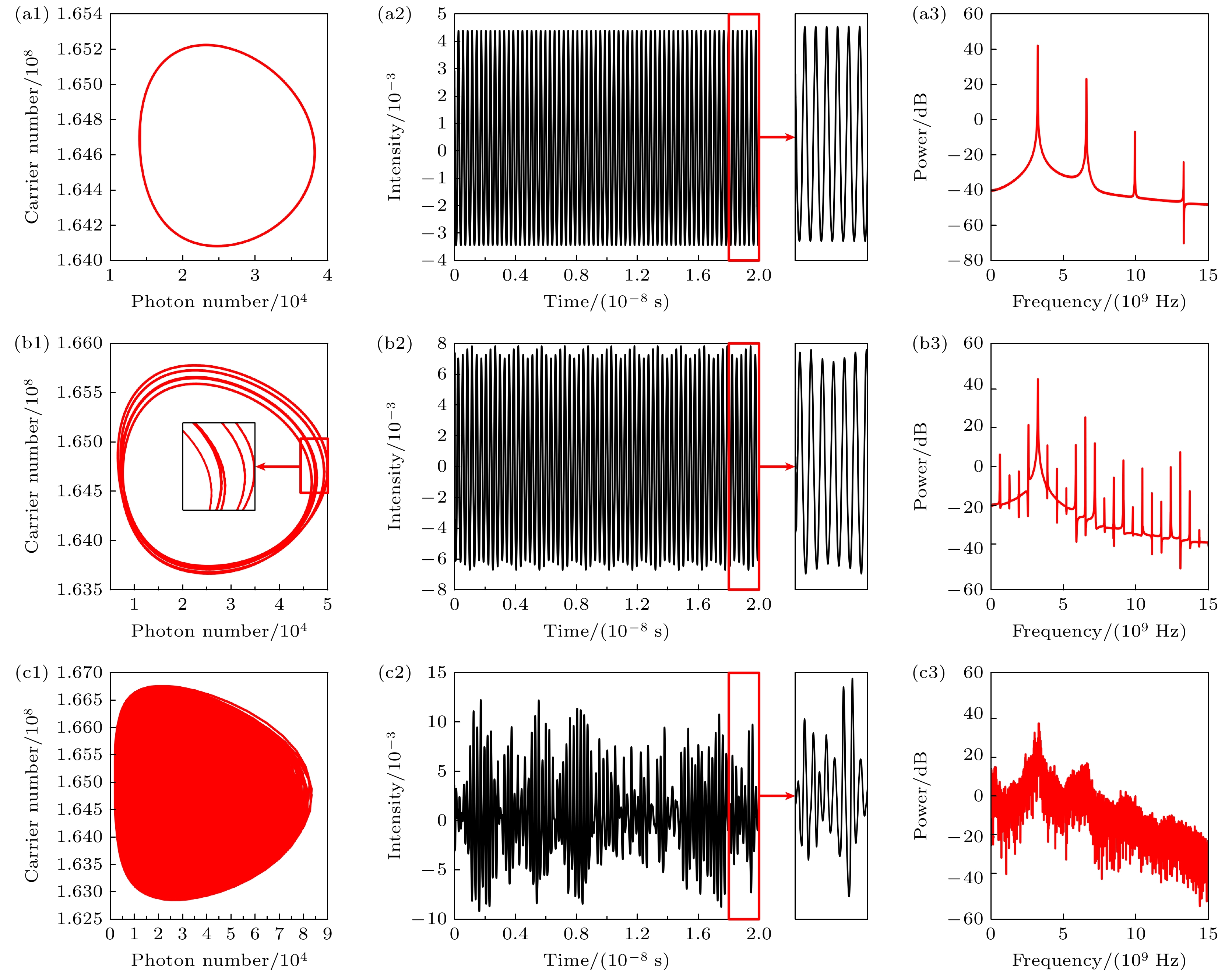
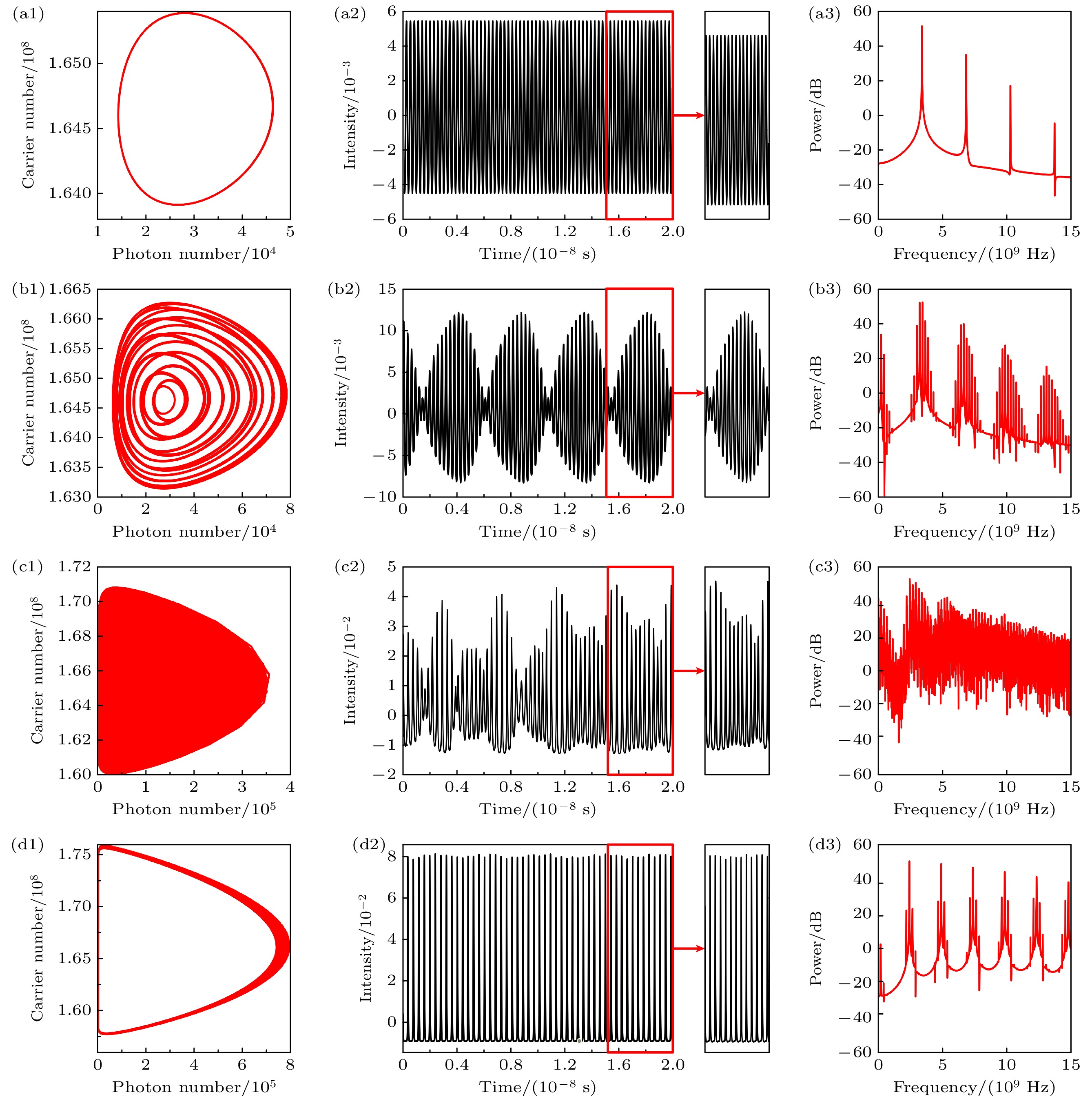
$\tau = 1 \times {10^{ - 9}}$ ,${\tau _{{\text{oe}}}} = 4 \times {10^{ - 9}}$ ,$I = 17 {\text{ mA}}$ . 改变光反馈强度$\kappa $ 分别为0.018, 0.044和0.059. 此时激光器腔内光子数与载流子数的关系图(S-N图)、激光器输出的时序图和频谱图如图3所示. 由图3(a)可以看出, S-N图只有一个环形轨迹, 对应的时序图为正弦型波, 每个波峰之间距离固定, 结合激光器功率谱中呈现出峰值频率$ {f_1} = 3.35 {\text{ GHz}} $ , 其他峰值为高阶频谱且功率低很多, 表明激光器处于单周期态. 图3(b)的S-N图具有5个闭合的环形轨迹, 时序图有明显的包络, 5个波峰为一个整体的周期, 其功率谱中, 对于同一阶次, 除f1频率成分外, 还包含了$ {f}_{2}=4{f}_{1}/5, {f}_{3}=3{f}_{1}/5, \;{f}_{4}=4{f}_{1}/5, \;{f}_{5}={f}_{1}/5 $ 频率成分, 表明激光器处于倍周期态. 从图3(c)可以看出, S-N图没有明显环路, 时序图杂乱无周期性, 功率谱几乎是连续的, 没有明显频谱分量, 表明激光器已经进入了混沌态.随着反馈强度的增大, 反馈光与腔模式的竞争变得更加剧烈, 导致激光器内部的光场和载流子浓度发生激烈变化. 在低反馈强度下, DFB-SL表现为稳态, 类似于自由输出, 输出光功率稳定且无明显波动. 当反馈强度增大到一定水平时, 激光器开始进入单周期状态. 在这个状态下, 输出信号呈现出规律性的波动, 频谱中出现一个主峰, 这个主峰对应着激光振荡的频率. 原因在于, 反馈光的引入打破了原本的稳定性, 以弛豫振荡为种子的模式被增强, 导致其输出出现周期性变化. 进一步增加反馈强度, 激光器可能会经历倍周期分叉. 这一现象表现为输出信号的频谱中出现多个谐波成分, 例如在基频(
$ {f_1} $ )之外, 出现频率为$ {f_1}/5 $ 的分量. 这种倍周期状态的形成源于内腔模式与反馈光之间的相互作用, 使得激光器出现新的、更复杂的振荡模式. 当反馈强度达到某个临界值, 激光器输出会经历相干崩溃, 最终演变为宽谱混沌状态. 在这个状态下, 频谱显示出几乎连续的状态, 没有明显的周期性特征. 混沌的出现是因为反馈光的强度已经使得激光器内不同模式间的竞争优势不易确定, 激光器输出变得极其复杂和混乱, 表现出混沌行为. 需要说明的是该混沌行为对初始条件很敏感, 该激光器的混沌状态可以被同步, 这与噪声展现出的随机性不一样[10]. -
固定以下参数值:
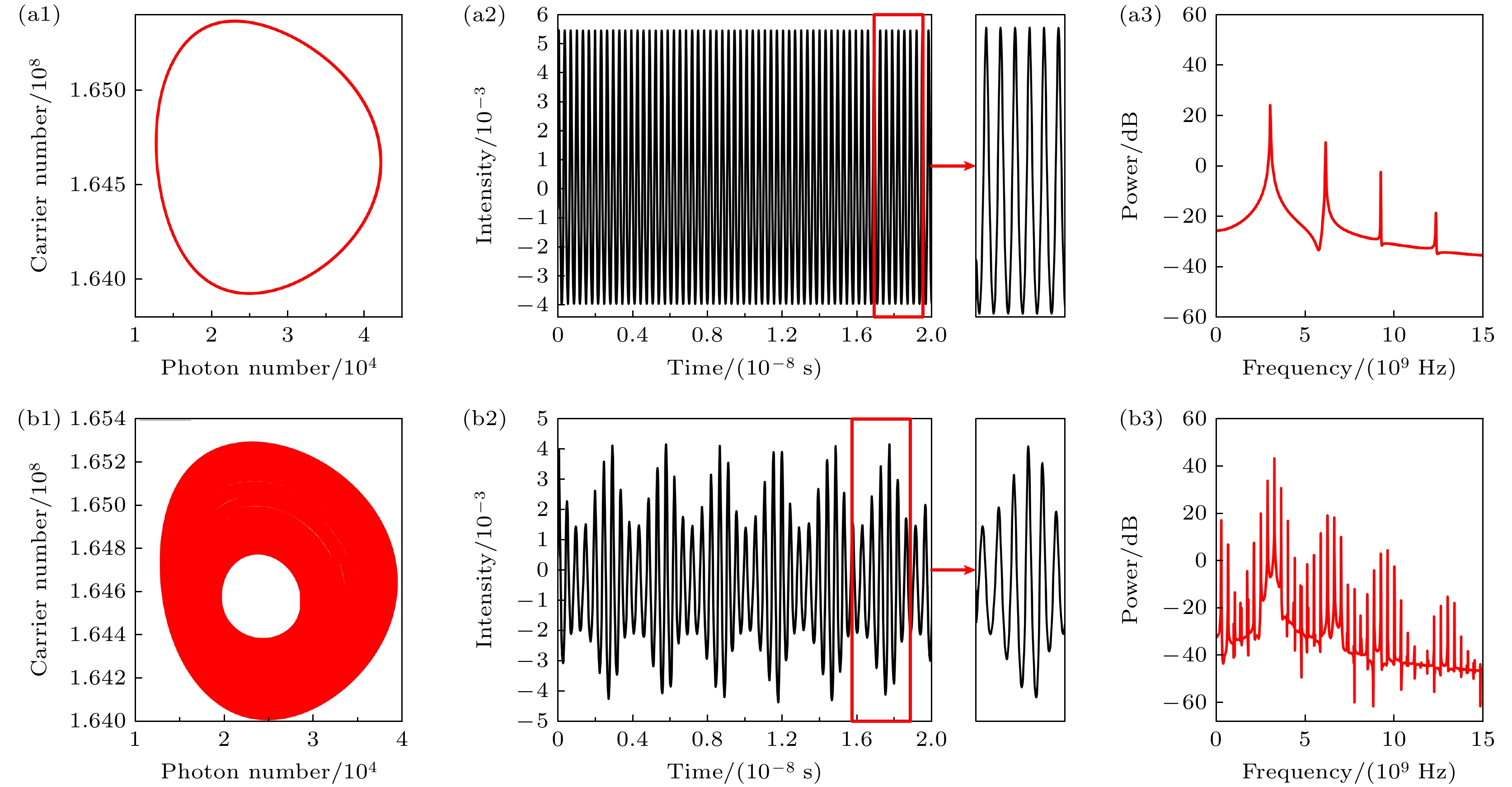
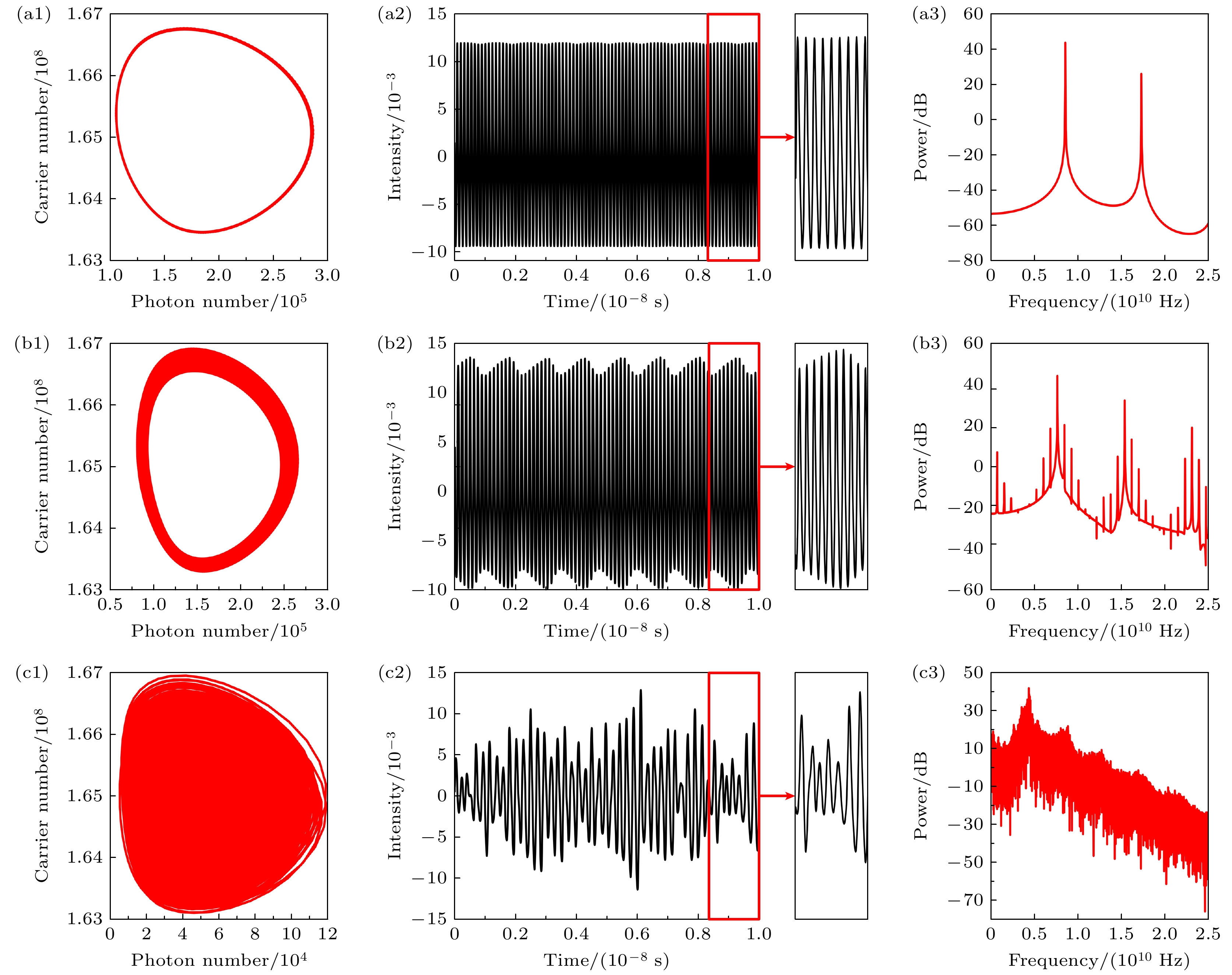
$\kappa = 0.02$ ,${\tau _{{\text{oe}}}} = 4 \times {10^{ - 9}}~{\text{s}}$ ,$I = 17\; {\text{mA}}$ . 设置光反馈时间$\tau $ 分别为2.18, 2.21 ns. 此时激光器腔内S-N图、激光器输出的时序图和频谱图如图4所示. 由图4(a)可以看出, S-N图只有一个环形轨迹, 对应的时序图为正弦型波, 没有明显的包络, 激光器功率谱同阶频率中只呈现出频率$ {f_1} = 3.0873\; {\text{GHz}} $ 的单峰, 表明激光器处于单周期态. 图4(b)的S-N图在一定范围内无法分辨内部结构, 或可视为较粗的一个环形轨迹, 时序图有明显的包络, 功率谱中的同阶频率中, 除$ {f_1} $ 频率成分外, 还包含了复杂的频率成分, 表明激光器处于多周期的状态, 有多个模式影响.随着光反馈时间继续增加, 激光器所处状态由单周期与多周期之间交替出现, 分别类似于图4(a), (b). 在激光器中, 不同的模式之间会存在竞争关系. 不同的光反馈时间意味着不同长度光纤接入回路, 随着光纤长度的变化反馈信号的时间延迟引起相位变化, 将使得不同模式之间的竞争关系有显著改变. 光纤长度直接影响光信号在反馈回路中的传播时间和相位关系[11–13]. 反馈时间延迟影响了激光器的反馈光与腔内模式的相位匹配. 当反馈光的相位与腔内模式相位同步时, 激光器输出信号的单周期态会被增强, 且变得更稳定, 当然光纤长度变化改变了环路的振荡模式[14,15].
-
图1中OC1上环路断开, 此时只有光电反馈的回路, 如图5所示. 此时(1)式和(3)式中光反馈强度
$\kappa = 0$ .固定以下参数值:
$\tau = 1 \times {10^{ - 9}}{\text{ s}}$ ,${\tau _{{\text{oe}}}} = 4 \times {10^{ - 9}}{\text{ s}}$ ,$I = 17 {\text{ mA}}$ . 设置光电反馈强度$\zeta $ 分别为0.045, 0.0555, 0.0973和0.19. 此时激光器腔内S-N图、激光器输出的时序图和频谱图如图6所示. 从图6(a)—(c)可看出, 随着光电反馈强度的增大激光器输出逐渐从单周期振荡过渡到多周期振荡, 再演化成混沌态. 图6(d)的S-N图看上去为一个环形轨迹, 但与P1的S-N图不同. 此时, 当载流子数剧烈变化时, 光子数无明显变化, 随后达到稳态, 时序图的脉冲宽度会显著减小, 脉冲间隔则保持稳定. 这种现象说明激光器能够在极短的时间内释放出大量的光子, 形成高频率的脉冲输出, 功率谱出现多个频率峰值, 带宽明显增大, 表明激光器处于锁模的状态, 此时激光器内部的不同振荡模式具有确定的相位关系, 产生短脉冲激光输出[16].调节反馈电流的幅度可以改变激光器的输出功率. 当反馈强度增大, 输出可能会达到一个新的稳定点, 但如果反馈过强, 也可能导致输出不稳定. 电反馈可以调整激光器的偏置工作点, 这会影响到激光器的光输出模式, 从而可能出现稳态、周期性振荡或者混沌行为[17–19]. 在电反馈作用下, DFB-SL内部的动态行为可能会发生剧烈变化. 适当的反馈可以增强激光器的稳定性, 但如果反馈强度过大, 可能导致自激振荡的产生, 从而使得激光输出呈现强烈的波动. 非线性效应会随着反馈强度的改变而变化, 可能导致多模态振荡或混沌现象出现. 在高反馈强度情况下激光器的输出模式可能变得更加复杂. 不同模式之间的竞争会导致输出光的强度和频率产生变化, 甚至可能引起模式的跳变, 这种模态竞争可能影响信号的整体质量和稳定性. 对于强烈的电反馈可以使得不同模式之间的相位关系保持一致[20,21]. 通过调节反馈信号的相位, 可以确保多个模式在特定时刻相互叠加, 形成强脉冲. 强烈的电反馈也可以引入频率调制, 使得激光器的输出频率在一定范围内变化, 不同频率的光波在相位上会产生干涉效应, 因此导致脉冲的形成. 强烈的电反馈会抑制激光器的相位噪声和频率噪声, 从而提高输出信号的稳定性, 这种噪声抑制有助于维持锁模状态.
-
光电反馈时的结构如图1所示, 我们将研究不同光电反馈强度、反馈延迟时间和偏置电流对各种动力学态的影响.
-
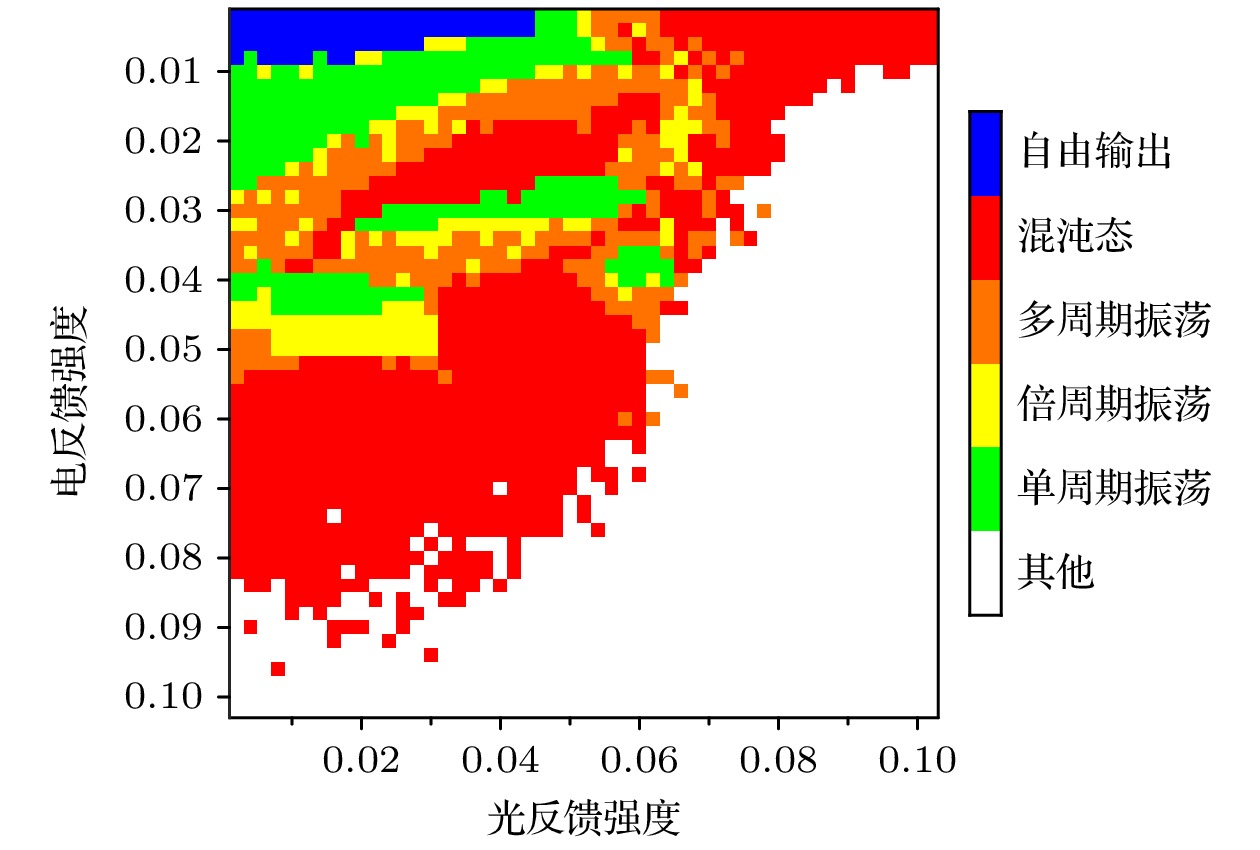
在图7中, 光、电反馈强度较低(
$\kappa \leqslant 0.06, 0.006 \leqslant \zeta \leqslant 0.05$ )时, 会出现P1、倍周期、多周期、混沌态之间的变化; 蓝色区域表示自由输出, 是因为在光、电反馈强度都小($\kappa \leqslant 0.06, \zeta \leqslant 0.006$ )时, DFB-SL接收到的反馈光、反馈电流很小, 不足以使激光器内部产生动力学变化; 白色区域受放大器增益、光纤耦合效率等实验的条件影响, 超出了参数允许范围, 本文不予讨论. 光、电反馈强度较高时, 激光器的输出为混沌态. 光反馈可以增强激光器的单周期振荡. 事实上, 反馈的光信号可能与腔模相干涉, 导致相位变化, 进而影响输出光的稳定性和强度. 电反馈可以通过调节激光器的驱动电流等参数, 实现对输出功率、谱宽和波长控制, 能够提高激光器的频率稳定性和抗扰动能力. 电反馈有助于抑制激光器输出的相位噪声, 从而增强信号的信噪比和稳定性. 当光反馈过强时, 可能引发激光器的自激振荡或产生不稳定的输出, 此时电反馈则可以通过调整增益或抑制噪声来恢复系统的稳定. 当反馈参数设置值在某些特定情况下, 光和电反馈之间的竞争可能导致激光器从稳定模式转变为混沌状态, 造成输出光强度和波长的剧烈波动. -
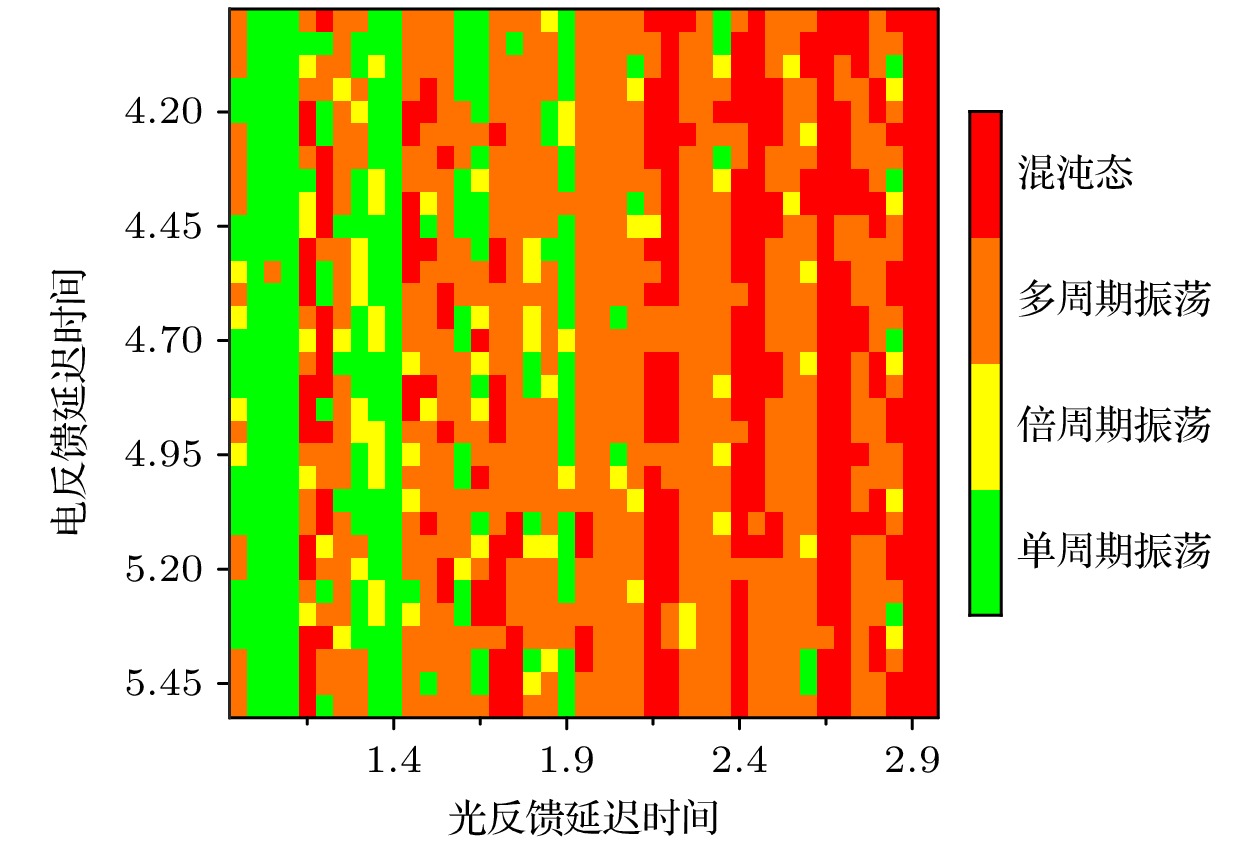
从图8可知, 单独改变光、电反馈延迟时间会有动力学态的变化, 但在一定条件下(如:
$\tau = 1.1 {\text{ ns, }} \tau {\text{ = 2}} {\text{ ns}}$ ), 只改变电反馈延迟时间激光器输出的动力学态不变, 均为P1或多周期态, 这与不同反馈延时引起的相位变化有关.光反馈和电反馈之间的相互作用影响到激光器的输出特性. 当二者的延迟时间相匹配时, 增强反馈能够稳定输出; 延迟时间不匹配时, 增强反馈可能引发混沌或不稳定状态. 混沌系统对初始条件极为敏感, 这种敏感性导致了轨道的不可预测性, 以及在相空间中轨迹的复杂性. 混沌谱中的特征包括: 非周期性、对周期或初始条件的小变化产生剧烈影响. 激光器的混沌特性可以应用于信息加密和信号处理(如混沌通信), 提高信息传输的安全性, 利用混沌激光器的高灵敏度, 其还可以用于化学传感器和环境监测等领域, 以检测微小的变化. 在单周期状态下, 激光输出表现为稳定的周期性波形, 这种状态易于控制与预测, 输出光强通常在固定的时间间隔内重复, 单周期激光信号可以用于高精度测量和通信时钟, 重力波探测、干涉测量等领域. 在激光加工和切割中, 提供稳定的激光输出能够增强加工精度和效率, 在光通信系统中, 单周期激光器可以用于信号的准确时序和调制, 确保信息的可靠传输.
图7和图8中, 多周期部分周期个数并不相同, 对比图6(b)与图4(b)可知, 多周期个数不同, 二者光反馈强度、光电反馈强度、电反馈延迟时间均不同, 改变部分参数可以达到改变多周期个数的效果, 但只通过单一参数, 无法改变多周期个数. 在激光器中, 反馈光一方面增强受激辐射, 另一方面在腔体内与新产生的光相互作用. 它们的相位关系会导致干涉现象的出现, 可能形成增强或减弱的效果. 这种干涉和叠加效应实际上是光波相位稳定性的基础. 在电反馈回路中, 激光器输出光强度被转化为电信号后再被反馈注入到激光器中, 从而影响激光器内部载流子. 这两种反馈机制的相互作用下, 激光器的输出特性变得更加复杂. 单一参数的变化(例如偏置电流大小), 往往不会导致输出周期数的显著变化. 这是因为激光器的输出不仅依赖于电流, 还受到腔内光波相互作用的影响. 同时改变多个参数, DFB激光器的输出才会产生预期的动力学态. 同时调整光反馈和电反馈可以更有效地控制激光器的增益和相位, 从而实现更精确的多周期个数调节. 通过调整延迟时间和光反馈, 可以改变激光器的谐振条件, 使得多周期个数的变化更加明显. 在实际应用中, 通过综合调节光反馈、电反馈和延迟时间等参数, 可以实现对激光器输出特性的精确控制进而改变多周期个数.
-
固定以下参数值:
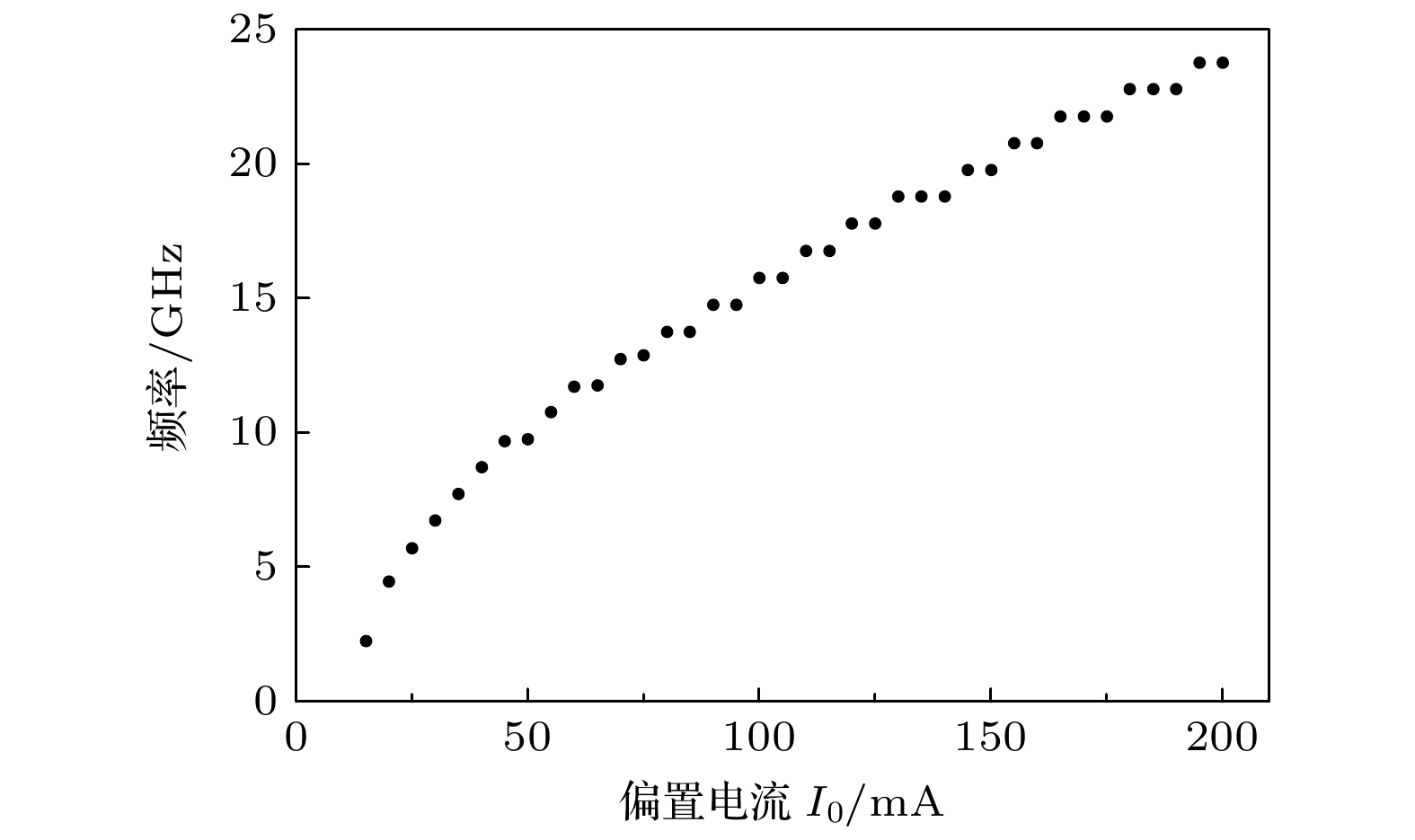
$\kappa = 0.08$ ,$\zeta = 0.01$ ,$\tau = 1 \times {10^{ - 9}}{\text{ s}}$ ,${\tau _{{\text{oe}}}} = 4 \times {10^{ - 9}}{\text{ s}}$ . 设置偏置电流$I$ 分别为40, 36和20 mA. 此时激光器腔内S-N图、激光器输出的时序图和频谱图如图9所示. 从图9(a)—(c)可看出, 随着偏置电流的逐渐增加DFB-SL可混沌态过渡到单周期态.这一变化主要归因于偏置电流的大小对增益系数和损耗之间平衡关系的显著影响. 当偏置电流处于较低水平时, 激光器的增益不足以有效抵消光腔内部的损耗, 此时激光器无法维持稳定的振荡输出, 输出的光信号在相位和幅度上表现出高度的混沌特征. 这种不稳定现象主要是由非线性相位-幅度耦合效应引起的. 在增益低于一个特定阈值时, 系统变得格外敏感, 容易受到外部干扰的影响, 这种影响进一步加剧了不确定性, 导致混沌状态的出现. 在这种状态下, 光的相干性显著降低, 激光器的输出光强度变得不稳定, 可能会在不同的模式之间快速切换. 此时激光器内载流子和光子状态极不稳定, 容易受到外界影响, 这使得激光器产生了一种难以预测的多种动力学态竞争的情况. 随着偏置电流的进一步提高, 增益逐渐增强, 载流子弛豫振荡起主导作用, 动力学态最终成为主导, 激光器表现为稳定的单周期状态. 需要说明的是, 随着偏置电流的增大单周期态的频率也随之增大, 如图10所示, 这一现象可能是多种物理机制作用的结果. 这是因为增大偏置电流会直接导致半导体激光器中载流子浓度的显著增大. 载流子浓度的提升不仅增大了激光增益, 还会引入光程差从而使腔模出现蓝移, 导致激光发射频率的提升.
-
光、电反馈DFB激光器在调制性能上表现优异, 可以通过调节光反馈和电反馈的多个参数, 灵活地调整激光器的工作波长, 可以集成多种反馈机制, 减少对复杂外部设备的依赖, 在面对外部干扰时表现出更强的抗干扰能力.
光反馈式DFB激光器在单周期应用中, 主要用于实现高稳定性和高精度的激光输出. 其工作原理是通过在激光器的有源区引入周期性的折射率变化, 形成光栅结构, 从而选择特定波长的光进行反馈. 这种单周期态的激光器能够在特定的工作条件下, 保持输出光的单模特性, 减少频率漂移, 广泛应用于光通信、传感器和精密测量等领域[22]. 相比之下, 光电反馈机制结合了光反馈和电反馈的特性, 使得激光器在动态响应和稳定性方面表现更佳. 光电式DFB激光器能够在更广泛的操作条件下保持输出的稳定性, 并且在面对外部扰动时, 能够迅速调整其输出特性. 在量子计算和量子通信领域, 多周期输出能够生成多种量子态, 支持量子比特的操作和传输, 推动量子技术的发展[23]. 电反馈式DFB激光器通过电流反馈实现激光输出的精确控制, 能够在量子态的生成和操控中提供稳定的激光源, 这对于量子比特的操作和量子态的测量至关重要. 然而, 光、电共同反馈式半导体激能够在更广泛的操作条件下保持激光的高稳定性和高效率. 这种激光器不仅提高了量子态的生成速率, 还增强了系统的抗干扰能力, 使其在量子通信和量子计算等前沿技术中展现出更大的应用潜力. 在混沌光通信中, 光反馈式半导体激光器由于其反馈机制的特性, 通常会引入时间延迟标签[24]. 这种时间延迟标签可能会影响信号的同步性和传输效率, 导致在接收端解码时出现困难. 而光电共同反馈式半导体激光器通过结合光反馈和电反馈的方式, 能够有效消除这种时间延迟标签. 光电共同反馈的机制使得激光器在生成混沌信号时, 能够实时调整反馈参数, 从而实现更快的响应和更高的信号稳定性. 这种特性在混沌光通信中尤为重要, 因为它不仅提高了数据传输的速度, 还增强了系统的抗干扰能力, 使得信息的传输更加可靠.
-
本文通过数值模拟的方法深入研究了DFB-SL在光反馈和电反馈作用下的各种非线性动力学行为. 研究结果揭示了不同的光、电反馈强度和延迟时间对激光器输出特性的显著影响, 特别是在光、电反馈强度, 光、电反馈延迟时间以及偏置电流等关键因素的作用下, 激光器的输出状态和性能会发生明显变化. 这些因素不仅影响激光器的稳定性和输出模式, 还可能导致复杂的动态行为, 如混沌状态或周期性振荡等. 在研究结果表明发现偏置电流对单周期信号频率的调谐性. 通过对这些非线性特性的研究, 本文为理解激光器在不同工作条件下的行为提供了重要的理论基础.
分布式反馈半导体激光器自延迟反馈下的非线性动力学态研究
Research on nonlinear dynamics of distributed feedback semiconductor laser under self-delayed feedback
-
摘要: 通过数值方法研究了自延迟光、电反馈作用下分布式反馈半导体激光器(DFB-SL)的各种非线性动力学行为. 结果表明, 在不同光反馈强度下DFB-SL输出呈现出单周期、准周期、多周期等多种非线性动力学态. 当外部光反馈达到一定强度后, 激光器输出表现为混沌态; 当光反馈强度较小时, 在不同的电反馈强度下DFB-SL输出也会出现多种非线性动力学态; 当光反馈强度较大时, 改变电反馈强度无法得到单周期的动力学态. 光反馈与电反馈延迟时间也对DFB-SL非线性动力学态有重要影响. 当二者的延迟时间相匹配时激光器的弛豫振荡被增强, 表现为单周期状态, 而在延迟时间不匹配的情况下, 可能引发混沌或不稳定状态. 偏置电流也会对动力学态产生影响, 但随着电流大小单向变化, 动力学态的演化方向不是单一的; 当DFB-SL处于单周期态时, 改变偏置电流会改变单周期振荡频率. 这些发现为自延迟反馈DFB-SL在微波光子信号处理和保密光通信等应用方面提供了重要理论基础, 也为各种非线性科学研究提供了实验手段.
-
关键词:
- 分布式反馈半导体激光器 /
- 自延迟反馈 /
- 非线性动力学态
Abstract: In this paper, various nonlinear dynamic behaviors of distributed feedback semiconductor laser (DFB-SL) subjected to self-delayed optical and electrical feedback are studied numerically. The results show that the DFB-SL output presents a variety of nonlinear dynamic states such as single-period, quasi-period, and multi-period under different optical feedback intensities. When the external light feedback reaches a certain intensity, the laser output enters a chaotic regime. When the optical feedback intensity is small, a variety of nonlinear dynamic states will appear in the DFB-SL output under different electrical feedback intensities. When the optical feedback intensity is large, the single-period dynamic state cannot be obtained by changing the electrical feedback intensity. The optical feedback and electrical feedback delay time also have a significant influence on the nonlinearity of DFB-SL. When their time delays match, the relaxation oscillation of the laser is enhanced and exhibits a single-period state. And time mismatch may lead to chaos or instability. The bias current also affects the dynamic state, however, the direction of evolution of the dynamic states is not unidirectional as the current changes unidirectionally. When the DFB-SL is in a single-period state, changing the bias current will result in the change of the single-cycle oscillation frequency. These findings provide an important theoretical basis for applying the self-delayed feedback DFB-SL to microwave photonic signal processing and secure optical communication, as well as experimental means for conducting various nonlinear scientific researches. -
-
图 1 DFB-SL自延迟光电反馈结构图
Figure 1. Diagram of the DFB-SL self-delay photoelectric feedback structure.
图 2 DFB-SL自延迟光反馈结构图
Figure 2. Diagram of the DFB-SL self-delay optical feedback structure.
图 3 不同光反馈强度下DFB激光器的S-N图及其输出的时序图和频谱图 (a1)—(a3)
$\kappa = 0.018$ ; (b1)—(b3)$\kappa = 0.044$ ; (c1)—(c3)$\kappa = 0.059$ Figure 3. Under different optical feedback intensities, S-N plots of DFB lasers and their output timing plots and spectrograms: (a1)–(a3)
$\kappa = 0.018$ ; (b1)–(b3)$\kappa = 0.044$ ; (c1)–(c3)$\kappa = 0.059$ .
图 4 不同光反馈时间下DFB激光器的S-N图及其输出的时序图和频谱图 (a1)—(a3)
$\tau = 2.18 {\text{ ns}}$ ; (b1)—(b3)$\tau = 2.21 {\text{ ns}}$ Figure 4. Under different optical feedback time, S-N plots of DFB lasers and their output timing plots and spectrograms: (a1)–(a3)
$\tau = 2.18 {\text{ ns}}$ ; (b1)–(b3)$\tau = 2.21 {\text{ ns}}$ .
图 5 DFB-SL自延迟电反馈结构图
Figure 5. Diagram of the DFB-SL self-delay electricity feedback structure.
图 6 不同光电反馈强度下DFB激光器的S-N图及其输出的时序图和频谱图 (a1)—(a3)
$\zeta = 0.045$ ; (b1)—(b3)$\zeta = 0.0555$ ; (c1)—(c3)$\zeta = 0.0973$ ; (d1)—(d3)$\zeta = 0.19$ Figure 6. Under different feedback intensity, S-N plots of DFB lasers and their output timing plots and spectrograms: (a1)–(a3)
$\zeta = 0.045$ ; (b1)–(b3)$\zeta = 0.0555$ ; (c1)–(c3)$\zeta = 0.0973$ ; (d1)–(d3)$\zeta = 0.19$ .
图 7 不同光-电反馈强度下的动力学态相图
Figure 7. Effect of photo-electrical feedback intensity on laser dynamics.
图 8 不同光-电反馈延迟时间条件下的动力学态相图
Figure 8. Effect of optical-electrical feedback delay time on laser dynamics.
图 9 不同偏置电流下DFB激光器的S-N图及激光器输出的时序图和频谱图 (a1)—(a3)
$I = 40 {\text{ mA}}$ ; (b1)—(b3)$I = 36 {\text{ mA}}$ ; (c1)—(c3)$I = 20 {\text{ mA}}$ Figure 9. Under different bias current, S-N plots of DFB lasers and their output timing plots and spectrograms: (a1)–(a3)
$I = 40 {\text{ mA}}$ ; (b1)–(b3)$I = 36 {\text{ mA}}$ ; (c1)–(c3)$I = 20 {\text{ mA}}$ .表 1 参数符号及取值
Table 1. Parameter symbols and their values.
参数 符号 取值 单位 光子数 $ S\left(t\right) $ — — 载流子数 $ N\left(t\right) $ — — 光功率 $ P\left(t\right) $ — — 微分增益 $ {G}_{{\mathrm{N}}} $ $ (3—4) \times {10}^{4}$ s–1 透明载流子数 $ {N}_{0} $ $ 1.36\times{10}^{8} $ — 阈值光子数 $ {S}_{0} $ $ 4.04\times{10}^{4} $ — 激光腔内反馈时间 $ {\tau }_{{\mathrm{i}}{\mathrm{n}}} $ 9 $ {\mathrm{p}}{\mathrm{s}} $ 光子寿命 $ {\tau }_{{\mathrm{p}}} $ 2 $ {\mathrm{p}}{\mathrm{s}} $ 载流子寿命 $ {\tau }_{{\mathrm{e}}} $ 2 $ {\mathrm{n}}{\mathrm{s}} $ 电子电荷 $ e $ $ 1.6\times{10}^{-19}$ C 限制因子 $ \varGamma $ 0.5 — 自发辐射因子 $ \beta $ $1\times {10}^{-5} $ — 饱和增益因子 $ \varepsilon $ $ (7—8)\times{10}^{-8} $ — 激光器的中心频率 $ {\omega }_{0} $ $ 1.938 \times {10}^{14}~{\mathrm{Hz}} $ — 线宽增强因子 $ a $ 4.5 — 
下载: 导出CSV
-
[1] Olesen H, Osmundsen J, Tromborg B 1986 IEEE J. Quantum Electron. 22 762 doi: 10.1109/JQE.1986.1073061 [2] 操良平, 邓涛, 林晓东, 吴加贵, 夏光琼, 吴正茂 2010 中国激光 37 939 doi: 10.3788/CJL20103704.0939 Cao L P, Deng T, Lin X D, Wu J G, Xia G Q, Wu Z M 2010 Chin. Lasers 37 939 doi: 10.3788/CJL20103704.0939 [3] 刘凌锋, 妙锁霞 2015 光电子·激光 26 86 doi: 10.16136/j.joel.2015.01.0728 Liu L F, Miao S X 2015 J. Optoelectron. Laser 26 86 doi: 10.16136/j.joel.2015.01.0728 [4] Lang R, Kobayashi K 1980 IEEE J. Quantum Electron. 16 347 doi: 10.1109/JQE.1980.1070479 [5] Soriano M C, Garcíaojalvo J, Mirasso C R, Fischer I, Soriano M C 2013 Rev. Mod. Phys. 85 421 doi: 10.1103/RevModPhys.85.421 [6] Saboureau P, Foing J P, Schanne P 1997 IEEE J. Quantum Electron. 33 1582 doi: 10.1109/3.622640 [7] Tang S, Liu J M 2001 IEEE J. Quantum Electron. 37 329 doi: 10.1109/3.910441 [8] Hizanidis J, Deligiannidis S, Bogris A, Syvridis D 2010 IEEE J. Quantum Electron. 46 1642 doi: 10.1109/JQE.2010.2055837 [9] Chen G C, Lu D, Guo L, Zhao W, Huang Y G, Zhao L J 2019 Optik 180 313 doi: 10.1016/j.ijleo.2018.11.109 [10] 包琪 2020 硕士学位论文 (杭州: 杭州电子科技大学) Bao Q 2020 M. S. Thesis (Hangzhou: Hangzhou Dianzi University [11] 张梦雨 2022 硕士学位论文 (郑州: 郑州大学) Zhang M Y 2022 M.S. Thesis (Zhengzhou: Zhengzhou University [12] Argyris A, Syvridis D, Larger L 2005 Nature 438 343 doi: 10.1038/nature04275 [13] 孔慧君, 吴正茂, 吴加贵, 林晓东, 谢瑛珂, 夏光琼 2006 中国激光 17 1490 doi: 10.3321/j.issn:0258-7025.2006.11.011 Kong H J, Wu Z M, Wu J G, Lin X D, Xie Y K, Xia G Q 2006 Chin. Lasers 17 1490 doi: 10.3321/j.issn:0258-7025.2006.11.011 [14] Argyris A, Hamacher M, Chlouverakis K E 2008 Phys. Rev. Lett. 100 194101 doi: 10.1103/PhysRevLett.100.194101 [15] Vicente R, Dauden J, Colet P, Toral R 2005 IEEE J. Quantum Electron. 41 541 doi: 10.1109/JQE.2005.843606 [16] 蔺玉雪, 高慧, 王龙生, 李腾龙, 赵彤, 常朋发, 王安帮, 王云才 2024 中国激光 51 0606002 doi: 10.3788/CJL230808 Lin Y X, Gao H, Wang L S, Li T L, Zhao T, Chang P F, Wang A B, Wang Y C 2024 Chin. Lasers 51 0606002 doi: 10.3788/CJL230808 [17] Heil T, Fischer I, Elsasser W, Gavrielides A 2001 Phys. Rev. Lett. 87 243901 doi: 10.1103/PhysRevLett.87.243901 [18] Lin F Y, Liu J M 2004 IEEE J. Quantum Electron. 40 815 doi: 10.1109/JQE.2004.828237 [19] Lin F Y, Liu J M 2003 IEEE J. Quantum Electron. 39 562 doi: 10.1109/JQE.2003.809338 [20] 韩韬, 刘香莲, 李璞, 郭晓敏, 郭龑强, 王云才 2017 物理学报 66 124203 doi: 10.7498/aps.66.124203 Han T, Liu X L, Li P, Guo X M, Guo Y Q, Wang Y C 2017 Acta Phys. Sin. 66 124203 doi: 10.7498/aps.66.124203 [21] Mork J, Tromborg B, Mark J 1992 IEEE J. Quantum Electron. 28 93 doi: 10.1109/3.119502 [22] 李增, 冯玉玲, 王晓茜, 姚治海 2018 物理学报 67 140501 doi: 10.7498/aps.67.20180035 Li Z, Feng Y L, Wang X Q, Yao Z H 2018 Acta Phys. Sin. 67 140501 doi: 10.7498/aps.67.20180035 [23] 戈杉杉, 王腾午, 戈静怡, 周沛, 李念强 2023 物理学报 72 164201 doi: 10.7498/aps.72.20230759 Ge S S, Wang T W, Ge J Y, Zhou P, Li N Q 2023 Acta Phys. Sin. 72 164201 doi: 10.7498/aps.72.20230759 [24] 张依宁, 徐艾诗, 冯玉玲, 赵振明, 姚治海 2020 光学学报 40 125 Zhang Y N, Xu A S, Feng Y L, Zhao Z M, Yao Z H 2020 Acta Opt. Sin. 40 125 -
计量
- 文章访问数: 35
- HTML全文浏览数: 35
- PDF下载数: 2
- 施引文献: 0