首页
登录
注册
-
光纤低频声传感系统因其具有较强的抗电磁干扰能力、较高灵敏度、较小体积等特点, 较传统电压、电容等压电类传感器具有明显优势, 成为近年来研究的热点[1], 在桥梁结构监测、地震、海啸等自然灾害的安全预警、生物医学成像等多个领域都有重要应用[2–4]. 目前, 光纤声传感系统大多数采用光纤干涉仪结构和光纤光栅结构[5–7]. 其中, 光纤干涉仪结构包括迈克耳孙(Michelson)干涉仪、萨尼亚克(Sagnac)干涉、马赫-曾德尔(Mach-Zehnder)干涉仪和法布里-珀罗(Fabry-Perot, F-P)干涉仪. 按照探测声场的频率, 光纤声传感系统通常分为高频声传感系统和低频声传感系统. 高频声传感系统大多数采用光纤激光器结构和F-P干涉仪结构. 光纤激光器结构对高频声信号探测较为灵敏[8,9], 在低频范围受相位噪声影响较大. FPI结构主要利用F-P腔内膜片接收声音振动, 使FPI的腔长产生周期性变化导致干涉光谱漂移. 该类方法通过在光纤内部形成F-P腔和对光纤末端镀膜来提高反射率, 制作难度较大, 主要用于高频声信号探测[10,11]. 低频声传感系统主要采用Sagnac干涉结构和光纤光栅结构, 目前基于Sagnac干涉结构和光纤光栅结构的声探测系统大多将声波直接作用于传感光纤, 声信号转换效率较低, 核心传感元件对声信号响应不足[12,13].
近年来, 本课题组和相关研究单位利用倾斜光纤光栅和长周期光纤光栅分别进行低频声场探测和振动探测[14,15], 研究表明该类特殊光纤光栅存在的多种包层模式容易受曲率变化影响而产生变化, 可有效进行振动或低频声场测量. 这些对声场或振动的探测方法, 都是基于声场对特殊光纤光栅多种模式的调制作用, 而对特种光纤模式进行调制并有效用于声场探测的研究较少. 级联特种光纤作为声传感光纤具有性能好、结构灵活、易制作、造价低等特点[16].
基于以上研究, 本文提出了一种基于光纤内马赫-曾德尔干涉仪的低频声传感方案, 利用光纤纤芯与包层折射率不同, 通过将不同类型特种光纤焊接在一起重组包层模式与纤芯模式, 形成了基于多模-超高数值孔径-多模光纤的微型马赫-曾德尔干涉仪结构. 然后将该干涉仪结构与聚对苯二甲酸乙二酯换能膜片进行结合, 当外界声压对传感光纤和换能膜片形成弯曲调制时, 由于包层和纤芯受到的应变不同, 产生了光程差, 使得干涉光谱发生变化, 通过对传感光谱进行解调可实现对低频声波信号的有效探测.
-
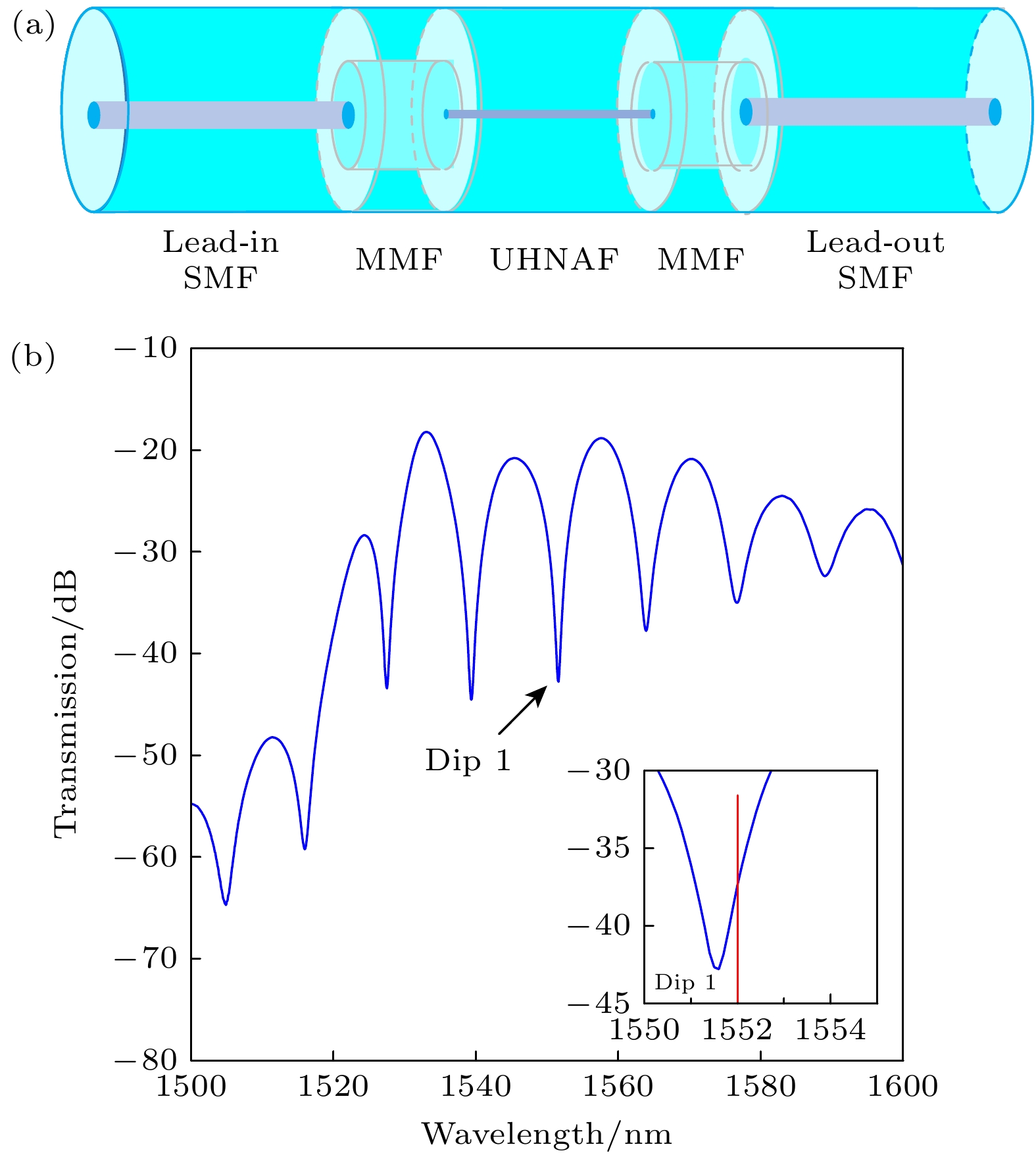
本文提出的基于多模光纤-超高数值孔径光纤-多模光纤级联的马赫-曾德尔干涉结构如图1(a)所示. 该结构将一段超高数值孔径光纤的两端通过光纤焊接机接上多模光纤, 形成光纤内马赫-曾德尔干涉仪结构. 信号光从单模光纤(single mode fiber, SMF)依次进入多模光纤(multimode fibers, MMF)、超高数值孔径光纤(ultra-high NA single-mode fibers, UHNAF), 由于二者芯径差, 光分两路分别进入UHNAF的包层和纤芯, 最后两路光进入多模光纤后形成干涉, 其中两端的多模光纤长度约为2 mm, 超高数值孔径光纤长度约为6 mm. 图1(b)为传感结构的透射光谱图, 图中Dip 1为随机选择的干涉谐振峰, 波长在1551.5 nm左右.
在多模光纤处产生的干涉为超高数值孔径光纤的纤芯模式与各阶包层模式的干涉, 根据干涉原理可得干涉光输出光强为
式中
${I_{{\text{core}}}}$ 为纤芯模式光强;${I_{{\text{clad}}}}$ 为各阶包层模式的总光强;$\Delta \varphi $ 为干涉光之间的相位差, 表示为其中
$\Delta {n_{{\text{eff}}}}$ 为纤芯和包层间的有效折射率差,${L_{\text{D}}}$ 为超高数值孔径光纤的长度,$\lambda $ 为入射光波长. 当相位差为$(2 m + 1){\text{π}}$ , 其中$m$ 为整数时, 得到谐振波长${\lambda _{\text{m}}}$ 为由此可知, 当选用超高数值孔径光纤时, 较大的数值孔径会使得折射率调制深度更大, 使得该结构更灵敏.
当干涉结构受到弯曲影响时, 光纤纤芯包层有效折射率差
$\Delta {n_{{\text{eff}}}}$ 发生变化, 其表示为[17]$\Delta {n_{{\text{eff}}}} = {k_{\text{c}}}\varepsilon $ , 其中${k_{\text{c}}}$ 为应变折射率系数, 应变$\varepsilon = {r_{\text{c}}}C$ ,${r_{\text{c}}}$ 为纤芯中心到包层中心的距离,$C$ 为曲率. 将这些参数代入(3)式整理后可得到:由(4)式可知, 谐振波长的漂移量与曲率变化成正比关系. 所以当声压作用在传感光纤上时, 曲率变化会使得谐振波长发生变化.
由于光纤直径较小, 受声压作用面积小, 因此需要使用换能元件. 本文利用聚对苯二甲酸乙二酯(PET)材质的膜片作为换能元件, 将传感光纤粘贴在膜片上, 在感知到外界声压时, 光纤和膜片同时发生周期性弯曲, 从而间接放大声压对传感光纤的影响.
根据受迫振动原理, 四周固定的圆形膜片振动时中心处最大形变量为[18]
其中
$E$ 为杨氏模量,$\mu $ 为泊松比,$r$ 为膜片半径,${f_{00}}$ 为一阶固有频率,$h$ 为膜片厚度,$\varsigma $ 为阻尼系数,$P$ 为声压,$f$ 为声波频率.根据几何关系进行计算, 当膜片弯曲时, 中心形变量
$\eta $ 、曲率半径${1}/{C}$ 以及膜片半径$r$ 之间的关系满足:${\Big(\dfrac{1}{C}\Big)^2} = {r^2} + {\Big(\dfrac{1}{C} - \eta\Big)^2}$ , 进而得到$C = \dfrac{{2\eta }}{{{r^2} + {\eta ^2}}}$ . 由于声压对光纤作用产生的形变量相对于膜片半径很小,${\eta ^2}$ 可忽略不计, 将(5)式代入后化简得到其中,
${I_{\text{D}}} = {I_{{\text{core}}}} + {I_{{\text{clad}}}}$ 为直流常数,$A = 2\sqrt {{I_{{\text{core}}}}{I_{{\text{clad}}}}} $ 为振幅, 由于在声波的作用下, 光纤产生的弯曲很小, 可将${I_{{\text{core}}}}$ 和${I_{{\text{clad}}}}$ 近似为固定值. 在傍轴条件下(7)式$ I = {I_{\text{D}}} + A\cos \left[ {\dfrac1\lambda\cdot {{2{\text{π}}{r_{\text{c}}}{k_{\text{c}}}{L_{\text{D}}}\left( {C + \dfrac{{\text{π}}}{{2}}-\dfrac{{\text{π}}}{{2}}} \right)}}} \right] $ 可以变为$ I = {I_{\text{D}}} + A\sin \Big(\dfrac{{2{\text{π}}{r_{\text{c}}}{k_{\text{c}}}{L_{\text{D}}}C}}{\lambda } + \dfrac{{{{\text{π}}^2}{r_{\text{c}}}{k_{\text{c}}}{L_{\text{D}}}}}{\lambda }\Big) $ . 由(7)式可知, 光强变化与曲率和波长两个参数相关. 当选定波长$\lambda $ 为谐振峰边沿线性区的固定波长后, 此时$\lambda $ 为定值, 光强变化只与曲率有关, 则(7)式可表示为其中
${I_{\text{O}}} = {I_{\text{D}}} + A\dfrac{{{{\text{π}}^2}{r_{\text{c}}}{k_{\text{c}}}{L_{\text{D}}}}}{\lambda }$ 为常数. 由(9)式可知, 在声波频率一定时, 光强$I$ 变化与声压$P$ 有关, 且为线性关系. 通过探测光强的变化可以检测动态变化的声波信号. -
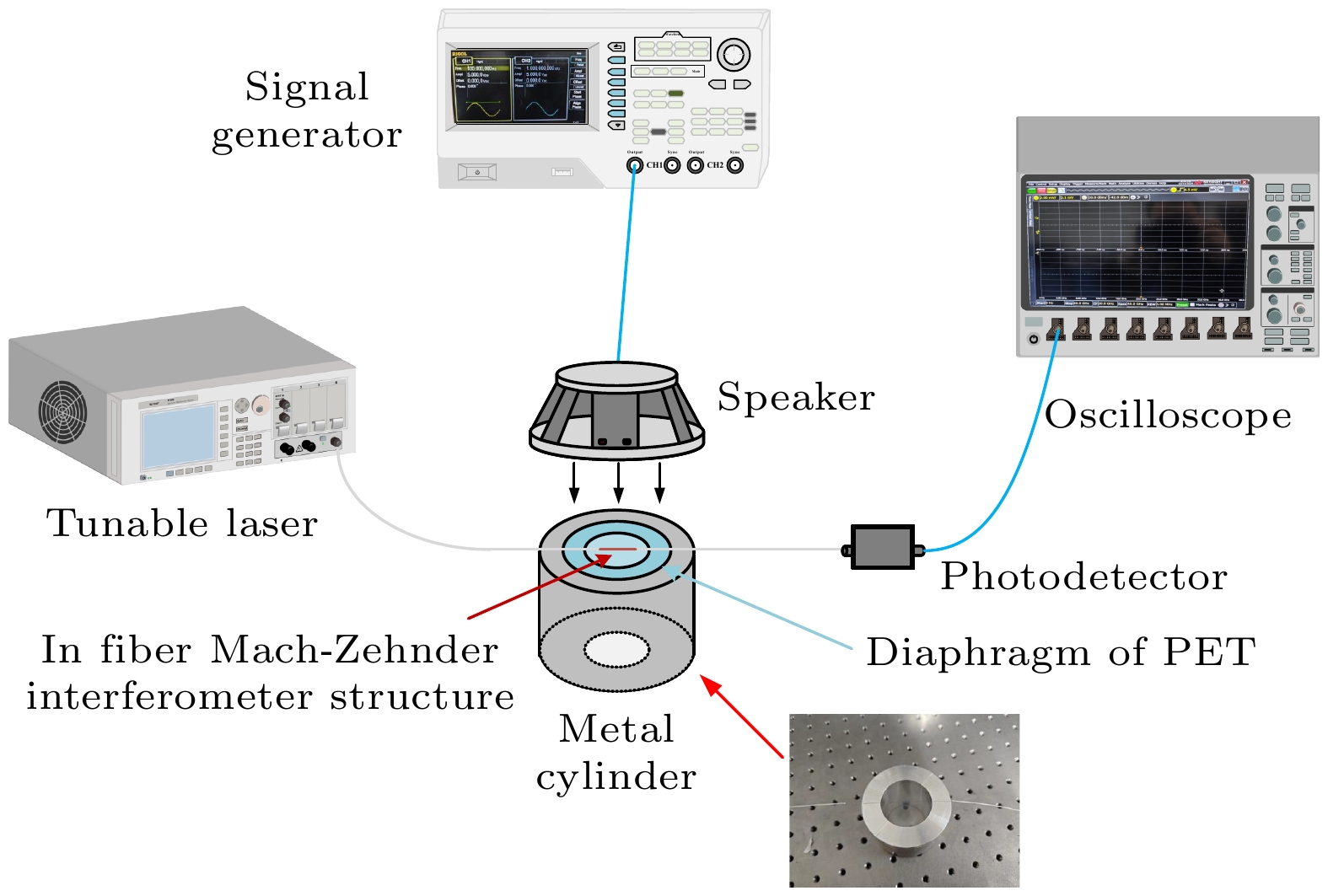
光纤低频声场探测原理如图2所示, 利用可调谐激光器(tunable laser)输出一束波长为1552 nm (Dip 1 附近)的窄线宽激光作为入射光进入单模光纤, 通过单模光纤后输入到传感头中, 出射的激光进入光电探测器(photodetector), 光电探测器将光信号转化为电信号, 进入示波器观察. 传感头部分是将焊接好的光纤内马赫-曾德尔干涉仪结构(in fiber Mach-Zehnder interferometer structure)与圆形换能膜片(diaphragm)粘贴在一起, 膜片半径约为2 cm, 厚度约为50 μm, 换能膜片固定在一个空心金属圆柱体(metal cylinder)顶部; 商用扬声器(speaker)为声源, 其调谐频率由信号发生器(signal generator)控制.
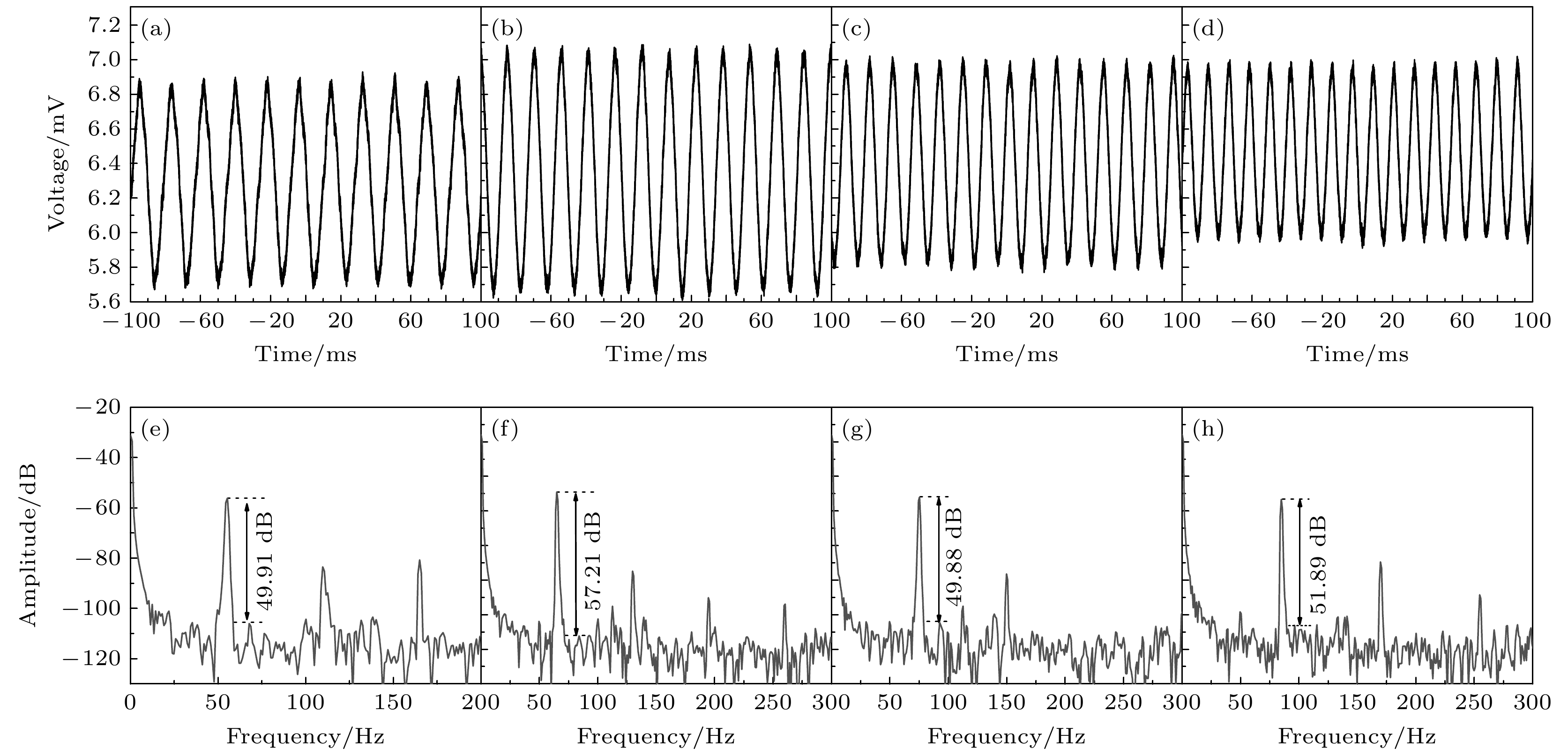
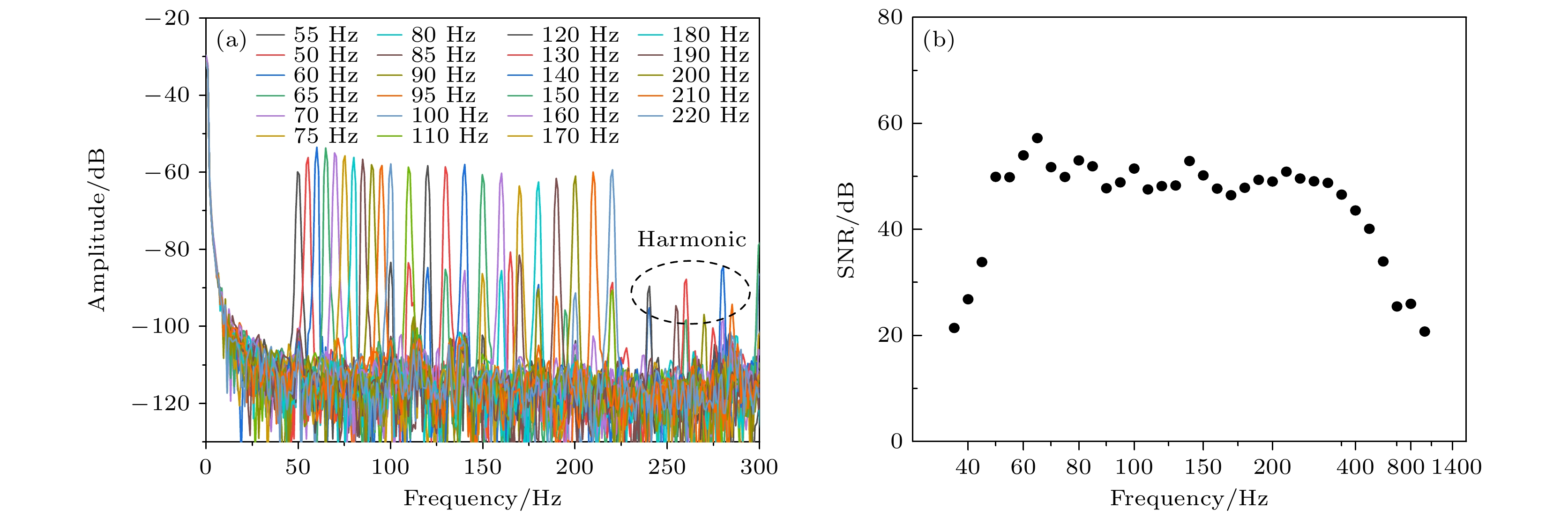
实验过程中为了测试该传感系统声响应能力, 首先随机测试不同频率的声波信号, 得到了输出时域信号和经快速傅里叶变化(FFT)的频谱图. 图3(a)—(d)所示声波频率为55 Hz, 65 Hz, 75 Hz, 85 Hz时对应示波器时域图, 图3(e)—(h)分别为对应FFT后的频谱图. 由图3可知, 在相同被测声压下固有频率65 Hz处信噪比较高约为57.2 dB, 而其他频率55 Hz, 75 Hz, 85 Hz分别为49.91 dB, 49.88 dB, 51.89 dB. 可以发现所提出的声波探测方案有较好的频率响应和较高信噪比. 为了进一步探究该系统在低频范围内对声信号的响应能力, 实验中通过随机选取35—1000 Hz范围内的声波信号进行测试, 得到了不同频率的信噪比如图4(b)所示, 在50—500 Hz范围内有较好的响应, 信噪比均在40 dB以上且频响范围较大且较平坦. 50—220 Hz频谱图如图4(a)所示. 可以发现所提出的传感方案对不同频率声波都有较好的响应, 实验过程中一直存在谐波效应, 推测是室内声波反射所致, 整个过程在室温环境下进行, 受温度影响较小.
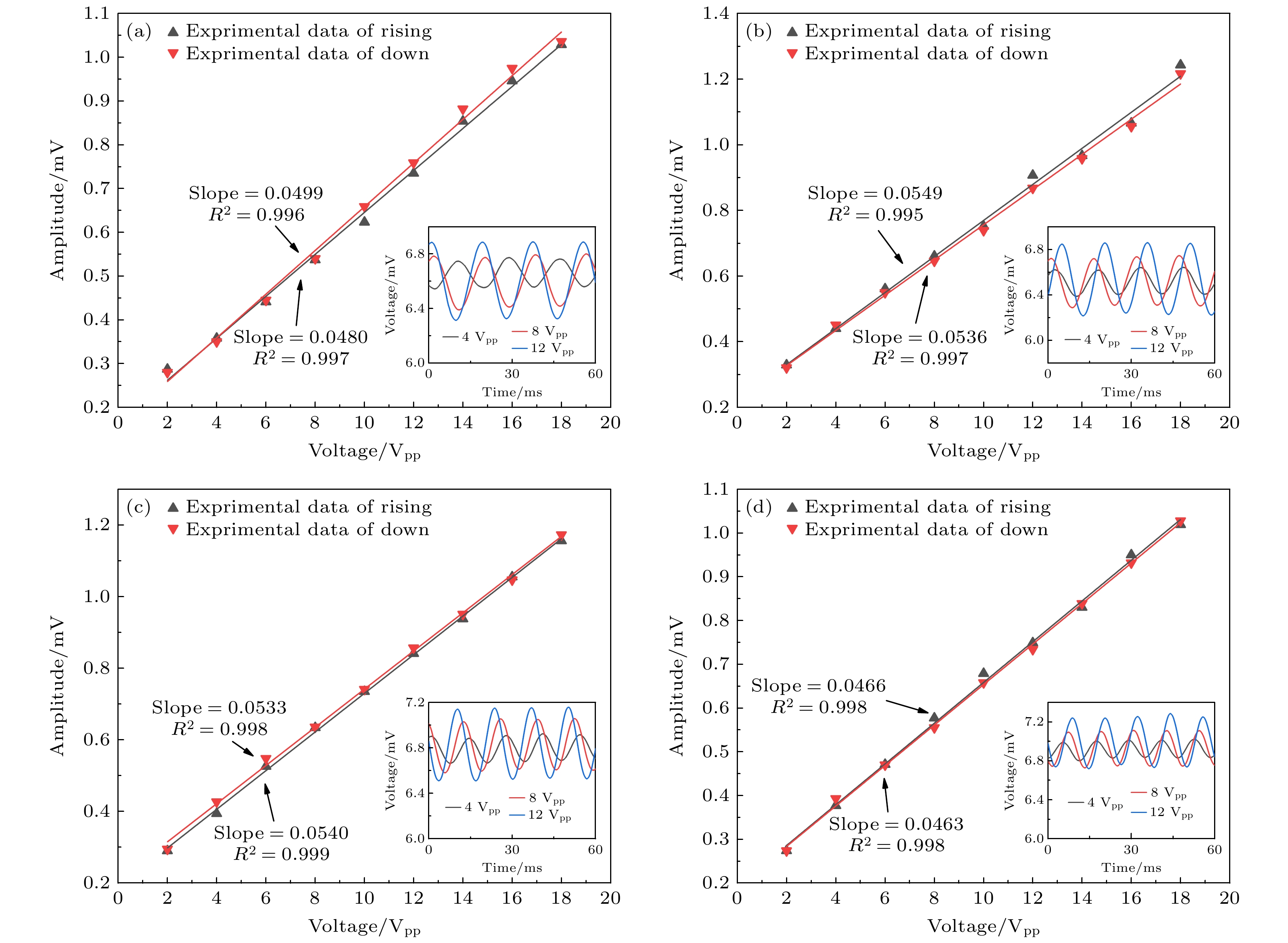
然后, 保持信号发生器输出频率不变, 改变输出电压从2 Vpp—18 Vpp (逐渐增大声压), 以及从18 Vpp 到2 Vpp (逐渐减小声压), 研究频率在55 Hz, 65 Hz, 75 Hz, 85 Hz时的声压灵敏度. 这里Vpp为信号发生器对扬声器施加的电压. 通过对示波器上正弦信号峰-峰值的最大值进行线性拟合, 图5(a)—(d)分别为55 Hz, 65 Hz, 75 Hz, 85 Hz的声压响应. 可以看出, 其声压增大过程的线性拟合优度分别为0.997, 0.995, 0.999, 0.998, 灵敏度分别为0.048 mV/Vpp, 0.0549 mV/Vpp, 0.0540 mV/Vpp, 0.466 mV/Vpp; 声压减小过程的线性拟合优度分别为0.996, 0.997, 0.998, 0.998, 灵敏度分别为0.0499 mV/Vpp, 0.0536 mV/Vpp, 0.0533 mV/Vpp, 0.463 mV/Vpp. 图5插图为对应频率在电压为4 Vpp, 8 Vpp, 12 Vpp时输出的时域图. 以上结果表明声压与信号强度有0.995以上的高线性拟合优度, 线性拟合优度越接近1, 表明与线性拟合曲线的方程越符合, 这与(9)式为线性方程的描述吻合.
最小可探测声压(minimum detectable pressure, MDP)表示为[19]
其中,
${\text{SNR}}$ 为信噪比,$\Delta f$ 为频谱图的频率分辨率. 本实验测量过程中, 利用标准声压计测得声压为0.238 Pa, 可得频率分辨率为1.5 Hz, 则在65 Hz处得到MDP为$267.9{\text{ μPa/H}}{{\text{z}}^{{{1/2}}}}$ .如表1所列, 将本文提出的传感方案与近年来相关光纤声传感方案的性能进行对比. 文献[20]是通过拉伸光纤, 使得中间部分光纤比两边细而形成锥形光纤. 文献[21]为基于金膜的法布里-珀罗干涉结构, 利用光纤套筒使光纤与金膜形成法布里-珀罗腔, 在受到声波影响时, 腔长发生变化而对声波进行探测. 文献[22]利用法布里-珀罗标准具作为传感元件. 文献[15]使用长周期光纤光栅受振动影响使得光纤光栅的耦合模式发生变化, 从而对声波进行探测. 文献[23]为基于COMS的微机械电容式传感器. 文献[24]通过双光子聚合直接3D打印在光纤尖端上形成法布里珀罗腔来对声波进行探测. 由表1可知, 本文提出的方案具有良好的信噪比、较低的最小可探测声压和较好的声响应能力.
-
本文提出了基于光纤内马赫-曾德尔干涉仪的低频声波探测方案, 利用光纤纤芯包层折射率不同, 通过将不同类型特种光纤焊接在一起重组包层模式与纤芯模式, 形成了基于多模-超高数值孔径-多模光纤的微型马赫-曾德尔干涉仪结构. 然后将该干涉结构与聚对苯二甲酸乙二酯换能膜片进行结合, 在感知到外界声压对传感光纤和换能薄膜形成弯曲调制时, 包层和纤芯受到的应变不同, 产生光程差, 使得干涉光谱发生变化, 通过对光谱变化进行解调实现对低频声波信号的有效探测. 本文分别从理论和实验两方面进行了论证, 得到该传感系统在65 Hz处信噪比约为57 dB, 最小可探测声压为
$267.9~{\text{μPa/Hz}}^{1/2}$ ; 在50—500 Hz的频率范围内, 对声波有较好响应, 信噪比均在40 dB以上, 信号较平坦. 该方案可显著提升传感系统声响应能力, 实现对低频声波的有效检测, 且具有制作简单、成本低的特点, 在声波探测相关应用领域有着很大的发展潜力.
一种基于光纤内马赫-曾德尔干涉仪的低频声传感方案
A low-frequency acoustic sensor scheme based on an in-fiber Mach-Zehnder interferometer
-
摘要: 提出了一种基于光纤内马赫-曾德尔干涉仪结构的低频声传感方案, 其中传感光纤是由多模-超高数值孔径-多模光纤焊接级联而成的微型马赫-曾德尔干涉仪, 可有效提高光纤弯曲灵敏度; 然后将该干涉仪结构与聚对苯二甲酸乙二酯换能膜片进行组合, 使得传感光纤在受到声压作用时与膜片同步产生曲率变化, 间接增大了光纤接收声场的面积. 文章推导了该系统的声传感理论, 并通过实验进行了验证, 得到传感系统在65 Hz处信噪比约为57 dB, 最小可探测声压为267.9 ${\text{μPa/H}}{{\text{z}}^{{\text{1/2}}}}$; 在50—500 Hz的频率范围内, 对声波有较好响应, 信噪比均在40 dB以上, 信号较平坦. 该方案可显著提升传感系统声响应能力, 实现对低频声波的有效检测, 且具有制作简单、成本低的特点, 在声波探测相关应用领域具有较大的发展潜力.Abstract: In this work, a low-frequency acoustic sensing scheme is proposed based on the structure of in-fiber Mach-Zehnder interferometer , in which the refractive index difference between fiber core and cladding is used to form a miniature Mach-Zehnder interferometer through fusion splicing of specialty optical fibers in a multi-mode-ultra-high numerical aperture-multi-mode configuration. This design achieves modal recombination between cladding and core modes, thereby effectively enhancing fiber bending sensitivity. The interferometer structure is then combined with a polyethylene terephthalate (PET) transducer diaphragm, enabling the sensing fiber to undergo curvature changes synchronously with the diaphragm under sound pressure, thereby indirectly increasing the area over which the fiber receives the acoustic field. When external acoustic pressure induces bending modulation on both the sensing fiber and transducer diaphragm, the differential strain distribution between the fiber cladding and core generates an optical path difference. This manifests itself in interference spectrum shifts, enabling the effective detection of low-frequency acoustic signals through demodulating the spectrum variations. In the paper, the theoretical framework for the acoustic sensing system is derived and validated experimentally. The results show that at 65 Hz, the system achieves a signal-to-noise ratio (SNR) of approximately 57 dB and a minimum detectable sound pressure of $267.9{\text{ μPa/H}}{{\text{z}}^{{{1/2}}}}$at 65 Hz. In a frequency range of 50–500 Hz, the system exhibits good acoustic response, with an SNR consistently above 40 dB and a relatively flat signal output. This scheme significantly enhances the acoustic response capability of the sensing system, enabling the effective detection of low-frequency acoustic waves. Additionally, it features simple fabrication and low cost, showing great potential for the development of acoustic wave detection applications.
-
Key words:
- optical fiber sensing /
- Mach-Zehnder interferometer /
- acoustic sensor /
- acoustic measurement .
-
-
图 1 (a) 传感光纤结构示意图; (b) 传感光纤光谱图
Figure 1. (a) Schematic diagram of optic sensing fiber structure; (b) spectral diagram of sensing fiber.
图 3 不同频率的频谱响应和时域波形 (a)—(d) 55 Hz, 65 Hz, 75 Hz, 85 Hz时对应的时域信号; (e)—(h) 55 Hz, 65 Hz, 75 Hz, 85 Hz时对应的频域信号
Figure 3. Frequency response and time domain signal at different frequencies: (a)–(d) Time domain signal at 55 Hz, 65 Hz, 75 Hz, 85 Hz; (e)–(h) frequency response at 55 Hz, 65 Hz, 75 Hz, 85 Hz.
图 4 传感系统对声波频率的频响 (a) 50—220 Hz部分频率的响应频谱图; (b) 35—1000 Hz的信噪比
Figure 4. Frequency response of the sensing system for acoustic wave: (a) The response of frequency spectrum during 50–220 Hz; (b) signal to noise ratio corresponding to different frequencies during 35–1000 Hz.
图 5 不同频率时传感结构对不同声压的灵敏度线性拟合及重复性测试 (a) 55 Hz; (b) 65 Hz; (c) 75 Hz; (d) 85 Hz
Figure 5. Linearly fitted sensitivities of the sensing structure to different acoustic pressures and repeatability test at (a) 55 Hz, (b) 65 Hz, (c) 75 Hz, (d) 85 Hz.
表 1 几种声传感方案的性能比较
Table 1. Performance comparison of several acoustic sensing systems.
传感结构 声压响应 信噪比/dB 最小探测声压/( ${\text{μPa}}\cdot{\text{Hz}}^{-1/2}$ )Tapered fiber[20] 36 mV/kPa 46.84 21.11×106@2500 Hz Gold diaphragm-based FPI with
a fiber-optic collimator[21]12.6 mV/Pa 51 470@150 Hz FP etalon[22] 177.6 mV/Pa 12.7 530@1 kHz LPBG[15] 0.064 nm/kPa 40.6 331.9@550 Hz CMOS micromachined capacitive[23] — — 1.35×106@2.4 MHz Two-photon 3D printed spring-based
Fabry-Perot cavity resonator[24]0.0883 mV/Vpp 56.2 2390@75 kHz 本工作 0.0549 mV/Vpp 57.21 267.9@65 Hz 
下载: 导出CSV
-
[1] Zhao Y, Chen M Q, Xia F, Lv R Q 2018 Sensor Acoust. A-Phys. 270 162 doi: 10.1016/j.sna.2017.12.057 [2] Shnaiderman R, Wissmeyer G, Seeger M, Soliman D, Estrada H, Razansky D, Rosenthal A, Ntziachristos V 2017 Optica 4 1180 doi: 10.1364/OPTICA.4.001180 [3] Basiri-Esfahani S, Armin A, Forstner S, Bowen W P 2019 Nat. Commun. 10 132 doi: 10.1038/s41467-018-08038-4 [4] Mydlarz C, Salamon J, Bello J P 2017 Appl. Acoustics 117 207 doi: 10.1016/j.apacoust.2016.06.010 [5] Jia J, Jiang Y, Zhang L, Gao H, Jiang L 2019 IEEE Sens. J. 19 7988 doi: 10.1109/JSEN.2019.2918570 [6] 刘欣, 蔡宸, 董志飞, 邓欣, 胡昕宇, 祁志美 2022 物理学报 71 094301 doi: 10.7498/aps.71.20212229 Liu X, Cai C, Dong Z F, Deng X, Hu X Y, Qi Z M 2022 Acta Phys. Sin. 71 094301 doi: 10.7498/aps.71.20212229 [7] Gong Z F, Chen K, Zhou X L, Yang Y, Zhao Z H, Zou H L, Yu Q X 2017 J. Lightwave Technol. 35 5276 doi: 10.1109/JLT.2017.2761778 [8] Xu Y P, Zhang L, Gao S, Lu P, Mihailov S, Bao X Y 2017 Opt. Lett. 42 1353 doi: 10.1364/OL.42.001353 [9] Li Y, Tian J J, Fu Q, Sun Y X, Yao Y 2019 J. Lightwave Technol. 37 1160 doi: 10.1109/JLT.2018.2888756 [10] Dass S, Chatterjee K, Kachhap S, Jha R 2021 J. Lightwave Technol. 39 3974 doi: 10.1109/JLT.2021.3051951 [11] Wu Y, Yu C B, Wu F, Li C, Zhou J H, Gong Y, Rao Y J, Chen Y F 2017 J. Lightwave Technol. 35 4344 doi: 10.1109/JLT.2017.2737639 [12] Feng G H, Chen W M 2016 Smart Mater. Struct. 25 055046 doi: 10.1088/0964-1726/25/5/055046 [13] Wang S, Lu P, Zhang L, Liu D M, Zhang J S 2014 J. Mod. Opt. 61 1033 doi: 10.1080/09500340.2014.919038 [14] Tian J, Zuo Y W, Zhou K M, Yang Q, Hu X, Jiang Y 2024 J. Lightwave Technol. 42 2538 doi: 10.1109/JLT.2023.3337127 [15] Fu X, Lu P, Ni W J, Liu L, Liao H, Jiang X Y, Liu D M, Zhang J S 2016 IEEE Photonics J. 8 7102811 doi: 10.1109/JPHOT.2016.2627546 [16] Yang Q, Tian J, Hu X, Tian J J, He Q Q 2024 Photonics 11 363 doi: 10.3390/photonics11040363 [17] Jiang B Q, Bai Z Y, Wang C L, Zhao Y H, Zhao J L, Zhang L, Zhou K M 2018 J. Lightwave Technol. 36 742 doi: 10.1109/JLT.2017.2776297 [18] Guo M, Chen K, Zhang G Y, Li C X, Zhao X Y, Gong Z F, Yu Q X 2022 J. Lightwave Technol. 40 4481 doi: 10.1109/JLT.2022.3164134 [19] Ren D P, Liu X, Zhang M Y, Gao R, Qi Z M 2021 IEEE Sens. J. 21 14655 doi: 10.1109/JSEN.2021.3073940 [20] Dass S, Jha R 2017 J. Lightwave Technol. 35 5411 doi: 10.1109/JLT.2017.2776519 [21] Xiang Z W, Dai W Y, Rao W Y, Cai X, Fu H Y 2021 IEEE Sens. J. 21 17882 doi: 10.1109/JSEN.2021.3086107 [22] Chen J M, Xue C Y, Zheng Y Q, Wu L Y, Chen C, Han Y 2021 Opt. Express 29 16447 doi: 10.1364/OE.418736 [23] Tang P K, Wang P H, Li M L, Lu M S C 2011 J. Micromech. Microeng. 21 025013 doi: 10.1088/0960-1317/21/2/025013 [24] Wei H M, Wu Z L, Sun K X, Zhang H Y, Wang C, Wang K M, Yang T, Pang F F, Zhang X B, Wang T Y, Krishnaswamy S 2023 Photonics Res. 11 780 doi: 10.1364/PRJ.481858 -
计量
- 文章访问数: 70
- HTML全文浏览数: 70
- PDF下载数: 0
- 施引文献: 0