-
全息技术, 作为20世纪中叶的一项物理发明, 通过记录光的振幅与相位等信息, 实现了物体的记录和复现. 相对于传统成像技术, 全息技术能捕捉物体的更多细节, 实现更具真实感的成像效果. 经过数十年的发展, 全息术在多种领域得到了广泛运用, 并展现出巨大的发展潜力[1–8]. 例如在增强和虚拟现实(AR/VR)中, 全息技术提供了更真实的影像和沉浸式的体验[9]; 在医学影像学中, 患者的三维数据实时全息显示为医生提供了更精准的病灶细节, 提高诊断的准确度[10,11]; 在数模传输中, 三维全息技术也得到了应用[12,13]; 在商业广告中, 三维全息的动态展示可以为顾客提供更多商品细节, 更加直观地展示商品优点[14,15].
尽管全息技术取得了显著的进展, 但仍然存在一些挑战和困难, 限制了其广泛应用和进一步发展. 第一, 传统全息技术使用光的波长和偏振编码不同的图像, 这种信息传输方式容易受到窃听和截取, 存在信息泄漏的风险, 因而在安全性方面仍有很大的提升空间[16]. 第二, 传统全息技术在信息容量方面也存在很多不足. 由于难以实现多路复用, 即在同一介质中同时存储多个全息图像的能力, 限制了其在信息传输和存储方面的容量扩展性[17]. 为了提升安全性、增大信息通量, 除了传统全息中使用的光学自由度[18], 如振幅[19]、偏振[20,21], 光学涡旋的轨道角动量(orbital angular momentum, OAM), 作为光的另外一种自由度, 可以用于全息加密[22–24]. OAM涉及光场的螺旋相位结构, 坡印亭矢量绕着主光轴螺旋向前. 信息可以被编码在携带不同OAM的光束通道中, 理论上存在无限个这样的光束通道, 并且携带不同OAM的光束通道之间相互正交[25–27]、相互不干扰, 这不仅提供了更大的密钥空间, 因而具有很高的安全性, 还能够增大信息通量, 提升信息储存、传播效率. 因此, OAM光学全息有助于解决上述的难题, 实现高安全性[28]、高信息通量[29,30]的光学全息. 此外, 传统全息技术大部分记录和复现二维图像, 而二维图像复原已无法满足人们对更高逼真视觉体验的需求. 而引入OAM有助于通过全息技术实现三维图像复原, 提供更真实的、更有立体感的视觉场景[31]
本文首先详细分析OAM光学全息技术的理论, 其次通过仿真计算, 实现了多幅二维图像的数字全息图编码, 制作了OAM多路复用全息图, 并验证了只能通过特定拓扑荷才能得到对应的图片信息, 从而同时验证了这种技术的安全性和高信息通量性. 然后, 这种技术被应用到三维物体上. 三维物体被切片之后, 以OAM复用的全息技术记录所有切面, 每个切面对应一个拓扑荷. 一张OAM复用的全息图能记录很多切面, 进而较为完整地复现出三维物体, 展示了高信息容量密度. 以拓扑荷为密钥保证了信息传输的安全性.
鉴于这些优势, OAM多路复用全息技术可以在光学和通信领域开辟出一系列新的应用, 例如在虚拟现实技术中生成高互动性的三维图像与环境.
-
在光学领域, 除了传统的高斯光束, 携带OAM信息的光束因其独特的螺旋相位结构而展现出广泛的应用前景. 这种光束的波前携带螺旋相位因子
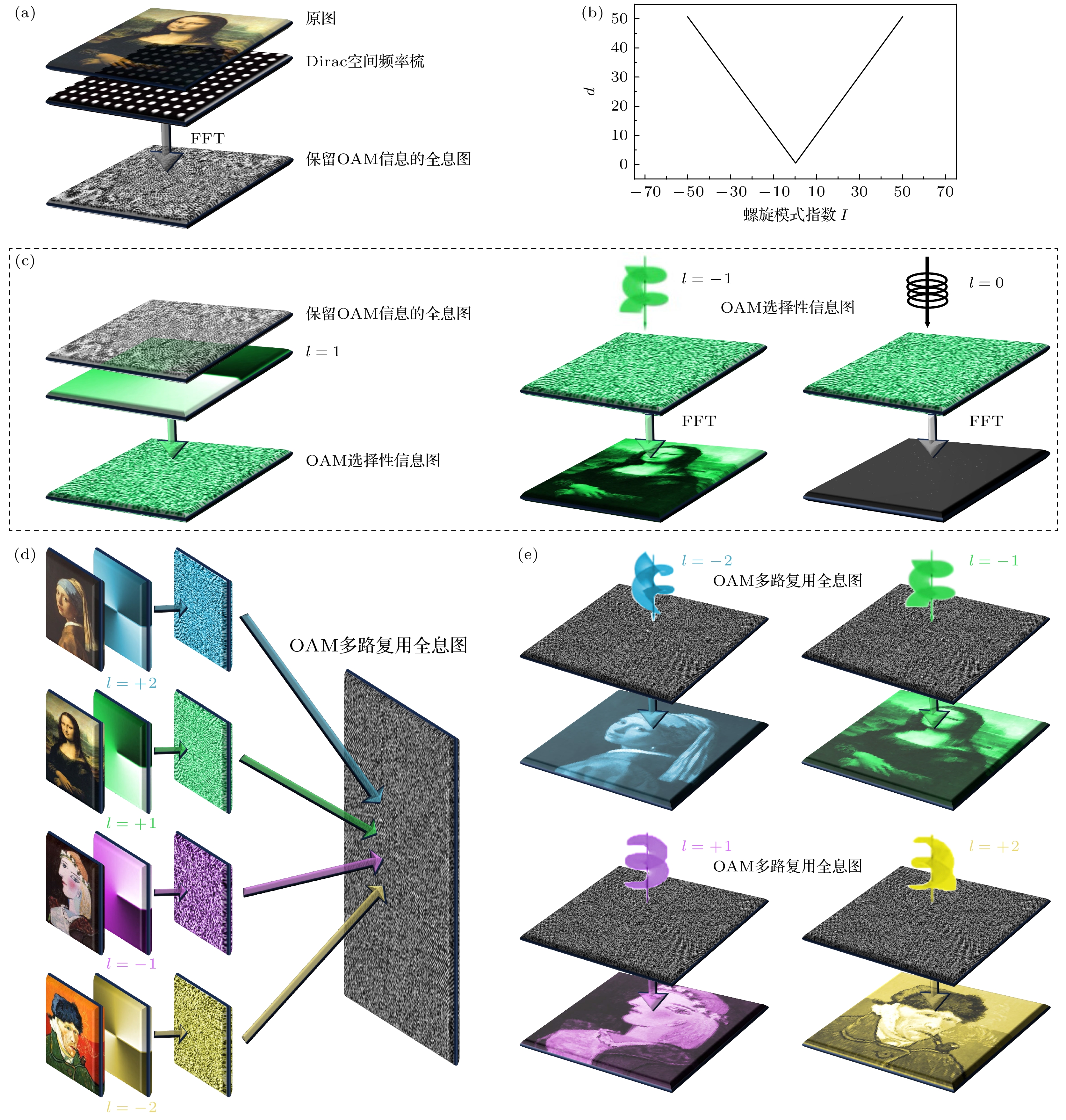
$ {{\mathrm{e}}}^{{\mathrm{i}}l\phi } $ (其中$ \phi $ 指方位角)[32], 相位沿着角向连续变化, 而沿着径向方向的相位相等, 其螺旋特性由拓扑荷l来标识. 由于这种螺旋波前结构, OAM光束的中心具有相位奇点, 形成了以几何中心为圆心的甜甜圈形状的强度分布, 并且拓扑荷越大, 光束中心的黑斑半径越大[33,34].携带OAM信息的光, 具有两大重要性质, 分别为固有正交性(inherent orthogonality)和无界状态(unboundedstates)[35]. 这些特性不仅为全息技术提供了新的自由度, 而且在信息安全和多通道复用方面具有显著优势. 然而, 由于传统光学全息技术中使用了连续或者准连续的波前分布, 重建之后相邻像素点之间存在较大的干涉. 入射的涡旋光经过重建的干涉相消、相长, 螺旋波前被破坏, 因此全息图不携带OAM信息. 为解决此问题, 首先应对图像乘上狄拉克梳函数, 进行空间离散采样, 再进行傅里叶变换, 进而得到离散全息图, 如图1(a)所示, 其能保留原图的OAM模式特征. 为了确保OAM性质不会被破坏, 采样点之间存在一最小间距d, 其与拓扑荷的关系如图1(b)所示, 最小间距随着拓扑荷绝对值线性增大[22].
携带特定OAM信息的全息图, 即OAM选择性全息图(OAM-selectivehologram)通过在离散全息图乘上螺旋相位因子
$ {{\mathrm{e}}}^{{\mathrm{i}}l\phi } $ 来构造, 如图1(c)左图所示. 由于光的螺旋波前遵循角动量守恒原理, 对于拓扑荷$ l $ 的OAM选择性全息图, 只有入射相反拓扑荷$ -l $ 的光才能复现出原始图像. 若使用的光波不具有匹配的拓扑荷, 只能观察到模糊或者杂乱的图样. 这一特性如图1(c)右图所示. OAM选择性全息图提供了一种独特的信息编码和解码方法, 允许选择性地操纵和传输特定OAM状态的光波. 以下公式可以说明其有选择性:其中
$ {P}_{} $ 代表原图的复振幅信息;$ {\mathrm{F}} $ 为进行傅里叶变换的操作;$ S\left({l}_{i}\right) $ 为对应拓扑荷$ {l}_{i} $ 加旋;$ S\left({l}_{j}\right) $ 为对应拓扑荷$ {l}_{j} $ 解旋;$ {\rm F}^{-1} $ 为进行逆傅里叶变换操作;$ \lambda $ 为进行操作的光的波长;$ u,\ v $ 为空间频率变量, 代表频域中的坐标;$ d$ 指远场条件下原始图像与选择性全息图之间距离.结果显示, 由于e指数函数积分的近似正交性, 只有当解旋对应拓扑荷与加旋对应拓扑荷相等时(
$ {l}_{j}={l}_{i} $ ), 选择性全息图才可以复现得到原图, 否则无法得到原图信息.通过叠加多幅具有不同拓扑荷的选择性全息图, 可以生成OAM多路复用全息图 (OAM-multiplexing hologram). 如图1(d)所示, 先将4幅不同的图片处理为OAM选择性全息图, 每个全息图对应独特的拓扑荷–2, –1, 1, 2. 叠加这4幅选择性全息图, 得到多路复用全息图. 这种复合全息图不仅集成了多种拓扑荷的信息, 还具备了复现特定图像的能力. 如图1(e)所示, 当采用与某一特定拓扑荷相匹配的光束照射多路复用全息图时, 能够成功复现出与该拓扑荷对应的原始图像. 以下公式可以说明其有多路复用性:
结果显示, 由于函数的近似正交性, 当使用特定拓扑荷解旋时, 多路复用全息图可以重新解码, 并经过傅里叶变化仅留下特定拓扑荷对应通道的原图成分. 通过调整拓扑荷
$ l $ , 可以选择性地分离和传输特定OAM的光, 实现对信息的安全编码和解码. OAM多路复用全息技术的这一特性为信息存储和传输提供了全新的可能性. 通过这种方式, 将多幅图片的信息有效地压缩到同一个全息图中. 理论上如果排除信息之间的串扰及其他干扰因素, 一张全息图可以承载无限个拓扑荷对应的图片, 实现了信息的高密度集成. 此外, 由于只有携带特定拓扑荷的光束才能复现对应的图像, 未经授权的光束无法获取全息图中存储的信息, 从而确保了数据的安全传输. 这些特性为实现高通量、高安全性的光学传输提供了坚实基础. -
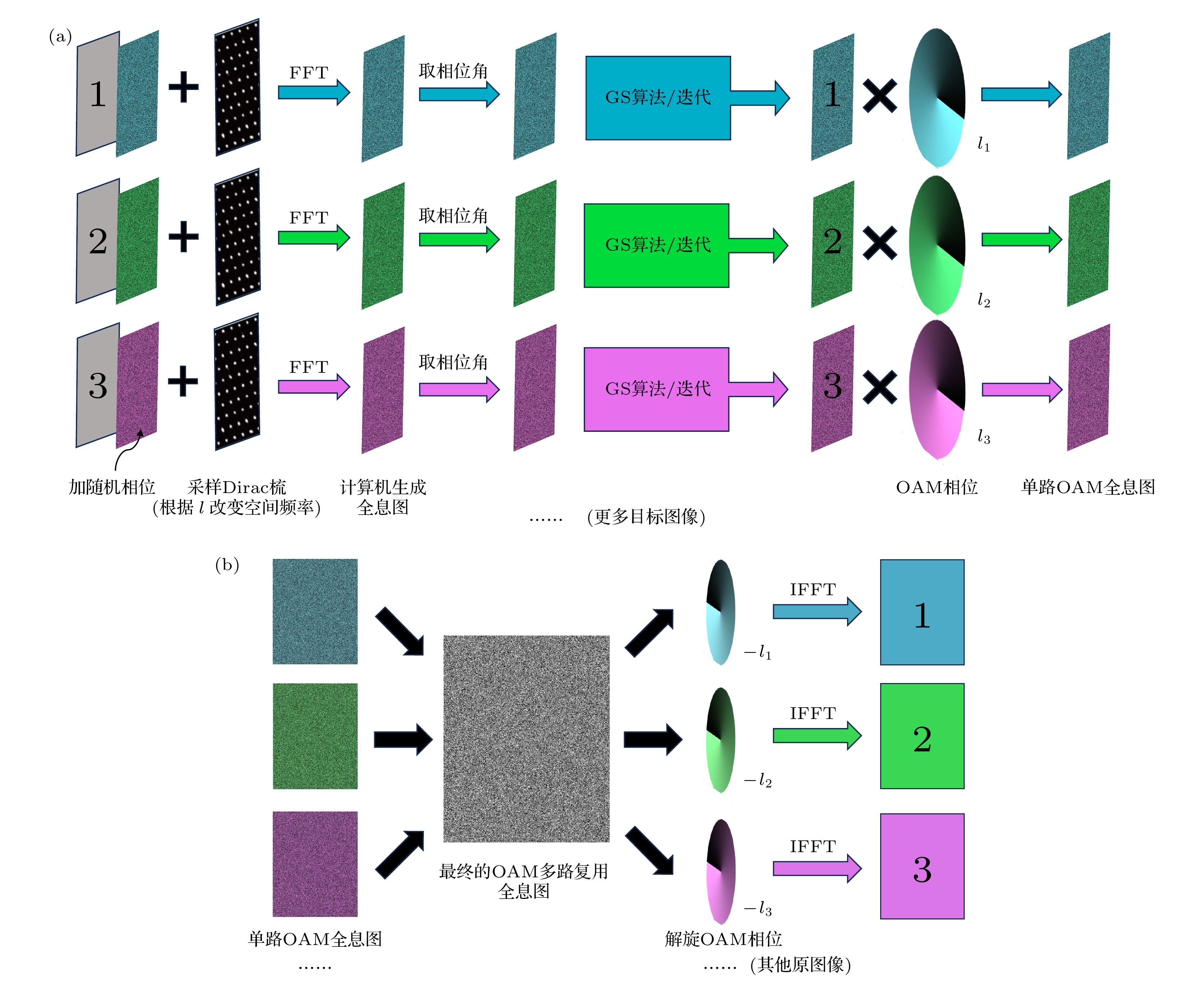
为制作OAM编码的2D加密全息图, 首先将目标图像转换为灰度图, 并将随机相位因子与图上灰度值相乘. 对于每条预处理完成的图片通道, 预先选定一个对应的拓扑荷
$ {l}_{i} $ , 将这张图与符合采样频率条件的狄拉克梳函数相乘, 以此保留OAM信息. 在远场近似下, 对图像进行快速傅里叶变换算法(FFT)[36]生成一张保留OAM信息的全息图. 为了使该全息图复原出来的图像还原度更高, 清晰度更好, 减少这个过程产生的信息误差, 完成FFT后, Gerchberg-Saxton (GS)算法被使用以对该全息图进行迭代[37]. 在仅保留该全息图的相位信息下根据相应拓扑荷对相位信息加旋, 即将目前得到的相位全息图乘上螺旋相位$ {{\mathrm{e}}}^{{\mathrm{i}}{l}_{i}\phi } $ , 得到具有特定拓扑荷的OAM选择性全息图. 例如, 对于第1张图, 选择拓扑荷为$ {l}_{1} $ , 通过上述方法得到拓扑荷为$ {l}_{1} $ 的第一张的第1张OAM选择性相位全息图. 重复上述步骤, 得到n张具有不同拓扑荷$ {(l}_{1}, {l}_{2}, \cdots , {l}_{n}) $ 的OAM选择性相位全息图, 如图2(a)所示.这n张OAM选择性相位全息图被叠加, 叠加产生的全息图再被取相位, 可得多路复用OAM相位全息图. 若使用若干束具有不同拓扑荷(
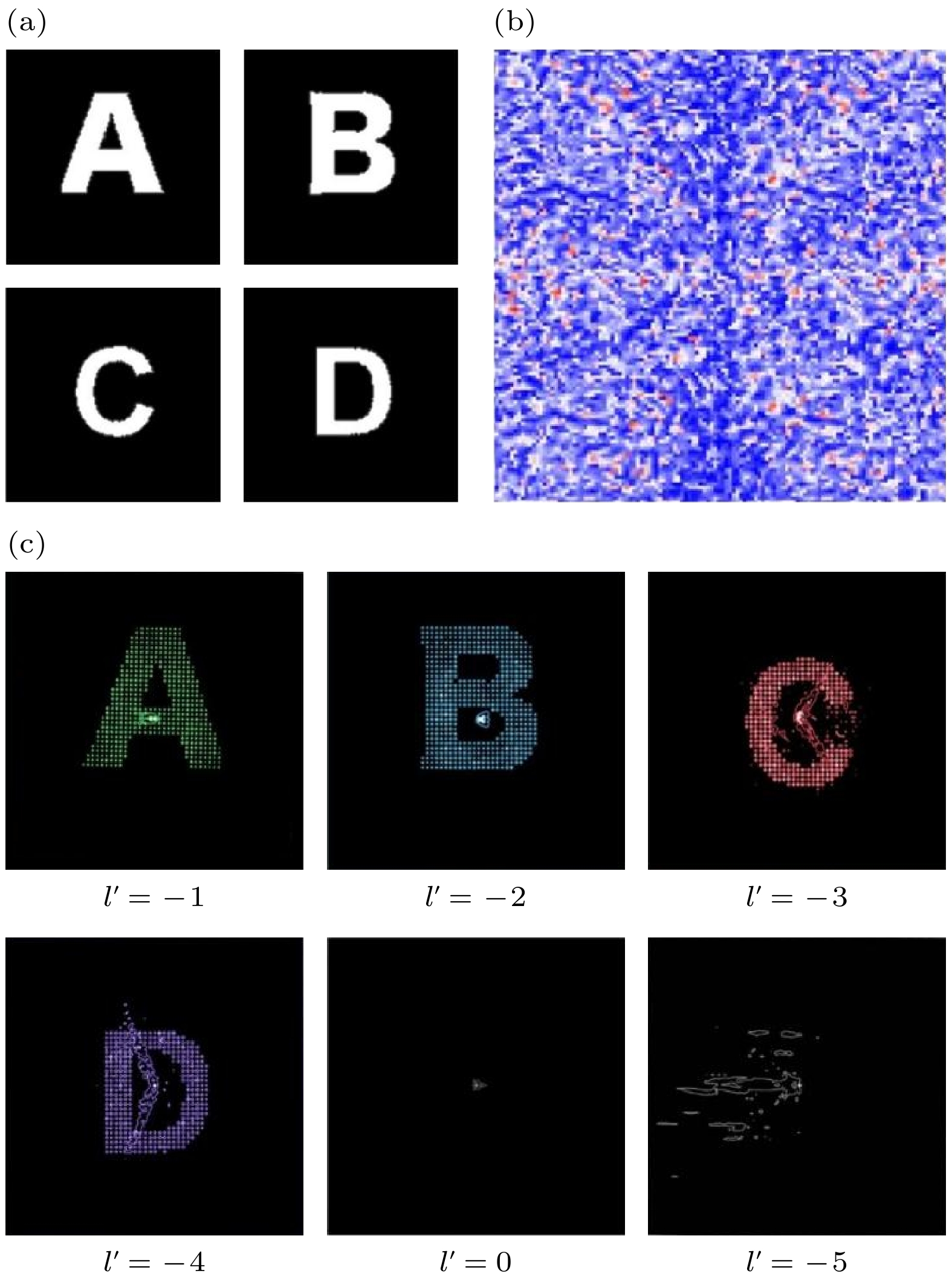
$ l'_{i} $ )的涡旋光对多路复用全息图进行照射还原, 即先将多路复用全息图乘上螺旋相位$ {{\mathrm{e}}}^{{\mathrm{i}}{l}_{i}'\phi } $ , 再使用快速傅里叶逆变换(IFFT), 可得到若干幅解密后的图像(比如$1', 2', 3' $ 等), 如图2(b)所示. 通过比较不同解旋的拓扑荷$ {l}_{i}' $ 与加旋的拓扑荷$ {l}_{i} $ 的关系以及他们对应的解密图像, 能够验证OAM编码全息图的理论.如图3(a)所示, 为4幅目标图像的原图. 目标图像的像素为128×128. 每幅图像预先与一个拓扑荷
$ {l}_{i} $ 相关联, 图像A的拓扑荷选取为$ {l}_{1} $ =1, 图像B的拓扑荷选取为$ {l}_{2}=2 $ , 图像C的拓扑荷选取为$ {l}_{3}=3 $ , 图像D的拓扑荷选取为$ {l}_{4}=4 $ . 根据上述操作, 利用Matlab软件进行仿真, 生成如图3(b)所示的多路复用相位全息图. 为了验证多路复用全息图的还原效果, 设置不同的复现光束的拓扑荷$ l'_{i} $ , 并观察解密图像. 将复现光束的拓扑荷先后取为$ l'_{1} = -1 $ ,$ l'_{2} = -2 $ ,$ l'_{3} = -3 $ ,$ l'_{4} = -4, \; l'_{5} = 0,\; l'_{6} = -5 $ , 得到如图3(c)示的6幅复现解密图像.可见当
对应拓扑荷为
$ {l}_{i} $ 的图像能够被复现, 而对应其他拓扑荷的图像几乎不显示. 这表明多路复用的OAM成像不同通道的串扰较低, 因此实现多通道全息图的传输复用. 当$ l'_{i} $ 和$ {l}_{i} $ 之和不等于0时, 复现图中几乎不显示任何原图所包含的有效信息. 这一特性使得该技术可以用于图像加密, 通过特定的拓扑荷作为密钥来解密相应的图像. 而图中字母中间的亮点以及类似于“钟表指针”的图案, 是由于OAM光的波前复振幅$ {{\mathrm{e}}}^{{\mathrm{i}}l\phi } $ 具有位于中心原点的相位奇点. 并且复现过程中由于引入了螺旋相位, 因而指针角度大小会随着$ l $ 的增大而增大. -
上述实验针对多幅无关联二维图像的OAM多路复用, OAM加密全息技术在高通量全息图传输与复现过程中的应用价值得以证明. 为了进一步挖掘这一技术的应用潜力, OAM加密全息可被用于实现3D物体的分层全息成像, 从而实现使用单个全息储存材质储存和复现三维物体信息. 直接处理三维物体的空间信息较为困难, 因此可将它转换为不同的平面信息. 通过分层法将其分为若干层二维平面, 每层二维平面到傅里叶透镜的距离都不同, 视作
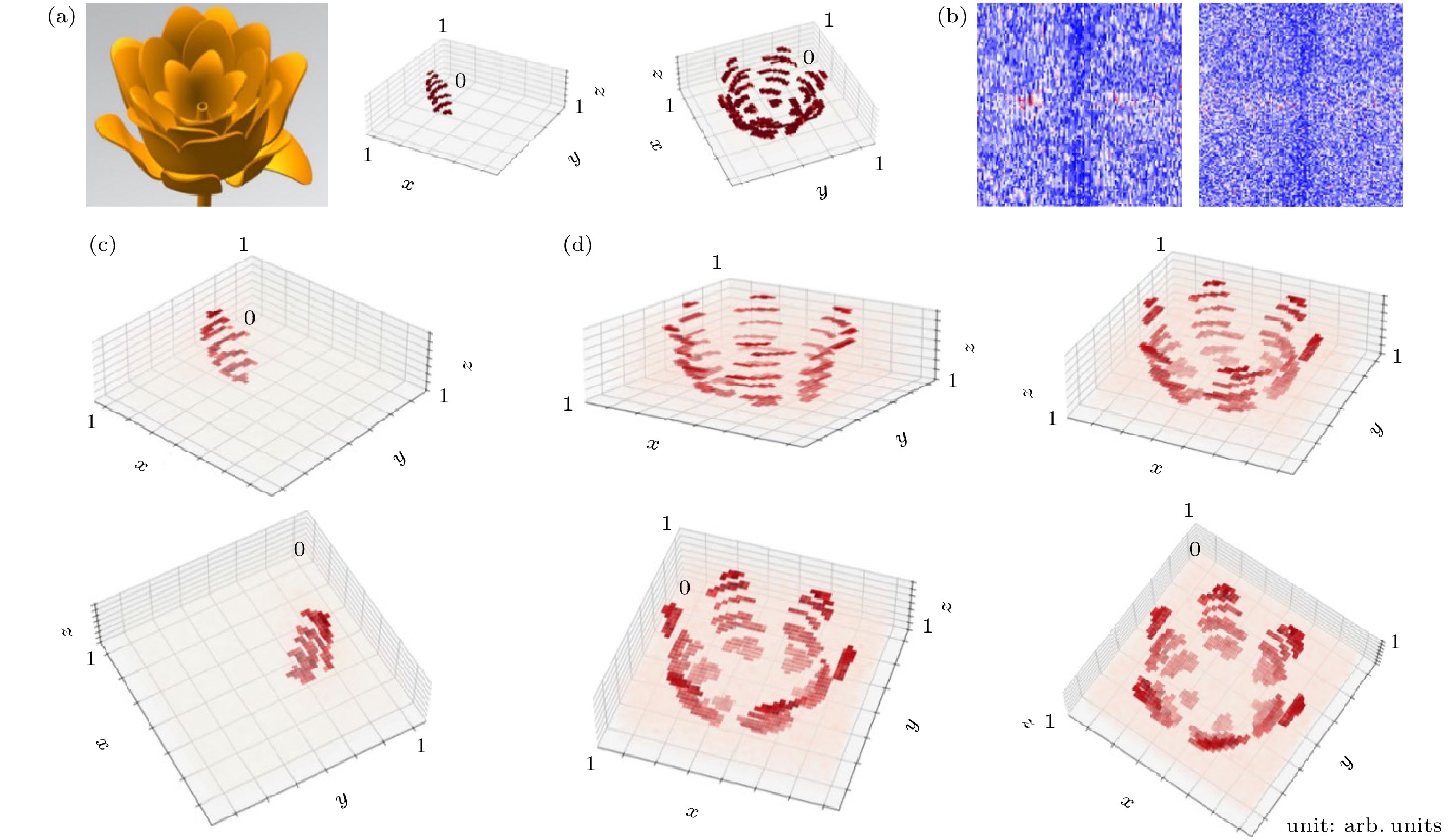
$ {z}_{i} $ , 不同平面层根据$ {z}_{i} $ 编号为$ 1, 2, \cdots, i, \cdots, n $ . 通过选择特定的$ i{\text{-}}l $ 关系,$ {l}_{i}=f\left(i\right) $ , 这些二维平面图被分别加旋并被计算得到OAM选择性全息图. 这些选择性全息图被叠加形成一幅多路复用OAM全息图. 这样, 可以将一个三维物体的全部信息保存在一张多路复用OAM全息图中, 实现了高容量且“降维”保存的效用. 而后在解旋的时候, 根据对应的拓扑荷以及$ f\left(i\right) $ 反解出片的标记$ i $ , 得到它应该处于的空间位置, 在计算机中处理并合成三维物体的完整信息. 在这个过程中, 不同平面的拓扑荷组成一串密钥, 同时函数$ f\left(i\right) $ 也可看成一密码函数, 只有采用对应的密钥和对应的函数才能完全解开三维物体的信息, 从而大大增加了信息的安全性. 理论上切片的多少, 即分层距离不同不会产生层间干扰, 但是实际上分层距离越短, 切片越多, 解旋过程中会存在串扰会越多, 因而合适的切片距离在可以保证获得足够的信息量的同时, 层间串扰也比较小. 此外, 通过选择特定的复现光的涡旋度l, 可以取出三维物体的特定部分信息, 例如, 如果需要观察一个三维物体的内部, 那可以只取三维物体内部切片的z对应的l进行复现. 由于还包含了3D模型的内部所有信息, 这种技术可以大大丰富3D模型的细节, 助力虚拟现实技术的应用化场景研究, 并推动光学通信、医学、游戏等各种领域的发展.如图4(a)所示的三维物体玫瑰经过处理, 得到一片花瓣和简化的玫瑰. 先按照上述方法获得花瓣的全息图, 并进行三维复现, 再对玫瑰进行同样的操作. 按图中垂直于z轴分别切片为7层, 根据每层对应z轴位置进行编号. 按以上方法将每层图片分别制作得到全息图, 之后进行加旋, 其拓扑荷分别设置为
$ {l}_{j} $ ,$ j=-3, -2, -1, 0, 1, 2, 3 $ , 再将每个加旋之后的全息图叠加形成一多通道复用全息图, 如图4(b)所示, 其中左图为单瓣花瓣的多路复用相位全息图, 右图为玫瑰的多路复用相位全息图. 接着通过不同的$ l'_{j} $ 对图形进行解旋复原, 根据(2)式, 基于不同需求, 不同的$ l'_{j} $ 能够被选择, 由此可以复现出对应的分层图形, 并根据$ l'_{j} $ 得到对应图形所在z轴的位置. 通过计算机处理, 将解旋得到的还原图在z轴方向上叠放, 得到三维的全息复现图. 对于不同视角下的三维复现结果, 花瓣如图4(c)所示, 玫瑰如图4(d)所示. 复现还原图已与原图十分接近, 说明三维物体可以被这种三维全息技术有效记录, 并保存在一张二维图形中, 实现信息安全高效存储和传递. 在第3和第4节中, 拓扑荷并没有被取到特别大, 是因为本实验的图片尺寸较小, 图片信息会被较大的拓扑荷加旋解旋破坏. 同时, 实际情况中, 高拓扑荷数的OAM光束可能更敏感于扰动, 如大气扰动或光学系统中的畸变, 这可能影响光束的质量和稳定性. -
通过对数字全息图编码, 实现了基于OAM性质的加密全息图和复现, 一种调控便捷、信息安全性高且存储空间需求小的技术得以开发. 基于OAM模式的正交性, 在Matlab仿真模拟中, 多幅二维图像通过OAM全息技术能被整合到一个OAM多路复用加密全息图中, 每个二维图像的复现依赖于特定的拓扑荷. 之后, 该技术被用于描述三维图像, 将三维物体的分层信息编码储存在同一幅OAM多路复用全息图中, 实现了对于三维物体的高通量信息储存, 并通过拓扑荷作为安全密钥, 不同的拓扑荷对应不同层次的三维信息, 极大地增强了信息传输的安全性. 这种技术可以在光学和通信领域开辟出一系列新的应用, 为光学、信息领域的研究和应用提供新的思路和方法.
轨道角动量复用三维加密全息图
Orbital angular momentum multiplexing three-dimensional encrypted hologram
-
摘要: 经过几十年的发展, 全息成像已成为展示信息的成熟光学技术. 然而, 仅通过光的波长和偏振作为信息传递的载体的传统全息技术, 在信息传播的安全性和容量方面存在一定的不足. 将一种新的光学维度, 轨道角动量(orbital angular momentum, OAM), 引入全息成像为这些问题提供了一个有效的解决方案. 通过使用OAM复用的全息技术进行理论分析和仿真计算, 二维图像被加密和存储. 然后三维物体被切片为多幅二维图像, 通过OAM复用的全息技术被存储于一个相位阵列中, 实现了信息存储维度的有效降低, 并且经过OAM复用的全息技术被成功复现, 因而三维全息被实现. 此外, 每幅图按照相应拓扑荷进行加密, 信息传递的安全性被显著提升. 这种具有OAM选择性的全息技术更为安全, 信息通量更大, 具有广泛的应用潜力.Abstract:
After decades of development, holography has evolved into a sophisticated optical technology for information display. Traditional holographic techniques, which rely solely on the wavelength and polarization of light as information carriers, are limited in both security and capacity of information. The introduction of orbital angular momentum (OAM) as an additional optical dimension into holography effectively addresses these challenges. In order to maintain the OAM mode characteristics of the original image, spatial discrete sampling must be performed first. The sampled image undergoes Fourier transform to generate a discrete hologram. An OAM-selective hologram is then constructed by multiplying the discrete hologram with a spiral phase factor. By superimposing multiple selective holograms with varying topological charges, an OAM-multiplexing hologram is generated. Using this approach, computer simulations of OAM-based holography demonstrate the encryption of multiple two-dimensional images with different topological charges ($ {l}_{i} $) into an OAM-multiplexing hologram for storage. Decryption is achieved by illuminating the multiplexing hologram with a reproduction beam of a specific topological charge. When the condition ($ l'_{i}+{l}_{i}= 0 $) is satisfied, the original image associated with the corresponding topological charge is successfully reproduced. Furthermore, a three-dimensional object, such as a rose in the article, can be decomposed into multiple two-dimensional planes by using a layering method. Holograms for each layer are generated based on their spatial positions and a custom function f that assigns topological charges ($ {l}_{j} $). These holograms are stored in a phase array through OAM-multiplexing holography, effectively reducing the dimensionality of information storage. By setting different reproduction charges ($ l'_{j} $), the holograms are successfully reconstructed. The spatial position of each layer is determined by the function f, enabling the replicating and stacking of layers to achieve a three-dimensional reconstruction of the rose, including its petals, from different perspectives. This process realizes three-dimensional holography. Notably, the combination of topological charge and the function f servesacts as a cryptographic key, significantly enhancing the security of information transmission. This OAM-selective holography technology not only improves security, but also achieves higher information throughput, indicating its enormous potential in various applications. -
Key words:
- orbital angular momentum /
- hologram /
- 3D imaging .
-

-
图 1 (a)得到离散全息图的示意图, 其能保留OAM模式特征; (b)最小采样间距-拓扑荷关系示意图; (c) OAM选择性全息图的示意图和使用不同拓扑荷进行解旋的效果示意图; (d)多路复用全息图制作示意图; (e)使用携带不同拓扑荷的光对多路复用全息图进行解旋的过程示意图
Figure 1. (a) Schematic of obtaining a discrete hologram, which preserves the OAM mode characteristics; (b) schematic of the relationship between the minimum sampling interval and topological charge; (c) schematic of an OAM-selective hologram and the effect of demodulating with different topological charges; (d) schematic of the process of creating a OAM-multiplexing hologram; (e) schematic of the process of demodulating the OAM-multiplexing hologram using light with different topological charges.
图 4 (a)左图为三维玫瑰建模图, 中间图为3D单瓣玫瑰原图, 右图为简化的3D玫瑰原图; (b)左图为单瓣玫瑰的OAM多通道复用相位全息图, 右图为简化玫瑰的OAM多通道复用相位全息图; (c)多视角下的单瓣花瓣的三维全息复现还原图; (d)多视角下的玫瑰的三维全息复现还原图, 每个坐标图的x, y, z坐标轴的单位是任意单位
Figure 4. (a) Left image shows a 3D rose model, the middle image is the original 3D single-petal rose, and the right image is a simplified version of the original 3D rose; (b) the left image is the OAM-multiplexing phase hologram of the single-petal rose, and the right image is the OAM-multiplexing phase hologram of the simplified rose; (c) 3D holographic reconstruction of the single-petal rose from multiple perspectives; (d) 3D holographic reconstruction of the rose from multiple perspectives, with the units of the x, y, z axes in each coordinate plot being arbitrary units.
-
[1] Lin S F, Wang D, Wang Q H, Kim E S 2020 Opt. Laser Eng. 126 105895 doi: 10.1016/j.optlaseng.2019.105895 [2] Lin X, Liu J, Jia J, Pan Y J, Wang Y T 2013 Opt. Express 21 20577 doi: 10.1364/OE.21.020577 [3] Shi L, Li B, Kim C, Kellnhofer P, Matusik W 2021 Nature 591 234 doi: 10.1038/s41586-020-03152-0 [4] Choi S, Gopakumar M, Peng Y, Kim J, Wetzstein G 2021 ACM Trans. 40 240 doi: 10.1145/3478513.3480542 [5] Li X P, Ren H R, Chen X, Liu J, Li Q, Li C M Y, Xue G L, Jia J, Cao L C, Sahu A, Hu B, Wang Y T, Jin G F, Gu M 2015 Nat. Commun. 6 6984 doi: 10.1038/ncomms7984 [6] Blanche P A 2021 Light Adv. Manuf. 2 28 doi: 10.37188/lam.2021.028 [7] Blinder D, Birnbaum T, Ito T, Shimobaba T 2022 Light Adv. Manuf. 3 35 doi: 10.37188/lam.2022.035 [8] Vyas S, Chia Y, Luo Y 2018 Opt. Express 26 21979 doi: 10.1364/OE.26.021979 [9] He Z H, Sui X M, Jin G F, Cao L C 2019 Appl. Opt. 58 A74 doi: 10.1364/AO.58.000A74 [10] Bruckheimer E, Rotschild C, Dagan T, Amir G, Kaufman A, Gelman S, Birk E 2016 Eur. Heart J. Card. Img. 17 845 doi: 10.1093/ehjci/jew087 [11] Gibby W, Cvetko S, Gibby A, Gibby C, Sorensen K, Andrews E G, Maroon J, Parr R 2021 J. Neurosurg. 137 489 doi: 10.3171/2021.9.JNS21510 [12] Wan Z S, Wang Z Y, Yang X L, Shen Y J, Fu X 2020 Opt. Express 28 31043 doi: 10.1364/OE.400587 [13] Ngcobo S, Litvin I, Burger L, Forbes A 2013 Nat. Commun. 4 2289 doi: 10.1038/ncomms3289 [14] Ahmed N H, Ahmed M S 2021 Int. Design J. 11 247 doi: 10.21608/idj.2021.152357 [15] Kong D Z, Cao L C, Jin G F, Javidi B 2016 Appl. Opt. 55 8296 doi: 10.1364/AO.55.008296 [16] 赫明钊, 曹良才, 谭峭峰, 何庆声, 金国藩 2009 光学学报 29 2709 doi: 10.3788/AOS20092910.2709 He M Z, Cao L C, Tan Q F, He Q S, Jin G F 2009 Acta Opt. Sin. 29 2709 doi: 10.3788/AOS20092910.2709 [17] Yan L, Xiao J, Plaskocinski T, Biabanifard M, Persheyev S, Askari M, Di Falco A 2022 Opt. Express 30 19145 doi: 10.1364/OE.456843 [18] Zhao R Z, Sain B, Wei Q S, Tang C C, Li X W, Weiss T, Huang LL, Wang Y T, Zentgraf T 2018 Light Sci. Appl. 7 95 doi: 10.1038/s41377-018-0091-0 [19] Chen W, Chen X D 2016 Appl. Opt. 55 6740 doi: 10.1364/AO.55.006740 [20] Kim J, Choi J, An J, Kim N, Lee K 2005 Opt. Commun. 247 265 doi: 10.1016/j.optcom.2004.11.066 [21] Zhou H, Sain B, Wang Y 2020 ACS Nano 14 5553 doi: 10.1021/acsnano.9b09814 [22] Fang X Y, Ren H R, Gu M 2020 Nat. Photonics 14 102 doi: 10.1038/s41566-019-0560-x [23] 程鹏雨 2023博士学位论文 (上海: 上海大学) Cheng P Y 2023 Ph. D. Dissertation (Shanghai: Shanghai University [24] Wen DD, Yue F Y, Li G X, Zheng G X, Chan K L, Chen S M, Chen M, Li K F, Wong P W H, Cheah K W, Pun E Y B, Zhang S, Chen X Z 2015 Nat. Commun. 6 8241 doi: 10.1038/ncomms9241 [25] Willner A E, Huang H, Yan Y 2015 Adv. Opt. Photon. 7 66 doi: 10.1364/AOP.7.000066 [26] 柯熙政, 谢炎辰, 张颖 2019 光学学报 39 0126017 doi: 10.3788/AOS201939.0126017 Ke X Z, Xie Y C, Zhang Y 2019 Acta Opt. Sin. 39 0126017 doi: 10.3788/AOS201939.0126017 [27] Lei T, Zhang M, Li Y, Jia P, Liu G N, Xu X, Li Z, Min C, Lin J, Yu C, Niu H, Yuan X 2015 Light Sci. Appl. 4 257 doi: 10.1038/lsa.2015.30 [28] Lim K T, Liu H, Liu Y, Yang J K 2019 Nat. Commun. 10 1 doi: 10.1038/s41467-018-07882-8 [29] Gibson G, Courtial J, Padgett M, Vasnetsov M , Pas’ko V 2004 Opt. Express 12 5448 doi: 10.1364/opex.12.005448 [30] Gong L, Zhao Q, Zhang H, Hu XY, Huang K, Yang JM, Li Y M 2019 Light Sci. Appl. 8 27 doi: 10.1038/s41377-019-0140-3 [31] Paturzo M, Memmolo P, Finizio A, Näsänen R, Naughton T J, Ferraro P 2010 Opt. Express 18 8806 doi: 10.1364/OE.18.008806 [32] Wang J, Liu J, Li S H, Zhao Y F, Du J, Zhu L 2022 Nanophotonics 11 645 doi: 10.1515/nanoph-2021-0527 [33] Zhong Z Q, Tang WH, Yuan H, Zhang B 2023 Opt. Laser Technol. 169 110081 doi: 10.1016/j.optlastec.2023.110081 [34] Raveh D, Pokharel S, Korotkova O 2023 Opt. Lett. 48 2405 doi: 10.1364/OL.488449 [35] Willner A E, Pang K, Song H, Zou K, Zhou H 2021 Appl. Phys. Rev. 8 041312 doi: 10.1063/5.0054885 [36] Pizzo A, Sanguinetti L, Marzetta T L 2022 IEEE Trans. Wire. Commun. 21 6890 doi: 10.1109/TWC.2022.3152965 [37] Salgado-Remacha F J 2016 Opt. Laser Technol. 85 30 doi: 10.1016/j.optlastec.2016.05.021 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: