光学非互易性的核心特点是方向依赖性, 即光在特定介质中沿一个方向的传输与沿相反方向的传输表现出不同的速度、吸收率或相位变化. 这一现象通常涉及到时间反演对称性的破坏, 经常通过施加外部磁场或利用磁光效应等手段实现^[1]. 光学非互易相关的研究具有较大的实际应用价值, 比如在信息通信技术领域的光隔离器和光二极管等的光学非互易器件^[2], 可以有效地减少信号的干扰, 提高通信系统的稳定性, 有利于帮助构建较为复杂的光学网络中心. 对于微尺度光学系统如集成光学器件和光子芯片^[3], 利用非互易性可以显著增强元器件的功能性, 推动更复杂的光路设计的出现, 进而推动光计算和光信息处理技术的发展. 在传感和量子信息系统^[4–6], 非互易光学元件具有能够提高系统灵敏度和抗干扰能力的优势.

近年来, 随着光子学和材料科学的发展, 尤其是在拓扑光子学和超材料等新兴领域的探索, 相关的科研工作者们开始研究能够更高效地实现非互易性的光学器件. 为实现这种非互易性, 常常需依赖特殊材料或结构设计, 如非中心对称晶体或特定的光子晶体. 然而, 光学非互易性通常不出现在自然界的大多数传统材料和系统中, 因为这些材料遵循时间反演对称性, 即物理过程在时间方向上是可逆的. 截至目前, 无磁光学非互易研究主要在光子晶体时空调制^[7,8]、非线性光学效应^[9]、手性量子光学^[10–13]、光与机械振动^[14]、拓扑光子学^[15–18]等领域进行. 而在原子体系中由于通过激光激发跃迁能存在很多非线性效应, 比如电磁诱导透明(EIT)^[19]、四波混频^[20]、拉曼效应^[21]等, 所以出现了很多在原子体系中进行光学非互易研究的成果. 比如2018年, 华东理工大学龚尚庆组^[22]把原子热运动和电磁诱导透明对双光子失谐特别敏感的特点相结合, 提出了热运动诱导非互易量子光学系统的方案. 2019年, 他们小组又开发了一个基于四能级原子的理论模型, 并使用热铷原子成功实现了光学非互易的非互易放大^[23]. 2020年, 他们小组利用热铷原子中的简单二能级系统, 通过耦合光激发, 成功实现了无磁光学非互易性, 实验上达到了最高20 dB的隔离效果^[24]. 此外, 该方案还允许通过调整耦合光参数灵活控制工作带宽、频率及隔离方向, 实现了可重构的操作^[24]. 同年, 该研究小组在无腔N型热⁸⁷Rb原子系统中通过调节两个耦合光的强度, 显著增强了探测光的非互易带宽^[25]. 2021年, 南京大学夏可宇教授团队^[26]在非互易原子气室中充入缓冲气体, 利用原子随热运动的强烈碰撞和原子的多能级结构, 实现了1.2 GHz的非互易工作带宽, 隔离比接近40 dB. 同年, Hu等^[27]发现了处于随机热运动的原子天然存在“速度选择的非线性”响应, 从而突破了无源非互易中动态互易的限制. 2022年, 南京大学夏可宇教授团队^[28]又通过在热铷原子中打破时间反演对称性实现EIT的光学非互易来区分和Autler-Townes分裂的区别. 同年, 李鑫等^[29]利用原子热运动的极化率-动量锁定和腔体的强耦合特性, 设计并实现了一种基于铯原子-腔复合系统的光学非互易传输转换方案. 尽管在原子体系中已经有了诸多的光学非互易研究成果, 但是在这些研究中涉及室温下的铯原子较少, 而且在铯原子体系中隔离比能达到20 dB以上的也不多.

相比于其他碱金属原子, 铯原子在进行光学非互易方面的研究具有几个明显的优势: 1)铯原子相比于其他碱性原子由于具有较小的饱和光强^[30,31], 在相同激光强度激发下的效率就高, 能够在不加热室温的情况下通过较小的激光功率进行激发, 那么将便于小型化和集成化. 2)铯原子的基态具有间隔大的超精细能级, 与光场的相互作用不易受周围能级的影响. 3)铯原子具有丰富的能级结构和易于控制的光学性质, 铯原子的激发态光谱通常没有多普勒展宽, 因此其光谱精度更高. 4)铯原子D1线激发所需要的894 nm波长与InAs量子点激子发射波段是一样的, 那么其将不仅可以成为原子和固态系统进行量子态交换的纽带, 也可以与非经典态光场相互作用实现量子信息过程.

因此, 本文提出在室温下铯原子体系中, 利用激光激发传输通过铯原子介质的Λ型能级配置实现EIT, 得到EIT信号的光学非互易传输并通过一系列光学可调参量进行非互易现象规律的调控研究. 通过对非互易现象规律的测量分析得到了该系统中隔离比随各类可调参量的变化曲线, 获得了26 dB的最大隔离比, 可在铯原子体系光学非互易调控方面提供实验上的有力证明, 为光学非互易器件的小型化和集成化提供实验上的支撑.

图1(a)所示为本次实验需要用到的铯原子Λ型原子能级图, 探测光和耦合光的频率各自对应铯原子D1线的超精细结构中两个跃迁能级产生光与原子的相互作用. 图1(b)是实验简易装置图, 一个铯原子气室被放在如图所示的光路中, 一台激光器产生探测光p, 激光波长设定为894.596 nm, 经过偏振分光棱镜(PBS)与耦合光共线同向或反向注入到铯原子气室中. c₁光束和c₂光束作为耦合光由同一台激光器产生, 激光波长设定为894.594 nm, 经过两个偏振分光棱镜(PBS)穿过铯原子后经偏振分光棱镜反射出去. 探测器APD用于探测在铯原子气室内探测光与耦合光相互作用后出射的探测光, 在示波器上进行显示测量. 探测光频率为ω_p, 作用于从基态$ \left| a \right\rangle $(6S_1/2, F = 4)到激发态$ \left| c \right\rangle $(6P_3/2, F = 5)的能级跃迁. 铯原子基态$ \left| a \right\rangle $与激发态$ \left| c \right\rangle $间的能级频率差为ω_ca, 探测光p光束的频率失谐: $ {\varDelta _{\text{p}}} = {\omega _{\text{p}}} - {\omega _{{\text{ca}}}} $. 耦合光c₁光和c₂光, 作用于从基态$ \left| b \right\rangle $(6S_1/2, F = 3)到激发态$ \left| c \right\rangle $(6P_3/2, F = 5)的能级跃迁, 能态$ \left| c \right\rangle $与$ \left| b \right\rangle $的能级频率差为ω_cb. c₁光频率为$ {\omega _{{{\text{c}}_1}}} $, 频率失谐: $ {\varDelta _{{{\text{c}}_1}}} = {\omega _{{{\text{c}}_1}}} - {\omega _{cb}} $; c₂光频率为$ {\omega _{{{\text{c}}_2}}} $, 频率失谐: $ {\varDelta _{{{\text{c}}_2}}} = {\omega _{{{\text{c}}_2}}} - {\omega _{{cb} }} $. 实验是在室温下进行的, 在26 ℃情况下对应的铯原子密度为$ 1.0 \times {10^{10}} \;{\text{c}}{{\text{m}}^{ - 3}} $.

在探测光传输过程中, 引入耦合光会在介质中形成透明窗口, 显著影响原子的极化率, 而在原子共振频率附近, 原子极化率对于弱探测光在介质中的传输特性又有着重要的影响. 因此, 重点分析在不同的耦合光条件下, 探测光通过铯原子一次时, 原子动力学行为的变化. 在不考虑原子热运动的条件下, 铯原子气室中原子速度为0, 此时在单向或双向耦合光的条件下, 通过应用三能级原子系统的哈密顿量和原子密度算符的动力学方程, 并考虑耦合光的强度远大于探测光强度的条件下, 可以有效计算探测光对应密度算符的稳态近似解. 在考虑探测光自缀饰作用$ {\varOmega _{\text{p}}}\varOmega _{\text{p}}^{\text{*}}/{\gamma _{{\text{aa}}}} $时, 分别打开耦合光c₁和c₂的情况下相应的稳态近似解分别为

其中$ {\varOmega _{{{\text{c}}_{1}}}} $是c₁光的拉比频率, $ {\varOmega _{{{\text{c}}_{2}}}} $是c₂光的拉比频率, $ {\gamma _{ab}} $是基态$ \left| a \right\rangle $和$ \left| b \right\rangle $能级间的退相干率, $ {\gamma _{ca}} $是激发态$ \left| c \right\rangle $到基态$ \left| a \right\rangle $能级间的衰减率, $ {\gamma _{aa}} $是由探测光激发引发自缀饰作用的相应能级衰减率. 考虑到由于原子运动引起的多普勒频移, 此时气室内铯原子运动速度不为0. 设定以特定速度v运动的原子与c₁光的运动方向相一致的为正向, 那么对于正向传输的p₁与c₁光的频率项, 需要考虑${\boldsymbol {kv}} $. 其中$ {\boldsymbol{k}} = \omega {\boldsymbol{v}}/{\boldsymbol{c}} $为光的波矢量, 因为$ {\omega _{{{\text{c}}_1}}} \approx {\omega _{{{\text{c}}_{2}}}} \gg {\delta _{\text{c}}} $, 且$ {\omega _{\text{c}}} - {\omega _{\text{p}}} \gg {\delta _{\text{c}}} $, 所以$ {{\boldsymbol{k}}_{{{\text{c}}_{1}}}} \approx {{\boldsymbol{k}}_{{{\text{c}}_{2}}}} \approx {{\boldsymbol{k}}_{\text{p}}} = {\boldsymbol{k}} $. 因此通过再计算可以得出探测光密度算符的稳态解为

(3)式和(4)式中$ {\varDelta '_{{\text{p(}}{{\text{c}}_{1}}{)}}} = {\varDelta _{{\text{p(}}{{\text{c}}_{1}}{)}}} + {\boldsymbol{kv}} $表示探测光p光(耦合光c₁光)以速度v运动的原子的频率失谐, $ {\varDelta '_{{{\text{c}}_2}}} = {\varDelta _{{{\text{c}}_2}}} - {\boldsymbol{kv}} $表示耦合光c₂以速度v运动的原子的频率失谐. 定义$ {\mu _{ca}} $是能级$ \left| a \right\rangle $到$ \left| c \right\rangle $的跃迁偶极矩, $ {\rho _{ca}} $表示密度算符$ {\rho _{11}} $或$ {\rho _{12}} $的通用表达式, 根据电动力学和非线性光学内容可以推出:

可得探测光的极化率和密度算符之间的关系为

规定$ {\varOmega _{\text{p}}} = {\mu _{ca}}{E_{\text{p}}}/{(}2\hbar {)} $, 考虑引入原子热运动导致的多普勒展宽效应, 能够求出原子对探测光p光和三能级原子间作用的复极化率是

式中, $ {\varepsilon _0} $表示真空介电常数, $ {k_{\text{B}}} $是玻尔兹曼常数, N表示铯原子泡中原子数密度, $ \hbar $是普朗克常数除以2π, m为相互作用的原子质量. 复极化率的虚部可以用来描述原子对探测光的吸收, 探测器探测到的探测光传输信号强度表达式为^[32]

其中P₀是探测光进入铯原子气室的功率强度, L是铯原子气室的长度, $ {\lambda _{\text{p}}} $是探测光的波长.

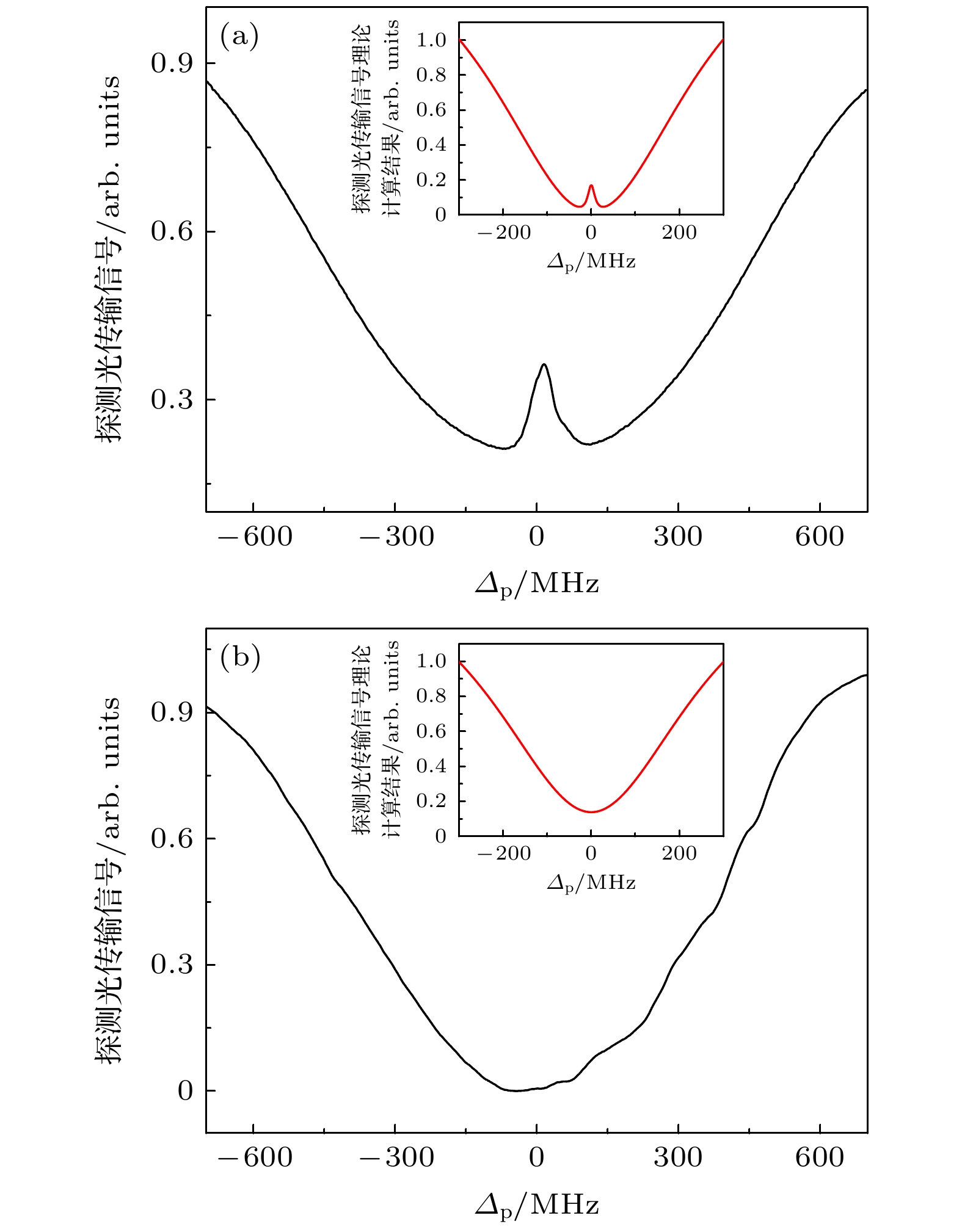
实验在26 ℃室温下, 首先在只有与探测光p同向的耦合光c₁存在的条件下, 接收分析探测器中得到的探测光传输信号. 接着又在仅有与探测光p反向的耦合光c₂存在的条件下观测了探测光传输信号. 从图2(a)可以看出, 当探测光和耦合光同向共线经过铯原子气室时, 耦合光场有效地降低了探测光在介质中的吸收, 在实验上观察到了EIT现象. 从图2(b)可以看到, 当探测光与耦合光共线反向经过铯原子气室时, 则几乎观测不到EIT现象. 通过对比可看出两种情况下EIT信号强弱差异较大, 表现出典型的方向依赖性, 显著地体现了光学非互易特征. 在理论方面, 探测光传输通道的输出是本文关注的重点, 相应的传输信号理论模拟图可通过在(8)式中分别代入$ {\rho _{11}} $(同向)或$ {\rho _{12}} $(反向)得到, 如图2(a), (b)插入的理论结果图所示. 由图2可知在$ {\varDelta _1} = 0 $处能够有效产生EIT峰值, 然后将耦合光束方向设置为与之前相反, 得到其EIT由于原子热运动速度发生了变化几乎消失. 理论模拟结果可表明该系统理论上具有非互易传输特性.

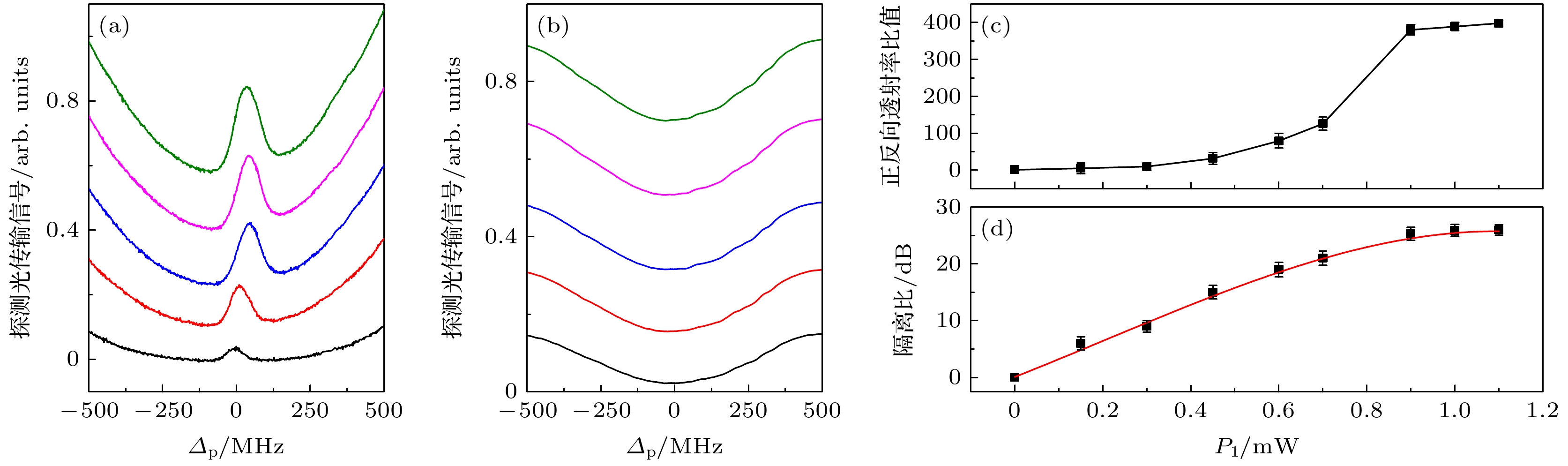
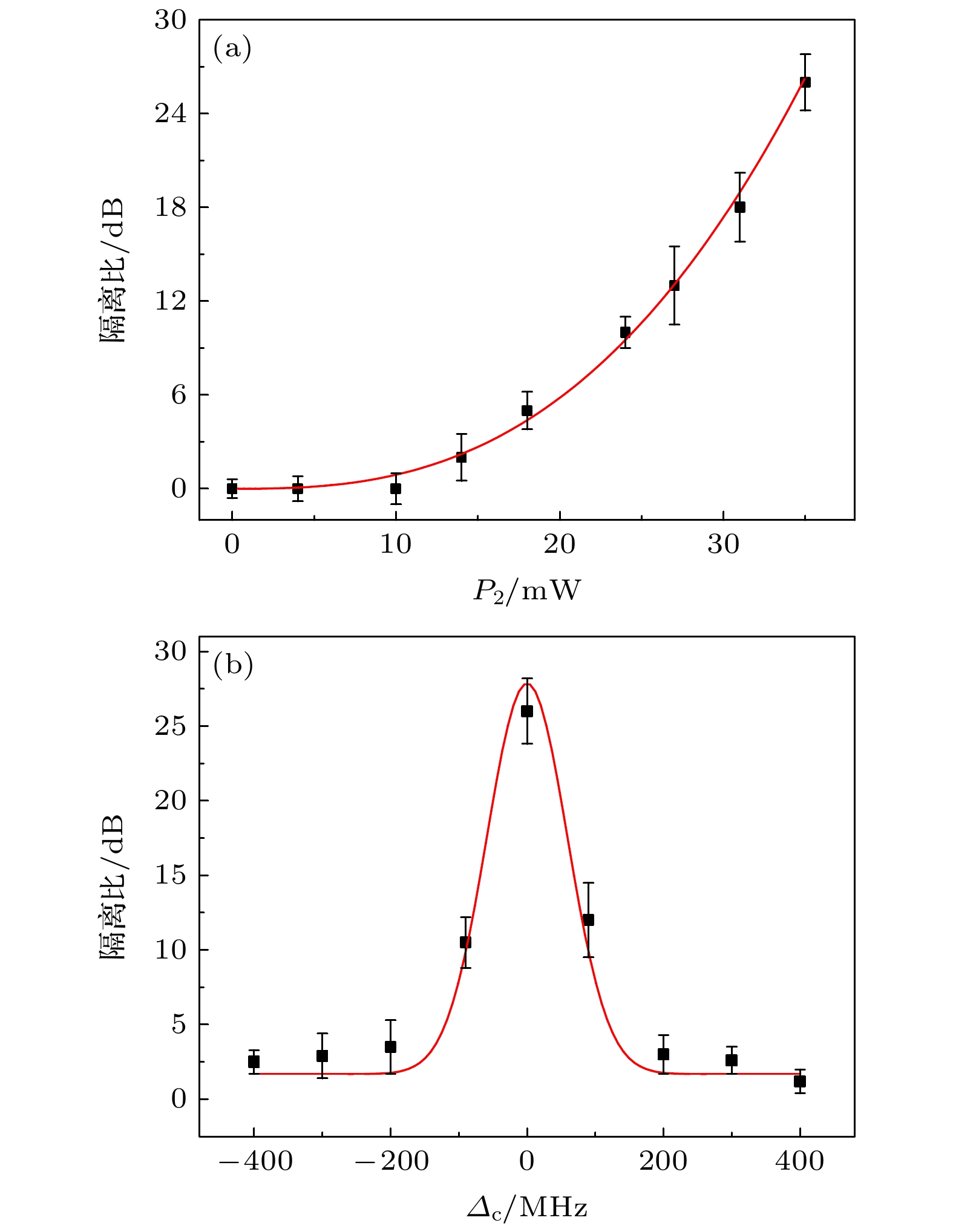
接下来进行一系列非互易传输的可调参量调控实验. 首先针对探测光功率进行调节, 固定耦合光的功率为35 mW, 固定$ {\varDelta _{{{\text{c}}_{1}}}} $, $ {\varDelta _{{{\text{c}}_{2}}}} $失谐为0, 得到图3所示的实验结果图. 图3(a)是不同探测光功率下同向传输的探测光传输信号图, 图3(b)是反向传输情况下不同探测光功率下的探测光传输信号图. 结果表明, 与近180°的反向传输情况相比, 同向传输操作中的激发共振条件可以得到更好的满足, 并获得可观的EIT信号. 在此过程中, 原子热运动引起激光的多普勒频移, 频率失谐$\varDelta _{\text{p}} $变化为$ {\varDelta '_{\text{p}}} = {\varDelta _{\text{p}}} +{\boldsymbol{ kv}} $, $ {\varDelta _{{{\text{c}}_{1}}{(}{{\text{c}}_{2}}{)}}} $变为$ {\varDelta '_{{{\text{c}}_{1}}{(}{{\text{c}}_{2}}{)}}} = {\varDelta _{{{\text{c}}_{1}}{(}{{\text{c}}_{2}}{)}}} \pm {\boldsymbol{kv}} $, 探测(耦合)光的波数为$ {k_{\text{p}}} = 2{\text{π}}/{\varLambda _{\text{p}}} $ ($ {k_{\text{c}}} = 2{\text{π}}/{\varLambda _{\text{c}}} $). 因此, 考虑到波数差异非常小($ {\varLambda _{\text{p}}} = {\varLambda _{\text{c}}} $), 在同向传输情况下, 探测光和泵浦光的多普勒频移几乎相同, 并且满足产生EIT的双光子共振条件$ {\varDelta '_{{{\text{c}}_{1}}}} - {\varDelta '_{\text{p}}} = {(}{\varDelta _{{{\text{c}}_{1}}}} + {\boldsymbol{kv}}{{) - (}}{\varDelta _{\text{p}}} + {\boldsymbol{kv}}{\text{) = }}{\varDelta _{{{\text{c}}_{1}}}} - {\varDelta _{\text{p}}} = 0 $, 是个一阶无多普勒构型. 然而, 对于反向传输的情况下, 探测光与耦合光($ {\varDelta '_{{{\text{c}}_{2}}}} = {\varDelta _{{{\text{c}}_{2}}}} - {\boldsymbol{kv}} $)之间的频率差变为$ {\varDelta '_{{{\text{c}}_{2}}}} - {\varDelta '_{\text{p}}} = {(}{\varDelta _{{{\text{c}}_{2}}}} - kv) - ({\varDelta _{\text{p}}} + {\boldsymbol{kv}}{\text{) = }}{\varDelta _{{{\text{c}}_{1}}}} - {\varDelta _{\text{p}}} - 2 {\boldsymbol{kv}}, $ 这破坏了在相同激光参数下产生EIT所需的双光子共振条件. 图3(c) 是实验上得到的同向传输和反向传输透射率相对于探测光功率P₁的变化图, 这里定义非互易对比度为$ (T_{{\mathrm{c o}}}- T_{{\mathrm{c o u}}}) /(T_{{\mathrm{c o}}}+T_{{\mathrm{c o u}}}) $, 隔离比为$ 10 \log _{10}\left(T_{{\mathrm{co}}} / T_{{\mathrm{c o u}}}\right) $, 其中$ T_{{\mathrm{c o}}}\left(T_{{\mathrm{c o u}}}\right) $表示相应实验参数下EIT信号的传输强度. 通过隔离比定义公式计算可得到如图3(d)所示的隔离比随着探测光功率的变化图. 可以看到, 光学非互易行为具有较高非互易对比度, 在较高的探测光功率P₁范围内产生理想的隔离功能, 其比值可达26 dB. 在初始阶段隔离比的值稳步增加, 直到在探测光功率0.9 mW附近, 隔离比曲线出现一个显著的峰值. 此时逐步加大探测光功率, 隔离比增大速度变缓. 隔离比的升高归因于在耦合光作用下, 铯原子系统对微弱入射探测光的非互易增强. 隔离比在峰值后增长显著趋于缓慢是因为强度高的探测光引起的能级自缀饰作用导致探测光传输信号的强度趋于饱和导致的. 因而适度的探测光功率有助于维持吸收强度曲线中EIT的强度, 保持高隔离比, 这为光学隔离器的性能指标提供了参考. 在实验过程中需要特别指出的是对于涉及相干制备原子气体的实际系统, 噪声可能通过激光功率和原子温度的波动以及光电探测器的电噪声引入. 外腔二极管激光器的输出功率波动通常小于$ \pm 0.5 {\text{%}} $, 导致隔离比的变化小于±0.07 dB. 原子温度的长期稳定性为±0.01 ℃, 原子密度N的变化率约为$ \pm 0.06 {\text{%}} $, 隔离比在±0.02 dB范围内波动. 系统参数波动引起的隔离比变化比测量值小得多. 同时, 在隔离比计算过程中, 去除光电探测器的电背景偏移(在两个探测光束都被阻挡的情况下测量)的影响, 即$ T_{{\mathrm{c o}}} \left(T_{{\mathrm{c o u}}}\right) $由同向传输(反向传输)探头的测量透射强度与平均背景偏移量之差得到.

然后固定探测光功率, 改变耦合光功率P₂进行隔离比的变化实验研究. 根据正、反向耦合光经过铯原子气室的条件, 控制耦合光功率作为实验变量, 研究EIT随耦合光功率的光谱曲线, 处理得到如图4(a)隔离比随耦合光功率变化的依赖曲线, 来呈现隔离比的改变趋势. 图4(a)实验条件设置为探测光具有1 mW功率, 失谐频率为0, 耦合光功率从0增至35 mW, 方形点和曲线分别代表实验值和相应的理论拟合曲线. 当功率从0增至35 mW时, 测量到的隔离比从0 dB增至26 dB, 根据密度矩阵公式与光场相应拉比频率成正比的原理, 很容易得到输出强度T_co随着耦合功率的提高呈现出线性增大. 在反向传输情况下, 由于原子密度不变, 只是耦合光功率影响了磁化率的虚部, 探测光束经历的吸收系数仍然很大. 很容易推断, 探测光的输出依赖于T_cou, 可以随着输入功率的增大而缓慢增大. 因此, 观察到的隔离比随着耦合功率的增大而增大, 与理论计算一致. 结果表明, 在一定的耦合光功率范围内, 实现了高性能的光学非互易系统.

最后, 研究了隔离比随耦合光失谐$ {\varDelta _{{{\text{c}}_{1}}{(}{{\text{c}}_{2}}{)}}} $的变化, 这些变化可以显著地改变同向传输探测光信号产生的效率, 但对反向传输探测光, 由于原子热运动引起激光的多普勒频移使得失谐对信号的影响很小. 图4(b)显示了在探测光功率为1 mW时, 耦合光功率35 mW, 通过对耦合光失谐进行离散操作得到的隔离比变化. 隔离比在失谐$ {\varDelta _{{{\text{c}}_{1}}{(}{{\text{c}}_{2}}{)}}} $为–200—200 MHz时变化较大, 在0 MHz处出现最大隔离比26 dB, 而这种变化趋势恰好和同向耦合光激发时的EIT信号强弱变化的趋势一致, 充分说明在耦合光失谐变化过程中隔离比的大小主要由同向传输激发时的EIT强度决定.

本文基于室温下的铯原子气体在三能级原子系统中通过调控耦合光的传输方向实现了光学非互易调控, 得到一系列的可调参量调节下隔离比的变化规律, 为光学隔离器的性能指标提供参考. 证明了在相干制备的铯原子系统中, 光学可调参量可以为实现高隔离比的理想光隔离提供有效途径. 与现有的基于原子相干性的高隔离比无腔非互易研究相比, 我们提出的实验方案在只需要室温下的三能级系统中就可以进行, 随着芯片级集成气室的发展, 更容易实现小型化和系统集成, 为光学非互易器件的小型化和集成化提供实验上的支撑^[33]. 因此, 通过满足双光子共振条件程度的调控而获得的光学非互易性调控, 无疑在实用而简单的优化和探索非互易光学功能方面发挥有利的作用.