高级搜索

基于梯度折射率微腔的色散调控

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

唐荻, 陈天赐, 康朝烽, 杨彬彬, 张磊, 杨煜, 王克逸. 基于梯度折射率微腔的色散调控[J]. 物理学报, 2025, 74(6): 064207-1. doi: 10.7498/aps.74.20241803
引用本文: 唐荻, 陈天赐, 康朝烽, 杨彬彬, 张磊, 杨煜, 王克逸. 基于梯度折射率微腔的色散调控[J]. 物理学报, 2025, 74(6): 064207-1. doi: 10.7498/aps.74.20241803
shu
Di TANG, Tianci CHEN, Zhaofeng KANG, Binbin YANG, Lei ZHANG, Yu YANG, Keyi WANG. Dispersion control based on gradient refractive index microresonators[J]. Acta Physica Sinica, 2025, 74(6): 064207-1. doi: 10.7498/aps.74.20241803
Citation: Di TANG, Tianci CHEN, Zhaofeng KANG, Binbin YANG, Lei ZHANG, Yu YANG, Keyi WANG. Dispersion control based on gradient refractive index microresonators[J]. Acta Physica Sinica, 2025, 74(6): 064207-1. doi: 10.7498/aps.74.20241803
shu

基于梯度折射率微腔的色散调控

  • 1.

    中国科学技术大学精密机械与精密仪器系, 合肥　230026

  • 2.

    合肥工业大学电气与自动化工程学院, 合肥　230009

    • 通讯作者: E-mail: kywang@ustc.edu.cn

  • 中图分类号: 42.50.-p, 42.60.Da, 42.65.-k, 42.81.Ht

Dispersion control based on gradient refractive index microresonators

  • 1.

    Department of Precision Machinery and Precision Instrumentation, University of Science and Technology of China, Hefei 230026, China

  • 2.

    School of Electrical Engineering and Automation, Hefei University of Technology, Hefei 230009, China

    • Corresponding author: E-mail: kywang@ustc.edu.cn

  • MSC: 42.50.-p, 42.60.Da, 42.65.-k, 42.81.Ht

  • 摘要: 回音壁模式微腔的色散调控是克尔光频梳生成的关键. 然而回音壁模式微腔色散设计主要是通过改变微腔结构调控模场分布, 方式较为单一. 本文将径向分布的梯度折射率$n(r)$引入回音壁模式微腔, 提出使用改变折射率分布调控梯度折射率微腔色散. 通过数值计算和有限元仿真结果表明, 折射率梯度的约束使微腔模场的位置远离微腔边缘, 梯度折射率微腔具有零几何色散特性. 基于设计不同折射率分布提出两种色散调控方式—修饰微腔边缘几何外形和构建双势阱. 并且研究了微腔半径、楔角大小、离子扩散和塑形工艺顺序、双势阱宽度和间距对色散的影响. 仿真结果表明两种方式均可以得到通信波段较大范围的反常色散, 梯度折射率微腔色散调控方式十分灵活, 在非线性光学应用领域具有极大潜力.
    Abstract: Kerr optical frequency combs based on whispering-gallery mode (WGM) microresonators have great potential for applications in various fields, such as precision measurement, spectral analysis, optical communication, and quantum technology. The interaction between dispersion and nonlinearity is crucial for determining the stability and bandwidth performance of optical frequency combs. In particular, the Kerr bright soliton optical frequency comb requires a suitable anomalous group velocity dispersion (GVD) to maintain the dissipative system. Therefore, designing the dispersion of the WGM microresonator is essential for generating the Kerr optical frequency comb. However, WGM microresonators typically have normal and fixed material dispersion, and their dispersion design is mainly based on modulating the mode field distribution by changing the microresonator structure to achieve anomalous dispersion, which limits their flexibility. In this paper, we introduce a radially distributed gradient refractive index n(r) into WGM microresonators and propose to use the refractive index profile for controlling the dispersion of gradient-index (GRIN) microresonators. Numerical simulations and finite element analysis demonstrate that the refractive index gradient constrains the mode field and pushes it away from the cavity edge, resulting in near-zero geometric dispersion in the GRIN microresonator. Two dispersion modulation methods are explored: modifying the microresonator’s geometric shape and constructing a dual potential well. The effects of microresonator radius, wedge angle, ion diffusion sequence, and potential well width and spacing on dispersion are systematically investigated. Simulation results show that both methods can achieve a wide range of anomalous dispersion within the communication band. In the first method, mode field leakage in the bilateral wedge-shaped GRIN microresonator produces anomalous dispersion, while no leakage results in normal dispersion. When the mode field is pushed away from the edge, near-zero dispersion is achieved. In the second method, energy coupling between the inner mode and the outer mode in the dual potential well structure leads to anomalous dispersion in the inner mode and normal dispersion in the outer mode. Our findings highlight the flexibility of GRIN microresonator dispersion control and indicate great potential for nonlinear optical applications.
  • 加载中

  • 图 1  (a) GRIN微腔的折射率分布, 从边缘到内部折射率由低变高, 模场远离微腔表面; (b) GRIN微腔沿径向折射率分布曲线n(r), 其中n(r)r曲线极点为基模位置

    Figure 1.  (a) Refractive index distribution of the GRIN microresonator, with low to high refractive indices from the edges to the interior, with the mode field away from the microresonator surface; (b) GRIN microresonator refractive index distribution curve n(r) along the radial direction, where n(r)r curve pole is the fundamental mode position.

    下载: 全尺寸图片 幻灯片

    图 2  (a)不同扩散时间下的折射率分布; (b)不同扩散时间下的势函数

    Figure 2.  (a) Refractive index distribution at different diffusion times; (b) potential function at different diffusion times

    下载: 全尺寸图片 幻灯片

    图 3  数值计算的WGM微腔和GRIN微腔的GVD

    Figure 3.  Numerically calculated GVD of WGM microresonators and GRIN microresonators.

    下载: 全尺寸图片 幻灯片

    图 4  (a) GRIN微腔的折射率分布; (b) GRIN微腔的基模模场; (c) WGM微腔的折射率分布; (d) WGM微腔的基模模场; (e) GRIN, WGM微腔几何色散

    Figure 4.  (a) Refractive index distribution of GRIN microresonator; (b) fundamental mode field of GRIN microresonator; (c) refractive index distribution of WGM microresonator; (d) fundamental mode field of WGM microresonator; (e) geometric dispersion of GRIN, WGM microresonator

    下载: 全尺寸图片 幻灯片

    图 5  不同半径和楔角大小的后扩散双边楔形GRIN微腔及其GVD　(a), (c), (e) GRIN 微腔折射率分布和基模模场; (b), (d), (f)对应的GRIN 微腔的 GVD

    Figure 5.  Diffusion-after bilateral wedge-shaped GRIN microresonator and their GVD with different radius and wedge angle sizes: (a), (c), (e) Refractive index distributions and fundamental mode fields of GRIN microresonators; (b), (d), (f) GVD of the corresponding GRIN microresonators

    下载: 全尺寸图片 幻灯片

    图 6  (a) 500 µm, 楔角半角正切1/2的先扩散微腔的折射率分布; (b) 500 µm, 楔角半角正切1/2的后扩散微腔的折射率分布; (c) 对应的先扩散微腔的基模模场; (d) 对应的后扩散微腔的基模模场; (e) 两种 GRIN 微腔的 GVD

    Figure 6.  (a) Refractive index distribution of a 500 µm, wedge-angle half-angle tangent 1/2 of the diffusion-first microresonator; (b) refractive index distribution of a 500 µm, wedge-angle half-angle tangent 1/2 of the diffusion-after microresonator; (c) corresponding fundamental mode fields of the first diffusion microresonator; (d) corresponding fundamental mode fields of the after-diffusion microresonator; (e) GVD of the two GRIN microresonators.

    下载: 全尺寸图片 幻灯片

    图 7  不同半径和楔角大小的先扩散双边楔形 GRIN 微腔及其GVD　(a), (c), (e) GRIN 微腔折射率分布和基模模场; (b), (d), (f)对应的GRIN 微腔的 GVD

    Figure 7.  Diffusion-first bilateral wedge-shaped GRIN microresonator and their GVD with different radius and wedge angle sizes: (a), (c), (e) Refractive index distributions and fundamental mode fields of GRIN microresonators; (b), (d), (f) GVD of corresponding GRIN microresonators.

    下载: 全尺寸图片 幻灯片

    图 8  (a)双势阱GRIN微腔的折射率分布$ n(r) $和势函数$ V(r) $; (b)内层基模径向模场; (c)外层基模径向模场

    Figure 8.  (a) Refractive index distribution $ n(r) $ and potential function $ V(r) $ of the GRIN microresonator with double-potential well; (b) radial mode field of the fundamental mode of the inner layer; (c) radial mode field of the fundamental mode of the outer layer.

    下载: 全尺寸图片 幻灯片

    图 9  双势阱GRIN微腔的内层模式色散和外层模式色散

    Figure 9.  Inner mode dispersion and outer mode dispersion of a double potential well GRIN microresonator

    下载: 全尺寸图片 幻灯片

    图 10  (a)双势阱GRIN微腔的折射率分布$ n(r) $和势函数$ V(r) $; (b)内层基模径向模场; (c)外层基模径向模场

    Figure 10.  (a) Refractive index distribution $ n(r) $ and potential function $ V(r) $ of the double-potential-well GRIN microresonator; (b) radial mode field of the inner fundamental mode; (c) radial mode field of the outer fundamental mode.

    下载: 全尺寸图片 幻灯片

    图 11  不同势阱间距对应的GVD

    Figure 11.  GVD corresponding to different potential well space

    下载: 全尺寸图片 幻灯片

    图 12  (a)改变外层势阱宽度对应的GVD; (b)改变内层势阱宽度对应的GVD

    Figure 12.  (a) GVD corresponding to changing the width of the outer potential wells; (b) GVD corresponding to changing the width of the inner potential wells

    下载: 全尺寸图片 幻灯片
  • [1] Vahala K 2003 Nature 424 839 doi: 10.1038/nature01939
    [2] 孟令俊, 王梦宇, 沈远, 杨煜, 徐文斌, 张磊, 王克逸 2020 物理学报 69 014203 doi: 10.7498/aps.69.20191265 Meng L J, Wang M Y, Shen Y, Yang Y, Xu W B, Zhang L, Wang K Y 2020 Acta Phys. Sin. 69 014203 doi: 10.7498/aps.69.20191265
    [3] Liu W, Li W, Wang R, Xing E, Jing N, Zhou Y, Tang J, Liu J 2021 Opt. Commun. 497 127148 doi: 10.1016/j.optcom.2021.127148
    [4] Wan H, Liu L, Ding Z, Wang J, Xiao Y, Zhang Z 2018 Opt. Laser Technol. 102 160 doi: 10.1016/j.optlastec.2017.12.039
    [5] Jiang S, Guo C, Fu H, Che K, Xu H, Cai Z 2020 Opt. Express 28 38304 doi: 10.1364/OE.412157
    [6] Strekalov D V, Marquardt C, Matsko A B, Schwefel H G L, Leuchs G 2016 J. Opt. 18 123002 doi: 10.1088/2040-8978/18/12/123002
    [7] Wu X Y, Wang K, Wang H, Lu B, Gao Y P, Wang C 2023 EPL 141 25001 doi: 10.1209/0295-5075/acaac5
    [8] Fuerst J U, Strekalov D V, Elser D, Aiello A, Andersen U L, Marquardt C, Leuchs G 2010 Phys. Rev. Lett. 105 263904 doi: 10.1103/PhysRevLett.105.263904
    [9] Cheng S, Zhang X, Shang M, Liu X, Jia K, Xie Z, Zhu S 2024 Phys. Rev. A 109 L011502 doi: 10.1103/PhysRevA.109.L011502
    [10] Del’Haye P, Schliesser A, Arcizet O, Wilken T, Holzwarth R, Kippenberg T J 2007 Nature 450 1214 doi: 10.1038/nature06401
    [11] Nakagawa Y, Mizumoto Y, Kato T, Kobatake T, Itobe H, Kakinuma Y, Tanabe T 2016 J. Opt. Soc. Am. B 33 1913 doi: 10.1364/JOSAB.33.001913
    [12] Xu L, Xie C, Wang M, Guo Z, Wei B, Zhang H, Zhang L, He X 2023 Opt. Express 31 38365 doi: 10.1364/OE.501129
    [13] Sturman B, Breunig I 2015 New J. Phys. 17 125006 doi: 10.1088/1367-2630/17/12/125006
    [14] Tian J, Lin G 2024 J. Lightwave Technol. 42 2118 doi: 10.1109/JLT.2023.3331256
    [15] Kippenberg T J, Gaeta A L, Lipson M, Gorodetsky M L 2018 Science 361 eaan8083 doi: 10.1126/science.aan8083
    [16] Fujii S, Tanabe T 2020 Nanophotonics 9 1087 doi: 10.1515/nanoph-2019-0497
    [17] Grudinin I S, Yu N 2015 Optica 2 221 doi: 10.1364/OPTICA.2.000221
    [18] Zhou C, Du J, He Z 2017 IEEE Photon. J. 9 7908008 doi: 10.1109/JPHOT.2017.2773120
    [19] Jin X, Wang J, Wang M, Dong Y, Li F, Wang K 2017 Appl. Opt. 56 8023 doi: 10.1364/AO.56.008023
    [20] Ke C, Ma J, Huang Y, Zeng Z, Xu C, Qin J 2019 Appl. Opt. 58 1522 doi: 10.1364/AO.58.001522
    [21] Ilchenko V, Savchenkov A, Matsko A, Maleki L 2003 J. Opt. Soc. Am. A 20 157 doi: 10.1364/JOSAA.20.000157
    [22] Zhu D, Zhou Y, Yu X, Shum P, Luan F 2012 Opt. Express 20 26285 doi: 10.1364/OE.20.026285
    [23] Chen T, Kang Z, Yang Y, Zhao S, Zhang J, Zhang L, Wang K 2023 J. Opt. Soc. Am. A 40 1208 doi: 10.1364/JOSAA.484595
    [24] Chen T, Kang Z, Zhang J, Huang Z, Tang D, Yang B, Yang Y, Wang K 2024 J. Opt. Soc. Am. B 41 486 doi: 10.1364/JOSAB.510347
    [25] Ba Q, Zhou Y, Li J, Xiao W, Ye L, Liu Y, Chen J H, Chen H 2022 eLight 2 19 doi: 10.1186/s43593-022-00026-y
    [26] Dadashi K, Kurt H, Ustun K, Esen R 2014 J. Opt. Soc. Am. B 31 2239 doi: 10.1364/JOSAB.31.002239
    [27] 王克逸, 汪景昌 1989 物理学报 38 1334 doi: 10.7498/aps.38.1334 Wang K Y, Wang J C 1989 Acta Phys. Sin. 38 1334 doi: 10.7498/aps.38.1334
    [28] Sellmeier W 1872 Annalen der Physik 223 386 doi: 10.1002/andp.18722231105
    [29] Nie M, Jia K, Xie Y, Zhu S, Xie Z, Huang S W 2022 Nat. Commun. 13 6395 doi: 10.1038/s41467-022-34103-0
  • 加载中
图( 12)
计量
  • 文章访问数:  104
  • HTML全文浏览数:  104
  • PDF下载数:  6
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-31
  • 刊出日期:  2025-03-20

基于梯度折射率微腔的色散调控

    通讯作者: E-mail: kywang@ustc.edu.cn
  • 1. 中国科学技术大学精密机械与精密仪器系, 合肥　230026
  • 2. 合肥工业大学电气与自动化工程学院, 合肥　230009
  • 收稿日期:  2024-12-31

摘要: 回音壁模式微腔的色散调控是克尔光频梳生成的关键. 然而回音壁模式微腔色散设计主要是通过改变微腔结构调控模场分布, 方式较为单一. 本文将径向分布的梯度折射率$n(r)$引入回音壁模式微腔, 提出使用改变折射率分布调控梯度折射率微腔色散. 通过数值计算和有限元仿真结果表明, 折射率梯度的约束使微腔模场的位置远离微腔边缘, 梯度折射率微腔具有零几何色散特性. 基于设计不同折射率分布提出两种色散调控方式—修饰微腔边缘几何外形和构建双势阱. 并且研究了微腔半径、楔角大小、离子扩散和塑形工艺顺序、双势阱宽度和间距对色散的影响. 仿真结果表明两种方式均可以得到通信波段较大范围的反常色散, 梯度折射率微腔色散调控方式十分灵活, 在非线性光学应用领域具有极大潜力.

English Abstract

    全文HTML

    1.   引　言

    • 回音壁模式(whispering-gallery mode, WGM)光学微腔通过共振循环将光束缚在小空间内[1], 极大增强了光与物质的相互作用. WGM微腔具有超高Q值和小模式体积, 已经广泛应用在传感器[2,3]、窄线宽激光器[4,5]和非线性光学[6,7]等多个领域. 微腔中群速度色散(group velocity dispersion, GVD)调控是许多非线性光子学应用的关键基础, 如光学参量振荡[8,9]、克尔光频梳[10–12]、受激布里渊激光器[13,14]等. 其中克尔亮孤子光频梳需要合适的反常 GVD 才能维持耗散系统[15].

      微腔的总群速度色散包括材料色散和几何色散[16], 材料色散一般是材料固有的特性, 难以改变. 因此, 在实际操作中主要通过改变几何色散来调控微腔的总色散. 常用调控WGM微腔几何色散的方式有修饰微腔边缘形状[17,18]、镀膜[19,20]等. 但WGM微腔具有均匀折射率分布, 调控自由度较少, 因此研究人员开始关注径向梯度折射率(gradient refractive index, GRIN)微腔. 2003年, Ilchenko等[21]提出用折射率沿径向减小的圆柱形材料制造微腔, 模场位置内移, 并且具有一阶等距频谱. 2012年, Zhu等[22]在光纤中使用折射率分布为$ n(r) = b/r $的包层提高倏逝场向微腔芯层的穿透. 2023年, 王克逸课题组提出了梯度折射率微腔形成的几何光学模型[23], 并且运用波动光学理论描述了单模与多模模场[24]. 尽管GRIN微腔的谐振特性已有较多研究[25,26], 但其色散特性及色散调控方式却 报道较少. 如图1(a)所示, GRIN微腔相比WGM微腔增加了一个新的自由度——微腔内部的折射率分布. 这也为调控微腔色散提供了一种新思路: 通过改变折射率分布来调控色散.

      本文第2节介绍GRIN微腔的理论基础和色散特性, 使用基于波动光学的差分法和有限元法分别计算GRIN微腔的色散. 第3节提出两种GRIN微腔的色散调控方式: 第1种是修饰几何外形, 使用有限元法对双边楔形GRIN微腔进行建模分析, 研究了离子扩散和塑形工艺顺序不同的两种微腔中半径、楔角对色散的影响; 第2种是构建双势阱, 在GRIN微腔中构建两个单模模式输出, 有效调控了内层模式的色散. 仿真结果表明两种色散调控方式都可以使GRIN微腔在通信波段(1550 nm附近)为反常色散, 色散调控方式十分灵活.

    2.   GRIN微腔的理论基础及基本色散特性

      2.1.   GRIN微腔的理论基础

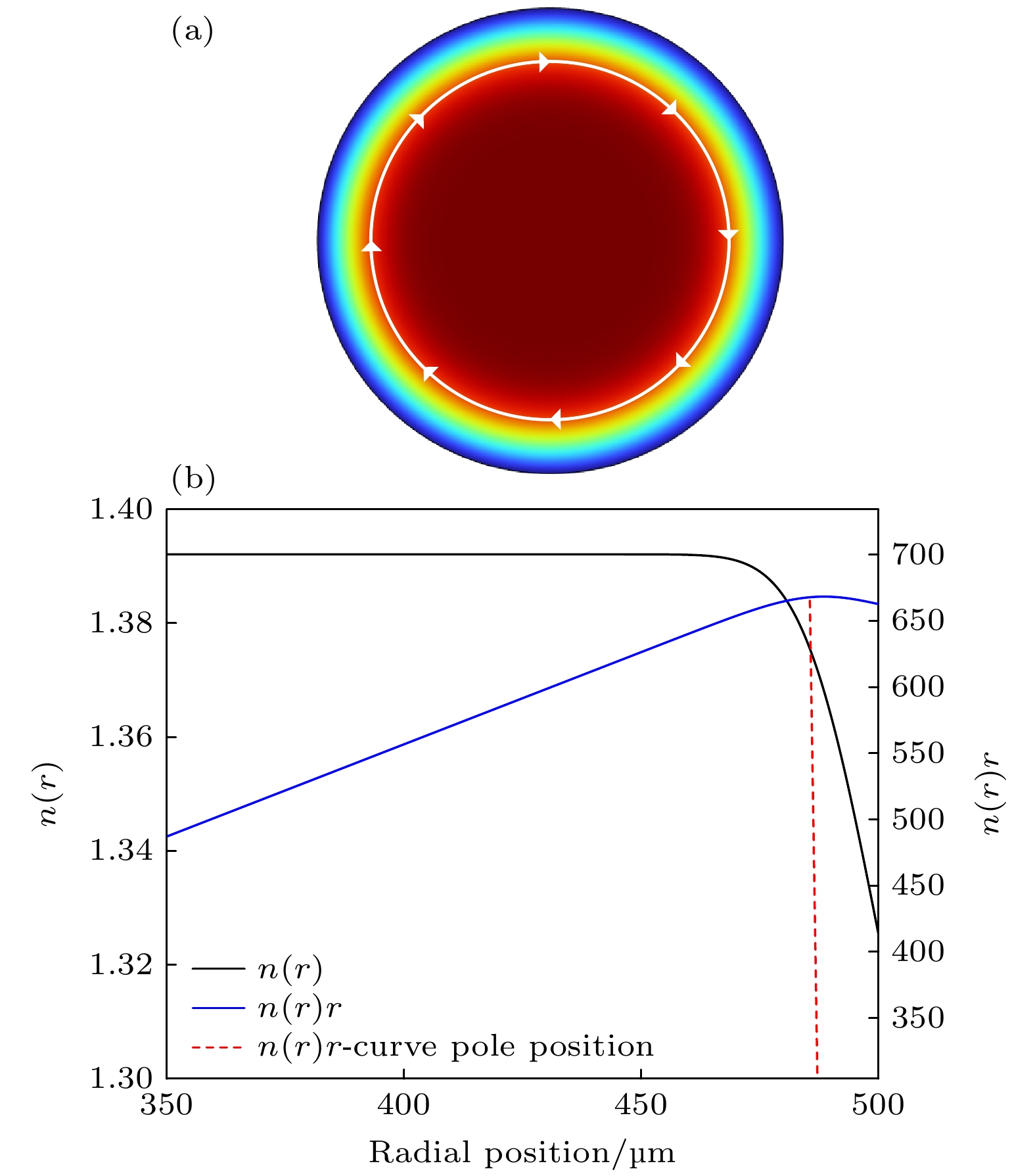
    • GRIN微腔具有轴对称径向折射率分布, 通过合理设计径向折射率梯度可以实现光线沿闭环圆周传输. 从几何光学出发推导出GRIN微腔的基模位置[23]:

      其中n为折射率, r为半径, $ \dot{n} $为n对r微分. GRIN微腔径向折射率为$ n(r) $, 若作出其$ n(r)r $曲线, 则曲线的极值点为基模位置, 如图1(b)所示.

      根据波动光学理论给出径向折射率为$ n(r) $的GRIN微腔TE和TM模的径向分布方程[24]:

      其中, $ V=\dfrac1{n^{2}(r)r^{2}} $为势函数, $ \gamma=\dfrac{k^2}{l^2} $为能级, l为角向模式数.

      (3)式和(4)式可以转化为类薛定谔方程, 进而求解GRIN微腔的模场分布和特征频率. 圆柱内折射率分布会引起势函数的弯曲, 在适当的条件下形成势阱, 势阱最低点对应$ {{\mathrm{d}}(nr)}/{{\mathrm{d}}r} = 0 $, 即GRIN微腔基模位置.

      GRIN微腔的折射率梯度分布类似于自聚焦透镜, 沿径向从内到外连续减小. 因此参考制作自聚焦透镜等梯度折射率介质的离子交换法来构造GRIN微腔的折射率分布. 柱坐标系下, 离子扩散满足Fick第二扩散理论[27]:

      其中u是归一化浓度, $ u=\dfrac{c-c_1}{c_0-c_1} $, $ c_0 $是交换初始浓度, $ c_1 $是交换平衡时的浓度; t是扩散时间; r是归一化半径; $ D(u) $是互扩散系数. 通过改变熔盐组成、扩散时间、初始条件和边界条件可以获得不同的折射率分布, 进而自由地设计势函数, 得到不同的GRIN微腔.

      • 2.2.   GRIN微腔的基本色散特性

    • GRIN微腔的色散包括材料色散和几何色散. 对于制造GRIN微腔的玻璃材料, 其材料色散难以获得. 为了便于研究, 假设将含氟化锂的圆柱形玻璃浸泡在熔融氟化钠熔盐中, 利用玻璃中的锂离子与熔盐中的钠离子进行交换, 以降低氟化锂玻璃表面的折射率形成梯度折射率分布. 使用差分法计算扩散形成的GRIN微腔的折射率分布和谐振 频率.

      首先根据Sellmeier公式[28]分别计算两种交换材料氟化锂和氟化钠的材料色散:

      其中, n是折射率, λ是波长, $ A_i $和$ B_i $是Sellmeier系数.

      接下来计算交换后半径为500 µm的圆柱形GRIN微腔的色散. 熔盐中的钠离子与玻璃中的锂离子进行交换时, 玻璃表面很快达到交换平衡. (5)式的初始条件为

      边界条件为

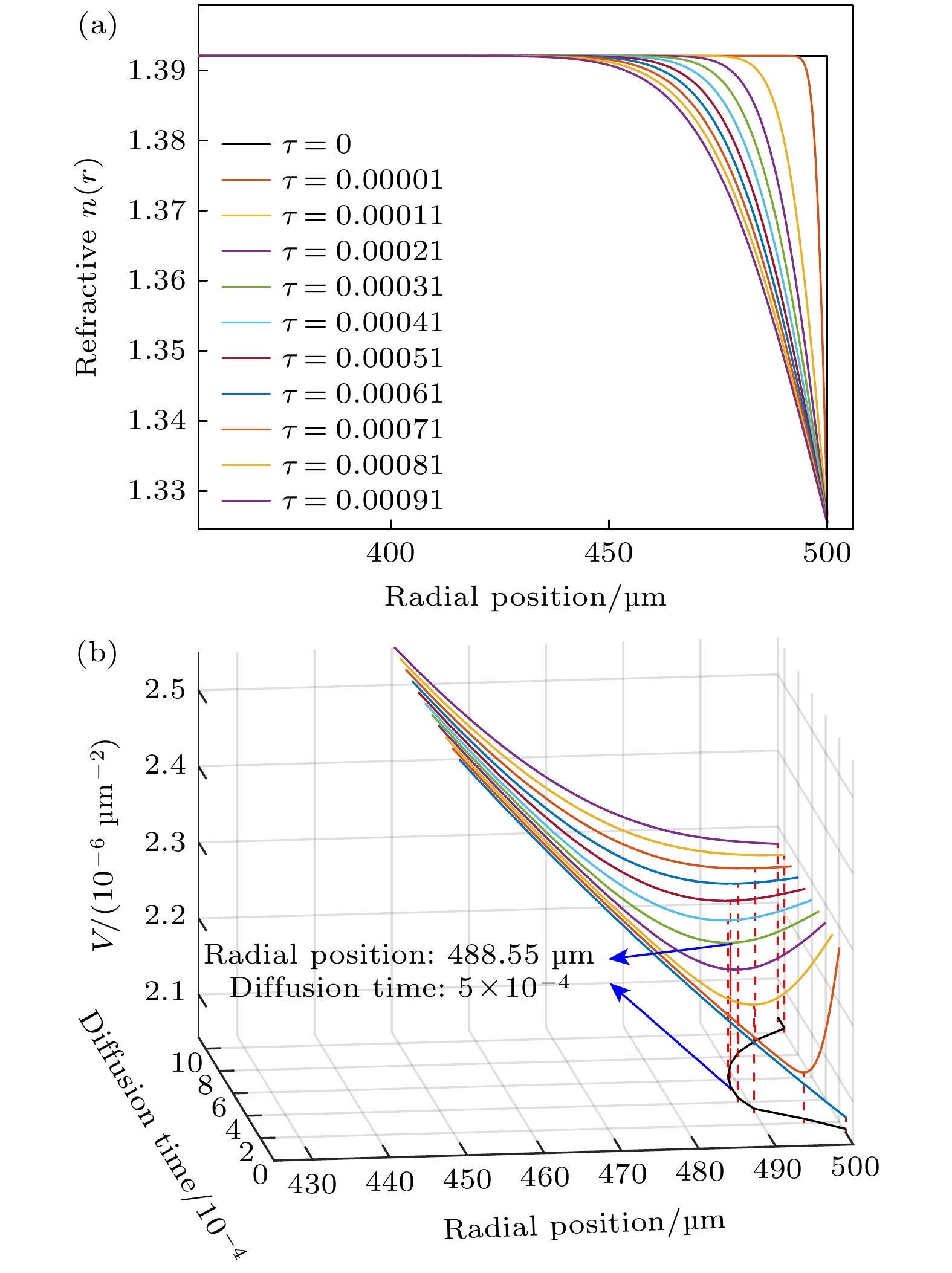
      由于改变熔盐中钠离子的浓度和交换温度可以将互扩散系数$ D(u) $控制在$ 10^{-14}—10^{-10} $m2/s[24], 因此计算中使用无量纲扩散时间$ \tau = {Dt}/{R^2} $而不是实际扩散时间t, 其中R为微腔半径. 从图2(a)可知, 随着扩散时间τ的增加, 氟化锂玻璃的边缘折射率从1.3921逐渐变低至1.3253, 对应的势阱由深变浅, 如图2(b)所示. 黑色线段表示势阱最低点即基模模场的位置, 其先向微腔内部移动到最深处, 再向外移动. 势阱深时会容纳多个模式, 导致高阶模出现; 势阱浅时模式体积较大, 有利于降低孤子光频梳的量子极限时间噪声, 从而降低时间抖 动[29], 但太浅会无法形成模式. 因此需要合理选择扩散时间. 本文选择势阱最低点最靠近微腔内部时对应的折射率分布, 扩散时间$ \tau = 5\times10^{-4} $(对应实际扩散时间$ t = 1250 $ s), 势阱最低点距离微腔边缘11.45 µm.

      交换形成的GRIN微腔的折射率分布为

      其中$ r = 488.55 $ µm, $ c_{{\mathrm{Li}}^+} $是$ \tau = 5\times10^{-4} $时对应的锂离子浓度分布.

      计算GRIN微腔包含材料色散的总色散[15]:

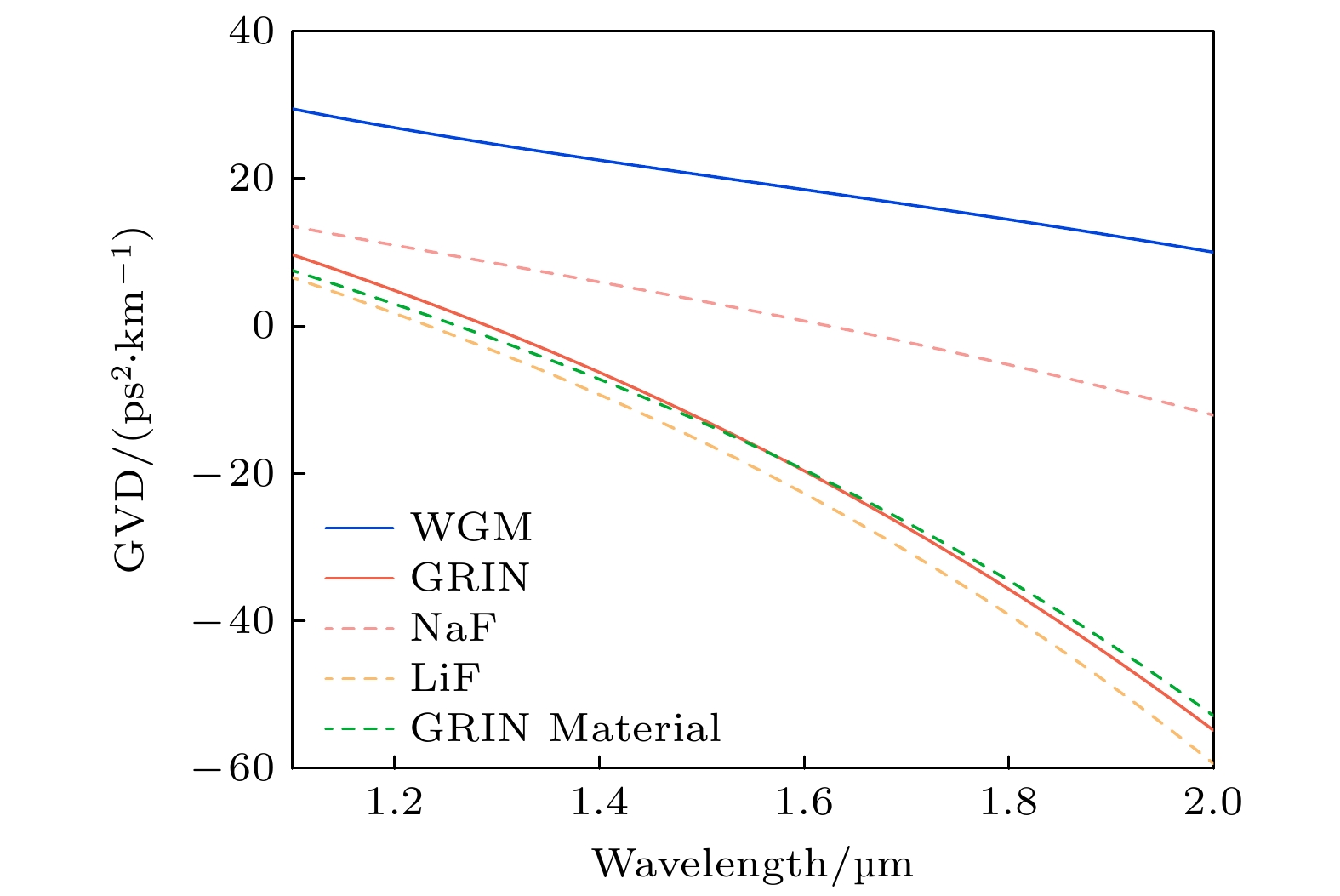
      其中$ \beta_2 $是群速度色散, 文中$ {{\beta_2}} < 0 $表示反常色散; $ f_m $是第m个模式的谐振频率; $ \Delta f_m= \dfrac{f_{m+1}-f_{m-1}}2 $, $ \Delta\left(\Delta f_m\right)=f_{m+1}-2 f_m+f_{m-1} $.

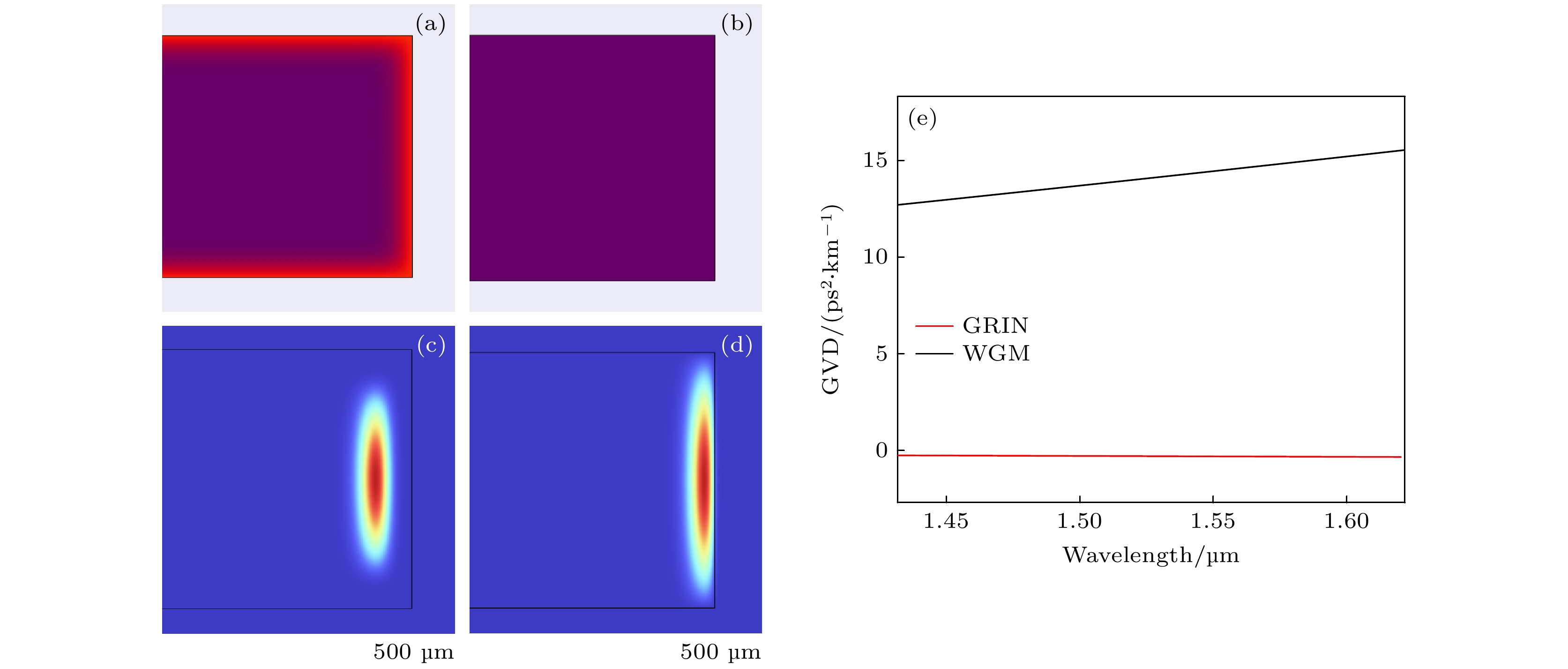
      图3中, 氟化锂的材料色散曲线为淡黄色线, 氟化钠的材料色散曲线为粉色线. 红线所示为GRIN微腔的总色散曲线, 在 1550 nm 附近具有较宽范围的反常色散. 同时计算了微腔径向 488.55 µm 即基模位置处, 氟化锂和氟化钠按照浓度比例混合的材料色散, 如绿色虚线所示. 绿色虚线与红线几乎重合. 这是因为GRIN微腔折射率梯度约束基模形成在腔的内部, 它始终具有固定的光程长度, 并且谐振波长始终满足等式$ 2\pi r_0 n_0=l\lambda $, 其中$ r_0 $为模式的径向位置, $ n_0 $为该位置的折射率. 因此它的几何色散为零, 只有材料色散. 红线与绿线微小的差距是因为模场位置处的等效折射率不严格等于该位置材料折射率. 作为对比, 计算了 500 µm 氟化镁WGM微腔的总色散, 如图3中深蓝色曲线所示, 在通信波段没有反常色散.

      使用差分法计算快速, 但无法直观显示模场分布情况. 因此使用有限元方法构建了沿轴向简化后半径均为 500 µm 的圆柱形WGM和GRIN微腔模型, 两种微腔材料和折射率分布是使用和差分法相同的参数. 图4所示为两种微腔折射率分布、模场分布和几何色散.

      从图4(a)和图4(b)看出, GRIN微腔的折射率梯度沿圆柱周围分布, 从微腔边缘到微腔内部折射率由低变高. 而WGM微腔的折射率是均匀的. 图4(c)和图4(d)为基模模场, GRIN微腔由于折射率的梯度将模场完全约束在微腔内部而没有泄漏到空气中, 不受全反射影响. 同时从微腔边缘到内部由低到高的折射率梯度使不同波长的光具有相同的几何光程长度, 因此GRIN微腔具有等距模式谱, 没有几何色散. 如图4(e)所示, 由于有限元网格划分精度有限, GRIN微腔几何色散并不是严格为0, 而是在0附近. 而在WGM微腔中, 由于光在微腔表面发生全反射, 短波长的光相比长波长的光在更靠近微腔表面的路径上传播, 相邻模态之间的频率间隔随着波长增大而增加, 几何色散表现为正常色散. 有限元的仿真结果支持上述差分数值计算的结论.

    3.   GRIN微腔的色散调控

      3.1.   修饰几何外形

    • GRIN微腔的材料色散特性由材料色散决定, 其性质难以改变. 因此在材料色散确定的情况下, 参考WGM微腔的色散调控方式, 通过修饰GRIN微腔的外形结构来改变几何色散, 进而调控微腔的总色散. 本文基于圆柱形GRIN微腔设计了双边楔形结构, 该双边楔形GRIN微腔是圆柱形玻璃先经过边缘磨削加工再经过离子交换得到的. 使用有限元方法构建了沿轴向简化后的二维微腔模型, 选择势阱最低点最靠近微腔内部时对应的折射率分布. 本节只关注微腔中不同参数所产生的几何色散, 因此假定折射率在 1.45—1.65 µm 波段为氟化锂玻璃交换后的折射率1.3253, 不随波长而改变.

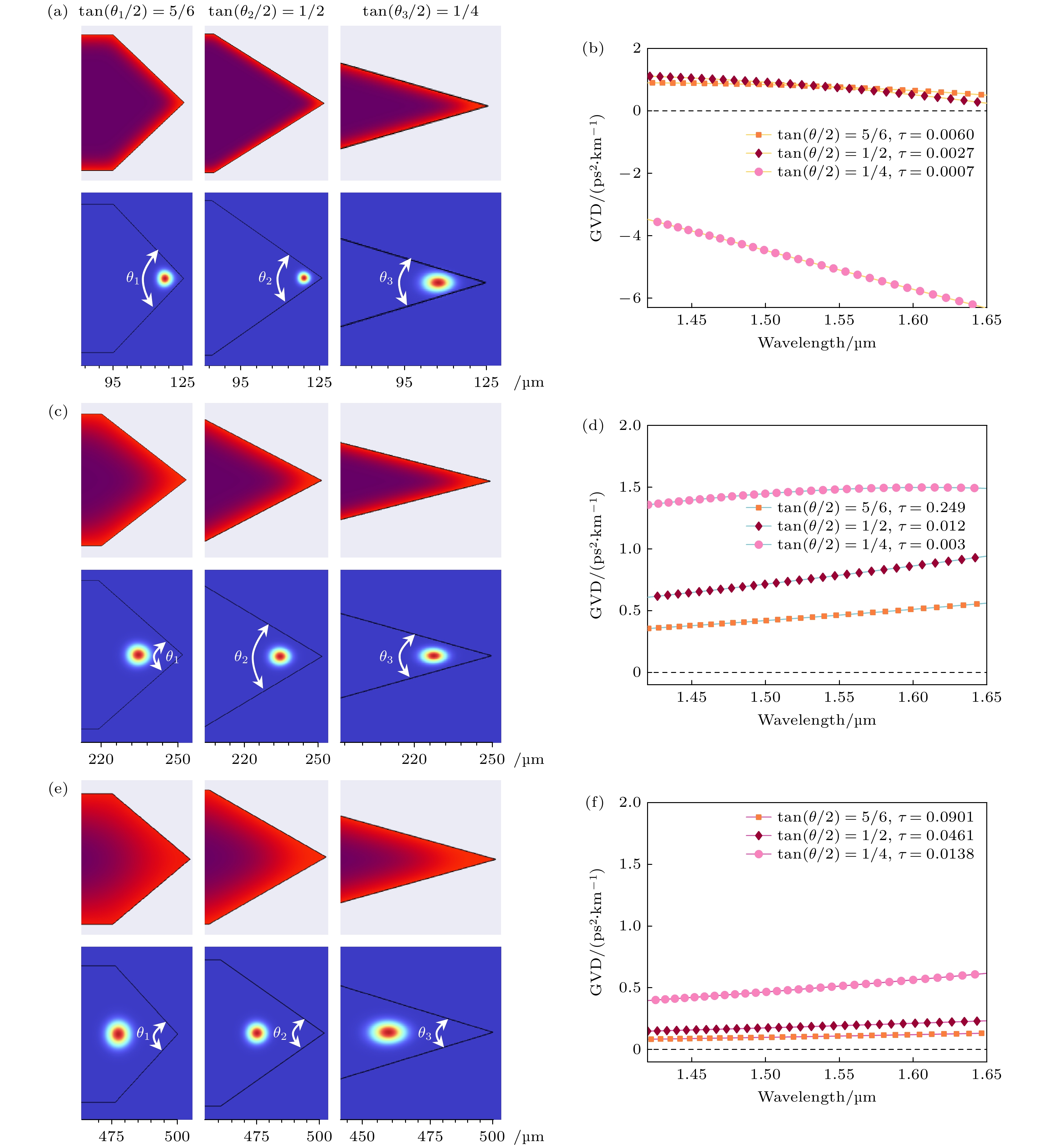
      微腔不同的几何结构参数对谐振频率、色散等均有影响, 因此改变上述双边楔形GRIN微腔半径、楔角角度大小, 仿真计算了不同结构参数的谐振频率, 然后求得GVD. 图5(a), (c), (e)所示为双边楔形微腔中的折射率分布和基模模场. 可以看出, 折射率梯度类似圆柱形微腔分布在微腔边缘 四周, 两条楔边均分布着折射率梯度. 折射率梯度和双楔边的双重约束不仅将模场压缩到微腔内部更小的区域还可以显著抑制轴向方向的高阶模. 图5(b), (d), (f)为在 125, 250和500 µm的半径下, 楔角半角正切值从大到小分别为5/6, 1/2和1/4时的GVD计算结果.

      对于半径 125 µm的微腔, 楔角半角正切值为1/4时为反常色散. 这是因为半径和楔角角度较小, 所以势阱最低点最靠近微腔内部对应的扩散时间短(折合扩散时间$ \tau = 0.0007 $), 折射率梯度分布浅, 基模模场靠近微腔边缘. 部分模场在两条楔边边缘发生全反射, 部分模场泄漏到空气中, 产生了反常色散. 楔角半角正切值为1/2 ($ \tau = 0.0027 $)和5/6($ \tau = 0.0060 $)时均为正常色散. 因为同一半径下, 楔角角度的增大使得扩散时间增大. 基模模场远 离微腔边缘, 轴向楔角对几何光程影响较小. 同 理, 对于半径 250 µm和 500 µm的微腔, 在1.45—1.65 µm 波段均为正常色散. 随着半径和楔角增加, GVD的值减小, 曲线更加平坦. 对于先经过边缘磨削加工再经过离子交换得到的双边楔形微腔, 半径和楔角越大, 模场分布越接近圆柱形GRIN微腔, 因此几何色散越接近零.

      GRIN微腔由离子扩散工艺形成, 因此对于双边楔形腔, 改变离子扩散工艺和边缘塑形顺序得到的折射率分布是不同的, 进而得到的模场分布和色散情况也不同. 将GRIN微腔先进行离子扩散后再磨削楔角记为先扩散微腔, 微腔先磨削楔角后再进行离子扩散记为后扩散微腔.

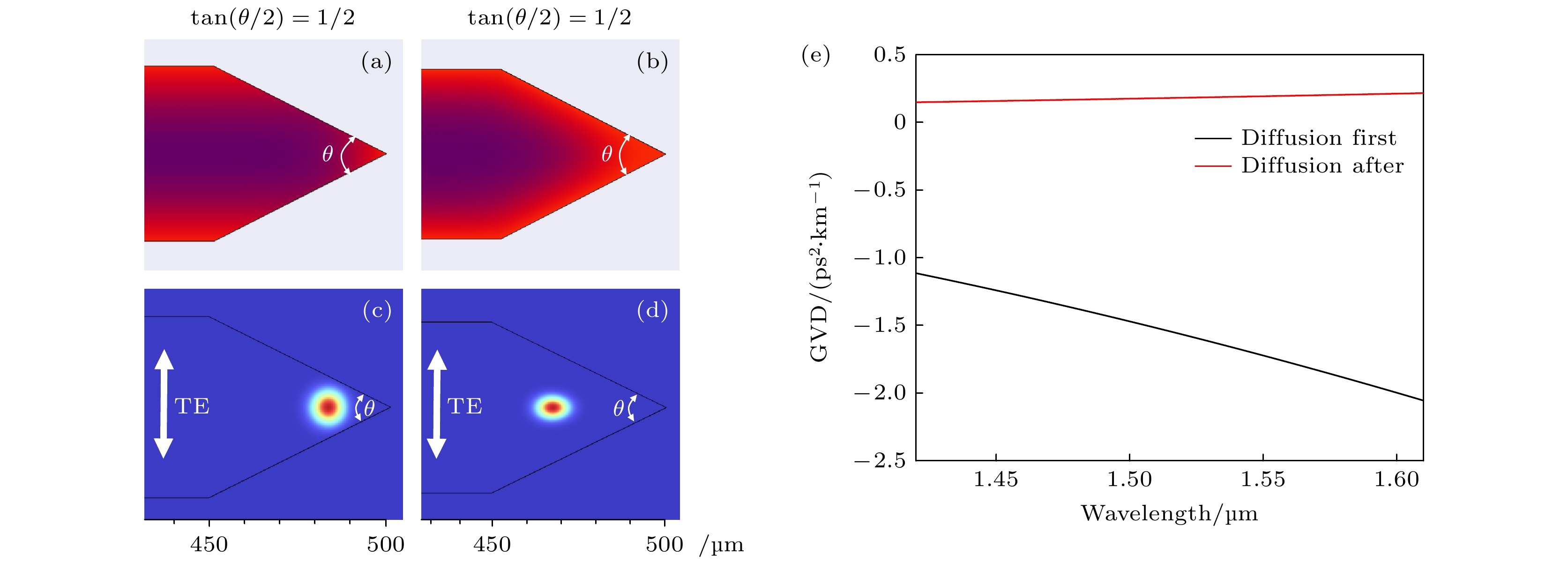
      图6(a)表示先扩散微腔, 两条楔边上的折射率分布被磨削掉, 折射率梯度主要分布在楔角顶端. 对应的基模模场也被约束在楔角顶端, 靠近微腔边缘, 如图6(c)所示; 图6(b)表示后扩散微腔, 不仅楔角顶端有折射率梯度分布, 在两个楔边上也有折射率分布, 对应的基模模场分布如图6(d)所示, 相比于图6(c)模场更加靠近微腔内部, 没有模场泄漏. 计算了两种GRIN微腔的GVD, 如图6(e)所示. 后扩散微腔在1.45—1.65 µm 波段为正常色散, 而先扩散微腔由于模场靠近微腔边缘, 部分模场泄漏到空气中, 产生了反常色散.

      改变半径、楔角角度大小, 计算了先扩散双边楔形GRIN微腔的折射率分布、基模模场和色散, 如图7所示.

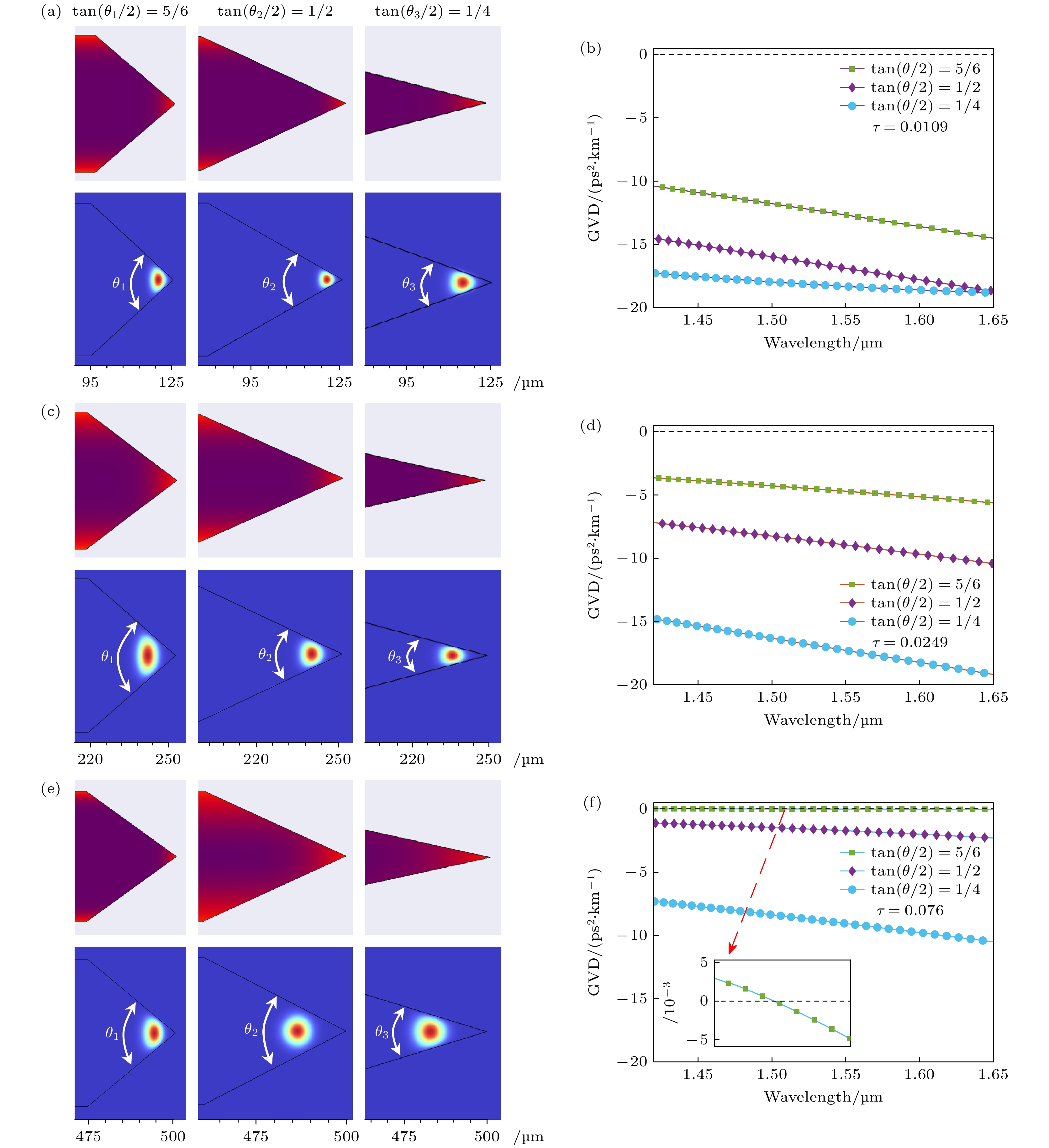
      从图7(b), (d)和(f)看出, 在 1.45—1.65 µm波段, 8种微腔呈现反常色散, 只有半径 500 µm楔角半切值5/6的微腔由正常色散变为反常色散, 零色散波长为 1.4909 µm. 随着波长的增加, GVD的绝对值增大. 更小的微腔半径和楔角都使微腔偏向反常色散. 由图7(a), (c)和(e)可知, 先扩散双边楔形GRIN微腔两条楔形边几乎没有梯度折射率的约束. 较小的半径和楔角使微腔模场靠近边缘泄漏到空气中, 产生反常色散. 然而, 微腔几何结构参数越小对加工要求越高, 因此需要合理选择. 随着微腔半径和楔角的增大, 模场泄漏减少, 微腔逐渐靠近零几何色散.

      因此, 对于GRIN微腔修饰几何边缘可以调控色散. 离子扩散和边缘塑形顺序对模场有影响, 对于先塑形后扩散的后扩散微腔由于模场远离边缘, 没有泄漏, 呈现正常色散. 而对于先扩散后塑形的先扩散微腔由于模场泄漏得到了通信波段内较大范围的反常色散. 对于这两种微腔, 较大的半径和楔角都使其模场远离边缘接近圆柱形GRIN微腔, 色散也接近零色散.

      • 3.2.   构建双势阱

    • 对于GRIN微腔, 通过设计离子扩散工艺可以得到不同的折射率梯度分布和势函数, 进而构建多个势阱. 本节在微腔中构造两个势阱形成两个单模, 利用它们之间的耦合特性调控色散.

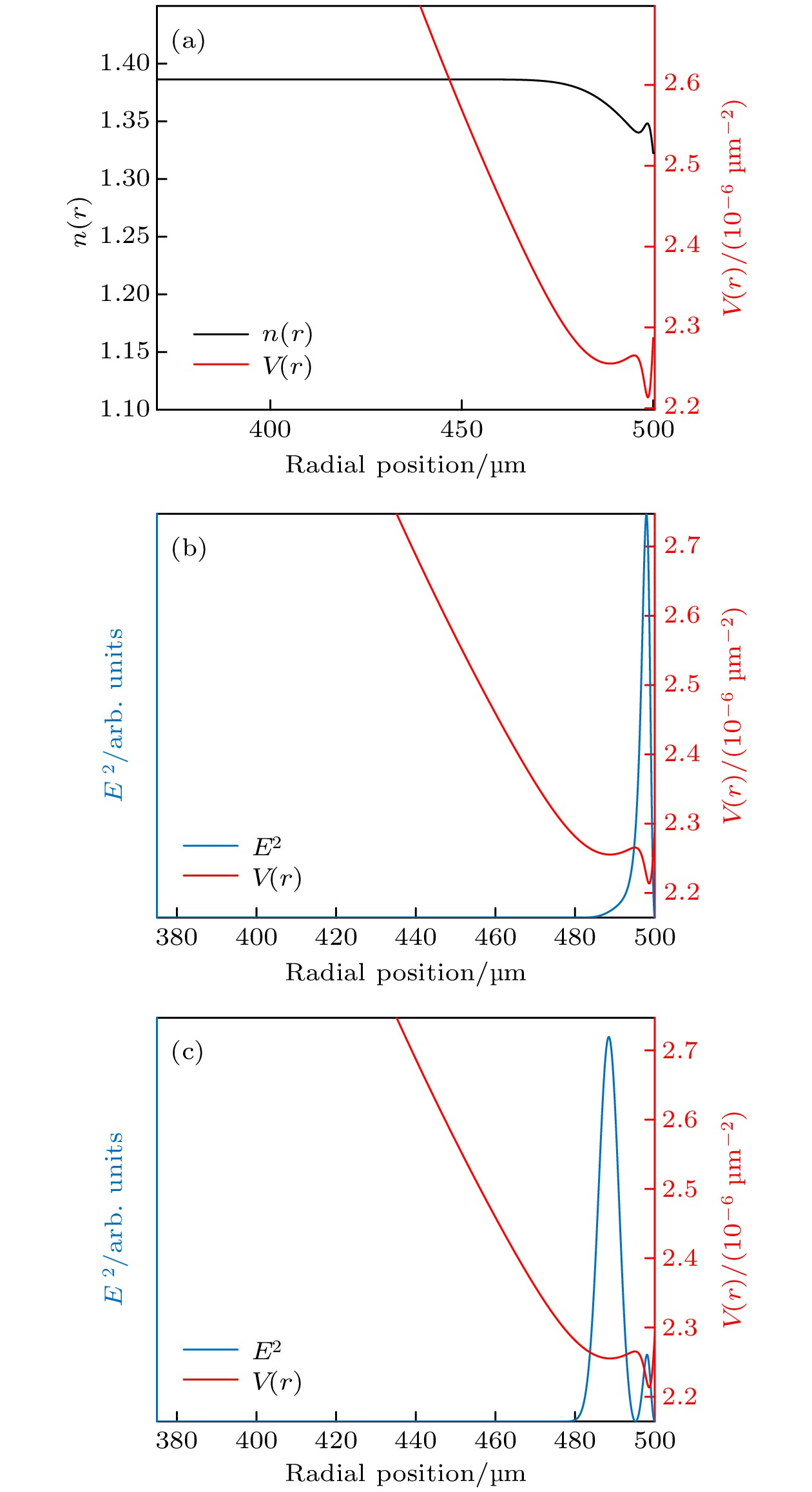
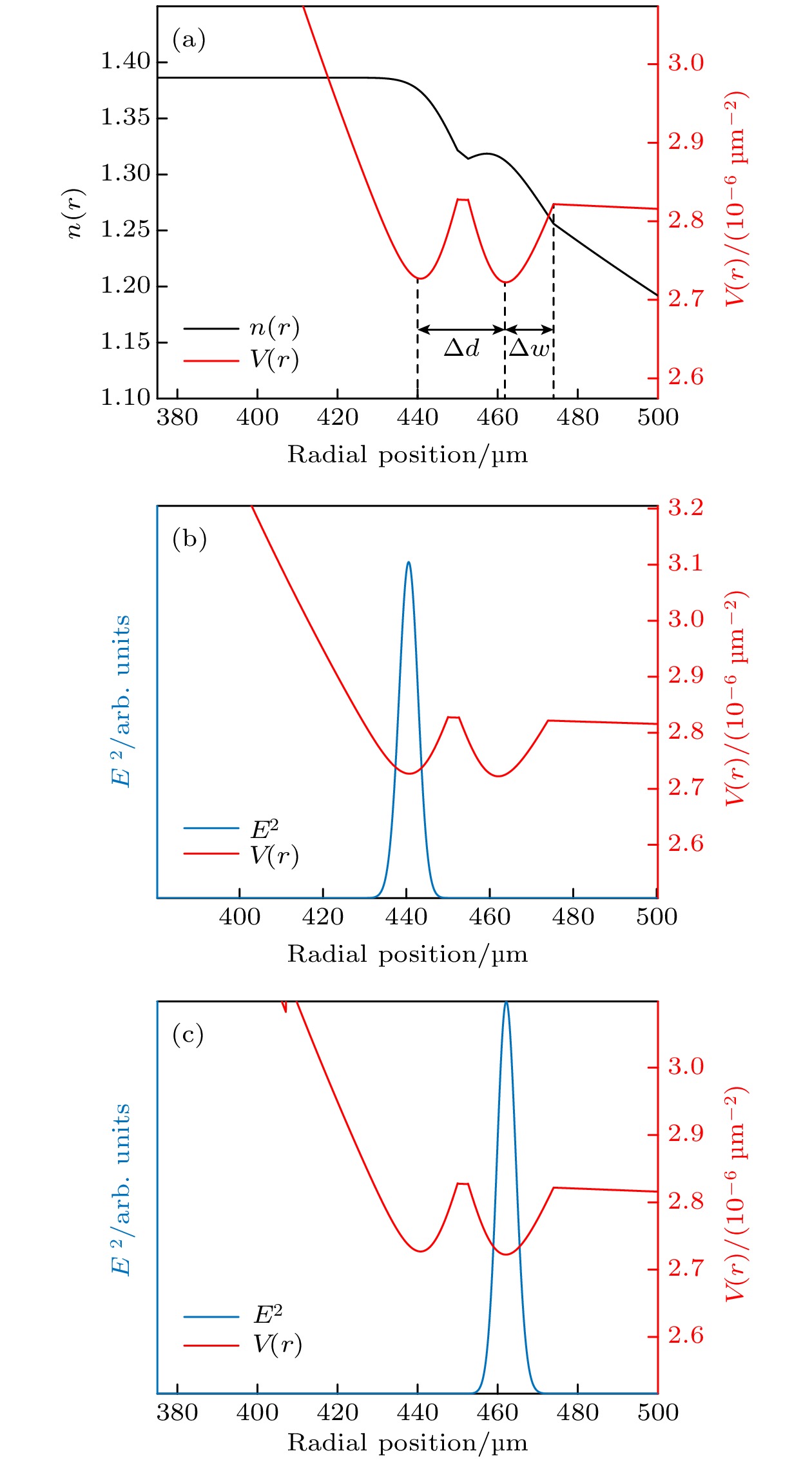
      在 500 µm 的GRIN微腔中通过扩散-反扩散-扩散工艺改变折射率分布构造双势阱. 使用差分方法计算扩散分布和谐振频率. 图8中红线为势函数, 黑线为折射率分布, 蓝线为径向电场. 图8(a)中改变微腔边缘折射率形成了两个形状不同的势阱, 每个势阱都可以形成基模, 如图8(b)和图8(c)中蓝色实线所示. 内外层各自形成独立模式, 并且内层模式能量可以通过外层模式耦合.

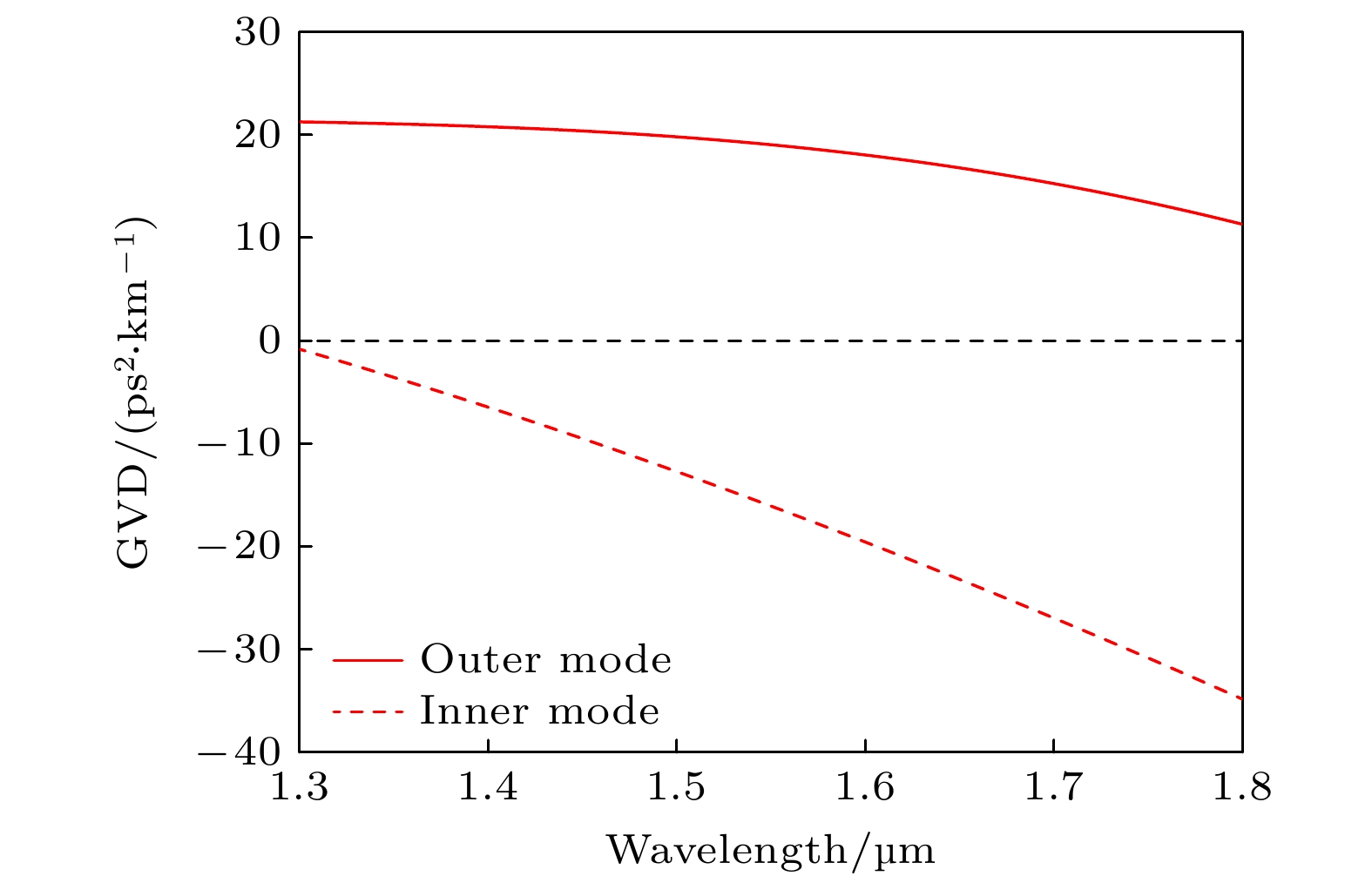
      计算该双势阱GRIN微腔的内层模式色散和外层模式色散, 结果如图9. 靠近微腔边缘的外层模式具有正常色散, 内层模式在1.3—1.8 µm 具有反常色散. 外层模式与邻近的内层模式之间需要有能量传输, 这种能量传输会影响相位, 进而影响两个模式的色散特性. 外层模式通过模式相互作用, 改变了内层模式的光程长度, 使内层模式具有反常色散, 且随波长增加内层模式反常色散会进一步 增加.

      两个势阱的间距和宽度会影响两个模式的 能量传输进而影响色散特性. 为排除微腔边缘全反射造成的模式泄漏的影响, 利用电场辅助扩散 将两个模式推进微腔内部. 通过优化扩散工艺, 在微腔中形成两个相同的势阱, 其中势阱宽度$ \Delta{w} $ 为从势阱最低点到右边界的距离, 两个势阱最低点距离为$ \Delta{d} $. 两个势阱都可以形成基模, 如图10 所示.

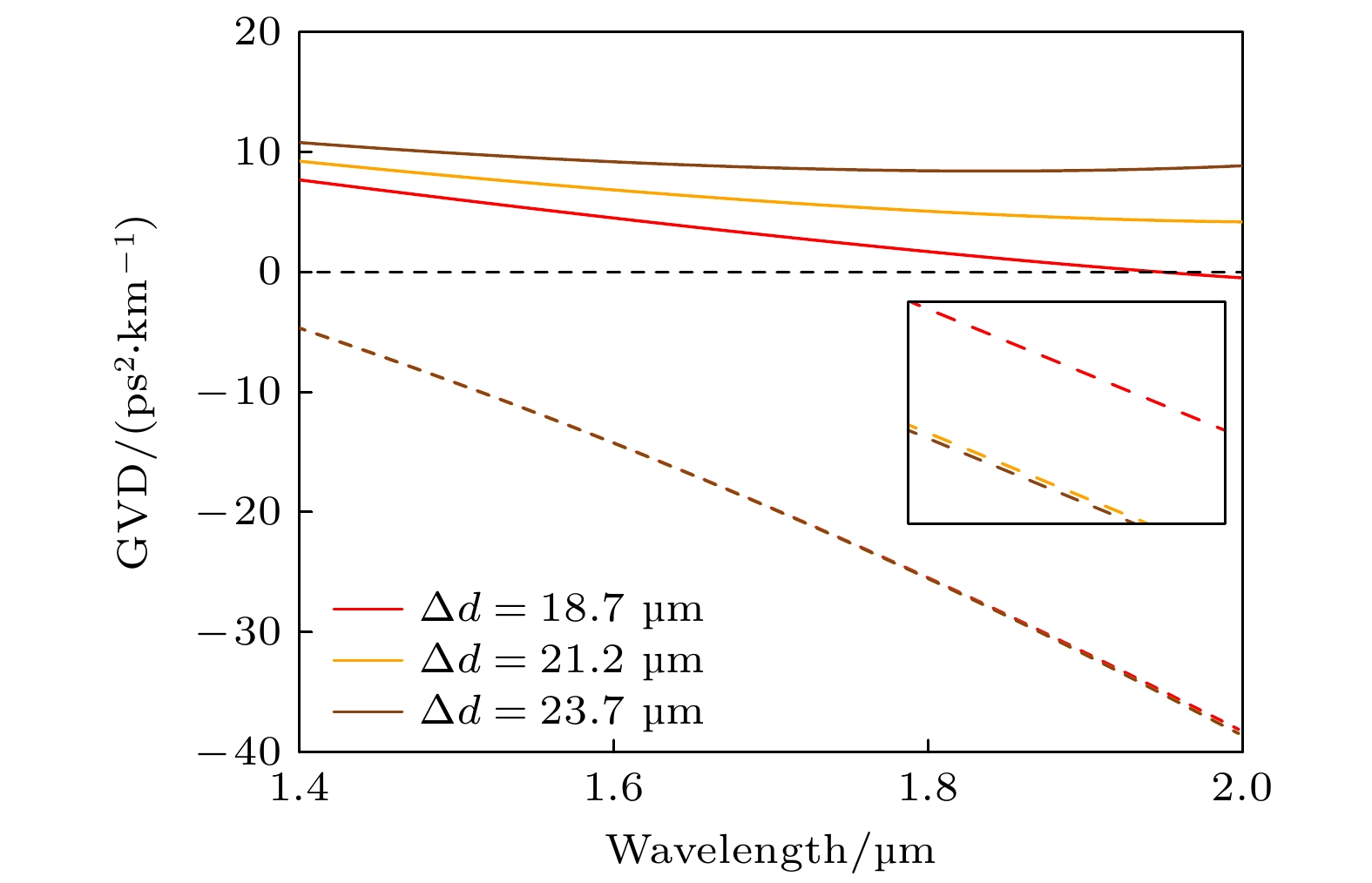
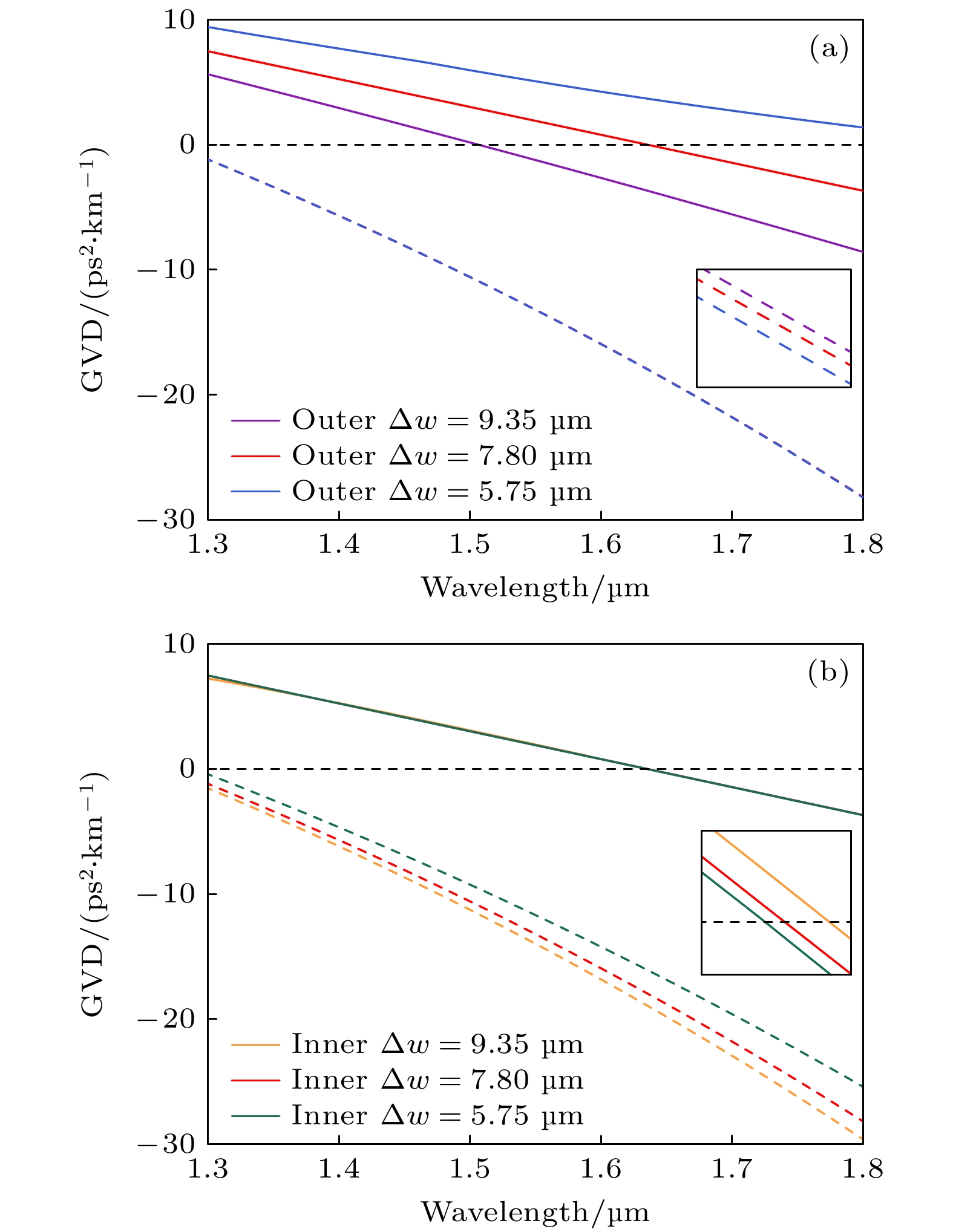
      首先研究势阱间距对色散的影响. 势阱宽度$ \Delta{w} = 9.35 $ µm, 改变两个势阱间距$ \Delta{d} $, 三种外层模式和对应的内层模式的色散曲线如图11所示. 外层模式的色散曲线为实线, 随着势阱间距的增加, 外层模式GVD的值增大, 零色散波长右移. 对应的三种内层模式GVD的值减小, 色散曲线几乎完全重合, 如虚线和内插图所示. 势阱间距增加, 两种模式之间的能量传输减弱, 使得外层模式更偏向正常色散, 内层模式更偏向反常色散, 但对内层模式的反常色散影响十分微弱.

      其次研究势阱宽度对色散的影响. 势阱间距是内层势阱宽度加外层势阱宽度. 首先保持内层势阱宽度为7.8 µm不变, 分别改变外层势阱宽度为9.35, 7.8和5.75 µm, 三种外层模式和对应的内层模式的色散曲线如图12(a)所示.

      内层势阱宽度为7.8 µm时, 内层模式在1.3—1.8 µm 均为反常色散, 其GVD绝对值随着外层势阱变窄而略微增大, 对应的外层模式由正 常色散变为反常色散. 外层势阱宽度为 9.35, 7.8和5.75 µm时, 对应的外层模式零色散波长分别 为 1.506, 1.636和1.915 µm. 即内层势阱宽度不变时, 随着外层势阱变窄, 外层模式零色散波长右移, 内层模式和外层模式之间GVD绝对值差值增大, 说明外层势阱变窄会减弱两种模式之间的能量 传输.

      然后保持外层势阱宽度为7.8 µm不变, 分别改变内层势阱宽度为9.35, 7.8和5.75 µm, 三种外层模式和对应的内层模式的色散曲线如图12(b)所示.

      外层势阱宽度为7.8 µm时, 内层模式在 1.3—1.8 µm 均为反常色散, GVD绝对值随着内层势阱变宽而增大, 对应的外层模式由正常色散变为反常色散. 内层势阱宽度为9.35, 7.8和5.75 µm时, 对应的外层模式零色散波长分别为 1.63594, 1.63563和1.63547 µm. 外层势阱宽度不变时, 随着内层势阱变宽, 外层模式零色散波长略微右移, 内层模式和外层模式之间GVD绝对值差值增大, 说明内层势阱变宽会减弱两种模式间的能量传输.

      通过操控势阱结构在微腔中形成了两个单模输出, 内层模式呈现反常色散, 外层模式呈现正常色散. 内外两个势阱间距和宽度影响着内外两个模式之间的能量传输, 并且对外层模式的影响较大. 两个势阱间距越大, 外层势阱越窄, 内层势阱越宽, 这种能量传输越弱. 通过调整内外两个势阱之间的间距和宽度, 可以使外层模式由正常色散变为反常色散. 双势阱结构可以为在微腔内通过激发三阶非线性和克尔效应产生光频双梳创造一个很好的平台.

    4.   结　论

    • 本文研究了基于离子扩散形成的GRIN微腔构造原理及色散特性. GRIN微腔相比传统的WGM微腔增加了折射率分布这一新自由度. 基于此, 本文提出了两种基于改变折射率分布的色散调控方式. 第1种方式是改变边缘几何外形, GRIN微腔模场泄漏到空气中发生全反射呈现反常色散, 不泄漏则呈现正常色散. 对于离子扩散和塑形工艺顺序不同的两种双边楔形微腔, 较大的半径和楔角都会使微腔接近零色散. 并且先塑形后进行离子扩散的微腔得到正常色散, 先进行离子扩散后塑形的微腔为反常色散. 第2种方式是构建双势阱, 利用势阱结构中的两个单模能量耦合来调控色散. 两个势阱间距越大, 外层势阱越窄, 内层势阱越宽, 两种模式之间能量传输越弱. 表现为外层模式偏向正常色散, 内层模式偏向反常色散, 但对外层模式影响较大. 两种方式显示了GRIN微腔可以灵活地调控色散, 在非线性光学应用中如生成克尔光频梳、精密光谱测量具有巨大潜力.

    参考文献 (29)

目录

/

返回文章
返回