首页
登录
注册
下载:
-
在托卡马克中, 等离子体的旋转及其速度剪切在决定等离子体低约束模式到高约束模式（L-H模）转换阈值、抑制磁流体力学不稳定性以及形成和维持等离子体内部输运垒等过程中都起着至关重要的作用[1-5]. 目前托卡马克装置中的主要动量源来自于外部中性束的动量注入. 然而对于国际热核聚变实验堆(international thermonuclear experimental reactor, ITER)来说, 由于装置的高密度和大尺寸, 中性束难以有效穿透等离子体进入其芯部, 导致中性束注入(netural beam injection, NBI)难以在实现Q值大于5的目标同时驱动足够大的环向旋转来抑制电阻壁模不稳定性[6,7]. 因此, 与湍流涨落有关的残余应力驱动的自发旋转成为了ITER维持高参数并致稳电阻壁模的关键. 研究人员已经在诸如JFT-2M, Alcator C-Mod, JET以及DIII-D等装置中开展了自发旋转的实验研究, 并建立了自发旋转大小与储能、等离子体电流的定标关系[8-15].
在DIII-D上, 研究人员发现在等离子体边界自发扭矩与台基压力梯度存在明显的相关性, 说明台基区域E × B剪切与残余应力的产生密切相关[11]. Rice等[16]在Alcator C-Mod托卡马克上展开对等离子体L-H转换以及L-I转换期间芯部自发旋转的定标研究, 并建立了马赫数与等离子体芯部速度随边界温度梯度、安全因子和环向磁场变化的定标关系. 研究人员在H模和I模数据库基础上对无量纲参数进行研究, 并且与JET和DIII-D的结果进行比较, 确定了自发扭矩存在与装置尺寸等相关的自发扭矩归一化规律[9]. 在DIII-D装置上, 研究人员就边界自发扭矩对无量纲参数如
$ \rho _{\ast } $ (归一化回旋半径)和$ \nu _{\ast } $ (归一化碰撞率)的依赖性做出了具体的定标关系[13]. 诸如DIII-D, Alcator C-Mod, ASDEX Upgrade, JET, JT-60U以及KSTAR等托卡马克装置都以探讨影响等离子体自发旋转的因素为目的进行了理论研究和实验观察, 这对于预测未来ITER运行中的自发旋转有着举足轻重的意义.EAST研究人员利用平衡中性束注入的方法在东方超环托卡马克(experimental advanced superconducting tokamak, EAST)上首次测量了L模等离子体中的自发扭矩[17]. 随后, 提出了一种平衡旋转的新经典验证方法[18]. 本研究基于平衡中性束注入和新经典验证的方法, 在EAST上建立了L模等离子体情况下自发扭矩与无量纲参数之间的定标关系. 相较于使用动量调制测量自发扭矩的实验方法, 使用平衡中性束注入的方式可以有效地避免动量扩散、对流项及其瞬时变化量对残余应力测量结果的影响, 也能避免瞬时
$ {\boldsymbol{J}}\times{\boldsymbol{B}} $ 力矩等因素对残余应力测量的干扰[19-21]. 本研究进一步扩充了托卡马克装置中等离子体自发旋转的实验数据, 并为未来如ITER等聚变反应堆中等离子 体自发旋转的预测提供参考. 本文第2节给出了EAST装置概述、诊断条件以及测量残余应力的理论方法. 第3节介绍了实验结果及数据处理. 第4节详细讨论了本文的实验结果, 与其他装置的结果进行比较, 并分析了可能存在的差异原因. 第5节总结了总体工作和研究发现. -
本文的实验在EAST上进行, EAST的大半径R ≈ 1.85 m, 小半径a ≈ 0.45 m, 等离子体电流
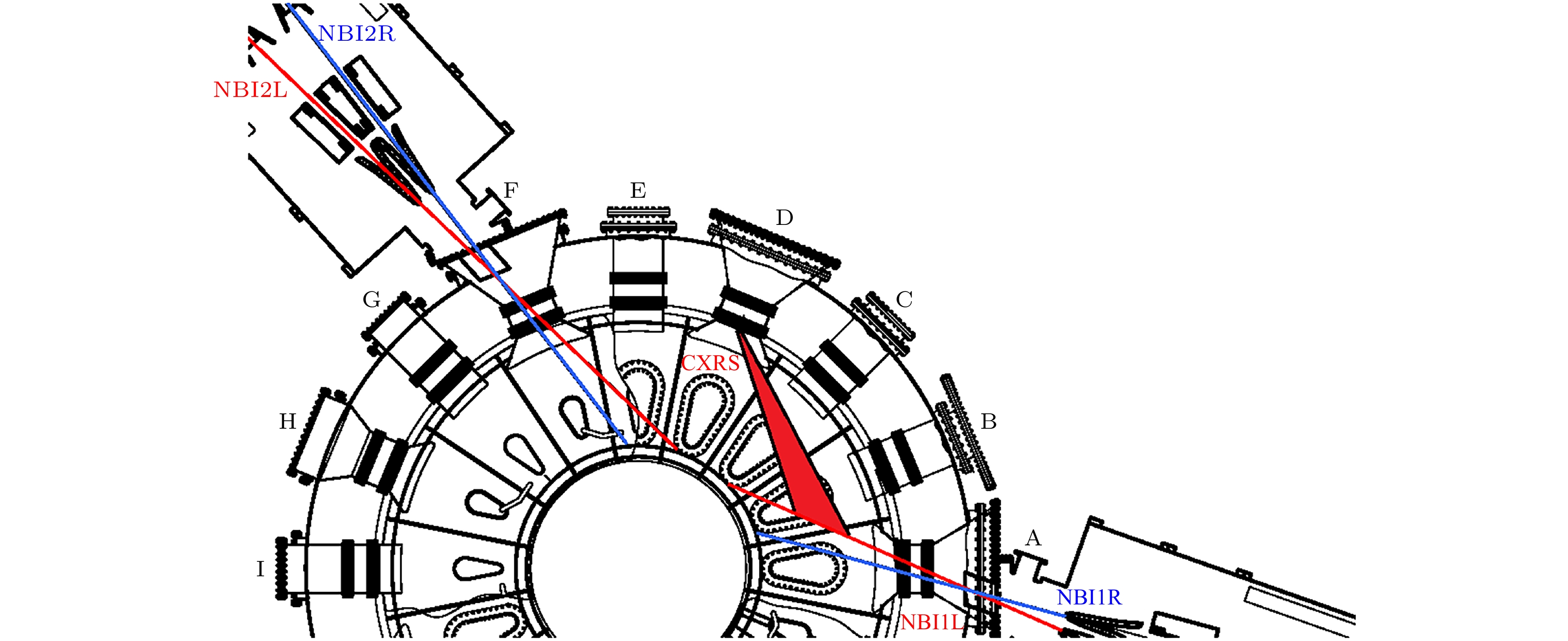
$ I_{\rm{p}}\leqslant 1 \ {\rm{MA}} $ , 环向磁场$ B_{\rm{T}}\leqslant 3.5 \ {\rm{T}}$ . EAST配备了多种加热系统, 包括低杂波电流驱动系统、电子回旋加热系统、离子回旋加热系统, 以及同向和反向的中性束注入(NBI)系统[22]. 本文的研究基于先前EAST的配置, 即NBI系统由位于A窗口和F窗口的两条注入束线组成, 每条注入线分别有左右两个离子源: 分布在A窗口的NBI1L和NBI1R进行同向注入; 分布在F窗口的NBI2L和NBI2R进行反向注入. 每条中性束的束流能量范围为50—80 keV, 束流电流在40—70 A之间, 脉冲宽度为10—100 s. 为了在EAST上开展等离子体物理实验研究, 采用了多种诊断方法来获取数据. 本文使用偏振干涉仪(POINT)测量等离子体密度[23], 由于POINT弦积分反演过程受到等离子体平衡重建结果的影响, 其测量相对误差约为5%. 汤姆孙散射[24]和电子回旋辐射诊断用于测量电子温度[25]. 通过EFIT (equilibrium fitting code)平衡重建得到安全因子q, 安全因子q的定义为磁场线沿环向绕行的圈数与极向绕行圈数的比值, 是描述等离子体磁场位形的重要物理量, 对磁约束稳定性具有重要意义. 电荷交换复合光谱(charge exchange recombination spectroscopy, CXRS)用于测量由NBI中性粒子与等离子体中离子之间的电荷交换反应发射的谱线, 以计算等离子体的环向速度和离子温度[26-28]. 图1展示了CXRS和NBI系统的布局, CXRS的测量区域显示为CXRS视线与NBI束线的交点.本文使用平衡中性束注入的方法来实现残余应力的测量, 原理可以从磁面平均的角动量守恒方程得出:
其中, n是等离子体密度, m是等离子体中主离子质量, R是托卡马克装置大半径, ω是等离子体环向旋转角频率, ρ是等离子体归一化坐标,
$V^{\prime} $ 是磁面所围体积对磁面坐标的导数. 方程左侧的时间导数项代表瞬时加速度. 方程右侧小括号内的第1项和第2项分别是由扩散和对流通量产生的扭矩, 小括号内第3项是由残余应力产生的自发扭矩, 括号外最后一项是来自NBI的外部力矩输入. 为了在实验中测量自发力矩, 必须将扩散、对流和残余应力项对总动量通量的贡献进行分离. 为了实现这一目标, 通常使用两种方法: 基于调制的方法研究[19-21,29-32]以及基于平衡中性束的实验研究[11,12]. 为了避免残余应力和其他瞬态扭矩对测量的时间依赖性影响, 本文采用了平衡中性束的方法. 在本研究中, 通过不同功率的同向、反向两条束线的四个离子源的结合注入, 使得环向旋转剖面足够平坦且接近于0$( {\partial\omega}/{\partial\rho}\sim0 , \omega\sim0 )$ . 因此, 可以忽略角动量守恒方程等号右边括号内的扩散项和对流项, 仅有自发扭矩密度平衡NBI力矩密度. 由于维持一个近乎零的环向旋转分布是非常理想的情况, 在托卡马克等离子体中并不容易实现. 因此, 为了验证旋转速度接近于零的情况下忽略动量扩散、对流项假设的合理性, 本文使用了基于Stacey-Sigmar理论开发的TransROTA代码来模拟所有与速度相关的项对环向角动量的贡献[33,34]. 本文利用TRANSP/NUBEAM计算NBI扭矩密度分布[35,36]. 在速度相关项可忽略的情况下, 自发扭矩等同于NBI扭矩的负值, 即$ \eta _{{\rm{intrinsic}}}\approx - \eta _{{\rm{NBI}}} $ . -
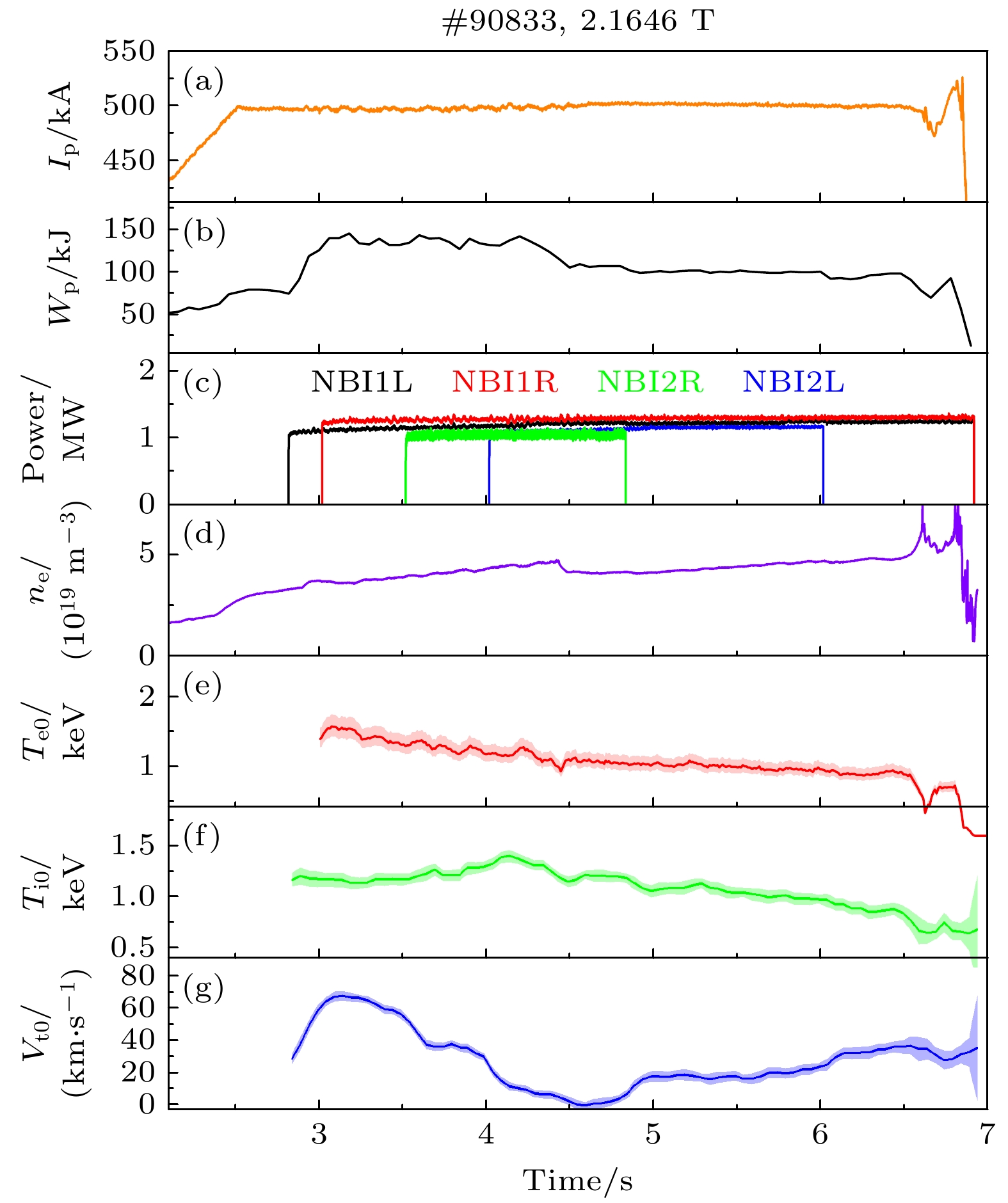
为了说明测量残余应力的过程, 图2展示了示例放电
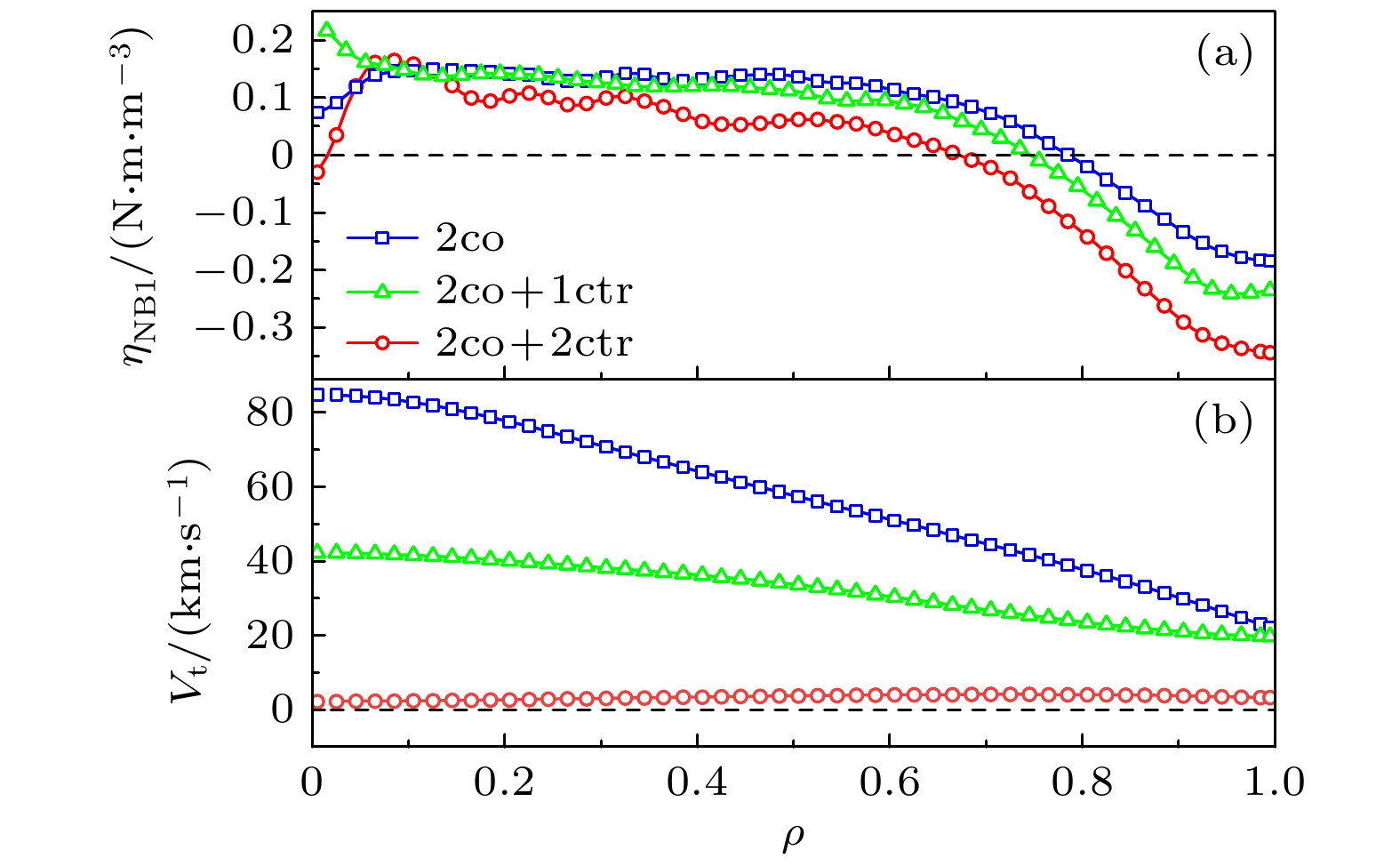
$ \# $ 90833的等离子体参数的时间演化. 等离子体电流在2.5 s时达到500 kA. NBI1L在等离子体电流平顶段注入, 随后是NBI1R, NBI2L和NBI2R. 两个同向NBI束的源功率分别为1.2和1.3 MW, 而两个反向NBI束的源功率则约为1.1 MW. 等离子体在注入两个同向NBI后进入H模, 储能为140 kJ, 并在注入两个反向NBI后转换回L模. 电子密度、电子温度和离子温度在中性束的连续注入过程中几乎保持稳定, 值分别为$ n_{{\rm{e}}}\sim4.1\times 10^{19}/{\mathrm{m}}^{3} $ ,$ T_{{\rm{e0}}}\sim1.6 \ {\rm{keV}} $ ,$ T_{{\rm{i0}}}\sim1.2 \ {\rm{keV}} $ . 在两个同向NBI的条件下, 旋转速度达到约80 km/s, 并随着两个同向和两个反向NBI的注入降低至0 km/s.图3展示了TRANSP/NUBEAM计算的在不同NBI组合下的NBI扭矩密度以及等离子体环向旋转速度分布. 三种不同NBI组合的总注入扭矩密度分布如图3(a)所示, 扭矩密度的正值和负值分别对应于同电流方向和反电流方向. 在所有三种组合下, 等离子体边界区域的扭矩密度主要由反向
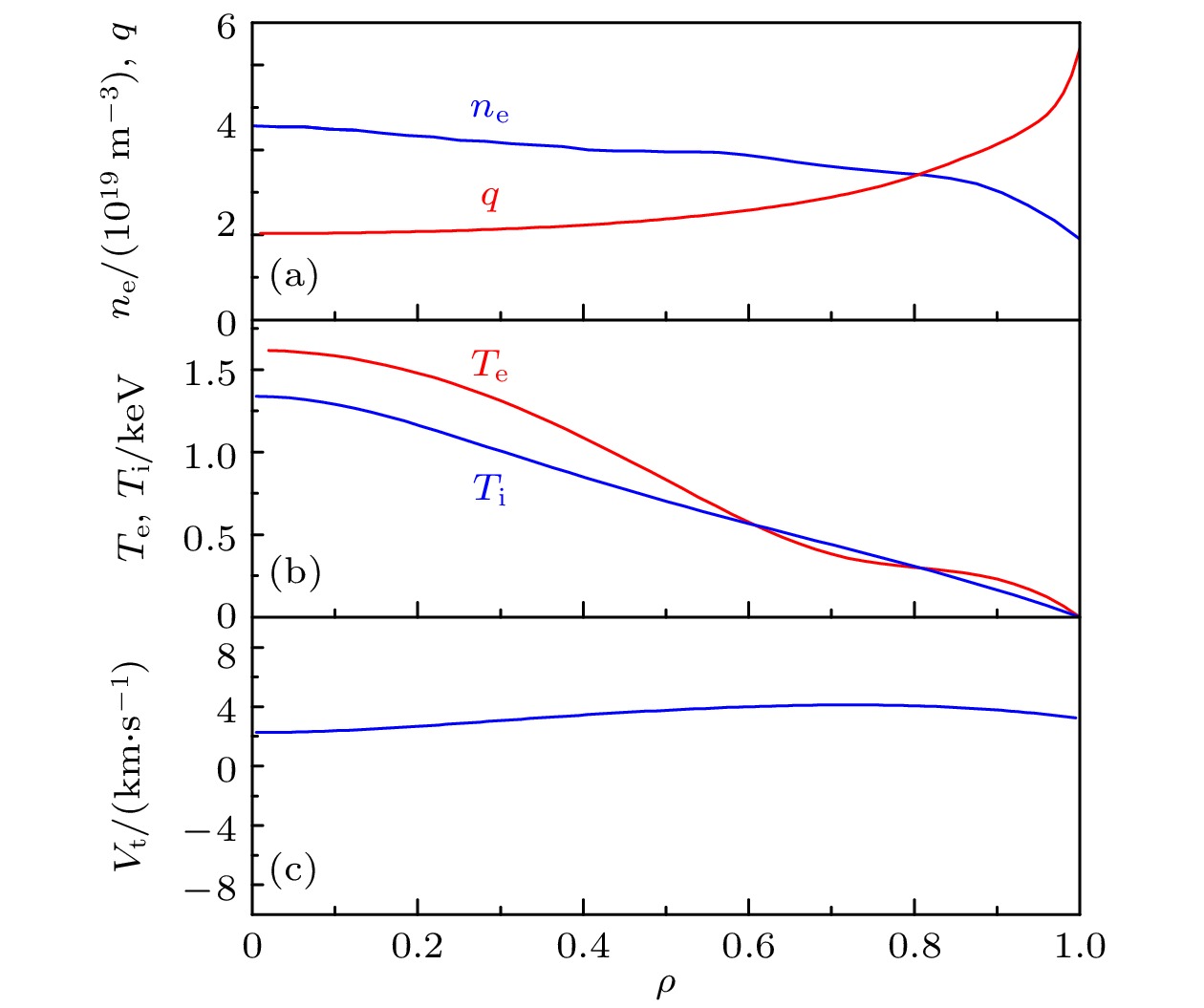
$ {\boldsymbol{J}}\times{\boldsymbol{B}} $ 力矩主导, 而在等离子体芯部区域, 则由同向$ {\boldsymbol{J}}\times{\boldsymbol{B}} $ 和碰撞扭矩主导. 图3(b)展示了在三种不同NBI条件下的环向旋转速度分布. 随着反向NBI的增加, 环向旋转速度逐渐降低至几乎为零. 最终, 在两个同向和两个反向NBI的条件下, 观察到在$ 0\leqslant \rho \leqslant1 $ 范围内的环向旋转速度几乎归零且分布平坦. 因此, 在这种情况下与速度相关的项, 即正比于速度梯度的扩散项和正比于速度的对流项对环向角动量通量的贡献可以忽略不计.如图3(b)所示, 在两个同向、两个反向NBI期间仍存在有限的环向旋转速度, 其峰值在4 km/s左右. 因此, 为了进一步验证在测量自发扭矩分布时忽略动量平衡方程中速度相关项这一假设的合理性, 本文使用了TransROTA模拟了速度相关项对动量平衡的贡献. 对图3中两个同向、两个反向中性束注入期间4.69 s的时刻使用TRANSP/NUBEAM和TransROTA开展动量平衡分析. 模拟所用的密度、安全因子q、温度、速度参数分布如图4所示. 图4(a), (b)展示了
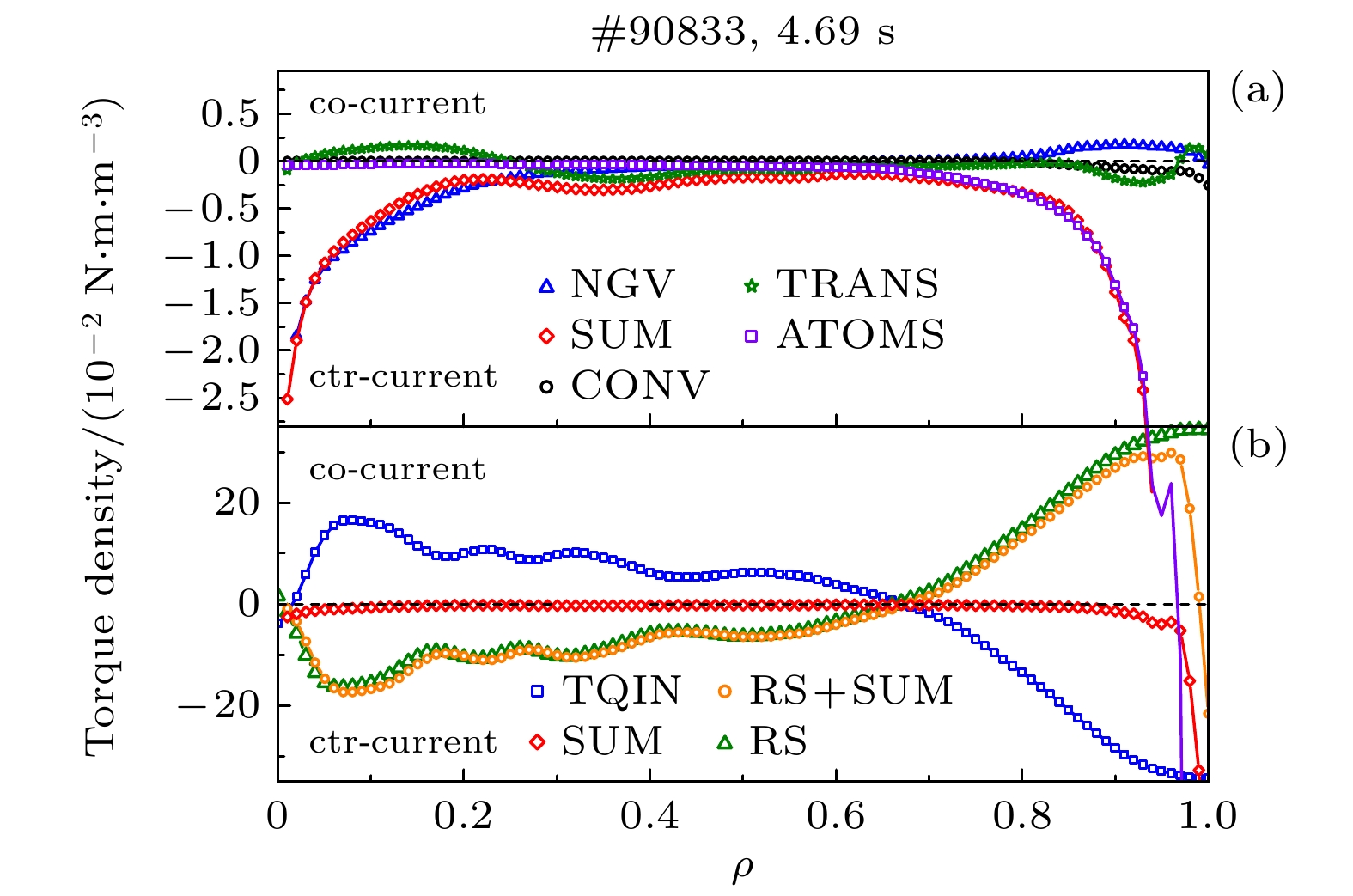
$ \# $ 90833的密度、温度分布. 可以看到在四个NBI投入期间, 尽管在0.8到1的范围内有梯度变化, 但并未形成典型的台基结构, 说明此时等离子体仍处于L模.图5(a)展示了TransROTA模拟结果, 其中NGV, CONV, TRANS, ATOMS和SUM分别对应于新经典回旋黏滞、对流、瞬态加速度、电荷交换动量损失和它们的总和所产生的力矩密度. 图5(b)显示了不同项对动量平衡贡献的力矩密度比较, 动量平衡表示为TQIN + SUM + RS = 0, 其中TQIN是来自TRANSP/NUBEAM模拟的中性束注入的总输入力矩密度, RS是由残余应力产生的自发力矩密度. 速度依赖项的总和SUM比外部扭矩密度注入TQIN小两个数量级, 进一步验证了等离子体环向旋转分布足够接近零, 因此可以忽略速度依赖项SUM. 在忽略速度相关项SUM后, 从动量平衡可知此时残余应力可表示为RS ≈ –TQIN, 如图5(b)所示.
在开始自发扭矩密度的定标分析之前, 有必要说明力矩密度与局部残余应力之间的关系. 通过对环向角动量守恒方程体积分可以得出
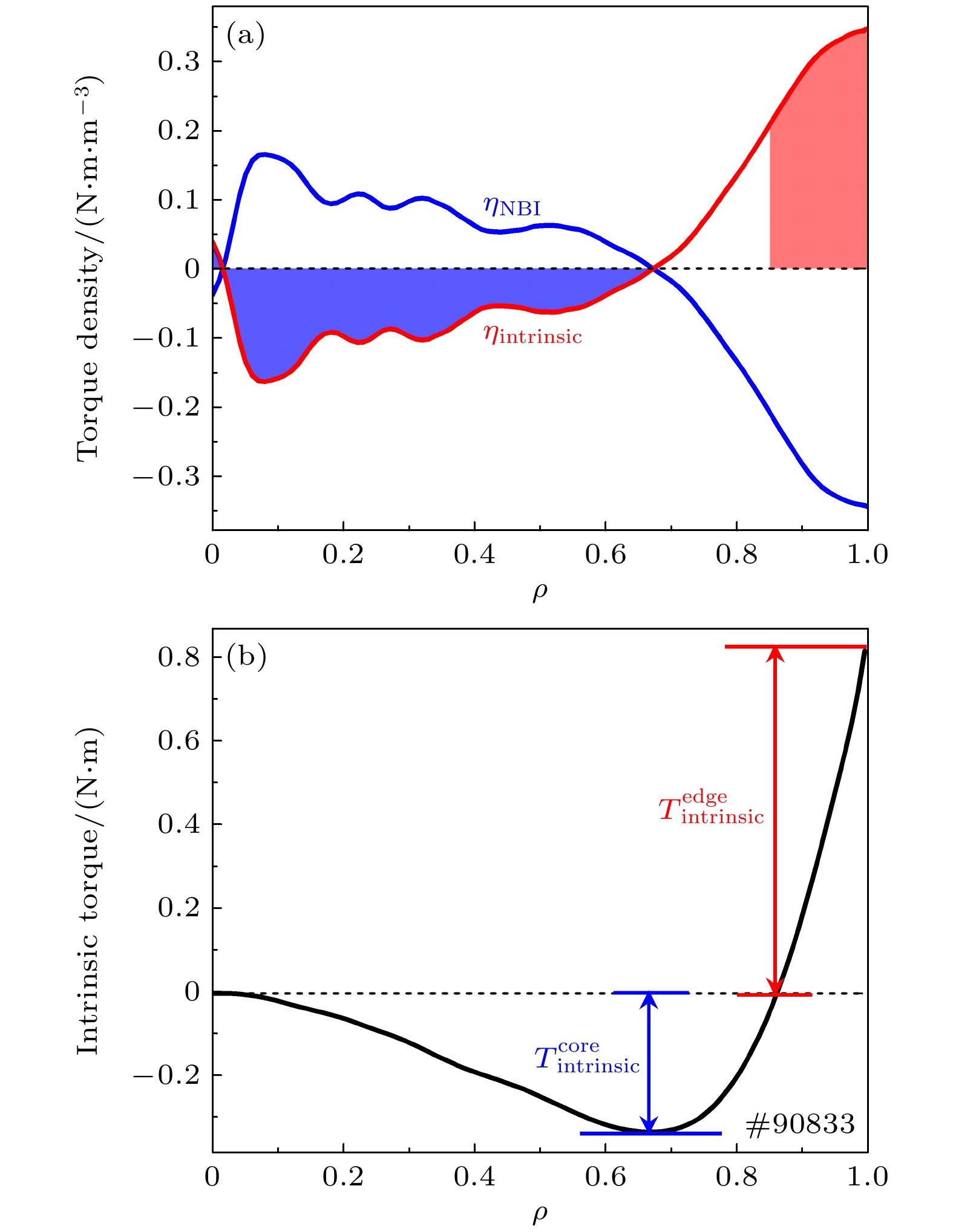
$ T_{{\rm{intrinsic}}} = \displaystyle \int \eta {\rm{d}}V\propto \varPi ^{{\rm{residual}}} $ . 本研究使用了两种不同积分区间的体积分自发扭矩的定义, 如图6所示. 将图(a)中自发扭矩密度从零积分到力矩密度为零点的区域内的积分值定义为图(b)所示的芯部自发扭矩$ T_{{\rm{intrinsic}}}^{{\rm{core}}} $ . 不难看出$ T_{{\rm{intrinsic}}}^{{\rm{core}}} $ 是自发扭矩体积分结果的第一个最大值. 而边界力矩$ T_{{\rm{intrinsic}}}^{{\rm{edge}}} $ 的积分区域覆盖整个最外闭合磁面内的等离子体, 如图6(a)中红色的积分区域所示. 与Solomon对边界自发扭矩的定义相比[37], 这一定义与等离子体自发旋转加速过程更相关, 如文献[2]所讨论.本文中归一化回旋半径
$ \rho_{\ast} $ 的计算公式为[9]对于芯部自发力矩,
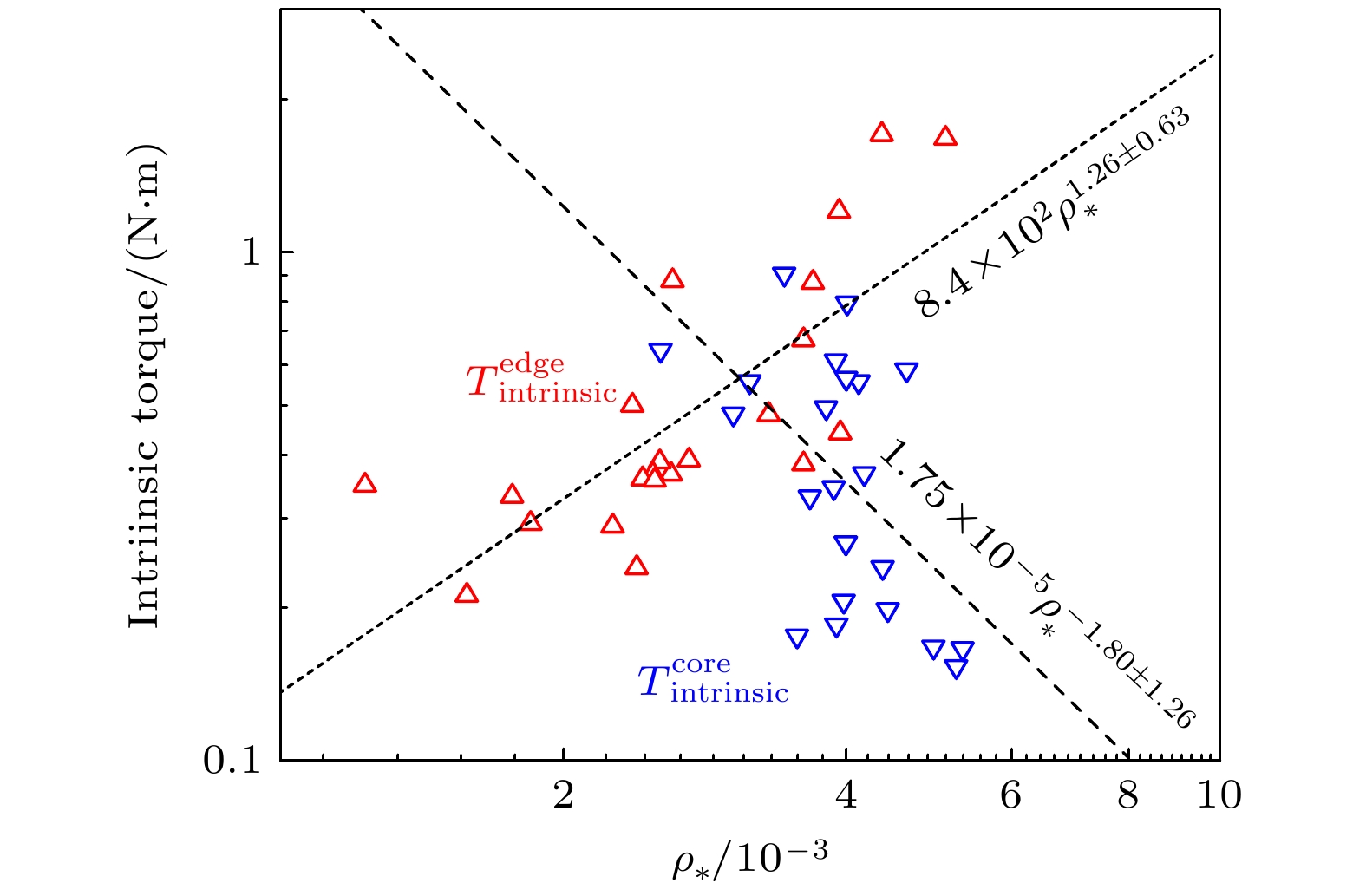
$ T_{{\rm{e}}} $ 取$ \eta _{{\rm{intrinsic}}} $ 等于零时的点, 而对于边界自发扭矩,$ T_{{\mathrm{e}}} $ 取$ T_{{\rm{intrinsic}}} $ 等于零时的点. 图7展示了等离子体芯部和边界自发旋转扭矩与$ \rho_{\ast} $ 之间的标定结果. 芯部和边界自发力矩与$ \rho_{\ast} $ 的定标结果分别为$ T_{{\rm{intrinsic}}}^{{\rm{core}}}\sim1.7\times10^{-5} \rho_{\ast}^{-1.80\pm1.26} $ 以及$ T_{{\rm{intrinsic}}}^{{\rm{edge}}}\sim8.4\times10^2 \rho_{\ast}^{1.26\pm0.63} $ . 由于$ \rho_{\ast} $ 随着装置尺寸的增大而减小, 定标结果表明, 在未来更大的聚变装置中芯部残余应力将增大, 而边界残余应力将减小.图8展示了自发力矩与归一化碰撞率
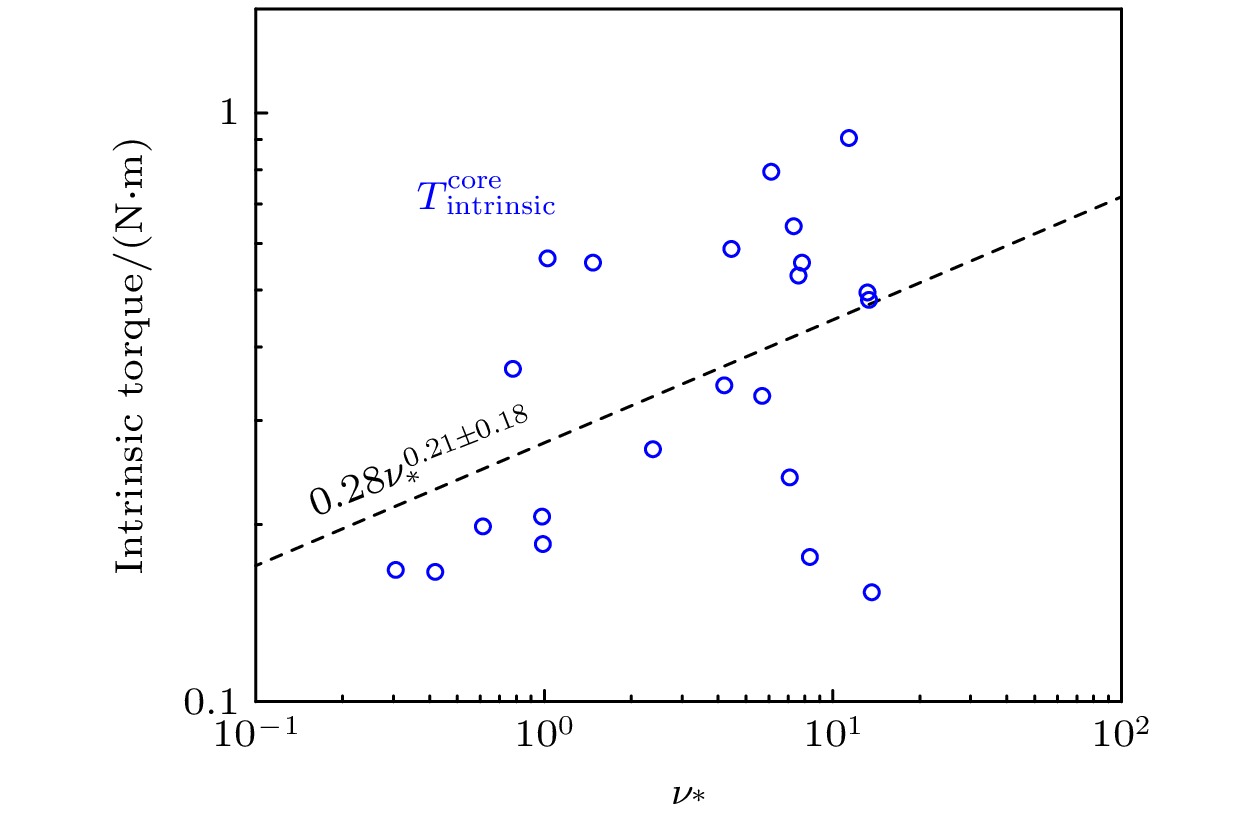
$ \nu _{\ast } $ 的定标结果,$ \nu _{\ast } $ 的计算公式为[9]其中Zeff为等离子体有效电荷数, 反映了等离子体中杂质对等离子体组分的贡献. 芯部自发扭矩的定标结果为
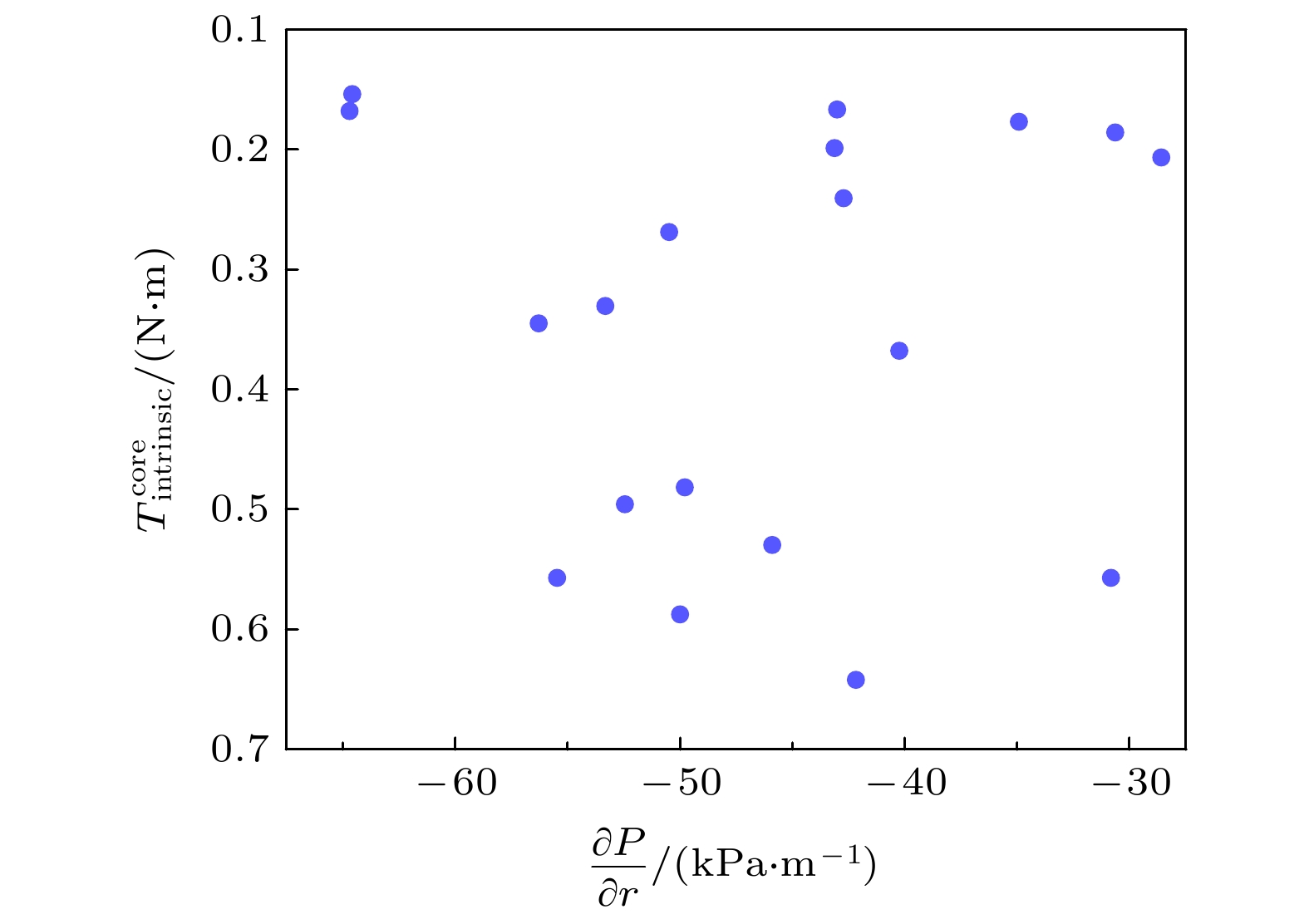
$ T_{{\rm{intrinsic}}}^{{\rm{core}}}\sim0.28\nu_{\ast}^{0.21\pm0.18} $ . 表明芯部自发扭矩与$ \nu_{\ast} $ 弱相关. 由于数据量偏少, 导致$ \nu_{\ast} $ 定标结果误差较大, 与C-MOD实验中的定标结果$ T_{{\rm{intrinsic}}}^{{\rm{core}}}\sim \nu_{\ast}^{0.09} $ 存在差异[9].图9展示了芯部自发扭矩与压力梯度之间的定标结果, 其中压力梯度的计算位置与
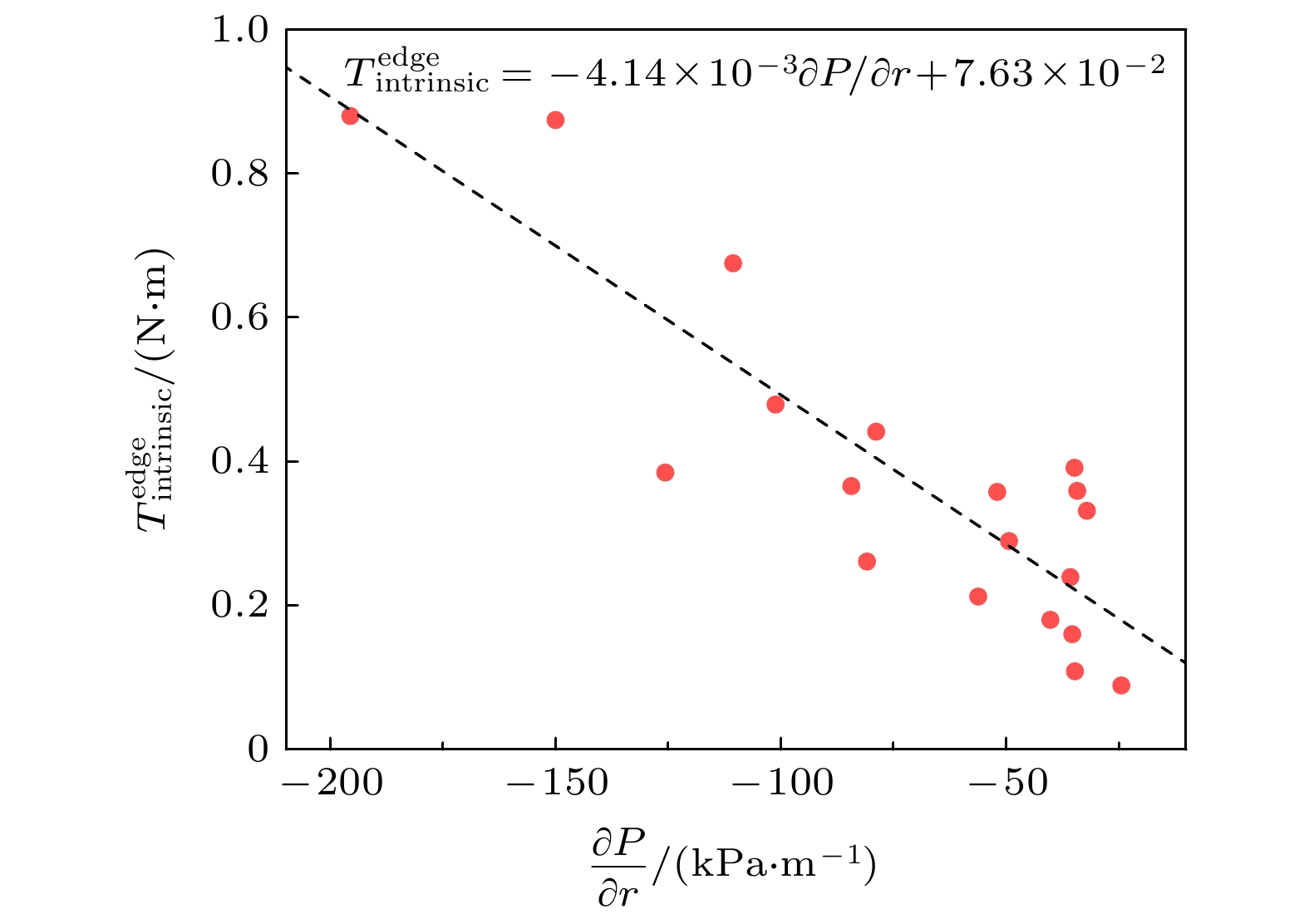
$ \rho_{\ast} $ 相同. 在芯部自发扭矩与压力梯度的定标结果中未发现明显趋势, 这一结果与DIII-D的结论一致. 边界自发力矩的定标结果如图10所示, 与芯部自发扭矩的定标结果不同, 边界自发扭矩与压力梯度定标呈线性关系, 说明压力梯度不仅为湍流的增长提供了自由能, 同时也为残余应力的产生提供了所需的对称性破坏机制. 边界自发扭矩反比于压力梯度这一定标结果也与DIII-D相似[11]. -
在本研究中, 利用EAST上平衡中性束研究了残余应力与无量纲参数
$ \rho_{\ast} $ ,$ \nu_{\ast} $ 之间的定标关系. 研究结果显示, 不同区域残余应力对$ \rho_{\ast} $ 的依赖性有所不同. 为了解释这些结果, 有必要将其与之前的实证研究、相关的理论框架进行比较, 并考虑可能影响结果的测量方法的差异.Solomon等[11]和Chrystalt等[13]在DIII-D上报告过自发扭矩与
$ \rho_{\ast} $ 的定标结果, 观察到自发扭矩对$ \rho_{\ast}^{-1.5} $ 的依赖关系. Rice等[14]在2021年的跨装置比较中也得到了类似的结果. 与本文的定标结果相比, EAST的实验中芯部自发扭矩与$ \rho_{\ast} $ 的定标结果为$ T_{{\rm{intrinsic}}}^{{\rm{core}}}\sim\rho_{\ast}^{-1.80} $ , 比较接近C-Mod的实验结果. 在跨装置的联合实验中, C-Mod测得的残余应力定标结果略小于其他装置. Rice曾将这一结果归因于等离子体参数、测量手段的不同. 然而使用与DIII-D相同的测量方法, EAST上残余应力的定标结果与C-Mod相似, 表明未来装置中残余应力的预测值可能要低于之前跨装置联合实验中的预测结果.芯部自发扭矩
$ T_{{\rm{intrinsic}}}^{{\rm{core}}} $ 与$ \rho_{\ast} $ 的定标关系同样可以从L-I, L-H中著名的Rice定标律得出[38]:$ \Delta V\sim {\Delta W_{{\rm{p}}} }/{I_{{\rm{p}}} }\sim {\rho _{\ast }^{-3}}/{\rho _{\ast }^{-1.5} } \sim\rho _{\ast }^{-1.5} $ (ΔV为等离子体环向旋转速度变化量, ΔW为等离子体储能变化量), 其中$ n\sim\rho_{\ast}^{-2} $ ,$ T\sim\rho_{\ast}^{-1} $ , 以及$ I_{{\mathrm{p}}}\sim\rho_{\ast}^{-1.5} $ . 而L-H, L-I转换过程中残余应力的产生机制主要为$ {\boldsymbol{E}}\times{\boldsymbol{B}} $ 剪切流, 在ITG主导的情况下残余应力与$ \rho_{\ast}T^{1/2}\chi_{\phi} $ 成正比[39]. 然而, 在定标结果中观察到$ \rho_{\ast} $ 的幂次存在细微差异. 这些差异可能归因于等离子体形状的影响. 理解这些差异至关重要, 未来的研究应旨在探索残余应力与等离子体形状之间的依赖关系.通过开展线性回归分析, 可以得到自发扭矩与
$ \rho_{\ast} $ ,$ \nu_{\ast} $ 的定标公式:从EAST的定标结果外推ITER的自发扭矩大小, 外推过程参考使用运行方案一中预测的等离子体参数[40], 其中密度、台基顶部温度、纵场强度、95%极向磁通对应磁面处的安全因子
$ q_{95} $ 、有效电荷数$ Z_{{\mathrm{eff}}} $ 、离子质量、装置大半径以及小半径分别为$ 11\times10^{19}\;{\mathrm{m}}^{-3} $ (15 MA时94%Greenwald密度极限), 5 keV(台基顶部), 5.3 T, 3, 2, 2.5 amu(氘-氚混合), 6.2 m以及2 m. 得到$ \rho_{\ast} \sim 0.0011 , \nu_{\ast} \sim 0.0055 $ 预估出ITER台基顶部的芯部残余应力大小约为$ (1.0\pm6.3) ~{\mathrm{N}}{\cdot} {\mathrm{m}} $ , 远小于之前Chrystal等[13]的预测结果. 造成这一结果的原因可能是由于本研究所统计的放电中均没有观察到明显的边界输运垒, 因此在台基区缺少$ {\boldsymbol{E}}\times{\boldsymbol{B}} $ 剪切流破坏湍流k谱对称性, 进而难以诱发残余应力的产生.与芯部区域自发力矩的定标结果相比, 边界自发力矩的定标趋势明显不同, 这意味着它在未来更大的装置中可能会变得更小. 芯部和边界自发力矩定标结果之间的不同可能是由于等离子体参数和加热功率的差异. 另外, 刮削层的差异也可能在平衡其他机制和生成边界自发力矩方面发挥重要作用[41], 这超出了本文的研究范围, 将在未来的实验中进一步研究.
与Zimmermann等[20]和Ohtani等[21]采用的基于调制分析提取时间变化传输系数的方法相比, 本研究中的残余应力测量基于使用平衡束的方法[11]. 这种方法可以可靠地测量残余应力. 然而, 该方法的一项局限性在于缺乏关于动量扩散率和对流速度的信息, 而稳态下的环向旋转速度分布与动量扩散、对流系数的分布密切相关[42], 所以仅靠当前自发扭矩的定标结果仍无法实现环向旋转速度分布的预测. 为了验证ITER中环向旋转能否有效地抑制电阻壁模不稳定性, 未来计划在EAST开展更多动量调制实验以扩展当前的自发旋转数据库, 从而进一步实现ITER旋转速度的预测.
-
EAST上使用平衡中性束开展了残余应力分布的测量以及其与无量纲参数之间定标关系的实验研究. 定标结果表明芯部残余应力与
$ \rho_{\ast}^{-1.80\pm1.26} $ 存在依赖关系, 表明芯部残余应力在未来更大的装置中对自发旋转的驱动起重要作用. 与芯部残余应力的定标结果相反, 边界残余应力则显示出对$ \rho_{\ast}^{1.26\pm0.63} $ 的依赖性. 结合芯部自发扭矩与归一化旋转半径、归一化碰撞率的定标结果, 得出芯部自发扭矩正比于$ \rho _{\ast}^{-1.39\pm 0.71}\nu _{\ast}^{0.11\pm 0.10} $ 的定标结果, 与JET, ASDEX, DIII-D以及C-Mod的联合实验中自发扭矩正比于$ \rho _{\ast}^{-1.5} $ 的定标结果相接近. 之前的联合实验中C-Mod测量的自发扭矩要小于其他装置的定标结果却与本文中EAST的定标结果接近, 说明导致C-Mod与JET, DIII-D定标结果不同的原因不是由于测量方式的不同. 使用EAST的定标结果预测得到的ITER参数下的自发扭矩要小于之前其他装置中的预测值, 使用ITER运行方案一中的等离子体参数预测而得到的芯部自发扭矩大小约为$( 1.0\pm6.3 )~ {\mathrm{N}}\cdot {\mathrm{m}} $ , 远小于之前DIII-D的预测结果. 仍需要更多实验数据以建立动量扩散、对流系数的定标律, 结合本文中自发扭矩的定标结果, 从而实现ITER环向旋转速度分布的预测.
EAST上基于平衡中性束注入方法的L模等离子体自发扭矩分布实验研究
Experimental study of intrinsic torque distribution of L-mode plasma based on balanced neutral beam injection on EAST
-
摘要: 等离子体旋转及其剪切是影响聚变装置的关键参数之一, 等离子体旋转的驱动和控制对未来聚变堆的稳定运行和约束改善都具有很大意义. 目前靠外部动量注入的方式不足以在满足Q大于5的同时抑制电阻壁模不稳定性. 因此, 有必要对不依赖外部动量注入的等离子体自发旋转展开实验研究. 为了更好地预测未来聚变装置中自发旋转速度的大小, 本文在东方超环托卡马克(EAST)上开展了残余应力与无量纲参数的定标研究, 利用平衡中性束的方法进行了多次自发扭矩的实验测量, 为未来托卡马克装置中等离子体自发旋转的预测提供实验依据. 实验定标结果表明, 芯部残余应力与$\rho _{\ast }^{-1.80\pm1.26}$相关, 而边界残余应力的定标则显示出对$\rho _{\ast }^{1.26\pm0.63}$的依赖性, 这表明随着装置尺寸的增大, 未来托卡马克聚变堆中芯部的残余应力可能会增大, 而边界残余应力则减小. 芯部与边界残余应力的定标结果差异表明, 在边界区域刮削层区残余应力的产生过程中, 有$\boldsymbol{E}\times\boldsymbol{B}$流剪切以外的对称性破坏机制起主导作用. 在自发扭矩与$\nu _{\ast }$的定标之间发现芯部自发扭矩依赖于$\nu _{\ast }^{0.21\pm0.18}$. 结合芯部自发扭矩与归一化旋转半径、归一化碰撞率的定标结果, 得到芯部自发扭矩的定标律为$\rho _{\ast }^{-1.39\pm0.71}\nu _{\ast }^{-0.11\pm0.10}$. 使用ITER氘-氚混合运行方案中的等离子体参数预测得到芯部自发扭矩大小为$(1.0\pm6.3)$ N$\cdot$m, 远小于之前DIII-D预测结果.Abstract: Plasma rotation and its shear are key parameters influencing the performance of fusion devices. The prediction and control of plasma rotation velocity are of great significance for improving the stable operation and confinement of future fusion reactors. External momentum injection methods are insufficient to suppress resistive wall mode instability while achieving Q greater than 5 in international thermonuclear experimental reactor (ITER). Therefore, it is necessary to conduct experimental research on intrinsic plasma rotation that does not rely on external momentum injection. To better predict the magnitude of intrinsic rotation velocity in future fusion devices, we conduct an experimental study on the scaling of residual stress and dimensionless parameters on EAST. Using the balanced neutral beam, multiple measurements of intrinsic torque are performed, providing experimental basis for predicting the intrinsic rotation in future tokamak devices. The scaling results indicate that the core residual stress is dependent on $\rho_{\ast}^{-1.80\pm1.26}$, while the scaling of edge residual stress shows an opposite trend with $\rho _{\ast }^{1.26\pm0.63}$. This suggests that as the device size increases, the core residual stress in future large devices can increase, while the edge residual stress can decrease. The difference in scaling results between the core and edge residual stress indicates that in the edge region, the symmetry-breaking mechanism other than $\boldsymbol{E}\times\boldsymbol{B}$ flow shear dominates the generation of residual stress in the scrape-off layer. A relationship is found between intrinsic torque and $\nu _{\ast }$, revealing that the core intrinsic torque depends on $\nu _{\ast }^{-0.21\pm0.18}$. Combining the scaling results of core intrinsic torque with the gyroradius and normalized collisionality, the scaling law for core intrinsic torque is obtained to be $\rho _{\ast }^{-1.39\pm0.71}\nu _{\ast }^{0.11\pm0.10}$. Using plasma parameters of ITER operation scenario 1, the core intrinsic torque in future ITER plasma is predicted to be $(1.0\pm6.3)~{\mathrm{N}}{\cdot} {\mathrm{m}}$, which is much smaller than the predicted magnitude at DIII-D.
-
Key words:
- tokamak /
- momentum transport /
- intrinsic rotation /
- scaling law .
-
-
图 2 (a)等离子体电流、(b)等离子体储能、(c)中性束功率、(d)平均电子密度、(e)芯部电子温度、(f)芯部离子温度和(g)芯部环向旋转速度随时间演化
Figure 2. Time evolutions of (a) plasma current, (b) stored energy, (c) neutral beam source power, (d) line-averaged electron density, (e) central electron temperature, (f) central ion temperature, and (g) central toroidal rotation velocity.
图 3
$ \# $ 90833不同驱动方案下NBI扭矩密度和环向旋转速度的比较 (a) NBI的总输入扭密度; (b)等离子体环向旋转速度Figure 3.
$ \# $ 90833 Comparison of NBI torque density and toroidal rotation velocity among different momentum driving schemes: (a) Total input torque densities from NBIs; (b) toroidal rotation velocities.
图 4 放电
$ \# $ 90833在4.69 s时, (a)电子密度和安全因子; (b)电子和离子温度; (c)环向旋转速度分布Figure 4. Profiles of (a) electron density and safety factor, (b) electron and ion temperature, and (c) toroidal rotation velocity at 4.69 s of discharge
$ \# $ 90833.
图 5 (a) TransROTA计算的速度相关项的径向分布; (b) TRANSP/NUBEAM计算的NBI力矩密度、速度相关项以及自发扭矩密度之间的对比
Figure 5. (a) Radial distributions of TransROTA-calculated velocity-dependent terms; (b) comparison among TRANSP/NUBEAM-calculated NBI injected torque densities, veolocity-dependent terms and intrinsic torque densities.
图 6 (a) NBI力矩密度和自发扭矩力矩密度的径向分布; (b) 体积分后的力矩分布. 两种不同自发扭矩积分区域及其定义如图(a)和(b)所示
Figure 6. (a) Radial distributions of NBI and intrinsic torque densities; (b) volume-integrated torque profiles. Two different integral ranges and definitions of intrinsic torque are shown in panel (a) and (b)
图 7 自发扭矩与
$ \rho_{\ast} $ 的定标结果Figure 7. Scaling results of intrinsic torques as a function of
$ \rho_{\ast} $ .
图 8 芯部自发扭矩与
$ \nu_{\ast} $ 的定标结果Figure 8. Scaling results of intrinsic torques as a function of
$ \nu_{\ast} $ 
图 9 芯部自发扭矩与压力梯度的定标关系
Figure 9. Scaling results of core intrinsic torques as a function of pressure gradients.
-
[1] Peeters A, Angioni C, Bortolon A, Camenen Y, Casson F, Duval B, Fiederspiel L, Hornsby W, Idomura Y, Hein T, Kluy N, Mantica P, Parra F, Snodin A, Szepesi G, Strintzi D, Tala T, Tardini G, De Vries P, Weiland J 2011 Nucl. Fusion 51 094027 doi: 10.1088/0029-5515/51/9/094027 [2] Diamond P, Kosuga Y, Gürcan Ö, McDevitt C, Hahm T, Fedorczak N, Rice J, Wang W, Ku S, Kwon J, Dif-Pradalier G, Abiteboul J, Wang L, Ko W, Shi Y, Ida K, Solomon W, Jhang H, Kim S, Yi S, Ko S, Sarazin Y, Singh R, Chang C 2013 Nucl. Fusion 53 104019 doi: 10.1088/0029-5515/53/10/104019 [3] Ida K, Rice J 2014 Nucl. Fusion 54 045001 doi: 10.1088/0029-5515/54/4/045001 [4] Rice J E 2016 Plasma Phys. Control. Fusion 58 083001 doi: 10.1088/0741-3335/58/8/083001 [5] Stoltzfus-Dueck T 2019 Plasma Phys. Control. Fusion 61 124003 doi: 10.1088/1361-6587/ab4376 [6] Garofalo A M, Strait E J, Johnson L C, La Haye R J, Lazarus E A, Navratil G A, Okabayashi M, Scoville J T, Taylor T S, Turnbull A D 2002 Phys. Rev. Lett. 89 235001 doi: 10.1103/PhysRevLett.89.235001 [7] Chapman I T, Liu Y Q, Asunta O, Graves J P, Johnson T, Jucker M 2012 Phys. Plasmas 19 052502 doi: 10.1063/1.4714877 [8] Ida K, Miura Y, Matsuda T, Itoh K, Hidekuma S, Itoh S I, Jft-2M Group 1995 Phys. Rev. Lett. 74 1990 doi: 10.1103/PhysRevLett.74.1990 [9] Rice J, Ince-Cushman A, deGrassie J, Eriksson L G, Sakamoto Y, Scarabosio A, Bortolon A, Burrell K, Duval B, Fenzi-Bonizec C, Greenwald M, Groebner R, Hoang G, Koide Y, Marmar E, Pochelon A, Podpaly Y 2007 Nucl. Fusion 47 1618 doi: 10.1088/0029-5515/47/11/025 [10] Yoshida M, Kamada Y, Takenaga H, Sakamoto Y, Urano H, Oyama N, Matsunaga G 2008 Phys. Rev. Lett. 100 105002 doi: 10.1103/PhysRevLett.100.105002 [11] Solomon W M, Burrell K H, deGrassie J S, Budny R, Groebner R J, Kinsey J E, Kramer G J, Luce T C, Makowski M A, Mikkelsen D, Nazikian R, Petty C C, Politzer P A, Scott S D, Van Zeeland M A, Zarnstorff M C 2007 Plasma Phys. Control. Fusion 49 B313 doi: 10.1088/0741-3335/49/12B/S29 [12] Solomon W M, Burrell K H, Garofalo A M, Kaye S M, Bell R E, Cole A J, deGrassie J S, Diamond P H, Hahm T S, Jackson G L, Lanctot M J, Petty C C, Reimerdes H, Sabbagh S A, Strait E J, Tala T, Waltz R E 2010 Phys. Plasmas 17 056108 doi: 10.1063/1.3328521 [13] Chrystal C, Grierson B A, Solomon W M, Tala T, deGrassie J S, Petty C C, Salmi A, Burrell K H 2017 Phys. Plasmas 24 042501 doi: 10.1063/1.4978563 [14] Rice J, Cao N, Tala T, Chrystal C, Greenwald M, Hughes J, Marmar E, Reinke M, Rodriguez Fernandez P, Salmi A 2021 Nucl. Fusion 61 026013 doi: 10.1088/1741-4326/abcb26 [15] Zimmermann C, McDermott R, Angioni C, Duval B, Dux R, Fable E, Salmi A, Stroth U, Tala T, Tardini G, Pütterich T, the ASDEX Upgrade Team 2023 Nucl. Fusion 63 126006 doi: 10.1088/1741-4326/acf387 [16] Rice J, Duval B, Reinke M, Podpaly Y, Bortolon A, Churchill R, Cziegler I, Diamond P, Dominguez A, Ennever P, Fiore C, Granetz R, Greenwald M, Hubbard A, Hughes J, Irby J, Ma Y, Marmar E, McDermott R, Porkolab M, Tsujii N, Wolfe S 2011 Nucl. Fusion 51 083005 doi: 10.1088/0029-5515/51/8/083005 [17] Wang X, Lyu B, Lu X, Li Y, Solomon W M, Hao B, Chen J, Wang F, Fu J, Zhang H, Yang J, Bin B, He L, Li Y, Wan S, Gong X, Wan B, Ye M 2020 Plasma Sci. Technol. 22 065104 doi: 10.1088/2058-6272/ab84eb [18] Bae C, Jin Y, Lyu B, Hao B, Li Y, Zhang X, Liu H, Zhang H, Wang F, Fu J, Fu J, Huang J, Zeng L, Zang Q, Li Y, He L, Lu D 2024 Plasma Phys. Control. Fusion 66 045020 doi: 10.1088/1361-6587/ad2d66 [19] Yang S, Na Y S, Na D, Park J K, Shi Y, Ko W, Lee S, Hahm T 2018 Nucl. Fusion 58 066008 doi: 10.1088/1741-4326/aab90e [20] Zimmermann C F B, McDermott R M, Fable E, Angioni C, Duval B P, Dux R, Salmi A, Stroth U, Tala T, Tardini G, Pütterich T 2022 Plasma Phys. Control. Fusion 64 055020 doi: 10.1088/1361-6587/ac5ae8 [21] Ohtani Y, Yoshida M, Honda M, Narita E 2021 AIP Adv. 11 085306 doi: 10.1063/5.0056982 [22] Wan B, Gong X, Liang Y, Xiang N, Xu G, Sun Y, Wang L, Qian J, Liu H, Zhang B, Xia T, Huang J, Ding R, Zhang T, Zuo G, Sun Z, Zeng L, Zhang X, Zang Q, Lyu B, Garofalo A, Li G, Li K, Yang Q, For The East Team And Collaborators 2022 Nucl. Fusion 62 042010 doi: 10.1088/1741-4326/ac2993 [23] Liu H, Jie Y, Ding W, Brower D, Zou Z, Qian J, Li W, Yang Y, Zeng L, Zhang S, Lan T, Wang S, Hanada K, Wei X, Hu L, Wan B 2016 JINST 11 C01049 doi: 10.1088/1748-0221/11/01/C01049 [24] Zang Q, Zhao J, Yang L, Hu Q, Xi X, Dai X, Yang J, Han X, Li M, Hsieh C L 2011 Rev. Sci. Instrum. 82 063502 doi: 10.1063/1.3599039 [25] Zhao H, Zhou T, Liu Y, Ti A, Ling B, Austin M E, Houshmandyar S, Huang H, Rowan W L, Hu L 2018 Rev. Sci. Instrum. 89 10H111 doi: 10.1063/1.5035452 [26] Li Y Y, Fu J, Lyu B, Du X W, Li C Y, Zhang Y, Yin X H, Yu Y, Wang Q P, von Hellermann M, Shi Y J, Ye M Y, Wan B N 2014 Rev. Sci. Instrum. 85 11E428 doi: 10.1063/1.4890408 [27] Yin X H, Li Y Y, Fu J, Jiang D, Feng S Y, Gu Y Q, Cheng Y, Lyu B, Shi Y J, Ye M Y, Wan B N 2016 Rev. Sci. Instrum. 87 11E539 doi: 10.1063/1.4962054 [28] Yin X, Li Y, Fu J, Jiang D, Lyu B, Shi Y, Ye M, Wan B 2019 Fusion Eng. Des. 148 111282 doi: 10.1016/j.fusengdes.2019.111282 [29] Yoshida M, Koide Y, Takenaga H, Urano H, Oyama N, Kamiya K, Sakamoto Y, Kamada Y, Team T J 2006 Plasma Phys. Control. Fusion 48 1673 doi: 10.1088/0741-3335/48/11/008 [30] Tala T, Crombé K, De Vries P C, Ferreira J, Mantica P, Peeters A G, Andrew Y, Budny R, Corrigan G, Eriksson A, Garbet X, Giroud C, Hua M D, Nordman H, Naulin V, Nave M F F, Parail V, Rantamäki K, Scott B D, Strand P, Tardini G, Thyagaraja A, Weiland J, Zastrow K D, JET-EFDA Contributors 2007 Plasma Phys. Control. Fusion 49 B291 doi: 10.1088/0741-3335/49/12B/S27 [31] Ryter F, Dux R, Mantica P, Tala T 2010 Plasma Phys. Control. Fusion 52 124043 doi: 10.1088/0741-3335/52/12/124043 [32] 杨进, 陈俊, 王福地, 李颖颖, 吕波, 向东, 尹相辉, 张洪明, 符佳, 刘海庆, 臧庆, 储宇奇, 刘建文, 王勋禺, 宾斌, 何梁, 万顺宽, 龚学余, 叶民友 2020 物理学报 69 055201 doi: 10.7498/aps.69.20191716 Yang J, Chen J, Wang F D, Li Y Y, Lyu B, Xiang D, Yin X H, Zhang H M, Fu J, Liu H Q, Zang Q, Chu Y Q, Liu J W, Wang X Y, Bin B, He L, Wan S K, Gong X Y, Ye M Y 2020 Acta Phys. Sin. 69 055201 doi: 10.7498/aps.69.20191716 [33] Bae C, Stacey W, Solomon W 2013 Nucl. Fusion 53 043011 doi: 10.1088/0029-5515/53/4/043011 [34] Bae C, Jin Y, Lyu B, Fu J, Wang F, Zhang H 2024 Comput. Phys. Commun. 296 108992 doi: 10.1016/j.cpc.2023.108992 [35] Goldston R J 1981 J. Comput. Phys. 43 61 doi: 10.1016/0021-9991(81)90111-X [36] Pankin A, McCune D, Andre R, Bateman G, Kritz A 2004 Comput. Phys. Commun. 159 157 doi: 10.1016/j.cpc.2003.11.002 [37] Solomon W, Burrell K, deGrassie J, Boedo J, Garofalo A, Moyer R, Muller S, Petty C, Reimerdes H 2011 Nucl. Fusion 51 073010 doi: 10.1088/0029-5515/51/7/073010 [38] Rice J E, Ince-Cushman A C, Reinke M L, Podpaly Y, Greenwald M J, LaBombard B, Marmar E S 2008 Plasma Phys. Control. Fusion 50 124042 doi: 10.1088/0741-3335/50/12/124042 [39] Kosuga Y, Diamond P H, Gürcan ff D 2010 Phys. Plasmas 17 102313 doi: 10.1063/1.3496055 [40] Green B J, Team I I, Teams P 2003 Plasma Phys. Control. Fusion 45 687 doi: 10.1088/0741-3335/45/5/312 [41] III R W B, Stoltzfus-Dueck T 2024 Plasma Phys. Control. Fusion 66 065011 doi: 10.1088/1361-6587/ad3e2b [42] Parra F I, Barnes M 2015 Plasma Phys. Control. Fusionn 57 045002 doi: 10.1088/0741-3335/57/4/045002 -
图( 10)
计量
- 文章访问数: 41
- HTML全文浏览数: 41
- PDF下载数: 1
- 施引文献: 0