理解物质间的相互作用, 并实现操控它们, 一直是物理学研究的重要目标之一. 近一百年以来, 随着量子力学的发展, 人类获得了研究微观世界的强有力工具. 在相互作用较弱的情况下, 微扰论^[1]能够较为精确地描述原子间的相互作用效应, 但在强相互作用体系下, 微扰论则不再适用. 冷原子物理的发展为研究可调控的强相互作用提供了理想平台. 通过激光冷却技术^[2,3], 人们可以在抑制热能效应的同时, 通过磁场或电场对原子间相互作用的强度进行精确调控, 甚至达到共振相互作用^[4]. 在这些共振附近, 无论是Feshbach共振^[5]还是形状共振^[6], 原子间的相互作用会发生显著变化. 这些共振的发现为调控原子间的相互作用提供了新的途径.

近几十年中, 人们对Feshbach共振的研究逐渐深入. 除了最常见的原子-原子体系, 如⁶Li的s波共振^[7,8], ⁴⁰K的p波共振^[9]等, 在分子-原子体系^[10], 甚至半导体体系^[11]中都发现了Feshbach共振. 将Feshbach共振作为控制原子相互作用的重要手段, 人们进一步研究了多体量子系统的性质^[12-14]. 另一方面, 描述原子间Feshbach共振存在多种理论框架: 耦合通道方法^[15] (coupled-channel)、有效场论^[16] (effective field theory)和多通道量子缺陷理论^[17,18] (MQDT)等. 其中耦合通道方法由于具有高精确性, 其结果经常与Feshbach共振实验进行对比^[19].

耦合通道方法的关键是建立原子间相互作用势具体的形式; 该形式的确立通常需要利用光缔合谱等实验数据^[20]. 使用确立的原子间相互作用势在实空间求解各个通道耦合在一起的薛定谔方程需要更多的计算资源. 相比之下, MQDT优势在于仅靠引入若干可由实验确定的参数即可相当精确地描述Feshbach共振的特征. 该方法在寻找和预言Feshbach共振方面被广泛应用.

本文采用MQDT方法, 预言⁷Li在高于$ 1000\;{\mathrm{G}} $ (1 G = 10^–4 T)磁场下存在两个d波Feshbach共振; 它们分别位于1039.24和1055.64 G, 共振宽度分别为0.6和61.5 mG. 之前关于⁷Li的实验主要关注入射通道aa在736.8 G的s波共振(见表A1), 未将磁场扫到超过1000 G的范围. 另一方面本文预言的两个d波共振宽度分别为0.6和60 mG左右, 在理论预言的指导下, 需在特定磁场范围内进行仔细扫描才能发现. 同时计算了表征Feshbach共振的各项参数及在共振点附近闭通道中两体束缚态的性质. 并进一步估算了d波中磁偶极矩相互作用导致的共振劈裂.

应用MQDT预测⁷Li原子发生Feshbach共振的外磁场值, 并给出描述Feshbach共振的各项参数. 在一般外磁场下, 对于电子处于空间基态轨道的单个⁷Li原子, 其内态可处于不同的超精细态. 我们将两个原子的内态定义为通道, 它们的内态能量和相对动能的总和称为通道能量. 两个入射原子所处的内态被定义为入射通道. 内态能量高于入射通道能量的通道定义为闭通道, 更低或相等则为开通道. 由于在实验中, 往往选取入射通道为内态能量最低的通道, 因此只需考虑一个开通道, 即入射通道. 在碰撞的过程中, 原子间的相互作用可以使在各通道中的概率幅发生转换. 若闭通道中存在一个和入射通道能量相同的束缚态, 两原子会发生共振散射, 这就是Feshabch共振.

MQDT将原子间相互作用分为长程和短程两部分: 在原子间距$ r > r_0 $的长程部分, 相互作用的形式可以很好地近似为 van der Waals 势; 对于$ r < r_0 $短程部分的效应, 则引入量子缺陷矩阵K来参数化. 该矩阵K确定了波函数及在$ r_0 $处的边界条件. 与有效场论相比, MQDT的处理方式通过严格求解$ r > r_0 $处的薛定谔方程从而记入van der Waals势的效应, 进而使得该理论在很大能量范围尺度内都可靠^[21]. 在$ r > r_0 $处, 描述两个相对角动量l分波中⁷Li原子内态和相对距离r自由度的哈密顿量为

式中μ是约化质量, $ C_6 $是van der Waals势能的参数. 对于处在具有外磁场$ \boldsymbol B $下的具有超精细多重态的原子, 其内态哈密顿量$ \hat{H}_{hz, j} (j = 1, 2) $为

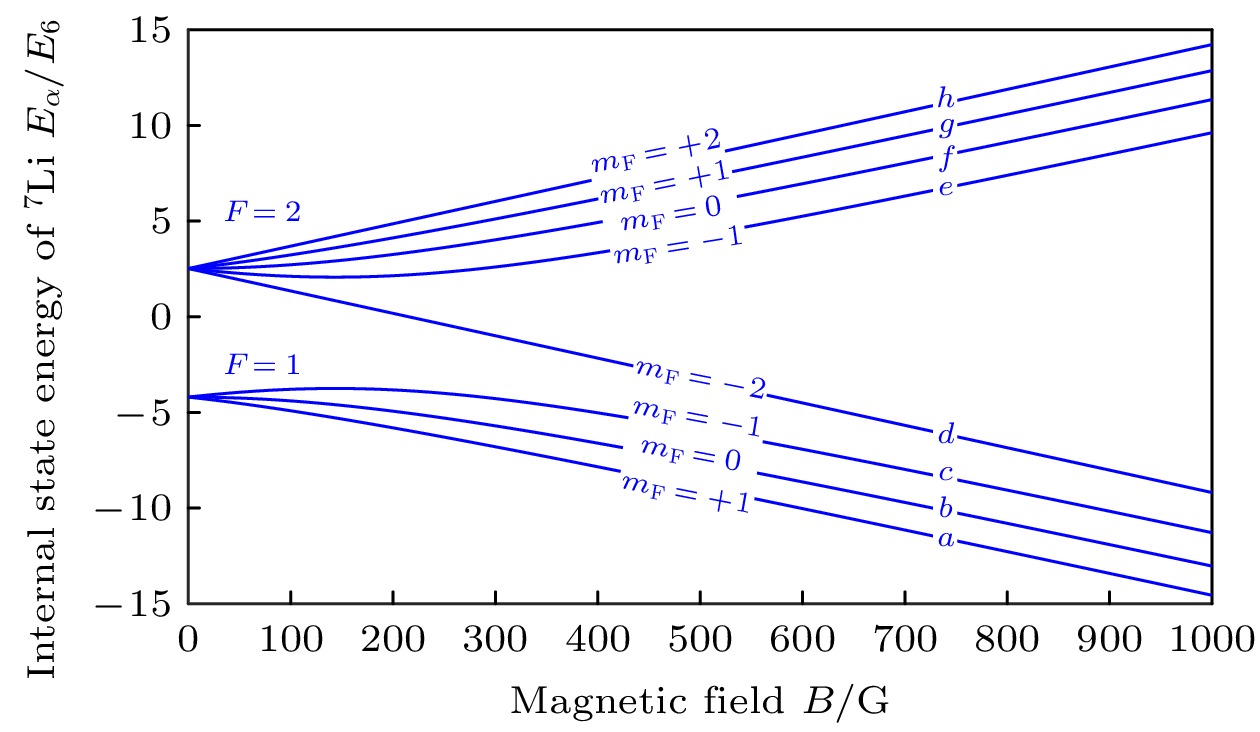
式中A, $ \gamma_{I} $和$ \gamma_{S} $分别是原子的超精细结构常数、核磁旋比和电子磁旋比, ${{ \boldsymbol {I}}_j} $和$ {{\boldsymbol {S}}_j} $分别是第j个原子的核自旋和电子自旋. 本征内态$ |\alpha\rangle $满足$ (\hat{H}_{hz, 1}+ \hat{H}_{hz, 2})|\alpha\rangle=E_\alpha |\alpha\rangle $, 其中$ E_\alpha $即为内态能量. 图1给出了⁷Li的本征内态(用字母$ a—h $表示)对应的内态能量随外磁场的变化.

如此, 在通道$ |\alpha\rangle $中的相对距离的空间波函数$ u_{l, \alpha}(r) $满足

其中$ \beta_6\equiv(2\mu C_6/\hbar^2)^{1/4} $ 并且$ \bar{\epsilon}_\alpha\equiv 2\mu \epsilon_\alpha/\hbar^2 $, $ \epsilon_\alpha $是通道能量. 这里将入射通道能量定义为能量零点. 由于实验中的入射动能及不同通道的内能差别通常远小于van der Waals能量, $ E_{\text{vdW}} \equiv {\hbar^2}/({2\mu R^2_{\text{vdW}}}) $, 其中$ R_{\text{vdW}} \equiv\dfrac{1}{2}\left( \dfrac{2\mu C_6}{\hbar^2}\right)^{{1}/{4}} $是van der Waals长度, 可以将$ \epsilon_\alpha/E_{\text{vdW}} $作为小量逐级展开^[22], 得到两组线性独立的解$ f_{l, \alpha}(r) $和$ g_{l, \alpha}(r) $. 详尽的数学解法参见文献[21].

这些线性独立解的相对系数则由近程相互作用决定. MQDT引入矩阵$ {\boldsymbol{K}}^{{c}} $, 即近程的K矩阵来参数化近程相互作用的效应^[21,23]. 由于在近程, 原子间相互作用被认为正比于$ \boldsymbol S_1\cdot\boldsymbol S_2 $, 且是典型电子能量的量级, 所以$ {\boldsymbol{K}}^{{c}} $在总自旋单态$ |S = 0\rangle $和三态$ |S = 1\rangle $的基矢下是对角的^[18], $ {\boldsymbol{K}}^{{c}} = K^{{c}}_{\mathrm{S}}|S = 0\rangle\langle S = 0 |+ K^{{c}}_{\mathrm{T}}|S = 1\rangle\langle S = 1 | $. 参数$ K^{{c}}_{\mathrm{S}} $和$ K^{{c}}_{\mathrm{T}} $可由实验中测得的零磁场下单态散射长度$ a_{\mathrm{s}} $和三态散射长度$ a_{\mathrm{t}} $确定. 当把闭通道都“积分”积去后, 可以得到开通道中的等效量子缺陷^[24]

这里α求和所有的闭通道c, $ \chi^c_l $由闭通道中的$ f_{l, \alpha}(r) $和$ g_{l, \alpha}(r) $组成^[25], 矩阵元$ K^c_{\alpha\beta}=\langle\alpha|K^c|\beta\rangle $.

对于l分波的散射相移$ \delta_l $做有效程展开,

其中$ {a}_l $和$ {r}_{{\mathrm{e}}, l} $是对应不同分波数的广义散射长度和有效距离. 在$ k\to 0 $的情况下, 只需要考虑首项与量子缺陷$ K^c_{\mathrm{eff}} $的联系^[26]

其中$ \bar{a}_l = \bar{a}_{{\mathrm{s}}, l}\beta_6^{2 l+1} $, 并且

当外磁场B趋向于$ K^c_{\mathrm{eff}}(B) $某个零点$ B_0 $时, 可以得到

其中$ a_{l, {\mathrm{bg}}} $为广义的背景散射长度, $ B_{0} $即是发生共振的磁场值, Δ表征共振的宽度.

进一步, 可以计算在闭通道中导致Feshbach共振的低能两体束缚态的能量$ E_{\mathrm{b}} $, 该能量满足^[27]

其中, $ K^c_{cc}=P_cK^cP_c $, 闭通道投影算符$ P_c= \displaystyle \sum\nolimits_{\alpha\in c} |\alpha\rangle\langle\alpha| $. 在共振磁场附近, 可以做线性展开

式中$ {\text{δ}}\mu $是闭通道束缚态与开通道中两个原子的磁矩差.

此外, Feshbach共振可区分为宽共振和窄共振^[28]. 通常而言, 共振宽度Δ并不能直接定义共振的宽窄, 而是由无量纲强度参数$ s_{\mathrm{res}} $决定. 考虑到磁矩差、背景散射长度对共振的影响, 它被定义为$ s_{\mathrm{res}} = \dfrac{a_{l, {\mathrm{bg}}}}{\bar{a}_{l}}\dfrac{\varDelta{\text{δ}}\mu}{\bar{E}} $, 其中$ \bar{E} = \dfrac{\hbar^2}{2\mu\bar{a}_{l}^2} $是与$ \bar{a}_{l} $相关的能量尺度. 若$ s_{\mathrm{res}} \gg 1 $, 称该共振属于入射通道主导的共振, 也就是宽共振(broad), 反之则为闭通道主导的共振, 也称窄共振(narrow). 通过$ s_{\mathrm{res}} $可以确定Feshbach共振的若干性质, 例如在共振磁场附近闭 通道的权重$ Z = \dfrac{1}{\zeta}\left\lvert\dfrac{B-B_0}{\varDelta}\right\lvert $, 其中$ \zeta \equiv \dfrac{1}{2}s_{\mathrm{res}}\left\lvert\dfrac{a_{l, {\mathrm{bg}}}}{\bar{a}_{l}}\right\lvert $. Z表征当磁场偏离共振点时, Feshbach分子态脱离入射通道主导的速率; 对于窄共振而言, Z在共振附近的变化率远大于宽共振, 即ζ值远小于1.

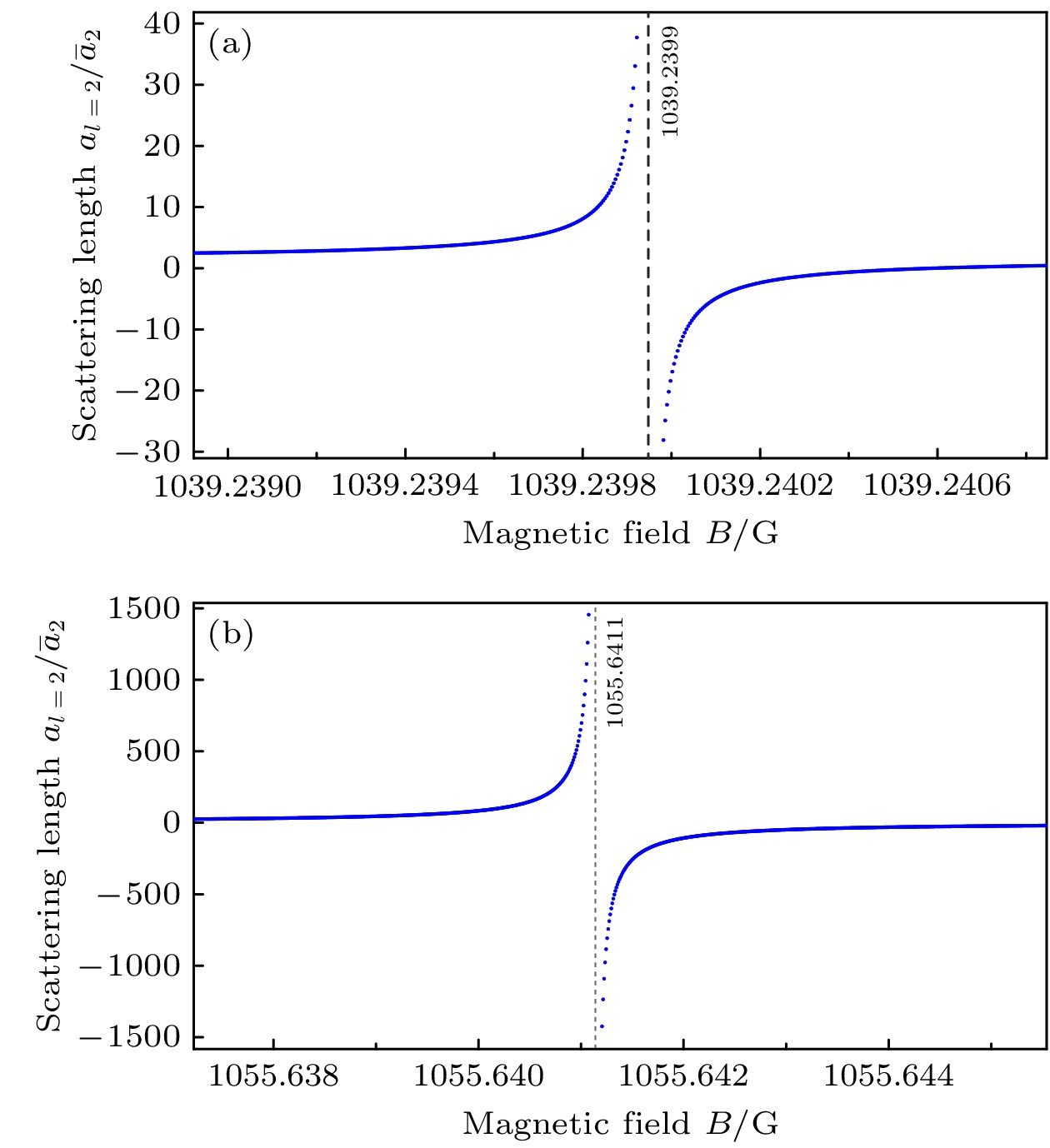
本文采用MQDT方法, 计算发现⁷Li在大于1000 G磁场下入射通道$ {\mathrm{aa}} $(即内态最低能级, 参看图1)中存在两个d波Feshbach共振: 其中一个共振位于1039.24 G, 另一个位于1055.64 G. 图2(a)和图2(b)给出了d波广义散射长度$ a_2(B) $在共振点附近随磁场的变化. 各物理量的计算结果如表1所列. 计算得到这两个Feshbach共振Δ分别为$ 6.397 \times 10^{-4} $和$ 6.15\times 10^{-2} \;{\rm G}$. 极小的$ s_{\mathrm{res}} $和ζ也表明了这两个共振都属于窄共振. 为确认MQDT数值计算的可靠性, 计算了先前已在实验中确认的Feshbach共振与之比对(详见附录A). 通过对比理论计算得到的Feshbach共振磁场$ B_0 $与实验观测到的共振磁场$ B_{\mathrm{ext}} $, 表明本文方法的精度在$ 0.2{\text{%}} $的水平. 并且我们对用于确定$ K^c $的参数$ a_{\mathrm{s}} $, $ a_{\mathrm{t}} $和$ C_6 $进行了优化(详见附录B).

从表面上看, 本文的计算结果似乎显示出共振宽度随磁场变大而变宽的趋势. 表A1中²³Na的两个s波共振也具有相同的趋势. 但在已知的其他Feshbach共振中存在违反该趋势的情况: ⁶Li和⁴⁰K原子间aa通道在$ 157.6 $和$ 168.2\;{\rm G} $的s波Feshbach共振宽度分别为$ 0.25 $和$ 0.15 \;{\rm G}$^[29]. 共振磁场与宽度之间没有单一的趋势, 正反映出Feshbach共振现象中多通道耦合而导致的复杂性.

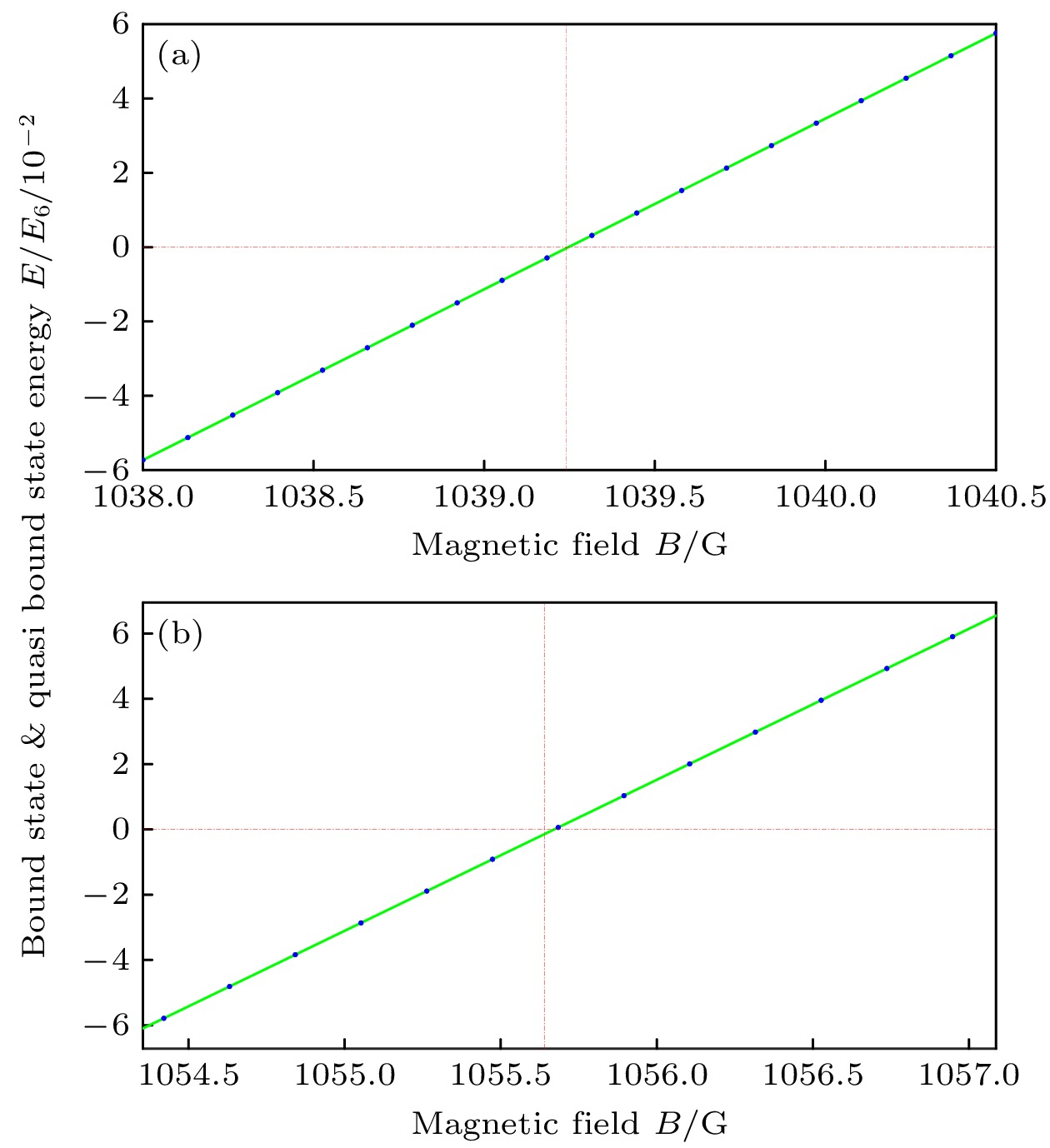
除了散射性质外, Feshbach共振的另一特征是共振点附近存在低能束缚态. 对于s波Feshbach共振, 束缚态的能量为$ E_{\mathrm{b}}(B) = -\dfrac{\hbar^2}{2\mu a_{l = 0}(B)^2} $^[29]. 对于高分波($ l\neq0 $), 通过将(5)式解析延拓到负能量可知, 低能束缚态能量$ E_{\mathrm{b}} $应与散射长度$ a_l $成反比. 因此, $ E_{\mathrm{b}} $在共振点附近($ B \to B_0 $)时, 与磁场呈线性关系. 图3(a)和图3(b)是利用(8)式计算得到的闭通道中导致共振的低能束缚态$ E_{\mathrm{b}} $在共振附近的行为, 其的确呈现出线性变化. 当考虑开通道时, $ E_{\mathrm{b}} > 0 $的区间对应的是“准”束缚态, 即具有有限的寿命. 这类“准”束缚态的性质已在之前p波Feshbach共振的实验中被测量^[30].

其次, 在之前高分波的共振实验中, 当分辨率足够高时, 发现共振会发生劈裂, 即在若干个相近的磁场发生共振^[6]. 这一劈裂的主要原因是磁偶极矩相互作用

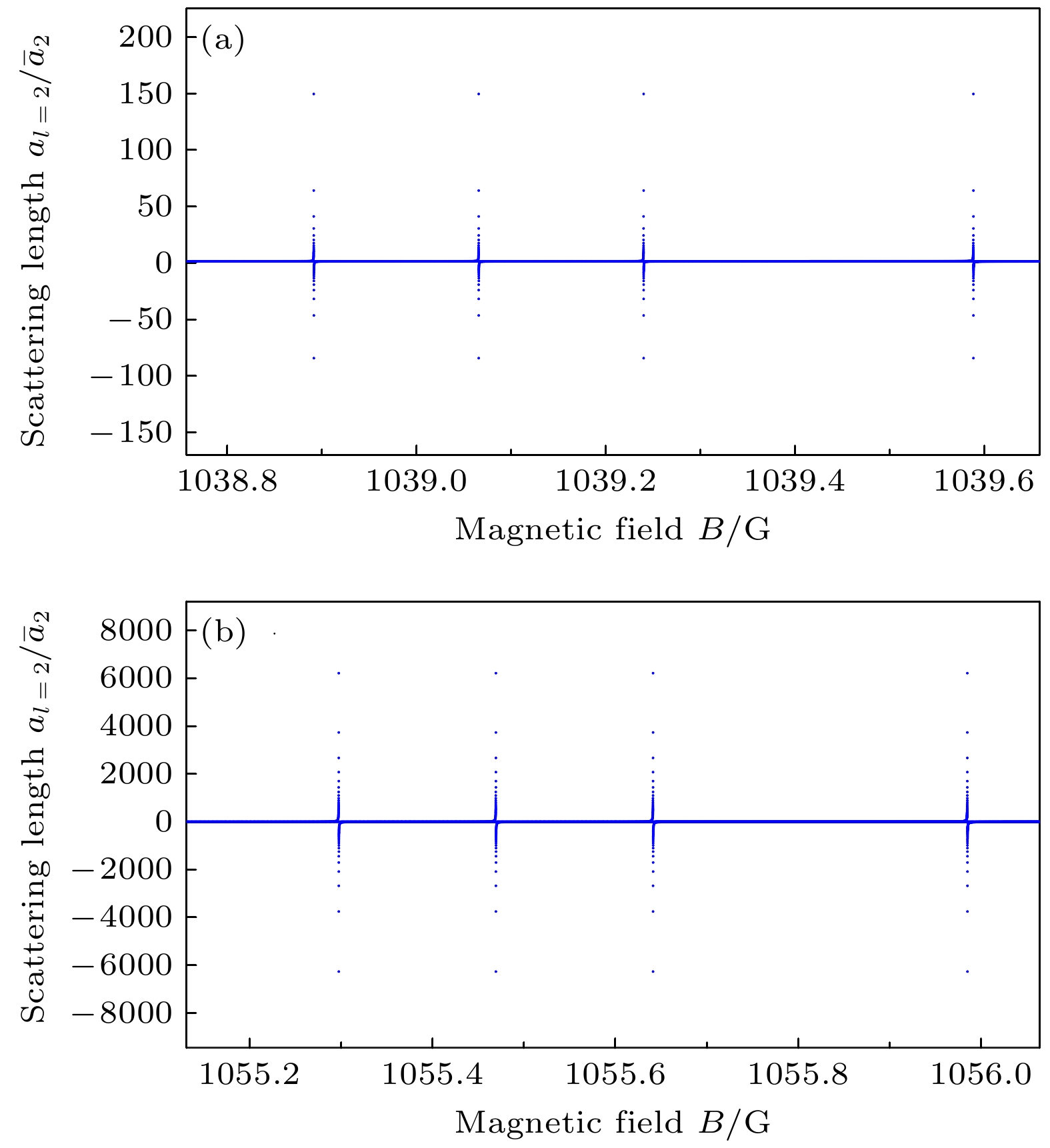
其中, $ a_{{\mathrm{d}}} $是磁偶极矩相互作用常数, θ是相对运动方向和偶极矩方向的夹角, r是两个原子间的距离. 由于磁偶极矩相互作用远弱于之前考虑的原子间相互作用, 本文采用了一阶定态微扰的方法来估算劈裂的大小.

我们发现, 对于⁷Li的d波Feshbach共振, 由于磁偶极矩相互作用, 共振点的位置发生了一定的变化, 如图4(a)和图4(b)所示. 对于1039.24 G的共振, $ m = 0 ,1,2$的$ B_0 $变化量分别为–0.349, –0.174和0.349 G; 对于1055.64 G的共振, $ m = 0 , 1,2 $的$ B_0 $变化量分别为–0.344, –0.172和0.344 G.

通过MQDT方法的计算, 发现⁷Li在磁场大于1000 G时存在两个d波Feshbach窄共振. 给出了表征这些共振性质的物理参数, 并计算得到了共振点附近闭通道中低能束缚态的行为. 此外, 估算了磁偶极矩相互作用导致的共振劈裂. 与宽共振相比, 窄共振由于通道间耦合相对较弱及耦合的通道数较少, 导致窄共振的半高宽较窄, 散射效应对于磁场依赖更为敏感, 在量子精密测量中具有应用前景. 作为计算方法, MQDT还可拓展研究其他原子(详见附录C)或其他系统的Feshbach共振研究, 如分子-原子^[10]、离子-原子^[31], 甚至空穴-激子^[32]等系统.

为了确认MQDT数值计算的可靠性, 计算了⁷Li和²³Na原子的s波Feshbach共振, 并与实验结果进行比对. 选择入射通道为$ {\mathrm{aa}} $和$ {\mathrm{ac}} $, 计算结果总结在表A1中. 考虑到实际实验条件, 只计算了磁场在0—1200 G之间的共振. 计算得到的共振磁场值与实验中观测到的值$ B_{\mathrm{ext}} $很好地符合.

我们发现对MQDT的参数值进行优化, 可以使计算结果更好与实验结果相符合, 从而提升其可靠性. 对计算结果有显著影响的主要有3个参数: 电子的单态和三态的s波散射长度$ a_{\mathrm{s}} $, $ a_{\mathrm{t}} $, 以及van der Waals常数$ C_6 $. 将现有精度下实验观测反推出的$ a_{\mathrm{s}} $, $ a_{\mathrm{t}} $, $ C_6 $数值作为初始值, 利用实验已观测到的Feshbach共振作为限制来优化$ a_{\mathrm{s}} $, $ a_{\mathrm{t}} $, $ C_6 $的取值, 从而确定共振矩阵$ K^c $的取值, 最后利用优化后$ K^c $的取值预测其他分波的新共振.

考虑到$ a_{\mathrm{s}} $, $ a_{\mathrm{t}} $以及$ C_6 $对共振点位置和宽度的映射是不寻常的多值函数, 同时缺乏解析的梯度表达式, 本文采用了Nelder-Mead单纯形法^[35], 它在解决这类问题时比数值梯度下降法更具优势. 应注意到的一点是, 电子的单态和三态的s波散射长度$ a_{\mathrm{s}} , a_{\mathrm{t}} $表征具有不同空间对称性的电子之间的相互作用强度, 而van der Waals常数$ C_6 $表示原子和原子间的相互作用强度, 对于不同的分波数l而言, 它们以上三个参数均相同. 因此, 在理论计算中, 利用已知的Feshbach共振位置对这些参数进行优化是充分且合理的. 本文的MQDT计算能给出之前实验中已观测到的“三个”s波Feshbach共振磁场位置在0.2%左右的误差, 不仅说明了MQDT方法的价值, 并佐证了实际计算的可靠性. 最终, 对于这两个新的d波Feshbach共振的预言归根结底需要通过实验来验证.

具体来说, 首先选择了⁷Li的s波共振点, 它的共振磁场为$ B_{0} = 736.8 \;{\mathrm{G}} $^[36]. 以这个共振点的位置作为目标进行优化, 选择被优化的输出函数形式为

其中B为每次迭代后的共振点位置, W为权重函数.

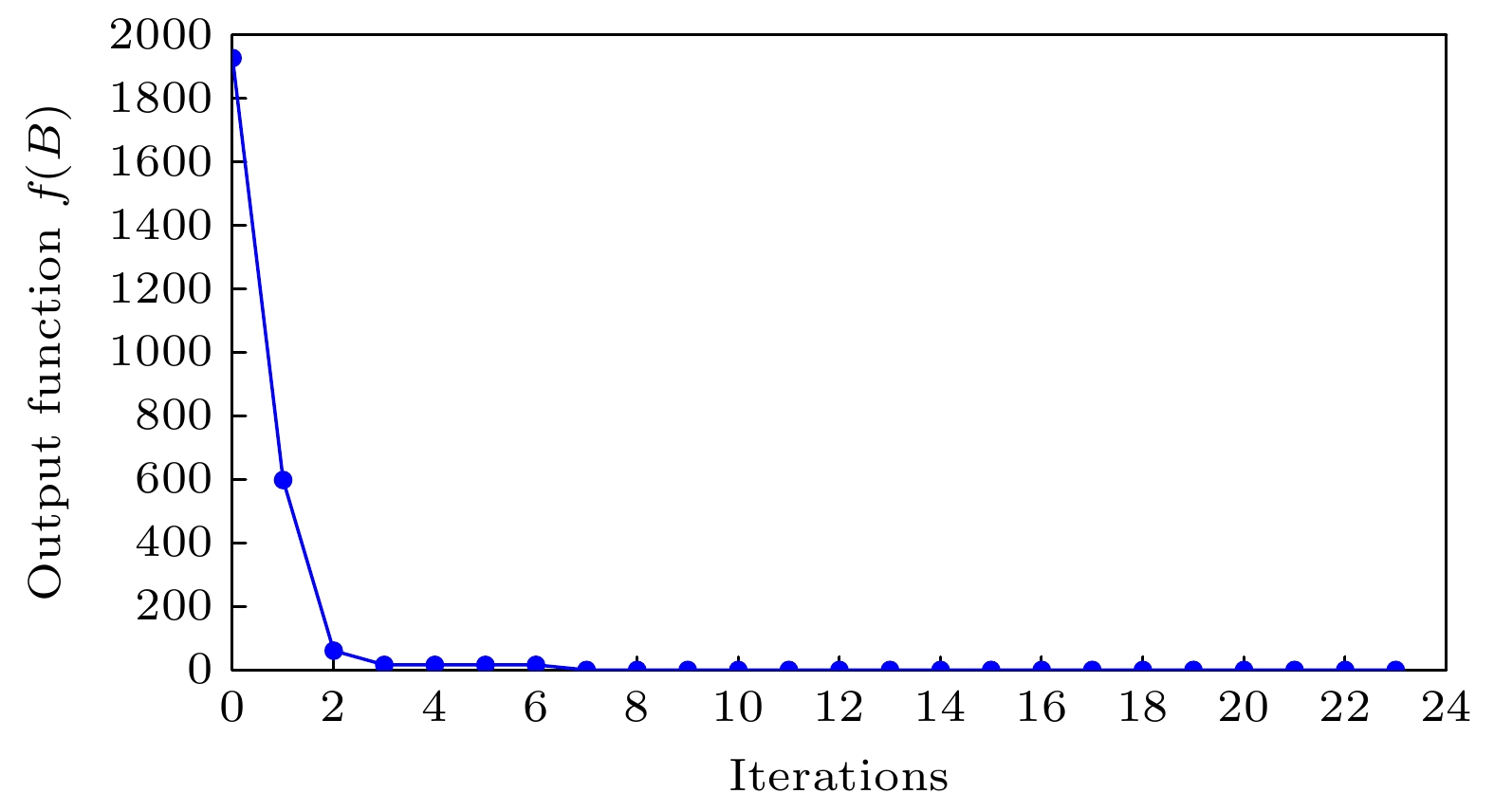
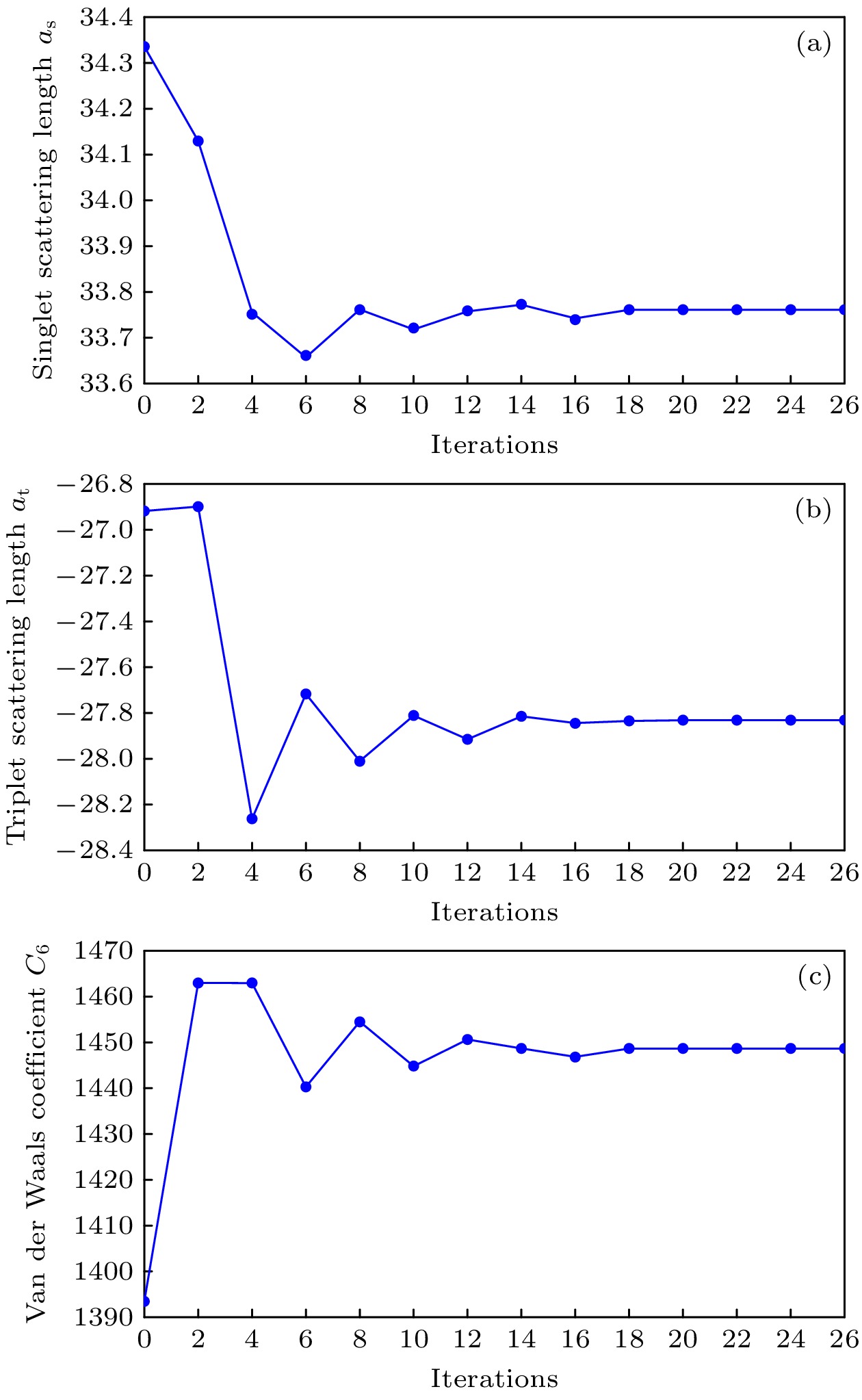
对于⁷Li的s波共振, 由于共振点仅有一个, 选择$ W = 1 $. 图B1给出了不同迭代次数时的系统状态, 系统在20次迭代后趋于稳定. 同时, 图B2给出了输出函数的变化, 它的值从初始化的$ 1918.14 $迭代到最后的$ 0.0232 $. 可以看出在使用Nelder-Mead 单纯形法的情况下, 输出函数在收敛非常快的同时, 收敛效果也非常好.

本文中的初始数据$ a_{\mathrm{s}} = 34.331 $, $ a_{\mathrm{t}} = -26.92 $, $ C_6 = 1393.39 $^[4], 迭代后的参数为$ a_{\mathrm{s}} = 33.737 $, $ a_{\mathrm{t}} = -27.896 $, $ C_6 = 1446.76 $. 计算得出优化前和优化后的共振点分别为$ B_{0} = 710.80\; {\mathrm{G}} $和$ B = 738.249\; {\mathrm{G}} $. 可见, 优化后的共振点位置明显优于优化前.

本工作的主旨是运用MQDT理论方法预言⁷Li入射通道aa中的d波Feshbach共振. 为突出该理论方法具有广泛适用性, 我们提及了在计算过程中发现的其他原子及通道中之前未曾报道过的Feshbach共振. 我们希望其中的预言能给实验学家寻找新的Feshbach共振提供帮助. 这些共振的各种性质被列在表C1中. 考虑了⁷Li和²³Na的三个低能量通道, 磁场从$ 0\; {\mathrm{G}} $到$ 1100\; {\mathrm{G}} $, 罗列出了入射通道、分波、共振点位置、共振宽度和背景散射长度.