首页
登录
注册
下载:
-
光学超表面(meta-surface)是一种人造二维材料, 通过对周期性微单元结构进行特殊的空间排布和参数设置[1–3], 可实现对反射或透射光场的全面调制. 由于其出色的光场调控能力, 超表面器件在光场的相位调制、极化调制、电磁波传播控制等方面具有重要的作用. 例如, 李绍和与李九生[4]制成了可多方向操纵太赫兹能量辐射的频率编码超表面; Malek等[5]将超表面应用于全息成像, 实现了更高的成像分辨率. 除此之外, 超表面还在提升太阳能效率[6]、多波段红外隐身[7]等领域蕴藏着巨大的发展潜力.
2016年, Khorasaninejad和Capasso[8]使用周期性分布的二维微单元阵列来控制各点的光场相位, 制作了可以与商用透镜类比的超表面透镜(meta-surface lens), 实现了对入射平面波的聚焦, 从而获得了一种亚波长厚度的微型化平面透镜. 在这之后, 超表面透镜引起了广泛的关注和深入的研究. 基于传输相位原理, Hu等[9]设计了一种具有增强效率的中波红外消色差双层超透镜; 徐平等[10]设计了长红外双波长共聚焦超透镜; 基于几何相位原理, Zhang等[11]设计了一种扩展焦深的毫米波超透镜. 这些超表面透镜很好地展示了超表面器件在微纳光学和集成光学中的应用潜力, 也实现了宽波段或消色差的功能. 不过, 上述超表面透镜都是通过相位调控来获得汇聚的球面波波前, 但并未对超表面透镜的聚焦性能和成像分辨率进行优化和提升.
为突破衍射极限, 进一步提升超表面透镜的聚焦性能, 本文将光瞳滤波超分辨成像技术融入超表面透镜设计, 可大幅压缩其横向焦斑尺寸, 实现超分辨聚焦的效果. 超分辨光瞳滤波器最早是由Di Francia[12]于1952年提出, 他所提出的光瞳滤波器是由多元同心环带所组成, 每个环带的延迟相位和透过率彼此不同, 理论上可以把衍射光斑的中心主瓣压缩到无限小, 从而提高光学系统的分辨率. 当前, 仍有许多课题组在对光瞳滤波超分辨成像技术领域展开研究. 按照调制的对象分类, 光瞳滤波器可以分为振幅型光瞳滤波器[13]、相位型光瞳滤波 器[14]和复振幅型光瞳滤波器[15]. 其中, 振幅型光瞳滤波器由于光线的部分吸收, 导致其光斑强度较低; 复振幅型光瞳滤波器可同时调控入瞳处的振幅和相位, 从而实现更好的超分辨效果, 但其仿真优化的难度较大, 且需要更为精确的加工精度; 相较而言, 相位型光瞳滤波器的能量利用率高、设计优化相对简单、加工难度低, 因此更适用于超分辨系统的初步设计, 特别是三区相位型光瞳滤波器.
本文将三区相位型光瞳滤波器融合于几何相位型单胞元超表面透镜的设计中, 同时实现二者的功能, 即在实现球面波波前的同时叠加相位型光瞳滤波器的功能, 由此实现横向超分辨聚焦. 首先, 利用时域有限差分法(finite-difference time-domain, FDTD)分析超表面微单元的结构参数对透射光场的相位调制作用, 选择合适的结构参数以确保微单元在180°的旋转角度内可以实现2π的相位改变; 其次, 根据工作波长和期望的焦距大小及通光口径, 对超表面透镜进行构建, 设计超表面透镜上各个位置所需的光学相位; 最后, 利用几何相位法, 计算不同位置处微单元的旋转角, 并在衬底上排列出微单元阵列, 完成超表面透镜的设计. 此外, 根据超表面透镜的口径, 设计并优化三区相位型光瞳滤波器, 再将其结构参数应用到融合型超表面透镜的设计, 构建出具有光瞳滤波功能的超表面透镜, 实现对入射光场的进一步调控. 比较发现, 融合型超表面透镜较原本的超表面透镜具有更小的焦斑尺寸, 提升了超表面透镜的聚焦性能和横向分辨率, 可广泛应用于各类微纳光学系统和光学仪器中.
-
作为比较目标, 首先利用几何相位设计一款单胞元超表面透镜, 用来比较融合光瞳滤波的超表面透镜聚焦性能的提升. 根据几何相位的原理 [14], 调整超表面上微单元的旋转角, 可实现光场的相位突变. 当圆偏振光射入到旋转角为θ的微单元时, 透射光场的琼斯矩阵可表示为
其中A, B分别为沿微单元结构长、短轴的反射或透射系数, 其构成的矩阵为微单元的偏振响应, 而入射圆偏光的旋向决定(1)式中正负号的取值. 当入射光波为左旋圆偏振时取正号, 反之为右旋圆偏振光时取负号. 从(1)式可看出, 当圆偏振光经过超表面后, 出射光由两部分构成, 其中一部分的出射光旋向与入射圆偏振光相同, 另一部分出射光旋向与入射圆偏振光相反. 当A = B时, 出射光中不含旋向相反的圆偏振光, 此时的琼斯矩阵对应于各向同性的光学元件; 当A = –B时, 则出射光只含旋向相反的圆偏振光, 并且相位延迟的绝对值正好等于两倍的光学元件朝向角. 因此, 调制微单元的结构参数, 使得A = –B, 因此当微单元结构旋转角为θ时, 旋向相反的圆偏振光会获得±2θ的附加相位.
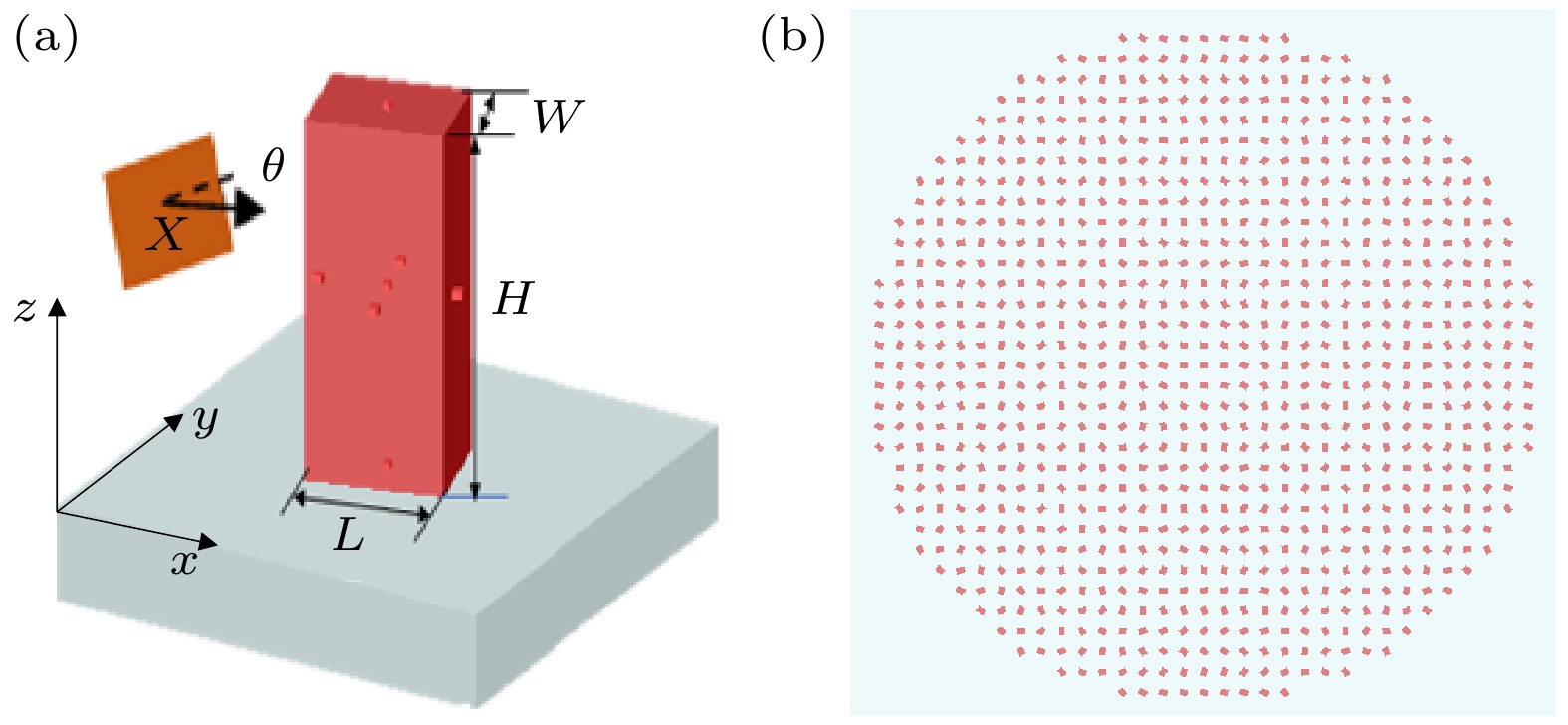
根据上述原理, 本文设计了以硅基纳米砖为微单元结构的超表面透镜, 其衬底材料为SiO2, 工作波长λ设置为633 nm, 透镜的口径D设置为10 μm, 透镜的焦距f设置为2 μm. 将微单元按二维阵列在衬底上周期排列, 并控制每一个微单元的旋转角度, 即可完成超表面透镜的设计, 其结构示意图和微单元的结构参数如图1所示.
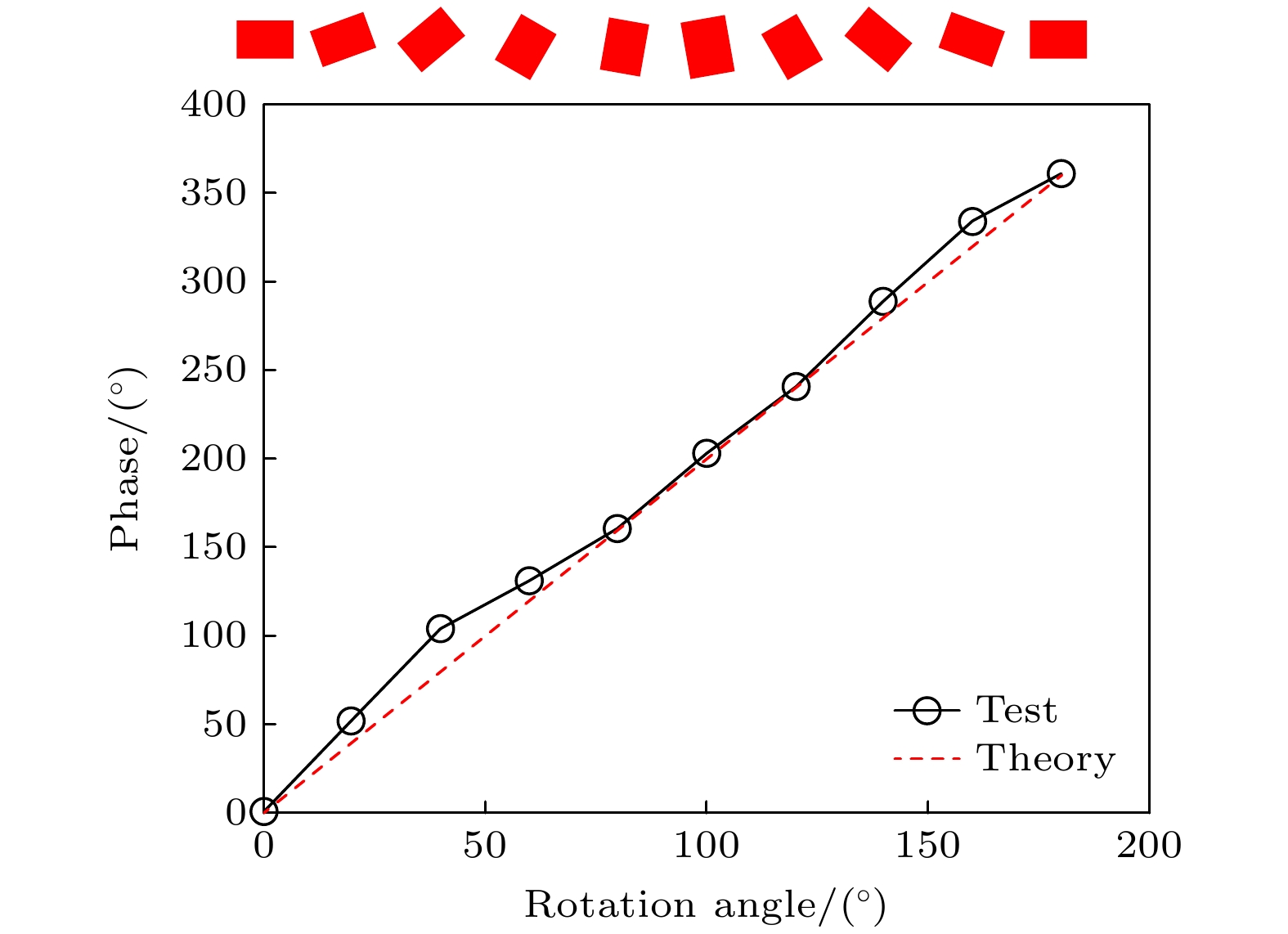
为实现微单元对入射光场的相位调控, 需设置微单元的结构参数, 以确保在其旋转角度范围内可实现2π的相位调制. 此外, 还需要避免超表面相邻微单元之间的耦合效应和超表面全息术的高阶衍射级, 并抑制透射光波中同向圆偏振光的比例. 综合考虑这两方面的影响, 利用FDTD算法对各种结构参数进行筛选和优化, 最终将微单元结构的周期设置为P = 300 nm, 微单元的高度设置为H = 400 nm, 长度设置为L = 120 nm, 宽度设置为W = 90 nm. 应用上述参数, 可实现2π的相位调制, 随着微单元旋转角度的改变, 透射光场的相位延迟随之变化, 如图2所示. 其中红色虚线为根据(1)式计算得到的理论曲线, 而黑色实线为使用FDTD算法采样仿真获得的计算结果, 二者吻合度较高, 可作为超表面透镜设计的参考.
根据超表面透镜的工作波长、通过口径及焦距大小, 为确保通过超表面透镜后形成汇聚的球面波波前, 可计算出超表面透镜不同位置所需的相位延迟, 而不同的相位延迟可通过调制该位置的微单元旋转角度来实现. 因此, 在超表面透镜表面坐标为(x, y)处微单元的旋转角θ 应设置为
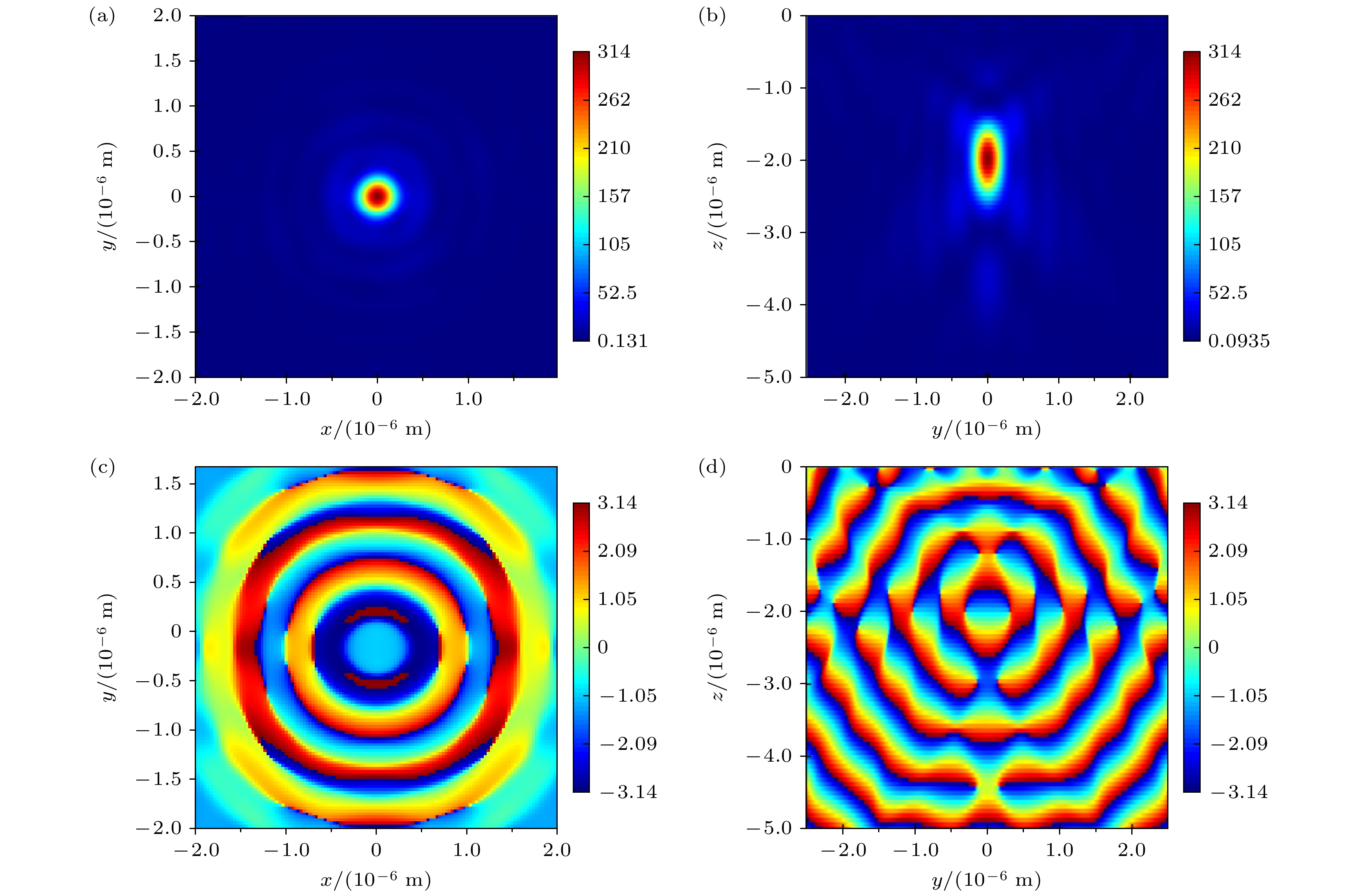
其中f为透镜焦距, λ为工作波长, 设置完成的超表面透镜如图1(b)所示. 为仿真其聚焦性能, 使用波长633 nm的右旋圆偏振光照射超表面透镜, 在焦平面上获得的光强分布如图3(a)所示, 相位分布如图3(c)所示; 而透镜后方y-z平面上的光强分布如图3(b)所示, 相位分布如图3(d)所示.
由y-z平面的光强分布可知, 会聚光斑的中心位置距离位于z = 0的超表面透镜约为2 μm, 与设计值基本一致. 在z = –2 μm平面, 即超表面透镜的焦平面, 可看出焦斑的大小尺寸和旁瓣的分布情况. 经过数据分析, 其焦斑的半高全宽(full width at half maximum, FWHM)约为376 nm, 且旁瓣的强度不超过中心强度的5%, 是较为理想的聚焦光斑.
-
根据Born和McCutchen的理论, 单色光照明条件下, 具有光瞳函数P(ρ)的成像系统[16–18], 其焦点附近的振幅分布可表示为
其中J0(ρ)为零阶贝塞尔函数, ρ为归一化半径, η对应接收面上的径向坐标r, u对应以焦点为原点的轴上坐标z, 且可以表示为
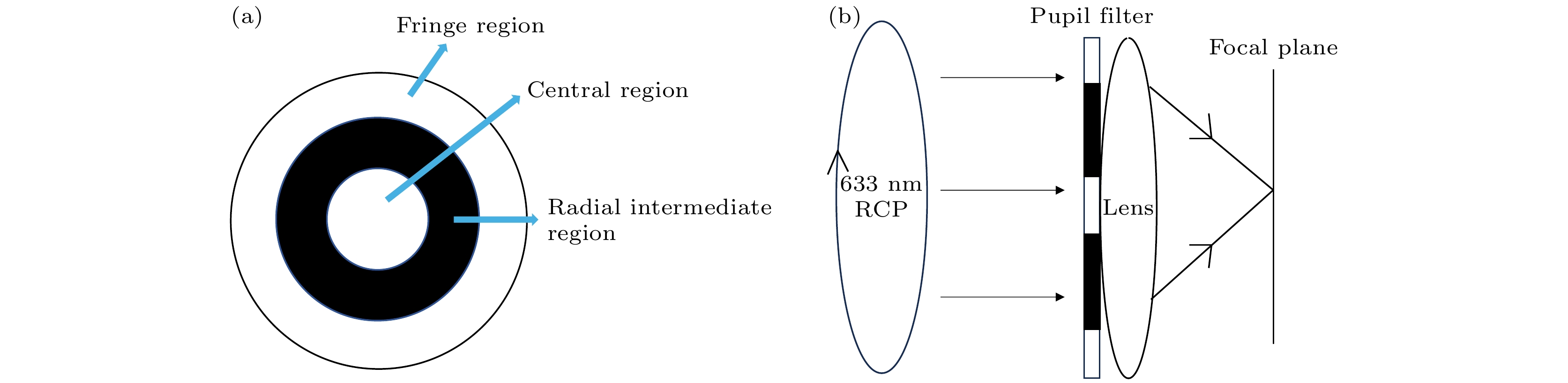
式中k为光的波矢, sinα代表系统的数值孔径. 通过对光瞳函数的设计和优化, 可在一定程度上减小焦斑尺寸, 起到超分辨聚焦和超分辨成像的效果. 一般来说, 评价超分辨光瞳滤波器的性能参数主要有: 横向超分辨因子(G(T))、轴向超分辨因子(G(A))和斯特列尔比(S), 分别表示在有无光瞳滤波器的情况下焦点附近横向强度分布函数的中心主瓣FWHM之比、轴向强度分布函数的中心主瓣FWHM之比, 以及有无滤波器时中心主瓣强度最大值之比[19]. 本文设计了一种三区相位型光瞳滤波器, 其结构如图4(a)所示, 其圆形孔径被分成3个同心圆或圆环, 分别为中心区、中间区和边缘区, 其对应的归一化半径分别为r1, r2和1. 图4(b)为光瞳滤波器的使用光路, 将其置于透镜的前方, 以调制入射光场的相位分布.
对于上述相位型光瞳滤波器, 可设定其中心区的透过率t1 = ei0、中间区透过率t2 = eiπ, 边缘区透过率t3 = ei0, 所对应区域的归一化半径大小分别为r1, r2和1, 因此其横向超分辨因子、轴向超分辨因子和斯特列尔比可表示为
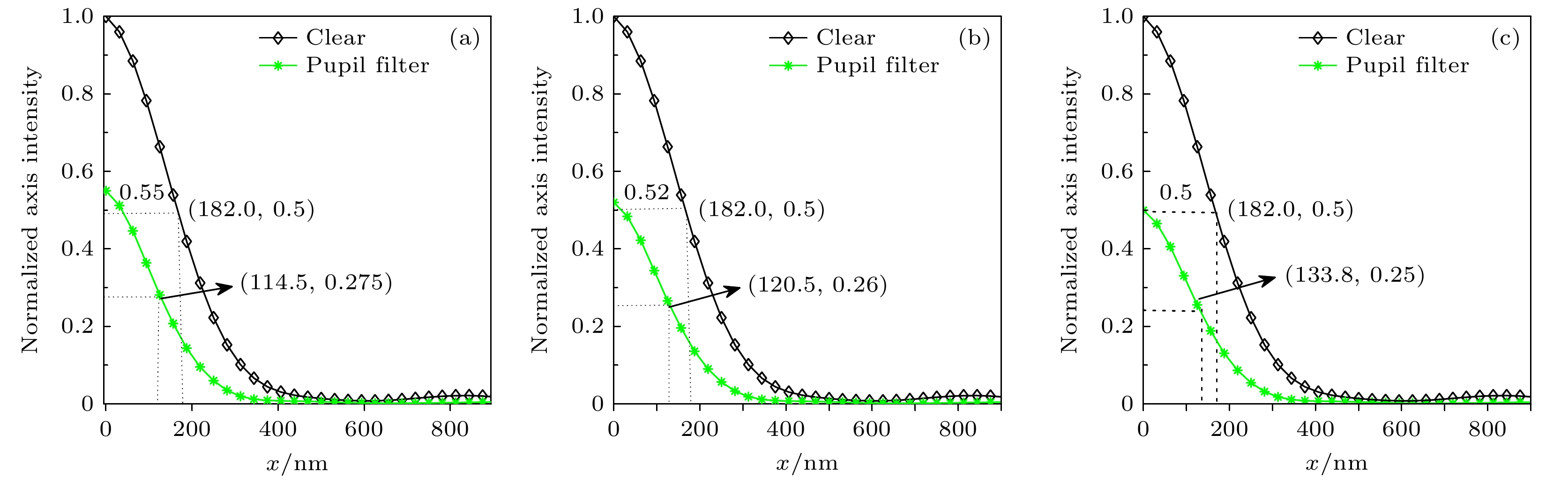
为提升透镜的横向分辨率, 并尽可能减少能量损失, 仿真优化过程中以横向超分辨因子和斯特列尔比作为优化目标, 即G(T)和S越大越好. 仿真中使用与超表面透镜相同的照明条件, 即入射光为633 nm右旋圆偏振光; 使用与超表面透镜参数相同的微透镜来仿真光瞳滤波器的效果, 即微透镜的口径为10 μm, 焦距为2 μm. 利用FDTD算法, 对不同半径参数的光瞳滤波器进行仿真分析, 获 得最佳参数为r1 = 0.33, r2 = 0.67, r3 = 1. 为此, 选择其附近的另外两组参数, 进行性能比较, 即3组参数分别为: 1) r1 = 0.33, r2 = 0.67, r3 = 1; 2) r1 = 0.2, r2 = 0.8, r3 = 1; 3) r1 = 0.1, r2 = 0.9, r3 = 1. 然后将加入光瞳滤波器后的归一化光强分布和未加入光瞳滤波器时透镜焦斑原本的归一化光强分布进行对比, 结果见图5.
从图5可以看出, 上述3组结构参数的光瞳滤波器对横向分辨率均有提高, 对应的横向超分辨因子分别为1.59, 1.51和1.36, 且斯特列尔比均保持在0.52左右. 由此可见, 调整光瞳滤波器中间区的宽度对斯特列尔比影响不大, 但对横向超分辨因子的影响较为明显, 因此在后续的融合型超表面透镜设计中, 将采用第1组结构参数.
-
受光瞳滤波器工作原理的启发, 对入射光场的相位进行调制后, 透镜的焦斑尺寸可大幅压缩, 因此在设计融合型超表面透镜时, 利用微单元的相位调制能力, 同时实现会聚的球面波波前和光瞳滤波器的相位调控. 具体来说, 将原本设计的超表面透镜根据光瞳滤波器的结构参数分成3个区域, 不同区域叠加不同的相位, 从而实现光瞳滤波器的功能, 而相位的叠加可通过微单元的方向旋转来实现.
根据前文光瞳滤波器半径参数的优选结果, 在透镜口径为10 μm的情况下, 中心区半径1.65 μm、径向中间区半径3.35 μm、边缘区的半径为5 μm为最优参数. 因此, 可将超表面透镜分成3个区域, 分别对应光瞳滤波器的中心区、中间区和边缘区, 结构如图6所示, 在不同区域叠加不同的相位, 其中边缘区和中心区保持相位不变, 而中间区增大π的相位延迟. 根据超表面微单元的相位调制特性, 即微单元的方位角旋转θ, 则入射的右旋圆偏振光相位改变2θ. 因此, 将中间区的每一个微单元都旋转90°, 可使该区域获得额外的相位延迟π.
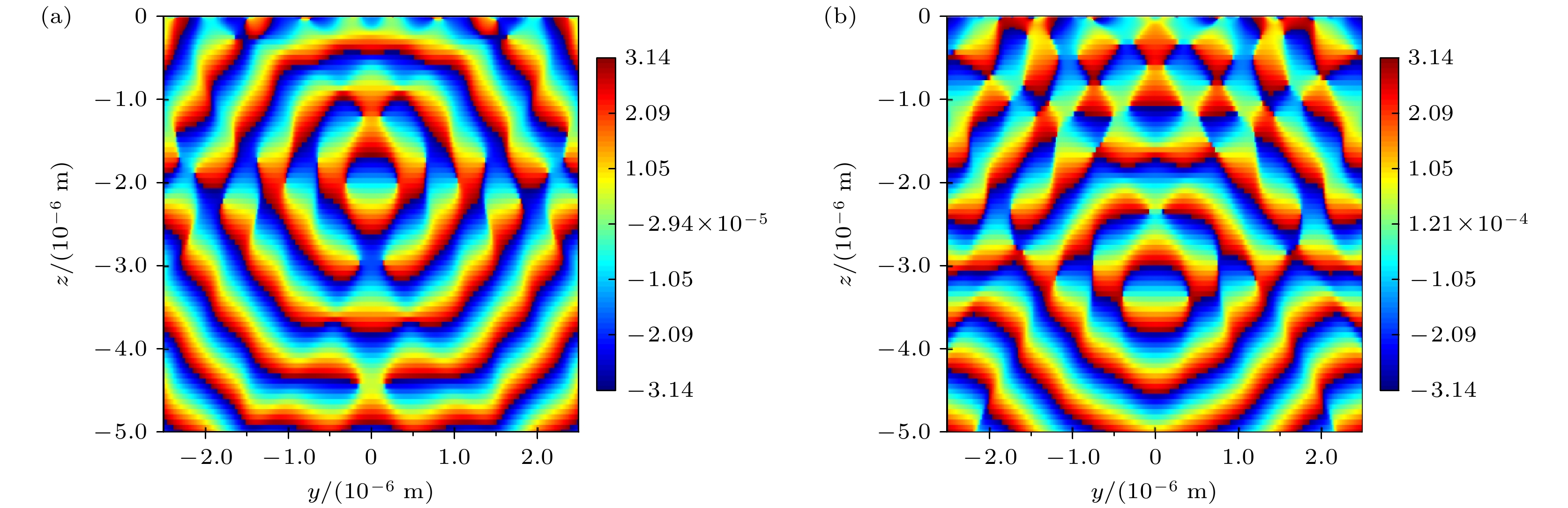
使用FDTD算法, 仿真分析融合型超表面透镜对入射光场的调控和会聚功能. 当波长为633 nm的右旋圆偏振光入射超表面透镜后, 其后方y-z平面的相位分布较原先的超表面透镜有所改变, 如图7所示. 在原先的超表面透镜后方, 产生的是汇聚的球面波, 其等相位面分布较为规整, 其焦点位置清晰可见, 如图7(a)所示; 在融合光瞳滤波的超表面透镜后方, 其相位分布如图7(b)所示, 其等相位面不再是连续的曲面, 而是被分割成若干个区域, 相邻区域间相位差为π, 并且其焦斑位置向下移动了约1.3 μm.
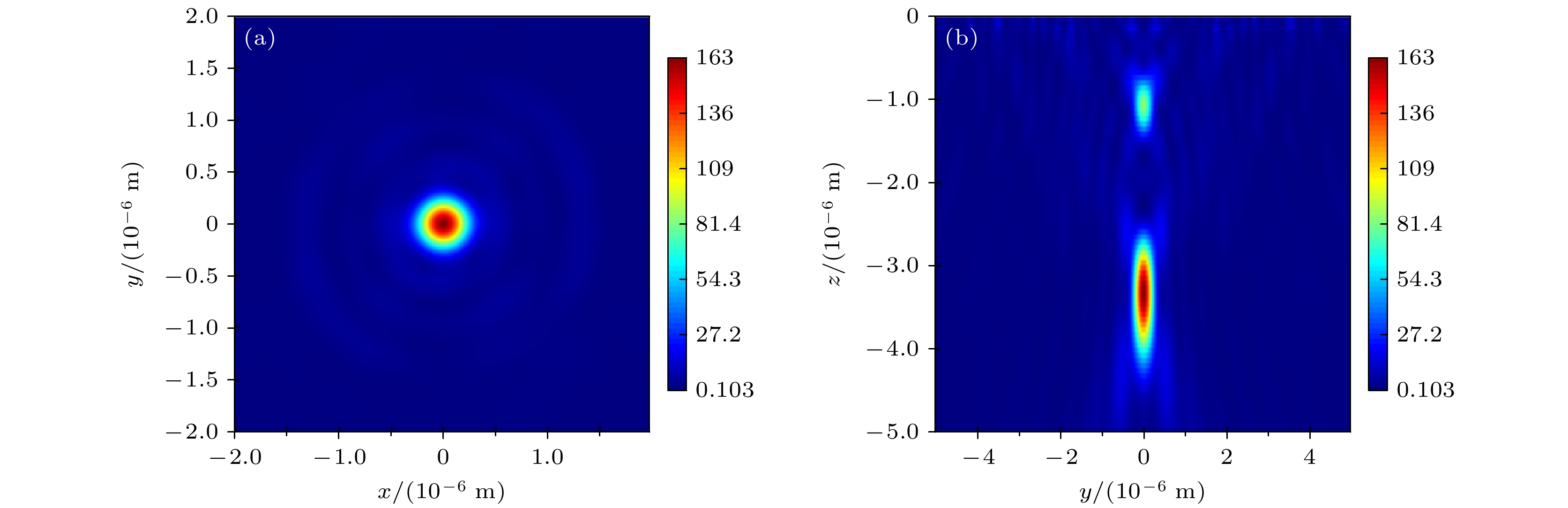
为精确描述融合型超表面透镜的聚焦性能, 可仿真分析焦平面上的光强分布和超表面透镜后方y-z平面内的光强分布, 分别如图8(a), (b)所示, 并与原先超表面透镜的焦斑特性进行比较. 从图8(a)可以发现, 融合型超表面透镜的焦斑尺寸明显小于原先的超表面透镜, 且其旁瓣的强度没有大幅提升, 因此仍然适用于宽场成像. 相较于原先的超表面透镜, 融合型超表面透镜的焦斑强度有所下降, 因此成像时需要更高的照明光强; 图8(b)为融合型超表面透镜后方y-z平面内的光强分布, 其焦斑位置较原先的超表面透镜发生了一定的位移, 且焦斑上方出现了一个亮度更弱的次焦点, 二者中心间距超过2 μm, 因此对微纳加工或超分辨成像的影响非常有限.
图8虽然直观地展示了融合型超表面透镜的焦斑特性和光强分布, 但无法定性分析其焦斑尺寸的改变量, 为此绘出焦平面中心的光强分布曲线, 并与原本的超表面透镜进行比较, 可定性地展示融合型超表面透镜的性能提升效果.
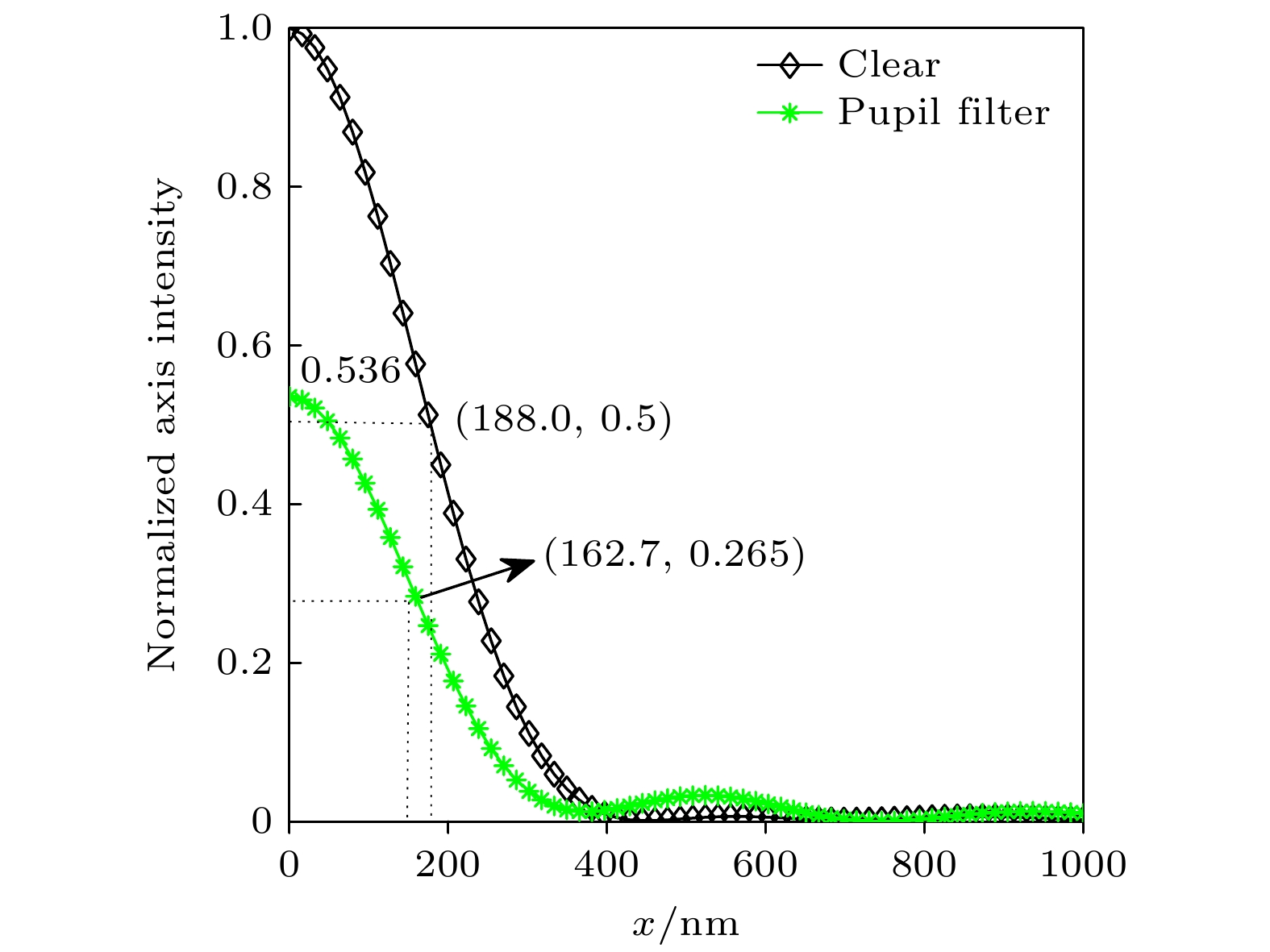
图9为两种超表面透镜焦平面中心处的光强分布归一化曲线, 其中黑色曲线代表原先的超表面透镜, 绿色代表融合了光瞳滤波的超表面透镜. 通过比较图中两条曲线可知, 原先超表面透镜的FWHM约为376 nm, 而融合光瞳滤波的超表面透镜FWHM约为323.4 nm. 由此可见, 融合型超表面焦斑主瓣的横向宽度得到一定的压缩, 横向超分辨因子计算结果约为1.29, 横向分辨率得到了约15%的提升, 但其中心亮度有所下降, 其斯特列尔比约为0.51. 随着焦斑尺寸的不断压缩, 其旁瓣强度将不断升高, 且中心亮度也会不断下降, 因此需要合理平衡各项参数, 在不影响成像质量的前提下尽可能地压缩焦斑尺寸, 从而实现更高的成像分辨率.
-
本文首先设计了一种以纳米硅阵列和SiO2衬底构成的单胞元超表面透镜, 针对633 nm的入射光实现了理想的聚焦光斑. 然后针对相同口径的光瞳滤波器进行仿真设计, 提出了一种三区相位型光瞳滤波器, 从内到外相位突变分别为0-π-0, 从而实现了对焦斑主瓣尺寸的压缩, 并对不同半径参数的光瞳滤波器进行仿真优选. 最后, 将上述超表面透镜与三区相位型光瞳滤波器融合得到一种新型融合型超表面透镜, 将其焦斑的FWHM压缩至323.4 nm (≈ 0.51λ), 不仅较普通超表面透镜的376.0 nm有巨大提升, 也超越衍射极限的0.61λ/NA (当NA = 0.9时, 约合429.0 nm), 该结果初步展示了融合型超表面透镜的超分辨效果. 随着对振幅、偏振、涡旋等多维信息的全面调控, 融合型超表面光学透镜将实现更加优异的超分辨聚焦和成像性能, 也将以其高分辨率、高集成度和微型化的特性, 广泛应用于超分辨成像、虚拟现实、三维光学显示 [20,21]等相关领域.
融合光瞳滤波的超表面透镜设计
Design of meta-surface lens integrated with pupil filter
-
摘要: 超表面透镜是一种通过调制表面微单元结构参数来实现对光波相位、振幅和偏振的精确调控的微型平面透镜. 相较于普通透镜, 具有尺寸小、重量轻、集成度高等优点, 是光子芯片的核心器件. 为突破衍射极限, 进一步提升超表面透镜的聚焦性能和成像分辨率, 需结合现有的光场调控技术, 对入射光场进行多维信息调控. 参考光瞳滤波器的超分辨成像原理, 设计了一种融合型超表面透镜, 可同时实现透镜聚焦和光瞳滤波器的功能, 从而获得超越衍射极限的聚焦光斑. 通过参数优化, 最终实现了半高全宽为323.4 nm (~0.51λ)的焦斑, 较未加光瞳滤波器的超表面透镜(半高全宽为376 nm)性能提升了近15%. 本文设计的融合型超表面透镜展示了全面光场调控对其光学性能的提升, 在未来有望代替传统透镜, 并在纳米显微成像、纳米光刻、虚拟现实以及3D显示等领域发挥重要作用.Abstract:
Metasurface lenses are miniature flat lenses that can precisely control the phase, amplitude, and polarization of incident light by modulating the parameters of each unit on the substrate. Compared with conventional optical lenses, they have the advantages of small size, light weight, and high integration, and are the core components of photonic chips. Currently, the hot topics for metasurface lens are broadband and achromatic devices, and there is still less attention paid to the resolution improvement. To break through the diffraction limit and further improve the focusing performance and imaging resolution of metasurface lenses, we use unit cells to perform multi-dimensional modulation of the incident light field. Specifically, in this paper, we combine phase modulation of metasurface lens with a pupil filtering, which has been widely applied to traditional microscopy imaging and adaptive optics and has demonstrated powerful resolution enhancement effects. The integrating of these two technologies will continue to improve the imaging performance of metasurface lenses and thus expanding their application fields. In this work, we firstly design a single-cell super-surface lens composed of a silicon nanofin array and a silica substrate as a benchmark for comparing the performance of integrated super-surface lens. The lens achieves an ideal focal spot for incident light at 633 nm, resulting in a full width at half maximum (FWHM) of 376.0 nm. Then, a three-zone phase modulating pupil filter is proposed and designed with the same aperture of metasurface lens, which has a phase jump of 0-π-0 from the inside to the outside of the aperture. From the simulation results, the main lobe size of the focal spot is compressed obviously. In the optimization, its structural parameters are scanned for the best performance, and an optimal set of structural parameters is selected and used in the integrated metasurface lens. Finally, the integrated metasurface lens is designed by combining the metasurface lens with a three-zone phase modulating pupil filter, and the FWHM of its focal spot is compressed to 323.4 nm (≈ 0.51λ), which is not only 15% smaller than original metasurface lens’s FWHM of 376.0 nm, but also much smaller than the diffraction limit of 0.61λ/NA (when NA = 0.9, it is approximately 429.0 nm). This result preliminarily demonstrates the super-resolution performance of the integrated super-surface lens. With the comprehensive regulation of multi-dimensional information, such as amplitude, polarization, and vortex, the integrated super-surface optical lens will achieve more excellent super-resolution focusing and imaging performance, and will also be widely used in the fields of super-resolution imaging, virtual reality, and three-dimensional optical display, due to its characteristics of high resolution, high integration, and high miniaturization. -
Key words:
- meta-lens /
- pupil filter /
- super-resolution imaging .
-
-
图 1 超表面透镜的微单元结构参数(a)和微单元的周期性排布(b)
Figure 1. Metasurface lens’ microcell structure parameters (a) and the periodic arrangement of microcells (b).
图 3 (a) x-y平面内焦斑的光强分布; (b) y-z平面成像内焦斑的光强分布; (c) x-y平面内的相位分布; (d) y-z平面内的相位分布
Figure 3. (a) Light intensity distributions in x-y plane for the focal spot; (b) light intensity distributions in y-z plane for the focal spot; (c) phase distributions in x-y plane for the focal spot; (d) phase distributions in y-z plane for the focal spot.
图 4 三区相位型光瞳滤波器的结构示意图(a)和使用光路(b)
Figure 4. Structural diagram (a) and optical path (b) of the three-zone phase pupil filter.
图 5 归一化光强分布对比 (a) r1 = 0.33, r2 = 0.67, r3 = 1; (b) r1 = 0.2, r2 = 0.8, r3 = 1; (c) r1 = 0.1, r2 = 0.9, r3 = 1
Figure 5. Comparison of normalized light intensity distribution: (a) r1 = 0.33, r2 = 0.67, r3 = 1; (b) r1 = 0.2, r2 = 0.8, r3 = 1; (c) r1 = 0.1, r2 = 0.9, r3 = 1.
图 7 (a)单胞元超表面透镜y-z平面相位分布; (b)融合型超表面透镜y-z平面相位分布
Figure 7. (a) Single cell metasurface lens y-z plane phase distribution; (b) integrated type metasurface lens y-z plane phase distribution
图 8 融合型超表面透镜焦斑处的光强分布 (a) 透镜焦平面上; (b) y-z平面
Figure 8. Light intensity distribution at the focal spot of integrated metasurface lens: (a) Focal plane image; (b) y-z plane.
-
[1] Feng M D, Wang J F, Ma H, Mo W D, Ye H J, Qu S B 2013 J. Appl. Phys. 114 074508 doi: 10.1063/1.4819017 [2] Lin D M, Fan P Y, Hasman E, Brongersma M L 2014 Science 345 298 doi: 10.1126/science.1253213 [3] West P R, Stewart J L, Kildishev A V, et al. 2014 Opt. Express 22 26212 doi: 10.1364/OE.22.026212 [4] Li S H, Li J S 2019 Aip Adv. 9 035146 doi: 10.1063/1.5089617 [5] Marlek S C, Ee H S, Agarwal R 2017 Nano Lett. 17 3641 doi: 10.1021/acs.nanolett.7b00807 [6] Cai B, Wu L, Zhu X W, Cheng Z Z, Cheng Y Z 2024 Res. Phys. 58 107509 [7] Li Y L, Xu J F, Liu, F H, Xu L Z, Fang B, Li, C X 2024 Phys. Scripta 99 075536 doi: 10.1088/1402-4896/ad5803 [8] Khorasaninejad M, Capasso F 2017 Science 358 6367 doi: DOI:10.1126/science.aam8100 [9] Hu T, Xia R, Wang S C, Yang Z Y, Zhao M 2024 J. Phys. D: Appl. Phys. 57 355103 doi: 10.1088/1361-6463/ad5023 [10] 徐平, 李雄超, 肖钰斐, 杨拓, 张旭琳, 黄海漩, 王梦禹, 袁霞, 徐海东 2023 物理学报 72 014208 doi: 10.7498/aps.72.20221752 Xu P, Li X C, Xiao Y F, Yang T, Zhang X L, Huang H X, Wang M Y, Yuan X, Xu H D 2023 Acta Phys. Sin. 72 014208 doi: 10.7498/aps.72.20221752 [11] Zhang Q S, Guo D, Shen C S, Chen Z F, Bai N F 2024 Phys. Scripta 99 015516 doi: 10.1088/1402-4896/ad1471 [12] di Francia G T 1952 Il Nuovo Cimento 9 426 doi: 10.1007/BF02903413 [13] Luo Z Y, Kuebler S M 2014 Opt. Commun. 315 176 doi: 10.1016/j.optcom.2013.11.009 [14] Chakraborty S, Bera S C, Chakraborty A K 2011 Optik 122 549 [15] 王吉明, 赫崇军, 刘友文, 杨凤, 田威, 吴彤 2016 物理学报 65 044202 doi: 10.7498/aps.65.044202 Wang J M, He C J, Liu Y W, Yang F, Tian Wei, Wu T 2016 Acta Phys. Sin. 65 044202 doi: 10.7498/aps.65.044202 [16] Liu S, Qi S X, Li Y K, Wei B Y, Li P, Zhao J L 2022 Light Sci. Appl. 11 219 [17] 丁洪萍, 李庆辉, 邹文艺 2004 光学学报 24 1177 doi: 10.3321/j.issn:0253-2239.2004.09.006 Ding H P, Li Q H, Zou W Y 2004 Acta Opt. Sin. 24 1177 doi: 10.3321/j.issn:0253-2239.2004.09.006 [18] Toshiyuki H, Katsuhiro H, Seitaro M 2019 Denki Kagaku oyobi Kogyo Butsuri Kagaku 63 536 [19] 赵丽娜 2018 博士学位论文 (成都: 电子科技大学) Zhao L N 2018 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China [20] 刘涛 2013 博士学位论文 (哈尔滨: 哈尔滨工业大学) Liu T 2013 Ph. D. Dissertation (Harbin: Harbin Institute of Technology [21] 陈俊林, 莫德锋, 蒋梦蝶, 朱海勇 2024 中国激光 51 1310001 doi: 10.3788/CJL231119 Chen J L, Mo D F, Jiang M D, Zhu H Y 2024 Chin. J. Lasers 51 1310001 doi: 10.3788/CJL231119 -
计量
- 文章访问数: 152
- HTML全文浏览数: 152
- PDF下载数: 2
- 施引文献: 0