-
被动锁模光纤激光器作为超快光学领域中的重要工具[1], 广泛应用于光通信[2]、精密测量[3]和生物成像等领域[4]. 与主动锁模相比, 被动锁模光纤激光器通过非线性效应或损耗机制来实现脉冲锁定, 具有结构简单、成本低、稳定性高的优势, 因此在产生超短脉冲方面备受关注[5,6]. 近年来, 随着光纤材料和非线性光学技术的进步, 掺铒、掺镱等稀土掺杂光纤进一步推动了被动锁模光纤激光器在更短脉冲和更高输出功率上的应用[7].
在被动锁模光纤激光器的研究中, 孤子和呼吸子是两种常见的非线性脉冲解[8]. 孤子是由于非线性和色散平衡而形成的稳定脉冲, 而呼吸子是一种周期性振荡的孤子解, 其脉冲宽度和光谱会随着时间和频率呈现周期性变化[9]. 近年来, 已有大量研究通过实验和数值模拟揭示了呼吸子形成的关键非线性效应, 并探讨了其在不同系统参数下的动态行为. 例如, Liu[10]通过实验观测和模拟研究了呼吸子在不同腔体和材料条件下的形成机制和演化规律. 然而, 呼吸子的复杂动力学特性[11,12], 例如其周期性振荡行为和在参数变化下的演变模式, 仍不完全清楚[13,14].
基于此, 本文通过搭建一个基于非保偏可饱和吸收体的锁模掺铒光纤激光器[15]实验装置, 并结合时间拉伸色散傅里叶变换(TS-DFT)技术[16–18], 系统地研究了呼吸子在时域和频域中的动力学行为及其周期性演化特征, 同时对不同系统参数条件下的呼吸子演化进行了深入的分析. 实验结果揭示了影响呼吸子形成与稳定的关键因素, 并表明调整系统参数能够有效地控制它们的演化模式, 为超快激光技术和非线性光纤系统中的呼吸子控制提供了重要参考.
-
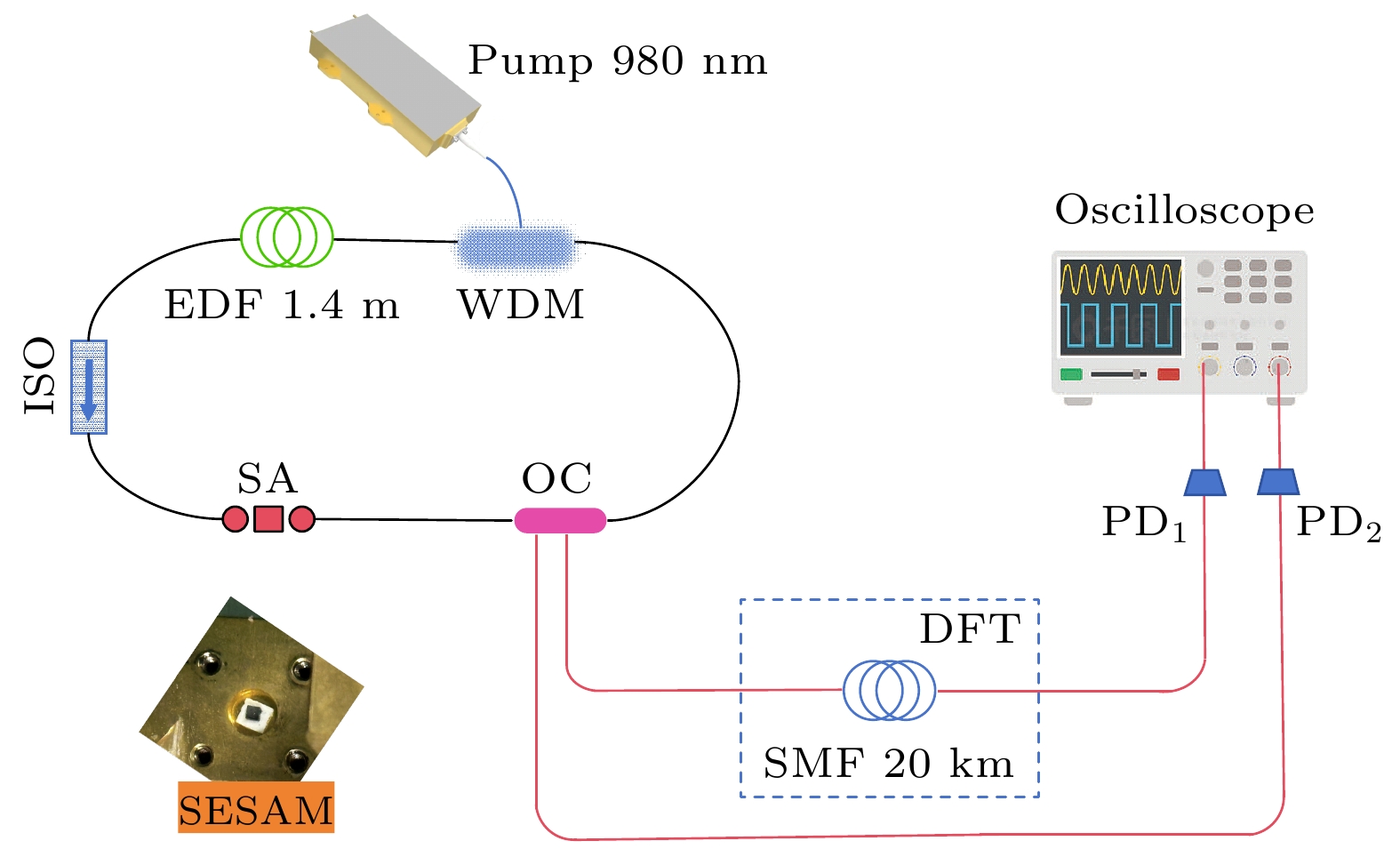
图1展示了一种基于可饱和吸收体锁模掺铒光纤激光器的实验装置和实时检测系统. 该激光器的总腔长为2.8 m, 完全由非保偏光纤和非保偏光纤器件组成, 采用980 nm波长的泵浦激光通过光纤耦合器(WDM)注入1.4 m长的掺铒光纤(EDF)中作为增益介质, 光纤环形腔通过引入可饱和吸收体(SA)实现锁模操作, SA由半导体可饱和吸收镜(SESAM)经过封装后与光纤集成, 该器件弛豫时间为3 ps, 饱和吸收率为30%, 插入损耗在23 ℃时为0.92 dB, 调制深度18%. 同时在环路中加入偏振相关隔离器(ISO), 确保激光器腔内的光信号单向运行, 避免反射引起干扰并提高系统稳定性. 输出信号通过50∶50耦合器(OC)提取, 随后进入20 km长的单模光纤(SMF), 光信号被光电探测器(PD1和PD2)转换为电信号, TS-DFT技术可以拉伸脉冲以将其频谱映射到时间波形实现对呼吸子动力学的单发实时监测. 激光器在1550 nm处的EDF群速度色散为 65 ps2⋅km–1, SMF群速度色散为–22 ps2·km–1, 腔内净色散量约为0.07 ps2.
-
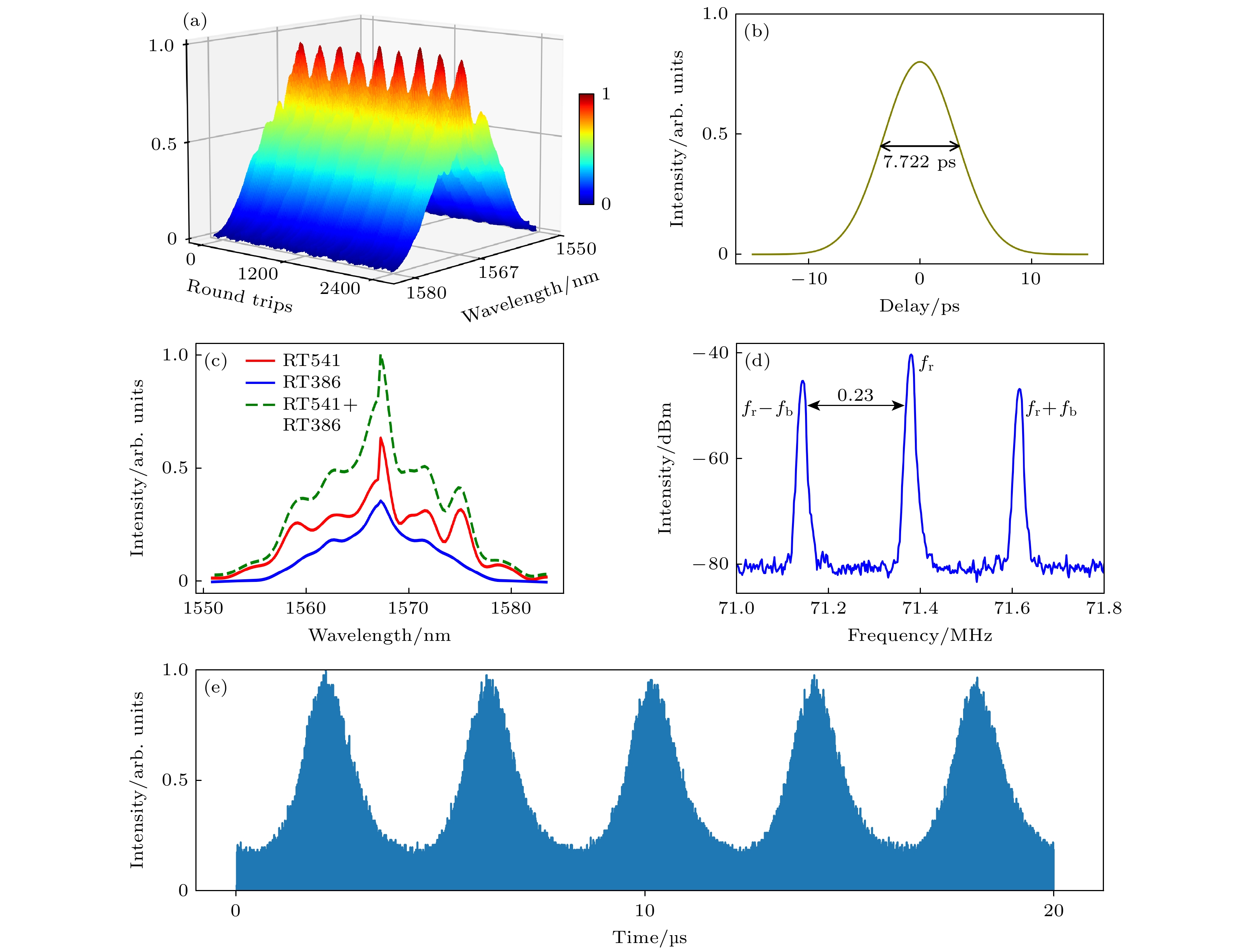
本文搭建的激光器在1567 nm下工作, 重复频率为71.38 MHz如图2(d)所示, 腔内往返一次周期为14 ns. 呼吸子的形成与调控主要受增益(泵浦功率)和腔体损耗(由可饱和吸收体调节)的影响. 图2(b)展示了通过调节泵浦功率来控制呼吸子状态变化的结果, 当泵浦功率在490—510 mW内时, 获得时间平均自相关宽度为7.722 ps的呼吸子. 实验采用群速度色散为–22 ps2/km的20 km长单模光纤对脉冲进行展宽, 同时通过实时监测系统记录其光谱和时域行为, 该光纤提供了总计–440 ps2的累积色散. 图2(a)和图2(c)分别展示了单激发光谱的傅里叶变换以及在一个振荡周期内最大往返次数与最小往返次数的单激发光谱. TS-DFT技术的基本原理是通过在色散介质中拉伸光脉冲, 使其累积足够大的群速度色散, 从而将光谱信息映射到时间域, 由于光电探测器具有极快的响应时间, DFT技术能够以远高于传统空间域光谱仪的扫描速率记录光谱信息, 这种高效的测量方法使得能够捕捉到往返分辨的光谱, 最近在揭示激光器中的各种快速动力学现象方面发挥了重要作用[17]. 图2(e)展示了呼吸子脉冲序列的包络, 周期性调制的包络揭示了呼吸子在时域内的能量调制特性. 这种周期性变化反映了呼吸子的“呼吸”行为, 即脉冲强度随时间产生周期性起伏.
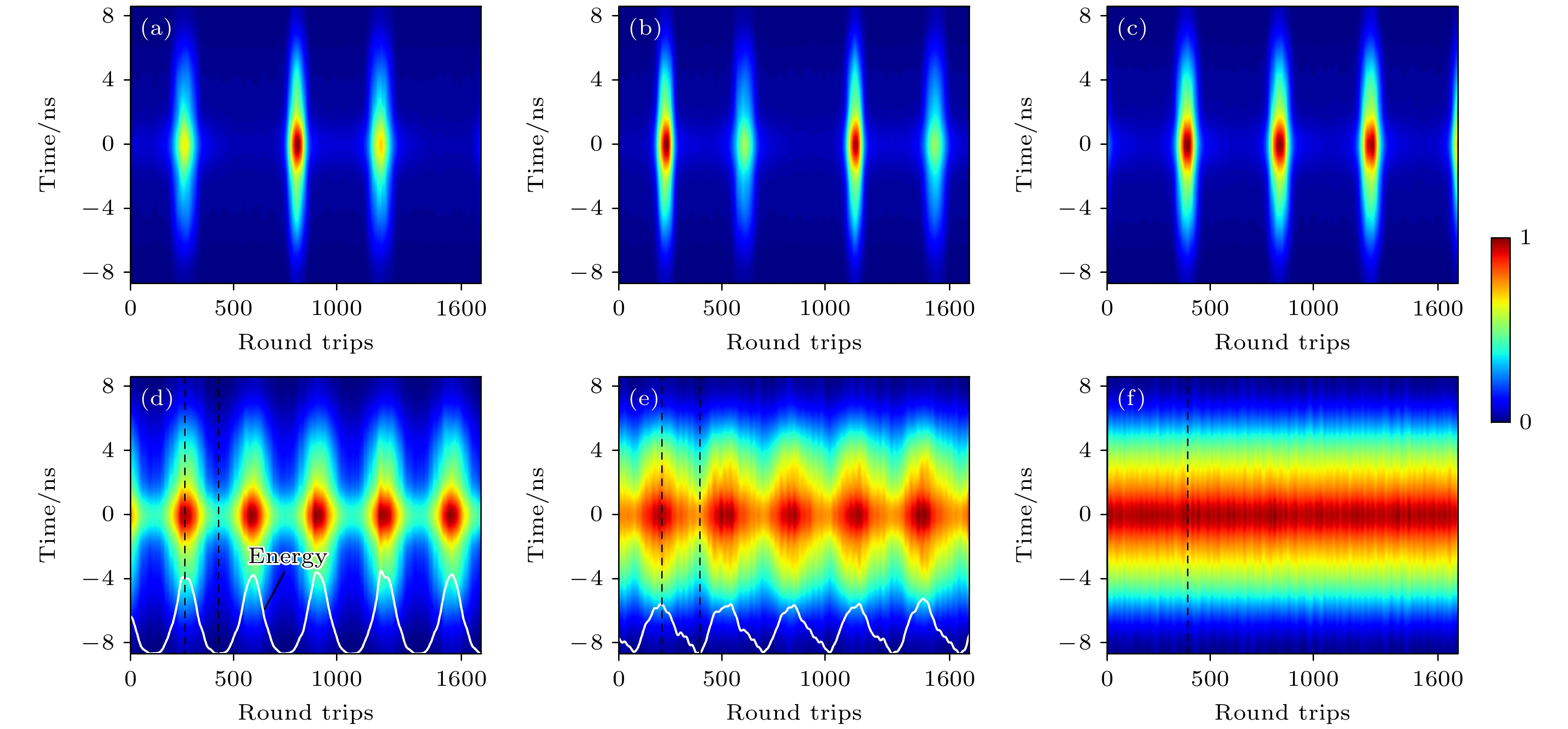
本实验利用TS-DFT结合自相关分析[19], 研究了泵浦功率在470—510 mW范围内对呼吸子高速演化动力学的影响. 图3(a)—(c)展示了呼吸子在形成初期的动态演化过程. 随着泵浦功率的调节和系统的进一步演化, 脉冲逐渐呈现交替变化的模式, 并最终表现出一定的周期性. 这一过程表明, 系统从无序波动状态逐步过渡到有序的呼吸子状态, 最终形成稳定的呼吸子演化模式. 该现象反映了非线性效应(如自相位调制和交叉相位调制)[20,21]在脉冲相互作用中的关键作用, 促进了系统向稳 定的呼吸子状态的演化. 图3(d)—(f)展示了通过TS-DFT记录的呼吸子在腔体往返过程中的时间演化特征. 脉冲的时域演化与能量变化(白色曲线)同步, 表现出周期性的压缩与拉伸现象, 这是呼吸子的显著特征, 周期大约为310次腔体往返. 图3(d)所示的周期性演化与图3(e)相似, 频率为
$ | {f_{\text{b}}} - {{{f_{\text{r}}}} {/ } {310}} | $ , 这意味着$ {f_{\text{b}}} = {{{f_{\text{r}}}} {/ } {310}} $ , 即呼吸周期正好是310次往返. 在每个周期内, 脉冲的时间曲线呈现出周期性演变, 峰值强度在每个周期内发生变化, 并且最大或最小峰值强度出现在脉冲宽度最大或最小的位置. 随着泵浦功率的增加, 图3(d)和图3(e)中所示的呼吸子周期性变化逐渐减弱, 最大带宽与最小带宽的呼吸比[22]逐渐减小, 图3(d)中的呼吸比为4.5, 而在图3(e)中则降至1.375. 当进一步增强非线性效应时, 如图3(f)所示, 呼吸比降至1, 表明系统已形成一个稳定的孤子状态.呼吸子的演变过程对于理解系统在不同泵浦功率下的动态特性至关重要. 为精确分析呼吸子在不同状态下的强度和相位变化, 采用频域特征提取技术对时域信号到频域的转换进行分析. 实验中使用采样率为10 GHz的示波器来记录2 ms时间窗口采样点的时域信号数据, 并使用逆离散傅里叶变换(IDFT)技术将频域信号转换回时域, 再令频率特性映射到时间域, 使时域中难以检测的频率特性显现. IDFT可以表示为[23]
其中
$ x\left(n\right) $ 为时域信号在第n个采样点的值,$ X\left(k\right) $ 为频域信号的第k个频率分量, N为信号的总采样点数, j为虚数单位(j =$ \sqrt{-1} $ ). 将频域信号转换回时域后, 使用三阶多项式拟合的Savitzky-Golay滤波器[24]对转化后的时域信号进行去滤波处理. 对窗口内的数据采用最小二乘法进行拟合, 能够使该滤波器保留信号的主要特征, 并可有效地去除噪声, 使得呼吸子的强度和相位特性能被更准确地提取和分析, 结果如图4所示. 通过计算功率谱密度(PSD)并进行积分, 还可以揭示能量集中的特性. 积分使用的公式为[25]其中
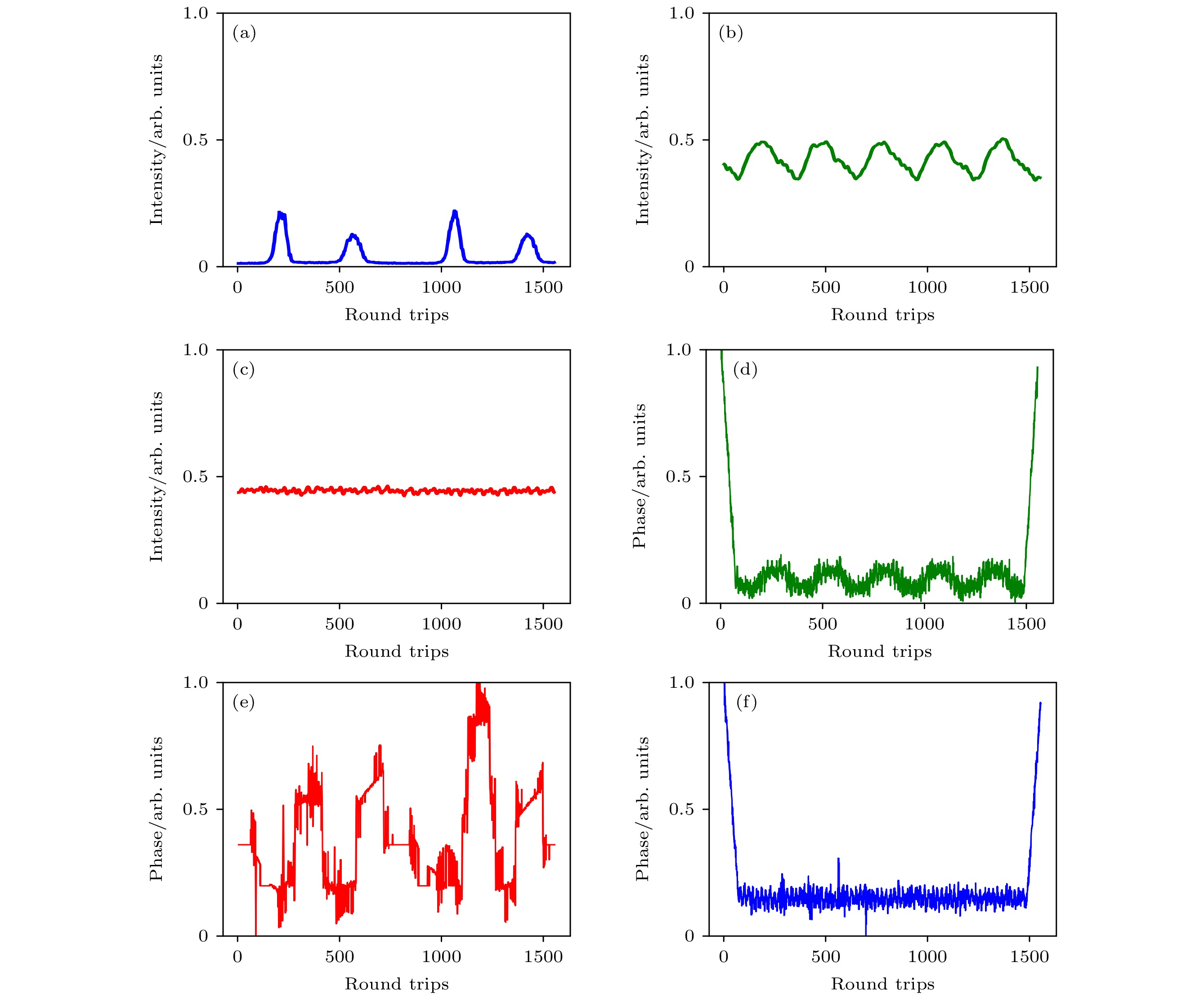
$ {\text{PSD}}\left( f \right) $ 为信号在频率f上的功率分布; T为时间长度;$ x\left( t \right) $ 为时域信号, t为时间;$ {{\text{e}}^{ - {\text{j}}2\pi ft}} $ 为复指数函数. 通过对时域信号进行傅里叶变换并计算其功率谱密度, 再对频率域上的PSD进行积分, 可以得到时域内的能量分布, 见图3 (白色曲线).图4(a)和图4(d)展示了在较低泵浦功率下, 脉冲强度和相位的变化. 尽管强度和相位表现为无序波动, 相位图显示出明显的相位漂移, 但可以观察到强度变化中出现周期性特征的萌芽, 系统正处于从无序到有序的过渡阶段, 非线性效应和色散效应的相互作用尚未达到平衡, 导致脉冲间出现不规则波动, 尚未形成稳定的周期性行为. 随着泵浦功率逐步提升至506 mW如图4(b)和图4(e)所示, 非线性效应逐渐增强, 脉冲强度和相位开始表现出清晰的周期性变化, 并且二者变化同步, 系统进入了稳定的呼吸子状态, 非线性动力学与色散效应达到平衡. 继续增加泵浦功率至510 mW时(图4(c)和图4(f)), 脉冲强度和相位趋于恒定, 系统转变为孤子状态.
这一系列变化展示了泵浦功率在调控系统动态特性中的作用, 泵浦功率的变化不仅影响非线性动力学过程与色散效应之间的平衡, 也影响了可饱和吸收体的动态响应. 可饱和吸收体通过其对脉冲强度的非线性响应, 有效地调控了脉冲的能量分布和频谱宽度, 其饱和效应能够抑制过高强度脉冲 的形成, 从而促进了系统中非线性与色散效应的平衡[26]. 在低功率情况下, 脉冲强度和相位的无序波动可能与可饱和吸收体未完全饱和, 导致其非线性吸收效应较弱有关. 随着泵浦功率的增加, 可饱和吸收体逐渐饱和, 增强了其对脉冲强度的调控作用, 从而帮助系统实现非线性与色散效应的平衡, 促进了脉冲的周期性变化[27], 进而加速了呼吸子的形成. 这一过程的内在联系和转换机制, 揭示了泵浦功率通过调节可饱和吸收体的吸收效应, 间接影响系统中非线性和色散的平衡, 进而影响呼吸子与孤子之间的可逆转换[17]. 具体而言, 呼吸子是在一定条件下由孤子演化而来的, 而当条件变化时, 呼吸子又可转变为孤子. 此过程的可逆性表明, 系统的稳定性不仅依赖于非线性与色散效应的平衡, 还可能受可饱和吸收体调控机制的影响.
-
呼吸子现象作为一种周期性脉冲行为, 是超快光纤激光器研究中的关键领域, 反映了非线性光学效应与腔内参数之间复杂的动力学特征[28]. 其独特之处在于能够输出被称为呼吸子的超短脉冲, 这些脉冲的能量随时间呈周期性变化, 这种周期性(即呼吸频率)与激光器的腔频(由激光器腔长决定)之间形成了一个天然的同步系统[16]. 通过调整激光器的泵浦功率、耗散等参数, 可以进一步调节呼吸子的特性和呼吸比的大小, 从而实现对激光输出的精确控制. 本文探讨了泵浦功率对非保偏可饱和吸收体锁模掺铒光纤激光器中呼吸子脉冲形成与演化的影响, 揭示了非线性效应在呼吸子稳定性中的核心作用, 在激光器内部, 呼吸子的周期性振荡特性导致了激光脉冲的非均匀分布, 这种非均匀分布的激光脉冲在脉冲整形、超短脉冲生成以及频率梳的精确控制方面展现出了巨大的应用潜力. 此外, 呼吸子的存在还可能对激光器的稳定性和能量转换效率产生影响, 从而为激光器的设计和优化提供新的视角.
基于可饱和吸收体锁模激光器中的呼吸子
Breathers in mode-locked lasers based on saturable absorbers
-
摘要: 呼吸子作为一种独特的非线性脉冲现象, 在激光器性能优化、非线性光学过程研究以及复杂信号传输中发挥着关键作用. 与稳定孤子不同, 呼吸子脉冲的能量随着时间发生周期性波动, 表现为脉冲频率和振幅的周期性变化. 通过适当的非线性效应, 激光器能够产生稳定的呼吸子脉冲, 实现呼吸锁模状态, 展现出类似“呼吸”的周期性模式. 基于此, 本文设计并搭建了一台基于可饱和吸收体作为锁模元件的光纤激光器, 并在较低泵浦功率下成功观察到稳定的呼吸态. 通过利用高速探测技术和时间拉伸色散傅里叶变换(TS-DFT)技术, 对快速脉冲进行了时间放大和频谱分析, 并实时监测呼吸子脉冲在时域和频域上的演化过程. 实验结果表明, 泵浦功率的变化显著地影响附加振荡引发的周期性调制, 从而调控呼吸比, 直至形成稳定的孤子. 当泵浦功率达到470—480 mW时, 实验首次观察到呼吸子的形成, 其呼吸比高达4.5. 随着泵浦功率的增加, 呼吸效应逐渐减弱, 并在510 mW时完全消失, 呼吸比降至1. 这一结果验证了泵浦功率对呼吸子状态及其转变过程的关键控制作用, 为超快激光技术和非线性光学领域提供新视角.Abstract:
Breathing pulses, as a unique nonlinear pulse phenomenon, play a key role in optimizing laser performance, nonlinear optical processes, and complex signal transmission. Unlike stable solitons, the breathing pulses fluctuates in energy periodically with time, and both pulse frequency and amplitude exhibit periodic changes. Through appropriate nonlinear effects, lasers can generate stable breathing pulses, achieving a mode-locked state that exhibits a periodic “breathing” pattern. Based on this, a fiber laser combining a saturable absorber as the mode-locking element is designed and built, and stable breathing states are successfully observed at lower pump power levels. High-speed detection techniques and time-stretched dispersive Fourier transform (TS-DFT) technology are used to time-amplify and spectrally analyze the rapid pulses, while monitoring the evolution of the breathing pulse in both time domain and frequency domain. Experimental results indicate that the change in pump power significantly affects the periodic modulation induced by additional oscillations, thereby controlling the breathing ratio and ultimately resulting in the formation of a stable soliton. When the pump power is between 470 and 480 mW, the formation of the breathing pulse is first observed, with a breathing ratio of up to 4.5. As the pump power increases, the breathing effect gradually diminishes, and at 510 mW, it completely disappears, with the breathing ratio dropping to 1. These results confirm the critical role of pump power in controlling the breathing pulse state and its transition, demonstrating the potential of controlling pump power in ultrafast laser technology and nonlinear optics. The breathing pulse phenomenon, as a periodic pulse behavior, reflects the complex dynamical characteristics between nonlinear optical effects and cavity parameters. Combined with the natural synchronization system formed between the breathing frequency and the cavity frequency (determined by the cavity length), the periodic change of the breathing pulse becomes a crucial factor for controlling laser output. By adjusting parameters such as the laser’s nonlinearity and dissipation, the characteristics of the breathing pulse and breathing ratio can be precisely controlled, thus achieving precise control of the laser output. The periodic oscillatory characteristics of the breathing pulse inside the laser cavity lead to the non-uniform distribution of pulses, a feature that demonstrates enormous potential in pulse shaping, ultrashort pulse generation, and precise frequency comb control. Additionally, the presence of the breathing pulse may affect the stability and energy conversion efficiency of the laser, providing new perspectives for designing and optimizing lasers. -
Key words:
- laser /
- breather /
- nonlinear fiber dynamics .
-

-
图 2 (a) 每个单次激发光谱的傅里叶变换; (b) 时间平均自相关宽度的测量结果; (c) 一个振荡周期内最大往返次数与最小往返次数单激发光谱; (d) 频谱特征; (e) 示波器记录的实验测量脉冲序列
Figure 2. (a) Fourier transform of each single excitation spectrum; (b) measurement of time-averaged autocorrelation width; (c) the maximum and minimum round-trip numbers within one oscillation period of a single-excitation spectrum; (d) spectral characteristics; (e) experimental measurement pulse sequences recorded by an oscilloscope.
图 3 呼吸子在470—510 mW泵浦功率范围内的高速动力学演化过程及其相对于1600次连续往返的时域演化 (a) Pp=470 mW; (b) Pp = 480 mW; (c) Pp = 490 mW; (d) Pp = 500 mW; (e) Pp = 506 mW; (d) Pp = 510 mW
Figure 3. The high-speed dynamical evolution of the breath pulse in the pump power range from 470 to 510 mW, and its temporal evolution relative to 1600 continuous round trips: (a) Pp = 470 mW; (b) Pp = 480 mW; (c) Pp = 490 mW; (d) Pp = 500 mW; (e) Pp = 506 mW; (f) Pp = 510 mW.
图 4 (a), (d) Pp = 480 mW未形成呼吸子状态下的脉冲强度和相位变化; (b), (e) Pp = 506 mW呼吸子稳定状态的脉冲强度和相位变化; (c), (f) Pp = 510 mW孤子状态下的脉冲强度和相位变化
Figure 4. (a), (d) The pulse intensity and phase variations at Pp = 480 mW in the non-breather state; (b), (e) the pulse intensity and phase variations at Pp = 506 mW in the stable breather state; (c), (f) the pulse intensity and phase variations at Pp = 510 mW in the soliton state.
-
[1] Ma Q Y, Yu H Y 2023 Nanomanuf. Metrol. 6 36 doi: 10.1007/s41871-023-00216-3 [2] Li Z X, Cao H Y, Wang Y Y, Dai C Q 2023 IEEE J. Sel. Top. Quantum Electron. 29 1100108 doi: 10.1109/JSTQE.2023.3248128 [3] Shimizu Y 2021 Nanomanuf. Metrol. 4 3 doi: 10.1007/s41871-020-00083-2 [4] Murakoshi H, Ueda H H, Goto R, Hamada K, Nagasawa Y, Fuji T 2023 Biomed. Opt. Express 14 326 doi: 10.1364/BOE.477322 [5] Liu F, Zhang Y, Wu X D, Li J F, Yan F, Li X H 2020 IEEE Photonics J. 12 1500910 doi: 10.1109/JPHOT.2020.2964981 [6] Keller U 2003 Nature 424 831 doi: 10.1038/nature01938 [7] Matniyaz T, Kong F, Kalichevsky-Dong M T, Dong L 2020 Opt. Lett. 45 2910 doi: 10.1364/OL.392786 [8] 王慧慧, 郭睿 2019 应用数学进展 8 2084 doi: 10.12677/AAM.2019.812239 Wang H H, Guo R 2019 Adv. Appl. Math. 8 2084 doi: 10.12677/AAM.2019.812239 [9] Chen T, Zhang Q L, Zhang Y P, Li X, Zhang H K, Xia W 2018 Photonics Res. 6 1033 doi: 10.1364/PRJ.6.001033 [10] Liu X M 2011 Phys. Rev. A 84 053828 doi: 10.1103/PhysRevA.84.053828 [11] Wu X Q, Peng J S, Boscolo S, Finot C, Zeng H P 2023 Phys. Rev. Lett. 131 263802 doi: 10.1103/PhysRevLett.131.263802 [12] Cui Y D, Zhang Y S, Huang L, Zhang A G, Liu Z M, Kuang C F, Tao C N, Chen D R, Liu X, Malomed B A 2023 Phys. Rev. Lett. 130 153801 doi: 10.1103/PhysRevLett.130.153801 [13] 吴修齐, 彭俊松, 张颖, 曾和平 2023 中国激光 50 1101006 doi: 10.3788/CJL230702 Wu X Q, Peng J S, Zhang Y, Zeng H P 2023 Chin. J. Lasers 50 1101006 doi: 10.3788/CJL230702 [14] Grelu P, Akhmediev N 2012 Nat. Photonics 6 84 doi: 10.1038/nphoton.2011.345 [15] Guo W Q, Zhang L, Xiao X S, Li X X, Yin Z G, Ning H, Zhang X, Zhang X W 2023 Photonics 10 610 doi: 10.3390/photonics10060610 [16] Xian T H, Zhan L, Wang W C, Zhang W Y 2020 Phys. Rev. Lett. 125 163901 doi: 10.1103/PhysRevLett.125.163901 [17] Peng J S, Boscolo S, Zhao Z, Zeng H P 2019 Sci. Adv. 5 11 doi: 10.1126/SCIADV.AAX1110 [18] Herink G, Kurtz F, Jalali B, Solli D R, Ropers C 2017 Science 356 50 doi: 10.1126/science.aal5326 [19] Apicella B, Bruno A, Wang X, Spinelli N 2013 Int. J. Mass Spectrom. 338 30 doi: 10.1016/j.ijms.2013.01.003 [20] Cui Y D, Zhang Y S, Song Y J, Tong L, Huang L, Qiu J R, Liu X M 2021 Laser Photonics Rev. 15 2000216 doi: 10.1002/lpor.202000216 [21] Lucas E, Karpov M, Guo H, Gorodetsky M L, Kippenberg T J 2017 Nat. Commun. 8 736 doi: 10.1038/s41467-017-00719-w [22] Qin Z P, Xie G Q, Gu H A, Hai T, Yuan P, Ma J G, Qian L J 2019 Adv. Photonics 1 065001 doi: 10.1117/1.AP.1.6.065001 [23] Auer G, Dammann A, Sand S 2003 Proceedings of the 14th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications Beijing, China, September 7–10, 2003 pp1954–1958 [24] Schafer R W 2011 IEEE Signal Process. Mag. 28 111 doi: 10.1109/MSP.2011.941097 [25] 黄旭方, 陈静开, 覃新贤 2012 电讯技术 52 1893 doi: 10.3969/j.issn.1001-893x.2012.12.006 Huang X F, Chen J K, Qin X X 2012 Telecommun. Eng. 52 1893 doi: 10.3969/j.issn.1001-893x.2012.12.006 [26] Woodward R I, Kelleher E J R 2015 Appl. Sci. 5 1440 doi: 10.3390/app5041440 [27] 江俊林, 乐文杰, 王玮琦, 丁翌辰, 吴波, 沈永行 2018 光子学报 47 0914001 doi: 10.3788/gzxb20184709.0914001 Jiang J L, Le W J, Wang W Q, Ding Y C, Wu B, Shen Y X 2018 Acta Photonica Sin. 47 0914001 doi: 10.3788/gzxb20184709.0914001 [28] Hu F T, Vinod A K, Wang W, Chin H H, McMillan J F, Zhan Z Y, Meng Y, Gong M, Wong C W 2024 Light Sci. Appl. 13 251 doi: 10.1038/s41377-024-01573-4 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: