-
隔离器由于具有单向导通特性被广泛用于保护反射敏感的光学系统中, 如激光器、光放大器等[1]. 光学器件一般是互易的, 即光路可逆, 实现单向导通必须打破非互易, 而打破非互易目前主要通过以下几个方案实现: 磁光方案[2-5]、非线性方案[6,7]、动态调制方案[8-10]、时间反演对称破缺方案[11,12]和片上集成设计方案[13,14]等. 其中, 片上集成方案一般是利用二维正方晶格光子晶体板之间的异质结与方向带隙失配和不同的模式转换实现光的非互易传输. 目前, 片上集成光隔离器已有诸多报道. 例如2020年, Mizumoto和Shoji[15]利用单晶磁光石榴石在硅片上取得了隔离度为16 dB的隔离器. 同年, Karki等[16]通过在石榴石中掺入镓和铕, 得到了不外加磁场的隔离器, 其在整个C波段上的隔离度为25 dB. 2021年, Tian等[17]在氮化铝(AlN)中利用三个氮化硅(
$ \mathrm{Si}_3\mathrm{N}_4 $ )微环谐振器进行时空调制, 取得隔离度为10 dB, 插入损耗为0.1 dB的结果. 2022年, Herrmann等[10]采用铌酸锂薄膜实现了系统频率特征模之间的转化, 在1550 nm处测得的隔离度为40 dB. 2023年, White等[6]利用氮化硅微环设计了一种基于克尔效应的隔离器, 取得了17—23 dB隔离度. 这些结果表明片上集成隔离器研究方面取得了很好的进展.但是, 目前仍然缺乏一种紧凑的、结构简单的片上硅基光隔离器方案. 为了得到超紧凑结构, 采用逆向算法设计是一个可能的途径. 与正向设计不同, 逆向算法设计是以目标为导向进行的算法设计思路, 目前逆向算法设计使用的方法有: 直接二进制搜索(direct binary search, DBS)算法[18-20]、伴随法(形状优化[21-24]与拓扑优化[25-28])、粒子群算法[29-31]和遗传算法[32-34]. 除上述算法外, 为追求器件的极致性能还开发出一些混合算法, 如Wang等[35]设计的超宽带宽的Y分支器件, 先后使用伴随法与DBS对Y分支进行优化, 取得了超低损耗与超宽带宽的结果; Peng等[36]讨论了使用单一算法和混合算法的区别, 通过混合算法得到的器件在性能上更有优势.
基于此, 本文基于遗传算法发展了引入分段设计适应度函数的自适应调整算法, 在标准的绝缘体上硅(silicon on insulator, SOI)基片, 通过设置简单的5种不同直径的圆孔结构而实现了光的定向传输. 在经典设计[13,14]的基础上, 本文获得的隔离器尺寸更小, 仅为
$ 4. 2\text{ μm}\times 3\text{ μm} $ , 且获得了更高的隔离度和更低的插入损耗. 在TE偏振模式下, 取得了隔离度约为31 dB、插入损耗仅为2 dB的结果. 这些结果对于发展结构超紧凑的、更利于光电融合的片上硅基光电子系统具有有益价值. -
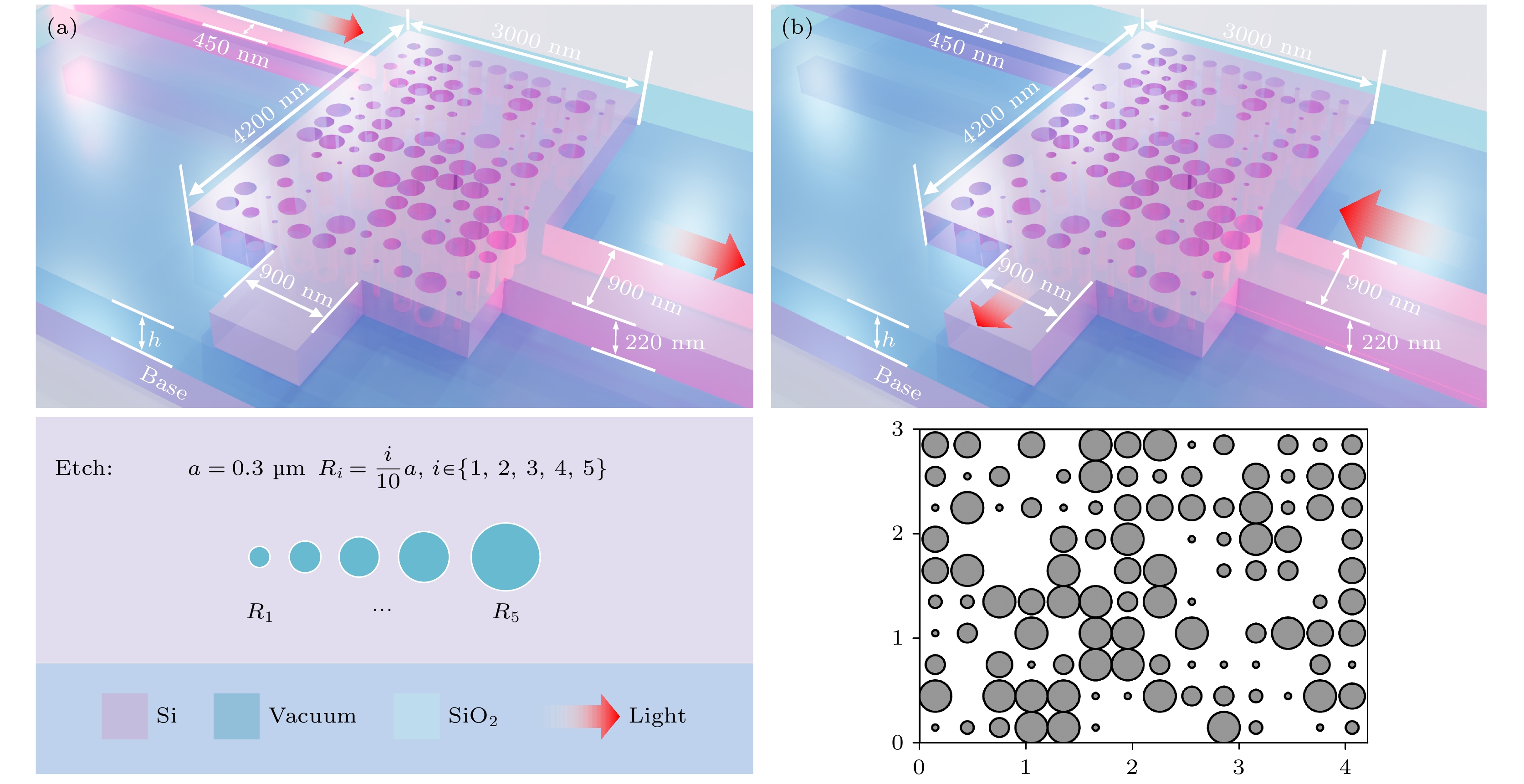
图1为基于SOI的片上隔离器示意图, 由三根直波导和一块方形波导组成, 分别为入射波导(450 nm)、出射波导(900 nm)、下方波导(900 nm)和中心波导(
$ 4. 2\text{ μm} \times 3\text{ μm} $ ). 通过在中心波导刻蚀不同半径的圆孔以实现隔离效果[13,14], 中心波导共有140个(14 × 10)位置可选择刻蚀与否, 为提高模型的表达能力, 刻蚀的圆孔直径提供了5种尺寸, 分别是60, 120, 180, 240和300 nm. 除了选择不同尺寸的圆孔刻蚀以外, 还可以不对该位置刻蚀. 图1(a)为正向通过该器件时的示意图, 其中紫色部分的材料为纯硅, 淡蓝色部分的材料为SiO2, 下方展示了5种可供遗传算法选择的尺寸; 图1(b)为反向通过该器件时的示意图, 下方给出了遗传算法通过1500次优化1550 nm TM偏振计算出来的结果, 观察该结构可以发现, 遗传算法充分使用了不同尺寸的圆孔. -
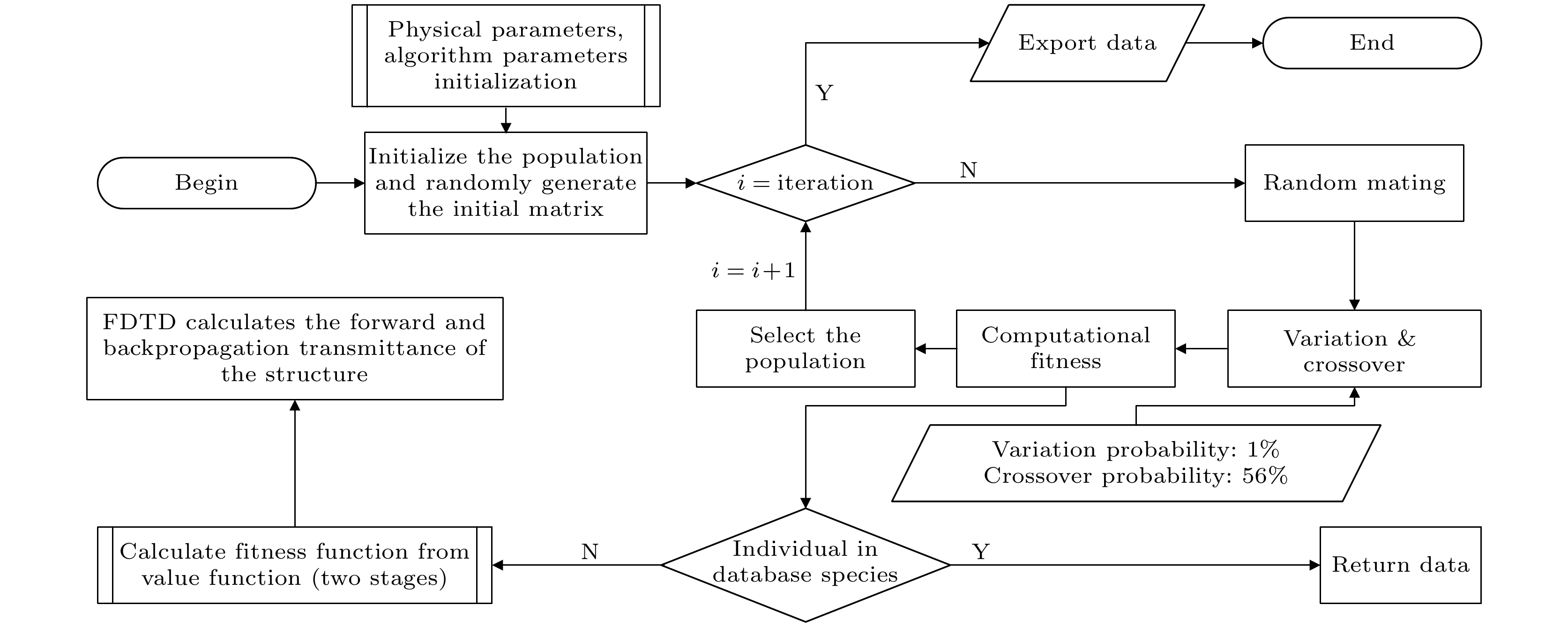
遗传算法被广泛用于光子器件优化[32-34], 这里设定种群环境容纳量为50, 种群进化1500代, 遗传算法的流程如图2所示, 首先随机生成一个数量为50个的初始种群, 种群之间随机进行基因交流, 产生一个数量为100的新种群, 将这个新种群代入时域有限差分(finite difference time domain, FDTD)中计算得到了整个种群的适应度, 以适应度为参考对种群内的个体进行选择, 选择出适应 度靠前的50个个体, 下一代以该50个个体作为迭代的初始种群(父代). 当迭代次数达到预设时, 程序结束并导出结果. 为满足隔离器单向传播的特性, 进一步发展为混合算法, 即在计算适应度函数(价值函数FOM)时, 算法考虑了两个阶段. 第一个阶段优先优化隔离度, 此时的价值函数设定为
$ \mathrm{FOM} = -10\log_{10}(p_1/p_2) $ , 式中$ p_1, p_2 $ 分别表示反向、正向通过器件的透射率. 经反复模拟发现当隔离度值较大时, 反向透射率$ p_1 $ 的减小速度要慢于正向透射率$ p_2 $ 的增大速度. 虽然隔离度值符合得很好, 但插入损耗却较大, 于是本文针对插入损耗设置了第二段价值函数. 在该阶段对$ p_1 $ 进行限制, 当$ p_1 < 1\times10^{-4} $ 时, 令$ p_1 = 1\times10^{-4} $ , 如此, 遗传算法会将优化重心转移到插入损耗上, 因而得到符合预期的隔离器性能.在种群演化更新中常常出现一些“未进化”的个体, 倘若再次对这些个体进行计算, 很大程度上会降低算法的优化效率, 于是进一步构建了基因库. 当计算出一个新结构的FOM后, 将这个结构和计算的结果保存至基因库中, 后续计算价值函数时, 首先查看该结构是否已存在于基因库中, 若存在则返回对应的值, 进而增加了算法的效率.
-
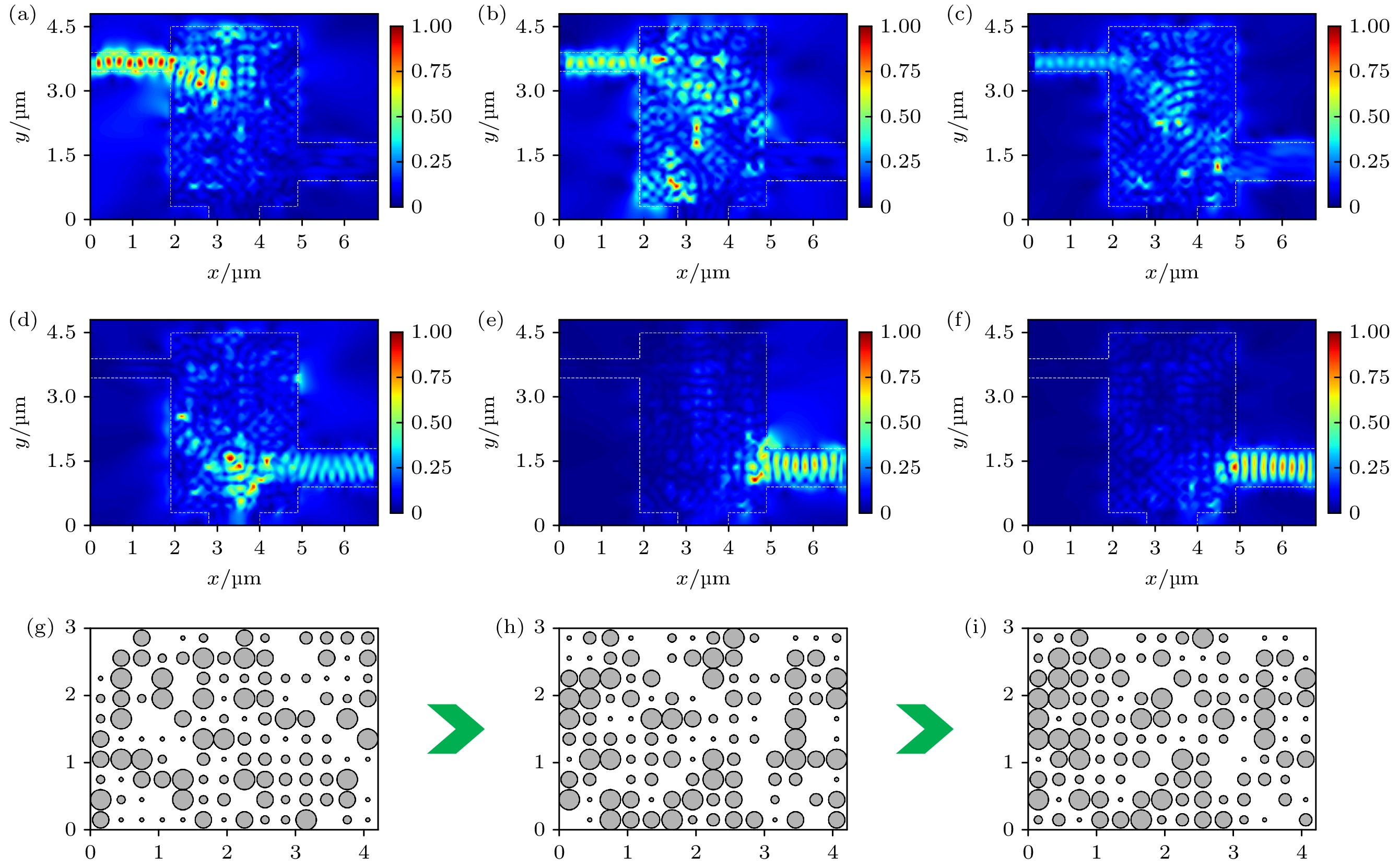
图3给出了遗传算法迭代1, 11和201次时的结果, 图3(a)—(c), 图3(d)—(f), 图3(g)—(i)分别是正向传播模场、反向传播模场与对应的结构分布. 模场分布随着迭代次数的增加, 正向通过的光强越来越大, 而反向通过的光强越来越小, 符合预期.
-
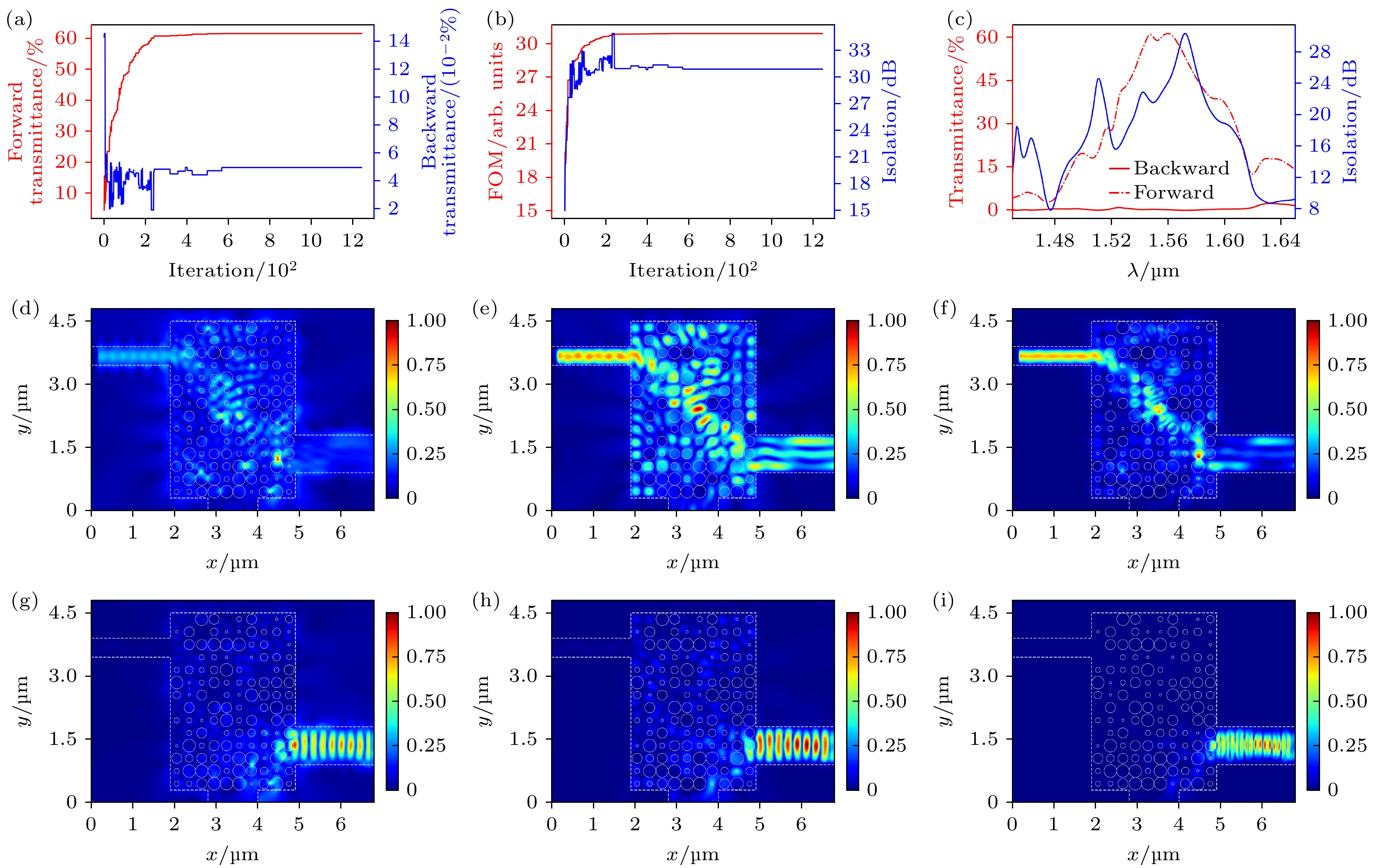
将光源设置为1550 nm处的TE偏振, 算法优化得到了图4所示的结果, 图4(a)是最优结构的正向和反向透射率, 正向透射率最终收敛在61.47%, 反向透射率收敛于
$ 5\times10^{-4} $ . 图4(b)红线是最优结构的价值函数随着迭代次数呈阶梯式单调递增趋势; 蓝线是最优结构的隔离度随迭代次数的变化曲线, 该曲线在细节上并不是单调递增, 这是由于第二阶段的价值函数限制作用, 优化重心转移至正向透射率的结果. 图4(c)是不同波长的光源正向(红色点线)、反向(红色实线)通过结构的透射率和隔离度(蓝色曲线)分布图, 红色点线 的值在1.53—1.58 μm之间都远远高于红色实线, 该器件的3 dB带宽约为50 nm. 图4(d)和图4(g)、 图4(e)和图4(h)、图4(f)和图4(i)分别为1550 nm TE模式的光正向和反向通过最优结构(白色圆孔)的电场、磁场、功率的模场分布, 从图4(d)—(f)可以看出正向通过该结构时, 不论是电场、磁场还是功率均能在出射波导中接收到电磁信号; 从图4(g)—(i)可观察到出射波导中并没有接受到大量电磁信号, 而是被反射回去或者进入到了下方波导中. 综上, 在TE偏振下1550 nm处取得了隔离度为30.89 dB, 插入损耗为2.11 dB的结果. -
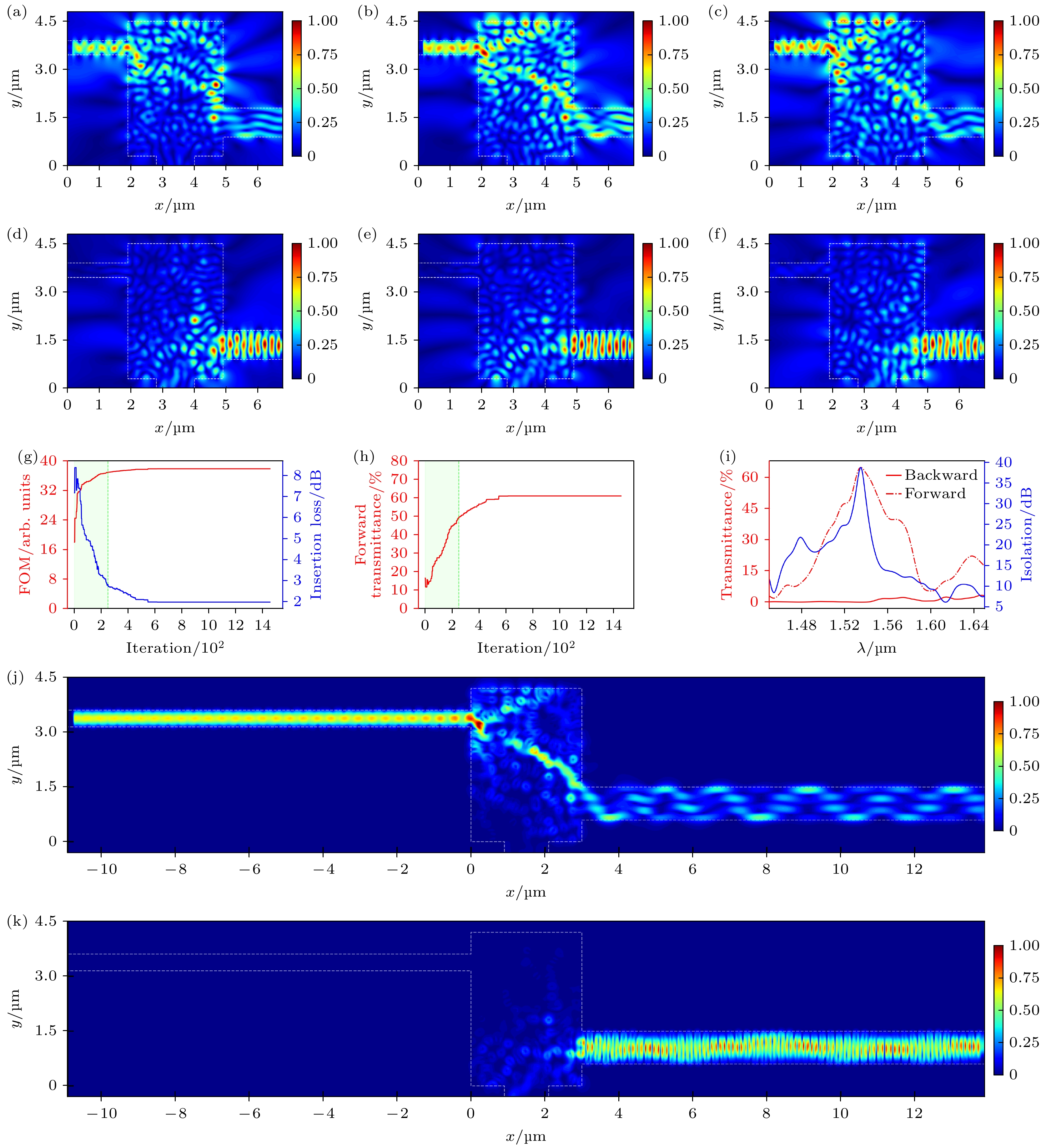
将光源设定为1550 nm的TM基模, 优化得到的结果见图5, 其中图5(a)和图5(d)、图5(b)和图5(e)以及图5(c)和图5(f)分别将光源波长设置为1535, 1555和1575 nm处, 光正向与反向通过隔离器的电场模分布, 整体均有隔离效果, 在细节上模场分布并不一致, 体现了不同波长的光在硅介质中传播规律的差别. 图5(g)红色曲线为每代最优结构的隔离度随着迭代次数的变化; 蓝色曲线为插入损耗随迭代次数的变化. 图5(h)是正向导通的透射率随着迭代次数的变化结果, 透射率随着迭代次数“阶梯式”增加. 图5(i)展示了不同波长的光源正向(红色点线)、反向(红色实线)通过结构的透射率分布和1450—1650 nm的各个波长(蓝色曲线)隔离度分布, 由图可得该器件的3 dB带宽约为50 nm, 正向通过器件时透射率值随波长的变化起伏较大, 而反向透射率相比于正向透射率均较小. 图5(j)和图5(k)分别是延长波导光源正向和反向通过这个器件的光场模场分布图, 光从入射波导进入器件后大部分光都从出射波导中透过, 少部分光从器件中散射出去, 图中白色圆圈标注处是透射监视器放置处, 经优化该处的最大透射率为61%. 由图5(k)可得反向入射的光多数被反射. 综上, 在TM偏振下1550 nm处取得了隔离度为37.86 dB, 插入损耗为1.96 dB的结果.
-
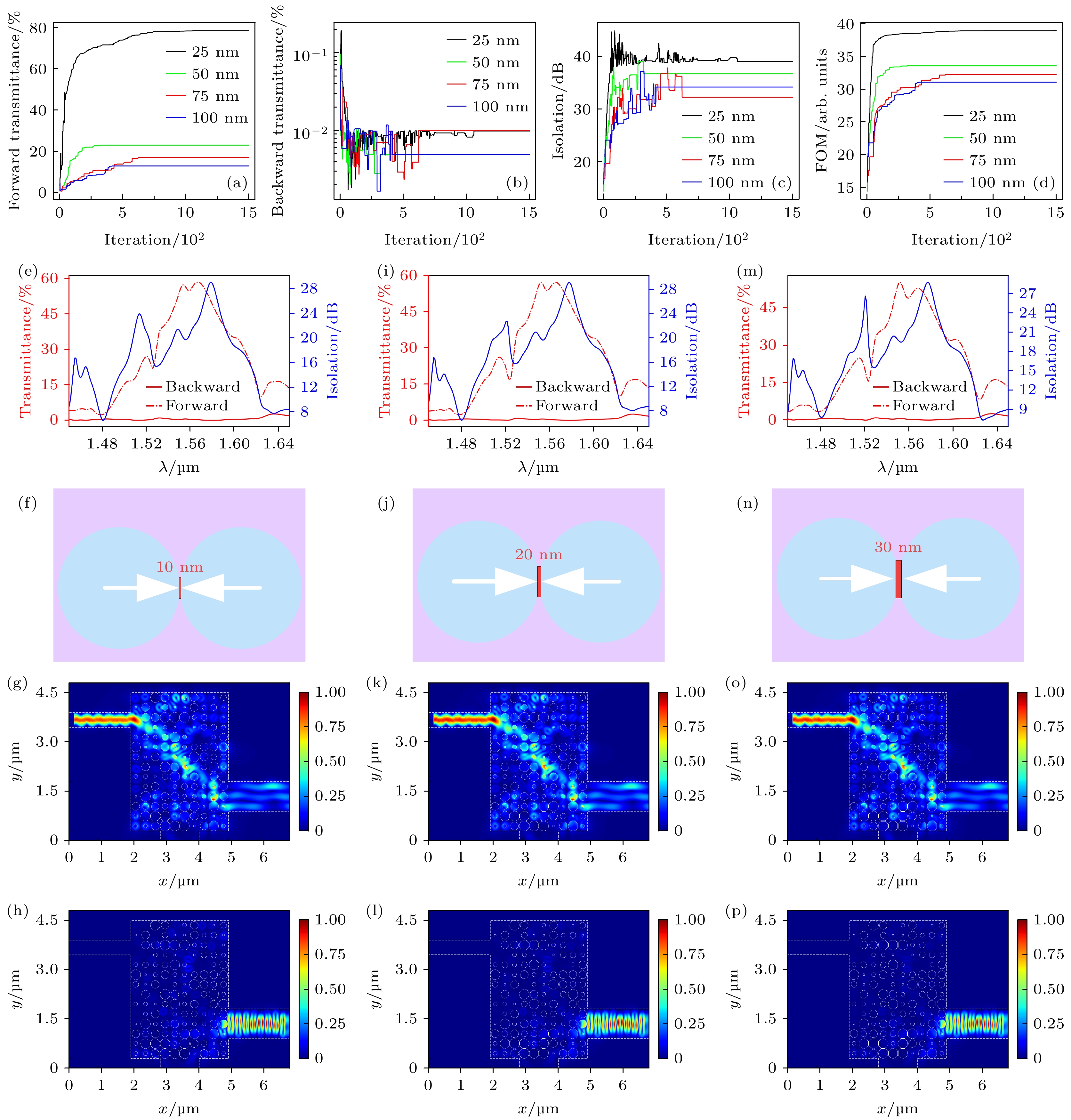
上述研究中, TE模式与TM模式使用的结构参数均一致, 其中最小的圆孔半径为30 nm, 为探究不同特征尺寸对隔离器效果的影响设置了4套不同的体系, 以最小半径25 nm为例, 在这套结构体系中还有半径为0×25 nm, 1×25 nm, 2×25 nm, 4×25 nm和5×25 nm的圆孔供算法选择, 最小半径还有50, 75和100 nm. 对这4套结构分别进行优化, 结果如图6所示. 图6(a)是正向透射率随迭代次数的变化曲线, 透射率值为上升趋势并收敛, 其中透射率取值最大的是25 nm对应的体系, 该体系最优结构的正向透射率(75%), 其次是50 nm (23%), 75 nm (17%)和100 nm (13%), 取值随尺寸的增大呈下降趋势. 图6(b)是反向透射率随着迭代次数的变化曲线, 可以看出整体呈下降趋势并收敛于价值函数限制处(
$ 10^{-4} $ ), 其中100 nm体系的反向透射率特别低, 体现了大尺寸体系将光传播到指定位置比较困难, 即该体系的表达能力不足. 图6(c)是隔离度随着迭代次数的变化曲线, 其中25 nm体系计算出来的隔离度有40 dB, 整体上看尺寸越大隔离度越小, 细节上不符的是100 nm体系和75 nm体系, 这是由于100 nm特征尺寸的通光能力过小, 导致计算出来的隔离度大于75 nm的结构, 这也证实了设置两段价值函数的必要性, 避免了通光能力小、插入损耗很大的器件. 图6(d)是4种特征尺寸的价值函数随迭代次数的变化曲线, 可以看出, 所有体系的价值函数都是随迭代的次数先阶梯式单调递增, 最后收敛到4个值, 体现了特征尺寸越小(表达能力强), 越符合本文对隔离器的期望.根据优化的数据可以看出: 结构尺寸越小, 隔离效果越好. 但同时需要考虑到现实工艺的限制, 器件结构尺寸并不能无限制得小, 正如上文使用的最小半径为30 nm的圆孔, 该尺寸的结构加工相对容易, 且隔离度较大而插入损耗较小, 基本满足实验的需求.
-
本文在设计中限定了刻蚀圆孔最小半径为30 nm, 而不同刻蚀孔的统一间距为300 nm. 因为方案中有了不同半径的刻蚀圆孔, 从而相邻圆孔间最小距离分别具有0, 30, 60, 120, 150, 180, 210, 240, 300 nm等9种可能. 对于孔间距离为0 nm的特殊情况, 会直接导致刻蚀穿透而实际不能加工. 如图6(f), (j)和(n)所示, 分别对应于刻蚀穿透区域为10, 20和30 nm的情况. 这覆盖了当前电子束工艺的极限加工尺寸约10 nm[37,38], 以及更成熟的30 nm特征尺寸[39]. 以30 nm刻蚀穿透为例, 如图6(n)所示, 两个圆孔相距为30 nm的区域被腐蚀掉而导致两个圆孔穿通. 通过仿真计算, 得到对应图6(o)的1550 nm TE模式的光正向通过结构的光场强分布, 以及图6(p)的1550 nm TE模式的光反向通过结构的光场强分布图. 图6(m)为结构的光透射率分布曲线, 可见在30 nm刻蚀穿透情况, 器件仍然保持了良好的隔离特性. 进一步与图6(e)和图6(i)比较可知, 10 nm刻蚀穿透和20 nm刻蚀穿透对器件光隔性能的总体影响不大. 当然可以预期, 随着刻蚀穿透区域越来越大, 器件的光隔离性能肯定会进一步劣化. 总之, 本文的结果初步显示, 当前较成熟的30 nm刻蚀工艺导致的刻蚀穿透是可以承受的.
-
本文在标准SOI平台上
$ 4. 2\text{ μm}\times 3\text{ μm} $ 区域内设计了一种高集成度、高隔离度的硅基光隔离器方案. 结合分段价值函数, 发展了改进的遗传算法, 在1550 nm TE偏振下取得了隔离度为30.89 dB, 插入损耗为2.11 dB 的结果; 此外还分析了1550 nm TM偏振模式下该光隔离器的结构参数, 取得了隔离度为37.86 dB, 插入损耗为1.96 dB的结果; 并进一步分析了不同尺寸体系对隔离器性能的影响, 得到了微纳结构尺寸越小, 体系的表达能力越强, 隔离效果越好的结论, 但同时也需要综合考虑实际加工工艺的限制. 总体而言, 这些结果有利于发展超紧凑的片上硅光单向传输方案, 有利于发展光电融合的集成硅基光电子系统.
基于改进遗传算法设计的超紧凑型片上硅光隔离器
Ultra-compact on-chip silicon photonics isolator designed using modified genetic algorithm
-
摘要: 片上集成型光隔离器的定向光传输特性在光通信、光信号处理等领域有广泛的应用价值. 本文通过改进遗传算法, 引入分段的适应度函数(阶段1设定隔离度; 阶段2设定插入损耗), 并建立基因库; 在仅为$4.2\text{ μm}\times 3\text{ μm}$的区域内获得了一种超紧凑的光隔离器方案. 在标准的绝缘体上硅(silicon on insulator, SOI)基片上, 通过设置5种直径(60 nm, 120 nm, 180 nm, 240 nm, 300 nm)的刻蚀圆孔排布, 在1550 nm TE偏振模式下, 取得了隔离度约为31 dB、插入损耗约为2 dB的结果; 在1550 nm TM偏振模式下, 取得了隔离度约为38 dB、插入损耗为2 dB的结果. 还进一步分析了不同尺寸组对隔离器性能的影响. 这些结果对于发展超小尺寸、高集成度的片上光信号定向传输方案有促进作用.Abstract: The directional optical transmission characteristics of on-chip integrated optical isolators have wide applications in fields such as optical communication and optical signal processing. At early stage, various schemes of on-chip optical isolators have been developed, such as single-crystal magneto-optical pomegranate scheme, and silicon nitride (Si3N4) micro-ring resonators. However, there is still lack of compact on-chip optical isolator solutions. Here, a compact and integrated silicon optical isolator on a standard silicon on insulator (SOI) substrate is proposed and designed by intelligent algorithms and a variety of micro-nano circular vias. A modified genetic algorithm is developed, a segmented design fitness function is induced, and a gene library is established to obtain an ultra-compact optical isolator scheme with a size of only 4.2 μm×3 μm. On a standard silicon on insulator substrate, a linear passive isolation scheme is achieved by etching circular holes with five different diameters: 60 nm, 120 nm, 180 nm, 240 nm, and 300 nm. In the TE polarization mode, the design achieves an isolation degree of approximately 31 dB and an insertion loss of about 2 dB. Furthermore, in TM polarization mode, the design achieves an isolation degree of approximately 38 dB and an insertion loss of 2 dB; Finally, the influence of different size groups on the performance of isolators is analyzed. The results show that the smaller the circular hole structure, the better the isolation performance is. However, at the same time, we also need to consider the real silicon etching process requirements. In practice, holes that are too small are difficult to etch the effects of etching penetration at 10 nm, 20 nm and 30 nm between circular vias on the performance of the isolator are also evaluated, and the preliminary results show that the etching penetration caused by the more mature 30 nm etching process is acceptable. Therefore, considering all factors, it is recommended that the minimum circular hole size be 30 nm and the minimum distance adjacent circular holes be 30 nm. These results can promote the development of highly integrated and ultra-small on-chip optical signal directional transmission schemes.
-
Key words:
- integrated optical isolator /
- ultra-compact /
- genetic algorithms .
-

-
图 1 隔离器结构示意图 (a)正向导通示意图, 下方是优化过程中可供选择的5种不同的圆孔孔径参数; (b)反向通光示意图. 下方是1550 nm的TM模式光源经过1500次迭代后最优价值函数对应的隔离器结构分布图
Figure 1. Isolator structure diagram: (a) Schematic diagram of the forward guide, below which are the five different round hole aperture parameters that can be selected during the optimization process; (b) reverse light passing diagram. The structure below is the distribution diagram of the isolator structure corresponding to the optimal value function of the 1550 nm TM mode light source after 1500 iterations.
图 3 遗传算法的最优结构在正向、反向传播时光场模场分布和对应的结构分布图 (a), (d), (g)迭代1次; (b), (e), (h)迭代11次; (c), (f), (i) 迭代201次
Figure 3. Optimal structure of genetic algorithm in the forward and backward propagation of power distribution and the corresponding structure distribution diagram: (a), (d), (g) Iteration 1 times; (b), (e), (h) 11 iterations; (c), (f), (i) 201 iterations.
图 4 将光源设置为1550 nm TE偏振的优化结果 (a) 透射率随着迭代次数的变化曲线; (b) 价值函数和隔离度随着算法的迭代的变化曲线; (c) 不同波长通过结构的透射率分布曲线; (d), (g) 正向、反向通光时的电场模场分布图; (e), (h) 正向、反向通光时的磁场分布图; (f), (i) 正向、反向通光时的光场模场分布图
Figure 4. Optimization results of setting the light source to 1550 nm TE polarization: (a) Transmittance with the number of iterations; (b) variation curve of the value function and isolation degree with the iteration of the algorithm; (c) transmittance distribution curves of different wavelengths through the structure; (d), (g) mode field distribution of the electric field when the light is transmitted in the forward and reverse directions; (e), (h) magnetic field distribution in forward and reverse transmission; (f), (i) power distribution diagram for forward and reverse transmission
图 5 TM偏振的优化结果 (a), (d) 1535 nm处的光场模场分布图; (b), (e) 1555 nm处的光场模场分布图; (c), (f) 1575 nm处的光场模场分布图; (g)隔离度、插入损耗的变化曲线; (h)透射率的变化曲线; (i)不同波长的光源通过结构的透射率和隔离度分布曲线; (j), (k) 1550nm TM光源正向和反向通过结构的光场模场分布图
Figure 5. Optimization results of TM polarization: (a), (d) Optical power distribution at 1535 nm; (b), (e) optical power distribution at 1555 nm; (c), (f) optical power distribution at 1575 nm; (g) variation curves of isolation and insertion loss; (h) variation curves of transmittance; (i) transmittance curves and isolation distribution curves of different wavelengths of the light source passing through the structure; (j), (k) mode-field distribution of the light field of a 1550 nm TM light source passing through the structure in the forward and reverse directions.
图 6 四种特征尺寸随迭代次数的变化曲线和刻蚀穿透间距离 (a) 正向透射率; (b) 反向透射率; (c) 隔离度; (d) 价值函数; (e)—(h) 刻蚀10 nm孔间距得到的透射率曲线、示意图和光场模场分布图; (i)—(l) 刻蚀20 nm得到的结果; (m)—(p) 刻蚀30 nm得到的结果
Figure 6. Variation curves of the four feature sizes with the number of iterations and the distance between the etched penetrations: (a) Forward transmittance; (b) reverse transmittance; (c) isolation; (d) FOM function; (e)–(h) transmittance curves, schematic and power distribution plots obtained by etching 10 nm pore spacing; (i)–(l) results obtained by etching 20 nm; (m)–(p) results obtained by etching 30 nm.
-
[1] Yu M, Cheng R, Reimer C, He L, Luke K, Puma E, Shao L, Shams-Ansari A, Ren X, Grant H R, Johansson L, Zhang M, Lončar M 2023 Nat. Photonics 17 666 doi: 10.1038/s41566-023-01227-8 [2] Huang D, Pintus P, Shoji Y, Morton P, Mizumoto T, Bowers J E 2017 Opt. Lett. 42 23 doi: 10.1364/OL.42.004901 [3] Pintus P, Huang D, Zhang C, Shoji Y, Mizumoto T, Bowers J E 2017 J. Lightwave Technol. 35 1429 doi: 10.1109/JLT.2016.2644626 [4] Bi L, Hu J, Jiang P, Kim D H, Dionne G F, Kimerling L C, Ross C 2011 Nat. Photonics 5 758 doi: 10.1038/nphoton.2011.270 [5] Onbasli M C, Beran L, Zahradník M, Kučera M, Antoš R, Mistrík J, Dionne G F, Veis M, Ross C A 2016 Sci. Rep. 6 23640 doi: 10.1038/srep23640 [6] White A D, Ahn G H, Gasse K V, Yang K Y, Chang L, Bowers J E, Vučković J 2023 Nat. Photonics 17 143 doi: 10.1038/s41566-022-01110-y [7] Abdelsalam K, Li T, Khurgin J B, Fathpour S 2020 Optica 7 209 doi: 10.1364/OPTICA.385639 [8] Dostart N, Gevorgyan H, Onural D, Popović M A 2021 Opt. Lett. 46 460 doi: 10.1364/OL.408614 [9] Lira H, Yu Z, Fan S, Lipson M 2012 Phys. Rev. Lett. 109 033901 doi: 10.1103/PhysRevLett.109.033901 [10] Herrmann J F, Ansari V, Wang J, Witmer J D, Fan S, Safavi-Naeini A H 2022 Nat. Photonics 16 603 doi: 10.1038/s41566-022-01026-7 [11] Yu Z, Fan S 2009 Nat. Photonics 3 91 doi: 10.1038/nphoton.2008.273 [12] Kang M S, Butsch A, Russell P S J 2011 Nat. Photonics 5 549 doi: 10.1038/nphoton.2011.180 [13] Wang C, Zhou C Z, Li Z Y 2011 Opt. Express 19 26948 doi: 10.1364/OE.19.026948 [14] Wang C, Zhong X L, Li Z Y 2012 Sci. Rep. 2 674 doi: 10.1038/srep00674 [15] Mizumoto T, Shoji Y 2020 Optical Fiber Communication Conference (OFC) 2020 San Diego, California, United States, March 8–12, 2020 pT3B.1 [16] Karki D, Stenger V, Pollick A, Levy M 2020 J. Lightwave Technol. 38 827 doi: 10.1109/JLT.2019.2949377 [17] Tian H, Liu J, Siddharth A, Wang R N, Blésin T, He J, Kippenberg T J, Bhave S A 2021 Nat. Photonics 15 828 doi: 10.1038/s41566-021-00882-z [18] Seldowitz M A, Allebach J P, Sweeney D W 1987 Appl. Opt. 26 2788 doi: 10.1364/AO.26.002788 [19] Yuan H, Wu J, Zhang J, Pu X, Zhang Z, Yu Y, Yang J 2022 Nanomaterials 12 669 doi: 10.3390/nano12040669 [20] Peng Z, Feng J, Yuan H, et al. 2022 Nanomaterials 12 1121 doi: 10.3390/nano12071121 [21] Lalau-Keraly C M, Bhargava S, Miller O D, Yablonovitch E 2013 Opt. Express 21 21693 doi: 10.1364/OE.21.021693 [22] Keraly C L, Bhargava S, Ganapati V, et al. 2014 CLEO: Science and Innovations 2014 San Jose, California, United States, June 8–13, 2014 pSTu2 M.6 [23] Liao J, Tian Y, Yang Z, Xu H, Tang C, Wang Y, Zhang X, Kang Z 2024 Chin. Opt. Lett. 22 011302 doi: 10.3788/COL202422.011302 [24] Wang Z, Feng J, Li H, Zhang Y, Wu Y, Hu Y, Wu J, Yang J 2023 Nanomaterials 13 2516 doi: 10.3390/nano13182516 [25] Piggott A Y, Lu J, Lagoudakis K G, Petykiewicz J, Babinec T M, Vučković J 2015 Nat. Photonics 9 374 doi: 10.1038/nphoton.2015.69 [26] Nanda A, Kues M, Calà Lesina A 2024 Opt. Lett. 49 1125 doi: 10.1364/OL.512100 [27] Vercruysse D, Sapra N V, Su L, Trivedi R, Vučković J 2019 Sci. Rep. 9 8999 doi: 10.1038/s41598-019-45026-0 [28] Cao J, Zhao Z, Sun H, Yang Y, Deng Y, Cao P 2023 J. Phys.: Conf. Ser. 2464 012019 doi: 10.1088/1742-6596/2464/1/012019 [29] Mak J C, Sideris C, Jeong J, Hajimiri A, Poon J K 2016 Opt. Lett. 41 3868 doi: 10.1364/OL.41.003868 [30] Yao R, Li H, Zhang B, Chen W, Wang P, Dai S, Liu Y, Li J, Li Y, Fu Q, Dai T, Yu H, Yang J, Pavesi L 2021 J. Lightwave Technol. 39 6253 doi: 10.1109/JLT.2021.3098346 [31] Lee I, Kim C, Ju K, Jun G, Yoon G 2023 Appl. Opt. 62 8994 doi: 10.1364/AO.500775 [32] Jia W, Jiang L, Li X 2010 Opt. Commun. 283 1537 doi: 10.1016/j.optcom.2009.11.054 [33] Yu Z, Cui H, Sun X 2017 Opt. Lett. 42 3093 doi: 10.1364/OL.42.003093 [34] Mirzaei A, Miroshnichenko A E, Shadrivov I V, Kivshar Y S 2014 Appl. Phys. Lett. 105 011109 doi: 10.1063/1.4887475 [35] Wang Z, Peng Z, Zhang Y, Wu Y, Hu Y, Wu J, Yang J 2023 Opt. Express 31 15904 doi: 10.1364/OE.489550 [36] Peng Z, Feng J, Du T, Cheng W, Wang Y, Zang S, Cheng H, Ren X, Shuai Y, Liu H, Wu J, Yang J 2022 Opt. Express 30 27366 doi: 10.1364/OE.462479 [37] Cakirlar C, Galderisi G, Beyer C, Simon M, Mikolajick T, Trommer J 2022 2022 IEEE 22nd International Conference on Nanotechnology (NANO) Palma de Mallorca, Spain, July 4–8, 2022 pp207–210 [38] Saifullah M, Subramanian K, Tapley E, Kang D J, Welland M, Butler M 2003 Nano Lett. 3 1587 doi: 10.1021/nl034584p [39] Wang K, Ren X, Chang W, Lu L, Liu D, Zhang M 2020 Photonics Res. 8 528 doi: 10.1364/PRJ.383887 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: