高级搜索

涡流场中气泡破碎对声空化效果的影响

,  , 

downloadPDF

上一篇

下一篇

邱春扬, 沈壮志, 姚博文. 涡流场中气泡破碎对声空化效果的影响[J]. 物理学报, 2025, 74(4): 044301-1. doi: 10.7498/aps.74.20241523
引用本文: 邱春扬, 沈壮志, 姚博文. 涡流场中气泡破碎对声空化效果的影响[J]. 物理学报, 2025, 74(4): 044301-1. doi: 10.7498/aps.74.20241523
shu
Chunyang QIU, Zhuangzhi SHEN, Bowen YAO. Influence of bubble breakup on cavitation effect in vortex flow field[J]. Acta Physica Sinica, 2025, 74(4): 044301-1. doi: 10.7498/aps.74.20241523
Citation: Chunyang QIU, Zhuangzhi SHEN, Bowen YAO. Influence of bubble breakup on cavitation effect in vortex flow field[J]. Acta Physica Sinica, 2025, 74(4): 044301-1. doi: 10.7498/aps.74.20241523
shu

涡流场中气泡破碎对声空化效果的影响

  • 陕西师范大学物理学与信息技术学院, 陕西省超声学重点实验室, 西安　710119

    • 作者简介: 邱春扬. E-mail: qcy6@snnu.edu.cn .
    通讯作者: E-mail: szz6@163.com.; 

  • 中图分类号: 43.20.+g, 43.35.+d, 47.10.ad, 47.11.Fg

Influence of bubble breakup on cavitation effect in vortex flow field

  • Shaanxi Key Laboratory of Ultrasonics, School of Physics & Information Technology, Shaanxi Normal University, Xi’an 710119, China

    • Corresponding author: E-mail: szz6@163.com.; 

  • MSC: 43.20.+g, 43.35.+d, 47.10.ad, 47.11.Fg

  • 摘要: 液态涡流场不仅可以传质传热影响声场分布, 还可以影响流场中气泡的行为特性, 进一步影响声空化效果. 以三维漏斗形涡流场中气泡的动力学方程并结合气泡破碎理论为基础, 研究了涡流场(搅拌产生的流场)对气泡破碎概率及其气泡空化效果的影响. 结果表明, 随着转速的增大, 气泡的破碎概率显著提高, 同时气泡破碎临界半径逐渐减小, 从600 rad/min时的200 μm降至2000 rad/min时的55.5 μm, 这意味着在高速旋转的涡流场中, 气泡在尚未膨胀到应达到的最大空化半径时就提前发生破碎, 导致其失去空化效应, 从而降低超声降解效果. 实验结果进一步验证了声空化效果在适中转速(600—1000 rad/min)下最佳, 而过高转速则会抑制降解效果. 这些发现为声空化技术的优化提供了理论基础和实验支持.
    Abstract: The liquid vortex flow field plays a crucial role not only in the transfer of matter and heat but also in significantly affecting the distribution of sound fields, which in turn influences the behavior of bubbles in the flow. This ultimately affects the phenomenon of acoustic cavitation. Based on the combination of the theory of bubble fragmentation and the theory of funnel-shaped vortex, in a three-dimensional vortex field. The effect of the vortex flow field (flow field generated by stirring) on the bubble breakup probability, as well as its modulation of acoustic cavitation, is investigated in this paper. In addition, the phenomena observed in experiments are explained. When the stirring speed reaches 1000 rad/min, the degradation effect no longer shows a monotonic increase, but instead begins to decline.It is demonstrated that with the increase of stirring speed, the probability of bubble breakup increases significantly. For instance, when the stirring speed is 1000 rad/min, the probability of bubble breakup is about 0.17%. At a stirring speed of 1500 rad/min, the breakup probability rises to 23%, and at 2000 rad/min, it reaches 44%. Moreover, the critical radius for bubble breakup decreases. The critical radius, as defined in this study, refers to the bubble radius at which the probability of breakup becomes nonzero. Experimental data show that at 600 rad/min, the critical radius for bubble breakup is about 200 μm, while at 2000 rad/min, it shortens to 55.5 μm. This indicates that in a high-speed rotating vortex field, bubbles may rupture before reaching their maximum cavitation radius, thus losing their effective cavitation effect.Further analysis shows that in the vortex flow field, for bubbles with an initial radius smaller than 22.5 μm, the temperature inside the bubbles upon collapse can reach as high as 2217.3 K (corresponding to an initial radius of 22.5 μm). For bubbles with an initial radius of 20 μm, the collapse temperature can even reach 2264.3 K. For bubbles with an initial radius of 40 μm, when the stirring speed does not exceed 1500 rad/min, the bubbles can still collapse under the action of the sound field, and the temperature inside the bubble upon collapse can reach 1659.6 K, which is sufficient to trigger off the cavitation effect. However, when the stirring speed exceeds 1500 rad/min, bubbles may break up too quickly and lose their cavitation capacity, thus failing to produce the expected cavitation effect.Experimental results further verify that at moderate stirring speeds (600—1000 rad/min), the acoustic cavitation effect is most pronounced, while excessively high stirring speeds suppress the enhancement of the degradation effect. This phenomenon suggests that the introduction of the vortex flow field makes the factors affecting acoustic cavitation more complex. The optimization of the acoustic cavitation effect requires not only the consideration of the sound field distribution and mass transfer but also the comprehensive factors such as gas entrainment, bubble aggregation, and breakup. Therefore, a thorough analysis and regulation of these factors are crucial for the widespread application of acoustic cavitation technology in engineering, with important theoretical value and practical significance, providing scientific basis and direction for further optimizing the acoustic cavitation process.
  • 加载中

  • 图 1  理论涡流场中质点运动粒子轨迹图

    Figure 1.  Trajectory diagram of particle motion in a theoretical vortex field.

    下载: 全尺寸图片 幻灯片

    图 2  不同转速下, 气泡破碎概率随气泡半径变化曲线

    Figure 2.  Bubble fragmentation probability as a function of bubble radius at different rotation speeds.

    下载: 全尺寸图片 幻灯片

    图 3  气泡初始半径破碎概率随转速的变化

    Figure 3.  Variation of bubble fragmentation probability with rotation speed for different initial bubble radii.

    下载: 全尺寸图片 幻灯片

    图 4  涡流场中声空化泡的破碎特性　(a) 1500 rad/min, 2000 rad/min转速下不同初始半径气泡破碎示意图; (b) 1000 rad/min, 1100 rad/min转速下不同初始半径气泡破碎示意图; (c) 1500 rad/min, 2000 rad/min转速下不同初始半径气泡破碎温度示意图; (d) 1000 rad/min, 1100 rad/min转速下不同初始半径气泡破碎温度示意图

    Figure 4.  Fragmentation characteristics of cavitation bubbles in a turbulent flow field: (a) Schematic diagram of bubble fragmentation with different initial radii at 1500 rad/min and 2000 rad/min speeds; (b) schematic diagram of bubble fragmentation with different initial radii at speeds of 1000 rad/min and 1100 rad/min; (c) schematic diagram of bubble fragmentation temperature at different initial radii at 1500 rad/min and 2000 rad/min speeds; (d) schematic diagram of bubble fragmentation temperature at different initial radii at speeds of 1000 rad/min and 1100 rad/min.

    下载: 全尺寸图片 幻灯片

    图 5  涡流场中声空化对亚甲基蓝降解效果

    Figure 5.  Effect of cavitation in a turbulent flow field on the degradation of methylene blue.

    下载: 全尺寸图片 幻灯片

    表 1  不同搅拌转速对应的气泡破碎半径

    Table 1.  Bubble fragmentation radius corresponding to different stirring speeds.

    搅拌转速/
    (rad·min–1)    		 破碎
    半径/μm    		 搅拌转速/
    (rad·min–1)    		 破碎
    半径/μm
    500 251.1 1200 90.6
    600 200.2 1300 85.4
    700 175.1 1400 82.5
    800 159.3 1500 78.0
    900 136.6 1600 71.5
    1000 122.1 1800 62.4
    1100 99.5 2000 55.5
    下载: 导出CSV
  • [1] 宗星星 2023 现代工业经济和信息化 8 197 doi: 10.16525/j.cnki.14-1362/n.2023.08.067 Zong X X 2023 Mod. Ind. Econ. Inf. 8 197 doi: 10.16525/j.cnki.14-1362/n.2023.08.067
    [2] Xu A, Wu Y H, Chen Z, Wu G, Wu Q, Ling F, Huang W E, Hu H Y 2020 Water Cycle 1 80 doi: 10.1016/j.watcyc.2020.06.004
    [3] Khan N, Pu J Y, Pu C S, Xu H X, Gu X Y, Zhang L, Huang F F, Nasir M A, Ullah R 2019 Ultrason. Sonochem. 56 350 doi: 10.1016/j.ultsonch.2019.04.018
    [4] Dehghani M H, Karri R R, Koduru J R, Manickam S, Tyagi I, Mubarak N M, Suhasf 2023 Ultrason. Sonochem. 94 106302 doi: 10.1016/j.ultsonch.2023.106302
    [5] Flores E M M, Cravotto G, Bizzi C A, Santos D, Iop G D 2021 Ultrason. Sonochem. 72 105455 doi: 10.1016/j.ultsonch.2020.105455
    [6] Nanzai B, Mochizuki A, Wakikawa Y, Masuda Y, Oshio T, Yagishita K 2023 Ultrason. Sonochem. 95 106357 doi: 10.1016/j.ultsonch.2023.106357
    [7] Pandit A V, Sarvothaman V P, Ranade V V 2021 Ultrason. Sonochem. 77 105677 doi: 10.1016/j.ultsonch.2021.105677
    [8] Ji H F, Xu Y F, Shi H F, Yang X D 2024 Appl. Surf. Sci. 652 0169 doi: 10.1016/j.apsusc.2024.159373
    [9] Pokhrel N, Vabbina P K, Pala N 2016 Ultrason. Sonochem. 29 104 doi: 10.1016/j.ultsonch.2015.07.023
    [10] Tian S, Li B, Dai Y, Wang Z L 2023 Mater. Today. 68 254 doi: 10.1016/j.mattod.2023.07.001
    [11] Suslick K S, Price G J 1999 Annu. Rev. Mater. Sci. 29 295 doi: 10.1146/annurev.matsci.29.1.295
    [12] 王双维, 冯若, 史群 1992 自然科学进展 3 267 Wang S W, Feng R, Shi Q 1992 Prog. Nat. Sci. 3 267
    [13] Zhang Z B, Gao T, Liu X Y, Li D W, Zhao J, Lei Y, Wang Y K 2018 Ultrason. Sonochem. 42 787 doi: 10.1016/j.ultsonch.2017.12.024
    [14] Moholkar V S 2009 Chem. Eng. Sci. 64 5255 doi: 10.1016/j.ces.2009.08.037
    [15] Ferkous H, Hamdaoui O, Pétrier C 2023 Ultrason. Sonochem. 99 106556 doi: 10.1016/j.ultsonch.2023.106556
    [16] Wong C Y, Raymond J L, Usadi L N, Zong Z, Walton S C, Sedgwick A C, Kwan J 2023 Ultrason. Sonochem. 99 106559 doi: 10.1016/j.ultsonch.2023.106559
    [17] Maghami S, Johansson Ö 2024 Ultrason. Sonochem. 103 106804 doi: 10.1016/j.ultsonch.2024.106804
    [18] Zhang X G, Hao C C, Ma C, Shen Z Z, Guo J Z, Sun R G 2019 Ultrason. Sonochem. 58 104691 doi: 10.1016/j.ultsonch.2019.104691
    [19] Madeleine J B, Zhang D K 2014 Ultrason. Sonochem. 21 485 doi: 10.1016/j.ultsonch.2013.09.011
    [20] Kojima Y, Asakura Y, Sugiyama G, Koda S 2010 Ultrason. Sonochem. 17 978 doi: 10.1016/j.ultsonch.2009.11.020
    [21] Liu J H, Shen Z Z, Lin S Y 2021 Phys. Rev. E 30 344 doi: 10.1088/1674-1056/abf4bb
    [22] 魏鑫鑫 2022 硕士学位论文 (西安: 陕西师范大学) Wei X X 2022 M. S. Thesis (Xi’an: Shaanxi Normal University
    [23] 王英瑞 2022 硕士学位论文 (西安: 陕西师范大学) Wang Y R 2018 M. S. Thesis (Xi’an: Shaanxi Normal University
    [24] Choi J K, Chahine G 2003 Comput. Mech. 32 281 doi: 10.1007/s00466-003-0485-5
    [25] 陈云良, 伍超, 叶茂, 李静 2005 水利学报 36 1269 doi: 10.3321/j.issn:0559-9350.2005.10.023 Chen Y L, Wu C, Ye M, Li J 2005 J. Hydraul. Eng. 36 1269 doi: 10.3321/j.issn:0559-9350.2005.10.023
    [26] Mih W C 2010 J. Hydraul. Res. 27 417
    [27] Hasan B O 2017 Chin. J. Chem. Eng. 25 698 doi: 10.1016/j.cjche.2017.03.008
    [28] Coolaloglou C, Tavlarides L 1977 Chem. Eng. Sci 32 1289 doi: 10.1016/0009-2509(77)85023-9
    [29] Hasan B O, Hamad M F, Majdi H S, Hathal M M 2021 Eur. J. Mech. B/Fluids 85 430 doi: 10.1016/j.euromechflu.2020.11.001
    [30] 陈志希, 谢明辉, 周国忠, 虞培清, 王抚华 2010 化学工程 38 38 Chen Z X, Xie M H, Zhou G Z, Yu P Q, Wang F H 2010 Chem. Eng. J. 38 38
    [31] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628 doi: 10.1121/1.384720
    [32] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 76 046309. doi: 10.1103/PhysRevE.76.046309
    [33] 刘金河, 沈壮志, 林书玉 2021 物理学报 70 224301 doi: 10.7498/aps.70.20211244 Liu J H, Shen Z Z, Lin S Y 2021 Acta Phys. Sin. 70 224301 doi: 10.7498/aps.70.20211244
    [34] Yusof N S M, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568 doi: 10.1016/j.ultsonch.2015.06.013
    [35] Song K, Liu Y J, Ahmad U, Ma H L, Wang H X 2024 Chemosphere 350 141024 doi: 10.1016/j.chemosphere.2023.141024
    [36] Lee D Y, Kang J, Son Y G 2023 Ultrason. Sonochem. 101 1350 doi: 10.1016/j.ultsonch.2023.106659
  • 加载中
图( 5) 表( 1)
计量
  • 文章访问数:  130
  • HTML全文浏览数:  130
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-30
  • 刊出日期:  2025-02-20

涡流场中气泡破碎对声空化效果的影响

    通讯作者: E-mail: szz6@163.com.; 
    作者简介: 邱春扬. E-mail: qcy6@snnu.edu.cn
  • 陕西师范大学物理学与信息技术学院, 陕西省超声学重点实验室, 西安　710119
  • 收稿日期:  2024-10-30

摘要: 液态涡流场不仅可以传质传热影响声场分布, 还可以影响流场中气泡的行为特性, 进一步影响声空化效果. 以三维漏斗形涡流场中气泡的动力学方程并结合气泡破碎理论为基础, 研究了涡流场(搅拌产生的流场)对气泡破碎概率及其气泡空化效果的影响. 结果表明, 随着转速的增大, 气泡的破碎概率显著提高, 同时气泡破碎临界半径逐渐减小, 从600 rad/min时的200 μm降至2000 rad/min时的55.5 μm, 这意味着在高速旋转的涡流场中, 气泡在尚未膨胀到应达到的最大空化半径时就提前发生破碎, 导致其失去空化效应, 从而降低超声降解效果. 实验结果进一步验证了声空化效果在适中转速(600—1000 rad/min)下最佳, 而过高转速则会抑制降解效果. 这些发现为声空化技术的优化提供了理论基础和实验支持.

English Abstract

    全文HTML

    1.   引　言

    • 随着工业化程度的不断深化, 工业水污染已经成为我们当前面临的严峻挑战之一. 据《2022—2028年我国污水处理行业市场行情动态及竞争战略分析报告》指出, 我国每年产生大量的工业废水, 排放总量甚至超过美国和印度[1]. 而这些废水中所含污染物种类繁多, 包括大量的重金属、有机物和无机盐等有害物质. 若这些有害物质未能得到有效处理, 将会对水质和土壤造成严重污染, 从而破坏生态系统的平衡, 给环境和人类健康带来极大威胁. 为了应对这一严峻挑战, 各个行业都在积极探索各种废水处理技术. 这些技术涵盖了物理、化学以及生物处理方法的多个领域[2]. 简而言之, 寻找高效、经济、绿色的废水处理方式对于保护环境、维护生态平衡以及保障人类健康至关重要.

      超声降解技术具备低能耗、无污染等特点, 且超声降解技术能将水体中有害有机物转变为CO2、H2O、无机离子或将它们转变为比原有机物毒性小的有机物[3], 因此超声波处理作为一种潜在替代方案, 被广泛应用于废水处理[4]、生物质处理[5]等领域, 以增强工业过程的效率, 特别是降解水中的有机污染物. 超声降解主要通过3条途径实现: 1)在超声过程中产生的空化气泡里热解, 借助理论计算可知气泡内的压力和温度在空化过程中上升到1000个大气压以上和5000 K以上[6,7]; 2)在超声处理过程中, 液体中的有机物受到超声波产生的⋅OH和⋅H自由基作用, 发生开环、断键、加成、取代和电子转移等化学反应, 这些反应最终将有机物降解为CO2和H2O, 从而实现污水的净化[8–10]; 3)被空化过程中形成的超临界态水氧化而降解[11].

      有研究发现, 在相同的声强输入下, 混响声场内的声化学产额比行波场高出6—10倍, 因此可知混响声场是提升超声降解效率的重要途径之一[12]. 为此, Zhang等[13]对不同定向组合超声声源下的声场进行了探究. 结果显示, 逆向平行源和底部源(LRY)能够实现声场的更均匀分布. 同时, 通过LRY声场激发, 声强相比单壁激发提高了约30倍, 可空化体积超过95%. Moholkar等[14]探究了双频声化学反应器中两个超声源之间的频率比和相位差, 以优化处理器中产生的声场, 结果表明当耦合频率的压缩阶段与基频引发的气泡瞬态坍塌相吻合时, 可以产生更多的自由基. Ferkous等[15]通过在声化学反应器顶部添加圆锥形反射器, 利用其声散射特性打乱驻波场, 成功提高了三碘化物声分解形成率. 此外, 一些学者尝试通过改变换能器的辐射方式来改善声场效果. 例如, Wong等[16]设计了一种换能器, 能够产生180°的超声波, 并在局部区域形成高声压振幅(15 MPa), 进而实现自发成核空化. Maghami和Johansson[17]设计了一种六方环形激励结构, 由六个换能器对称排布, 为流通式超声波反应器提供了更均匀的声压分布, 并降低了耦合损耗.

      近年来, 一些学者开始尝试采用超声辐射与机械搅拌相结合的方式来处理水溶液中的有机污染物. 通过机械搅拌产生的涡声散射和传质效应, 可以实现声场的均匀分布, 从而提高超声降解的效率, 这种操作简便的改进方法引起了许多学者的关注, 为废水处理技术的进一步改善应用提供了新思路. Zhang等[18]研究了不同反应容器、溶液初始浓度、搅拌速度和超声频率等不同因素对水溶液中罗丹明B降解率的影响, 研究发现最佳实验条件为: 搅拌速度为700 rad/min, 初始浓度为10 mg/L, 超声频率为40 kHz. 在该条件下, 罗丹明B的最佳降解率可在1 h内达到98%. Madeleine和Zhang[19]探讨了在超声化学反应器中不同频率、不同功率下的搅拌对声化学活性的影响. 通过碘化物剂量法测量的过氧化氢产量和声化学发光成像来确定声化学活性, 研究发现, 低频反应器中的搅拌能够改善氢过氧化物的产量, 而在高频下却无法观察到相同的效果. Kojima等[20]利用激光片技术和激光多普勒测速仪对490 kHz下的矩形声化学反应器进行了可视化和流动分布测量, 研究发现引入搅拌器后液体流动受到干扰, 但声化学效率约提高了两倍. 研究结果表明液体流动模式和引入搅拌器对声化学效率有显著影响. 刘金河等[21]通过对40 kHz频率下声场分布的分析, 并结合有限元方法的模拟, 确认了搅拌可以改善驻波声场, 进而提高了超声降解效率. 研究还发现随着搅拌速度的增大, 降解速率先增大, 达到600 rad/min时降解效率最高. 然而, 继续增大转速并没有进一步提高处理效率. 这一实验结果与Madeleine和Zhang[19]在40 kHz频率下的研究一致, 即在900 rad/min时达到最佳降解效率. 尽管频率相同, 但由于搅拌头类型、搅拌器放置位置不同, 导致最佳降解效率所对应的转速不同, 这表明搅拌条件对超声降解效率的影响存在一定的差异. 目前对该实验现象的解释仅停留在定性的分析上, 并未有研究针对该现象进行详细的理论分析.

      一些学者通过研究涡流现象对超声降解效果的影响, 探讨了涡流场的涡声散射效应及其对声场的调节作用. 魏鑫鑫[22]提出了基于小马赫数、不可压缩、无黏条件下的涡流场声散射理论, 利用仿真模拟分析了Hill球涡和涡环的声压分布, 结果表明涡流场能够有效均匀化声场分布, 从而提升声化学反应器中的降解速率. 王英瑞[23]则采用时域有限差分法模拟了声波在涡流场中的传播特性, 研究发现通过增加同向旋转的涡流并使其垂直于入射波排列, 可以显著改善声场分布, 进而增强声化学反应的效率. 此外, 研究者还关注涡流场对气泡行为的影响, 尤其是气泡的涡空化效应. Choi和Chahine[24]通过二维和三维数值模型, 深入分析了涡流气蚀气泡的生长、振荡和塌缩过程, 发现气泡的振荡周期、幅度及最终半径对涡流特性及压力变化高度敏感, 且气泡的形态和体积振荡与涡流的时间尺度密切相关. 这些研究为进一步优化超声降解过程提供了理论依据.

      声场中的涡流场不仅起到传质效果, 同时对声空化也产生不利的因素. 本文将三维涡流场(搅拌产生的涡流场)中的气泡空化理论与气泡破碎理论相结合, 研究转速对气泡破碎的影响, 以及气泡破碎对声空化效果的影响. 确定涡流场与声空化之间的耦合关系, 使涡流场不仅可以传质, 更重要的是不对声空化效应产生负面影响, 这一研究将为未来优化超声在水净化工程中应用提供理论指导依据.

    2.   数学模型与数值方法

      2.1.   涡流场的数学模型

    • 虽然Choi和Chahine[24]使用二维Lamb涡模型来描述螺旋浆产生的涡流场, 并将其引入Rayleigh-Plesset方程中进行推导, 然而这一模型仅适用于二维情况, 与实际三维涡流场存在一定差异. 因此, 为了研究涡流场声空化处理效果, 以更符合搅拌索形成的立轴水涡流场为模型, 并借鉴文献[25]的改进理论, 得到了柱坐标系下涡流场内的速度方程:

      这里, v为黏性系数, 涡环常量Γ = 2.8πDc0Ma, 马赫数Ma = 2πrN/60c0, c0为声速, N为搅拌器转速. 立轴水涡流的水面线(水气交界面)轨迹方程为

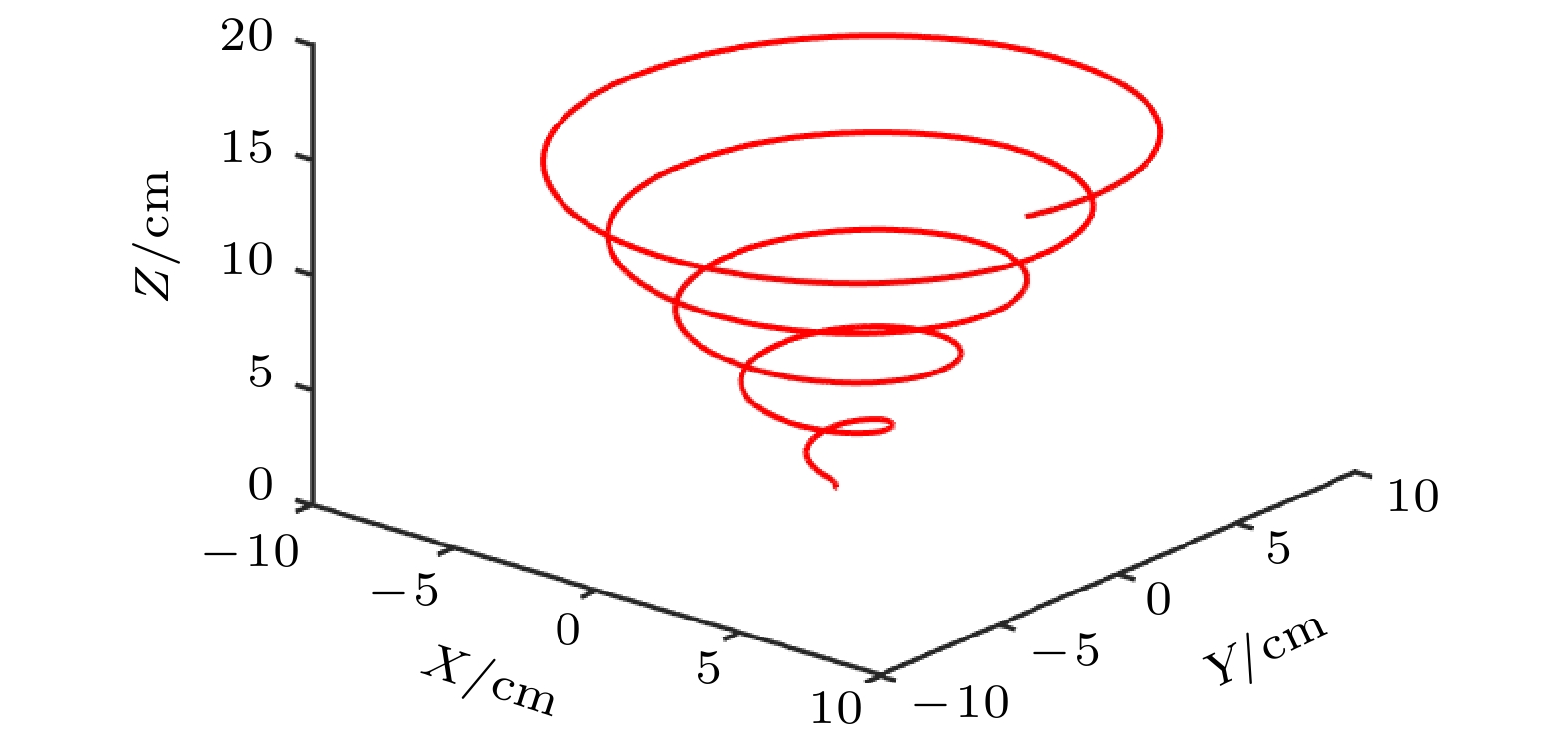
      其中$ r $为气泡到涡中心的距离, $ z $为气泡所在高度, $ h $为液面高度, 与实验对应取值为0.12 m, $ {r_{\text{m}}} $为涡核半径, 根据文献[26]的结论$ {r_{\text{m}}} = 0.5 D $, D为最大切向速度所对应的直径, 由文献[21]所展示的速度截面图可知, 搅拌器边缘处即为最大切向速度位置, 因此确定涡核半径为0.02 m. $ \bar r $为无量纲半径, $ \bar r = r/{r_{\text{m}}} $; $ \bar z $为无量纲水深, $ \bar z = z/h $; e为自然数.

      基于上述涡流场内速度分布方程, 得到涡流场内一质点的运动轨迹, 如图1所示, 这一轨迹可以描述整个三维涡流模型的特征.

      • 2.2.   涡流场中气泡破碎理论

    • Hasan[27]研究表明涡流场中气泡破碎主要分为以下4个机制: 1)湍流波动和碰撞; 2) 层流剪切应力; 3) 叶轮叶片的剪切力; 4) 颗粒与叶片碰撞造成的断裂. Coolaloglou和Tavlarides[28]基于气泡周围液体的湍流动能超过特定阈值而导致气泡破碎的现象, 提出的气泡破碎模型为

      式中$ {t_{\text{b}}} $为气泡破碎时间, $ {{\Delta N\left( d \right)} {/ } {N\left( d \right)}} $为气泡破碎概率, 其中$ {c_1} $, $ {c_2} $为比例系数, 基于单液滴实验的拟合[29]取值分别为0.543和0.091, $ d $是气泡直径, $ \sigma $是气液表面张力系数, $ \varepsilon $为湍流动能耗散率, 搅拌对气泡破碎的影响即体现在湍流动能耗散率上, 即用单位质量液体的搅拌功率来表征湍流动能的耗散[29]:

      其中Np为搅拌准数, 可通过对应文献[30]中雷诺数与搅拌准数曲线获得, 此处选择二叶平桨模型, 取值为1.9, $ N $为转速, $ D $为搅拌器直径此处取4.2 cm, $ V $为搅拌液体体积, 此处取0.0086 m3 (与实验保持一致).

      • 2.3.   涡流场中气泡空化模型

    • 通过能量守恒得出涡流场中的伯努利方程:

      式中, ${P_{{\text{vortex}}}}$为涡流场中任一点处涡流的压力值.

      将气泡在涡流场中所受到的压力代入气泡动力学方程[31,32]中, 可得涡流场中单个气泡的动力学方程:

      这里, ${P_{\text{s}}}$是$(R, \dot R, t)$函数:

      其中P0为环境大气压, Pv是泡内蒸气压, $\sigma $是表面张力, μ是黏滞系数, c是声速, ρ是液体密度, $\kappa $是泡内气体的多方指数, R0是气泡初始半径, R是任意时刻泡的运动半径, PA为辐射声压幅值, f为声波频率.

      采用龙格-库塔法模拟群内气泡的运动特性. 初始条件t = 0时, R = R0, ρ = 103 kg/m3, σ = 0.0725 N/m, μ = 0.001 Pa⋅s, P0 = 105 Pa, c = 1500 m/s, γ = 4/3, f = 40 kHz, PA = 1.2×105 Pa.

    3.   结果与讨论

      3.1.   涡流场中转速对气泡破碎概率的影响

    • 液态流场中声空化效果本身就受到很多因素的影响, 而复杂的涡流场会导致溶解于其中微气泡产生破碎, 为了探究微气泡破碎可能对声空化效果的影响, 这里研究了不同初始半径下, 涡流特性(以搅拌为例)对气泡破碎的影响.

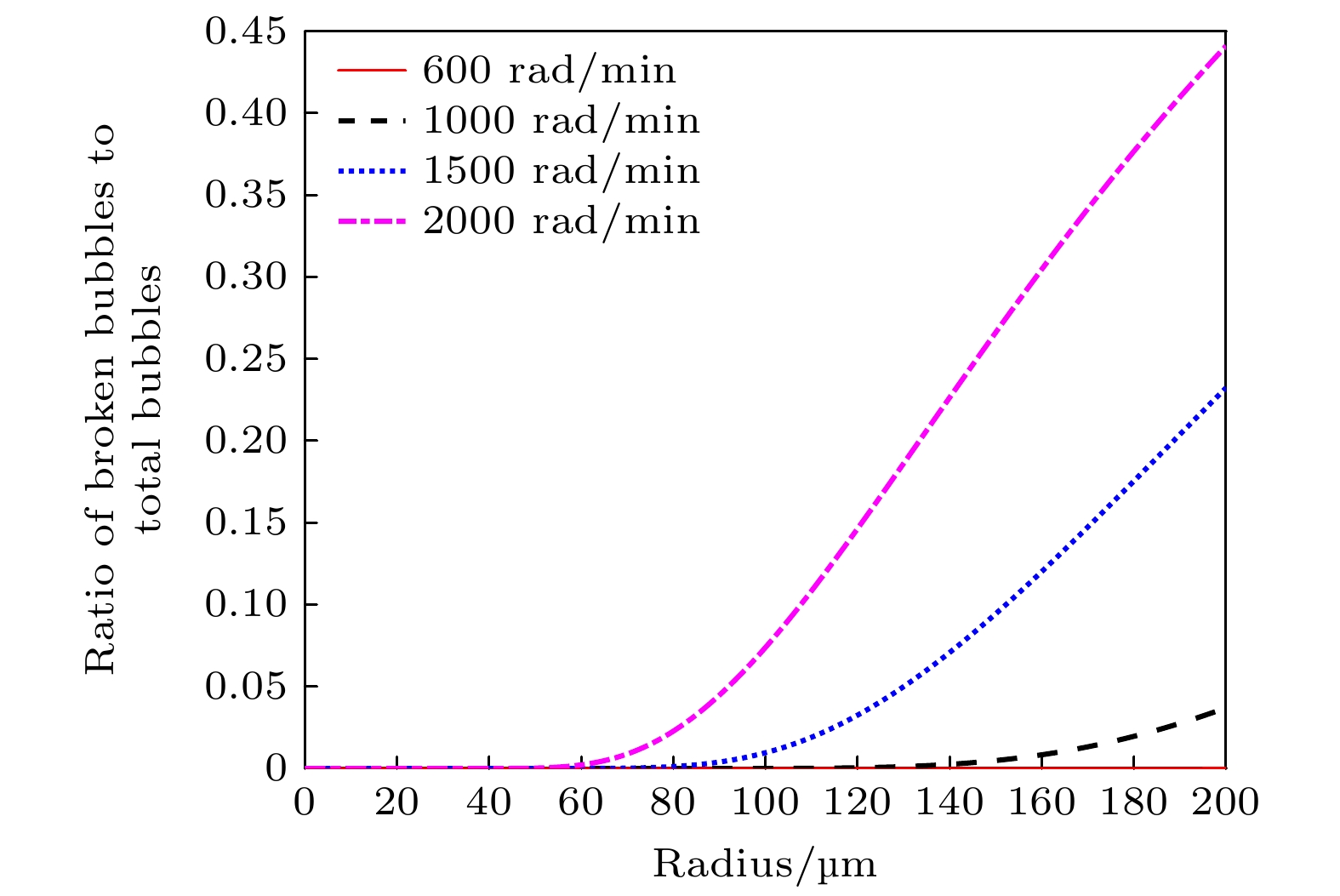
      实际液体中, 气泡以气泡群的形式溶解于其中的, 因而初始气泡大小不一. 图2为初始半径为200 μm以下的气泡, 在不同的转速下气泡破碎的概率是不同的. 当转速为600 rad/min时, 气泡发生破碎的概率很小, 几乎没有发生破碎现象; 当转速为1000 rad/min, 气泡破碎的概率也很小. 从图2可知, 初始半径约小于122.5 μm气泡, 不会发生破碎, 而初始半径约大于122.5 μm的气泡将会发生破碎, 该转速下气泡破碎半径的临界值约为122.5 μm; 当转速为1500 rad/min时, 初始半径约小于78.0 μm的气泡, 不会发生破碎, 大于78.0 μm的气泡, 将会发生破碎, 所以气泡破碎半径的临界值约78.0 μm; 当转速为2000 rad/min时, 初始半径约小于55.5 μm, 不会发生破碎, 约大于55.5 μm时, 会发生破碎现象, 因此该参数下, 破碎半径的临界值约55.5 μm. 另外从图2可知, 初始半径为200 μm的气泡在转速为600 rad/min时, 破碎概率约为0.01%; 当转速为1000 rad/min时, 气泡破碎概率大约只有0.17%; 当转速为1500 rad/min时, 破碎概率约高达23%; 而当转速为2000 rad/min时, 气泡的破碎概率高达44%; 结果表明, 转速越大, 气泡破碎的概率也越大, 大气泡更容易发生破碎, 且气泡半径越大, 破碎概率也越大.

      • 3.2.   转速对大气泡破碎概率的影响

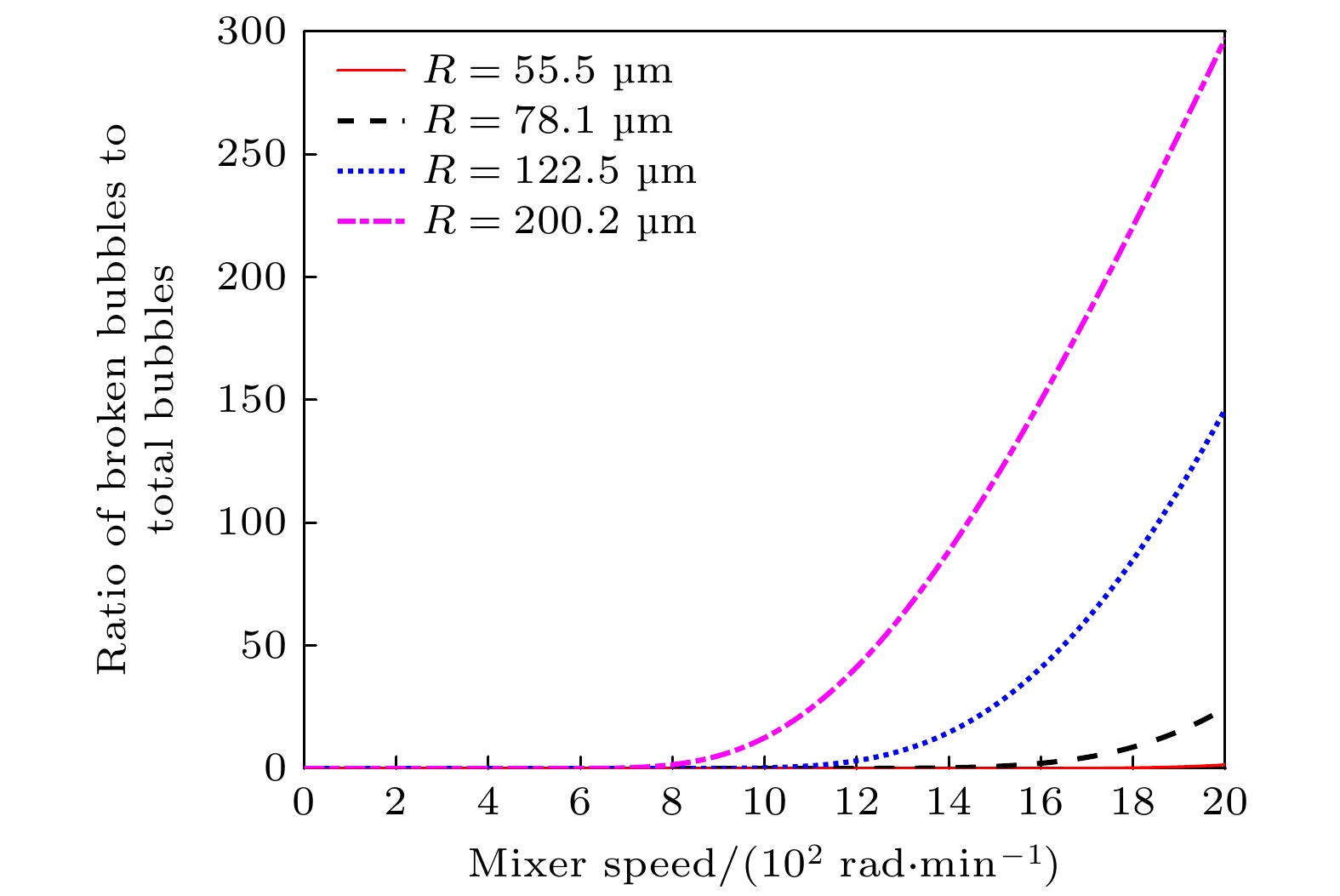
    • 图3为转速对大气泡破碎程度的影响. 这里所谓的大气泡是指在不同转速下约处于临界破碎状态的气泡, 以临界破碎气泡作为初始半径, 研究转速对这类气泡的破碎程度的影响. 由于气泡群内的气泡半径大小不一, 在声场作用下, 微气泡可能会膨胀到处于临界破碎状态, 并在搅拌状态下可能会影响着声空化的处理效果. 从图3可知, 初始半径55.5 μm时, 在转速高达2000 rad/min下, 破碎气泡只占据0.09%; 当气泡初始半径为78.0 μm, 在转速在2000 rad/min下, 破碎的气泡也只占据1.9%; 当气泡初始半径为122.5 μm时, 在转速为2000 rad/min下, 破碎的气泡已占据液体中总气泡数量的15.6%; 当气泡初始半径为200 μm时, 在同样的转速2000 rad/min下, 破碎的气泡已约占据液体中总气泡的44.0%. 图4结果表明, 大气泡容易破碎, 且随着转速越大, 气泡破碎的程度也越高.

      • 3.3.   涡流场中声空化泡的破碎特性

    • 能产生声空化效应的气泡叫空化泡, 而声空化效果不仅取决于声空化泡的崩溃程度也取决于能发生强烈崩溃的空化泡数量, 而涡流场的存在既可以提高液体的传质效果, 也对声空化效果产生一定负面影响, 即阻碍声空化的有效发生, 因此研究涡流场中声空化泡特性具有重要的意义.

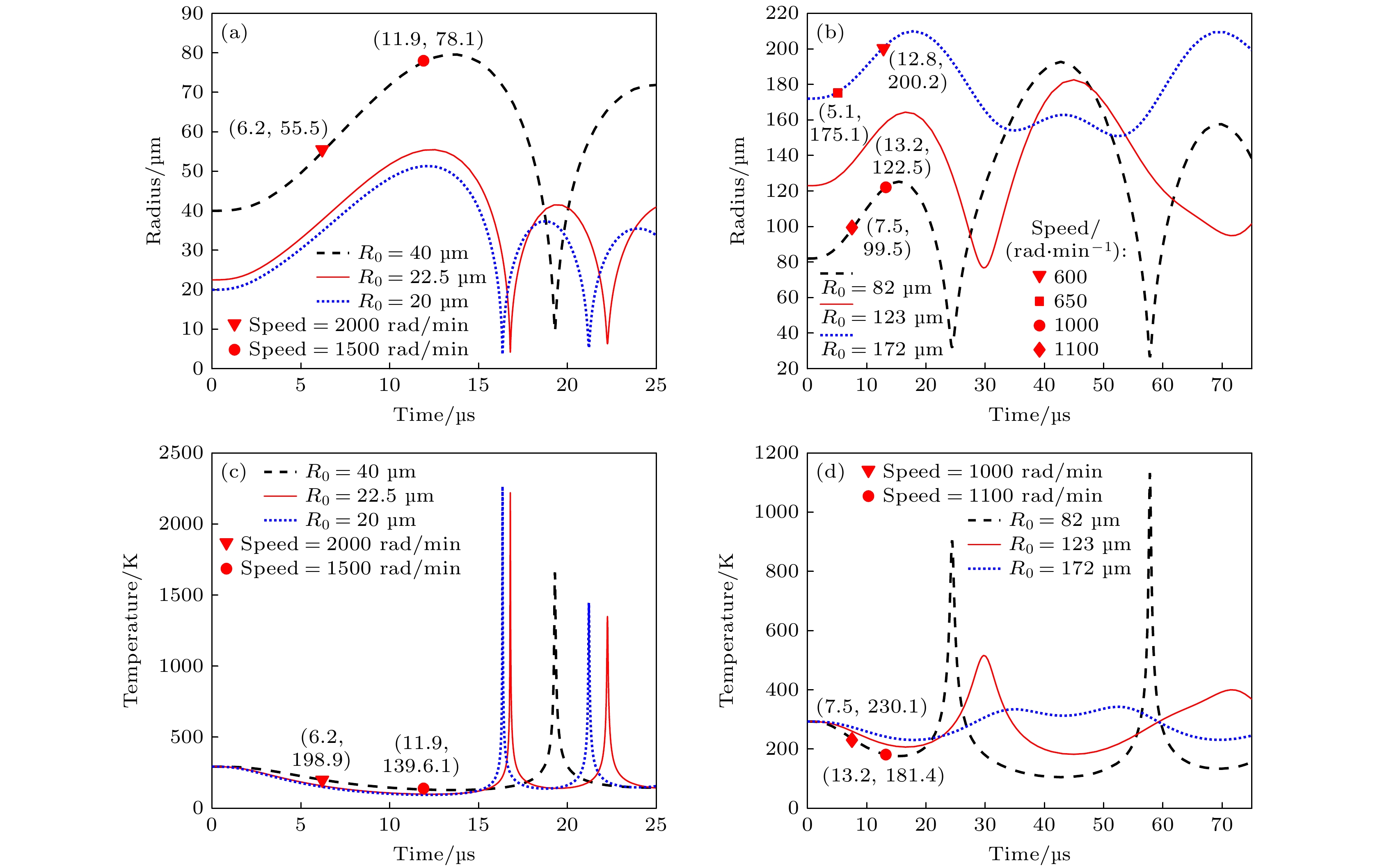
      图4是涡流场中声空化泡的破碎特性. 图4(a)表明频率为40 kHz的声场条件下, 初始半径为22.5 μm的气泡在16.78 μs时刻, 膨胀到最大半径为55.5 μm. 研究发现半径为55.5 μm的气泡在转速为2000 rad/min的涡流场中刚好发生破碎, 而在低于2000 rad/min转速的涡流场中, 55.5 μm的气泡是不会发生破碎, 因此在转速低于为2000 rad/min的涡流场中, 初始半径为22.5 μm的气泡, 在声场作用下不会发生破碎现象, 这样的气泡能发生有效的空化效应. 图4(a)也显示气泡初始半径低于22.5 μm时, 在转速低于2000 rad/min的涡流场中, 空化泡不会发生破碎现象, 这有利于声空化发生. 而初始半径高于22.5 μm的气泡, 涡流场的存在有可能发生破碎, 影响声空化的发生. 图4(a)中初始半径为40 μm的气泡, 没有涡流场时, 该气泡完全可以发生声空化, 但涡流场的存在可能会导致气泡提前破碎而不发生空化, 如在转速为2000 rad/min的涡流场中, 声空化泡, 膨胀到约6.2 μs发生破碎, 在转速为1500 rad/min的涡流场中, 声空化泡, 膨胀到约11.9 μs发生破碎, 也就是说在这两种情况下, 气泡都没有膨胀到最大值就直接破碎了, 声空化无法发生, 这样的气泡就失去了空化效应. 从图中发现, 转速越大, 气泡破碎的时间越早, 在转速低于1500 rad/min的涡流场中, 该气泡不会发生破碎现象, 有利于声空化的发生. 这种情况下气泡崩溃时, 泡内的温度特性如图4(c)所示, 在低于2000 rad/min转速的涡流场中, 初始半径小于22.5 μm的气泡, 崩溃时泡内的温度约达2217.3 K (对应初始半径22.5 μm的气泡)及2264.3 K (对应初始半径20 μm的气泡). 就40 μm的初始半径的气泡来说, 如果没有高于1500 rad/min转速的涡流场, 在声场作用下, 它完全可以发生崩溃, 且崩溃时泡内温度约为1659.6 K, 这样的高温也足以产生空化效应, 但如果存在转速高于1500 rad/min的涡流场, 则将失去产生声空化效果. 图4(b)显示, 初始半径为82 μm的气泡, 在转速为1100 rad/min的涡流场中, 声空化泡, 膨胀到约7.5 μs发生破碎, 而在转速为1000 rad/min的涡流场中, 声空化泡, 膨胀到约13.2 μs发生破碎. 同样在这两种涡流场中, 声空化无法发生, 只有在转速低于1000 rad/min的涡流场中, 声空化泡不会发生破碎, 声空化效果如期发生. 而初始半径为123 μm的气泡在转速低于1000 rad/min的涡流场, 气泡不会发生破碎, 而初始半径为172 μm气泡, 在转速为650 rad/min和600 rad/min的涡流场中, 气泡容易发生破碎, 且这两种气泡在40 kHz的声场中不易发生空化现象. 这种情况下气泡的崩溃特性如图4(d)所示, 在转速低于1000 rad/min的涡流场中, 初始半径过大的气泡, 就算不易破碎, 崩溃时泡内的温度过低, 产生的空化效果也非常不明显. 由此可见, 在转速低于1000 rad/min的涡流场中, 初始半径约高于123 μm的气泡, 不易发生声空化现象, 只有初始半径低于123 μm的气泡才能发生声空化现象, 由于空化泡是以空化群形式出现的, 这类空化泡不仅种类多而且数量也大, 有利于提高空化效果. 根据文献[27]的研究, 气泡在液涡流场中受到剪切应力的作用, 它在气泡周围产生速度差从而导致气泡变形与破碎. 若气泡只有一小部分位于尾流区域内, 则尾流边界上的剪切应力可能使气泡拉伸, 最终导致气泡破碎; 湍流的特征是存在高速旋转的流体微元组成的高动能涡流. 当涡流与气泡产生相互作用时其结果不仅取决于相互作用的强度, 还受到相互作用时间的影响, 在涡流的产生到消失过程中这种相互作用都一直存在从而导致气泡拉伸与形变. 搅拌桨叶片能够在气泡未发生形变或刚开始形变时直接将其击碎. 空化过程中的气泡同样会受到上述因素的影响, 使得其膨胀到临界半径时达到气泡破碎的条件而发生破碎.

      值得注意的是, 气泡破碎仅仅是高转速导致降解效率降低的原因之一, 其他原因还涉及超声场中的空化阈值、空化屏蔽、过饱和空化、掺气减蚀、还有时空尺度等问题, 将会在后续研究继续进行探究. 因此要产生很好的声空化效果, 需要适当的涡流场和适合范围的初始半径.

      表1列出了不同转速下对应的气泡破碎半径. 气泡破碎半径是指气泡达到该半径时, 破碎的概率不再为0. 如图3所示, 在转速为1000 rad/min的曲线中, 当横坐标表示的半径达到122.1 μm时, 曲线开始上升, 破碎概率也不再为0. 采用相同的绘图方法, 分别绘制了500—2000 rad/min转速条件下的初始半径与破碎概率的关系图, 通过确定破碎概率不再为0时的对应坐标得到了表1中的气泡破碎半径数据. 由表1可知, 当转速为2000 rad/min时, 溶解于水中半径为55.5 μm的气泡会发生破碎, 同样在转速为2000 rad/min的涡流场中, 声空化泡膨胀到约55.5 μm, 可能还没有膨胀到最大值就发生破碎现象. 而声空化效果是大量空化泡产生空化效应的累积结果. 原本有更多的微气泡在声场的作用下产生空化效应, 却因在高速旋转的涡流场中, 致使气泡在膨胀的过程中发生破碎, 失去空化效应, 造成整体上空化效果降低, 所以强涡流场不利于声空化发生.

      • 3.4.   气泡破碎理论与实验结果的验证

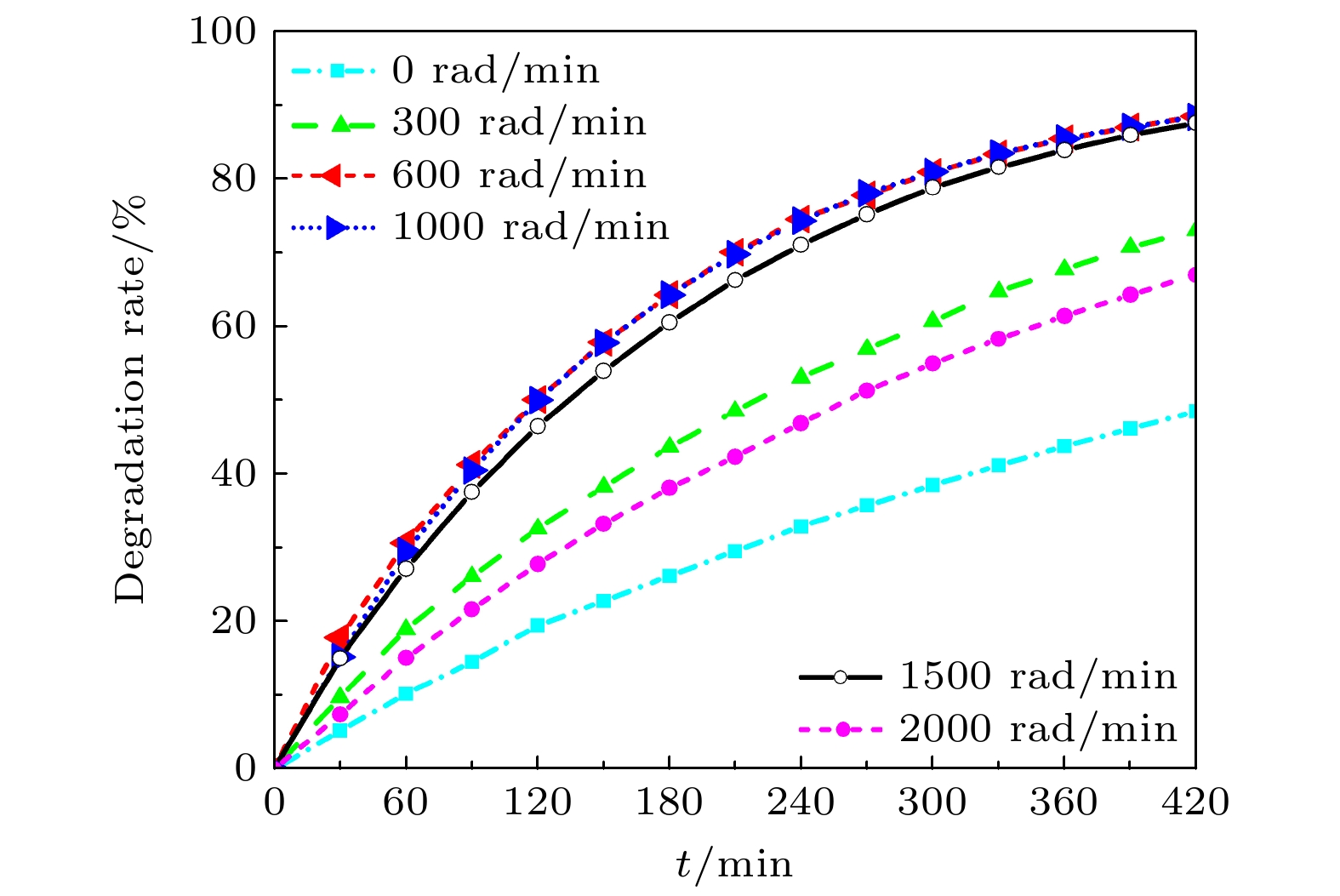
    • 为了验证涡流场对声空化效果的影响, 设计了超声协同机械搅拌来测量亚甲基蓝溶液的降解率的实验(用去离子水配成10 mg/L的亚甲基蓝水溶液). 诚如文献[33–35]所说, 搅拌作用在物理上一方面改变了清洗槽内的声场分布, 使得声场分布变得均匀, 从而扩大了空化效应的区域, 另一方面搅拌也增强了传质效果, 同时该文发现, 过高的转速反而不利于声空化的发生, 最佳的转速应在600—1000 rad/min之间. 图5的研究结果就是这种情况的体现. 这也可以从气泡的破碎机理上来阐述这样的实验结果, 如表1所示, 随着转速的提高, 气泡破碎半径越小, 这样一来, 声场作用下的气泡还没有来得及膨胀到最大值就发生了破碎现象, 从而导致声空化效应无法发生, 所以过高的转速不利于产生声空化效果, 这与文献[33]的研究结果一致. 另外, 随着转速越高, 中间的涡旋使液面下降, 轴线处出现低压区, 通常会卷吸气体进入水中, 在紊动流体的作用下卷吸的气泡破碎产生了掺气效应, 减弱了空化泡的溃灭强度, 进而也减弱了降解效果; 同时, 溶解在液体中的气泡在涡流作用下会向涡流中心聚集, 在聚集的过程中, 气泡会膨胀, 膨胀的气泡可能会破碎, 就算不破碎, 聚集的气泡也会影响声能的传递[36], 导致空化效果降低, 进而也降低了有机物的降解效果.

      综上所述, 涡流场的引入使影响声空化效果的因素变得更加复杂. 涡流场是否有利于声空化效应, 不仅要考虑声场分布和传质因素, 还要考虑气体的掺入, 以及气泡的聚集、破碎等因素, 只有综合考虑多方面的因素, 才能拓展声空化的工程应用.

    4.   结　论

    • 基于涡流场(搅拌产生的流场)中气泡空化理论以及气泡破碎理论, 对声空化引起亚甲基蓝溶液降解实验结果进行了理论分析. 研究表明, 随着搅拌器转速的增大, 涡流场对气泡施加的压力增大, 导致气泡的溃灭压强和溃灭温度提升, 从而增强了空化效果和超声降解效率. 然而, 一旦转速达到临界值, 气泡可能在达到最大半径前就发生破碎, 从而降低超声降解效率. 气泡的半径越大, 气泡的破碎概率会随之增大. 并且随着转速的增大, 气泡的破碎临界半径呈现减小趋势, 这意味着高转速下气泡发生破碎的概率增大, 从而导致声空化效果降低, 不利于空化对污染物的降解. 研究表明, 初始半径小于22.5 μm的气泡, 在转速低于2000 rad/min的涡流场中, 声空化泡不易发生提前破碎的现象, 有利于声空化对污染物的降解. 总之涡流场的存在不仅要考虑它的传质传热效果, 还要考虑气泡破碎所带来的不利声空化因素, 只有综合考虑各方面的影响, 才能为未来拓宽声空化在工程中广泛应用提供理论依据和改进指导.

    参考文献 (36)

目录

/

返回文章
返回