高级搜索

基于巨磁阻抗效应的双模态型低噪声大量程磁传感器

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

温涛, 马宇航, 王德全, 谌浩然, 李艳芳, 许洋, 王志广. 基于巨磁阻抗效应的双模态型低噪声大量程磁传感器[J]. 物理学报, 2025, 74(3): 038501-1. doi: 10.7498/aps.74.20241498
引用本文: 温涛, 马宇航, 王德全, 谌浩然, 李艳芳, 许洋, 王志广. 基于巨磁阻抗效应的双模态型低噪声大量程磁传感器[J]. 物理学报, 2025, 74(3): 038501-1. doi: 10.7498/aps.74.20241498
shu
Tao WEN, Yuhang MA, Dequan WANG, Haoran CHEN, Yanfang LI, Yang XU, Zhiguang WANG. Dual-mode low noise large range magnetic sensor based on giant magnetoimpedance effect[J]. Acta Physica Sinica, 2025, 74(3): 038501-1. doi: 10.7498/aps.74.20241498
Citation: Tao WEN, Yuhang MA, Dequan WANG, Haoran CHEN, Yanfang LI, Yang XU, Zhiguang WANG. Dual-mode low noise large range magnetic sensor based on giant magnetoimpedance effect[J]. Acta Physica Sinica, 2025, 74(3): 038501-1. doi: 10.7498/aps.74.20241498
shu

基于巨磁阻抗效应的双模态型低噪声大量程磁传感器

  • 1.

    北方自动控制技术研究所, 太原　030006

  • 2.

    西安交通大学电子科学与工程学院, 西安　710049

  • 3.

    武汉长盈通光电技术股份有限公司, 武汉　430071

  • 4.

    杭州电子科技大学通信工程学院, 杭州　310000

    • 作者简介: 温 涛: 844300915@qq.com .
    通讯作者: E-mail: zgwang18@xjtu.edu.cn.

  • 中图分类号: 85.70.Ay, 84.37.+q, 84.30.-r, 06.30.Ft

Dual-mode low noise large range magnetic sensor based on giant magnetoimpedance effect

  • 1.

    North Automatic Control Technology Institute, Taiyuan 030006, China

  • 2.

    School of Electronic Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China

  • 3.

    Yangtze Optical Electronic Co., Ltd., Wuhan 430071, China

  • 4.

    School of Communication Engineering, Hangzhou Dianzi University, Hangzhou 310000, China

    • Corresponding author: E-mail: zgwang18@xjtu.edu.cn.

  • MSC: 85.70.Ay, 84.37.+q, 84.30.-r, 06.30.Ft

  • 摘要: 磁传感器在导航、交通运输、机器人、自动化、医疗设备等领域有着广泛的应用, 对传感器的性能要求越来越高. 本文提出了一种具有两种工作模式的磁传感器, 兼具大量程和低噪声两种优点. 该传感器由一个640 μH磁芯绕线电感与一个100 pF电容串联构成. 传感器工作于阻抗模式时, 具有噪声低的优点, 当传感器驱动信号频率为1 MHz, 偏置磁场为7.66 Oe (1 Oe = 103/(4π) A/m)时, 传感器等效磁噪声水平最小, 约为200 $ {\text{pT/}}\sqrt {{\text{Hz}}} @1 \;{\text{Hz}} $, 线性范围为2 Oe; 工作于频率模式时, 具有量程大的优点, 量程可以达到25 Oe, 当偏置磁场为7.66 Oe时, 传感器灵敏度最大, 约为47 kHz/Oe. 该传感器与多种型号的商用磁传感器相比, 其低噪声、大量程、低成本的优点依然具有显著的市场竞争力.
    Abstract: Magnetic sensors are widely used in the fields of navigation, transportation, robotics, automation, and medical equipment, and the performance requirements of sensors are getting higher and higher. In this work, a bimodal magnetic sensor with two operating modes, which has the advantages of large range and low noise, is proposed. The sensor consists of a 640 μH core-wound inductor in series with a 100 pF capacitor. When the external magnetic field changes, the magnetization state of the iron core in the inductor will change, the inductance value will change accordingly. The resonant frequency and impedance value of the sensor will also change with the magnetic field. In this work, the giant magnetic impedance characteristics of an RLC series circuit are analyzed, and the relationship between magnetic permeability, inductance value, and external magnetic field is established, and the series resonant frequency of the circuit is simulated to calculate the characteristics of the circuit with respect to the inductance variation. Then, two testing systems are set up to test the relationship between resonance frequency and magnetic field, as well as the noise characteristics of the sensor. In the impedance mode, the effects of capacitance, drive signal frequency, and static bias magnetic field on the sensor noise floor are first analyzed to determine the optimal parameters of the sensor. When the series capacitance of the sensor is 100 pF, the drive signal frequency will be 1 MHz and the static bias magnetic field will be 7.66 Oe. The sensor has the optimal performance with an equivalent noise floor of about $ {200}\;{\text{pT/}}\sqrt {{\text{Hz}}} @1 \;{\text{Hz}} $, an impedance rate of change sensitivity of 160.6%/Oe, and a linear range of about 2 Oe. In the frequency mode, the sensor operates linearly up to 25 Oe. A logistic regression model is used to fit the resonant frequency to the magnetic field variation, and the fitted value reaches 0.9974. When the static bias magnetic field is about 7.66 Oe, the sensor sensitivity will be about 47 kHz/Oe. Moreover, compared with other common types of magnetic sensors on the market, this sensor has the commercial component cost of only ¥10, and excellent performance, and huge market potential.
  • 加载中

  • 图 1  电感与电容串联后的等效电路模型

    Figure 1.  Equivalent circuit model of inductor and capacitor in series.

    下载: 全尺寸图片 幻灯片

    图 2  等效电路串联谐振仿真　(a) RLC串联等效电路模型仿真结果; (a) 串联谐振频率随电感的变化

    Figure 2.  Equivalent circuit series resonance simulation: (a) Simulation results obtained by RLC series equivalent circuit model; (b) variation of series resonance frequency with inductance.

    下载: 全尺寸图片 幻灯片

    图 3  电感元件特征　(a) 电感实物图; (b) 电感值随磁场的变化

    Figure 3.  Inductor characteristic: (a) Physical drawings of inductors; (b) variation of inductance value with magnetic field.

    下载: 全尺寸图片 幻灯片

    图 4  谐振频率-磁场传感器测试平台

    Figure 4.  Resonant frequency-magnetic field sensor test platform.

    下载: 全尺寸图片 幻灯片

    图 5  阻抗-磁场传感器测试平台

    Figure 5.  Impedance-magnetic field sensor test platform.

    下载: 全尺寸图片 幻灯片

    图 6  不同条件下的最小等效磁噪声与激励信号频率关系　(a) 电容为91 pF; (b) 电容为100 pF; (c) 电容为110 pF; (d) 电容为120 pF

    Figure 6.  Relationship between minimum equivalent magnetic noise and frequency of excitation signal under different conditions: (a) The capacitance is 91 pF; (b) the capacitance is 100 pF; (c) the capacitance is 110 pF; (d) the capacitance is 120 pF.

    下载: 全尺寸图片 幻灯片

    图 7  GMI传感器特性　(a)不同频率激励信号时GMI传感器的阻抗随磁场的变化; (b) 不同频率激励信号时GMI传感器阻抗变化率随磁场的变化; (c) 不同频率激励信号时GMI传感器阻抗变化率灵敏度随磁场的变化; (d) 在施加3 nT和300 pT的微弱磁信号时GMI传感器的等效磁噪声幅度谱; (e) 传感器阻抗随外加磁场的变化以及线性拟合曲线; (f) 施加1 Hz正弦交流磁信号时传感器的阻抗变化量随磁场强度的变化

    Figure 7.  GMI sensor characteristics: (a) The impedance of GMI sensor vs. magnetic field for different frequency excitation signals; (b) the impedance variation of GMI sensor vs. magnetic field for different frequency excitation signals; (c) impedance change rate sensitivity of GMI sensor vs. magnetic field for different frequency excitation signals; (d) the equivalent magnetic noise amplitude spectrum of the GMI sensor when a weak magnetic signal of 3 nT or 300 pT is applied; (e) sensor impedance vs. applied magnetic field and corresponding linear fitting curve; (f) sensor impedance variation vs. magnetic field intensity when 1 Hz sinusoidal AC magnetic signal is applied.

    下载: 全尺寸图片 幻灯片

    图 8  磁传感器谐振频率随磁场强度的变化及拟合曲线

    Figure 8.  Resonance frequency of magnetic sensor vs. magnetic field intensity curve and corresponding fitting curve.

    下载: 全尺寸图片 幻灯片

    图 9  谐振频率-磁场数值拟合曲线及灵敏度曲线

    Figure 9.  Resonance frequency vs. magnetic field fitting curve and sensitivity curve.

    下载: 全尺寸图片 幻灯片

    表 1  最小等效磁噪声及其对应参数

    Table 1.  Minimum equivalent magnetic noise and its corresponding parameters.

    电容值/pF最小等效磁
    噪声/nT    		激励信号
    频率/MHz    		偏置磁场/Oe
    910.550.87.66
    1000.4917.66
    1100.7515.9
    1200.5917.66
    下载: 导出CSV

    表 2  双模态磁传感器与商用磁传感器对比

    Table 2.  Comparison of dual-mode magnetic sensor and commercial magnetic sensor.

    类型 型号 厂家 本底噪声/
    (nT@1 Hz)    		 量程/
    ±Oe    		 灵敏度 截止频率 价格
    ￥
    AMR MMC5983MA 美新半导体 40 8 — 1 kHz ~34
    AMR HMC1001 霍尼韦尔 0.5 5 3.2 mV/(V·Oe) 5 MHz ~100
    GMR AA002 NVE 2 15 36 mV/(V·Oe) 1 MHz ~150
    TMR TMR2901 多维 2 8 25 mV/(V·Oe) — ~350
    TMR TLI5590-A6W 英飞凌 — 50 1.85 mV/(V·Oe) 5 kHz ~20
    TMR CT815X Allegro — 80 5 mV/(V·Oe) 100 Hz ~10
    Microfluxgate DRV425 德州仪器 4 20 1.22 mA/Oe 32 kHz ~30
    Fluxgate Mag651 Bartington ~0.02 0.6 5 V/Oe 5 Hz >35000
    Hall DRV5055
    A1/Z1    		 德州仪器 130 210 10 mV/Oe 20 kHz ~10
    GMI MI-CB-1DJ Aichi ~0.1 0.02 500 V/Oe 10 kHz ~10000
    GMI GC-CC-101A 国创智能 ~0.06 0.6 — 2 kHz ~5000
    LC串联磁传感器 阻抗模式 — ~0.2 6—8 Oe 160.6%/Oe — ~10
    频率模式 — — 5—30 Oe 47 kHz/Oe(max) — ~10
    下载: 导出CSV
  • [1] Auster H U, Glassmeier K H, Magnes W, Aydogar O, Baumjohann W, Constantinescu D, Fischer D, Fornacon K H, Georgescu E, Harvey P, Hillenmaier O, Kroth R, Ludlam M, Narita Y, Nakamura R, Okrafka K, Plaschke F, Richter I, Schwarzl H, Stoll B, Valavanoglou A, Wiedemann M 2008 Space Sci. Rev. 141 235 doi: 10.1007/s11214-008-9365-9
    [2] Du A M, Zhang Y, Li H Y, Qiao D H, Yi Z, Zhang T L, Meng L F, Ge Y S, Luo H, Zhao L, Sun S Q, Ou J M, Li Z, Feng X, Dai J L 2020 Space Sci. Rev. 216 135 doi: 10.1007/s11214-020-00766-8
    [3] Fimbombaya H S, Mvungi N H, Hamisi N Y, Iddi H U 2018 Modell. Simul. Eng. 2018 2591304 doi: 10.1155/2018/2591304
    [4] Kim H J, Hirayama H, Kim S, Han K J, Zhang R, Choi J W 2017 IEEE Access 5 21264 doi: 10.1109/ACCESS.2017.2757267
    [5] Kuwahata A, Tanaka R, Matsuda S, Amada E, Irino T, Mayanagi S, Chikaki S, Saito I, Tanabe N, Kawakubo H, Takeuchi H, Kitagawa Y, Kusakabe M, Sekino M 2020 Sci. Rep. 10 1798 doi: 10.1038/s41598-020-58530-5
    [6] Limes M E, Foley E L, Kornack T W, Caliga S, McBride S, Braun A, Lee W, Lucivero V G, Romalis M V 2020 Phys. Rev. Appl. 14 011002 doi: 10.1103/PhysRevApplied.14.011002
    [7] Liu X Y, Liu C H, Han W, Pong P W T 2019 IEEE Sens. J. 19 1683 doi: 10.1109/JSEN.2018.2883708
    [8] Wang S X, Peng D L, Wu Z Y 2019 IEEE Sens. J. 19 9818 doi: 10.1109/JSEN.2019.2928336
    [9] Sekino M, Kuwahata A, Ookubo T, Shiozawa M, Ohashi K, Kaneko M, Saito I, Inoue Y, Ohsaki H, Takei H, Kusakabe M 2018 Sci. Rep. 8 1195 doi: 10.1038/s41598-018-19480-1
    [10] Tsukada K, Hayashi M, Nakamura Y, Sakai K, Kiwa T 2018 IEEE Trans. Magn. 54 6202205 doi: 10.1109/TMAG.2018.2845864
    [11] Ennen I, Kappe D, Rempel T, Glenske C, Hütten A 2016 Sensors 16 904 doi: 10.3390/s16060904
    [12] 韩秀峰, 张雨, 丰家峰, 陈川, 邓辉, 黄辉, 郭经红, 梁云, 司文荣, 江安烽, 魏红祥 2022 物理学报 71 238502 doi: 10.7498/aps.71.20221278 Han X F, Zhang Y, Feng J F, Chen C A, Deng H, Huang H, Guo J H, Liang Y, Si W R, Jiang A F, Wei H X 2022 Acta Phys. Sin. 71 238502 doi: 10.7498/aps.71.20221278
    [13] Han X F, Zhang Y, Wang Y Z, Huang L, Ma Q L, Liu H F, Wan C H, Feng J F, Yin L, Yu G Q, Yu T, Yan Y 2021 Chin. Phys. Lett. 38 128501 doi: 10.1088/0256-307X/38/12/128501
    [14] Khan M A, Sun J, Li B D, Przybysz A, Kosel J 2021 Eng. Res. Express 3 022005 doi: 10.1088/2631-8695/ac0838
    [15] Lenz J, Edelstein A S 2006 IEEE Sens. J. 6 631 doi: 10.1109/JSEN.2006.874493
    [16] Narod B B, Miles D M 2024 Geosci. Instrum. Methods Data Syst. 13 131 doi: 10.5194/gi-13-131-2024
    [17] Wang Z G, Wen T, Su W, Hu C J, Chen Y C, Hu Z Q, Wu J G, Zhou Z Y, Liu M 2021 IEEE Trans. Ind. Electron. 68 7577 doi: 10.1109/TIE.2020.3007097
    [18] Panina L V, Mohri K 1994 Appl. Phys. Lett. 65 1189 doi: 10.1063/1.112104
    [19] Phan M H, Peng H X 2008 Prog. Mater Sci. 53 323 doi: 10.1016/j.pmatsci.2007.05.003
    [20] Kurlyandskaya G V, Sánchez M L, Hernando B, Prida V M, Gorria P, Tejedor M 2003 Appl. Phys. Lett. 82 3053 doi: 10.1063/1.1571957
    [21] Panina L V, Mohri K, Bushida K, Noda M 1994 J. Appl. Phys. 76 6198 doi: 10.1063/1.358310
    [22] Wen T, Wang Z G, Du Q, Su W, Guan M M, Zhao, S S, Wu J, Hu Z Q, Zhou Z Y, Liu M 2022 Adv. Mater. Technol. 7 2100919 doi: 10.1002/admt.202100919
    [23] Vazquez M, Knobel M, Sanchez M L, Valenzuela R, Zhukov A P 1997 Sens. Actuator A Phys. 59 20 doi: 10.1016/S0924-4247(97)80143-4
    [24] Butta M, Yamashita S, Sasada I 2011 IEEE Trans. Magn. 47 3748 doi: 10.1109/TMAG.2011.2152379
    [25] Malatek M, Dufay B, Saez S, Dolabdjian C 2013 Sens. Actuator A Phys. 204 20 doi: 10.1016/j.sna.2013.10.001
    [26] Malátek M, Kraus L 2010 Sens. Actuator A Phys. 164 41 doi: 10.1016/j.sna.2010.09.011
    [27] Dufay B, Saez S, Dolabdjian C P, Yelon A, Ménard D 2013 IEEE Sens. J. 13 379 doi: 10.1109/JSEN.2012.2216521
    [28] Ding L H, Saez S, Dolabdjian C, Melo L G C, Yelon A, Ménard D 2009 IEEE Sens. J. 9 159 doi: 10.1109/JSEN.2008.2011067
    [29] Dufay B, Saez S, Dolabdjian C, Yelon A, Ménard D 2013 IEEE Trans. Magn. 49 85 doi: 10.1109/TMAG.2012.2219579
    [30] Dufay B, Saez S, Dolabdjian C P, Yelon A, Ménard D 2011 IEEE Sens. J. 11 1317 doi: 10.1109/JSEN.2010.2084996
    [31] Melo L G C, Ménard D, Yelon A, Ding L, Saez S, Dolabdjian C 2008 J. Appl. Phys. 103 033903 doi: 10.1063/1.2837106
    [32] Traoré P S, Asfour A, Yonnet J P, Dolabdjian C P 2017 IEEE Sens. J. 17 6175 doi: 10.1109/JSEN.2017.2739480
    [33] Traore P S, Asfour A, Yonnet J P 2021 Sens. Actuator A Phys. 331 112972 doi: 10.1016/j.sna.2021.112972
    [34] Jin F, Wang J C, Zhu L, Mo W Q, Dong K F, Song J L 2019 IEEE Sens. J. 19 9172 doi: 10.1109/JSEN.2019.2925738
    [35] Fernández E, García-Arribas A, Barandiarán J M, Svalov A V, Kurlyandskaya G V, Dolabdjian C P 2015 IEEE Sens. J. 15 6707 doi: 10.1109/JSEN.2015.2463254
    [36] Kim J Y, Cho I K, Lee H J, Lee J, Moon J I, Kim S M, Kim S W, Ahn S, Kim K 2020 IEEE Access 8 193091 doi: 10.1109/ACCESS.2020.3032702
  • 加载中
图( 9) 表( 2)
计量
  • 文章访问数:  134
  • HTML全文浏览数:  134
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-25
  • 刊出日期:  2025-02-05

基于巨磁阻抗效应的双模态型低噪声大量程磁传感器

    通讯作者: E-mail: zgwang18@xjtu.edu.cn.
    作者简介: 温 涛: 844300915@qq.com
  • 1. 北方自动控制技术研究所, 太原　030006
  • 2. 西安交通大学电子科学与工程学院, 西安　710049
  • 3. 武汉长盈通光电技术股份有限公司, 武汉　430071
  • 4. 杭州电子科技大学通信工程学院, 杭州　310000
  • 收稿日期:  2024-10-25

摘要: 磁传感器在导航、交通运输、机器人、自动化、医疗设备等领域有着广泛的应用, 对传感器的性能要求越来越高. 本文提出了一种具有两种工作模式的磁传感器, 兼具大量程和低噪声两种优点. 该传感器由一个640 μH磁芯绕线电感与一个100 pF电容串联构成. 传感器工作于阻抗模式时, 具有噪声低的优点, 当传感器驱动信号频率为1 MHz, 偏置磁场为7.66 Oe (1 Oe = 103/(4π) A/m)时, 传感器等效磁噪声水平最小, 约为200 $ {\text{pT/}}\sqrt {{\text{Hz}}} @1 \;{\text{Hz}} $, 线性范围为2 Oe; 工作于频率模式时, 具有量程大的优点, 量程可以达到25 Oe, 当偏置磁场为7.66 Oe时, 传感器灵敏度最大, 约为47 kHz/Oe. 该传感器与多种型号的商用磁传感器相比, 其低噪声、大量程、低成本的优点依然具有显著的市场竞争力.

English Abstract

    全文HTML

    1.   引　言

    • 随着科学和技术的进步, 对于磁传感器的研究越来越深入, 性能不断提升, 应用范围越来越广, 在军事、工程、消费电子等方面具有不可替代的作用, 在地磁探测、空间探测、无损检测、交通运输、无线通讯、医疗设备、工业智能、物联网等诸多领域具有广泛应用[1–10]. 随着技术的不断进步和市场规模的持续增长, 对磁传感器的性能提出了越来越高的要求, 其中灵敏度、噪声水平、量程是关键指标. 高灵敏度的特点可以实现对磁场的更高精度检测; 低噪声特性能够确保磁传感器在微弱磁场环境下获取准确的信号; 大量程的特点可以提高传感器抗强磁场干扰的能力. 目前市场上最常用的磁传感器元件, 如霍尔(Hall)传感器, 其量程通常较大, 可以达到几百奥斯特(Oe), 但是其本底噪声较大; 磁阻传感器的灵敏度高, 噪声水平更低, 但是其基本处于nT量级[11–15]. 此外, 磁通门传感器的噪声水平只有几十pT, 甚至可以到10 pT[16], 但是它的量程有限, 仅有几Oe.

      如果可以将低噪声和大量程两种重要特性集成到一种传感器中, 既可以满足微弱磁场探测的需要, 也可以满足大磁场信号探测的需求, 而且有效地扩展了传感器的使用场景, 降低使用成本. 在文献[17]中, 我们研究了磁芯绕线电感元件的巨磁阻抗特性, 验证了磁芯电感元件的LC谐振特性与磁阻抗特性之间的关系[17]. 在之前研究的基础上, 本文提出了一种基于巨磁阻抗(GMI)效应的双模态磁传感器, 通过工作模式的改变, 使得该传感器兼具了大量程和低噪声的优点, 可以满足不同工况下对传感器性能的要求. 该传感器由一个商用电感元件串联电容后构成, 当改变外部磁场时, 电感中磁芯材料的磁导率发生变化, 导致电感元件的电感值发生改变, 使得电感与电容的谐振状态发生变化, 串联谐振频率随之改变, 进一步引起传感器的阻抗值变化. 当传感器工作在阻抗模式时, 传感器的阻抗值随外加磁场变化, 传感器具有本底噪声低的特点, 传感器的等效磁噪声水平约为200 $ {\text{pT/}}\sqrt {{\text{Hz}}} @1~{\text{Hz}} $; 传感器工作在频率模式时, 传感器的谐振频率随外加磁场变化, 传感器具有量程大的优点, 量程可以达到25 Oe.

    2.   传感器设计与原理

    • 巨磁阻抗效应是指, 当铁磁导体被施加一定频率的交流信号后, 其交流复阻抗Z会随外部磁场Hex的变化而变化. 在恒流交流电流信号激励下, 非晶丝两端的电压值随直流磁场的变化发生相应的变化, 在1994年, Panina和Mohri[18]首次提出了巨磁阻抗效应这一概念. 典型的GMI传感器的灵敏度可以达到500%/Oe, 比巨磁阻(GMR)传感器的灵敏度高两个数量级以上[19]. 由于GMI传感器具有高灵敏度、低噪声的特点, 基于GMI效应的磁传感器也得到了研究者的广泛研究[20–23].

      传统的GMI传感器通常采用非对角驱动方式, 敏感单元主要由软磁材料制成的磁芯和缠绕在磁芯材料外部的铜线圈组成, 其物理结构与传统磁芯绕线电感元件一致. 在之前研究的基础上, 本文继续研究商用电感的GMI特性, 针对GMI传感器的噪声、灵敏度、量程等特性展开研究.

      当电感元件与电容串联构成LC串联电路后, 其等效电路模型如图1所示, RLC串联电路的总阻抗可以由(1)式表示:

      当RLC电路发生串联谐振时, 阻抗中的电抗分量应该等于0, 即(1)式中虚数部分等于0, 同时可以计算得到电路串联谐振频率为

      RLC电路串联谐振时, 电路能量在电路内部的电场和磁场之间进行交换, 此时电路的阻抗最小, 等于电阻的值. 电路的谐振频率由发生谐振的电容、电感决定, 电路的阻抗值由驱动信号频率、电容、电感共同决定. 因此, 当LC串联电路的电容和驱动信号频率确定时, 只有电感的变化会引起谐振频率和阻抗的变化. 由于电感元件选用的是磁芯绕线电感, 外部磁场会改变电感中磁芯的磁导率, 从而导致电感值发生变化, 进而影响串联电路的谐振状态, 引起谐振频率和阻抗改变. 由此可知, LC串联电路的谐振频率、电感磁芯的磁导率、电感值、外部磁场之间的关系为

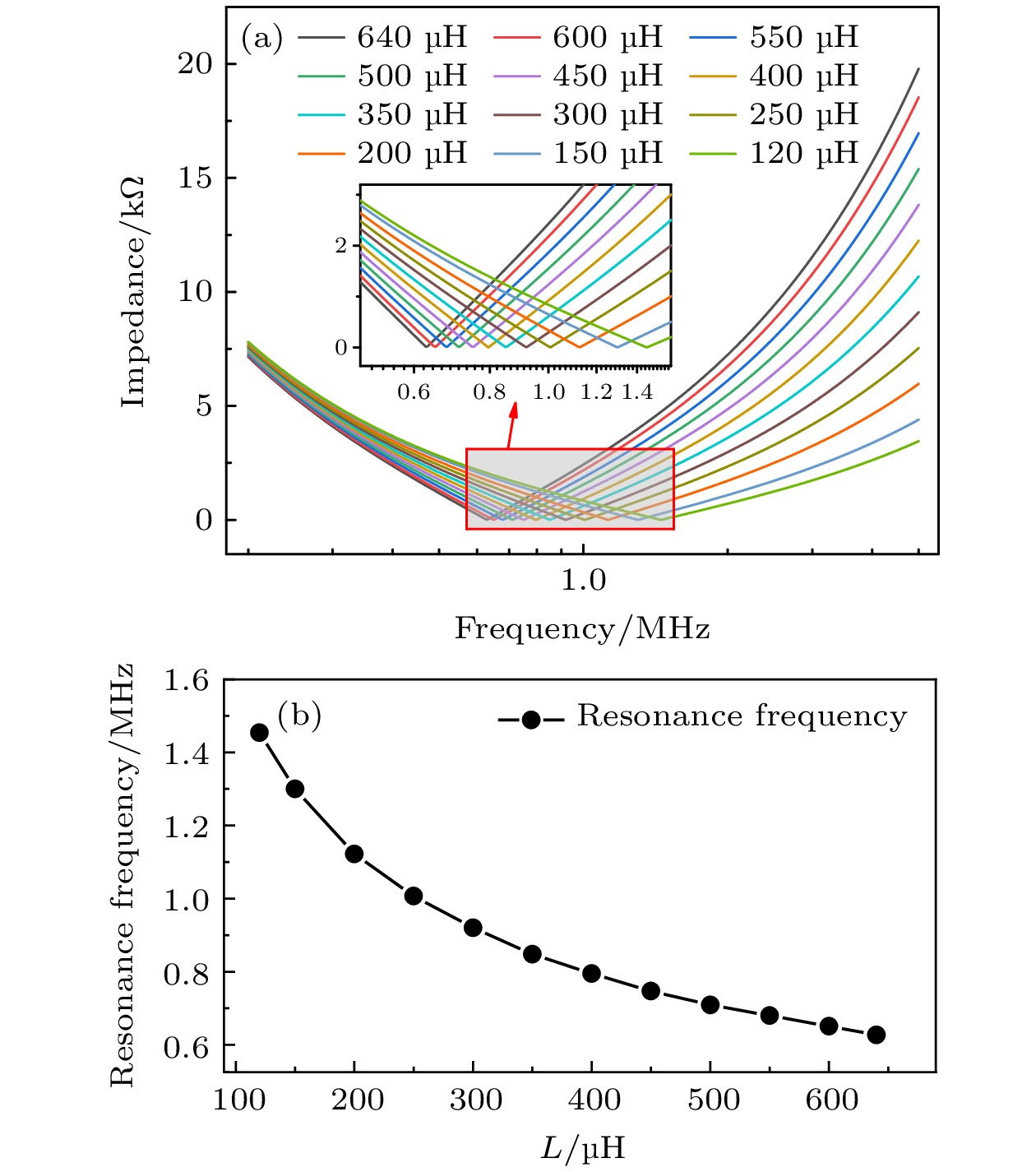
      进一步使用Multisim仿真软件对RLC电路模型进行仿真分析, 以电感值的变化等效模拟外部磁场的变化, 仿真结果如图2所示. 图中模拟了当电感值为120—640 μH时, RLC等效电路的阻抗值与信号频率之间的关系. 从图2可以看出, RLC电路的串联谐振频率处的阻抗值等于电阻的阻抗, 而且随着电感值的减小, 串联谐振频率逐渐增大; 如果固定某一信号频率, 可以看到随着电感值的变化, RLC串联电路的阻抗值呈现单向的变化趋势.

      通过以上分析可知, 当外部磁场发生变化时, LC串联电路的谐振频率和固定驱动信号频率下的阻抗值都会发生改变. 因此串联合适的电感、电容构成的LC串联磁传感器具有两种工作模式: 1)阻抗模式, 通过阻抗的变化来测量磁场强度变化; 2)频率模式, 通过谐振频率的变化来测量磁场强度变化.

    3.   实验方法

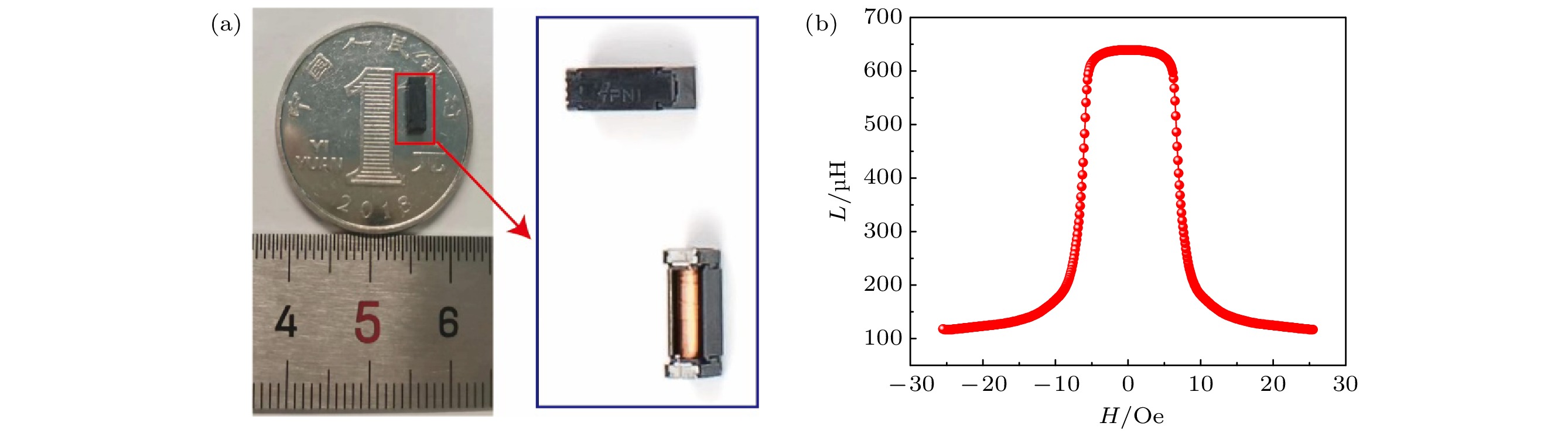
    • 根据前文的分析, 选用PNI公司生产的640 μH电感元件, 如图3(a)所示, 该电感元件长度约为10 mm, 侧面为2 mm×2 mm的矩形封装, 使用软磁非晶薄带作为磁芯材料, 将该电感与一个电容串联后构成一个LC串联式磁传感器. 图3(b)所示为该电感元件的电感值随磁场的变化. 当磁场强度小于5 Oe时, 电感磁芯材料的磁化曲线在线性区域, 磁导率基本不变. 当磁场强度大于5 Oe后, 磁芯材料的磁化强度开始逐渐趋于饱和, 磁导率变化开始进入非线性区域内. 随着磁场的增大, 磁芯材料的磁导率逐渐减小, 在5—10 Oe范围内, 磁导率变化较快, 所以电感值随磁场迅速减小; 随着磁场强度继续增大, 磁导率继续减小, 而且变化趋势减缓, 所以电感值变化趋势变缓, 逐渐趋近于饱和.

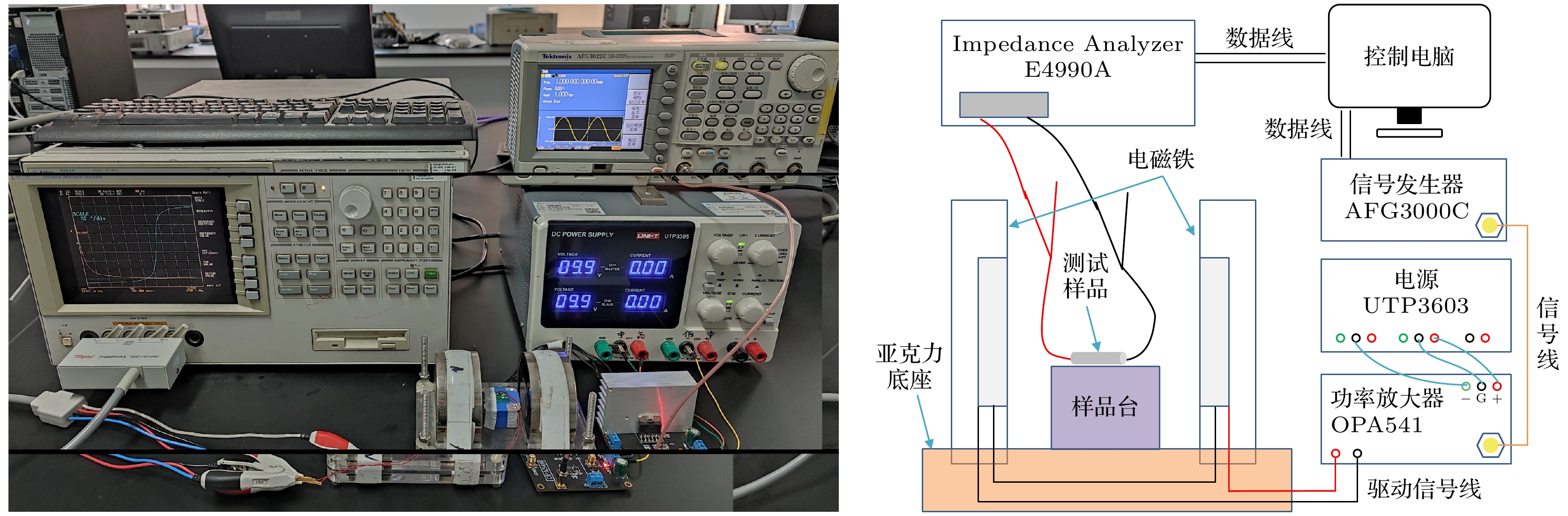
      为了进一步研究传感器的谐振频率-阻抗-磁场等几种参数之间的关系, 搭建了两组测试系统, 即如图4所示系统, 用于测试传感器的阻抗值-磁场-激励信号频率之间的关系; 如图5所示系统, 用于测试传感器的本底噪声特性.

      图4所示的测试系统硬件平台, 采用功率放大器驱动一对小型电磁铁, 可以产生最大约300 Oe的磁场; 使用AFG3000 C任意函数发生器产生特定波形的信号, 经过功率放大器后驱动电磁铁, 可以产生具有相同波形变化趋势的磁场信号; 待测GMI传感器样品放置于平台上, 使用E4990A阻抗分析仪测试传感器的阻抗随频率或者外部磁场的变化. 在该测试系统中没有使用高斯计来实时监测电磁铁产生的磁场强度, 是因为电感中有软磁磁芯, 当磁芯被磁化后, 产生的磁感应强度与外加的磁场强度相比通常会大得多, 导致高斯计探头在样品附近测得的磁场强度并不是电磁铁产生的磁场强度. 为了知道电磁铁产生的磁场强度的具体大小, 在测试系统不放置样品的情况下, 利用Lakeshore425高斯计对测试系统中预定放置样品的位置处的磁场强度与信号发生器输出电压之间的关系进行了标定, 可知电压信号与磁场关系:

      该测试系统使用LabVIEW软件设计了自动化测试控制程序. 通过数据线将电脑与阻抗分析仪和信号发生器连接, 在测试控制软件中设置测试参数: 激励信号频率、外加磁场强度、外加磁场频率、电压与磁场转换参数等. 在自动化测试软件控制下, 可以测试阻抗随磁场变化的数据, 阻抗随激励信号频率变化的数据.

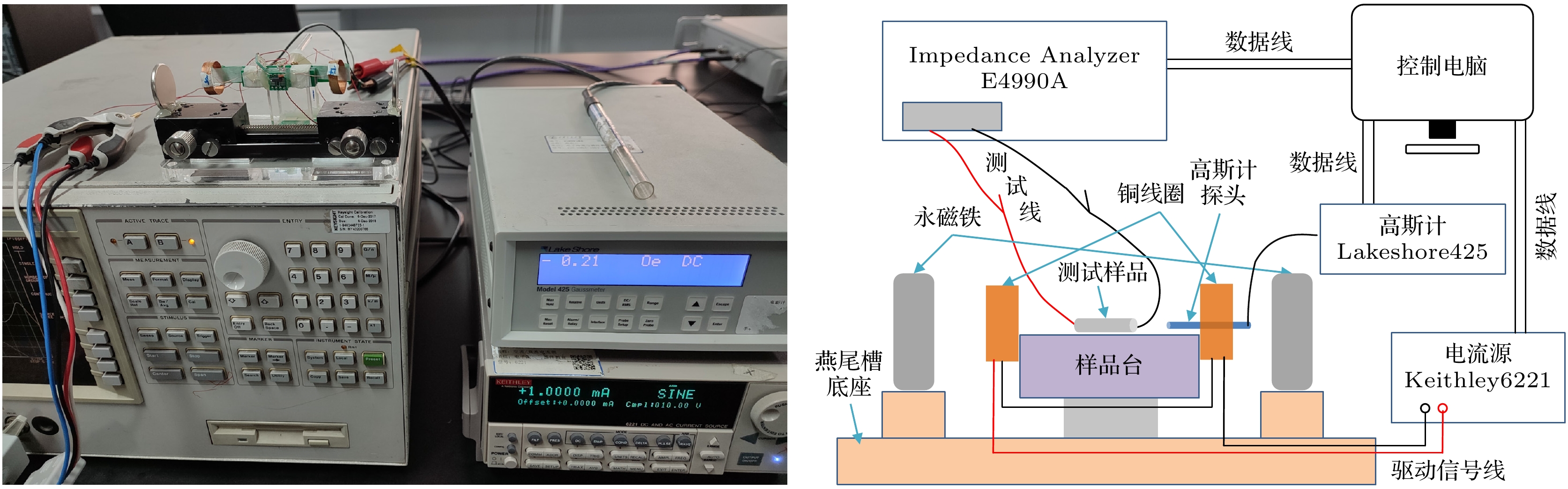
      在测试传感器本底噪声的实验中, 需要对传感器施加直流偏置和微弱的交流磁场小信号. 图4所示的测试系统, 使用电磁铁产生磁场, 由于信号发生器和功率放大模块自身性能的限制, 无法同时输出直流磁场和交流磁场小信号. 所以需要开发新的微弱磁场探测性能测试平台, 如图5所示. 微弱磁场探测性能测试平台使用一对固定于滑动燕尾槽上的永磁铁提供直流偏置磁场, 使用 Lakeshore425高斯计测试中心位置磁场强度. 在中间位置设置一对空心铜线圈构成一组亥姆霍兹线圈, 亥姆霍兹线圈在 Keithley6221电流源驱动下产生微弱的交流磁场. 在测试前对亥姆霍兹线圈感应磁场能力进行了标定: 7.5 Oe/A = 0.75 nT/μA.

      图5测试系统同样使用LabVIEW软件设计了自动化测试控制软件. 使用数据线将电脑与阻抗分析仪和电流源相连, 在电脑端的测试控制软件中设置测试参数: 激励信号频率、激励线圈电流频率和幅值. 在控制软件中, 加入了快速傅里叶变换(FFT)计算子程序, 通过对采集的传感器的阻抗值数据进行FFT分析, 观测数据的频域特性, 可以观测到在时域数据中由于噪声干扰无法直接观测的特征信号幅值.

    4.   结果与分析

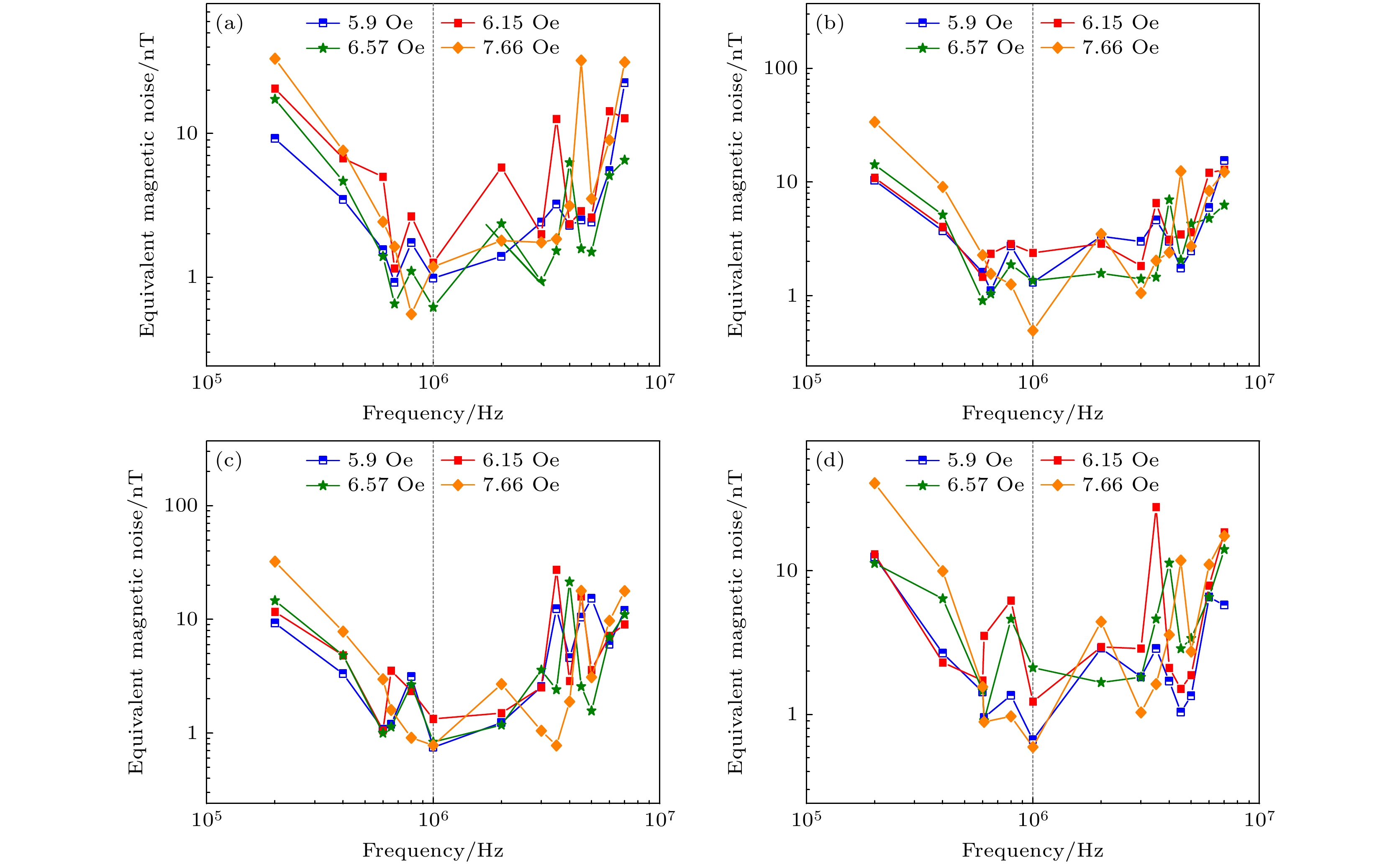
    • 当LC串联磁传感器工作在阻抗模式时, 串联的电容会改变谐振频率和阻抗, 从而影响磁传感器的传感性能. 不仅如此, GMI传感器的噪声主要来源于磁畴的磁化波动、本征热噪声造成的磁化热涨落、激励信号的幅值和相位波动、外部磁噪声等, 而且激励信号频率和偏置磁场的变化会引起传感器灵敏度的显著变化, 会进一步导致等效磁噪声的变化. 所以选择合适的串联电容在传感器设计中是十分重要的. 图6(a)—(d)所示结果表明, 在串联不同大小的电容时, 不同频率的激励信号驱动下所表现出的等效磁噪声并没有随着偏置磁场的增大发生明显的单调变化, 反而呈现出对激励信号频率的较强依赖性. 在激励信号频率低于800 kHz时, 随着偏置磁场强度增大, 等效磁噪声随之增大. 当激励信号频率为1 MHz时, 在不同偏置磁场和不同电容值时都表现出很低的磁噪声特性, 出现这一现象的主要原因与磁芯材料的本征磁化特性相关. 不同类型或不同长度与直径的非晶材料作为GMI传感器时, 传感器出现最小噪声时的激励信号频率从几百kHz到几十MHz不等, 彼此之间呈现明显的差异, 导致这一差异的原因主要有材料的磁导率、磁畴分布等因素[24–27]. 此外, 对于GMI传感器来说, GMI传感器的噪声主要来源于磁畴的磁化波动、本征热噪声造成的磁化热涨落、外部磁噪声等[27–31]. 在GMI传感器的实际测试中, 除了GMI传感器本征磁噪声外, 信号源噪声和测试系统噪声是主要的噪声来源[32,33]. 此外, GMI传感器的静态工作点即偏置磁场对于传感器的噪声特性也有较大的影响[34]. GMI传感器的这一噪声特征与图6中的测试结果相一致, 即激励信号频率和静态偏置磁场与GMI传感器的等效磁噪声具有强相关性. 当激励信号频率大于3 MHz时, 等效磁噪声开始呈现散点分布状态, 其对激励信号频率、电容值、偏置磁场的依赖性变得模糊.

      特别说明, 传感器的等效磁噪声由输出的阻抗噪声除以传感器的转换比(即传感器的阻抗-磁场灵敏度)换算得到[35,36].

      根据图6(a)—(d)所示结果, 将其中的最小等效磁噪声及其对应激励参数列入表1中. 在串联不同大小的电容时, 传感器能测到的最小等效磁噪声基本集中于0.6 nT附近, 而且对应的激励信号频率主要集中于1 MHz. 说明了电容值对于激励信号频率的选择影响相对较小. 当等效磁噪声最小时, 偏置磁场强度主要集中于7.66 Oe. 在串联电容为110 pF条件下, 在偏置磁场强度为5.9 Oe时, 等效磁噪声最小为0.75 nT. 但是从图6(a)可以看出, 在1 MHz频率时对应的等效磁噪声基本集中于0.8 nT左右, 仅在偏置磁场强度为6.15 Oe时, 等效磁噪声增大到1.3 nT, 相比于0.8 nT, 仅增加了0.5 nT. 所以串联电容为110 pF、偏置磁场强度为5.9 Oe时, 最小等效磁噪声对应的偏置场异变并不能视作偏置磁场导致的显著变化. 所以根据以上测试结果和分析, 可以得出阻抗模式下传感器的最佳工作条件: 串联电容值为100 pF、激励信号频率为1 MHz、偏置磁场强度为7.66 Oe.

      根据以上的测试和分析, 可以发现将640 μH电感和100 pF电容串联后组成的LC串联磁传感器在阻抗模式时, 具有较低的噪声水平. 证明其作为低噪声的LC串联磁传感器具有一定的可行性.

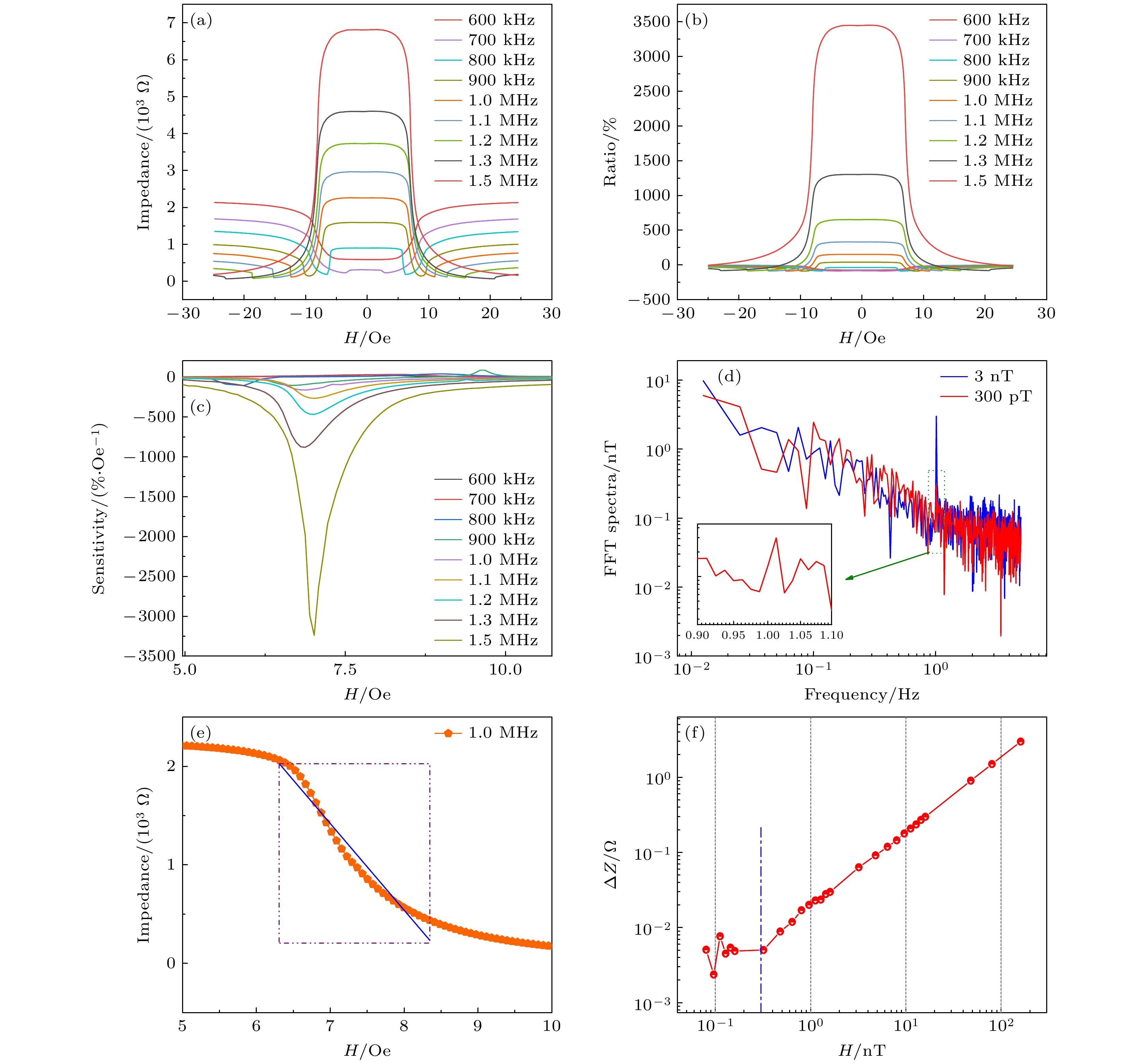
      进一步对工作在阻抗模式下的LC串联磁传感器性能进行了测试, 结果如图7所示. 图7(a)为该传感器的阻抗值随传感器外加磁场强度的变化. 可以看到传感器的阻抗值基本都在几千欧姆范围内, 最大阻抗值仅有6800 Ω. 不仅如此, 在激励信号为600 kHz时, 阻抗值随着磁场强度增强逐渐增大, 出现这一现象的原因是激励信号频率小于LC串联电路的初始谐振频率. 当磁场逐渐增大, 电感值逐渐减小、谐振频率逐渐增大, 体现在坐标轴上等效于阻抗-频率曲线向右移动, 所以LC串联电路的阻抗值逐渐增大. 增大激励信号频率, 阻抗值变化曲线逐渐呈现双峰现象. 在不同的激励信号频率下, 阻抗值在不同磁场强度时达到最小, 此阻抗最小值与LC串联电路的串联谐振频率相对应; 当激励信号频率达到1.5 MHz时, 激励信号频率逐渐逼近LC串联电路在磁饱和状态下的串联谐振频率, 串联谐振频率随磁场变化趋势减缓, 双峰现象消失. 图7(b)为传感器的阻抗变化率曲线. 随着激励信号频率的增大, 阻抗变化率越来越大.

      通过对传感器阻抗变化率-磁场关系曲线进行微分, 计算得到阻抗变化率灵敏度随磁场的变化, 如图7(c)所示. 在5—10 Oe磁场范围内, 阻抗变化率灵敏度的幅度随磁场变化呈现先增大后减小的趋势. 随着激励信号频率的增大, 传感器的灵敏度不断变大, 当激励信号频率为1.5 MHz时, 灵敏度达到了3240%/Oe, 但当激励信号频率为1 MHz时, 其灵敏度仅有160.6%/Oe. 虽然在1.5 MHz时, 传感器具有更高的灵敏度, 但是从图6可知, 在该激励信号频率时, 传感器的等效磁噪声更大, 这极大地限制传感器对于微弱磁信号的探测能力. 以上的测试分析表明LC串联磁传感器在阻抗模式下的灵敏度和磁噪声之间不存在正向依赖关系.

      图7(d)所示为阻抗模式的磁传感器对于微弱磁信号的等效幅度谱, 即根据传感器的传递函数, 将测得的阻抗数据转换为磁场强度数据, 然后幅度谱计算, 获得等效幅度谱. 对传感器施加7.66 Oe静态偏置磁场, 同时对传感器施加1 Hz正弦交流磁信号, 对采集到的时域信号进行FFT分析. 可以看出, 传感器等效磁噪声约为200 pT@1 Hz; 当外加的正弦交流磁信号强度为3 nT时, 可以在图中看到蓝色曲线在1 Hz处有一个明显的信号峰, 信噪比约为1500; 当交流磁信号强度减小到300 pT时, 从红色曲线及其放大图可看出, 在1 Hz处依然存在一个明显的信号, 其信噪比约为1.5.

      继续对传感器的输出特性进行测试, 如图7(e)所示, 可以看到6—8 Oe范围内, 传感器的阻抗随磁场呈线性变化, 拟合线性度可以达到0.964. 如图7(f)所示, 对传感器施加7.66 Oe的偏置磁场, 在1 Hz微弱磁场信号作用下, 可以看到随着磁场信号强度逐渐减弱, 传感器阻抗变化量呈线性减小趋势, 当外部磁场强度小于0.3 nT后, 阻抗变化量呈散点分布, 不再具有线性特征.

      通过以上的测试和分析可知, 当640 μH电感和100 pF电容串联后组成的LC串联磁传感器在阻抗模式时, 在频率为1 MHz的激励信号驱动下, 传感器的线性区间约为2 Oe, 线性度为0.964, 阻抗变化率灵敏度约为160.6%/Oe, 等效磁噪声约为200 pT@1 Hz, 检测极限约为300 pT.

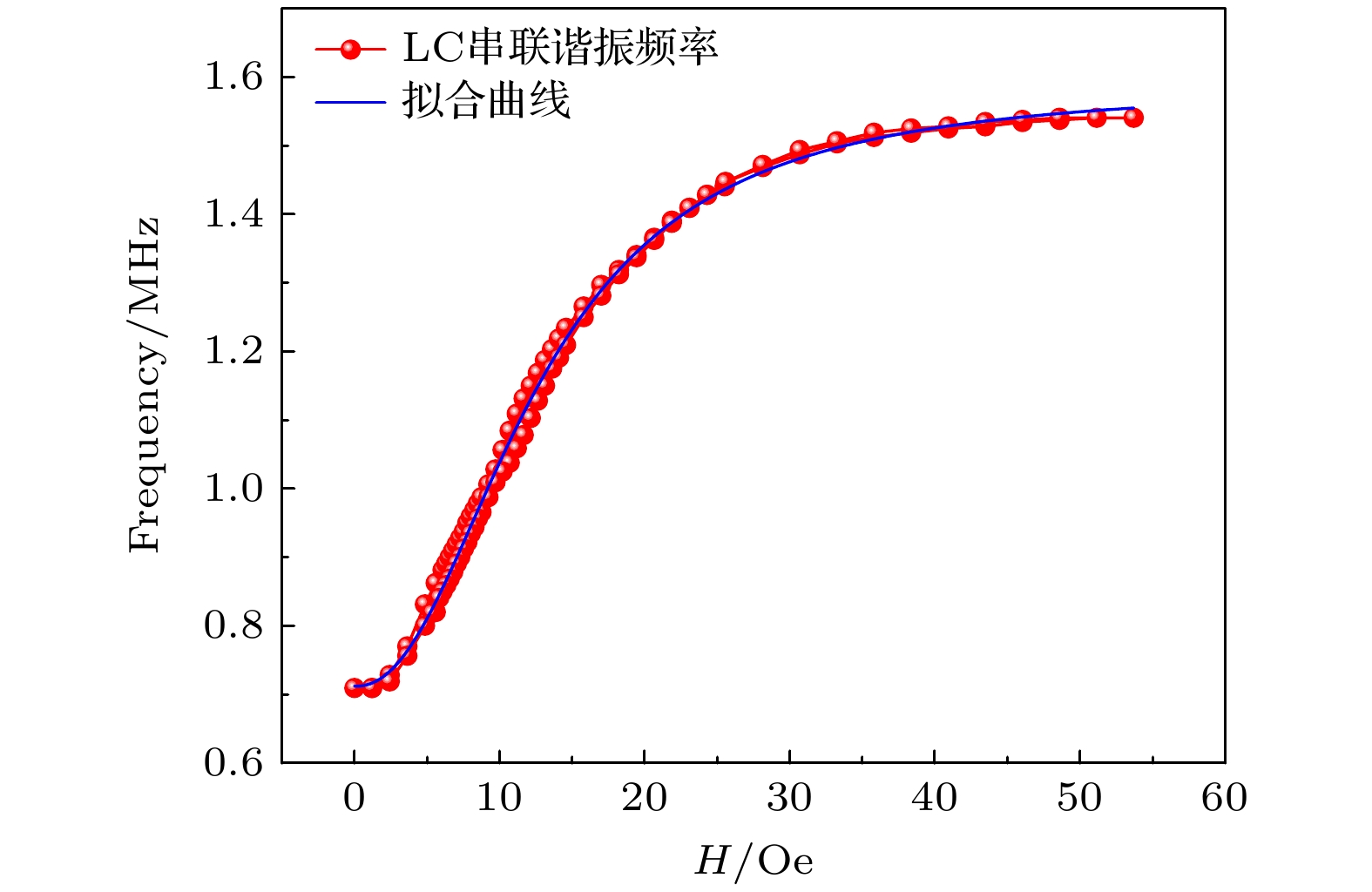
      当LC串联磁传感器工作于频率模式时, 对传感器串联谐振频率随磁场变化特性进行测试和分析. 图8中红色曲线是传感器的串联谐振频率随磁场的变化. 可以看到谐振频率在0—40 Oe范围内整体呈现单调变化趋势, 而且在很大的磁场范围内呈现线性变化. 图8中的串联谐振变化趋势与图2中电路仿真的结果一致, 在线性区域内, 串联谐振频率随磁场强度增大(电感值减小)而增大. 所以如果将LC串联电路的频率变化作为反应磁场强度的传感量, 将极大地提高传感器的量程, 实现几十Oe的磁场检测范围.

      对传感器的谐振频率随磁场的变化曲线进行非线性拟合, 如图8中蓝色拟合曲线. 从图8测试结果可以看出, 曲线变化规律并不是常规的函数 变化趋势, 不能通过常见的简单函数来描述, 所以在拟合计算时, 需要考虑应用其他非线性拟合模型对数据进行拟合, 在尝试多种非线性拟合模型后, 最终确定使用Logistic回归模型对谐振频率-磁场数据进行拟合. Logistic回归模型的拟合函数为

      式中Y表示因变量, 即谐振频率; X表示自变量, 即磁场强度; a, b, c, p是4个常数. 根据拟合结果可知对应的数值分别是: a = 1580000, b = 710000, c = 12.65, p = 2.22. 在数据拟合中, 拟合优度理论最大值为1, 该数值越接近1, 表明回归直线对观测值的拟合程度越好. Logistic模型的拟合优度R2 = 0.9974, 其数值趋近于1, 表明该模型的拟合结果与实验数据之间的差异极小, 可以很好地描述两个变量之间的关系. 将常量参数代入(5)式可以得到谐振频率与磁场之间的关系:

      需要注意的是, (6)式中频率变量f的单位为Hz, 磁场变量H的单位为Oe.

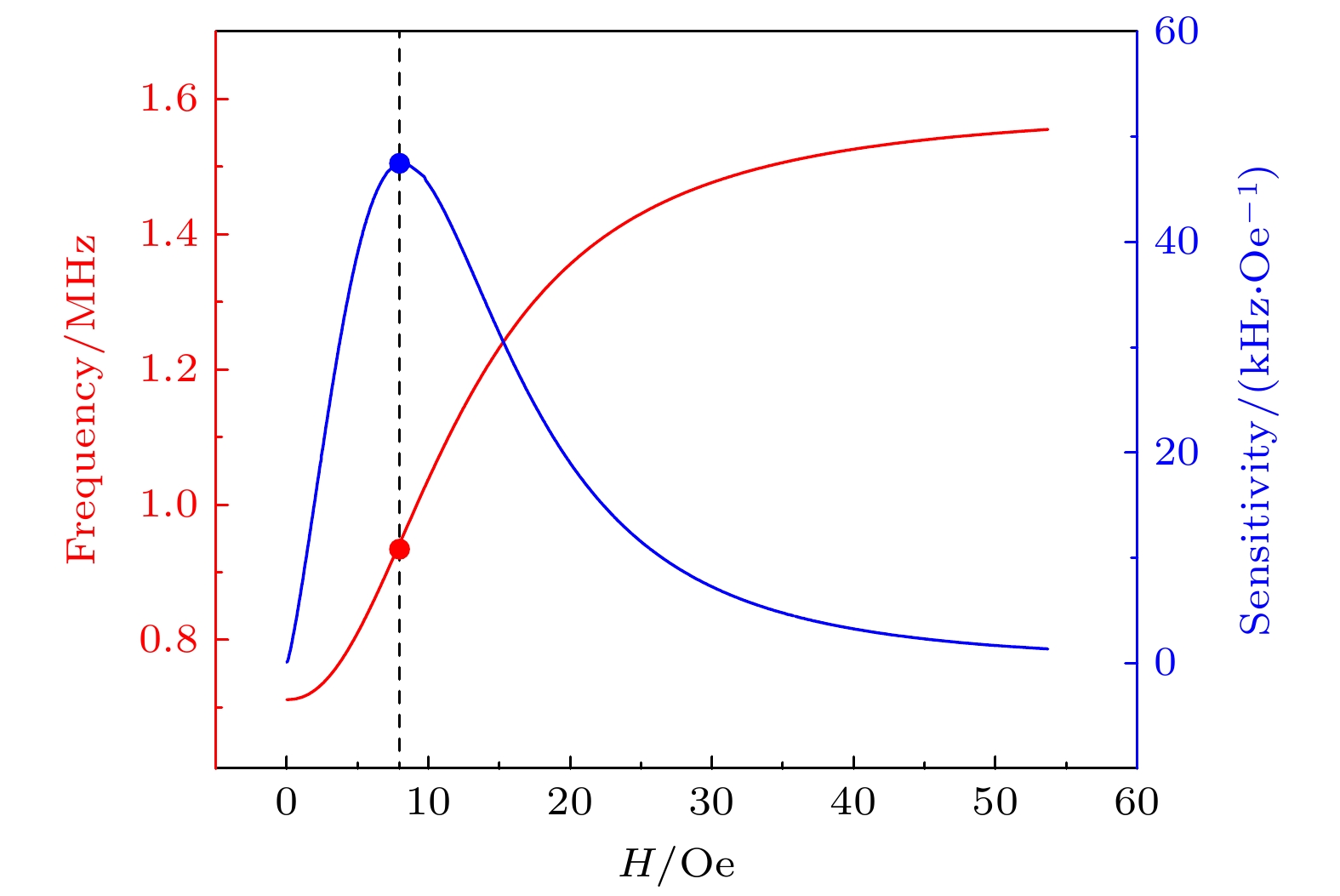
      在实验数据的基础上进行非线性拟合后, 得到如(6)式所示的函数, 该式给出了磁场与谐振频率之间的关系. 良好的拟合结果, 明确的关系式, 证明了LC串联磁传感器在频率模式下作为磁传感器的设计可行性. 进一步对拟合函数所表征的频率和磁场关系, 采用数值计算方式分析其拟合灵敏度, 如图9所示. 因为谐振频率随磁场的变化趋势和拟合函数都呈现非线性变化特征, 所以其灵敏度必然会随着磁场的变化而发生改变. 因为(6)式很好地拟合了频率与磁场之间的变化关系, 所以在分析灵敏度非线性时, 在(6)式的基础上进行数值模拟. 对谐振频率-磁场拟合曲线进行微分计算, 得到频率灵敏度随磁场的变化. 从图9可以看到, 灵敏度随磁场变化呈现先增大后降低的趋势, 当磁场小于7.66 Oe时, 灵敏度随磁场强度的增大迅速增大, 当磁场强度大于7.66 Oe时, 灵敏度随磁场强度增大而缓慢减小; 当外加磁场强度约为7.66 Oe时, 灵敏度达到最大值, 约为47 kHz/Oe.

      当LC串联磁传感器处于灵敏度最高的工作状态时, 其灵敏度为0.47 Hz/nT. 假设当传感器需要检测1000 nT的微弱磁场信号时, 磁场引起的谐振频率的偏移量约为470 Hz, 此时LC谐振式磁传感器的串联谐振频率约为950 kHz, 所以谐振频率偏移量约为0.49‰. 这一频率偏移量对于目前现有的谐振频率检测方法来说, 很难区分其谐振频率的变化. 从技术实现上基本否定了LC串联磁传感器作为微弱磁场探测器的可行性. 但是需要强调的一点是, 在5—30 Oe磁场范围内, LC串联磁传感器具有明显的单调递增变化规律. 通过检测传感器的串联谐振频率, 根据谐振频率-磁场拟合(6)式, 可以计算出外部磁场强度的大小, 表明LC串联磁传感器在频率模式下, 可以作为一种大量程的磁传感器.

      当LC串联元件作为一个传感器使用时, 具有两种工作模态: 1)阻抗模式, 通过阻抗的变化来测量磁场强度变化, 具有噪声低、灵敏度高的特点; 2)频率模式, 通过谐振频率的变化来测量磁场强度变化, 具有线性范围宽、量程大的特点. 值得注意的是, 当LC串联磁传感器工作在频率模式时, 其在偏置磁场为7.66 Oe时, 频率对磁场变化的灵敏度处于最大值; 当LC串联磁传感器工作在阻抗模式时, 在7.66 Oe偏置磁场条件下, 传感器具有最小的本底噪声. LC串联磁传感器在两种工作模式下所需的静态偏置磁场是一致的.

      本文设计的LC串联磁传感器兼具了低噪声和大量程的优点, 具有较大的应用价值和市场潜力, 与目前市场上应用广泛的霍尔传感器、磁阻传感器、磁通门传感器相比, 具有明显的差异化优势. 表2对比了本文中设计的LC串联磁传感器与多种商用磁传感器性能和价格. 双模态磁传感器工作在磁阻抗模式时, 与几种磁阻传感器(各向异性磁阻(AMR)、GMR、隧穿磁阻(TMR))相比, 本底噪声明显要更低; 与磁通门传感器相比, 其本底噪声远小于微型磁通门传感器(DRV425), 是传统磁通门传感器(Mag651)的10倍; 与同类型的巨磁阻抗(GMI)传感器相比, 其本底噪声性能依然具有较大的差距. 但是本文中设计的磁传感器在价格上具有明显的优势. 噪声性能优异的几种磁传感器(磁通门、GMI), 价格基本都在千元以上, 甚至达到上万元, 严重阻碍了高性能磁传感器的推广应用. 本文中设计的磁传感由商用电感和电容串联组成, 电感元件市场价格约为10元, 电容价格更是低至不足0.1元. 10元的价格与一个霍尔传感器的价格接近, 但是其本底噪声相比霍尔传感器降低了近650倍. 双模态磁传感器工作在LC谐振模式时, 其量程为5—30 Oe, 测试范围可以达到25 Oe, 与表2中所列的多种商用磁传感器相比, 其在量程上都具有明显的优势. 所以, 本文中设计的LC串联磁传感器在噪声特性、量程、价格3个方面都具有一定的差异化竞争优势, 在规模越来越大的磁传感器市场的激烈竞争中, 将会是一个不错的选择.

    5.   结论和展望

    • 本文设计了一种由640 μH电感和100 pF电容串联后构成的LC串联磁传感器. 该传感器具有两种工作模式, 当传感器工作于阻抗模式时, 传感器通过阻抗变化来探测磁场强度变化, 具有灵敏度高、噪声小的特点. 当传感器激励信号频率为1 MHz, 静态偏置磁场为7.66 Oe时, 其阻抗变化率灵敏度约为160.6%/Oe, 等效磁噪声约为200 pT@1 Hz, 量程为6—8 Oe. 当传感器工作于频率模式时, 传感器通过串联谐振频率的变化来探测磁场强度变化, 具有量程大的优点, 线性范围可以达到25 Oe, 测试量程为5—30 Oe. 一个传感器, 通过切换检测的传感器特征参数, 实现两种传感模式的切换, 使得该传感器即具有低噪声和高灵敏度的特点, 也具备了大量程检测的能力. 不仅如此, 该磁传感器构成采用了成熟的商用的电感和电容元件, 无需额外的加工制造环节, 极大的节约了传感器的制造成本, 其价格仅为10元人民币. 该传感器是一款性能优异, 价格低廉的磁传感器, 在未来磁传感器市场中将有很大大的应用价值和竞争优势.

    参考文献 (36)

目录

/

返回文章
返回