高级搜索

锂离子电池颗粒尺度下电化学-热-力过充模型

,  ,  ,  , 

downloadPDF

上一篇

下一篇

张袆柔, 曾晓淇, 李家星, 任怡茂, 吴伟雄. 锂离子电池颗粒尺度下电化学-热-力过充模型[J]. 物理学报, 2025, 74(3): 038201-1. doi: 10.7498/aps.74.20240984
引用本文: 张袆柔, 曾晓淇, 李家星, 任怡茂, 吴伟雄. 锂离子电池颗粒尺度下电化学-热-力过充模型[J]. 物理学报, 2025, 74(3): 038201-1. doi: 10.7498/aps.74.20240984
shu
Huirou ZHANG, Xiaoqi ZENG, Jiaxing LI, Yimao REN, Weixiong WU. Electrochemical-thermal-mechanical overcharge model on a scale of particle for lithium-ion batteries[J]. Acta Physica Sinica, 2025, 74(3): 038201-1. doi: 10.7498/aps.74.20240984
Citation: Huirou ZHANG, Xiaoqi ZENG, Jiaxing LI, Yimao REN, Weixiong WU. Electrochemical-thermal-mechanical overcharge model on a scale of particle for lithium-ion batteries[J]. Acta Physica Sinica, 2025, 74(3): 038201-1. doi: 10.7498/aps.74.20240984
shu

锂离子电池颗粒尺度下电化学-热-力过充模型

  • 暨南大学国际能源学院, 珠海　519070

    • 作者简介: 张袆柔: zyr011117@stu2022.jnu.edu.cn .
    通讯作者: E-mail: weixiongw@126.com.

  • 中图分类号: 82.80.Fk, 81.70.Pg, 82.47.Aa, 91.65.Lc

Electrochemical-thermal-mechanical overcharge model on a scale of particle for lithium-ion batteries

  • International School of Energy, Jinan University, Zhuhai 519070, China

    • Corresponding author: E-mail: weixiongw@126.com.

  • MSC: 82.80.Fk, 81.70.Pg, 82.47.Aa, 91.65.Lc

  • 摘要: 锂离子电池过充时, 负极超过最大嵌锂浓度会发生表面析锂, 而正极则处于贫锂状态导致颗粒内部应力升高, 从而引发严重的寿命和安全问题. 本文基于单层电芯颗粒尺度, 建立了镍钴锰正极和石墨负极颗粒尺度下的三维电化学-力-热耦合过充模型, 能够准确地反映充电过程中析锂和应力-应变规律. 基于此, 分析了充电倍率和负极颗粒半径设计参数对负极表面析锂的影响. 结果表明: 高倍率下析锂的触发电压较低, 而低倍率下由于极化和温度较低的影响, 过充至4.8 V时析锂浓度较高; 相较于大粒径颗粒, 小颗粒表面呈现最大锂离子浓度高、析锂过电位低、平均冯·米塞斯应力大, 更容易发生析锂. 在应力方面, 探究了正极颗粒空间分布和热效应的影响, 定义了接触深度因子${J_{\text{r}}}$, 发现颗粒的接触深度与接触界面区域的应力成反比关系; 而且, 随着充电倍率增大, 温度相关电化学参数显著变化, 在计算颗粒层面应力时不能忽略. 相关结果可为优化电池设计和充电管理策略提供理论依据和指导.
    Abstract: During overcharging of lithium-ion batteries, lithium plating can occur on the anode surface when the maximum lithium intercalation concentration is exceeded, while the cathode is in a lithium-poor state, which can result in shortened battery lifespan and safety. In this work, the geometric structure of the positive electrode particles is designed based on the tomography data, while the negative electrode particles are represented by spheres with different sizes. The homogenization method is used, with the carbon filler, binder and electrolyte regarded as a single porous conductive adhesive domain. Based on the main mechanism of lithium-ion battery overcharge, a coupled three-dimensional electrochemical-mechanical-thermal overcharge model on a particle scale is developed for NCM cathode and graphite anode. The coupled mathematical model consists of four parts, namely the electrochemical model, the lithium plating model, the thermal model and the stress-strain model. In terms of lithium precipitation, the particle radius parameter and charging rates are investigated. The results show that the lithium plating concentration of the particles near the separator is higher, following the “principle of proximity” , namely the sequence of lithium deintercalation is related to the migration path. The surface of anode particles with small particle size is more prone to lithium precipitation due to the high maximum lithium ion concentration on the surface of the particles, the low surface lithium precipitation overpotential, and the high average Von Mises stress. At high charging rate, fast charge transfer rate and ion diffusion rate result in a low voltage at the anode, triggering off lithium precipitation. At a low rate, polarization and low temperature can lead to the precipitation of more lithium on the surface of the anode particles. In terms of stress, the spatial distribution between particles and thermal effects are investigated. The ratio of the distance from the contact surface to the center of the particle to the particle radius is calculated and defined as the contact depth ($ J_{\rm r} $), in order to better describe the law of particle contact stress. It is shown that the contact depth between particles is inversely proportional to the stress on the contact area. When the heat generation effect is considered, the temperature of the battery rises faster with the increase of the charging rate. The electrochemical parameters related to temperature and the lithium concentration diffusion gradient increase significantly, and the influence of temperature on the particle stress is also more significant. The relevant results can provide theoretical basis and guidance for designing battery and optimizing charge strategies.
  • 加载中

  • 图 1  模型几何图和耦合关系图　(a) 几何模型; (b) 网格; (c) 数学模型之间的耦合关系

    Figure 1.  Geometric shape and coupling relationship diagram of the model: (a) Geometric shape; (b) mesh; (c) coupling relationship between mathematical models.

    下载: 全尺寸图片 幻灯片

    图 2  NCM和石墨随化学计量系数x变化的熵系数(a)[12]和平衡电位曲线 (b) [13]

    Figure 2.  Entropy coefficient (a) [12] and the equilibrium potential (b) [13] as a function of the chemical composition coefficient x of NCM and graphite.

    下载: 全尺寸图片 幻灯片

    图 3  NCM111和石墨随化学计量系数x变化的体积变化率[31,32]

    Figure 3.  Volume change rate of NCM111 and graphite as a function of stoichiometry coefficient x [31,32].

    下载: 全尺寸图片 幻灯片

    图 4  电压的仿真数据与实验数据的对比　(a) 充电至4.2 V时, 充电倍率为0.2C, 0.5C, 1C和1.5C的电压变化图; (b) 充电至4.8 V时, 充电倍率为0.2C, 0.5C的电压变化图

    Figure 4.  Comparison between simulated and experimental data of voltage: (a) Voltage variation graphs charging to 4.2 V at charging rates of 0.2C, 0.5C, 1C and 1.5C; (b) voltage variation graphs charging to 4.8 V at charging rates of 0.2C and 0.5C.

    下载: 全尺寸图片 幻灯片

    图 5  (a) 负极颗粒表面析出锂金属浓度分布; (b) 负极颗粒表面析锂过电位绝对值分布; (c) 不同粒径颗粒位置示意(蓝色标记)

    Figure 5.  (a) Lithium metal concentration on the particle surface; (b) the absolute value of overpotential of lithium plating on the particle surface; (c) position of particles with different sizes (the blue area).

    下载: 全尺寸图片 幻灯片

    图 6  在负极两个颗粒表面的过充过程　(a) 析出锂金属浓度; (b) 最大锂离子浓度; (c) 平均析锂过电位; (d) 平均冯·米塞斯应力

    Figure 6.  Overcharging process on the surfaces of two negative particles: (a) Concentration of lithium metal precipitated; (b) maximum lithium ion concentration; (c) average lithium precipitation overpotential; (d) average von Mises stress.

    下载: 全尺寸图片 幻灯片

    图 7  不同倍率下的负极整个表面析出的锂金属浓度(a)和负极颗粒的温度(b)

    Figure 7.  (a) Lithium metal concentration precipitated on the whole surface of the negative electrode and (b) the temperature of the negative electrode particles at different charging rates.

    下载: 全尺寸图片 幻灯片

    图 8  (a) 0.5C充电至4.8 V的正极与负极应力; (b) 0.5C充电至4.8 V的正极应力-应变

    Figure 8.  (a) Stress of the cathode and anode charged to 4.8 V at 0.5C; (b) stress-strain of the cathode charged to 4.8 V at 0.5C.

    下载: 全尺寸图片 幻灯片

    图 9  0.5C充电至3.9 V, 4.2 V, 4.5 V, 4.8 V的正极颗粒应力-应变分布图

    Figure 9.  Stress-strain distribution diagrams of cathode particles charged to 3.9 V, 4.2 V, 4.5 V and 4.8 V at 0.5C.

    下载: 全尺寸图片 幻灯片

    图 10  A, B, C和D四组颗粒的接触应力-应变(a)和位置(b)

    Figure 10.  (a) Contact stress and strain of particles and (b) corresponding position in groups A, B, C and D.

    下载: 全尺寸图片 幻灯片

    图 11  0.2C (a), (c) 和0.5C (b), (d)倍率下, 正极颗粒平均冯·米塞斯应力, 以及温度相关系数随充电过程变化

    Figure 11.  Average von Mises stress of positive electrode particles and temperature-dependent coefficient at (a), (c) 0.2C and (b), (d) 0.5C.

    下载: 全尺寸图片 幻灯片

    表 1  电化学过充模型中的几何参数和结构

    Table 1.  Geometric parameters and structure of the electrochemical overcharge model.

    参数 负极 隔膜 正极
    长度 L/μm 80 30 95
    颗粒平均半径 Rs_avg/μm 4.15 — 6.19
    颗粒最大/最小半径Rsmax/min/μm 14.61/1.03 — 14.25/1.62
    颗粒面积 Ap/μm2 24997 — 20553
    颗粒体积 Vp/μm3 37892 — 36193
    电池截面长度 Lcross/μm 37
    电池截面宽度 Wcross/μm 34.4
    比表面积 av/m–1 2.52×105 — 1.69×105
    固相体积分数 ψs 0.3833 — 0.2984
    液相体积分数 ψe 0.6167 — 0.7015
    下载: 导出CSV

    表 4  电化学过充模型中的热力学参数[27-30]

    Table 4.  Thermal mechanical parameters of the electrochemical overcharge model[27-30].

    参数 负极 隔膜 正极
    密度 ρ/kg·m–3 2300 1000 4530
    杨氏模量 E/GPa 10 78
    泊松比 ν 0.3 0.25
    热膨胀系数 αT/K–1 4.06×10–6 1.2×10–5
    电池比热容 Cp/(J·kg–1·K–1) 881 1260 1009.21
    对流系数 h/(W·m–2·K–1) 10
    下载: 导出CSV

    表 2  电化学过充模型中的电化学参数[12,13,16]

    Table 2.  Electrochemical parameters of the electrochemical overcharge model[12,13,16].

    参数 负极 隔膜 正极
    固相电子电导率 σs/(S·m–1) 100 — 3.8
    固相有效电子电导率 σs,eff/(S·m–1) $\psi_{\rm s}^{1.5}\sigma_{\mathrm{s}} $ $\psi_{\rm s}^{1.5}\sigma_{\mathrm{s}} $
    液相离子电导率 σe/(S·m–1) $c_{\rm e}(5.38- 3.49 \times 10^{-4}c_{\rm e} + 2.3 \times 10^{-7} c_{\rm e}^2)^2 \times 10^{-4} $
    液相有效离子电导率 σe, eff/(S·m–1) $\psi_{\rm e}^{1.5}\sigma_{\mathrm{e}} $
    液相电子电导率 σca/(S·m–1) 10
    σe的活性能 Ea,σe/(kJ·mol–1) 30
    初始电解质浓度 ce,0/(mol·m–3) 1200
    最大固相锂浓度 cs,max/(mol·m–3) 24407 — 30017
    化学计量系数 x 在1/0 SOC 0.115/0.98 — 0.92/0.222
    容量比 N/P 1.09
    固相扩散系数 Ds/(m2·S–1) 1.45×10–13 — 2×10–13
    液相扩散系数 De/(m2·S–1) $ 10^{[-8.43-54/(59.15-0.05c_{\text{e}})-2.2\times10^{-4}c_e^2]} $
    液相有效扩散系数 De,eff/(m2·S–1) $\psi_{\rm e}^{1.5}D_{\mathrm{e}} $
    De的活化能 Ea,De/(kJ·mol–1) 72
    下载: 导出CSV

    表 3  电化学过充模型中的动力学参数[13]

    Table 3.  Dynamics parameters of the electrochemical overcharge model[13].

    参数 负极 隔膜 正极
    反应的传递系数 αa,1, αc,1 0.5, 0.5 0.5, 0.5
    反应速率常数 k1,ref/(m·s–1) 2×10–11 2×10–11
    k1 的活化能 Ea,k1/(kJ·mol–1) 71 45
    析锂反应传递系数 αa,2, αc,2 0.3, 0.7
    析锂反应速率常数 k2,ref/(m·s–1) 2.5×10–7
    k2的活化能Ea,k2/(kJ·mol–1) 50
    锂的摩尔质量 Mpl/(kg·mol–1) 6.94×10–5
    锂的密度 ρpl/(kg·m–3) 534
    电导率 σfilm/(S·m–1) 6×10–5
    析锂的平衡电位 Eeq,Li/V 0
    下载: 导出CSV
  • [1] Yong J Y, Ramachandaramurthy V K, Tan K M, Mithulananthan N 2015 Renew. Sust. Energ. Rev. 49 365 doi: 10.1016/j.rser.2015.04.130
    [2] Crabtree G 2019 Science 366 422 doi: 10.1126/science.aax0704
    [3] Huang W S, Feng X N, Han X B, Zhang W F, Jiang F C 2021 Cell Rep. Phys. Sci. 2 100285 doi: 10.1016/j.xcrp.2020.100285
    [4] Wang Q S, Mao B B, Stoliarov S I, Sun J H 2019 Prog. Energ. Combust. 73 95 doi: 10.1016/j.pecs.2019.03.002
    [5] Belova I V, Murch G E 1995 J. Appl. Phys. 77 127 doi: 10.1063/1.359379
    [6] Zhao Y, Stein P, Bai Y, Al-Siraj M, Yang Y Y W, Xu B X 2019 J. Power Sources 413 259 doi: 10.1016/j.jpowsour.2018.12.011
    [7] Pastor-Fernández C, Uddin K, Chouchelamane G H, Widanage W D, Marco J 2017 J. Power Sources 360 301 doi: 10.1016/j.jpowsour.2017.03.042
    [8] 王其钰, 王朔, 周格, 张杰男, 郑杰允, 禹习谦, 李泓 2018 物理学报 67 128501 doi: 10.7498/aps.67.128501 Wang Q Y, Wang S, Zhou G, Zhang J N, Zheng J Y, Yu X Q, Li H 2018 Acta Phys. Sin. 67 128501 doi: 10.7498/aps.67.128501
    [9] Honbo H, Takei K, Ishii Y, Nishida T 2009 J. Power Sources 189 337 doi: 10.1016/j.jpowsour.2008.08.048
    [10] Mei W X, Duan Q L, Qin P, Xu J J, Wang Q S, Sun J H 2019 J. Electrochem. Soc. 166 A3319 doi: 10.1149/2.0741914jes
    [11] Arora P, Doyle M, White R E 1999 J. Electrochem. Soc. 146 3543 doi: 10.1149/1.1392512
    [12] Ren D S, Smith K, Guo D X, Han X B, Feng X N, Lu L G, Ouyang M G, Li J Q 2018 J. Electrochem. Soc. 165 A2167 doi: 10.1149/2.0661810jes
    [13] Mei W X, Zhang L, Sun J H, Wang Q S 2020 Energy Storage Mater. 32 91 doi: 10.1016/j.ensm.2020.06.021
    [14] Yang S, Hua Y, Qiao D, Lian Y, Pan Y, He Y 2019 Electrochim. Acta 326 134928 doi: 10.1016/j.electacta.2019.134928
    [15] Wang Y N, Li H, Wang Z K, Lian C, Xie Z F 2021 J. Energy Storage 43 103214 doi: 10.1016/j.est.2021.103214
    [16] Schmidt A, Ramani E, Carraro T, Joos J, Weber A, Kamlah M, Ivers-Tiffée E 2021 Energy Technology 6 2000881 doi: 10.1002/ente.202000881
    [17] Ebner M, Geldmacher F, Marone F, Stampanoni M, Wood V 2013 Adv. Energ. Mater. 3 845 doi: 10.1002/aenm.201200932
    [18] 李涛, 程夕明, 胡晨华 2021 物理学报 70 138801 doi: 10.7498/aps.70.20201894 Li T, Cheng X M, Hu C H, 2021 Acta Phys. Sin. 70 138801 doi: 10.7498/aps.70.20201894
    [19] Yang F Q 2016 Sci. China Phys. Mech. 59 44 doi: 10.1007/s11433-016-0198-6
    [20] Newman J S, Tobias C W 1962 J. Electrochem. Soc. 109 1183 doi: 10.1149/1.2425269
    [21] Ge H, Aoki T, Ikeda N, Suga S, Isobe T, Li Z, Tabuchi Y, Zhang J 2017 J. Electrochem. Soc. 164 A1050 doi: 10.1149/2.0461706jes
    [22] David W I F, Thackeray M M, De Picciotto L A, Goodenough J B 1987 J. Solid State Chem. 67 316 doi: 10.1016/0022-4596(87)90369-0
    [23] Yang F 2005 Mater. Sci. Eng. A 409 153 doi: 10.1016/j.msea.2005.05.117
    [24] Wu B, Lu W 2017 J. Power Sources 360 360 doi: 10.1016/j.jpowsour.2017.05.115
    [25] Guo M, Sikha G 2010 J. Electrochem. Soc. 158 A122 doi: 10.1149/1.3521314
    [26] 蒋跃辉, 艾亮, 贾明, 程昀, 杜双龙, 李书国 2017 物理学报 66 118202 doi: 10.7498/aps.66.118202 Jang Y H, Ai L, Jia M, Cheng J, Du S L, Li S G 2017 Acta Phys. Sin. 66 118202 doi: 10.7498/aps.66.118202
    [27] Wu W, Xiao X, Huang X, Yan S 2014 Comp. Mater. Sci. 83 127 doi: 10.1016/j.commatsci.2013.10.002
    [28] Samba A, Omar N, Gualous H, Capron O, Van B P, Van M J 2014 Electrochim. Acta 147 319 doi: 10.1016/j.electacta.2014.08.115
    [29] Lai Y, Du S, Ai L, Cheng Y, Tang Y, Jia M 2015 Int. J. Hydrogen Energy 40 13039 doi: 10.1016/j.ijhydene.2015.07.079
    [30] Mei W X, Chen H, Sun J H, Wang Q S 2018 Appl. Therm. Eng. 142 148 doi: 10.1016/j.applthermaleng.2018.06.075
    [31] Hahn M, Buqa H, Ruch P W, Goers D, Spahr M E, Ufheil J, Novák P, Kötz R 2008 Electrochem. Solid State Lett. 11 A151 doi: 10.1149/1.2940573
    [32] Kondrakov A O, Schmidt A, Xu J, Geßwein H, Mönig R, Hartmann P, Sommer H, Brezesinski T, Janek J 2017 J. Phys. Chem. C 121 3286 doi: 10.1021/acs.jpcc.6b12885
    [33] Hosseinzadeh E, Genieser R, Worwood D, Barai A, Marco J, Jennings P 2018 J. Power Sources 382 77 doi: 10.1016/j.jpowsour.2018.02.027
    [34] Yang Y, Zhong X L, Xu L 2024 J. Energy Chem. 97 453 doi: 10.1016/j.jechem.2024.06.005
    [35] 魏振伟, 毛烁源, 汪宇, 韩雪冰, 卢兰光, 欧阳明高 2024 上海理工大学学报 46 1 doi: 10.13255/j.cnki.jusst.20230915001 Wei Z W, Mao L Y, Wang Y, Lu L G, Ouyang M G 2024 J. Univ. Shanghai Sci. Tech. 46 1 doi: 10.13255/j.cnki.jusst.20230915001
    [36] Mao S, Wang Y, Lu Y, et al. 2025 InfoMat 7 e12612 doi: 10.1002/inf2.12612
    [37] Wu W, Ma R, Liu J, Liu M, Wang We, Wang Q 2021 Int. J. Heat Mass Tran. 170 121024 doi: 10.1016/j.ijheatmasstransfer.2021.121024
    [38] 骆晨旭, 师晨光, 余志远, 黄令, 孙世刚 2022 电化学 28 2006131 doi: 10.13208/j.electrochem.200613 Luo C X, Shi C G, Yu Z Y, Huang L, Sun S G 2022 J. Electrochem. 28 2006131 doi: 10.13208/j.electrochem.200613
    [39] Manthiram A 2020 Nat. Commun. 11 1550 doi: 10.1038/s41467-020-15355-0
  • 加载中
图( 11) 表( 4)
计量
  • 文章访问数:  128
  • HTML全文浏览数:  128
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-15
  • 刊出日期:  2025-02-05

锂离子电池颗粒尺度下电化学-热-力过充模型

    通讯作者: E-mail: weixiongw@126.com.
    作者简介: 张袆柔: zyr011117@stu2022.jnu.edu.cn
  • 暨南大学国际能源学院, 珠海　519070
  • 收稿日期:  2024-07-15

摘要: 锂离子电池过充时, 负极超过最大嵌锂浓度会发生表面析锂, 而正极则处于贫锂状态导致颗粒内部应力升高, 从而引发严重的寿命和安全问题. 本文基于单层电芯颗粒尺度, 建立了镍钴锰正极和石墨负极颗粒尺度下的三维电化学-力-热耦合过充模型, 能够准确地反映充电过程中析锂和应力-应变规律. 基于此, 分析了充电倍率和负极颗粒半径设计参数对负极表面析锂的影响. 结果表明: 高倍率下析锂的触发电压较低, 而低倍率下由于极化和温度较低的影响, 过充至4.8 V时析锂浓度较高; 相较于大粒径颗粒, 小颗粒表面呈现最大锂离子浓度高、析锂过电位低、平均冯·米塞斯应力大, 更容易发生析锂. 在应力方面, 探究了正极颗粒空间分布和热效应的影响, 定义了接触深度因子${J_{\text{r}}}$, 发现颗粒的接触深度与接触界面区域的应力成反比关系; 而且, 随着充电倍率增大, 温度相关电化学参数显著变化, 在计算颗粒层面应力时不能忽略. 相关结果可为优化电池设计和充电管理策略提供理论依据和指导.

English Abstract

    全文HTML

    1.   引　言

    • 鉴于全球气候上升和能源枯竭危机, 新型储能技术的发展与大规模应用正逐渐成为未来发展趋 势[1–3]. 锂离子电池具有能量密度高、循环寿命长和低自放电率等优点, 作为储能器件在移动和固定场景得到广泛应用[3]. 目前学术和产业界认为电池本质安全是该领域面临的核心挑战[4]. 其中, 根源之一为过充现象, 即电池在充电时超过其设计电压, 可导致电池寿命缩短和性能下降, 甚至引发内部产生过热、短路及爆炸风险.

      锂离子电池过充致失效的主导模式中, 一般认为由内部电极颗粒产生的扩散诱导应力和负极表面析锂直接或间接导致[5]. 一方面, 过大的扩散应力会造成活性颗粒破碎、活性层开裂、以及活性层与集流体的分层剥离等多种失效形式, 从而导致电池容量衰减、内阻增大、寿命缩短等失效现象[6]. 另一方面, 析锂会造成可循环锂的大量损失[7], 导致容量衰减[8]; 进一步, 析出的锂会演变成锂枝晶[9], 穿透隔膜, 造成内部短路而引发热失控. 因此, 开展锂离子电池过充过程析锂和应力的研究对其安全高效使用至关重要.

      电池充电过程涉及到内部电化学反应等多尺度多物理场问题. 在锂离子电池研究领域, 尽管X射线成像等先进测试技术可以观察内部微观情况, 但是获得的现象基本上是静态的, 难于定量反映电池微观动态演变情况. 与实验不同, 精细化模型可以获取和计算颗粒层级的内部应力和锂浓度等数值, 有利于评估其对电池性能的影响[10]. 由于电化学模型可用于析锂预测和应力计算, 许多学者构建相应的应力和析锂模型开展仿真研究. Arora等[11]首先构建了电化学模型来研究电池过充电过程的析锂情况, 将Butler-volmer方程和阴极Tafel速率表达式描述的析锂反应作为副反应纳入Doyle和Newman开发的伪二维(P2D)模型中. Ren等[12]建立了在负极表面加入析锂和锂溶解反应作为副反应的电化学模型, 研究了低温充电后电压弛豫曲线的特征平台以及电压平台出现的原因, 证明不同温度下可逆锂的容量与时间存在线性关系. Mei等[13]建立NCM(1∶1∶1)/石墨电池P2D电化学模型模拟电池过充析锂过程, 并采用差示热分析和扫描电子显微镜形貌观察等实验进行验证. 发现析锂首先发生在负极-隔膜界面, 随后到负极和集流体界面, 并且可通过合理的负极/正极厚度比来减轻析锂. 上述模型在析锂方面提供了一种在P2D模型上预测电池析锂的方法, 然而, 目前尚未应用于颗粒水平的三维非均质模型的析锂计算.

      在锂离子电池电化学-力仿真的研究领域中, 前人建立多种维度的模型深入分析了锂离子电池在充放电过程中的微观变化和应力-应变的影响因素. Yang等[14]采用了一维电化学-热-力耦合模型, 包括负极的副反应和正极活性物质的损失. 研究发现高倍率扩散引起的应力明显增加并导致严重的正极活性材料损失, 在298 K和318 K的环境温度和低循环电流下, 正极材料的应变能几乎不会超过其临界极限. Wang等[10]建立了LiMn2O4/石墨微观结构的三维电化学-力模型, 考虑了集流体和邻近颗粒的限制, 分析了放电过程中负极和正极的锂离子浓度、电流密度、过电位、应力和应变. Li等[15]基于锂离子电池三维电化学-力模型, 研究了充电速率和负极结构设计参数对锂电池性能的影响, 提出小倍率电流、较小的压实密度和电极厚度、较大的扩散系数有助于减小充电过程中负极颗粒中的应力. 尽管前期研究构建了基于P2D模型的三维应力计算模型, 但其忽略了温度依赖的动态电化学参数的改变对应力的影响, 以及颗粒之间的设计参数对颗粒接触处应力的影响.

      综上, 在本研究中, 考虑锂离子扩散和迁移过程、析锂反应、温度和扩散诱导应力的产生, 采用Li(NiCoMn)1/3O2-石墨电池作为模型开发的物理基础, 建立颗粒尺度下的三维非均质电化学过充模型, 分析该模型在恒流过充至4.8 V时电池析锂和力学特性, 探究在不同充电速率和不同颗粒粒径下负极颗粒表面的析锂变化, 以及颗粒粒径接触深度和温度对正极颗粒的应变和应力的影响.

    2.   模型建立

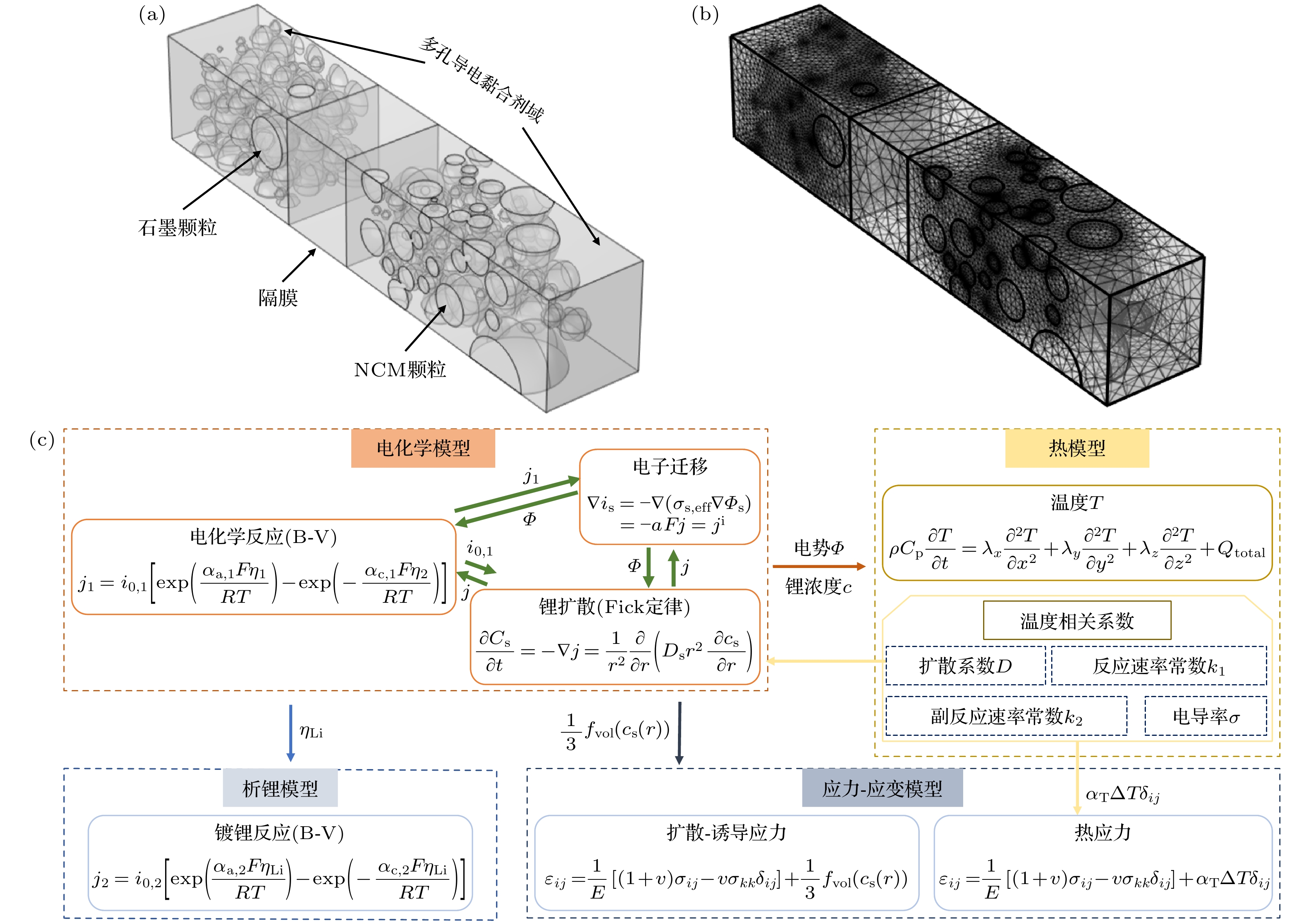
    • 如图1所示, 本文建立的模型为电极颗粒尺度下的三维非均质异构模型, 单层电芯包含正极(Li(NiCoMn)1/3O2)、负极(石墨)、隔膜、电解质(LiPF6 in 0.1PC:0.27EC:0.63EMC). 按照Schmidt等[16]所述的部分均质化方法, 将碳填料、黏合剂和电解质视为单个多孔导电黏合剂域. 正极颗粒几何结构基于层析成像数据生成异构NCM电极结构[17], 而负极颗粒为大小不一的球体. 模型在恒流充电工况下充至4.8 V, 可复现浸润在电解液中正负极颗粒之间的电化学反应, 以及描述颗粒产生的扩散-诱导应力和负极表面的析锂情况.

      图1(c)所示为数学模型包括的4个部分: 电化学模型、析锂模型、热模型和应力-应变模型. 模型间耦合关系描述如下: 电化学模型根据电迁移、电荷平衡以及锂离子扩散和迁移相关控制方程模拟内部电化学行为, 可计算锂离子浓度分布、电势分布、热量分布[18]. 析锂模型为当负极电位相对于Li/Li+下降到0 V时, 触发析锂副反应, 还需要注意的是, 由于不考虑容量衰减, 因此未涉及固体电解质界面(SEI)生长引起的副反应. 热模型通过电化学模型中的电流密度、电压和过电势等计算得到极化热、化学反应热和欧姆热, 这3种热量的变化导致电池温度上升, 而温度变化反作用于电化学模型中的温度敏感参数, 实现电化学模型和热模型双向耦合. 应力-应变模型由扩散-诱导应力和热应力构成, 一是通过菲克定律计算电极颗粒锂浓度及分布, 进而获得因颗粒内部锂浓度差引起的扩散-诱导应力; 二是热模型中的温度梯度使颗粒发生膨胀和收缩, 导致热应力的产生和变化.

      • 2.1.   电荷和质量守恒方程

    • 锂离子由于浓度梯度在电极活性材料球形颗粒内部扩散, 该过程的质量平衡由菲克定律描述:

      式中, $ {c_{\text{s}}} $为多孔电极固相锂离子浓度, ${D_{\text{s}}}$为多孔电极固相锂离子扩散系数.

      锂离子在电解液中的扩散和迁移过程, 应用浓溶液理论和菲克第二定律来描述:

      式中, $\psi _{\text{e}}^{}$为多孔电极液相体积分数, $D_{{\text{e, eff}}}^{}$为液相有效扩散系数, ${c_{\text{e}}}$为多孔电极液相锂浓度, ${t_ + }$为锂离子迁移系数, ${j^{\text{i}}}$为多孔电极电流密度, F为法拉第常数.

      在电极固相中, 电荷平衡遵循欧姆定律:

      式中, $\sigma _{{\text{s, eff}}}^{}$为多孔电极固相有效电子电导率, ${\phi _{\text{s}}}$为固相电势.

      液相电势平衡描述如下:

      式中, $\sigma _{{\text{e, eff}}}^{}$为液相有效离子电导率, R为普适气体常数, $T$为电池温度, $ {\phi _{\text{e}}} $为液相电势.

      • 2.2.   电化学动力学方程

    • 析锂的实现可以通过在电化学模型中加入析锂动力学来表示. 析锂被认为是在过充电过程中负极表面发生的副反应. 当电池过充时会导致电池内部发生一系列化学反应, 部分锂离子无法完全嵌入负极材料中, 而以金属锂的形式析出. 化学反应式用下面的方式来定义:

      局部电流总密度${j^{\text{i}}}$可定义为

      式中, ${j_1}$为嵌锂反应的局部电流密度, ${j_2}$为析锂反应的局部电流密度.

      在活性粒子与电解质界面处, 界面处的过电势作为反应动力, 锂嵌入反应引起的局部电流密度${j_1}$可由Butler-Volmer动力学方程描述[19,20]:

      式中, ${i_{0, 1}}$为交换电流密度; ${\alpha _{{\text{a, 1}}}}$和${\alpha _{{\text{c, 1}}}}$分别为阳极和阴极的电荷转移系数, 其值均为0.5; ${\eta _1}$为嵌入反应的过电位; ${k_1}$为反应速率常数; ${c_{\text{e}}}$为电解质浓度; ${c_{{\text{s, max}}}}$和${c_{{\text{s, surf}}}}$分别为最大固相锂浓度和表面固相锂浓度; ${E_{{\text{eq}}}}$为平衡电势.

      根据Arora等[11]的研究, 析锂反应的速率也遵循Butler-Volmer方程, 只有当析锂过电位为负时才发生此反应, 由以下方程描述:

      式中, ${i_{0, 2}}$为析锂反应的交换电流密度; ${k_2}$为反应速率常数; ${\alpha _{{\text{a,2}}}}$和${\alpha _{{\text{c,2}}}}$分别为反应的阳极和阴极的电荷转移系数, 分别为0.3和0.7 [21]; ${\eta _{{\text{Li}}}}$为析锂过电位. 当负极电位继续下降到0 V vs. Li/Li+时, 发生析锂副反应.

      析锂反应中的析锂过电位为

      式中, ${R_{{\text{film}}}}$表示广义的薄膜电阻, 其中薄膜是在电极活性材料表面析出锂金属.

      式中, ${M_{{\text{film}}}}$和${\rho _{{\text{film}}}}$为固体锂的摩尔质量和密度. 薄膜电阻由薄膜的厚度和电导率${\delta _{{\text{film}}}}$决定:

      式中, ${\delta _{{\text{film,0}}}}$为薄膜的初始厚度, ${\delta _{{\text{film}}}}$为膜厚变化量.

      • 2.3.   应力-应变方程

    • 充放电循环过程中, 当电极颗粒内存在锂浓度梯度, 会导致不均匀的弹性变形, 从而产生应力. 由于锂离子在固相中的扩散速率显著低于弹性形变速率, 因此力学平衡的建立要比扩散快得多. 故而, 力平衡可以看作是一个静力平衡问题. 在下面的分析中, 假设球形电极颗粒是各向同性的线弹性固体[22]. 材料的体积变化率通常与固相锂浓度有关. 其中固相锂浓度根据菲克定律计算, NCM111和石墨的体积变化率被认为是与固相锂浓度的相关函数:

      随着浓度梯度的存在, 应力-应变关系可描述为[23]

      式中, ${\varepsilon _{ij}}$为应变分量; ${\sigma _{ij}}$为应力分量; $E$为杨氏模量; $\nu$为泊松比; $ {c_{\text{s}}}\left( r \right) $为固相锂浓度; ${\delta _{ij}}$为狄拉克函数, 当$i \ne j$时, 取值为0, 当$i = j$时, 取值为1. 假设这些弹性性质与锂浓度无关. 球形粒子可以用球坐标系表示, 径向分量和切向分量[24]应变计算为

      式中, ${\varepsilon _r}\left( r \right)$为径向应变分量, ${\sigma _r}\left( r \right)$为径向应力分量, $ {\varepsilon _\theta }\left( r \right) $为切向应变分量, ${\sigma _\theta }\left( r \right)$为切向应力分量.

      对于半径为${r_{\text{p}}}$的球形粒子, 满足以下边界条件: 颗粒表面径向应力为零((19)式)、颗粒中心和集流体边界处的位移不变((20)式和(21)式),

      在没有任何外力的情况下求解静力力学平衡方程, 其径向应力和切向应力的表达式为[24]

      这里第1个积分$ \displaystyle\int_0^{{r_{\text{p}}}} {{\text{d}}r'} $是对球形粒子的整个体积积分, 第2个积分$\displaystyle \int_0^r {{\text{d}}r'} $是对半径为$r$球形粒子的体积积分.

      • 2.4.   能量守恒方程

    • 电池温度的变化遵循能量守恒方程:

      式中, $T$为电池温度; $\rho $为电池密度; ${C_{\text{p}}}$为电池热容; ${\lambda _x}$, $ {\lambda _y} $和$ {\lambda _z} $分别为电池沿长宽高三个方向的导热系数; $a$为电池比表面积; ${Q_{{\text{total}}}}$为平均内部产热, ${Q_{{\text{rev}}}}$, ${Q_{{\text{act}}}}$和$ {Q_{{\text{Ohm}}}} $分别表示极化热、反应热和欧姆热; $U$为热力学平衡电势.

      • 2.5.   温度相关参数

    • 电化学模型中的一些参数依赖于温度[25], 如扩散系数、电导率和反应速率常数. 它们在一定温度T下的值可由Arrhenius方程计算[26]:

      式中, ${Y_{\text{T}}}$为与温度相关参数, ${Y_{{\text{ref}}}}$为参考温度${T_{{\text{ref}}}}$下参数值, ${E_{{\text{a, Y}}}}$为${Y_{\text{T}}}$对应的活化能.

    3.   模型参数与有效性验证

      3.1.   模型设计参数

    • 在仿真建模中, 仿真对象的物性参数尤为重要, 表1—表4分别所示为电池几何参数和结构、电化学参数、动力学参数和热力学参数, 其中法拉第常数F = 10 C/mol, 理想气体常数R = 8.314 J·mol–1·K–1, 参考温度Tref = 298.15 K. 图2和图3分别为正负极平衡电位和熵系数、颗粒体积变化率随LixC6/Lix(NiCoMn)1/3O2中化学计量系数x的变化.

      • 3.2.   网格独立性验证

    • 模型在COMSOL Multiphysics 6.0软件中开发, 模型的几何和网格如图1(a), (b)所示. 为了简化, 通过电流边界条件将虚拟集流体简化为电极与电解液之间的边界. 采用自由四面体网格构建网格, 由845202个四面体单元、127151个三角形单元、19000个边缘单元和2309个顶点单元组成. 该网格通过了网格独立性测试: 当对原始网格进行2倍加密或粗化时, 仿真结果相差小于2%.

      • 3.3.   模型验证

    • 该模型为电极颗粒尺度下的三维异构模型, 选取文献[13]在不同倍率下的充电实验电压数据与本模型的模拟结果进行对比. 如图4(a), (b)所示, 在不同的充放电倍率下电压模拟结果与实验数据相符合, 验证了模型的可靠性. 该数值的最大误差为3.8%, 与Hosseinzadeh等[33]开路电压误差5.7%相比处于较低的水平, 进一步保证了模型的精确度.

    4.   结果与讨论

      4.1.   过充模型的析锂分析

      4.1.1.   不同颗粒粒径对析锂的影响

    • 锂离子电池充电过程中, 正极活性材料晶格中的Li失去电子变成Li+, Li+从正极脱嵌后在电解液中迁移/扩散, 通过隔膜后再嵌入到负极材料. 达到截止电压后继续充电, 多余的Li+将迁移到负极而无法嵌入, 此时会在颗粒表面还原析出, 形成锂金属沉积. 图5(a)为0.5C倍率过充到4.8 V时负极颗粒表面析锂浓度分布图. 可以看到, 靠近隔膜处的颗粒析锂浓度较高, 遵循“就近原则”——锂的脱嵌顺序与迁移路径相关[34]. 由方程(10)可知, 析锂反应在析锂过电位为负时触发, 之后的析锂浓度与析锂过电位绝对值呈正相关趋势. 该结果亦可从图5(b)进一步看出, 隔膜处颗粒析锂过电位绝对值较高. 同时, 图5(a)还观察到一个有趣的现象, 即末端颗粒的析锂浓度略有上升, 特别是小粒径颗粒尤为明显. 因此, 选取离隔膜距离一致, 但不同粒径的2个负极颗粒进行分析, 粒径分别为2.28 μm和6.11 μm, 如图5(c)所示.

      图6(a)为不同粒径负极颗粒过充至4.8 V时, 颗粒表面析锂浓度的动态变化趋势. 小粒径颗粒的析锂触发电压约为4.453 V, 低于大粒径颗粒的4.466 V, 而且小粒径颗粒的析锂浓度在过充阶段始终高于大粒径颗粒. 颗粒表面的锂离子浓度、析锂过电位和应力对析锂有重要影响[11,35], 后续从这3个方面进行分析. 小粒径颗粒的比表面积大, 表面有更多的活性位点与电解液接触[36], 有利于锂离子嵌入, 所以小颗粒的最大表面锂离子浓度高于大颗粒, 导致表面锂离子浓度更快达到饱和状态, 如图6(b)所示. 负极颗粒表面的锂离子浓度与颗粒平衡电位成负相关(见图2), 因此小颗粒表面的析锂过电位会比大颗粒提前下降到0 V, 如图6(c)所示. 此外, 大颗粒表面锂离子浓度呈上升趋势, 而小颗粒曲线则波动显著且具有较大的浓度梯度变化, 导致其平均冯·米塞斯应力大, 如图6(d)所示. 过大应力带来结构不稳定, 导致颗粒产生裂缝或破碎, 形成更小粒径颗粒表面而产生析锂反应. 基于以上三点可得出: 在同一个电极中, 小粒径颗粒在过充时更加容易析锂.

      • 4.1.2.   不同充电倍率对析锂的影响

    • 图7(a)为不同充电倍率下负极表面平均析锂浓度曲线. 从图7(a)可看出, 高倍率充电可更快地达到析锂触发电压, 但最终析出的锂金属浓度显著降低. 例如, 在0.2C, 0.35C和0.5C倍率下, 负极颗粒表面分别在4.488 V, 4.4713 V和4.442 V时开始析锂, 而充电至4.8 V时, 析出的锂金属浓度依次为1.08 mol/m2, 0.702 mol/m2和0.251 mol/m2.

      分析认为, 初始充电阶段, 高倍率充电触发负极析锂的电压低. 充电倍率增大导致电极表面处的$ {j_1} $上升, 反应速率加快, 电解液到电极表面的锂离子浓度梯度${{\delta c}}/{{\delta r}}$增大; 随着浓度梯度增大, 根据菲克第二定律, 扩散通量J增大, 这意味着锂离子从电解液向电极迁移的速度加快. 然而, 高倍率条件下, 颗粒内部动力学过程无法与电荷转移和离子扩散保持同步, 使得锂离子在负极表面的积累速率超过其嵌入颗粒内部速率. 这种不平衡导致负极表面锂离子浓度增大, 在较低电位处发生析锂.

      随后过充阶段, 低倍率充电导致负极析出锂金属的浓度高. 低倍率下充电引起的极化小, 因此在相同电压下低倍率具有更大的理论容量[13]. 由于颗粒内嵌锂容量有限, 低倍率过充时负极剩余容量相比高倍率更容易耗尽, 使得析出的锂金属浓度更高. 同时, 低倍率充电的电池产热比高倍率充电少, 并且较长的充电时间使得电池向环境散出更多的热量, 因此低倍率充电下的电池温度低, 如图7(b)所示. 而低温环境下锂离子的扩散动力学受阻, 嵌入效率变低, 更容易在负极表面积累, 从而加剧锂的析出现象[37].

      • 4.2.   过充模型的应力-应变分析

      4.2.1.   不同颗粒接触深度对最大应力-应变的影响

    • 充电过程中, 锂离子在正负极颗粒内不断脱出和嵌入, 在颗粒内部锂扩散引起的浓度梯度和外部约束(相邻的颗粒、黏结剂、导电剂等)的综合作用下, 颗粒内部会产生扩散应力. 如图8(a)所示, 电池在过充后, 正负极应力开始急剧上升, 而且当充电至4.34 V时, 正极应力开始大于负极应力, 原因为过充状态下正极材料的化学和结构特性比负极更容易发生变化[38]. 前期研究集中在石墨、硅碳等负极材料膨胀机制, 而正极材料直接影响电池的能量密度、功率密度和循环寿命[39], 因此本文应力部分重点分析NCM正极. 图8(b)为过充过程正极的应变-应力曲线, 电池在过充后, 正极应力开始急剧上升, 而应变开始急剧下降.

      颗粒的三维图形能够直观反映正极应力-应变的变化. 图9为正极颗粒在3.9, 4.2, 4.5, 4.8 V电压下应力-应变分布图. 可以看出电池过充后应力和应变急剧增大, 应力最大部分达到120 MPa以上, 且分布不均匀性加剧. 在颗粒互相接触区域, 表现出较大的局部应力, 同时收缩的颗粒在接触部位出现了正应变, 导致颗粒间接触区域容易发生破裂, 难于维持颗粒内和颗粒间的结构稳定性. 值得注意的是, 当粒径不同的正极颗粒直接接触时, 其在脱锂化过程中的体积变化不一致. 由于接触界面区域缺乏足够的空间来容纳这种体积变化, 收缩的颗粒可能会对邻近的颗粒施加拉伸力, 在接触处存在一个较高的应力集中区. 本文选取不同粒径的颗粒组合进行分析.

      图10(a)为4组相互接触的颗粒在接触处的应力-应变曲线, 对应的颗粒组合位置如图10(b)所示. 按照与隔膜的距离依次排列, 颗粒粒径分 别为9.55 μm-5.31 μm(A), 9.55 μm-6.80 μm(B), 6.80 μm-3.18 μm(C), 6.80 μm-5.85 μm(D). 从 图10(a)可以看到, 4组颗粒接触应力大小的总体关系为: A > D > C > B, 但该应力关系与靠近隔膜的距离不一致. 对比4组颗粒的体积比, 其大小关系为: C (46.7%) < A (55.6%) < B (71.2%) < D (86%), 同样与应力大小关系不同. 可以推断, 除颗粒靠近隔膜的距离与颗粒组合体积差外, 存在影响接触应力特性的其他因素. 本文为了更好地描述颗粒接触应力规律, 计算了接触面到颗粒中心的距离与颗粒半径的比例, 定义为接触深度${J_{\text{r}}}$:

      式中, $ r_{{\mathrm{pl}}-{\mathrm{o}}} $和$ r_{\mathrm{p2}-0} $分别为接触面到颗粒中心的距离, $ r_{{\mathrm{pl}}} $和$ r_{{\mathrm{P}} 2} $分别为两个颗粒的半径. 根据计算结果对接触深度进行比较, 从小到大排序为A (1.6%) < D (1.8%) < C (2.9%) < B (8.8%), 表现出与接触应力大小的完全负相关特性. 此外, 从图10可见, A, C, D接触处的应变随充电进程而增大, 而B组应变表现为缓慢的下降趋势, 原因可能是两个颗粒接触得越深, 有更多的空间来应对两个颗粒间体积的变化, 从而避免了应力集中. 因此, 提出的接触深度计算方法能够反映过充时正极颗粒间应力特性, 即接触应力与接触深度成反比关系, 可为电池材料设计提供参考.

      • 4.2.2.   电池产热对应力-应变的影响

    • 如模型构建部分所述, 充电过程中内部电化学反应会产生热量, 导致温度变化, 进而引起正极材料的热膨胀. 由于各组分材料热膨胀系数的差异, 并且温度分布不均匀, 电极不同部分的热膨胀程度不一致, 直接影响正极颗粒的应力-应变大小. 图11(a), (b)对比了是否考虑产热效应的冯·米塞斯应力, 并进行了归一化处理. 其中, 实线代表考虑了产热与换热边界条件(环境温为293 K)的应力, 虚线则表示不考虑产热且保持温度恒为293 K时的应力. 从图11可以看出, 在0.2C和0.5C倍率下过充至4.8 V时, 考虑了热效应的应力分别比不考虑的情况高出2.01%和6.03%.

      高倍率充电会产生更多热量, 从而引起更显著的温度变化(见图7). 电化学反应和物性参数, 如负极反应速率系数(${Y_{{\text{k1\_neg}}}}$)、正极反应速率系数(${Y_{{\text{k1\_pos}}}}$)、析锂反应速率系数(${Y_{{\text{k2\_neg}}}}$)、液相离子电导率系数(${Y_{{\text{σe}}}}$)和液相扩散系数(${Y_{{\text{De}}}}$)等, 均为温度的函数, 可通过Arrhenius方程(见(28)式)计算. 图11(c), (d)展示了0.2C和0.5C倍率充电过程中温度相关系数随时间的变化. 在0.2C和0.5C倍率下, 这些值分别增大1.508, 1.296, 1.334, 1.188和1.517倍以及3.224, 2.096, 2.277, 1.637和3.278倍. 可以看出, 高倍率下温度相关参数增加更为显著, 导致内部电化学反应速率增大, 使得颗粒内部锂离子浓度梯度增大, 对应力的影响增大.

    5.   结　论

    • 本文建立了Li(NiCoMn)1/3O2/石墨电池在颗粒水平上的三维电化学-热-力耦合过充模型, 分析了模型在过充过程中的负极析锂和正极应力-应变特性. 得出以下结论: 1)由于颗粒粒径小的负极颗粒表面最大锂离子浓度高、表面析锂过电位低和平均冯·米塞斯应力大, 小颗粒表面更加容易析锂. 在高倍率下由于电荷转移和离子扩散速率快使得负极触发析锂时的电压低, 低倍率下由于极化和温度低使得负极表面析出的锂浓度更大. 2)锂离子电池过充的后半阶段, 正极应力大于负极应力, 并且正极颗粒接触紧密的区域有足够的空间适应颗粒的体积变化, 可减轻应力集中. 当考虑产热效应时, 与温度相关的电化学参数和锂浓度扩散梯度发生变化, 将导致正极应力发生改变.

    参考文献 (39)

目录

/

返回文章
返回