首页
登录
注册
-
微放电是放电空间在亚毫米以下量级的一种放电形式, 包括微介质阻挡放电、微电晕放电和微空心阴极放电等放电结构[1–4]. 微空心阴极放电(MHCD)是一种阴极为空腔状电极的微放电形式[5]. 由于空腔阴极结构, 放电时正离子团会在电场的作用下于孔中心形成“虚拟阳极”, 在阴极和“虚拟阳极”的综合影响下, 电子会在阴极孔腔内径向往复振荡, 增加了电子碰撞电离的频率, 从而产生高密度、高能量的电子. 这个过程又称“空心阴极效应”[5–7]. 因此微空心阴极放电与其他放电结构相比具有更高的带电粒子密度, 在废气处理、表面处理和光谱分析等领域有着广泛的应用[7,8].
在微空心阴极放电中, 一定条件下即使使用直流电源也会发生脉冲模式的放电现象, 即自脉冲放电. Truscott等[9]首先在氩气直流微空心阴极放电中观察到了自脉冲放电现象, 其自脉冲电流峰值可达到300 mA. 在其后的时间内, 人们对这种现象进行了广泛的研究. Aubert等[10]根据实验结果指出, 对于给定的MHCD几何形状和气体压强, 脉冲频率仅取决于平均电流. Qin等[11,12]通过实验研究发现, 如果镇流电阻过小, 气体击穿后放电立即转变为辉光放电或弧光放电, 不能实现自脉冲放电; 自脉冲的上升时间受工作气体、电极材料和气体压强的影响. 该上升时间随着压强的增加而减小, 但与放电电流无关. 同时, 在实验研究中, 人们发现自脉冲放电的电压和电流波形非常近似于电容器的充放电电压和电流波形, 因此人们认为这种放电模式可以等效于电容器的充放电过程, 在此基础上对其形成机理进行了分析. Hsu与Graves[13]利用可变电阻、电容器和电感器组成的放电单元, 通过将自脉冲放电假设为电容充放电以及自感现象, 构建电路模型模拟了微空腔阴极放电的自脉冲现象. Taylan与Berberoglu[14]发现, 将放电单元等效为与放电电流相关的双指数衰减函数时得到的模拟结果与实验更加接近. Lazzaroni与Charbrert[15]利用一种微空心阴极自脉冲放电等效电路模型, 研究了该放电结构的自脉冲放电现象, 并提出了自脉冲的产生机制与电容器充放电原理相似.
由上所述, 目前人们对微空心阴极自脉冲放电的模拟研究主要是从RLC电路出发, 将放电单元等效为电容、可变电阻和电感等, 从而模拟得到放电的电流和电压波形. 但是该模拟方法只能从电容器充放电角度对自脉冲放电的形成进行解释, 并不能揭示自脉冲放电形成的微观机制. Aubert等[10]利用高速相机拍摄得到了微空心阴极自脉冲放电的发光图像. 结果表明电流较高时阴极外表面有较强的发光, 而电流较低时阴极外表面没有发光. 但是由于特殊的空腔状结构, 无法从实验上测量得到空腔内的放电情况. 同时只是通过阴极外表面发光的变化也无法从微观角度解释自脉冲的形成机制. 因此为了进一步揭示自脉冲放电的微观机制, 本文利用实验与模拟相结合的方法, 研究了纯氩气环境中微空心阴极放电自脉冲放电的微观时空动力学过程.
-
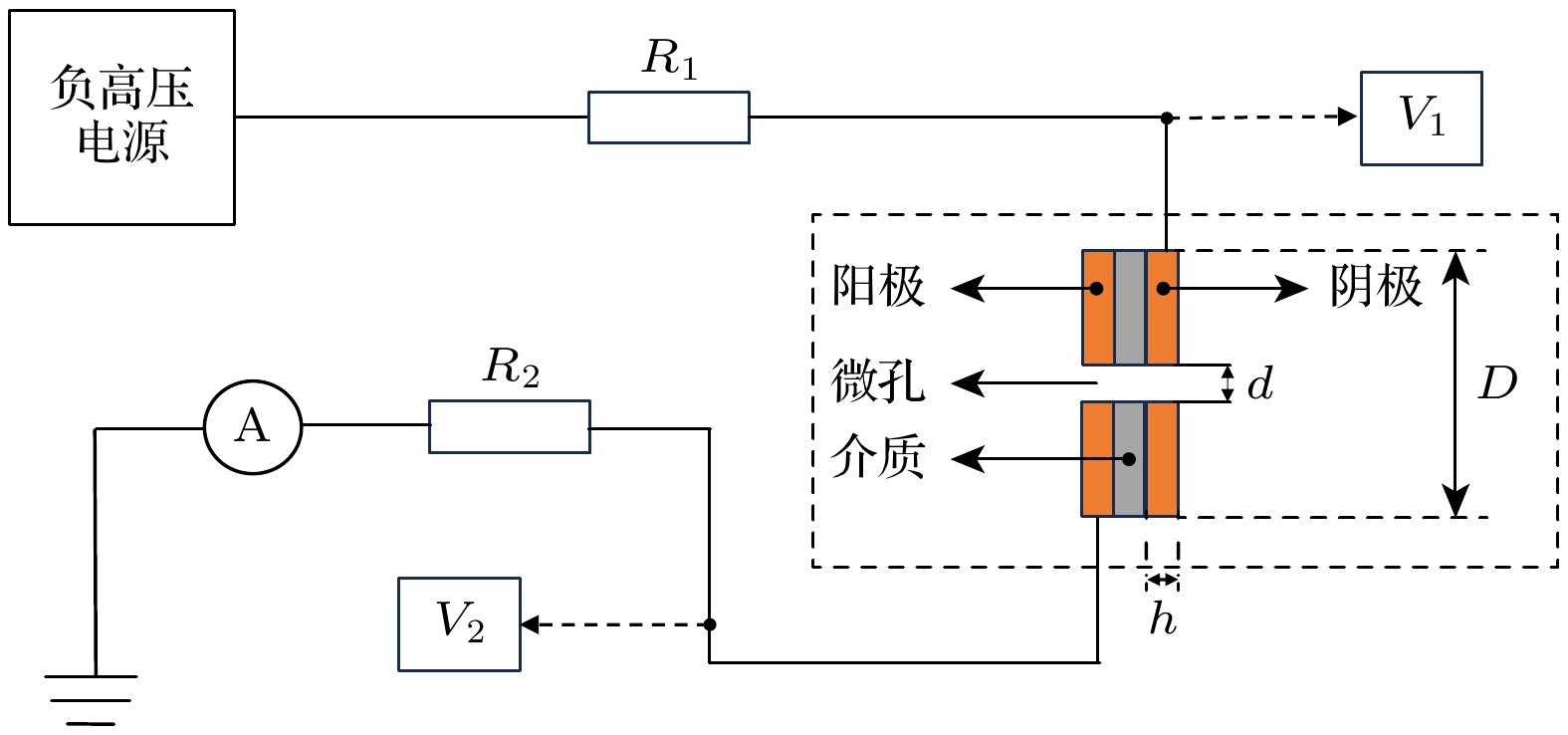
实验装置如图1所示, 放电电极是一种金属-电介质-金属夹层, 中间开有一直径d为1 mm的微孔. 阴极和阳极都是直径D为15 mm, 厚度h为1 mm的圆形钼箔, 电介质是厚度为1 mm的Al2O3陶瓷片. 电极系统放在真空室中. 直流负高压电源施加在阴极上, 阳极接地. 限流电阻R1 = 500 kΩ与阴极串联, 采样电阻R2 = 10 kΩ与阳极串联. 示波器通过电压探针记录V1和V2的电压波形, 放电电流通过采样电阻R2两端的电压V2来计算: I2 = V2/R2, 安培表与阳极串联, 以测量平均放电电流. 实验所使用的气体为纯度达到99.999%的氩气. 实验研究表明, 当气体压强为10 Torr (1 Torr = 133 Pa)时自脉冲放电较为稳定. 因此本文选取气体压强为10 Torr 时的结果为例进行介绍.
-
模型中参与反应的粒子包括电子(e)、氩原子(Ar)、氩离子(Ar+)、亚稳态原子(Ar*、Ar2*). 反应类型及方程参见表1.
本文采用迁移-扩散近似二维流体模型进行模拟研究. 该模型通过粒子密度的连续性方程、电子能量密度的连续性方程以及泊松方程进行联合求解, 具体模型参见文献[21,22]. 模型使用的电极结构和气压与实验一致.
粒子密度的连续性方程:
其中
${n_j}$ 表示粒子密度;${S_j}$ 表示粒子源项;$ {\varGamma _j} $ 表示粒子流密度. 直接电离反应速率${S_{}} = \alpha \left| {{\varGamma _{\mathrm{e}}}} \right|$ .$\alpha $ 和${\varGamma _{\mathrm{e}}}$ 分别表示汤生电离系数和电子流密度.电子能量密度的连续性方程:
其中
${n_{\text{e}}}$ 表示电子数密度;$\varGamma _{\varepsilon, {\mathrm{e}}}$ 表示电子能量流密度;$S_{\varepsilon ,{\text{e}}}$ 表示能量源项;${\varepsilon _{\mathrm{e}}}$ 表示电子平均能量.泊松方程:
其中
$\varphi $ 表示电势;$\varepsilon $ 表示介电常数;${q_{\mathrm{e}}}$ 表示基本电荷常量;${n_{\text{p}}}$ 和${n_{\text{e}}}$ 分别表示正电荷和电子密度. -
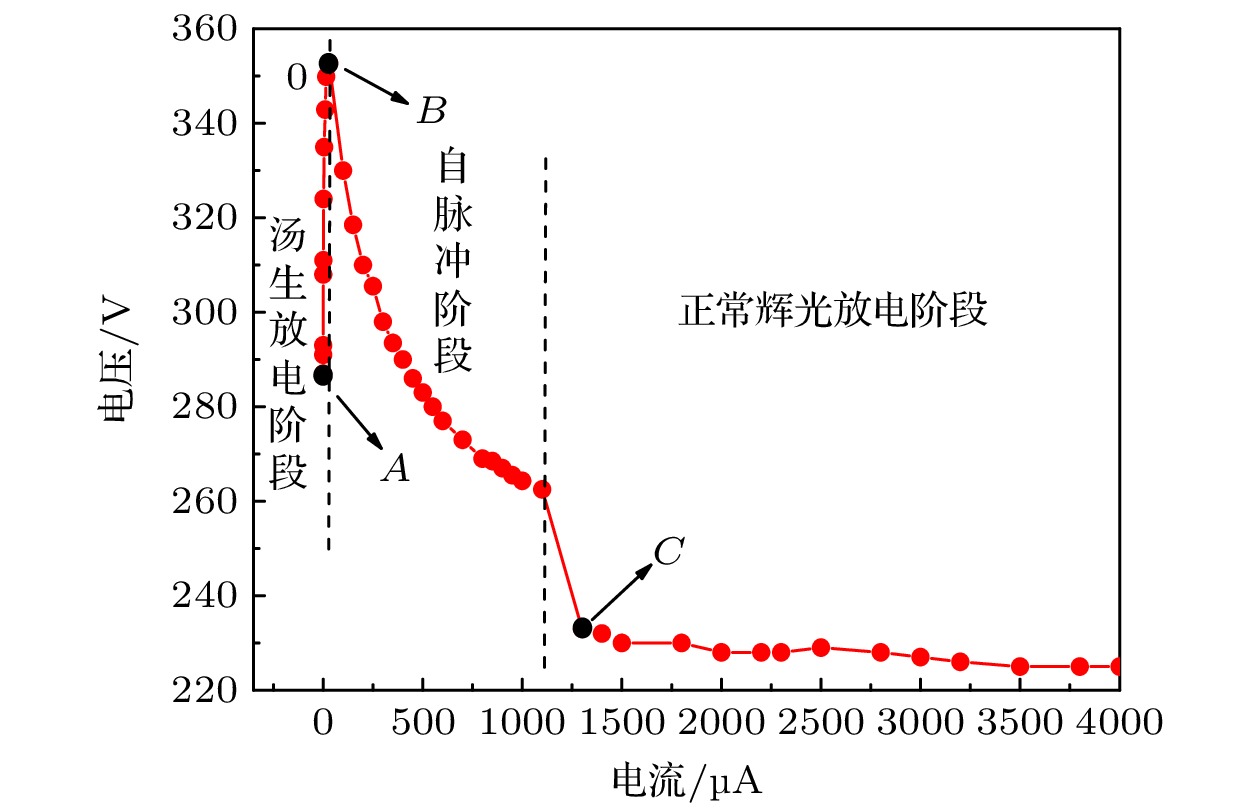
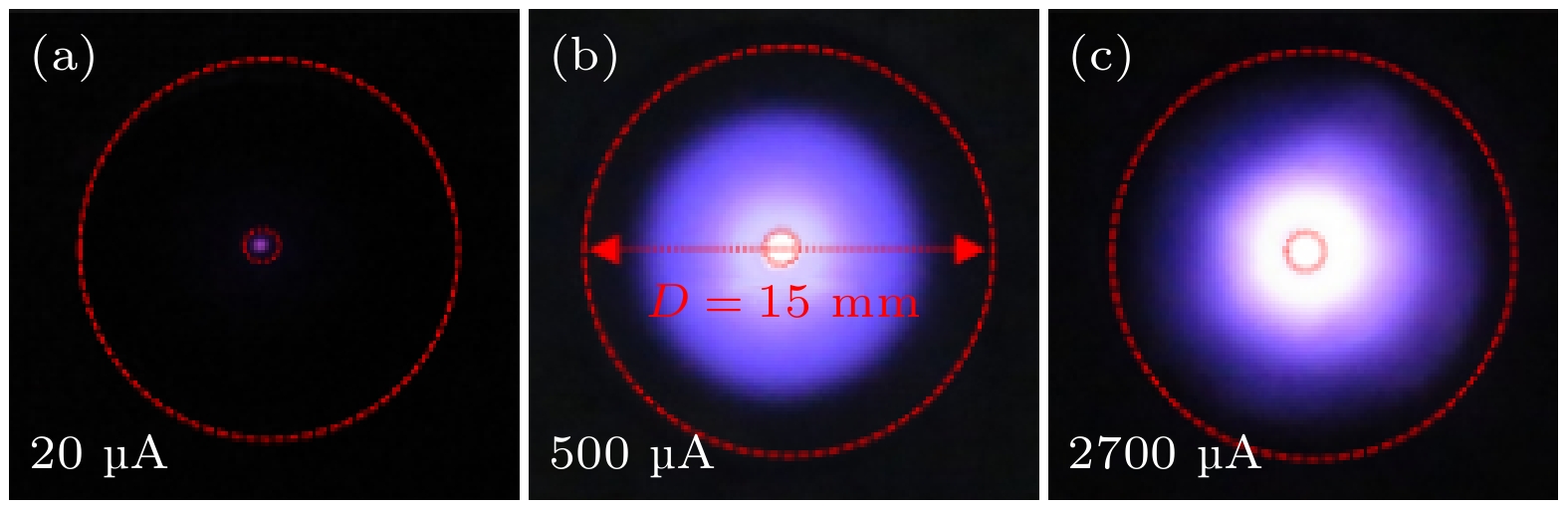
图2为实验测量得到的伏安特性曲线. 当平均电流小于30 μA时, 放电位于孔内, 放电很弱, 如图3(a)所示. 极间电压随着平均电流的增大而上升, 该阶段为汤生放电阶段, 即图2中的AB段. 结合下面模拟可知, 此阶段放电空间以较弱的轴向电场为主. 电场强度和电流的升高源于极间电压的不断升高. 当平均电流逐渐增大到30 μA, 极间电压升高到350 V时, 放电空间气体被完全击穿, 电离和激发速率迅速升高, 放电电流随之出现越变升高. 此时放电由稳态放电转变为自脉冲放电模式, 电压与电流呈现出稳定的脉冲波形. 由于外部限流电阻的作用, 极间电压迅速降低. 但是此阶段空间电荷层开始对空间电场产生扰动, 放电空间的电场主要由空间电荷层决定, 而不再依赖于外部电压. 因此, 随着平均电流的升高, 空间电荷层对电场的扰动增强, 造成放电空间特别是阴极位降区电场强度不断增强, 而极间平均电压反而逐渐减小. 当平均电流大于1100 μA时, 自脉冲现象消失, 放电转为直流放电模式, 极间电压出现明显的降低. 放电模式由自脉冲放电阶段转换为正常辉光放电阶段. 此阶段在阴极外表面已经具有较强的放电, 如图3(c)所示. 在正常辉光放电模式下, 放电电流的升高依赖于阴极表面放电面积的增加, 极间电压基本不随放电电流的升高发生明显变化.
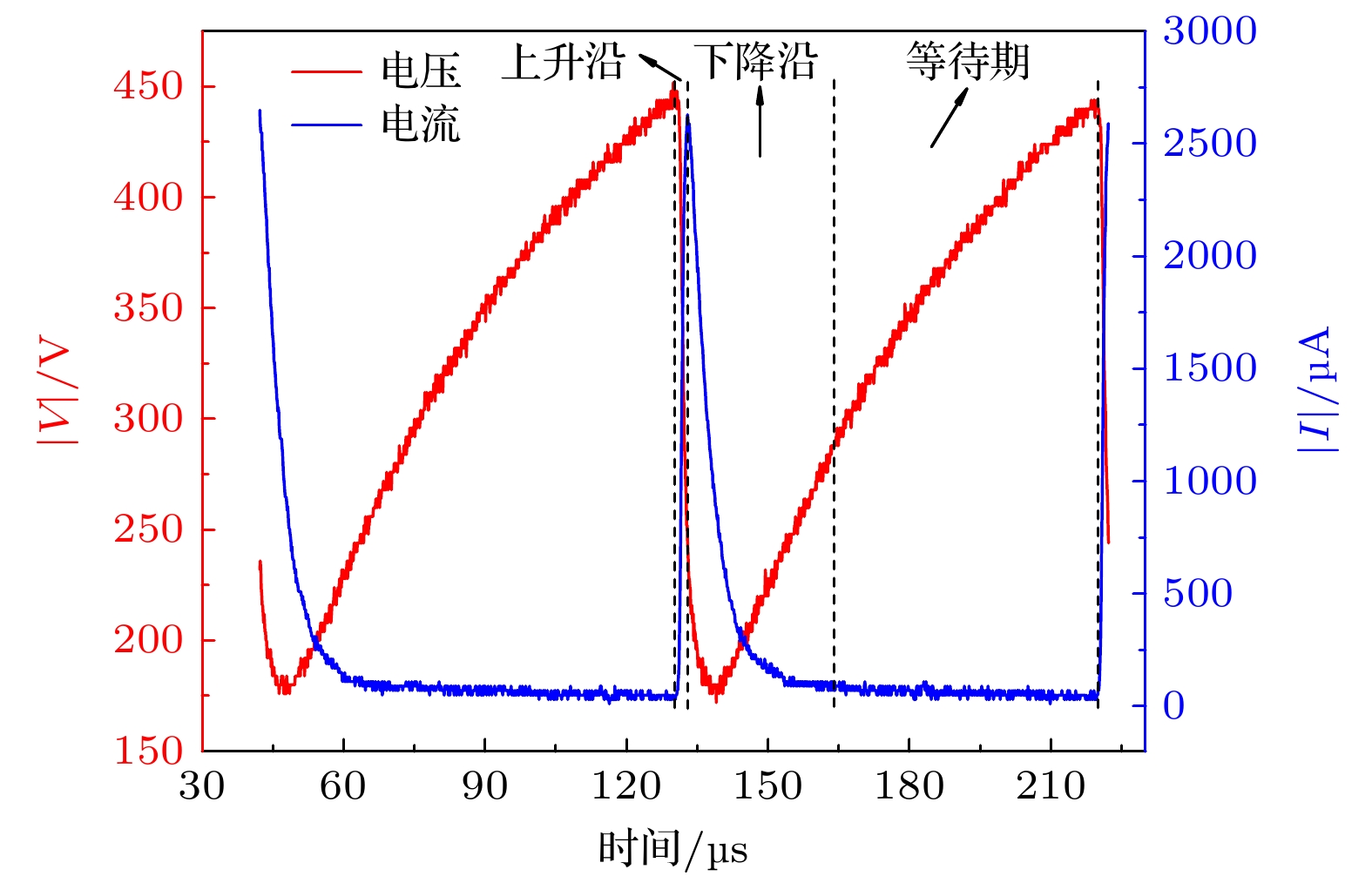
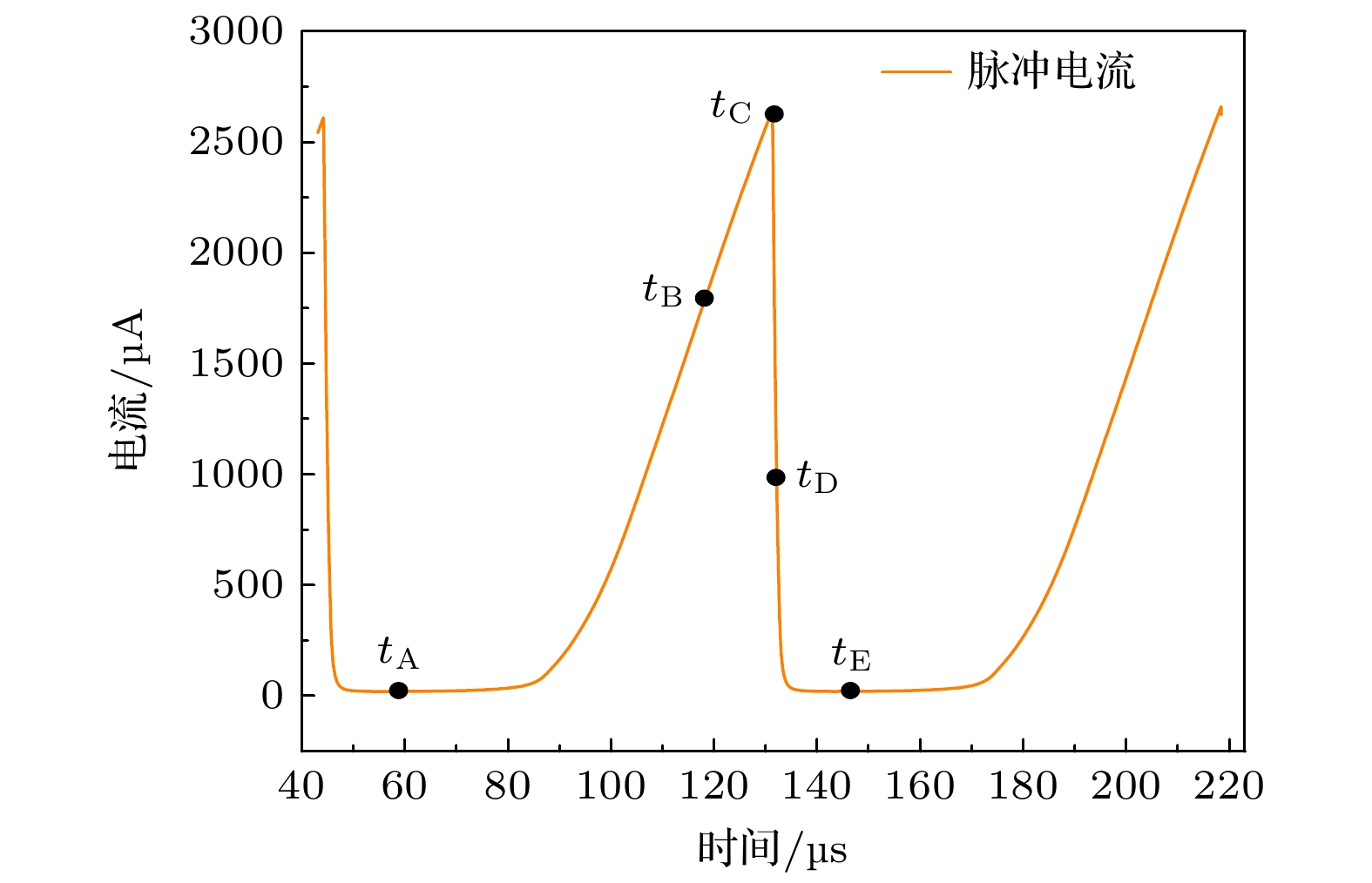
在自脉冲放电阶段, 放电电流呈现出规则的脉冲模式. 为了便于分析, 实验数据进行了取绝对值处理. 如图4所示, 一个完整的自脉冲放电周期可以分为三个阶段: 放电电流上升的上升沿, 放电电流下降的下降沿, 以及放电电流比较平稳的等待期. 当自脉冲放电电压从236 V缓慢增大到442 V期间, 电压还没有达到峰值, 放电间隙还没有击穿, 自脉冲放电电流处于放电等待期, 电流较低, 为28 μA, 放电等待期持续时间为65 μs. 当自脉冲放电电压继续增大到峰值时, 自脉冲放电电流迅速增大直至达到峰值2610 μA, 此为电流脉冲的上升沿阶段, 这一阶段变化快速, 持续时间约为2.3 μs. 当自脉冲放电电流达到峰值之后开始逐渐下降, 自脉冲放电电压也会继续下降, 此阶段为脉冲电流的下降沿, 将会持续25 μs, 直至下降到自脉冲放电电流的最小值, 进入到脉冲电流的等待期.
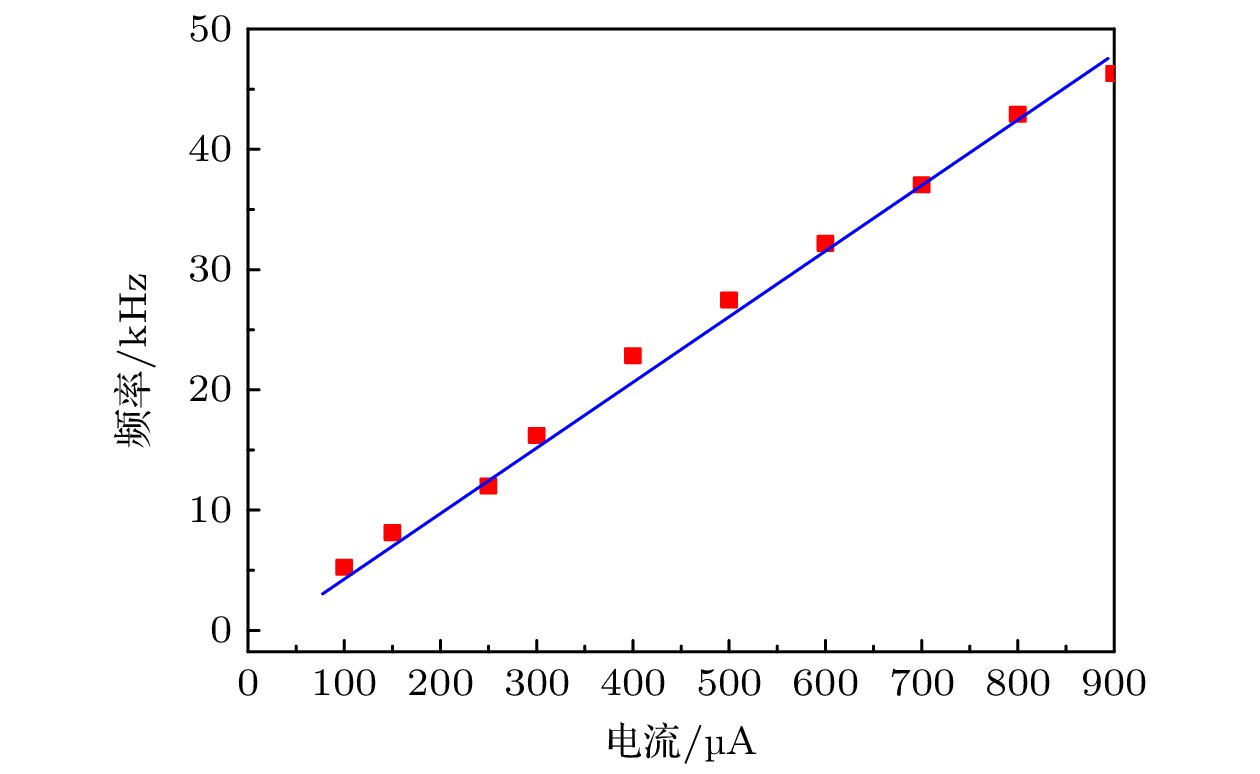
实验结果同时表明, 自脉冲放电频率随着平均电流的升高近似线性升高, 如图5所示, 这与已有文献结果相符[10,11,23]. 随着平均电流的升高, 放电空间电场强度增强, 因此更加有利于放电的击穿, 从而使自脉冲的等待期不断降低, 自脉冲频率升高[11,12].
-
不同课题组建立了不同的等效电路模型对自脉冲放电进行了仿真, 但是模拟得到的自脉冲电流波形和实验相差较大. 同时无论何种电路模型, 从放电本质而言, 自脉冲放电是在极间电压的作用下气体放电产生的. 部分文献也表明自脉冲放电应该源于放电的某些内部机制[23]. 本文主要目的是分析自脉冲放电的时空发展动力学过程, 因此本文在模拟部分将实验测量得到的极间电压作为阴极输入电压, 对自脉冲放电特性进行了模拟研究. 下面的模拟结果也表明利用本模型得到的模拟结果与实验结果也比较符合. 由于阳极外侧等离子体参量变化很小, 因此下面的模拟结果将截取主要放电空间的区域进行讨论.
-
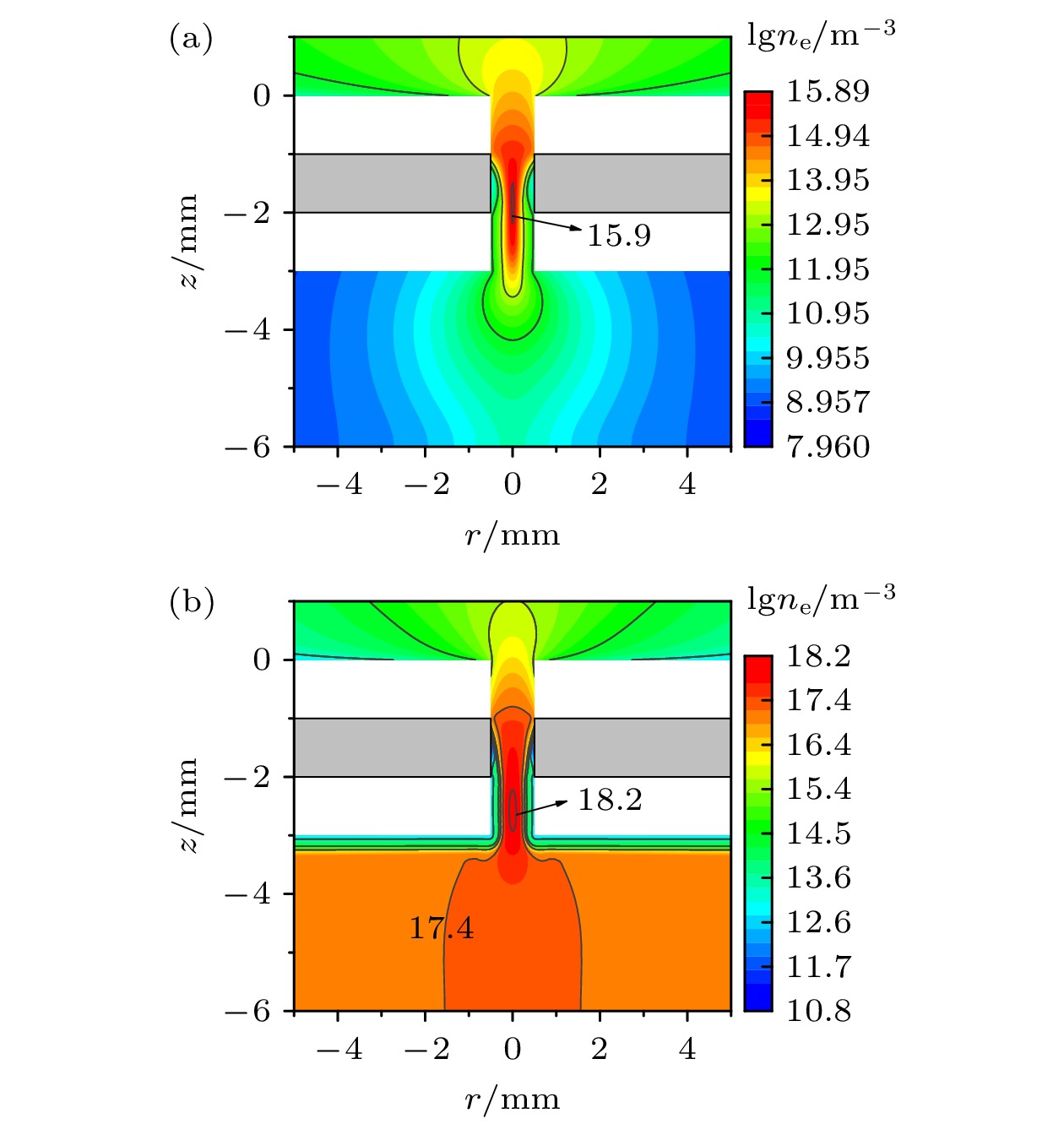
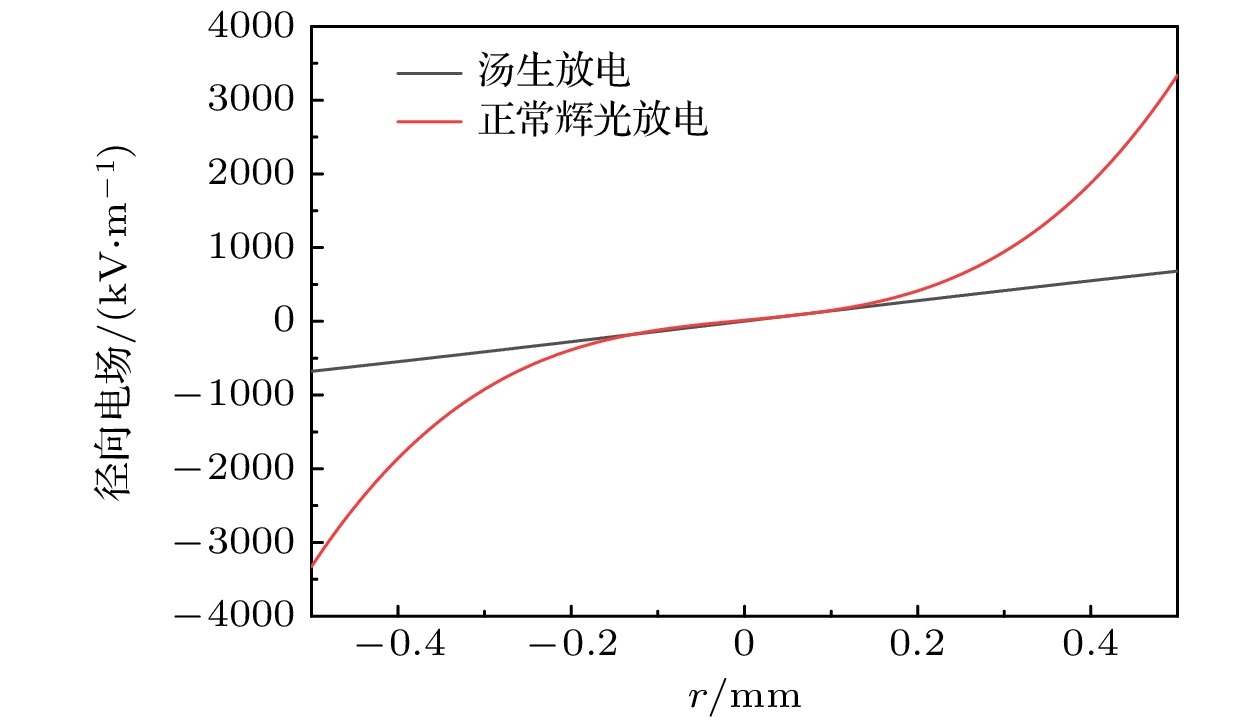
图6和图7为汤生放电模式和正常辉光放电模式下电子密度和径向电场分布图. 图6(a)为模拟得到的放电电流为20 μA汤生放电模式下的电子密度分布. 此阶段, 整个放电空间的电子密度很低, 在阴极孔内电子密度较高, 但是其峰值也仅为7.94
$ \times $ 1015 m–3. 此放电模式下径向电场较弱, 径向电场峰值仅为670 kV/m, 没有明显的阴极鞘层形成. 由以上分布特性可知, 此阶段只有在放电孔内具有较强的放电, 孔外基本没有明显的放电, 与实验测量结果图3(a)相符. 图6(b)为模拟得到的放电电流为3000 μA时的正常辉光放电模式下的电子密度分布. 此阶段, 虽然电子密度峰值仍然位于孔内, 但是此时阴极孔外也出现了较大面积的高密度等离子体, 阴极孔外的电子密度达到1017 m–3. 同时阴极孔内径向电场强度大大提高, 径向电场强度峰值达到3330 kV/m, 阴极孔内已经形成显著的阴极鞘层结构. 由以上结果可知, 此阶段阴极孔外已经具有较强的放电, 与实验测量结果图3(c)相符. -
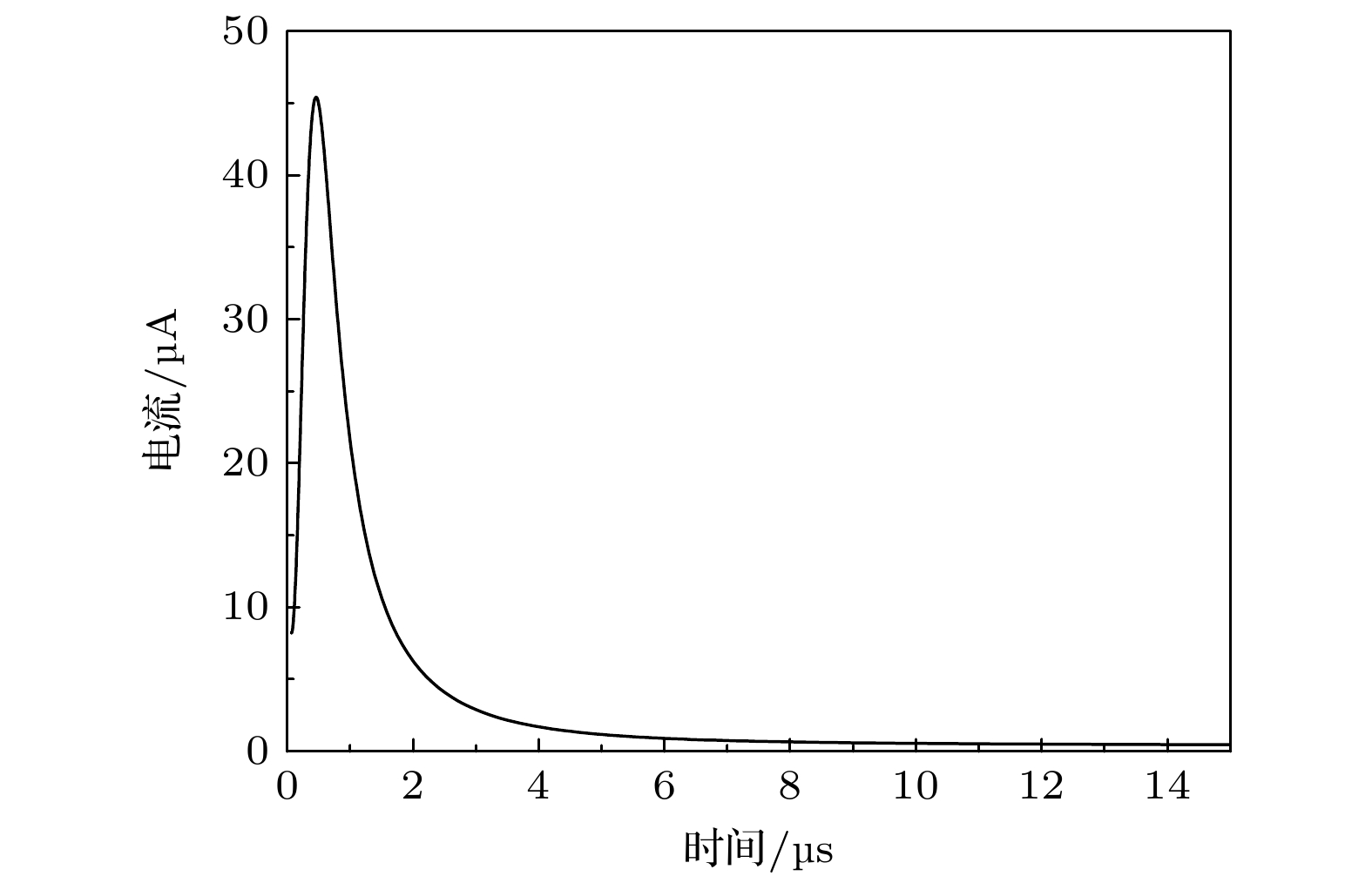
本部分以平均电流250 μA为例, 对自脉冲放电的时空分布特性进行模拟研究. 图8为平均电流为250 μA时模拟得到的自脉冲放电电流.
与图4所示实验结果相比, 模拟得到的放电电流波形能够比较好地反映出一个自脉冲周期的三个阶段: 脉冲上升期, 下降期, 以及等待期. 模拟得到的自脉冲电流峰值和最低值与图4中所示实验结果也符合较好. 实验测量得到的自脉冲电流峰值为2610 μA, 电流最低值为28 μA; 模拟得到自脉冲电流峰值为2644 μA, 最低值为23 μA.
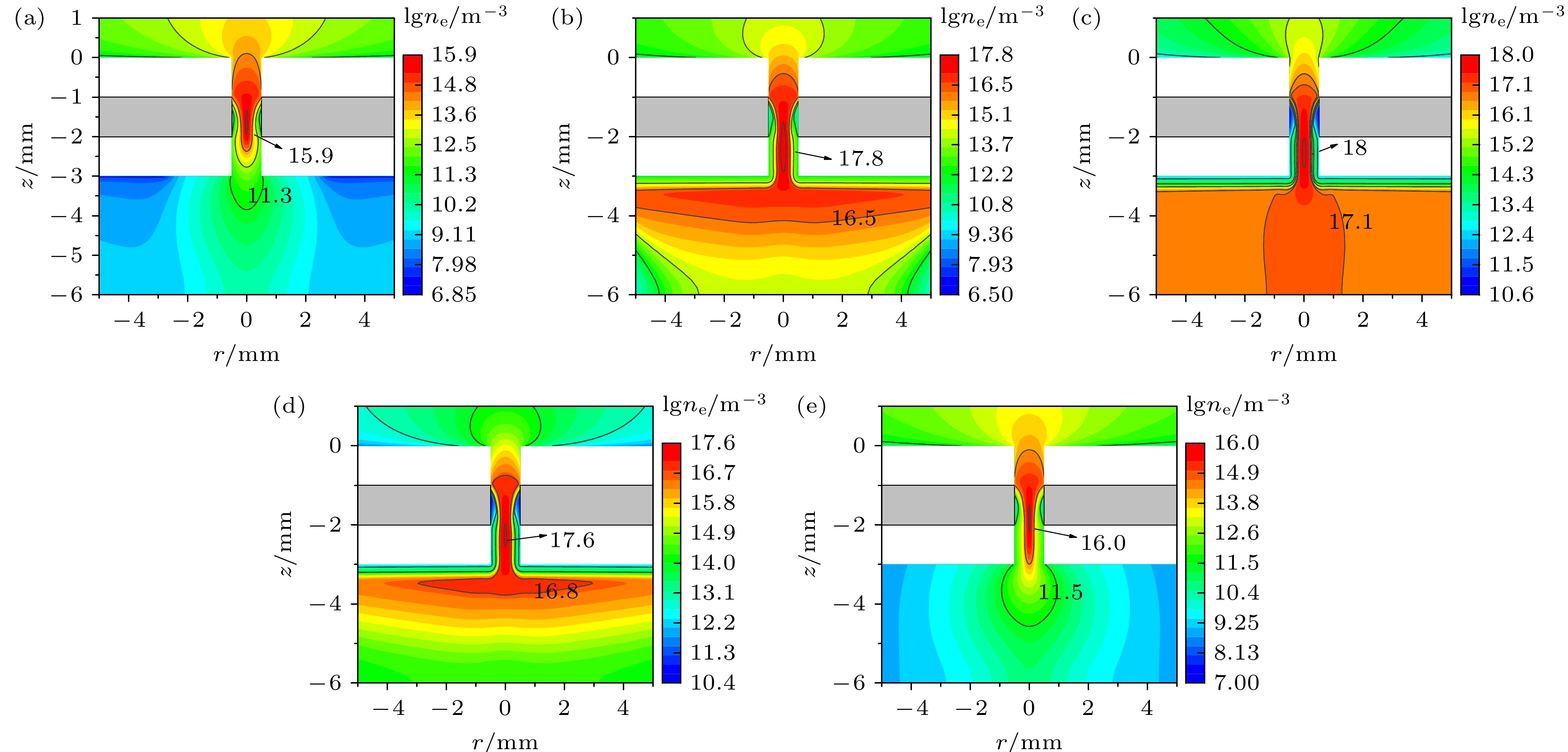
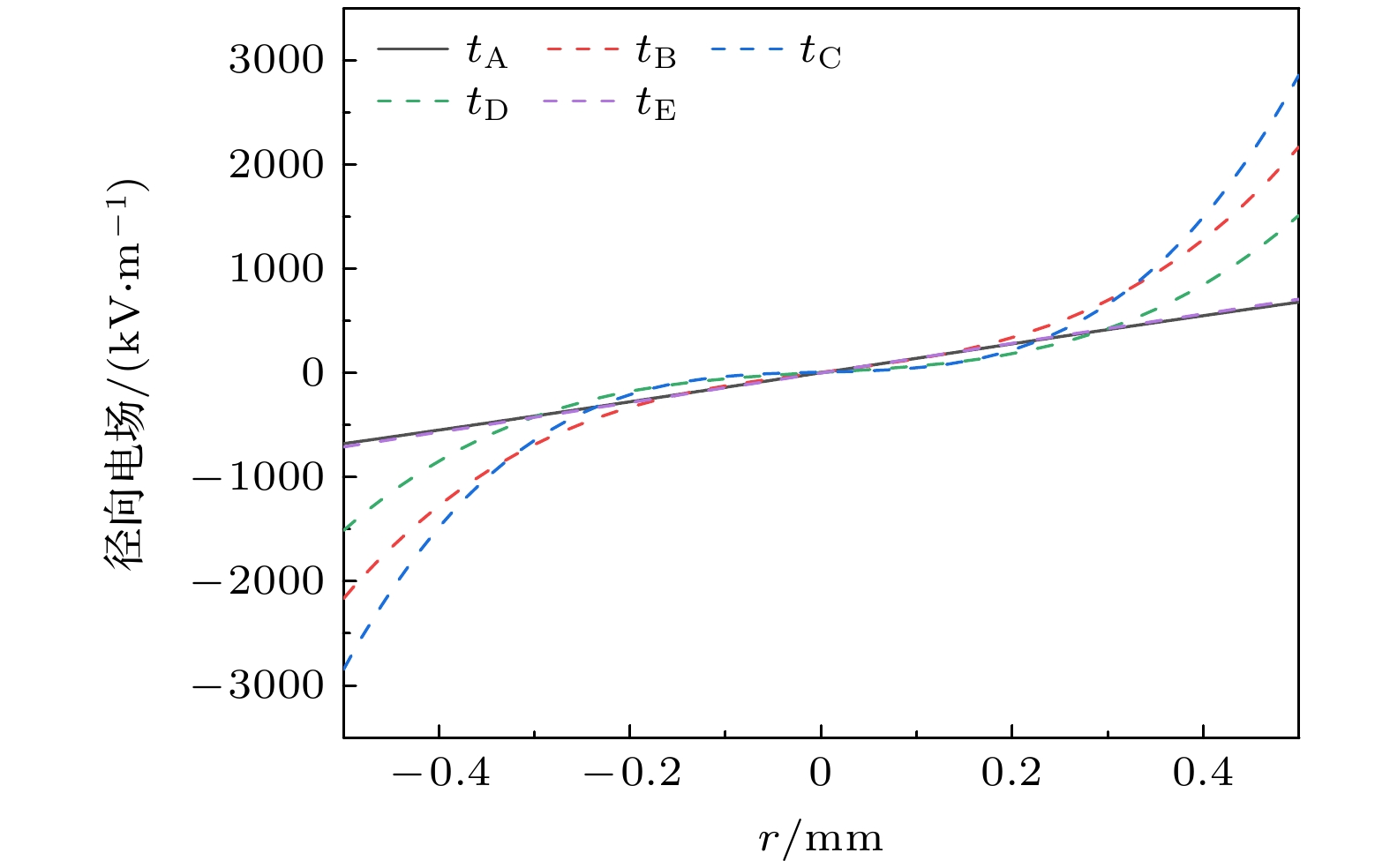
图9和图10是图8中对应的不同时刻的电势和电子密度分布图. 图11为z = –2.5 mm处径向电场随时间变化的一维分布图.
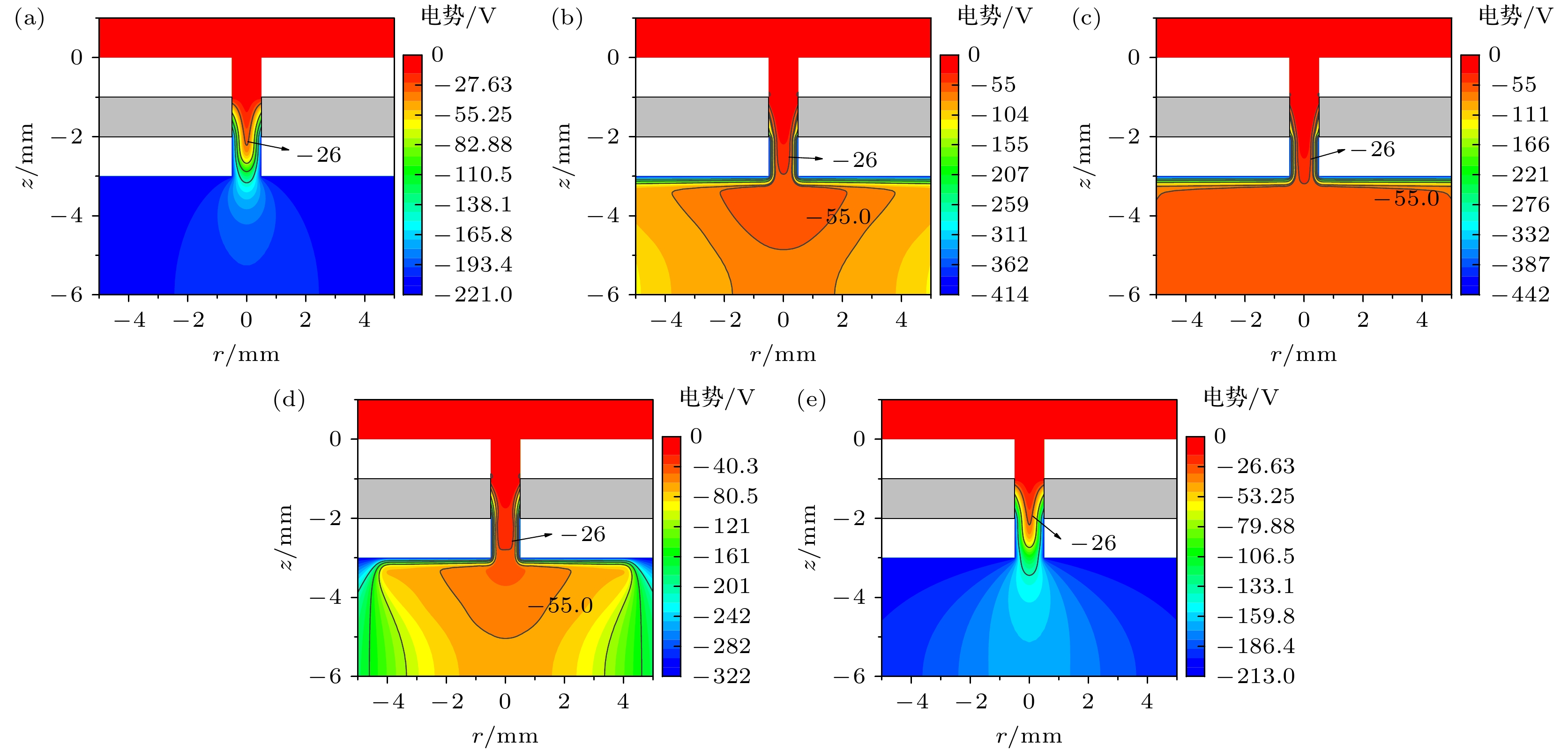
图9(a)是tA = 58.9 μs时, 自脉冲电流最小时的电势分布图. 该时刻在阴极孔中轴线上的等势线比较密集, 说明该区域在轴向上存在较大的电势梯度, 即存在较高的轴向电场. 同时–26 V的电势线刚发展到阴极边缘. 阴极孔内径向电场强度处于较低值, 只有677 kV/m. 由图10(a), 高密度电子主要集中在阴极孔内, 其峰值为1
$ \times $ 1016 m–3, 孔外的电子密度很低, 其值在1012 m–3以下. 电势和电子密度的分布特征说明了此时放电被限制在阴极孔内. 该阶段放电特性和图6(a)所示低电流时的稳态汤生放电模式相似.随着放电的继续发展, 当tB = 118.1 μs时, 由图9(b)可知, 高电势等势线从阴极孔内向外扩张. 在tA时刻位于介质和阴极交汇处的–26 V的电势线沿着阴极孔中心线向下发展, 已经到达阴极中心位置. 同时阴极外表面已形成较密集的等势线, 说明在阴极外表面附近已经存在较强的电场. 与tA时刻相比, 阴极孔内的电子密度显著升高, 此时电子密度峰值达到6.31
$ \times $ 1017 m–3, 阴极孔外的电子密度也处于较高值, 其电子密度超过1016 m–3, 如图10(b)所示. 同时阴极孔内径向电场峰值由677 kV/m增大到2164 kV/m, 而阴极鞘层也初步形成. 由上所述可知此时刻放电区域已经延伸到阴极孔外. 在tC = 131.3 μs, 放电电流达到了最大值2644 μA. 由图9(c)可知, 高电势进一步向阴极方向发展, –26 V电势线已经发展到阴极孔口, 孔内阴极鞘层变窄, 电势降升高. 因此径向电场强度较tB时刻进一步增强, 达到2846 kV/m. 同时阴极外表面电势线变密, –55 V的电势线向阴极外表面靠近, 这表明阴极外表面附近电场强度得到了进一步增强. 由图10(c), 电子密度与tB时刻相比继续升高, 孔内峰值已经达到1$ \times $ 1018 m–3. 放电区域继续向阴极孔外延伸, 孔外的电子密度继续增大到1017 m–3量级. 此时刻放电特性与图6(b)所示正常辉光放电模式下的放电特性相似.当放电电流上升到最大值后, 随着放电继续进行, 自脉冲电流出现下降的情况. 在tD时刻, 放电空间的电势、电子密度以及径向电场强度都出现下降. 与tC时刻相比, 该时刻的放电强度明显减弱了. 该时刻的高电势等势线开始由孔外向孔内收缩, –26 V电势线移至阴极轴向中心区域, 而–55 V电势线已经向内收缩到阴极孔口附近. 该时刻孔内的电子密度比tC时刻电子密度明显降低, 峰值已经下降到3.98
$ \times $ 1017 m–3, 同时孔外高电子密度电子向孔内收缩. 径向电场强度也降低到1511 kV/m.在tE时刻, 放电电流已经减小到了23 μA, 与tA时刻对应的脉冲电流大小基本一致. 由图9(e)、图10(e)和图11可知, 此时刻电势、电子密度和电场与tA时刻接近: 阴极附近电势降较低, 径向电场减弱, 没有明显的阴极鞘层结构; 只有在孔内具有较高密度的电子.
-
利用本模型模拟得到的自脉冲放电的电流上升沿比实验测量得到的结果要长. 这主要是由于放电模拟过程中的电流衰减延迟效应造成的. 图12为极间电压270 V时模拟得到的放电电流随时间变化图. 在实验中, 只有当电压超过击穿电压时放电空间才能被击穿并产生明显的放电电流. 但是在气体放电的模拟中即使极间电压低于击穿电压, 由于电势差的存在, 放电空间也存在较弱的电场. 而在自脉冲放电的等待期, 放电电流不为零, 存在一微弱的电流, 即存在一定数量的带电粒子. 这些种子电子在电场的作用下向阳极运动, 而正离子向阴极运动. 由于电子和离子运动速度的差别, 在空间会产生一弱的正空间电荷层, 从而会在局部增强放电. 因此即使在较弱的电场和较低的电子能量下, 空间电荷和电场强度在放电开始的短时间内也会出现升高, 从而造成放电电流的微弱升高, 如图12所示. 但是由于极间电压过低, 其产生的空间电场不足以维持放电的持续增强. 同时由于电荷在边界的扩散以及电极表面带电粒子损失等因素的存在. 整个空间的电场强度和带电粒子密度达到一定值后会逐渐减弱. 放电电流随之降低到极低值或者为零, 如图12所示. 这种在较低电压下的放电延迟衰减或熄灭现象是气体放电中模拟中的一种常见现象[24,25]. 因此在一低于击穿电压的恒定电压下, 放电最终会维持在一个电流极低或者熄灭的状态.
以上结果说明, 在较低的电压下, 虽然放电最终会达到一个极低或者为零的电流值, 但是需要一定的时间延迟. 由于自脉冲放电过程中, 极间电压是连续上升的, 而且电压和放电电流最低值也不为0. 因此即使极间电压低于击穿电压, 由于放电熄灭延迟效应的存在, 在自脉冲的等待期放电电流也不为0. 并且在到达击穿电压之前, 当极间电压达到较高值时, 随着极间电压的升高放电电流会出现明显的升高, 造成模拟得到的自脉冲电流的上升沿要比实验中测量得到的略长.
实际上, 在其他放电结构关于自脉冲放电模拟的研究中自脉冲电流的上升沿时间一般也比实验要长很多[26,27]. 但是文献表明, 这种模拟和实验的差别对分析自脉冲放电特性没有显著影响. 而本文模拟得到自脉冲放电电流的波形比已有文献的报道更接近实验波形. 模拟得到的自脉冲放电电流波形可以比较好地反映自脉冲放电的基本过程: 上升期、下降期和等待期. 同时如上所述利用本模型模拟得到的稳态放电模式下的汤生放电和正常辉光放电模式下的放电特性与实验测量结果相符; 而模拟得到的自脉冲放电在孔外的演化过程与Aubert等[10]拍摄得到的自脉冲放电的发光图像也相吻合. 特别是本文主要目的为分析不同自脉冲阶段的等离子体参量演化过程, 而模拟得到的自脉冲电流峰值和最低值与实验结果符合较好. 实验测量得到的自脉冲电流峰值和最低值分别为2610 μA和28 μA; 模拟得到自脉冲电流峰值和最低值分别为2644 μA和23 μA. 综上所述, 本模型模拟得到的结果与实验结果是比较相符的.
-
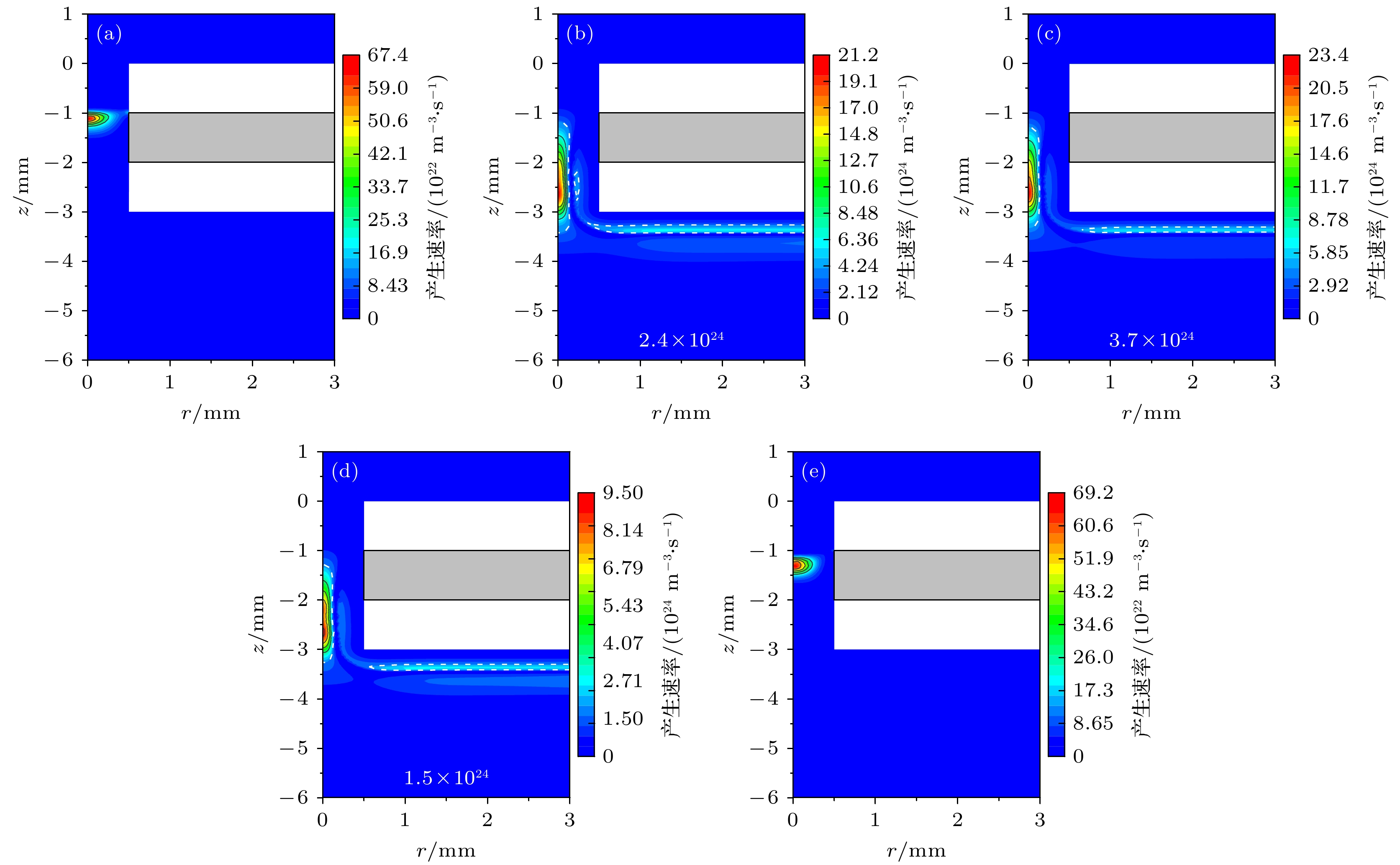
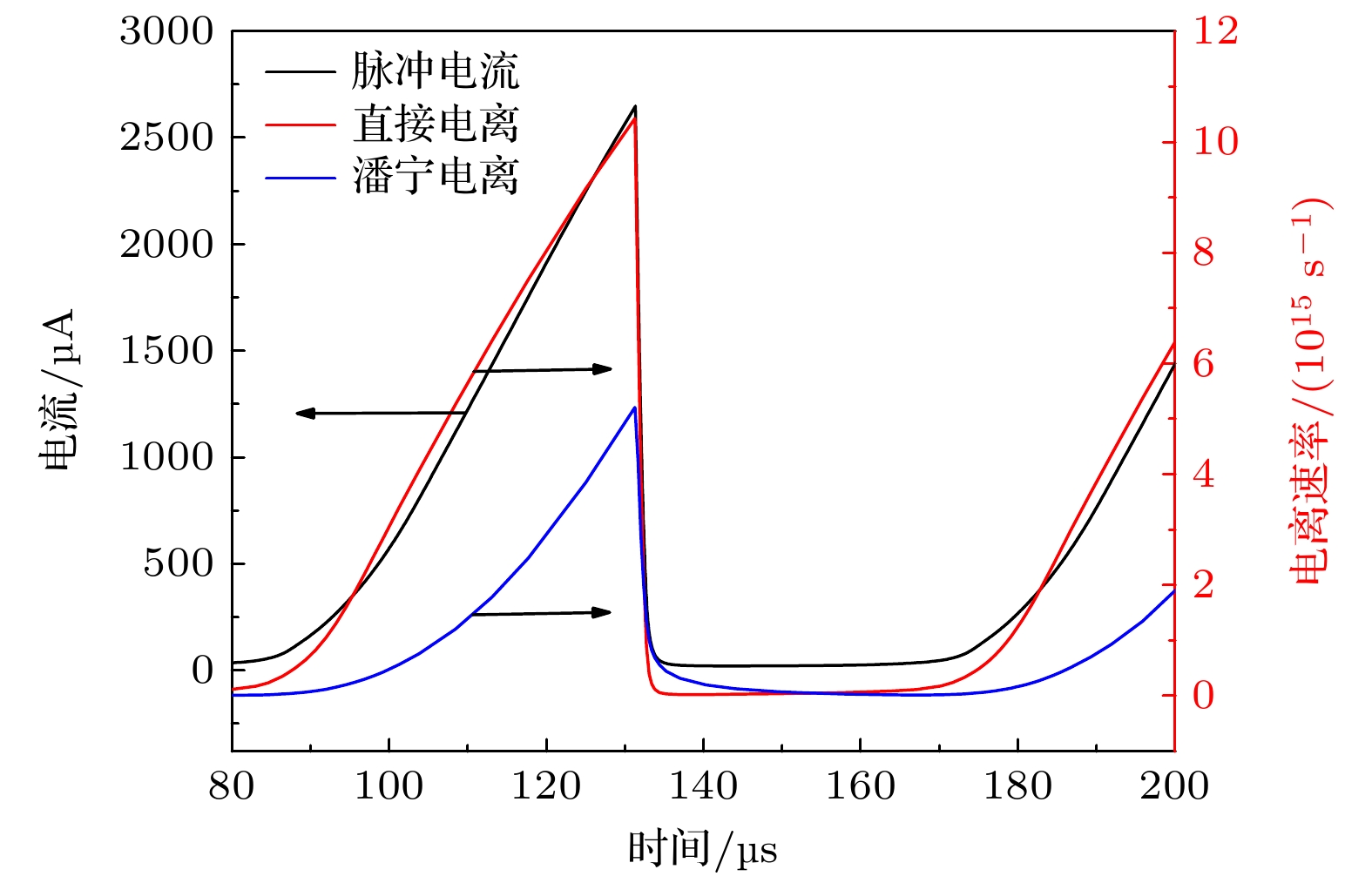
放电模式的转化与电子的产生直接相关, 图13为不同时刻的电子产生速率分布图. tA时刻电子产生速率相对较低, 速率峰值只有6.74
$ \times $ 1023/(m3·s), 并且高速率主要位于阴极孔中心区域. 因此该阶段放电很弱, 类似于低电流汤生放电模式. 而tB时刻的电子产生速率与tA时刻相比明显升高, 速率峰值增加到2.12$ \times $ 1025/(m3·s). 除了在孔的中心区域存在很高的电子产生速率, 在阴极外表面附近区域也存在较高的电子产生速率, 该区域的电子产生速率可以达到2.4$ \times $ 1024/(m3·s). 这主要是由于该阶段阴极外表面附近已存在较强的电场和电子能量, 因此促进了碰撞电离的产生. tC时刻的孔内和孔外的电子产生速率均达到一个脉冲周期的最大值, 孔内峰值为2.34$ \times $ 1025/(m3·s). 阴极外表面的电子产生速率可以达到3.7$ \times $ 1024/(m3·s). 这说明此阶段孔外也存在大量新电子的产生, 因此该时刻无论是孔内还是孔外均存在很强的放电, 该阶段为强放电的正常辉光放电模式. tD时刻的孔内和孔外电子产生速率均出现下降, 放电减弱. tE时刻的电子产生速率继续下降, 孔内峰值减小为6.92$ \times $ 1023/(m3·s), 同时速率分布特征与tA时刻相似, 阴极孔外不再分布有较高的电子产生速率, 放电模式转变为弱汤生放电.另外, 模拟研究表明, 自脉冲放电的不同阶段电子的电离源不同. 图14为自脉冲电流和不同电离反应速率的时间演化图. 本模型包括的电离反应包括直接电离Ar+e = Ar++2e, 分步电离Ar*+e = Ar++2e和潘宁电离Ar*+Ar* = Ar++Ar+e. 在整个脉冲周期内, 直接电离速率和潘宁电离速率远高于分步电离速率. 因此图14中未给出分步电离速率. 图14的反应速率为直接电离和潘宁电离分别在空间内总的积分电离速率, 即
$ {S_{tj}} = \displaystyle\int {{S_j}} {\text{d}}V $ . 由图14可知, 自脉冲放电的不同阶段, 电子的电离源不同. 当电流较高时, 直接电离速率要明显高于潘宁电离速率, 即新电子主要源于直接电离反应. 在自脉冲电流处于最低值的脉冲等待期, 潘宁电离速率要高于直接电离速率, 新电子的产生主要源于潘宁电离反应. 这主要是由于直接电离与电场和电子能量直接相关, 电场和电子能量越高, 电离速率系数越大. 如上所述, 电场强度和电子能量随放电电流的升高而升高. 因此当自脉冲处于等待期时, 整个空间电场强度和电子能量很低, 因此很难发生电子和氩原子的直接碰撞电离反应. 但是潘宁电离反应不受电子能量影响, 因此在脉冲等待期其反应速率要高于直接电离反应. 虽然根据模拟结果潘宁电离只有在放电电流最低的这一段很短的时间内高于直接电离速率, 但是本模型模拟得到的脉冲等待期时间要短于实验中的脉冲等待时间. 因此可以预期在实验中潘宁电离对于维持放电具有更加重要的作用. -
本文通过实验和数值模拟方法对纯氩气微空心阴极放电中的自脉冲放电现象进行了研究. 主要得到以下结论.
1)随着放电的进行, 放电分为汤生放电、自脉冲放电和正常辉光放电这三个阶段. 一个完整的自脉冲放电周期可以分为放电电流上升的上升沿, 放电电流下降的下降沿, 以及放电电流比较平稳的等待期.
2)实验和模拟结果表明, 低电流和高电流稳态放电模式分别为位于孔内的汤生放电和放电延伸至孔外的正常辉光放电模式.
3)模拟结果表明, 当自脉冲放电电流处于最小值时, 放电被限制在阴极孔内, 电场强度、电子密度均较低, 为汤生放电模式; 随着放电电流的增高, 孔内放电逐渐增强, 同时放电由孔内逐渐向孔外延伸. 当电流最高时, 孔外已经具有较强的放电: 孔外电子密度可以达到1017 m–3量级, 阴极外表面附近也形成明显的阴极鞘层结构, 存在很高的电场. 当放电电流降低时, 放电由孔外向孔内收缩. 当电流达到最低值时, 放电恢复到汤生放电模式.
4)不同自脉冲放电阶段电离源不同: 电流较高时直接电离起主要作用, 电流处于最低值时的脉冲等待期潘宁电离起主要作用.
5)微空心阴极自脉冲放电源于放电模式的转换, 为由低电流孔内汤生放电模式向高电流孔外正常辉光放电模式的转换过程. 电子产生速率对放电模式的转换具有重要的影响.
微空心阴极自脉冲放电微观动力学过程
Experiment and simulation on spatiotemporal microscopic dynamics of self-pulsing discharge in micro-hollow cathode
-
摘要: 为了进一步揭示自脉冲放电机理, 本文对氩气环境下的微空心阴极自脉冲放电进行了实验研究. 结果表明, 随着放电电流的升高, 放电分为汤生放电、自脉冲放电和正常辉光放电三个阶段. 一个完整的自脉冲放电周期可以分为电流的上升期、下降期以及放电的等待期. 本文同时利用流体模型对自脉冲放电的时空动力学特性进行了模拟研究. 模拟结果表明, 当自脉冲放电电流处于最小值时, 放电被限制在阴极孔内, 电场强度、电子密度和电子产生速率均较低, 为汤生放电模式; 随着放电电流的增高, 孔内放电逐渐增强, 同时放电由孔内逐渐向孔外延伸. 当脉冲电流最高时, 阴极孔外具有较强的放电, 阴极外表面附近形成明显的阴极鞘层, 阴极腔外部存在较高的电子产生速率. 当放电电流降低时, 放电由孔外向孔内收缩, 并逐步恢复到汤生放电模式. 模拟结果同时表明, 不同自脉冲放电阶段电离源不同: 电流较高时直接电离起主要作用, 电流处于最低值时的脉冲等待期潘宁电离起主要作用. 实验和模拟结果表明, 微空心阴极自脉冲放电实质上是放电被限制在孔内的汤生放电模式与放电区域延伸到孔外的正常辉光放电模式相互转换的过程.Abstract: To further explore the mechanism of self-pulsing discharge, a sandwiched microcavity cathode is used to study this phenomenon in argon. With the increases of discharge current, the discharge undergoes Townsend discharge, self-pulsing discharge and normal glow discharge. A complete self-pulsing discharge consists of the rising edge, the falling edge of the discharge current, and the waiting period of the discharge. The spatiotemporal dynamic characteristic of self-pulsing discharge is simulated by using a fluid model. The simulated results indicate that when the self-pulsing discharge current reaches its minimum value, the discharge is confined inside the cathode cavity. The electric field, electron density and electron generate rate are low, resulting in a Townsend discharge mode. As the discharge current increases, the discharge inside the cavity is strengthened, and the discharge gradually extends from the inside of the cavity to the outside. When the current reaches its maximum value, there exists a strong discharge outside the cavity, and an obvious cathode sheath is formed near the outer surface of the cathode, resulting in a high electron generate rate outside the cavity. When the discharge current decreases, the discharge shrinks from the outside to the inside of the cavity, and finally returns to the Townsend discharge mode. The simulated results also indicate that the ionization source varies depending on the stage of self-pulsing discharge, specifically, direct ionization is dominant when the current is high, and Penning ionization plays a major role in the pulse waiting period when the current reaches its minimum value. The experimental and simulation results indicate that the self-pulsing discharge in a micro-cavity cathode is essentially a process of mode transition between the Townsend discharge mode where the discharge is confined within the cavity and the normal glow discharge mode where the discharge region extends to the outside of the hole.
-
Key words:
- self-pulsing discharge /
- hollow cathode discharge /
- mode transition /
- fluid model .
-
-
图 3 不同放电模式下放电图像(红线小圆: 微孔; 红线大圆: 电极片)
Figure 3. The discharge images at different discharge modes (small red circle: cavity; large red circle: cathode electrode).
图 4 平均电流250 μA时的电压和电流脉冲波形图
Figure 4. Voltage and current pulse waveforms at an average current of 250 μA.
图 5 自脉冲频率随平均电流变化
Figure 5. The self-pulsing frequency as a function of average discharge current.
图 6 不同稳态放电模式下电子密度 (a)汤生放电模式I = 20 μA; (b)正常辉光放电模式I = 3000 μA
Figure 6. Electron density at different stable discharge modes: (a) Townsend discharge at I = 20 μA; (b) normal glow discharge I = 3000 μA.
图 7 稳态放电模式下z = –2.5 mm处一维径向电场
Figure 7. One dimensional radial electric field at z = –2.5 mm in stable discharge mode.
图 8 自脉冲放电电流模拟波形. tA = 58.9 μs, tB = 118.1 μs, tC = 131.3 μs, tD = 132.1 μs, tE = 146.3 μs
Figure 8. The simulated discharge current waveform. tA = 58.9 μs, tB = 118.1 μs, tC = 131.3 μs, tD = 132.1 μs, tE = 146.3 μs.
图 9 不同时刻电势分布图 (a) 58.9 μs; (b) 118.1 μs; (c) 131.3 μs; (d) 132.1 μs; (e) 146.3 μs
Figure 9. Electric potential at different time: (a)58.9 μs; (b) 118.1 μs; (c) 131.3 μs; (d) 132.1 μs; (e) 146.3 μs.
图 10 不同时刻电子密度分布图 (a) 58.9 μs; (b) 118.1 μs; (c) 131.3 μs; (d) 132.1 μs; (e) 146.3 μs
Figure 10. Electron density distribution at different time: (a) 58.9 μs; (b) 118.1 μs; (c) 131.3 μs; (d) 132.1 μs; (e) 146.3 μs.
图 11 不同时刻z = –2.5 mm处径向电场分布图
Figure 11. Radial electric field distribution at z = –2.5 mm at different time.
图 12 极间电压270 V时放电电流随时间变化图
Figure 12. Discharge current evolution with time at a voltage of 270 V.
图 13 不同时刻电子产生速率分布图 (a) 58.9 μs; (b) 118.1 μs; (c) 131.3 μs; (d) 132.1 μs; (e) 146.3 μs
Figure 13. Electron generation rate at different times: (a) 58.9 μs; (b) 118.1 μs; (c) 131.3 μs; (d) 132.1 μs; (e) 146.3 μs.
图 14 脉冲电流和不同电离速率时间演化图
Figure 14. The evolution of pulse current and different ionization rates with time.
表 1 碰撞反应类型
Table 1. Collision reactions in the model.
反应类型 反应方程 直接电离 $\rm Ar+e = Ar^+ + 2e $ [16]分步电离 $\rm Ar^*+e = Ar^+ + 2e $ [16]基态激发 $\rm Ar + e = Ar^* + e $ [16]弹性碰撞 $\rm Ar + e = Ar + e $ [16]潘宁电离 $\rm Ar^*+Ar^* = Ar^+ + Ar + e $ [17]两体碰撞 $\rm Ar^* +Ar = Ar+Ar $ [18]三体碰撞 $\rm Ar^*+2Ar = Ar_2^*+Ar $ [19]解激发 $\rm Ar^* + e = Ar + e + {\it hv} $ [19]复合反应 $ \rm Ar^+ + e + e = Ar + e $ [20]
下载: 导出CSV
-
[1] 王震, 赵志航, 付洋洋 2024 物理学报 73 125201 doi: 10.7498/aps.73.20240392 Wang Z, Zhao Z H, Fu Y Y 2024 Acta Phys. Sin. 73 125201 doi: 10.7498/aps.73.20240392 [2] Wei H C, Wang N, Duan Z C, He F 2018 Phys. Plasmas 25 123513 doi: 10.1063/1.5063450 [3] 邝勇, 章程, 胡修翠, 任晨华, 陈根永, 邵涛 2023 电工技术学报 38 3960 Kuang Y, Zhang C, Hu X C, Ren C H, Chen G Y, Shao T 2023 Trans. Chin. Electrotech. Soc. 38 3960 [4] 郭昱均, 季启政, 何锋, 廖劲松, 张宇, 欧阳吉庭 2019 高电压技术 45 820 Guo Y J, Ji Q Z, He F, Liao J S, Zhang Y, Ouyang J T 2019 High Voltage Eng. 45 820 [5] Saifutdinov A I, Sysoev S S 2023 Plasma Sources Sci. Technol. 32 114001 doi: 10.1088/1361-6595/ad05f6 [6] 赵立芬, 哈静, 王非凡, 李庆, 何寿杰 2022 物理学报 71 025201 doi: 10.7498/aps.71.20211150 Zhao L F, Ha J, Wang F F, Li Q, He S J 2022 Acta Phys. Sin. 71 025201 doi: 10.7498/aps.71.20211150 [7] Schoenbach K H, Kurt B 2016 Eur. Phys. J. D 70 29 doi: 10.1140/epjd/e2015-60618-1 [8] 欧阳吉庭, 张宇, 秦宇 2016 高电压技术 42 673684 Ouyang J T, Zhang Y, Qin Y 2016 High Voltage Eng. 42 673684 [9] Schoenbach K H, El-Habachi A, Shi W, Ciocca M 1997 Plasma Sources Sci. Technol. 6 468 doi: 10.1088/0963-0252/6/4/003 [10] Aubert X, Bauville G, Guillon J, Lacour B, Puech V, Rousseau A 2007 Plasma Sources Sci. Technol. 16 23 doi: 10.1088/0963-0252/16/1/004 [11] Qin Y, He F, Jiang X X, Xie K, Ouyang J T 2014 Phys. Plasmas 21 073501 doi: 10.1063/1.4885640 [12] Qin Y, Xie K, Zhang Y, Ouyang J T 2016 Phys. Plasmas 23 023501 doi: 10.1063/1.4941281 [13] Hsu D D, Graves D B 2003 J. Phys. D: Appl. Phys. 36 2898 doi: 10.1088/0022-3727/36/23/006 [14] Taylan O, Berberoglu H 2014 J. Appl. Phys. 116 043302 doi: 10.1063/1.4891250 [15] Lazzaroni C, Charbrert P 2011 Plasma Sources Sci. Technol. 20 2033 [16] Hagelaar G J M, Pitchford L C 2005 Plasma Sources Sci. Technol. 14 722 doi: 10.1088/0963-0252/14/4/011 [17] Ferreira C M, Loureiro L, Richard A 1985 J. Appl. Phys. 57 82 doi: 10.1063/1.335400 [18] Karoulina E V, Lebedev Y A 1992 J. Phys. D: Appl. Phys. 25 401 doi: 10.1088/0022-3727/25/3/010 [19] Biondi M A 1963 Phys. Rev. 129 1181 doi: 10.1103/PhysRev.129.1181 [20] Shon Jong W, Kushner M J 1994 J. Appl. Phys. 75 1883 doi: 10.1063/1.356334 [21] He S J, Wang P, Ha J, Zhang B M, Zhang Z, Li Q 2018 Plasma Sci. Technol. 20 054006 doi: 10.1088/2058-6272/aab54b [22] Fu Y Y, Verboncoeur J P, Christlieb A J 2017 Phys. Plasmas 24 103514 doi: 10.1063/1.5004681 [23] Cui R L, He F, Miao J S, Ouyang J T 2017 Phys. Plasmas 24 103524 doi: 10.1063/1.4997262 [24] Chen S, Li K L, Nijdam S 2019 Plasma Sources Sci. Technol. 28 055017 doi: 10.1088/1361-6595/aae554 [25] 高嘉懋 2022 硕士学位论文 (武汉: 华中科技大学) Gao J M. 2022 M. S. Thesis (Wuhan: Huazhong University of Science and Technology [26] Levko D, Raja L 2021 J. Phys. D: Appl. Phys. 54 235201 doi: 10.1088/1361-6463/abed0a [27] Arslanbekov R R, Kolobov V I 2003 J. Phys. D: Appl. Phys. 36 2986 doi: 10.1088/0022-3727/36/23/020 -
计量
- 文章访问数: 86
- HTML全文浏览数: 86
- PDF下载数: 0
- 施引文献: 0