-
20世纪90年代的ROSAT卫星从3个能带(1/4, 3/4和1.5 keV)探测宇宙弥漫热气体的分布[1,2], 但在1/4 keV能带的原始巡天观测数据中发现了大量不规则的带状结构[1], 这完全不同于3/4 keV波段的全天观测特征, 这说明1/4 keV波段的辐射与观测方向和时间相关, 而且这种辐射亮度变化的时间尺度也非常复杂、没有规律可循, 有数小时、数天或数月的不等周期, 被称为长期增强现象(long-term enhancement)[1]. Freyberg[3]发现这种亮度增强现象与太阳风参数存在关联, 随后Lisse等[4]在冷暗的百武彗星(Hyakutake)的观测中首次发现了X射线辐射信号. 这一发现颠覆了天体物理学家对X射线辐射的常规认识, 即通常认为X射线辐射是源于一个炽热(温度约百电子伏特)的等离子体源, 或是受到强辐射源(如黑洞、活动星系核、X射线双星等)的辐照产生的光电离辐射. 为解释彗星中观测到的X射线辐射, Cravens[5]提出了太阳风离子与彗星中氢原子和水气分子电荷交换的辐射机制, 即彗发中水蒸气分子(H2O)中一个电子在碰撞时被太阳风中的高电荷态离子(如O8+)俘获, 变成O7+的高激发量子态, 该量子态不稳定退激发产生X射线. 于是, Cox[6]和Cravens[7]进一步提出宇宙X射线背景中的长期增强现象可能就是源于太阳风与地球磁鞘层氢原子的电荷交换辐射所致. 随后, Wargelin等[8]利用月球暗夜区的钱德拉(Chandra)观测数据发现其X射线亮度变化与ROSAT巡天数据中3/4 keV波段的背景辐射相当, 证实了地球邻近空间是背景辐射的重要来源之一. 随后, 利用高能谱分辨、高探测效率的钱德拉(Chandra, NASA)、X射线多镜面-牛顿(XMM-Newton, ESO)空间望远镜, 天体物理学家在太阳系所有行星的观测中均发现了这种X射线辐射, 并获得了线辐射的观测证据[9]. 理论数值分析揭示这种X射线辐射主要来源于太阳风与行星大气相互作用的行星磁鞘层[10], 因此, 天体物理学家建议将这种X射线辐射用于研究行星大气鞘层大尺度结构, 因为其是一种很好的、廉价的远端探测太阳风与行星大气全局性结构的手段, 这为中欧联合联学卫星——太阳风与地球磁层相互作用全景成像卫星(SMILE)奠定了坚实的科学基础[11]. 这种辐射与太阳风的成分、速度、行星大气的成分、密度紧密相关, 因此观测数据的也可以用来诊断太阳风在当地的特征信息[12,13].
针对宇宙天体的观测, 这种辐射与太阳邻近空间(100 pc)热气泡和银河系晕热气体的辐射完全混合在一起, 难以从观测上分辨. 30年来, X射线观测天文学家借助于空间物理模型或太阳不同活动周期的观测数据对太阳风电荷交换贡献进行非常有限的约束, 一直没有很好地限定这种辐射对目标源分析的干扰. 这种辐射与热气体的辐射只有在高分辨的能谱上才有明显的区分特征, 比如类氦离子的三重线比值, 即电荷交换的禁戒线比共振线强, 而热辐射中禁戒线较弱. 近年来, Jin等[14]提出中国空间站银河系热重子探寻计划(DIXE), 其探测器具有<6 eV的能谱分辨能力, 可以有效地分辨类氦离子的三重线, 并有望在其巡天观测数据中从能谱的维度分离太阳风电荷交换对宇宙天体的前景干扰.
综上所述, 无论是SMILE卫星的成像数据反演[15], 还是爱因斯坦探针(EP)
1 和DIXE的能谱分析, 电荷交换辐射因子是核心物理参数. Schwadron和Cravens[16]利用类氢近似总截面、两步级联和平均分配各级联跃迁截面的方法给出了一些重要辐射线的辐射率研究彗星的电荷交换X射线辐射. Smith等[17]利用类氢近似获得恒定总截面的方法和电子俘获通道的近似处理方法, 结合其AtomDB原子数据库2 实现了高分辨电荷交换光谱计算的通用性. Gu等[18]通过收集公开的电荷交换截面数据给出了速度相关的电荷交换光辐射模型. Cumbee等[19]将团队20多年系列的、高精度计算截面结果整理形成了Kronos电荷交换截面数据库3 , 极大地提高了辐射因子计算结果的准确性. Liang等[20]发展的SASAL工具包提供了不同的电荷交换截面数据, 并考虑了双电子俘获的精确辐射因子计算模型[21]. 但最新的这些电荷交换模型应用于实测太阳风电荷交换辐射因子计算的工作极少, Whittaker和Sembay[22]采用实验截面研究了美国先进太阳风成分探测器(advanced composition explorer, ACE) 13年(1998—2011年)实测的O7+, 8+离子的辐射因子, 但该工作中没有考虑级联效应. 2024年, Koutroumpa[23]利用其发展的完备的电荷交换模型分类研究了ACE探测器13年的太阳风粒子不同起源的辐射因子, 但显示了与之前结果的巨大差异.本文利用我们近年来发展起来的电荷交换辐射计算方法, 通过收集ACE探测器13年的实测太阳风数据研究了SMILE和DIXE探测器能谱范围的太阳风离子与氢原子碰撞的辐射因子, 并探讨了其随太阳风粒子特征参数的统计分布关系. 中性氦原子在行星大气和行星际空间的数密度要小一些, 对总辐射的贡献也相对小些[24], 后续工作中将计算与氦原子碰撞的辐射因子. 结构安排如下: 第2节介绍了辐射因子的计算方法与电荷交换截面数据来源, 第3节讨论了ACE探测器实验太阳风粒子的统计分布, 第4节给出了电荷交换辐射因子及讨论分析.
-
太阳风离子(
$ X^{q+} $ )电荷交换辐射率可以表示为如下公式:单位是
$ {\rm eV\cdot cm^{-3}\cdot s^{-1}} $ , 其中$ n_{{\mathrm{sw}}}(r) $ 表示以地球为坐标中心不同空间位置r处太阳风质子数密度;$ n_{\rm H}(r) $ 表示不同空间位置r处中性氢原子数密度; 太阳风平均速度$ v_{{\mathrm{av}}}=\sqrt{v^2_{{\mathrm{sw}}}+v^2_{{\mathrm{th}}}} $ , 其取决于太阳风整体速度与离子热速度($ v_{{\mathrm{th}}}=\sqrt{{3 k_{\mathrm{B}}T}/{m_{\mathrm{p}}}} $ );$ \alpha^{q+} $ 是电荷为$ q+ $ 的太阳风离子电荷交换辐射因子, 文献[22]中采用如下公式:由于ACE数据中心提供的数据给出了这些元素(除H外)与O元素的丰度比, 所以
$ \left[\dfrac{{{X}}}{{\mathrm{H}}}\right] $ 可通过$ \left[\dfrac{{{X}}}{{\mathrm{H}}}\right]=\left[\dfrac{{{X}}}{{\mathrm{O}}}\right]\left[\dfrac{{\mathrm{O}}}{{\mathrm{He}}}\right]\left[\dfrac{{\mathrm{He}}}{{\mathrm{H}}}\right] $ 计算获得, 此外该公式中没有考虑辐射级联效应, 本文将(2)式中的$ \sigma^{q+}\; E $ 更换为$ \displaystyle\sum\nolimits_{ij}\epsilon_{ij}^{(q-1)+}\Delta E_{ij}/v_{av} $ , 其中俘获电子后$ {\mathrm{X}}^{(q-1)+} $ 离子线辐射率$ \epsilon_{ij}^{(q-1)+}\equiv\; N_jA_{ij} $ 是俘获电子后离子量子态j的布居数和自发跃迁速率$ A_{ij} $ 的乘积, 俘获电子后$ X^{(q-1)+} $ 离子量子态j的布居$ N_j $ 通过求解速率方程获得, 即其中r表示离子和中性气体数密度球对称分布情况下的不同空间距离. 该方法自洽地考虑了俘获电子后的级联过程. 从中可以看出, 除俘获电子后离子的能级与辐射系数
$ A_{ij} $ 外, 量子态分辨的电荷交换俘获截面是精确计算辐射因子的关键. 能级与辐射系数数据来源于我们早期的Sasal数据库[20], 该数据库类似于天体物理领域广泛使用的AtomDB数据库2 . 电荷交换截面数据主要采用我们发展电荷交换模型过程中收集的数据[21], C, N, O和Ne离子数据采用精确全量子的原子/分子轨道耦合计算结果, 对于Si, Mg和Fe的数据采用修正的Muller & Salzborn方法获得其总截面数据[25](见该文(1)式), 其总截面数值与Schwadron和Cravens[16]表1中所列出的结果一致. 对这些离子, 我们也采用Wargelin等[26]工作中描述的经验公式, 即$ \sigma=q\dfrac{A{\mathrm{ln}}(B/\tilde{E})}{1+C\tilde{E}^2+D\tilde{E}^{4.5}} $ (式中$ \tilde{E}=E/q^{0.5} $ , q是离子电荷, A, B和C是系数), 该公式是基于经典轨迹蒙特卡罗计算结果, 其精度在临界碰撞能量($ E_{{\mathrm{crit}}}\sim 25\sqrt{q} $ keV/amu)下好于30%. 截面数据具体来源情况在表1列出.Janev和Winter[31]揭示电子俘获通道具有选择性, 其俘获后的最大主量子数是:
其中
$ I_{\rm neu} $ 是碰撞中性气体的电离势(采用原子单位), 即本文中氢原子, q是碰撞前离子的电荷. 总截面在轨道量子态的分配方法与文献[17, 18]的方法一样, 这里不再详述. -
本文采用ACE官方网站上提供的1998年至2011年8月的探测数据
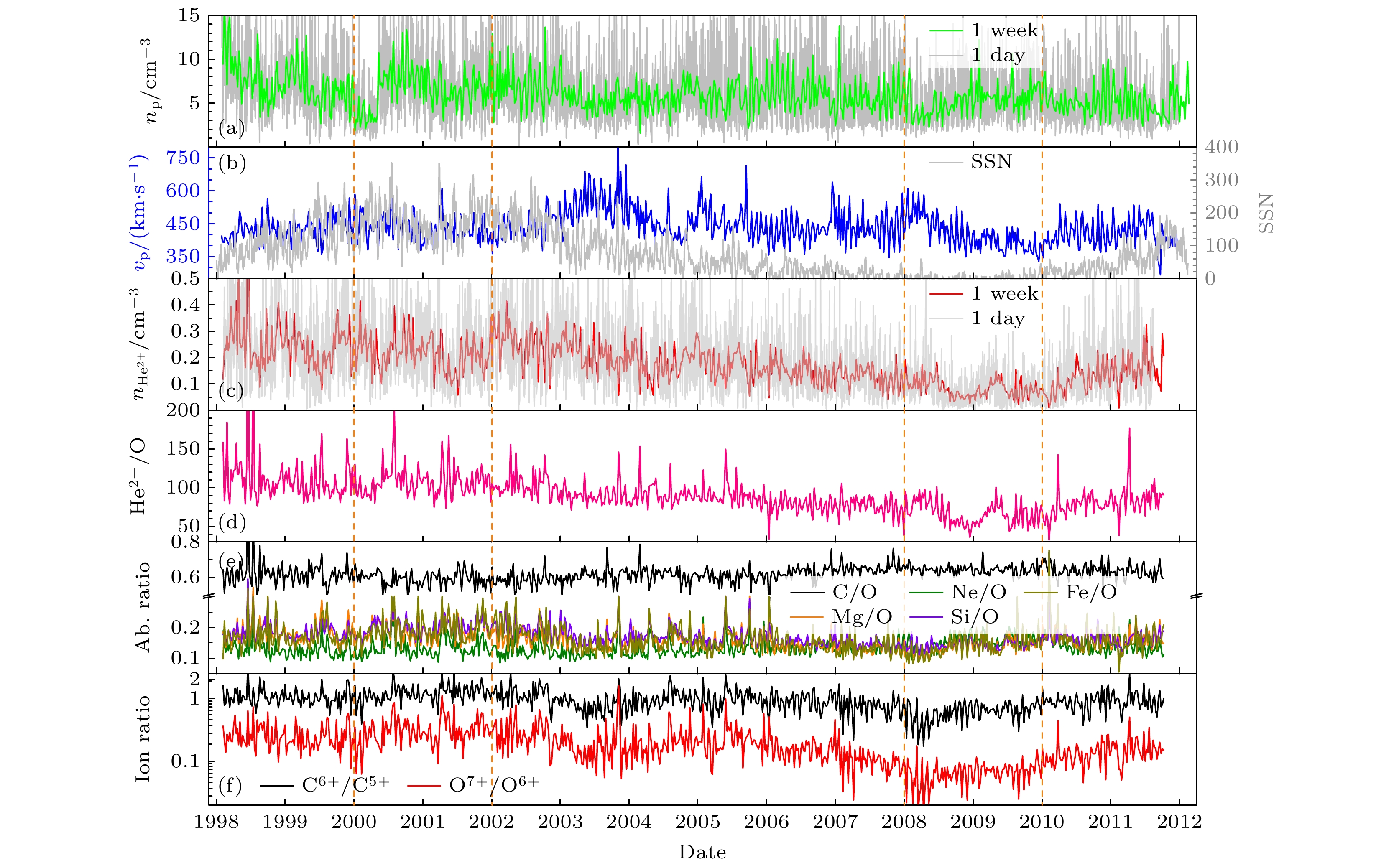
4 , 之后的数据由于探测器故障使得数据不全面而没有被采用. 对于重粒子数据采用2 h平均数据, 而质子数据采用可获得的12 min平均数据, 并依据时间标识匹配重组成2 h平均数据. 表征太阳风状态的ACE数据主要有质子数密度、速度、He2+数密度、不同元素与氧元素丰度比、离子丰度比值(C6+/C5+, O7+/O6+)等, 如图1所示. 为了揭示太阳活动性情况在图中也显示了太阳黑子数(SSN), 该数据来源于比利时太阳黑子指数和长期太阳观测中心5 . 从图1各参数的时间序列数据可以看出, 没有规律可循, 只有太阳黑子指数表现了明显的长时标(约11年)的周期性, 说明太阳风的高度变化复杂性. 除此之外, He2+离子数密度在长时标上与太阳黑子数密度展现了一定的相关性, 即太阳活动强的年份(2000— 2002年) He2+离子数密度整体偏大, 而太阳活动弱的年份(2008—2010年) He2+离子数密度整体偏小. 同样O7+/O6+离子丰度比也表现了与太阳黑子数密度相关的特征.为了探讨这些看似没有规律的时间序列数据, 我们利用2 h平均数据统计研究了不同物理参数之间的关系, 如图2所示. 因为同一元素相邻电荷态丰度比与等离子体的温度紧密相关, 且由于高电荷态离子在离开太阳表面(0.05—0.5)
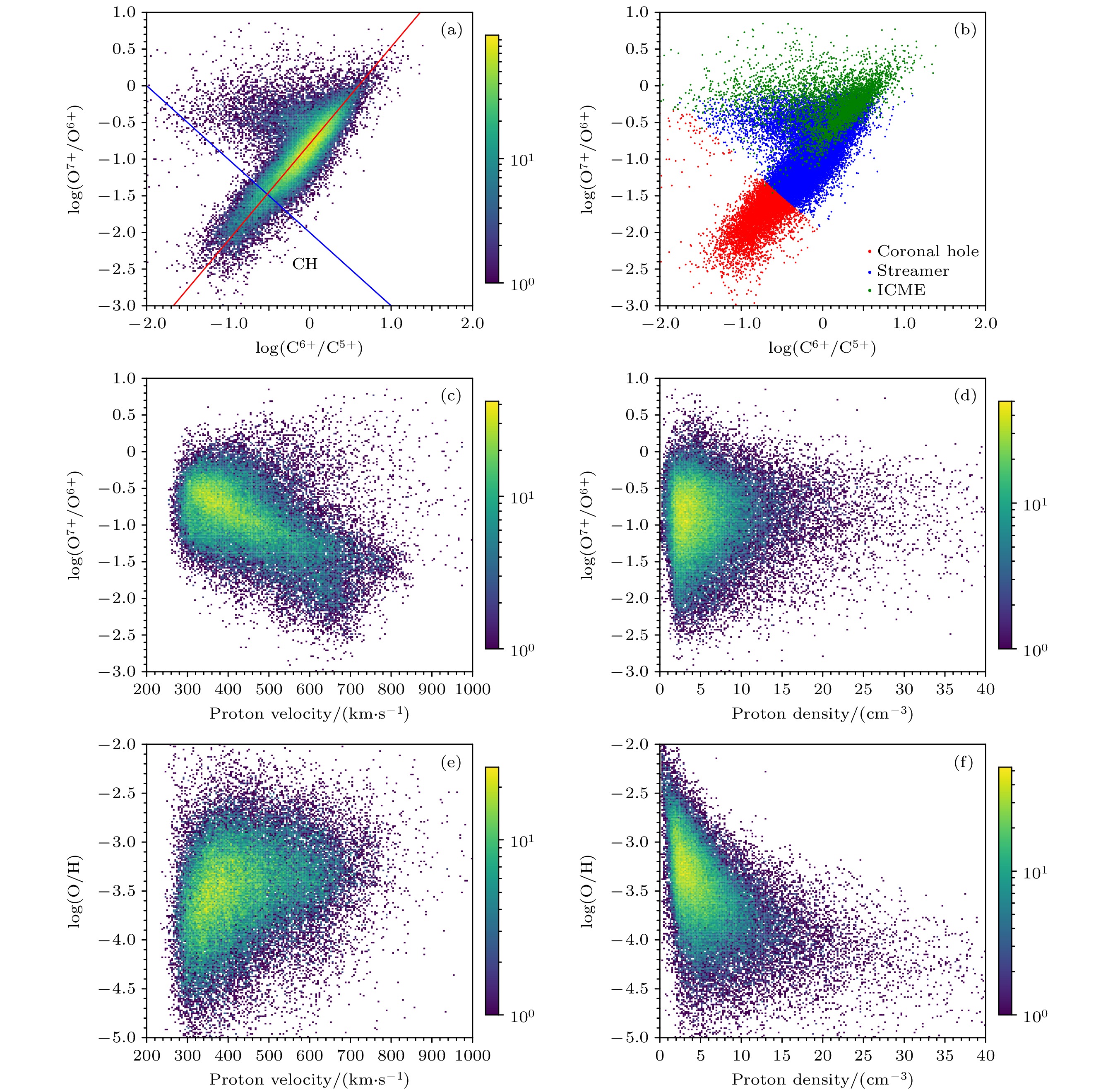
$ R_{\odot} $ 处就 处于‘冻结’状态[33], 因此Zhao等[34]以离子丰度比值O7+/O6+和太阳风速度建立了一个标准来分辨太阳风在太阳表面的起源, 即冕洞(coronal hole, CH)、冕流(Streamer)、行星际冕物质抛射(ICME). 2024年, Koutroumpa[23]提出以C和O离子丰度乘积$ {\rm \left({O^{7+}}/{O^{6+}}\right)}\times{\rm \left({C^{6+}}/{C^{5+}}\right)} \leqslant 0.01 $ 作为区分冕洞和冕流起源的判据, 本文采用这一方法重新分类了源于冕流和冕洞的数据点, 而ICMEs的数据点直接采用ACE数据中心提供的分类标签. 所以图2(a)以二维直方图显示了所有ACE 2 h平均数据的这两个离子丰度比在$ 200\times200 $ 网格坐标空间数据点的统计分布关系, 其颜色表示每个小方隔空间所包含的数据点数目. 利用Koutroumpa[23]和Zhao等[34]的分类方法(详情见该文表2), 图2(b)以不同颜色给出这3种太阳风粒子起源的所有数据点(共56641条)的分布, 其中冕流的统计记录最多. 除少数数据点外, 绝大多数数据点都位于一条丰度比对数值的线性区域, 其斜率约1.32, 见图2(a)中红色斜线. 针对这些偏离的数据点(Outliers)的起源, Zhao等[35]的详尽分析揭示其可能是来源于太阳冕区的磁重联事件导致太阳风电离度降低.太阳风的质子数密度和速度是太阳风的两个非常重要的特征能数, 图2(c)和图2(d)给出了
$ {\rm {O^{7+}}/{O^{6+}}} $ 值与质子数密度和速度关系的统计分 布.$ {\rm {O^{7+}}/{O^{6+}}} $ 值与速度存在强关联, 即高电荷态 O7+越少(即温度越低)其速度越大, 而与质子数密度没有显示任何相关性. (2)式中决定辐射因子大小的另一个重要参数是元素丰度, 其中O元素是太阳风中丰度最高的重元素, 因此, 我们也研究了O丰度(指相对H丰度)随太阳风质子速度和密度的关系, 如图2(e)和图2(f), 整体上质子速度越大, 记录的数据不仅快速减少, 且整体O丰度偏高些. 而O丰度与质子数密度的关系却是整体快速减小. -
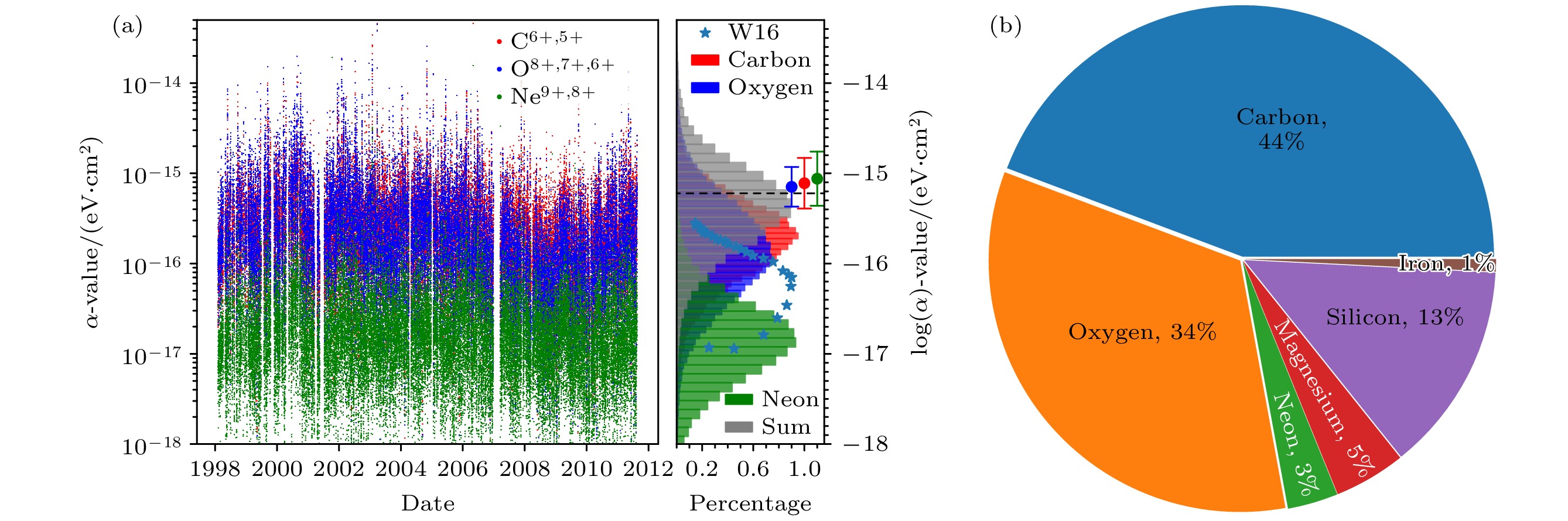
基于第2节、第3节, 获得了辐射光子能段0.1—2.0 keV的辐射因子, 如图3所示, 这也是SMILE 卫星(0.2—5.0 keV)[11]、中国空间站DIXE载荷(0.1—10.0 keV)[14]和EP卫星(0.5—4.0 keV)[36]覆盖的重要观测能段. 图3(a)给出了2 h平均1998—2011年所有高质量有效数据ACE记录的C(红色)、O(蓝色)和Ne(深绿色)元素的α值, 图3(a)右侧给出了这些α对数值的统计分布. 我们1998—2011年时间段的平均结果(
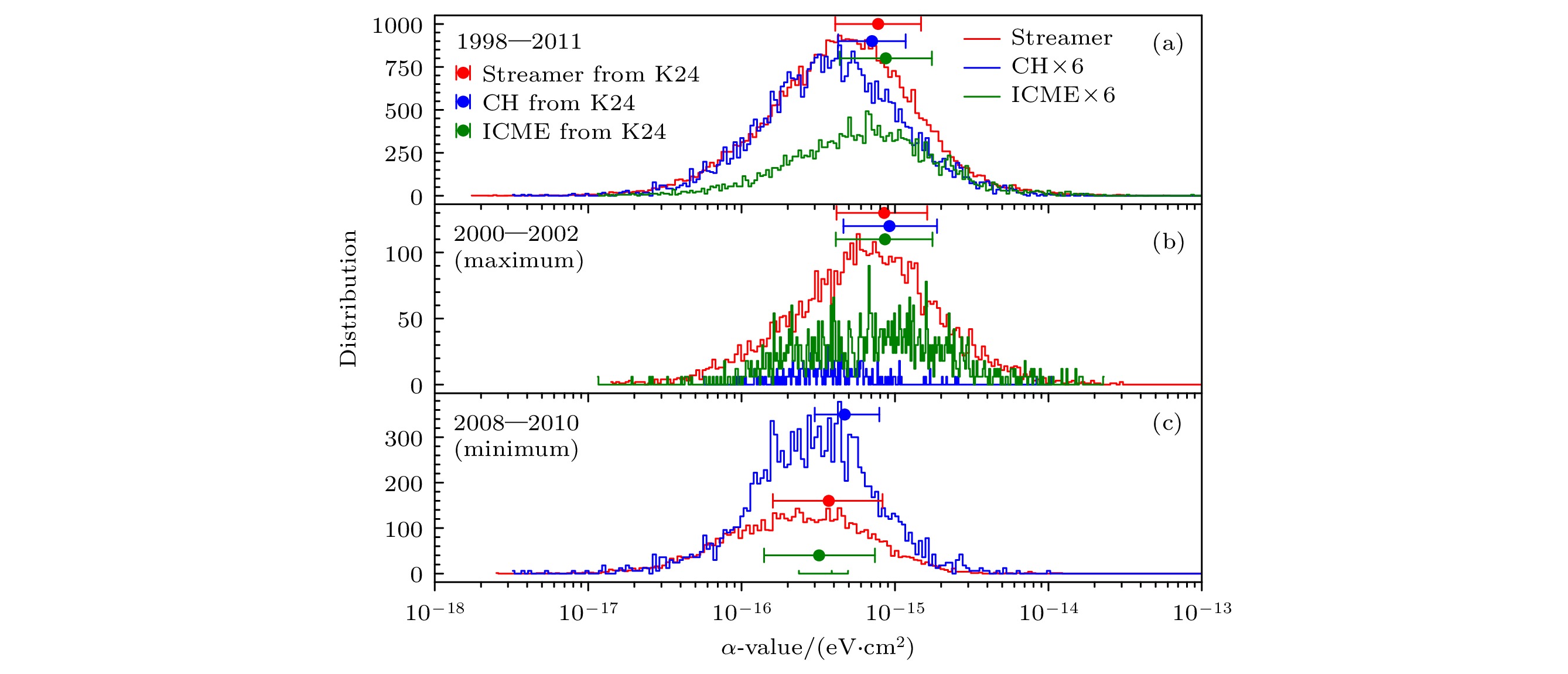
$ 4.6_{-3.1}^{+9.9}\times 10^{-16} $ eV·cm2)小于Koutroumpa[23]的结果($ 7.1_{-2.9}^{+4.7} \times10^{-16} $ (冕洞)、$ 7.8_{-3.7}^{+7.0}\times10^{-16} $ (冕流)以及$ 8.8_{-4.4}^{+8.8}\times 10^{-16} $ eV·cm2(冕物质抛射)), 但在误差范围内. 这个值也与空 间物理学家采用的经典值($ 6.0\times10^{-16} $ eV·cm2)相一致, 即图中的黑色水平虚线. 但这些基于ACE 实测数据结果远远大于Whittaker和Sembay[22]的统计分布结果, 如图中$\star $ 形点分布. 百分比分布图(图3(b))清晰地说明C和O是该波段辐射辐射因子α值的主要贡献来源, 分别是44%和34%.进一步研究了不同时间段和不同太阳风起源的辐射因子α值, 如图4所示. 在全观测周期中(1998—2011年), 源于冕物质抛射的辐射因子α值均值(6.3×10–16 eV·cm2)大于冕流(4.6×10–16 eV·cm2)和冕洞(3.9×10–16 eV·cm2), 这与Koutroumpa[23]的结论相一致, 主要是由于冕物质抛射中高电荷态离子相对多些, 即冕物质抛射中
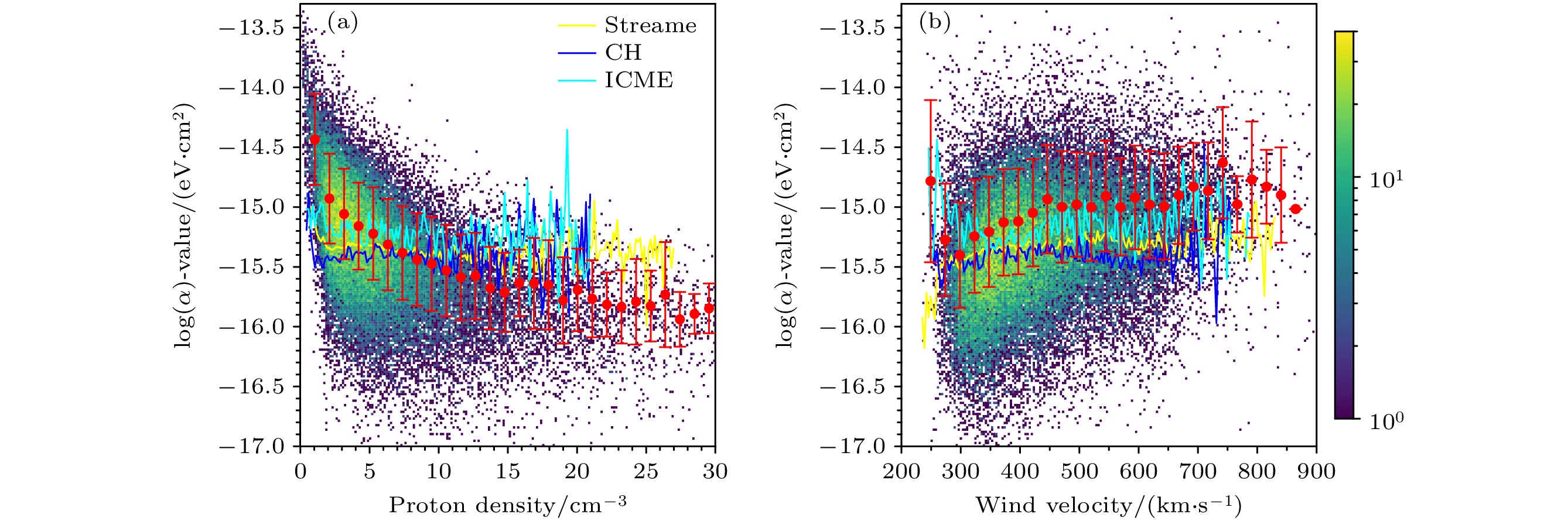
${{\rm O}^{7+}}/{{\rm O}^{6+}} $ 平均值比冕流和冕洞中的大, 如图2(b)所示, 辐射光子的能量偏大导致的, 也与太阳风起源分辨标准(文献[34]中表2)一致. 但该均值比Koutroumpa[23]的结果小30%—45%. 在太阳活动强周期(2000—2002年), 本文的辐射因子均值分别是7.2×10–16 eV·cm2 (星际冕物质抛射)、6.5×10–16 eV·cm2(冕流)和3.9×10–16 eV·cm2(冕洞), 比Koutroumpa[23]的结果分别小16%, 24%和58%, 即源于冕洞太阳风粒子的数据差异最大. 在太阳活动弱周期(2008—2010年), 冕物质抛射、冕流和冕洞的辐射因子平均值分别是3.6×10–16, 2.4×10–16和3.0×10–16 eV·cm2, 与Koutroumpa[23]的结果相比, 冕物质抛射的α值一致, 而冕流和冕洞的α值小约35%. 太阳活动强周期的辐射因子是弱周期的α均值的2.0、2.7和1.3倍, 这主要是由于太阳活动强周期离子丰度整体较高所致[23]. 在上述辐射因子均值中, 太阳活动强周期源于冕流的辐射因子大于冕洞的值, 而在太阳活动弱周期冕洞的辐射因子略高于冕流, 这与Koutroumpa[23]的结果不同, 即在强和弱周期都是冕洞的辐射因子均值大. 弱周期源于冕洞的辐射因子略偏大主要是由于太阳风中C6+离子相对增丰所致, 这与图2(a)$ {\rm O^{7+}}/{\rm O^{6+}} $ 与$ {\rm C^{6+}}/{\rm C^{5+}} $ 关系拟合直线的斜率(1.32)大于1相一致. 整体上来说, 全观测周期和太阳活动强周期的星际冕物质抛射的辐射因子差异小些、其次是冕流, 差异较大的是冕洞. 不同结果的差异, 可能是由于采用的原子结构和碰撞参数不同所致, 总碰撞截面向量子态分辨分配截面处理方法不同也是一个重要原因, 如Liang等[21]揭示300 eV以下的辐射线强度对量子态的选择效应存在近2倍的差异. 但可获得的精确量子态nl分辨的碰撞截面数据仍然很少, 天文应用分析仍然需要借助于一些近似处理方法[17,18]. 由于宽能段辐射因子计算中涉及到了19个离子的数据, 很难推断是由于哪个离子的数据差异所引起, 这需要逐个离子逐个原子参数的精细比较才能辨明, 这也是国际上不同辐射模型(包括热辐射)未来需要解决的前沿问题, 这不是本文的主要研究内容. 此外, 不同太阳风起源的辐射因子统计均值差异的大小不一样, 说明ACE数据处理方法的不同也是一种原因, 比如, 本文处理ACE数据时没有进一步区分上层弱风(upper depleted wind, UDW)和磁重联慢太阳风(Outliers)[35].我们进一步分析了总辐射因子α值随太阳风特征参数(质子速度与数密度)的统计分布, 如图5所示. α值的平均值随质子数密度的增大快速变小, 在
$ n_{\mathrm{p}}>13 $ cm–3以上达到相对稳定的值(log(α) ≈–15.7 eV·cm2). 随质子速度的增大, α值的平均值也存在增大的趋势(低速度且统计数据少的两个点除外), 但相对缓慢, 并在$ v_{{\mathrm{sw}}}>430\; $ km/s以上时趋于恒定. 在较高统计的质子数密度和速度区域, 源于冕物质抛射的辐射因子平均值大于冕流和冕洞的值. 这种关系与图2中O元素丰度的表现很相似, 这主要是由于0.1—2.0 keV能段的总辐射因子主要是由太阳风中高电荷态O (34%)和C (44%)离子的贡献所主导所致. -
本文通过分析美国先进成分空间探测器数据13年(1998—2011)的实测数据, 研究了这些ACE数据中电离态和元素丰度与太阳风特征参数的统计分布, 发现电离度整体上与太阳风速度存在强相关性, 即速度越大电离度越低, 即温度越小. 冕流的高统计值说明太阳风更多起源于电离度高(温度高)的冕流. 而O元素丰度却与质子数密度存在强相关性, 即质子密度越大, O丰度越小. 基于ACE实测太阳风参数计算的电荷交换辐射因子与Koutroumpa最新的计算结果[23]相比整体偏低些(30%—48%). 不同太阳风起源α值统计平均的分析揭示冕物质抛射的α值比冕流和冕洞的大, 太阳活动强周期的辐射因子是弱周期的1.3—2.7倍. 此外, 统计分析发现α值与太阳风质子速度和密度的关系与O丰度的表现相一致, 即随质子数密度的增大快速变小, 随质子速度的增大缓慢变大, 并分别在
$ n_{\mathrm{p}}>13 $ cm–3和$ v_{{\mathrm{sw}}}>430 $ km/s时趋于恒定, 这种一致性是由于宽能带的总辐射因子α值, 主要是由高电荷态O和C离子所主导. 这些基于可获得的精确碰撞截面所计算的α值, 将对中欧联合科学卫星SMILE、中国空间站银河系热重子探寻计划DIXE, 以及爱因斯坦探针EP观测数据的分析起到重要支撑作用.
基于ACE观测数据的太阳风电荷交换X射线辐射因子
Solar wind charge-exchange X-ray emission factor based on ACE observation data
-
摘要: 太阳风电荷交换是太阳风粒子与行星大气中性粒子碰撞过程中的一种非弹性碰撞过程, 碰撞相伴产生软X射线辐射, 对行星大气的演化起着重要的影响. 中欧联合卫星——太阳风与地球磁层相互作用全景成像(SMILE)正是利用这种X射线辐射研究太阳风与地球大气相互作用的全局性结构. 但这种辐射对天体弥散X射线源研究是一种重要的干扰, 直接影响对目标源的观测分析. 电荷交换辐射因子是分析空间X射线探测器观测数据(包括中国空间站建议载荷—银河系热重子探寻计划(DIXE)和爱因斯坦探针(EP))的关键物理量. 本文采用美国先进成分空间探测器(ACE) 13年(1998—2011年)的探测数据, 结合前期发展的辐射分析模型, 研究了不同时间段和不同太阳风起源的电荷交换辐射因子, 并与前人结果进行比较, 统计分析揭示了其随太阳风参数的变化规律, 即平均辐射因子随太阳风质子数密度增大快速变小并达到稳定值, 而随太阳风速度增大而缓慢变大并在vsw > 430 km/s趋于恒定. 冕物质抛射的辐射因子比冕流和冕洞的大, 太阳活动强周期的辐射因子比弱周期的大.Abstract:
This study aims to quantify the solar wind charge-exchange (SWCX) X-ray emission factor (denoted as α-value) and its dependence on solar wind parameters, solar activity cycle, and solar wind origin. By analyzing 13-year (1998–2011) in-situ measurements from the advanced composition explorer (ACE) spacecraft, we investigate the statistical correlations between solar wind ionization states, elemental abundances (particularly oxygen), and bulk plasma parameters (proton speed, density). The derived α-values are critical for explaining the data from solar wind and magnetosphere interaction linker explorer (SMILE), and disentangling SWCX foreground emissions from diffuse astrophysical X-ray sources observed by Einstein Probe (EP) and proposed diffuse X-ray explorer (DIXE) payload on Chinese space station. In this work, high-resolution solar wind ion composition data and plasma parameters from ACE are investigated. Events are categorized by solar wind origin (coronal holes, streamers, interplanetary coronal mass ejections (ICMEs)) and solar cycle phase (minimum vs. maximum). The α-value, defined as the total soft X-ray photon emission cross section per solar wind proton, is computed using an updated charge-exchange model that combines the state-resolved cross-section for highly charged ions. The model takes into consideration the velocity-dependent cross-section of solar wind-neutral interaction. Statistical method and bin-averaging techniques are adopted to extract the relations between α, solar wind speed (vsw), proton density (np), and oxygen abundance. The main results are as follows. 1) Ionization state dynamics: A strong anti-correlation exists between solar wind ionization degree and bulk speed: high-speed winds (> 500 km/s) exhibit lower ionization states than slow-speed winds (< 400 km/s). 2) Elemental abundance trends: Oxygen abundance ([O/H]) is inversely correlated with np: the [O/H] of denser solar wind plasmas (np > 13 cm–3) decreases by 30%–50%, indicating the presence of fractionation during plasma acceleration. No significant speed dependence of [O/H] is observed, compared with earlier research results. 3) Emission factor (α-value) behavior: α-value decreases rapidly with the increase of np and stabilizes for np > 13 cm−3. Conversely, α-value increases gradually with vsw up to 430 km/s, beyond which it plateaus. The ICME-associated α exceeds streamer and coronal hole values by 35%–60%, which is attributed to higher averaged ionic state in transient ejecta. Solar maximum α (2000–2002) is 1.3–2.7 times higher than solar minimum (2008–2010), reflecting cycle-dependent ion composition changes. By bridging in-situ solar wind measurements and X-ray emission physics, this work enhances the ability to diagnose solar wind-magnetosphere coupling and diffuse X-ray background. The validated α-value will be of benefit to the data analysis for Chinese aerospace projects in the 2020s, such as SMILE, DIXE, and EP. -
Key words:
- solar wind /
- charge-exchange /
- X-ray emission factor .
-

-
图 1 美国先进成分空间探测器1998—2011年监测的太阳风粒子状态数据, 除时序间隔外, 该图与Koutroumpa[23]文中图2基本一致 (a) 质子数密度 (cm–3), 灰线是1天平均, 绿线是1周平均; (b) 质子速度(km/s, 蓝线)和太阳表黑子计数(右纵轴, 灰线, 1天平均数据), 其来源于比利时太阳黑子指数和长期太阳观测中心[32]; (c) He2+ 离子数密度(cm–3), 灰线是1天平均, 红线是1周平均; (d), (e) 不同元素(He, C, Ne, Mg和Si)与O元素丰度比; (f) 高电荷态的C6+/C5+和O7+/O6+离子比; 竖直点划线分隔的2个区域(2000—2002年和2008—2010年)分别是太阳活动最大和最小时间段
Figure 1. Status of solar wind particles from ACE during 1998 and 2012. This figure is basically similar with Fig. 2 of Koutroumpa[23] with exception of time step: (a) Proton density (cm–3), gray line is 1-day averaged, while green line is 1-week averaged; (b) proton bulk velocity (km/s, blue line) and sun splot number (SSN, righ-axis) with 1-day averaged from the World Data Center SILSO[32]; (c) He2+ density (in cm–3), gray and red lines refer to 1-day and 1-week averaged; (d), (e) element (He, C, Ne, Mg and Si) abundance ratios relative to oxygen; (f) ion fraction ratio of C6+/C5+ and O7+/O6+. Vertical dashed-dot lines separate two regions (i.e. 2000–2002 year and 2008–2010 year) for solar maximum and minimum, respectively.
图 2 ACE卫星13年的太阳风粒子监测数据二维直方图或点分布图, 数据采用ACE网站的2小时平均数据, 其中太阳风质子速度和密度采用12 min平均数据重新分组获得. (a), (b) 分别为log(O7+/O6+)与log(C6+/C5+)关系的柱状分布和点分布, 图(a)中蓝色斜线是源于冕洞数据的分隔线, 即
$({{\rm O}^{7+}}/{{\rm O}^{6+}})\times ({{\rm C}^{6+}}/{{\rm C}^{5+}})\leqslant 0.01 $ , 红色斜线是斜率为1.32的线性拟合线; 图(b)中按Koutroumpa[23]和Zhao等[34]的方法对来源于冕洞(红)、冕流(蓝)和星际冕物质抛射物(深绿)的不同数据进行了分类. (c), (d) 分别为log(O7+/O6+)与太阳风速度和密度关系的二维直方图. (e), (f) 分别为O元丰度与太阳风速度和密度关系的二维柱状分布Figure 2. 2D histograms and scatter distribution plots of ACE mission data from Feb. 1998 to Aug. 2011. Element and ion fraction data are from the ACE science center with 2-hour averaged, while proton bulk velocity and density are obtained by rebinning the 12-minute data available from the website. (a), (b) The log(O7+/O6+) vs. log(C6+/C5+) in 2D histogram and scatter, respectively. The oblique blue line in panel (a) refers to the criterion value of
$({{\rm O}^{7+}}/{{\rm O}^{6+}})\times ({{\rm C}^{6+}}/{{\rm C}^{5+}})\leqslant 0.01 $ for coronal hole (CH) and streamer sources, amd the red line is a linear fit line with a slope of 1.32. Panel (b) shows the ACE data points of solar wind from different source in Sun by using the distinguise methods of Koutroumpa[23] and Zhao et al.[34], e.g. coronal holes (red), streamters (blue) and interplanetary coronal mass ejections (dark green). (c), (d) The log(O7+/O6+) vs. proton velocity and density in 2D histogram, respectively. (e), (f) The O abundance (in log) vs. Proton velocity and density in 2D histogram, respectively.图 3 (a) 1998年至2011年ACE监测到的不同太阳风离子(C6+, 5+, O8+, 7+, 6+和Ne9+, 8+)电荷交换X射线辐射在0.1—2.0 keV能带的辐射因子α值的点分布图(左)和统计百分比分布(右).
$ \star $ 形点来源于Whittaker和Sembay的结果[22], 标记为W16; 水平虚线是经典结果($ 6\times10^{-16} $ eV·cm2); 带误差棒的实心圆点是来源于Koutroumpa的不同太阳风起源的结果[23], 即冕流(红色)、冕洞(蓝色)和星际冕物质抛射(绿色), 其能带宽是0.1—2.0 keV. (b) 所有记录点统计的平均辐射因子中各元素贡献百分比Figure 3. (a) Scatter plot and statical distribution of the charge-exchange emission factor α-value of the ACE solar wind particles (C6+, 5+, O8+, 7+, 6+ and Ne9+, 8+) in the energy ranges of 0.1–2.0 keV.
$ \star $ symbol points are from the results of Whittaker & Sembay[22], marked as W16. Horizontal dashed line is the empirical value of$ 6\times10^{-16} $ eV·cm2. Filled circles with errorbar refers to the calculation by Koutroumpa[23] for different solar wind (e.g. streamers (red), CH (blue), and ICMEs (green)). (b) Percentage contribution from the different elements to the mean emission factor α-value of all recored data.图 4 不同观测时间段和不同太阳风起源的电荷交换辐射因子α值的统计分布, 及其与Koutroumpa[23]结果(K24)的比较. 冕流: 红色阶梯线和带误差棒的实心圆点; 冕洞: 蓝色; 星际冕物质抛射: 绿色. 由于冕洞和星际冕物质抛射的统计数值小, 为便于比较, 均乘了6倍的任意数值. (a) 1998—2011年全时间段; (b)太阳活动强周期2000—2002年; (c)太阳活动弱周期2008—2010年
Figure 4. Statistical distribution of solar wind charge-exchange emission factor α-value during different observational period and for different solar wind sources, as well as its comparison with the results of Koutroumpa[23] (K24). Streamer: red step lines and filled circles with errorbars, CH: blue lines and symbols, ICMEs: green lines and symbols. For comparison, the statistical distribution of CH and ICMEs are multiplied by an arbitrary value of six. (a) Full period of 1998—2011; (b) 2000—2002 of solar maximum; (c) 2008—2010 of solar minimum.
图 5 1998—2011年2小时平均的不同太阳风离子电荷交换X射线总辐射因子α值与质子数密度(a)和速度(b)的二维直方图. 带误差棒实心圆点表示质子数密度和速度相应网格辐射因子的平均值和其方差, 折线分别表示冕物质抛射(青色)、冕流(黄色)和冕洞(蓝色)的辐射因子平均值
Figure 5. 2D histograms of the charge-exchange emission factor α-value of all particles in solar wind versus proton density (a) and velocity (b) for 2-hour averaged data in 1998–2011. Filled symbols with errorbars refer to mean and standard variance of the α distribution at the grids of the proton density and velocity. Broken curves denotes mean α-value for ICMEs (cyan), Streamer (yellow) and CH (blue).
表 1 不同太阳风离子与中性氢原子碰撞电荷交换截面数据来源
Table 1. Charge exchange cross-setion sources of different solar wind ions with neutral hydrogen.
-
[1] Snowden S L, Freyberg M J, Plucinsky P P, Schmitt J H M M, Trümper J, Voges W, Edgar R J, McCammon D, Sanders W T 1995 Astrophys. J. 454 643 doi: 10.1086/176517 [2] Snowden S L, Egger R, Freyberg M J, McCammon D, Plucinsky P P, Sanders W T, Schmitt J H M M, Trümper J, Voges W 1997 Astrophys. J. 485 125 doi: 10.1086/304399 [3] Breitschwerdt D, Freyberg M J, Trümper J 1998 The Local Bubble and Beyond (Berlin: Springer [4] Lisse C M, Dennerl K, Englhauser J, Harden M, Marshall F E, Mumma M J, Petre R, Pye J P, Ricketts M J, Schmitt J, Trümper J, West R G 1996 Science 274 205 doi: 10.1126/science.274.5285.205 [5] Cravens T E 1997 Gelphys. Res. Lett. 24 105 doi: 10.1029/96GL03780 [6] Breitschwerdt D, Freyberg M J, Trümper J 1998 The local bubble and beyond: proceedings of the IAU Colloquim no. 166 Garching, Germany, April 21–25 1997 p121 Breitschwerdt D, Freyberg M J, Trümper J 1998 The local bubble and beyond: proceedings of the IAU Colloquim no. 166 Garching, Germany, April 21–25 1997 p121 [7] Cravens T E 2000 Astrophys. J. 532 L153 doi: 10.1086/312574 [8] Wargelin B J, Markevitch M, Juda M, Kharchenko V, Edgar R & Dalgarno A 2004 Astrophys. J. 607 596 doi: 10.1086/383410 [9] Bhardwaj A, Gladstone G R, Elsner R F, et al. 2002 Proc. ESLAB 36 Symposium: Earth-Like Planets and Moons Noordwijk, Netherlands, June 3–8, 2002 pp215–226 [10] Robertson I P, Cravens T E 2003 Gelphys. Res. Lett. 30 1439 doi: 10.1029/2002GL016740 [11] Sembay S, Alme A L, Agnolon D, et al. 2024 Earth Planet. Phys. 8 5 doi: 10.26464/epp2023067 [12] Beiersdorfer P, Boyce K R, Brown G V, Chen H, Kahn S M, Kelley R L, May M, Olson R E, Porter F S, Stahle C K, Tillotson W A 2003 Science 300 1558 doi: 10.1126/science.1084373 [13] Zhang R T, Liao T, Zhang C J, Zhou L P, Guo D L, Gao Y, Gu L Y, Zhu X L, Zhang S F, Ma X 2023 Mon. Not. R. Astron. Soc. 520 1417 doi: 10.1093/mnras/stad040 [14] Jin H, Mao J J, Chen L B, Chen N H, Cui W, Gao B, Li J J, Li X F, Liu J J, Quan J, Jiang C Y, Wang G L, Wang L, Wang Q, Wang S F, Xiao A M, Zhang S 2024 J. Low Temperature Phys. 215 256 doi: 10.1007/s10909-024-03095-0 [15] Sun T R, Connor H, Samsonov A 2024 Earth Planet. Phys. 8 1 doi: 10.26464/epp2023089 [16] Schwadron N A, Cravens T E 2000 Astrophys. J. 544 558 doi: 10.1086/317176 [17] Smith R K, Foster A R, Brickhouse N S 2012 Astron. Nachr 333 301 doi: 10.1002/asna.201211673 [18] Gu L Y, Kaastra J, Raassen A J J 2016 Astron. Astrophys. 588 A52 doi: 10.1051/0004-6361/201527615 [19] Cumbee R, Stancil P, Mcilvane S 2021 American Astronomical Society Meeting 238 12601 [20] Liang G Y, Li F, Wang F L, Wu Y, Zhong J Y, Zhao G 2014 Astrophys. J. 783 124 doi: 10.1088/0004-637X/783/2/124 [21] Liang G Y, Zhu X L, Wei H G, Yuan D W, Zhong J Y, Wu Y, Hutton R, Cui W, Ma X W, Zhao G 2021 Mon. Not. R. Astron. Soc. 508 2194 doi: 10.1093/mnras/stab2537 [22] Whittaker I C, Sembay S 2016 Gelphys. Res. Lett. 43 7328 doi: 10.1002/2016GL069914 [23] Koutroumpa D 2024 Earth Planet. Phys. 8 105 doi: 10.26464/epp2023056 [24] Liang G Y, Sun T R, Lu H Y, Zhu X L, Wu Y, Li S B, Wei H G, Yuan D W, Zhong J Y, Cui W, Ma X W, Zhao G 2023 Astrophys. J. 943 85 doi: 10.3847/1538-4357/acac7e [25] Midha J M, Gupta S C 1994 J. Quant. Spectrosc. Radiat. Transfer 52 897 doi: 10.1016/0022-4073(94)90054-X [26] Wargelin B J, Beiersdorfer P, Brown G V 2008 Can. J. Phys. 86 151 doi: 10.1139/p07-125 [27] Zhang R T, Seely D G, Andrianarijaona V M, Draganić I N, Havener C C 2022 Astrophys. J. 931 1 doi: 10.3847/1538-4357/ac6876 [28] Wu Y, Stancil P C, Schultz D R, Hui Y, Liebermann H P, Buenker R J 2012 J. Phs. B: At. Mol. Opt. Phys. 45 235201 doi: 10.1088/0953-4075/45/23/235201 [29] Nolte J L, Stancil P C, Liebermann H P, Buenker R J, Hui Y, Schultz D R 2012 J. Phs. B: At. Mol. Opt. Phys. 45 245202 doi: 10.1088/0953-4075/45/24/245202 [30] Liu L, Wu Y, Wang J G, Janev R K 2022 At. Data & Nuclear Data Tables 143 101464 doi: 10.1016/j.adt.2021.101464 [31] Janev R K, Winter H 1985 Phys. Rep. 117 265 doi: 10.1016/0370-1573(85)90118-8 [32] Royal Observatory of Belgium, Brussels (Sunspot Number catalogue ‘1998-2012’) http://www.sidc.be/SILSO/ [33] Landi E, Gruesbeck J R, Lepri S T, Zurbuchen T H, Fisk L A 2012 Astrophys. J. 761 48 doi: 10.1088/0004-637X/761/1/48 [34] Zhao L, Zurbuchen T H, Fisk L A 2009 Gelphys. Res. Lett. 36 L14104 doi: 10.1029/2009GL039181 [35] Zhao L, Landi E, Lepri S T, Kocher M, Zurbuchen T H, Fisk L A, Raines M J 2017 Astrophys. J. Supp. Ser. 228 4 doi: 10.3847/1538-4365/228/1/4 [36] Zhang C, Ling Z X, Sun X J, et al. 2022 Astrophys. J. Lett. 941 L2 doi: 10.3847/2041-8213/aca32f -


 首页
首页 登录
登录 注册
注册



 下载:
下载: